RBSE Class 9 Science Important Questions Chapter 8 गति

Rajasthan Board RBSE Class 9 Science Important Questions Chapter 8 गति Important Questions and Answers.

RBSE Class 9 Science Chapter 8 Important Questions गति

बहुचयनात्मक प्रश्न:

प्रश्न 1. 
वेग में परिवर्तन की दर है।
(अ) बल
(ब) संवेग
(स) त्वरण
(द) विस्थापन
उत्तर: 
विस्थापन

 

प्रश्न 2. 
समान वेग से गतिमान वस्तु का वेग एवं समय के साथ आरेख है।

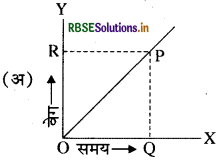
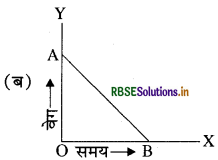
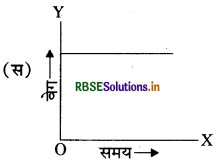
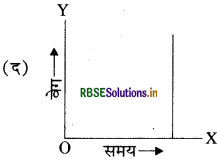
उत्तर: 

प्रश्न 3. 
एक पत्थर को किसी मीनार से गिराते हैं। मीनार से 20 मीटर गिरने पर इसका वेग कितना होगा? \(\mathrm{g}=10\) मीटर / सेकण्ड ²
(अ) -10 मीटर / सेकण्ड
(ब) 10 मीटर / सेकण्ड
(स) -20 मीटर / सेकण्ड
(द) 20 मीटर / सेकण्ड
उत्तर: 
10 मीटर / सेकण्ड

प्रश्न 4. 
जब कोई गेंद ऊर्ध्वाधर दिशा में ऊपर की ओर फेंकी जाती है तो गुरुत्वीय त्वरण
(अ) उसकी गति की दिशा के विपरीत दिशा में होता है।
(ब) उसकी गति की ही दिशा में होता है।
(स) गेंद के नीचे आते समय बढ़ता जाता है।
(द) गेंद की उच्चतम स्थिति पर शून्य हो जाता है।
उत्तर: 
गेंद के नीचे आते समय बढ़ता जाता है।

प्रश्न 5. 
दूरी - समय आलेख से प्राप्त क्षैतिज सीधी रेखा किस गति से सम्बन्धित है?
(अ) शून्य वेग
(ब) नियत वेग
(स) बढ़ता हुआ वेग
(द) घटता हुआ वेग।
उत्तर:
बढ़ता हुआ वेग 

प्रश्न 6. 
एक वस्तु 5 मी./से. के वेग से चलना प्रारम्भ करती है। यदि वस्तु का त्वरण 2 मी./से.² हो तो 8 सेकण्ड बाद उसका वेग होगा
(अ) 21 मी./से.
(ब) 18 मी./से.
(स) 10.5 मी./से.
(द) 9 मी./से.
उत्तर: 
10.5 मी./से.

प्रश्न 7. 
एक रेलगाड़ी का वेग 10 सेकण्ड में 20 मी./से. से बढ़कर 60 मी./से. हो जाता है। रेलगाड़ी का त्वरण ज्ञात करो।
(अ) 4 m/sec²
(ब) 12 m/sec²
(स) 2m/sec² 
(द) 6m/sec²
उत्तर: 
12 m/sec²

प्रश्न 8. 
एक गेंद 2 मी./से.²  के त्वरण से 10 मीटर दूरी तय करती है। यदि गेंद का प्रारम्भिक वेग 3 मी./से. हो तो उसका अन्तिम वेग ज्ञात कीजिए।
(अ) 7
(ब) 6
(स) 5
(द) 4
उत्तर: 
5

प्रश्न 9. 
एक किलोग्राम का एक पत्थर तथा 2 किलोग्राम का दूसरा पत्थर दोनों साथ-साथ एक ही ऊँचाई से स्वतन्त्रतापूर्वक छोड़े जाते हैं। पृथ्वी पर गिरने में लगे पत्थरों के समय का अनुपात क्या होगा?
(अ) 1 :1
(ब) 1: \(\sqrt{2}\)
(स) 1: 2
(द) 1: 3
उत्तर: 
1: 2

प्रश्न 10. 
यदि दो राशियों का परस्पर ग्राफ सरल रेखा हो तो दोनों राशियाँ।
(अ) अचर होती हैं।
(ब) बराबर होती हैं।
(स) अनुक्रमानुपाती होती हैं।
(द) व्युत्क्रमानुपाती होती हैं।
उत्तर: 
अनुक्रमानुपाती होती हैं।

प्रश्न 11. 
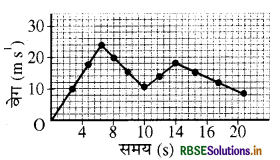
एक कण की एक विमीय गति के लिये वेग - समय ग्राफ चित्र के अनुसार है। कण का त्वरण है (मी./से.² में) 

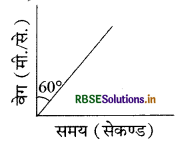
(अ) \(\sqrt{3}\)
(ब) \(\frac{1}{\sqrt{3}}\)
(स) शून्य
(द) \(\frac{\sqrt{3}}{2}\)
उत्तर: 
\(\frac{1}{\sqrt{3}}\)

प्रश्न 12. 
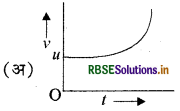
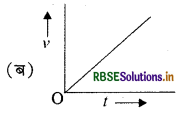
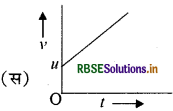
u प्रारम्भिक वेग और समान त्वरण a से गतिशील एक कण का वेग-समय ग्राफ है।




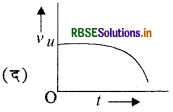
उत्तर: 

प्रश्न 13. 
किसी पिण्ड का तात्क्षणिक वेग मापा जा सकता है।
(अ) स्पीडोमीटर द्वारा
(ब) ग्राफ द्वारा
(स) वेक्टर विधि द्वारा
(द) इनमें से कोई नहीं
उत्तर: 
ग्राफ द्वारा

प्रश्न 14. 
किसी गतिमान वस्तु का त्वरण ज्ञात किया जा सकता है।
(अ) दूरी - समय ग्राफ के ढाल द्वारा
(ब) वेग - समय ग्राफ के ढाल द्वारा
(स) वेग - समय ग्राफ के क्षेत्रफल द्वारा
(द) दूरी - समय ग्राफ के क्षेत्रफल द्वारा
उत्तर: 
दूरी - समय ग्राफ के ढाल द्वारा

प्रश्न 15. 
यदि एक एथलीट r त्रिज्या वाले वृत्तीय पथ का एक चक्कर लगाने में t सेकण्ड समय लेता है, तो उसका वेग (v) क्या होगा?
(अ) \(v=2 \pi r\)
(ब) \(v=\frac{t}{2 \pi}\)
(स) \(v=\frac{2 \pi r}{t}\)
(द) \(v=\frac{2 \pi}{r}\)
उत्तर: 
\(v=\frac{t}{2 \pi}\)

रिक्त स्थान वाले प्रश्न:

निम्नलिखित प्रश्नों में रिक्त स्थानों की पूर्ति कीजिए:

प्रश्न 1. 
किसी वस्तु की स्थिति को बताने के लिए हमें एक निर्देश बिन्दु की आवश्यकता होती है, जिसे ..................... बिन्दु कहा जाता है।
उत्तर: 
मूल

प्रश्न 2. 
वस्तु की प्रारम्भिक व अन्तिम स्थिति के बीच की न्यूनतम दूरी को वस्तु का ............................. कहते हैं।
उत्तर: 
विस्थापन

प्रश्न 3. 
एक समान चाल के लिये, समय के साथ तय की गई दूरी का ग्राफ .................... है।
उत्तर: 
एक सरल रेखा

प्रश्न 4. 
वेग - समय ग्राफ का क्षेत्रफल दिये गये समयांतराल में तय की ..................... को बताता है।
उत्तर: 
दूरी 

प्रश्न 5. 
असमान त्वरित गति की स्थिति में वेग-समय ग्राफ किसी भी ..................... का होता है।
उत्तर: 
आकृति

प्रश्न 6. 
जब एक वस्तु वृत्तीय रास्ते पर एक समान चाल से चलती है, तब उसकी गति को एकमान ................... कहा जाता है।
उत्तर: 
वृत्तीय गति।

सत्य / असत्य कथन वाले प्रश्न:

निम्नलिखित कथनों में सत्य तथा असत्य कथन छाँटिए:

प्रश्न 1. 
प्रारम्भिक स्थिति और अन्तिम स्थिति आपस में मिल जाती है तब विस्थापन शून्य होता है। 
उत्तर:
सत्य

प्रश्न 2. 
स्वचलित वाहनों में एक यंत्र लगा होता है जो उनके द्वारा तय की गई दूरी को प्रदर्शित करता है। इस यंत्र को ओडोमीटर कहते हैं।
उत्तर:
सत्य

प्रश्न 3. 

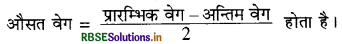
उत्तर:
असत्य

प्रश्न 4. 
त्वरण \(a=\frac{v+u}{t}\) होता है।
उत्तर:
असत्य

प्रश्न 5. 
असमान त्वरित गति की स्थिति में वेग - समय ग्राफ किसी भी आकृति का हो सकता है।
उत्तर:
सत्य

मिलान वाले प्रश्न:

निम्नलिखित प्रश्नों में भाग (अ) का मिलान भाग (ब) से करके सही कृट ( कोड ) का चयन कीजिए:

प्रश्न 1. 

भाग (अ)	भाग (ब)
(i) विस्थापन	(a) अदिश राशि होती है।
(ii) चाल	(b) सदिश राशि होती है।
(iii) औसत वेग \(\left(v_{a v}\right)\)	(c) समान होता है।
(iv) चाल और वेग का मात्रक	(d) \(\frac{u+v}{2}\)
(v) एक समान त्वरित के लिये वेग-समय ग्राफ	(e) सीधी रेखा है।

उत्तर:

भाग (अ)	भाग (ब)
(i) विस्थापन	(b) सदिश राशि होती है।
(ii) चाल	(a) अदिश राशि होती है।
(iii) औसत वेग \(\left(v_{a v}\right)\)	(d) \(\frac{u+v}{2}\)
(iv) चाल और वेग का मात्रक	(c) समान होता है।
(v) एक समान त्वरित के लिये वेग-समय ग्राफ	(e) सीधी रेखा है।

​
अतिलघूत्तरात्मक प्रश्न:

प्रश्न 1. 
गाड़ी द्वारा तय की गई दूरी किसके द्वारा मापी जाती है?
उत्तर:
ओडोमीटर से।

प्रश्न 2. 
विस्थापन - समय आरेख का ढाल किस राशि के मान को प्रकट करता है?
उत्तर:
वेग को।

प्रश्न 3. 
एक समान चाल के लिए समय के साथ तय की गई दूरी का ग्राफ कैसा होता है?
उत्तर:
एक सरल रेखा।

प्रश्न 4. 
दूरी - समय ग्राफ से क्या जाना जा सकता है?
उत्तर:
वस्तु की चाल को।

प्रश्न 5. 
एक समान त्वरित गतियों के लिए वेग-समय ग्राफ कैसा होता है?
उत्तर:
एक सीधी रेखा।

प्रश्न 6. 
मंदन किसे कहते हैं?
उत्तर:
ऋणात्मक त्वरण मंदन कहलाता है।

प्रश्न 7. 
वेग - समय ग्राफ का ढाल किसे प्रदर्शित करता है?
उत्तर:
त्वरण को।

प्रश्न 8. 
वेग से क्या अभिप्राय है?
उत्तरं:
विस्थापन के परिवर्तन की दर वेग कहलाती है।

प्रश्न 9. 
क्या किसी समय कोई पिंड स्थिर एवं गतिशील दोनों हो सकता है?
उत्तर:
हाँ, क्योंकि गति सापेक्ष होती है।

प्रश्न 10. 
क्या किसी समान त्वरित वस्तु का तात्क्षणिक वेग शून्य हो सकता है?
उत्तर:
हाँ, समान त्वरित वस्तु का तात्क्षणिक वेग शून्य हो सकता है।

प्रश्न 11. 
किसी गतिमान वस्तु के वेग - समय ग्राफ तथा समय - अक्ष के बीच स्थित क्षेत्रफल किसके बराबर होता है?
उत्तर:
वस्तु के विस्थापन के या तय की गई दूरी के।

प्रश्न 12. 
वेग - समय आरेख यदि सरल रेखा हो तो गति कैसी है तथा रेखा का ढाल क्या निरूपित करेगा?
उत्तर:
गति, समान त्वरण गति होगी एवं रेखा का ढाल त्वरण निरूपित करेगा।

प्रश्न 13. 
उस भौतिक राशि का नाम लिखो जिसका परिमाण एवं दिशा द्नों ही होते हैं।
उत्तर:
वेग द्वारा परिमाण व दिशा दोनों का ज्ञान होता है।

प्रश्न 14. 
समान गति का दूरी-समय आलेख का ढाल क्या प्रदर्शित करता है?
उत्तर:
चाल प्रदर्शित करता है।

प्रश्न 15. 
गति किसे कहते हैं?
उत्तर:
जब कोई वस्तु समय के साथ अपनी स्थिति में परिवर्तन करती है तो उसे गति कहते हैं।

प्रश्न 16. 
गति का सबसे साधारण प्रकार कौन - सा है?
उत्तर:
सरल रेखीय गति।

प्रश्न 17. 
वस्तु की दूरी को जानने के लिए किस बात की आवश्यकता नहीं होती है?
उत्तर:
गति की दिशा की आवश्यकता नहीं पड़ती है।

प्रश्न 18. 
वस्तु का विस्थापन क्या है?
उत्तर:
वस्तु का प्रारम्भिक और अन्तिम स्थिति के बीच की न्यूनतम दूरी को वस्तु का विस्थापन कहते हैं।

प्रश्न 19. 
एकसमान गति किसे कहते हैं?
उत्तर:
जब कोई वस्तु समान समयांतराल में समान दूरी तय करती है तो उसकी गति को एकसमान गति कहते हैं।

प्रश्न 20. 
असमान गति के कोई दो उदाहरण लिखिए।
उत्तर:

1. सड़क पर जा रही मोटरकार।
2. पार्क में व्यायाम कर रहा एक व्यक्ति।

प्रश्न 21. 
यदि त्वरण वेग की दिशा में हो तो उसे किस प्रकार लिया जा सकता है?
उत्तर:
धनात्मक।

प्रश्न 22. 
यदि त्वरण वेग की विपरीत दिशा में हो तो इसे किस प्रकार लिया जाता है?
उत्तर:
ऋणात्मक।

प्रश्न 23. 
ग्राफ से क्या अभिप्राय है?
उत्तर:
एक भौतिक राशि से दूसरी भौतिक राशि के सापेक्ष परिवर्तन को दो विभिन्न अक्षों पर चित्रित करना ग्राफ कहलाता है।

प्रश्न 24. 
वेग - समय ग्राफ से क्या दिखाया जाता है?
उत्तर:
एक सरल रेखा में चल रही वस्तु के वेग में समय के साथ परिवर्तन को।

प्रश्न. 25. 
कोई वस्तु सूर्य के इर्द - गिर्द अचर चाल से वृत्ताकार परिपथ में घूम रही है। इसकी गति त्वरित है या नहीं?
उत्तर:
वस्तु की गति की दिशा निरन्तर बदल रही है, अतः वेग भी निरन्तर बदल रहा है। गति त्वरित है।

प्रश्न 26. 
एक वस्तु r त्रिज्या के वृत्ताकार पथ पर गमन कर रही है। एक चक्कर पूरा करने में इसका विस्थापन क्या और दूरी क्या होगी?
उत्तर:
विस्थापन शून्य होगा, क्योंकि अन्तिम बिन्दु और प्रारम्भिक बिन्दु एक ही हैं और दूरी \(2 \pi r\) होगी।

प्रश्न 27. 
किसी एथलीट को षट्कोणीय पथ के अनुदिश दौड़ते हुए एक चक्कर पूरा करने में कितनी बार अपनी दिशा बदंलनी पड़ेगी?
उत्तर:
छः बार।

प्रश्न 28. 
एकसमान वृत्तीय गति से क्या तात्पर्य है?
उत्तर:
जब एक वस्तु वृत्तीय रास्ते पर एकसमान चाल से चलती है तब उसकी गति को एकसमान वृत्तीय गति कहते हैं।

प्रश्न 29. 
क्या विस्थापन - समय आरेख में वक्र समय अक्ष के लम्बवत् हो सकता है?
उत्तर:
नहीं। क्योंकि वक्र का ढाल अनन्त नहीं हो सकता है।

प्रश्न 30. 
किस स्थिति में वस्तु के विस्थापन का मान, वस्तु द्वारा तय की गई दूरी के बराबर होता है?
उत्तर:
एक विमीय गति में, जब वस्तु की दिशा नहीं बदले।

प्रश्न 31. 
वेग - समय वक्र का क्षेत्रफल क्या बताता है?
उत्तर:
विस्थापन का मान।

प्रश्न 32. 
वर्षा के दिनों में वर्षा की बूँदे एकसमान वेग से गिरती हैं अथवा एकसमान त्वरण से?
उत्तर:
एकसमान त्वरण से गिरती हैं।

प्रश्न 33. 
संलग्न चित्र द्वारा वस्त के वेग तथा त्वरण के बारे में क्या निष्कर्ष निकलता है?

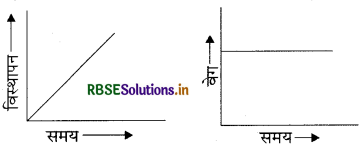
उत्तर:
दोनों में वस्तु एकसमान वेग से गतिमान है तथा त्वरण शून्य है।

प्रश्न 34. 
दो स्कूटरों का समय-वेग ग्राफ संलग्न चित्रों (अ) व (ब) में प्रदर्शित है। इनके त्वरणों में क्या सम्बन्ध है?

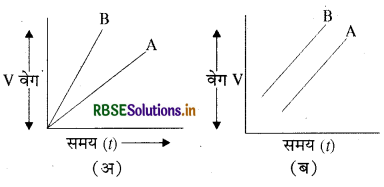
उत्तर:
चित्र (अ) में त्वरण A, त्वरण B से कम होगा तथा चित्र (ब) में दोनों का त्वरण समान होगा क्योंकि दोनों आपस में समान्तर हैं (ढाल समान है)।

प्रश्न 35. 
क्या तारक्षणिक वेग का मान सदैव तात्क्षणिक चाल के बराबर होता है? 
उत्तर:
हाँ।

प्रश्न 36. 
एक विमीय गति का कोई एक उदाहरण दीजिए, जिसमें त्वरण, वेग के विपरीत दिशा में हो। 
उत्तर:
जब हम किसी वस्तु को ऊपर की ओर फेंकते हैं, उस समय त्वरण, वेग के विपरीत दिशा में होता है। 

प्रश्न 37. 
क्या किसी समान त्वरित वस्तु का तात्क्षणिक वेग शून्य हो सकता है?
उत्तर:
हाँ।

प्रश्न 38. 
किसी बस का चाल मापक औसत चाल का मापन करता है या तात्क्षणिक चाल का?
उत्तर:
तात्क्षणिक चाल का।

लघूत्तरात्मक प्रश्न:

प्रश्न 1. 
गुरुत्वीय त्वरण क्या है?
उत्तर:
गुरुत्वीय त्वरण-पृथ्वी की तरफ गिरते समय वस्तु पर पृथ्वी के आकर्षण बल के कारण जो त्वरण उत्पन्न होता है, वह गुरुत्वीय त्वरण कहलाता है। इसका मात्रक मीटर / सेकण्ड ² होता है और इसका मान 9.8 मीटर / सेकण्ड² होता है।

प्रश्न 2. 
चाल से क्या अभिप्राय है? औसत चाल का मान किस प्रकार प्राप्त कर सकते हैं?
उत्तर:
चाल - किसी वस्तु द्वारा किसी भी दिशा में इकाई समय में तय की गई दूरी को चाल कहते हैं। इसका मात्रक मी./से. होता है। अधिकांश वस्तुओं की गति असमान होती है, इस कारण से इन वस्तुओं की गति की दर को उनकी औसत चाल कहा जाता है। वस्तु की औसत चाल को उसके द्वारा तय की गई कुल दूरी में कुल समयावधि का भाग देकर प्राप्त किया जा सकता है। 
अत: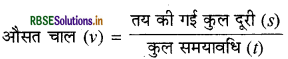 

प्रश्न 3. 
गति के समीकरण लिखिए। 
उत्तर:
गति के तीन समीकरण हैं। 
\(\begin{aligned} v &=u+a t \\ s &=u t+\frac{1}{2} a t^{2} \\ 2 a s &=v^{2}-u^{2} \end{aligned}\)

प्रश्न 4. 
गति क्या है? दैनिक जीवन में गति के उदाहरण दीजिए।
उत्तर:
गति - जब कोई वस्तु समय के साथ अपनी स्थिति में परिवर्तन करती है, तो उसे गति कहते हैं। दैनिक जीवन में गति के उदाहरण:दैनिक जीवन में गति के कई उदाहरण देखने को मिलते हैं, जैसे 

1. पंखे की घूमती पंखुड़ियाँ
2. वायु में उड़ते वायुयान
3. सड़क पर चलती मोटर - कारें

प्रश्न 5. 
(i) एक ऐसी वस्तु का उदाहरण दीजिए जो किसी व्यक्ति को गतिशील दिखे और अन्य को स्थिर।
(ii) उपर्युक्त उदाहरण से गति के बारे में हम क्या कह सकते हैं?
उत्तर:
(i) किसी गतिशील बस या रेलगाड़ी में बैठे यात्रियों को लगता है कि बाहरी भंवन, पेड़ - पौधे और मनुष्य पीछे की ओर गतिशील हैं। बाहर चलते लोगों को बस या रेलगाड़ी में बैठे यात्री उनके साथ ही आगे की दिशा में गति करते प्रतीत होते हैं। ठीक इसी समय गतिशील बस या रेलगाड़ी में बैठे सभी यात्री स्वयं को गतिहीन पाते हैं।

(ii) गति के बारे में स्पष्ट निष्कर्ष निकलता है कि वह सापेक्ष होती है।

प्रश्न 6. 
विराम और गति को उदाहरण देकर स्पष्ट कीजिए।
उत्तर:
विराम - यदि कोई वस्तु अपने परिवेश के सापेक्ष अपनी स्थिति में परिवर्तन नहीं करती, तो वह वस्तु विराम स्थिति में होती है।
उदाहरण:
मेज पर रखी हुई पुस्तक, फर्श पर रखी हुई कुर्सी या मेज। गति - यदि कोई वस्तु अपने परिवेश के सापेक्ष अपनी स्थिति में परिवर्तन करती है तो वह वस्तु गतिशील कहलाती है। उदाहरण: एक स्थान से दूसरे स्थान पर जाना, सड़क पर चलती मोटर - कारें।

प्रश्न 7. 
गतियाँ कितने प्रकार की होती हैं? उनके नाम लिखकर उन्हें परिभाषित कीजिए।
उत्तर:
सामान्यतया गतियाँ तीन प्रकार की होती हैं।

1. रेखीय या स्थानान्तरीय गति:  जब कोई वस्तु एक सीधी रेखा में गतिमान होती है, तब उसकी गति सरल रेखीय या स्थानान्तरीय गति कहलाती है। जैसे - सीधी सड़क पर गतिमान कार।
2. वृत्तीय या घूर्णात्मक गति: जब कोई वस्तु किसी वृत्ताकार पथ पर गति करती है, तो उस बस्तु की गति वृत्तीय गति कहलाती है। जैसे - गोलक के परिवृत गति।
3. वक्रीय या दोलनी गति: जब कोई वस्तु किसी वक्रीय मार्ग के साथ - साथ गतिमान हो, तो उसकी गति वक्रीय गति कहलाती है। जैसे - लोलक की गति।

प्रश्न 8. 
दूरी और विस्थापन में अन्तर स्पष्ट कीजिए।
उत्तर:
दूरी और विस्थापन में निम्न अन्तर हैं।

दूरी	विस्थापन
1. किसी वस्तु द्वारा दिशा के सापेक्ष तय की गई पथ की वास्तविक लम्बाई तय की गई दूरी कहलाती है।	1. किसी गतिमान पिण्ड की प्रारम्भिक स्थिति और अन्तिम स्थिति के मध्य सबसे कम दूरी विस्थापन कहलाती है।
2. दूरी एक अदिश राशि है।	2. विस्थापन एक सदिश राशि है।

प्रश्न 9. 
एक एथलीट r त्रिज्या वाली एक गोलाकार पट्टी का एक चक्कर 40 सेकण्ड में लगाता है। 12 मिनट 40 सेकण्ड की समाप्ति पर दूरी और विस्थापन कितने होंगे?
उत्तर:
(i)  \(\because\)40 सेकण्ड में तय की गई वास्तविक दूरी = 2\( \pi \)r
∴ 1 सेकण्ड में तय की गई वास्तविक दूरी = \(\frac{2 \pi r}{40}\)
\(\therefore\) 160 सेकण्ड में तय की गई वास्तविक दूरी = \(\frac{2 \pi r}{40} \times 160\) 
\(\because\) मिनट 4 सेकण्ड = 160 सेकण्ड = 8\( \pi\)r उत्तर

(ii) 2 मिनट 40 सेकण्ड में विस्थापन = शुन्य क्योंकि प्रारम्भिक बिन्दु और अन्तिम बिन्दु एक ही हैं।

प्रश्न 10. 
एक वस्तु r त्रिज्या के गोले में गतिमान है। आधे चक्कर में इसके विस्थापन का विस्तार और तय की गई दूरी कितनी होगी? यह भी बताइए कि क्या विस्थापन हमेशा धनात्मक होता है?
उत्तर:
पूरे चक्कर में तय की गई दूरी = 2\( \pi \)r
आधे चक्कर में तय की गई दूरी = \(\pi \)r
पूरे चक्कर में विस्थापन = शून्य
आधे चक्कर में विस्थापन = 2r
विस्थापन हमेशा धनात्मक नहीं होता है। यह धनात्मक और ऋणात्मक दोनों ही हो सकते हैं।

प्रश्न 11. 
निम्न की परिभाषा दीजिये
(i) विस्थापन 
(ii) वेग।
उत्तर:
(i) विस्थापन: वस्तु की प्रारम्भिक एवं अन्तिम स्थिति के बीच की दूरी को वस्तु का विस्थापन कहते हैं। यह सदिश राशि है।
(ii) वेग: किसी निश्चित दिशा में किसी वस्तु द्वारा एकांक समय में तय की गई दूरी को उसका वेग कहते हैं। वेग सदिश राशि है।

\(v=\frac{S}{t}\)

प्रश्न 12. 
त्वरण किसे कहते हैं?
उत्तर:
त्वरण: प्रति इकाई समय में किसी वस्तु के वेग में परिवर्तन की दर को त्वरण कहते हैं। यदि किसी वस्तु का प्रारम्भिक वेग u है तथा t समय पश्चात् वस्तु का वेग v हो जाता है तो वस्तु का त्वरण होगा

प्रश्न 13. 
वृत्तीय गति किसे कहते हैं? वस्तुओं की एक समान वृत्तीय गति के कोई तीन उदाहरण लिखिए।
उत्तर:
वृत्तीय गति: जब कोई वस्तु किसी वृत्ताकार पथ पर गति करती है, तो उसकी गति वृत्तीय गति कहलाती है।
वृत्तीय गति के उदाहरण:

1. चन्द्रमा एवं पृथ्वी की गति।
2. पृथ्वी के चारों ओर घूर्णन करता हुआ उपग्रह
3. वृत्तीय पथ पर नियत चाल से चलता हुआ साइकिल सवार।

प्रश्न 14. 
आरम्भिक बिन्दु से 100 सेमी. दूर स्थित एक वस्तु का विराम में दूरी - समय आरेख बनाइए।
उत्तर:
y अक्ष पर दूरी और x अक्ष पर समय दर्शाते हुए एक आरेख खींचते हैं। चूँकि वस्तु अपने आरम्भिक बिन्दु से 100 सेमी. दूर विराम की स्थिति में है। इसका अर्थ है कि विभिन्न कालखण्डों में वस्तु की दूरी 100 सेमी. ही रहेगी। किसी वस्तु के लिए दूरी - समय आरेख निम्न
प्रकार से होगा:

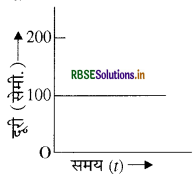
निबन्धात्मक प्रश्न:

प्रश्न 1. 
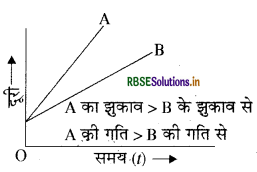
समान एवं असमान गतियों से चलती दो वस्तुओं (A और B) का दूरी - समय आरेख खींचिए।
उत्तर:
(i) जब दो वस्तुएँ A और B समान गतियों से चलती हैं, तब दोनों के लिए खींचा गया दूरी - समय आरेख एक सरल रेखा प्राप्त होता है।

(ii) जब दोनों वस्तुएँ A और B असमान गतियों से चलती हैं, तब यह दोनों वस्तुएँ समान समय अंतराल से भिन्न - भिन्न दूरियाँ तय करेंगी। अतः दोनों वस्तुओं के दूरी-समय ग्राफ में ढाल अलग - अलग प्राप्त होंगे। दोनों में से तेज चलने वाली वस्तु का ढाल अधिक प्राप्त होगा। चूंकि वस्तुएँ A और B समान गति से गतिमान हैं। इनके लिए खींचे गए दूरी-समय ग्राफ में A का ढाल B की अपेक्षा अधिक है। अतः A की गति B की तुलना में तेज है।

प्रश्न 2.
वेग - समय ग्राफ के अध्ययन से एक विमीय गति कर रहे कण के लिये क्या महत्वपूर्ण निष्कर्ष प्राप्त किये जा सकते हैं? समझाइये।
उत्तर:
यदि वेग - समय ग्राफ समय अक्ष के समानान्तर सरल रेखा है। जैसा कि चित्र (अ) में दिखाया गया है। तब यह नियत वेग से गति को दर्शाता है। जहाँ वेग - समय ग्राफ का ढाल त्वरण के बराबर होता है।

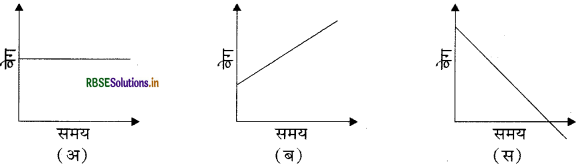
चित्र (ब) में ढाल धनात्मक है अर्थात् त्वरण की दिशा, वेग की दिशा में ही है। और वेग में समय के साथ वृद्धि हो रही है।
चित्र (स) में ढाल ऋणात्मक है। इसमें कण की गति मंदित है। इसमें त्वरण की दिशा वेग की दिशा के विपरीत है। इस स्थिति में कण का वेग घटकर शून्य हो जाता है। वेग - समय ग्राफ में वक्र और समय अक्ष के मध्य के विभिन्न भागों के क्षेत्रफलों के मानों का योग, कण द्वारा तय की गई दूरी के बराबर होता है, जबकि विभिन्न भागों के क्षेत्रफल का बीजगणितीय योग विस्थापन के बराबर होता है।

प्रश्न 3.
वेग - समय आलेख से विस्थापन कैसे ज्ञात करेंगे? समझाइये।
उत्तर:
एक समान गति में वेग और समय के मध्य खींचे गये ग्राफ (सरल रेखा) व समय अक्ष के बीच बन रहे आयत का क्षेत्रफल, पिण्ड द्वारा तय की गई दूरी (विस्थापन) के बराबर होता है। समय अन्तराल (t₂ -t₁) में पिण्ड द्वारा तय की गई दूरी ही विस्थापन होगी। चूँकि यहाँ पर एक विमीय में गति हो रही है और दिशा परिवर्तित नहीं हो रही है। अतः
दूरी = वेग x समय
S = AD X DC
S = V (t₂ - t₁)
= आयत A B C D का क्षेत्रफल

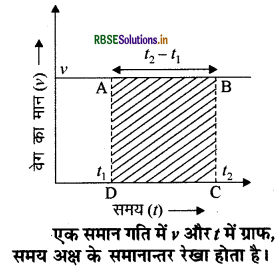
समय (t) व्यापक वेग - समय ग्राफ में भी वक्र और समय अक्ष के चित्र-एक समान गति में v और में ग्राफ, मध्य का क्षेत्रफल विस्थापन के बराबर होता है। समय अक्ष के समानान्तर रेखा होता है।

प्रश्न 4.
एक समान त्वरित एक विमीय गति के लिए गति के तीनों समीकरणों को व्युत्पन्न कीजिए।
हल - समान त्वरित गति के समीकरणों की व्युत्पत्ति: यदि u वेग से गतिशील कण का t समय में वेग । हो जाता है तो औसत त्वरण
वेग का मान (v)
\(a=\frac{v-u}{t}\)
या
v - u = at
v = u + at ...............(1)
यह गति का प्रथम समीकरण है।
पुनः कण का औसत वेग \(=\frac{u+v}{2}\)

समीकरण (1) से y का मान रखने पर
औसत वेग \(=\frac{u+u+a t}{2}\)
\(\begin{aligned} &=\frac{2 u+a t}{2} \\ &=u+\frac{1}{2} a t \end{aligned}\)
∴ दूरी
s = औसत वेग x समय
\(s=\left(u+\frac{1}{2} a t\right) \times t\)
\(s=u t+\frac{1}{2} a t^{2}\) .....................(2)
यह गति का द्वितीय समीकरण है।
गति के प्रथम समीकरण से 
v = u + at
दोनों तरफ वर्ग करने पर
\(\begin{aligned} (v)^{2} &=(u+a t)^{2} \\ &=u^{2}+2 u a t+(a t)^{2} \\ &=u^{2}+2 u a t+a^{2} t^{2} \\ v^{2} &=u^{2}+2 a\left(u t+\frac{1}{2} a t^{2}\right)=u^{2}+2 a s \end{aligned}\)
(समीकरण 2 से) यह गति का तीसरा समीकरण है।

प्रश्न 5.
समान गति व असमान गति को दूरी - समय आलेख से समझाइए।
उत्तर:
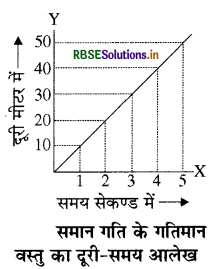
समान गति - यदि कोई गतिशील वस्तु निश्चित समयान्तरालों में समान दूरियाँ तय करती है तो वस्तु की गति को समान गति कहते हैं। उदाहरण के लिए, एक कार 10 मी./से. की समान चाल से गतिमान है। अर्थात् यह कार प्रति सेकण्ड 10 मीटर दूरी तय करती है। अतएव इस कार की गति एकसमान गति है। इस कार द्वारा तय की गई दूरी निम्नलिखित प्रकार से है

समय	दूरी
0 सेकण्ड में	0 मीटर
1 सेकण्ड में	10 मीटर
2 सेकण्ड में	20 मीटर
3 सेकण्ड में	30 मीटर
4 सेकण्ड में	40 मीटर
5 सेकण्ड में	50 मीटर

यदि कार द्वारा तय दूरी और समय में आलेख खींचें तो चित्र में दर्शाए अनुसार एक सीधी रेखा प्राप्त होती है। यह सीधी रेखा समान गति को प्रदर्शित करती है। दूरी - समय आलेख का ढाल (झुकाव) वस्तु की चाल को दर्शाता है।

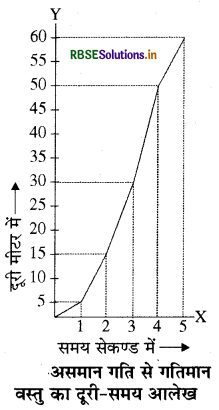
असमान गति: यदि कोई गतिशील वस्तु निश्चित समयान्तरालों में असमान दरियाँ तय करती है, तो वस्तु की गति को असमान गति कहते हैं। उदाहरण के लिए, यदि कोई कार असमान चाल से गतिमान है तो कार द्वारा प्रति सेकण्ड तय की गई दूरी भिन्न - भिन्न होगी। तब इस कार की गति असमान होगी। इस प्रकार गतिमान कार द्वारा तय की गई दूरी निम्नानुसार है

समय	दूरी
0 सेकण्ड में	0 मीटर
1 सेकण्ड में	5 मीटर
2 सेकण्ड में	15 मीटर
3 सेकण्ड में	30 मीटर
4 सेकण्ड में	50 मीटर
5 सेकण्ड में	60 मीटर

यदि कार द्वारा तय दूरी और समय में ग्राफ खींचें तो चित्र में दर्शाए अनुसार आलेख वक्र रूप में प्राप्त होता है। आलेख की वक्र आकृति वस्तु की असमान गति को प्रदर्शित करती है। वस्तुतः असमान गति को त्वरित गति कहते हैं। यदि दूरी-समय ग्राफ का ढाल समय के साथ बढ़ता है तो समय सेकण्ड मेंवस्तु की बढ़ती चाल को प्रदर्शित करता है और यदि ढाल समय के साथ चित्र-असमान गति से गतिमान घटता है तो वह वस्तु की घटती चाल को प्रदर्शित करता है।


 प्रश्न 6.
समान एवं असमान गति को समझाइये। वेग - समय ग्राफ की सहायता से गति के समीकरण ज्ञात कीजिये।
उत्तर:
समान गति-यदि कोई गतिशील वस्तु निश्चित समयान्तरालों में समान दूरियाँ तय करती है तो वस्तु की गति को समान गति कहते हैं।

असमान गति-यदि कोई गतिशील वस्तु निश्चित समयान्तराल में असमान दूरियाँ तय करती है तो वस्तु की गति को असमान गति कहते हैं।

प्रथम समीकरण की व्युत्पत्ति-एकसमान त्वरित गति में वेग में परिवर्तन की दर नियत रहती है। अर्थात्
\(\frac{d v}{d t}=a=\)नियत
इस कारण वेग और समय में ग्राफ एक सरल रेखा होती है, जिसकी ढाल त्वरण के बराबर होती है। अर्थात्
tan θ = a होती है
चित्र से
\(\frac{\mathrm{BC}}{\mathrm{CA}}\) = tan θ  = a

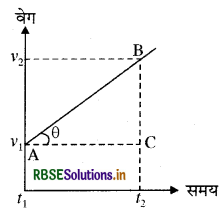
 या \(\frac{v_{2}-v_{1}}{t_{2}-t_{1}}=\mathrm{a}\)
या  \(v_{2}-v_{1}=\mathrm{a}\left(\mathrm{t}_{2}-\mathrm{t}_{1}\right)\)
या  \(v_{2}=v_{1}+\mathrm{a}\left(\mathrm{t}_{2}-\mathrm{t}_{1}\right)\)
उपर्युक्त में t₁ = 0, V₁ = u, t₂ = t
और v₂ = v
लिखने पर V = u + at .....(1)
यह गति का प्रथम समीकरण है।
द्वितीय समीकरण की व्युत्पत्ति:
एक समान त्वरण (a) से एक विमीय गतिशील कण के लिये वेग - समय ग्राफ एक सरल रेखा होती है। समय t₁ = 0 पर यदि वेग ॥ तथा समय t₂ = t पर वेग । है, तब यह सरल रेखा AB से दिखाई गई है। वेग-समय ग्राफ में, वक्र और समय अक्ष के मध्य का क्षेत्रफल कण के विस्थापन के बराबर होता है। समय अन्तराल 1 में विस्थापन s होता है तब,
s = समलम्ब चतुर्भुज ABCDEA का क्षेत्रफल
= \(\frac{1}{2}\)(समान्तर भुजाओं का योग) उनके बीच की दूरी
\(\begin{aligned} &=\frac{1}{2}(\mathrm{EA}+\mathrm{BD}) \times \mathrm{AC} \\ &=\frac{1}{2}(u+v) \times(t-0) \\ s &=\frac{1}{2}(u+v) \times t \end{aligned}\)

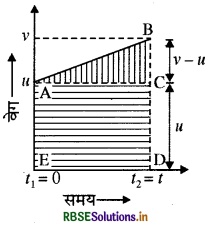
लेकिन गति के प्रथम समीकरण से v = u + at होता है।
अत: मान रखने पर
\(\begin{aligned} s &=\frac{1}{2}(u+u+a t) \times t \\ &=\frac{1}{2}(2 u+a t) \times t=\frac{2 u t}{2}+\frac{1}{2} a t^{2} \end{aligned}\)
\(s=u t+\frac{1}{2} a t^{2}\)   ...................(2)
यह गति का द्वितीय समीकरण है।
गति का तृतीय समीकरण:
\(s=u t+\frac{1}{2} \mathrm{at}^{2}\)

समीकरण (2) में समीकरण (1) से t का मान \(\left(\frac{v-u}{a}\right)\) रखने पर
\(\begin{aligned} s &=u\left(\frac{v-u}{a}\right)+\frac{1}{2} a\left(\frac{v-u}{a}\right)^{2} \\ s &=\frac{u(v-u)}{a}+\frac{1}{2} \frac{(v-u)^{2}}{a} \\ s &=\frac{2 u(v-u)+(v-u)^{2}}{2 a} \\ 2 a s &=2 u v-2 u^{2}+v^{2}-2 u v+u^{2} \end{aligned}\)

⇒ \(v^{2}=u^{2}+2 a s\)  .....................(3)
समीकरण (3) गति का तीसरा समीकरण है।

प्रश्न 7.
त्वरण किसे कहते हैं? धनात्मक एवं ऋणात्मक त्वरण से क्या आशय है? समान त्वरण व असमान त्वरण को लेखाचित्र की सहायता से समझाइए।
उत्तर:
त्वरण-किसी गतिशील वस्तु के वेग में परिवर्तन की दर को त्वरण कहते हैं। इसे हम निम्न प्रकार समझ सकते हैंमाना समय t₁ पर किसी वस्तु का वेग है एवं समय v₁ पर वस्तु का वेग t₂ है तो v₂ वेग में परिवर्तन

\(\mathrm{a}=\frac{v_{2}-v_{1}}{t_{2}-t_{1}}=\frac{v-u}{t}\)

यहाँ  वस्तु का अन्तिम वेग है और ॥ वस्तु का प्रारम्भिक वेग है तथा a वस्तु का औसत त्वरण है। यदि v को मीटर / सेकण्ड और समय (t) को सेकण्ड में व्यक्त करें तो त्वरण का मात्रक मीटर / सेकण्ड² होगा।

धनात्मक एवं ऋणात्मक त्वरण: यदि त्वरण, वेग की दिशा में है, तो इसे धनात्मक लिया जाता है अर्थात् प्रारम्भिक वेग में वृद्धि होने पर त्वरण धनात्मक होता है एवं प्रारम्भिक वेग में कमी आने पर त्वरण ऋणात्मक होता है। ऋणात्मक त्वरण को 'मंदन' भी कहते हैं।

समान त्वरण (Uniform Acceleration): यदि गतिशील वस्तु के वेग में परिवर्तन समान समयान्तराल में समान हो, तो वस्तु के त्वरण को समान त्वरण कहते हैं। ऐसी गति को समान त्वरित गति कहते हैं। समान त्वरण से गतिमान वस्तु के वेग और समय में आलेख खींचने पर चित्र (अ) में दर्शाए अनुसार एक सीधी रेखा प्राप्त होती है। इस सीधी रेखा का झुकाव या ढाल ( ढाल = \(\frac{\mathrm{PQ}}{\mathrm{OQ}}\) ) वस्तु के त्वरण को दर्शाता है। अर्थात्
त्वरण = PO

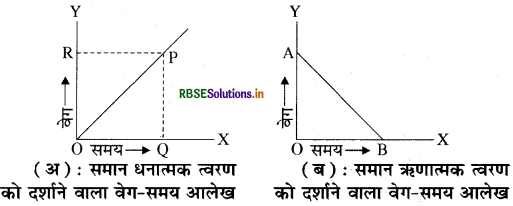
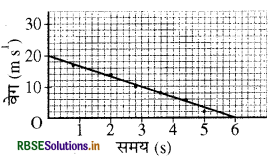
 यदि गतिशील वस्तु के वेग: समय आलेख से प्राप्त सीधी रेखा का ढाल ऊपर की ओर है तो वह वस्तु के समान त्वरण को दर्शाता है (चित्रअ)। परन्तु गतिशील वस्तु के वेग - समय आलेख से प्राप्त सीधी रेखा का ढाल नीचे की ओर है तो वह समान ऋणात्मक त्वरण (मंदन) को दर्शाता है (चित्र-ब)।

असमान त्वरण (Non-uniform Acceleration): यदि गतिशील वस्तु के वेग में परिवर्तन समान समयान्तराल में असमान हो तो वस्तु के त्वरण को असमान त्वरण कहते हैं। ऐसी गति को असमान त्वरित गति कहते हैं। असमान त्वरण से गतिशील वस्तु के वेग और समय में आलेख खींचें तो चित्र (स) में दर्शाए अनुसार वक्रीय रेखा प्राप्त होती है।

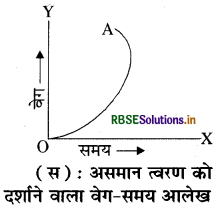
प्रश्न 8.
एक बस \(s_{1}\) दूरी \( v_{1}\) चाल से तथा \(s_{2}\) दूरी \(v_{2}\) चाल से तय करती है । बस की औसत चाल क्या है? यदि दूरियाँ आपस में बराबर हों तो सिद्ध कीजिए कि औसत चाल का मान \(\frac{2 v_{1} v_{2}}{v_{1}+v_{2}}\) होगा।
उत्तर:

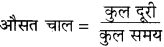
\(=\frac{s_{1}+s_{2}}{t_{1}+t_{2}}\)

जहाँ \(t_{1}\) प्रथम दूरी को पार करने का समय है और \(t_{2}\) द्वितीय दूरी को पार करने का समय है।

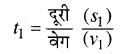
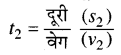
अतः औसत चाल   \(v=\frac{\left(s_{1}+s_{2}\right)}{\left(\frac{s_{1}}{v_{1}}+\frac{s_{2}}{v_{2}}\right)}\)

यदि दूरियाँ बराबर हैं। \(s_{1}=s_{2}\) अर्थात् बस अपनी यात्रा की प्रथम आधी दूरी चाल \(v_{1}\) से और द्वितीय आधी दूरी चाल \(v_{2}\) से तय करती है, तब

औसत चाल =  \(\frac{2 v_{1} v_{2}}{v_{1}+v_{2}}\)