RBSE Class 9 Science Important Questions Chapter 11 Work and Energy

Rajasthan Board RBSE Class 9 Science Important Questions Chapter 11 Work and Energy Important Questions and Answers.

RBSE Class 9 Science Chapter 11 Important Questions Work and Energy

Objective Type Questions

Question 1.
When a body falls freely towards the Earth, then its total energy :
(a) increases
(b) decreases
(c) remains constant
(d) first increases and then decreases
Answer:
(c) remains constant

Question 2.
A car is accelerated on a levelled road and attains a velocity 4 times of its initial velocity. In this process the potential energy of the car :
(a) does not change
(b) becomes twice to that of initial
(c) becomes 4 times that of initial
(d) becomes 16 times that of initial
Answer:
(a) does not change

Question 3.
In case of negative work the angle between the force and displacement is :
(a) 0°
(b) 45°
(c) 90°
(d) 180°
Answer:
(d) 180°

Question 4.
An iron sphere of mass 10 kg has the same diameter as an aluminium sphere of mass is 3.5 kg. Both spheres are dropped simultaneously from a tower. When they are 10 m above the ground, they have the same :
(a) Acceleration
(b) Momentum
(c) Potential energy
(d) Kinetic energy
Answer:
(a) Acceleration

Question 5.
A girl is carrying a school bag of 3 kg mass on her back and moves 200 m on a levelled road. The work done against the gravitational force will be (g = 10 m s^-2) :
(a) 6 × 10³ J
(b) 6 J
(c) 0.6 J
(d) Zero
Answer:
(d) Zero

Question 6.
Which one of the following is not the unit of energy?
(a) Joule
(b) Newton metre
(c) Kilowatt
(d) Kilowatt hour
Answer:
(c) Kilowatt

Question 7.
The work done on an object does not depend upon the :
(a) Displacement
(b) Force applied
(c) Angle between force and displacement
(d) Initial velocity of the object
Answer:
(d) Initial velocity of the object

Question 8.
Water stored in a dam possesses :
(a) No energy
(b) Electrical energy
(c) Kinetic energy
(d) Potential energy
Answer:
(d) Potential energy

Question 9.
A body is falling from a height h. After it has fallen a height 2 m, it will possess:
(a) Only potential energy
(b) Only kinetic energy
(c) Half potential and half kinetic energy
(d) More kinetic and less potential energy
Answer:
(c) Half potential and half kinetic energy

Question 10.
A stone of mass m is dropped freely to a distance d, the value of its kinetic energy will be.:
(a) mgd
(b) \(\frac{1}{2}\)md²
(c) \(\frac{m g}{d}\)
(d) zero
Answer:
(a) mgd

Question 11.
The rate of doing work or rate of transfer of energy is called :
(a) work
(b) power
(c) \(\frac{\text { power }}{\text { work }}\)
(d) \(\frac{\text { work }}{\text { power }}\)
Answer:
(b) power

Question 12.
The value of kinetic energy depends :
(a) only on the mass of the object
(b) only on the velocity of the object
(c) on both mass and velocity
(d) None of these
Answer:
(c) on both mass and velocity

Question 13.
A bullet fired from the gun has energy :
(a) only due to its mass
(b) due to its mass and velocity
(c) due to gravitational force acting on it
(d) only potential
Answer:
(b) due to its mass and velocity

Question 14.
A 5 N force moves on object in the direction of force by 2 m, then the work done by the force will be (in joules) :
(a) 0.4
(b) 2.5
(c) 20
(d) 10
Answer:
(d) 10

Question 15.
When the value of velocity is doubled of an object, then the value of its kinetic energy :
(a) is reduced to half
(b) unchanged
(c) becomes four times
(d) becomes double
Answer:
(c) becomes four times

Question 16.
Fill in the blanks :
(a) Work done by force is defined as the .................. of force and displacement.
(b) 1 kWh = .................
(c) ................ energy is required to do 1 joule of work.
(d) The value of kinetic energy possessed by an object of mass m and moving with velocity v is ..................
(e) Potential energy of an object at a height is ....................
Ans. :
(a) product
(b) 3.6 × 10⁶ J
(c) 1 joule
(d) KE = \(\frac{1}{2}\)mv²
(e) PE = mgh

Question 17.
Match the column (A) with the column (B).

Column (A)	Column (B)
(i) Unit of work	(a) \(\frac{1}{2}\)mv2
(ii) Kinetic energy of a moving object	(b) mgh
(iii) Work done	(c) Joule
(iv) Potential energy	(d) Force × displacement

Answer:

Column (A)	Column (B)
(i) Unit of work	(c) Joule
(ii) Kinetic energy of a moving object	(a) \(\frac{1}{2}\)mv2
(iii) Work done	(d) Force × displacement
(iv) Potential energy	(b) mgh

Question 18.
Read the statements carefully and identify whether they are True or False-
1. The work done is equal to the change in kinetic energy of the object.
2. 1 Joule is the amount of work done on an object when the force of 1 N displaces the object 1 meter in the direction of force.
3. The work done on the object is equal to 2mgh.
4. Commercial unit of energy is known as joule.
5. An oscillating simple pendulum, possess only potential energy at its extreme position because there kinetic energy will be zero.
Answer:
1. True
2. True
3. False
4. False
5. True

Very Short Answer Type Questions

Question 1.
Does work done depend upon the velocity of the body.
Answer:
No.

Question 2.
State the law of conservation of energy.
Answer:
It states that energy can neither be created nor destroyed. It can only change its form.

Question 3.
In a tug-of-war one team gives way to the other. What work is being done and by whom?
Answer:
The winning team does work. The work is equal to the product of the resultant force and the displacement undergone by the losing team.

Question 4.
What will cause greater change in kinetic-energy of a body; changing its mass or changing its velocity?
Answer:
Changing its velocity.

Question 5.
List two essential conditions for work to be done.
Answer:
(i) A force must act and (ii) there should be displacement in the body.

Question 6.
When is 1 joule of work said to be done?
Answer:
When a force of 1 Newton acting on a body displaces it lm in its own direction.

Question 7.
What is the SI unit of work done and power?
Answer:
Joule and watt.

Question 8.
What is power? What is its SI unit?
Answer:
It is defined as the rate of doing work. Its unit is watt.

Question 9.
Find the energy in kWh consumed in 10 hours by a machine of power 500 W.
Answer:
W = P × t
= 500 × 10
= 5000 Wh
= 5 kWh.

Question 10.
When is work -said to be done against the force of gravity?
Answer:
When a body is lifted, the work is done against the force of gravity.

Question 11.
Write an expression for the work done in lifting a body of mass ‘m’ through a vertical height 'h'.
Answer:
Work done W = mgh, where g is .acceleration due to gravity.

Question 12.
Is it possible that some force is acting on a body but still the work done is zero?
Answer:
Yes, when force acts at an angle of 90° with the displacement.

Question 13.
What is the work done on a body moving in a circular path?
Answer:
Zero, because force and displacement are perpendicular to each other.

Question 14.
When do we say that work is done?
Answer:
Work is said to be done when a force causes displacement of an object in the direction of applied force.

Question 15.
What is the kinetic energy of an object?
Answer:
The energy possessed by a body by virtue of its motion is called kinetic energy.

Question 16.
Define 1 watt of power.
Answer:
When a work of 1 joule is done in 1 s, the power is said to be one watt.

Question 17.
Define energy.
Answer:
Energy is the ability of a body to do work. It is also defined as tfte capacity to do work.

Question 18.
What is the SI unit of energy?
Answer:
The SI unit of energy is joule.

Question 19.
Does a body at rest possess any kinetic energy?
Answer:
No.

Question 20.
By how much will the speed of a body, of fixed mass, increase if its kinetic energy becomes four times its initial kinetic energy?
Answer:
The speed is doubled.

Question 21.
Can a body possess energy even if it is not in motion?
Answer:
Yes, it can possess potential energy.

Question 22.
Define potential energy.
Answer:
It is defined as the energy possessed by a body by virtue of its position or change in shape.

Question 23.
Name the energy possessed by a stretched rubber hand lying on the table.
Answer:
Potential energy.

Question 24.
A cell converts one form of energy into another. Name the two forms.
Answer:
It converts chemical energy into electrical energy.

Question 25.
Name one unit of power bigger than watt.
Answer:
A unit bigger than watt is kilowatt.

Question 26.
Name at least three commonly used units of energy.
Answer:

• Joule,
• Erg,
• Kilowatt hour.

Question 27.
Name at least six forms of energy.
Answer:

1. Chemical energy
2. Heat energy
3. Light energy
4. Electrical energy
5. Sound energy
6. Solar energy

Question 28.
How many watt are there in 1 horsepower?
Answer:
746 watt.

Question 29.
A light and a heavy body have equal kinetic energy. Which one is moving fast?
Answer:
The lighter body is moving fast.

Question 30.
State the relation between kWh and joule. Define 1 watt.
Answer:
1 kWh - 1000 Wh = 1000 Js^-1 × 60 × 60 s = 3.6 × 10⁶ J
1 watt is the power of an agent which can do one joule of work in one second.

Question 31.
How much work is done by a force of 10 N in moving an object through a distance of 4 m in the direction of the force?
Answer:
Work done = Force × displacement = Fs = (10 N) × (4 m) = 40 joule or 40 J.

Question 32.
What is power? How do you differentiate kilowatt from kilowatt hour?
Answer:
Power is the rate of doing work. Kilowatt is the unit of power and kilowatt hour is the emit of energy.

Question 33.
What kind of energy transformation takes place when a body is dropped from a certain height?
Answer:
When a body falls, its potential energy gradually gets converted into (kinetic energy. On reaching the ground, the whole of the potential energy of the body gets converted into kinetic energy.

Question 34.
Can kinetic energy of a body be negative?
Answer:
No, as mass and velocity cannot be negative.

Question 35.
How does the kinetic energy of a body change if the mass of the body is halved?
Answer:
If the mass of a body is halved the kinetic energy is also halved.

Question 36.
A car and a truck are moving with the same velocity of 60 km/hr-1, which one has more kinetic energy?
Answer:
Truck has more kinetic energy as kinetic energy is directly proportional to the mass.

Question 37.
Give the mathematical relation between power, force and velocity.
Answer:
Power (P) = Force (F) × velocity (v)

Question 38.
At what rate is electrical energy consumed by a bulb of 60 watt?
Answer:
A 60 watt bulb consume electrical energy at the rate of 60 joule per second.

Question 39.
Which type of energy is present in an atom?
Answer:
Nuclear energy.

Question 40.
Which type of energy is present in a battery?
Answer:
Chemical energy.

Question 41.
Name the energy present in an object due to its position or configuration.
Answer:
Potential energy.

Question 42.
What type of energy is possessed by a flying bird and a flying aeroplane?
Answer:
Both potential energy and kinetic energy.

Question 43.
Does the potential energy of a spring increase or decrease when it is compressed?
Answer:
The potential energy of the spring increases because work is done on it when it is compressed.

Question 44.
A spring is compressed, what change is expected in the potential energy of the spring?
Answer:
When a spring is compressed, its potential energy is used up to changing its shape.

Question 45.
What is the amount of work done by a force when a body moves in a circular path?
Answer:
Work done is given by the expression W = Fs cos θ. When a body moves in a circular path, then the displacement (s) is zero. Therefore, work done is W = F × 0 = 0.

Short Answer Type Questions

Question 1.
Define work. How is work measured? When is work done by a force negative?
Answer:
Work is said to be done if force acting on an object displaces it through a certain distance. It is measured as the product of force and displacement.
Work done is negative if force and displacement are in the opposite direction.

Question 2.
Name the transformation of energy involved in the following cases :
(a) When a body is thrown upwards.
(b) When a body falls from the top of a hill.
(c) When coal burns.
(d) When a gas burns.
(e) When water falls from a height.
Answer:
(a) Kinetic energy into potential energy.
(b) Potential energy into kinetic energy.
(c) Chemical energy into heat energy.
(d) Chemical energy into heat energy.
(e) Potential energy into kinetic energy.

Question 3.
What are the factors on which the work done depends?
Answer:
The work done by a force depends upon :

• The magnitude of the force.
• The magnitude of the displacement.
• The angle between force and displacement.

Question 4.
How are kinetic energy and momentum related?
Answer:
Kinetic energy is given by the relation K = \(\frac{1}{2}\)mv². Multiplying and dividing the right hand side of the equation by m, we have K = \(\frac{m^{2} v^{2}}{2 m}=\frac{p^{2}}{2 m}\) (mv = p is momentum of a body), therefore, p = \(\sqrt{2 m K}\).

Question 5.
What is the work done by a coolie walking on a horizontal platform with a load on his head?
Answer:
In order to balance the load on his head, the coolie applies a force on it in the upward direction, equal to its weight. His displacement is along the horizontal direction. Thus, the angle between force F and displacement is 90°. Therefore, work done W = Fs cos θ = Fs cos 90° = 0.

Question 6.
We wind our watch once a day, what happens to the energy?
Answer:
When we wind our watch, we wind the spring inside the watch. As a result, energy is stored in the spring in the form of elastic potential energy. This elastic potential energy is used to make the watch work the whole day.

Question 7.
Distinguish between work, energy and power. State the SI units for each of these quantities.
Answer:
Work s It is defined as the product of force applied and the distance moved by the body on the application of the force. In SI unit it is measured in joule.
Energy : It is defined as the capacity of a body to do work. In SI unit it is measured in joule.
Power : It is defined as the rate of doing work. It measures how fast Or slow the work is done. In SI unit it is measured in watt unit.

Question 8.
A girl sits and stands repeatedly for 5 minutes. Draw a graph to show variation of potential energy with time.
Answer:

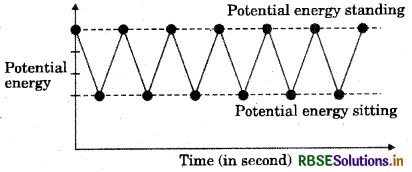
Question 9.
(i) What is a closed system?
(ii) State the law of conservation of energy.
Answer:
(i) A system that does not interact with another is a closed system. Energy m a closed system is neither taken out of it nor taken in from outside. However, energy transformation may occur inside a closed system.

(ii) The law of conservation of energy states that “the energy can neither be created nor destroyed, but can be transformed from one form to another. In other words, the total energy of a closed system remains constant. Therefore, whenever one form of energy disappear, an equivalent amount of another form appears.

Question 10.
When an arrow is shot from its bow, it has kinetic energy. From where does it get the kinetic energy?
Answer:
A stretched bow possesses potential energy on account of a change in its shape. To shoot an arrow; the bow is released. The potential energy of the bow is converted into the kinetic energy of the arrow.

Question 11.
Can any object have mechanical energy even if its momentum is zero? Explain.
Answer:
Yes, mechanical energy comprises of both potential energy and kinetic energy. Zero momentum means that velocity is zero. Hence, there is no kinetic energy but the object may possess potential energy.

Question 12.
A rocket is moving up with a velocity v. If the velocity of this rocket is suddenly tripled, what will be the ratio of two kinetic energies?
Answer:

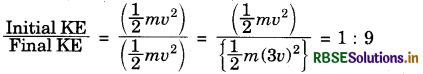
Question 13.
Give one example each of potential energy (i) due to position (ii) due to shape.
Answer:
(i) Potential energy due to position: Water stored in dam has potential energy.
(ii) Potential energy due to shape: In a toy car, the wound spring possesses potential energy and as the spring is released, its potential energy changes into kinetic energy due to which the car moves.

Question 14.
Define kinetic energy. Give any three examples.
Answer:
The energy possessed by an object by virtue of its motion is called the kinetic energy. It increases with the increase in velocity.
Examples :

• Fast-moving vehicles
• Moving bullet
• Flowing water etc.

Question 15.
Define Potential energy. Give any three examples.
Answer:
The energy possessed by an object by virtue of its motion or configuration or change thereof is called the potential energy.
Examples :

• Water stored in the overhead tank.
• A stretched rubber band.
• An archer’s bow with the string pulled back.

Question 16.
When is the work done by a force said to be negative? Give one situation in which one of the forces acting on the object is doing positive work and the other is doing negative work.
Answer:
We know that work done W = Fs cos θ, where θ is the angle between F and s. Clearly, W will be -ve, if θ is between 90° and 180° because then cos θ will be -ve. Consider the case of a body falling under gravity. The body experiences an upward frictional force and downward force due to gravity. Since, the body is moving downwards, the work done by force to gravity will be +ve but that is against the upward thrust will be -ve.

Long Answer Type Questions

Question 1.
Can any object have mechanical energy even if its momentum is zero? Explain.
Answer:
Yes, mechanical energy comprises both potential energy and kinetic energy. Momentum is zero which means velocity is zero. Hence, there is no kinetic energy but the object may possess potential energy.
Mechanical energy = Potential energy + Kinetic energy
Momentum = mv
Given, Momentum is zero which means velocity is zero.
Therefore, Kinetic energy = \(\frac{1}{2}\)mv²
As v = 0 (given)
Kinetic energy = \(\frac{1}{2}\) × m × 0
KE = 0
Mechanical energy = Potential energy + Kinetic energy
Mechanical energy = Potential energy + 0
Mechanical energy = Potential energy
Therefore, we can say that an object can have mechanical energy even if its momentum is zero.

Question 2.
The velocity of a body moving in a straight line is increased by applying a constant force F, for some distance in the direction of the motion. Prove that the increase in the kinetic energy of the body is equal to the work done by the force on the body.
Answer:
Consider that a force ‘F’ is applied on a body having mass 'm' and the distance travelled be ‘s’.
Work done (joules) = Force (Newton) × Distance (metre)
W = F × s ............ (1)
As,
Force (F) = ma .............. (2)
By substituting (2) in (1), we get
W = ma × s ............(3)
Using the Newton’s third equation of motion,
v² - u² = 2as
\(\frac{v^{2}-u^{2}}{2}\) = as .............(4)
Substituting (3) in (4), we get
W = \(m\left(\frac{v^{2}-u^{2}}{2}\right)\) .............. (5)
W = \(\frac{1}{2}\)mv² - \(\frac{1}{2}\)mu²
W = Final kinetic energy - Initial kinetic energy
Work done = change in kinetic energy

Question 3.
A light and a heavy object have the same momentum. Find out the ratio of their kinetic energies. Which one has a larger kinetic energy?
Answer:
Consider the mass and velocity of the light object to be m₁ and v₁ respectively.
Similarly, let the mass and velocity of the heavy object to be m₂ and v₂ respectively
Momentum = mass × velocity
i.e., p = mv ...........(1)
Momentum of light object = m₁v₁
Momentum of heavy object = m₂v₂
Given, light and a heavy object have the same momentum
Therefore,
m₁v₁ = m₂v₂
But, we know that
Kinetic energy = \(\frac{1}{2}\)mv²
Thus,
Kinetic energy of light object (KE₁) = \(\frac{1}{2}\)pv₁ [From (1)] ............(2)
Kinetic energy of heavy object (KE_h) = \(\frac{1}{2}\)pv₂ [From (1)] ............(3)
Given that m₁ < m₂; then v₁ > v₂ ............(4)
P = m₁v₁ = m₂v₂ = P, then \(\frac{v_{1}}{v_{2}}=\frac{m_{2}}{m 1}\) > 1
Ratio of kinetic energy of light and heavy object = \(\frac{\text { Equation (2) }}{\text { Equaiton (3) }}\)
= \(\frac{\left(\frac{1}{2} p v_{1}\right)}{\left(\frac{1}{2} p v_{2}\right)}\)
= \(\frac{v_{1}}{v_{2}}\)
But, v₁ > v₂ {from (4)}
Therefore, (KE)_l > (KE)_h
The lighter one will have more kinetic energy than the heavy one. Moreover, kinetic energy is directly proportional to the mass of the object.

Question 4.
(i) Derive a formula for kinetic energy.
(ii) Derive a formula for gravitational potential energy.
Answer:
(i) Expression for kinetic energy :
Let us consider an object of mass m lying at rest on a surfact. Let a constant force F be applied on the object so that it can attain a velocity v after displacement s in the direction of force
∵ Work done, W = F × s ............(i)
From Newton’s second law of motion, F = ma .............(ii)
and according to third equation of motion, v² - u² = 2as
⇒ s = \(\frac{v^{2}-u^{2}}{2 a}\) .........(iii)
Putting the value of F and s from equation (ii) and (iii) in equation (i),
W = ma × \(\frac{v^{2}-u^{2}}{2 a}=\frac{1}{2} m v^{2}-\frac{1}{2} m u^{2}\)
W = \(\frac{1}{2} m\left(v^{2}-u^{2}\right)\)
If body starts moving from rest, then u = 0
∴ W = mv² = K.E.
It is a scalar quantity.

(ii) Gravitational potential energy: It is defined as the work done in raising an object from ground to a point against gravity.
Expression for gravitational potential energy :
Consider an object of mass m, let it be raised through a height h.
Force applied on the object,
F = m × g (upward)
∴ Work done against gravity in raising the object through a height h above the ground to upwards.
Work, W = F × h
∴ W = m × g × h = P.E

Solved Numericals

Question 1.
A hammer of mass 1 kg falls freely from a height of 2 m. Calculate (I) The velocity and (II) The kinetic energy of the hammer just before it touches the ground. Does the velocity of hammer depend on the mass of hammer?
Answer:
PE = mgh = 1 × 9.8 × 2 = 19.6 J
PE = KE = 0.5 mv²
19.6 = 0.5 × 1 × v²
39.2 = v²
v = 6.29 m/s
No, velocity of hammer does not depend on the mass of the hammer as v = u + at

Question 2.
Calculate the change that should be affected in the velocity of a body to maintain the same KE, if mass of the body is increased to 4 times.
Answer:
Original KE = \(\frac{1}{2}\) mv₁²
Now, if mass if increase 4 times then,
New KE = 4 × \(\frac{1}{2}\)mv₂²
\(\frac{1}{2}\)mv₁² = 4 × \(\frac{1}{2}\)mv₂² ⇒ v₁² = 4v₂²
⇒ v₂ = \(\frac{v_{1}}{2}\)
Hence, new velocity will be half of the original velocity.

Question 3.
A rickshaw puller pulls the rickshaw by applying a force of 100 N. If the rickshaw moves with constant velocity of 36 kmh^-1. Find the power of rickshaw puller.
Answer:
Force = 100 N
Velocity = 36 km/h = 36 × 5 /18 = 10 m/s
Power = Force × Velocity
Power = 100 × 10 = 1000 Watt .
Therefore, power of rickshaw puller = 1000 Watt

Question 4.
An athlete weighing 60 kg runs up a staircase having 10 steps each of 1 m in 30 sec. Calculate power (g = 9.8ms^-1).
Answer:
h = 10 × 1m = 10 m
Work done = Potential energy = mgh = 60 × 9.8 × 10 = 5880 J
Power = \(\frac{W}{t}=\frac{5880}{30}\) = 196 W

Question 5.
The heart does 1.5 J of work in each heartbeat. How many times per minute does it beat if its power is 2 watt?
Answer:
Total work = P × t = 120 J,
Number of times heart beat in 1 min. = Total work done/work done in each beat
= \(\frac{120}{1.5}\) = 80 times

Question 6.
Calculate the time taken by 60 W bulb to consume 3000 J of energy.
Answer:
Power = 60 W and Energy consumed = 3000 J
We know that

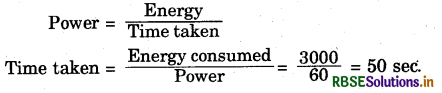
Question 7.
A horse exert a force of 200N to pull the cart. If the horse cart system moves with velocity 36 kmh^-1 on the level road, then find the power of horse in term of horsepower (1 HP = 746 W).
Answer:
Velocity = 36 kmh^-1 = 10 m/s
W = F × s = 200 × 10 = 2000J
P = \(\frac{\mathrm{W}}{\mathrm{t}}=\frac{2000 \mathrm{~J}}{1 \mathrm{sec}}\) = 2000 W
746 W = 1 HP
So, 2000 W = \(\frac{2000}{746}\) = 2.68 HP

Question 8.
In an experiment to measure his power, a student records the time taken by him in running up a flight of steps on a staircase.
Answer:
Use the following data to calculate the power of the student:
Number of steps = 28,
Height of each step = 20 cm,
Time taken = 5.4 s,
Mass of student = 55 kg,
Acceleration due to gravity = 9.8 ms^-2

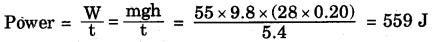
Question 9.
A bullet of mass 15 g has a speed of 400 m/s. What is its kinetic energy? The bullet strikes a thick target and is brought to rest in 2 cm, calculate the average net force acting on the bullet. What happens to kinetic energy originally in the bullet?
Answer:
KE = \(\frac{1}{2}\)mv² = 0.5 × 0.015 kg × (400 × 400) = 1200 J.
Work done = Change in K.E. .
As final velocity = 0.
So, change in KE = K_f - K_i = 1200 J
Therefore, F × d = 1200 (where F is the average force.)
F = \(\frac{1200}{2 \times 10^{-2}}\) = 6 x 10⁴N.
The kinetic energy is eventually converted to heat energy.

Question 10.
The power of a heart which beats 72 times in a minute is 1.2 kW. Calculate the work done by heart for each beat.
Answer:
P = 1200 W and t = 60 s
W = P × t = 1200 × 60 = 72000 J
In 72 times heartbeats 72000 J energy used
In 1 beat = \(\frac{72000}{72}\) = 1000J
Work done by the heart in every beat is 1 KJ.

Question 11.
When loading a truck, a man lifts boxes of 100 N each through a height of 1.5 m.
(a) How much work does he do in lifting one box?
(b) How much energy is transferred when one box is lifted?
(c) If the man lifts 4 boxes per minute, at what power is he forking? (g = 10 m s^-2)
Answer:
(a) Work done in lifting one box = F × d = 100 × 1.5 = 150 J.
(b) W = E = 150 J.
(c) Power = \(\frac{\text { Work done }}{\text { Time }}=\frac{150 \times 4}{60}\) = 10 W

Question 12.
Calculate the electricity bill amount for a month of 31 days, if the following devices are used as specified.
(a) 3 bulbs of 40 W for 6 hours.
(b) 4 tubelights of 50 W for 8 hours,
(c) A TV of 120 W for 6 hours.
The rate of electricity is ₹ 2.50 per unit.
Answer:
E₁ = P × t = 0.04 × 6 × 3 = 0.72 kWh
E₂ = P × t = 0.05 × 8 × 4 = 1.60 kWh
E₃ = 0.12 × 6 = 0.72 kWh
Total E = 0.72 + 1.6 + 0.72 = 3.04 kWh
Cost in 31 days = rate × E
= 3.04 × 2.50 × 31 = ₹ -235.60

Question 13.
Calculate the amount of work required to stop a car of 1000 kg moving with a speed of 72 km/h.
Answer:
Given m = 1000 kg, u = 72 km h^-1 = 20 ms^-1, v = 0
Work done = change in kinetic energy
= \(\frac{1}{2}\)m(v² - u²) = \(\frac{1}{2}\) × 1000 × (0²- 20²)
= -200000 J = -2 × 10⁵J

Question 14.
(a) What is the work done to increase the velocity of a car from 36 km h^-1 to 72 kmh^-1 if the mass of the car is 1500 kg? Does the work done by the force have a negative or a positive magnitude?
(b) Where does an oscillating pendulum have maximum PE and KE?
Answer:
(a) Given, m = 1500 kg, u = 36 kmh^-1 = 10 ms^-1, v = 72 k mh^-1 = 20 ms^-1, W = ?
Work done = Change in kinetic energy = \(\frac{1}{2}\)m(v² - u² ) = \(\frac{1}{2}\) × 1500 × (20² - 10²) = 225000 J
The work done is positive.
(b) It has maximum potential energy at its extreme position and maximum kinetic energy at the mean position.

Question 15.
A rocket is moving up with a velocity v. If the velocity of this rocket is suddenly tripled, what will be the ratio of two kinetic energies?
Answer:
Initial velocity = u; final velocity (v) = 3u
Final kinetic energy (KE_i) = \(\frac{1}{2}\)mv²
Final kinetic energy (KE_f) = \(\frac{1}{2}\)m(3u)²
Final kinetic energy = \(\frac{1}{2}\) × m × 9 u² = 9 × (\(\frac{1}{2}\)mu²)
Therefore, ratio of the two kinetic energies = KE_i : KE_f = 1 : 9

Question 16.
Avinash can run with a speed of 8 ms^-1 against the frictional force of 10 N, and Kapil can move with a speed of 3 ms^-1 against the frictional force of 25 N. Who is more powerful and why?
Answer:
As work equals to product of force and distance, you can write the equation for power in the following way, assuming that the force acts along the direction of travel:

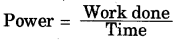
But, Work done = Force × distance
Therefore, P = \(\frac{W}{t}=\frac{F s}{t}\)
Where s is the distance travelled.
As

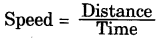
Therefore, the object’s speed, 'v' is
P = \(\frac{W}{t}=\frac{F s}{t}\) = Fv
Power of Avinash = 10 × 8 = 80 W
Power of Kapil = 25 × 3 = 75 W
Therefore, Avinash is more powerful than Kapil.

Question 17.
A boy is moving on a straight road against a frictional force of 5 N. After travelling a distance of 1.5 km he forgot the correct path at a roundabout figure of radius 100 m. However, he moves on the circular path for one and half cycle and then he moves forward upto 2.0 km. Calculate the work done by him.
Answer:

F = 5N
As work equals force times distance
W = F.s
W = 5 × [1500 + 200 + 2000] = 18500 J
Here, 1.5 km = 1500 m; 2 km = 2000 m

Question 18.
The power of a motor pump is 2 kW. How much water per minute the pump can raise to a height of 10 m? (Given, g = 10 m s^-2)
Answer:
Given, power of the pump = 2 kW = 2000 W; t = 1 min = 60 sec; height = 10 m; g = 10 ms^-2
Power = Work done per unit time
(The force on an object of mass m at the surface of the Earth is mg, from F = ma,
when acceleration is g, the acceleration at the surface of the Earth. If the object falls through a distance h, then the work done on the object by the force of gravity is mg times h, force times distance.)
Work = mgh
P = \(\frac{m g h}{t}\)
2000 W = m × 10 m s^-2 × 10 m
2000 W = \(\frac{m \times 100 \mathrm{~m}}{60 \mathrm{~s}}\)
m = \(\frac{2000 \times 60}{100}\)
m = 1200 kg
Therefore, the pump can raise 1200 kg of water in one minute.

Question 19.
The weight of a person on a planet A is about half that on the Earth. He can jump up to 0.4 m height on the surface of the Earth. How high he can jump on the planet A?
Answer:
As per the definition of force, the equation of force due to gravity is given by,
W = mg, i.e. weight is equal to mass times gravitational acceleration.
In this case, the force is better known as the weight of the object.
Weight of a person on Earth = W = mg₁ (given);
Height the person can jump (h₁) = 0.4 m
U = potential energy from height, m = mass of the object, g = gravity and height = h
U = mgh
Therefore, Potential energy = mg₁h₁
where (h₁) = 0.4 m; g₁ = g ............(1)
Now,
Weight of the person on planet A = \(\frac{\mathrm{W}}{2}=\frac{m g_{2}}{2}\)
Let the height the person can jump = h₂, g₂ = \(\frac{1}{2}\)g₁ = \(\frac{1}{2}\)g ...............(2)
Therefore,
Potential energy on planet A = mg₂h₂
Potential energy of the person on the Earth = mg₁h₁ ..........(3)
Substituting (1) in (3), we get
mg₁h₁ = m × g × 0.4
Now,
Potential energy of the person on the planet A = mg₂h₂ .............(4)
Substituting (2) in (4), we get
mg₂h₂ = m × \(\frac{1}{2}\)g × h₂
As potential energy of the person will remain the same on the Earth and on planet A.
Thus, mg₁h₁ = mg₂h₂
As mass remains the same,
Therefore, mg₁h₁ = mg₂h₂
g₁h₁ = g₂h₂
Therefore, by substituting the values, we get
g × 0.4 = \(\frac{1}{2}\) g × h₂
h₂ = \(\frac{g \times 0.4}{g / 2}\)
h₂ = \(\frac{g \times 0.4 \times 2}{g}\)
h₂ = 0.4 × 2 = 0.8 m
Hence, he can jump double the height with the same muscular force. 

Question 20.
A ball is dropped from a height of 10 m. If the energy of the ball reduces by 40% after striking the ground, how much high can the ball bounce back? (g = 10 m s^-2)
Answer:
Given, g = 10 ms^-2; h = 10 m
Energy possessed by the ball = mgh = m × 10 × 10 = 100 m joules
Energy left in the ball after striking the ground = \(\frac{100-40}{100}=\frac{60}{100}\)
(As energy is reduced by 40% after striking the ground)
Therefore, remaining energy = 60 m joules ...........(1)
Let the height at which the ball bounces back = h₁ ...........(2)
Therefore,
Energy possessed by the ball = mgh
Using (1) and (2), we get
60 m = m × 10 × h₁
h₁ = 6 metres.
Thus, the height at which the ball bounces back = 6 m

Question 21.
If an electric iron of 1200 W is used for 30 minutes every day, find electric energy consumed in the month of April.
Answer:
Given,
Power (P) = 1200 W = \(\frac{1200}{1000}\) = 1.2 kW;
Time (t) = 30min = \(\frac{30}{60}\)hr = \(\frac{1}{2}\)hr = 0.5 hr
Number of days in April = 30 days
We need the time for a month (April):
Therefore, 0.5 × 30 = 15 hr
Power = \(\frac{\text { Energy }}{\text { Time }}\)
Therefore, Energy = Power × Time
E = 1.2 × 15 = 18 kWh
The speed of the car (B) just after the collision = 10 m s^-1

Question 22.
A girl having mass of 35 kg sits on a trolley of mass 5 kg. The trolley is given an initial velocity of 4 ms^-1 by applying a force. The trolley comes to rest after traversing a distance of 16 m. (a) How much work is done on the trolley? (b) How much work is done by the girl?
Answer:
Given,
Mass of the girl = 35 kg;
Mass of the trolley = 5 kg;
Initial velocity (u) = 4 m s^-1;
Final velocity (v) = 0 (as it comes to rest); Distance (s) = 16 m
Therefore, by uSing equation of motion, we get
v² = u² + 2 as
0 = (4)² + 2 × a × (16)
0= 16 + 32a
-16 = 32a
\(-\frac{16}{32}\) = a
\(-\frac{1}{2}\) = a
- 0.5 m/s² = a
(Acceleration is negative, therefore, retardation)
Force exerted (F) = ma
F = 40 × \(-\frac{1}{2}\)
F = - 20N
(a) Work done = force × distance
W = F × d
W = Mass (As F = ma)
Total mass of the trolley = Mass of girl + mass of trolley = 35 + 5 = 40 kg
Therefore,
Work done on the trolley = 40 × \(\frac{1}{2}\) × 16 = 20 × 16 = 320 J

(b) Work done by the girl = F × d × mass
Work done by the girl = 35 × 0.5 × 16
Work done by the girl = 280 J

Question 23.
Four men lift a 250 kg box to a height of 1 m and hold it without raising or lowering it.
(a) How much work is done by the men in lifting the box?
(b) How much work do they do in just holding it?
(c) Why do they get tired while holding it? (g = 10 ms^-2)
Answer:
(a) Given, mass = 250 kg; Height(s) = 1 m; g = 10 ms^-2
F = mg (g = gravity)
F = 250 kg × 10 ms^-2 = 2500 N
W = F.s
= 2500 N × 1 m = 2500 J
(b) The men did not do any work in just holding it because the box does not move at all. Therefore, kinetic energy is zero (when the box is held up, it is at rest, no movement, thus it has zero speed).
(c) In order to hold the box, men are applying a force which is opposite and 1 equal to the gravitational, force acting on the box. They are working against gravity, air friction, etc. to hold the box up thereby making them feel tired.

Question 24.
How is the power related to the speed at which a body can be lifted? How many kilograms will a man working at the power of 100 W, be able to lift at constant speed of 1 m s^-1 vertically? g = 10 m/s^-2
Answer:
Given, power = 100 W, speed = 1 m s^-1; g = 10 m/s^-2

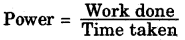
(here, work done = potential energy gained)
Therefore, Power = \(\frac{m g h}{t}\) .............(1)
But, \(\frac{h}{t}\) = Speed at which the body is being lifted. .........(2)
By substituting (2) in (1), we get
Power = m × g × speed
m = \(\frac{\text { Power }}{\text { g } \times \text { speed }}\)
m = \(\frac{100}{10 \times 1}\)
m = 10 kg

Question 25.
Compare the power at which each of the following is moving upwards against the force of gravity, (given g = 10 ms^-2)
(i) A butterfly of mass 1.0 g that flies upward at a rate of 0.5 ms^-1.
(ii) A 250 g squirrel climbing up on a tree at a rate of 0.5 ms^-1.
Answer:
(i) Given, mass of butterfly = 1 g = \(\frac{1}{1000}\) kg, g = 10 ms^-2; speed (v) = 0.5 ms^-1
Power = Force × speed
But, Force = mg
Therefore, Power = mg × v
P = \(\frac{1}{1000}\) × 10 × 0.5
P = \(\frac{0.5}{100}\) = 5 × 103W

(ii) Given, mass of squirrel = 250 g = \(\frac{250}{1000}\) kg = \(\frac{1}{4}\) kg, g = 10 ms^-2;
speed (v) = 0.5 ms^-1
Power = force × speed
But, Force = mg
Therefore, Power = mg × v
P = \(\frac{1}{4}\) × 10 × 0.5
P = 1.25 W
Thus, the power with which the squirrel is climbing is more than that of a butterfly flying.