RBSE Class 9 Science Important Questions Chapter 10 Gravitation

Question 5.
In the relation F = G Mm/d², the quantity G :
(a) depends on the value of g at the place of observation
(b) is used only when the Earth is one of the two masses
(c) is greatest at the surface of the Earth
(d) is universal constant of nature
Answer:
(d) is universal constant of nature

Question 6.
Law of gravitation gives the gravitational force between :
(a) the Earth and a point mass only
(b) the Earth and Sim only
(c) any two bodies having some mass
(d) two charged bodies only
Answer:
(c) any two bodies having some mass

Question 7.
The value of quantity G in the law of gravitation :
(a) depends on mass of Earth only
(b) depends on radius of Earth only
(c) depends on both mass and radius of Earth
(d) is independent of mass and radius of the Earth
Answer:
(d) is independent of mass and radius of the Earth

Question 8.
Two particles are placed at some distance. If the mass of each of the two particles is doubled, keeping the distance between them unchanged, the value of gravitatipnal force between them will be :
(a) 1/4 times
(b) 4 times
(c) 1/2 times
(d) Unchanged
Answer:
(b) 4 times

Question 9.
The atmosphere is held to the Earth by :
(a) gravity
(b) wind
(c) clouds
(d) earth’s magnetic field
Answer:
(a) gravity

Question 10.
The force of attraction between two unit point masses separated by a unit distance is called :
(a) gravitational potential
(b) acceleration due to gravity
(c) gravitational field
(d) universal gravitational constant
Answer:
(d) universal gravitational constant

Question 11.
The weight of an object at the centre of the Earth of radius R is :
(a) Zero
(b) Infinite
(c) R times the weight at the surface of the Earth
(d) 1/R² times the weight at surface of the Earth
Answer:
(a) Zero

Question 12.
An object weighs 10 N in air. When immersed fully in water, it weighs only 8 N. The weight of the liquid displaced by the object will be :
(a) 2 N
(b) 8 N
(c) 10 N
(d) 12 N
Answer:
(a) 2 N

Question 13.
A girl stands on a box having 60 cm length, 40 cm breadth and 20 cm width in three ways. In which of the following cases, pressure exerted by the brick will be :
(a) maximum when length and breadth form the base
(b) maximum when breadth and width form the base
(c) maximum when width and length form the base
(d) the same in all the above three cases
Answer:
(b) maximum when breadth and width form the base

Question 14.
An apple falls from a tree because of gravitational attraction between the Earth and apple. If F₁ is the magnitude of force exerted by the Earth on the apple and F₂ is the magnitude of force exerted by apple on Earth, then :
(a) F₁ is very much greater than F₂.
(b) F₂ is very much greater than F₁.
(c) F₁ is only a little greater than F₂.
(d) F₁ and F₂ are equal.
Answer:
(d) F₁ and F₂ are equal.

Question 15.
Which of the following is a correct formula, if d shows the density of earth?
(a) g = \(\frac{4}{3}\) πGd
(b) g = \(\frac{4}{3}\) πR Gd
(c) g= \(\frac{4}{3} \frac{\pi d G}{R}\)
(d) g = \(\frac{4}{3} \frac{\pi d G}{R^{2}}\)
Answer:
(d) g = \(\frac{4}{3} \frac{\pi d G}{R^{2}}\)

Question 16.
Fill in the blanks :
(a) Value of g is ............... at the poles and ............... at equater.
(b) In the state of weightlessness, apparent weight is ...............
(c) The formula of gravitational force between two objects is, F = ...............
(d) When an object immersed in a liquid, an upward force acts on it, which is called ............... force.
(e) The mass of a 60 kg person on earth will be ............... on moon.
Answer:
(a) maximum, minimum
(b) zero
(c) G \(\frac{m_{1} m_{2}}{d^{2}}\)
(d) buoyant
(e) 60 kg

Question 17.
Match the column (A) with the column (B).

Column (A)	Column (B)
(i) Attraction between two planets	(a) Gravity
(ii) Attraction between a body and a planet	(b) Weightlessness
(iii) Free fall	(c) Gravitational force
(iv) Weight	(d) Gravitation

Answer:

Column (A)	Column (B)
(i) Attraction between two planets	(d) Gravitation
(ii) Attraction between a body and a planet	(a) Gravity
(iii) Free fall	(b) Weightlessness
(iv) Weight	(c) Gravitational force

Question 18.
Read the statements carefully and identify whether they are True or False-
1. The value of g, acceleration due to gravity is 1.57 m/s² on moon.
2. The force on bodies falling freely in vacuum is same.
3. The force required for the circular motion of an object is centripetal force.
4. The gravitational force between two bodies does not depend on the sum of the masses of them.
5. The velocity of the object thrown vertically upwards is minimum at the maximum height.
Answer:
1. True
2. False
3. True
4. True
5. False

Very Short Answer Type Questions

Question 1.
Write SI unit of G.
Answer:
We know,
F = Gm₁m₂/r²
or G = Fr²/m₁m₂
In SI system, force F is measured in N, distance r in m and masses m₁ and m₂ in kg, therefore-
SI unit of G = Nm²/kg.kg = Nm²kg^-2

Question 2.
Why is G called ‘a universal gravitational constant’?
Answer:
The value of G is same for any pair of objects in the universe. Also its value does not depend on the nature of the intervening medium. That is why constant G is called ‘universal gravitational constant’.

Question 3.
Why should we be sent flying in space if the force of gravity somehow vanishes today?
Answer:
The centripetal force required to keep us rotating along with the Earth would not be available in the absence of force of gravity. We would then fly off along the tangent to the Earth into the space.

Question 4.
What is weightlessness?
Answer:
A body is said to be in a state of weightlessness when the reaction of the supporting surface is zero or its apparent weight is zero.

Question 5.
Is value of “g” same at all places on the Earth? Give reason for your answer.
Answer:
No, the value of “g” is maximum at the poles and minimum at equator. This variation is because to the oblong shape of the Earth and its rotation about its own axis.

Question 6.
Define the weight of an object on Moon.
Answer:
The weight of an object on the Moon is the force with which the Moon attracts that object.

Question 7.
What is the relation between gravitational force of the Moon with the Earth?
Answer:
The gravitational force of the Moon is about one-sixth of what it is on the Earth.

Question 8.
Name the scientist in whose honor the SI unit of pressure is named.
Answer:
The SI unit of pressure is named after Blaise Pascal.

Question 9.
Why does a mug full of water feel lighter inside, water?
Answer:
A mug of water appears lighter inside the water because a buoyant force acts on the mug when placed inside the water.

Question 10.
Name the force which accelerates a body in free fall.
Answer:
Gravitational force of Earth.

Question 11.
What is the unit of “g”?
Answer:
The unit of “g” is ms^-2.

Question 12.
Why value of “g” more or less constant on or near the Earth?
Answer:
Radius of Earth does not change much; “g” is more or less constant on or near the Earth.

Question 13.
Name the force which is necessary for the plants to revolve around the sun.
Answer:
Gravitational force.

Question 14.
Write the formula of pressure.
Answer:

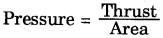
Question 15.
What is the unit of relative density?
Answer:
Since, relative density is the ratio of same quantities, it has no unit.

Question 16.
Write the formula to find the value of g.
Answer:
g = G \(\frac{m}{R^{2}}\)
where m = mass of earth
R = distance between object and earth

Question 17.
What is thrust?
Answer:
The force perpendicular to the surface of an object is called thrust (net force).

Question 18.
If an object is thrown vertically upwards from the bottom, what will be the form of equations of motion?
Answer:
(i) v = u - gt
(ii) h = ut - \(\frac{1}{2}\) gt²
(iii) v² = u² - 2gh

Question 19.
Do liquids exert pressure?
Answer:
Yes, liquids exert the pressure on the walls of vessel in which they are kept.

Question 20.
In which direction do liquids exert pressure?
Answer:
liquids exert pressure in all directions.

Question 21.
What is the effect of buoyant force on the weight of an object?
Answer:
Due to the buoyant force exerted on an object immersed in a liquid, the weight of an object is felt less than its actual weight.

Question 22.
Which object floats in water and which object sinks? Answer.
Answer:
If the density of an object is less than the fluid then object floats and if it is more than the fluid then object sinks in it.

Question 23.
What is the reason for the movement of the moon around file earth?
Answer:
Due to centripetal force, which arises due to the attraction force of the earth.

Question 24.
What does the effect of thrust depend on?
Answer:
The effect of thrust depend on the area on which it is applied.

Question 25.
Using the principle of Archimedes, write a formula for the relative density of an object.
Answer:

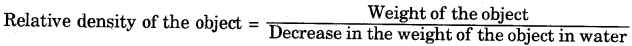
Question 26.
Write Kepler’s law of orbital period.
Answer:
The cube of the mean distance of a planet from the sun is proportional to the square of its orbital period (T).
Or, r³ ∝ T²
\(\frac{r^{3}}{T^{2}}\) = constant

Question 27.
What is the main reason for the tides in the sea?
Answer:
The gravitational effect of moon.

Question 28.
A person can jump higher on the moon, what is the reason for this?
Answer:
The value of g is 6 times less than earth on moon.

Question 29.
What will be the value of gravitational acceleration at the centre of Earth?
Answer:
The value of g will be zero at the centre of earth.

Question 30.
Where did Archimedes use his knowledge?
Answer:
He used his knowledge to measure the purity of gold used in the king’s crown.

Question 31.
How does the force of gravitation between two objects change when the distance between them is reduced to half?
Answer:
When the distance between the objects is reduced to half the gravitational force increases by four times the original force.

Question 32.
The gravitational force acts on all objects in proportion to their masses. Why, then, a heavy object does not fall faster than a light object?
Answer:
Acceleration due to gravity does not depend on mass of object. Hence, all bodies fall with the same acceleration provided there is no air or other resistance.

Question 33.
The cork floats on water while the nail sinks. Why?
Answer:
The density of nail is higher than the density of cork, which causes the nail to sink.

Question 34.
Why is the weight of objects on the moon is less than the weight of objects on the Earth?
Answer:
The mass of the moon is less than that of the Earth, so the moon applies less attraction force on objects.

Question 35.
Which scientist’s law did Newton use to calculate the gravitational force?
Answer:
Kepler’s third law.

Question 36.
What is gravitational acceleration?
Answer:
The acceleration due to the gravitational force of Earth is called gravitational acceleration.

Question 37.
Whom does the moon revolve around?
Answer:
Earth.

Question 38.
Why is the gravitational acceleration (g) is higher than the equator at the poles?
Answer:
The radius of earth increases from the poles to the equator, so the value of g is higher at the poles.

Question 39.
Write the formula of weight.
Answer:
W = mg

Short Answer Type Questions

Question 1.
Derive a relationship between “g” and “G”.
Answer:
Let a body of mass m be dropped from a distance R from the centre of the Earth.
Therefore, F exerted by the Earth on the body is;
F = \(\frac{G \times M_{e} \times m}{R^{2}}\)
Where, Me is the mass of the Earth then, the acceleration of the body (a) is given by :

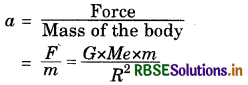
Thus, a is independent of the mass of the object falling towards the Earth. This acceleration “a” developed by a falling object is called the acceleration due to gravity. It is denoted by “g”.
g = \(\frac{G \times M_{e}}{R}\)

Question 2.
Discuss the variation of weight of a body with the Latitude of Earth and Altitude of Earth.
Answer:

• Earth is not a perfect sphere.
• Its radius at equator is longer than at the poles.
• The acceleration due to gravity is inversely proportional to the square of the radius.
• Therefore, the value of “g” at the poles is higher than that at the equator.
• As a result, the weight of an object increases if it moves from the equator to the poles.

Question 3.
Why are the ends of tools like knives, pins and nails pointed?
Answer:
The ends of tools such as pins, knives and nails are made pointed to increase the effect of the force. Because the pointed ends have much smaller areas. As result for a certain amount of force applied, the pressure becomes very large. That is why sharp edges needs very small force to cut fruits or vegetables.

Question 4.
Explain : Centrifugal force and Centripetal force.
Answer:
A force which is required to move a body uniformly in a .circle is known as centripetal force. This force acts along the radius and towards the centre of the circle, centrifugal force arises when a body is moving actually along a circular path, by virtue of tendency of the body to regain its natural straight line path. This force acts along the radius and away from the centre of the circle.

Question 5.
A certain particle has a weight of 30N at a place where the acceleration due to gravity is 9.8 m/s² : (a) What are its mass and weight at a place where acceleration due to gravity is 3.5 m/s²? (b) What are its mass and weight at a place where acceleration due to gravity is 0?
Answer:
(a) Weight of the body, W = 30, W = mg, Mass of the body, m = \(\frac{W}{g}=\frac{30}{3.5}\) = 8.5 kg
New weight of the body, W' = mg' = (3.06) (3.5) = 10.71 N
(b) Mass remains the same but weight becomes zero.

Question 6.
What is gravitation?
Answer:
Gravitation is the force of attraction between two objects in the universe :
(i) Gravitation may be the attraction of objects by the Earth.
Example : If a body is dropped from a certain height, it falls downwards due to Earth’s gravity. If a body is thrown upwards, it reaches a certain height and then falls downwards due to the Earth’s gravity.

(ii) Gravitation may be the attraction between objects in outer space : Attraction between the Earth and Moon. Attraction between the Sun and planets.

Question 7.
Two objects of masses M₁ and M₂ are dropped in vacuum from a height above the surface of Earth (M₁ is greater than M₂). Which one will reach the ground first and why?
Answer:
Since acceleration is the rate of change of velocity, and velocity is the rate of change of position, objects dropped from the same height will feel the same acceleration, and so move with the same rate of increasing velocity, and so hit the ground at the same time, independent of their masses.

Question 8.
What is the source of centripetal force that a planet requires to revolve around the Sun? On what factors does that force depend?
Answer:
Gravitational force is the source of centripetal force that a planet requires to revolve around the Sun.
It depends upon the following factors :

• Mass of the planet and the Sun, i.e. depends on the product of the masses of the planet and the Sun.
• Distance between the planet and the Sun, i.e. depends on the square of distance between the planet and the Sun.

Question 9.
Suppose gravity of Earth suddenly becomes zero, then in which direction will the Moon begin to move if no other celestial body affects it?
Answer:
If gravity of Earth suddenly becomes zero then Moon will begin to move in a straight line in the direction in which it was moving at that instant. This straight line will be a tangent to the circular path. This change happens because the circular motion of the Moon is due to the centripetal force provided by the gravitational force of the Earth.

Question 10.
Identical packets are dropped from two aeroplanes, one above the equator and the other above the north pole, both at height h. Assuming, all conditions are identical, will those packets take same time to reach the surface of Earth. Justify your answer.
Answer:
At a given place, the value of acceleration due to gravity is constant but it varies from one place to another place on the Earth surface. It is due to this fact that Earth is not a perfect sphere. It is flattened at the poles and bulges out at the equator (ellipsoidal shaped) Thus, the value of ‘g’ is minimum at the equator and maximum at the poles. It mgans ‘g’ increases as we go from equator to pole. Therefore, the packet falls slowly at equator compared to the poles. Thus, the packet will remain in air for a lunger time, when it is dropped at the equator.

Question 11.
Give difference between ‘g’ and ‘G’ in a tabular form.
Answer:

Gravity (g)	Gravitational constant (G)
1. Acceleration acquired by a body due to Earth’s gravitational pull on it.	1. Numerically equal to the force of attraction between two masses of 1 kg each apart of 1 m.
2. Not a universal constant. Different at different places.	2. G is a universal constant. Value is 6.67 × 10-11 N-m2kg-2.
3. Vector quantity	3. Scalar quantity

Question 12.
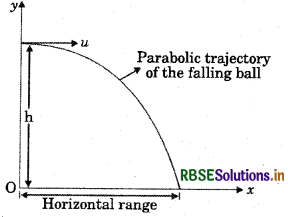
A ball moving on a table reaches the edge and falls. Sketch the path it will follow while falling.
Answer:
As the ball falls, it has a horizontal velocity and a vertical downward acceleration due to gravity. Under the combined effect of these two motion the ball moves along a parabolic trajectory as shown in figure :

Question 13.
What is the importance of universal law of gravitation?
Or
Write four phenomenons which were successfully explained using universal law of gravitation.
Answer:
Many unconnected phenomenon can be explained by gravitational law successfully.

• Force binds us with Earth
• Motion of Moon around Earth
• Motion of planet around Sun
• Tides due to the Moon and Sun

Question 14.
Write Kepler’s laws.
Answer:
Kepler’s laws :
(i) The orbit of a planet is an ellipse with the sun at one of the foci.
(ii) The fine joining the planet and the sun sweep equal areas in equal intervals of time.
(iii) The cube of the mean distance of a planet from the sun is proportional to the square of its orbital period (T).
Or, \(\frac{r^{3}}{T^{2}}\) = constant

Question 15.
The Earth is acted upon by gravitation of Sun, even though it does not fall into the Sun. Why?
Answer:
According to Newton’s first law of motion, an object in motion tries to move in straight-line at a constant speed unless external pressure is not applied. When the Earth comes dose to the Sun that has a large gravitational force, the path of the Earth is altered due to the unbalanced force of gravity on it. The Sun exerts an attractive force on the Earth, accelerating the Earth directly towards the Sun. It moves towards the Sim as described by Newton’s second law. To avoid falling into the Sun, the Earth also counteracts the force that is pulling it towards the Sun. Thus, a force which tends to make a body move in a curved path, is called a centripetal force is applied by the Earth.

Therefore, we can say that the gravitational force is responsible for providing the necessary centripetal force which allows the Earth to move around the Sun in a defined orbit. Gravitational attraction of the Sun deflects the Earth from a straight path.

Question 16.
What do you mean by relative density?
Answer:
The relative density of a substance is the ratio of its density to that of water.

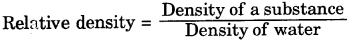
Since the relative density is a ratio of similar quantities, it has no unit.

Question 17.
What is the universal law of gravitation? Write.
Answer:
Universal law of gravitation : According to this law, ‘Every mass in the universe attracts every other mass with a force which is directly proportional to the product of two masses and inversely proportional to the square of the distance between them.’ This force acts along the line joining centres of two masses.

Long Answer Type Questions

Question 1.
Prove that the time of fall and the time of going up are equal for an object.
Answer:
When an object goes upwards-
Final velocity, v = 0
acceleration, a = -g
then, from equation u = u + at,
0 = u - gt
or, t = \(\frac{u}{g}\)
When object falls from maximum height, then time taken for coming back-
initial velocity, u = 0
and height h = \(\frac{u^{2}}{2 g}\) ............(i)
∴ From, vh = ut + \(\frac{1}{2}\) gt²
equation,
h = 0 + \(\frac{1}{2}\) gt²
⇒ h = \(\frac{1}{2}\) gt² ...........(ii)
Equating both the equations (i) and (ii)
\(\frac{u^{2}}{2 g}=\frac{1}{2} g t^{2}\)
or t² = \(\frac{u^{2}}{g^{2}}\)
∴ t = \(\sqrt{\frac{u^{2}}{g^{2}}}=\frac{u}{g}\)
t = \(\frac{u}{g}\)
Hence the time of fall is equal to the time of going up.

Question 2.
On the Earth, a stone is thrown from a height in a direction parallel to the Earth’s surface while another stone is simultaneously dropped from the same height. Which stone would reach the ground first and why?
Answer:
Both the stones will take the same time to reach the ground because the two stones fall from the same height.
As both the stones will have initial velocity (u) = 0, a = g (acceleration due to gravity), distance (s) = s; t = ?
Using equation of motion,
s = ut + \(\frac{1}{2}\) at²
Time taken for the first stone to travel,
s = ut + \(\frac{1}{2}\) at²
s = 0 × t + \(\frac{1}{2}\) gt²
s = 0 + \(\frac{1}{2}\) gt²
\(\frac{2 s}{g}\) = t²
\(\sqrt{\frac{2 s}{g}}\) = t
Time taken for the second stone to travel,
s = ut + \(\frac{1}{2}\) at²
s = 0 × t + \(\frac{1}{2}\) gt²
s = 0 + \(\frac{1}{2}\) gt²
\(\frac{2 s}{g}\) = t²
\(\sqrt{\frac{2 s}{g}}\) = t
Therefore, time taken for both the stones to reach the ground will be the same.

Question 3.
Calculate the average density of the Earth in terms of g, G and R. ‘g’ is related to Earth’s mass “M” and radius “R”.
Answer:
By the equation;
g = \(\frac{G M}{R^{2}}\)
Therefore, M = \(\frac{g R^{2}}{G}\) ..............(i)
Average density of Earth,
From (i), we get

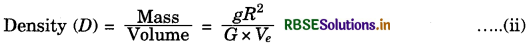
Where Ve is the volume of the Earth
The Earth is approximately a sphere (actually it is sphere slightly flattened at the poles).
Use the equation for the volume of a sphere which is
V = \(\frac{4}{3} \pi\) × Radius³
V = \(\frac{4}{3} \pi\) × R³ ..............(iii)
Therefore, by substituting equation (iii) in equation (ii), we get
D = \(\frac{g R^{2}}{G} \div \frac{4}{3} \pi \times \mathrm{R}^{3}\)
D = \(\frac{3 g}{4 \pi G R}\)

Question 4.
How does the weight of an object vary with respect to mass and radius of the Earth? In a hypothetical case, if the diameter of the Earth becomes half of its present value and its mass becomes four times of its present value, then how would the weight of any object on the surface of the Earth be affected?
Answer:
From Newton’s law of gravitation, we get
Weight of an object is directly proportional to the mass of the Earth and inversely proportional to the square of the radius of the Earth.
Weight of a body = Mass of the body × gravity of the Earth
W = mg ...........(i)
Mass of the Earth is same everywhere
Weight of a body = \(\frac{G M m}{R^{2}}\) .............(ii)
Where M = mass of Earth; m = mass of the body; R = radius of the Earth; G = universal gravitational constant; g = 9.8 m/s² on Earth.
Thus,
Weight of a body ∝ M
Weight of a body ∝ \(\frac{1}{R^{2}}\)
Original weight W₀ = mg = \(\frac{m G M}{R_{2}}\) (∵ \(g=\frac{G M}{R^{2}}\)) ..........(iii)
When diameter of the Earth becomes half of its present value R becomes R/2, its mass (M) becomes 4 M.
Then, weight becomes (W_n) = m G 4M/(R/2)² = (16 m G) M/R² = 16 x W₀
The weight of the same object will become 16 times its original weight.

Question 5.
Two objects of masses m₁ and m₂ having the same sizes are dropped simultaneously from heights h₁ and h₂ respectively. Find out the ratio of time they would take in reaching the ground. Will this ratio remain the same if (i) one of the objects is hollow and the other one is solid and (ii) both of them are hollow, size remaining the same in each case? Give reason.
Answer:
Two objects of masses m₁ and m₂ having the same sizes are dropped, therefore, initial velocity (u) = 0 and a = g (Acceleration due to gravity - falling object) and it is independent of mass.
By using Newton’s equation of motion namely
s = ut + \(\frac{1}{2}\) at²
For object 1,
h₁ = \(\frac{1}{2} g t_{1}^{2}\) ............(1)
where t₁ = time taken by object 1 to reach the ground
For object 2,
h₂ = \(\frac{1}{2} g t_{2}^{2}\) ............(2)
where t₂ = time taken by object 2 to reach the ground
Therefore, the ratio of time they would take in reaching the ground
\(\frac{h_{1}}{h_{2}}=\frac{\frac{1}{2} g t_{1}^{2}}{\frac{1}{2} g t_{2}^{2}}\)
\(\frac{t_{1}}{t_{2}}=\sqrt{\frac{h_{1}}{h_{2}}}\)

(i) This ratio of time will be the same even if one of the objects is hollow and the other one is solid. This is because acceleration due to gravity is independent of the mass of the falling body.
(ii) This ratio of time will be the same even if both of them are hollow, size remaining the same in each case. This is because acceleration due to gravity is independent of the mass of the falling body.

Question 6.
Prove that the weight of an object on the moon is equal to the -g-th of the weight of an object on the Earth.
Answer:
The weight of an object on the earth is the force with which the earth attracts the object. In the same way, the weight of an object on the moon is the force with which the moon attracts that object. The mass of the moon is less than that of earth. Due to this the moon exerts lesser force of attraction on objects.

Let the mass of an object be m. Let its weight on the moon be W_m, the mass of moon be Mm and its radius be r_m.
By using the universal law of gravitation, weight of the object on the moon will be
Wm = G \(\frac{M_{m} \times m}{r_{m}^{2}}\) .............(i)
Let the weight of same object on earth be We and the mass of earth be M and its radius be r.
Then the weight of the object on the earth will be
We = G \(\frac{M \times m}{r^{2}}\) .............(ii)
Here, mass of earth = 5.98 × 10²⁴ kg
r = 6.37 × 10⁶ m
and, mass of moon = 7.36 × 10²² kg
rm = 1.74 × 10⁶
From equation (i) and (ii),



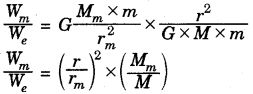
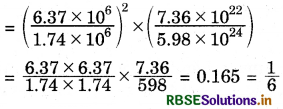
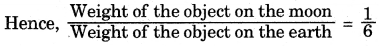
Weight of the object on the moon = \(\frac{1}{6}\) × its weight on the earth.

Question 7.
Explain the Newton’s law of gravitation. Derive a relation among acceleration due to gravity g, gravitational constant G, mass of earth Me and the radius of the earth Re with the help of suitable diagram. How does the value of g change on earth?
Answer:
Newton proposed the law of gravitation of earth.
According to his law, “an attraction force acts between two particles, which is called gravitational force.” He explained this force as follows :
Every mass in this universe attracts every other mass with a force which is directly proportional to the product of two masses and inversely proportional to the square of the distance between them. The force is along the line joining the centres of two masses.

Consider masses of two objects A and B are M and m and they lie at a distance of d from each other as shown in figure.

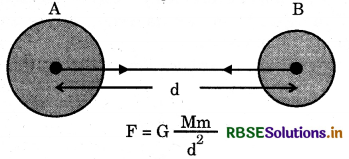
The gravitational force between two unifrom objects is directed along the line joining their centres.
According to the Newton’s law of gravitation, force F acting between the objects-
F ∝ M_m ............(i)
and F ∝ \(\frac{1}{d^{2}}\) .............(ii)
From both equations (i) and (ii)
F ∝ \(\frac{M_{m}}{d^{2}}\)
or, F = G \(\frac{M_{m}}{d^{2}}\)
Where G is a proportional constant and is called the universal gravitation constant. Its value is 6.67 × 10^-11 Nm²/kg².
Relation among acceleration due to gravity g, constant G, mass of earth Me and radius of earth Re :
According to the universal law of gravitation,
F = G \(\frac{M_{m}}{d^{2}}\) ...........(i)
If the value of gravitational acceleration is g, then the gravitational force F acting on the object of mass m will be-
F = mg ............(ii)
From both equations (i) and (ii)
mg = G \(\frac{M_{m}}{d^{2}}\)
or, g = G \(\frac{M}{d^{2}}\) ............(iii)
Above equation shows that the value of gravitational acceleration of a freely falling object does not depend on the value of the mass of that object. It only depends on the mass of the earth and the distance between the centre of the earth and the object. If the value of gravitational acceleration on earth be g_e, mass of earth be M_e and the radius of earth be R_e, then
g_e = G \(\frac{M_{e}}{R_{e}^{2}}\) [from equation (iii)]
The value of g decreases with increase in height. It also decreases with increase in the depth of earth. At the surface of earth, it will be maximum.

Question 8.
Derive a formula to calculate the value of acceleration due to gravity on a planet.
Answer:
We know that, mass of earth Me, gravitational constant G, and radius of earth Re has following relation :
g_e = G \(\frac{M_{e}}{R_{e}^{2}}\) ...........(i)
If the value of gravitational acceleration is g_p for a planet, M_p is the mass of planet and R_p is the radius of planet,
then, \(g_{p}=G \frac{M_{p}}{R_{p}^{2}}\) ...........(ii)
From equations (i) and (ii)

So, the value of gravitational acceleration g can be calculated from equation (iii) for any planet.

Question 9.
Explain the change in the value of g due to the shape of earth.
Answer:
We know that earth is not a perfect sphere or equatorial radius of earth is greater than its polar radius.

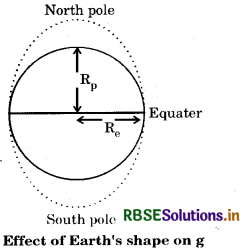
∵ Acceleration due to gravity, g = G \(\frac{M}{R^{2}}\) .............(i)
and value of g at poles, gp = G \(\frac{M}{R_{p}^{2}}\) ........ (ii)
and value of g at equator, ge = G \(\frac{M}{R_{e}^{2}}\) ............(iii)
But R_p < R_e
Therefore g_p > g_e
Hence, as the radius of the earth increases from the poles to the equater, therefore the value of g is greater at poles than at the equater.

Solved Numericals

Question 1.
The gravitational force between two objects is 49 N. How much distance between these objects be decreased so that the force between them becomes double?
Answer:
Let V be the distance between the object of mass m₁ and m₂.
F = G \(\frac{m_{1} m_{2}}{r^{2}}\)
49 = G \(\frac{m_{1} m_{2}}{r^{2}}\) ...........(i)
Now, the distance is reduced to 'x' so that the force becomes twice, then
2 F = G \(\frac{m_{1} m_{2}}{x^{2}}\)
98 = G \(\frac{m_{1} m_{2}}{x^{2}}\) ...........(ii)
Dividing equation (i) by (ii)

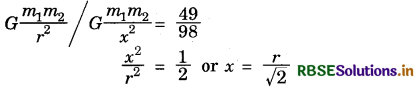
So, the distance must decrease by \(\frac{1}{\sqrt{2}}\) times the original distance.

Question 2.
Two bodies A and B having masses 2 kg and 4 kg respectively are separated by 2 m. Where should a body of mass 1 kg be placed so that the gravitational force on this body due to bodies A and B is zero?
Answer:
Mass of body A is M_A = 2 kg
Mass of body B is M_B = 4 kg
Mass of body C is M_C = 1 kg
Separation between A and B = 2 m
Let the body C be placed at a distance d from body A
Gravitational force between A and C

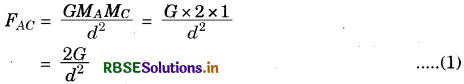
Gravitational force between B and C is

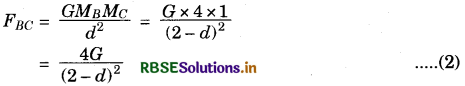
For body C the gravitational force is 0.
Hence, F_AC = F_BC
\(\frac{2 G}{d^{2}}=\frac{4 G}{(2-d)^{2}}\)
(2 - d)² = 2d²
2 - d = \(\sqrt{2} d\)
(\(\sqrt{2}\) + 1)d = 2
d = 0.83

Question 3.
Calculate the force of gravitation due to a child of mass 25 kg on his mother of mass 75 kg if the distance between their centres is 1 m from each other. Given G = (20/3) × 10^-11 Nm² kg^-2.
Answer:
Here, m₁ = 25 kg; m₂ = 75 kg; d = 1 m;
G = \(\frac{20}{3}\) × 10^-11 Nm² kg^-2
Using, F = G \(\frac{m_{1} m_{2}}{(d)^{2}}\)
F = \(\frac{\frac{20}{3} \times 10^{-11} \times 25 \times 75}{(1)^{2}}\)
F = 12500 × 10^-11
or, F = 1.25 × 10^-7 N

Question 4.
A boy drops a stone from the edge of the roof. It passes a window 2 m high in 0.1 s. How far is the roof above the top of the window?
Answer:
Let a stone be dropped from the edge of the roof A. Let it passes over B with a velocity say u. Consider motion BC.
u = ?, a = 9.8 ms^-2; s = h = 2 m; t = 0.1 s
Using
s = ut + \(\frac{1}{2}\) gt², we have
2 = u(0.1) + \(\frac{9.8}{2}\) (0.1)²
2 = 0.1u + 0.049
0.1u = 2 - 0.049
or, u = 19.51 ms^-1
This initial velocity at B in motion BC is the final velocity in motion AB. Considering motion AB, we have
u = 0; v = 19.51 ms-¹; s = ?; a = 9.8 ms^-2
Using v² - u² = 2as, we have
(19.51)² - (0)² = 2 × 9.8 s
or, s = 19.4 m
Roof is 19.4 m above the window.

Question 5.
A ball thrown up is caught by the thrower after 4 s. With what velocity was it thrown up? How high did it go? Where was it after 3 s ? (g = 9.8 ms^-2)
Answer:
Since, the time of going up is the same as that of coming down, therefore, time of going up = 4/2 = 2 s. Let it starts upward with velocity u.
Here u = ?; a = - 9.8 ms^-2; t = 2 s; v = 0 (at the top); s = h
Using v = u' + at
or 0 = u - 9.8 × 2
or u = 19.6 ms^-1
Again v² - u² = 2as
0 - (19.6)² = 2 (-9.8) h
h = 19.6 m
After 2 s, it starts coming downwards (starting with u = 0). Considering downward motion,
u = 0; a = 9.8 ms^-2; t = 3 - 2 = 1 s; s = ?
s = ut + \(\frac{1}{2}\) at²
or, s = 0 × \(\frac{9.8}{2}(1)^{2}\) = 4.9 m from top.

Question 6.
Coconut is hanging on a tree at a height of 15 m from the ground. A boy launches a projectile vertically upwards with a velocity of 20 ms^-1. After what time the projectile pass by coconut? Explain the two answer in this problem.
Answer:
Here u = 20 ms^-1; a = -10 ms^-2; s = 15 m; t = ?
Using, s = ut + \(\frac{1}{2}\) at², we have
15 = 20t + \(\frac{1}{2}\) (-10) t²
Dividing throughout by 5, we have
3 = 4t - t²
or, t² - 4t + 3 = 0
or (t - 1) (t - 3) = t - 1 = 0 or t = 1 s
or t - 3 = 0 or t = 3 s
After 1 s, it will cross coconut while going up and after 3 s while coming down.

Question 7.
A sealed can of mass 600 g has a volume of 500 cm³. Will this can sink in water? Density of water is 1 g cm^-3.
Answer:
Here, mass of can, M = 600 g
Volume of can, V = 500 cm³
Density of can, D = \(\frac{M}{V}=\frac{600 \mathrm{~g}}{500 \mathrm{~cm}^{3}}\) = 1.2 g cm^-3
Since, density of the can is greater than the density of water, so the can will sink in water.

Question 8.
A force of 200 N is applied perpendicular to its surface having area 4 square metres. Calculate the pressure.
Answer:
Thrust = 200 N
Area = 4 m²
Pressure = ?
Pressure = Thrust/Area = 200 N/4 m²
= 50 Nm^-2 = 50 Pa

Question 9.
A plastic bottle of 500 g has a volume of 450 cm³. Will the bottle float or sink in water? Density of water is 1 g cm^-3. Also calculate the mass of the water displaced by the bottle. 
Answer:
Mass, M = 500 g
Volume, V = 450 cm³
Density of bottle, D = \(\frac{M}{V}=\frac{500 \mathrm{~g}}{450 \mathrm{~cm}^{3}}\) = 1.11 g cm^-3
Since, density of bottle is greater than the density of water (1 g cm^-3), so the bottle will sink in water.
Mass of water displaced by the bottle = Volume of water displaced × Density of water
= Volume of bottle × Density of water
= 450 cm³ × 1 g cm^-3
= 450 g.

Question 10.
What is the force of gravitation between two point masses of 1 kg and 2 kg kept 1 m apart?
Answer:
Given : m₁ = 1 kg, m₂ = 2 kg, r = 1 m

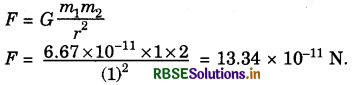
This is an extremely small force.

Question 11.
A particle is thrown up vertically with a velocity of 50 m/s.
(a) What will be its velocity at the highest point of its journey?
(b) How high would the particle rise?
(c) What time would it take to reach the highest point?
Answer:
At the highest point the velocity will be zero.
Considering activity A to B
Using v = u + at
0 = 50 - 9.8 × t
t = 5.1 sec
Also, v² - u² = 2as
0² - (50)² = 2 (-9.8) × s
s = 127.5 m

Question 12.
A hall is dropped from the top of a tower 40 m high. What is its velocity when it has covered 20 m? What would be its velocity when it hits the ground? Take g = 10 m/s².
Answer:
Let the point B be at a height of 20 m.
Activity from A to B : u₁ = 0, a₁ = 10 ms^-2, s₁ = 20 m, v₁ = ?
\(v_{1}^{2}-u_{1}^{2}\) = 2a₁s₁
\(v_{1}^{2}-0^{2}\) = 2 (10) (20)
\(v_{1}^{2}\) = 20²
v₁ = 20 m/s
Activity from A to C : C is a point on the ground
u₂ = 0, a₂ = 10 ms^-2, s₂ = 40 m, v₂ = ?
\(v_{2}^{2}-u_{2}^{2}\) = 2a₂s₂
\(v_{2}^{2}\) - 0² = 2 (10) (40)
\(v_{2}^{2}\) = 800
v₂ = 28.28 ms^-1

Question 13.
A body is thrown up with a speed 29.4 ms^-1.
(i) What is its speed after (a) t = 1 s, (b) t = 2 s and (c) t = 3 s?
(ii) What is its height after (a) t = 1 s, (b) t = 2 s and (c) t = 3 s?
Answer:
(i) (a) u = 29.4 ms^-1, a = - 9.8 ms^-2, t₁ = 1 s, v₁ = ?
v₁ = u + at₁
= 29.4 (- 9.8) × 1 = 19.6 ms^-1
(b) u = 29.4 ms^-1, a = - 9.8 ms^-2, t₂ = 2 s, v₂ = ?
v₂ = u + at₂
= 29.4 + (- 9.8) × 2 = 9.8 ms^-1
(c) u = 29.4 ms^-1, a = - 9.8 ms^-2, t₃ = 3 s, v₃ = ?
v₃ = u + at₃
= 29.4 + (- 9.8) × 3 = 0

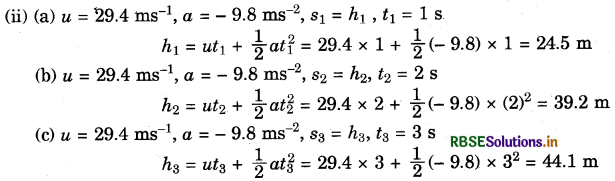
Question 14.
Weight of an object is 294 N on the surface of the Earth. What is its weight at a height of 200 km from the surface of the Earth? Radius of the Earth = 6400 km.
Answer:
Weight on Earth = W_e = 294 N
Radius of Earth = R_e = 6400 km
We have to find the weight at height 200 km from the surface of Earth
∴ Total distance = 200 + 6400
d = 6600 km
Weight at height 200 km = W_h = ?
We know

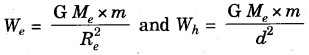
G and Me are constant,

∴ Weight of the object at the height 200 km from the surface of the Earth is 276.45 N.

Question 15.
The gravitational force between, two objects is F. How will this force change, when :
(i) distance between them is reduced to half?
(ii) the mass of each object is quadrupled?
Answer:
(i) According to Newton’s law of gravitation, gravitational force F between two objects distance r apart is \(\frac{\mathrm{G} \mathrm{Mm}}{\mathrm{r}^{2}}\)
Thus, F' = 4F
i.e. force becomes 4 times its previous value.
Again, according to Newton’s law of gravitation, the gravitational force F between two objects of masses m₁ and m₂ is F ∝ m₁m₂
When mass of each object is quadrupled,
m'₁ = 4m₁
and m'₂ = 4m₂
The force, F' ∝ m'₁ m'₂
or, F' = 16 F
i.e. force becomes 16 times its previous value.

Question 16.
A sphere of mass 40 kg is attracted by a second sphere of mass 15 kg when their centres are 20 cm apart, with a force of 0.1 milligram weight. Calculate the value of gravitational constant.
Answer:
Here, m₁ = 40 kg, m₂ = 15 kg
r = 20 cm = 2 × 10^-1 m
F = 0.1 milligram weight = 0.1 × 10^-3 gram weight
= 10^-4 × 10^-3 kg wt = 10^-7 × 9.8 N (1 kg wt = 9.8 N)
From F = \(\frac{G M m}{r^{2}}\)
9.8 × 10^-7 = \(\frac{G \times 15 \times 40}{(0.2)^{2}}\)
9.8 × 10^-7 = \(\frac{\mathrm{G} \times 600}{0.04}\)
9.8(0.040) × 10^-7 = 600G
3.92 × 10^-7 = 600G
G = 6.53 × 10^-11 Nm²/kg²

Question 17.
Calculate the force of gravity acting on your friend of mass 60 kg. Given mass of Earth = 6 × 10²⁴ kg and radius of Earth = 6.4 × 10⁶ m.
Answer:
Here, m = 60 kg, M = 6 × 10²⁴ kg
R = 6.4 × 10⁶ m, F = ?
G = 6.67 × 10^-11 Nm²/kg²
F = \(\frac{\mathrm{GMm}}{R^{2}}\)
= \(\frac{6.67 \times 10^{-11} \times 6 \times 10^{24} \times 60}{\left(6.4 \times 10^{6}\right)^{2}}\)
Thus, F = 58.62 N

Question 18.
A block weighing 1.0 kg is in the shape of a cube of length 10 cm. It is kept on a horizontal table. Find the pressure on the portion of the table where the block is kept.
Answer:
Here, force acting on the table, F = 1.0 kg = 10 N
Area of the table on which this force acts, A = 10 cm × 10 cm = 100 cm²
= 100 × 10^-4 m² = 10^-2 m² (1 cm² = 10^-4 m²)
P = \(\frac{F}{A}=\frac{10}{10^{-2}}\)
Pressure on the table, P = 1000 Pa

Question 19.
The mass of brick is 2.5 kg and its dimensions are 20 cm × 10 cm × 5 cm. Find the pressure exerted on the ground when it is placed on the ground with different faces.
Answer:
Given, Mass of the brick (m) = 2.5 kg
Dimensions of the brick = 20 cm × 10 cm × 5 cm
∴ Weight of the brick (Thrust/Force)
⇒ F = mg = 2.5 × 9.8 = 24.5 N
(i) When the surface area 10 cm × 5 cm is in contact with the ground, then
Area = 10 × 5 = 50 cm²
= \(\frac{50}{10000}\) = 0.005 m²
⇒ P = \(\frac{F}{A}=\frac{24.5}{0.005}\) = 4900N/m2
(ii) When the surface area 20 cm × 10 cm is in contact with the ground, then
Area = 20 × 10 = 200 cm²
\(\frac{200}{10000}\) = 0.02 m²
⇒ P = \(\frac{F}{A}=\frac{24.5}{0.02}\) = 1225 N/m²

Question 20.
An object is thrown vertically upwards and reaches a height of 78.4 m. Calculate the velocity at which the object was thrown? (g = 9.8 m/s²)
Answer:
Given, h = 78.4 m
v = 0
g = - 9.8 m/s²
Now, v² = u² - 2gh

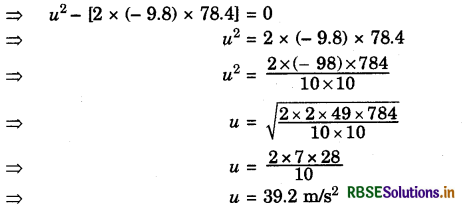
Question 21.
What is the mass of an object whose weight is 49 Newton?
Answer:
Given, Weight of object W = 49N
g = 9.8 m/s²
Now, W = mg
⇒ m = \(\frac{W}{g}=\frac{49}{9.8}\) = 5kg

Question 22.
The volume of 50 g of a substance is 20 cm³. If the density of water is 1 g cm^-3, will the substance float or sink?
Answer:
Mass = 50 g
Volume = 20 cm³
Density = ?
\(\frac{\text { Mass }}{\text { Volume }}=\frac{50 \mathrm{~g}}{20 \mathrm{~cm}^{3}}\)
= 2.5 g cm^-3
As the density of substance is greater than water, so it will sink.