RBSE Class 9 Science Important Questions Chapter 10 गुरुत्वाकर्षण

Rajasthan Board RBSE Class 9 Science Important Questions Chapter 10 गुरुत्वाकर्षण  Important Questions and Answers.

RBSE Class 9 Science Chapter 10 Important Questions  गुरुत्वाकर्षण

बहुचयनात्मक प्रश्न:

प्रश्न 1. 
यदि दो वस्तुओं के बीच की दूरी 'r ' है तो उन वस्तुओं के बीच गुरुत्वाकर्षण बल समानुपातिक होता है।
(अ) r²के
(ब) r के
(स) \(\frac{1}{r}\) के
(द) \(\frac{1}{\mathrm{r}^{2}}\) के
उत्तर:
 \(\frac{1}{\mathrm{r}^{2}}\) के

प्रश्न 2. 
एकं पंत्थर को किसी मीनार से गिराते हैं। मीनार से 20 मीटर गिरने पर इसका वेग कितना होंगा? g = 10 मीर्टर \ सेकण्ड² 
(अ) -10 मीटर / सेकण्ड
(ब) 10 मीटर / सेकण्ड
(स) -20 मीटर / सेकण्ड
(द) 20 मीटर / सेकण्ड
उत्तर:
20 मीटर / सेकण्ड

 

प्रश्न 3. 
जब कोई गेंद ऊर्ध्वाधर दिशा में ऊपर की ओर फेंकी जाती है तो गुरुत्वीय त्वरण।
(अ) उसकी गति की दिशा के विपरीत दिशा में होता है।
(ब) उसकी गति की ही दिशा में होता है।
(स) गेंद के नीचे आते समय बढ़ता जाता है।
(द) गेंद की उच्चतम स्थिति पर शून्य हो जाता है।
उत्तर:
उसकी गति की दिशा के विपरीत दिशा में होता है।

प्रश्न 4. 
दो वस्तुओं के मध्य लगने वाला गुरुत्वाकर्षण बल निर्भर नहीं करता है।
(अ) वस्तुओं के मध्य दूरी पर।
(ब) वस्तुओं के द्रव्यमान के गुणनफल पर।
(स) वस्तुओं के द्रव्यमान के योग पर।
(द) गुरुत्वाकर्षण स्थिरांक पर।
उत्तर:
वस्तुओं के द्रव्यमान के योग पर।

प्रश्न 5. 
यदि दो वस्तुओं का द्रव्यमान दुगुना कर दिया जाए और उनके मध्य दूरी को भी दुगुना कर दिया जाए तो दोनों वस्तुओं के मध्य लगने वाला बल पहले की अपेक्षा हो जाएगा।
(अ) 8 गुना
(ब) 4 गुना
(स) 2 गुना
(द) 1 गुना
उत्तर:
1 गुना

प्रश्न 6. 
दो द्रव्यमानों के बीच की दूरी दोगुनी करने पर द्रव्यमानों के बीच गुरुत्वाकर्षण बल।
(अ) अपरिवर्तित रहेगा 
(ब) चौथाई हो जाएगा 
(स) आधा रह जाएगा 
(द) दोगुना हो जाएगा 
उत्तर:
(ब) चौथाई हो जाएगा 

प्रश्न 7. 
निम्न में से कौनसा सूत्र सही है - d पृथ्वी का घनत्व है।
(अ) \(\mathrm{g}=\frac{4}{3} \pi \mathrm{Gd}\)
(ब) \(\mathrm{g}=\frac{4}{3} \pi \mathrm{RGd}\)
(स) \(\mathrm{g}=\frac{4}{3} \frac{\pi \mathrm{dG}}{\mathrm{R}}\)
(द) \(\mathrm{g}=\frac{4}{3} \frac{\pi \mathrm{dG}}{\mathrm{R}^{2}}\)
उत्तर:
\(\mathrm{g}=\frac{4}{3} \pi \mathrm{RGd}\)

प्रश्न 8. 
चन्द्रमा की सतह से पलायन वेग का मान पृथ्वी की सतह की अपेक्षा कम होता है। क्योंकि।
(अ) चन्द्रमा पर वायुमण्डल नहीं होता है जबकि पृथ्वी पर है।
(ब) चन्द्रमा की त्रिज्या पृथ्वी की त्रिज्या से कम है।
(स) चन्द्रमा सूर्य के निकट है।
(द) चन्द्रमा का द्रव्यमान कम है।
उत्तर:
चन्द्रमा की त्रिज्या पृथ्वी की त्रिज्या से कम है।

प्रश्न 9. 
केप्लर के तृतीय नियमानुसार किसी ग्रह के परिक्रमण काल का वेग।
(अ) r के अनुक्रमानुपाती है।
(ब) r² के अनुक्रमानुपाती है।
(स) r³ के अनुक्रमानुपाती है।
(द) r के व्युत्क्रमानुपाती है।
उत्तर:
r² के अनुक्रमानुपाती है।

प्रश्न 10. 
एक वस्तु पृथ्वी से चन्द्रमा पर ले जाई जाती है।
(अ) इसका द्रव्यमान नियत रहता है।
(ब) इसका भार नियत रहता है।
(स) गुरुत्वीय त्वरण नियत रहता है।
(द) उपर्युक्त में से कोई नहीं।
उत्तर:
इसका द्रव्यमान नियत रहता है।

प्रश्न 11. 
गुरुत्वीय त्वरण का मान अधिकतम होता है।
(अ) पृथ्वी की भूमध्य रेखा पर।
(ब) पृथ्वी के ध्रुवों पर।
(स) किसी पहाड़ की चोटी पर।
(द) पृथ्वी के अन्दर गहरी खान में।
उत्तर:
किसी पहाड़ की चोटी पर।

प्रश्न 12. 
गुरुत्वीय त्वरण का मान ध्रुवों की अपेक्षा भूमध्य रेखा पर।
(अ) पृथ्वी की आकृति व चक्रण दोनों के कारण घटता है।
(ब) पृथ्वी की आकृति के कारण बढ़ता है, पर चक्रण के कारण घटता है।
(स) पृथ्वी की आकृति के कारण घटता है, पर चक्रण के कारण बढ़ता है।
(द) पृथ्वी की आकृति व चक्रण दोनों के कारण बढ़ता है।
उत्तर:
पृथ्वी की आकृति व चक्रण दोनों के कारण घटता है।

प्रश्न 13. 
g  का मान सबसे अधिकतम कहाँ पर होता है?
(अ) पृथ्वी की सतह - पर  
(ब) ऊँचाई पर 
(स) गहराई में
(द) केन्द्र पर।
उत्तर:
पृथ्वी की सतह - पर  

प्रश्न 14. 
न्यूटन का गुरुत्वाकर्षण का नियम सार्वत्रिक होता है, क्योंकि।
(अ) वह सदेव आकषण का हैता है।
(ब) वह सौरमण्डल के सभी सदस्यों व कणों पर लागू होता है।
(स) यह सभी द्रव्यमान पर सभी दूरियों पर लागू होता है तथा माध्यम से प्रभावित नहीं होता है।
(द) उपरोक्त में से कोई नहीं।
उत्तर:
यह सभी द्रव्यमान पर सभी दूरियों पर लागू होता है तथा माध्यम से प्रभावित नहीं होता है।

प्रश्न 15. 
गुरुत्वाकर्षण के सार्वत्रिक नियतांक G का मान निर्भर करता है।
(अ) कणों की प्रकृति पर।
(ब) कणों के मध्य उपस्थित माध्यम पर।
(स) समय पर।
(द) किसी पर निर्भर नहीं करता।
उत्तर:
किसी पर निर्भर नहीं करता।

प्रश्न 16. 
पृथ्वी सतह पर किसी व्यक्ति का भार 60N है तो चन्द्रमा की सतह पर व्यक्ति का भार क्या होगा?
(अ) 60N
(ब) 30N
(स) 20N
(द) 10N
उत्तर:
10N

रिक्त स्थान वाले प्रश्न:

निम्नलिखित प्रश्नों में रिक्त स्थानों की पूर्ति कीजिए:

प्रश्न 1. 
दो पिण्डों के मध्य गुरुत्वाकर्षण बल का सूत्र....................होता है।
उत्तर:
\(\frac{\mathrm{Gm}_{1} \mathrm{~m}_{2}}{\mathrm{~d}^{2}}\)

प्रश्न 2. 
गुरुत्वाकर्षण के सार्वत्रिक नियतांक..........................नहीं करता है।
उत्तर:
निर्भर

प्रश्न 3. 
वह अवस्था जब वस्तु का भार शून्य हो जाता है......................कहलाती है।
उत्तर:
भारहीनता

प्रश्न 4. 
जब वस्तुयें पृथ्वी की ओर गुरुत्वीय आकर्षण बल के कारण गिरती हैं, तब उनकी गति कहलाती है।
उत्तर:
मुक्तपतन

प्रश्न 5. 
60 किग्रा. द्रव्यमान के किसी मनुष्य का चन्द्रमा पर द्रव्यमान.....................होगा।
उत्तर:
60 kg

प्रश्न 6. 
भारहीनता की अवस्था में प्रतिक्रिया बल...................होता है।
उत्तर:
शून्य

सत्य / असत्य कथन वाले प्रश्न:

निम्नलिखित कथनों में सत्य तथा असत्य कथन छाँटिए:

प्रश्न 1. 
वस्तु की वृत्ताकार गति के लिये आवश्यक बल अभिकेन्द्र बल होता है।
उत्तर:
सत्य

प्रश्न 2. 
निर्वात में स्वतंत्रतापूर्वक गिरते हुए पिण्डों का बल समान होता है।
उत्तर:
असत्य

प्रश्न 3. 
चन्द्रमा पर गुरुत्वीय त्वरण का मान 1.57 मीटर / से² होता है।
उत्तर:
सत्य

प्रश्न 4. 
ऊर्ध्वाधर ऊपर फेंके गये पिण्ड का महत्तम ऊँचाई पर वेग न्यूनतम होता है।
उत्तर:
असत्य

प्रश्न 5. 
दो पिण्डों के मध्य गुरुत्वाकर्षण बल उन दोनों के द्रव्यमानों के योग पर निर्भर नहीं करता है। 
उत्तर:
सत्य

प्रश्न 6. 
चन्द्रमा पर गुरुत्वीय त्वरण का मान, पृथ्वी पर गुरुत्वीय त्वरण के मान का\( \frac{1}{6}\) भाग होता है। 
उत्तर:
सत्य

मिलान वाले प्रश्न:

निम्नलिखित प्रश्नों में भाग (अ) का मिलान भाग ( ब ) से करके सही कृट (कोड ) का चयन कीजिए:

प्रश्न 1.

भाग (अ)	भाग (ब)
(i) गुरुत्वाकर्षण का नियम	(a) भास्कराचार्य
(ii) प्रयोगशाला में G के मान की गणना	(b) कॉपरनिकस
(iii) खगोल पिण्डों की गति का मॉडल	(c) हैनरी कैवेंडिस
(iv) भूकेन्द्रीय मॉडल	(d) आर्यभट्ट
(v) सिद्धान्त शिरोमणि	(e) न्यूटन

उत्तर:

भाग (अ)	भाग (ब)
(i) गुरुत्वाकर्षण का नियम	(e) न्यूटन
(ii) प्रयोगशाला में G के मान की गणना	(c) हैनरी कैवेंडिस
(iii) खगोल पिण्डों की गति का मॉडल	(d) आर्यभट्ट
(iv) भूकेन्द्रीय मॉडल	(b) कॉपरनिकस
(v) सिद्धान्त शिरोमणि	(a) भास्कराचार्य

प्रश्न 2.
 

भाग (अ)	भाग (ब)
(i) गुरुत्वीय त्वरण g का मान =	(a)  6 x 1024 kg
(ii) पृथ्वी का द्रव्यमान M =	(b) 6.4 x 106 kg
(iii) पृथ्वी की त्रिज्या R =	(c) \(\frac{\mathrm{GM}}{\mathrm{R}^{2}}\)  होता है।
(iv) वस्तु का चन्द्रमा पर भार =	(d)  \(\frac{1}{6}\) इसका पृथ्वी पर भार
(v) पानी का घनत्व =	(e) 103 kg m-3

उत्तर:

भाग (अ)	भाग (ब)
(i) गुरुत्वीय त्वरण g का मान =	(c) \(\frac{\mathrm{GM}}{\mathrm{R}^{2}}\)  होता है।
(ii) पृथ्वी का द्रव्यमान M =	(a)  6 x 1024 kg
(iii) पृथ्वी की त्रिज्या R =	(b) 6.4 x 106 kg
(iv) वस्तु का चन्द्रमा पर भार =	(d)  \(\frac{1}{6}\) इसका पृथ्वी पर भार
(v) पानी का घनत्व =	(e) 103 kg m-3

अतिलघूत्तरात्मक प्रश्न:

प्रश्न 1.
उस बल का नाम बताइए जो ग्रहों का सूर्य के चारों तरफ चक्कर काटते रहने के लिए आवश्यक है।
उत्तर:
गुरुत्वाकर्षण बल।

प्रश्न 2.
वस्तुओं का पृथ्वी की ओर गिरने के लिए कौनसा बल उत्तरदायी है?
उत्तर:
गुरुत्वाकर्षण बल।

प्रश्न 3.
चन्द्रमा किसकी परिक्रमा करता है ?
उत्तर:
पृथ्वी की परिक्रमा।

प्रश्न 4.
गुरुत्वाकर्षण बल के तथ्य को सबसे पहले किसने समझा था?
उत्तर:
आइजक न्यूटन ने।

प्रश्न 5.
न्यूटन को गुरुत्वाकर्षण के बारे में सोचने के लिए किस क्रिया ने प्रेरित किया था ?
उत्तर:
पेड़ से सेब नीचे गिरने की क्रिया ने।

प्रश्न 6.
दाब का सूत्र लिखिए।
उत्तर:


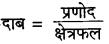
प्रश्न 7.
यदि पृथ्वी के द्वारा सेब अपनी ओर आकृष्ट किया जाता तो सेब की ओर पृथ्वी क्यों नहीं खिंच पाती ?
उत्तर:
पृथ्वी की अपेक्षा सेब का द्रव्यमान नगण्य होता है, इसलिए सेब की तरफ पृथ्वी नहीं खिंच पाती है।

प्रश्न 8.
गुरुत्वाकर्षण बल क्या है?
उत्तर:
विश्व के सभी पिण्ड एक - दूसरे को आकर्षित करते हैं। वस्तुओं के बीच यह आकर्षण बल गुरुत्वाकर्षण बल कहलाता है।

प्रश्न 9.
गुरुत्वाकर्षण का बल किस दिशा में लगता है?
उत्तर:
यह बल दोनों पिण्डों को मिलाने वाली रेखा की दिशा में लगता है।

प्रश्न 10.
न्यूटन ने किस वैज्ञानिक के नियम का उपयोग गुरुत्वाकर्षण बल के परिकलन में किया था?
उत्तर:
कैप्लर के तीसरे नियम का उपयोग किया था।

प्रश्न 11.
गुरुत्वीय त्वरण g का मान ध्रुवों पर विषुवत वृत्त की अपेक्षा अधिक क्यों होता है?
उत्तर:
पृथ्वी की त्रिज्या ध्रुवों से विषुवत वृत्त की ओर जाने पर बढ़ती है, इसलिए g का मान ध्रुवों पर अधिक है।

प्रश्न 12.
मुक्त पतन क्या है?
उत्तर:
पृथ्वी के गुरुत्वीय बल से वस्तुओं का पृथ्वी पर गिरना मुक्त पतन कहलाता है।

प्रश्न 13.
गुरुत्वीय त्वरण किसे कहते हैं?
उत्तरं:
पृथ्वी के गुरुत्वीय बल के कारण उस्पन्न त्वरण गुरुत्वीय त्वरण कहलाता है।

प्रश्न 14.
गुरुत्वीय बल की परिमाण F का मान किसके बराबर होता है?
उत्तर:
\(\mathrm{F}=\mathrm{Hlg}\)

प्रश्न 15.
g का मान किस सूत्र से ज्ञात किया जाता है। 
उत्तर:
\( \mathrm{g}=\mathrm{G} \frac{\mathrm{m}}{\mathrm{R}^{2}}\)
जहाँ M पृथ्वी का द्रव्यमान, R वस्तु के बीच की दूरी है।

प्रश्न 16.
किसी ऊँचाई से पृथ्वी पर वस्तुओं के गिरने की दर क्या होनी चाहिए?
उत्तर:
एकसमान होनी चाहिए।

प्रश्न 17. भार किसे कहते हैं?
उत्तर:
किसी वस्तु का भार वह बल है जिससे यह पृथ्वी की ओर आकर्षित होती है।

प्रश्न 18.
भार के परिमाण तथा दिशा क्यों होते हैं?
उत्तर:
भार एक बल है जो ऊर्ध्वाधर दिशा में नीचे की ओर लगता है इसलिए इसमें परिमाण एवं दिशा दोनों जे हैं।

प्रश्न 19.
चन्द्रमा पर वस्तुओं का भार पृथ्वी पर वस्तुओं के भार से कम क्यों होता है?
उत्तर:
चन्द्रमा का द्रव्यमान पृथ्वी की अपेक्षा कम है इसलिए चन्द्रमा वस्तुओं पर कम आकर्षण बल लगाता है।

प्रश्न 20.
चन्द्रमा पर पृथ्वी की अपेक्षा किसी वस्तु का भार कितना होता है?
उत्तर:
छः गुणा कम।

प्रश्न 21.
प्रणोद किसे कहते हैं?
उत्तर:
किसी वस्तु की सतह के लम्बवत् लगने वाले बल को प्रणोद (नेट बल) कहते हैं।

प्रश्न 22.
प्रणोद का प्रभाव किस पर निर्भर करता है?
उत्तर:
प्रणोद का प्रभाव उस क्षेत्रफल पर निर्भर करता है, जिस पर वह लगता है।

प्रश्न 23.
यदि किसी वस्तु को नीचे से ऊर्ध्वाधर ऊपर की ओर फेंका जाता है, तो गति के समीकरणों के स्वरूप खेए।
उत्तर:
1. v = u - g t
2. \(h = u t -\frac{1}{2} g t^{2}\)
3. \(v^{2}=u^{2}-2 g h\)

प्रश्न 24.
उत्प्लावन बल किसे कहते हैं ?
उत्तर:
किसी वस्तु पर पानी के द्वारा ऊपर की ओर लगाये जाने वाला बल उत्प्लावन बल कहलाता है।

प्रश्न 25.
उत्प्लावन बल का परिमाण किस पर निर्भर करता है?
उत्तर:
तरल के घनत्व पर निर्भर करता है।

प्रश्न 26.
पानी में कॉर्क तैरता है जबकि कील डूब जाती है। क्यों?
उत्तर:
कील का घनत्व कॉर्क के घनत्व से अधिक होता है। इस कारण से कील डूब जाती है।

प्रश्न 27.
किसी द्रव में कौनसी वस्तुएँ तैरती हैं और कौनसी वस्तु डूब जाती है?
उत्तर:
किसी वस्तु का घनत्व यदि द्रव से कम होता है तो वह वस्तु तैरती है और यदि अधिक होता है तो वह स्तु उसमें डूब जाती है।

प्रश्न 28.
पृथ्वी के चारों ओर चन्द्रमा की गति किसके कारण है?
उत्तर:
अभिकेन्द्र बल के कारण, जो पृथ्वी के आकर्षण बल के कारण उत्पन्न होता है।

प्रश्न 29.
क्या तरल पदार्थ दबाव आरोपित करते हैं?
उत्तर:
हाँ, तरल पदार्थ उस बर्तन की दीवारों पर दबाव आरोपित करते हैं, जिस बर्तन में इन्हें रखा जाता है।

प्रश्न 30.
तरल पदार्थ किस दिशा में दबाव आरोपित करते हैं?
उत्तर:
तरल पदार्थ सभी दिशाओं में दबाव आरोपित करते हैं।

प्रश्न 31.
किसी तरल में डुबाई जाने वाली वस्तु के भार पर उत्प्लावक बल का क्या प्रभाव पड़ता है?
उत्तर:
किसी तरल में डुबाई जाने वाली वस्तु पर लगने वाले उत्प्लावक बल के कारण ही वस्तु का भार उसके स्तविक भार से कम महसूस होता है।

प्रश्न 32.
पानी से भरा मग पानी के अन्दर हल्का क्यों महसूस होता है?
उत्तर:
ऐसा मग को पानी में रखने पर उस पर ऊपर की ओर आरोपित होने वाले उत्प्लावक बल के कारण होता है।

प्रश्न 33.
आपेक्षिक घनत्व का मात्रक लिखिए।
उत्तर:
चूँकि आपेक्षिक घनत्व समान राशियों का अनुपात है, अत: इसका कोई मात्रक नहीं होता है।

प्रश्न 34.
पृथ्वी के केन्द्र पर गुरुत्वीय त्वरण का मान क्या होगा?
उत्तर:
गुरुत्वीय त्वरण g का मान शून्य होगा इसलिए इसका भार भी शून्य होगा।

प्रश्न 35.
केपलर के आवर्तकाल के नियम का आलेख कीजिए।
उत्तर:
ग्रह के आवर्तकाल का वर्ग \(\left(\mathrm{T}^{2}\right)\) इसके सूर्य से माध्य दूरी के धन  \(\left(\mathrm{r}^{3}\right)\)के समानुपाती होता है। अर्थात् \(\mathrm{T}^{2} \propto \mathrm{r}^{3}\)

प्रश्न 36.
चन्द्रमा पर पृथ्वी का गुरुत्वाकर्षण बल लगता है तो भी चन्द्रमा पृथ्वी पर क्यों नहीं गिरता?
उत्तर:
चन्द्रमा स्थिर कक्षा में है तथा पृथ्वी का गुरुत्वाकर्षण बल चन्द्रमा की गति के लम्बवत् लगता है।

प्रश्न 37.
समुद्र में उत्पन्न ज्वार - भाटे का प्रमुख कारण क्या है?
उत्तर:
चन्द्रमा का गुरुत्वाकर्षण प्रभाव।

प्रश्न 38.
एक व्यक्ति चन्द्रमा पर अधिक ऊँची छलाँग लगा सकता है, इसका क्या कारण है?
उत्तर:
चन्द्रमा पर g का मान पृथ्वी तल से 6 गुणा कम होता है।

प्रश्न 39.
पृथ्वी तल से अन्दर केन्द्र की ओर जाने पर g का मान दूरी के साथ कैसे बदलता है?
उत्तर:
रेखीय रूप में एकसमान परिवर्तन होता है।

प्रश्न 40.
आर्किमिडीज के सिद्धान्त का प्रयोग करके किसी वस्तु का आपेक्षिक घनत्व का सूत्र लिखिए।
उत्तर:


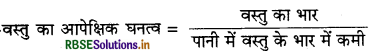
प्रश्न 41.
आर्किमिडीज ने अपने ज्ञान का उपयोग कहाँ पर किया?
उत्तर:
उन्होंने अपने ज्ञान का उपयोग राजा के मुकुट में उपयोग हुए सोने की शुद्धता को मापने के लिए किया।

लघूत्तरात्मक प्रश्न:

प्रश्न 1.
गुब्बारे पर सुई चुभोने पर वह फट जाता है, परन्तु दबाने पर नहीं । ऐसा क्यों होता है?
उत्तर:
सुई की नोक का क्षेत्रफल बहुत कम होता है। इस कारण इससे लगने वाले बल का प्रभाव भी अधिक होता है। परन्तु गुब्बारे को हाथ से दबाने से हाथों का क्षेत्रफल गुब्बारे के बड़े क्षेत्र को घेरता है, जिससे लगने वाला बल अधिक क्षेत्र में वितरित हो जाता है। इस कारण गुब्बारा फटता नहीं है।

प्रश्न 2.
आर्किमिडीज का सिद्धान्त लिखिए।
उत्तर:
आर्किमिडीज का सिद्धान्त-यदि किसी वस्तु को किसी तरल में पूर्ण या आंशिक रूप से डुबोया जाता है तो वह ऊपर की दिशा में एक बल का अनुभव करती है, जो वस्तु द्वारा हटाए गए तरल के भार के बराबर होता है।

प्रश्न 3.
G की परिभाषा दो। इसका मान और मानक इकाई लिखिए।
उत्तर:
दो वस्तुओं के बीच लगने वाला गुरुत्वाकर्षण बल
\(F=G \frac{m_{1} m_{2}}{R^{2}} \) होता है। 
यदि m₁ = m₂ = 1 इकाई और R = 1 इकाई
तब F = G

अत: गुरुत्वाकर्षण स्थिरांक G वह आकर्षण बल है जो इकाई द्रव्यमान वाली दो वस्तुओं के मध्य क्रिया करता है, जो कि एक - दूसरे से इकाई दूरी पर स्थिर होती है। CGS प्रणाली में G का मान 6.67 x 10^-8 डाइन सेमी² / ग्राम² है। मानक इकाई में इसका मान \(6.67 \times 10^{-11} \)\(\mathrm{Nm}^{2} / \mathrm{kg}^{2}\) है। ।



प्रश्न 4.
गुरुत्वाकर्षण नियम से न्यूटन के तीसरे नियम की व्याख्या किस प्रकार करते हैं?
उत्तर:
न्यूटन के तीसरे नियम के अनुसार प्रत्येक क्रिया के लिए बराबर और विपरीत दिशा में प्रतिक्रिया होती है। क्रिया और प्रतिक्रिया के ऐसे बलों को न्यूटोनियम बल कहते हैं। आक़र्षण का गुरुत्वाकर्षण बल दो वस्तुओं में अपना होता है। यदि एक वस्तु A दूसरी वस्तु B को किसी बल से आकर्षित करती है तो वस्तु B भी वस्तु A को उसी बल में आकर्षित करेगी। वस्तुओं में उत्पन्न प्रवेग भिन्न होगा और यह उनके द्रव्यमानों पर निर्भर करेगा लेकिन दोनों वस्तुओं द्वारा बल बराबर महसूस किया जायेगा।

प्रश्न 5.
गुरुत्व g तथा गुरुत्वाकर्षण (G) में क्या अन्तर है ?
उत्तर:

गुरुत्व (g)	गुरुत्वाकर्षण (G)
1. यह गुरुत्वीय त्वरण को प्रदर्शित करता है।	1. यह गुरुत्वाकर्षण स्थिरांक को प्रदर्शित करता है।
2. इसका मान भिन्न-भिन्न स्थानों पर भिन्न-भिन्न होता है।	2. इसका मान सभी स्थानों पर समान होता है, इसलिए इसे सार्वत्रिक स्थिरांक भी कहते हैं।
3. इसका पृथ्वी पर मान 9.8m/s2 होता है।	3. इसका मान \( 6.67 \times 10^{-11} \mathrm{Nm}^{2} / \mathrm{kg}^{2}\) होता है।

प्रश्न 6.
G को सार्वत्रिक स्थिरांक क्यों कहा जाता है?
उत्तर:
चूँकि \(\mathrm{F}=\mathrm{G} \frac{\mathrm{m}_{1} \mathrm{~m}_{2}}{\mathrm{R}^{2}}\)
इसमें G एक स्थिरांक है। G का मान m₁ , m₂ या R के मान पर निर्भर नहीं करता। इसका मान इस बात पर ती निर्भर नहीं करता कि F को किसने मापा, कब मापा और कहाँ मापा। ब्रह्माण्ड में स्थित किन्हीं भी दो वस्तुओं के लिए G का मान स्थिर रहता है। F तथा  \(\frac{\mathrm{m}_{1} \mathrm{~m}_{2}}{\mathrm{R}}\)का अनुपात जो कि G के बराबर होता है, किन्हीं भी दो वस्तुओं के लिए समान होता है इसलिए G को सार्वत्रिक स्थिरांक कहा जाता है।

प्रश्न 7.
केपलर के नियम लिखिए।
उत्तर:
केपलर के नियम:

1. प्रत्येक ग्रह सूर्य के चारों ओर दीर्घ वृत्ताकार कक्षा में परिक्रमण करता है तथा सूर्य कक्षा के एक फोकस र होता है।
2. किसी भी ग्रह को सूर्य में मिलाने वाली रेखा समान समय अन्तराल में समान क्षेत्रफल पार करती है अर्थात् ह का क्षेत्रीय वेग \(\left(\frac{\mathrm{dA}}{\mathrm{dt}}\right)\) नियत रहता है।
3. सूर्य से किसी ग्रह की औसत दूरी (r) का घन, उस ग्रह के सूर्य के परितः परिक्रमण काल T के वर्ग के मानुपाती होता है।
4. अथवा \(\frac{\mathrm{r}^{3}}{\mathrm{~T}^{2}}=\) स्थिरांक

प्रश्न 8.
द्रव्यमान और भार के अभिलक्षण लिखिए।
उत्तर:
द्रव्यमान के अभिलक्षण-किसी वस्तु में उपस्थित द्रव्य की मात्रा को द्रव्यमान कहते हैं। इसके प्रमुख अभिलक्षण निम्नलिखित हैं।

1. यह प्रत्येक स्थान पर समान रहता है।
2. यह एक अदिश राशि है तथा इसे भौतिक तुला में तोला जाता है।

भार के अभिलक्षण: किसी वस्तु का भार वह बल है जिससे पृथ्वी उसे अपनी ओर खींचती है। इसके प्रमुख अभिलक्षण निम्नलिखित होते हैं।

1. यह एक सदिश राशि है, जिसे कमानीदार तुला से तोला जाता है।
2. यह स्थान - स्थान पर बदलता है।
3. यह द्रव्यमान के अनुक्रमानुपाती होता है।

प्रश्न 9. 
प्रणोद् किसे कहते हैं? इसके दैनिक जीवन में उपयोग लिखिए।
उत्तर:
किसी वस्तु की सतह के लम्बवत् लगने वाले बल को प्रणोद कहते हैं। इसकी हमारे दैनिक जीवन में बहुत उपयोगिता है। जैसे

1. साइकिल या फुटबॉल में पम्प के द्वारा हवा भरने के लिए इसके द्वारा पिस्टन के पूरे क्षेत्रफल पर बल लगाते हैं।
2. ड्राइंग पिन को लगाते समय इसके चपटे भाग के क्षेत्रफल पर बल लगाते हैं। यह बल सतह के लम्बवत् होता है।

प्रश्न 10. 
दाब किसे कहते हैं? इसकी प्रमुख विशेषताएँ लिखिए।
उत्तर:
इकाई क्षेत्रफल पर लगने वाले बल को दाब कहते हैं।

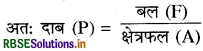
बल का मात्रक न्यूटन और क्षेत्रफल का मात्रक मीटर²
इस प्रकार दाब का मात्रक न्यूटन / मीटर² होता है । इसका SI मात्रक पास्कल Pa होता है। पिन, कुल्हाड़ी, कील, चाकू, कैंची आदि औजारों में बल का प्रभाव बढ़ाने के लिए उस क्षेत्रफल को कम किया जाता है, जिंस पर ये क्रिया करते हैं। क्षेत्रफल कम होने से दाब बढ़ जाता है।

प्रश्न 11. 
उत्प्लावन बल किसे कहते हैं? यह कैसे मापा जाता है?
उत्तर:
जब किसी वस्तु को द्रव में डुबोया जाता है तो वस्तु पर ऊपर की ओर एक बल लगता है, जिसे उत्प्लावन बल कहते हैं।
उत्प्लावन बल का मापन: एक ठोस बेलन लेकर एक कमानीदार तुला से उसका भार नोट करते हैं। माना उसका भार W₁ ग्राम है। अब बीकर में पानी लेते हैं और बेलन को बीकर में रखे पानी में धीरे - धीरे ले जाते हैं। पानी में धीरेधीरे डालने से बेलन का भार कम प्रतीत होने लगता है, जो कि कमानीदार तुला के सूचक से प्रकट होता है। जब बेलन पूरी तरह से पानी में डूब जाये तो कमानीदार तुला के सूचक का पाठ्यांक नोट करते हैं। माना यह पाठ्यांक W₂ है।
अत: उत्प्लावन बल = बेलन का वायु में भार - बेलन का पानी में भार
 = (W₁ - W₂) ग्राम

प्रश्न 12. 
कलन (Calculus) से क्या अभिप्राय है?
उत्तर:
न्यूटन ने गणित की एक नई शाखा की खोज की, जिसे कलन कहते हैं। इसका उपयोग उन्होंने यह सिद्ध करने के लिए किया कि किसी एकसमान घनत्व वाले गोले के बाहर स्थित वस्तुओं के लिए गोले का व्यवहार इस प्रकार का होता है, जैसे कि उसका सम्पूर्ण द्रव्यमान उसके केन्द्र में स्थित हो।

प्रश्न 13. 
गुरुत्वाकर्षण का सार्वत्रिक नियम क्या है? लिखिए।
उंत्तर:
गुरुत्वाकर्षण का सार्वत्रिक नियम-विश्व का प्रत्येक पिण्ड प्रत्येक अन्य पिण्ड को एक बल से आकर्षित करता है, जो दोनों पिण्डों के द्रव्यमानों के गुणनफल के समानुपाती तथा उनके बीच की दूरी के वर्ग के व्युत्क्रमानुपाती होता है। यह बल दोनों पिण्डों को मिलाने वाली रेखा की दिशा में लगता है। यह नियम सार्वत्रिक इस अभिप्राय से है कि यह सभी वस्तुओं पर लागू होता है, चाहे वे वस्तुएँ छोटी हों या बड़ी, खगोलीय हों या पार्थिव।

प्रश्न 14. 
क्या कारण है कि किसी दिए हुए स्थान पर हम वस्तु के भार को उसके द्रव्यमान की माप के रूप में उपयोग कर सकते हैं?
उत्तर:
चूँकि किसी दिए हुए स्थान पर गुरुत्वीय त्वरण g का मान स्थिर रहता है, इसलिए किसी दिए हुए स्थान पर, वस्तु का भार, वस्तु के द्रव्यमान m के समानुपाती होता है, अर्थात् \(\mathrm{W} \propto m\)। इसी कारण किसी दिए हुए स्थान पर हम वस्तु के भार को उसके द्रव्यमान की माप के रूप में उपयोग कर सकते हैं। किसी वस्तु का द्रव्यमान प्रत्येक स्थान पर, चाहे पृथ्वी पर या किसी अन्य ग्रह पर उतना ही रहता है, जबकि वस्तु का भार इसके स्थान पर निर्भर करता है।

प्रश्न 15. 
आपेक्षिक घनत्व से क्या अभिप्राय है?
उत्तर:
आपेक्षिक घनत्व-किसी पदार्थ का आपेक्षिक घनत्व, उस पदार्थ का घनत्व एवं पानी के घनत्व का अनुपात होता है। अर्थात्

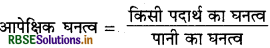
चूँकि आपेक्षिक घनत्व समान राशियों का एक अनुपात है, अतः इसका कोई मात्रक नहीं होता है।

प्रश्न 16. 
भारी वाहनों के पहियों के टायर काफी चौड़े क्यों बनाए जाते हैं?
उत्तर:
भारी वाहनों के पहियों के टायर काफी चौड़े बनाए जाते हैं क्योंक भारी वाहनों के टायर चौड़े होने से सड़क ( जमीन) पर इनके द्वारा लगने वाला दाब कम हो जाता है। चूँकि वाहन का भार अधिक क्षेत्रफल पर लगता है, इसलिए वाहन के पहिए जमीन में धंसने से बच जाते हैं।

प्रश्न 17. 
लोहे से बना जहाज समुद्र में तैरता रहता है। क्यों?
उत्तर:
लोहे के जहाज का ढाँचा अवतल होता है तथा वह अन्दर से खोखला बनाया जाता है। जैसे ही जहाज समुद्र में प्रवेश करता है, उसके द्वारा (उसकी बनावट के कारण) इतना जल हटा दिया जाता है कि उसके द्वारा हटाए गए जल का भार, जहाज (जहाज एवं उसके समस्त सामान सहित) के कुल भार के बराबर हो जाता है। इसी कारण प्लवन के सिद्धान्त के अनुसार लोहे का जहाज जल में डूबता नहीं है, वरन् तैरता रहता है।

प्रश्न 18. 
रेलगाड़ी की पटरियों के नीचे लकड़ी अथवा लोहे के चौड़े स्लीपर क्यों लगाए जाते हैं?
उत्तर:
रेलगाड़ी की पटरियों के नीचे चौड़े स्लीपर नहीं लगाने पर रेल की पटरियाँ अधिक दबाव के कारण जमीन में धँस सकती हैं। पटरियों के नीचे लकड़ी अथवा लोहे के चौड़े स्लीपर लगाने से क्षेत्रफल अधिक हो जाता है, जिस कारण रेलगाड़ी का दबाव पटरियों पर कम पड़ता है और रेल की पटरियाँ जमीन में नहीं धँसतीं।

प्रश्न 19. 
कुएं से पानी खींचते समय, पानी से भरी बाल्टी, कुएं के पानी से बाहर आती है, तो वह अधिक भारी क्यों लगती है?
उत्तर:
जब बाल्टी जल में डूबी होती है, तब उस पर उसके द्वारा हटाए गए जल के भार के बराबर उत्प्लावन बल लगता है। जैसे - जैसे बाल्टी जल से बाहर निकलती है, उस पर लगने वाले उत्प्लावन बल का मान भी कम होने लगता है, जिस कारण बाल्टी भारी लगने लगती है।

प्रश्न 20. 
जब हम ढीली रेत पर खड़े होते हैं, तो हमारे पैर रेत में गहरे धँस जाते हैं, परन्तु रेत पर लेटने पर हमारा शरीर अपेक्षाकृत कम धँसता है। क्यों ?
उत्तर:
चूँकि किसी वस्तु की सतह के लम्बवत् लगने वाला बल प्रणीद कहलाता है। अतः जब हम ढीली रेत पर खड़े होते हैं, तब बल अर्थात् हमारे शरीर का भार, हमारे पैरों के क्षेत्रफल के बराबर क्षेत्रफल पर लग रहा होता है। परन्तु जब हम रेत पर लेटते हैं, तब वही बल हमारे पूरे शरीर के सम्पर्क क्षेत्रफल के बराबर क्षेत्रफल पर लगता है, जो कि हमारे पैरों के क्षेत्रफल से अधिक है। चूँकि रेत पर प्रणोद का प्रभाव लेटे हुए की अपेक्षा खड़े होने की स्थिति में अधिक है। इसलिए खड़े होने पर हमारे पैर जमीन में धँस जाते हैं।

निबन्धात्मक प्रश्न:

प्रश्न 1. 
सिद्ध कीजिए कि गुरुत्व-त्वरण का मान वस्तु के द्रव्यमान के मान से स्वतन्त्र होता है।
उत्तर:
पृथ्वी तल पर m द्रव्यमान वाली एक वस्तु पर विचार करते हैं। माना M तथा R पृथ्वी का द्रव्यमान और त्रिज्या है।

वस्तु पर क्रिया कर रहा F गुरुत्व बल है।
तब 
\(\mathrm{F}=\mathrm{G} \frac{\mathrm{Mm}}{\mathrm{R}^{2}}\)
वस्तु का त्वरण IMM
या
\(=\frac{G \frac{M m}{R^{2}}}{m}\)

त्वरण = \(\mathbf{G} \frac{\mathrm{M}}{\mathrm{R}^{2}}\)
इसे ही गुरुत्व - त्वरण कहते हैं।
∴  \(g=G \frac{M}{R^{2}}\)

इस समीकरण में वस्तु का द्रव्यमान m शामिल नहीं है। इससे सिद्ध होता है कि गुरुत्व बल के कारण किसी वस्तु द्वारा प्राप्त गुरुत्वीय त्वरण इसके द्रव्यमान से स्वतन्त्र होता है। अतः हम कहते हैं कि सभी आकार और द्रव्यमान वाली वस्तुएँ किसी भी स्थान पर समान त्वरण से गिरती हैं।

प्रश्न 2.
जब किसी वस्तु को सीधे ऊपर फेंका जाता है तो उसके द्वारा प्राप्त अधिकतम ऊँचाई ज्ञात करने के लिए समीकरण लिखिए।
उत्तर:
अधिकतम ऊँचाई के लिए व्यंजक: जब किसी वस्तु को आरम्भिक वेग u से ऊपर फेंका जाता है, तो वह अधिकतम ऊँचाई पर जाकर थोड़े समय के लिए रुक जाती है और उसी समय नीचे गिरना प्रारम्भ करती है। यहाँ पर वस्तु का अन्तिम वेग v शून्य हो जाता है। यहाँ पर गुरुत्व वेग g ऋणात्मक होगा। यदि अधिकतम ऊँचाई h हो तो गति के तीसरे नियम से

\(\begin{aligned} v^{2} &=u^{2}+2 g h \text { } \\ (0)^{2} &=(u)^{2}+2(-g) \times h \\ 0 &=u^{2}-2 g h \\ u^{2} &=2 g h \end{aligned}\)

∴  \(h=\frac{u^{2}}{2 g}\)

प्रश्न 3. 
सिद्ध कीजिए कि गिरने का समय और ऊपर जाने का समय समान होता है? 
उत्तर:
जब वस्तु नीचे से ऊपर जाती है:
अन्तिम वेग v = 0
त्वरण a = -g 
तब समीकरण v = u + at से
0 = u - gt.
\(t=\frac{u}{g}\)
जब वस्तु अधिकतम ऊँचाई से नीचे गिरती है, तब वापस आने में लगा समय
आरम्भिक वेग u = 0
और ऊँचाई = \(h=\frac{u^{2}}{2 g}\) ..............(1)
\(\mathrm{h}=\mathrm{ut}+\frac{\mathrm{l}}{2} \mathrm{gt}^{2} \text { }\)
\(h=0+\frac{1}{2} g t^{2}=\frac{1}{2} g t^{2}\)  ................(2)
 समीकरण (1) तथा (2) को बराबर करने पर
\(\frac{u^{2}}{2 g}=\frac{1}{2} g t^{2}\)
अत: जाने का समय और वापस आने का समय बराबर होता है।
   \(t^{2}=\frac{u^{2}}{g^{2}}\)
\(t=\sqrt{\frac{u^{2}}{g^{2}}}=\frac{u}{g}\)
\(\mathrm{t}=\frac{\mathrm{u}}{\mathrm{g}}\)

प्रश्न 4.
गुरुत्वीय त्वरण 'g' का मान पृथ्वी के माध्य घनत्व व त्रिज्या पर किस प्रकार निर्भर करता है? सूत्र द्वारा बताइये।
उत्तर:
हल - गुरुत्वीय त्वरण पृथ्वी की सतह या उसके पास स्थित वस्तुओं के लिये
\(g=G \frac{M}{R^{2}}\)    ................(1)
लेकिन पृथ्वी का द्रव्यमान = पृथ्वी का आयतन x घनत्व
\(M=\frac{4}{3} \pi R^{3} \times d\)
\(M=\frac{4}{3} \pi R^{3} d\)  ..............(2)
समीकरण (1) से M का मान समीकरण (2) में रखने पर
\(g=\frac{G \times \frac{4}{3} \pi R^{3} d}{R^{2}}\)
\(g=\frac{4}{3} \pi \mathrm{GR} \mathrm{d}\)
यहाँ पर \(\frac{4}{3} \pi \mathrm{G}\) का मान नियत प्राप्त होता है। अतः g का मान माध्य घनत्व व पृथ्वी की त्रिज्या के समानुपाती होता है।

प्रश्न 5.
किसी ग्रह पर गुरुत्वीय त्वरण का मान ज्ञात करने के लिए सूत्र की स्थापना कीजिए।
उत्तर:
हल - हम जानते हैं कि पृथ्वी का द्रव्यमान M. गुरुत्वीय नियतांक G व पृथ्वी की त्रिज्या R. में निम्न सम्बन्ध है
\(\mathrm{g}_{\mathrm{e}}=\mathrm{G} \frac{\mathrm{M}_{\mathrm{e}}}{\mathrm{R}_{\mathrm{e}}^{2}}\)  ..............(1)
यदि किसी ग्रह (प्लेनेट) पर गुरुत्वीय त्वरण का मान g_p है, ग्रह का द्रव्यमान M_p है और उसकी त्रिज्या R_p है तो
\(g_{p}=G \frac{M_{p}}{R_{p}^{2}}\)    ..................(2)
समीकरण (1) व (2) से
\(\frac{\mathrm{g}_{\mathrm{p}}}{\mathrm{g}_{\mathrm{e}}}=\frac{\mathrm{GM}_{\mathrm{p}}}{\mathrm{R}_{\mathrm{p}}^{2}} \times \frac{\mathrm{R}_{\mathrm{e}}^{2}}{\mathrm{GM}_{\mathrm{e}}}\)
या  \(\frac{g_{p}}{g_{e}}=\frac{M_{p}}{M_{e}} \times\left(\frac{R_{e}}{R_{p}}\right)^{2}\) .............(3)
समीकरण (3) की सहायता से गुरुत्वीय त्वरण का मान किसी भी ग्रह पर ज्ञात किया जा सकता है।

प्रश्न 6.
एक ग्रह की त्रिज्या और द्रव्यमान दोनों ही पृथ्वी की त्रिज्या और द्रव्यमान के आधे हैं तो ग्रह पर गुरुत्वीय त्वरण का मान पृथ्वी की तुलना में कितना होगा?
उत्तर:
हल - पृथ्वी का द्रव्यमान = Me
तब ग्रह का द्रव्यमान  \(\mathbf{M}_{\mathrm{p}}=\frac{\mathrm{M}_{\mathrm{e}}}{2}\)
पृथ्वी की त्रिज्या = Re
तब ग्रह की त्रिज्या \(\mathrm{R}_{\mathrm{p}}=\frac{\mathrm{R}_{\mathrm{e}}}{2}\)
ग्रह पर गुरुत्वीय त्वरण g_p ज्ञात करना है।
 ∴   \(\frac{g_{p}}{g_{e}}=\left(\frac{M_{p}}{M_{e}}\right) \times\left(\frac{R_{e}}{R_{p}}\right)^{2}\)
 या   \(\frac{g_{p}}{g_{e}}=\left(\frac{M_{e}}{2 M_{e}}\right) \times\left(\frac{2 R_{e}}{R_{e}}\right)^{2}\)
  या    \(\frac{g_{p}}{g_{e}}=\frac{1}{2} \times \frac{4}{1}=2\)
या g_p = 2 ge
अतः ग्रह पर गुरुत्वीय त्वरण का मान पृथ्वी के गुरुत्वीय त्वरण से दुगना होगा। इस प्रकार पृथ्वी पर 1.5 मीटर की छलांग लगाने वाला व्यक्ति इस ग्रह पर 0.75 मीटर की छलांग ही लगा पाएगा क्योंकि g_p = 2g_e है।

प्रश्न 7.
पृथ्वी के आकार के कारण g के मान में परिवर्तन को समझाइए।
उत्तर:
वस्तुतः पृथ्वी ध्रुवों पर चपटी होती है अर्थात् पृथ्वी की विषुवतीय त्रिज्या (Re) अधिक तथा ध्रुवीय । त्रिज्या (Rp) कम होती है।
उत्तरी ध्रुव 
 ∴  गुरुत्वीय त्वरण  \(g=\mathrm{G} \frac{\mathrm{M}}{\mathrm{R}^{2}}\) ...............(1)
एवं ध्रुवों पर g का मान  \(g_{p}=\mathrm{G} \frac{\mathbf{M}}{\mathbf{R}_{\mathbf{p}}^{2}}\)   .............(2)
तथा भूमध्य रेखा पर g का मान  \(g_{e}=\mathbf{G} \frac{\mathbf{M}}{\mathbf{R}_{\mathrm{e}}^{2}}\) .............(3)

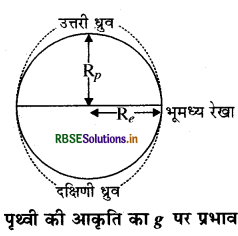
\(\mathbf{R}_{p}<\mathbf{R}_{e}\) 
इसलिए  \(g_{p}>g_{e}\)
अतः पृथ्वी की त्रिज्या ध्रुवों से विषुवत रेखा की ओर जाने पर बढ़ती है, इसलिए ध्रुवों पर g का मान अधिक होता है।

प्रश्न 8.
न्यूटन के गुरुत्वाकर्षण के नियम को समझाइये। आवश्यक चित्र बनाकर गुरुत्वीय जनित त्वरण g, गुरुत्वाकर्षण स्थिरांक G, पृथ्वी के द्रव्यमान M_e और पृथ्वी की त्रिज्या R_e में सम्बन्ध ज्ञात कीजिये। 'g' का मान पृथ्वी पर कैसे परिवर्तित होता है? .
उत्तर:
न्यूटन ने पृथ्वी के गुरुत्वाकर्षण के नियम का प्रतिपादन किया था। इस नियम के अनुसार "दो कणों के मध्य एक बल कार्य करता है जिसे गुरुत्वाकर्षण बल कहते हैं।" इस बल को न्यूटन ने निम्न प्रकार समझाया

ब्रह्माण्ड में प्रत्येक कण, दूसरे कण को अपनी ओर आकर्षित करता है। यह आकर्षण बल दोनों कणों के द्रव्यमान के गुणनफल के समानुपाती होता है और उनके मध्य की दूरी के वर्ग के व्युत्क्रमानुपाती होता है।
यह आकर्षण बल दोनों कणों को जोड़ने वाली रेखा की दिशा की ओर होता है। माना दो वस्तुओं (कणों) का द्रव्यमान क्रमशः m₁ और m₂ हैं और उनके मध्य दूरी R है। उन दोनों वस्तुओं के मध्य लगने वाला गुरुत्वाकर्षण बल वस्तुओं के मध्य F न्यूटन के नियमानुसार:

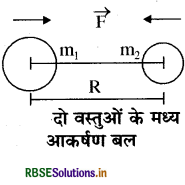
आकर्षण बल Fα m₁m₂ ............(1)
और
\(\mathrm{F} \propto \frac{1}{\mathrm{R}^{2}}\)   ......(2)
(1) और (2) को एक साथ लिखने पर
\(\mathrm{F} \propto \frac{\mathrm{m}_{1} \mathrm{~m}_{2}}{\mathrm{R}^{2}}\)
या   \(F=G \frac{m_{1} m_{2}}{R^{2}}\)
यहाँ G एक समानुपाती स्थिरांक है जिसको गुरुत्वाकर्षण नियतांक कहते हैं। इसका मान 6.67 x 10^-11 न्यूटन मी./ किग्रा. होता है।
गुरुत्वीय त्वरण g_e स्थिरांक G, पृथ्वी का द्रव्यमान M_e और पृथ्वी की त्रिज्या R_e में सम्बन्ध:
M द्रव्यमान की पृथ्वी के केन्द्र से R दूरी पर स्थित m द्रव्यमान की वस्तु पर पृथ्वी द्वारा लगने वाले बल का मान होगा
\(\mathrm{F}=\mathrm{G} \frac{\mathrm{Mm}}{\mathrm{R}^{2}}\) ............(1)
यदि गुरुत्वीय त्वरण का मान g है तो m द्रव्यमान वाली वस्तु पर लगने वाला गुरुत्वीय बल F का मान होगा
F= mg  ............(2)
समीकरण (1) व (2) से
\(\begin{aligned} m g &=G \frac{M I}{R^{2}} \\ \end{aligned}\)
\(g=G \frac{M}{R^{2}}\) ..........(3)
समीकरण (3) से स्पष्ट है कि
स्वतन्त्रतापूर्वक गिरती हुई वस्तु के गुरुत्वीय त्वरण का मान वस्तु के द्रव्यमान पर निर्भर नहीं करता है। यह केवल पृथ्वी के द्रव्यमान व पृथ्वी के केन्द्र से वस्तु की दूरी पर निर्भर करता है। यदि पृथ्वी के धरातल पर गुरुत्वीय त्वरण का मान g_e है, पृथ्वी का द्रव्यमान M_e है और पृथ्वी की त्रिज्या R. है तो समीकरण (3) से
\(\mathrm{g}_{\mathrm{e}}=\mathrm{G} \frac{\mathrm{M}_{\mathrm{e}}}{\mathrm{R}_{\mathrm{e}}^{2}}\)
g का मान ऊँचाई पर जाते समय घटता है। g का मान पृथ्वी के भीतर (गहराई पर) जाने पर भी घटता है।g का मान पृथ्वी तल पर अधिकतम होता है।

प्रश्न 9.
पृथ्वी का द्रव्यमान चन्द्रमा से 81 गुना है तथा व्यास चन्द्रमा के व्यास का 3.6 गुना है। पृथ्वी तथा चन्द्रमा के गुरुत्वीय त्वरणों की तुलना करिये।
उत्तर:
हल - यदि पृथ्वी का द्रव्यमान M_e गुरुत्वीय नियतांक G व पृथ्वी की त्रिज्या R_e हो, तो

पृथ्वी का गुरुत्वीय त्वरण \(\mathrm{g}_{\mathrm{e}}=\mathrm{G} \frac{\mathrm{M}_{\mathrm{e}}}{\mathrm{R}_{\mathrm{e}}^{2}}\)  ...........(1)
 यदि चन्द्रमा पर गुरुत्वीय त्वरण का मान g_m है, चन्द्रमा का द्रव्यमान M_m है और उसकी त्रिज्या R_m हो

चन्द्रमा का गुरुत्वीय त्वरण \(g_{m}=G \frac{M_{m}}{R_{m}^{2}}\) ..........(2)
समीकरण (1) में समी (2) का भाग
\(\frac{\mathrm{g}_{\mathrm{e}}}{\mathrm{g}_{\mathrm{m}}}=\frac{\mathrm{GM}_{\mathrm{e}}}{\mathrm{R}_{\mathrm{e}}^{2}} \times \frac{\mathrm{R}_{\mathrm{m}}^{2}}{\mathrm{GM}}\)
 ∴    \(\frac{g_{\mathrm{c}}}{g_{m}}=\left(\frac{M_{e}}{M_{m}}\right) \times\left(\frac{R_{m}}{R_{c}}\right)^{2}\)
लेकिन दिया गया है
\(\begin{aligned} &M e=81 \mathrm{M}_{\mathrm{m}} \\ &\mathrm{Re}=3.6 \mathrm{Rm} \end{aligned}\)
मान रखने पर
  ∴   \(\frac{g_{e}}{g_{m}}=81 \times\left(\frac{1}{3.6}\right)^{2}\)
\(\begin{aligned} &\frac{g_{\mathrm{c}}}{g_{\mathrm{m}}}=\frac{81}{3.6 \times 3.6} \times \frac{81 \times 100}{36 \times 36} \\ &\frac{g_{\mathrm{e}}}{g_{\mathrm{m}}}=\frac{100}{4 \times 4}=\frac{25}{4} \end{aligned}\)
अतः पृथ्वी तथा चन्द्रमा के गुरुत्वीय त्वरणों का अनुपात 25/4 होगा।

प्रश्न 10.
सिद्ध कीजिए किसी वस्तु का चन्द्रमा पर भार, उस वस्तु का पृथ्वी पर \(\frac{1}{6}\) भार के बराबर होता है।
उत्तर:
किसी वस्तु का चन्द्रमा पर भार: पृथ्वी पर किसी वस्तु का भार वह बल है, जिससे पृथ्वी उस वस्तु को अपनी ओर आकर्षित करती है। इसी प्रकार से चन्द्रमा पर किसी वस्तु का भार वह बल है, जिससे चन्द्रमा उस वस्तु को अपनी ओर आकर्षित करता है। चन्द्रमा का द्रव्यमान पृथ्वी की अपेक्षा बहुत कम होता है। यही कारण है कि चन्द्रमा वस्तुओं पर कम आकर्षण बल लगाता है।
माना किसी वस्तु का द्रव्यमान m है तथा चन्द्रमा पर इसका भार W_m है और यह भी माना कि चन्द्रमा का द्रव्यमान M_n है तथा इसकी त्रिज्या R_m है।
गुरुत्वाकर्षण के सार्वत्रिक नियम से
चन्द्रमा पर वस्तु का भार होगा
\(\mathrm{W}_{\mathrm{m}}=\mathrm{G} \frac{\mathrm{M}_{\mathrm{m}} \times \mathrm{m}}{\mathrm{R}_{\mathrm{m}}^{2}}\) ...............(1)
माना उसी वस्तु का पृथ्वी पर भार W_e है और पृथ्वी का द्रव्यमान M तथा इसकी त्रिज्या R है।
 तब पृथ्वी पर उस वस्तु का भार
\(\mathrm{W}_{\mathrm{e}}=\mathrm{G} \frac{\mathrm{M} \times \mathrm{m}}{\mathrm{R}^{2}}\) ................(2)
यहाँ पर पृथ्वी का द्रव्यमान = 5.98 x 10²⁴ और त्रिज्या R = 6.37 x 10⁶ तथा चन्द्रमा का द्रव्यमान = 7.36 x 10²² और त्रिज्या R = 1.74 x 10⁶ है, तो समीकरण (1) तथा (2) से
\(\begin{aligned} \frac{W_{\mathrm{m}}}{\mathrm{W}_{\mathrm{e}}} &=\mathrm{G} \frac{\mathrm{M}_{\mathrm{m}} \times \mathrm{m}}{\mathrm{R}_{\mathrm{m}}^{2}} \times \frac{\mathrm{R}^{2}}{\mathrm{G} \times \mathrm{M} \times \mathrm{m}} \\ \frac{\mathrm{W}_{\mathrm{m}}}{\mathrm{W}_{\mathrm{e}}} &=\left(\frac{\mathrm{R}}{\mathrm{R}_{\mathrm{m}}}\right)^{2} \times\left(\frac{\mathrm{M}_{\mathrm{m}}}{\mathrm{M}}\right) \\ &=\left(\frac{6.37 \times 10^{6}}{1.74 \times 10^{6}}\right)^{2} \times\left(\frac{7.36 \times 10^{22}}{5.98 \times 10^{24}}\right) \\ &=\frac{6.37 \times 6.37}{1.74 \times 1.74} \times \frac{7.36}{598}=0.165=\frac{1}{6} \end{aligned}\)


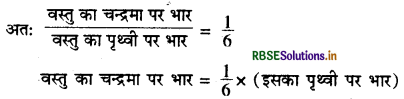
आंकिक प्रश्न:

प्रश्न 1. 
पृथ्वी का द्रव्यमान 6 x 10²⁴ kg है तथा चन्द्रमा का द्रव्यमान 7.4 x 10²² kg है। यदि पृथ्वी तथा चन्द्रमा के बीच की दूरी 3.84 x 10 km है तो पृथ्वी द्वारा चन्द्रमा पर लगाये गये बल का परिकलन कीजिए।
G = 6.7 x 10^-11 Nm-kg²
उत्तर:
हल - पृथ्वी का द्रव्मयान M_e = 6 x 10²⁴ kg
चन्द्रमा का द्रव्यमान m = 7.4 x 10²² kg
पृथ्वी तथा चन्द्रमा के बीच की दूरी
d या R = 3.84 x 10⁵ km
= 3.84 x 10⁵ x 10³m 
= 33.84 x 10⁸ m
G = 6.7 x 10¹¹ Nm-kg-2
पृथ्वी द्वारा चन्द्रमा पर लगाया गया बल निम्न सूत्र से ज्ञात करेंगे
\(F=G \frac{M_{e} m}{R^{2}}\)

मान रखने पर
\(\begin{aligned} &=\frac{6.7 \times 10^{-11} \times 6 \times 10^{24} \times 7.4 \times 10^{22}}{\left(3.84 \times 10^{8}\right)^{2}} \\ &=\frac{6.7 \times 6 \times 7.4 \times 10^{24+22-11}}{3.84 \times 3.84 \times 10^{16}} \\ &=\frac{6.7 \times 6 \times 7.4 \times 10^{35}}{3.84 \times 3.84 \times 10^{16}} \end{aligned}\)

\(\begin{aligned} &=\frac{6.7 \times 6 \times 7.4 \times 10^{35-16}}{3.84 \times 3.84} \\ &=\frac{6.7 \times 6 \times 7.4 \times 10^{19}}{3.84 \times 3.84}=20.17 \times 10^{19} \end{aligned}\)
या \(=2.017 \times 10^{20} \mathrm{~N}\)
अत: पृथ्वी द्वारा चन्द्रमा पर लगाया गया बल
= 2.017 x 10²⁰ N है।

प्रश्न 2. एक कार किसी कगार से गिरकर 0.5 s में धरती पर आ गिरती है। परिकलन में सरलता के लिए g का मान 10 m/s² लीजिए।
(i) धरती पर टकराते समय कार की चाल क्या होगी?
(ii) 0.5 s के दौरान इसकी औसत चाल क्या होगी?
(iii) धरती से कगार कितनी ऊँचाई पर है?
उत्तर:
हल - दिया गया है।
समय t = 0.5s
प्रारम्भिक वेग u = 0 m/s
गुरुत्वीय त्वरण g = 10 m/s²
कार का त्वरण a = + 10 m/s² (अधोमुखी)
(i) कार की चाल
v = u + at 
= 0 + 10 x 0.5
v = 5 m/s
अत: धरती पर टकराते समय कार की चाल होगी = 5 मीटर / सेकण्ड
प्रारम्भिक वेग + अन्तिम वेग

(ii) औसत चाल

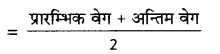
\(=\frac{0+5}{2}=2.5 \mathrm{~m} / \mathrm{s}\)
अत: 0.5 s के दौरान कार की औसत चाल होगी = 2.5 मीटर / सेकण्ड

(iii) तय की गई दूरी
\(s=u t+\frac{1}{2} a t^{2}\)
\(\begin{aligned} &=0 \times 0.5+\frac{1}{2} \times 10 \times(0.5)^{2} \\ &=0+5 \times 0.25=1.25 \mathrm{~m} \end{aligned}\)
अतः धरती से कगार की ऊँचाई h = 1.25 m

(i) धरती पर टकराते समय इसकी चाल = 5 ms^-1

(ii) 0.5 सेकण्ड के दौरान इसकी औसत चाल = 2.5 ms^-1
(iii) धरती से कगार की ऊँचाई = 1.25 m

प्रश्न 3.
एक वस्तु को ऊर्ध्वाधर दिशा में ऊपर की ओर फेंका जाता है और यह 10 m की ऊँचाई तक पहुँचती है। परिकलन कीजिए
(i) वस्तु कितने वेग से ऊपर फेंकी गई तथा
(ii) वस्तु द्वारा उच्चतम बिन्दु तक पहुँचने में लिया गया समय।
उत्तर:
हल - दिया गया है।
तय की गई ऊँचाई h = 10 m
वस्तु का प्रारम्भिक वेग u = ?
उच्चतम ऊँचाई पर वस्तु का अन्तिम वेग v = 0 m/s
गुरुत्वीय त्वरण g = 9.8 m/s²
वस्तु का त्वरण a = - 9.8 m/s² (ऊर्ध्वमुखी)
गति के तीसरे समीकरण से
\(v^{2}=u^{2}+2 g h\) से
चूँकि वस्तु नीचे से ऊपर की ओर फेंकी गई है, अतः g का मान ऋणात्मक होगा।
\(\begin{aligned} 0 &=u^{2}+2 \times(-9.8) \times 10 \\ 0 &=u^{2}-196 \\ u^{2} &=196 \\ u &=\sqrt{196}=14 \mathrm{~m} / \mathrm{s} \text { } \end{aligned}\)
गति के प्रथम समीकरण से
\(\begin{aligned} 0 &=14+(-9.8) \mathrm{t} \\ 9.8 \mathrm{t} &=14 \\ \mathrm{t} &=\frac{14}{9.8}=\frac{140}{98} \\ \mathrm{t} &=1.43 \mathrm{~s} \end{aligned}\)
अत: (i) वस्तु का प्रारम्भिक वेग u = 14 m/s
(ii) लिया गया समय t = 1.43 s

प्रश्न 4.
एक वस्तु का द्रव्यमान 10 kg है। पृथ्वी पर इसका भार कितना होगा?
उत्तर:
हल - दिया गया है।
वस्तु का द्रव्यमान (m) = 10 kg
गुरुत्वीय त्वरण (g) = 9.8 m/s²
पृथ्वी पर वस्तु का भार (W) = mg
= 10 kg x 9.8 = 98 N
अतः वस्तु का भार 98 N है।

प्रश्न 5.
एक वस्तु का भार पृथ्वी के पृष्ठ पर मापने पर 10 N आता है। इसका भार चन्द्रमा की सतह पर मापने पर कितना होगा?
उत्तर:
हल - हम जानते हैं कि चन्द्रमा पर किसी वस्तु का भार = \(\frac{1}{6}\) x (पृथ्वी पर इसका भार)
अर्थात्
\(\begin{aligned} \mathbf{W}_{\mathrm{m}} &=\frac{1}{6} \times \mathrm{W}_{\mathrm{e}} \\ &=\frac{1}{6} \times 10=\frac{10}{6}=\frac{5}{3}=1.67 \mathrm{~N} \end{aligned}\)
अतः चन्द्रमा पर वस्तु का भार 1.67 N होगा।

प्रश्न 6.
एक लकड़ी का गुटका मेज पर रखा है। लकड़ी के गुटके का द्रव्यमान 5 Kg है तथा इसकी विमायें 40 cm x 20 cm x 10 cm हैं। लकड़ी के टुकड़े द्वारा मेज पर लगने वाले दाब को ज्ञात कीजिए, यदि इसकी निम्नलिखित विमाओं की सतह मेज पर रखी जाती है
(a) 20 cm x 10 cm (b) 40 cm x 20 cm

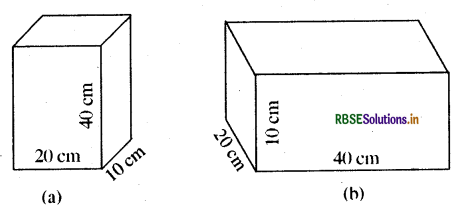
उत्तर:
हल - (a) दिया गया है
लकड़ी के गुटके का द्रव्यमान m= 5 kg
g= 9.8 m/s
यहाँ लकड़ी के गुटके का भार मेज की सतह पर प्रणोद लगाता है। अर्थात्
प्रणोद F = m xg
= 5 x 9.8
= 49 N
सतह का क्षेत्रफल A = लम्बाई x चौड़ाई
= 20 cm x 10 cm
= 200 cm²
जब cm² को m² में बदलते हैं तब 10000 से भाग देते हैं।
 ∴  \(=\frac{200}{10 00}=0.02 \mathrm{~m}^{2}\)
100NO = 0.02 m2
∵ दाब \(\mathbf{P}=\frac{\mathbf{F}}{\mathbf{A}}\)
49N_49x100
दाब
\(\begin{aligned} P &=\frac{49 \mathrm{~N}}{0.02}=\frac{49 \times 100}{2} \\ &=49 \times 50 \mathrm{~N} / \mathrm{m}^{2} \\ &=2450 \mathrm{~N} / \mathrm{m}^{2} \text { } \end{aligned}\)

(b) जब गुटके की 40 cm x 20 cm विमाओं की सतह मेज पर रखी जाती है। यह मेज की सतह पर पहले जितना ही प्रणोद लगाता है।
क्षेत्रफल (A) = लम्बाई x चौड़ाई
= 40 cm x 20 cm
= 800 cm²
\(=\frac{800}{100 \times 100} \mathrm{m}^{2}=0.08 \mathrm{~m}^{2}\)
दाब

\(\begin{aligned} &=\frac{p}{A}=\frac{49 \mathrm{~N}}{0.08 \mathrm{~m}^{2}} \\ &=612.5 \mathrm{~N} / \mathrm{m}^{2} \end{aligned}\)

 अतः सतह 20 cm x 10 cm द्वारा लगाया गया दाब 2450 N/m² है तथा सतह 40 cm x 20 cm द्वारा लगाया गया दाब 612.5 Nm² है।

प्रश्न 7.
चाँदी का आपेक्षिक घनत्व 10.8 है। पानी का घनत्व 10 kg/m² है। SI मात्रक में चाँदी का घनत्व क्या होगा?
उत्तर:

प्रश्न 8. सिद्ध कीजिए कि पृथ्वी के केन्द्र से समान दूरी पर रखी दो वस्तुओं A एवं B को पृथ्वी यदि समान बल से आकर्षित करती है तो दोनों वस्तुओं के द्रव्यमान बराबर होंगे।
उत्तर:
हल - माना पहली वस्तु A का द्रव्यमान = m₁
और दूसरी वस्तु B का द्रव्यमान = m₂ तो
वस्तु A तथा पृथ्वी के बीच लगने वाला आकर्षण बल
\(F_{1}=G \frac{M_{e} \times m_{1}}{R^{2}}\)
 जहाँ पर R, पृथ्वी के केन्द्र से वस्तु A की दूरी। पुन: वस्तु B तथा पृथ्वी के बीच लगने वाला आकर्षण बल
\(\mathrm{F}_{2}=\mathrm{G} \frac{\mathrm{M}_{\mathrm{e}} \times \mathrm{m}_{2}}{\mathrm{R}^{2}}\)
या
चूँकि दोनों बल F₁ तथा F₂ बराबर हैं।
अतः
\(\begin{aligned} G \frac{M_{e} \times m_{1}}{R^{2}} &=G \frac{M_{e} \times m_{2}}{R^{2}} \\ m_{1} &=m_{2} \end{aligned}\)
अत: समान बल से आकर्षित वस्तुओं का द्रव्यमान बराबर होता है।

प्रश्न 9.
g तथा G के बीच सम्बन्ध का उपयोग करते हुए गुरुत्वीय त्वरण g का मान ज्ञात कीजिए।
उत्तर:
हल - गुरुत्वीय त्वरण g के मान का परिकलन
चूँकि गुरुत्वीय त्वरण g = \(\mathrm{G} \frac{\mathrm{M}_{\mathrm{e}}}{\mathrm{R}_{\mathrm{e}}^{2}}\)
यहाँ पर गुरुत्वीय स्थिरांक G = 6.7 x 10^-11 Nm²/kg²
पृथ्वी का द्रव्यमान M. = 6 x 10²⁴ kg
पृथ्वी की त्रिज्या R. = 6.4 x 10⁶ m
इसलिए \(g=G \frac{M_{e}}{R_{e}^{2}}\) में मान रखने पर
\(\begin{aligned} g &=\frac{6.7 \times 10^{-11} \times 6 \times 10^{24}}{\left(6.4 \times 10^{6}\right)^{2}} \\ &=\frac{6.7 \times 6 \times 10^{-11+24}}{6.4 \times 6.4 \times 10^{12}} \\ &=\frac{6.7 \times 6 \times 10^{13-12}}{6.4 \times 6.4}=\frac{67 \times 6}{40.96} \\ &=\frac{402}{40.96}=9.81 \mathrm{~m} / \mathrm{s}^{2} \end{aligned}\)
अतः \(\mathrm{g}=9.8 \mathrm{~m} / \mathrm{s}^{2}\)
अतः पृथ्वी के गुरुत्वीय त्वरण का मान g = 9.8 m/s²

प्रश्न 10.
चन्द्रमा की सतह पर गुरुत्वीय त्वरण के मूल्य की गणना कीजिए। दिया गया है - चन्द्रमा का द्रव्यमान = 7.4 x 10²² Kg चन्द्रमा की त्रिज्या = 1740 km,
G = 6.7 x 10^-11 Nm² / kg²
उत्तर:
हल - गुरुत्वीय त्वरण g = GM
यहाँ पर,
G = 6.7 x 10^-11 Nm- / kg²
\(\begin{aligned} \mathrm{M} &=7.4 \times 10^{22} \mathrm{~kg} \\ \mathrm{R} &=1740 \mathrm{~km}=1740 \times 10^{3} \mathrm{~m} \\ &=1.74 \times 10^{6} \mathrm{~m} \end{aligned}\)
अब उपर्युक्त सूत्र में G, M और R के इन मानों को रखने पर
\(\begin{aligned} g &=\frac{6.7 \times 10^{-11} \times 7.4 \times 10^{22}}{\left(1.74 \times 10^{6}\right)^{2}} \\ &=\frac{6.7 \times 7.4 \times 10^{22-11}}{1.74 \times 1.74 \times 10^{12}} \\ &=\frac{6.7 \times 7.4 \times 10^{11}}{1.74 \times 1.74 \times 10^{12}} \\ &=\frac{6.7 \times 7.4}{1.74 \times 1.74 \times 10}=\frac{49.58}{30.28} \\ &=1.64 \mathrm{~m} / \mathrm{s}^{2} \end{aligned}\)
अतः चन्द्रमा की सतह पर गुरुत्वीय त्वरण g = 1.64 m/s² है।

प्रश्न 11.
नदी के ऊपर पुल की ऊँचाई ज्ञात करने के लिए पुल से एक पत्थर को नदी में स्वतन्त्र रूप से गिराया जाता है। नदी में जल की सतह को छूने में पत्थर 2 सेकण्ड लेता है। जल - स्तर से पुल की ऊँचाई की गणना कीजिए
g = 9.8 m/s²
उत्तर:
हल - पत्थर को नदी में स्वतन्त्र रूप से गिराया जाता है। इसलिए पत्थर का प्रारम्भिक वेग
u = 0
लिया गया समय (t) = 2 s
गुरुत्वीय त्वरण g = - 9.8 m/s²
पुल की ऊँचाई (h) = ?
मुक्त पतन पिण्ड के लिए
ऊँचाई \((h)=u t+\frac{1}{2} g t^{2}\)
मान रखने पर
\(\begin{aligned} &h=0 \times 2+\frac{1}{2} \times(-9.8) \times(2)^{2} \\ &h=0-4.9 \times 4=0-19.6 \\ &h=-19.6 \mathrm{~m} \end{aligned}\)
 अतः जलस्तर के ऊपर पुल की ऊँचाई – 19.6 मीटर है। ऊँचाई के साथ ऋणात्मक चिह्न दर्शाता है कि वह अधोमुखी दिशा में है।

प्रश्न 12.
एक गेंद को 15 m/s की चाल से ऊपर फेंका जाता है। वह गिरना आरम्भ करने से पहले कितनी ऊँचाई तक जायेगा?
उत्तर:
हल - दिया गया है।
गेंद की प्रारम्भिक चाल u = 15 m/s
गेंद की अन्तिम चाल v = 0 m/s
यहाँ पर गेंद रुक जाती है। गुरुत्वीय त्वरण g = - 9.8 m/s²
ऊँचाई h = ?
गति के तीसरे समीरण से,
\(v^{2}=u^{2}+2 g h\)
मान रखने पर
\(\begin{aligned} (0)^{2} &=(15)^{2}+2 \times(-9.8) \times h \\ 0 &=225-19.6 \mathrm{~h} \\ 19.6 \mathrm{~h} &=225 \\ \mathrm{~h} &=\frac{225}{19.6} \\ \mathrm{~h} &=11.48 \mathrm{~m} \end{aligned}\)

 अत: गेंद उसके गिरना आरम्भ होने से पहले 11.48 मीटर की अधिकतम ऊँचाई तक जाएगी।

प्रश्न 13.
एक आदमी का पृथ्वी पर भार 500 N है। उसका द्रव्यमान क्या है ? (g = 10 m/s² लें) यदि उसे चन्द्रमा पर ले जाया जाये, उसका भार 100 N होगा। चन्द्रमा पर उसका द्रव्यमान क्या है ? चन्द्रमा पर गुरुत्वीय त्वरण क्या है?
उत्तर:
हल - (i) दिया गया है- पृथ्वी पर मनुष्य का भार, W = 500 - N
पृथ्वी पर मनुष्य का द्रव्यमान m = ?
और गुरुत्वीय त्वरण पृथ्वी पर g = 10 m/sहम जानते हैं
∵ W = mg
\(\begin{aligned} \therefore \quad \mathrm{m} &=\frac{\mathrm{W}}{\mathrm{g}} \\ &=\frac{500}{10}=50 \mathrm{~kg} \end{aligned}\)
अत: पृथ्वी पर मनुष्य का द्रव्यमान 50 kg है।
चूँकि किसी पिण्ड का द्रव्यमान प्रत्येक स्थान पर समान रहता है। इसलिए इस आदमी का द्रव्यमान चन्द्रमा पर भी 50 kg होगा।

(ii) चन्द्रमा पर गुरुत्वीय त्वरण:
∵ W = m xg
चन्द्रमा पर मनुष्य का भार W = 100 N
चन्द्रमा पर मनुष्य का द्रव्यमान m = 50 kg
गुरुत्वीय त्वरण (चन्द्रमा पर) g = ?
मानं रखने पर
100 = 50 xg
\(g=\frac{100}{50}=2 \mathrm{~m} / \mathrm{s}^{2}\) 
अतः चन्द्रमा की सतह पर गुरुत्वीय त्वरण 2 m/s² है।

प्रश्न 14.
60 kg के मनुष्य का चन्द्रमा के ऊपर कितना भार होगा? पृथ्वी पर तथा चन्द्रमा पर उसका द्रव्यमान क्या होगा? (चन्द्रमा पर गुरुत्वीय त्वरण = 1.63 m/s²)
उत्तर:
हल - दिया गया है।
चन्द्रमा पर मनुष्य का द्रव्यमान = 60 kg
गुरुत्वीय त्वरण = 1.63 m/s²)

\(\begin{aligned} \mathbf{ W} &=\mathrm{m} \times \mathbf{g} \\ \mathbf{W} &=60 \times 1.63 \\ &=97.80 \mathbf{N} \end{aligned}\)

प्रश्न 15. 
पृथ्वी का द्रव्यमान चन्द्रमा का 80 गुना है। पृथ्वा का त्रज्या चन्द्रमा स चार गुना है याद पृथ्वा
पर \(\mathrm{g}\) का मान 9.8 मी. / स.² है तो चन्द्रमा पर g का मान क्या होगा?
उत्तर:
माना कि चन्द्रमा का द्रव्यमान = M और त्रिज्या = R
दिया गया है
पृथ्वी का द्रव्यमान = 80M
और पृथ्वी की त्रिज्या = 4R
अत: \(\cdot \mathrm{g}_{\mathrm{m}}\) (चन्द्रमा के तल पर गु. बल) \(=\mathrm{G} \frac{\mathrm{M}}{\mathrm{R}^{2}}\)
(पृथ्वी के तल पर गु. बल) = \(\mathrm{G} \frac{80 \mathrm{M}}{(\Delta \mathrm{R})^{2}}\)
\(\begin{aligned} \frac{g_{m}}{g_{e}} &=\frac{G \frac{M}{R^{2}}}{G \frac{80 M}{(4 R)^{2}}} \\ \frac{g_{m}}{g_{e}} &=\frac{M}{R^{2}} \times \frac{16 R^{2}}{80 M} \\ \frac{g_{m}}{g_{e}} &=\frac{16}{80} \end{aligned}\)

या  \(\frac{g_{m}}{g_{e}}=\frac{1}{5}\)

∴  \(g_{m}=\frac{1}{5} g_{\mathrm{e}}\)  

\(\begin{aligned} g_{m} &=\frac{1}{5} \times 9.8 \\ &=1.96 \end{aligned}\)

अतः चन्द्रमा पर गुरुत्वाकर्षण बल 1.96 मीटर / सेक² होगा।

प्रश्न 16.
पृथ्वी की सतह पर किसी वस्तु का भार 90 किग्रा. है। एक अन्य ग्रह जिसका द्रव्यमान पृथ्वी के द्रव्यमान का 1/9व त्रिज्या उसकी आधी है, की सतह पर रखी इस वस्तु का भार कितना होगा?
उत्तर:
हल - पृथ्वी जिस बल से वस्तु को अपनी ओर आकर्षित करती है,उसे वस्तु का भार कहते हैं। माना कि पृथ्वी का द्रव्यमान व त्रिज्या क्रमश: M व R हैं।
वस्तु का द्रव्यमान m हो तब न्यूटन के गुरुत्वाकर्षण बल के नियम से
\(F=G \frac{M m}{R^{2}}=m g\) ............(1)
प्रश्नानुसार F = 90 किग्रा
भार = 90 x 9.8 न्यूटन
अन्य ग्रह का द्रव्यमान = \(\frac{\mathbf{M}}{9}\) त्रिज्या \(\frac{R}{2}\)
माना कि उस वस्तु का अन्य ग्रह की सतह पर भार x न्यूटन है, तब
\(x=\frac{G \frac{M}{9} \times m}{\left(\frac{R}{2}\right)^{2}}\)
\(=G \frac{\frac{4}{9} \mathrm{Mm}}{R^{2}}\) ..................(2)
समीकरण (2) में समीकरण (1) का भाग देने पर
\(\frac{x}{F}=\frac{4}{9}\)
\(F=90 \times 9.8\) न्यूटन है।

⇒   \(\frac{x}{90 \times 9.8}=\frac{4}{9}\)

⇒  \(\begin{aligned} \therefore \quad x &=\frac{4}{9} \times 90 \times 9.8 \\ x &=40 \times 9.8 \end{aligned}\)
या x = 40 किग्रा.
अतः अन्य ग्रह पर उस वस्तु का भार 40 किग्रा. होगा।

प्रश्न 17.
दो वस्तुएँ A तथा B क्रमशः m और 4 m द्रव्यमान की 30 सेमी. की दूरी पर रखी हैं। इनको मिलाने वाली रेखा पर M द्रव्यमान की एक अन्य वस्तु A से कितनी दूरी पर रखें कि उस पर A तथा B का गुरुत्वाकर्षण बल बराबर व विपरीत हो?

उत्तर: दिया गया है।

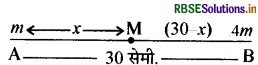
माना कि M द्रव्यमान की वस्तु A से x सेमी. दूरी पर रखी है। इस बिन्दु पर वस्तु A तथा B का गुरुत्वाकर्षण बल बराबर है।
\(F=G \frac{m \times M}{x^{2}}\) ...........(1)
\(F=G \frac{M \times 4 m}{(30-x)^{2}}\) ..............(2)
समीकरण (1) तथा समीकरण (2) से
\(\begin{aligned} G \frac{m \times M}{x^{2}} &=G \frac{M \times 4 m}{(30-x)^{2}} \\ (30-x)^{2} &=4 x^{2} \end{aligned}\)
 या \(30-x=2 x\)
 या  30 = 30x
\(x=\frac{30}{3}=10\)
 सेमी. अत: M द्रव्यमान की एक अन्य वस्तु A से 30 सेमी. की दूरी पर रखनी होगी।