RBSE Class 12 Physics Notes Chapter 7 Alternating Current

These comprehensive RBSE Class 12 Physics Notes Chapter 7 Alternating Current will give a brief overview of all the concepts.

RBSE Class 12 Physics Chapter 7 Notes Alternating Current

Alternating Current and Emf:
The electric current whose magnitude changes with time and direction reverses periodically are called alternating current and the emf or voltage is called alternating emf.
i.e I = I₀ sin ωt
or I = I₀ cos ωt
Similarly E = E₀ sin ωt
or E = E₀ cos ωt
I₀ (or E₀) is the peak value of current (or emf).

Mean/Average value of A.C.:
It is equal to that steady current which when passed through a circuit for half the period of A.C. will send the same amount of charge by alternating current in the same time through the same circuit.

For half cycle
I_m = \(\frac{2 \mathrm{I}_0}{\pi}\) = 0.636 I₀
and E_m = \(\frac{2 \mathrm{E}_0}{\pi}\) = 0.636 E₀
During next half cycle the mean value of o.c. will be equal in magnitude but opposite in direction. So average value of a.c. over a complete cycle is zero.

R.M.S./Virtual value of A.C.:
It is the root of mean square values of different instants.
It is that steady value of current which produces the same quantity of heat in a certain resistance in a given time as is done by A.C. in the same time.
I_rms = I_eff = I_v = \(\frac{\mathrm{I}_0}{\sqrt{2}}\) = 0.707 I₀
or E_rms = E_eff = E_v = \(\frac{\mathrm{E}_0}{\sqrt{2}}\) = 0.707 E₀

Phasor diagram is a diagram by which voltages and currents can be represented by vector.
Angle between them gives the phase difference between voltage and current.

Lag and lead is alternating current
In dc supply the e.m.f. and current are always in the same phase but in a.c. although the e.m.f. and current have the same frequency, yet they may be out of phase with each other. If the peak value of e.m.f. occurs before the peak value of current, the e.m.f. is said to ‘lead’ the current or current lag behind the e.m.f. by certain angle of fraction of time period.

In a.c. circuit containing resistance only
If E = E₀ sin ωt
then I = I₀ sin ωt
i.e. the voltage and current are in the same phase.

In a.c. circuit containing inductance only
If E = E₀ sin ωt
then I = I₀ sin (ωt - π/2)
i.e. current (I) lags behind the e.m.f. (E) by a phase angle by π/2.

In a.c. circuit containing capacitance only
i.e. current (I) leads the e.m.f. (E) by a phase angle by π/2.

Inductive reactance:
The effective opposition offered by the inductor to the flow of a.c. in the circuit is called inductive reactance.
It is denoted bv X_L.
And X_L = ωL = 2πv L,
v is the frequency of a.c.
For d.c. v = 0, so X_L = 0
For a.c. X_L ∝ v
So an inductor is an easy path for d.c. but a resistive path for a.c.

Capacitive reactance:
The effective opposition offered by the capacitor to the flow of a.c. in the circuit is called capacitive reactance.
It is denoted by X_C.
And X_C = \(\frac{1}{\omega \mathrm{C}}=\frac{1}{2 \pi v \mathrm{C}}\)

For d.c
v = 0
X_C = \(\frac{1}{0}\) = ∞

For a.c
X_C ∝
So a capacitor is an easy path for a.c. but a resistive path for d.c.

A.C. circuit containing LCR:
The effective resistance Z called impedance of the circuit is given by
Z = \(\frac{\mathrm{E}_0}{\mathrm{I}_0}=\sqrt{\mathrm{R}^2+\left(\omega \mathrm{L}-\frac{1}{\omega \mathrm{C}}\right)^2}\)

And phase angle Φ is given by
tan Φ = \(\frac{\mathrm{X}_L-\mathrm{X}_C}{\mathrm{R}}\)

• When X_L = X_C, tan Φ = 0 or Φ = 0. The voltage and current are in the same phase and the a.c. circuit is called non-inductive.
• When X_L > X_C, tan Φ = +ve, or Φ is positive, the voltage lead the current by phase angle Φ and the circuit is called inductive dominant circuit.
• When X_L < X_C, tan Φ = -ve, or Φ is negative, the voltage lags behind the current by phase angle Φ and the circuit is called capacitive dominant circuit.

Resonance series LCR-circuit:
A series LCR circuit, which admits maximum current corresponding to a particular angular frequency ω₀ of the a.c. source is called series resonance circuit.
i.e I₀ = I_max = \(\frac{E_0}{\mathrm{R}}\)

In series LCR circuit at resonance
ωL = \(\frac{1}{\omega \mathrm{C}}\)
or 2πv₀L = \(\frac{1}{2 \pi \mathrm{C}}\)
or v₀ = \(\frac{1}{2 \pi \sqrt{\mathrm{LC}}}\)

Resonance parallel LC circuit:
The LC parallel circuit, which allows no current to flow corresponding to a particular angular frequency &>0 of the a.c. source is called resonance parallel LC circuit. i.e.
i.e I₀ = 0
and ωL = \(\frac{1}{\omega \mathrm{C}}\)
or v₀ = \(\frac{1}{2 \pi \sqrt{L C}}\)

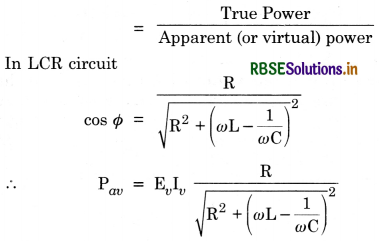
Average power in LCR circuit:
P_True = P_av = E_vI_v cos Φ
True power = apparent power × power factor

Electrical Devices:
A.C. Generator

• A.C. generator or a.c. dynamo is a device used to produce alternating current energy from mechanical energy.
• A.C. generator is based on the phenomenon of electromagnetic induction i.e., whenever magnetic flux linked with a coil changes, an induced e.m.f. is produced in the coil.

The induced emf produced in the coil of a.c. generator is given by
e = NAB ωsin ωt ...(i)
where N is number of turns of the coil having area of cross-section A rotating in a magnetic field B with angular velocity ω.

The induced emf will be maximum, when
sin ωt = 1
or e_max = e₀ = NBAω

So (i) can be written an
e = e₀ sin ωt

Armature:
Armature is a rectangular coil consisting of a large number of turns wound over a soft iron core, to increase the magnetic flux.

Transformer:
Transformer is an electrical device used for changing the a.c. voltage. It is based on the principle of mutual induction i.e. whenever magnetic flux linked with a coil is changed, an induced emf is produced in the neighbouring coil.

Step up and step down transformer
In a step up transformer, the voltage increases and proportionally current decreases.
In a step down transformer, the voltage decreases and proportionally current increases.
If E_p, I_p and E_s, I_s be voltage and current in the primary and secondary coils of a transformer respectively then
I_sE_s = I_pE_p
or \(\frac{E_S}{E_p}=\frac{I_P}{I_S}\)
Thus as voltage in the secondary increases, the current proportionately falls and vice versa i.e. whatever is gained in voltages is lost in current.

Energy losses in a transformer
A transformer suffers from the following energy losses :

• Copper loss. Energy is lost due to production of heat in the winding of the coils.
• Iron loss due to eddy currents.
• Magnetic flux leakage due to imperfect insulation.
• Humming loss due to vibrations in the case and production of sound.