RBSE Class 12 Physics Notes Chapter 6 Electromagnetic Induction

These comprehensive RBSE Class 12 Physics Notes Chapter 6 Electromagnetic Induction will give a brief overview of all the concepts.

RBSE Class 12 Physics Chapter 6 Notes Electromagnetic Induction

Electromagnetic Induction:
Electromagnetic induction is the process of production of current with the help of magnetic field by the method of induction.

Magnetic flux (Φ):
Magnetic flux (Φ) through any surface is the total number of magnetic lines passing through that surface.
If a surface has area A and magnetic field B is passing through the surface, then
Magnetic flux, Φ = B. A = BA cos θ
In SI, the unit of Φ is Wb.
Since Φ = BA
So 1 Wb = 1Tm²

Dimensional formula of (Φ)
Since Φ = BA cos θ
or [Φ] = \(\left[\frac{\mathrm{FA}}{q v}\right]=\left[\frac{\mathrm{FA}}{\mathrm{I} t v}\right]=\frac{\left[\mathrm{MLT}^{-2}\right]\left[\mathrm{L}^2\right]}{[\mathrm{A}][\mathrm{T}]\left[\mathrm{LT}^{-1}\right]}\)
[Φ] = [ML²T^-2A^-1]

Faraday’s laws of electromagnetic Induction

• First law. Whenever magnetic flux linked with a closed circuit changes, an induced e.m.f. (or current) is produced and it lasts so long as the change in magnetic flux continues.
• Second law. The magnitude of induced e.m.f. is directly proportional to the rate of change of magnetic flux linked with the circuit.

Mathematically,
e ∝ \(\frac{\phi_2-\phi_1}{t-0}\)
or e ∝ -k\(\left(\frac{\phi_2-\phi_1}{t}\right)\)
or e = -\(\frac{d \phi}{d t}\)
If the coil has N turns
e = -N\(\frac{d \phi}{d t}\)

Lenz’s law:
Lenz’s law states that the induced current produced in a circuit always flows in such a direction that it opposes the change that produces it.

Methods of producing induced e.m.f.

• By changing the magnetic field
• By changing the area
• By changing the orientation (θ) of the coil w.r.t the magnetic field.

Motional emf:
Motional emf is the induced emf produced by changing the area of a closed circuit by the movement of the circuit or part of it in a uniform magnetic field.
Motional e.m.f. e = B l v
And induced current
I = \(\frac{e}{\mathrm{R}}=\frac{\mathrm{B} l v}{\mathrm{R}}\)

Eddy currents:
Eddy currents are the induced currents produced in a conductor when magnetic flux linked with the conductor changes.
Magnitude of eddy current is
i = \(\frac{e}{\mathrm{R}}=\frac{d \phi / d t}{\mathrm{R}}\)

Eddy currents are used in

• Electromagnetic damping
• Induction furnace
• Magnetic brakes
• Electric power meters and
• Induction motor.

Self And Mutual Induction:
Self induction is the property of a coil by virtue of which, the coil opposes any change in the current flowing through it by inducing an e.m.f. in the coil.

Coefficient of self induction (or self inductance) of a coil is numerically equal to the amount of magnetic flux linked with the coil when unit current flows through it.
In a coil, the magnetic flux linked with it when current I is passing through it is given by
Φ ∝ I
or Φ = LI
[where L is called coefficient of self induction]
The induced e.m.f. produced in the coil due to self inductance is given by
e = -\(\frac{d \phi}{d t}=-\frac{d}{d t}(LI) = -L\frac{d I}{d t}\)

Units of self inductance:
The self inductance of coil is said to be 1H if a change of current equal to 1 ampere per second causes an induced e.m.f. equal to one volt in the circuit.

Self inductance of a solenoid:
Self inductance of a solenoid of radius r having n number of turns per unit length and a current I flowing through it has coefficient of self induction L given by
L = µ₀n²lA

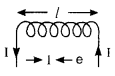
If the coil is wound on a material having relative permittivity fir, then
L = µ₀µ_rn²lA

Mutual induction:
Mutual induction is the phenomenon of producing an induced current in a coil or circuit by changing current in a neighbouring circuit.

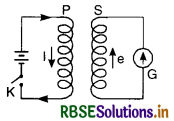
In a pair of coil as shown in the given figure, we find that the magnetic flux linked with S coil is proportional to the current I flowing in P coil. i.e. Φ ∝ I
or Φ = MF
[where M is called coeffcient of mutual induction]

The induced emf produced in S (secondary) coil is given by
e = -\(\frac{d \phi}{d t}=-\frac{d}{d t}(MI) = -\frac{\mathrm{M} d \mathrm{I}}{d t}\)
or M = -\(\frac{e}{d \mathrm{I} / d t}\)

Units of mutual inductance
Mutual inductance in a pair of coils is said to be 1 henry if a current changing at the rate of 1 As-1 in one coil induces an e.m.f. of IV in the neighbouring coil.

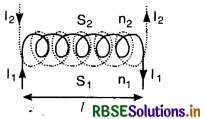
Mutual inductance of two long solenoids
Consider two long co-axial solenoids of length l having n₁, I₁ and n₂, I₂ be respective number of turns per unit length and current. Then the mutual inductance M is given by
M = µ₀n¹n²lA

Energy stored in an inductor:
Let L be coefficient of an inductor and current is changing at a rate \(\frac{dI}{dt}\) is passed through it, the induced emf produced in the inductor is given by
e = L\(\frac{dI}{dt}\) (in magnitude)

Work done by source, when I changes from 0 to I is given by
W = L \(\int_0^{\mathrm{I}}\) I dI = \(\frac{1}{2}\) LI²

This work done is stored in the form of energy
U = \(\frac{1}{2}\)LI²