RBSE Class 12 Physics Notes Chapter 5 Magnetism and Matter

These comprehensive RBSE Class 12 Physics Notes Chapter 5 Magnetism and Matter will give a brief overview of all the concepts.

RBSE Class 12 Physics Chapter 5 Notes Magnetism and Matter

Magnets And Earth’S Magnetism:
Earth behaves as a magnet with the magnetic field pointing approximately from geographic south to the north. And when a bar magnet is freely suspended, it points in the north-south direction.
Magnetism is the phenomenon of attraction of small pieces of iron, steel, Co, Ni etc. towards the ore. This phenomena is called magnetism.
Magnets are natural as well as artificial.

Properties of magnetism

• Earth behaves as a magnet.
• A freely suspended magnet always points along north direction.
• Like poles repel and unlike poles attract each other.
• Magnetic poles exist in pairs.
• Repulsion is the surest test for distinguishing between a magnet and a piece of iron.

Coulomb’s law in magnetism
Force of interaction between two poles of strengths m₁ and m₂ separated by a distance r is given by
F ∝ \(\frac{m_1 m_2}{r^2}\)
or F = \(\frac{\mu_0}{4 \pi} \frac{m_1 m_2}{r^2}\)

Magnetic field is the space abound a magnet, in which a magnetic force can be experienced. Its unit in SI is tesla.
And IT = 1NA^-1m^-1.
Magnetic field fine is the path through which an isolated north pole will tend to move if free to do so. Magnetic lines are closed, continuous loops and never intersect each other.

Magnetic dipole consists of unlike poles of equal strength and separated by a small distance 2\(\vec{l}\).
Magnetic dipole moment
\(\vec{M} = m(2\vec{l})\)

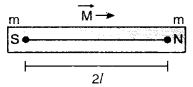
Its direction is from S to N and is a vector quantity.

Magnetic field on the axial line of a bar magnet
B_axial = \(\frac{\mu_0}{4 \pi} \frac{2 \mathrm{M} r}{\left(r^2-l^2\right)^2}\)
When l < < r
B_axial = \(\frac{\mu_0}{4 \pi} \frac{2 \mathrm{M}}{r^3}\)

Magnetic field on the equatorial line of a bar magnet
B_eq = \(\frac{\mu_0}{4 \pi} \frac{\mathrm{M}}{\left(r^2+l^2\right)^{3 / 2}}\)
When l < < r
B_eq = \(\frac{\mu_0}{4 \pi} \frac{\mathrm{M}}{r^3}\)

A current loop behaves like a magnetic pole, and the magnetic moment is given by
M = nIA
where n is number of turns of the loop carrying current I having area A.
or
\(\overrightarrow{\mathrm{M}}\) = nIA n̂
n̂ is unit vector perpendicular to the plane of the loop and its direction is given by right hand screw rule.

Torque on bar magnet placed in a magnetic field B is given by
\(\vec{\tau}=\vec{M} \times \vec{B}\)
or r = MB sin θ

and potential energy of a magnetic dipole is given
U = -MB cos θ
or U = -\(\overrightarrow{\mathrm{M}} \cdot \overrightarrow{\mathrm{B}}\)

Atom as magnetic dipole
The magnetic moment of an atom is given by
M = n\(\left(\frac{e h}{4 . \pi m_e}\right)\) = nµ_B
where µ_B = \(\frac{e h}{4 \pi m_e}\) magneton and
µ_B = 9.27 × 10^-24 Am²

Gauss’s law in magnetism
It means that Φ_B = ∮\(\overrightarrow{\mathrm{B}} \cdot d \overrightarrow{\mathrm{S}}\)

• Isolated magnetic poles do not exist.
• Magnetic poles always exist in pairs of equal strength.

Magnetic elements of earth at a place are the quantities which describe completely in magnitude and direction of the magnetic field at the place. There are threee magnetic elements.

• Magnetic declination (θ) at a place is the angle between geographical meridian and magnetic meridian.
• Magnetic inclination or dip (δ) at a place is the angle which the direction of total magnetic field of earth’s magnetic field make with the horizontal line of magnetic meridian.
• Horizontal component of earth’s magnetic field (H) is the component of earth magnetic field along the horizontal direction.
  And tan δ = \(\frac{V}{H}\)
• Neutral point is that point where the magnetic field due to magnet is completely neutralized by the horizontal component of earth’s magnetic field.
  At neutral point
  B = H

Classification of Magnetic Materials
Magnetic flux through a surface is the number of magnetic field lines passing normally through the surface and is given as Φ = \(\overrightarrow{\mathrm{B}} d \vec{s}\) Its unit is weber (Wb).

Magnetic intensity (H) is the degree to which a magnetic field can magnetise a material.
And H = \(\frac{\mathrm{B}_0}{\mu_0} \)Am^-1 (or Nm^-2 T^-1 or N Wb^-1 or Jm^-1 Wb^-1).

Intensity of magnetisation (I): It is the magnetic moment per unit volume of the material placed in the magnetising field.
And I = \(\frac{\mathrm{M}}{\mathrm{V}}=\frac{m \times 2 l}{a \times 2 l}=\frac{m}{a}\)
Units of I is Am^-1

Magnetic susceptibility 0f (χ_m) of a magnetic substance is the ratio of intensity of magnetisation to the magnetic intensity.
i.e. χ_m = I/H and has no units.

Magnetic permeability (μ):
Magnetic permeability (μ) of a substance is the ratio of the magnetic induction (B) to the magnetic intensity
i.e μ = \(\frac{B}{H}\) (units Tm A^-1)

Relation between μ and χ_m is
μ = μ₀ (1 + χ_m)
or \(\frac{\mu}{\mu_0}\) = 1 + χ_m
or μ_r = (1 + χ_m)

Classification of magnetic materials
All substances possess magnetic properties and on the basis of their behaviour, Faraday divided the magnetic materials into three classes, namely

• Diamagnetic susbtances
• Paramagnetic substances and
• Ferromagnetic substances.

Diamagnetic substances:
Diamagnetic substances when placed in a magnetising field are feebly magnetised in a direction opposite to the magnetising field e.g. Sb, Bi, Co, Pb, Ag, Au etc.

Pararnagnetic substances:
Pararnagnetic substances when placed in a magnetising field are feebly magnetised in the direction of magnetising field e.g. Al, Cr, Mn, Mg, Na, K etc.

Ferromagnetic substances:
Ferromagnetic substances when placed in a magnetising field are strongly magnetised in the direction of magnetising field e.g. Co, Ni, Fe etc.

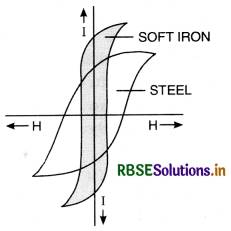
Hysteresis:
It is the lag of intensity of magnetisation behind the magnetising field during the process of magnetisation and demagnetisation of a ferromagnetic material.

The given figure shows the magnetisation curve of a ferromagnetic material, when it undergoes a complete cycle of magnetisation. The area of the hysteresis loop is the loss of energy per unit volume. From the figure we find that energy loss per unit volume for soft iron is much smaller than that for steel.