RBSE Class 12 Physics Notes Chapter 4 Moving Charges and Magnetism

These comprehensive RBSE Class 12 Physics Notes Chapter 4 Moving Charges and Magnetism will give a brief overview of all the concepts.

RBSE Class 12 Physics Chapter 4 Notes Moving Charges and Magnetism

Magnetic Effect of Current:
Magnetic effect of current was discovered by Oersted. He observed that when a current carrying wire is placed above and parallel to a magnetic needle it is deflected in a certain direction. When the current carrying wire is placed below the needle, the needle is deflected in the opposite direction.

Magnetic’s Field:
Magnetic’s Field is the space around a conductor carrying current (or a magnet) in which its magnetic effect can be felt.

Biot-Savart’s law:
It states that the magnitude of magnetic flux density dB at a point P at a distance r from a small current element Idl is given by

Direction of d \(\overrightarrow{\mathrm{B}}\) is perpendicular to the plane containing \(\overrightarrow{d l}\) and \(\vec{r}\) and is directed inwards.

Magnetic flux or magnetic induction:
It is the total number of magnetic lines of forces passing normally through a given area and is given by
Φ = \(\overrightarrow{\mathrm{B}} \cdot \overrightarrow{\mathrm{A}}\)
Its unit in SI is weber (Wb).

Magnetic field due to straight long conductor carrying current is given by
B = \(\frac{\mu_0 \mathrm{I}}{4 \pi r}\)(sinΦ₁ + sinΦ₂)

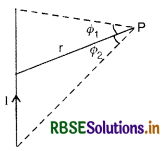
If the wire is infinitely long conductor
B = \(\frac{\mu_0 \mathrm{I}}{2 \pi r}\) [∵ Φ₁ = Φ₂ = 90°]

Magnetic field due to a solenoid carrying current I at any point P on its axis is
B = µ₀nI
Magnetic field at one end of solenoid
B_end = \(\frac{1}{2}\)µ₀nI

Magnetic field due to a toroid:
Magnetic field within the turns of toroid
B = \(\frac{\mu_0 n \mathrm{I}}{2 \pi r}\)
where r is average radius.
Magnetic field outside the toroid is zero.

Ampere circuital law states that line integral of magnetic field \(\vec{B}\) around a closed path in vacuum is equal to µ₀ times the total current I passing through the closed path
i.e. \(\vec{B} \cdot \overrightarrow{d l}\) = µ₀I

Force on a current carrying conductor of length l placed in a uniform magnetic field B is given by
F = BIl sin θ

Force On A Charge
Lorentz force is the force experienced by a charged particle at a place where both electric and magnetic fields exists.

Force due to electric field
If a charged particle having charge q is moving in an electric field \(\overrightarrow{\mathrm{E}}\), it experiences a force \(\overrightarrow{\mathrm{F}}_e\), given by
\(\overrightarrow{\mathrm{F}}_e = q\overrightarrow{\mathrm{E}}\)
Here, the direction of \(\overrightarrow{\mathrm{F}}_e\) is the same as that of \(\overrightarrow{\mathrm{E}}\).

Force due to magnetic field
If a charged particle having charge q is moving in a magnetic field \(\overrightarrow{\mathrm{B}}\), with a velocity \(\vec{v}\), it experiences force \(\overrightarrow{\mathrm{F}}_m\) given by
\(\overrightarrow{\mathrm{F}}_m=q(\vec{v} \times \overrightarrow{\mathrm{B}})\)

Here, the direction of \(\overrightarrow{\mathrm{F}}_m\) is perpendicular to plane containing \(\vec{v}\) and \(\vec{B}\).

Force due to both, electric and magnetic fields:
It a charged particle having charge q is moving in both electric and magnetic fields, the total force experienced by q will be

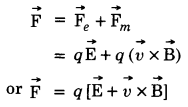
Force between two infinitely long straight parallel conductors carrying current in the same direction attract each other and if the current is flowing in opposite directions, they repel each other.
Force per unit length between two parallel conductors is given by
F = \(\frac{\mu_0}{4 \pi} \frac{2 \mathrm{I}_1 \mathrm{I}_2}{r}\) [conductors are infinitely long]

Torque on a rectangular current carrying coil:
Consider a rectangular coil suspended in a uniform magnetic field B having length l and breadth b carrying current as shown in the below figure.

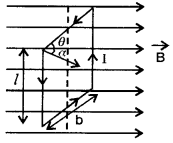
If the rectangular coil has n-turns, then the torque in the coil is given by
r = nIBA cos θ
where θ is the angle which the plane of the coil makes with the direction of magnetic field.
If the normal drawn on the plane of the coil makes an angle θ with the magnetic field, then
θ + α = 90° or θ = (90° - α)
τ = nIBA cos (90 - α)
or τ = nIBA sin α

Galvanometer:
Galvanometer is an electrical instrument used to detect and measure small currents.

Moving coil galvanometer is based on the principle that whenever a loop carrying current is placed in a magnetic field, it experiences a torque which tends to
In moving coil galvanometer, the current is proportional to the deflection produced in the coil i.e.
I ∝ θ
or I = kθ
where, k = \(\frac{\mathrm{C}}{n \mathrm{BA}}\) is the constant of proportionality and is called galvanometer constant.

Conversion of a galvanometer into an ammeter
Here a low resistance S is connected parallel with the galvanometer G and here
P.D. across the galvanometer = P.D. across the shunt

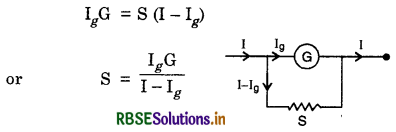
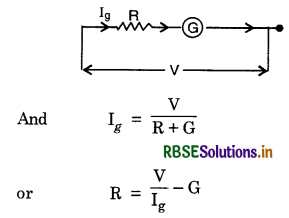
Conversion of a galvanometer into a voltmeter:
Here a high resistance R is connected in series with the galvanometer.

Cyclotron is a device used to accelerate charged particles or ions to high energy and it is based on the principle that a charged particle moving at right angle to a uniform magnetic field is acted upon by a force perpendicular to its direction of motion and follow a circular path.
The time period of charged particle is :
T = \(\frac{2 \pi m}{\mathrm{~B} q}\)
And frequency of oscillator field
v = \(\frac{1}{\mathrm{~T}}=\frac{\mathrm{B} q}{2 \pi m}\)
Electrons and neutrons cannot be accelerated with cyclotron.