RBSE Class 12 Physics Notes Chapter 2 Electrostatic Potential and Capacitance

These comprehensive RBSE Class 12 Physics Notes Chapter 2 Electrostatic Potential and Capacitance will give a brief overview of all the concepts.

RBSE Class 12 Physics Chapter 2 Notes Electrostatic Potential and Capacitance

Electrostatic Potential:
Electric potential is the degree of electrification and it determines the flow of charge from one point to another in an electric field. Electric potential at a point in an electric field is defined as the amount of work done in bringing a unit positive charge from infinity to that point against the electric force.
So, electric potential = \(\frac{\text { Work done }}{\text { Charge }}\)

SI unit of electric potential is volt (or JC^-1) and its dimensional formula is [ML² T^-3].

Electrostatic potential difference between two points in an electric field is defined as the amount of work done in moving a unit positive test charge from one point to the other (without acceleration) against the electrostatic force. The potential difference between two points A and B at distances r_A and r_B from point charge q having potentials V_A and V_B (V_B - V_A) is given by
V_B - V_A = \(\frac{q}{4 \pi \varepsilon_0}\left[\frac{1}{r_{\mathrm{B}}}-\frac{1}{r_{\mathrm{A}}}\right]\)

Electric potential due to electric dipole at any point P is given by
V = \(\frac{p \cos \theta}{4 \pi \varepsilon_0 r^2}\)

On the axial line, θ = 0°

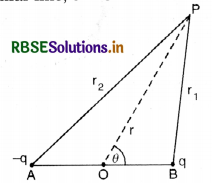
∴ V = \(\frac{p}{4 \pi \varepsilon_0 r^2}\)

On the equatorial line, θ = 90°
∴ V = 0

Characteristics of potential (V)

• Potential is a scalar quantity.
• Its value at infinity is zero.
• Potential is positive if q > 0 and negative if q < 0
• Potential depends only on the distance from the source charge.

Equipotential surfaces
An equipotential surface is that at every point of which electric potential is the same.

Characteristics of equipotential surface

• No work is done in moving a test charge over an equipotential surface
  i.e W_AB = 0
• Electric field intensity E is perpendicular to the equipotential surface.
• Equipotential surfaces help us to distinguish regions of strong field from those of weak fields.

Electrostatic shielding:
Electrostatic shielding is the phenomenon in which a certain region of space is protected from the
electric field. Since electric field inside a conductor is zero, so to protect delicate instruments from external electric field, we enclose them in hollow' conductor. For example, in electronic devices, certain circuits or components are shielded by covering them with metal shields.

Electric Potential Energy:
Electric potential energy of a system of point charges is the total amount of work done in bringing the various charges to their respective positions from infinitely large mutual separations.

Electric potential energy of a system of two point charges is given by
U = W = \(\frac{1}{4 \pi \varepsilon_0} \frac{q_1 q_2}{r_{12}}\)

Electrical Capacitance:
Capacitance of a conductor
The capacitance of a conductor is the ratio of the charge on the conductor to its potential.
i.e C = \(\frac{q}{V}\)
And the unit of capacitance of capacitor in SI is farad.
And IF = \(\frac{1C}{1V}\) = 1C V^-1

Capacitor:
A capacitor is an arrangement for storing large amount of electric charge and hence electrical energy, in a small space.

Capacitance of a capacitor:
Capacitance of a capacitor is defined as the ratio of charge q on the plates of capacitor to the potential difference V across its plate i.e. C = q/V.

Capacitance of a capacitor:
Capacitance of a capacitor is also given by

• Capacitance of a spherical capacitor of radius r is given by C = 4πε₀r
• Capacitance of a parallel plate capacitor separated by small distance d is given by
  C = \(\frac{\varepsilon_0 \mathrm{~A}}{d}\) (medium between capacitor plates is air or vaccum)
• If medium between plates is other than air having dielectric constant K, then
  C = \(\frac{\varepsilon_0 \mathrm{KA}}{d}\)

Dielectric:
A dielectric is a material that does not conduct electric current through it. Molecules of a dielectric are of two types.

• Polar molecule is one in which the centre of gravity of positive charges does not coincide with the centre of gravity of negative charge e.g. HCl, NH₃, H₂O, CO etc.
• Non-polar molecule is one, in which the centre of gravity of positive charges coincide with the centre of gravity of the negative charges e.g. O₂, H₂, N₂, etc.

Effect of dielectric in a capacitor
When a slab of a dielectric is introduced between the plates of a parallel plate capacitor, the capacitance of capacitor becomes
C = \(\frac{\mathrm{K} \varepsilon_0 \mathrm{~A}}{\mathrm{~K}(d-t)+t}\)
If t = d, C = \(\frac{\mathrm{KA} \varepsilon_0}{d}\)

Grouping of Capacitors:
Capacitors can be grouped in series or in parallel as per the requirement.
(i) Capacitors in series. Capacitors are said to be connected in series if the second plate of one capacitor is connected to the first plate of the next and so on as shown in the figure ahead.

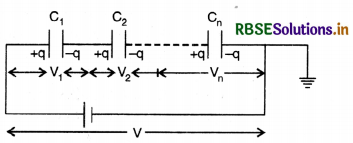
Resultant capacitance will be
\(\frac{1}{\mathrm{C}}=\frac{1}{\mathrm{C}_1}+\frac{1}{\mathrm{C}_2}+\ldots \ldots \ldots \ldots \ldots \ldots+\frac{1}{\mathrm{C}_n}\)

(ii) Capacitors in parallel
Capacitors are said to be connected in parallel if the “positively charged plates” of all the capacitors are connected together at a point A, while the ‘earthed’ plates are connected together at another point B as shown in the figure.

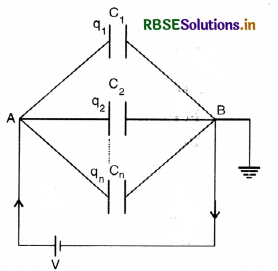
Resultant capacitance will be
C = C₁ + C₂ + .......... + C_n

Energy stored in a capacitor is given by
U= \(\frac{1}{2}\)CV² = \(\frac{1}{2} \frac{q^2}{\mathrm{C}}=\frac{1}{2}\) qV
Both in series combination and parallel combinations, the total energy stored is equal to sum of the energies stored in individual capacitors.
i.e. U = C₁ + C₂ + .......... + C_n

Van de Graaff electrostatic:
Van de Graaff electrostatic generator is based on the principle that

• If a charged conductor is in internal contact with another hollow conductor the hollow conductor accept all charge of the conductor irrespective of its own potential
• The electric discharge takes place in air or gases readily at pointed conductors.