RBSE Class 12 Physics Notes Chapter 1 वैद्युत आवेश तथा क्षेत्र

These comprehensive RBSE Class 12 Physics Notes Chapter 1 वैद्युत आवेश तथा क्षेत्र will give a brief overview of all the concepts.

RBSE Class 12 Physics Chapter 1 Notes वैद्युत आवेश तथा क्षेत्र

भूमिका (Introduction):
आकाश में गर्जन विद्युत विसर्जन की सामान्य घटना है। हम सभी को शुष्क मौसम में स्वेटर या संश्लेषित वस्त्र जैसे नॉयलान, पॉलिएस्टर के वस्त्रों को उतारते समय चट-चट की ध्वनि सुनाई देती है। शुष्क सर्द मौसम में ऊनी कंबलों पर हाथ रगड़ने पर चिंनगारियाँ (Sparks) देखने का अनुभव होता है। विद्युत झटके का अनुभव उस समय भी होता है जब हम किसी कार का दरवाजा खोलते हैं अथवा बस की सीट पर खिसकने के पश्चात उसमें लगी लोहे की छड़ को पकड़ते हैं। इसी प्रकार हवा से भरे गुब्बारे को वस्त्र पर रगड़कर सूखी दीवार से सटाने पर गुब्बारा घण्टों दीवार से चिपका रहता है। विद्युत विसर्जन के इन सभी अनुभवों का कारण विद्युतरोधी पृष्ठों पर रगड़ के कारण एकत्र वैद्युत आवेश है। इस अध्याय तथा अगले अध्याय में हम इसी वैद्युत आवेश के विषय पर चर्चा करेंगे। हमारे अनुभव की ये सभी घटनाएँ वैद्युत आवेश के स्थिर प्रभाव का परिणाम है। स्थिर से तात्पर्य है वह सब कुछ जो समय के सापेक्ष परिवर्तित अथवा गतिमान नहीं होता है। "स्थिर-वैद्युतिकी (Electrostatics) के अन्तर्गत स्थिर आवेशों द्वारा उत्पन्न बलों, क्षेत्रों (Fields) एवं विभवों (Potentials) के विषय में अध्ययन किया जाता है।"

क्या आप जानते है?
सामान्य तौर पर सभी विद्यार्थियों द्वारा प्रयोग में ली गई फोटोस्टेट मशीन जिसे इलेक्ट्रोस्टेट मशीन भी कहा जाता है, स्थिर वैद्युतिकी का अनुप्रयोग है। इसके अलावा कम्प्यूटर प्रिंटर, स्थिर वैद्युत स्मृति (Electrostatic Memory), भूकम्प लेखी (Seismograph) उल्लेखनीय अनुप्रयोग हैं।

 

विद्युत आवेश (Electric Charge):
लगभग 600 ई.पू. यूनान (ग्रीस) देश के मिलेटस प्रांत के दार्शनिक थेल्स (Thales) को विद्युत आवेश की खोज का श्रेय दिया जाता है। उन्होंने इस तथ्य की खोज अम्बर (Amber) नामक पदार्थ की छड़ को ऊनी अथवा रेशमी वस्त्र से रगड़ने पर की। उन्होंने पाया कि ऊन अथवा रेशमी वस्त्र से रगड़ा गया अम्बर हल्की वस्तुओं को आकर्षित करता है। बाद में सन् 1600 में वैज्ञानिक गिलबर्ट (Gilbert) ने यह दर्शाया कि यह अद्भुत आकर्षण का गुण अम्बर में ही नहीं बल्कि लगभग सभी पदार्थों में थोड़ा बहुत उपस्थित होता है। उदाहरण के लिए कांच की छड़ को रेशम से तथा एबोनाइट को फ्लालेन (Flannel) या बिल्ली के समूर (बालों का आवरण) से रगड़ा जाये तो दोनों ही पदार्थों की छड़ें भूसे के तिनकों, सरकंडे की गोलियों, कागज के छोटे टुकड़ों को आकर्षित करने लगती हैं। चूँकि ग्रीक भाषा में अम्बर को इलेक्ट्रॉन (ElektronElectron) कहा जाता है। अतः आकर्षण के इस अद्भुत गुण को 'इलेक्ट्रिसिटी' की संज्ञा दी गई। यह नामकरण 1646 में सर थॉमस ब्राउन (Sir Thomas Brown) ने दिया था।

क्रियाकलाप:
विद्युत आवेश के प्रभाव को एक क्रियाकलाप द्वारा समझा जा सकता है। सफेद कागज की लम्बी पतली पट्टियाँ काटकर उन पर धीरे से इस्तरी कीजिए। इन पट्टियों को टेलीविज़न की स्क्रीन अथवा कम्प्यूटर के मॉनीटर के निकट लाइए। आप देखेंगे कि पट्टियाँ स्क्रीन या मॉनीटर की ओर आकर्षित होती हैं। वास्तव में वे कुछ समय तक स्क्रीन से चिपकी रहती हैं।

रगड़ (rubbing) से उत्पन्न होने वाली विद्युत को घर्षण विद्युत (Frictional electricity) कहते हैं। जिन वस्तुओं में हल्के पदार्थों को आकर्षित करने का गुण होता है, उन्हें 'आवेशित (charged)' कहते हैं। विद्युत आवेशों की मौजूदगी और इस प्रवाह से जुड़े भौतिक परिघटनाओं के समुच्चय को विद्युत (Electricity) कहा जाता है। अर्थात् इसे न तो देखा जा सकता है और न ही स्पर्श किया जा सकता है केवल इसके प्रवाह से अनुभव किया जा सकता है। यदि वस्तु में उत्पन्न विद्युत आवेश को अन्य वस्तु में प्रवाहित न होने दिया जाये, तो इस विद्युत को स्थित वैद्युत (Static electricity) कहते हैं। "विद्युत की वह शाखा जिसमें आवेश की स्थिर (गतिहीन) अवस्था में होने वाले प्रभावों एवं घटनाओं का अध्ययन किया जाता है।"

• विद्युत आवेश एक अदिश राशि है जिसे से प्रदर्शित किया जाता है।
• विद्युत आवेश का S.I. मात्रक कूलॉम (C) तथा CGS मात्रक मात्रक स्टेट कूलॉम या e.s.u. (electrostatic unit) होता है।
• विद्युत आवेश का विमीय सूत्र [AT] है।

विद्युत आवेश के मात्रकों से संबंधित स्मरणीय बिन्दु

• 1 कूलॉम (C) = 3 × 10⁹ e.s.u. या स्टेट कूलॉम या फ्रैंकलिन।
• आवेश का वैद्युत चुम्बकीय मात्रक-emu (electromagnetic unit) या ऐब कूलॉम (ab coulomb)
  1 emu = 3 × 10¹⁰ esu = 10 कूलॉम
  1 कूलॉम = \(\frac{1}{10}\) ऐब कूलॉम या emu
• आवेश का प्रायोगिक मात्रक ऐम्पियर × घण्टा (Ah)
• आवेश का सबसे बड़ा मात्रक फैराडे है।
  1 फैराडे = 96500 कुलॉम

धन तथा ऋण आवेश (Positive and Negative Charge):
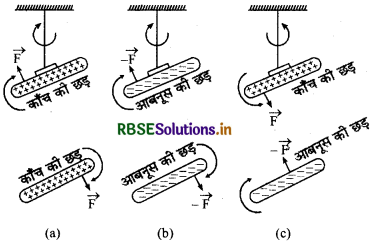
यदि ऊन अथवा रेशम के कपड़ों से रगड़ी हुई दो काँच की छड़ों को एक-दूसरे के निकट लाएँ तो वे एक-दूसरे को प्रतिकर्षित करती हैं। (चित्र (a))। ऊन की लड़ियाँ अथवा रेशम के कपड़े के टुकड़े अथवा आबनूस की छड़े भी एक-दूसरे को प्रतिकर्षित करती हैं परन्तु काँच की छड़ तथा ऊन अथवा आबनूस की छड़े एक-दूसरे को आकर्षित करती है (चित्र 1.1(b))।
इसी प्रकार, बिल्ली की समूर (खाल पर बालों का आवरण) (ब्रेकेट) से रगड़ी हुई दो प्लास्टिक छड़े एक-दूसरे को प्रतिकर्षित करती हैं। जबकि प्लास्टिक छड़ समूर को आकर्षित करती है। अमेरिकी वैज्ञानिक बैंजामिन फ्रैंकलिन (सन् 1750) ने अपने अध्ययनों के पश्चात् निष्कर्ष निकाला कि इस घटना का कारण एक राशि है, जिसे वैद्युत आवेश कहते है और यह केवल दो प्रकार के ही हो सकते हैं। उन्होंने स्पष्ट किया कि

• सजातीय आवेश एक-दूसरे को प्रतिकर्षित तथा
• विजातीय आवेश एक-दूसरे को आकर्षित करते हैं। वह गुण जो दो प्रकार के आवेशों में भेद करता है, आवेश की ध्रुवता कहलाता है। इस प्रकार आवेशों को दो प्रकार का बताया गया :

(i) धनावेश (Positive charge)
(ii) ऋणावेश (Negative charge)

तालिका : 1.1 रगड़ी गई वस्तुओं के युग्मों पर आवेश

धनावेश	ऋणावेश
1. काँच की छड़	1. संश्लेषित वस्त्र
2. फर या ऊनी वस्त्र	2. अम्बर या रबड़
3. नायलॉन	3. प्लास्टिक की शीट
4. सूखे बाल	4. कंघा
5. बिल्ली की समूर	5. काँच की छड़ 6. प्लास्टिक की छड़ 7. एबोनाइट की छड
6. ऊनी कपड़ा	8. अम्बर 9. एबोनाइट 10. प्लास्टिक 11. रबड़

इलेक्ट्रॉन सिद्धान्त के आधार पर विद्युतीकरण की व्याख्या (Explanation of electrification on the basis of electron theory):
इलेक्ट्रॉन सिद्धान्त के अनुसार प्रत्येक पदार्थ अतिसूक्ष्म परमाणुओं से मिलकर बना होता है। परमाणु का केन्द्रीय भाग (central part) नाभिक (nucleus) कहलाता है जो प्रोटॉनों (Protons) तथा न्यूट्रॉनों (Neutrons) से मिलकर बना होता है। प्रोटॉन धनावेशित मूल कण तथा न्यूट्रॉन आवेश-रहित मूल कण होते हैं इसलिए नाभिक में सम्पूर्ण 'धनावेश' होता है। नाभिक के चारों ओर कुछ विशिष्ट कक्षाओं में ऋणावेशित इलेक्ट्रॉन परिक्रमा करते हैं। इलेक्ट्रॉनों पर ऋणावेश की मात्रा उतनी ही होती है जितनी प्रोटॉन पर धन आवेश की होती है अर्थात् इलेक्ट्रॉन पर आवेश e = -1.6 × 10^-19

कूलॉम तथा प्रोटॉन पर आवेश e = - 1.6 × 10^-19

कूलॉम होता है। सामान्य अवस्था में परमाणु में इलेक्ट्रॉनों व प्रोटॉनों की संख्या ठीक बराबर होती हैं, इसलिए सामान्य अवस्था में परमाणु विद्युत उदासीन होता है। जब किसी परमाणु से किसी भी प्रकार से एक अथवा अधिक इलेक्ट्रॉन निकल जाते हैं तो वह परमाणु 'धनावेशित' हो जाता है। इसके विपरीत किसी परमाणु को बाहर से एक अथवा अधिक इलेक्ट्रॉन दे देने पर वह ऋणावेशित हो जाता है। इस प्रकार किसी वस्तु का धनावेशित हो जाना उसके परमाणुओं में 'इलेक्ट्रॉनों की कमी' प्रदर्शित करता है तथा वस्तु का ऋणावेशित हो जाना उसके परमाणुओं में 'इलेक्ट्रॉनों की वृद्धि' को प्रदर्शित करता है।

जब हम दो वस्तुओं को आपस में रगड़ते हैं तो उनके पृष्ठों के मध्य घर्षण के विरुद्ध आपेक्षिक गति होती है। इस परिस्थिति में ऋणात्मक कार्य होता है। यदि इन वस्तुओं के युग्म भिन्न इलेक्ट्रॉन बन्धुता के परमाणुओं से निर्मित हैं तो जिस वस्तु की इलेक्ट्रॉन बंधुता कम होती है वह इलेक्ट्रॉन का त्याग कर 'धनावेशित' हो जाती है जबकि इसके विपरीत अधिक इलेक्ट्रॉन बन्धुता वाली वस्तु इलेक्ट्रॉन ग्रहण कर ऋणावेशित हो जाती है।

विद्युत तथा चुम्बकत्व का एकीकरण विद्युत के अन्तर्गत तड़ित, बैटरी, काँच की छड़ों, बिल्ली की समूर आदि के आवेशों पर चर्चा होती है जबकि चुम्बकत्व के अन्तर्गत चुम्बकीय पदार्थों, चुम्बकीय सुई आदि में अन्योन्य क्रिया का वर्णन है। डेनमार्क के वैज्ञानिक ऑर्टेड ने पाया कि चुम्बकीय सुई के निकट रखे धारावाही चालक तार से विद्युत धारा प्रवाहित करने पर चुम्बकीय सुई विक्षेपित हो जाती है। ऐम्पियर तथा फैराडे ने इस प्रेक्षण की व्याख्या करते हुए बताया कि गतिशील आवेश चुम्बकीय क्षेत्र उत्पन्न करते हैं तथा गतिशील चुम्बक विद्युत धारा उत्पन्न करत हैं। विद्युत तथा चुम्बकत्व में एकीकरण का सिद्धांत स्कॉटलैंड के भौतिकविद् मैक्सवेल तथा हॉलैंड के भौतिकविद् लॉरेन्ज ने प्रतिपादित किया। इस क्षेत्र को वैद्युत चुम्बकत्व (Electromagnetism) कहते हैं। हमारे चारों ओर की अधिकांश परिघटनाओं के लिए उत्तरदायी बलों का उद्भव वैद्युत-चुम्बकीय बलों से हुआ है। वैद्युत-चुंबकीय बल प्रकृति के मूल बलों में से एक है।

वैद्युत चुम्बकत्व आधुनिक प्रौद्योगिक युग की नींव है। विद्युत शक्ति, दूरसंचार, रेडियो, टेलीविजन तथा दैनिक जीवन में उपयोग होने वाली प्रायोगिक युक्तियाँ इसी विज्ञान के सिद्धान्तों पर आधारित हैं।

स्वर्ण-पत्र विद्युतदर्शी (Gold Leaf Electroscope):
स्वर्ण-पत्र विद्युतदर्शी का कार्य-यह एक ऐसा उपकरण है जिसकी सहायता से किसी आवेशित वस्तु पर आवेश की उपस्थिति (presence) एवं आवेश की प्रकृति (nature) का पता लगाया जा सकता है। इसकी सहायता से विभवान्तर की माप भी की जा सकती है।

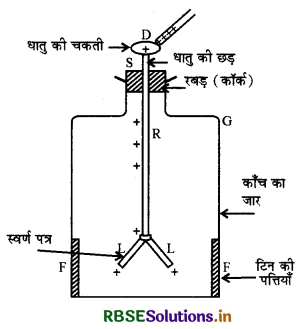
संरचना-इसकी संरचना चित्र 1.2 में प्रदर्शित की गई है।
इसमें एक काँच का जार G होता है जिसके मुख में एक अचालक पदार्थ का ढक्कन S लगा होता है और इस ढक्कन से होकर एक धातु की छड़ R जार के अन्दर जाती है। इस छड़ के निचले सिरे पर अत्यन्त पतले दो स्वर्ण-पत्र (L-L) लगे रहते हैं और ऊपरी सिरे पर एक धातु की चकती (D) लगी रहती है। विद्युतदर्शी की सुग्राहिता (sensitivity) बढ़ाने के लिए स्वर्ण-पत्रों के सामने जार की दीवार में दो टिन की पत्तियाँ (F-F) चिपका दी जाती हैं।

कार्यविधि-स्वर्ण-पत्र अत्यन्त हल्के होते हैं और चालक होने के कारण वे बहुत कम स्थिर वैद्युत बल का भी शीघ्रता से प्रभाव प्रदर्शित करने लगते हैं। जब कोई आवेशित छड़ धातु की चकती D से स्पर्श करायी जाती है, तो छड़ का आवेश छड़ R के माध्यम से स्वर्ण-पत्रों तक पहुँच जाता है और स्वर्ण-पत्र एक-दूसरे को प्रतिकर्षित करने लगते हैं तथा वे फैल जाते हैं। स्वर्ण-पत्रों का फैलना चकती D से स्पर्श करायी गई छड़ के आवेशित होने का प्रमाण है। स्वर्ण-पत्रों का फैलाव आवेश के परिमाण (magnitude) के अनुपात (ratio) में होता है।

स्वर्ण-पत्र विद्युतदर्शी के स्वर्ण-पत्रों को ज्ञात आवेश देने के बाद यदि कोई अन्य छड़ चकती D से स्पर्श कराई जाती है और पत्तियों का फैलाव बढ़ता है तो छड़ पर समान प्रकृति का आवेश होगा और यदि पत्तियों का फैलाव कम होता है तो छड़ पर विपरीत प्रकृति का आवेश होगा।

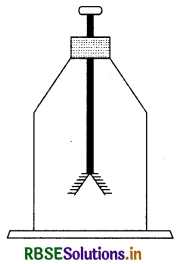
कैसे बनाएँ विद्युतदर्शी ? विद्यार्थी स्वयं सरल सूक्ष्मदर्शी बना सकते हैं। परदे लटकाने वाली ऐलुमिनियम की एक बारीक छड़ लीजिए। इस छड़ के दोनों सिरों पर ऐलुमिनियम के गोले जुड़े होने चाहिए। इसका लगभग 20 सेमी लंबा एक टुकड़ा इस प्रकार काटिए जिससे छड़ का एक सिरा चपटा तथा दूसरा सिरा गोले का बना रहने देते हैं। एक बड़ी बोतल लेते हैं जिसके मुँह पर कॉर्क लगा हो। कॉर्क में छेद करके इस छड़ को चित्र में दर्शाए अनुसार सेट कर लेते हैं। छड़ के गोले वाला सिरा बोतल के बाहर तथा कटा सिरा बोतल के भीतर रखना चाहिए। लंबा ऐलुमिनियम पत्र लेकर इसे बीच में मोड़ लेते हैं। इस पत्र को छड़ के चपटे सिरे पर सेलो टेप के साथ जोड देते हैं। अब कॉर्क को बोतल के मुख पर इस प्रकार फिट करते हैं कि छड़ का गोले वाला सिरा कॉर्क से लगभग 5 से 6 सेमी बाहर निकला रहे। बोतल के भीतर एक कागज का पैमाना पहले से ही पत्रों की पृथकता को मापने के लिए लगाया जा सकता है। पत्रों की पृथकता (Separation) विद्युतदर्शी पर आवेश की मात्रा की एक माप होती है।

चालक, अचालक एवं परावैद्युत (Conductors, Insulators and Dielectrics):
प्रकृति में पाये जाने वाले अधिकांश पदार्थों को दो भागों में बाँटा गया है

• चालक एवं
• अचालक। चालक (conductors)

"वह पदार्थ जो आवेश को ले जाने या आवेश को एक स्थान से दूसरे स्थान तक ले जाने के लिए प्रयोग किया जाता है, चालक कहलाता है।" चाँदी सर्वोत्तम चालक है, इसके अलावा सभी धातुएँ चालक की श्रेणी में आती हैं, जैसे ताँबा, लोहा, ऐलुमिनियम, पारा आदि। पृथ्वी भी वैद्युत की सुचालक (good conductor) है और मानव शरीर भी विद्युत का सुचालक है। सभी लवणों, अम्लों एवं क्षारों के जलीय घोल (water soluble salts, acids and bases) विद्युत के सुचालक हैं। इन घोलों में मौजूद आयन आवेश वाहक (charge carriers) का कार्य करते हैं।

धातुओं में मौजूद मुक्त इलेक्ट्रॉन (free electrons) आवेश वाहक का कार्य करते हैं। मुक्त इलेक्ट्रॉन परमाणुओं की सबसे बाहरी कक्षा के इलेक्ट्रॉन होते हैं जो थोड़ी भी ऊर्जा पाकर संगत परमाणु को छोड़कर चालक की परिसीमाओं (boundary) के अन्दर कहीं भी घूम सकते हैं लेकिन चालक को छोड़कर नहीं जा सकते हैं। इन मुक्त (free) इलेक्ट्रॉनों की तुलना किसी बर्तन में बन्द गैस के अणुओं से की जा सकती है, अतः इनके समूह को इलेक्ट्रॉन गैस भी कह सकते हैं।

महत्त्वपूर्ण बिन्दु-विद्युत्-अपघट्यों (electrolytes) में गतिमान आवेश इलेक्ट्रॉन और आयन दोनों होते हैं।

अचालक (Insulators):
अचालक वे पदार्थ होते हैं जिनसे होकर विद्युत प्रवाह नहीं हो सकता है। अचालकों के सामान्य उदाहरण काँच, रबर, प्लास्टिक, एबोनाइट, अभ्रक, मोम आदि हैं। इन पदार्थों में नगण्य संख्या में मुक्त इलेक्ट्रॉन होते हैं। दूसरे शब्दों में यह कह सकते हैं कि इन पदार्थों के परमाणुओं में सभी इलेक्ट्रॉन बद्ध इलेक्ट्रॉन (bound electrons होते हैं और वे मुक्त रूप से गति नहीं कर सकते हैं। चूँकि अचालकों में मुक्त रूप से विचरण (movable) करने वाले आवेश नहीं होते हैं इसलिए इनसे होकर विद्युत् का चालन सम्भव नहीं है।

परावैद्युत (Dielectric):
अचालकों को ही परावैद्युत (dielectric) पदार्थ कहते हैं। स्वाभाविक है कि परावैद्युत माध्यमों से भी विद्युत् प्रवाह सम्भव नहीं है लेकिन बाहरी वैद्युत क्षेत्र (external electric field) में रखने पर इनकी सतह पर प्रेरित आवेश एकत्र हो जाता है। इस प्रकार हम परावैद्युत पदार्थ की परिभाषा निम्न प्रकार कह सकते हैं, "वे अचालक पदार्थ जो चालन के बिना वैद्युत प्रभाव का प्रदर्शन करते हैं, परावैद्युत पदार्थ कहलाते हैं।"

जब चालक पदार्थ को कोई आवेश दिया जाता है तो यह बहुत शीघ्र उसकी सतह पर फैल जाता है, लेकिन अचालक को दिया गया आवेश वहीं पर ठहर कर रह जाता है।

भूसम्पर्कण (Grounding or Earthing)
जब हम किसी आवेशित वस्तु को पृथ्वी के सम्पर्क में लाते हैं तो आवेश चालक में से होते हुए भूमि में चला जाता है। आवेश का इस प्रकार भूमि में जाना भूसम्पर्कण (Grounding or Earthing) कहलाता है। भूसम्पर्कण विद्युत परिपथों एवं युक्तियों की सुरक्षा के लिए प्रदान की एक व्यवस्था है। भूसम्पर्कण के लिए धातु की एक मोटी प्लेट को भूमि में गहराई तक गाड़ा (buried) जाता है तथा इस प्लेट से मोटे तारों को निकालकर भवनों में इन तारों का उपयोग मुख्य आपूर्ति (Main Supply) के निकट भूसम्पर्कण के लिए किया जाता है। घरों में प्रयुक्त तीन तारों की सप्लाई में दो तार विद्युत शक्ति को मुख्य लाइन से युक्तियों तक ले जाते हैं तथा तीसरा तार भूमिगत प्लेट से जोड़ा जाता है। विद्युत इस्तरी (प्रेस), रेफ्रिजरेटर, टेलीविजन के धातु के आवरण भूसंपर्क तार से जुड़े होते हैं। परिपथ में कोई त्रुटि होने पर अथवा विद्युन्मय तार का धातु के आवरण से स्पर्श होने पर आवेश भूमि में प्रवाहित हो जाता है। इन अनुप्रयुक्तियों को कोई हानि नहीं होती तथा मनुष्यों को कोई क्षति भी नहीं होती।

अर्द्धचालक (Semiconductor):
पदार्थों की एक तीसरी श्रेणी अर्द्धचालक कहलाती है। ये पदार्थ कुचालक एवं चालक दोनों ही पदार्थों के गुण प्रदर्शित करते हैं। सिलिकॉन तथा जर्मेनियम अर्द्धचालकों के उदाहरण हैं।

आवेशन की विधियाँ (Methods of Charging):
किसी वस्तु में स्थैतिक आवेश (Static Charge) निम्न विधियों के द्वारा अस्तित्व में हो सकता है

प्रेरण द्वारा आवेशन (Charging by Induction)
उद्देश्य-किसी आवेशित वस्तु को अनावेशित वस्तु से स्पर्श किये बिना विपरीत आवेश उत्पन्न करना।

प्रेरण द्वारा आवेश उत्पन्न करने की विधि:
"प्रेरण द्वारा आवेशन की घटना में आवेशित वस्तु A जब अनावेशित वस्तु B के पास लाई जाती है तो दोनों के सम्पर्क के बिना अनावेशित वस्तु B में वस्तु A के निकट वाले पृष्ठ पर विपरीत प्रकृति (opposite nature) का कुछ आवेश उत्पन्न हो जाता है। चूंकि दोनों वस्तुएँ सम्पर्क में नहीं लायी जाती हैं अत: A के आवेश में कोई कमी नहीं आती है।"

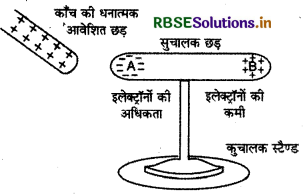
सुचालक छड़ को दूसरी सुचालक छड़ के पास लाने पर प्रेरण द्वारा आवेशन

एक चालक गोले को प्रेरण द्वारा आवेशित करने की स्थितियाँ चित्र में प्रदर्शित हैं। विभिन्न स्थितियों की विवेचना निम्न प्रकार है।

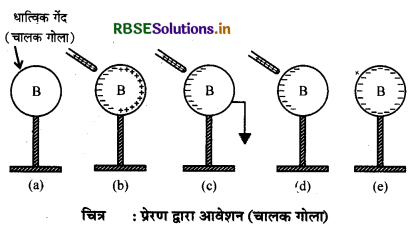
• एक चालक गोला B एक अचालक स्टैण्ड पर स्थित है।
• जब एक धनावेशित काँच की छड़ A गोले B के निकट लायी जाती है तो छड़ के पास वाले गोलीय पृष्ठ (spherical surface) पर ऋण आवेश प्रेरित हो जाता है। ऐसा इसलिए होता है कि छड़ A का धनावेश गोले B के मुक्त इलेक्ट्रॉनों को आकर्षित करता है जिससे गोले के दूर वाले पृष्ठ से इलेक्ट्रॉन A के निकट वाले पृष्ठ पर एकत्र होने लगते हैं। जैसे ही गोले के इलेक्ट्रॉनों पर परिणामी (resultant) बल शून्य हो जाता है यह क्षणिक क्रिया तुरन्त बन्द हो जाती है। इस प्रकार गोले B का छड़ A के पास वाला पृष्ठ ऋणावेशित एवं दूर वाला पृष्ठ धनावेशित हो जाता है [चित्र (b)] ।
• जब गोले B का सम्पर्क पृथ्वी से कर देते हैं तो उसका समस्त धनावेश पृथ्वी में चला जाता है अर्थात् पृथ्वी से इलेक्ट्रॉन आकर गोले के धनावेश को उदासीन (neutral) बना देते हैं। इस प्रकार अब गोले B पर A के पास वाला ऋणावेश रह जाता है
• अब गोले B का सम्पर्क पृथ्वी से हटा देते हैं तो भी ऋणावेश A के निकट वाले भाग पर ही रहता है
• जब काँच की छड़ को हटा लेते हैं तो गोले B का ऋणावेश पूरे पृष्ठ पर समान रूप से (equally) फैल जाता है

इसी प्रकार यदि गोले B को प्रेरण द्वारा धनावेशित करना है तो हमें उसके निकट ऋणावेशित छड़ लानी होगी।

महत्वपूर्ण बिन्दु

• विद्युतीकरण का सही परीक्षण प्रतिकर्षण है न कि आकर्षण क्योंकि एक आवेशित तथा एक अनावेशित वस्तु के मध्य भी आकर्षण ही होता है।
• आवेश का संसूचन एवं मान, स्वर्णपत्र विद्युत्दर्शी, इलेक्ट्रोमीटर, वोल्टामीटर तथा प्रक्षेप धारामापी द्वारा किया जा सकता है।
• जब X-किरणें (0.1Å से 10Å के मध्य तरंगदैर्ध्य परास के विद्युत चुम्बकीय प्रेरण) एक धातु सतह पर आपतित होती हैं तो धातु में से इलेक्ट्रॉन उत्सर्जित होते हैं। अतः सतह धनावेशित हो जाती है।

घर्षण द्वारा आवेशन (Charging by Friction):
दो उचित पदार्थों को उचित दशाओं (proper conditions) में रगड़ने (या घर्षण) से उत्पन्न विद्युत को घर्षण विद्युत कहते हैं। जब उचित पदार्थों को रगड़ा जाता है तो वह विद्युतीकृत (electrified) हो जाते हैं, इनमें से एक पदार्थ इलेक्ट्रॉनों का त्याग करता है तथा दूसरा पदार्थ इलेक्ट्रॉनों को ग्रहण करता है। जो पदार्थ इलेक्ट्रॉनों का त्याग करता है वह धनावेशित तथा जो पदार्थ इलेक्ट्रॉनों को ग्रहण करता है वह ऋणावेशित कहलाता है।

आवेशन का मूल कारण वास्तव में एक पदार्थ से दूसरे पर रगड़ने के दौरान इलेक्ट्रॉनों का स्थानान्तरण है। रगड़ने (या घूर्णन) के दौरान प्रोटॉनों का स्थानान्तरण नहीं होता है क्योंकि प्रोटॉन नाभिक के अन्दर होते हैं।
अग्र सारणी में कुछ पदार्थ दर्शाए गए हैं जिन्हें आपस में रगड़ने पर दो प्रकार के आवेश प्राप्त होते हैं

I(+)	II(-)
काँच की छड़	रेशमी कपड़ा
बिल्ली की खाल द्वारा	(i) प्लास्टिक छड़ (ii) ऐबोनाइट छड़
ऊनी कपड़ा	(i) अम्बर (ii) एबोनाइट (iii) प्लास्टिक (iv) रबड़

चालन (स्पश) द्वारा आवेशन (Charging by Conduction (Contact))
यदि किसी अनावेशित चालक को आवेशित चालक से स्पर्श कराया जाता है तो अनावेशित चालक पर आवेशित चालक के बराबर आवेश प्राप्त किया जा सकता है। ऐसा इसलिए होता है क्योंकि स्पर्श बिन्दु पर कुछ 'इलेक्ट्रॉन स्थानान्तरित हो जाते हैं। कोई आवेशित पिण्ड या वस्तु जब किसी आवेशित चालक के सम्पर्क (contact) में आती है तो वह आवेश का कुछ वितरण (distribution) कर सकती है।

सम्पर्क में स्थित दो वस्तुओं में एक वस्तु से दूसरी वस्तु को सीधे आवेश स्थानान्तरण को 'सम्पर्क द्वारा आवेशन' कहते हैं। यदि हम दो चालक वस्तुएँ लें जो कुचालक स्टैण्डों पर हैं इनमें एक आवेशित है तथा दूसरी अनावेशित है। इन्हें परस्पर स्पर्श कराने पर आवेश (चाहे धन हो या ऋण) अपने स्वयं के प्रतिकर्षण के कारण दोनों चालकों पर वितरित हो जाता है। अत: दोनों चालकों पर समान प्रकृति का आवेश हो जाता है।

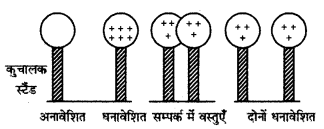
चित्र: चालन द्वारा आवेशन

विशेष नोट

• जब किसी चालक को धनावेशित किया जाता है तो उसका द्रव्यमान घट जाता है क्योंकि उस चालक से इलेक्ट्रॉन चले जाते हैं।
• जब किसी चालक को ऋणावेशित किया जाता है तो उसका द्रव्यमान बढ़ जाता है क्योंकि वह चालक इलेक्ट्रॉनों को ग्रहण (gain) कर लेता है।
• समान आवेश एक-दूसरे को प्रतिकर्षित करते हैं जबकि विपरीत आवेश एक-दूसरे को आकर्षित करते हैं। इस नियम को "कैवेण्डिश का स्थिर-विद्युत आकर्षण एवं प्रतिकर्षण का नियम" कहते हैं।
• आवेश हमेशा द्रव्यमान से सम्बद्ध (bound) होता है।

वैद्युत आवेश के मूल गुण (Fundamental Properties of Electric Charge)
हम जानते हैं कि वैद्युत आवेश दो प्रकार का होता है-धनावेश तथा ऋणावेश और ये दोनों एक-दूसरे को प्रभावहीन (neutralise) करने की प्रवृत्ति (tendency) भी रखते हैं। इस गुण के अतिरिक्त आवेश के कुछ अन्य गुणों पर भी विचार करना आवश्यक है जो कि निम्नलिखित हैं

आवेशों की योज्यता (Additivity of Charge):
"आवेशों की योज्यता वह गण है जिसके द्वारा किसी निकाय (system) का कुल आवेश उसके विभिन्न आवेशों के बीजीय योग (algebraic sum) से प्राप्त किया जाता है।" इसका अर्थ यह है कि आवेशों को वास्तविक संख्याओं (real numbers) की भाँति जोड़ा जा सकता है अर्थात् आवेश द्रव्यमान की भाँति अदिश राशि (scalar quantitiy) है। यदि किसी निकाय में n आवेश क्रमशः q₁, q₂, q₃, ..., q_n है तो निकाय का कुल आवेश
q = q₁ + q₂ + q₃ + ... + q_n होगा।

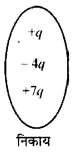
द्रव्यमान की भाँति आवेश में केवल परिमाण (magnitude)होता है दिशा (direction) नहीं। किसी वस्तु का द्रव्यमान केवल धनात्मक होता है लेकिन आवेश धनात्मक एवं ऋणात्मक दोनों प्रकार का हो सकता है। अतः निकाय का आवेश ज्ञात करते निकाय समय उचित चिह्न (sign) का प्रयोग करना आवश्यक होता है। उदाहरण के लिए, यदि किसी निकाय में + q - 4q व + 7q आवेश हैं तो निकाय का कुल आवेश
q = +q - 4q + 7q = + 4q होगा।

वैद्युत आवेश का संरक्षण (Conservation of Electric Charge)
"आवेश का संरक्षण वह गुण है जिसके कारण किसी विलगित निकाय (isolated system) का कुल आवेश नियत (constant) रहता है।" किसी विलगित निकाय में मौजूद अनेक आवेशित वस्तुओं के आवेश अन्योन्य क्रियाओं के कारण पुनर्वितरित हो सकते हैं लेकिन निकाय का कुल आवेश नियत रहेगा। उदाहरण के लिए, जब दो वस्तुओं को रगड़ते हैं तो एक वस्तु आवेश ग्रहण करती है और दूसरी वस्तु उतना ही आवेश खो देती है। इस प्रकार, "किसी विलगित निकाय के कुल आवेश को न तो नष्ट (nor be destroyed) किया जा सकता है और न ही उत्पन्न (neither be created) किया जा सकता है।" हालांकि आवेश वाहक कणों को किसी प्रक्रम (process) में नष्ट भी किया जा सकता है और उत्पन्न भी किया जा सकता है। उदाहरण के लिए, कोई न्यूट्रॉन एक प्रोटॉन एवं एक इलेक्ट्रॉन में बदल जाता है तो दोनों पर परिमाण में समान किन्तु प्रकृति में विपरीत आवेश होता है। इस प्रकार युग्म उत्पादन (pair production) से पूर्व एवं बाद में कुल आवेश शून्य ही रहता है। "समान एवं विपरीत प्रकृति के युग्म रूप (in pairs) में ही आवेश को उत्पन्न किया जा सकता है और उदासीन (neutral) भी किया जा सकता है।"

उदाहरण:
जब कैल्सियम (⁴⁴₂₀Ca) पर त्वरित प्रोटॉनों की बमबारी की जाती है तो न्यूट्रॉन उत्सर्जित होते हैं तथा निम्न प्रकार स्कैण्डियम बनता है

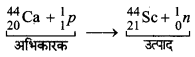
अभिकारकों पर कुल आवेश
= कैल्सियम पर आवेश + प्रोटॉन पर आवेश
= 20e + e=21e

उत्पादों पर कुल आवेश
= स्कैण्डियम आवेश + न्यूट्रॉन पर आवेश
= 21e + 0 = 21e

अतः अभिकारकों पर तथा उत्पादों पर कुल आवेश संरक्षित रहता है।

क्या आप जानते हैं ?

• आवेश का संरक्षण यह बताता है कि विद्युत आवेश का संरक्षण प्रकृति का वास्तविक नियम है। यह प्रकृति के सभी डोमेनों (Domains) के लिए सत्य है। यह उच्च ऊर्जा भौतिकी के डोमेनों के लिए जिसमें द्रव्यमान, ऊर्जा में एवं ऊर्जा, द्रव्यमान में बदलती है, के लिए भी सत्य है।
• आवेश का संरक्षण सार्वभौमिक (global) घटना है अर्थात् समस्त ब्रह्माण्ड (universe) का आवेश नियत है।
• आवेश का संरक्षण सभी बड़े से बड़े (macroscopic) से लेकर छोटे से छोटे (microscopic) प्रक्रमों के लिए सत्य है।

वैद्युत आवेश का क्वाण्टमीकरण (Quantization of Electric Charge)
"आवेश का क्वाण्टमीकरण वह गुण है जिसके कारण सभी मुक्त आवेश मूल आवेश (e) के पूर्ण-गुणज (integral multiple) होते हैं।" अर्थात् किसी वस्तु पर आवेश q हमेशा निम्न प्रकार होगा
q = ne ....(1)
जहाँ n = 0 ± 1 ± 2 ± 3 .......
जहाँ n एक पूर्ण संख्या है और e मूल आवेश (fundamental charge) है। इलेक्ट्रॉन अथवा प्रोटॉन के आवेश को ही मूल आवेश कहते हैं। परम्परा के अनुसार इलेक्ट्रॉन के आवेश को ऋणात्मक एवं प्रोटॉन के आवेश को धनात्मक रूप में लिया जाता है और इन्हें क्रमशः (- e) व (+ e) से व्यक्त किया जाता है।
e = 1.6 × 10^-19 कूलॉम ...(2)

यह प्रकृति के महत्त्वपूर्ण नियतांकों में से एक है।
यदि किसी वस्तु में n1 इलेक्ट्रॉन एवं 12 प्रोटॉन हैं तो उस पर कुल आवेश q= n₂ (e) + n₁ (-e) = (n₂ - n₁) होगा। चूँकि n₁ व n₂ पूर्ण संख्याएँ हैं अतः इनका अन्तर (n₂ - n₁) भी पूर्ण संख्या (whole number) होना चाहिए। इस प्रकार किसी आवेशित वस्तु पर आवेश सदैव e का पूर्ण गुणज होगा तथा आवेश की वृद्धि अथवा कमी भी e के पदों में ही होगी।

किसी वस्तु पर आवेश का सम्भव मान ±e, ± 2e, ± 3e,.... इत्यादि ही होगा अर्थात् सम्भव आवेश निम्नलिखित प्रकार होंगे
q = ±e = + 1.6 × 10^-19C
q = 2e = 2 × 1.6 × 10^-19 = +3.2 × 10^-19c
q = 3e = +3 × 1.6 × 10^-19 = +4.8 × 10^-19c
..............................................
..............................................
इन आवेशों के मध्य आवेश का कोई मान सम्भव नहीं है। दूसरे शब्दों में, आवेशित कण पर आवेश का मान e का भिन्नात्मक (fractional) गुणक (जैसे ±1.5e; ± 9.2e आदि) सम्भव नहीं है।
“आवेश के क्वाण्टमीकरण का कारण यह है कि इलेक्ट्रॉनों की पूर्ण संख्या ही एक वस्तु से दूसरी वस्तु को स्थानान्तरित हो सकती है।"

आवेश के क्वाण्टमीकरण का विचार सबसे पहले वैज्ञानिक फैराडे (Faraday) ने विद्युत्-अपघटन (electrolysis) के प्रायोगिक नियमों के आधार पर प्रस्तुत किया था लेकिन बाद में मिलिकन (Millikan) ने तेल बून्दक प्रयोग (Oil droplet Experiment) द्वारा इसका प्रायोगिक प्रदर्शन किया। इस प्रकार आवेश का क्वाण्टमीकरण प्रकृति के सभी डोमेनों में प्रयोग किया हुआ सिद्ध नियम है।

क्या आप जानते हैं
1. क्वार्क-गैलमेन तथा ज्वीग नामक वैज्ञानिकों ने एक कण क्वार्क की खोज की। उन्होंने बताया कि सभी कण अन्य मूल अवयवों से मिलकर बने हैं, जिनको क्वार्क (Quark) कहते हैं। परन्तु ये कण मुक्त अवस्था में प्रेक्षित नहीं होते। इन कणों को up quark, down quark, strange quark, top quark, bottom quark तथा charm quark के नाम से जाना जाता है। इनके आवेश क्रमशः + 2e/3,-e/3,-e/3, +2e/3,-e/3 तथा + 2e/3 होते हैं। क्वार्क मॉडल के अनुसार,

2. बड़े आवेशों (macroscopic charges) के प्रयोग के दौरान हम विद्युत आवेश के क्वाण्टमीकरण को छोड़ देते हैं, क्योंकि मूल आवेश e बहुत छोटा होता है और n बहुत बड़ा अतः अधिक प्रायोगिक स्थितियों में 4 सतत होता है अर्थात् बहुत अधिक आवेश का प्रवाह हो रहा है। आवेश का क्वाण्टमीकरण बहुत छोटे आवेशों (microscopic charges) के लिए महत्त्वपूर्ण है, जहाँ आवेश e की कोटि tens या hundreds में होती है
4. e का वास्तविक मान 1.602192 × 10^-19 C होता है तथा C.GS. पद्धति में - 4.8 × 10^-10 e.s.u. होता है।

आंकिक उदाहरण
(वैद्युत आवेश के क्वाण्टमीकरण पर आधारित आंकिक उदाहरण के लिए
(1) प्रयुक्त सूत्र
(a) q = ±ne
(b) आवेशन के समय द्रव्यमान का स्थानान्तरण
= m_e × n

(2) प्रयुक्त इकाईयाँ
q व e कूलॉम में एवं n एक वास्तविक संख्या है।

(3) प्रयुक्त नियतांक e= 1.6 × 10^-19 C, m_e = 9.1 × 10^-31kg

वैद्युत आवेश की अचरता (Invariance of Electric Charge)
विद्युत आवेश निर्देश तन्त्र में स्वतन्त्र होते हैं अर्थात् किसी वस्तु पर आवेश परिवर्तित नहीं होता है, वस्तु या प्रेक्षक की चाल चाहे जो भी हो।

विरामावस्था में आवेश = गतिमान अवस्था में आवेश
अर्थात् q विरामावस्था गतिमान अवस्था
हीलियम परमाणु तथा हाइड्रोजन अणु दोनों में ही 2 प्रोटॉन तथा 2 इलेक्ट्रॉन होते हैं, दोनों प्रोटॉन की गति में विभिन्नता होती है, जबकि इलेक्ट्रॉनों की गति समान होती है, परन्तु दोनों ही उदासीन होते हैं जो यह प्रदर्शित करता है कि गति के कारण आवेशों पर प्रभाव नहीं पड़ता है।

आवेश पर वेग का प्रभाव (Effect of Velocity on Charge)
आवेश की मात्रा पर वेग का कोई प्रभाव नहीं पड़ता है। उदाहरण के लिए, इलेक्ट्रॉन पर आवेश -1.6 × 10^-19 कूलॉम होता है, इलेक्ट्रॉन का वेग चाहे कुछ भी हो। त्वरित आवेश (accelerated charges) ऊर्जा को वितरित (radiate) करता है।।

महत्त्वपूर्ण बिन्दु
आवेश हमेशा द्रव्यमान से सम्बद्ध होता है अर्थात् द्रव्यमान के बिना आवेश का अस्तित्व संभव नहीं है किन्तु आवेश रहित द्रव्यमान संभव है जैसे फोटॉन पर न तो आवेश है और न ही
द्रव्यमान। न्यूट्रॉन पर द्रव्यमान है पर आवेश नहीं।

कूलॉम का नियम (Coulomb's Law):
फ्रांसीसी वैज्ञानिक कूलॉम ने सन् 1785 में आवेशित वस्तुओं के मध्य कार्य करने वाले आकर्षण (attraction) एवं प्रतिकर्षण (repulsion) बलों का परिमाणात्मक (magnitudinal) अध्ययन ऐंठन तुला प्रयोग (torsion balance experiment) द्वारा किया और प्राप्त प्रेक्षणों के आधार पर एक नियम की स्थापना की जो कूलॉम का व्युत्क्रम वर्ग नियम (Coulomb's inverse square law) कहलाया। इस नियम के अनुसार, "दो स्थिर बिन्दु आवेशों के मध्य कार्य करने वाला विद्युत (आकर्षण या प्रतिकर्षण) बल दोनों आवेशों की मात्राओं के गुणनफल के अनुक्रमानुपाती एवं उनके बीच की दूरी के वर्ग के व्युत्क्रमानुपाती होता है। यह बल दोनों आवेशों को मिलाने वाली रेखा के अनुदिश (along) होता है।"

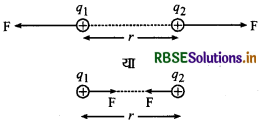
इस प्रकार यदि बिन्दु आवेशों q₁ व q₂ के बीच की दूरी न हो तो कूलॉम के नियमानुसार उनके मध्य लगने वाला आकर्षण या प्रतिकर्षण बल
F ∝ q₁q₂
एवं F ∝ \(\frac{1}{r^2}\)
या F ∝ \(\frac{q_1 q_2}{r^2}\)
या F = k \(\frac{q_1 q_2}{r^2}\) ....(1)
जहाँ {k} समानुपातिक (proportional) नियतांक है।
(i) यदि दोनों आवेश निर्वात् या वायु में रखे हों और बल को न्यूटन में, दूरी r को मीटर में तथा आवेशों को कूलॉम में व्यक्त किया जाये तो
k = \(\frac{1}{4 \pi \varepsilon_0}\) = 9 × 10⁹ न्यूटन मी/कूलॉम²

जहाँ ε₀ (एप्साइलन जीरो) निर्वात् की विद्युत्शीलता (permittiyity of free space) है। यदि निर्वात् या वायु में आवेशों के मध्य लगने वाले बल को F₀ से व्यक्त करें तो समी. (1) से,
F₀ = \(\frac{1}{4 \pi \varepsilon_0} \frac{q_1 q_2}{r^2}\) न्यूटन ...(2)

(ii) यदि आवेश किसी अन्य माध्यम में रखें हों तो
k = \(\frac{1}{4 \pi \varepsilon}\)
जहाँ ε, माध्यम की विद्युतशीलता है।
अतः समी. (1) से कूलॉम बल ।
F = \(\frac{1}{4 \pi \varepsilon} \cdot \frac{q_1 q_2}{r^2}\) न्यूटन ..(3)

प्रयोगों से यह देखा गया कि दो बिन्दु आवेशों के मध्य किसी निश्चित दूरी के लिए कार्य करने वाला बल निर्वात् में सबसे अधिक होता है। किसी माध्यम के लिए,
\(\frac{\mathrm{F}_0}{\mathrm{~F}}\) = नियतांक = K = माध्यम का परावैद्युतांक (dielectric constant of the medium)
समी. (2) व (3) से क्रमशः F₀ व F के मान रखने पर,
\(\frac{\varepsilon}{\varepsilon_0}\) = K
या ε = ε₀ यही निर्वात् की विद्युतशीलता (ε₀) एवं माध्यम की निरपेक्ष (absolute) विद्युतशीलता (ε) के मध्य सम्बन्ध है।
इस प्रकार समी. (3) में ६ का मान रखने पर कूलॉम बल के लिए व्यापक सूत्र प्राप्त होता है
F = \(\frac{1}{4 \pi \varepsilon_0 \mathrm{~K}} \frac{q_1 q_2}{r^2}\) ...(5)

जहाँ K को विशिष्ट परावैद्युतांक कहते हैं तथा कुचालक पदार्थ को परावैद्युत (dielectric) कहते हैं। सभी परावैद्युतों के लिए K का मान 1 से अधिक होता है। अतः यदि आवेशों के मध्य कोई परावैद्युत माध्यम हो तो उनके बीच वैद्युत बल घट जाता है।

माध्यमों के लिए K का मान

निर्वात	1
काँच	5 से 9
वायु	1.00054
अम्रक	3 से 6
कागज	3.5
पैराफिन मोम	2 से 2.5
पानी	80
ग्लिसरीन	42.5
धातुएँ	अनन्त (∞)
रबर	7

कूलॉम के नियम का महत्त्व (Importance of Coulomb's Law)
कलॉम के नियम से निम्नलिखित बलों को सरलतापूर्वक समझा जा सकता है

• किसी परमाणु के नाभिक तथा उसके परितः घूमने वाले इलेक्ट्रॉनों के मध्य लगने वाला बल।
• अणु बनाने वाले परमाणुओं के मध्य बन्धन (binding) बल।
• परमाणुओं या अणुओं को परस्पर सम्बद्ध कर द्रव अथवा ठोस बनाने वाले बल।

महत्त्वपूर्ण बिन्दु
कूलॉम का नियम बहुत बड़ी दूरियों से लेकर बहुत छोटी दूरियों, यहाँ तक कि परमाण्वीय (atomic) दूरियों (≈10^-11 m) तथा नाभिकीय (nuclear) दूरियों (≈10^-15 m) के लिए भी सत्य है।

आवेश का मात्रक (कूलॉम) (Unit of Charge : Coulomb)
निर्वात् में दो आवेशों के मध्य लगने वाला बल
F₀ = 9 × 10⁹ 9192
यदि q₁ = q₂ = 1 C; r = 1 m
तो F₀ = 9 × 10⁹ न्यूटन
अर्थात् “यदि निर्वात् में 1 मीटर की दूरी पर रखे दो समान परिमाण (magnitude) के आवेशों के मध्य 9 × 10⁹ न्यूटन का वैद्युत बल कार्य करे तो प्रत्येक आवेश 1 कूलॉम के बराबर होगा।" निर्वात् की वैद्युतशीलता, ε₀ (Permittivity of free space, to)

क्या आप जानते हैं?

• यदि आवेशित वस्तुओं का रेखीय आकार उनके बीच की दूरी से बहुत छोटा है तो उनके आकार को गणना में नहीं लाते और आवेशित वस्तुओं को बिन्दु आवेश कहा जाता है।
• कूलॉम का नियम केवल बिन्दु आवेशों के लिए सत्य है।
• 4πε₀ का S.I. इकाई में वास्तविक मान \(\frac{10^7}{c^2}\)C²N^-1m^-2 होता है। जहाँ c = निर्वात् में प्रकाश का वेग
• ऐसा कोई माध्यम नहीं है जिसके लिए K < 1 हो।

सदिश रूप में कूलोंम का नियम (Coulomb's Law In Vector Form)
कूलॉम के नियमानुसार, दो बिन्दु आवेशों q₁ व q₂ के मध्य लगने वाला वैद्युत बल आवेशों के गुणनफल के अनुक्रमानुपाती (proportional) एवं उनके मध्य दूरी के वर्ग के व्युत्क्रमानुपाती (inversely proportional) होता है अर्थात् यहाँ पर आवेशों के परिमाण |q₁| व |q₂| का प्रयोग किया गया है क्योंकि आवेश धनात्मक एवं ऋणात्मक कुछ भी हो सकते हैं और तद्नुसार बल भी आकर्षण या प्रतिकर्षण हो सकता है।
F = \(\frac{k\left|q_1\right|\left|q_2\right|}{r^2}\)
जहाँ k, स्थिरवैद्युत बल नियतांक है।
F ∝ \(\frac{\left|q_1\right|\left|q_2\right|}{r^2}\) या F ∝ \(\frac{q_1 q_2}{r^2}\)
चूँकि बल सदिश (vector) राशि है अतः कूलॉम बल को सदिश रूप में लिखना बेहतर होगा। माना समान प्रकृति के दो आवेश q₁ व q₂ बिन्दुओं A व B पर रखे हैं। ये दोनों आवेश एक-दूसरे पर प्रतिकर्षण बल आरोपित (impose) करेंगे। चित्र 1.10 में इनकी स्थितियाँ दिखायी गई हैं।

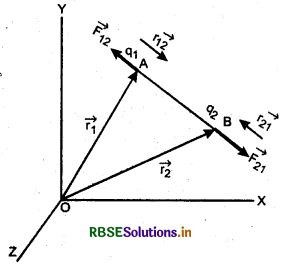
बिन्दु A का स्थिति वेक्टर \(\overrightarrow{r_1}=\overrightarrow{O A}\)
बिन्दु B का स्थिति वेक्टर \(\overrightarrow{r_2}=\overrightarrow{O B}\)
अतः q₁ से q₂ की ओर अर्थात् A से B की ओर वेक्टर
\(\overrightarrow{\mathrm{AB}}=\overrightarrow{r_{12}}=\overrightarrow{r_2}-\overrightarrow{r_1}\)

इसी प्रकार q₂ से q₁ की ओर वेक्टर
\(\overrightarrow{\mathrm{BA}}=\vec{r}_{21}=\overrightarrow{r_1}-\overrightarrow{r_2}\)

\(\overrightarrow{r_{12}}\) का परिमाण \(|\overrightarrow{r_{12}}|\) एवं \(\overrightarrow{r_{21}}\) का परिमाण \(|\overrightarrow{r_{21}}|\) होगा।
चूँकि किसी वेक्टर की दिशा एकांक वेक्टर (unit vector) द्वारा निर्धारित होती है, जिसकी दिशा उसी वेक्टर के अनुदिश होती है, अतः

इसी प्रकार यदि q₁ व q₂ विपरीत प्रकृति (opposite nature) के आवेश हैं तो वे एक-दूसरे को आकर्षित करेंगे अर्थात् q₁ q₂ < 0 (चित्र)। इस दशा में कूलॉम बल

महत्त्वपूर्ण बिन्दु

• ∵ \(\overrightarrow{\mathrm{F}_{12}}=-\overrightarrow{\mathrm{F}_{21}}\); अतः कूलॉम बल हमेशा न्यूटन के तृतीय नियम का पालन करता है।
• कूलॉम बल केन्द्रीय बल है अर्थात् दो वस्तुओं के बीच आरोपित कूलॉम बल उनको मिलाने वाली रेखा के अनुदिश कार्य करता

बहुल आवेशों के बीच बल (Forces between MultipleCharges) या अध्यारोपण का सिद्धान्त (Principle of Superposition)
दो बिन्दु आवेशों के बीच पारस्परिक (mutual) वैद्युत बल कूलॉम के नियम द्वारा प्राप्त होता है। जब आवेशों का एक समूह किसी आवेश पर बल लगाता है तो अध्यारोपण का सिद्धान्त उस आवेश पर लगने वाले बल को प्रदान करता है। इस सिद्धान्त के अनुसार, “जब कई आवेश किसी विशेष आवेश (special charge) पर बल लगाते हैं तो उस आवेश पर लगने वाला परिणामी बल उन सभी बलों का सदिश योग होता है जो वे सभी आवेश अलग-अलग उस आवेश पर स्वतन्त्र रूप से बल लगाते हैं। किसी एक आवेश द्वारा लगाया गया विशिष्ट बल (specific force) अन्य आवेशों की उपस्थिति (presence) के कारण प्रभावित (effected) नहीं होता।"

किन्हीं दो आवेशों के मध्य लगने वाला बल अन्य आवेशों की उपस्थिति से प्रभावित नहीं होता है।
माना n बिन्दु आवेशों का समूह क्रमशः q₁, q₂, q₃, ..., q_n आकाश में वितरित है (चित्र)। सभी आवेश एक-दूसरे पर बल लगाते हैं।

माना q₂, q₃, ..., q_n, आवेशों द्वारा आवेश q₁ पर आरोपित बल

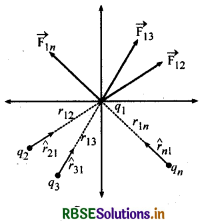
चित्र

क्रमशः \(\overrightarrow{\mathrm{F}_{12}}, \overrightarrow{\mathrm{F}_{13}}, \overrightarrow{\mathrm{F}_{14}}, \ldots, \overrightarrow{\mathrm{F}_{1 n}}\) हैं तो अध्यारोपण के सिद्धान्त के अनुसार आवेश q पर लगने वाला परिणामी बल निम्न समीकरण से प्राप्त होगा
\(\overrightarrow{\mathrm{F}_1}=\overrightarrow{\mathrm{F}_{12}}+\overrightarrow{\mathrm{F}_{13}}+\ldots \ldots+\overrightarrow{\mathrm{F}_{1 n}}\) ...(1)

यदि आवेश q₁ से आवेशों q₂, q₃, ..., q_n की दूरियाँ क्रमश:। r₁₂, r₁₃, ..., r_1n हों तथा सभी आवेशों से q₁ की ओर एकांक वेक्टर क्रमश: r̂₂₁, r̂₃₁, ... r̂_n1 हों तो

इसी प्रकार आवेश q₂ पर अन्य आवेशों द्वारा लगने वाले बलों का परिणामी बल

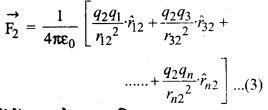
स्थिति सदिश के पदों में अध्यारोपण का सिद्धान्त (Superposition principle in terms of position vector),
माना q₁, q₂, q₃, ..., q_n बिन्दु आवेश किसी माध्यम में रखे हुए हैं। उनके स्थिति सदिश क्रमशः \(\overrightarrow{r_1}, \overrightarrow{r_2}, \overrightarrow{r_3}, \ldots \quad \overrightarrow{r_n}\), हैं। माना आवेश q₂ से q₁ की ओर एकांक सदिश r̂₂₁, q₃ से q₁ की ओर एकांक सदिश r̂₃₁ ....... एवं q_n, से q₁ की ओर r̂_n1 हैं। अतः

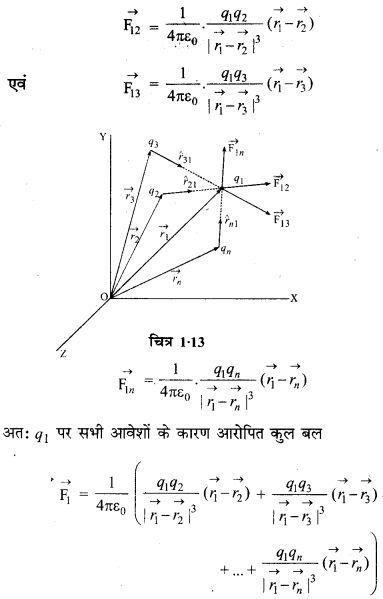
स्थिति सदिश (position vector) के पदों में i वें आवेश पर सभी (N - 1) आवेशों द्वारा आरोपित बल

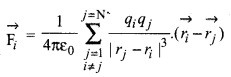
i ≠ j इसलिए है क्योंकि आवेश स्वयं पर कोई बल आरोपित नहीं करता है।

आंकिक उदाहरण
कूलॉम नियम पर आधारित आंकिक उदाहरण के लिए
1. प्रयुक्त सूत्रi.

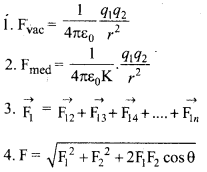
2. प्रयुक्त इकाइयाँ
q₁ व q₂ कूलॉम में, F-न्यूटन में, 7-मीटर में
3. प्रयुक्त नियतांक k = \(\frac{1}{4 \pi \varepsilon_0}\) = 9 × 10⁹ Nm²C^-2

स्थायी व अस्थायी सन्तुलन से सम्बन्धित प्रश्नों के लिए विशेष युक्तियाँ (Tricks) यदि दो आवेश नीचे दिखाये गये चित्रानुसार रखे हैं और एक तीसरा आवेश q₃ इस तरह से रखना है कि वे सभी आवेश सन्तुलन (equi| librium) में हों अर्थात् प्रत्येक आवेश पर नेट बल सदैव शून्य हो।

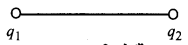
स्थिति I.
यदि q₁ व q₂ समान प्रकृति के हैं (धनात्मक या ऋणात्मक) और q₃ असमान प्रकृति का है, तो q₃ को उन आवेशों को मिलाने वाली रेखा के मध्य में रखना होगा।

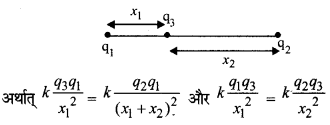
(यदि हम q₁ व q₃ के सन्तुलन को ले रहे हैं)

स्थिति II.
यदि q₁ व q₃ असमान प्रकृति के हैं, तो q₃ को अवश्य ही q₁ से पहले या q₂ से बाहर की ओर रखना होगा।

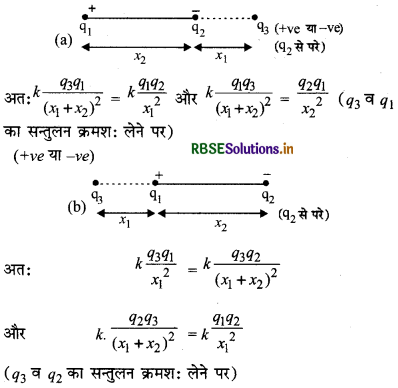
विद्युत् क्षेत्र (Electric Field):
किसी आवेश अथवा आवेश समूह (group of charges) के परितः वह क्षेत्र जहाँ तक उसके वैद्युत प्रभाव (electrical effect) का अनुभव किया जा सकता है अर्थात् जहाँ तक वह आवेश अथवा आवेश समूह किसी अन्य आवेश पर वैद्यत बल लगा सकता है, उस आवेश अथवा आवेश समूह का वैद्युत क्षेत्र कहलाता है। यह एक सदिश राशि है और इसकी दिशा धन परीक्षण (test) आवेश (+q₀) पर लगने वाले बल की दिशा से व्यक्त होती है। विद्युत क्षेत्र वैद्युत बल रेखाओं (electric lines of force) द्वारा व्यक्त (represent) किया जाता है।

यदि किसी बिन्दु पर धन परीक्षण आवेश कोई बल अनुभव नहीं करता है तो उस बिन्दु पर अन्य किसी आवेश द्वारा उत्पन्न विद्युत क्षेत्र शून्य होगा। विद्युत क्षेत्र की अभिधारणा (concept) सर्वप्रथम फैराडे (Faraday) ने प्रस्तुत की थी।

आवेश q, जो वैद्युत क्षेत्र उत्पन्न करता है, स्त्रोत आवेश (Source charge) कहलाता है और +q₀ आवेश, जो स्रोत आवेश के प्रभाव का परीक्षण करता है, परीक्षण आवेश (Test charge) कहलाता है। परीक्षण का स्वयं का अपना विद्युत क्षेत्र नहीं होता परन्तु स्रोत आवेश के विद्युत में प्रभावित होता है। स्रोत आवेश केवल एक आवेश हो सकता है और आवेश समूह भी हो सकता है।

विद्युत् क्षेत्र की तीव्रता-विद्युत् क्षेत्र में किसी बिन्दु पर धन परीक्षण आवेश (+q₀) पर यदि \(\vec{F}\) वैद्युत बल कार्य करे तो उस बिन्दु पर वैद्युत क्षेत्र की तीव्रता \(\vec{E}\) की परिभाषा निम्न प्रकार होगी
\(\vec{E} = \frac{\overrightarrow{\mathrm{F}}}{q_0}\) ..........(1)

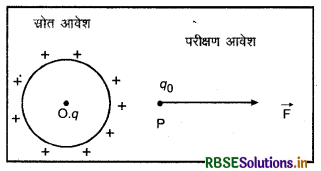
अर्थात्, "किसी बिन्दु पर विद्युत् क्षेत्र की तीव्रता उस बिन्दु पर स्थित आवेश पर लगने वाले बल तथा आवेश के अनुपात के बराबर होती है।"
विद्युत् क्षेत्र की दिशा धनावेश से दूर (away) की ओर और ऋणावेश की ओर (along) होती है

समीकरण (1) में यदि
q₀ = + 1 C तो \(\overrightarrow{\mathrm{E}}=\overrightarrow{\mathrm{F}}\)
अर्थात्, "किसी बिन्दु पर विद्युत् क्षेत्र की तीव्रता उस बल के तुल्य (equal) होती है जो उस बिन्दु पर एकांक (unit) धनावेश (positive charge) पर कार्य करता है।"
समीकरण (1) से स्पष्ट है कि
\(\overrightarrow{\mathrm{F}}=\overrightarrow{\mathrm{E}}\)q₀ या F = q₀E ...(2)

अर्थात् यदि कोई आवेश किसी विद्युत क्षेत्र में रखा है तो उस पर लगने वाला बल समी. (2) से प्राप्त होगा। धनावेश पर यह बल क्षेत्र की दिशा में (in the direction of force field) एवं ऋणावेश पर क्षेत्र की विपरीत दिशा (opposite direction) में कार्य करेगा (चित्र (c))।

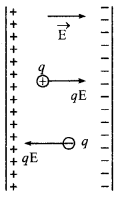
चूँकि परीक्षण आवेश +q₀ का स्वयं का विद्युत क्षेत्र किसी बिन्दु पर स्रोत आवेश के कारण उत्पन्न विद्युत क्षेत्र को प्रभावित (influence) करेगा। अतः इस प्रभाव को कम-से-कम करने के लिए हम समी. (1) को निम्न प्रकार लिख सकते हैं

महत्त्वपूर्ण बिन्दु
यहाँ विशेष बात यह याद रखने की है कि विद्युत् क्षेत्र की दिशा धनात्मक आवेश से दूर (away) जाती है और ऋणात्मक आवेश की दिशा में (along) होती है :
उदाहरण- (+q) → वैद्युत क्षेत्र की दिशा
(-q) - वैद्युत क्षेत्र की दिशा

बिन्दु आवेश के कारण उत्पन्न विद्युत् क्षेत्र की तीव्रता । (Intensity of Electric Field due to a Point Charge):
माना एक बिन्दु आवेश +q मूलबिन्दु O पर रखा है और r दूरी पर स्थित बिन्दु P पर बिन्दु आवेश +q के कारण विद्युत् क्षेत्र की तीव्रता ज्ञात करनी है।
P पर वैद्युत क्षेत्र की तीव्रता ज्ञात करने के लिए इस बिन्दु पर अति लघु धन परीक्षण आवेश +q₀ रखा हुआ मानते हैं तो कूलॉम के नियम से इस परीक्षण आवेश पर लगने वाला वैद्युत बल

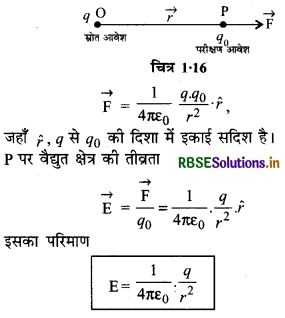
अतः E ∝ \(\frac{1}{r^2}\), अतः बिन्दु आवेश के चारों ओर खींचे गये गोलीय पृष्ठ पर स्थित सभी बिन्दुओं के लिए E का परिमाण समान होगा और यह है की दिशा पर निर्भर नहीं होगा। इस प्रकार का क्षेत्र गोलीय सममित (spherically symmetric) या त्रिज्यीय क्षेत्र (radial field) कहलाता है। यदि आवेश q से देखा जाये और इसका परिमाण आवेश से दूरी के वर्ग के व्युत्क्रमानुसार घटता है।
विद्युत क्षेत्र की तीव्रता एवं दूरी के साथ आरेख चित्र के अनुसार दर्शाते हैं

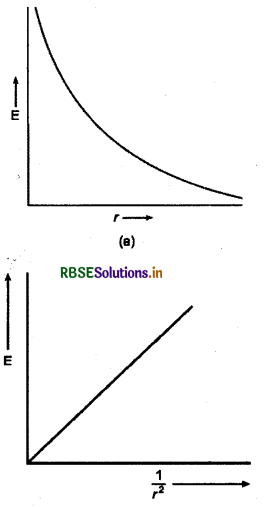
विद्युत क्षेत्र में परिवर्तन

यदि बिन्दु आवेश ६, परावैद्युतांक के माध्यम में स्थित है तब विद्युत क्षेत्र

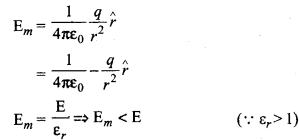
अर्थात् परावैद्युत माध्यम में विद्युत क्षेत्र की तीव्रता का मान निर्वात में तीव्रता की अपेक्षा ε_r गुणांक हो जाता है।।

विद्युत क्षेत्र की तीव्रता के कार्तीय घटक (Cartesian components):
यदि चित्र में बिन्दु P के निर्देशांक (x, y, z) हैं अतः बिन्दु P का स्थिति वेक्टर
\(\vec{r}\) = xî + yĵ + zk̂
और इसका परिमाण

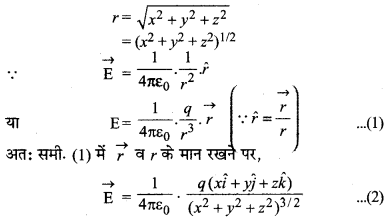
यदि E के कार्तीय अक्षों x, y, z के अनुदिश घटकों के परिमाण E_x, E_y, E_z, हों तो
\(\vec{E}\) = E_x î + E_yĵ + E_zk̂
समी. (2) व (3) की तुलना करने पर,

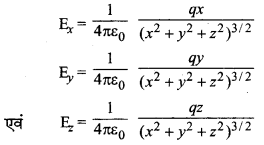
स्रोत आवेश एवं प्रेक्षण बिन्दु के स्थिति वेक्टरों के पदों में विद्युत् क्षेत्र (Electric field in Terms of Position Vectors of Source Charge and test Charge):
माना बिन्दु आवेश +q बिन्दु A पर स्थित है जिसका स्थिति वेक्टर \(\overrightarrow{\mathrm{OA}}=\overrightarrow{r^{\prime}}\) है और प्रेक्षण बिन्दु P का स्थिति वेक्टर \(\overrightarrow{\mathrm{OP}}=\vec{r}\) है। यदि बिन्दु P पर एक अत्यन्त लघु परिमाण (small magnitude) का धन परीक्षण आवेश +q₀ रखा जाये तो स्रोत आवेश q द्वारा उस पर आरोपित बल

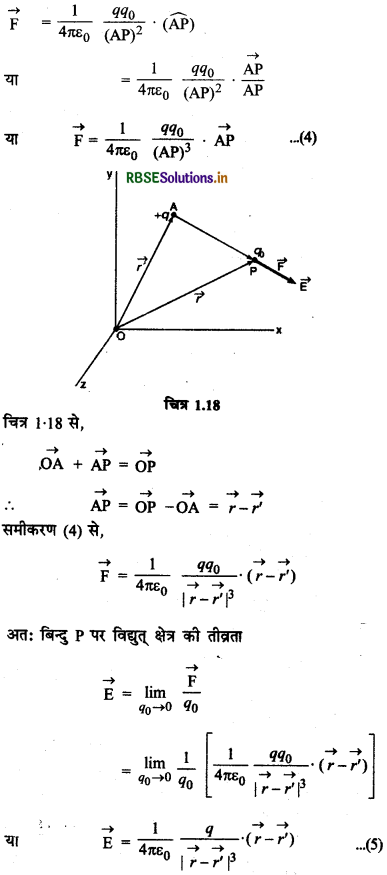
क्या आप जानते हैं ?

• परीक्षण आवेश भी अपना विद्युत् क्षेत्र उत्पन्न करता है, परन्तु यह नगण्य होता है।
• यदि q > 0 तो तीव्रता सदिश बिन्दु से त्रिज्यीय बाहर की ओर होगा।

आवेशों के निकाय के कारण विद्युत् क्षेत्र (Electric Field due to System of Charges)
विद्युत् क्षेत्र सदिश राशि है अतः यदि किसी बिन्दु P पर कई बिन्दु आवेश q₁, q₂, ...., q_n अलग-अलग विद्युत् क्षेत्र \(\overrightarrow{\mathrm{E}}_1, \overrightarrow{\mathrm{E}}_2, \ldots, \overrightarrow{\mathrm{E}}_n\), उत्पन्न कर रहे हों तो P का परिणामी विद्युत् क्षेत्र इन सभी विद्युत् क्षेत्रों के सदिश योग के बराबर होगा, अर्थात्

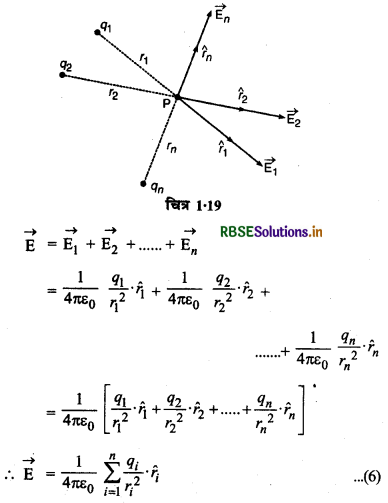
स्रोत आवेशों के स्थिति वेक्टरों के पदों में विद्युत क्षेत्र (Electric field in terms of position vector of source charges):
माना प्रेक्षण बिन्दु P पर कई बिन्दु आवेश q₁, q₂, ...., q_n, विद्युत् क्षेत्र उत्पन्न करते हैं। ये क्षेत्र क्रमशः \(\overrightarrow{\mathrm{E}}_1, \overrightarrow{\mathrm{E}}_2, \ldots, \overrightarrow{\mathrm{E}}_n\), हैं और बिन्दु आवेशों के स्थिति वेक्टर क्रमशः \(\overrightarrow{r_1}, \overrightarrow{r_2}, \ldots, \overrightarrow{r_n}\) है तथा प्रेक्षण बिन्दु का स्थिति वेक्टर \(\vec{r}\) है। जब स्रोत आवेश का स्थिति वेक्टर \(\vec{r}\) और प्रेक्षण बिन्दु \(\vec{r}\) होता है तो प्रेक्षण बिन्दु पर उत्पन्न विद्युत् क्षेत्र समी. (5) से,

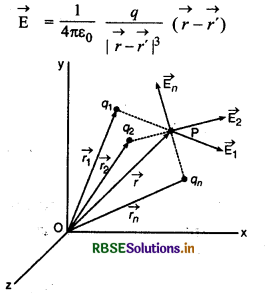
अतः सभी आवेशों के कारण प्रेक्षण बिन्दु पर उत्पन्न विद्यत् क्षेत्र की तीव्रता,

आंकिक उदाहरण
वैद्युत क्षेत्र की तीव्रता पर आधारित आंकिक उदाहरण के लिए प्रयुक्त सूत्र ,
1. (a) \(\overrightarrow{\mathrm{E}}=\frac{\overrightarrow{\mathrm{F}}}{q_0}\)
(b) बिन्दु आवेश के कारण विद्युत क्षेत्र
E = \(\frac{1}{4 \pi \varepsilon_0} \frac{q}{r^2}\)
(c) \(\overrightarrow{\mathrm{E}}=\overrightarrow{\mathrm{E}}_1+\overrightarrow{\mathrm{E}}_2+\overrightarrow{\mathrm{E}}_3+\ldots+\overrightarrow{\mathrm{E}}_n,\)
2. प्रयुक्त इकाई, ___E की इकाई NC^-1 या Vm^-1
3. प्रयुक्त नियतांक k = \(\frac{1}{4 \pi \varepsilon_0}\) = 9 × 10⁹ Nm²C^-2

विद्युत क्षेत्र का भौतिक अभिप्राय (Physical Significance of Electric Field)
आवेशों के किसी निकाय के लिए मापने योग्य राशि किसी आवेश पर आरोपित बल है जिसे हम सीधे ही कूलॉम के नियम तथा अध्यारोपण के सिद्धांत द्वारा निर्धारित कर सकते हैं। फिर विद्युत क्षेत्र नामक राशि को क्यों प्रस्तावित किया जाता है?
स्थिर-वैद्युतिकी के लिए विद्युत क्षेत्र की अविधारणा सुगम तो है पर वास्तव में आवश्यक नहीं है। विद्युत क्षेत्र आवेशों के किसी निकाय के परिवेश को अभिलक्षित करने का उपाय है। आवेशों के निकाय के चारों ओर के दिकस्थान में किसी बिन्दु पर विद्युत क्षेत्र यह दर्शाता है कि निकाय को विक्षुब्ध (Disturbance) किए बिना यदि उस बिन्दु पर कोई एकांक धनात्मक परीक्षण आवेश रखे तो वह कितना बल अनुभव करेगा। भौतिकी में क्षेत्र (Field) शब्द का उपयोग व्यापक रूप से उस राशि को निर्दिष्ट करने के लिए किया जाता है, जो दिक्स्थान के प्रत्येक बिन्दु पर परिभाषित किया जा सके तथा एक बिन्दु से दूसरे बिन्दु पर परिवर्तित होती हो। चूँकि बल सदिश राशि है, अतः विद्युत क्षेत्र भी एक सदिश राशि है।

विद्युत क्षेत्र की अभिधारणा की वास्तविक भौतिक सार्थकता तभी प्रकट होती है जब हम स्थिर-वैद्युतिकी से बाहर निकलकर कालाश्रित (time dependent) वैद्युत चुम्बकीय परिघटनाओं से व्यवहार करते हैं। मान लो हम त्वरित गति से गतिमान दो दूरस्थ आवेशों q₁ तथा q₂ के मध्य बल पर चर्चा करते हैं। अब, वह अधिकतम चाल जिसमें कोई संकेत (Signal) अथवा सूचना एक स्थान से दूसरे स्थान तक जा सके, वह प्रकाश की चाल c है। इस प्रकार q₂ पर q₁ की किसी गति का प्रभाव

तात्क्षणिक उत्पन्न नहीं हो सकता। कारण तथा प्रभाव के बीच कुछ न कुछ काल विलंब अवश्य होता है। यहीं पर सार्थक रूप में विद्युत क्षेत्र की अवधारणा स्वाभाविक एवं अति उपयोगी है।

वैद्युत क्षेत्र रेखाएँ (Electric Lines of Field)
“वैद्युत क्षेत्र में स्वतन्त्रतापूर्वक (freely) छोड़ा गया धन परीक्षण आवेश जिस मार्ग का अनुसरण (follow) करता है, उसे उस क्षेत्र की वैद्युत क्षेत्र-रेखा या विद्युत बल रेखा कहते हैं।" वैद्युत क्षेत्र रेखाओं की निम्नलिखित विशेषताएँ (characteristics) होती हैं

• वैद्युत क्षेत्र रेखा के किसी बिन्दु पर खींची गई स्पर्श रेखा उस बिन्दु पर परिणामी विद्युत् क्षेत्र की दिशा व्यक्त करती है।
• वैद्युत क्षेत्र रेखाएँ धन आवेश से ऋण आवेश की ओर चलती हैं।
• दो क्षेत्र रेखाएँ कभी एक-दूसरे को नहीं काटती (intersect) हैं क्योंकि यदि वे काटेंगी (चित्र) तो कटान बिन्दु (point of intersection) पर दोनों वक्रों पर खींची गई स्पर्श रेखाएँ दो परिणामी विद्युत् क्षेत्र व्यक्त करेंगी जो कि सम्भव नहीं है। अतः क्षेत्र रेखाओं का काटना भी सम्भव नहीं है।

• वैद्युत क्षेत्र रेखाएँ खुले वक्र (open curves) के रूप में होती हैं क्योंकि ये धनावेश से चलकर ऋणावेश पर समाप्त हो जाती हैं।
• वैद्युत क्षेत्र रेखाएँ किसी पृष्ठ से लम्बवत् बाहर निकलती हैं और पृष्ठ पर लम्बवत क्षेत्र ही समाप्त होती है।
• किसी स्थान पर वैद्युत बल रेखाओं का पृष्ठ घनत्व (surface density) (एकांक क्षेत्रफल से गुजरने वाली क्षेत्र रेखाओं की संख्या) उस स्थान पर 'वैद्युत' क्षेत्र की तीव्रता के अनुपात में होता है अर्थात् क्षेत्र रेखाएँ जितनी सघन (dense) होंगी, वहाँ विद्युत् क्षेत्र उतना ही प्रबल (strong) होगा। क्षेत्र रेखाओं की संख्या के पदों में विद्युत् क्षेत्र की तीव्रता की परिभाषा निम्न प्रकार की जा सकती है

"किसी स्थान पर क्षेत्र रेखाओं की दिशा के लम्बवत् एकांक क्षेत्रफल (unit area) से गुजरने वाली क्षेत्र रेखाओं की संख्या, उस स्थान पर विद्युत् क्षेत्र की तीव्रता के तुल्य होती है।"

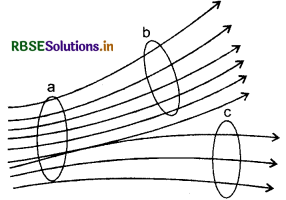
पर क्षेत्र अधिकतम तथा c पर न्यूनतम

• ये खिंची हुई लचकदार डोरी (flexible string) की तरह लम्बाई में सिकुड़ने (contract) का प्रयत्न करती हैं। इसी कारण विपरीत आवेशों में आकर्षण होता है।
• ये अपनी लम्बाई की लम्ब दिशा में एक-दूसरे से दूर रहने (for apart) का प्रयास करती हैं। इसलिए समान आवेशों के मध्य प्रतिकर्षण होता है।

क्या आप जानते हैं?

• क्षेत्र रेखाएँ काल्पनिक (imaginary) वक्र हैं, परन्तु उनके द्वारा प्रदर्शित क्षेत्र (field) वास्तविक (real) होता है।
• क्षेत्र रेखाएँ त्रिविमीय (three-dimensional) आकाश वक्र हैं।
• अगर क्षेत्र रेखाएँ किसी पृष्ठ के लम्बवत् नहीं हैं तो E का घटक पृष्ठ के समान्तर होगा और इलेक्ट्रॉन के प्रवाह को बढ़ायेगा अतः पृष्ठ पर धारा का प्रवाह होने लगेगा परन्तु सन्तुलन की अवस्था में कोई धारा प्रवाहित नहीं होती है।

(वैधत क्षेत्र रेखाओं के कछ उदाहरण)
(i) विलगित (isolated) बिन्दु आवेश के कारण क्षेत्र रेखाएँ-विलगित बिन्दु आवेश के कारण वैद्युत बल-रेखाएँ निम्न चित्र [(a) तथा (b)] में प्रदर्शित की गई हैं

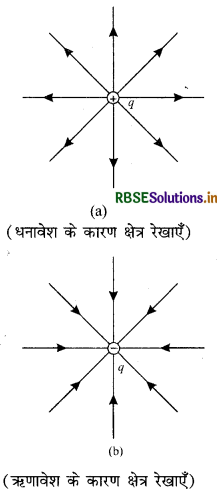
(ii) आवेश युग्म (pair of charges) के वैद्युत क्षेत्र के कारण क्षेत्र रेखाएँ
(a) यदि दोनों आवेश धनात्मक हों और परिमाण समान हों तो उनकी वैद्युत क्षेत्र रेखाएँ चित्र (a) के अनुसार होंगी।

(b) यदि दोनों आवेश परिमाण में समान किन्तु प्रकृति में ऋणात्मक हैं तो उनकी क्षेत्र रेखाएँ चित्र (b) की भाँति होंगी।

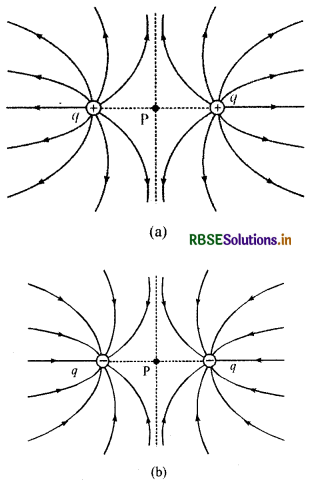
उक्त दोनों चित्रों में बिन्दु P को उदासीन बिन्दु (neutral point) कहते हैं क्योंकि इस बिन्दु पर परिणामी विद्युत् क्षेत्र शून्य है। यदि इस बिन्दु पर कोई अन्य आवेश रख दें तो उस पर कोई विद्युत् बल कार्य नहीं करेगा, अतः आवेश किसी भी दिशा में नहीं चलेगा क्योंकि इस बिन्दु पर परिणामी बल शून्य हो जाता है।

(c) यदि दोनों आवेश धनात्मक हैं लेकिन परिमाण में समान (equal) नहीं हैं तो उदासीन बिन्दु P छोटे आवेश (smaller charge) की ओर खिसक जायेगा और क्षेत्र रेखाएँ चित्र (a) की भाँति होंगी (q₁ < q₂)।

(d) यदि आवेश परिमाण में समान किन्तु प्रकृति में विपरीत (opposite) हैं तो वैद्युत क्षेत्र रेखाएँ चित्र (b) की भाँति होंगी।

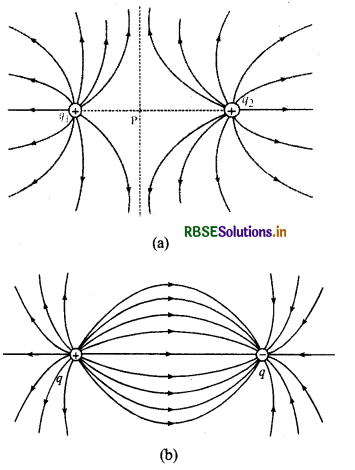
(e) यदि आवेश परिमाण (magnitude) व प्रकृति (nature) दोनों में । भिन्न हैं तो बल रेखाएँ चित्र की भाँति होंगी।

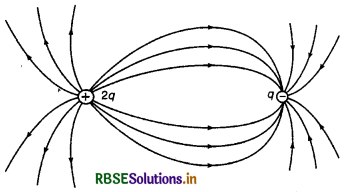
(iii) विस्तृत (large) आवेशित पृष्ठ के कारण वैद्युत क्षेत्र रेखाएँ-विस्तृत आवेशित पृष्ठ (धनात्मक) के परिच्छेद (section) के कारण वैद्युत क्षेत्र रेखाएँ चित्र 1.29 की भाँति होंगी।

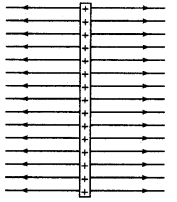
वैधुत क्षेत्र रेखाओं का आपेक्षिक घनत्व | (Relative Density of Electric Field Lines)
किसी आवेश के निकट विद्युत् क्षेत्र रेखाओं का घनत्व अधिक होता है और वे सघन होती हैं। आवेश से दूरी बढ़ने पर क्षेत्र दुर्बल हो जाता है और क्षेत्र रेखाओं का घनत्व कम होता है तथा क्षेत्र रेखाएँ दूर-दूर होती हैं। यदि हम कुछ त्रिज्यीय क्षेत्र रेखाओं का समुच्चय खींचें तो विभिन्न बिन्दुओं पर क्षेत्र रेखाओं का आपेक्षिक संख्या घनत्व उन बिन्दुओं पर विद्युत् क्षेत्र की आपेक्षिक प्रबलता दर्शाता है। चित्र 1:30 में कोई छोटा

अनुप्रस्थ रेखा अवयव Δl बिन्दु O से दूरी पर रखा जाता है। बिन्दु O द्वारा रेखा अवयव Δl द्वारा अंतरित कोण Δθ = Δl/r है। इसी प्रकार तीन विमाओं (Three dimensions) में किसी छोटे लम्बवत् क्षेत्र Δs द्वारा दूरी r पर अंतरित घन कोण को ΔΩ = ΔS/r² द्वारा व्यक्त करते हैं।

चित्र 1:30 में माना दो बिन्दुओं P₁, तथा P₂, के लिए घन कोण ΔΩ द्वारा P₁ पर अंतरित क्षेत्र अवयव r₁ Δ2 तथा P₂, पर अंतरित क्षेत्र अवयव r₂²ΔΩ है। इन क्षेत्र अवयवों को काटने वाली संख्या माना n है।

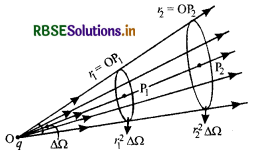
अतः P₁ बिन्दु पर एकांक क्षेत्रफल को काटने वाली क्षेत्र रेखाओं की संख्या = \(\frac{n}{r_1^2 \Delta \Omega}\)
एवं P₂ बिन्दु पर एकांक क्षेत्रफल को काटने वाली क्षेत्र रेखाओं की संख्या = \(\frac{n}{r_2^2 \Delta \Omega}\)
∵ विद्युत् क्षेत्र की तीव्रता क्षेत्र रेखाओं के घनत्व के अनुक्रमानुपाती होती है अतः

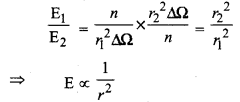
क्षेत्रफल सदिश (Area Vector)
किसी समतलीय क्षेत्रफल, जैसे ds में परिमाण के साथ-साथ दिशा भी होती है। क्षेत्रफल की दिशा पृष्ठ पर खींचे गये अभिलम्ब की दिशा में बाहर की ओर होती है।
क्षेत्रफल वेक्टर को d \(\overrightarrow{\mathrm{S}}\) से निरूपित कर सकते हैं। यदि

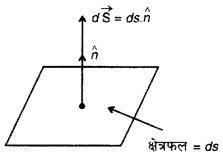
पृष्ठ की लम्ब दिशा में एकांक वेक्टर । हो और क्षेत्रफल का मान ds हो तो d \(\overrightarrow{\mathrm{S}}\) = ds. n̂

वैद्युत फ्लक्स (Electric Flux):
"विद्युत् क्षेत्र में रखे किसी पृष्ठ के लम्बवत् गुजरने वाली वैद्युत क्षेत्र रेखाओं की संख्या को उस पृष्ठ से सम्बद्ध वैद्युत फ्लक्स कहते हैं।" इसे 5 से व्यक्त करते हैं और यह एक अदिश राशि है।

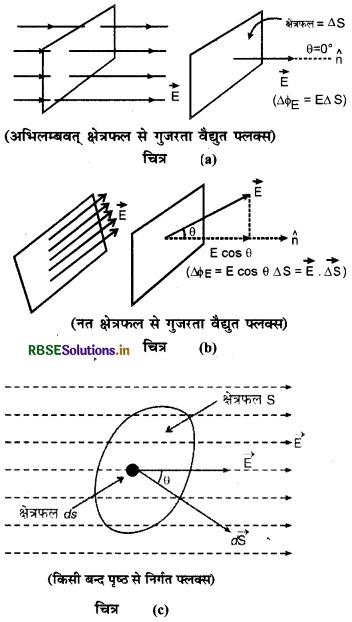
वैद्युत क्षेत्र बल रेखाओं की दिशा के लम्बवत् एकांक क्षेत्रफल से गुजरने वाली वैद्युत क्षेत्र रेखाओं की संख्या को फ्लक्स घनत्व (flux, density) या विद्युत् क्षेत्र की तीव्रता (E) कहते हैं। अतः वैद्युत क्षेत्र \(\overrightarrow{{E}}\) में स्थित किसी पृष्ठ के क्षेत्रफल के अल्पांश d\(\overrightarrow{\mathrm{S}}\) से सम्बद्ध वैद्युत फ्लक्स वेक्टर \(\overrightarrow{{E}}\) व d\(\overrightarrow{\mathrm{S}}\) के अदिश गुणन (scalar product) से प्राप्त होगा अर्थात्
dΦ_E = \(\overrightarrow{\mathrm{E}} \cdot d \overrightarrow{\mathrm{S}}\) = E . ds cos θ ....(1)
(i) यदिए θ = 0° = हो तो cos θ = 1
अतः dΦ_E = Eds जो कि अधिकतम मान है।

(ii) जब θ = 90° तो cos θ = 0
dΦ_E = 0 जो कि न्यूनतम मान है।
यदि कोई पृष्ठ असमान वैद्युत क्षेत्र में रखा है तो पृष्ठ से सम्बद्ध वैद्युत फ्लक्स ज्ञात करने के लिए अनेक अल्पांशों में बाँटकर उनसे सम्बद्ध वैद्युत फ्लक्स के मानों को जोड़कर कुल फ्लक्स ज्ञात करेंगे, अतः
Φ_E = \(\lim _{d s \rightarrow 0} \Sigma d \phi_{\mathrm{E}}=\lim _{d s \rightarrow 0} \Sigma \overrightarrow{\mathrm{E}} \cdot d \overrightarrow{\mathrm{S}}\)
Φ_E = \(\oint_{\mathrm{S}} \overrightarrow{\mathrm{E}} \cdot d \overrightarrow{\mathrm{S}}\) .........(2)

उपर्युक्त समाकल \(\oint_{\mathrm{S}}\) को वैद्युत क्षेत्र \(\overrightarrow{\mathrm{E}}\) का पृष्ठ समाकलन (surface integral) कहते हैं। यह समाकलन यह बताता है कि क्षेत्रफल S को d\(\overrightarrow{\mathrm{S}}\) क्षेत्रफल के सूक्ष्म पृष्ठों में विभाजित किया जाता है और अदिश राशि \(\overrightarrow{\mathrm{E}}.d\overrightarrow{\mathrm{S}}\) की गणना प्रत्येक सूक्ष्म क्षेत्रफल (elemental area) के लिए करके उनका योग लिया जाता है जो सम्पूर्ण पृष्ठ से सम्बद्ध वैद्युत फ्लक्स को व्यक्त करता है।

पुनः समीकरण (1) से स्पष्ट है कि वैद्युत फ्लक्स एक अदिश राशि है तथा किसी सूक्ष्म पृष्ठ से सम्बद्ध वैद्युत फ्लक्स dΦ_E का मान धनात्मक, शून्य अथवा ऋणात्मक हो सकता है जो E व ds के मध्य कोण θ पर निर्भर करता है। यदि कोण θ न्यूनकोण (< 90°) है तो फ्लक्स धनात्मक होता है, यदि θ = 90° हो तो फ्लक्स शून्य होता है और यदि θ अधिक कोण (> 90°) हो तो फ्लक्स ऋणात्मक होता है।

महत्त्वपूर्ण बिन्दु
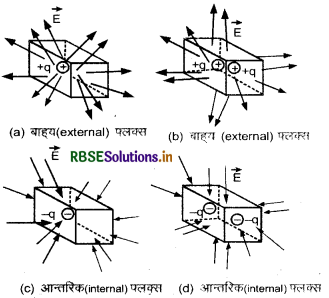
यदि क्षेत्र रेखाएँ पृष्ठ से बाहर (outwards) निकल रही हैं तो क का मान धनात्मक होता है और यदि क्षेत्र रेखाएँ पृष्ठ में प्रवेश कर रही हैं तो + का मान ऋणात्मक होता है। . एक घन के पृष्ठ पर विद्युत् क्षेत्र जबकि,
(a) घन के अन्दर एकल धनात्मक आवेश है।
(b) घन के अन्दर दो धनात्मक आवेश हैं।
(c) घन के अन्दर एकल ऋणात्मक आवेश है।
(d) घन के अन्दर दो ऋणात्मक आवेश हैं।

मात्रक एवं विमीय सूत्र (Unit and dimensional formula):
∵ वैद्युत फ्लक्स dΦ_E = \(\overrightarrow{\mathrm{E}} \cdot d \overrightarrow{\mathrm{S}}\)
अतः वैद्युत फ्लक्स का मात्रक
= E का मात्रक × ds का मात्रक

= Nm²C^-1

यदि E का मात्रक Vm^-1 लें तो
dΦ_E का मात्रक- Vm^-1m² = Vm

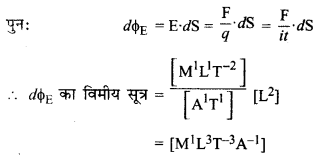
आकिक उदाहरण
वैद्युत फ्लक्स पर आधारित आंकिक उदाहरण के लिए, प्रयुक्त सूत्र|
(1) (a) Φ_E = \(\overrightarrow{\mathrm{E}} \cdot \vec{S}\) = ES cose
(b) फ्लक्स घनत्व

(2) प्रयुक्त इकाईयाँ (a) Φ_E = Nm²C^-1
(b) फ्लक्स घनत्व = NC^-1

(3) प्रयुक्त नियतांक
k = \(\frac{1}{4 \pi \varepsilon_0}\) Nm²C^-1

वैद्युत द्विध्रुव (Electric Dipole):
"जब परिमाण में समान किन्तु प्रकृति में विपरीत (equal in magnitude but differ in nature) दो आवेश किसी अल्प दूरी (small distance) पर रखे होते हैं तो वे वैद्युत द्विध्रुव की रचना करते हैं। किसी आवेश एवं दोनों आवेशों के मध्य दूरी का गुणनफल वैद्युत द्विध्रुव आघूर्ण (electric dipole moment) कहलाता है।" इसे p से व्यक्त करते हैं। यह सदिश राशि है जिसकी दिशा ऋण आवेश से धन आवेश की ओर होती है।

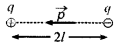
माना कि वैद्युत द्विध्रुव के आवेश -q व +q कूलॉम हैं तथा उनके बीच की अल्प दूरी 21 हो तो -21वैद्युत द्विध्रुव आघूर्ण
p = q × 2l ...(1)
वैद्युत द्विध्रुव आघूर्ण का मात्रक = Cm तथा वैद्युत द्विध्रुव आघूर्ण का विमीय सूत्र
= [A¹T¹L¹]
= [M⁰L¹T¹A¹]

वैद्युत द्विध्रुव के कारण उत्पन्न विद्युत क्षेत्र की तीव्रता (Intensity of Electric Field Produced due to an Electric Dipole):
(a) अक्षीय स्थिति (axial position) में:
माना एक वैद्युत द्विध्रुव AB, + q तथा -कूलॉम के आवेशों का बना है जिनके बीच की दूरी 21 है। द्विध्रुव के मध्य-बिन्दु 0 से दूरी पर स्थित बिन्दु P पर विद्युत् क्षेत्र
की तीव्रता ज्ञात करनी है।

+q आवेश के कारण P पर उत्पन्न विद्युत् क्षेत्र की तीव्रता का परिमाण

-q आवेश के कारण P पर उत्पन्न विद्युत् क्षेत्र की तीव्रता का परिमाण
E₂ = \(\frac{1}{4 \pi \varepsilon_0} \frac{q}{(r+l)^2}\)(PA दिशा में) ..(2)
P पर परिणामी विद्युत् क्षेत्र
\(\overrightarrow{\mathrm{E}}=\overrightarrow{\mathrm{E}_1}+\overrightarrow{\mathrm{E}_2}\)

∵ \(\overrightarrow{\mathrm{E}_1} \)व \(\overrightarrow{\mathrm{E}_2}\), की दिशाएँ परस्पर विपरीत हैं तथा E₁ > E₂
∴ P पर परिणामी विद्युत् क्षेत्र की तीव्रता का परिमाण
E = E₁ - E₂

∵ \( \vec{p}\) की दिशा ऋण आवेश से धन आवेश की ओर होती है अतः \( \vec{p}\) व \(\vec{E}\) एक ही दिशा में होंगे। इस प्रकार सदिश रूप में समी. (3) को निम्न प्रकार व्यक्त करेंगे
\(\overrightarrow{\mathrm{E}}=\frac{1}{4 \pi \varepsilon_0} \frac{2 r \cdot \vec{p}}{\left(r^2-l^2\right)^2}\) .......(4)
दीर्घ दूरियों के लिए r >> 1 ∴ r² >>> l²

अतः l² को r² की तुलना में छोड़ने पर समी. (3) से,

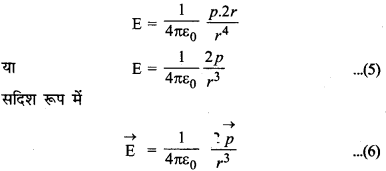
महत्त्वपूर्ण बिन्दु
अक्षीय स्थिति में विद्युत् द्विध्रुव आघूर्ण और विद्युत् क्षेत्र की दिशा एक ही होंगी।

(b) निरक्षीय स्थिति (equatorial position) में-
वैद्युत द्विध्रुव की निरक्षीय स्थिति में r दूरी पर स्थित बिन्दु P पर विद्युत् क्षेत्र की तीव्रता ज्ञात करनी है। बिन्दु P से दोनों आवेशों की दूरियाँ समान (\(\sqrt{r^2+l^2}\)) होंगी। अतः P पर +q आवेश के कारण उत्पन्न विद्युत् क्षेत्र की तीव्रता का परिमाण

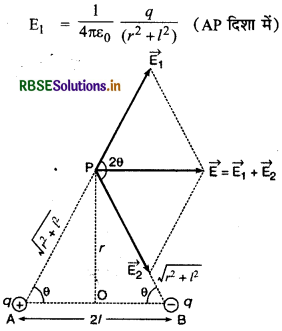
और -q आवेश के कारण P पर उत्पन्न विद्युत् क्षेत्र की तीव्रता का परिमाण
E₂ = \(\frac{1}{4 \pi \varepsilon_0} \frac{q}{\left(r^2+l^2\right)}\) (PB दिशा में)
इस प्रकार \(\left|\overrightarrow{E_1}\right|=\left|\overrightarrow{E_2}\right| \) या E₁ = E₂

बिन्दु P पर परिणामी विद्युत् क्षेत्र की तीव्रता
\(\overrightarrow{\mathrm{E}}=\overrightarrow{\mathrm{E}_1}+\overrightarrow{\mathrm{E}_2}\)

समान्तर चतुर्भुज के नियम से परिणामी विद्युत् क्षेत्र की तीव्रता का परिमाण

चित्र में \(\overrightarrow{\mathrm{E}}\) की दिशा द्विध्रुव की अक्ष के समान्तर होगी। चूँकि \(\vec{p}\) की दिशा ऋण आवेश से धन आवेश की ओर होती है अत: \(\overrightarrow{\mathrm{E}}\) व \(\vec{p}\) की दिशाएँ परस्पर विपरीत होंगी। इस प्रकार समी. (7) को सदिश रूप में निम्न प्रकार लिख सकते हैं
\(\overrightarrow{\mathrm{E}}=\frac{1}{4 \pi \varepsilon_0} \frac{\vec{p}}{\left(r^2+l^2\right)^{3 / 2}}\) .........(8)

दीर्घ दूरियों के लिए r > > l
∴ r² > > l²
अतः l² को r² की तुलना में छोड़ने पर समी. (7) से,
E = \(\frac{1}{4 \pi \varepsilon_0} \frac{p}{r^3}\) .........(9)
सदिश रूप में
\(\overrightarrow{\mathrm{E}}=-\frac{1}{4 \pi \varepsilon_0} \frac{\vec{p}}{r^3}\) ...........(10)

महत्त्वपूर्ण बिन्दु

• निरक्षीय स्थिति (equatorial position) में विद्युत् क्षेत्र और विद्युत् द्विध्रुव आघूर्ण की दिशा विपरीत होंगी।
• निरक्षीय रेखा को उदासीन (neutral) अक्ष (axis) भी कहते हैं।

(c) वैद्युत द्विध्रुव के कारण किसी बिन्दु पर विद्युत् क्षेत्र की तीव्रता (Intensity of electric field on any point due to electric dipole):
जैसा कि चित्र 1:37 में दिखाया गया है, AB एक वैद्युत द्विध्रुव है जिसकी अक्ष से 0 कोण एवं मध्य-बिन्दु 0 से दूरी पर स्थित बिन्दु P पर वैद्युत क्षेत्र की तीव्रता ज्ञात करनी है।

वैद्युत द्विध्रुव आघूर्ण \(\vec{p}\) को निम्न दो घटकों (components) में विभाजित किया जा सकता है

• p cos θ, दिशा OP में
• p sin θ, दिशा OP की लम्ब दिशा में।

p वैद्युत द्विध्रुव आघूर्ण वाले वैद्युत द्विध्रुव AB को दो द्विध्रुवों

• p cos θ द्विध्रुव आघूर्ण वाले द्विध्रुव A, B और
• p sin θ द्विध्रुव आघूर्ण वाले द्विध्रुव A,B, के संयोजन से मिलकर बना हुआ मान सकते हैं। ये दोनों द्विध्रुव परस्पर लम्बवत् हैं।

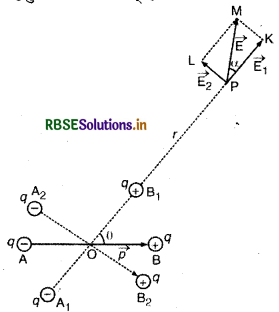
बिन्दु P द्विध्रुव A₁B₁ की अक्ष पर और A₂B₂ की निरक्षीय रेखा (equatorial ]ine) पर स्थित है अतः द्विध्रुव A₁B₁ के कारण P पर उत्पन्न विद्युत् क्षेत्र की तीव्रता का परिमाण
E₁ = \(\frac{1}{4 \pi \varepsilon_0} \frac{2 p \cos \theta}{r^3}\) (PK दिशा में) ...(11)
और द्विध्रुव A,B, के कारण इसकी निरक्षीय स्थिति में विद्युत् क्षेत्र की तीव्रता का परिमाण
E₂ = \(\frac{1}{4 \pi \varepsilon_0} \frac{p \sin \theta}{r^3}\) ....(12)
(PL दिशा में जो कि PK के लम्बवत् है)

अतः P बिन्दु पर परिणामी विद्युत् क्षेत्र की तीव्रता
\(\overrightarrow{\mathrm{E}}=\overrightarrow{\mathrm{E}_1}+\overrightarrow{\mathrm{E}_2} \because \overrightarrow{\mathrm{E}_1} \perp \overrightarrow{\mathrm{E}_2}\)
अतः \(\overrightarrow{\mathrm{E}}\) का परिमाण

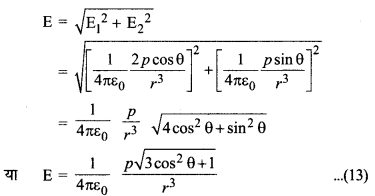
द्विध्रुव के कारण परिणामी विद्युत् क्षेत्र की दिशा ज्ञात करने के लिए माना कि परिणामी विद्युत् क्षेत्र E वेक्टर E के साथ a कोण बनाता है तो चित्र 1.37 के समकोण त्रिभुज PKM में,

इस समीकरण से a का मान ज्ञात कर सकते हैं।

आंकिक उदाहरण
विद्युत् द्विध्रुव आघूर्ण के कारण उत्पन्न विद्युत् क्षेत्र पर आधारित आंकिक उदाहरण के लिए
1. प्रयुक्त सूत्र
(a) अक्षीय स्थिति में

2. प्रयुक्त इकाइयाँ
E - NC^-1 या Vm^-1

द्विध्रुवों की भौतिक सार्थकता (Physical Significance of Dipoles):
ध्रुवी एवं अध्रुवी अणु-जब किसी अणु में धन एवं ऋण आवेश अणु के सभी भागों में समान रूप से वितरित होते हैं तो दोनों आवेशों का प्रभावी केन्द्र एक ही होता है। ऐसे अणु विद्युत्-उदासीन (electrically neutral) होते हैं और इन्हें अधुवी अणु (non-polar molecule) कहते हैं।

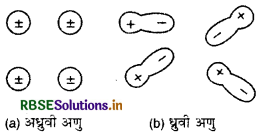
कुछ पदार्थों के अणुओं में धन एवं ऋण आवेशों का वितरण समरूप (uniform) नहीं होता है। इसमें धन एवं ऋण आवेशों के प्रभावी केन्द्र भिन्न होते हैं, ऐसे अणु ध्रुवी अणु (polar molecule) कहलाते हैं।

उदाहरण के लिए, HCl अणु ध्रुवी होता है, इसमें एक H⁺ आयन और दूसरा Cl^- आयन परस्पर वैद्युत आकर्षण से बँधे रहते हैं। इसमें धन एवं ऋण आवेशों के प्रभावी केन्द्रों के मध्य लगभग 10-11 m की दूरी रहती है। इसी प्रकार सभी विद्युत्-अपघट्य (electrolytes) पदार्थों के अणु ध्रुवी होते हैं। सभी ध्रुवी अणु जैसे-HCl, H₂O, NaCl, AgNO₃ आदि वैद्युत द्विध्रुव के उदाहरण हैं।

महत्त्वपूर्ण बिन्दु-

• परमाणु (atom) में धनावेश (नाभिक) का केन्द्र तथा ऋणावेश (इलेक्ट्रॉनों) का केन्द्र परस्पर सम्पाती (coincide) होते हैं। अत: परमाणु द्विध्रुव नहीं होता है। परन्तु यदि परमाणु को वैद्युत क्षेत्र में रख दें तो धन एवं ऋण आवेशों के केन्द्र एक-दूसरे के सापेक्ष हट जाते हैं और परमाणु द्विध्रुव बन जाता है।
• यदि आवेश q काफी बड़ा हो जाये और आवेशों के मध्य दूरी 21 बहुत अल्प हो जाये तो ऐसा समायोजन (arrangement) एक आदर्श वैद्युत द्विध्रुव (ideal electric dipole) कहलाता है।

एकसमान बाह्य क्षेत्र में द्विध्रुव (Dipole in a Uniform External Field)
(a) समरूप विद्युत् क्षेत्र में द्विध्रुव पर लगने वाले बलयुग्म का आघूर्ण-चित्र में एक समरूप विद्युत् क्षेत्र में एक वैद्युत द्विध्रुव

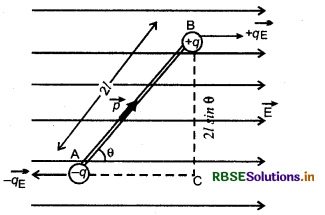
θ विक्षेप (deflection) की स्थिति में दिखाया गया है। द्विध्रुव के आवेशों (+q) व (-4) पर लगने वाले वैद्युत बल (qE) परिमाण में समान एवं दिशा में विपरीत हैं तथा दोनों की क्रिया रेखाएँ (line of action) भिन्न (different) हैं। अतः ये दोनों बल बलयुग्म बनाते हैं। इस बल युग्म का आघूर्ण
τ = बल x बलों की क्रिया रेखाओं के मध्य दूरी
τ = qE BC
चित्र से, \(\frac{\mathrm{BC}}{\mathrm{AB}}\) = sin θ
या BC = AB sin θ
अतः BC = 2l. sin θ
τ = qE × 2l sin θ
= q.2l. E sin θ
τ = pE sin θ न्यूटन × मीटर

चित्र की सहायता से सदिश रूप (vecter form) में बलयुग्म के आघूर्ण को निम्न प्रकार लिख सकते हैं

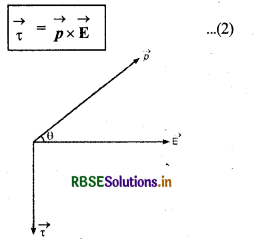
सदिश राशि बल आघूर्ण \(\vec{τ}\) की दिशा दक्षिणावर्त पेंच के नियमानुसार (according to right handed screw rule) \(\vec{p}\) व \(\vec{E}\) के तल के लम्बवत् होती है (चित्र)।
(i) जब θ = 0 तो sin θ = 0
अतः = pE sin θ = 0
या θ = 0
यही स्थायी सन्तुलन (stable equilibrium) की अवस्था है।

(ii) यदि θ = 90° तो sin θ = 1 .
τ_max = pE

(iii) ∵ τ = pE sin θ
यदि E = 1 NC^-1, sin θ = 1
अर्थात् θ = 90°
तो τ = p
अर्थात् “वैद्युत द्विध्रुव आघूर्ण उस बलयुग्म के आघूर्ण (torque) के तुल्य है जो द्विध्रुव पर तब कार्य करता है जब वह एकांक तीव्रता के समरूप (uniform) वैद्युत क्षेत्र में क्षेत्र के लम्बवत् रखा होता है।"

(b) जब वैद्युत द्विध्रुव असमान (non-uniform) विद्युत् क्षेत्र में होता है
(i) जब विद्युत् क्षेत्र \(\vec{p}\) की दिशा में बढ़ता है-इस दशा में यदि (-q) आवेश की स्थिति में विद्युत् क्षेत्र E₁ और (+q) की स्थिति में E₂ है और E₂ > E₁, अतः (-q) पर बल qE₂, आवेश (+q) पर बल qEसे कम होगा और फलस्वरूप नेट बल = qE₂ - qE₁, होगा (चित्र)

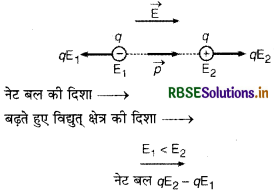
(ii) जब विद्युत् क्षेत्र \(\vec{p}\) की विपरीत दिशा में बढ़ता है-इस दशा में (-q) पर लगने वाला बल qE₁, आवेश (+q) पर लगने वाले बल qE₂, से अधिक होगा क्योंकि E₁ > E₂, अतः नेट बल = qE₁ - qE₂ होगा (चित्र)।

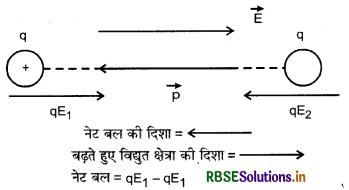
उक्त दोनों स्थितियों में द्विध्रुव पर नेट बल युग्म का आघूर्ण τ = pE sin θ = 0 होगा क्योंकि θ = 0° ।

महत्त्वपूर्ण बिन्दु

• यदि विद्युत क्षेत्र असमान हैं तो द्विध्रुव पर बलयुग्म के साथ नेट बल भी कार्य करता है। अतः जब \(\vec{p}\) क्षेत्र \(\vec{E}\) के समान्तर है तो द्विध्रुव पर बढ़ते क्षेत्र की दिशा (direction of increasing field) में एक नेट बल कार्य करता है। जब क्षेत्र \(\vec{E}\) के प्रतिसमान्तर (anti parallel) होता है तो द्विध्रुव पर घटते क्षेत्र की दिशा में (direction of decreasing field) एक नेट बल कार्य करता है। वास्तव में बल, \(\vec{E}\) के सापेक्ष \(\vec{p}\) के द्विक्विन्यास (double orientation) पर निर्भर करता है।
• किसी एकसमान विद्युत क्षेत्र में कोई वैद्युत द्विध्रुव एक बल आघूर्ण का अनुभव करता है। परन्तु किसी नेट बल का अनुभव नहीं करता।

वैद्युत क्षेत्र में द्विध्रुव को घुमाने में किया गया कार्य (Work Done in Rotating Dipole in an Electric Field)
यदि कोई वैद्युत द्विध्रुव समरूप वैद्युत क्षेत्र में क्षेत्र के साथ θ विक्षेप की स्थिति में रखा है तो उस पर लगने वाले बलयुग्म का आघूर्ण
τ = pE sin θ

इस स्थिति से dθ कोणीय विस्थापन (angular displacement) देने में किया गया कार्य
dw = τ.dθ

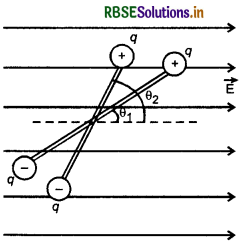
अतः θ₁ विक्षेप की स्थिति से θ₂ विक्षेप की स्थिति तक द्विध्रुव को घुमाने में किया गया कार्य

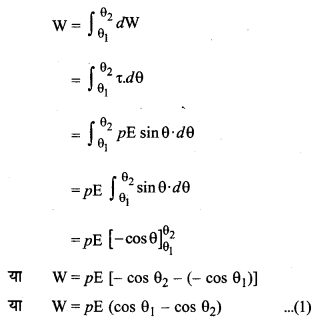
(i) स्थायी सन्तुलन (stable equilibrium)(अर्थात् θ₁ = 0) से θ विक्षेप देने में (अर्थात् θ₂ = 0) कृत कार्य
W = pE (cos 0 - cos θ)
या W = pE (1 - cos θ) ...(2)

(ii) स्थायी सन्तुलन से 90° विक्षेप देने में कृत कार्य
W = pE (1 - cos 90°)
W = pE

(iii) स्थायी सन्तुलन से 180° विक्षेप देने में कृत कार्य
W = PE (1 - cos 180°)
या W = pE [1 - (-1)] = pE (1 + 1)
या W = 2pE

समरूप विद्युत् क्षेत्र में वैद्युत द्विध्रुव की स्थितिज ऊर्जा (Potential Energy of Electric Dipole in a Uniform Electric Field)
"विद्युत क्षेत्र में किसी वैद्युत द्विध्रुव की स्थितिज ऊर्जा उस कार्य के तुल्य है जो द्विध्रुव को अनन्त (infinite) से उस स्थिति (position) तक लाने में करना पड़ता है।" वैद्युत स्थितिज ऊर्जा को इस प्रकार भी परिभाषित कर सकते हैं "विद्युत क्षेत्र में शून्य ऊर्जा की स्थिति से किसी स्थिति विशेष तक द्विध्रुव को ले जाने में अर्थात् घुमाने में किया गया कार्य उस स्थिति में द्विध्रुव की स्थितिज ऊर्जा के बराबर होता है।" यह सिद्ध किया जा सकता है कि द्विध्रुव की स्थितिज ऊर्जा तब शून्य होगी जब वह क्षेत्र के साथ लम्बवत् होती है।

θ विक्षेप की स्थिति में द्विध्रुव पर लगने वाले बलयुग्म का आघूर्ण
τ = pE sin θ

इस स्थिति से dθ कोणीय विस्थापन (angular displacement) देने में किया गया कार्य
dw = τ.dθ

∴ शून्य ऊर्जा की स्थिति (अर्थात् θ = 90°) से विक्षेप की स्थिति तक द्विध्रुव को घुमाने में कृत कार्य अर्थात् θ विक्षेप की स्थिति में वैद्युत द्विध्रुव की स्थितिज ऊर्जा

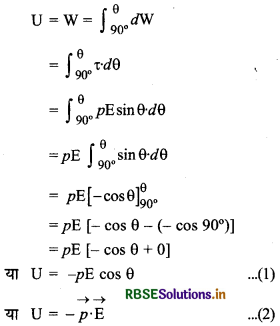
स्पष्ट है कि द्विध्रुव की वैद्युत स्थितिज ऊर्जा अदिश (scalar) राशि है। इसकी माप (measure) जूल में की जाती है।
(i) जब θ = 0° तो cos θ = 1
U = -pE

(ii) जब θ = 90° तो cos θ = 0
U = 0.

(iii) समी. (1) की सहायता से द्विध्रुव को विद्युत् क्षेत्र में घुमाने में किया गया कार्य ज्ञात कर सकते हैं।
यदि θ₁, विक्षेप की स्थिति में स्थितिज ऊर्जा U₁, और θ₂, विक्षेप में U₂, है तो θ₁ से θ₂ तक द्विध्रुव को घुमाने में कृत कार्य
W₂ = U₂ - U₁
= - pE cos θ₂ - (- pE cos θ₁)
=pE cos θ₁ - pE cos θ₂
W = pE (cos θ₁) - cos θ₂)) ...(3)

(वैद्युत क्षेत्र में वैद्युत द्विध्रुव पर आधारित आंकिक उदाहरण के लिए,
1. प्रयुक्त सूत्र:
(a) विद्युत द्विध्रुव आघूर्ण p = q × 2l
(b) बल युग्म का आघूर्ण
τ = pE sin θ

(c) द्विध्रुव की स्थितिज ऊर्जा
U = - pE cos θ

(d) स्थायी सन्तुलन की स्थिति से q कोणीय विस्थापन में किया गया कार्य
W = PE (1 - cos θ)

2. प्रयुक्त इकाईयाँ
विद्युत् द्विध्रुव आघूर्ण-C-m
द्विध्रुव की स्थितिज ऊर्जा-जूल

संतत आवेश वितरण (Continuous Charge Distribution):
व्यवहार में, हम इलेक्ट्रॉन के आवेश के परिमाणों का बड़े आवेशों की समस्याओं में उपयोग करते हैं अतः हम आवेश की क्वाण्टम प्रकृति को नगण्य (neglegible) मानते हैं और यह मान लेते हैं कि आवेश एक संतत तरीके से क्षेत्र में फैला हुआ है। इस तरह का आवेश का वितरण (distribution of charge) संतत आवेश वितरण कहलाता है। .

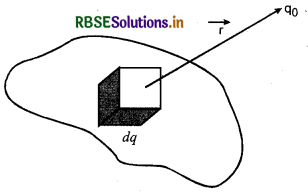
चित्र 144 आवेश का संतत वितरण (continuous distribution) एकविमीय, द्विविमीय तथा त्रिविमीय हो सकता है। एक-विमीय (one dimensional) वितरण को आवेश का रेखीय वितरण (linear charge distribution), द्विविमीय वितरण (two dimensional distribution) को आवेश का पृष्ठीय वितरण (surface charge distribution) तथा त्रिविमीय (three dimensional) वितरण को आवेश का आयतनिक वितरण (volumetric charge distribution) कहते हैं।

(a) रेखीय आवेश घनत्व (Linear Charge Density)-जब आवेश का वितरण एक रेखा (सीधी अथवा वक्र) के अनुदिश होता है तो प्रति एकांक (per unit) लम्बाई आवेश की मात्रा को रेखीय आवेश घनत्व कहते हैं।
यदि q आवेश किसी रेखा की l लम्बाई पर समान रूप से वितरित हो, तो

आवेश का रेखीय घनत्व,

λ का मात्रक-कूलॉम/मीटर (Cm^-1) होता है।
उदाहरण-यदि q आवेश R त्रिज्या के एक वलय पर समान रूप से वितरित हो, तो वलय पर आवेश का रेखीय घनत्व \(\frac{q}{2 \pi R}\), होगा।

(b) पृष्ठीय आवेश घनत्व (Surface Charge Density):
जब आवेश का वितरण किसी समतल अथवा वक्र पृष्ठ (curvature surface) पर होता है, तो प्रति एकांक क्षेत्रफल आवेश की मात्रा को आवेश का पृष्ठ घनत्व कहते हैं। यदि q आवेश किसी पृष्ठ के A क्षेत्रफल पर समान रूप से वितरित हो, तो आवेश का पृष्ठ घनत्व,

σ = क्षेत्रफल A का मात्रक-कूलॉम/मीटर² (Cm^-2) होता है।
उदाहरण-यदि q आवेश R त्रिज्या के गोले के पृष्ठ पर समान रूप से वितरित हो, तो गोले पर आवेश का पृष्ठ घनत्व \(\frac{q}{4 \pi \mathrm{R}^2}\) होगा।

(c) आयतनिक आवेश घनत्व (Volumetric Charge Density):
जब आवेश का वितरण वस्तु के आयतन में होता है, तो प्रति एकांक आयतन आवेश की मात्रा को आवेश का आयतन घनत्व कहते हैं।

यदि q आवेश किसी वस्तु के V आयतन में समान रूप से वितरित हो, तो आवेश का आयतन घनत्व,
ρ का मात्रक-कूलॉम/मीटर³ (Cm^-3) होता है।
उदाहरण-यदि q आवेश R त्रिज्या के एक गोले में समान रूप से वितरित हो, तो गोले में आवेश का आयतन घनत्व होगा।

(d) समान रूप से वितरित रेखीय आवेश के कारण विद्युत् क्षेत्र (Electric field due to uniformally distributed linear charge):
माना L लम्बाई का एकसमान रूप से वितरित रेखीय आवेश है और इसका λ रेखीय आवेश घनत्व (एकांक लम्बाई पर आवेश) λ है। इस रेखीय आवेश पर एक dl लम्बाई का अति सूक्ष्म आवेश है जिस पर आवेश
dq = λ.dl

यदि अति सूक्ष्म आवेश dq का स्थिति वेक्टर \(\vec{r}\) और अति सूक्ष्म धन आवेश का परीक्षण आवेश +q₀ का स्थिति वेक्टर \(\vec{r}\) है तो आवेश अल्पांश dq द्वारा q₀ पर आरोपित बल


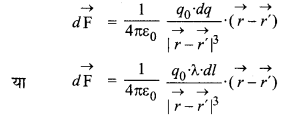
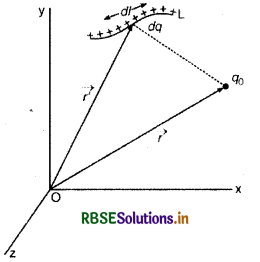
∴ पूरे रेखीय आवेश द्वारा q₀ पर आरोपित बल

(e) आवेश के पृष्ठीय वितरण (surface distribution) के कारण विद्युत् क्षेत्र:
माना कि किसी पृष्ठ S पर आवेश समान रूप से वितरित है। इस आवेश वितरण के कारण धन परीक्षण आवेश +q₀ पर लगने वाला बल ज्ञात करना है। +q₀ आवेश का स्थिति वेक्टर \(\vec{r}\) एवं dq आवेश से युक्त एक सूक्ष्म आवेश का स्थिति वेक्टर \(\vec{r}\) है। यदि आवेशित पृष्ठ पर आवेश का पृष्ठ घनत्व (एकांक पृष्ठीय क्षेत्रफल पर मौजूद आवेश) σ है तो आवेशित पृष्ठ पर सूक्ष्म (small) पृष्ठ dS पर उपस्थित आवेश,
dq = σ.dS

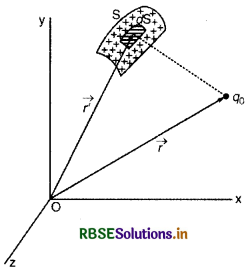
इस सूक्ष्म आवेश dq के कारण +q₀पर लगने वाला बल,

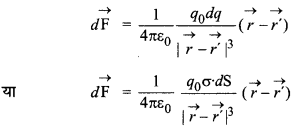
गाउस प्रमेय या गाउस नियम (Gauss's Theorem or Gauss's Law):
गाउस का नियम स्थिर वैद्युत बलों के सम्बन्ध में कूलॉम नियम का दूसरा रूप है। यह प्रमेय किसी स्थिर वैद्युत क्षेत्र में स्थित किसी काल्पनिक एवं स्वेच्छगृहीत बन्द पृष्ठ से सम्बद्ध (bound) गुजरने वाले सम्पूर्ण वैद्युत फ्लक्स (या सम्पूर्ण अभिलम्बवत् वैद्युत प्रेरण) तथा सतह के अन्दर विद्यमान कुल आवेश में सम्बन्ध प्रदर्शित करती है। यह काल्पनिक तथा स्वेच्छ बन्द पृष्ठ (closed surface) गाउसीय पृष्ठ (Gaussian surface) कहलाता है। इस प्रमेय की सहायता से आवेशित वस्तुओं के वैद्युत क्षेत्रों की गणना सरलतापूर्वक की जा सकती है।

कथन-गाउस प्रमेय के अनुसार, किसी बन्द पृष्ठ से गुजरने वाला वैद्युत फ्लक्स, उस पृष्ठ द्वारा परिबद्ध (bounded) कुल नेट आवेश का \(\frac{1}{\varepsilon_0}\) गुना होता है।
गणितीय रूप में, विद्युत् क्षेत्र में बन्द लूप के लिए विद्युत् क्षेत्र का पृष्ठीय समाकलन (surface integration) विद्युत् फ्लक्स के बराबर होता है।
Φ_E = ∮_S.\(\overrightarrow{\mathrm{E}} \cdot d \overrightarrow{\mathrm{S}}=\frac{q}{\varepsilon_0}\)
जहाँ ε₀ = निर्वात् में विद्युतशीलता है।
यदि बन्द पृष्ठ द्वारा परिबद्ध कुल आवेश शून्य है (अथवा बन्द पृष्ठ के भीतर कोई आवेश न हो या आवेश बन्द पृष्ठ के बाहर हो) तो पृष्ठ से बाहर निकलने वाला कुल अभिलम्बवत् फ्लक्स शून्य होता है अर्थात्
Φ_E = ∮_S.\(\overrightarrow{\mathrm{E}} \cdot d \overrightarrow{\mathrm{S}}\) = 0 .....(2)
उपपत्ति (Proof)

(i) जब आवेश बन्द पृष्ठ के अन्दर स्थित है (when charge is inside closed surface): माना कि S क्षेत्रफल का एक बन्द पृष्ठ है जिसके अन्दर O बिन्दु पर एक बिन्दु आवेश q रखा है (चित्र)। सम्पूर्ण पृष्ठ को अनन्त सूक्ष्म पृष्ठ अवयवों (infinitely small surface elements) dS से मिलकर बना माना जा सकता है। पृष्ठ पर स्थित बिन्दु P पर एक सूक्ष्म पृष्ठ अवयव \(\overrightarrow{d \mathrm{~S}}\) पर विद्युत् क्षेत्र की तीव्रता \(\vec{E}\) है। क्षेत्रफल वेक्टर \(\overrightarrow{d \mathrm{~S}}\) व विद्युत् क्षेत्र \(\vec{E}\) के मध्य कोण θ है। O से P की दूरी r है अतः
\(\overrightarrow{\mathrm{E}}=\frac{1}{4 \pi \varepsilon_0} \frac{q}{r^2} \cdot \hat{r}\)
जहाँ r̂, OP दिशा में एकांक वेक्टर है।

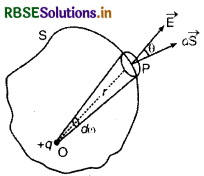
अब सूक्ष्म क्षेत्रफल dS के अभिलम्बवत् बाहर निकलने वाला कुल वैद्युत फ्लक्स

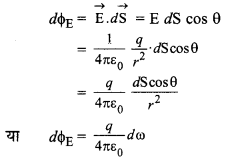
जहाँ dω = \(\frac{d \mathrm{~S} \cos \theta}{r^2}\) = सूक्ष्म क्षेत्रफल dS द्वारा O पर बना घन कोण अतः सम्पूर्ण बन्द पृष्ठ से निर्गत वैद्युत फ्लक्स

यही गाउस प्रमेय का कथन है।
यदि बन्द पृष्ठ के भीतर अनेक बिन्दु आवेश q₁, q₂, ..., q_n, हों तो । प्रत्येक बिन्दु आवेश के कारण पृष्ठ से वैद्युत फ्लक्स बाहर निकलेगा। अतः कुल फ्लक्स इन सभी फ्लक्सों के योग के बराबर होगा अर्थात्

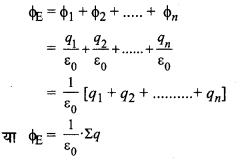
जहाँ Σq बन्द पृष्ठ के अन्दर कुल आवेशों का बीजगणितीय योग

महत्त्वपूर्ण बिन्दु
घन कोण (Solid Angle)-किसी गोलीय पृष्ठ द्वारा गोले के केन्द्र पर जो कोण अन्तरित होता है, उसे घन कोण कहते हैं। इसे ω से व्यक्त करते हैं और इसका मात्रक स्टेरेडियन (Steradian) होता है। इसका मान निम्न सूत्र से प्राप्त होता है
dω = \(\frac{d \mathrm{~S}}{r^2}\)
यदि घन कोण गोलीय पृष्ठ के केन्द्र के अतिरिक्त अन्य किसी बिन्दु O पर अन्तरित होता है तो

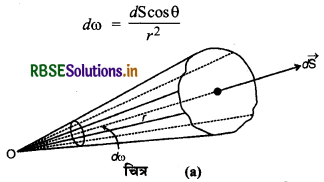
किसी सम्पूर्ण गोलीय पृष्ठ द्वारा उसके केन्द्र पर अन्तरित कुल घन कोण

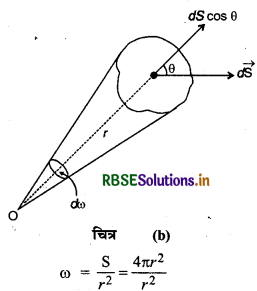
या ω = 4π स्टेरेडियन

(ii) जब आवेश बन्द पृष्ठ के बाहर स्थित हो (when charge is outside closed surface):
माना +q आवेश चित्र 1.49 की भाँति एक बन्द पृष्ठ के बाहर बिन्दु O पर स्थित है। बिन्दु O से dω घन कोण बनाता हुआ एक शंकु (cone) इस प्रकार खींचते हैं कि बन्द पृष्ठ को चार बिन्दुओं P, Q, R.व S पर क्रमशः dS₁, dS₂, dS₃ a dS₄ क्षेत्रफलों से काटता है।

बिन्दु P पर dS₁, क्षेत्रफल से गुजरने वाला वैद्युत फ्लक्स
dΦ₁ = - \(\frac{q}{4 \pi \varepsilon_0}\)dω

बिन्दु Q पर dS₂ क्षेत्रफल से गुजरने वाला वैद्युत फ्लक्स
dΦ₂ = + \(\frac{q}{4 \pi \varepsilon_0}\)dω

बिन्दु R पर dS₃, क्षेत्रफल से गुजरने वाला वैद्युत फ्लक्स
dΦ₃ = - \(\frac{q}{4 \pi \varepsilon_0}\)dω

बिन्दु S पर dS₄ क्षेत्रफल से गुजरने वाला वैद्युत फ्लक्स
dΦ₄ = + \(\frac{q}{4 \pi \varepsilon_0}\)dω

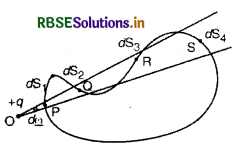
अतः dω घन कोण में पृष्ठ से गुजरने वाला कुल वैद्युत फ्लक्स
dΦ_E = dΦ₁+ dΦ₂ + dΦ₃ + dΦ₄
= - \(\frac{q}{4 \pi \varepsilon_0}\)dω + \(\frac{q}{4 \pi \varepsilon_0}\)dω - \(\frac{q}{4 \pi \varepsilon_0}\)dω + \(\frac{q}{4 \pi \varepsilon_0}\)dω
या dΦ = 0
अतः सम्पूर्ण बन्द पृष्ठ से गुजरने वाला कुल वैद्युत फ्लक्स (total electric flux)
Φ_E = ∮_SdΦ = ∮_S\(\overrightarrow{\mathrm{E}} \cdot \overrightarrow{\mathrm{S}}\) = 0
या Φ_E =∮_S\(\overrightarrow{\mathrm{E}} \cdot \overrightarrow{\mathrm{S}}\) = 0
इस प्रकार गाउस प्रमेय सिद्ध हो जाती है।

क्या आप जानते हैं?

• गाउस की प्रमेय किसी भी आकार के बन्द पृष्ठ एवं किसी भी सामान्य आवेश वितरण के लिए सिद्ध है।
• किसी बन्द पृष्ठ के बाहर स्थित आवेशों के लिए बन्द पृष्ठ से निर्गत फ्लक्स का मान शून्य होगा।
• गाउस के प्रमेय में E सभी आवेशों के लिए चाहे वे बन्द पृष्ठ के अन्दर या बाहर हैं, के लिए है, लेकिन आवेश व केवल बन्द पृष्ठ के अन्दर उपस्थित आवेशों के लिए है।
• गाउस की प्रमेय व्युत्क्रम वर्ग नियम का पालन करती है।
• किसी परावैद्युतांक K वाले माध्यम के लिए
  Φ_E =∮_S\(\overrightarrow{\mathrm{E}} \cdot \overrightarrow{\mathrm{S}} = \overrightarrow{\mathrm{E}} \cdot \overrightarrow{\mathrm{S}}\)

गाउस की प्रमेय का ग्राफीय अर्थ निर्वचन (Graphical Meaning Interpretation of Gauss's Theorem)
किसी वैद्युत क्षेत्र के लिए वैद्युत फ्लक्स को एक बन्द पृष्ठ से होकर गुजरने वाली वैद्युत क्षेत्र-रेखाओं द्वारा मापा जाता है। यदि क्षेत्र-रेखाएँ प्रत्येक स्थान पर बाहर की ओर दिष्ट होती हैं तो किसी बन्द पृष्ठ के लिए वैद्युत फ्लक्स का मान धनात्मक होता है। इस दशा में \(\vec{E}\) तथा dS के बीच θ न्यूनकोण (अर्थात् (θ < 90°) होने के कारण \(\vec{E} . d\vec{S}\) का मान ऋणात्मक होता है।

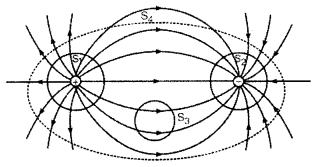
इसे स्पष्ट करने के लिए हम दो समान तथा विपरीत आवेशों तथा उनकी क्षेत्र-रेखाओं पर चित्र के अनुसार विचार करते हैं। उपर्युक्त कथनानुसार (statement) पृष्ठों S₁, व S₂ के लिए वैद्युत फ्लक्स क्रमशः धनात्मक तथा ऋणात्मक हैं। पृष्ठ S₃ किसी भी आवेश को परिबद्ध नहीं करता है और इसमें भीतर की ओर प्रवेश करने वाली क्षेत्र-रेखाओं की संख्या पृष्ठ से बाहर निकलने वाली क्षेत्र-रेखाओं की संख्या के बराबर होने के कारण शुद्ध फ्लक्स शून्य है। पृष्ठ S₄ दो बराबर तथा विपरीत आवेशों को परिबद्ध (bound) करता है तथा इससे बाहर निकलने वाले नैट फ्लक्स तथा परिबद्ध नेट आवेश दोनों शून्य हैं।

नोट:
(1) यदि किसी बन्द पृष्ठ में कोई आवेश न हो, तो q = 0 तब
Φ_E = ∮_S\(\overrightarrow{\mathrm{E}} \cdot d \overrightarrow{\mathrm{S}}=\frac{q}{\varepsilon_0}\) से
q = 0 ∴ Φ_E = 0

(2) यदि बंद पृष्ठ में दो आवेश जो परिमाण में बराबर हैं लेकिन आवेश विपरीत हो तो कुल आवेश बन्द पृष्ठ में शून्य होगा

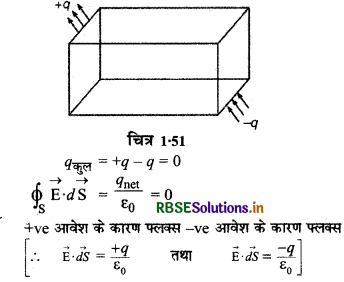
(3) बन्द पृष्ठ का कुल वैद्युत फ्लक्स बन्द पृष्ठ में रखे आवेश की मात्रा पर निर्भर करता है लेकिन बन्द पृष्ठ की आकृति (shape) पर निर्भर नहीं करता।
बन्द पृष्ठ B पर वैद्युत फ्लक्स = 2 × बन्द पृष्ठ A पर वैद्युत फ्लक्स

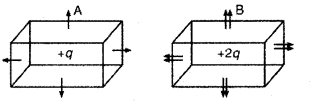
(4) यदि किसी बन्द पृष्ठ से आने वाली विद्युत् क्षेत्र-रेखाओं की संख्या पृष्ठ से निकलने वाली विद्युत् क्षेत्र-रेखाओं की संख्या से कम है तो बन्द पृष्ठ में धनावेश रखा हुआ है जैसा कि चित्र में प्रदर्शित है।

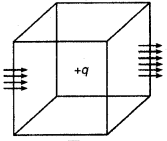
(5) यदि किसी बन्द पृष्ठ से आने वाली विद्युत् क्षेत्र-रेखाओं की संख्या पृष्ठ से निकलने वाली विद्युत् क्षेत्र-रेखाओं की संख्या से अधिक हो तो बन्द पृष्ठ में ऋणावेश रखा हुआ है जैसा कि चित्र 1.54 में प्रदर्शित

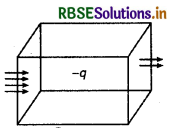
(6) किसी बन्द पृष्ठ से बाहर निकलने वाला कुल वैद्युत फ्लक्स Φ_E हो, तो
Φ_E = क्षेत्र से बाहर निकलने वाली विद्युत क्षेत्र-रेखाओं की संख्या - क्षेत्र के भीतर जाने वाली विद्युत् क्षेत्र-रेखाओं की संख्या।

कूलॉम के नियम से गाउस प्रमेय की उपपत्ति । (Gauss's Theorem Proof by Coulomb's Law)
विद्युत् फ्लक्स की परिभाषा से,
Φ_E = \(\oint_{\mathrm{S}} \overrightarrow{\mathrm{E}} \cdot \overrightarrow{d \mathrm{~S}}=\oint_{\mathrm{S}}\)EdS cos θ

किसी बिन्दु आवेश q से समान दूरी पर |\(\vec{E}\)| का मान नियत रहता है और गोलीय पृष्ठ के लिए θ = 0° होता है,
अत: Φ_E = E \(\oint_{\mathrm{S}}\) dS cos 0 = E \(\oint_{\mathrm{S}}\) dS = E. 4πr²
क्योंकि \(\oint_{\mathrm{S}}\) dS = E.4πr²
या Φ_E = E.4πr² ...(3)

कूलॉम के नियम से बिन्दु आवेश q से दूरी पर विद्युत् क्षेत्र की तीव्रता

यही गाउस का प्रमेय है।

आकिक उदाहरण
गाउस प्रमेय पर आधारित आंकिक उदाहरण के लिए प्रयुक्त सूत्र
(1) Φ_E = \(\oint_{\mathrm{S}}\overrightarrow{\mathrm{E}} \cdot \overrightarrow{d \mathrm{~S}}=\frac{q}{\varepsilon_0}\)

(2) प्रयुक्त इकाई
Φ_E = Nm²C^-1

(3) प्रयुक्त नियतांक
ε₀ = \(\frac{1}{4 \pi \times 9 \times 10^{-9}}\)
= 8.85 × 10^-12 C² N^-1m^-2

गाउसीय पृष्ठ (Gaussian Surface)
कूलॉम के नियम के द्वारा केवल सरल परिस्थितियों में विद्युत् क्षेत्र की तीव्रता का व्यंजक प्राप्त किया जा सकता है। उन परिस्थितियों में जहाँ कूलॉम के नियम तथा अध्यारोपण के सिद्धान्त (principle of super position) के द्वारा विद्युत् क्षेत्र की गणना नहीं कर सकते, वहाँ इन्हें गाउस के प्रमेय की सहायता से प्राप्त कर सकते हैं। इसके लिए, सबसे पहले पृष्ठ समाकलन (surface integral) की गणना करनी पड़ती है। आवेश वितरण के चारों ओर कुशलतापूर्वक एक ऐसा बन्द पृष्ठ (closed surface) चुनना पड़ता है, जिससे पृष्ठ समाकलन को आसानी से प्राप्त किया जा सके, जिस पृष्ठ को चुना जाता है, वही गाउसीय पृष्ठ (Gaussian surface) कहलाता है।

इस प्रकार आवेश वितरण (एक बिन्दु आवेश, एक रेखीय आवेश, एक पृष्ठीय आवेश या एक आयतनीय आवेश हो सकता है) के चारों ओर का वह बन्द पृष्ठ (closed surface) जिसके प्रत्येक बिन्दु पर विद्युत् क्षेत्र की तीव्रता समान होती है और उस पृष्ठ से गुजरने वाला विद्युत् फ्लक्स पृष्ठ के लम्बवत् हो तो उस पृष्ठ को गाउसीय पृष्ठ (Gaussian surface) कहते हैं।

गाउस के नियम के अनुप्रयोग (Applications of Gauss's Law)
अनन्त लम्बाई के एकसमान आवेशित सीधे तार के कारण विद्युत क्षेत्र (Electric Field due to a uniformly charged straight wire of Infinite Length)
माना AB एक अनन्त लम्बाई का सीधा तार है जिसकी एकांक लम्बाई (unit length) पर आवेश अर्थात् आवेश का रेखीय घनत्व λ है। इस रेखीय आवेश से r दूरी पर स्थित बिन्दु P पर विद्युत् क्षेत्र की तीव्रता ज्ञात करनी है। अब P बिन्दु पर विद्युत् क्षेत्र ज्ञात करने के लिए l लम्बाई एवं r त्रिज्या के एक बेलनाकार गाउसीय पृष्ठ की कल्पना करते हैं (चित्र), जिसके बेलनाकार पृष्ठ (cylindrical surface) पर बिन्दु P स्थित है।

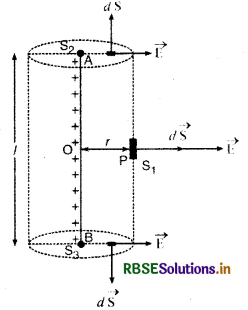
चूँकि आवेश का रेखीय घनत्व (linear density) λ है, अतः गाउसीय पृष्ठ द्वारा परिबद्ध आवेश (bounded charge)
q = λ.l फ्लक्स की परिभाषानुसार,
Φ = \(\oint_{\mathrm{S}} \overrightarrow{\mathrm{E}} \cdot d \overrightarrow{\mathrm{S}}=\oint_{\mathrm{S}}\) Eds cos θ ...(1)
समीकरण (1) को हल करने के लिए गाउसीय पृष्ठ को निम्न तीन भागों में बाँट सकते हैं

(i) बेलनाकार पृष्ठ S, जिस पर विद्युत् क्षेत्र की तीव्रता हर जगह समान है एवं θ = 0° ∴ cos 0° = 1
(ii) सूक्ष्म पृष्ठ S, जहाँ वैद्युत क्षेत्र पृष्ठ के अनुदिश (along) है अतः θ = 90° ∴ cos 90° = 0

(iii) सूक्ष्म पृष्ठ S, जहाँ θ = 90° ∴ cos 90° = 0 अतः समी. (1) से,

यदि रेखीय आवेश की लम्ब दिशा (perpendicular direction) में एकांक वेक्टर n̂ हो तो सदिश रूप में
\(\overrightarrow{\mathrm{E}}=\frac{1}{4 \pi \varepsilon_0 \mathrm{~K}} \cdot \frac{2 \lambda}{r} \hat{n}\) .....(5)
स्पष्ट है कि E ∝ \(\frac{1}{r}\)
अर्थात् अनन्त लम्बाई के रेखीय चालक के निकट बिन्दु पर विद्युत् क्षेत्र की तीव्रता चालक से बिन्दु की दूरी के व्युत्क्रमानुपाती (inversely proportional) होती है लेकिन आवेश की लम्बाई पर निर्भर नहीं करती है। दूरी के साथ विद्युत् क्षेत्र की तीव्रता का परिवर्तन (variation) चित्र में दिखाया गया है।

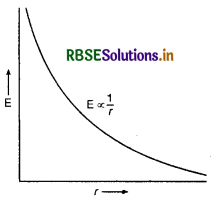
एकसमान आवेशित अनन्त समतल चादर के कारण विद्युत क्षेत्र (Electric Field due to an Uniformly Charged Infinite Plane Sheet)
(a) अनन्त विस्तार की आवेशित चालक परत के कारण वैद्युत क्षेत्र की तीव्रता (Intensity of Electric Field due to any Infinite Extent Charged Conducting Sheet): जब अनन्त विस्तार (infinite extent) की चालक परत को आवेश दिया जाता है तो आवेश पट्टिका के बाहरी पृष्ठ पर समान रूप से वितरित हो जाता है जिससे चालक के अन्दर विद्युत् क्षेत्र शून्य हो जाता है। चालक के पृष्ठ पर तथा उसके निकट बाह्य बिन्दु पर वैद्युत क्षेत्र परत के पृष्ठ के लम्बवत् होता है।

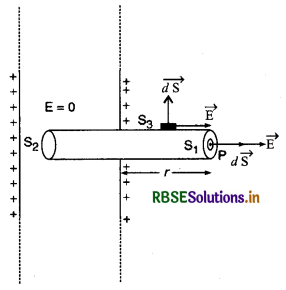
माना परत पर आवेश का पृष्ठ घनत्व σ है। इस परत के कारण लम्बवत् दूरी r पर स्थित किसी बिन्दु P पर वैद्युत क्षेत्र की तीव्रता ज्ञात करनी है।
अब एक बेलनाकार गाउसीय पृष्ठ की कल्पना करते हैं जिसका एक सूक्ष्म पृष्ठ S₁ बिन्दु P पर तथा दूसरा सूक्ष्म पृष्ठ S₂ परत के अन्दर स्थित है। इस गाउसीय पृष्ठ का अनुप्रस्थ परिच्छेद क्षेत्रफल S है अतः बेलनाकार गाउसीय पृष्ठ द्वारा परिबद्ध आवेश
q = σ. S ...(1)

अब फ्लक्स की परिभाषानुसार,
Φ_E = \(\oint_{\mathrm{S}} \overrightarrow{\mathrm{E}} \cdot \overrightarrow{d \mathrm{~S}}=\oint_{\mathrm{S}}\) EdS.cos θ ...(2)
समी. (2) को हल करने के लिए हम गाउसीय पृष्ठ को तीन भागों में बाँट सकते हैं
(i) प्लेट के पृष्ठ के बाहर सूक्ष्म पृष्ठ S₁, जहाँ θ = 0 ∴ cos θ = 1

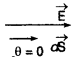
(ii) चालक प्लेट के अन्दर सूक्ष्म पृष्ठ S₂, जहाँ E = 0 तथा

(iii) बेलनाकार पृष्ठ S₃, जहाँ θ = 90°, अत: cos θ = 0

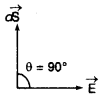
∴ समीकरण (2) से,
Φ_E = \(\oint_{S_1}\)E.dScos θ + \(\oint_{S_2}\)E.dScos θ + \(\oint_{S_3}\)Eds.cos θ
= E\(\oint_{S_1}\)ds cos 0° + 0 + 0
= E\(\oint_{S_1}\)dS
या Φ_E = E.S (क्योंकि \(\oint_{S_1}\).dS = S) ..(3)

गाउस के प्रमेय से,
Φ = \(\frac{1}{\varepsilon_0}\) × परिबद्ध आवेश
= \(\frac{q}{\varepsilon_0}=\frac{\sigma S}{\varepsilon_0}\) (∵ q = σS)...(4)

समी. (3) व (4) की तुलना करने पर
ES = \(\frac{\sigma \mathrm{S}}{\varepsilon_0}\) या E = \(\frac{\sigma}{\varepsilon_0}\) ........(5)

यदि चालक के पृष्ठ के लम्बवत् एकांक सदिश n हो तो सदिश रूप में विद्युत् क्षेत्र
\(\overrightarrow{\mathrm{E}}=\frac{\sigma}{\varepsilon_0}\)n̂ ....(6)

इस प्रकार अनन्त विस्तार की आवेशित प्लेट के निकट किसी बिन्दु पर वैद्युत क्षेत्र की तीव्रता परत के क्षेत्रफल एवं परत से उस बिन्दु की दूरी पर निर्भर नहीं करती है।

(b) अनन्त विस्तार की आवेशित परावैद्युत परत के कारण वैद्युत क्षेत्र की तीव्रता (Electric Field Intensity due to any Infinite Extent Charged Dielectric Sheet) चित्र में पतली, अनन्त विस्तार की समान रूप से आवेशित परावैद्युत परत प्रदर्शित की गयी है। जिस पर एकसमान आवेश का पृष्ठ घनत्व ० है। इस परत से r दूरी पर स्थित बिन्दु P पर विद्युत क्षेत्र की तीव्रता ज्ञात करनी है।

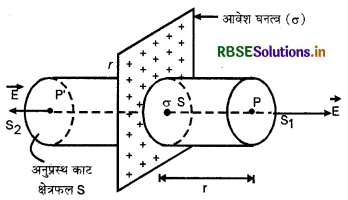
सममिति से, विद्युत् क्षेत्र की तीव्रता परत से बाहर की ओर होगी। इसके अतिरिक्त परत से समान दूरी पर स्थित दो बिन्दुओं P और P' के लिए E का परिमाण समान पर दिशा में विपरीत होगा।
हम एक बेलनाकार गाउसीय पृष्ठ को चुनते हैं जिसकी अनुप्रस्थ काट का क्षेत्रफल S और लम्बाई 2r है, इसका अक्ष परत के लम्बवत् है।

चूँकि क्षेत्र रेखायें बेलन के वक्र पृष्ठ के समान्तर होंगी अतः वक्र पृष्ठ से निर्गत फ्लक्स शून्य होगा। बेलन के अन्त्यफलक (plane-end faces) S, व S₂ से निर्गत फ्लक्स
Φ_E = ES + ES = 2ES

गाउसीय पृष्ठ से परिबद्ध आवेश
q = σS

गाउस की प्रमेय से,
Φ_E = \(\frac{q}{\varepsilon_0}\)
2EA = \(\frac{\sigma S}{\varepsilon_0}\) या E = \(\frac{\sigma}{2 \varepsilon_0}\)
अतः E, r पर निर्भर नहीं है।

एकसमान आवेशित गोलीय कोश के कारण विद्युत् क्षेत्र की citarat (Electric Field Intensity Due to a Uniformly Charged Spherical Shell)
माना R त्रिज्या का एक गोलीय कोश है जिस पर +q आवेश समान रूप से वितरित है। कोश के केन्द्र O से r दूरी पर स्थित बिन्दु P पर वैद्युत क्षेत्र की तीव्रता \(\vec{E}\) ज्ञात करनी है। बिन्दु P की निम्न स्थितियाँ ली जा सकती हैं
(i) जब बिन्दु P गोलीय कोश के बाहर (Outside Spherical Shell) स्थित है (r >R):
इस दशा में कोश के केन्द्र O को केन्द्र मानकर r त्रिज्या के गोलीय गाउसीय पृष्ठ की कल्पना करते हैं। इस पृष्ठ में परिबद्ध आवेश q होगा तथा बिन्दु P इस पृष्ठ पर होगा। अतः गाउस प्रमेय से इस गाउसीय पृष्ठ का निर्गत कुल वैद्युत फ्लक्स
Φ_E = \(\frac{0_3}{b}\) ...(1)
गाउसीय पृष्ठ के प्रत्येक बिन्दु पर विद्युत् क्षेत्र की तीव्रता समान होगी और त्रिज्या की दिशा बाहर की ओर होगी। बिन्दु P पर एक लघु क्षेत्रफल अवयव (element) dS लें तो इससे गुजरने वाला वैद्युत फ्लक्स
Φ_E =\( \overrightarrow{\mathrm{E}} \cdot d \overrightarrow{\mathrm{S}}\)

अतः सम्पूर्ण पृष्ठ (whole surface) से निर्गत (exit) वैद्युत फ्लक्स
Φ_E = \(\oint_{\mathrm{S}} \overrightarrow{\mathrm{E}} \cdot d \overrightarrow{\mathrm{S}}=\oint_{\mathrm{S}}\) E.dS cos θ

∵ गोलाकार गाउसीय पृष्ठ के प्रत्येक बिन्दु पर E नियत रहता है और θ = 0°, अतः

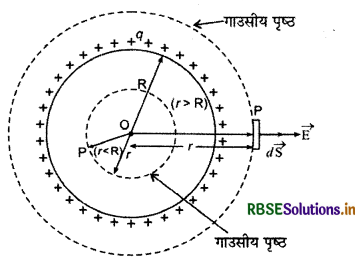
Φ_E = E\(\oint_{\mathrm{S}}\)dS cos 0
= E\(\oint_{\mathrm{S}}\)dS = E.4πr²
या Φ_E = E.4πr² ........(2)

समी. (1) व (2) की तुलना करने पर,
E.4πr² = \(\frac{q}{\varepsilon_0}\)
E = \(\frac{1}{4 \pi \varepsilon_0} \cdot \frac{q}{r^2}\) ...(3)
सदिश रूप में, \(\overrightarrow{\mathrm{E}}=\frac{1}{4 \pi \varepsilon_0} \cdot \frac{q}{r^2} \cdot \hat{r}\) ......(4)

जहाँ r̂ = OP दिशा में एकांक (unit) वेक्टर। यदि कोश पर आवेश का पृष्ठ घनत्व (surface density) σ हो, तो
q =4πR²σ
अतः समीकरण (4) से,
E = \(\frac{\sigma}{\varepsilon_0} \frac{\mathrm{R}^2}{r^2}\) ....(5)

(ii) जबबिन्दुPगोलीयकोश के पृष्ठपर स्थित है (Onthe Surface of Spherical Shell) (r = R) – इस स्थिति में गाउसीय पृष्ठ की त्रिज्या R होने पर भी परिबद्ध आवेश q ही रहेगा अतः समी. (3) में r = R रखने पर,
E = \(\frac{1}{4 \pi \varepsilon_0} \frac{q}{\mathrm{R}^2}\) ..........(6)
सदिश रूप में (vectorially),
\(\overrightarrow{\mathrm{E}}=\frac{1}{4 \pi \varepsilon_0} \frac{q}{\mathrm{R}^2} \hat{r}\) ...(7) अर्थात् E का मान नियत होता है और यह अधिकतम मान होता है।

(iii) जब बिन्दु Pगोलीय कोश के अन्दर (Inside the Spherical Shell) स्थित है (r < R)-चूँकि गोलीय कोश को दिया गया समस्त
आवेश कोश के पृष्ठ पर समान रूप से वितरित होता है तथा कोश के अन्दर कोई आवेश मौजूद नहीं होता है, अतः यदि O को केन्द्र मानकर r त्रिज्या (r < R) का कोई गाउसीय पृष्ठ खींचें तो इस पृष्ठ से परिबद्ध आवेश शून्य होगा, अर्थात् गाउसीय पृष्ठ से निर्गत फ्लक्स

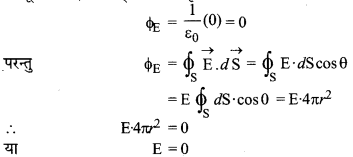
अर्थात् गोलीय कोश के अन्दर प्रत्येक बिन्दु पर विद्युत् क्षेत्र की तीव्रता शून्य होगी।

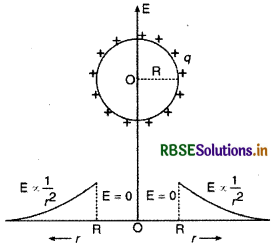
आवेशित गोलीय कोश के कारण उत्पन्न विद्युत् क्षेत्र की तीव्रता E कोश के केन्द्र O से दूरी । पर चित्र 1.60 की भाँति निर्भर करती है।

→ वस्तु का आवेशन (Charging of bodies):
इलेक्ट्रॉनों की कमी हो जाने पर वस्तु धनावेशित एवं इलेक्ट्रॉनों की अधिकता होने पर वस्तु ऋणावेशित हो जाती है। इलेक्ट्रॉन के आवेश के परिमाण (e = 1.6 × 10^-19 कूलॉम) को मूल आवेश (fundamental charge) कहते हैं।

→ चालक एवं अचालक (Conductor and insulator):
वे पदार्थ जिनसे होकर विद्युत् प्रवाह सम्भव है, चालक कहलाते हैं और जिन पदार्थों से होकर विद्युत् प्रवाह नहीं हो सकता है, अचालक कहलाते हैं।

→ वैद्युत आवेश का संरक्षण(Conservation of electric charge):
आवेश का संरक्षण वह गुण है जिसके कारण किसी विलगित (isolated) निकाय का कुल आवेश नियत रहता है। किसी विलगित निकाय के कुल आवेश को न तो नष्ट किया जा सकता है और न ही उत्पन्न किया जा सकता है।

→ वैद्युत आवेश का क्वाण्टमीकरण(quantisation of electric charge):
आवेश का क्वाण्टमीकरण वह गुण है जिसके कारण सभी मुक्त आवेश मूल आवेश (e) के पूर्ण गुणज (integral multiple) होते हैं अर्थात् q = ± ne

→ कूलॉम का नियम-निर्वात् (vacuum) में स्थित किन्हीं दो बिन्दु आवेशों के मध्य लगने वाला वैद्युत आकर्षण या प्रतिकर्षण बल आवेशों के परिमाणों के गुणनफल के अनुक्रमानुपाती एवं उनके बीच की दूरी के वर्ग के व्युत्क्रमानुपाती होता है।
कूलॉम बल F = \(\frac{1}{4 \pi \varepsilon_0} \cdot \frac{q_1 q_2}{r^2}\)
जहाँ \(\frac{1}{4 \pi \varepsilon_0}\) = 9 × 10⁹ N.m²C^-2

→ बहल आवेशों के मध्य बल-आवेशों के समूह (group of charges) में किसी एक आवेश पर लगने वाला परिणामी बल समूह के अन्य आवेशों द्वारा उस पर लगने वाले बलों के सदिश योग (addition of vector) से प्राप्त होता है। आवेश q₁ पर परिणामी बल
\(\overrightarrow{\mathrm{F}_1}=\overrightarrow{\mathrm{F}_{12}}+\overrightarrow{\mathrm{F}_{13}}+\ldots \ldots . .+\overrightarrow{\mathrm{F}_{1 n}}\)

→ वैद्युत क्षेत्र की तीव्रता-(i) वैद्युत क्षेत्र में किसी बिन्दु पर एकांक धनावेश पर कार्य करने वाला बल ही उस बिन्दु पर वैद्युत क्षेत्र की तीव्रता के बराबर होता है, अतः
\(\overrightarrow{\mathrm{E}}=\frac{\overrightarrow{\mathrm{F}}}{q_0}\) NC^-1
जहाँ \(\vec{F}\), धन परीक्षण (test) आवेश (+q₀) पर लगने वाला बल है

→ वैद्युत फ्लक्स-(i) वैद्युत क्षेत्र \(\vec{E}\) में स्थित किसी पृष्ठ के क्षेत्रफल के अल्पांश d \(\overrightarrow{\mathrm{S}}\) से सम्बद्ध (bound) वैद्युत फ्लक्स \(\vec{E}\) व d \(\overrightarrow{\mathrm{S}}\) के अदिश गुणन (scalar multiplication) से प्राप्त होता है अर्थात्
dΦ_E = \(\overrightarrow{\mathrm{E}} \cdot d \overrightarrow{\mathrm{S}}\) = E.ds.cos 0

(ii) असमान वैद्युत क्षेत्र में रखे होने पर किसी पृष्ठ से सम्बद्ध वैद्युत फ्लक्स
Φ_E = \(\oint_{\mathrm{S}} \overrightarrow{\mathrm{E}} \cdot d \overrightarrow{\mathrm{S}}=\oint_{\mathrm{S}}\) E dS cos θ

(iii) वैद्युत फ्लक्स का मात्रक-Nm²C^-1 या Vm

(iv) वैद्युत फ्लक्स का विमीय सूत्र = [ML³T^-3A^-1]

→ वैद्युत द्विध्रुव एवं द्विध्रुव आघूर्ण-परिमाण में समान (equal in magnitude) किन्तु प्रकृति में विपरीत (differ in nature) दो आवेश जब किसी अल्प दूरी पर रखे होते हैं तो वे वैद्युत द्विध्रुव की रचना करते हैं। एक आवेश एवं दोनों आवेशों के बीच की दूरी के गुणनफल को वैद्युत द्विध्रुव आघूर्ण कहते हैं।
द्विध्रुव आघूर्ण p = q × 2l
p एक सदिश राशि है जिसकी दिशा ऋण आवेश से धन आवेश की ओर होती है।

→ वैद्युत द्विध्रुव के कारण उत्पन्न विद्युत् क्षेत्र की तीव्रता
(i) अक्षीय (axial) स्थिति में दीर्घ दूरियों के लिए,
E = \(\frac{1}{4 \pi \varepsilon_0} \frac{2 p}{r^3}\)
सदिश रूप में, \(\overrightarrow{\mathrm{E}}=\frac{1}{4 \pi \varepsilon_0} \frac{2 \vec{p}}{r^3}\)

(ii) निरक्षीय (equatorial) स्थिति में दीर्घ दूरियों के लिए,
E = \(\frac{1}{4 \pi \varepsilon_0} \frac{p}{r^3}\)
सदिश रूप में, \(\overrightarrow{\mathrm{E}}=-\frac{1}{4 \pi \varepsilon_0} \frac{\vec{p}}{r^3}\)

(iii) किसी अन्य स्थिति में विद्युत् क्षेत्र की तीव्रता
E = \(\frac{1}{4 \pi \varepsilon_0} \frac{p \sqrt{3 \cos ^2 \theta+1}}{r^3}\)

→ गाउस प्रमेय-विद्युत् क्षेत्र में स्थित किसी स्वगृहीत बन्द पृष्ठ से अभिलम्बवत् निर्गत वैद्युत फ्लक्स उस पृष्ठ द्वारा परिबद्ध आवेश का \(\frac{1}{\varepsilon_0}\) गुना होता है।
Φ = \(\oint_{\mathrm{S}} \overrightarrow{\mathrm{E}} \cdot d \overrightarrow{\mathrm{S}}=\frac{1}{\varepsilon_0}\)(Σq)

→ गाउस-प्रमेय के अनुप्रयोग:
(a) समान आवेशित गोलीय कोश (uniformly charged spherical shell) के कारण विद्युत् क्षेत्र की तीव्रता
(i) पृष्ठ के बाहर स्थित बिन्दु पर

(iii) कोश के अन्दर स्थित किसी बिन्दु पर
E = 0

(b) अनन्त विस्तार (infinite extent) की आवेशित चालक प्लेट के कारण वैद्युत क्षेत्र की तीव्रता
E = \(\frac{\sigma}{\varepsilon_0}\)या E = \(\frac{\sigma}{\varepsilon_0}\)n̂
जहाँ σ आवेश का पृष्ठ घनत्व है।

(c) अनन्त विस्तार की आवेशित परावैद्युत परत (dielectric sheet) के कारण वैद्युत क्षेत्र
E = \(\frac{\sigma}{2 \varepsilon_0}\)
या \(\overrightarrow{\mathrm{E}}=\frac{\sigma}{2 \varepsilon_0}\)n̂

(d) अनन्त लम्बाई के रेखीय आवेश (linear charge) के कारण विद्युत् क्षेत्र
E = \(\frac{1}{4 \pi \varepsilon_0} \frac{2 \lambda}{r} \)n̂
\(\overrightarrow{\mathrm{E}}=\frac{1}{4 \pi \varepsilon_0} \cdot \frac{2 \lambda}{r}\)

→ समरूप वैद्युत क्षेत्र में रखे वैद्युत द्विध्रुव पर आरोपित बल युग्म का आघूर्ण (Torque)
τ = pE sin θ
सदिश रूप में \(\vec{\tau}=\overrightarrow{\mathrm{P}} \times \overrightarrow{\mathrm{E}}\)

→ वैद्युत क्षेत्र में θ₁ विक्षेप की स्थिति से विक्षेप की स्थिति तक द्विध्रुव को घुमाने में कृत कार्य
W = pE(cos θ₁ - cos θ₂)

स्थायी सन्तुलन (θ₁ = 0) से θ विक्षेप देने में कृत कार्य
W = pE(1 - cos θ)

→ समरूप वैद्युत क्षेत्र में द्विध्रुव की वैद्युत स्थितिज ऊर्जा
U = - pE cos θ

→ आवेश का क्वाण्टमीकरण q = ne

→ कूलॉम का नियम F = \(\frac{1}{4 \pi \varepsilon_0} \frac{q_1 q_2}{r^2}\)
सदिश रूप
\(\overrightarrow{\mathrm{F}_{\mathrm{L} 2}}=\frac{1}{4 \pi \varepsilon_0} \frac{q_1 q_2}{r^2} \hat{r}_{21} \overrightarrow{\mathrm{F}}_{21}=\frac{1}{4 \pi \varepsilon_0} \frac{q_1 q_2}{r^2} \hat{r}_{12}\)

→ वैद्युत् क्षेत्र की तीव्रता E = \(\frac{\mathrm{F}}{q_0}=\frac{1}{4 \pi \varepsilon_0} \frac{q}{r^2} \hat{r}\)
सदिश रूप \(\overrightarrow{\mathrm{E}}=\frac{1}{4 \pi \varepsilon_0} \cdot \frac{q}{r^2} \hat{r}\)

→ वैद्युत् फ्लक्स
Φ = \(\oint_{\mathrm{S}} \overrightarrow{\mathrm{E}} \cdot \overrightarrow{d \mathrm{~S}}\)
= \(\oint_{\mathrm{S}}\) EdS cos θ

→ वैद्युत् द्विध्रुव आघूर्ण p = q × 2l

→ वैद्युत् द्विध्रुव के कारण उत्पन्न विद्युत् क्षेत्र की तीव्रता

• अक्षीय स्थिति में, E = \(\frac{1}{4 \pi \varepsilon_0} \frac{2 p}{r^3}\)
• निरक्षीय स्थिति में, E = \(\frac{1}{4 \pi \varepsilon_0} \frac{p}{r^3}\)
• किसी अन्य स्थिति में विद्युत् क्षेत्र की तीव्रता E = \(\frac{1}{4 \pi \varepsilon_0} \frac{p \sqrt{3 \cos ^2 \theta+1}}{r^3}\)

→ गाउस की प्रमेय Φ = \(\oint_{\mathrm{S}} \overrightarrow{\mathrm{E}} \cdot \overrightarrow{d \mathrm{~S}}=\frac{(\Sigma q)}{\varepsilon_0}\)

→ समान आवेशित गोलीय कोश के कारण विद्युत् क्षेत्र की तीव्रता

• E = \(\frac{1}{4 \pi \varepsilon_0} \cdot \frac{q}{r^2}\)(r > R)
• E = \(\frac{1}{4 \pi \varepsilon_0} \cdot \frac{q}{R^2}\) (r = R)
• E = 0(r < R)

→ अनन्त विस्तार की आवेशित चालक परत के कारण वैद्युत क्षेत्र की तीव्रता
E = \(\frac{\sigma}{\varepsilon_0}\)

→ अनन्त विस्तार की आवेशित परावैद्युत् परत के कारण विद्युत् क्षेत्र की तीव्रता E = \(\frac{\sigma}{2 \varepsilon_0}\)

→ अनन्त लम्बाई के रेखीय आवेश के कारण विद्युत् क्षेत्र की तीव्रता
E = \(\frac{1}{4 \pi \varepsilon_0} \cdot \frac{2 \lambda}{r}\)

→ वैद्युत द्विध्रुव पर लगने वाले बलयुग्म का आघूर्ण
\(\vec{\tau}=\vec{P} \times \vec{E}\) = pE sin θ

→ वैद्युत द्विध्रुव को घुमाने में किया गया कार्य
W = pE(cos θ₁ - cos θ₂)

→ समरूप वैद्युत क्षेत्र में द्विध्रुव की वैद्युत स्थितिज ऊर्जा
U = -pE cos θ

→ स्थिर-वैद्युतिकी (Electrostatics):
स्थिर आवेशों द्वारा उत्पन्न बलों, क्षेत्रों, विभवों का अध्ययन।

→ परावैद्युत (Dielectric):
अचालकों को ही परावैद्युत कहते हैं पर ये चालन के बिना वैद्युत प्रभाव का प्रदर्शन करते हैं।

→ प्रेरण (Induction):
बगैर स्पर्श कराये हुए दूसरी वस्तु पर विपरीत आवेश उत्पन्न करना।

→ विद्युतशीलता (Permittivity):
किसी माध्यम में स्थित बिन्दु आवेशों के मध्य लगने वाले वैद्युत बल का परिमाण, माध्यम के जिस विद्युत् गुण के व्युत्क्रमानुपाती होता है उस वैद्युत गुण को माध्यम की विद्युतशीलता कहते हैं।

→ स्रोत आवेश (Source charge):
जो वैद्युत क्षेत्र उत्पन्न करता है।

→ परीक्षण आवेश (Test charge):
जो स्रोत आवेश के प्रभाव का परीक्षण करता है।

→ वैद्युत क्षेत्र रेखा (Electric field lines):
वैद्युत क्षेत्र में स्वतन्त्रतापूर्वक छोड़े गये धन परीक्षण आवेश द्वारा अपनाया गया मार्ग।

→ उदासीन बिन्दु (Neutral point):
उदासीन बिन्द पर परिणामी विद्युत् क्षेत्र शून्य होता है।

→ आवेश का संतत् वितरण (Continuous distribution of charge):
किसी वस्तु को दिये गये आवेश का उस पर समान रूप से वितरित हो जाना।

→ वैद्युत द्विध्रुव (Electric dipole):
परिमाण में समान किन्तु प्रकृति में विपरीत दो आवेश अल्प दूरी पर वैद्युत द्विध्रुव बनाते हैं।

→ ध्रुवी अणु (Polar molecule):
इसमें धन व ऋण आवेशों के प्रभावी केन्द्र भिन्न होते हैं।

→ अधुवी अणु (Non-polar molecule):
इसमें धन व ऋण आवेशों का प्रभावी केन्द्र एक ही होता है।

→ वैद्युत फ्लक्स (Electric flux):
किसी वैद्युत क्षेत्र में स्थित किसी पृष्ठ से लम्बवत् गुजरने वाली वैद्युत क्षेत्र रेखाओं की संख्या को उस पृष्ठ से बद्ध वैद्युत फ्लक्स कहते हैं।

→ घन कोण (Solid angle):
गोलीय पृष्ठ के क्षेत्रफल द्वारा गोले के केन्द्र पर अन्तरित कोण।

→ गाउसीय पृष्ठ (Gaussian surface):
काल्पनिक तथा स्वेच्छ बन्द पृष्ठ।