RBSE Class 12 Physics Notes Chapter 1 Electric Charges and Fields

These comprehensive RBSE Class 12 Physics Notes Chapter 1 Electric Charges and Fields will give a brief overview of all the concepts.

RBSE Class 12 Physics Chapter 1 Notes Electric Charges and Fields

Electrostatics:
Electrostatics is the branch of physics which deals with the study of forces and potentials arising from static charges. Such charges cannot flow from one body to another. And electric charges are produced due to friction between two insulating bodies which are rubbed against each other. These charges are found to generate in equal pairs of positive and negative charges e.g. when glass rod is rubbed with silk cloth, glass rod acquires positive charge and silk cloth acquires equal negative charge.

Properties of Charge

• Additive property of charge: Total charge on a body is the algebraic sum of all the charges distributed over the body as it is a scalar quantity.
• Charge quantization: The charge on a body is an integral multiple of charge on an electron or a proton i.e. q = ±ne, where n is an integer and ‘e’ is the smallest possible unit of charge (1.6 × 10^-19 C).
• Conservation of charge: The algebraic sum of the positive and negative charges in an isolated system always remains constant.

Electrostatic induction:
The process of charging a conductor with the help of a charged conductor without any physical contact is called electrostatic induction e.g. if we want to charge a conductor positively permanently by induction, we bring a negatively charged conductor near an uncharged conductor (Fig. (a)). Near end A acquires positive charge and end B acquires equal negative charge. Now connect end B to the earth. The free charges (i.e. electrons) flow to the earth (Fig. (b)). Now disconnect the conductor from earth (Fig. (c)).

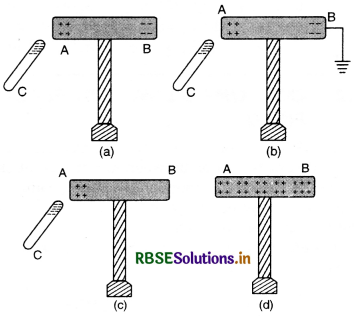
Finally, remove the charged conductor C, the positive induced charge will immediately spread uniformly over the whole conductor. Thus conductor AB is charged positively by induction. Similarly, the conductor AB can be charged negatively by using a positively charged conductor C.

Coulomb’S Law And Electric Field:
Coulomb’s law: It states that the force of attraction or repulsion between any two point charges at rest is directly proportional to the product of the charges and inversely proportional to the square of the distance between them.
If two point charges q₁ and q₂ are separated by distance r, then
Force of interaction F is given by
F q₁q₂
and F ∝ \(\frac{1}{r^2}\)
or F ∝ \(\frac{q_1 q_2}{r^2}\)
or F ∝ k\(\frac{q_1 q_2}{r^2}\)
where k is the constant of proportionality and in SI in vacuum (or air)
k = \(\frac{1}{4 \pi \varepsilon_0}\) = 9 × 10⁹ Nm² C^-2
and ε₀ = 8.85 × 10^-12 C² N^-1 m^-2 is called permittivity of free space.

In vector form, Coulomb’s law is given by

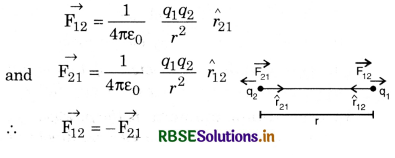
One coulomb is a charge which repels equal and similar charge placed at lm away in vacuum with a force of 9 × 10⁹ N.
Dielectric: constant of a medium (Relative Permittivity).may be defined as the ratio of force between two charges separated by a certain distance in air to the force between the same charges separated by the same distance in the medium.
i.e k = \(\frac{\mathrm{F}_{\text {air }}}{\mathrm{F}_{\text {medium }}}\)

Electric Field and Electric Field Intensity:
Electric field due to a charge + q is the space around the charge + q within which any other charge + q0 (called test charge) experiences a force of attraction or repulsion.

Electric field intensity \(\vec{E}\) at any point in the field is the force experienced by unit positive charge (or vanishingly small charge) placed at that point.

Mathematically:

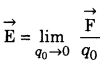
SI unit of \(\vec{E}\) is newton/coulomb.

Electric field due to a point charge:
\(\overrightarrow{\mathrm{E}}=\frac{1}{4 \pi \varepsilon_0} \frac{q}{r^3} \vec{r}=\frac{1}{4 \pi \varepsilon_0} \frac{q}{r^2} \hat{r}\)

• If q > 0, the direction of \(\vec{E}\) is away from q.
• If q < 0, the direction of \(\vec{E}\) is towards q.

Electric lines of force:
An electric line of force, in general, is a straight or curved, the tangent to which at any point gives the direction of the electric field intensity at that point. Important properties

• Electric lines of force start from + ve charge and end at - ve charge.
• Electric lines are continuous curves without any break.
• They never cross each other.
• They do not form any closed loops.

Electric dipole:
Electric dipole is a system of two equal and opposite charges separated by a certain distance. Electric dipole moment: Electric dipole moment is the product of either charge and the length of the electric dipole and its direction is from negative charge to positive charge as shown in the figure.

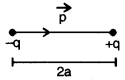
Electric field intensity on axial line of electric dipole:
Electric field intensity at point P from the centre of dipole on the axial line at a distance r is given by

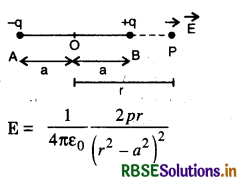
For a short dipole r >> a, so (r² - a²)² - r⁴
E = \(\frac{1}{4 \pi \varepsilon_0} \frac{2 p r}{r^4}=\frac{1}{4 \pi \varepsilon_0} \frac{2 p}{r^3}\)

Electric field intensity on equatorial line of electric dipole:
Electric field intensity at point P from the centre of the dipole on the equatorial line at a distance r is given by

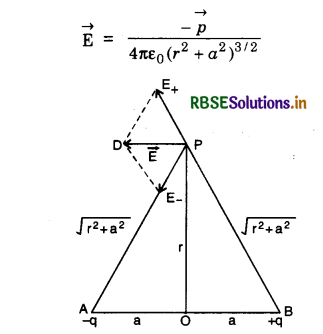
For a short dipole, r > > a, so
\(\overrightarrow{\mathrm{E}}=-\frac{\vec{p}}{4 \pi \varepsilon_0 r^3}\)
(-ve sign means that the direction of \(\overrightarrow{\mathrm{E}}\) is opposite to \(\overrightarrow{\mathrm{E}}\)).

Torque and potential energy of an electric dipole in a uniform electric field.
The torque on an electric dipole of dipole moment \(\overrightarrow{\mathrm{p}}\) when placed in a uniform electric field \(\overrightarrow{\mathrm{E}}\) such that \(\overrightarrow{\mathrm{p}}\) makes an angle θ with is \(\overrightarrow{\mathrm{E}}\) given by
\(\vec{\tau}=\vec{p} \times \overrightarrow{\mathrm{E}}\)
Or τ = pE sin θ
When θ = 0, τ = 0
When θ = 90°, τ = pE

Potential energy, U of the electric dipole is the total work done in turning a dipole in uniform electric field from its stable position.
U = - pE cos θ
where θ is the angle through which the dipole is rotated against the torque.

Gauss’Theorem:
Electric flux (Φ) through an area is defined as the total number of electric lines of force passing through the area normally.
Mathematically.
Φ = E S cos θ = \(\overrightarrow{\mathrm{E}} \cdot \overrightarrow{\mathrm{S}}\)

Gauss' Theorem:
It states that the net electric flux through any gaussian surface is equal to \(\frac{1}{\varepsilon_0}\) times the magnitude of the charge enclosed.
Φ = ∮\(\overrightarrow{\mathrm{E}} \cdot d \overrightarrow{\mathrm{S}}=\frac{q}{\varepsilon_o}\)

Gauss' theorem for a spherically symmetric closed surface.
The electric field \(\overrightarrow{\mathrm{E}}\) at point P due to a charge q placed at the centre of the sphere of radius r is given by 4πε₀ r²
\(\overrightarrow{\mathrm{E}} = \frac{1}{4 \pi \varepsilon_0} \frac{q}{r^2} \hat{r}\)

Electric flux through area element d \(\overrightarrow{\mathrm{S}}\) is given by

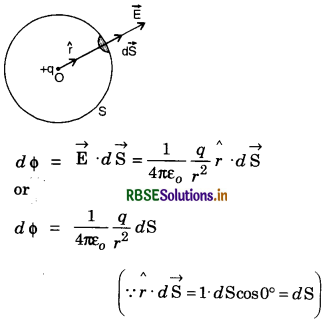
Total electric flux through the closed surface of the sphere,
Φ = ∫dΦ = \(\frac{1}{4 \pi \varepsilon_0} \frac{q}{r^2}\) ∫dS = \(\frac{1}{4 \pi \varepsilon_0} \frac{q}{r^2}\) 4πr²
or Φ = \(\frac{q}{\varepsilon_0}\)

Gaussian surface:
Gaussian surface is the surface of arbitrary shape drawn in the electric field to evaluate the closed surface integral of the electric field intensity to apply the Gauss' law.

Importance of gaussian surface:
The concept of gaussian surface helps in evaluating the electric field strength due to some symmetric charge distribution.

Electric field:
Electric field due to an infinite long straight wire is given by
E = \(\frac{\lambda}{2 \pi \varepsilon_0 r}\)