RBSE Class 12 Physics Important Questions Chapter 9 किरण प्रकाशिकी एवं प्रकाशिक यंत्र

Rajasthan Board RBSE Class 12 Physics Important Questions Chapter 9 किरण प्रकाशिकी एवं प्रकाशिक यंत्र Important Questions and Answers.

RBSE Class 12 Physics Chapter 9 Important Questions किरण प्रकाशिकी एवं प्रकाशिक यंत्र

अति लघुत्तरीय प्रश्न

प्रश्न 1.
एक समतल दर्पण की फोकस दूरी कितनी होती है?
उत्तर:
अनन्त

प्रश्न 2.
लेन्स की क्षमता एवं फोकस दूरी में संबंध लिखिए।
उत्तर:

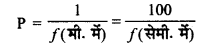
प्रश्न 3.
सूक्ष्मदर्शी की आवर्धन क्षमता से क्या तात्पर्य है?
उत्तर:
सूक्ष्मदर्शी की नेत्रिका पर अंतिम प्रतिबिम्ब द्वारा बने दर्शन कोण (ß) तथा स्पष्ट दृष्टि की न्यूनतम दूरी पर रखे विम्ब द्वारा नेत्र पर बने दर्शन कोण (α) का अनुपात सूक्ष्मदी की आवर्धन क्षमता (M) कहलाती है।

प्रश्न 4.
माध्यम के अपवर्तनांक की परिभाषा लिखिए।
उत्तर:
वायु या निर्वांत में प्रकाश की चाल (c) तथा माध्यम में प्रकाश की चाल (v) का अनुपात उस माध्यम का अपवर्तनांक कहलाता है।

प्रश्न 5.
प्रकाश के प्रकीर्णन से आप क्या समझते हैं?
उत्तर:
जब प्रकाश किसी ऐसे अणु पर आपतित होता है जिसका आकार प्रकाश की तरंगदैर्ध्य (λ) की तुलना में बहुत छेया होता है तो अणु प्रकाश को अवशोषित कर लेता है और अवशोषण के पश्चात् सभी दिशाओं में नवीन तरंगदैर्ध्य का प्रकाश उत्सर्जित करता है। यह परिघटना प्रकीर्णन कहलाती है।

प्रश्न 6.
प्रकाश के पूर्ण आन्तरिक परावर्तन की आवश्यक शर्ते लिखिए।
उत्तर:
पूर्ण आन्तरिक परावर्तन के लिए आवश्यक है कि आपतन कोण का मान क्रांतिक कोण से अधिक होना चाहिए तथा प्रकाश सघन माध्यम से विरल माध्यम में प्रवेश करें।

प्रश्न 7.
यदि बैंगनी रंग के आपतित प्रकाश को लाल प्रकाश से प्रतिस्थापित कर दिया जाए तो कांच के प्रिज्म का न्यूनतम विचलन कोण किस प्रकार परावर्तित होता है? कारण दीजिए।
उत्तर:
बैंगनी प्रकाश की तरंगदैर्ध्य लाल रंग के प्रकाश से कम होती है। न्यूनतम विचलन कोण का मान
δ_m = (µ - 1) A
अर्थात् δ_{m ∝ µ}
जैसा कि µ < µ_v
∴ (δ_m)R < (δ_m)v
अतः स्पष्ट है लाल रंग के लिए न्यूनतम विचलन का मान घट जायेगा।

प्रश्न 8.
सूर्योदय तथा सूर्यास्त के समय सूर्य रक्ताभ लाल क्यों दिखाई देता है?
उत्तर:
सूर्योदय तथा सूर्यास्त के दौरान, प्रकाश कोण वायुमंडल में अधिक दूरी तय करनी पड़ती है क्योंकि उस समय सूर्य क्षितिज पर होता है। रैले के नियम के अनुसार, प्रकीर्णन ∝ \(\frac{1}{\lambda_2}\)। जैसा कि लाल रंग के अलावा सभी रंग के प्रकाश का प्रकीर्णन हो जाता है। लाल रंग का प्रकाश ही बिना प्रकीर्णित हुए हमारी आँख में प्रवेश करता है। इसी कारण सूर्योदय तथा सूर्यास्त के समय सूर्य लाल रंग का प्रतीत होता है।

प्रश्न 9.
इन्द्रधनुष दिखाई देने का क्या कारण है?
उत्तर:
जल की बूंदों द्वारा सूर्य के प्रकाश का विक्षेपण ही इन्द्रधनुष का कारण है।

प्रश्न 10.
प्रकीर्णित प्रकाश की तीव्रता किस भौतिक राशि पर निर्भर करती है?
उत्तर:
रैले के अनुसार प्रकीर्णिन प्रकाश की तीव्रता
I ∝ \(\frac{1}{\lambda^4}\)
अत: तीव्रता तरंगदैर्ध्य पर निर्भर करती है।

प्रश्न 11.
उस सिद्धान्त का नाम लिखिए जिस पर प्रकाशिक तन्तु कार्य करता है?
उत्तर:
पूर्ण आन्तरिक परावर्तन।

प्रश्न 12.
प्रकाश के अपवर्तन का कारण बताइये।
उत्तर:
प्रकाश के अपवर्तन का कारण है प्रकाश की चाल विभिन्न माध्यमों में भिन्न - भिन्न होती है।

प्रश्न 13.
किस लेन्स का आवर्धन सदैव 1 से कम होता है?
उत्तर:
अवतल लेंस में प्रतिबिम्ब सदैव सीधा एवं वस्तु से छोटा बनता है अत: अवतल लेंस का आवर्धन सदैव 1 से कम होता है।

प्रश्न 14.
क्रांतिक कोण किसे कहते हैं?
उत्तर:
सघन माध्यम में वह आपतन कोण जिसके संगत विरल माध्यम में अपवर्तन कोण 90° होता है, क्रांतिक कोण कहलाता है।

प्रश्न 15.
किसी प्रिज्म के लिए न्यूनतम विचलन की शर्त लिखिए।
उत्तर:
आपतन कोण एवं निर्गमन कोण बराबर होना चाहिए।

प्रश्न 16.
खतरे का निशान लाल होता है, क्यों?
उत्तर:
रेले के प्रकीर्णन नियमानुसार I_s ∝\(\frac{1}{\lambda^4}\)

प्रश्न 17.
दूरदर्शी के अभिदृश्यक का द्वारक यथा सम्भव बड़ा लिया जाता है, क्यों?
उत्तर:
बड़े द्वारक के अभिदृश्यक के दो लाभ है-
(a) आवर्धन क्षमता बढ़ जाती है
(b) विभेदन क्षमता बढ़ जाती है।

लघु उत्तरीय प्रश्न

प्रश्न 1.
दर्पण सूत्र का प्रयोग करते हुए व्याख्या कीजिए उत्तल दर्पण सदैव ही बिम्ब का आभासी प्रतिबिम्ब क्यों बनाते हैं?
उत्तर:
दर्पण सूत्र के अनुसार \(\frac{1}{v}+\frac{1}{u}=\frac{1}{f}\)
\(\frac{1}{v}=\frac{1}{f}-\frac{1}{u}\)
v = \(\frac{u f}{u-f}\)
और जैसा कि हम जानते हैं कि उत्तल दर्पण के लिए फोकस दूरी f धनात्मक तथा बिम्ब की दूरी u ऋणात्मक होती है।
इसलिए v का मान हमेशा धनात्मक होगा। इसका अर्थ है कि उत्तल दर्पण से हमेशा आभासी प्रतिबिम्ब बनता है।

प्रश्न 2.
अपवर्ती दूरदर्शक की तुलना में परावती दूरदर्शक के दो लाभों की व्याख्या कीजिए।
उत्तर:
परावर्तक दूरदर्शक की अपवर्तन दूरदर्शक से श्रेष्ठता-

• परावर्ती दूरदर्शी से बना प्रतिबिम्ब वर्ण विपथन के दोष से मुक्त होता है।
• परावर्ती दूरदर्शी में प्रकाश का अवशोषण बहुत कम होता है फलस्वरूप इससे बनने वाला प्रतिबिम्ब अपवर्ती दूरदर्शी की अपेक्षा अधिक चमकीला होता है।

प्रश्न 3.
किसी टेलीस्कोप के अभिदृश्यक की फोकस दूरी अधिक और द्वारक अधिक क्यों चाहिए? अपने उत्तर की पुष्टि कीजिए।
उत्तर:
दूरदर्शी की आवर्धन क्षमता
m = -\(\frac{f_0}{f_e}\)
अतः स्पष्ट है कि दूरदर्शी की आवर्धन क्षमता बढाने के लिए अभिदृश्यक की फोकस दूरी f₀ का मान अधिक होना चाहिए।
दूरदर्शी को विभेदन क्षमता ∝ \(\frac{d}{\lambda}\)
अतः स्पष्ट है कि दूरदर्शी को विभेदन क्षमता बढ़ाने के लिए अभिदृश्यक का द्वारक d अधिक होना चाहिए।

प्रश्न 4.
वर्ण विक्षेपण क्या है? विक्षेपण का कारण लिखिए।
उत्तर:
जब श्वेत प्रकाश किरण प्रिज्म के अपवर्तक पृष्ठ पर आपतित होती है तो प्रिज्म द्वारा उसका विक्षेपण हो जाता है अर्थात् वह अपने अवयवी रंगों में विभक्त हो जाती है। यह क्रिया वर्ण विक्षेपण (Dispersion) कहलाती है।

चूँकि बैंगनी रंग की तरंगदैर्ध्य सबसे कम और लाल रंग की तरंगदैर्ध्य सबसे अधिक होती है। इसलिए लाल रंग के लिए विचलन कोण सबसे कम तथा बैंगनी रंग के लिए सबसे अधिक होता है। फलस्वरूप जय श्वेत प्रकाश किरण प्रिज्म से अपवर्तित होती है तो विभिन्न रंगों के लिए विचलन कोण भिन्न - भिन्न होने के कारण विभिन्न रंगों के मार्ग भिन्न हो जाते हैं अर्थात् प्रकाश किरण अपने अवयवी घटकों में वियोजित हो जाती है। वर्ण विक्षेपण का यही कारण है।

प्रश्न 5.
संयुक्त सूक्ष्मदर्शी की आवर्धन क्षमता कैसे बढायी जा सकती है?
उत्तर:
संयुक्त सूक्ष्मदर्शी की आवर्धन क्षमता बढ़ाने के लिए f₀ व f_e दोनों के मान कम होने चाहिए। दृश्य क्षेत्र को बढ़ाने के लिए f_o < f_e होना चाहिए।

प्रश्न 6.
दर्पण की फोकस दूरी एवं वक्रता त्रिज्या में संबंध स्थापित कीजिए।
उत्तर:
गोलीय दर्पणों की फोकस दूरी एवं वक्रता त्रिज्या में संबंध (Relation Between Focal Length and Radius of Curvature of a Spherical Mirror)
(i) उत्तल दर्पण के लिए: माना एक उत्तल दर्पण की फोकस दूरी f व वक्रता त्रिज्या R है। OA एक मुख्य अक्ष के समान्तर आने वाली आपतित किरण है और AS परावर्तित किरण है जो फोकस F से आती हुई प्रतीत होती है। AN मुख्य अक्ष पर अभिलम्ब है। परावर्तन के नियम से,

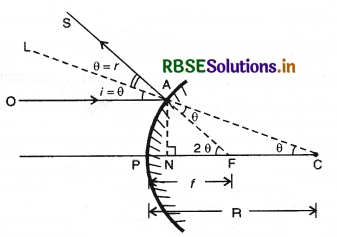
i = r = θ (मान लिया)
∆AFC में,
∠FAC = ∠LAS = θ (शौर्षाभिमुख (vertically opposite) कोण हैं)
∠ACF = ∠OAL = θ (संगत (corresponding) कोण हैं)
∆AFC में,
बहिष्कोण (exterior angle) AFP = अन्त:कोण (interior angle) ( ∠FAC+ ∠ FCA)
= θ + θ = 2θ
समकोण ∆ANC से,
tan θ = \(\frac{\mathrm{AN}}{\mathrm{NC}}\frac{\mathrm{AN}}{\mathrm{NC}}\)
यदि θ छोटा है तो 
(i) tan θ ≈ θ,  (ii) बिन्दु P व N सम्पाती (coincident) होंगे
∴ θ = \(\frac{\mathrm{AN}}{\mathrm{PC}}=\frac{\mathrm{AN}}{\mathrm{R}}\) ..........................(1)
इसी प्रकार समकोण ∆ANF से,
tan 2θ = \(\frac{\mathrm{AN}}{\mathrm{NF}}\)
यदि 2θ छोटा है तो
(ii) tan 2θ = 20, (ii) N व P सम्पाती (coincident) होंगे
∴ 2θ = \(\frac{\mathrm{AN}}{\mathrm{PF}}=\frac{\mathrm{AN}}{f}\) ......................(2)
समी. (1) व (2) से,

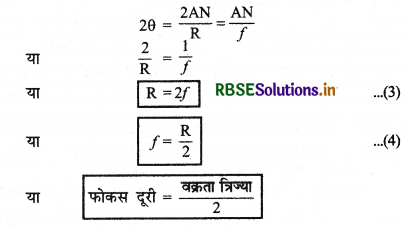
(ii) अवतल दर्पण के लिए: इसमें भी OA आपतित किरण एवं AF परावर्तित किरण है। AN मुख्य अक्ष पर अभिलम्ब है। f फोकस दूरी एवं वक्रता त्रिज्या है। परावर्तन के नियम से,
∠i = ∠r = θ (मान लिया)
∴ ∠OAF = i + r = θ + θ = 2θ
और ∠OAF = ∠AFP = 2θ (क्योंकि दोनों एकान्तर (alternate interior angle) कोण है)

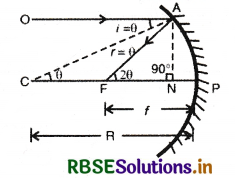
इसी प्रकार
∠OAC = ∠ACP = θ (ये भी एकान्तर कोण हैं)
समकोण ∆ANC में,
tanθ = \(\frac{\mathrm{AN}}{\mathrm{CN}}\)
यदि कोण θ छोटा है, तो 
(i) tanθ ≈ θ और (ii) N व P सम्पाती होंगे।
∴ θ = \(\frac{\mathrm{AN}}{\mathrm{CP}}=\frac{\mathrm{AN}}{\mathrm{R}}\) ..............................(1)
इसी प्रकार समकोण ∆ANF से,
tan 2θ = \(\frac{\mathrm{AN}}{\mathrm{FN}}\)
यदि 2θ छोटा है, तो
(i) tan 2θ ≈ 2θ और 
(ii) N व P सम्पाती होंगे।
अतः 2θ = \(\frac{\mathrm{AN}}{\mathrm{FP}}=\frac{\mathrm{AN}}{f}\) .......................(2)
समी. (1) व (2) से,
2θ = \(\frac{2 \mathrm{AN}}{\mathrm{R}}=\frac{\mathrm{AN}}{f}\)
या \(\frac{2}{\mathrm{R}}=\frac{1}{f}\)

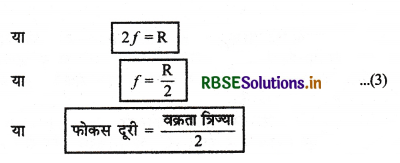
अतः स्पष्ट है कि गोलीय दर्पण की फोकस दूरी वक्रता त्रिज्या की आधी होती है।

प्रश्न 7.
किसी लेन्स की फोकस दूरी किन - किन कारणों पर निर्भर करती है?
उत्तर:
लेन्स की फोकस दूरी \(\frac{1}{f}=(\mu-1)\left(\frac{1}{R_1}-\frac{1}{R_2}\right)\)
अत: फोकस दूरी (f) का मान निम्न कारकों पर निर्भर करता है-

• लेन्स की वक्रता त्रिज्याओं पर
• लेन्स के पदार्थ के अपवर्तनांक पर
• उस माध्यम के अपवर्तनांक पर जिसमें लेन्स रखा है।

प्रश्न 8.
द्वितीयक इन्द्रधनुष में रंगों का क्रम प्राथमिक की तुलना में उल्टा क्यों होता है?
उत्तर:
द्वितीयक इन्द्रधनुष तब बनता है जब प्रकाश किरण जल की बूंद में निचले भाग में प्रवेश करती है और उसका दो बार पूर्ण आन्तरिक परावर्तन होता है जबकि प्राथमिक इन्द्रधनुष बनने पर बूंद के ऊपरी भाग में प्रकाश प्रवेश करता है और इसका पूर्ण आन्तरिक परावर्तन एक बार होता है। इसीलिए द्वितीयक इन्द्रधनुष में रंगों का क्रम उल्टा होता है।

प्रश्न 9.
किसी संयुक्त सूक्ष्मदर्शी के अभिदृश्यक तथा नेत्रिका लेन्स की फोकस दूरी कम क्यों होनी चाहिए?
उत्तर:
अभिदृश्यक की आवर्धन क्षमता का परिणाम
m₀ = \(\frac{v_0}{u_0}\)
संयुक्त सूक्ष्मदशी में वस्तु अभिदृश्यक लेन्स के प्रथम फोकस तल के बराबर उसके निकट रखी जाती है अत:
u₀ ≈ f₀
∴ m₀ = \(\frac{v_0}{f_0}\)
स्पष्ट है कि अभिदृश्यक का m₀ उतना ही अधिक होगा जितना f₀ का मान कम होगा।
अभिनेत्र लेन्स की आवर्धन क्षमता
m_e = \(\left(1+\frac{D}{f_e}\right)\)
इसमें भी f_e का मान जितना कम होगा, m_e का मान उतना ही अधिक होगा।
स्पष्ट है कि संयुक्त सूक्ष्मदर्शी की आवर्धन क्षमता बढ़ाने के लिए अभिदृश्वक एवं नेत्रिका लेन्स दोनों की फोकस दूरियाँ कम ली जाती हैं।

प्रश्न 10.
चित्र द्वारा प्राथमिक इन्द्रधनुष बनने की प्रक्रिया दर्शाइए और व्याख्या कीजिए कि किस कोण पर प्राथमिक इन्द्रधनुष दिखाई देता है।
उत्तर:
प्राथमिक इन्द्रधनुष बनने की प्रक्रिया निम्न चित्र में समझायी गई है। प्रक्षेक की आँख पर बूंद 1 से लाल प्रकाश एवं बूंद 2 से बैंगनी प्रकाश पहुँचता है। बूंद 1 से बैंगनी एवं बूंद 1 से लाल प्रकाश आँखों के ऊपर एवं नीचे से गुजराता है, अतः इन्द्रधनुष में हमें ऊपरी किनारा लाल तथा निचला किनारा बैंगनी दिखायी देता है। इस प्रकार प्राथमिक इन्द्रधनुष तीन चरणीय प्रक्रम (अपवर्तन, पूर्ण आन्तरिक परावर्तन तथा पुनः अपवर्तन) का परिणाम है।

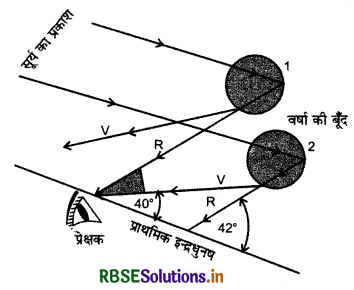
बैंगनी तथा लाल रंग के प्रकाश क्रमश: 40° व 42° पर फैलते हैं।

प्रश्न 11.
मोटर वाहनों के पीछे के ट्रैफिक को देखने हेतु चालक किस दर्पण का उपयोग करते हैं और क्यों?
उत्तर:
उत्तल दर्पण क्योंकि इससे बनने वाला प्रतिबिम्ब सीधा, आभासी एवं छोटा होता है जिसके फसस्वरूप पीछे का दृश्य क्षेत्र बड़ा हो जाता है।

दीर्घ उत्तरीय प्रश्न

प्रश्न 1.
प्रिज्म से गुजरने वाले प्रकाश के लिए आपतन कोण के फलन के रूप में विचलन कोण में विचरण को दर्शाने के लिए ग्राफ खींचिए। प्रिज्म कोण और न्यूनतम विचलन कोण के पदों में अपवर्तनांक के लिए व्यंजक व्युत्पन्न कीजिए।
उत्तर:
प्रिज्म में अपवर्तन (Refraction through Prism )
"किसी कोण पर झुके हुये दो समतल अपवर्तक फलकों के मध्य घिरे समांगी (homogeneous) एवं पारदर्शी (transparent) माध्यम को प्रिज्म कहते हैं।"

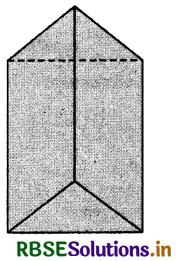
प्रिज्म एक ऐसा पारदशी माध्यम (सामान्यतः काँच) होता है जो दो त्रिभुजाकार (triangular) एवं तीन आयताकार (rectangular) अपवर्तक फलकों (faces) से घिरा होता है। प्रिज्म को इस प्रकार रखा जाता है कि उसके आयताकार फलक ऊधिर एवं त्रिभुजाकार फलक तिज (horizontal) रहें। प्रिण्य के आयताकार फलकों से अपवर्तन होता है, अत: इन्हें अपवर्तक फलक (refracting surfaces) कहते हैं। जिस कोर पर दोनों अपवर्तक फलक मिलते हैं, उसे अपवर्तक कोर (refracting edge) कहते है तथा इन फलकों के मध्य जो कोण बनता है उसे प्रिज्म कोण (angle of prism) कहते हैं। प्रिज्य कोण को ही अपवर्तक कोण (refracting angle) भी कहते हैं। अपवर्तक कोर के सामने वाले फलक को आधार (base) कहते है जिसकी पहचान के लिए प्रायः इसे घिस दिया जाता है। अपवर्तक फलकों के लम्बवत् प्रिज्म के परिच्छेद (cross - section) को प्रिज्म का मुख्य परिचोद (principal section) कहते हैं। यदि प्रिज्य कोण 60° है तो यह मुख्य परिच्छेद समबाहु त्रिभुज (equilateral triangle) के आकार का होता है। इसीलिए सामान्यतः प्रिज्म को एक समबाहु त्रिभुज द्वारा व्यक्त किया जाता है।

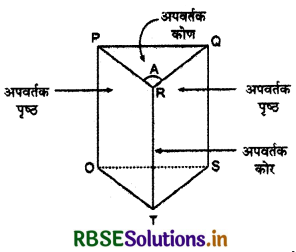
प्रिज्म की क्रिया: जब प्रिम द्वारा कोई प्रकाश अपवर्तित होता है तो निम्नलिखित दो क्रियाएँ सम्भव है-

• विचलन, 
• विक्षेपण।

1. प्रिज्म द्वारा विद्यालय (Deviation by Prism): जब एकवर्णीय (monochromatic) प्रकाश की कोई किरण प्रिज्य के अपवर्तक पृष्ठ पर आपत्तित होती है तो किरण का दो बार अपवर्तन होता है जिससे किरण की दिशा में विचलन उत्पन्न हो जाता है। "निर्गत किरण (emergentray) की दिशा एवं आपतित किरण (incident ray) की दिशा के मध्य जो कोण बनता हैउसे विचलन कोण (deviation angle) कहते है।" चित्र में इसे 8 से प्रदर्शित किया गया है।

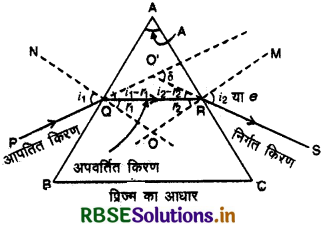
चित्र 9.54(b) में,
PQ = आपतित किरण, QR = अपवर्तित किरण, RS = निर्गत किरण, i₁ = आपतन कोण, r₁ व r₂ = अपवर्तन कोण, i₂ या e = निर्गमन कोण, δ = विचलन कोण
आपतन कोण, विचलन कोण तथा प्रिज्य कोण में सम्बन्ध - ∆O QR में,
बहिष्कोण (exterior angle) = δ, 
सामने के अन्त:कोण (interior angle)
∠O'QR = (i₁ - r₁) 
और ∠O'RQ = (i₂ - r₂)
∵ त्रिभुज में बहिष्कोण सामने के अन्त:कोणों के योग के बराबर होता है अत:
δ = ∠O'QR + ∠O'RQ 
या δ = (i₁ - r₁) + (i₂ - r₂)
या δ = (i₁ + i₂) - (r₁ + r) ....................(1)
∆AQR में,
∠AQR = ∠AQO - ∠OQR
= 90° - r₁
इसी प्रकार ∠ARQ = 90° - r₂
∵ त्रिभुज के तीनों अन्त:कोणों का योग 180° होता है।
∴ ∠QAR + ∠AQR + ∠ARQ = 180°
या A + 90° - r₁ + 90° - r₂ = 180°
या A - (r₁ + r₂) + 180° = 180° 
या A = (r₁ + r₂) = 180° - 180° = 0
या A = (r₁ + r₂) ...................(2)
समी. (1) व (2) से,
δ = (i₁ + i₂) - A

न्यूनतम विचलन कोण (Angle of Minimum Deviation) (D_m): यदि प्रिज्य पर प्रकाश का आपतन कोण बदल - बदल कर संगत विचलन कोणों के मान ज्ञात करके उन्हें ग्राफ पर प्लॉट किया जाये तो प्राप्त वक्र की भाँति मिलता है। वक्र से स्पष्ट है कि आपतन कोण बढ़ने के साथ विचलन कोण का मान घटता है और एक न्यूनतम मान के बाद फिर बढ़ने लगता है। विचलन कोण के इसी न्यूनतम मान को न्यूनतम विचलन कोण (angle of minimum deviation) कहते हैं और δ_m से व्यक्त करते हैं।

ग्राफ से यह स्पष्ट है कि किसी भी विचलन कोण के संगत (corresponding) आपतन कोण के दो मान i₁ व i₂ प्राप्त होते हैं लेकिन न्यूनतम विचलन कोण के संगत आपतन कोण का केवल एक ही मान 
(i) प्राप्त होता है। आपतन कोण के दो मानों i₁ व i₂ में एक आपतन कोण होता है और दूसरा निर्गमन कोण होता है, क्योंकि प्रकाश का पथ उत्क्रमणीय (reversible) होता है। जब आपतन कोण i₁ = i₂ होंगे

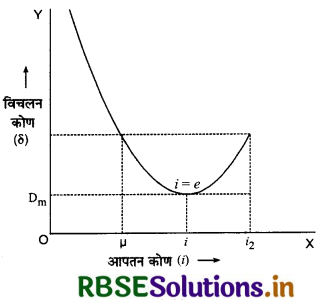
तो अपवर्तन कोण r₁ = r₂ होंगे। अतः न्यूनतम विचलन की अवस्था में,
(i) आपतन कोण निर्गमन कोण के बराबर होता है। (∠i = ∠e)
(ii) अपवर्तित किरण प्रिज्म के आधार (base) के समान्तर होती है।

प्रिज्म के पदार्थ के अपवर्तनांक के लिए सूत्र (Formula for Refractive Index of the Prism ): न्यूनतम विचलन की दशा में प्रिज्म से किरण आरेख चित्र 9.56 में दिखाया गया है। स्नेल के नियम से प्रिज्म के पदार्थ का अपवर्तनांक,
n = \(\frac{\sin i}{\sin r}\) .................(1)
∆QOR में,
∠r + ∠r + ∠O = 180°

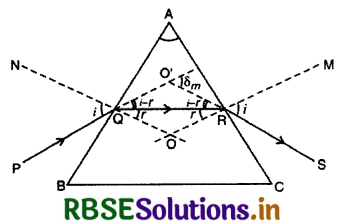
या 2r + ∠O = 180° .................(2)
□ AQOR में अन्त: कोण
∠AQO = ∠ARO = 90°
∴ ∠A + ∠O = 180° .......................(3)
( क्योंकि चतुर्भुज के चारों अन्तः कोणों का योग चार समकोण होता है।)
समी. (2) व (3) की तुलना करने पर,
2r + ∠O = A + ∠O
या 2r = A ................(4)
या r = A/2
अब ∆O'QR में बहिष्कोण
δ_m = (i - r) + (i - r) = 2i - 2r
या δ_m = 2i -A [समी. (4) से]
या 2i = A + δ_m
या i = \(\frac{\mathrm{A}+\delta_m}{2}\) ...................(5)
समी. (4) व (5) से r व i के मान समी. (1) में रखने पर,

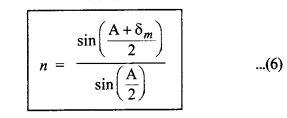
इस सूत्र को प्रिज्म - सूत्र (prism formula) भी कहते हैं।
पतले प्रिज्म द्वारा उत्पन्न विचलन (Deviation Produced by a Thin Prism)
प्रिज्म के पदार्थ का अपवर्तनांक
n = \(\frac{\sin \left(\frac{\mathrm{A}+\delta_m}{2}\right)}{\sin \left(\frac{\mathrm{A}}{2}\right)}\)
पतले प्रिज्म के लिए प्रिज्म कोण का मान बहुत कम (लगभग 5°) होता है अत: δm का मान भी बहुत कम होगा। अत:
\(sin\left(\frac{\mathrm{A}+\delta_m}{2}\right) ≈ \frac{\mathrm{A}+\delta_m}{2}\) और \(sin\frac{\mathrm{A}}{2} \approx \frac{\mathrm{A}}{2}\)

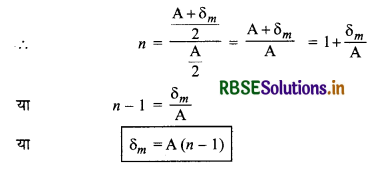
स्पष्ट है कि पतले प्रिज्म द्वारा उत्पन्न विचलन कोण का मान केवल प्रिज्म कोण (A) व प्रिज्म के पदार्थ के अपवर्तनांक (n) पर निर्भर करता है। यद्यपि उक्त समीकरण में न्यूनतम विचलन कोण पतले प्रिज्म के लिए प्राप्त किया गया है लेकिन पतले प्रिज्म के लिए इसे हम व्यापक रूप दे सकते हैं जिसके अनुसार,

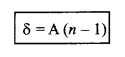
प्रश्न 2.
जरा दृष्टि दोष किसे कहते हैं? परावर्तक दूरदशी की बनावट एवं कार्यविधि का वर्णन कीजिए। आवश्यक किरण चित्र बनाइए।
उत्तर:
प्रमुख दृष्टि दोष निम्नलिखित हैं जो अनेक असावधानियों एवं सुरक्षात्मक उपायों की अनदेखी से उत्पन्न होते हैं-
(i) निकट दृष्टि दोष (Myopia or Short Sightedness)
जब आँख में निकट दृष्टि दोष उत्पन्न होता है तो निकट की वस्तुएँ तो स्पष्ट दिखायी देती हैं लेकिन दूर की वस्तुएँ स्पष्ट दिखायी नहीं देती है। दोष के कारण - यह दोष तब उत्पन्न होता है जब (i) नेत्र लेन्स एवं रेटिना के बीच की दूरी बढ़ जाती है अथवा (ii) नेत्र लेन्स की फोकस दूरी कम हो जाती है। इनमें से कोई कारण होने पर दूर अर्थात् अनन्त से आने वाली किरणे रेटिना से पहले फोकस हो जाती हैं और वस्तु स्पष्ट दृष्टिगोचर नहीं होती है। इस दोष से युक्त लेन्स का दूर बिन्दु (F) अनन्त पर न होकर लेन्स से कुछ दूरी (x) पर होता है।

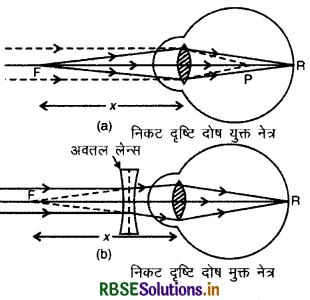
दोष दूर करने के उपाय: निकट दृष्टि के दोष से मुक्ति पाने के लिए नेत्र लेन्स के पास अवतल लेन्स का प्रयोग किया जाता है ताकि दूर से आने वाली किरणें कुछ अपवर्तित होकर नेत्र लेन्स पर पहुंचे और वे रेटिना पर प्रतिबिम्ब बनायें। अनन्त से आने वाली समान्तर किरणे अवतल लेन्स द्वारा दूर बिन्दु F पर प्रतिबिम्ब बनाती हैं जो नेत्र लेन्स के लिए आभासी वस्तु (virtual object) का कार्य करता है और दूरस्थ वस्तु (far object) का प्रतिबिम्ब रेटिना पर बन जाता है तथा वस्तु स्पष्ट दिखायी देने लगती है। इस प्रकार निकट दृष्टि का दोष दूर हो जाता है| 
दोष निवारण के लिए प्रयुक्त लेन्स की शक्ति: यदि नेत्र लेन्स से दूर बिन्दु की दूरी हो, तो अवतल लेन्स के लिए,
u = -∞ एवं v= -x
∴ अवतल लेन्स की फोकस दूरी
\(\frac{1}{f}=\frac{1}{-x}-\frac{1}{-\infty}=-\frac{1}{x}\)
या f = -x
यदि x को cm में नापा जाये तो लेन्स की क्षमता
P = \(\frac{100}{f}\)

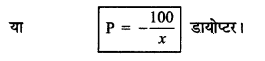
(ii) दूर दृष्टि दोष (Hypermetropia or Long Sightedness): नेत्र में दूर दृष्टि दोष उत्पन्न होने पर दूर की वस्तुएँ तो स्पष्ट दिखायी देती हैं लेकिन पास की वस्तुएँ स्पष्ट दिखायी नहीं देती हैं।
दोष के कारण: यह दोष तब उत्पन्न होता है जब (i) नेत्र लेन्स तथा रेटिना के बीच की दूरी कम हो जाती है अथवा (ii) नेत्र लेन्स की फोकस दूरी बढ़ जाती है।
दोष दूर करने के उपाय: इनमें से कोई कमी उत्पन्न होने पर नेत्र के निकट बिन्दु N पर रखी वस्तु से चलने वाली किरणे रेटिना के पीछे बिन्दु P पर मिलकर प्रतिबिम्ब बनाती हैं और वस्तु स्पष्ट दिखायी नहीं देती है जबकि N पर वस्तु यदि स्थित हो तो उसका प्रतिबिम्ब रेटिना पर बनेगा और वह स्पष्ट दिखायी देगी। स्पष्ट है कि N से चलने वाली किरणों को एक समुचित उत्तल लेन्स द्वारा कुछ अभिसरित (converge) कर दिया जाये ताकि वे N' से आती प्रतीत हों तो वस्तु का प्रतिबिम्ब रेटिना पर बन जायेगा और वह स्पष्ट रूप से दृष्टिगोचर (visible) हो जायेगी तथा दूर दृष्टि का दोष समाप्त हो जायेगा।

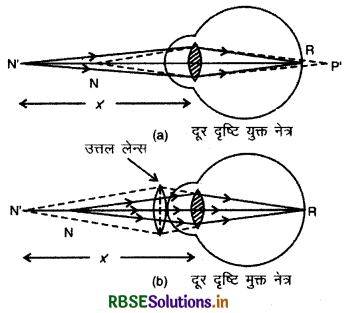
निवारण के लिए प्रयुक्त लेन्स की शक्ति (power of used lens to remove defect): माना दोष युक्त नेत्र के निकट बिन्दु N' की नेत्र लेन्स से दूरी x' है और सामान्य आँख की स्पष्ट दृष्टि की न्यूनतम दूरी D है तथा प्रयुक्त उत्तल लेन्स की फोकस दूरी है f तो
u = -D और v = -x'
∴ लेन्स - सूत्र से,

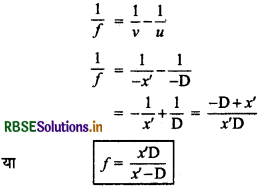
∵ x' > D ∴ f का मान धनात्मक होगा अर्थात् प्रयुक्त लेन्स उत्तल लेन्स होगा। यदि दूरियाँ सेमी में नापी जाए तो प्रयुक्त लेन्स की शक्ति
P = +\(\frac{100}{f}\)

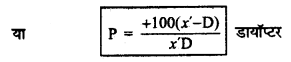
(iii) जरा दृष्टि दोष (Presbyopia): इस दोष के उत्पन्न होने पर न तो बहुत दूर की वस्तुएँ स्पष्ट दिखायी देती है और न ही बहुत पास की वस्तुएँ स्पष्ट दिखायी देती है अर्थात् दूर बिन्दु अनन्त से हटकर नेत्र के पास आ जाता है और निकट बिन्दु नेत्र से दूर हट जाता है।

दोष के कारण: दोष का मुख्य कारण वृद्धावस्था में मांसपेशियों का शिथिल हो जाना है। दोष का निवारण - जरा दृष्टि दोष में निकट दृष्टि एवं दूर दृष्टि दोनों प्रकार के दोष शामिल हैं, अत: इस दोष को दूर करने के लिए दो चश्मे प्रयोग किये जाते हैं जिनमें से एक में उत्तल लेन्स और दूसरे में अवतल लेन्स का प्रयोग किया जाता है। यदि एक ही चश्मा पहनना है तो द्विफोकसी - लेन्स (bifocal lens) का प्रयोग करना होगा।

(iv) अबिन्दुकता दोष (Astigmatism): जब आँखों में अबिन्दुकता का दोष उत्पन्न हो जाता है तो या तो क्षैतिज दशा में स्पष्ट (clear) और ऊर्ध्व दिशा में धुंधला (dimmer) अथवा ऊर्ध्व दिशा में स्पष्ट और क्षैतिज दिशा में धुंधला दिखाई देने लगता है।
दोष का कारण: दोष का कारण कॉर्निया की सतह का गोलाकार च रहना है (comea has unequal curvature), किसी एक दिशा में उसको त्रिज्या अधिक और दूसरी दिशा में कम हो जाती है।
दोष के निवारण का उपाय: दोष के निवारण के लिए मोटे गोलीय बेलनाकार लेन्स (thick sphero - cylindrical lens) प्रयोग किये जाते हैं।

दूरदर्शी (Telescope)
दूरदर्शी वह प्रकाशिक उपकरण है जो दूर की वस्तुओं को देखने के लिए प्रयोग किया जाता है। खगोलीय दूरदर्शी का उपयोग खगोल वैज्ञानिक आकाशीय पिण्डों को देखने के लिए करते हैं। जब खगोलीय वस्तुओं जैसे चन्द्रमा या अन्य किसी ग्रह को देखा जाता है तो उनके उल्टे प्रतिबिम्ब से कोई असुविधा नहीं होती क्योंकि ये वस्तुएँ गोलाकार हैं। यह दूरदर्शी संरचना के आधार पर दो प्रकार के होते हैं-
(1) अपवर्ती प्रकार का दूरदर्शी
(2) परावर्ती प्रकार का दूरदर्शी।

(1) अपवर्ती प्रकार का दूरदशी (Refracting Telescope)
रचना: इस दूरदर्शी में दो लेन्स होते हैं जिनमें एक का मुख्य फोकस एवं मुख्य व्यास (द्वारक) बड़ा होता है और यह वस्तु की ओर रहता है, इसे अभिदृश्यक (Objective lens or field lens) कहते हैं। दूसरा लेन्स छोटे मुख्य फोकस एवं छोटे द्वारक का होता है और यह आँख की और रहता है, इसे अभिनेत्र लेन्स (eye lens) कहते हैं। दोनों लेन्स एक नली के दोनों सिरों पर लगे होते हैं और इनके बीच की दूरी दण्ड चक्रीय क्रम (rack and pinion) से घटायी या बढ़ाई जा सकती है।

समायोजन एवं किरण आरेख - सबसे पहले नेत्रिका को आगे - पीछे खिसकाकर क्रॉस - वार (cross wire) पर समायोजित कर लेते हैं। इसके बाद अभिदृश्यक का रुख दृश्य (जो वस्तु देखनी है) की ओर करके छोटी नली को लम्बी नली में इतना आगे या पीछे खिसकाते हैं कि वस्तु का प्रतिबिम्ब क्रॉस - तार पर बनने लगे। इस दशा में वस्तु स्पष्ट दृष्टिगोचर होने लगती है।
दूरदर्शी से प्रतिबिम्ब बनने की क्रिया चित्र 9.72 में दिखाई गई है।

अनन्त पर रखी किसी वस्तु AB से आने वाली समान्तर किरणें अभिदृश्यक से अपवर्तित होकर इसके फोकस F₀ पर वस्तु का उल्य, छोटा एवं वास्तविक प्रतिबिम्ब A'B' बनाती हैं। नेत्रिका को इतना आगे या पीछे खिसकाते हैं कि यह प्रतिबिम्ब उसके प्रथम फोकस F_e' के अन्दर आ जाये। इस स्थिति में A'B' का सीधा, बड़ा एवं काल्पनिक प्रतिबिम्ब A"B" बनता है। यही अन्तिम प्रतिबिम्ब होता है।

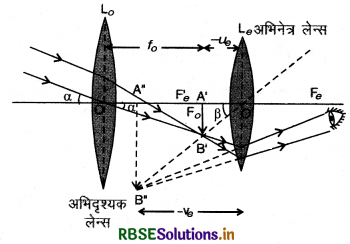
आवर्धन क्षमता (Magnifying Power): दूरदर्शी की आवर्धन क्षमता की परिभाषा निम्न प्रकार की जाती है-

(i) जब अन्तिम प्रतिबिम्ब स्पष्ट दृष्टि की न्यूनतम दूरी पर बने: अन्तिम प्रतिबिम्ब स्पष्ट दृष्टि की न्यूनतम दूरी (D) पर बनता है तो
v_e = -D
∴अभिनेत्र लेन्स के लिए लेन्स सूत्र से,
\(\frac{1}{v_e}-\frac{1}{u_e}=\frac{1}{f_e}\)

इस अवस्था में दूरदर्शी को निकट बिन्दु समायोजन की स्थिति में कहा जाता है (Near - point adjustment)।
(ii) जब अन्तिम प्रतिबिम्ब अनन्त पर बने: जब अन्तिम प्रतिबिम्ब अनन्त पर बनेगा तो माध्यमिक प्रतिबिम्ब AB' अभिनेत्र लेन्स के फोकस F_e' पर बनेगा, अत:
u_e = f_e
समी. (1) से,

इस स्थिति में किरण आरेख निम्न प्रकार होगा:

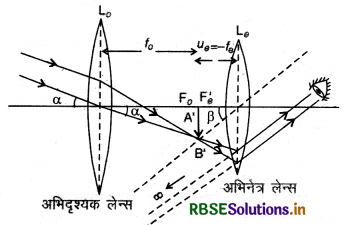
यदि अन्तिम प्रतिबिम्ब अनन्त (Infinity) पर बनता है तो इस अवस्था में दूरदर्शी को सामान्य समायोजन की स्थिति में कहा जाता है (Normal adjustment)।

प्रश्न 3.
दर्पण समीकरण का व्यंजक व्युत्पन्न कीजिए। आवश्यक किरण चित्र बनाइए।
उत्तर:
दर्पण समीकरण (Mirror Equation) 
(A) उत्तल दर्पण के लिए दर्पण - सूत्र (Mirror Formula for Convex Mirror): M₁M₂ उत्तल दर्पण है। इसके सामने रखी वस्तु AB का प्रतिबिम्ब A'B' बनता है। मुख्य अक्ष के समान्तर किरण के आपतन बिन्दु E से मुख्य अक्ष पर डाला गया अभिलम्ब EN है।

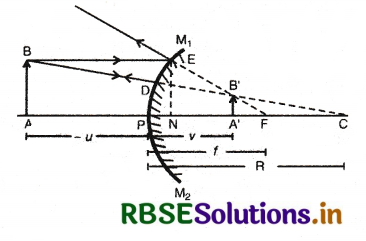
अब ∆ABC व ∆A'B'C में,
∠BAC = ∠B'A'C = 90°
∠C दोनों में उभयनिष्ठ (Common) है।
अतः त्रिभुजों के तीसरे कोण ∠ABC व ∠ABC स्वतः बराबर हो जायेंगे। इस प्रकार ∆ARC व ∆A'B'C समरूप (similar) त्रिभुज होंगे। इन समरूप त्रिभुजों में,
\(\frac{\mathrm{AB}}{\mathrm{A}^{\prime} \mathrm{B}^{\prime}}=\frac{\mathrm{AC}}{\mathrm{A}^{\prime} \mathrm{C}}\) ...............(1)
अब ∆ENF व ∆A'B'F में,
∠ENF = ∠B'A'F = 90°
∠F दोनों में उभयनिष्ठ (common) है।
अत: ∆ENF व ∆A'B'F भी समरूप (similar) त्रिभुज होंगे। इन समरूप त्रिभुजों से,
\(\frac{\mathrm{EN}}{\mathrm{A}^{\prime} \mathrm{B}^{\prime}}=\frac{\mathrm{NF}}{\mathrm{A}^{\prime} \mathrm{F}}\) ................(2)
∵ EN = AB
∴ \(\frac{\mathrm{AB}}{\mathrm{A}^{\prime} \mathrm{B}^{\prime}}=\frac{\mathrm{NF}}{\mathrm{A}^{\prime} \mathrm{F}}\) .............(3)
ध्रुव P के काफी निकट (very near) होगा, अत: NF = PF ले सकते हैं, अतः
\(\frac{\mathrm{AB}}{\mathrm{A}^{\prime} \mathrm{B}^{\prime}}=\frac{\mathrm{PF}}{\mathrm{A}^{\prime} \mathrm{F}}\) ................(4)
अब समी. (1) व (4) की तुलना करने पर,
\(\frac{\mathrm{AC}}{\mathrm{A}^{\prime} \mathrm{C}}=\frac{\mathrm{PF}}{\mathrm{A}^{\prime} \mathrm{F}}\) ..................(5)
या \(\frac{\mathrm{AP}+\mathrm{PC}}{\mathrm{PC}^{-} \mathrm{PA}^{\prime}}=\frac{\mathrm{PF}}{\mathrm{PF}-\mathrm{PA}^{\prime}}\) ................(6)
चिह्न परिपाटी के अनुसार,
AP = -u
PA' = +v
PF = +f
PC = +R = 2f
समी. (6) में मान रखने पर,

(B) अवतल दर्पण के लिए दर्पण - सूत्र (Mirror Formula for Concave Mirror): M1M2 एक अवतल दर्पण है जिसके सामने रखी वस्तु AB का प्रतिबिम्ब A'B' बनता है।

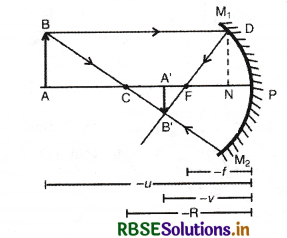
∆ARC व ∆CA'B' में,
∠BAC = ∠CA'B' = 90°
∠BCA = ∠A'CB' (शीर्षाभिमुख (vertically opposite) कोण हैं)
अत: ∆ABC व ∆A'B'C समरूप त्रिभुज हैं। इन समरूप त्रिभुजों से,
\(\frac{\mathrm{AB}}{\mathrm{AB}^{\prime}}=\frac{\mathrm{AC}}{\mathrm{CA}^{\prime}}\) ..........................(1)
अब ∆A'B'F व ∆FDN में,
∠BAF = ∠ENF = 90°
∠A'FB' = ∠DFN (शीर्षाभिमुख कोण हैं)
अत: ∆A'B'F व ∆FDN समरूप त्रिभुज हैं। 
इन समरूप त्रिभुजों से,
\(\frac{\mathrm{DN}}{\mathrm{A}^{\prime} \mathrm{B}^{\prime}}=\frac{\mathrm{FN}}{\mathrm{FA}^{\prime}}\) ........................(2)
∵ DN = AB
∴ \(\frac{\mathrm{AB}}{\mathrm{A}^{\prime} \mathrm{B}^{\prime}}=\frac{\mathrm{FN}}{\mathrm{FA}^{\prime}}\) ...................(3)
यदि दर्पण का द्वारक बहुत छोटा है तो N व P अति निकट (very near) होंगे, अत: FN = FP ले सकते हैं।
∴\(\frac{\mathrm{AB}}{\mathrm{A}^{\prime} \mathrm{B}^{\prime}}=\frac{\mathrm{FP}}{\mathrm{FA}^{\prime}}\) ....................(4)
समी. (1) व (4) से,
\(\frac{\mathrm{AC}}{\mathrm{CA}^{\prime}}=\frac{\mathrm{FP}}{\mathrm{FA}^{\prime}}\)
या \(\frac{\mathrm{PA}-\mathrm{PC}}{\mathrm{PC}-\mathrm{PA}^{\prime}}=\frac{\mathrm{FP}}{\mathrm{A}^{\prime} \mathrm{P}-\mathrm{PF}}\) .......................(5)
चिहन परिपाटी के अनुसार,
PA = -u
PC = -R = -2f
PA' = -v
PF = -f
∴समीकरण (5) में मान रखने पर,
\(\frac{-u-(-2 f)}{-2 f-(-v)}=\frac{-f}{-v-(-f)}\)

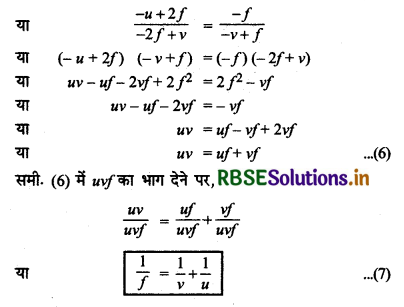
प्रश्न 4.
लेंस मेकर सूत्र का उपयोग करके किसी पतले उभयोत्तल लेन्स के सूत्र \(\frac{1}{f}=\frac{1}{v}-\frac{1}{u}\) को व्युत्पन्न कीजिए।
उत्तर:
पतले लेंस के लिए सूत्र
चित्र 9.43 में एक पतला लेन्स दिखाया गया है जिसके दोनों ओर एक ही माध्यम वायु है। इसके दोनों पृष्ठों की वक्रता त्रिज्याएँ क्रमश: R₁ व R₂ हैं। लेन्स की अक्ष पर रखी एक बिन्दु वस्तु O का प्रतिबिम्ब पृष्ठ AP₁B द्वारा I' बनता है और I' का प्रतिविम्ब पृष्ठ AP₂B द्वारा I बनता है। इस प्रकार पूरे लेन्स द्वारा O का प्रतिबिम्ब I बनता है।

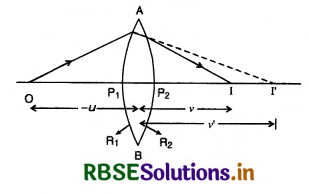
अतः प्रथम पृष्ठ पर अपवर्तन के लिए,
\(\frac{n_{g a}}{v^{\prime}}-\frac{1}{u}=\frac{n_{g a}-1}{\mathrm{R}_1}\) ....................(1)
पहले पृष्ठ द्वारा बना प्रतिबिम्ब I' दूसरे पृष्ठ के लिए आभासी वस्तु का कार्य करता है और अन्तिम प्रतिबिम्ब I बनता है, अत: दूसरे पृष्ठ पर अपवर्तन के लिए,
\(\frac{n_{a g}}{v}-\frac{1}{\left(v^{\prime}-t\right)}=\frac{n_{a g}-1}{\mathrm{R}_2}\)
क्योंकि दूसरे पृष्ठ से I' की दूरी = (v' - t) जहाँ t पतले लेन्स की मोटाई है।
पतले लेन्स के लिए t का मान उपेक्षणीय होता है, अतः

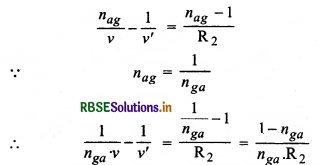
n_ga का समी. के दोनों ओर गुणा करने पर,
\(\frac{1}{v}-\frac{n_{g a}}{v^{\prime}}=\frac{1-n_{g a}}{\mathrm{R}_2}\)
समी. (1) व (2) को जोड़ने पर,

यदि लेन्स की फोकस दूरी f हो तो
\(\frac{1}{v}-\frac{1}{u}=\frac{1}{f}\) ......................(4)
समी (3) व (4) की तुलना करने पर
\(\frac{1}{f}=\left(n_{g a}-1\right)\left(\frac{1}{\mathrm{R}_1}-\frac{1}{\mathrm{R}_2}\right)\) .......................(5)
इसे लेन्स निर्माताओं का सूत्र (Lens maker's formula) कहते हैं। सामान्य रूप से उक्त सूत्र (5) को व्यापक रूप से निम्न प्रकार लिख सकते हैं-

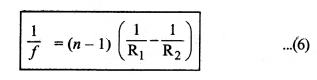
इसे लेन्स सूत्र कहते हैं। यदि लेन्स किसी द्रव जैसे पानी में रखा हो तो लेन्स की फोकस
दूरी

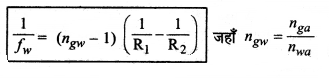
प्रश्न 5.
संयुक्त सूक्ष्मदर्शी की बनावट का वर्णन कीजिए। इसकी कुल आवर्धन क्षमता का सूत्र व्युत्पन्न कीजिए। संयुक्त सूक्ष्मदर्शी द्वारा प्रतिबिम्ब बनने का किरण आरेख बताइये।
उत्तर:
संयुक्त या यौगिक सूक्ष्मदर्शी (Compound Microscope)
संयुक्त सूक्ष्मदर्शी ऐसा उपकरण है जिसका उपयोग अत्यन्त सूक्ष्म वस्तुओं के उच्च आवर्धित प्रतिबिम्ब (highly magnified images) देखने के लिए किया जाता है। 
रचना: इसमें दो उत्तल लेन्स होते हैं। एक लेन्स जो झेटी फोकस, दूरी एवं छोटे द्वारक का होता है और वस्तु की ओर रहता है, इसे अभिदृश्यक लेन्स (Objective lens or field lens) कहते हैं। दूसरा लेन्स बड़ी फोकस दूरी एवं बड़े द्वारक का होता है और आँख की ओर रहता है, यह अभिनेत्र लेन्स (eye lens) कहलाता है। दोनों लेन्स समाक्ष रूप से एक नली के दो सिरों पर लगे होते हैं। दोनों लेन्सों के बीच की दूरी को दण्ड चक्रीय क्रम (rack and pinion) विधि से घटाया या बढ़ाया जा सकता है।

समायोजन (Adjustments) एवं प्रतिबिम्ब का बनना: समायोजन की प्रक्रिया में सबसे पहले नेत्रिका का समायोजन करते हैं। इसके लिए नेत्रिका को इतना आगे या पीछे गति देते हैं कि क्रॉस - तार (cross - wire) स्पष्ट रूप से दिखायी देने लगे। अब वस्तु को अभिदृश्यक के सामने रखकर अभिदृश्यक (objective) की वस्तु से दूरी, अभिदृश्यक को चलाकर, इस प्रकार समायोजित करते हैं कि वस्तु का स्पष्ट प्रतिबिम्ब दिखायी देने लगे। इस दशा में वस्तु का उल्टा, बड़ा एवं आभासी प्रतिविम्ब क्रॉस - तार पर बनता है।
प्रतिबिम्ब बनने की प्रक्रिया निम्न किरण आरेख में प्रदर्शित की गई है।

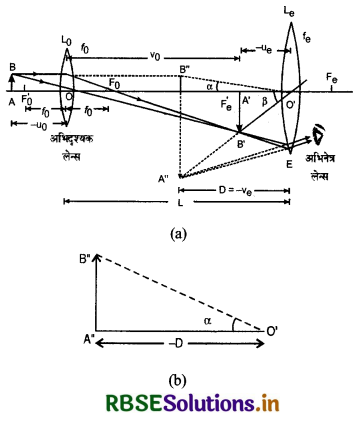
AB एक सूक्ष्म वस्तु है जिसका प्रतिबिम्ब अभिदृश्यक द्वारा बड़ा, उल्टा, वास्तविक A'B' बनता है। यही प्रतिबिम्ब अभिनेत्र लेन्स के लिए वस्तु का कार्य करता है, अत: अभिनेत्र लेन्स को इतना आगे या पीछे खिसकाते हैं कि यह प्रतिबिम्ब अभिनेत्र लेन्स के फोकस के अन्दर आ जाये। इस स्थिति में A'B' का सीधा, बड़ा एवं काल्पनिक (virtual and magnified) प्रतिबिम्ब अभिनेत्र लेन्स के इंसी ओर A"B" बन जाता है। यही अन्तिम प्रतिबिम्ब होता है।

आवर्धन क्षमता (Magnifying power):संयुक्त सूक्ष्मदर्शी की आवर्धन क्षमता की परिभाषा अग्र प्रकार की जाती है

समरूप ∆ABO व ∆OA'B' से,
\(\frac{\mathrm{A}^{\prime} \mathrm{B}^{\prime}}{\mathrm{AB}}=\frac{\mathrm{A}^{\prime} \mathrm{O}}{\mathrm{OA}}=\frac{v_o}{-u_o}\)
∴ समी. (1) से,

(i) यदि अन्तिम प्रतिबिम्ब स्पष्ट दृष्टि की न्यूनतम दूरी (D) पर बने तो
v_e = -D 
अतः अभिनेत्र लेन्स के लिए लेन्स के सूत्र से,

(ii) यदि अन्तिम प्रतिबिम्ब अनन्त पर बने: अन्तिम प्रतिबिम्ब अनन्त पर तभी बनेगा जब अभिदृश्यक द्वारा बनने वाला प्रतिबिम्ब A'B' अभिनेत्र लेन्स के प्रथम फोकस F_e' पर बने, अत:
u_e = f_e
∴ समी. (2) से,

इस स्थिति में किरण आरेख निम्न चित्र 9.71 के अनुसार होगा-

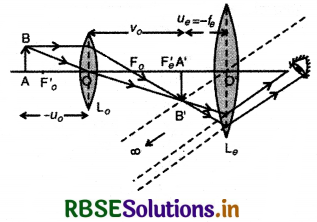
वस्तु AB अभिदृश्यक के आगे उसके प्रथम फोकस F₀' के काफी निकट रहती है अत:
AO ≈ F0'O या u₀ = f₀
इसी प्रकार माध्यमिक प्रतिबिम्ब A'B' अभिनेत्र के काफी निकट बनता है अतः
v₀ = OA' ≈ OO'  ≈ सूक्ष्मदर्शी की लम्बाई (L)
या v0 ≈ L
अत: समी. (3) से आवर्धन क्षमता
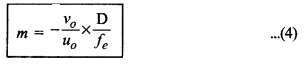
m = \(\frac{\mathrm{L}}{-f_o}\left(1+\frac{\mathrm{D}}{f_e}\right)\) .......................(5)
आंकिक रूप से,
m = \(\frac{\mathrm{L}}{f_o}\left(1+\frac{\mathrm{D}}{f_e}\right)\) ......................(6)

विवेचना (Discussion):
(i) आवर्धन क्षमता m का मान ऋणात्मक होने का अर्थ है कि सूक्ष्मदशी में वस्तु के सापेक्ष प्रतिबिम्ब उल्टा बनता है।
(ii) चूँकि माध्यमिक प्रतिबिम्ब (intermediate image) दोनों लेसों के मध्य बनता है, अत: क्रॉस - तार या मापक स्केल (measuring scale) का प्रयोग किया जा सकता है।
(iii) अधिक आवर्धन क्षमता के लिए f₀ व f_e दोनों के मान कम होने चाहिए। दृश्य क्षेत्र को बढ़ाने के लिए f₀ < f_e लेना चाहिए।
(iv) चूँकि सूक्ष्मदर्शी में दोनों लेन्सों का द्वारक (aperture) छोटा होता है अतः प्रतिबिम्ब का गोलीय विपथन दोष (spherical aberration defect) भी कम हो जाता है।
(v) एक अच्छे संयुक्त सूक्ष्मदर्शी में अभिदृश्यक एवं नेत्रिका दोनों को संयुक्त लेन्सों के रूप में प्रयोग करते हैं जिसके प्रतिबिम्ब का वर्ण विपथन दोष (एक अकेले लेन्स में वर्ण विपथन दोष होता है) समाप्त हो जाता है।
(vi) वस्तु अभिदृश्यक के फोकस तल के बाहर होनी चाहिए अर्थात् u₀ > f₀ अन्यथा माध्यमिक प्रतिबिम्ब (A'B') लेन्सों के मध्य नहीं बनेगा। इसीलिए अभिदृश्यक लेन्स की फोकस दूरी (f_e) कम ली जाती है।

प्रश्न 6.
अपवर्ती दूरदर्शी द्वारा किसी दूरस्थ बिम्ब का प्रतिबिम्ब बनना दर्शाने के लिए किरण आरेख खींचिए। उपयोग किए गए लेंसों की फोकस दूरी के पदों में कोणीय आवर्धन के लिए व्यंजक लिखिए। अधिक विभेदन प्राप्त करने के लिए आवश्यक महत्वपूर्ण तथ्यों और उनकी परिणामी सीमाओं का उल्लेख कीजिए।
उत्तर:
दूरदर्शी (Telescope)
दूरदर्शी वह प्रकाशिक उपकरण है जो दूर की वस्तुओं को देखने के लिए प्रयोग किया जाता है। खगोलीय दूरदर्शी का उपयोग खगोल वैज्ञानिक आकाशीय पिण्डों को देखने के लिए करते हैं। जब खगोलीय वस्तुओं जैसे चन्द्रमा या अन्य किसी ग्रह को देखा जाता है तो उनके उल्टे प्रतिबिम्ब से कोई असुविधा नहीं होती क्योंकि ये वस्तुएँ गोलाकार हैं। यह दूरदर्शी संरचना के आधार पर दो प्रकार के होते हैं-
(1) अपवर्ती प्रकार का दूरदर्शी
(2) परावर्ती प्रकार का दूरदर्शी।

(1) अपवर्ती प्रकार का दूरदशी (Refracting Telescope)
रचना: इस दूरदर्शी में दो लेन्स होते हैं जिनमें एक का मुख्य फोकस एवं मुख्य व्यास (द्वारक) बड़ा होता है और यह वस्तु की ओर रहता है, इसे अभिदृश्यक (Objective lens or field lens) कहते हैं। दूसरा लेन्स छोटे मुख्य फोकस एवं छोटे द्वारक का होता है और यह आँख की और रहता है, इसे अभिनेत्र लेन्स (eye lens) कहते हैं। दोनों लेन्स एक नली के दोनों सिरों पर लगे होते हैं और इनके बीच की दूरी दण्ड चक्रीय क्रम (rack and pinion) से घटायी या बढ़ाई जा सकती है।

समायोजन एवं किरण आरेख - सबसे पहले नेत्रिका को आगे-पीछे खिसकाकर क्रॉस - वार (cross wire) पर समायोजित कर लेते हैं। इसके बाद अभिदृश्यक का रुख दृश्य (जो वस्तु देखनी है) की ओर करके छोटी नली को लम्बी नली में इतना आगे या पीछे खिसकाते हैं कि वस्तु का प्रतिबिम्ब क्रॉस - तार पर बनने लगे। इस दशा में वस्तु स्पष्ट दृष्टिगोचर होने लगती है।
दूरदर्शी से प्रतिबिम्ब बनने की क्रिया चित्र 9.72 में दिखाई गई है।

अनन्त पर रखी किसी वस्तु AB से आने वाली समान्तर किरणें अभिदृश्यक से अपवर्तित होकर इसके फोकस F₀ पर वस्तु का उल्य, छोटा एवं वास्तविक प्रतिबिम्ब A'B' बनाती हैं। नेत्रिका को इतना आगे या पीछे खिसकाते हैं कि यह प्रतिबिम्ब उसके प्रथम फोकस F_e' के अन्दर आ जाये। इस स्थिति में A'B' का सीधा, बड़ा एवं काल्पनिक प्रतिबिम्ब A"B" बनता है। यही अन्तिम प्रतिबिम्ब होता है।

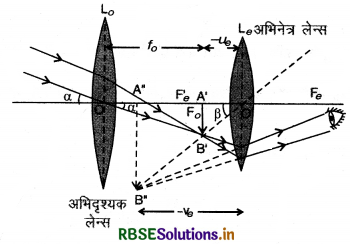
आवर्धन क्षमता (Magnifying Power): दूरदर्शी की आवर्धन क्षमता की परिभाषा निम्न प्रकार की जाती है-

(i) जब अन्तिम प्रतिबिम्ब स्पष्ट दृष्टि की न्यूनतम दूरी पर बने: अन्तिम प्रतिबिम्ब स्पष्ट दृष्टि की न्यूनतम दूरी (D) पर बनता है तो
v_e = -D
∴अभिनेत्र लेन्स के लिए लेन्स सूत्र से,
\(\frac{1}{v_e}-\frac{1}{u_e}=\frac{1}{f_e}\)

इस अवस्था में दूरदर्शी को निकट बिन्दु समायोजन की स्थिति में कहा जाता है (Near - point adjustment)।
(ii) जब अन्तिम प्रतिबिम्ब अनन्त पर बने: जब अन्तिम प्रतिबिम्ब अनन्त पर बनेगा तो माध्यमिक प्रतिबिम्ब AB' अभिनेत्र लेन्स के फोकस F_e' पर बनेगा, अत:
u_e = f_e
समी. (1) से,

इस स्थिति में किरण आरेख निम्न प्रकार होगा:

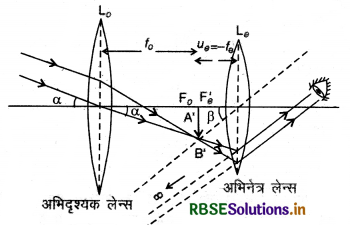
यदि अन्तिम प्रतिबिम्ब अनन्त (Infinity) पर बनता है तो इस अवस्था में दूरदर्शी को सामान्य समायोजन की स्थिति में कहा जाता है (Normal adjustment)।

प्रश्न 7.
R वक्रता त्रिज्या के गोलीय पृष्ठ के उत्तल तल के सामने उसकी मुख्य अक्ष पर स्थिति किसी बिन्दु विम्य का प्रतिविम्य बनने की स्थिति ज्यामिति किरण आरेख द्वारा दर्शाइए। n₁ अपवर्तनांक के माध्यम से आपतित किरण अपवर्तनांक के पदार्थ में प्रवेश करती है। दर्शाइए-
\(\frac{n_2}{v}-\frac{n_1}{u}=\frac{n_2-n_1}{R}\)
जहाँ सभी प्रतीक सामान्य अर्थ में है।
उत्तर:
गोलीय पृष्ठों से अपवर्तन (Refraction Through Spherical Surfaces)
(1) उत्तल गोलीय पृष्ठ पर अपवर्तन का सूत्र (Formula for Refraction at Convex Spherical Surface): माना AB एक उत्तल गोलीय पृष्ठ है जिसके बायीं ओर एक माध्यम (बिरल) एवं दायीं ओर

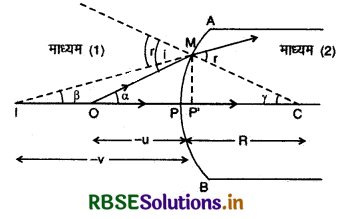
दूसरा माध्यम (सघन) है। P गोलीय पृष्ठ का ध्रुव (pole) है तथा C वक्रता केन्द्र (centre of curvature) है। चित्र 9.36 के किरण आरेख के अनुसार मुख्य अक्ष पर स्थित एक बिन्दु वस्तु (point object) O का प्रतिबिम्ब I बनता है। M से मुख्य अक्ष पर डाला गया अभिलम्ब (normal) MP' है।
अब स्नेल के नियमानुसार,
n₂₁ = \(\frac{\sin i}{\sin r}\) 
जहाँ n₂₁ = प्रथम माध्यम के सापेक्ष दूसरे माध्यम का अपवर्तनांक है।
या n = \(\frac{\sin i}{\sin r}\)
(अस्थायी रूप से n₂₁ के स्थान पर केवल n रखने पर)
यदि i व r छोटे हैं तो sini ≈ i और sinr ≈ r
∴ n = \(\frac{i}{r}\)
या i = nr .......................(1)
∵ त्रिभुज में बहिष्कोण (exterior angle) सामने के अन्त:कोणों (interior angles) के योग के बराबर होता है।
∆MOC से,
i = α + γ ...................(2) 
और ∆MIC से,
r = ß + γ .....................(3)
समी. (1) में समी- (2) व (3) से मान रखने पर,
(α +γ) = n(ß + γ)
यदि बिन्दु M मुख्य अक्ष से अधिक दूर नहीं है तो 
(i) बिन्दु P व P' सम्पाती होंगे और 
(ii) कोण α, ß व γ छोटे होंगे।

इस सूत्र को उत्तल पृष्ठ का अपवर्तन सूत्र कहते हैं। यदि प्रथम व द्वितीय माध्यमों के निरपेक्ष अपवर्तनांक क्रमश: n₁ व n₂
n₂₁ = \(\frac{n_2}{n_1}\)
∴ समी. (5) से,
\(\frac{n_2}{n_1 v}-\frac{1}{u}=\frac{\frac{n_2}{n_1}-1}{\mathrm{R}}=\frac{n_2-n_1}{n_1 \mathrm{R}}\)
पूरे समीकरण में n₁ का गुणा करने पर,

चूँकि उत्तल पृष्ठ के लिए R धनात्मक होता है अतः यदि u का मान \(\frac{\mathrm{R}}{(n-1)}\) से कम है तो v का मान ऋणात्मक होगा तथा प्रतिबिम्ब पहले माध्यम में बनेगा और आभासी (virtual) होगा। इसके विपरीत यदि u का मान \(\frac{\mathrm{R}}{(n-1)}\) से अधिक है तो v का मान धनात्मक होगा तथा प्रतिबिम्ब दूसरे माध्यम में बनेगा और वह वास्तविक (real) होगा।

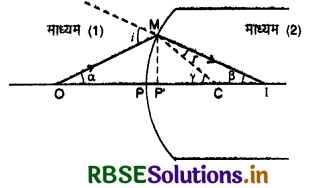
(2) अवतल गोलीय पृष्ठ पर अपवर्तन का सूत्र (Formula for Refraction at Concave Spherical Surface): माना AB एक अवतल गोलीय पृष्ठ है जिसके बायीं ओर विरल माध्यम (1) एवं दायीं ओर सघन माध्यम (2) है। P ध्रुव एवं C वक्रता केन्द्र है। मुख्य अक्ष पर रखी वस्तु O का आभासी प्रतिबिम्ब I बनता है। MP' मुख्य अक्ष पर अभिलम्ब है।

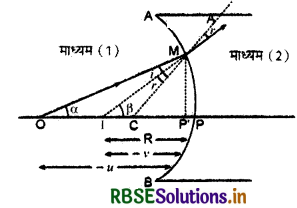
अब स्नेल के नियम से,
n₂₁ = \(\frac{\sin i}{\sin r}\)
या n = \(\frac{\sin i}{\sin r}\)
(अस्थायी रूप से n₂₁ के स्थान पर केवल n रखने पर)
यदि i व r छोटे हैं तो
sin i ≈ i व sin r ≈ r
∴ n = \(\frac{i}{r}\)
या i = nr ....................(1)
∵ त्रिभुज में बहिष्कोण सामने के अन्त:कोणों के योग के बराबर होता है।
∴ ∆MOC से,
α + i = γ
या i = (γ - α) ....................(2)
इसी प्रकार ∆MIC से,
r + ß = γ
∴ r = (γ - ß) .....................(3)
समी. (2) व (3) से समी. (1) में मान रखने पर,
(γ - α) = n (γ - ß)
यदि बिन्दु M मुख्य अक्ष से अधिक दूर नहीं है तो 
(i) P व P' सम्पाती होंगे और
(ii) α, ß, γ छोटे होंगे।

इस सूत्र को अवतल पृष्ठ का अपवर्तन सूत्र कहते हैं।
इस सूत्र के अनुसार, v का मान कोण α पर निर्भर नहीं करता है। अतः बिन्दु O से चलने वाली सभी किरणे भेटे व्यास के अवतल पृष्ठ से अपवर्तित होकर एक ही बिन्दु I से आती हुई प्रतीत होती है। अतः I वस्तु O का आभासी प्रतिबिम्ब है। चूंकि अवतल पृष्ठ के लिए R ऋणात्मक होता है अतः u के सभी ऋणात्मक मानों के लिए v का मान भी ऋणात्मक होगा अर्थात् प्रतिबिम्ब सदैव पहले माध्यम में ही बनेगा तथा आभासी (virtual) होगा।

आंकिक प्रश्न

प्रश्न 1.
अवतल दर्पण का वक्रता त्रिज्या 40 सेमी. है। इसकी फोकस दूरी ज्ञात कीजिए।
उत्तर:
दिया है: R = -40 सेमी
फोकस दूरी f = \(\frac{R}{2}=-\frac{40}{2}\)
= -20 सेमी.

प्रश्न 2.
किसी बिम्ब को 60 cm वक्रता त्रिज्या के अवतल दर्पण के सामने 20 cm दूरी पर रखा गया है। बनने वाले प्रतिबिम्ब की प्रकृति और स्थिति ज्ञात कीजिए।
उत्तर:
दिया है, R = -60 cm, u = - 20 cm
अत: फोकस दूरी f = \(\frac{R}{2}=-\frac{60}{2}\) = -30 cm 
दर्पण सूत्र से \(\frac{1}{f}=\frac{1}{v}+\frac{1}{u}\)

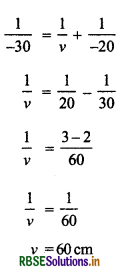
आवर्धनता m = -\(\frac{v}{u}\)
m = \(\frac{-60}{-20}\) = 3
अत: प्रतिबिम्ब आभासी, सीधा, दर्पण के पीछे तीन गुना आवर्धित बनेगा।

प्रश्न 3.
20 cm वक्रता त्रिज्या के किसी अवतल दर्पण के सामने h ऊँचाई के किसी बिम्ब की दर्पण से वह दूरी परिकलित कीजिए जिस पर बिम्ब को रखने पर आवर्धन 2 का वास्तविक प्रतिबिम्ब प्राप्त हो। प्रतिबिम्ब की स्थिति ज्ञात कीजिए।
उत्तर:
दिया है - अवतल दर्पण की वक्रता त्रिज्या R = - 20 cm
वास्तविक प्रतिबिम्ब के लिए रेखीय आर्थन m = - 2
∴m = -\(\frac{v}{u}\) से
-2 = \(\frac{v}{u}\)
v = 2u
दर्पण सूत्र से \(\frac{1}{f}=\frac{1}{v}+\frac{1}{u}\)

प्रतिबिम्ब की स्थिति
v = 2u = -2 x 15
v = -30 cm

प्रश्न 4.
10 cm वक्रता त्रिज्या के गोलीय दर्पण की फोकस दूरी ज्ञात कीजिए।
उत्तर:
दिया है: R = 10 cm
∴ f = \(\frac{R}{2}=\frac{10}{2}\) = 5 cm 

प्रश्न 5.
किसी बिम्ब को 15 cm फोकस दूरी के अवतल दर्पण के सामने रखा गया है। इस दर्पण द्वारा इस बिम्ब का तीन गुना वास्तविक प्रतिबिम्ब बनता है। दर्पण से बिम्ब की दूरी परिकलित कीजिए।
उत्तर:
दिया है: दर्पण की फोकस दूरी f = 15 cm
m = -3
∴ m = -\(\frac{v}{u}\)
-3 = -\(\frac{v}{u}\)
v = 3u
दर्पण सूत्र से \(\frac{1}{f}=\frac{1}{v}+\frac{1}{u}\)
\(\frac{1}{-15}=\frac{1}{3 u}+\frac{1}{u}\)
\(\frac{1}{-15}=\frac{4}{3 u}\)
u = -20 cm 

प्रश्न 6.
उस माध्यम में प्रकाश के वेग की गणना करो, जिसका क्रांतिक कोण 30° है।
उत्तर:
अपवर्तनांक µ = \(\frac{c}{v}=\frac{1}{\sin i_c}\)
v = c sin i_c
= 3 x 10⁸ sin 30°
= 3 x 10⁸ x \(\frac{1}{2}\)
v = 1.5 x 10⁸ m/s

प्रश्न 7.
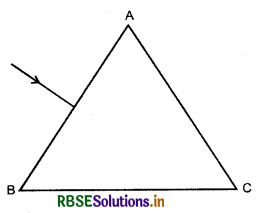
\(\frac{4}{3}\) अपवर्तनांक के जल में स्थित \(\frac{3}{2}\) अपवर्तनांक के काँच के किसी समबाहु प्रिज्म के फलक AB पर कोई प्रकाश किरण चित्रानुसार अभिलम्बवत आपतन करती है। फलक AC से टकराने पर क्या वह किरण पूर्ण आंतरिक परावर्तन होगी? अपने उत्तर की पुष्टि कीजिए।

उत्तर:
AB पर किरण लम्बवत आपतित है अत: अपवर्तन की कोई घटना नहीं होगी। इस स्थिति किरण BC फलक के साथ 30° का कोण बनाते हुए BC पर आपतित होती है जिसका आपतन कोण i = 60° होगा।
काँच का जल के सापेक्ष अपवर्तनांक
_wµ_g = \(\frac{{ }_a \mu_g}{{ }_a \mu_w}=\frac{3 / 2}{4 / 3}\)
_wµ_g = \(\frac{9}{8}\)
क्रान्तिक कोण i_c हो तो

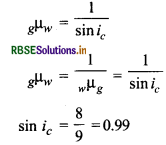
∴ i > i_c अत: आपतित किरण पूर्ण आंतरिक परावर्तन होगा।

प्रश्न 8.
1.55 अपवर्तनांक के कॉच से कोई उभयोत्तल लेंस बनाया गया है जिसके दोनों फलकों की वक्रता त्रिज्या समान है। यदि इस लेंस की फोकस दूरी 20 cm है, तो आवश्यक वक्रता त्रिज्या ज्ञात कीजिए।
उत्तर:
दिया है- n = 1.55, f = 20 cm
R₁ = R₂ = R
उभयोत्तल लेंस के लिए
\(\frac{1}{f}=(n-1) \frac{2}{R}\)
\(\frac{1}{20}=(1.55-1) \frac{2}{R}\)
R = 0.55 x 10
R = 5.50 cm

प्रश्न 9.
10 cm फोकस दूरी के किसी उत्तल लेन्स से 12 cm दूरी पर, मुख्य अक्ष पर कोई बिन्दुकित बिम्ब स्थित है। लेस के दूसरी ओर 10 cm दूरी पर किसी उत्तल दर्पण को समक्ष रखा गया है। यदि अंतिम प्रतिबिम्ब संपाती है तो किरण आरेख खींचिए और उत्तल दर्पण की फोकस दूरी ज्ञात कीजिए।
उत्तर:

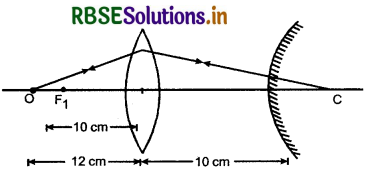
10 cm फोकस दूरी के लेंस के सामने 12 cm पर बिन्दुकित बिम्ब रखा है। अतः लेन्स सूत्र से

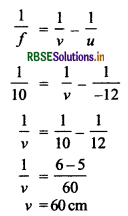
लेंस से बना प्रतिबिम्ब दर्पण के वक्रता केन्द्र C पर बनेगा तभी आपतित किरण उसी मार्ग से परावर्तित होकर O पर संपाती प्रतिबिम्बित होगी।
अत: दर्पण की वक्रता त्रिज्या R = 60 - 10
= 50 cm 
अत: उत्तल दर्पण को फोकस दूरी f = \(\frac{R}{2}=\frac{50}{2}\)
f = 25 cm

प्रश्न 10.
एक बिम्ब उत्तल लेंस से 20 सेमी. दूरी पर रखा है। यदि लेंस द्वारा 3 गुना आवधित वास्तविक प्रतिबिम्ब प्राप्त होता है तो लेंस की फोकस दूरी ज्ञात करो।
उत्तर:
दिया है: उत्तल लेंस से बिम्ब की दूरी u = -20 cm 3 गुना आवर्धित वास्तविक प्रतिबिम्ब बनता है अत:
m = -3
हम जानते हैं \(\frac{1}{v}-\frac{1}{u}=\frac{1}{f}\)

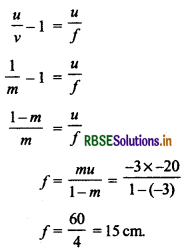
प्रश्न 11.
कोई पर्दा किसी बिम्ब से 90 cm कर दूरी पर स्थित है। किसी उत्तल लेंस द्वारा लेंस की दो विभिन्न स्थितियों, जिनके बीच 20 cm का पृथकन है, के लिए बिम्ब का पर्दे पर प्रतिबिम्ब बनता है। लेंस की फोकस दूरी परिकलित कीजिए।
उत्तर:
दिया है: a = v + u = 90 cm
लेंस की दो स्थितियों के मध्य अन्तराल, जब प्रतिबिम्ब पर्दे पर बनता है।
b = v - u = 20 cm
तब लेंस की फोकस दूरी f = \(\frac{a^2-b^2}{4 a}\)
f = \(\frac{(90)^2-(20)^2}{4 \times 90}=\frac{8100-400}{360}\)
= \(\frac{7700}{360}\)
f = 21.38 cm

प्रश्न 12.
एक अभिसारी लेंस की वायु में फोकस दूरी 25 cm है। यदि इसको जल में डुबो दें तो लेंस की फोकस दूरी ज्ञात करें।
उत्तर:
ज्ञात है जल का अपवर्तनांक _aµ_w = 1.33
हम जानते हैं, द्रव में किसी लेंस की फोकस दूरी

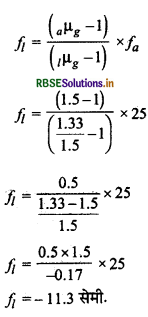
अतः द्रव में बुलाने पर लेंस की प्रकृति अपसारी (अवतल) लेंस की तरह होगी।

प्रश्न 13.
+15 D एवं -5 D क्षमता के दो लेन्सों को सम्पर्क में रखा गया है। (a) संयोजन की फोकस दूरी ज्ञात कीजिए।
उत्तर:
दिया है: P₁ = + 15 D; P₂ = -5 D
संयोजन की क्षमता P = P₁ + P₂ = +15 - 5
P = +10 D 
अतः संयोजन की फोकस दूरी F = \(\frac{100}{\mathrm{P}}\) = 10 सेमी.

प्रश्न 14.
+10 cm और -5 cm फोकस दूरियों वाले दो पतले लेन्सों को एक - दूसरे के सम्पर्क में रखा गया है। इस संयोजन की फोकस दूरी तथा शक्ति कितनी है?
उत्तर:
दिया है- f₁ = + 10 cm, f₂ = -5 cm
अतः संयोजन की फोकस दूरी \(\frac{1}{F}=\frac{1}{f_1}+\frac{1}{f_2}\)

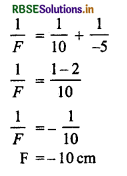
प्रश्न 15.
60° प्रिज्म कोण वाले प्लास्टिक प्रिज्म का पीले प्रकाश के लिए अपवर्तनांक \sqrt{2} है। अल्पतम विचलन की स्थिति में ज्ञात कीजिए-
(a) अल्पतम विचलन कोण
(b) आपतन कोण 
(c) प्रिज्म के भीतर अपवर्तन कोण 
उत्तर:
दिया है: प्रिज्म कोण A = 60°
µ = \(\sqrt{2}\)
(a) प्रिज्म के माध्यम का अपवर्तनांक
µ = sin \(\left(\frac{\left(\frac{\mathrm{A}+\delta_m}{2}\right)}{\sin \frac{\mathrm{A}}{2}}\right)\)

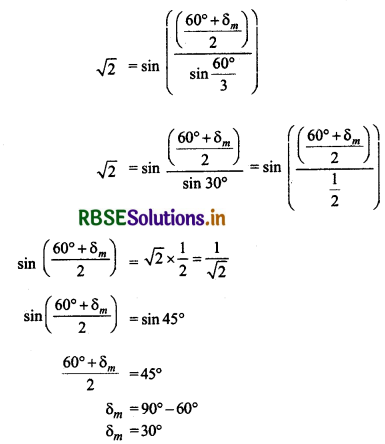
(b) न्यूनतम विचलन की स्थिति में आपतन कोण
i = \(\frac{A+\delta_m}{2}=\frac{60^{\circ}+30^{\circ}}{2}\) = 45°

(c) स्नैल के नियम से µ = \(\frac{\sin i}{\sin r}\)
जहाँ µ = \(\sqrt{2}=\frac{\sin 45^{\circ}}{\sin r}\)
sin r = \(\frac{1}{\sqrt{2} \times \sqrt{2}}=\frac{1}{2}\)
sin r = sin 30°
r = 30°

प्रश्न 16.
एक संयुक्त सूक्ष्मदर्शी के निर्माण के लिए 1.25 cm और 5 cm फोकस दूरियों के लेन्स प्रयुक्त किये गये हैं। यदि वांछित आवर्धन क्षमता 30 है, तो अभिदृश्यक और अभिनेत्रिका के मध्य दूरी ज्ञात करो।
उत्तर:
संयुक्त सूक्ष्मदर्शी की अधिकतम आवर्धन क्षमता
m = \(\frac{v_0}{u_0}\left[1+\frac{D}{f_e}\right]\)
इसलिए m = 30 के लिए, दिया है f₀ = 1.25 cm तथा f = 5 cm
30 = \(\frac{v_0}{u_0}\left[1+\frac{25}{5}\right]\)
\(\frac{v_0}{u_0}=\frac{30}{6}\) = 5
v₀ = 5 u₀
अभिदृश्यक लेंस के लिए

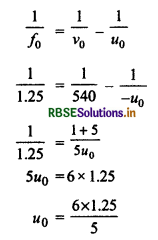
u₀ = 1.5 cm
तथा v₀ = 5 u₀ = 5 x 1.5
∴ v₀ = 7.5 cm
अधिकतम आवर्धन के लिए नेत्रिका से अंतिम प्रतिबिम्ब की दूरी
v_e = D = -25 cm
पुनः लैंस सूत्र से \(\frac{1}{f_e}=\frac{1}{v_e}-\frac{1}{u_e}\)
\(\frac{1}{5}=\frac{1}{-25}-\frac{1}{-u_e}\)
\(\frac{1}{u_e}=\frac{1}{5}+\frac{1}{25}=\frac{5+1}{25}\)
u_e = \(\frac{25}{6}\) = 4.67 cm
∴दोनों लेंसों के मध्य दूरी या नलिका की लम्बाई
L = v₀ + u_e
L = 7.5 cm + 4.67 cm
L = 11.67 cm

प्रश्न 17.
एक दूरदशी की आवर्धन क्षमता है। जब इसे समान्तर किरणों के लिए समजित करते हैं जब नेत्रिका और अभिदृश्यक लेंस के बीच की दूरी 18 cm है। दोनों लेंसों की फोकस दूरियाँ ज्ञात कीजिए।
उत्तर:
प्रश्नानुसार, दूरदर्शी की आवर्धन क्षमता m = 18 cm 
नेत्रिका तथा अभिदृश्यक के बीच दूरी L = 18 cm
अतः m = -\(\frac{f_0}{f_e}\) = -8
f₀ = 8f_e ......................(i)
नेत्रिका तथा अभिदृश्यक के बीच दूरी
l = f₀ + f_e
18 = f₀ + f_e
18 = 8f_e + f_e = 9f_e (समी. (i) से)
f_e = 2 cm
समी (i) से f₀ = 8f_e = 2 x 8 
f₀ = 16 cm

प्रश्न 18.
एक छोटी दूरबीन के अभिदृश्यक तथा नेत्रिका की फोकस दूरियाँ क्रमशः 192 cm व 8 cm हैं। इसकी आवर्धन क्षमता तथा दोनों लेंसों के बीच दूरी ज्ञात कीजिए।
उत्तर:
दिया है: अभिदृश्यक की फोकस दूरी f₀ = 192 cm 
नेत्रिका को फोकस दूरी f_e = 8 cm
∴आवर्धन क्षमता लग m = -\(\frac{f_0}{f_e}=-\frac{192}{8}\) = -24
दोनों लेंसों के बीच दूरी l = f₀ + f_e
l = 192 + 8 = 200 cm

प्रतियोनी परीक्षा संबंधी प्रश्न

प्रश्न 1.
लघु प्रिज्म कोण A के एक पृष्ठ पर आपतन कोण i से एक किरण आपतित होती है और विपरीत पृष्ठ से अभिलम्बवत निर्गत होती है। यदि प्रिज्म के पदार्थ का अपवर्तनांक µ_s हो तो आपतन कोण बराबर होगा-
(A) µA
(B) \(\frac{\mu \mathrm{A}}{2}\)
(C) \(\frac{A}{2 \mu}\)
(D) \(\frac{2 A}{\mu}\)
उत्तर:
(A) µA

प्रश्न 2.
प्रारंभ में एक बिम्ब को उत्तल लेंस से 10 cm दूरी पर रखा गया है। लेंस से 10 cm दूरी पर पर्दे पर स्पष्ट प्रतिबिम्ब बनता है। अब µ = 1.5 और 1.5 cm मोटाई की कॉच की प्लेट बिम्ब और लेंस के मध्य रख दी जाती है। पर्दे को कितना खिसकाया जाये कि पर्दे पर स्पष्ट प्रतिबिम्ब बन सके।
(A) \(\frac{9}{5}\) cm
(B) \(\frac{5}{9}\) cm
(C)1cm 
(D) 5 cm
उत्तर:
(B) \(\frac{5}{9}\) cm

प्रश्न 3.
150 mm लम्बाई की नली की एक संयुक्त सूक्ष्मदर्शी से वांछित आवर्धन 375 है और अभिदृश्यक की फोकस दूरी 5 mm है, तो नेत्रिका की फोकस दूरी होगी-
(A) 22 mm
(B) 2 mm 
(C) 12 mm
(D) 33 mm 
उत्तर:
(A) 22 mm

प्रश्न 4.
F फोकस दूरी वाले दो समान पतले उभयोत्तल लेंस समाक्षीय इस प्रकार रखे हैं कि संयोजन की फोकस दूरी F₁ रहे। यदि दोनों के बीच स्थान में ग्लिसरीन भर दी जाती है (जिसका अपवर्तनांक काँच के अपवर्तनांक के बराबर µ = 1.5 हो) तो तुल्य फोकस दूरी F₂ हो जाती है। F₁ : F₂ होगा-
(A) 1 : 2
(B) 2 : 3
(C) 3 : 4
(D) 2 : 1
उत्तर:
(A) 1 : 2

प्रश्न 5.
एक खगोलीय अपवर्ती दूरदर्शी बड़े कोणीय आवर्धन तथा उच्च कोणीय विभेदन की है, जब इसका अभिदृश्यक लेंस होगा-
(A) अधिक फोकस दूरी व अधिक व्यास का 
(B) अधिक फोकस दूरी व कम व्यास का
(C) कम फोकस दूरी व अधिक व्यास का
(D) कम फोकस दूरी व कम व्यास का
उत्तर:
(B) अधिक फोकस दूरी व कम व्यास का

प्रश्न 6.
प्रिज्म के किसी अपवर्तक पृष्ठपर किसी प्रकाश किरण के लिये आपतन कोण का मान 450 है। प्रिज्म कोण का मान 60° है यदि यह किरण प्रिज्म से न्यूनतम विचलित होती हैं, तो न्यूनतम विचलन कोण तथा प्रिज्म के पदार्थ का अपवर्तनांक क्रमशः हैं-
(A) 45°, \(\frac{1}{\sqrt{2}}\)
(B) 45°, \(\sqrt{2}\)
(C) 45°\(\sqrt{2}\)
(D) 30°, \(\frac{1}{\sqrt{2}}\)
उत्तर:
(B) 45°, \(\sqrt{2}\)

प्रश्न 7.
एक प्रयोग करके तथा i - δ ग्राफ बनाकर एक कांच से बने प्रिज्म का अपर्वतनॉक निकाला जाता है। तब एक किरण को 35° पर आपतित करने पर वह 40° से विचलित होती है तथा यह 79° पर निर्गम होती है। इस स्थिति में निम्न में से कौनसा मान अपर्वनांक के अधिकतम मान से सबसे पास है-
(A) 1.6
(B) 1.7
(C) 1.8
(D) 1.5
उत्तर:
(D) 1.5

प्रश्न 8. 
वायु से आती प्रकाश की एक समानान्तर किरण पुंज एक समकोण त्रिभुजीय प्रिज्म जिसका अपवर्तनांक n = \(\sqrt{2}\) है के PQ तल पर α की न्यूनतम मान 45° है तो प्रिज्म की PR सतह पर पूर्ण आन्तरिक परार्वतन होता है। प्रिज्म का कोण θ क्या होगा-

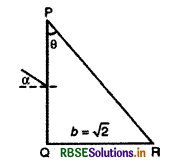
(A) 150 
(B) 22.5°
(C) 30°
(D) 45°
उत्तर:
(A) 150

प्रश्न 9.
किसी प्रिज्म का कोण A है। इस प्रिज्म के एक अपवर्तक (फलक) रजतित कर परावर्तक बना दिया गया है, इसके पृष्ठ पर, 2A कोण पर आपतित, प्रकाश की किरणें, रजतित सतह से परावर्तन के पश्चात् अपने मार्ग पर वापस आ जाती हैं। प्रिज्म के पदार्थ का अपवर्तनांक µ होगा- 
(a) 2 cos A 
(b) \(\frac{1}{2}\) cos A 
(c) tan A
(d) 2 sin A 
उत्तर:
(A) 2 cos A

प्रश्न 10. 
0.25 x 10 W ऊर्जा फ्लक्स का प्रकाश, किसी पूर्णतः परावर्तक पृष्ठ (सतह) पर लम्बवत् आपतित होता है। यदि इस पृष्ठ का क्षेत्रफल 15 cm² हो तो, पृष्ठ पर आरोपित औसत बल होगा:
(A) 2.50 x 10^-6 N
(B) 1.20 x 10^-6 N
(C) 3.0 x 10^-6 N
(D) 1.25 x 10^-6 N
उत्तर:
(A) 2.50 x 10^-6 N

प्रश्न 11.
क्राउन काँच (µ = \(\frac{3}{2}\)) से निर्मित एक पतले उत्तल लेन्स की फोकस दूरी f है। जब इसे \(\frac{4}{3}\) तथा \(\frac{5}{3}\) अपवर्तनांक वाले दो भिन्न - भिन्न द्रवों में मापा जाता है, तब इसकी फोकस दूरी क्रमशः f₁ तथा f₂ है। फोकस दूरियों के मध्य सही सम्बन्ध है:
(A) f₁ - f₂ < f
(B) f₁ > f तथा f₂ ऋणात्मक हैं
(C) f₂ > f तथा f₁ ऋणात्मक है
(D) f₁ तथा f₂ दोनों प्राणात्मक हैं
उत्तर:
(B) f₁ > f तथा f₂ ऋणात्मक हैं

प्रश्न 12.
एक हरा प्रकाश क्रान्तिक कोण (θ) पर जल से वायु - जल अन्तराफलक पर आपतित होता है। सही कथन का चयन कीजिए।
(A) दृश्य प्रकाश का सम्पूर्ण स्पैक्ट्रम अभिलम्ब से 90° कोण पर जल से बाहर आएगा
(B) दृश्य प्रकाश का स्पैक्ट्रम जिसकी आवृत्ति हरे प्रकाश की आवृत्ति से कम है, वायु मामा से बाहर आएगा
(C) दृश्य प्रकाश का स्पैक्ट्रम जिसकी आवृत्ति हरे प्रकाश की आवृत्ति से अधिक है, वायु माध्यम से बाहर आएगा
(D) दृश्य प्रकाश का सम्पूर्ण स्पैक्ट्रम अभिलम्ब से विभिन्न कोणों पर जल से बाहर आएगा।
उत्तर:
(C) दृश्य प्रकाश का स्पैक्ट्रम जिसकी आवृत्ति हरे प्रकाश की आवृत्ति से अधिक है, वायु माध्यम से बाहर आएगा