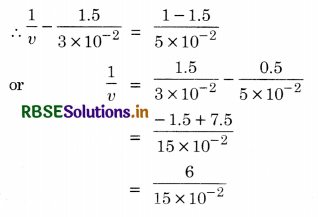RBSE Class 12 Physics Important Questions Chapter 9 Ray Optics and Optical Instruments

Rajasthan Board RBSE Class 12 Physics Important Questions Chapter 9 Ray Optics and Optical Instruments Important Questions and Answers.

RBSE Class 12 Physics Chapter 9 Important Questions Ray Optics and Optical Instruments

Multiple Choice Questions

Question 1.
Focal length of the plane mirror is:
(A) negative
(B) positive
(C) zero
(D) infinite.
Answer:
(D) infinite.

Question 2.
Which of the following phenomenon is used in optical fibre?
(A) Total internal reflection
(B) Scattering
(C) Reflection
(D) Interference.
Answer:
(A) Total internal reflection

Question 3.
Out of the following, of which colour, sensitivity of human eye is the highest:
(A) green
(B) red
(C) violet
(D) white.
Answer:
(A) green

Question 4.
If a lens is cut into two pieces perpendicular to the principal axis and only one part is used the new focal length:
(A) remains the same
(B) becomes \(\frac{1}{2}\) time
(C) becomes 2 times 
(D) infinite.
Answer:
(C) becomes 2 times 

Question 5.
Optical fibre works on:
(A) Total internal reflection
(B) Reflection
(C) Refraction
(D) Dispersion.
Answer:
(A) Total internal reflection

Question 6.
The velocity of light in vacuum can be changed by changing:
(A) Frequency
(B) Amplitude
(C) Wavelength
(D) None of these.
Answer:
(D) None of these

Question 7.
Total internal reflection takes place, when light travels from:
(A) Water to glass
(B) Glass to diamond
(C) Water to air
(D) Air to mercury.
Answer:
(C) Water to air

Question 8.
Velocity of light is maximum in:
(A) diamond
(B) water
(C) glass
(D) vacuum.
Answer:
(D) vacuum.

Question 9.
When light passes from one medium to another medium, which one of these quantities, remains unchanged.
(A) Refractive index
(B) Frequency
(C) Wavelength
(D) Velocity.
Answer:
(B) Frequency
 
Question 10.
The sky appears blue, because:
(A) Red light is absorbed
(B) Blue light is scattered the most
(C) It is a natural colour
(D) Blue light is absorbed.
Answer:
(B) Blue light is scattered the most

Question 11.
The blue colour of the sky is due to the phenomenon of:
(A) Reflection
(B) Refraction
(C) Scattering
(D) Dispersion.
Answer:
(C) Scattering

Question 12.
Red colour is used for danger sgnals, because of its:
(A) Highest frequency
(B) Highest wavelength
(C) Lowest wavelength
(D) None of these.
Answer:
(B) Highest wavelength

Question 13.
Glittering of diamond is due to:
(A) Total internal reflection
(B) Dispersion
(C) Diffraction
(D) None of these.
Answer:
(A) Total internal reflection

Question 14.
An air bubble inside the water behaves as:
(A) convex lens
(B) concave lens
(C) a planoconvex lens
(D) A concave mirror.
Answer:
(B) concave lens

Question 15.
A convex lens becomes less converging, when placed in:
(A) Oil
(B) Water
(C) Both (A) and (B)
(D) None of them.
Answer:
(C) Both (A) and (B)

Question 16.
Linear magnification of plane mirror is:
(A) +1
(B) - 1
(C) < 0
(D) zero.
Answer:
(A) +1

Question 17.
Pencil in a beaker filled with water seems to be broken or bent due to:
(A) Reflection
(B) Diffraction
(C) Total internal reflection
(D) Refraction.
Answer:
(D) Refraction.

Question 18.
If angle between two plane mirrors is 60°, then number of images formed are:
(A) 5
(B) 6
(C) infinite
(D) none of these.
Answer:
(A) 5

Question 19.
In dispersion of light through a glass prism angle of deviation is minimum for:
(A) red
(B) green
(C) violet
(D) orange.
Answer:
(A) red

Question 20.
Which of the following colours is the least scattered?
(A) Violet
(B) Blue
(C) Red
(D) Yellow.
Answer:
(C) Red

Question 21.
To get five images of a single object, one should have two plane mirrors at an angle of:
(A) 30°
(B) 60°
(C) 90°
(D) 120°.
Answer:
(A) 30°

Question 22.
‘Mirage’ is a phenomenon due to:
(A) reflection of light
(B) refraction of light
(C) total internal reflection
(D) diffraction of light
Answer:
(C) total internal reflection

Question 23.
Brilliance of a diamond is due to:
(A) shape
(B) cutting
(C) reflection
(D) total internal reflection.
Answer:
(D) total internal reflection.

Question 24.
Sky appears to be blue in clear atmosphere due to:
(A) diffraction
(B) dispersion
(C) scattering
(D) polarisation.
Answer:
(C) scattering

Question 25.
The formation of rainbow in due to the phenomenon of:
(A) reflection
(B) dispersion
(C) refraction
(D) interference.
Answer:
(B) dispersion

Fill in the blanks

Question 1.
A plane mirror can be considered as a spherical mirror of ............................. focal length.
Answer:
infinite.

Question 2.
The mirror formula holds for a spherical mirror of ............................. aperture only.
Answer:
large.

Question 3.
The focal length of a plane glass plate is .............................
Answer:
infinite.

Question 4.
The power of a ............................. lens is smaller than that of a ............................. lens.
Answer:
thick, thin.

Question 5.
The phenomenon of splitting of white light into its constituent colours is called .............................
Answer:
dispersion.

Question 6.
The magnifying power and ............................. produced by a lens are different from each other.
Answer:
magnification.

Question 7.
............................. is called natural optical instrument.
Answer:
Human eye.

Question 8.
Two lenses of powers +15D and -15D are in contact with each other. The focal length of combination is .............................
Answer:
10 cm.

Question 9.
A substance has critical angle 45° for yellow light, its refractive index is .............................
Answer:
1.414.

Question 10.
Locus of all the points in same phase is called .............................
Answer:
wavefront.

Very Short Answer Type Questions

Question 1.
State Snell's law of refraction.
Answer:
It states that the ratio of sine of angle of incidence to the sine of angle of refraction is equal to the refractive index of the medium.

Question 2.
Define refractive index.
Answer:
Refractive index of a medium is the ratio of velocity of light in vacuum to the velocity of light in that medium
i.e., µ = \(\frac{c}{v}\)

Question 3.
What is the significance of refractive index?
Answer:
The refractive index of a medium shows the direction of bending of light i.e. whether the light will bend towards or away from the normal.

Question 4.
What is the principle of reversibility of light?
Answer:
It states that when final path of a ray of light after any number of reflections and refractions is reversed, the ray retraces back its entire path.

Question 5.
If refractive index of glass w.r.t. air is 1.55 then what is the refractive index of air w.r.t. glass.
Answer:
\(\frac{1}{1.55}\).

Question 6.
What happens to the wavelength of light when it goes from rarer to denser medium?
Answer:
Wavelength of light decreases because
λ_medium = \(\frac{\lambda_{v a c}}{\mu}\)
As µ > 1
∴ λ_medium < λ_vac.

Question 7.
What is the unit of refractive index?
Answer:
Since µ = \(\frac{c}{v}\) i.e. ratio of the same quantities. so it has no unit.

Question 8.
What is the angle of reflection when a ray falls normally on a plane mirror?
Answer:
Angle of reflection, r = 0°.

Question 9.
What is the focal length of a plane mirror?
Answer:
Infinity.

Question 10.
What is the number of images of an object held between two parallel plane mirrors?
Answer:
Infinity.

Question 11.
What happens to the image if aperture of a spherical mirror is large?
Answer:

• The condition R = 2f will not hold good and
• Various defects like spherical aberrations etc. in the image formed by the spherical mirror will be produced.

Question 12.
What should be the minimum size of a plane mirror to produce full image of a person having height h?
Answer:
\(\frac{h}{2}\) i.e. half of the height of the person.

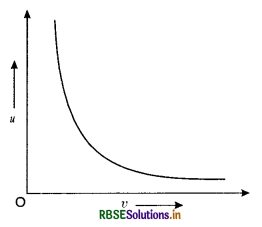
Question 13.
Draw a graph between u and v in case of a concave mirror.
Answer:
The graph is a shown in figure VSAQ 13.

Question 14.
What do you mean by deviation?
Answer:
The bending of rays of light from its original path is called deviation.

Question 15.
Does the apparent depth of a tank of water change, if viewed obliquely?
Answer:
Yes, it decreases.

Question 16.
What do you mean by critical angle?
Answer:
The critical angle is that angle of incidence in the denser medium for which angle of refraction is 90° and the refractive ray travels parallel to the interface of the two media.

Question 17.
What will be the focal length and power of a plane glass plate?
Answer:
Focal length, f = ∞
Power, P = 0.

Question 18.
Whether the power of a lens will be more in air or in water?
Answer:
Since ^aµ_g > ^wµ_g
So the power of the lens will be more in air.

Question 19.
What is power of a lens? Give its unit.
Answer:
The power of a lens is its ability to diverge or converge the incident ray. It is defined as the reciprocal of focal length in metre.
i.e. P = \(\frac{1}{f(\text { in metre })}=\frac{100}{f(\mathrm{~cm})}\)
Unit. Its unit is dioptre.
The power of a lens is said to be one dioptre if the focal length is 1 m.

Question 20.
What is the major use of optical fibres?
Answer:
The major use of optical fibre is the internal examination of the human body. The instrument used is called endoscope.

Question 21.
What is the deviation produced by a thin lens of a ray passing through the optical centre?
Answer:
The ray goes undeviated.

Question 22.
Write the formula for refraction at a thin lens.
Answer:
\(-\frac{1}{u}+\frac{1}{v}=\frac{1}{f}\)
where u = distance of object,
v = distance of image
f = focal length of the lens.

Question 23.
A convex lens forms a virtual image of an object. What is the position of the object?
Answer:
The object is placed between the focus and optical centre of the lens.

Question 24.
Why does an air bubble in a jar of water shine brightly?
Answer:
A ray of light undergoes total internal reflection when it goes from water to air and the ray is reflected back as if from a mirror, hence the air bubble shines like a mirror.

Question 25.
A lens when immersed in a transparent liquid become invisible. Under what condition does it happen?
Answer:
It happens when the refractive index of the liquid is equal to the refractive index of the material of lens.

Question 26.
Can light travelling from air to water suffer total internal reflection?
Answer:
No, because, total internal reflection takes place only when a ray of light is travelling from denser to a rarer medium.

Question 27.
A portion of a lens is broken. Will we get a complete image of an object with such a lens?
Answer:
Yes, but the intensity of image will be lesser.

Question 28.
Under what conditions a concave lens can behave as a converging lens?
Answer:
A concave lens can behave as converging lens when it is placed in a medium whose refractive index is more than the refractive index of material of lens.

Question 29.
A lens is of focal length - 0.5 m. What is the nature and power of the lens?
Answer:
Since power of lens, P = \(\frac{1}{f}\)
∴ P = \(-\frac{1}{0.5}\) = -2D
As the power is -ve, so it is concave lens.

Question 30.
What is dispersion of light?
Answer:
The phenomenon of splitting up of white light into its constituent colours is called dispersion of light. The bands of colours produced on the screen is called spectrum.

Question 31.
Which of the violet and red lights will be deviated more by a prism and why?
Answer:
Violet light will deviate more than red light because
µ_v > µ_r
So δ_v > µ_r [∵ δ = (µ - 1) A]

Question 32.
What is the significance of dispersive power of a prism?
Answer:
The dispersive power is the ability of a prism to split white light into its constituent colours.

Question 33.
Is the angle of minimum deviation produced by a prism different for different wavelengths/colours?
Answer:
Yes.

Question 34.
On what factors does the chromatic aberration of a lens depend?
Answer:
It depends upon (i) focal length and (ii) the dispersive power of the material of the lens.

Question 35.
Out of crown and flint glasses, which has the larger value of dispersive power?
Answer:
Flint glass.

Question 36.
What is the cause of formation of a rainbow?
Answer:
Dispersion, refraction and total internal reflection of light.

Question 37.
What is a pure spectrum?
Answer:
The spectrum in which no overlapping of colours takes place is called pure spectrum.

Question 38.
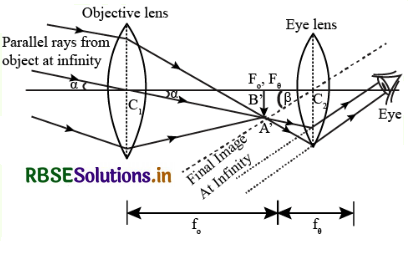
What is the magnifying power of an astronomical telescope in normal adjustment? What is its length?
Answer:
Magnifying power of an astronomical telescope is the ratio of the angle subtended by the image at the eye as seen through the telescope to the angle suhstended by the object at the unaided eye, the object and the image both being at infinity. M = \(\frac{f_0}{f_e}\). Its length is l = f₀ + f_e.

Question 39.
What is mangnifying power of a microscope? What is it equal to?
Answer:
Magnifying power of a compound microscope is defined as the ratio of an angle subtended on the eye by the final image to the angle subtended on the eye by the object when both are placed at least distance of distinct vision from the eye.
m = \(-\frac{\mathrm{L}}{f_0}\left(1+\frac{\mathrm{D}}{f_e}\right)\)

Question 40.
What is the magnifying power of an astronomical telescope when the final image of a distant object is formed at least distance of distinct vision?
Answer:
Magnifying power of a telescope is defined as the ratio of the angle subtended on the eye by the final image at least distance of distinct vision to the angle subtended on the eye by the object at infinity when seen directly.
m = \(-\frac{f_0}{f_e}\left(1+\frac{f_e}{\mathrm{D}}\right)\)

Question 41.
What is the normal adjustment of a telescope?
Answer:
When final image is formed at infinity, the telescope is said to be in normal adjustment position.

Question 42.
Eye is more sensitive to yellow colour. Why are then the danger signals red?
Answer:
The scattering (Rayleigh’s) of light is inversely proportional to the fourth power of the wavelength of light. So. the scattering of red light is much less than the yellow light and the signals of red light can be seen upto a longer distance. That is why the danger signals are red in colour.

Question 43.
Which lens has positive and which lens has negative power?
Answer:
Convex lens of denser medium has positive power. Concave lens of denser medium has negative power.

Question 44.
Under what conditions will a convex lens have a negative and a concave lens a positive power?
Answer:
In a denser medium, a convex lens has a negative and a concave lens has a positive power.

Question 45.
Write expressions for the focal length and power of a lens combination.
Answer:
The required expressions are:
\(\frac{1}{f}=\frac{1}{f_1}+\frac{1}{f_2}\)
and P = P₁ + P₂

Question 46.
Define a lens system.
Answer:
An arrangement of two or more lenses placed separated from each other on a common axis, is called a lens system.

Question 47.
What is power of a parallel faced glass slab?
Answer:
A parallel faced glass slab has zero power.

Question 48.
Name the seven colours produced by the dispersion of white light.
Answer:
The colours can be remembered by the word VIBGYOR i.e., voilet, indigo, blue, green, yellow, orange and red.

Question 49.
Write expression for the angular dispersion produced by a prism.
Answer:
The required expression is (µ_v - µ_r) A.

Question 50.
Write expression for the magnificiation produced by a lens system.
Answer:
The required expression is
M = m₁ x m₂ x m₃.

Question 51.
Which surface has a positive and which surface has a negative power?
Answer:
A converging surface has a positive power. A diverging surface has a negative power.

Question 52.
Write formula for refraction of light from a single spherical surface.
Answer:
The required formula is
\(-\frac{\mu_1}{u}+\frac{\mu_2}{v}=\frac{\mu_2-\mu_1}{\mathrm{R}}.\)

Question 53.
Define optical centre of a lens.
Answer:
It is a point on the principal axis of the lens such that a ray of light passing through it goes undeviated.

Question 54.
If a telescope is inverted, will it serve as a microscope?
Answer:
No.

Question 55.
What is the distance between object and eye lens, when the telescope is on normal adjustment?
Answer:
Length of telescope, L = f₀ + f_e.

Question 56.
What is the range of vision for normal eye?
Answer:
The range is from 25 cm (least distance of distinct vision) to inifinity.

Question 57.
A glass lens of refractive index 1.5 is placed in a trough of liquid. What must be the refractive index of the liquid in order to make the lens diappear.    
Answer:
The same as that of the lens i.e. 1.5.

Question 58.
Converging lens of refractive index 1.5 is kept in a liquid medium having the same refractive index what would be the focal length of the lens in this medium?
Answer:
Infinite, because
\(\frac{1}{f}=\left(\frac{\mu_2}{\mu_1}-1\right)\left(\frac{1}{\mathrm{R}_1}-\frac{1}{\mathrm{R}_2}\right)\)
= (1 - 1) \(\left(\frac{1}{R_1}-\frac{1}{R_2}\right)\) = 0
 ∴ f = ∞

Question 59.
How does the power of a convex lens vary if the incident red light is replaced by violet light?
Answer:
Power increases because the focal length is minimum for violet light. Because
P = \(\frac{1}{f}=\left({ }^a \mu_g-1\right)\left(\frac{1}{\mathrm{R}_1}-\frac{1}{\mathrm{R}_2}\right)\)

Question 60.
An object is held at the principal focus of a concave lens of focal length F. Where is the image formed?
Answer:
Between the optical centre and the focus on the same side as that of the object.

Question 61.
A diverging lens of focal length f is cut in two identical parts each part forming a piano-concave lens. What is the focal length of each part?
Answer:
2f.
∵ For a diverging lens
\(\frac{1}{f}=(\mu-1)\left(-\frac{1}{\mathrm{R}}-\frac{1}{\mathrm{R}}\right)=-\frac{(\mu-1)^2}{\mathrm{R}}\)
or f = \(\frac{\mathrm{R}}{(\mu-1)^2}\)
For each plano convex lens
\(\frac{1}{f^{\prime}}=(\mu-1)\left(-\frac{1}{R}-\frac{1}{\infty}\right)=-\frac{(\mu-1)}{R}\)
or f' = \(-\frac{\mathrm{R}}{(\mu-1)}\) = 2f

Question 62.
A double convex lens made from a material of refractive index µ₁ is immersed in a liquid of refactive index µ₂ where µ₂> µ₁. What change, if any, would occur in the nature of the lens?
Answer:
The lens behave as a concave lens.

Question 63.
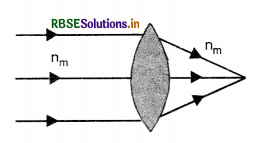
In the given figure VSAQ 63 below the path of a parallel beam of light passing through a convex lens of refractive index n_g kept in a medium of refractive index nm is shown. Is (1) n_g = n_m or (ii) n_g > n_m or (iii) n_g < n_m.

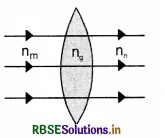
Answer:
Since the rays after refraction pass undeflected so n_g = n_m.

Question 64.
In the figure VSAQ 64 given below the path of a parallel beam of light passing through a convex lens of refractive index n_g kept in a medium of refractive' index n is shown. Is (i) n_g = n_m or (ii) n_g > n_m or (iii) n_g < n_m.

Answer:
Since a parallel beam of light is diviated towards the principal axis, so n_g > n_m.

Question 65.
The refractive index of a material of a concave lens is n₁. It is immersed in medium of refractive index n₂. A parallel beam of light is incident on the lens. Trace the path of the emergent lays when
(i) n₂ = n₁
(ii) n₂ > n₁
(iii) n₂ < n₁
Answer:

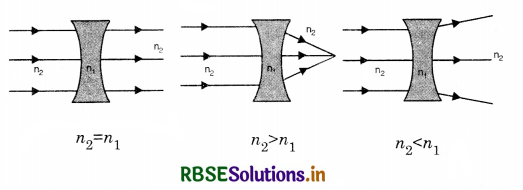
Question 66.
How does the frequency of a beam of ultraviolet light change when it goes from air to glass?
Answer:
Frequency of light remains unchanged.

Question 67.
When light undergoes refraction, what happens to its frequency?
Answer:
Frequency of light remains unchanged.

Question 68.
A concave mirror is placed in water will there be any change in focal length? Give reason.
Answer:
Focal length of the concave mirror remains constant.

Question 69.
How does the focal length of a convex lens change if monochromatic red light is used instead of monochromatic blue light?
Answer:
Since λ_red > λ_blue, so the focal length would increase.

Question 70.
What is the focal length of a plane mirror?
Answer:
Infinite.

Question 71.
Two thin lenses of power + 5D and -3D are in contact. What is the focal length of the combination.
Answer:
P = P₁ + P₂ = 5 - 3 = 2
or P = \(\frac{1}{f}\) = 2
or f = \(\frac{1}{2}\) m = 50 cm

Question 72.
A convex lens made of material of refractive index n₁ is kept in a medium of refractive index n₁. Parallel rays of light are incident on the lens. Complete the path rays of light emerging from the convex lens, if
(i) n₁ > n₂ (ii) n₁ = n₂ (iii) n₁ < n₂
Answer:

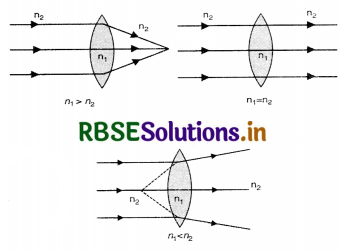
Question 73.
A lens shown in the figure VSAQ 9.73 is made of two different materials. A point object is placed on its axis. How many images will it form?

Answer:
The given lens will form minimum two images.

Question 74.
An object is placed at the focus of concave lens. Where will its image be formed?
Answer:
Between focus and optical centre.

Question 75.
Which spherical mirror is called a divergent mirror - concave or convex?
Answer:
A divergent mirror is called convex mirror.

Question 76.
How is the focal length of a spherical mirror affected, when the wavelength of the light used is increased?
Answer:
The focal length of the mirror is independent of wavelength of incident light.

Question 77.
Which of the main parts of an optical fibre has a higher value of refractive index?
Answer:
The value of refractive index of the fibre material is higher than that of the coating material.

Question 78.
What happens to the focal length of convex lens, when it is immersed in water?
Answer:
The focal length of the lens increases when it is immersed in water.

Question 79.
Write the relation for the refractive index of the prism in terms of the angle of minimum deviation and the angle of prism.
Answer:
µ = \(\frac{\sin \left(\frac{\mathrm{A}+\delta_m}{2}\right)}{\sin \mathrm{A} / 2}\)

Question 80.
Out of red and blue lights, for which colour is the refractive index of glass greater?
Answer:
µ_b > µ_r.

Question 81.
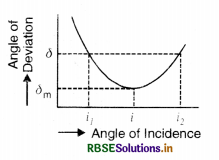
Plot a graph to show the variation of the angle of deviation as a function of angle of incidence for light rays passing through a prism.
Answer:
The graph is as shown in Fig. VSAQ 81.

Question 82.
What is the length of telescope in normal adjustment?
Answer:
Length of telescope = f₀ + f_e.

Question 83.
A glass of refractive index 1.45 disappears when immersed in a liquid. What is the value of refractive index of the liquid?
Answer:
The refractive index of the liquid is also 1.45.

Question 84.
Calculate the speed of light in a medium whose critical angle is 30°.
Answer:

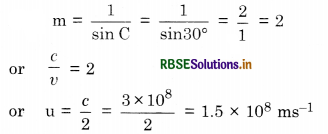
Question 85.
Sketch the emergent wavefront.

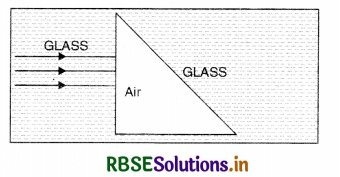
Answer:
After refraction from face AB, the ray go straight and on face AC, the refraction is from rarer to denser medium, hence they go towards the normal.

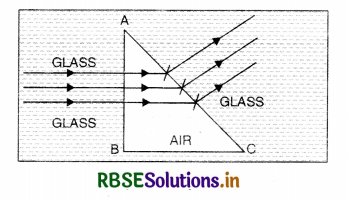
Question 86.
Define the magnifying power of a compound microscope when the final image is formed at infinity. Why must both the objective and the eye piece of a compound microscope has short focal length? Explain.
Answer:
Magnifying power is defined as the angle subtends at the eye by the image to the angle subtended by the object.
m = m₀ × m_e = \(\frac{L}{f_0} \times \frac{D}{f_e}\)
To increase the magnifying power both objective and eye piece must have short focal lengths such as,
m = \(\frac{L}{f_0} \times \frac{D}{f_e}\)

Short Answer Type Questions

Question 1.
What do you mean by refraction of light?
Answer:
The phenomenon of bending of light rays as they pass from one medium to another is called refraction of light. The bending of light rays is due to the fact that the speed of light changes as it passes from one medium to another. If the light goes from rarer medium to denser medium, it bends towards the normal and if it goes from denser to rarer medium, it bends away from the normal. The refraction of light obey two laws (a) the incident ray, r refracted ray and the normal at the point of incidence all lie on the same plane and (b). The ratio of sine of angle of incidence and sine of angle of refraction is constant for a given pair of media.

Question 2.
Define absolute refractive index of a medium.
Answer:
The absolute refractive index of a medium (µ) is defined as the ratio of velocity of light in vacuum (c) to the velocity of light in the medium (v)
i.e. µ = \(\frac{c}{v}\)
As c > v ∴ µ > 1.

Question 3.
Define refractive index of a medium w.r.t. another medium.
Answer:
If v₁ is velocity of light in medium 1 and v₂ is velocity of light in medium 2, then refractive index of medium 2.w.r.t. medium 1 is defined as
¹µ₂ = \(\frac{v_1}{v_2}\)

Question 4.
What is law of refraction in terms of angles i and r?
Answer:
sin i ∝ sin r
or sin i = µ sin r or \(\frac{\sin i}{\sin r}\) = µ
where µ is a constant called refractive index.

Question 5.
Define refractive index in terms of velocity of light.
Answer:
Refractive index is the ratio of velocity of light in vacuum to the velocity of light in other medium.
µ = \(\frac{\text { Velocity of light in vacuum }(c)}{\text { Velocity of light in medium }(v)}\)
µ of glass is 1.5. If the velocity of light in vacuum is 3 x 10⁸ ms^-1, velocity of light in glass will be
1.5 = \(\frac{3 \times 10^8}{v_g}\)
or v_g = \(\frac{3 \times 10^8}{1.5}\) = 2 x 10⁸ ms^-1

Question 6.
What is the relation between critical angle and refractive index? What is critical angle for diamond?
Answer:
µ = \(\frac{1}{\sin C}\) or sin C = \(\frac{1}{\mu}\)
Refractive index of diamond is 2.42, hence critical angle is 24.6°.

Question 7.
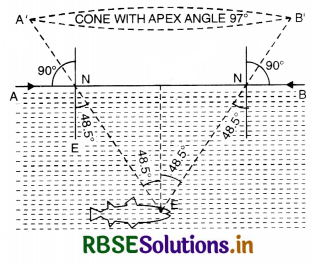
How does the surface of the earth appear to a fish or a person sitting inside clear water?
Answer:
Whole of the earth will appear to he within 97° instead of actual 180°. A ray of light from A incident at angle of 90° at N' will go towards NE at an angle of 48.5°. [Refractive index of water is 1.33 and critical angle is 48.5°]. It shall appear to fish to come from A instead of A'. Similarly another ray from B will apear to come from B'. Whole of the earth will appear to he within a cone of apex angle 48.5° + 48.5° = 97°.

Question 8.
An empty test tube is placed slanting in the water and viewed from above, what will you observe?
Answer:
The portion of the tube within water will shine like a mirror due to total internal reflection. If the tube is partially filled with water, the portion of tube containing water will no longer show this effect.

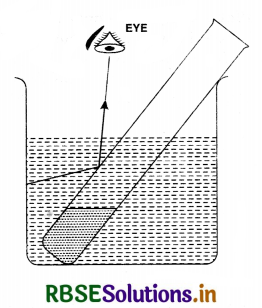
Question 9.
What happens if angle of incidence is more than critical angle?
Answer:
If angle of incidence is more than critical angle in going from denser to rarer medium the ray of light will be completely reflected back in the denser medium.

Question 10.
Explain the brilliance of a diamond.
Answer:
The refractive index of diamond is 2.42 and the critical angle for diamond is given by
sin C = \(\frac{1}{\mu}=\frac{1}{2.42}\) = 0.4132 or C = 24.4°.
As the value of critical angle is very small so the diamond is cut in such a way that it has multiple faces at suitable angles. A ray of light on entering into the diamond suffers total internal reflection from other faces and comes out of the diamond as an intense beam from selected directions and the faces shine when viewed from outside.

Question 11.
Does the critical angle depend on the wavelength of light?
Answer:
Yes. Since critical angle depends upon the refractive index of the medium and refractive index of the medium depends upon the wavelength of light. So critical angle also depends upon the wavelength of light.

Question 12.
Why does a convex lens of glass µ = 1.5 behave as a diverging lens when immersed in carbon disulphide of µ = 1.65?
Answer:
The lens formula is given by
\(\frac{1}{f}=\left(\frac{\mu_2}{\mu_1}-1\right)\left(\frac{1}{\mathrm{R}_1}-\frac{1}{\mathrm{R}_2}\right)\)
here \(\frac{\mu_2}{\mu_1}=\frac{\mu_g}{\mu_c}=\frac{1.5}{1.65}<1\)
Hence f becomes -ve, so the lens behaves like a diverging lens.

Question 13.
What are the uses of optical fibre?
Answer:
Following are the main uses of optical fibre.

• It is used for internal examination of the human body. This equipment is called endoscope.
• In surgery optical fibre is used to transmit light.
• To measure the blood flow in the heart, the optical fibres are used in the form of photometric sensors.
• Optical fibres are used in medical examination.
• Optical fibres are used in optical signal transmission.

Question 14.
State the condition of total internal reflection to take place at an interface separating two transparent media. Hence derive the expression for the critical angle in terms of speed of light in two media.
Answer:
Conditions for total internal reflection. There are two conditions to be satisfied for the total internal reflection to take place:
(i) Ray of light should proceed from optically denser to optically rarer medium.
(ii) Angle of incidence must be greater than the critical angle for the pair of media.
If a and b are optically rarer and optically denser media respectively, and C is the critical angle, then
sin C = \(\frac{1}{a}\) = ^bµ_a
or sin C = \(\frac{v_b}{v_a}\)
= \(\frac{\text { velocity in optically denser medium }}{\text { velocity in optically rarer medium }}\)

Question 15.
What are the advantages of total reflecting prism over a plane mirror?
Answer:

• It reflects whole light i.e. its reflection is 100%
• No silvering is required for reflection of light through total reflecting prisms.
• In reflecting prism, multiple reflection does not take place and the single image formed is bright.

Question 16.
When observed from under water, all the objects above the surface can be seen within a cone of 97°. Why? Explain.
Answer:
Since the critical angle C and refractive index µ is given by
sin C = \(\frac{1}{\mu}\)
for water, µ = 1.33
∴ sin C = \(\frac{1}{1.33}\) = 0.7519
or C = 48.75°
∴ Angle of the cone = 48.75° x 2 = 97°.

Question 17.
What are the assumptions followed to study refraction from spherical surfaces?
Answer:

• The object is taken a point object on the principal axis.
• The aperture of the spherical refracting surface is small.
• Incident and refracted rays make small angles with principal axis.

Question 18.
A concave mirror and a convex lens are hold in water. What change, if any, do you expect to find in the focal length of either?
Answer:
The focal length of a mirror is half its radius of curvature and has nothing to do with the external medium. The focal length of a convex lens will increase because the refractive index of glass with respect to water is less than refractive index of glass with respect to air.

Question 19.
A curved glass piece of uniform thickness has a zero power. Why?
Answer:
Glass slab has zero power. A curved glass piece of uniform thickness is equivalent to combination of a convex and a concave lens having powers numerically equal. The sum of equal and opposite powers makes the combination to have a zero power. It behaves like a glass slab with curved parallel face.

Question 20.
Why are ‘haloes'(rings) observed sometimes round the sun or moon?
Answer:
When the sun or the moon is seen through a thin veil of the high cloud haloes are formed. A large number of icy crystals are present in the clouds. The haloes are due to the refraction of light from the icy crystals.

Question 21.
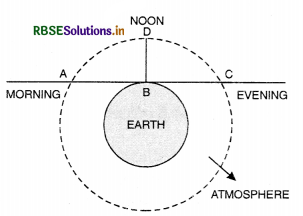
Explain with reason, why (i) sun appears reddish at sun set or sun rise and (ii) sun is observed earlier to actual sun rise and after sun set.
Answer:
(i) In morning and in the evening, the sun rays have to cover more distance through air AB or BC than at the noon time (BD). Therefore, blue colour scattered from the air more than red since scattering ∝ \(\frac{1}{\lambda^4}\).

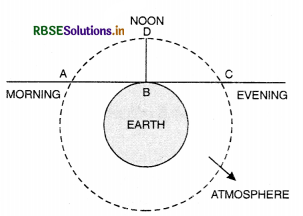
For blue λ is the least and scattering is maximum.

(ii) The sun is visible before actual rise and after sun set. This is due to refraction of light produced by atmosphere. Whereas the sun is actually at (and hence should be invisible) but it will appear to be at S'. Thus it is visible even before sun rise and similarly it is visible after sun set.

Question 22.
A concave mirror and a convex lens are held separately in water. What changes, if any, do you expect in the focal length of either?
Answer:
The focal length of concave mirror will remain constant because its focal length f = \(\frac{\mathrm{R}}{2}\), so f does not depend upon µ.
The focal length of convex lens will increase, because, in this case focal length is given by \(\frac{1}{f}=(\mu-1)\left(\frac{1}{R_1}-\frac{1}{R_2}\right)\). As µ of lens decreases with reference to water.

Question 23.
What is the cause of dispersion of light?
Answer:
The refractive index of a material depends upon the wavelength as the velocity of light in a material depends upon wavelength, since white light is composed of different colours, so different colours are deviated through different angles and we get dispersion of light.

Question 24.
A telescope has an objective of diameter of 60 cm. The focal lengths of the objective and eye piece are 2.0 m and 1.0 cm respectively. The telescope is directed to view two distant almost point sources of light (e.g. two stars of a binary). The sources are at roughly the same distance (= 10⁴ light years) along the line of sight but separated transverse to the line of sight by a distance of 10¹⁰ m. Will the telescope resolve the two objects i.e. will it see two distinct stars?
Answer:
Distance between two stars, d = 10¹⁰ m
Distance of stars from objective,
D = 10⁴ light years
= 10⁴ x 10¹⁶ m (∵ 1 light year ≃ 10¹⁶ m)
Objective diameter (aperture),
a = 60 cm = 0.60 m
Wavelength of light used,
λ = 5500 x 10^-8 m
Angle subtended by the stars on the telescope; objective.
\(\frac{d}{\mathrm{D}}=\frac{10^{10}}{10^{20}}\) = 10^-10 radians
Limit of angular resolution of telescope objective,
dθ = \(\frac{1.22 \lambda}{a}\)
= \(\frac{1.22 \times 5500 \times 10^{-8}}{0.60}\)
= 1.118 x 10^-6 radians.

Question 25.
The image of a candle is formed by a convex lens on a screen. The lower half of the lens is painted black to make it completely opaque. Draw the ray diagram to show the image formation. How will this image be different from one obtained when the lens is not painted black?
Answer:
The ray diagram is shown in Fig. SAQ 25.

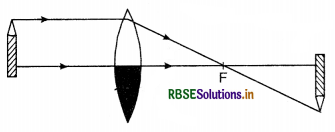
Here the light received from only upper half and hence the image formed will be faint and its intensity will be half of what it can have with full lens.

Question 26.
A figure divided into squares each of size 1 mm², is being viewed at a distance of 9 cm through magnifying lens of focal length 10 cm, held close to the eye.
(a) Draw the ray diagram showing the formation of the image.
(b) What is the magnification produced by the lens? How much is the area of each square in the virtual image?
(c) What is the angular magnification of the lens?
Answer:
(a) The ray diagram is shown in figure SAQ 26. The virtual image A'B' of real object AB is formed on the same side.


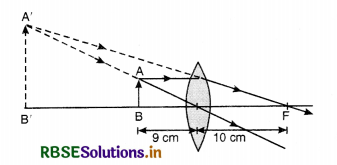
(b) u = -9 cm, f = 10 cm, v = ?

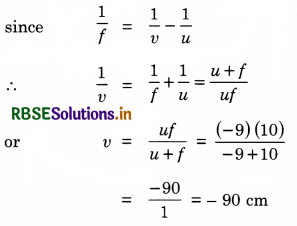
∴ Magnification, m = \(-\frac{v}{u}=\frac{-90}{9}\) = -10
i.e. the image will be erect, virtual and three times bigger.
Magnification in area = (-10)² = 100
Area of the image will be
1 mm² x 100 = 100 mm² = 1 cm²

(c) Angular magnification
= \(\frac{\beta}{\alpha}=\frac{\mathrm{I}}{\mathrm{O}}\)
= 10.

Question 27.
A converging lens has a focal length of 20 cm in air. It is made of a material of refractive index 1.6. If it is immersed in a liquid of refractive index 1.3, what will be its new focal length?
How does the nature of the lens change, if this lens is immersed in a liquid of refractive index 1.8?

From (1) and (2), we get
f = 52 cm
When the converging lens is immersed in a liquid of refractive index 1.3, it will behave like divergent lens of focval length say f'
∴ \(\frac{1}{f^{\prime}}=\left(\frac{1.6}{1.8}-1\right)\left(\frac{1}{\mathrm{R}_1}-\frac{1}{\mathrm{R}_2}\right)\)
or \(\frac{1}{f^{\prime}}=-\frac{1}{9}\left(\frac{1}{R_1}-\frac{1}{R_2}\right)\) ..........................(3)
From (1) and (3)
f' = -108 cm
i.e. the focal length of divergent lens is -108 cm.

Question 28.
Why parabolic mirrors are used in search lights?
Answer:
Parabolic mirrors produce a parallel beam of light of wide cross-section, if a light source is placed at its focus. Also the intensity of search light practically remains constant over the long distances.

Question 29.
If the wavelength of incident light on a (i) concave mirror and (ii) convex lens is increased, how will the focal length of each of these change?
Answer:
For concave mirror, there is no change in the focal length.
For convex lens, the focal length will increase, because the refractive index decreases with the increase in wavelength and as \(\frac{1}{f}\) ∝ µ so f will increase.

Question 30.
How will you explain twinkling of stars ?
Answer:
The light from stars undergoes number of refractions before reaching the earth. Due to change in temperature conditions and density of the atmosphere, the star light has to travel through fluctuating masses of air in motion, hence the apparent position of the star constantly keeps on changing. This give rise to twinkling of stars.

Question 31.
The sun is seen a little before, it rises and for a short while after it sets. Explain, Why?
Or
Watching the sunset on a beach, one can see for several minutes after it has 'actually set'. Explain.
Answer:
(ii) The sun is visible before actual rise and after sun set. This is due to refraction of light produced by atmosphere. Whereas the sun is actually at (and hence should be invisible) but it will appear to be at S'. Thus it is visible even before sun rise and similarly it is visible after sun set.

Question 32.
Why the sun looks to be red at the time of setting?
Answer:
(i) In morning and in the evening, the sun rays have to cover more distance through air AB or BC than at the noon time (BD). Therefore, blue colour scattered from the air more than red since scattering ∝ \(\frac{1}{\lambda^4}\).

For blue λ is the least and scattering is maximum.

Question 33.
Show that a concave lens will always form a virtual image of a real object.
Answer:
Let u' be distance of real object from concave lens of focal length f.
From new sign conventions
v = -u' and f = -f'
Using lens formula.

Since v is negative number irrespective of value of u', the image formed is always virtual.

Question 34.
A prism can produce spectrum of white light but a glass slab having the same material as prism cannot produce any spectrum. Why?
Answer:
In case of a prism, when white light is incident on it, the white light breaks up into constituent colours. And the emergent light is not parallel to incident light, so the different colours for deviation at different angles and we get a spectrum of white light.
In case of glass slab, when white light is incident on it, it also breaks up into its constituent colours, after refraction in the glass slab, but the emergent ray is parallel to incident ray, so all the different colours are deviated through the same angle and image formed is white in colour and no spectrum of white light is observed.

Question 35.
A virtual image cannot be obtained on screen. But when we see a virtual image, it is obtained on the screen i.e. the retina of our eye. Is there any contradiction?
Answer:
No, there is no contradiction. The eye lens forms the real image of the virtual object and converges the divergent rays and focus them on the retina (i.e. screen).

Question 36.
How does a combination of lenses affect the size, position and nature of the image?
Answer:
Two or more lenses may be combined by placing them in contact or at a finite distance apart. We can find size, nature and position of the final image by considering refraction through individual lenses. The image formed by first lens acts as an object for second lens. Similarly, the image formed by second lens acts as an object for third lens and so on. The standard formulae can be applied in case of individual lenses to obtain the final size, nature and position of the image.
If m₁, m₂, m₃ ............................. are the magnifications produced by the individual lenses, then total magnification produced by the combination is
M = m₁ x m₂ x m₃ x .............................

Question 37.
What is meant by chromatic aberration? How is this defect removed?
Answer:
Chromatic aberration is an optical defect by virtue of which image of an object seen in white light through a lens appears coloured.
It arises on account of inability of a lens to focus all the colours (in white light) at the same point. In Fig. red rays are focussed at f_r and violet rays are focused at f_v, all other colours being focussed in between.
The difference in focal lengths of the lens for red and violet rays i.e. (f_r - f_v) is a measure of longitudinal chromatic aberration of the lens. It is positive in case of a convex lens and negative in case of a concave lens.

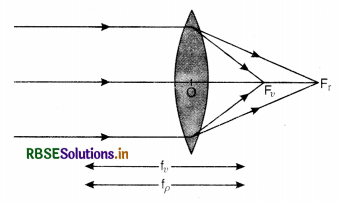
To remove chromatic aberration, we use an achromatic doublet. This is a combination of a convex lens of crown glass and concave lens of flint glass with their focal lengths adjusted suitably so that net chromatic aberration of the combination is zero.
The achromatic doublet will thus focus all the colours at the same point. Hence the image seen in white light shall not be coloured i.e. it will be free of chromatic aberration.

Question 38.
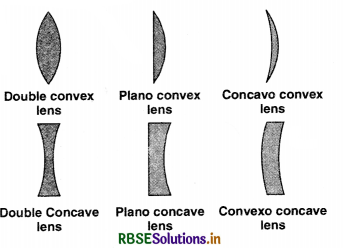
Show diagrammatically the various types of convex and concave lenses.
Answer:

Question 39.
Draw a labelled ray diagram of a reflecting type telescope. Write its any one advantage over refracting type telescope.
Answer:
Diagram:

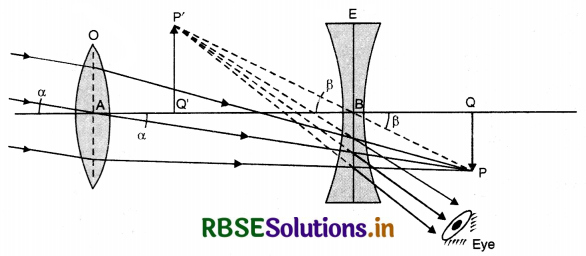
Advantage over refracting type telescope. It is free from chromatic aberration, spherical aberration and astigmatism.

Question 40.
Violet light is incident on a converging lens of focal length f. State with reasons how focal length of the lens will change, if the violet light is replaced by red light.
Answer:
The focal length of a lens is given by
\(\frac{1}{f}=(\mu-1)\left(\frac{1}{\mathrm{R}_1}-\frac{1}{\mathrm{R}_2}\right)\)
Since µ_r < µ_v
∴ \(\frac{1}{f_r}<\frac{1}{f_v}\)
or f_r > f_v
Thus, the focal length will increase.

Question 41.
What is the cause of the blue colour of the sky?
Or
Why does the sky appear blue?
Answer:
Blue colour of the sky can be explained due to Rayleigh scattering. The amount of scattering is inversely proportional to the fourth power of the wavelength. When light from the sun travels through earth's atmosphere, it gets scattered by large number of gaseous molecules. The blue light of shorter wavelength is scattered more than the red light of larger wavelength. Due to this, blue colour predominates and the sky appears blue.

Question 42.
Draw path of rays for astronomical telescope in normal adjustment.

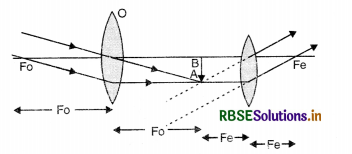
Answer:
In an astronomical telescope, the objective is a convex lens of large focal length. The eye lens is also a convex lens of small focal length. The position of the eye piece is adjusted so that final image is seen at infinity. Then distance between two lenses
d = f₀ + f_e.

Question 43.
Draw a labelled diagram of a telescope which gives erect images of distant objects.
Answer:
We use a Galileo telescope to get an erect image of objects. The objective is a convex lens while the eye piece is a concave.

Question 44.
Draw a labelled ray diagram to show the image formation by an astronomical telescope in the near point adjustment.
Or
Draw a ray diagram to illustrate image formation by an astronomical telescope used in near point position.
Or
Draw a ray diagram of an astronomical telescope in the normal adjustment position. Write down the expression for its magnifying power.
Answer:
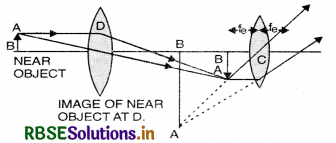
Image of the near object can be formed at infinity or at D.
Image of near object at infinity.

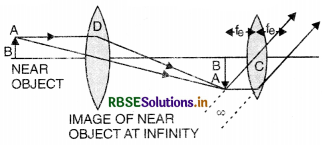
Magnifying power for normal adjustment
M = \(-\frac{f_0}{f_e}\)
Image formed at least distance of distinct vision.

Question 45.
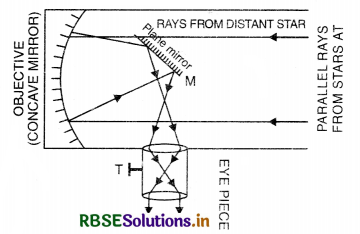
Draw a ray diagram of a reflecting type telescope. State two advantages of this telescope over a refracting telescope.
Or
Modern telescopes prefer using suitable mirrors over using suitable lenses. Give two reasons of this preference.
Answer:
Ray diagram of reflecting type telescope is given in Fig.
Advantages
1. The image is free from chromatic aberration.
2. The image is free from spherical aberrations.

Question 46.
Draw a ray diagram of an astronomical telescope in the normal adjustment position. State two drawbacks of this type of telescope.
Answer:
Ray diagram of an astronomical telescope for normal adjustment is given in Fig. SAQ 47.

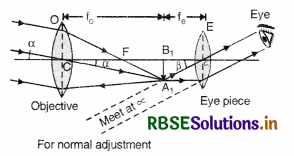
Drawbacks.
1. The image is inverted and fainter.
2. Spherical aberration and chromatic aberrations present.

Question 47.
Draw a ray diagram of a compound microscope. Write the expression for its magnifying power.

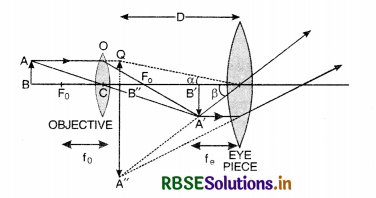
Magnifying power, M = \(\frac{l}{f_0}\left(1 \times \frac{\mathrm{D}}{f_e}\right)\).

Question 48.
State the condition for total internal reflection. Calculate the speed of light in the medium whose critical angle in 45°.
Or
State the condition of total internal reflection to take place at an interface separating two transparent media. Hence derive the expression for the critical angle in terms of speed of light in two media.
Or
State the conditions for the phenomenon of total internal reflection to occur.
Answer:
Conditions for total internal reflection. There are two conditions to be satisfied for the total internal reflection to take place:
(i) Ray of light should proceed from optically denser to optically rarer medium.
(ii) Angle of incidence must be greater than the critical angle for the pair of media.
If a and b are optically rarer and optically denser media respectively, and C is the critical angle, then
sin C = \(\frac{1}{a}\) = ^bµ_a
or sin C = \(\frac{v_b}{v_a}\)
= \(\frac{\text { velocity in optically denser medium }}{\text { velocity in optically rarer medium }}\)

Question 49.
The image of a candle is formed by a convex lens on a screen. The lower half of the lens is painted black to make it completely opaque. Draw the ray diagram to show the image formation. How will this image be different from one obtained when the lens is not painted black?
Answer:
The ray diagram is shown in Fig. SAQ 25.

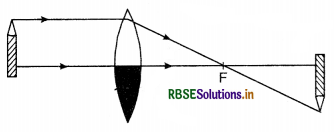
Here the light received from only upper half and hence the image formed will be faint and its intensity will be half of what it can have with full lens.

Question 50.
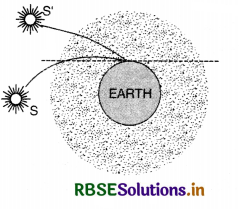
The sun is seen a little before sunrise and after a short while after it sets. Explain why?
Answer:
The sun is visible before actual sunrise and after sunset. This is due to refraction of light produced by atmosphere. Whereas the sun is actually at S (and hence should be invisible) but it will appear to be at S'. Thus it is visible even before sunrise and similarly it is visible after sunset.

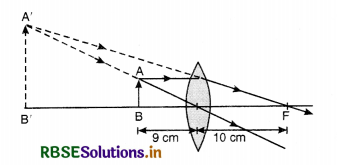
Question 51.
A figure divided into squares each of size 1 mm², is being viewed at a distance of 9 cm though magnifying lens of focal length 10 cm, held close to the eye.
(a) Draw the ray diagram showing the formation of the image.
(b) What is the magnification produced by the lens? How much is the area of each square in the virtual image?
(c) What is the angular magnification of the lens?
Answer:
(a) The ray diagram is shown in figure SAQ 26. The virtual image A'B' of real object AB is formed on the same side.


(b) u = -9 cm, f = 10 cm, v = ?

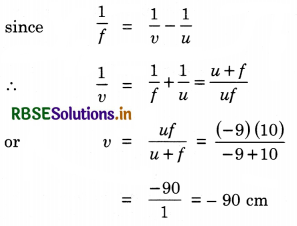
∴ Magnification, m = \(-\frac{v}{u}=\frac{-90}{9}\) = -10
i.e. the image will be erect, virtual and three times bigger.
Magnification in area = (-10)² = 100
Area of the image will be
1 mm² x 100 = 100 mm² = 1 cm²

(c) Angular magnification
= \(\frac{\beta}{\alpha}=\frac{\mathrm{I}}{\mathrm{O}}\)
= 10.

Question 52.
If the wavelength of incident light on a (i) concave mirror and (ii) convex lens is increased, how will the focal length of each of these change?
Answer:
The light from stars undergoes number of refractions before reaching the earth. Due to change in temperature conditions and density of the atmosphere, the star light has to travel through fluctuating masses of air in motion, hence the apparent position of the star constantly keeps on changing. This give rise to twinkling of stars.

Question 53.
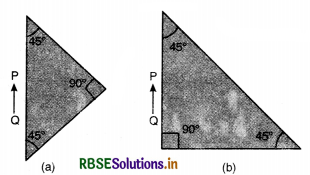
A right angled crown glass prism with critical angle 41°. is placed before an object PQ in two positions are shown in figure SAQ 54 (a) and (b). Trace the path of the rays P and Q passing through the prisms in the two cases.

Answer:
The curve of rays P and Q passing through the prism is shown in Fig. SAQ 54 (c, a)

Question 54.
A converging and a diverging lens of equal focal lengths are placed co-axially in contact. Find the power and the focal length of the combination.
Answer:
If f and -f be the focal length of coverging and diverging lenses respectively, then Power of combination,
P = P₁ + P₂ = \(\frac{1}{f}-\frac{1}{f}\) = 0 
∴ Focal length of combination
F = \(\frac{1}{\mathrm{P}}=\frac{1}{0}\) = ∞

Question 55.
Define resolving power of a compound microscope. How does the resolving power of a compound microscope change when
(i) refractive index of medium between the object and objective lens increases.
(ii) Wavelength of radiation used is increased.
Answer:
Resolving power of a microscope is defined as the reciprocal of the least separation between two close objects, so that they appear just separated, when seen through the microscope.
Resolving power of microscope
= \(\frac{2 \mu \sin \theta}{1.22 \lambda}\)
(i) Since resolving power ∝ µ, so when µ between object and objective lens is increased, the resolving power of the microscope is also increased.
(ii) Since resolving power of microscope ∝ \(\frac{1}{\lambda}\), so as the wavelength of radiation is increased, the resolving power of the microscope is decreased.

Question 56.
Draw a graph to show variation of angle of deviation D with that of angle of incidence i for a monochromatic ray of light passing through a prism of reflecting angle A. Hence deduce the relation.
µ = \(\frac{\sin \left(\frac{\mathrm{D}_m+\mathrm{A}}{2}\right)}{\sin \mathrm{A} / 2}\)
Answer:
(a) The graph between D and i is as shown in Fig. SAQ 57.


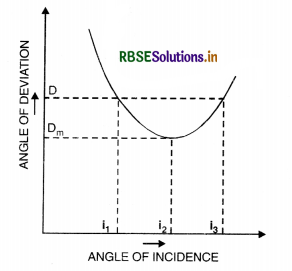
(b) From the graph, we find that D is the same for two angles of incidence i₁ and i₂ but at minimum deviation D, there is only one angle of incidence.
It is found that at minimum deviation positions,
i.e. at D = D_m
e = i and r₁ = r₂ = r (say)
Since D = i + e - A
∴ At minimum deviation position,
we have
D_m = i + e - A = i + i - A
or D_m = 2i - A
or 2i = A D_m
or i = \(\frac{\mathrm{A}+\mathrm{D}_m}{2}\) ..........................(1)
Also at minimum deviation position
A = r₁ + r₂ = r + r = 2r
or  r = \(\frac{\mathrm{A}}{2}\) ..........................(2)
If µ is the refractive index of the prism, then from Snell's law at surface AB, we have
µ = \(\frac{\sin i}{\sin r}\)
Using Eqs. (1) and (2), we get
µ = \(\frac{\sin \frac{\mathrm{A}+\mathrm{D}_m}{2}}{\sin \mathrm{A} / 2} \)

Question 57.
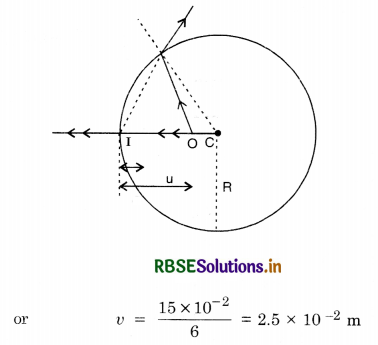
A spherical convex surface of radius of curvature 20 cm, made of glass (µ = 1.5) is placed in air. Find the position of the image formed, if a point object is placed at 30 cm in front of the convex surface on the principal axis.

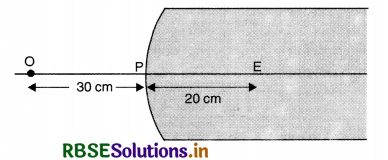
Answer:
Given u = -30 cm, R = 20 cm, µ = 1.5, v = ?

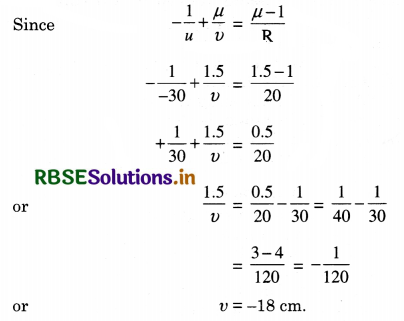
Question 58.
How does the angle of minimum deviation of a glass prism vary, if the incident violet light is replaced by red light? Give reason.
Answer:
(δ_m)_Violet > (δ_m)_red
We know that
λ_red > λ_violet
Since λ ∝ \(\frac{1}{\mu}\)
So µ_red < µ_violet
As µ = \(\frac{\sin \left(\frac{\mathrm{A}+\delta_m}{2}\right)}{\sin \mathrm{A} / 2}\)
So (δ_m)_red < (δ_m)_violet
or (δ_m)_violet > (δ_m)_red.

Question 59.
(a) Draw a ray diagram depicting the formation of the image by an astronomical telescope in normal adjustment.
Or
(b) You are given the following three lenses. Which two lenses will you use as an eye piece and as an objective to construct an astronomical telescope? Give reason.

Lenses	Power (D)	Aperture (cm)
L1	3	8
L2	6	1
L3	10	1

Answer:
(a)

(b) For eye piece, we use L₃ as it has high power and hence more magnification.
For objective, we use L₁ as it has high aperture and hence high resolving power.

Long Answer Type Questions

Question 1.
(a) Define spherical mirror, centre of curvature, radius of curvature, pole, principal axis and focal length of spherical mirror.
(b) What are sign conventions used in mirrors?
Answer:
(a) 1. A spherical mirror is a part of a spherical reflecting surface.
Two types of spherical mirrors are:

• Concave mirror, whose reflecting surface is towards the centre of the sphere of which the mirror is a part. Fig. LAQ 1 (a).
• Convex mirror, whose reflecting surface is away from the centre of the sphere of which the mirror is a part; Fig. LAQ 1 (b).

2. Centre of curvature. The centre of the sphere, of which the mirror forms a part is called the centre of curvature of the mirror.
It is represented by C [Fig. LAQ 1 (a) & (b)].
3. Radius of curvature. The radius of the sphere, of which the mirror forms apart is called the radius of curvature of the mirror.

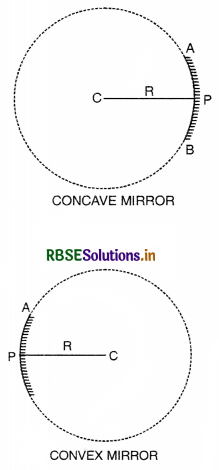
It is denoted by R. In Fig. and the distance PC = R represents the radius of curvature of the mirror.
4. Pole. The middle point of the spherical mirror is called its pole.
It is denoted by P [Fig. LAQ 1 (a) and (b)].
5. Principal axis. The line joining the pole and the centre of curvature of the mirror is called the principal axis of the mirror.
The line PC extended both ways in Fig. represents the principal axis of the mirror.
6. Aperture. The diameter of the mirror is called aperture of the mirror.
7. Principal Focus. It is a point on the principal axis where the rays of light parallel to the principal axis after reflection from the spherical mirror either converge to that point or appear to diverge from that point.
In case of concave mirror rays of light converge to point F, therefore, principal focus is real. In case of convex mirror, rays of light appear to diverge from point F, therefore, principal focus is virtual as shown in Fig. LAQ 1 (c).

Focal length. It is the distance of the principal focus from the pole of mirror. It is denoted by f.

(b) Sign Conventions used in Spherical Mirrors

• All the distances are to be measured from the pole of the mirror.
• The distances measured in the same direction as incident light are taken as +ve.
• The distances measured in the direction opposite to the incident light are taken as -ve.

Question 2.
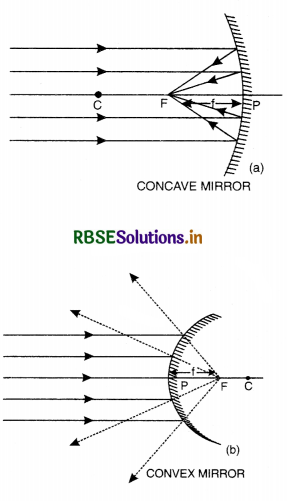
Show that for a spherical concave mirror f = \(\frac{\mathrm{R}}{2}\).
Answer:
Case of Concave Mirror
Consider a ray AB parallel to principal axis incident on a concave mirror at point B and is reflected along BF. The line CB is a normal to the mirror as shown in Fig. LAQ 2.

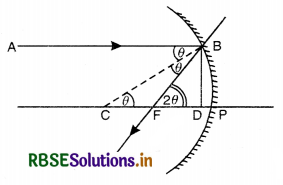
Let θ be angle of incidence, ∠ABC.
∴ ∠ABC = ∠BCP = ∠θ (Alt. ∠S)
Draw BD ⊥ CP.
In right angled ∆ BCD,
tan θ = \(\frac{\mathrm{BD}}{\mathrm{CD}}\) ...........................(i)
In right angled ∆ BFD,
tan 2θ = \(\frac{\mathrm{BD}}{\mathrm{FD}}\) ...........................(ii)
Dividing (i) and (ii), we get
\(\frac{\tan 2 \theta}{\tan \theta}=\frac{\mathrm{CD}}{\mathrm{FD}}\) ...........................(iii)
If θ is very small, then
tan θ = θ and tan 2θ = 2θ
Since the aperture of the mirror is small, therefore, point B lies very close to P.
∴ CD ≈ CP and FD ≈ FP.
From (iii), \(\frac{2 \theta}{\theta}=\frac{\mathrm{PC}}{\mathrm{PF}}=\frac{\mathrm{R}}{f}\)
R = 2f

Question 3.
Show that for a spherical convex mirror f = \frac{\mathrm{R}}{2}.
Answer:
Case of Convex Mirror
A ray AB is incident at a point B on a convex mirror and is reflected along BX. It appears to diverge from F as in Fig. LAQ 3.

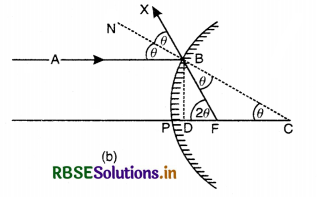
CBN is a normal to the convex mirror.
∠ABC = ∠NBX = ∠θ (∠i = ∠r)
∠NBX = ∠FBC = ∠θ (V. Opp. ∠s)
∠ABN = ∠BCF = ∠θ (Corresponding ∠s)
Draw BD ⊥ CD,
In rt. ∠d ∆BCD, tan θ = \(\frac{\mathrm{BD}}{\mathrm{CD}}\) ...........................(i)
In rt. ∠d ∆BFD, tan 2θ = \(\frac{\mathrm{BD}}{\mathrm{FD}}\) ...........................(ii)
Dividing (i) and (ii)
\(\frac{\tan 2 \theta}{\tan \theta}=\frac{\mathrm{CD}}{\mathrm{FD}}\)
If θ is small tan θ = θ, tan 2θ = θ
\(\frac{2 \theta}{\theta}=\frac{\mathrm{CD}}{\mathrm{FD}}\)
Since aperture is small and point B is very close to point P,
∴ CD = PC, FD = PF
∴ \(\frac{2 \theta}{\theta}=\frac{\mathrm{CD}}{\mathrm{PF}}\)
∴ PC = 2PF
R = 2f
Radius of curvature = 2 x Focal length of Spherical Mirror.

Question 4.
(a) What is a mirror formula?
(b) Derive mirror formula for Concave mirror stating assumptions.
Answer:
(a) Mirror Formula. A formula which gives the relation between the image distance (v), the object distance (u) and the focal length (f) of a mirror is known as mirror formula
\(\begin{aligned} \frac{1}{\text { Focal length }}= & \frac{1}{\text { Image distance }} \\ & +\frac{1}{\text { Object distance }} \end{aligned}\)
\(\frac{1}{f}=\frac{1}{v}+\frac{1}{u}\)

(b) Assumptions

1. Aperture of mirror is small.
2. Incident ray makes small angles with principal axis.
3. Object lies on the principal axis.
4. Object lies on left hand side of the mirror.

Case of Concave Mirror
Consider an object AB placed beyond centre of curvature of a concave mirror, on its principal axis and on the left hand side.
A ray AD parallel to principal axis is incident on the mirror at point D and is reflected to pass through F. Another ray AE passing through centre of curvature C is reflected along the same path. Two rays of light intersect at point A₁. Thus A₁B₁ is real, inverted and diminished image of AB formed between C and F.

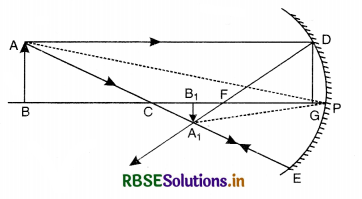
Draw DG ⊥ on principal axis.
∆s DGF and A₁B₁F are similar,
∴ \(\frac{\mathrm{DG}}{\mathrm{A}_1 \mathrm{~B}_1}=\frac{\mathrm{GF}}{\mathrm{FB}_1}\)
But DG = AB
\(\frac{\mathrm{AB}}{\mathrm{A}_1 \mathrm{~B}_1}=\frac{\mathrm{GF}}{\mathrm{FB}_1}\) ..........................(i)
Again ∆s ABC and A₁B₁C are similar
∴ \(\frac{\mathrm{AB}}{\mathrm{A}_1 \mathrm{~B}_1}=\frac{\mathrm{CB}}{\mathrm{CB}_1}\) ......................(ii)
Comparing (i) and (ii)
\(\frac{\mathrm{GB}}{\mathrm{FB}_1}=\frac{\mathrm{CB}}{\mathrm{CB}_1}\)
Since the aperture is small, therefore, point D and point G lie very close to P.
∵ GF = PF
∴ \(\frac{\mathrm{PF}}{\mathrm{FB}_1}=\frac{\mathrm{CB}}{\mathrm{CB}_1}\) .........................(iii)
Since FB₁ = PB₁ - PF
CB = PB - PC
CB₁ = PC - PB₁
Substituting in (iii), we get
\(\frac{\mathrm{PF}}{\mathrm{PB}_1-\mathrm{PF}}=\frac{\mathrm{PB}-\mathrm{PC}}{\mathrm{PC}-\mathrm{PB}_1}\)
Applying sign conventions, we get
PF = -f, PC = -2f, PB = -u and PB1 = -v
\(\frac{-f}{-v-(-f)}=\frac{-u-(-2)}{-2 f-(-v)}\)
\(\frac{-f}{-v+f}=\frac{-u+2 f}{-2 f+v}\)
2f² -vf = uv - uf - 2fv + 2f²
or uv - uf - 2fv = -vf
-uf - vf = -uv
uf + vf = uv
Dividing both sides by uvf, we get
\(\frac{u f}{u v f}+\frac{v f}{u v f}=\frac{u v}{u v f}\)
\(\frac{1}{v}+\frac{1}{u}=\frac{1}{f}\)

Question 5.
Derive mirror formula for a convex mirror.
Answer:
Case of Convex Mirror
Consider an object AB placed on the principal axis of a convex mirror. A ray AD is incident on the mirror at point D and is reflected along DX. It appears to come from F. Another ray AE is directed towards C and it retraces its path.

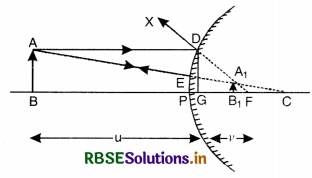
These rays of light appear to meet at A₁. Thus A₁B₁ is virtual, erect image of AB.
Draw DG ⊥ on principal axis.
∆s DGF and A₁B₁F are similar.
∴ \(\frac{\mathrm{DG}}{\mathrm{A}_1 \mathrm{~B}_1}=\frac{\mathrm{GF}}{\mathrm{B}_1 \mathrm{~F}}\)
But DG = AB
\(\frac{\mathrm{AB}}{\mathrm{A}_1 \mathrm{~B}_1}=\frac{\mathrm{GF}}{\mathrm{B}_1 \mathrm{~F}}\) .......................(i)
Again ∆s ABC and A₁B₁C are similar
∴ \(\frac{\mathrm{AB}}{\mathrm{A}_1 \mathrm{~B}_1}=\frac{\mathrm{BC}}{\mathrm{B}_1 \mathrm{C}}\) .....................(ii)
Comparing (i) and (ii), we get
\(\frac{\mathrm{GF}}{\mathrm{B}_1 \mathrm{~F}}=\frac{\mathrm{BC}}{\mathrm{B}_1 \mathrm{C}}\)
Since aperture of mirror is small, therefore, points G and D are close to point P
GF = PF
\(\frac{\mathrm{PF}}{\mathrm{B}_1 \mathrm{~F}}=\frac{\mathrm{BC}}{\mathrm{B}_1 \mathrm{C}}\)
B₁C = PC - PB₁
BC = PB + PC
B₁F = PF - PB₁
\(\frac{\mathrm{PF}}{\mathrm{PF}-\mathrm{PB}_1}=\frac{\mathrm{PB}+\mathrm{PC}}{\mathrm{PC}-\mathrm{PB}_1}\) ........................(iii)
Using sign coventions, we get
PF = +f, PB = -u, PB₁ = v, PC = +2f
Substituting in (iii), we get
\(\frac{+f}{+f-v}=\frac{-u+2 f}{+2 f-v}\)
2f² - vf = -uf + uv + 2f² - 2fv
uf + vf = uv
Dividing both sides by uvf, we get
\(\frac{u f}{u v f}+\frac{v f}{u v f}=\frac{u v}{u v f}\)
\(\frac{1}{v}+\frac{1}{u}=\frac{1}{f}\)

Question 6.
What is meant by linear magnification of a spherical mirror? Derive expressions for it.
Answer:
Linear magnification or simply magnification of a spherical mirror is the ratio of the size of the image formed by the mirror to the size of the object.
It is represented by m.
Thus
m = \(\frac{\text { size of image }\left(h_2\right)}{\text { size of object }\left(h_1\right)}=\frac{\mathrm{A}_1 \mathrm{~B}_1}{\mathrm{AB}}\)
Fig. LAQ 4 or 5, ∆s ABP and A₁B₁P are similar.
\(\frac{\mathrm{A}_1 \mathrm{~B}_1}{\mathrm{AB}}=\frac{\mathrm{PB}_1}{\mathrm{~PB}}\)
In case of concave mirror. Using new cartesian sign conventions,
A₁B₁ = -h₂, AB = +h₁
PB₁ = -v, PB = -u
∴ \(\frac{-h_2}{h_1}=\frac{-v}{-u}=\frac{v}{u}\)
∴ m = \(\frac{h_2}{h_1}=-\frac{v}{u}\)
In case of a convex mirror, using new cartesian sign conventions,
A₁B₁ = +h₂, AB = +h₁
PB₁ = +v, PB = -u
∴ \(\frac{h_2}{h_1}=\frac{v}{-u}\)
∴ m = \(\frac{h_2}{h_1}=-\frac{v}{u}\)
When m > 1, image formed in enlarged.
When m < 1, image formed in diminished.
Again, when m is +ve, image must be erect (i.e. virtual).
When m is -ve, image must be inverted (i.e. real)
Other formulae for magnification.
From mirror formula,
\(\frac{1}{u}+\frac{1}{v}=\frac{1}{f}\)
Multiplying both sides by v,

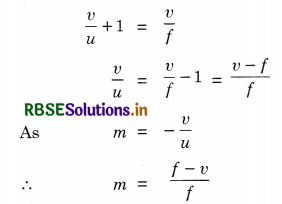
Again, multiplying both sides of mirror formula by u,

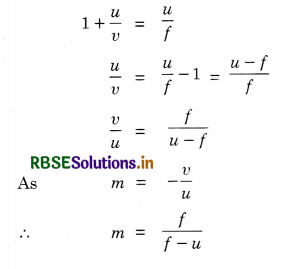
Hence m = \(-\frac{v}{u}=\frac{f-v}{f}\)
= \(\frac{f}{f-u}\)

Question 7.
State and explain the phenomenon of refraction of light with examples.
Answer:
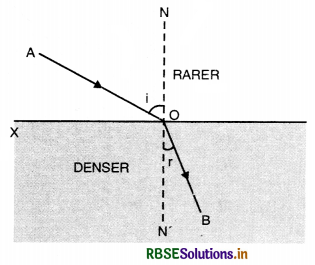
Refraction. The phenomenon of bending of rays of light as they pass from one medium into another is called refraction of light.
Let a ray AO goes from optically rarer medium to an optically denser medium (Fig. LAQ 7 (a)). It is found that most of light passes through the denser medium but it bends towards the normal along OB. This bending of light is called refraction.
∠AON = i, which the incident ray makes with the normal is called angle of incidence.
∠BON' = r, which refracted ray makes with the normal is called angle of refraction.
Water is called optically denser medium and air is called optically rarer medium.
As ray of light goes from optically rarer medium to optically denser medium, it bends towards the normal and when the ray goes from denser medium to rarer medium, it bends away from the normal.


Illustrative Examples
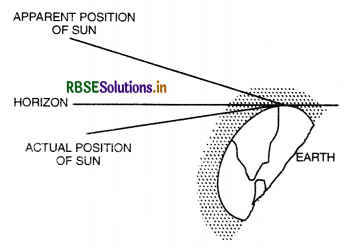
1. Atmospheric Refraction. Rays of light coming from the sun through space bend very slightly towards the normal. The density of air is higher near the surface of the earth and gradually becomes less higher up. The sun rays, therefore, follow a curved path as they enter the atmosphere. The angle through which the rays actually bend is not more than 2°, but this is greater than the sun’s angular diameter so that the sun appears higher on the horizon than it really is. The sun, therefore, appears to set several minutes after it has actually sunk below the horizon, and can be seen a few minutes before it actually rises above the horizon. Fig. LAQ 7 (b).

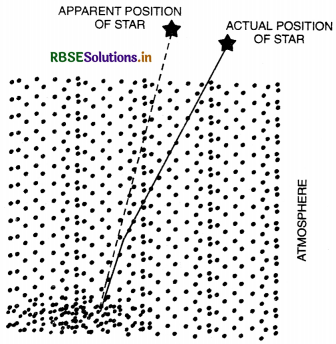
2. Twinkling of Stars. Unless a star is directly above and the rays from it are normal to the atmosphere, atmospheric refraction causes an angular displacement of nearly 1/2° and a star is not where it appears to be Fig. LAQ 7 (c). This effect has to be taken into account by astronomers and navigators.

The atmosphere consists of several moving masses of air, some hot and some cold, some dense and some rarer. When light from a distant star enters the Earth's atmosphere, it is bent as it passes from one mass of air to another. The masses themselves are in motion. This gives rise to the twinkle in stars.

Question 8.
State laws of refraction. Deduce Snell's law.
Answer:
Laws of refraction
1. Incident ray, refracted ray and the normal all lie in one plane.
2. Ratio of sine of angle of incidence to the sine of angle of refraction is constant.
\(\frac{\sin i}{\sin r}\) = constant = ¹µ₂
This constant denoted by is called refractive index of medium 2 (in which refracted ray lies) w.r.t. medium 1 (in which incident ray lies).
This law is also called Snell's law.
Let us consider refraction of light as a plane beam of light passing from air to water. (Fig. LAQ 8).

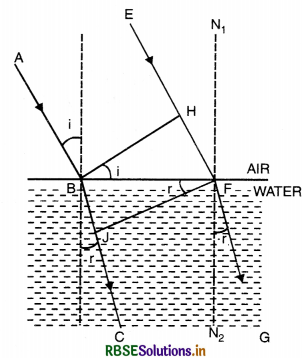
The incident rays AB, EF make an angle i at B, F with the normal to the plane separating air and water. The refracted rays BC and FG are at angle r with respect to the normal, r is the angle of refraction. BH is normal to EF and FJ normal to BC. Note that the incident ray, the refracted ray and the normal to the plane at the point of incidence lie in the same plane. The phase of the plane light wavefront is the same all along BH (in air) as also along the refracted waterfront JF (in water). Therefore, by the time the ray HF travels in air, the corresponding ray BJ travels in water.
∠HBF = i and ∠BFJ = r
In ∆ HBF, sin i = \(\frac{\mathrm{HF}}{\mathrm{BF}}\)
In ∆ BFJ, sin r = \(\frac{\mathrm{BJ}}{\mathrm{BF}}\)
Therefore, \(\frac{\sin i}{\sin r}=\frac{\mathrm{HF}}{\mathrm{BJ}}=\frac{v_1 t}{v_2 t}\) = ¹µ₂
where \(\frac{v_1}{v_2}\) = ¹µ₂ the refractive index of water with respect to air.

Question 9.
State the principle of reversibility of light. Hence show that ^aµ_b = \(\frac{1}{{ }^b \mu_a}\).
Answer:
Principle. When final path of a ray of light after any number of reflections and refractions is reversed, the ray retraces back its entire path.
In Fig. LAQ 9 a ray of light travelling along AO in medium a is refracted along OB in medium b, at the interface XY.
Let ∠AON = i and ∠BON' = r
For incident ray
From Snell's law of refraction,
\(\frac{\sin i}{\sin r}\) = ^aµ_b ............................(1)
Let a plane mirror M be held ⊥ to OB. The ray retraces its path and emerges along OA.
For the reversed beam
Angle of incidence i = angle of refraction r.

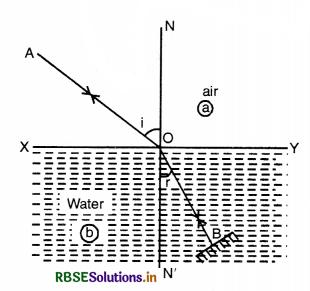
According to Snell's law,
\(\frac{\sin r}{\sin i}\) = ^bµ_a ...........................(2)
Multiplying (1) and (2),
\(\frac{\sin i}{\sin r} \times \frac{\sin r}{\sin i}\) = ^aµ_b x ^bµ_a
i.e. 1 = ^aµ_b x ^bµ_a
or ^aµ_b = \(\frac{1}{b \mu_a}\)

Question 10.
Show that ray of light emerging out from glass slab is parallel to incident light.
Or
Discuss refraction through a glass slab and show that emergent ray is parallel to the incident ray but displaced.
Answer:
Refraction through glass slab. Let a ray of light travel from one medium to a second medium and then to a third medium and refraction occurs at both the interfaces. Figure LAQ 10 traces the path of light as it travels through a parallel glass slab.
At point B
From Snell's law, we have
\(\frac{\sin i}{\sin r}\) = ^aµ_g .............................(1)
Since this ray emerges from the glass slab at point C making angle of emergence 'e', so

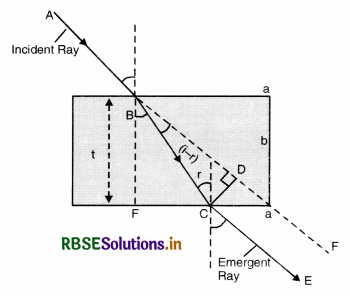
At Point C
From Snell's law, we have
\(\frac{\sin r}{\sin e}\) = ^gµ_a .........................(2)
Multiplying (1) and (2), we get
\(\frac{\sin i}{\sin r} \times \frac{\sin r}{\sin e}\) = ^aµ_g x ^gµ_a
or \(\frac{\sin i}{\sin e}\) = 1 [∵ ^aµ_g x ^gµ_a = 1]
or sin i = sin e
or i = e
i.e. incident and emergent rays are parallel but displaced.

Question 11.
Discuss the refraction of light through a compound slab and show that ^aµ_g = ^aµ_w x _wµ_g.
Answer:
Let us consider a compound slab made of two transparent media say water (w) and glass (g) bounded by parallel faces as shown in Fig. Let this compound slab be held in air (a).

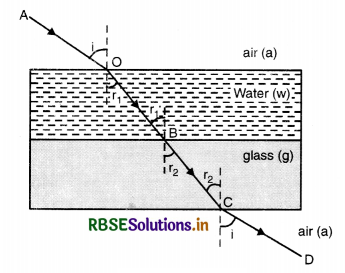
A ray AO incident on the slab at O making an angle of incidence i and is refracted at angle r₁ along OB. At point B, it is again refracted at angle r₂ and finally refracted at C making an angle of refraction i at C because the medium on both sides of the slab is the same. So
At point O
From Snell's law, we have
\(\frac{\sin i}{\sin r_1}\) = ^aµw ..............................(1)
At point B
\(\frac{\sin r_1}{\sin r_2}\) = ^wµ_g .........................(2)
AT point C
From Snell's law, we have
\(\frac{\sin r_2}{\sin i}\) = ^gµ_a ........................(3)
Multiplying eqns. (1), (2) and (3), we get
\(\frac{\sin i}{\sin r_1} \times \frac{\sin r_1}{\sin r_2} \times \frac{\sin r_2}{\sin i}\) = ^aµ_w x ^wµ_g x ^gµ_a
or 1 = ^aµ_w x ^wµ_g x ^gµ_a
or ^aµ_w x ^wµ_g = \(\frac{1}{{ }^g \mu_a}\)
or ^aµ_w x ^wµ_g = ^aµ_g [∵ ^aµ_g = \(\frac{1}{{ }^g \mu_a}\)]
or ^aµ_g = ^aµ_w x ^wµ_g.

Question 12.
Show that apparent depth of a water tank is less than real depth.
Answer:
Consider a point 0 at the bottom of a tank. A ray OA falls normally on XY and goes without refraction. Another ray OB is incident at B and suffers refraction. Two rays of light appear to meet at D.
When seen through water, O appears at D. Therefore, apparent depth = AD, which is less than the real depth OA.

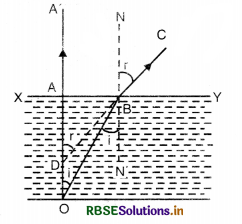
∠AOB = ∠OBN' = i (alt. ∠s)
∠ADB = ∠NBC = r (Corres. ∠s)
In ∆ OAB,
sin i = \(\frac{\mathrm{AB}}{\mathrm{OB}}\)
In ∆ DAB,
sin r = \(\frac{\mathrm{AB}}{\mathrm{DB}}\)
∴\( \frac{\sin i}{\sin r}=\frac{\mathrm{AB}}{\mathrm{OB}} \cdot \frac{\mathrm{DB}}{\mathrm{AB}}=\frac{\mathrm{DB}}{\mathrm{OB}}\) ................(1)
From Snell's law, we have
\(\frac{\sin i}{\sin r}\) = ^wµ_a
Using eq. (1), we get
\(\frac{\mathrm{DB}}{\mathrm{OB}}\) = ^wµ_a
When angle i and r are small, point B is close to A.
So DB ≃ DA and OB ≃ OA
So \(\frac{\mathrm{DA}}{\mathrm{OA}}\) = ^wµ_a
or ^aµ_w = \(\frac{\mathrm{OA}}{\mathrm{DA}}\)
= \(\frac{\text { Real depth }}{\text { Apparent depth }}\)
or \(\frac{\mu_w}{\mu_a}=\frac{\text { Real depth }}{\text { Apparent depth }}\) [∵ ^aµ_w = \(\frac{\mu_w}{\mu_a}\)]
If refractive index of air is 1 (i.e. µ_a = 1) and writing the refractive index of water as µ (i.e. µ_w = µ)
Then
Refractive index of water,
µ = \(\frac{\text { Real depth in water }}{\text { Apparent depth in water }}\)

Question 13.
(a) Explain total internal reflection. What are its conditions?
(b) Give illustrative examples for total internal reflection.
Answer:
(a) Total internal reflection. When a ray of light travels from denser medium to rarer medium, the refracted ray is bent away from the normal

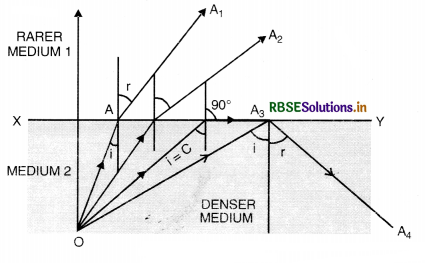
Consider an object in the denser medium. A ray OA incident on XY bends away from the normal. As the angle of incidence is increased, the angle of refraction goes on increasing. For a certain angle of incidence, the refracted ray becomes parallel to the surface XY or angle of refraction is 90°. This angle of incidence in the denser medium for which the angle of refraction is 90° in the rarer medium is called critical angle.

When the angle of incidence is further increased, the ray is not refracted but is totally reflected back in the denser medium. This phenomenon is called total internal reflection. Thus the total internal reflection is the phenomenon in which a ray of light from denser to rarer medium strike the interface at an angle greater than critical angle for that medium, then it is totally reflected back into denser medium.

Conditions for total internal reflection
(i) Ray of light must proceed from denser medium to rarer medium and
(ii) Angle of incidence should be greater than critical angle.

Relation between refractive index and critical angle
Let C be critical angle for any two media '1' and ‘2’. Let media ‘2’ is denser than '1'. We know that at critical angle, the angle of refraction is 90°.
Thus when a ray incident at the interface of two media at angle C, then
For Snell's law,
\(\frac{\sin C}{\sin 90^{\circ}}\) = ²µ₁
or sin C = ²µ₁
or ¹µ₂ = \(\frac{1}{\sin C}\)
If medium '1' is air having refractive index 1 and the denser medium 2 has refractive index µ, then the above equation becomes
µ = \( \frac{1}{\sin C}\)

Illustrative Examples
1. Mirror effect in test tube. An empty test tube placed slanting in water and viewed from above will appear mirrored because total internal reflection takes place between the water-air interface outside the test tube (Fig. LAQ 13 (a))
If the tube is filled with water, it no longer gives the miror effect.

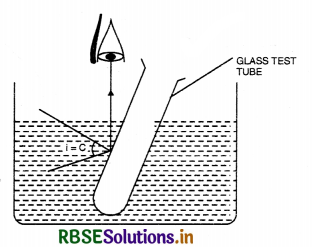
2. Mirage. The mirage or optical illusion caused by the total internal reflection of light at layers of air of different densities.
In the desert, the sand becomes very hot during the day time and it rapidly heats the layer of air which is in its contact. The layer of air, on being heated, expands and its density decreases. As a result, the successive upward layers are denser than those below them.

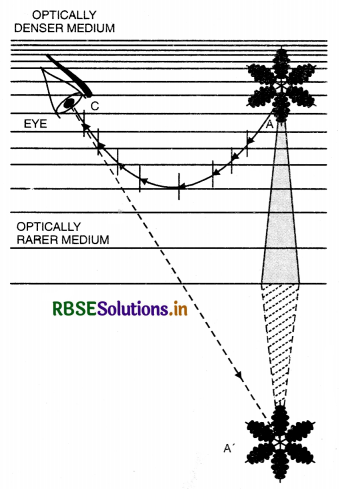
When a beam of light travelling from the top of a tree enters a rarer layer, it is refracted away from the normal. As a result, at the surface of separation of successive layers of air, each time the angle of incidence increases and ultimately a stage is reached when the angle of incidence becomes greater than the critical angle between the two layers. At the stage, the incident ray suffers total internal reflection and is directed upwards. (Fig. LAQ 13 (b)). When this reflected beam of light enters the eye of the observer, it appears as if an inverted image of the tree is formed and the same looks like a pool of water to the observer.

Totally Reflecting Prisms. We know the critical angle of glass is aborit 41°. If prism is so designed that its angles are 45°, 45°, 90°, it is said to be a totally reflecting prism. Its principal section is a right-angled isosceles triangle. Since the rays are incident at angle of 45° i.e., greater than critical angle of glass (42° nearly), the rays suffer total internal reflection and the plane surfaces act as mirrors.


In Figure LAQ 13 (c), the reflecting face ac acts as a mirror which can produce a deviation of 90°. If we use the prism as shown in figure LAQ 13 (d). both faces ab and be act as mirrors. The emergent rays get inverted and also a deviation of 180° is introduced between incident rays and emergent rays. If prism is placed as in Fig. LAQ 13 (e), the face acts as a mirror and inverts the image without producing any deviation. Such prisms are called erecting prisms.

Question 14.
What are fibre optics? Mention some of their applications.
Or
State principle of optical fibre and write their applications.
Answer:
Principle. The working of optical fibre is based on the phenomenon of total internal reflection. Optical fibres consist of many thousands of verjr long fine quality, glass/quartz fibres. They are coated with a thin layer of a material of low refractive index. For example, the strand can be 0.0001 cm in diameter and the refractive index of the main fibre 1.7 and that of coating 1.5 (Fig. LAQ 14).

When the light is incident on one end of the fibre at a small angle, the light passes inside. It undergoes repeated total internal reflections along the fibre and finally comes out. The angle of incidence here is larger than the critical angle of the fibre material with respect of its coating. Even if the fibre is bent, the light can easily travel through along the fibre.

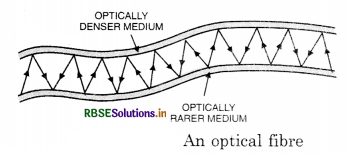
Uses of Optical Fibre

• A bundle of optical fibres can be used as a ‘light pipe’ in medical and optical examination called endoscopy.
• It can also be used for optical signal transmission.
• Optical fibres have also been used for transmission and receiving electrical signals which are converted to light by suitable transducers. The main requirement is that thereby very little absorption of light as it travels for long distances inside the optical fibre. This has been achieved by purification and special preparation of materials such as quartz.

Question 15.
What is spherical refracting surface? What do you mean by pole, centre of curvature, radius of curvature, aperture and principal axis.
Answer:
Spherical refracting surface. A spherical refracting surface is formed when the refracting surface forms a part of a sphere. It is of two types:
(i) Convex spherical surface. If the convex surface is towards the rarer medium, it is called convex spherical refracting surface, Fig. LAQ 15 (a).
(ii) Concave spherical surface. If the concave 1 surface is towards the rarer medium, it is called concave spherical refracting surface, Fig. LAQ 15 (b).

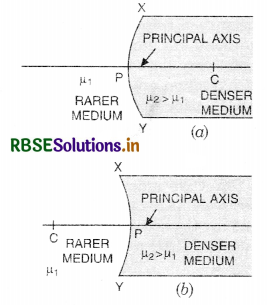
1. Pole (P). The centre of spherical refracting 1 surface is called its pole.
2. Centre of curvature (C). It is the centre of the | sphere from which the curved surface is taken a part.
3. Radius of curvature (PC). It is the radius of the sphere from which the curved surface is taken a part.
4. Aperture (XY). The diameter of the curved surface is called its aperture.
5. Principal axis. The principal axis is the line joining the pole and centre of curvature of refracting surface.

Question 16.
Derive the relation between distance of object, distance of image and radius of curvature of a convex spherical surface when refraction takes place from 1 rarer medium of refractive index µ₁ to a denser medium of refractive index µ₂ and the image produced is real. State assumptions and conventions of sign used.
Or
Derive the expression
\(-\frac{\mu_1}{\mathbf{u}}+\frac{\mu_2}{v}=\frac{\mu_2-\mu_1}{\mathbf{R}}\)
when refraction occurs from rarer to denser medium at convex spherical refracting surface (µ₁ < µ₂) and real image is formed.
Answer:
Sign Conventions

1. All the distances are to be measured from the pole of spherical surface.
2. The distances measured in the same direction as the incident light are taken as positive.
3. Distances measured in the direction opposite to the direction of the incident light are taken as negative.

Asumptions:

1. Object is a point object lying on the principal axis.
2. The aperture of refracting edge is small.
3. The indcident ray from the object strikes the surface at a point very close to point so that angles of incidence and refraction are very small.

Derivation. Consider a point object O be situated on the principal axis of the convex spherical surface. Let P be pole and C be centre of curvature and PC = R be the radius of curvature of the surface. Let µ₁ and µ₂ be refractive indexes of rarer and denser medium respectively as shown in the figure.
Let incident ray OA refracts at point A and bends towards the normal CAN and real image is formed at I.
From Snell’s law, for small i and r, we have
\(\frac{\sin i}{\sin r}=\frac{i}{r}=\frac{\mu_2}{\mu_1}\)
or µ₁ i = µ₂ r ..............................(1)

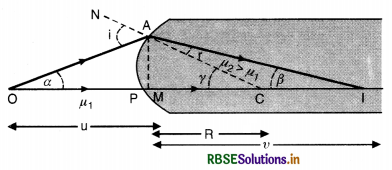
In ∆ AOC,
i = α + γ
In ∆ AIC,
γ = r + ß
or r = γ - ß
Putting the values of i and r in equation (1), we get
µ₁ (α + γ) = µ₂ (γ - ß)
or µ₁α + µ₁γ = µ₂γ - µ₂ß
or µ₁α + µ₂ß = (µ₂ - µ₁) γ ...............................(2)
Since α, ß and γ are small, so they can be replaced by their tangents. So equation (2) becomes
µ₁ tan α + µ₂ tan ß = (µ₂ - µ₁) tan γ
or µ₁ \(\frac{\mathrm{AM}}{\mathrm{MO}}\) + µ₂ \(\frac{\mathrm{AM}}{\mathrm{MI}}\) = (µ₂ - µ₁) \(\frac{\mathrm{AM}}{\mathrm{MC}}\)
or \(\frac{\mu_1}{\mathrm{MO}}+\frac{\mu_2}{\mathrm{MI}}=\frac{\mu_2-\mu_1}{\mathrm{MC}}\)
Since M is very close to the pole P,
so MO ≃ PO, MI ≃ PI and MC ≃ PC
∴ \(\frac{\mu_1}{\mathrm{PO}}+\frac{\mu_2}{\mathrm{PI}}=\frac{\mu_2-\mu_1}{\mathrm{PC}}\)
Using sign conventions,
PO = -u, PI = v and PC = R,
we get

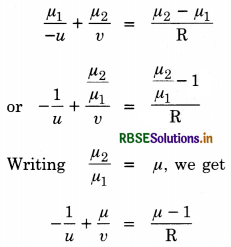
Question 17. 
Derive the relation between u, v and R at a convex spherical refracting surface, when the ray travels from rarer to denser medium and virtual image is formed.
Or
Derive the expression
\(-\frac{\mu_1}{u}+\frac{\mu_2}{v}=\frac{\mu_2-\mu_1}{\mathbf{R}}\),
when refraction occurs from rarer to denser medium at convex spherical refracting surface (µ₁ < µ₂) and virtual image is formed.
Answer:
Let a point object 0 be situated on the principal axis of the convex spherical surface. Let P be pole and C be centre of curvature and PC = R be the radius of curvature. Let µ₁ and µ₂ be refractive indices of rarer and denser medium respectively as shown in the figure.

The incident ray OA refracts at A and bends towards the normal along AQ and when produced in the backward direction, it meets at point I on the principal axis. Then I will be the virtual image of point O.
From Snell's law for small i and r

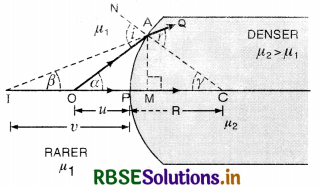
\(\frac{\sin i}{\sin r}=\frac{i}{r}=\frac{\mu_2}{\mu_1}\)
or µ₁i = µ₂r .............................(1)
In ∆ AOC,
i = α + γ
In ∆ AIC,
r = ß + γ
Putting the values of i and r in Eq. (1), we get
µ1 (α + γ) = µ₂ (ß + γ)
or µ₁α + µ₁γ = µ₂ß + µ₂γ
or µ1α - µ₂ß = (µ₂ - µ₁) γ
Since α, ß and γ are small, so they can be replaced by their tangents.
Hence 
µ₁ tan α - µ₂ tan ß = (µ₂ - µ₁) tan γ
or µ₁ \(\frac{\mathrm{AM}}{\mathrm{MO}}\) - µ₂ \(\frac{\mathrm{AM}}{\mathrm{MI}}\) = (µ₂ - µ₁) \(\frac{\mathrm{AM}}{\mathrm{MC}}\)
or \(\frac{\mu_1}{\mathrm{MO}}+\frac{\mu_2}{\mathrm{MI}}=\frac{\mu_2-\mu_1}{\mathrm{MC}}\)
Since M is very close to the pole P,
so MO ≃ PO, MI ≃ PI and MC ≃ PC
∴ \(\frac{\mu_1}{\mathrm{PO}}+\frac{\mu_2}{\mathrm{PI}}=\frac{\mu_2-\mu_1}{\mathrm{PC}}\)
Using sign conventions,
PO = -u, PI = v and PC = R, we get

Question 18.
Discuss briefly refraction from rarer to denser medium at a concave spherical refracting surface.
Or
Prove that:
\(-\frac{\mu_1}{u}+\frac{\mu_2}{v}=\frac{\mu_2-\mu_1}{\mathrm{R}}\),
when refraction occurs from rarer to denser medium at a concave spherical refracting surface.
Answer:
Let a point object O be situated on the principal axis of a concave spherical refracting surface. Let P be pole and C be centre of curvature and PC = R be radius of curvature. Let µ₁ and µ₂ be refractive indices of rarer and denser medium respectively as shown in the figure. Let incident ray OA refracts at A and bends towards the normal along AQ and when produced in backward direction it meets at point I. So I is the virtual image of point object O.

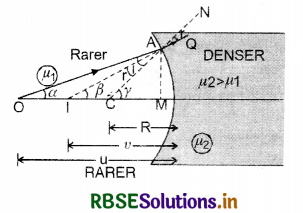
From Snell's law for small i and r, we have
\(\frac{\sin i}{\sin r}=\frac{i}{r}=\frac{\mu_2}{\mu_1}\)
or µ₁ i = µ₂ r ........................(1)
In ∆ AOC,
γ = i + α
or i = γ - α
In ∆ AIC,
γ = r + ß
or r = γ - ß.
Putting the values of i and r in Eq. (1), we get
µ₁(γ - α) = µ₂(γ - ß)
or µ₁γ - µ₁α = µ₂γ - µ₂ß
or -µ₁α + µ₂ß = (µ₂ - µ₁) γ
Since α, ß and γ are small, so they can be replaced by their tangents, So
-µ₁ tan α + µ₂ tan ß = (µ₂ - µ₁) tan γ
or -µ₁ \(\frac{\mathrm{AM}}{\mathrm{MO}}\) + µ₂ \(\frac{\mathrm{AM}}{\mathrm{MI}}\) = (µ₂ - µ₁) \(\frac{\mathrm{AM}}{\mathrm{MC}}\)
or \(\frac{\mu_1}{\mathrm{MO}}+\frac{\mu_2}{\mathrm{MI}}=\frac{\mu_2-\mu_1}{\mathrm{MC}}\)
Since M is very close to the pole P, so
MO ≃ PO, MI ≃ PI and MC ≃ PC
∴ \(\frac{\mu_1}{\mathrm{PO}}+\frac{\mu_2}{\mathrm{PI}}=\frac{\mu_2-\mu_1}{\mathrm{PC}}\)
Using sign conventions,
PO = -u, PI = -v and PC = -R,
we get

Question 19.
What do you mean by a lens? What are concave and convex lenses? What do you mean by Principal axis, Optical centre and Principal focus and focal length of a lens?
Answer:
Lens. A lens is a portion of a transparent medium bounded by two spherical surfaces or one spherical and other plane surface. Lenses are divided in following classes:

• If both the surfaces are convex, we call it a convex lens or convergent lens as shown in fig. LAQ 19 (a).
• If both the surfaces are concave, we call it a concave lens or divergent lens as shown in figure. LAQ 19 (b).
• If one surface is plane and other is concave (or convex), we call it plano-concave (or piano-convex) lens as shown in fig. LAQ 19 (c).

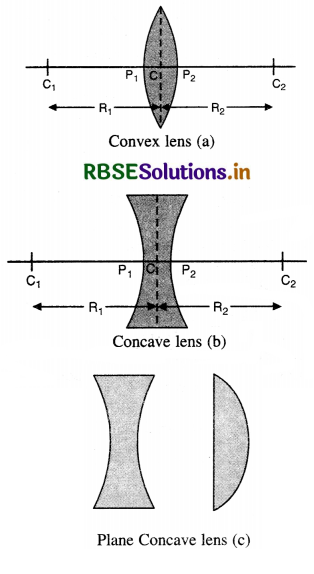
A double convex or double concave lens has two radii of curvature namely R₁ and R₂ as shown in Figs. LAQ 19 a & b.
1. Principal axis. It is a straight line passing through the centre of curvature of two surfaces of a lens.
2. Optical centre (C). Optical centre is a point inside or outside the lens on the principal axis such that any ray of light passing through this point moves undeviated.
3. Principal focus. A narrow beam of light incident on a lens in a direction parallel to its principal axis, after refraction through the lens, the rays converge to a point (in case of convex lens) or appear to diverge from a point (in case of concave lens) on the principal axis. This point is called principal focus of the lens. Clearly, principal focus is a real point in case of a convex lens and a virtual point in case of a concave lens as shown in the figure. 19 (d, e).

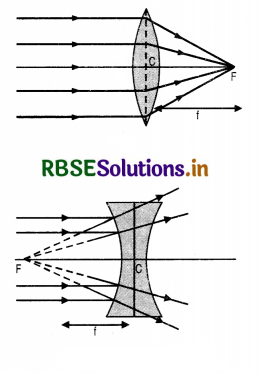
4. Focal length (f). The distance of principal focus from the optical centre of the lens is called focal length of the lens. In the above figure, the focal length f = CF.

Question 20.
What is a lens maker's fromula? Why it is called so? Derive it for a thin convex lens.
Or
Show by a diagram the image formation of a point object by a thin double convex lens having radii of  curvature R₁ and R₂. Hence derive the formula \(\frac{1}{f}=(n-1)\left[\frac{1}{R_1}-\frac{1}{R_2}\right]\), where f is the focal length and n is refractive index of material of the lens.

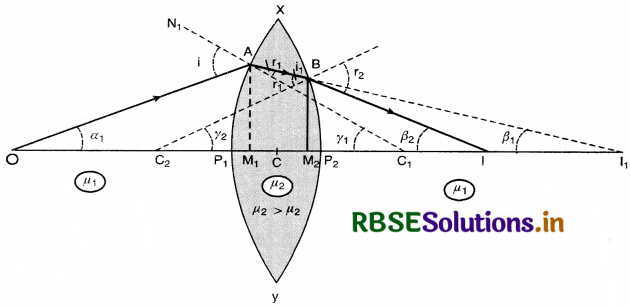
Answer:
Lens maker’s formula
It is given by
\(\frac{1}{f}=(\mu-1)\left(\frac{1}{\mathrm{R}_1}-\frac{1}{\mathrm{R}_2}\right)\)
This formula relates the focal length of the lens of the radii of curvature of the surfaces and the refractive index of the material of the lens.
Why is it called lens maker’s formula?
It is so called because this formula is used by the manufacturers to prepare lenses of desired focal lengths.

Sign conventions

• All the distances are measured from the optical centre of lens.
• Distance measured in the direction of incident light is taken +ve.
• Distance measured in the direction opposite to the direction of incident light is taken -ve.

Assumptions

1. Object is a point object.
2. Lens is thin so that distances are measured from the poles of its surfaces.
3. The aperture of the lens is small.
4. Angles of incidence and refraction are small.

Let C₁ and C₂ be centres of curvature of two spherical surfaces XP₁Y and XP₂Y with optical centre C. Let µ₂ be the refractive index of the material of the lens and µ₁ that of the medium surrounding the lens where µ₂ > µ₁.

Refraction at surface XP₁Y
Let a ray OA starts from the point object O which is placed on the principal axis of the convex lens and it refracts into the denser medium at point A. The refracted ray AB goes undeviated to meet at point I₁, if the lens material were continued. Then I₁ would be the real image of point object O.
From Snell’s law for small i₁ and r₁, we have
\(\frac{\sin i_1}{\sin r_1}=\frac{i_1}{r_1}=\frac{\mu_2}{\mu_1}\)
or µ₁ i₁ = µ₂ r₁ ...........................(1)
In ∆ AOC1,
i₁ = α₁ + γ₁
In ∆ AI₁C₁,
γ₁ = ß₁ + r₁
or r₁ = γ₁ - ß₁
Putting the values of i₁ and r₁ in Eq.(1), we get
µ₁ (α₁ + γ₁) = µ₂ (γ₁ - ß₁)
or µ₁α₁ + µ₁γ₁ = µ₂γ₁ - µ₂ß₁
or µ₁α₁ + µ₂ß¹ = (µ₂ - µ₁) γ¹
Since α₁, ß₁ and γ₁ are small, so they can be replaced by their tangents.
∴ µ₁ tan α₁ + µ₂ tan ß₁ = (µ₂ - µ₁) tan γ₁
or µ₁\(\frac{\mathrm{AM}_1}{\mathrm{M}_1 \mathrm{O}}\) + µ₂ \(\frac{\mathrm{AM}_1}{\mathrm{M}_1 \mathrm{I}_1}\) = (µ₂ - µ₁) \(\frac{\mathrm{AM}_1}{\mathrm{M}_1 \mathrm{C}_1}\)
or \( \frac{\mu_1}{\mathrm{M}_1 \mathrm{O}}+\frac{\mu_2}{\mathrm{M}_1 \mathrm{I}_1}=\frac{\mu_2-\mu_1}{\mathrm{M}_1 \mathrm{C}_1}\)
Since the lens isa very thin,
so M₁O ≃ CO, M₁I₁ ≃ CI₁
and M₁C₁ ≃ CC₁
∴ \(\frac{\mu_1}{\mathrm{CO}}+\frac{\mu_2}{\mathrm{CI}_1}=\frac{\mu_2-\mu_1}{\mathrm{CC}_1}\) .............................(2)

Refraction at surface XP₂Y
Actually the lens is not continuous and the ray AB suffer refraction at B and finally meet at I. So I is the real image of the virtual object I₁ (placed in the material of the lens).
From Snell’s law for small i₂ and r₂, we have
\(\frac{\sin i_2}{\sin r_2}=\frac{i_2}{r_2}=\frac{\mu_1}{\mu_2}\)
or µ₁r₂ = µ₁i₂ ..........................(3)
In ∆ BC₂I₁,
i₂ = ß₁ + γ₂
In ∆ BC₂I, r² = ß² + γ²
Putting the value of i₂ and r₂ in Eq. (3), we get
µ₁ (ß₂ + γ₂) = µ₂ (ß₁ + γ₂)
or µ₁ß₂ + µ₁γ₂ = µ₂ß₁ + µ₂γ₂
or µ₁ß₂ - µ₂ß₁ = (µ₂ - µ₁) γ₂
Since ß₂, ß₁ and γ₂ are small, so they can be replaced by their tangents, so
µ₁ tan ß₂ - µ₂ tan ß₁ = (µ₂ - µ₁) tan γ₂
or µ₁ \(\frac{\mathrm{BM}_2}{\mathrm{M}_2 \mathrm{I}}\) - µ₂ \(\frac{\mathrm{BM}_2}{\mathrm{M}_2 \mathrm{I}_1}\) = (µ₂ - µ₁) \(\frac{\mathrm{BM}_2}{\mathrm{M}_2 \mathrm{C}_2}\)
or \(\frac{\mu_1}{\mathrm{M}_2 \mathrm{I}}-\frac{\mu_2}{\mathrm{M}_2 \mathrm{I}_1}=\frac{\mu_2-\mu_1}{\mathrm{M}_2 \mathrm{C}_2}\)
Since the lens is thin, So
M₂I ≃ CI, M₂I₁ ≃ CI₁ and M₂C₂ ≃ CC₂
∴ \(\frac{\mu_1}{\mathrm{CI}}-\frac{\mu_2}{\mathrm{CI}_2}=\frac{\mu_2-\mu_1}{\mathrm{CC}_2}\) ..............................(4)
Adding Eq. (2) and (4), we get
\(\frac{\mu_1}{\mathrm{CO}}+\frac{\mu_1}{\mathrm{CI}}=\left(\mu_2-\mu_1\right)\left[\frac{1}{\mathrm{CC}_1}+\frac{1}{\mathrm{CC}_2}\right]\)
Dividing both sides by µ₁, we get
\(\frac{1}{\mathrm{CO}}+\frac{1}{\mathrm{CI}}=\left(\frac{\mu_2}{\mu_1}-1\right)\left(\frac{1}{\mathrm{CC}_1}+\frac{1}{\mathrm{CC}_2}\right)\)
Using sign conventions,
CO = -u, CI = v, CC₁ = R₁ and CC₂ = -R₂ and writing \(\frac{\mu_2}{\mu_1}\) = µ, we get
\(\frac{1}{-u}+\frac{1}{v}=(\mu-1)\left(\frac{1}{\mathrm{R}_1}+\frac{1}{-\mathrm{R}_2}\right)\)
or \(\frac{1}{-u}+\frac{1}{v}=(\mu-1)\left(\frac{1}{\mathrm{R}_1}-\frac{1}{\mathrm{R}_2}\right)\)
Since \(-\frac{1}{u}+\frac{1}{v}=\frac{1}{f}\), where f is the focal length of the lens
∴ \(\frac{1}{f}=(\mu-1)\left(\frac{1}{\mathrm{R}_1}-\frac{1}{\mathrm{R}_2}\right)\)
Note: This is the required lens maker's formula for thin convex lens. If n is taken as refractive index of the material of lens then
\(\frac{1}{f}=(n-1)\left[\frac{1}{\mathrm{R}_1}-\frac{1}{\mathrm{R}_1}\right]\)

Question 21.
Derive lens maker's formula for a thin concave lens.
Answer:
Let C₁ and C₂ be centres of curvature of two spherical surfaces of the concave lens having optical centre C as shown in the figure LAQ 21. Let µ₂ be the refractive index of the material of the lens and µ₁ that of medium surrounding the lens (µ₂ > µ₁)

Refraction at surface X₁Y₁
Let a ray OA starts from the point object O which is placed on the principal axis of the concave lens and it refracts into the denser medium at point A. The refracted ray AB goes undeviated if the lens material were continuous. When AB is produced back it meets at I₁. So I₁ would be the virtual image of point object O.

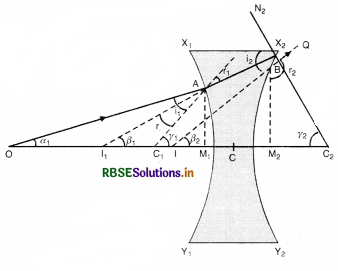
From Snell's law for small i₁ and r₁, we have
\(\frac{\sin i_1}{\sin r_2}=\frac{i_1}{r_1}=\frac{\mu_2}{\mu_1}\)
or µ₁i₁ = µ₂r₁ ..............................(1)
In ∆ AOC₁,
γ₁ = i₁ + α₁
or i₁ = γ₁ - α₁
In ∆ AI₁C₁,
γ₁ = ß₁ + r₁
or r₁ = γ₁ - ß₁
Putting the values of i₁ and r₁ in Eq.(1), we get
µ₁ (γ₁ - α₁) = µ₂ (γ₁ - ß₁)
or µ₁γ₁ - µ₁α₁ = µ₂γ₁ - µ₂ß₁
or -µ₁α₁ + µ₂ß₁ = (µ₂ - µ₁)γ₁
Since α₁, ß₁ and γ₁ are small, so they can be replaced by their tangents
so -µ₁ tan α₁ + µ₂ tan ß₁ = (µ₂ - µ₁) tan γ₁
or -µ₁\(\frac{\mathrm{AM}_1}{\mathrm{M}_1 \mathrm{O}}\) + µ₂\(\frac{\mathrm{AM}_1}{\mathrm{M}_1 \mathrm{I}_1}\) = (µ₂ - µ₁) \(\frac{\mathrm{AM}_1}{\mathrm{M}_1 \mathrm{C}_1}\)
or \(-\frac{\mu_1}{\mathrm{M}_1 \mathrm{O}}+\frac{\mu_2}{\mathrm{M}_1 \mathrm{I}_1}=\frac{\left(\mu_2-\mu_1\right)}{\mathrm{M}_1 C_1}\)
Since point M₁ is very close to C, so
M₁O ≃ CO, M₁I₁ ≃ CI₁ and M₁C₁ ≃ CC₁
∴ \(-\frac{\mu_1}{\mathrm{CO}}+\frac{\mu_2}{\mathrm{CI}_1}=\frac{\mu_2-\mu_1}{\mathrm{CC}_1}\) ............................(2)

Refraction at X₂Y₂
Actually the lens material is not continuous and the ray AB suffers refraction at B and bend away from the normal along BQ. When BQ is produced in backward direction, it meets at I on the principal axis and I is the virtual image of virtual object I₁
From Snell's law for small i₂ and r₂, we have
\(\frac{\sin i_2}{\sin r_2}=\frac{i_2}{r_2}=\frac{\mu_1}{\mu_2}\)
or µ₁r₂ = µ₂i₂ ............................(3)
In ∆ BC₂I₁,
i₂ = ß₁ + γ₂
In ∆ BC₂I, r₂ = ß₂ + γ₂
Putting the value of i₂ and r₂ in Eq. (3), we get
µ₁ (ß₂ + γ₂) = µ₂ (ß₁ + γ₂)
or µ₁ß₂ + µ₁γ₂ = µ₂ß₁ + µ₂γ₂
or µ₁ß₂ - µ₂ß₁ = (µ₂ - µ₁) γ₂
Since ß₂, ß₁ and γ₂ are small, so they can be replaced by their tangents. So,
µ₁ tan ß₂ - µ₂ tan ß₁ = (µ₂ - µ₁) tan γ₂
µ₁\(\frac{\mathrm{BM}_2}{\mathrm{M}_2 \mathrm{I}}\) - µ_{2\(\frac{\mathrm{BM}_2}{\mathrm{M}_2 \mathrm{I}_1}\)} = (µ₂ - µ₁) \(\frac{\mathrm{BM}_2}{\mathrm{M}_2 \mathrm{C}_2}\)
or \(\frac{\mu_1}{\mathrm{M}_2 \mathrm{I}}-\frac{\mu_2}{\mathrm{M}_2 \mathrm{I}_1}=\frac{\mu_2-\mu_1}{\mathrm{M}_2 \mathrm{C}_2}\)
Since point M₂ is very close to C, so
\(\frac{\mu_1}{\mathrm{CI}}-\frac{\mu_2}{\mathrm{CI}_1}=\frac{\mu_2-\mu_1}{\mathrm{CC}_2}\) .............................(4)
Adding Eqs.(2) and (4), we get
\(-\frac{\mu_1}{\mathrm{CO}}+\frac{\mu_1}{\mathrm{CI}}=\left(\mu_2-\mu_1\right)\left[\frac{1}{\mathrm{CC}_1}+\frac{1}{\mathrm{CC}_2}\right]\)
Using sign conventions,
CO = -u, CI = v
CC₁ = -R₁ and CC₂ = -R₂

Since \(-\frac{1}{u}+\frac{1}{v}=\frac{1}{f}\), where f is the focal length of the lens.
so \(\frac{1}{f}=(\mu-1)\left(\frac{1}{\mathrm{R}_1}-\frac{1}{\mathrm{R}_2}\right)\)
This is required lens maker's formula for the concave lens.

Question 22.
Distinguish between a real image and a virtual image. Describe the formation of real and virtual images by a convex lens with the help of diagrams at different positions of the object.
Answer:
Real Image. Real image is the image formed due to actual interaction of refracted light rays, and real image can be formed on a screen. Fig. (c), (d), (e)
Virtual Image. Virtual image is the image formed due to apparent interaction of refracted light rays when they are produced in backward directions, and virtual image cannot be obtained on the screen. Fig. (a).

Rules for forming the images by convex lens

• A ray parallel to the principal axis, passes through the principal focus after refraction.
• A ray passing through the principal focus, becomes parallel after refraction.
• A ray passing through the optical centre of the lens goes undeviated after refraction.

Let us discuss following cases:
(1) When object is placed between optical centre and the principal focus of the convex lens.
The incident ray AL which is parallel to the principal axis, passes through the principal focus F after refraction and ray AD which is passing through the optical centre goes undeviated. These two rays when produced in backward direction, meet at B', so A'B' is the virtual image of real object AB.

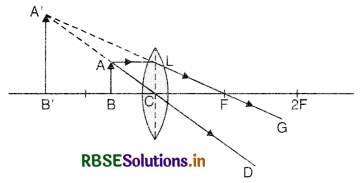
Here the image is virtual, erect, magnified and is formed behind, the object.

(2) When object is placed at the principal focus of the convex lens.
The incident ray AL, which is parallel to the principal axis, passes through the focus F after refraction and ray AD. which passes through the optical centre C, goes undeviated. These two rays are parallel and they meet at infinity. Thus real image of object AB is formed at infinity.

Here the image is real, inverted, highly enlarged and is formed at infinity.

(3) When object is placed between F and 2F
The incident ray AL, which is parallel to the principal axis, passes through the focus P₁ after refraction and ray AA', which passes through the optical centre C, goes undeviated. These two rays meet at point A'. So A'B' is the real image of object AB.

Here the image is real, inverted, magnified and is formed beyond 2F.

(4) When object is placed at 2F
The incident ray AL, which is parallel to the principal axis, passes through the focus F after refraction and ray AA', which passes through the optical centre C goes undeviated. These two rays meet at point A'. So A'B' is the real image of object AB.

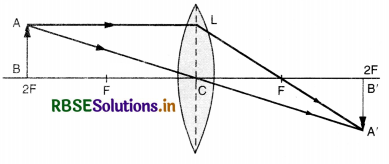
Here the image is real, inverted, equal to the size of object and is formed at 2F on the other side of the lens.

(5) When the object is placed beyond 2F
The incident ray AL, which is parallel to the principal axis, passes through the principal focus F after refraction, and the ray AA' which passes through the optical centre C goes undeviated. These two rays meet at point A'. So'A'B' is the real image of object AB.

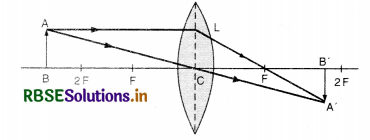
Here, the image is real, inverted, smaller in size and is formed between F and 2F on the other side of the lens.

Question 23.
Describe the formation of image by a concave lens.

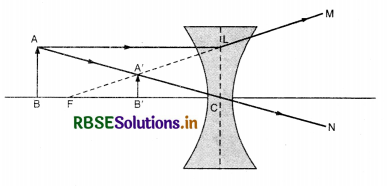
Answer:
Consider a concave lens of focal length F and optical centre C as shown in Fig 9.81. Let a ray of light AL be incident parallel to the principal axis of the concave lens, and is refracted along LM. When this ray is produced in backward direction it meets af F, i.e. the ray LM appears to be coming from the focus F. Other ray AN which passes through the optical centre C of the concave lens, goes undeviated and these two refracted rays meet at A'. So A'B' is the virtual image of object AB.
Here the image is always virtual (independent of position of object), erect, diminished and is formed infront of the lens. If the object is moved closer to the lens, the image moves towards the optical centre and is always formed in front of the lens.

Question 24.
What is a lens formula? Derive an expression for lens formula for a convex lens forming a real image.
Answer:
Lens formula. Lens formula is an equation relating the distance of object, distance of image formed and the focal length of the lens, and is given by
\(-\frac{1}{u}+\frac{1}{v}=\frac{1}{f}\)
where u is the distance of object from optical centre of the lens, v is the distance of image from the optical centre of the lens and f is the focal length of the lens.
When image formed is real
Consider a convex lens of focal length f and optical centre C. Let an object AB be placed perpendicular to the principal axis at a point between F and 2F. The real image of this object A'B' is formed beyond 2F on the other side of the lens. The image is real, inverted and magnified as shown in fig. LAQ 24.

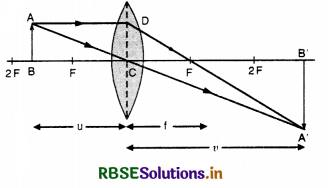
∆ ABC and ∆ AB'C are similar, so we have
\(\frac{\mathrm{A}^{\prime} \mathrm{B}^{\prime}}{\mathrm{AB}}=\frac{\mathrm{CB}^{\prime}}{\mathrm{CB}}\) .........................(1)
∆ DCF and ∆ A'B'F are similar, so we have
\(\frac{\mathrm{A}^{\prime} \mathrm{B}^{\prime}}{\mathrm{DC}}=\frac{\mathrm{FB}^{\prime}}{\mathrm{CF}}\)
But DC = AB
∴ \(\frac{\mathrm{A}^{\prime} \mathrm{B}^{\prime}}{\mathrm{AB}}=\frac{\mathrm{FB}^{\prime}}{\mathrm{CF}}\) ......................(2)
From Eq. (1) and (2), we have
\(\frac{\mathrm{CB}^{\prime}}{\mathrm{CB}}=\frac{\mathrm{FB}^{\prime}}{\mathrm{CF}}\)
or \(\frac{\mathrm{CB}^{\prime}}{\mathrm{CB}}=\frac{\mathrm{CB}^{\prime}-\mathrm{CF}}{\mathrm{CF}}\) ........................(3)
Using sign conventions,
Let CB' = v, CB = -u, CF = f
so Eq. (3) becomes
\(\frac{v}{-u}=\frac{v-f}{f}\)
or vf = -uv + uf
Dividing both sides by u v f, we get

Question 25.
Derive lens formula for a convex lens forming a virtual image.
Answer:
Consider a convex lens of focal length f and optical centre C. Let an object AB be placed perpendicular to the principal axis at a point between C and F. The virtual image of this object A'B' is formed on the same side of the lens. The image is virtual, erect and is behind the object as shown in Fig. LAQ 24.

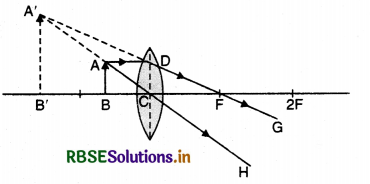
∆ ABC and ∆ A'B'C are similar, so
\(\frac{\mathrm{A}^{\prime} \mathrm{B}^{\prime}}{\mathrm{AB}}=\frac{\mathrm{CB}^{\prime}}{\mathrm{CB}}\) ........................(1)
∆ DCF and ∆  A'B'F are smililar, so
\(\frac{\mathrm{A}^{\prime} \mathrm{B}^{\prime}}{\mathrm{DC}}=\frac{\mathrm{B}^{\prime} \mathrm{F}}{\mathrm{CF}}\)
But DC = AB
∴ \(\frac{\mathrm{A}^{\prime} \mathrm{B}^{\prime}}{\mathrm{AB}}=\frac{\mathrm{B}^{\prime} \mathrm{F}}{\mathrm{CF}}\) ...................(2)
From Eqs. (1) & (2), we have
\(\frac{\mathrm{CB}^{\prime}}{\mathrm{CB}}=\frac{\mathrm{B}^{\prime} \mathrm{F}}{\mathrm{CF}}\)
or \(\frac{\mathrm{CB}^{\prime}}{\mathrm{CB}}=\frac{\mathrm{CB}^{\prime}+\mathrm{CF}}{\mathrm{CF}}\) ......................(3)
Using sign conventions,
Let CB' = -v, CB = -u, CF = f
So Eq. (3) becomes
\(\frac{-v}{-u}=\frac{-v+f}{f}\)
or vf = -uv + uf
Dividing both sides by uvf, we get

Question 26.
Derive lens formula relating object distance image distance and focal length of the concave lens.
Answer:
Consider a concave lens of focal length f and optical centre C. Let an object AB be placed perpendicular to the principal axis at any suitable distance. The image formed by this lens is always virtual, erect and on the same side of the lens as shown in Fig. LAQ 26.

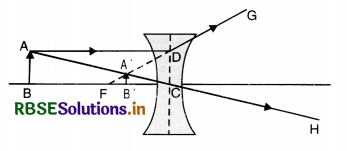
∆ ABC and ∆ A'B'C are similar, so
\(\frac{\mathrm{A}^{\prime} \mathrm{B}^{\prime}}{\mathrm{AB}}=\frac{\mathrm{CB}^{\prime}}{\mathrm{CB}}\) .........................(1)
∆ DCF and ∆ A'B'F are similar, so
\(\frac{\mathrm{A}^{\prime} \mathrm{B}^{\prime}}{\mathrm{DC}}=\frac{\mathrm{B}^{\prime} \mathrm{F}}{\mathrm{CF}}\)
But DC = AB
∴ \(\frac{\mathrm{A}^{\prime} \mathrm{B}^{\prime}}{\mathrm{AB}}=\frac{\mathrm{B}^{\prime} \mathrm{F}}{\mathrm{CF}}\) ......................(2)
From Eq. (1) and (2), we have
\(\frac{\mathrm{CB}^{\prime}}{\mathrm{CB}}=\frac{\mathrm{B}^{\prime} \mathrm{F}}{\mathrm{CF}}\)
or \(\frac{\mathrm{CB}^{\prime}}{\mathrm{CB}}=\frac{\mathrm{CF}-\mathrm{CB}^{\prime}}{\mathrm{CF}}\) .........................(3)
Using sign conventions,
Let CB' = -v, CB = -u, CF = -f
So Eq.(3) becomes
\frac{-v}{-u}=\frac{-f+v}{-f}
or -vf = -uf + uv
Dividing both sides by uvf, we get

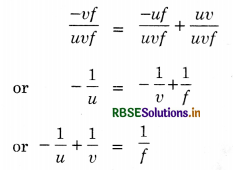
Question 27.
What do you mean by linear magnification produced by a lens? Derive its various expressions.
Answer:
Linear magnification. The linear magnification of a lens is the ratio of size of image formed by the lens to the size of object.
If I = Size of image formed by the lens
O = Size of object.
Then,
Linear magnification = \(\frac{\text { size of image }}{\text { size of object }}\)
or m =\( \frac{\mathrm{I}}{\mathrm{O}}\) ...........................(1)
Let us discuss different cases.

(i) When image formed by convex lens is real
From Fig. LAQ 24 we find that
\(\frac{\mathrm{A}^{\prime} \mathrm{B}^{\prime}}{\mathrm{AB}}=\frac{\mathrm{CB}^{\prime}}{\mathrm{CB}}\)
Using sign conventions,
Let A'B' = - I (Inverted), AB = O, CB' = v, CB = -u

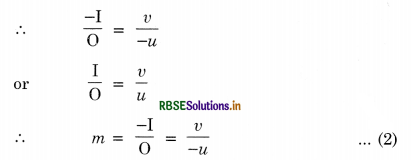
i.e. for real image, the magnification is -ve

(ii) When image formed by convex lens is virtual
From LAQ 25 we find that
\(\frac{\mathrm{A}^{\prime} \mathrm{B}^{\prime}}{\mathrm{AB}}=\frac{\mathrm{CB}^{\prime}}{\mathrm{CB}}\)
Using sign conventions,
Let A'B' = I, AB = O, CB' = -v, CB = -u

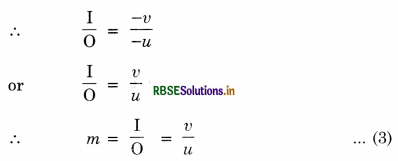
i.e. for virtual image, the magnification is +ve

(iii) When image is formed by concave lens
From LAQ 26 we find that
\(\frac{\mathrm{A}^{\prime} \mathrm{B}^{\prime}}{\mathrm{AB}}=\frac{\mathrm{CB}^{\prime}}{\mathrm{CB}}\)
Using sign conventions,
Let A'B' = I, AB = O, CB' = -v, CB = -u

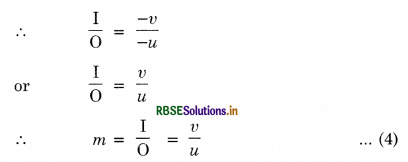
A concave lens always forms a virtual image, so the magnification in case of a concave lens is always + ve.
(iv) Other formulae

Thus we find that in case of a lens, u is always negative, v is positive for real image and negative for virtual image, so magnification is -ve for real image and +ve for virtual image.

Question 28.
Define power of lens and give its units.
Answer:
Power of lens. Power of a lens is defined as its bending ability and is measured as reciprocal of focal length in metre
If f = focal length of lens in metres
∴ Power of lens, P = \(\frac{1}{f}\)
Since the focal length of convex lens is +ve.
∴ Power of convex lens is +ve.
The focal length of concave lens is -ve, hence its power is -ve.
The lens maker’s formula is
\(\frac{1}{f}=\frac{\mu_2-\mu_1}{\mu_1}\left(\frac{1}{\mathrm{R}_1}-\frac{1}{\mathrm{R}_2}\right)\)
Since P = \(\frac{1}{f}=\frac{\mu_2-\mu_1}{\mu_1}\left(\frac{1}{\mathrm{R}_1}-\frac{1}{\mathrm{R}_2}\right)\)
or P = \(\left(\frac{\mu_2}{\mu_1}-1\right)\left(\frac{1}{\mathrm{R}_1}-\frac{1}{\mathrm{R}_2}\right)\)
where µ = \(\frac{\mu_2}{\mu_1}\), refractive index of medium of lens with respect to outside medium.
If outside medium is air, then µ₁ = 1 and µ₂ = µ, then
P = (µ - 1) \(\left(\frac{1}{\mathrm{R}_1}-\frac{1}{\mathrm{R}_2}\right)\)
For convex lens, P is +ve and for concave lens P is -ve.
Units: In S.I., the unit of power of a lens is dioptre (D)
So if f = 1 m, P = \(\frac{1}{1 \mathrm{~m}}\) = 1m^-1
= 1D
Thus power of a lens is said to be one dioptre, if its focal length is 1m.
1D = m^-1.
Note. The focal length of a lens is given in cm, then
P = \(\frac{100}{f}\) D.

Question 29.
Derive the relation \(\frac{1}{f}=\frac{1}{f_1}+\frac{1}{f_2}\) for a combination of two thin lenses.
Answer:
Derivation of the relation
\(\frac{1}{f}=\frac{1}{f_1}+\frac{1}{f_2}\)
Consider an object O placed at a distance u on principal axis of the lens A. Rays of light starting from O form the image I₁.
∴ \(\frac{1}{v_1}-\frac{1}{u}=\frac{1}{f_1}\) ...............................(1)
Place the lens B in contact with A. The image I₁, will serve as virtual object and forms a real image I.

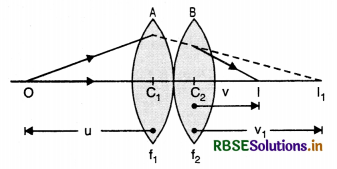
∴ Again apply lens formula,
\(-\frac{1}{v_1}+\frac{1}{v}=\frac{1}{f_2}\) .............................(2)
Adding (1) and (2), we have
\(\frac{1}{v}-\frac{1}{u}=\frac{1}{f_1}+\frac{1}{f_2}\) ............................(3)
But \(\frac{1}{v}-\frac{1}{u}=\frac{1}{f}\)
where f is the focal length of combination
From (3), \(\frac{1}{f}=\frac{1}{f_1}+\frac{1}{f_2}\)
The total power of the lens combination is given by
P = P₁ + P₂
If the two lens of focal lengths f₁ and f₂ are placed at a distance x apart, then the focal length of the combination will be:

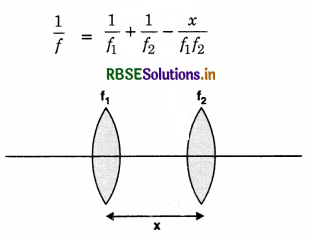
The power of combination is given by
P = P₁ + P₂ - xP₁P₂

Question 30.
What is meant by chromatic aberration? How is this defect removed?
Answer:
Chromatic aberration is an optical defect by virtue of which image of an object seen in white light through a lens appears coloured. It arises on account of inability of a lens to focus all the colours (in white light) at the same point. In Fig. LAQ 30 a red rays are focussed at F_r and violet rays are focussed af F, all other colours being focussed in between. The difference in focal lengths of the lens for red and violet rays i.e. (f_r - f_v) is a measure of longitudinal chromatic aberration of the lens. It is positive in case of a convex lens and negative in case of a concave lens.

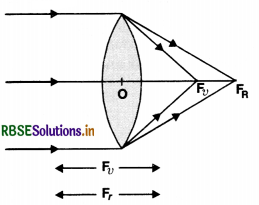
To remove chromatic aberration, we use an achromatic doublet. This is a combination of a convex lens of crown glass and concave lens of flint glass with their focal lengths adjusted suitably so that net chromatic aberration of the combination is zero.
The achromatic doublet will thus focus all the colours at the same point. Hence the image seen in white light shall not be coloured i.e. it will be free of chromatic aberration.

Question 31.
(a) What is a prism, refracting faces and angle of prism?
(b) For a prism prove that
A + δ = i + e.
(c) For a prism prove that
µ = \(\frac{\sin \frac{A+\delta_m}{2}}{\sin A / 2}\)
Or
Derive prism formula for a prism of small angle.
Answer:
(a) Prism. A prism is a wedge-shaped body made from a refracting medium bounded by two plane faces inclined to each other at some angle. The two plane faces are called the refracting faces. The angle included between these two faces is called the angle of prism or refracting angle. ABC represents the principal section of a glass prism having ZA as refracting angle.

(b) A ray EF is incident on the face AB at the point F where N₁FO is the normal and so i is the angle of incidence. The refracted ray FG bends towards the normal such that r₁ is the angle of refraction. The ray FG suffers refraction from face AC at G bends away from the normal and goes along GH such that e is the angle of emergence. 


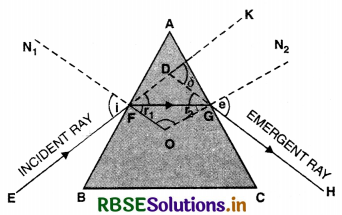
In the absence of the prism, the incident ray EF would have proceeded straight but due to refraction through the prism, it changes its path along the direction DGH. Thus ∠KDH gives the angle of deviation i.e. the angle through which the incident ray gets deviated in passing through the prism.
Now in ∆ DFG, external angle,
δ = ∠DFG + ∠DGF
or δ = i - r₁ + e - r₂
or δ = i + e - (r₁ + r₂) ...................(1)
In quadrilateral AFOG, we have
∠AFO + A + ∠AGO + ∠O = 360°
or 90° + A + 90° + ∠O = 360°
or A + ∠O = 180°
Also, in triangle FGO,
r₁ + r₂ + ∠O = 180°
∴ A + ∠O = r₁ + r₂ + ∠O
or A = r₁ + r₂ .......................(2)
Substituting in equation (1), we have
δ = i + e - A .......................(3)
or A + δ = i + e .........................(4)
Here δ is the angle through which a ray deviates on passing through a small angled prism, and the angle of deviation depends not only upon the material of the prism but also upon the angle of incidence and of prism.

(c) It is found that if the angle of incidence is increased gradually, there is variation in the angle of deviation, it decreases first, attains a minimum value dm and then it starts increasing. So minimum deviation is the angle at which the deviation of ray of light is minimum and the prism is said to be in minimum deviation position.

If we plot a graph between angle of incidence and angle of deviation, the graph is as shown in Fig. 9.89. From the graph, we find that δ is same for two angles of incidence i₁ and i₂ but at minimum deviation δ_m, there is only one angle of incidence.
It is found that at minimum deviation position.
i.e. at δ = δ_m
e = i and r₁ = r₂ = r (say)

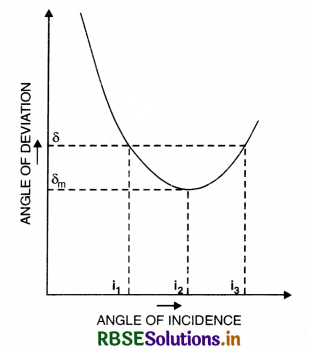
Since δ = i + e - A
∴ At minimum deviation position,
we have
δ_m = i + e - A = i + i - A
or δ_m = 2i - A
or 2i = A + δ_m
or i = \(\frac{\mathrm{A}+\delta_m}{2}\) ...........................(5)
Also at minimum deviation position
A = r₁ + r₂ = r + r = 2r
or r = \(\frac{\mathrm{A}}{2}\) .......................(6)
If µ is the refractive index of the prism, then from Snell's law at surface AB, we have
µ = \(\frac{\sin i}{\sin r}\)
Using Eqs. (5) and (6), we get
µ = \(\frac{\sin \frac{\mathrm{A}+\delta_m}{2}}{\sin \mathrm{A} / 2}\)

Question 32.
What is dispersion of light? Explain it with a diagram. Also explain the cause of dispersion.
Answer:
Dispersion of Light. The phenomenon of splitting of white light into its constituent colours, on passing through a prism is called dispersion of light. The band of colours so obtained is called a spectrum.

White light, e.g. light from the sun, when seen through a prism, appears coloured. Thus white light is split into different colours, on passing through a prism. The colours in the order of decreasing deviation are Violet, Indigo, Blue, Green, Yellow, Orange and Red, Fig. LAQ 32. Obviously, the deviaition is maximum for violet colour and minimum for red colour.


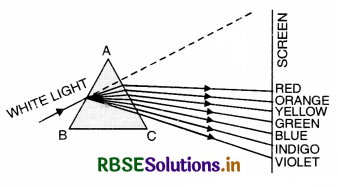
Casue of Dispersion
The wavelength of red light (in the visible spectrum) is much larger than that of violet light and the wavelength of orange, yellow, green, blue and indigo colours lying in between red and violet light gradually decreases in the above order.
According to Cauchy's formula
µ = a + \(\frac{b}{\lambda^2}+\frac{c}{\lambda^4}\)
where λ is the wavelength of light and µ is the refractive index for the particular wavelength i.e. velocity of light is different for different wavelengths. As the wavelength of violet light is smaller than that of red light, the refractive index for violet light is greater than that for red light. i.e. since λ_v < λ_r
∴ µ_v > µ_r
We know that, the deviation δ for a small angled prism is given by δ = (µ - 1) A
So δ_v > δ_r
The other colours will deviate through angles having values between δ_r and δ_v.

Question 33.
Define and explain angular dispersion and dispersive power in a prism.
Answer:
Angular dispersion. Angular dispersion produced by a prism is the difference in the angles of deviation of two extreme colours i.e. violet and red colours.
If δ_v = deviation of violet colour
δ_r = deviation of red colour
∴ Angular dispersion θ = δ_v - δ_r ....................(1)
Since deviation produced by a small angled prism of refractiven index µ is given by:
δ = (µ - 1) A
∴ δ_v = (µ_v - 1) A
and δ_r = (µ - 1) A
so Eq. (1) becomes
θ = (µ_v - 1) A - (µ_r - 1) A
= (µ_v A - A - µ_r A + A)
or θ = (µ_v - µ_r) A
It depends upon nature of material and angle of prism.

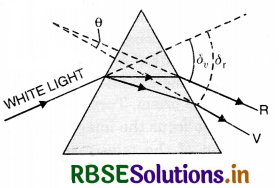
Dispersive power. The dispersive power of a prism is defined as the ratio of angular dispersion to the mean deviation produced by the prism. It is represented by ω.
Let A = Angle of prism, µ_v, µ_r and µ be refractive indices of prism for violet, red and yellow (mean), Mean deviations, δ = (µ - 1) A
Angular dispersion,
θ = δ_v - δ_r = (µ_v - µ_r) A
Dispersive power,

Hence we find that the dispersive power is independent of angle of prism but depends only on the refractive index (i.e. nature of material of the prism) for red, violet and mean colour.
Note. Refractive index for mean colour is given by µ = \(\frac{\mu_v+\mu_r}{2}\)

Question 34.
What do you mean by impure and pure spectrum? How is pure spectrum produced?
Or
What is spectrum? State the necessary conditions to produce a pure specturm.
Answer:
(i) Impure spectrum
The spectrum in which overlapping of various colours take place is called impure spectrum as shown in Fig. LAQ 34 (a).

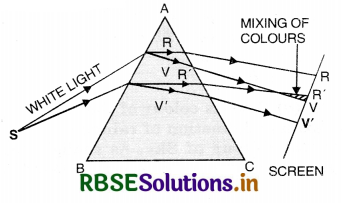
(ii) Pure spectrum
The spectrum in which there is no overlapping of one colour on other is called pure spectrum as shown in Fig. LAQ 34 (b).

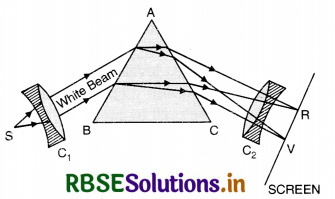
Production of pure spectrum

1. The source of light should be narrow.
2. The prism should be placed in minimum deviation position.
3. The incident beam should be parallel.
4. An achromatic convex lens should be used to make incident beam parallel and another achromatic convex lens to bring emergent light of a given colour to focus at one point.

Question 35.
Describe Spectrometer. How will you use it to determine the refractive index of prism?
Answer:
Spectrometer
It is an instrument used for the production and study of pure spectrum and to find the refractive index of transparent solids and liquids. Fig. 9.93 (a).
The essential parts of spectrometer are

1. Collimator
2. Prism table
3. Telescope.

1. Collimator
It consists of a tube which carries at one end a narrow adjustable slit S, and at the other an achromatic convex lens L. The slit is illuminated by a source of light, the spectrum of which is to be examined. The distance between the slit and the lens can be adjusted with the help of rack and pinion arrangement P. The distance between the slit and the lens is adjusted till the slit is at focus of the lens and the light emerges from the lens as a parallel beam.


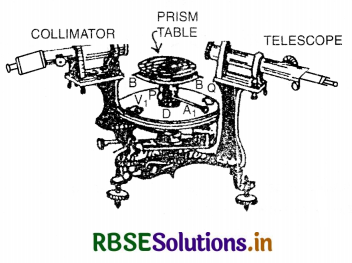
2. Prism table
The prism table D is a circular plane table which can be rotated about the axis of the instrument independently of the collimater C and the telescope T, Fig. LAQ 35 (b). The height of the prism table can be adjusted by raising or lowering the rod carrying the table and then clamping it in position. It can be leveled by means of three leveling screws attached to the bottom. The rotation of the prism table and hence the prism can be read by means of the verniers and V₂ attached to it on the circular space. The prism is placed on the table so that it receives the parallel pencil of light from the collimator. Dispersion is produced by it and from the face, AC emerge various systems of parallel rays which can be brought to focus by a telescope T.


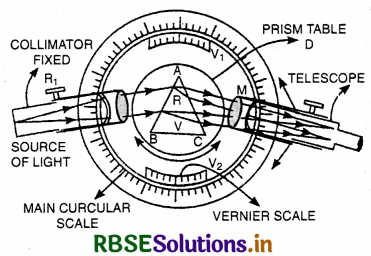
3. Telescope
It is an astronomical type of telescope fitted with Ramsden’s eye piece. The telescope is mounted with its axis horizontal and pointing towards the centre of the prism table on an arm attached to the spectrometer. It can be rotated about the vertical axis of the prism table. Parallel light emerges from the prism falls on the lens M, and is thereby brought to focus at F, the principal focus of the lens, so that a real image of the slit is formed in the focal plane. Another lens E (eye piece) is used to give a magnified virtual image of this real image. The two lenses M and E, mounted in the tube, together constitute a telescope.
Determination of µ of material of a prism is given by
The refractive index of the material of a prism is given by
µ = \(\frac{\sin \left(\mathrm{A}+\delta_m\right) / 2}{\sin \mathrm{A} / 2}\)
where A is the angle of the prism and δ_m is the angle of minimum deviation. 
Hence, for the determination of µ of the prism we must determine δ_m and A.

(i) Determination of 'δ_m'. Set the prism in the minimum deviation position as explained above. Turn the telescope, so as to focus it on the mean (yellow) colour of the spectrum, as in the position T₁. (Fig. LAQ 35 (c)). Note the telescope reading in this position. Remove the prism. Turn the telescope to the position T₂, so as to focus the image of the slit direct. Read the position of the telescope. The difference between the two readings of the telescope gives us the angle of minimum deviation, δ_m.

(ii) Determination of‘A’. To determine the angle of prism A, place the prism ABC on the prism table, such that light from the collimator falls symmetrically on the faces AB and AC of the prism. Look for the brightest image of the slit as seen from the reflection of light as faces AB and AC.

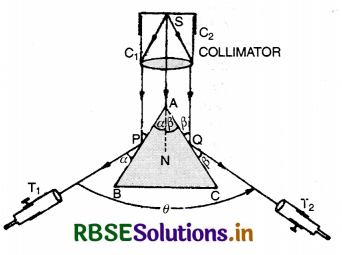
Set the telescope in position T₁, so as to focus the image of the slit from face AB. Turn the telescope to the position T₂, so as to focus the image of the slit from face AC. Let O be the angle through which telescope is turned.
Then A = \(\frac{\theta}{2}\)
Proof. ∠APC₁ = ∠BPT₁ = α
∠AQC₂ = ∠CQT₂ = ß
∠NAP = ∠APC₂ = α (alt. ∠s)
∠NAQ = ∠AQC₂ = ß (alt. ∠s)
So θ = (α + α) + (ß + ß)
= 2 (α + ß) = 2A
A = _{\(\frac{\theta}{2}\)}.

Question 36.
(a) Discuss colour of the sky.
(b) Explain formation of rainbow.
Answer:
(a) Colour of Sky. As sunlight travels through the earth’s atmosphere, gets scattered by the large number of molecules present. This scattering of sunlight is responsible for the colour of the sky, during sunrise and sunset etc. The light of shorter wavelength is scattered much more than light of larger wavelength. Scattering ∝ 1/λ⁴. This scattering is known as Rayleigh scattering. Most of blue light is scattered, hence the bluish colour of the sky predominates.
At sunset or sunrise, sun’s rays must pass through a larger atmospheric distance (Fig. LAQ 36 (a)). More of the blue colour is scattered away. Only red colour which is least scattered appears to come from sun. Hence it appears red.


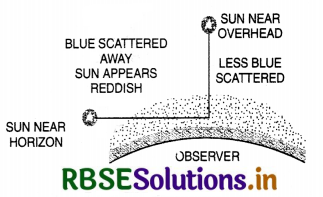
(b) Formation of Rainbow. The rainbow is a classic example of the dispersion of sunlight by the water drops in the atmosphere. This is a combined phenomenon of the refraction of sunlight by the spherical water droplets behaving in a prism-like manner. Fig. shows how the sunlight is broken into its segments in the process and a rainbow appears. The dispersion of the violet and the red rays after internal reflection in the drop is shown in the Fig. LAQ 36 (b).


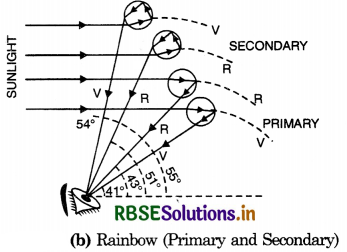
The red rays emerge from the drops of water at one angle (43°) and the violet rays emerge at another angle (41°). The large number of water drops in the sky especially just after it has rained makes for a prominent rainbow. The parallel beam of sunlight getting dispersed at these angles produces a cone of rays at the observer as seen in the figure. The rainbow, therefore, appears semicircular for an observer on earth. A secondary rainbow will sometimes be formed, with inverted colours. Here the light is reflected twice within the drop as shown in the figure. The secondary rainbow is fainter than the primary rainbow.
 
Question 37.
Explain the working of simple microscope and find an expression for its magnifying power. What are the uses of simple microscope?
Answer:
Microscope. Microscope is a device which is used to see very small objects which cannot be seen with naked eye.
Simple Microscope
Principle. When an object is placed between principal focus and optical centre of a convex lens, a vitual and erect image will be formed on the same side of the object.

Construction and Action
An ordinary convex lens of small focal length held close to the eye can be used as magnifying glass or a simple microscope. The object is made to lie between the lens and its focus so that image formed is virtual, erect and magnified. As the object is to be seen clearly, the image is made to lie at the distance of distinct vision from the eye. The course of rays indicating the formation of image is shown in the figure.

Magnifying Power
Magnifying Power of a microscope is defined as the ratio of the angle subtended at the eye by the image to the angle subtended by the object when both are placed at the least distance of distinct vision and seen directly.
In Fig. LAQ 37, the image A'B' is formed at the distance of distinct vision and subtends an ∠A'CB' = ß on the eye as it is held close to the lens. If the object AB is also moved to the distance of distinct vision i.e., to the position EB', it would subtend an ∠ECB' = α at the eye.

Magnifying power,

or M = \(\frac{\mathrm{CB}^{\prime}}{\mathrm{CB}}\) (∵ AB = EB')
M = \(\frac{v}{u}\)

Using the lens formula

Since image is formed at least distance of distinct vision D and is virtual,
∴ v = -D
So m = 1 - \(\frac{-\mathrm{D}}{f}\)
or m = 1 + \(\frac{\mathrm{D}}{\mathrm{f}}\) ...........................(1)
This shows that smaller the focal length of the lens, greater will be the magnifying power of microscope.

Uses.
1. Jewellers and watch makers use simple microscope.
2. In science laboratory, a magnifying glass (a simple microscope) is used to see vernier scale attached to the instrument.
3. The image formed by simple microscope is bright and sharp because the object is held close to the lens, and without the lens the object is not clearly visible.

Question 38.
Draw a course of rays through a compound microscope. Obtain an expression for the magnifying power of a microscope. When image is formed at least distance of distinct vision.
Or
Explain the construction and working of a compound microscope and find the expression for its magnifying power.
Answer:
It is an instrument used to see highly magnified image of tiny objects.
Principle. It is based on the principle that when a small object is placed just outside the focus of objective lens, its real, inverted and magnified image is formed on the other side of the lens. This image acts as an object for eye lens, the eye lens is so adjusted that the final image is produced at least distance of distinct vision.

Construction. It consists of two convex lenses of shorter focal lengths arranged co-axially at the ends of two sliding tubes.
(i) Objective. It is a convex lens of very short focal length and of small aperture and is placed near the object to be magnified.

(ii) Eye piece. It is a convex lens of short focal length and of comparatively large aperture and is placed near the eye for seeing the final image which is formed at least distance of distinct vision.

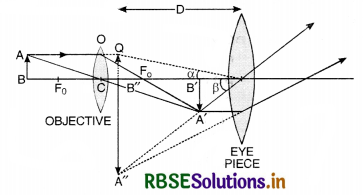
The distance between the two lenses can be adjusted by rack and pinion arrangement.
Let a tiny object AB be placed in front of objective at a distance more than f0. Its real and enlarged image is formed at A' B'. This image A'B' acts as an object for eye piece and forms final image at A"B" i.e. at a distance D, the distance of distinct vision.

Magnifying Power of Microscope is defined as the ratio of the angle subtended on the eye by the final image to the angle subtended on the eye by the object, when both the final image and the object are situated at least distance of distinct vision.
Magnifying power, M = \frac{\beta}{\alpha}
Since angles are small, therefore, tan ß ≃ ß and tan α ≃ α.

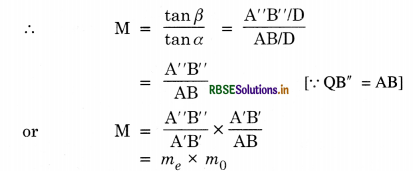
where m_e and m₀ are the magnifying powers of eye piece and the objective.
m₀ = \(\frac{\mathrm{A}^{\prime} \mathrm{B}^{\prime}}{\mathrm{AB}}=\frac{\mathrm{CB}^{\prime}}{\mathrm{CB}}\)
But CB is nearly equal to (-f₀) and CB' is equal to the length of the tube L [since the image A'B' is formed very close to eye lens]
m₀ = \(\frac{\mathrm{L}}{\left(-f_0\right)}\)
Also m_e = 1 + \(\frac{\mathrm{D}}{f_e}\) [As in simple microscope]
∴ M = \(-\frac{\mathrm{L}}{f_0}\left(1+\frac{\mathrm{D}}{f_e}\right)\)
(Negative sign shows that final image is inverted with respect to the object.)
Thus we find that, if the focal length of objective lens and eye lens are short, the magnifying power will be large. Magnifying power of compound microscope when final image is at infinity. Magnifying power is defined as the angle subtended on the eye by the final image to the angle subtanded on the eye by the object, at the unaided eye, when final image is formed at infinity. When final image is formed at infinity.

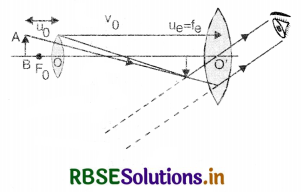
The angular magnification due to eye piece m_e = \(\frac{\mathrm{D}}{f_e}\)
The angular magnification due to objective lens m₀ = \(\frac{\mathrm{L}}{f_0}\)
∴ M = m₀m_e = \(\frac{\mathrm{L}}{f_0} \times \frac{\mathrm{D}}{f_e}\)
Thus we find that, to have large magnification, the focal length of the objective lens nad eye lens must be small.

Question 39.
What is a telescope? Describe astronomical telescope. Calculate magnifying power of the telescope in normal adjustment and for formation of image at least distance of distinct vision.
Or
Draw a ray diagram of an astronomical telescope in the normal adjustment position. Write down the expression for its magnifying power.
Answer:
Telescope. A telescope is an optical instrument used for observing distant objects very dearly.
Astronomical telescope. It produces virtual and inverted image and is used to see heavenly bodies like sun, stars, planets etc. so the inverted image does not affect the observation.
Principle. It is based on the principle that when rays of light are made to incident on objective from a distant object, the objective forms the real and inverted image at its focal plane. The eye lens is so adjusted that the final image is formed at least distance of distinct vision.

Construction. The refracting type astronomical telescope consists of two convex lenses one of which is called the objective and the other eye piece. The objective is a convex lens of large focal length and large aperture. It is generally a combination of two lenses in contact so as to reduce spherical and chromatic aberrations. The eye piece is also a convex lens but of short focal length and small aperture. The objective is mounted at one end of a brass tube and the eye piece at the other end in a smaller tube which can slide inside the bigger tube carrying the objective.


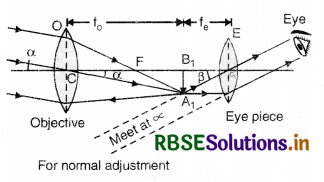
(i) When the final image is formed at infinity. (i.e. for normal adjustments). The distance between the image A₁B₁ and the eye piece is adjusted equal to the focal length of the eye piece so that the final image is formed at infinity. In this case, telescope is said to be in normal adjustment or focussed to infinity. In normal adjustment, distance between two lenses = (f₀ + f_e).
The magnifying power of a telescope in normal adjustment is defined as the ratio of the angle subtended by the image at the eye as seen through the telescope to the angle subtended by the object at the unaided eye, the object and the image both lying at infinity.

Angle subtended by object at eye piece or at eye ∠A₁, CB₁ = α
The angle subtended by the image at the eye
∠B₁C₁A₁ = ß
∴ Magnifying power, M = \(\frac{\beta}{\alpha}\)
As the angles are small, therefore, they can be replaced by their tangents. Hence
M = \(\frac{\tan \beta}{\tan \alpha}\)
= \(\frac{A_1 B_1}{B_1 C_1} \times \frac{B_1 C}{A_1 B_1}=\frac{B_1 C}{B_1 C_1}\) .........................(i)
When the rays emerging from the eye piece are parallel, the image A2B2 lies at infinity and the distance B₁C₁ is equal to f_e the focal length of the eye piece, as shown in Fig. LAQ 39a. Also the distance B₁C = f₀, the focal length of the objective.
∴ M = \(\frac{\mathrm{B}_1 \mathrm{C}}{\mathrm{B}_1 \mathrm{C}_1}=-\frac{f_0}{f_e}\)
= \(-\frac{\text { Focal length of the objective }}{\text { Focal length of the eye piece }}\)
Thus to increase the magnifying power of a telescope the objective must have a very large focal length and the eye piece a very small focal length.

(ii) When final image is formed at least distance of distinct vision.
The objective O forms a real, inverted and diminished image A₁B₁ of a far object at focal plane B₁ of the objective in front of the eye piece E. The rays incident on the objective are taken in the form of a parallel beam as they are coming from a far off object. The distance between the eye lens and this image formed is adjusted so that it is less than the focal length of eye piece which, therefore, forms a magnified, virtual image A₁₁B₁₁ at the least distance of distinct vision. Fig. LAQ 39a (a).

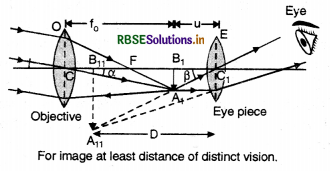
Magnifying power of a telescope is the ratio of angle subtended by the image at the eye formed at least distance of distinct vision to the angle subtended by the object (seen directly) at the eye lying at infinity.
Angle subtended at the eye by the image formed at least distance of distinct vision ∠A₁₁C₁B₁₁ = ß = ∠A₁C₁B₁
Angle subtended at the eye by the object seen directly lying at infinity ∠A₁CB₁ = α
∴ Magnifying power, M = _{\(\frac{\beta}{\alpha}\)}
Since α and ß are small, so they can be replaced by their tangents.

So, the magnification will be large, if focal length of objective (f₀) is very large as compared to focal length of eye piece (f_e).
Since 1 + \(\frac{f_e}{D}\) > 1 , so we find that the amplification produced is more when final image is formed at least distance of distinct vision than when final image is formed at infinity.
In both cases, the final image is inverted hence it is not suitable for seeing terrestrial objects.

Question 40.
Describe a Terrestrial telescope. Calculate its magnifying power.
Answer:
Terrestrial telescope
It is used to see erect image of distant earthly

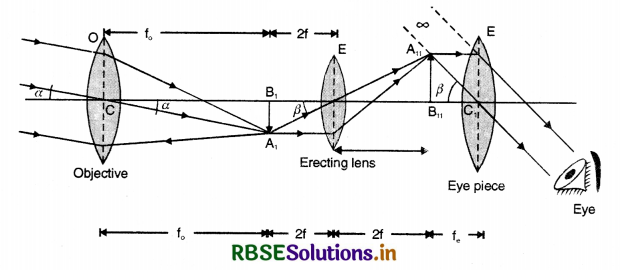
objects. For obtaining erect image an extra convex lens is placed between objective and eye piece.
Principle. Same as in astronomical telescope.
Construction. It consists of an objective and an eye piece Objective is of large aperture and focal length and eye piece is of small focal length and aperture. An erecting lens placed at a distance 2f from the image to form erect image. The distance between the objective and eye piece can be adjusted by using a rack and pinion arrangement.

The course of rays is as shown in Fig 9.101. The objective produces real and inverted image A₁B₁ on its focal plane of distant object. In order to form erect image A₁₁B₁₁, a convex lens called erecting lens is placed at a distance. 2f from image A₁B₁ and a real image A₁₁B₁₁ is formed at 2f on other side of the lens. The eye piece is placed at such a distance so that the image is either formed at infinity (for normal adjustment) or at least distance of distinct vision.
For normal adjustment
Total length of the telescope = f₀ + 4f + f_e
And magnification (similar as in case of astronomical telescope)
M = \(\frac{f_0}{f_e}\)
When image is formed at least distance of distinct vision.
For normal adjustment, eye lens is placed at a distance exactly equal to its focal length from the image PQ which forms the virtual object for the concave lens. So the diverged rays become parallel to each other and the final image is formed at infinity. In this position, the length of telescope is f₀ - f_e, where f₀ is focal length of objective and fe is focal length of eye lens.
Magnifying Power Magnifying Power,
M = \(\frac{\text { Angle subtended by the image }}{\text { Angle subtended by the object }}\)
Magnification, M = \(\frac{f_0}{f_e}\left[1+\frac{f_e}{\mathrm{D}}\right]\)

Question 41.
Discuss Galileo telescope and calculate its magnifying power.
Answer:
Galileo's Telescope. It is used to observe distant objects on the earth.
Construction
In this telescope, objective is a convex lens of long focal length and large aperture. The eye piece is a concave lens of short focal length. Both the lenses are fixed at the ends of two tubes. The tube carrying eye lens can slide into the tube carrying the objective lens. As the rays of light from a distant object strike the objective in a parallel beam, they are converged to the point P. In this way objective lens forms real, diminished and inverted image PQ at its focal plane.

The concave lens or eye lens is placed in between the image PQ and the objective so that it intercepts the rays which would have converged to P in its absence. So the rays are diverged by the eye lens as shown in Fig. LAQ 41. As illustrated in the figure the rays appear to reach eye of the observer from P', so that P'Q' is finally erect, virtual and magnified image. Position of the eye lens is adjusted in such a way that final image is formed at the least distance of distinct vision. 

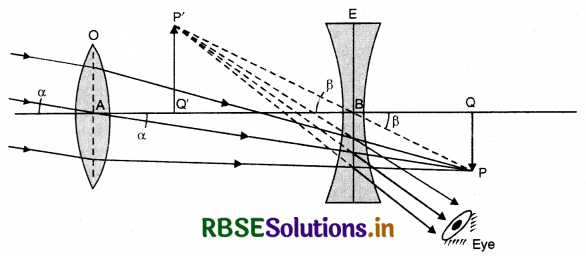
Angle subtended bv the image at the eye = ß
Angle subtended by the object at the eye = α
∴ Magnification,
M = \(\frac{\beta}{\alpha}\)
Since α and ß are small, so they can be replaced by their tangents.
∴ M = \(\frac{\tan \beta}{\tan \alpha}\)
or M = \(\frac{\mathrm{PQ}}{\mathrm{QB}} \times \frac{\mathrm{QA}}{\mathrm{PQ}}=\frac{\mathrm{QA}}{\mathrm{QB}}\)
The object is at a very large distance. So QA = f₀, the focal length of the objective. For normal adjustment, the image is formed at infinity. So QB = f_e, the focal length of eye lens.
Hence M = \(\frac{f_0}{f_e}\)
= \(\frac{\text { Focal length of objective }}{\text { Focal length of eye lens }}\)

Question 42.
Describe a reflecting telescope. Give its merits and demerits
Answer:
It is a telescope which uses a converging mirror to view distant objects like stars etc.
This telescope was initially constructed by Newton for observing distant stars, and was modified from time to time. In Fig. LAQ 42. Cassegrainian type of telescope is shown.

Construction
It consists of an objective and eye piece. Objective is a concave mirror of large aperture and large focal length fixed at one
end of a long tube. A plane mirror M is placed before the formation of image by the concave mirror at 45° to the axis of the tube. This mirror deviates the rays towards the eye piece which consists of two plano-convex lenses capable of moving in and out with the help of rack and pinion arrangement T as shown in the figure.


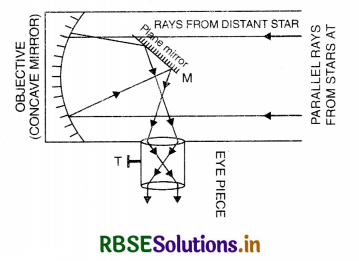
Working
Parallel rays from distant objects like stars are made to fall on the concave mirror. These rays are reflected towards the focus F, but the plane mirror M deviates the rays towards the eye piece and real image I is formed in front of eye piece. The rays after passing through the eye piece become parallel. The eye piece acts as a magnifier and the final image is virtual, erect and magnified.

Merits

1. The image is free from chromatic aberration.
2. The image is free from spherical aberration.
3. Concave mirror of large aperture can be easily made.
4. The objective i.e. concave mirror does not absorb light.
5. The image is stable.

Demerits

• It cannot be used for general purpose.
• It is less convenient to use.
• Large area of sky cannot be photographed.

Question 43.
Describe briefly the human eye from an optical point of view.
Answer:
Eye. The eye is the most common and the most remarkable optical instrument, and in many respects it is similar to a camera. An image of an object is formed on the retina of the eye and is transmitted to the brain by way of optic nerves. It consists of following parts:

Cornea. The outermost coating made of a tough and opaque white substance called sclerotic. The front transparent part is called cornea.

Choroid. The second coating inside the sclerotic is called choroid. It is a black, opaque membrane, which serves to darken the interior of the eye.

Iris. The front part of choroid is divided into two layers. Iris is the disc-like front part. It is coloured giving the characteristic colour to the eye. The hole in the centre is called pupil of the eye.

Ciliary Muscles. This is second layer of choroid. These muscles along with suspensory ligaments help in changing the power of accommodation of the lens.

Lens. It is the transparent bi-convex lens, having back surface more curved than the front one. It is composed of flexible material arranged in layers, with increasing refractive index towards the centre.

Retina. It is the rose coloured innermost membrane of the eye ball. It is very sensitive to light. The point which is most sensitive to light is called fovea centralis or yellow spot. The point which is least sensitive is the called blind spot.

Anterior and Posterior Chamber. The space between cornea and lens is called anterior chamber and is filled with a liquid called aqueous humour. The space between lens and retina is called posterior chamber which is filled with a liquid called vitreous humour.


Focussing action. The cornea, the aqueous humour, the crystalline lens and the vitreous humour together constitute a single converging lens, and the image is formed by the eye lens on the sensitive retina. The iris automatically adjusts the size of the pupil according to the intensity of light falling on it. The inverted image formed on the retina when sent to the brain by optic nerves is transformed into erect image.

Accommodation. The process by which the eye can adapt itself to see objects at different distances is called accommodation. It is defined as the power of a lens to adjust its value according to needs.

Far and near points. The most distant point upto which an eye can see is called the far point (it is upto infinity) and the point at the shortest distance from the eye upto which the eye can accommodate itself and, therefore can see clearly is called the near point (for normal eye it is 15 cm).

Range of vision. The distance between the far and the near point is called the range of vision. Within this range, however, there is a certain distance where the objects are most distinctly seen with fully relaxed eyes. This distance for normal eye is about 25 cm and is called the least distance of distinct vision.

Question 44.
What are main defects of vision? Describe clearly with diagrams how are they corrected?
Answer:
The major defects of vision are:

1. Short sightedness or myopia.
2. Long sightedeness or Hypermetropia
   The other minor defects are:
3. Astigmatism
4. Presbyopia
5. Phorias
6. Colour blindness.

We shall discuss only major defects and their corrections.
A person with normal eye sight can see clearly distant objects as well as near objects.
Short-sightedness or Myopia and its correction.
A person with this defect can see near objects clearly and distinctly and distant objects are not clearly visible. This defect arises due to following reasons.
(i) The length of eye ball becomes larger than that of the normal eye, or
(ii) The limiting (the largest) focal length of the eye lens becomes too short.

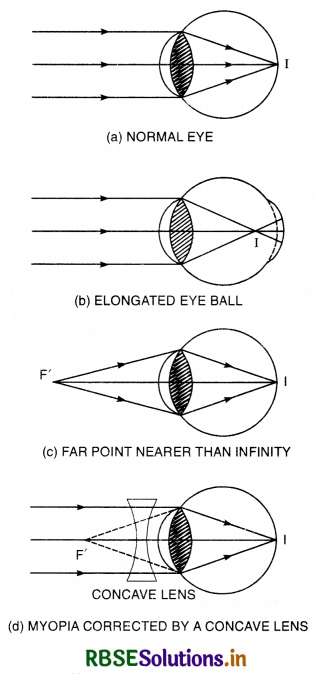
A person suffering from myopia, the eye brings a parallel beams of light to focus at I in front of the retina Fig. (b) but the rays from the normal near point F' are focussed on the reetina Fig. LAQ 44 (c).

Remedy. In order to correct this defect a divergent lens of suitable focal length is placed in front of the eye Fig. (d) so that parallel rays coming from infinity appear, after refraction through the lens, to come from the far point (F') when eye is unaccommodated.
Calculation
If x = distance of far point F' from eye,
Then from lens to be used,
u = ∞ and v = -x
If f is the focal length of concave lens, then
\(\frac{1}{f}=-\frac{1}{u}+\frac{1}{v}=-\frac{1}{\infty}-\frac{1}{x}\)
or f = -x.

(2) Long-sightedness or Hypermetropia and its correction.
A person suffering from this defect can see distant objects quite clearly and distinctly and near objects are not clearly visible. This defect arises due to following reasons:
(i) The size of eye ball becomes smaller than that in the normal eye; or
(ii) The eye lens becomes too thin so that its limiting (smallest) focal length becomes abnormally large.
(a) Eye ball too short
(b) Eyes own near point farther than 25 cm
(c) Hypermetropia corrected by convex lens


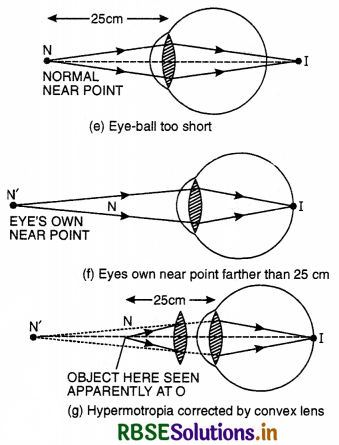
A person suffering from hypermetropia, the eye brings the rays coming from normal point N (25 cm) to a focus at point I behind the retina (Fig. LAQ 44 (e)), but the rays from its own near point (N') are focussed on the retina (Fig. LAQ 44 (f))
Remedy. In order to correct this defect a convergent lens of suitable focal length is placed infront of the eye Fig. LAQ 44 (g) so that the rays diverging from N appear to come after refraction, from near point N'.
If x = distance of near point N' from eye
Then, for lens to be used
u = -D, v = -x
If f is the focal length of convex lens, then
\(\frac{1}{f}=-\frac{1}{u}+\frac{1}{v}=-\frac{1}{-\mathrm{D}}-\frac{1}{x}\)
or \(\frac{1}{f}=\frac{x-\mathrm{D}}{x \mathrm{D}}\)
or f = \(\frac{x \mathrm{D}}{x-\mathrm{D}}\)

Question 45.
Describe a photographic camera.
Answer:
Photographic camera
A photographic camera is essentially a converging lens system used for producing a real image on the photographic film.
Construction. A photographic camera consists of following parts:

(а) A light proof box. This box is blackened inside to absorb only stray radiations and to control internal reflections.
(b) Objective. Photographic objective is a converging lens system fitted in front of camera and the lens system is corrected for spherical and chromatic aberrations. It forms real, inverted and diminished image of the object on the photographic film.

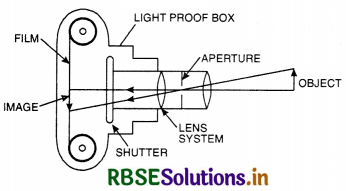
(c) Shutter. It is placed between the lens and the film. It opens and closes quickly when photograph of an object is taken.
In a camera following adjustments and controls are provided.

(i) Exposure time. In order to obtain a clear image for a given aperture, the film has to be exposed for a certain time. It determines the total amount of light falling on the film. If the photographer is taken in bright sun light the exposure time should be small and it should be large (i) shade condition or for indoor photography. The normal, exposure times used in camera are:
\(\frac{1}{500} s, \frac{1}{200} s, \frac{1}{125} s, \frac{1}{60} s, \frac{1}{30} s \text { etc. }\)

(ii) Aperture of the lens (f-numbers).
It refers to diameter of circular opening through which light passes into the camera. It is generally expressed in f-numbers, f-number indicates the light generating power, hence is referred to as the speed of the lens.
If D is diameter of the circle of lens and f is focal length, then
f-number = \(\frac{\text { focal length of the lens }}{\text { diameter of the aperture }}\)
= \(\frac{f}{\mathrm{D}}\)
So, amount of light per unit area of image is proportional to \(\frac{\mathrm{D}^2}{f^2}\)

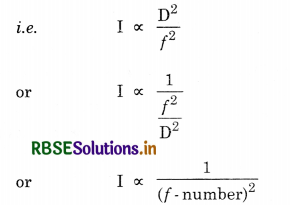
It means, smaller the f-number, higher the speed of the lens of the camera.
In almost all cameras, the aperture used are
\(\frac{f}{2}, \frac{f}{2.8}\left(\frac{f}{2 \sqrt{2}}\right), \frac{f}{4}, \frac{f}{5.6}\left(\frac{f}{4 \sqrt{2}}\right), \frac{f}{8}, \frac{f}{11.2}\left(\frac{f}{8 \sqrt{2}}\right), \frac{f}{16}\)
f-number 16 means that the focal length is 16-times the diameter.

(iii) Film speed. Film speed is a measure of how quickly the film be exposed when in use. A fast film requires comparatively slow time exposure while a slow film requires relatively longer time. Thus fast films are used in poor light conditions and very slow films for all still object photography.

(iv) Exposure meter. Modern cameras have built in exposure meters. It has light sensitive surface. When light falls over it, a current, proportional to the quantity of light falling, flows in the meter and photographer can adjust a suitable combination of aperture and exposure times for correct exposure.

(v) Depth of focus. It indicates the range of object distances over which the focussing is reasonably good. This factor becomes important when the aperture has to be made large due to poor light conditions. Under such condtions, the image is not focussed in a single plane but gets spread out due to aberrations.

Question 46.
Give principle, construction, working and merits of a prism binocular.
Answer:
Principle
A prism binocular is a double, field telescope for seeing final image erect in large field of view by using two totally reflecting prisms to get erect image of an inverted image without lateral inversion.

Construction. It consists of two objective lenses of large focal length and large aperture. To totally reflecting prisms are provided with each objective as shown in the figure. The eye pieces in the left and right sections are separated by some distance as the normal distance between the two eyes. Both eye pieces are movable forward and backward simultaneously.

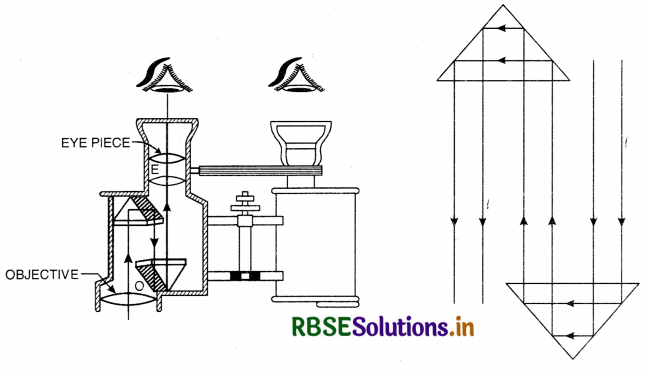
Working
The rays from the objective O, travel thrice the length of the tube by means of two prisms before reaching the erecting eye peice E. The purpose of the terrestrial telescope is served in a short length and by using an objective of large focal length, sufficient magnification and a wider field of view can be obtained.

It has a benefit of binoculars vision (vision with two eyes). High magnification is achieved by increasing effective length by the pair of totally reflecting prisms in between the two lenses. Field of view is increased by using convex eye pieces instead of concave. The use of prisms, in addition to the help given in increasing the magnifying power of the instrument, also helps us in increasing the field of view, because it allows use of convex eye pieces without any lateral inversion. The inverted image formed by the object is made erect by the first prism and second prism corrects the same for lateral inversion as shown in the figure.
Merits

• It has a benefit of binocular vision (vision with two eyes).
• Field of view is large due to the use of convex eye pieces instead of concave eye prieces.
• Roundness of object seen becomes more clear as we see through two widely separated objectives.
• It is suitable for terrestrial observations because the final image seen is erect without lateral inversion.

Question 47.
Trace the rays of light showing the formation of an image due to a point object placed on the axis of a spherical surface separating the two media of refractive indices n₁ and n₂. Establish the relation between the distances of the object, the image and the radius of curvature from the central point of the spherical surface. Hence derive the expression of the lens maker’s formula.
Answer:
Lens maker’s formula
It is given by
\(\frac{1}{f}=(\mu-1)\left(\frac{1}{\mathrm{R}_1}-\frac{1}{\mathrm{R}_2}\right)\)
This formula relates the focal length of the lens of the radii of curvature of the surfaces and the refractive index of the material of the lens.
Why is it called lens maker’s formula?
It is so called because this formula is used by the manufacturers to prepare lenses of desired focal lengths.

Sign conventions

• All the distances are measured from the optical centre of lens.
• Distance measured in the direction of incident light is taken +ve.
• Distance measured in the direction opposite to the direction of incident light is taken -ve.

Assumptions

1. Object is a point object.
2. Lens is thin so that distances are measured from the poles of its surfaces.
3. The aperture of the lens is small.
4. Angles of incidence and refraction are small.

Let C₁ and C₂ be centres of curvature of two spherical surfaces XP₁Y and XP₂Y with optical centre C. Let µ₂ be the refractive index of the material of the lens and µ1 that of the medium surrounding the lens where µ₂ > µ₁.

Refraction at surface XP₁Y
Let a ray OA starts from the point object O which is placed on the principal axis of the convex lens and it refracts into the denser medium at point A. The refracted ray AB goes undeviated to meet at point I₁, if the lens material were continued. Then I₁ would be the real image of point object O.
From Snell’s law for small i₁ and r₁, we have
\(\frac{\sin i_1}{\sin r_1}=\frac{i_1}{r_1}=\frac{\mu_2}{\mu_1}\)
or µ₁ i₁ = µ₂ r₁ ...........................(1)
In ∆ AOC₁,
i₁ = α₁ + γ₁
In ∆ AI₁C₁,
γ₁ = ß₁ + r₁
or r₁ = γ₁ - ß₁
Putting the values of i₁ and r₁ in Eq.(1), we get
µ₁ (α₁ + γ₁) = µ₂ (γ₁ - ß₁)
or µ₁α₁ + µ₁γ₁ = µ₂γ₁ - µ₂ß₁
or µ₁α₁ + µ₂ß₁ = (µ₂ - µ₁) γ₁
Since α₁, ß₁ and γ₁ are small, so they can be replaced by their tangents.
∴ µ₁ tan α₁ + µ₂ tan ß₁ = (µ₂ - µ₁) tan γ₁
or µ₁\(\frac{\mathrm{AM}_1}{\mathrm{M}_1 \mathrm{O}}\) + µ₂ \(\frac{\mathrm{AM}_1}{\mathrm{M}_1 \mathrm{I}_1}\) = (µ₂ - µ₁) \(\frac{\mathrm{AM}_1}{\mathrm{M}_1 \mathrm{C}_1}\)
or \(\frac{\mu_1}{\mathrm{M}_1 \mathrm{O}}+\frac{\mu_2}{\mathrm{M}_1 \mathrm{I}_1}=\frac{\mu_2-\mu_1}{\mathrm{M}_1 \mathrm{C}_1}\)
Since the lens is a very thin,
so M₁O ≃ CO, M₁I₁ ≃ CI₁
and M₁C₁ ≃ CC₁
∴ \(\frac{\mu_1}{\mathrm{CO}}+\frac{\mu_2}{\mathrm{CI}_1}=\frac{\mu_2-\mu_1}{\mathrm{CC}_1}\) .............................(2)

Refraction at surface XP₂Y
Actually the lens is not continuous and the ray AB suffer refraction at B and finally meet at I. So I is the real image of the virtual object I₁ (placed in the material of the lens).
From Snell’s law for small i₂ and r₂, we have
\(\frac{\sin i_2}{\sin r_2}=\frac{i_2}{r_2}=\frac{\mu_1}{\mu_2}\)
or µ₁r₂ = µ₁i₂ ..........................(3)
In ∆ BC₂I₁,
i₂ = ß₁ + γ₂
In ∆ BC₂I r₂ = ß₂ + γ₂
Putting the value of i₂ and r₂ in Eq. (3), we get
µ₁ (ß₂ + γ₂) = µ₂ (ß₁ + γ₂)
or µ₁ß₂ + µ₁γ₂ = µ₂ß₁ + µ₂γ₂
or µ₁ß₂ - µ₂ß₁ = (µ₂ - µ₁) γ₂
Since ß₂, ß₁ and γ₂ are small, so they can be replaced by their tangents, so
µ₁ tan ß₂ - µ₂ tan ß₁ = (µ₂ - µ₁) tan γ₂
or µ₁ \(\frac{\mathrm{BM}_2}{\mathrm{M}_2 \mathrm{I}}\) - µ₂ \(\frac{\mathrm{BM}_2}{\mathrm{M}_2 \mathrm{I}_1}\) = (µ₂ - µ₁) \(\frac{\mathrm{BM}_2}{\mathrm{M}_2 \mathrm{C}_2}\)
or \(\frac{\mu_1}{\mathrm{M}_2 \mathrm{I}}-\frac{\mu_2}{\mathrm{M}_2 \mathrm{I}_1}=\frac{\mu_2-\mu_1}{\mathrm{M}_2 \mathrm{C}_2}\)
Since the lens is thin, So
M₂I ≃ CI, M₂I₁ ≃ CI₁ and M₂C₂ ≃ CC₂
∴ \(\frac{\mu_1}{\mathrm{CI}}-\frac{\mu_2}{\mathrm{CI}_2}=\frac{\mu_2-\mu_1}{\mathrm{CC}_2}\) ..............................(4)
Adding Eq. (2) and (4), we get
\(\frac{\mu_1}{\mathrm{CO}}+\frac{\mu_1}{\mathrm{CI}}=\left(\mu_2-\mu_1\right)\left[\frac{1}{\mathrm{CC}_1}+\frac{1}{\mathrm{CC}_2}\right]\)
Dividing both sides by µ₁, we get
_{\(\frac{1}{\mathrm{CO}}+\frac{1}{\mathrm{CI}}=\left(\frac{\mu_2}{\mu_1}-1\right)\left(\frac{1}{\mathrm{CC}_1}+\frac{1}{\mathrm{CC}_2}\right)\)}
Using sign conventions,
CO = -u, CI = v, CC₁ = R₁ and CC₂ = -R₂ and writing \frac{\mu_2}{\mu_1} = µ, we get
\(\frac{1}{-u}+\frac{1}{v}=(\mu-1)\left(\frac{1}{\mathrm{R}_1}+\frac{1}{-\mathrm{R}_2}\right)\)
or \(\frac{1}{-u}+\frac{1}{v}=(\mu-1)\left(\frac{1}{\mathrm{R}_1}-\frac{1}{\mathrm{R}_2}\right)\)
Since \(-\frac{1}{u}+\frac{1}{v}=\frac{1}{f}\), where f is the focal length of the lens
∴ \(\frac{1}{f}=(\mu-1)\left(\frac{1}{\mathrm{R}_1}-\frac{1}{\mathrm{R}_2}\right)\)
Note: This is the required lens maker's formula for thin convex lens. If n is taken as refractive index of the material of lens then
\(\frac{1}{f}=(n-1)\left[\frac{1}{\mathrm{R}_1}-\frac{1}{\mathrm{R}_1}\right]\)
Take µ₁ = n₁ and µ₂ = n₂

Question 48.
Draw the labelled ray diagram for the formation of image by a compound microscope. Derive the expression for the total magnification of a compound micro-scope. Explain why both the objective and the eyepiece of a compound microscope must have short focal lengths.
Answer:
It is an instrument used to see highly magnified image of tiny objects.
Principle. It is based on the principle that when a small object is placed just outside the focus of objective lens, its real, inverted and magnified image is formed on the other side of the lens. This image acts as an object for eye lens, the eye lens is so adjusted that the final image is produced at least distance of distinct vision.

Construction. It consists of two convex lenses of shorter focal lengths arranged co-axially at the ends of two sliding tubes.
(i) Objective. It is a convex lens of very short focal length and of small aperture and is placed near the object to be magnified.
(ii) Eye piece. It is a convex lens of short focal length and of comparatively large aperture and is placed near the eye for seeing the final image which is formed at least distance of distinct vision.

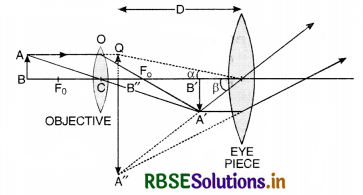
The distance between the two lenses can be adjusted by rack and pinion arrangement.
Let a tiny object AB be placed in front of objective at a distance more than f₀. Its real and enlarged image is formed at A' B'. This image A'B' acts as an object for eye piece and forms final image at A"B" i.e. at a distance D, the distance of distinct vision.

Magnifying Power of Microscope is defined as the ratio of the angle subtended on the eye by the final image to the angle subtended on the eye by the object, when both the final image and the object are situated at least distance of distinct vision.
Magnifying power, M = \(\frac{\beta}{\alpha}\)
Since angles are small, therefore, tan ß ≃ ß and tan α ≃ α.

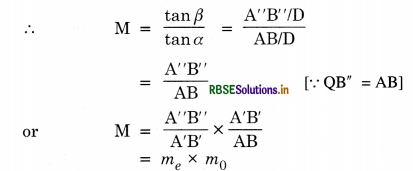
where m_e and m₀ are the magnifying powers of eye piece and the objective.
m₀ = \(\frac{\mathrm{A}^{\prime} \mathrm{B}^{\prime}}{\mathrm{AB}}=\frac{\mathrm{CB}^{\prime}}{\mathrm{CB}}\)
But CB is nearly equal to (-f₀) and CB' is equal to the length of the tube L [since the image A'B' is formed very close to eye lens]
m₀ = \(\frac{\mathrm{L}}{\left(-f_0\right)}\)
Also m_e = 1 + \(\frac{\mathrm{D}}{f_e}\) [As in simple microscope]
∴ M = \(-\frac{\mathrm{L}}{f_0}\left(1+\frac{\mathrm{D}}{f_e}\right)\)
(Negative sign shows that final image is inverted with respect to the object.)

Thus we find that, if the focal length of objective lens and eye lens are short, the magnifying power will be large. Magnifying power of compound microscope when final image is at infinity. Magnifying power is defined as the angle subtended on the eye by the final image to the angle subtanded on the eye by the object, at the unaided eye, when final image is formed at infinity. When final image is formed at infinity.

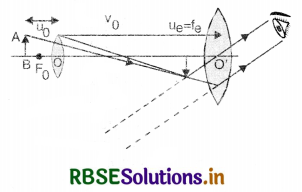
The angular magnification due to eye piece m_e = \(\frac{\mathrm{D}}{f_e}\)
The angular magnification due to objective lens m₀ = \(\frac{\mathrm{L}}{f_0}\)
∴ M = m₀m_e = \(\frac{\mathrm{L}}{f_0} \times \frac{\mathrm{D}}{f_e}\)
Thus we find that, to have large magnification, the focal length of the objective lens and eye lens must be small.

Question 49.
Derive the lens formula \(\frac{1}{f}=\frac{1}{v}-\frac{1}{u}\) for a concave lens, using the necessary ray diagram. 
Two lenses of powers 10D and -5D are placed in contact.
(i) Calculate the power of the new lens.
(ii) Where should an object be held from the lens, so as to obtain a virtual image of magnification 2?
Answer:
Consider a concave lens of focal length f and optical centre C. Let an object AB be placed perpendicular to the principal axis at any suitable distance. The image formed by this lens is always virtual, erect and on the same side of the lens as shown in Fig. LAQ 26.

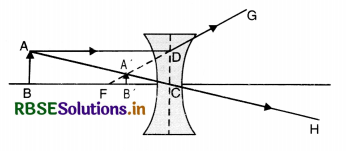
∆ ABC and ∆ A'B'C are similar, so
\(\frac{\mathrm{A}^{\prime} \mathrm{B}^{\prime}}{\mathrm{AB}}=\frac{\mathrm{CB}^{\prime}}{\mathrm{CB}}\) .........................(1)
∆ DCF and ∆ A'B'F are similar, so
\(\frac{\mathrm{A}^{\prime} \mathrm{B}^{\prime}}{\mathrm{DC}}=\frac{\mathrm{B}^{\prime} \mathrm{F}}{\mathrm{CF}}\)
But DC = AB
∴ \(\frac{\mathrm{A}^{\prime} \mathrm{B}^{\prime}}{\mathrm{AB}}=\frac{\mathrm{B}^{\prime} \mathrm{F}}{\mathrm{CF}}\) ......................(2)
From Eq. (1) and (2), we have
\(\frac{\mathrm{CB}^{\prime}}{\mathrm{CB}}=\frac{\mathrm{B}^{\prime} \mathrm{F}}{\mathrm{CF}}\)
or \(\frac{\mathrm{CB}^{\prime}}{\mathrm{CB}}=\frac{\mathrm{CF}-\mathrm{CB}^{\prime}}{\mathrm{CF}}\) .........................(3)
Using sign conventions,
Let CB' = -v, CB = -u, CF = -f
So Eq.(3) becomes
\(\frac{-v}{-u}=\frac{-f+v}{-f}\)
or -vf = -uf + uv
Dividing both sides by uvf, we get


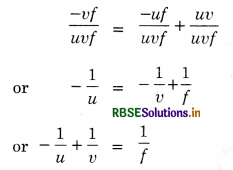
(i) Power of the combination
= P₁ + P₂ = 10D + (-5D) = 5D

(ii) So focal length of the combination
f = \(\frac{100}{P}=\frac{100}{5}\) = 20 cm
Given m = \(\frac{v}{u}\) so v = mu = 2u
since \(\frac{1}{f}-\frac{1}{u}+\frac{1}{24}\)
or u = 10 cm

Question 50.
(i) Define the term power of a lens. Write its SI units.
(ii) Derive the expression for the power of two thin lenses placed in contact with each other.
Answer:
(i) Power of lens is the reciprocal of its focal length in metre.
i.e. P = \(\frac{1}{f(\text { in } m)}\)
SI units of power is dioptre (D).
(ii) Power of two thin lenses in contact
Derivation of the relation
\(\frac{1}{f}=\frac{1}{f_1}+\frac{1}{f_2}\)
Consider an object O placed at a distance u on principal axis of the lens A. Rays of light starting from O form the image I₁.
∴ \(\frac{1}{v_1}-\frac{1}{u}=\frac{1}{f_1}\) ...............................(1)
Place the lens B in contact with A. The image I₁, will serve as virtual object and forms a real image I.

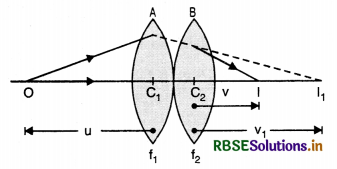
∴ Again apply lens formula,
\(-\frac{1}{v_1}+\frac{1}{v}=\frac{1}{f_2}\) .............................(2)
Adding (1) and (2), we have
\(\frac{1}{v}-\frac{1}{u}=\frac{1}{f_1}+\frac{1}{f_2}\) ............................(3)
But \(\frac{1}{v}-\frac{1}{u}=\frac{1}{f}\)
where f is the focal length of combination
From (3), \(\frac{1}{f}=\frac{1}{f_1}+\frac{1}{f_2}\)
The total power of the lens combination is given by
P = P₁ + P₂
If the two lens of focal lengths f₁ and f₂ are placed at a distance x apart, then the focal length of the combination will be:

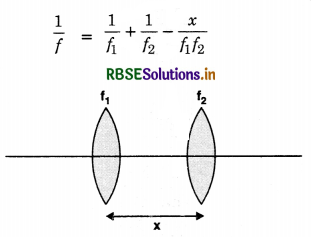
The power of combination is given by
P = P₁ + P₂ - xP₁P₂

Question 51.
A spherical surface of radius of curvature R, separates a rarer and a denser medium as shown in the figure. Complete the path of the incident ray of light, showing the formation of a real image. Hence derive the relation connecting object distance ‘u’, image distance ‘v’, radius of curvature R and the refractive indices n₁ and n₂ of two media.
Briefly explain how the focal length of a convex lens changes, with increase in wavelength of incident light.
Answer:
Sign Conventions

• All the distances are to be measured from the pole of spherical surface.
• The distances measured in the same direction as the incident light are taken as positive.
• Distances measured in the direction opposite to the direction of the incident light are taken as negative.

Asumptions:

• Object is a point object lying on the principal axis.
• The aperture of refracting edge is small.
• The indcident ray from the object strikes the surface at a point very close to point so that angles of incidence and refraction are very small.

Derivation. Consider a point object O be situated on the principal axis of the convex spherical surface. Let P be pole and C be centre of curvature and PC = R be the radius of curvature of the surface. Let µ₁ and µ₂ be refractive indexes of rarer and denser medium respectively as shown in the figure.
Let incident ray OA refracts at point A and bends towards the normal CAN and real image is formed at I.
From Snell’s law, for small i and r, we have
\(\frac{\sin i}{\sin r}=\frac{i}{r}=\frac{\mu_2}{\mu_1}\)
or µ₁ i = µ₂ r ..............................(1)

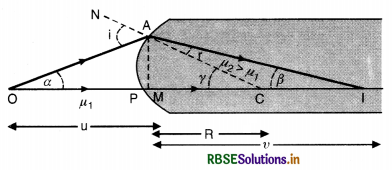
In ∆ AOC,
i = α + γ
In ∆ AIC,
γ = r + ß
or r = γ - ß
Putting the values of i and r in equation (1), we get
µ₁ (α + γ) = µ₂ (γ - ß)
or µ₁α + µ₁γ = µ₂γ - µ₂ß
or µ₁α + µ₂ß = (µ₂ - µ₁) γ ...............................(2)
Since α, ß and γ are small, so they can be replaced by their tangents. So equation (2) becomes
µ₁ tan α + µ₂ tan ß = (µ₂ - µ₁) tan γ
or µ₁ \(\frac{\mathrm{AM}}{\mathrm{MO}}\) + µ₂ \(\frac{\mathrm{AM}}{\mathrm{MI}}\) = (µ₂ - µ₁) \(\frac{\mathrm{AM}}{\mathrm{MC}}\)
or \(\frac{\mu_1}{\mathrm{MO}}+\frac{\mu_2}{\mathrm{MI}}=\frac{\mu_2-\mu_1}{\mathrm{MC}}\)
Since M is very close to the pole P,
so MO ≃ PO, MI ≃ PI and MC ≃ PC
∴ \(\frac{\mu_1}{\mathrm{PO}}+\frac{\mu_2}{\mathrm{PI}}=\frac{\mu_2-\mu_1}{\mathrm{PC}}\)
Using sign conventions,
PO = -u, PI = v and PC = R,
we get

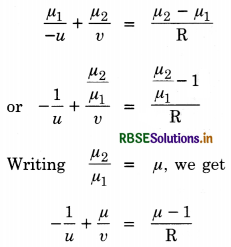
When wavelength is increased, the value of n decreases and hence the focal length of the lens increases with increase in wavelength.

Question 52.
Draw a graph to show the angle of deviation d with the variation of angle of incidence i for a monochro-matic ray of light passing through a prism of refracting angle A. Deduce the relation 
n = \(\frac{\sin \frac{A+\sin \delta_m}{2}}{\sin \frac{A}{2}}\)
Answer:
(a) Prism. A prism is a wedge-shaped body made from a refracting medium bounded by two plane faces inclined to each other at some angle. The two plane faces are called the refracting faces. The angle included between these two faces is called the angle of prism or refracting angle. ABC represents the principal section of a glass prism having ∠A as refracting angle.

(b) A ray EF is incident on the face AB at the point F where N₁FO is the normal and so i is the angle of incidence. The refracted ray FG bends towards the normal such that r₁ is the angle of refraction. The ray FG suffers refraction from face AC at G bends away from the normal and goes along GH such that e is the angle of emergence. 

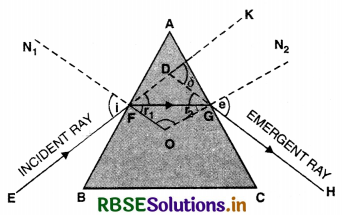
In the absence of the prism, the incident ray EF would have proceeded straight but due to refraction through the prism, it changes its path along the direction DGH. Thus ∠KDH gives the angle of deviation i.e. the angle through which the incident ray gets deviated in passing through the prism.
Now in ∆ DFG, external angle,
δ = ∠DFG + ∠DGF
or δ = i - r₁ + e - r₂
or δ = i + e - (r₁ + r₂) ...................(1)
In quadrilateral AFOG, we have
∠AFO + A + ∠AGO + ∠O = 360°
or 90° + A + 90° + ∠O = 360°
or A + ∠O = 180°
Also, in triangle FGO,
r₁ + r₂ + ∠O = 180°
∴ A + ∠O = r₁ + r₂ + ∠O
or A = r₁ + r₂ .......................(2)
Substituting in equation (1), we have
δ = i + e - A .......................(3)
or A + δ = i + e .........................(4)
Here δ is the angle through which a ray deviates on passing through a small angled prism, and the angle of deviation depends not only upon the material of the prism but also upon the angle of incidence and of prism.

(c) It is found that if the angle of incidence is increased gradually, there is variation in the angle of deviation, it decreases first, attains a minimum value dm and then it starts increasing. So minimum deviation is the angle at which the deviation of ray of light is minimum and the prism is said to be in minimum deviation position.

If we plot a graph between angle of incidence and angle of deviation, the graph is as shown in Fig. 9.89. From the graph, we find that δ is same for two angles of incidence i₁ and i₂ but at minimum deviation δ_m, there is only one angle of incidence.
It is found that at minimum deviation position.
i.e. at δ = δ_m
e = i and r₁ = r₂ = r (say)

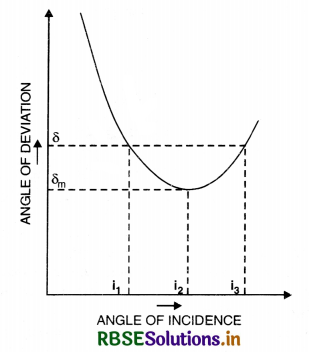
Since δ = i + e - A
∴ At minimum deviation position,
we have
δ_m = i + e - A = i + i - A
or δ_m = 2i - A
or 2i = A + δ_m
or i = \(\frac{\mathrm{A}+\delta_m}{2}\) ...........................(5)
Also at minimum deviation position
A = r₁ + r₂ = r + r = 2r
or r = \(\frac{\mathrm{A}}{2}\) .......................(6)
If µ is the refractive index of the prism, then from Snell's law at surface AB, we have
µ = \(\frac{\sin i}{\sin r}\)
Using Eqs. (5) and (6), we get
µ = \(\frac{\sin \frac{\mathrm{A}+\delta_m}{2}}{\sin \mathrm{A} / 2}\)

Question 53.
Draw a ray diagram to show the working of a compound microscope. Deduce an expression for the total magnification when the final image is formed at the near point.
Answer:
It is an instrument used to see highly magnified image of tiny objects.
Principle. It is based on the principle that when a small object is placed just outside the focus of objective lens, its real, inverted and magnified image is formed on the other side of the lens. This image acts as an object for eye lens, the eye lens is so adjusted that the final image is produced at least distance of distinct vision.

Construction. It consists of two convex lenses of shorter focal lengths arranged co-axially at the ends of two sliding tubes.
(i) Objective. It is a convex lens of very short focal length and of small aperture and is placed near the object to be magnified.
(ii) Eye piece. It is a convex lens of short focal length and of comparatively large aperture and is placed near the eye for seeing the final image which is formed at least distance of distinct vision.

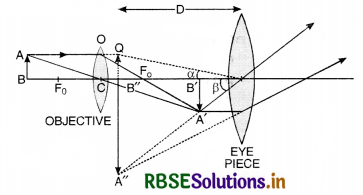
The distance between the two lenses can be adjusted by rack and pinion arrangement.

Let a tiny object AB be placed in front of objective at a distance more than f₀. Its real and enlarged image is formed at A' B'. This image A'B' acts as an object for eye piece and forms final image at A"B" i.e. at a distance D, the distance of distinct vision.

Magnifying Power of Microscope is defined as the ratio of the angle subtended on the eye by the final image to the angle subtended on the eye by the object, when both the final image and the object are situated at least distance of distinct vision.
Magnifying power, M = \(\frac{\beta}{\alpha}\)
Since angles are small, therefore, tan ß ≃ ß and tan α ≃ α.

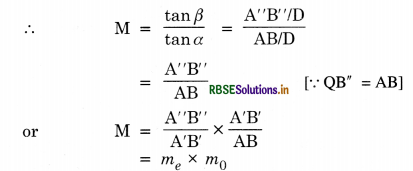
where m_e and m₀ are the magnifying powers of eye piece and the objective.
m₀ = \(\frac{\mathrm{A}^{\prime} \mathrm{B}^{\prime}}{\mathrm{AB}}=\frac{\mathrm{CB}^{\prime}}{\mathrm{CB}}\)
But CB is nearly equal to (-f₀) and CB' is equal to the length of the tube L [since the image A'B' is formed very close to eye lens]
m₀ = \(\frac{\mathrm{L}}{\left(-f_0\right)}\)
Also m_e = 1 + \(\frac{\mathrm{D}}{f_e}\) [As in simple microscope]
∴ M = \(-\frac{\mathrm{L}}{f_0}\left(1+\frac{\mathrm{D}}{f_e}\right)\)
(Negative sign shows that final image is inverted with respect to the object.)
Thus we find that, if the focal length of objective lens and eye lens are short, the magnifying power will be large. Magnifying power of compound microscope when final image is at infinity. Magnifying power is defined as the angle subtended on the eye by the final image to the angle subtanded on the eye by the object, at the unaided eye, when final image is formed at infinity. When final image is formed at infinity.

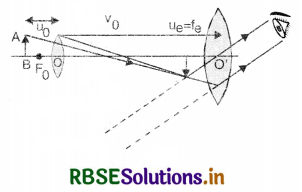
The angular magnification due to eye piece m_e = \(\frac{\mathrm{D}}{f_e}\)
The angular magnification due to objective lens m₀ = \(\frac{\mathrm{L}}{f_0}\)
∴ M = m₀m_e = \(\frac{\mathrm{L}}{f_0} \times \frac{\mathrm{D}}{f_e}\)
Thus we find that, to have large magnification, the focal length of the objective lens and eye lens must be small.

Question 54.
Define the magnifying power of a compound microscope. Why should both the objective and the eye piece have small focal lengths in a microscope?
Answer:
It is an instrument used to see highly magnified image of tiny objects.
Principle. It is based on the principle that when a small object is placed just outside the focus of objective lens, its real, inverted and magnified image is formed on the other side of the lens. This image acts as an object for eye lens, the eye lens is so adjusted that the final image is produced at least distance of distinct vision.

Construction. It consists of two convex lenses of shorter focal lengths arranged co-axially at the ends of two sliding tubes.
(i) Objective. It is a convex lens of very short focal length and of small aperture and is placed near the object to be magnified.
(ii) Eye piece. It is a convex lens of short focal length and of comparatively large aperture and is placed near the eye for seeing the final image which is formed at least distance of distinct vision.

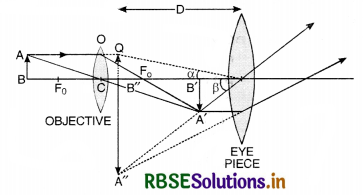
The distance between the two lenses can be adjusted by rack and pinion arrangement.
Let a tiny object AB be placed in front of objective at a distance more than f₀. Its real and enlarged image is formed at A' B'. This image A'B' acts as an object for eye piece and forms final image at A"B" i.e. at a distance D, the distance of distinct vision.

Magnifying Power of Microscope is defined as the ratio of the angle subtended on the eye by the final image to the angle subtended on the eye by the object, when both the final image and the object are situated at least distance of distinct vision.
Magnifying power, M = \(\frac{\beta}{\alpha}\)
Since angles are small, therefore, tan ß ≃ ß and tan α ≃ α.

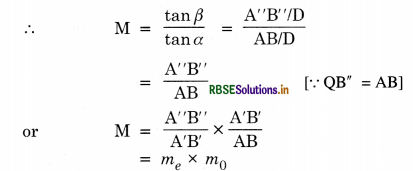
where m_e and m₀ are the magnifying powers of eye piece and the objective.
m₀ = \(\frac{\mathrm{A}^{\prime} \mathrm{B}^{\prime}}{\mathrm{AB}}=\frac{\mathrm{CB}^{\prime}}{\mathrm{CB}}\)
But CB is nearly equal to (-f₀) and CB' is equal to the length of the tube L [since the image A'B' is formed very close to eye lens]
m₀ = \(\frac{\mathrm{L}}{\left(-f_0\right)}\)
Also m_e = 1 + \(\frac{\mathrm{D}}{f_e}\) [As in simple microscope]
∴ M = \(-\frac{\mathrm{L}}{f_0}\left(1+\frac{\mathrm{D}}{f_e}\right)\)
(Negative sign shows that final image is inverted with respect to the object.)
Thus we find that, if the focal length of objective lens and eye lens are short, the magnifying power will be large. Magnifying power of compound microscope when final image is at infinity. Magnifying power is defined as the angle subtended on the eye by the final image to the angle subtanded on the eye by the object, at the unaided eye, when final image is formed at infinity. When final image is formed at infinity.

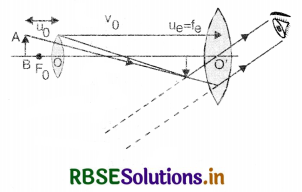
The angular magnification due to eye piece m_e = \(\frac{\mathrm{D}}{f_e}\)
The angular magnification due to objective lens m₀ = \(\frac{\mathrm{L}}{f_0}\)
∴ M = m₀m_e = \(\frac{\mathrm{L}}{f_0} \times \frac{\mathrm{D}}{f_e}\)
Thus we find that, to have large magnification, the focal length of the objective lens and eye lens must be small.

Question 55.
(a) Draw a ray diagram to show refraction of a ray of monochromatic light passing through a glass prism. Deduce the expression for the refractive index of glass in terms of angle of prism and angle of minimum deviation.
(b) Explain briefly the phenomenon of total internal reflection used in fibre optics.
Answer:
(a) Prism. A prism is a wedge-shaped body made from a refracting medium bounded by two plane faces inclined to each other at some angle. The two plane faces are called the refracting faces. The angle included between these two faces is called the angle of prism or refracting angle. ABC represents the principal section of a glass prism having ∠A as refracting angle.

(b) A ray EF is incident on the face AB at the point F where N₁FO is the normal and so i is the angle of incidence. The refracted ray FG bends towards the normal such that r₁ is the angle of refraction. The ray FG suffers refraction from face AC at G bends away from the normal and goes along GH such that e is the angle of emergence. 

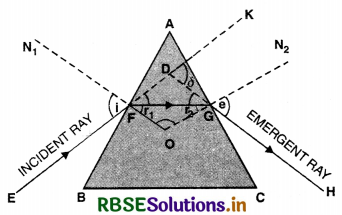
In the absence of the prism, the incident ray EF would have proceeded straight but due to refraction through the prism, it changes its path along the direction DGH. Thus ∠KDH gives the angle of deviation i.e. the angle through which the incident ray gets deviated in passing through the prism.
Now in ∆ DFG, external angle,
δ = ∠DFG + ∠DGF
or δ = i - r₁ + e - r₂
or δ = i + e - (r₁ + r₂) ...................(1)
In quadrilateral AFOG, we have
∠AFO + A + ∠AGO + ∠O = 360°
or 90° + A + 90° + ∠O = 360°
or A + ∠O = 180°
Also, in triangle FGO,
r₁ + r₂ + ∠O = 180°
∴ A + ∠O = r₁ + r₂ + ∠O
or A = r₁ + r₂ .......................(2)
Substituting in equation (1), we have
δ = i + e - A .......................(3)
or A + δ = i + e .........................(4)

Here δ is the angle through which a ray deviates on passing through a small angled prism, and the angle of deviation depends not only upon the material of the prism but also upon the angle of incidence and of prism.

(c) It is found that if the angle of incidence is increased gradually, there is variation in the angle of deviation, it decreases first, attains a minimum value dm and then it starts increasing. So minimum deviation is the angle at which the deviation of ray of light is minimum and the prism is said to be in minimum deviation position.

If we plot a graph between angle of incidence and angle of deviation, the graph is as shown in Fig. 9.89. From the graph, we find that δ is same for two angles of incidence i₁ and i₂ but at minimum deviation δ_m, there is only one angle of incidence.
It is found that at minimum deviation position.
i.e. at δ = δ_m
e = i and r₁ = r₂ = r (say)

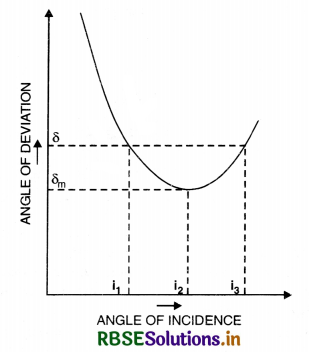
Since δ = i + e - A
∴ At minimum deviation position,
we have
δ_m = i + e - A = i + i - A
or δ_m = 2i - A
or 2i = A + δ_m
or i = \(\frac{\mathrm{A}+\delta_m}{2}\) ...........................(5)
Also at minimum deviation position
A = r₁ + r₂ = r + r = 2r
or r = \(\frac{\mathrm{A}}{2}\) .......................(6)
If µ is the refractive index of the prism, then from Snell's law at surface AB, we have
µ = \(\frac{\sin i}{\sin r}\)
Using Eqs. (5) and (6), we get
µ = \(\frac{\sin \frac{\mathrm{A}+\delta_m}{2}}{\sin \mathrm{A} / 2}\)

Principle. The working of optical fibre is based on the phenomenon of total internal reflection. Optical fibres consist of many thousands of verjr long fine quality, glass/quartz fibres. They are coated with a thin layer of a material of low refractive index. For example, the strand can be 0.0001 cm in diameter and the refractive index of the main fibre 1.7 and that of coating 1.5 (Fig. LAQ 14).

When the light is incident on one end of the fibre at a small angle, the light passes inside. It undergoes repeated total internal reflections along the fibre and finally comes out. The angle of incidence here is larger than the critical angle of the fibre material with respect of its coating. Even if the fibre is bent, the light can easily travel through along the fibre.

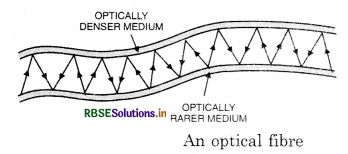
Uses of Optical Fibre

1. A bundle of optical fibres can be used as a ‘light pipe’ in medical and optical examination called endoscopy.
2. It can also be used for optical signal transmission.
3. Optical fibres have also been used for transmission and receiving electrical signals which are converted to light by suitable transducers. The main requirement is that thereby very little absorption of light as it travels for long distances inside the optical fibre. This has been achieved by purification and special preparation of materials such as quartz.

Question 56.
(a) Draw a ray diagram of compound microscope for the final image formed at least distance of distinct vision?
(b) An angular magnification of 30X is desired using an objective of focal length 1.25 cm and an eye piece of focal length 5 cm. How will you set up the compound microscope for the final image formed at least distance of distinct vision?
Answer:
Ray diagram of compound microscope when final image is formed at least distance of distinct vision:

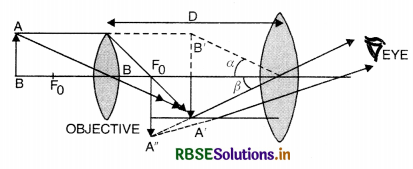
Question 57.
(a) Draw a ray diagram to show image formation when the concave mirror produces a real, inverted and magnified image of the object.
(b) Obtain the mirror formula and write the expression for the linear magnification.
(c) Explain two advantages of a reflecting telescope over a refracting telescope.
Answer:
(a) Ray diagram for real inverted and magnified image with concave mirror.

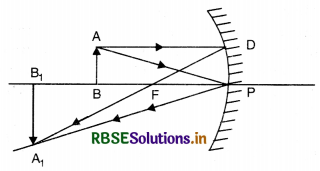
(b) Mirror formula

Mirror Formula. A formula which gives the relation between the image distance (v), the object distance (u) and the focal length (f) of a mirror is known as mirror formula
\(\frac{1}{\text { Focal length }}=\frac{1}{\text { Image distance }}\) + \(\frac{1}{\text { Object distance }}\)
\(\frac{1}{f}=\frac{1}{v}+\frac{1}{u}\)

Assumptions

• Aperture of mirror is small.
• Incident ray makes small angles with principal axis.
• Object lies on the principal axis.
• Object lies on left hand side of the mirror.

Case of Concave Mirror
Consider an object AB placed beyond centre of curvature of a concave mirror, on its principal axis and on the left hand side.
A ray AD parallel to principal axis is incident on the mirror at point D and is reflected to pass through F. Another ray AE passing through centre of curvature C is reflected along the same path. Two rays of light intersect at point A₁. Thus A₁B₁ is real, inverted and diminished image of AB formed between C and F.

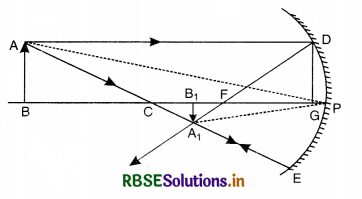
Draw DG ⊥ on principal axis.
∆s DGF and A₁B₁F are similar,
∴ \(\frac{\mathrm{DG}}{\mathrm{A}_1 \mathrm{~B}_1}=\frac{\mathrm{GF}}{\mathrm{FB}_1}\)
But DG = AB
\(\frac{\mathrm{AB}}{\mathrm{A}_1 \mathrm{~B}_1}=\frac{\mathrm{GF}}{\mathrm{FB}_1}\) ..........................(i)
Again ∆s ABC and A₁B₁C are similar
∴ \(\frac{\mathrm{AB}}{\mathrm{A}_1 \mathrm{~B}_1}=\frac{\mathrm{CB}}{\mathrm{CB}_1}\) ......................(ii)
Comparing (i) and (ii)
\(\frac{\mathrm{GB}}{\mathrm{FB}_1}=\frac{\mathrm{CB}}{\mathrm{CB}_1}\)
Since the aperture is small, therefore, point D and point G lie very close to P.
∵ GF = PF
∴ \(\frac{\mathrm{PF}}{\mathrm{FB}_1}=\frac{\mathrm{CB}}{\mathrm{CB}_1}\) .........................(iii)
Since FB₁ = PB₁ - PF
CB = PB - PC
CB₁ = PC - PB₁
Substituting in (iii), we get
\(\frac{\mathrm{PF}}{\mathrm{PB}_1-\mathrm{PF}}=\frac{\mathrm{PB}-\mathrm{PC}}{\mathrm{PC}-\mathrm{PB}_1}\)
Applying sign conventions, we get
PF = -f, PC = -2f, PB = -u and PB₁ = -v
\(\frac{-f}{-v-(-f)}=\frac{-u-(-2)}{-2 f-(-v)}\)
\(\frac{-f}{-v+f}=\frac{-u+2 f}{-2 f+v}\)
2f² -vf = uv - uf - 2fv + 2f²
or uv - uf - 2fv = -vf
-uf - vf = -uv
uf + vf = uv
Dividing both sides by uvf, we get
\(\frac{u f}{u v f}+\frac{v f}{u v f}=\frac{u v}{u v f}\)
\(\frac{1}{v}+\frac{1}{u}=\frac{1}{f}\)
Since As ABP and A, B, P are similar (in fig LAQ 57)
∴ \(\frac{\mathrm{A}_1 \mathrm{~B}_1}{\mathrm{AB}}=\frac{\mathrm{PB}_1}{\mathrm{~PB}}\)
or \(-\frac{h_2}{h_1}=\frac{-v}{-u}=\frac{v}{u}\)
∴ m = \(\frac{h_2}{h_1}=-\frac{v}{u}\)
(c) (i) In reflecting telescope, the image is free from chromatic and spherical aberration.
(ii) In reflecting telescope, the concave mirror is of large aperture and hence its resolving power is high.

HOTS QUESTIONS

Question 1.
(a) A short linear object of length b lies along the axis of a concave mirror of focal length f at a distance u from the pole. What is the size of the image?
(b) If object begins to move with speed v₀, what will be the speed of its image?
Answer:
(a) Since \(\frac{1}{u}+\frac{1}{v}=\frac{1}{f}\) (mirror formula) ....................(i)
Differentiating both sides, we get
\(-\frac{1}{u^2} d u-\frac{1}{v^2} d v=0\)
or dv = \(-\frac{v^2}{u^2}\)du  ..............................(ii)
Multiplying both sides of eq. (i) with u, we get
\(\frac{u}{v}\) + 1 = \(\frac{u}{f}\)
∴ \(\frac{v}{u}=\frac{f}{u-f}\) ............................(iii)
Putting eq.(iii) in (ii) and taking length of the object on axis du = b, we get:
dv = \(-\left(\frac{f}{u-f}\right)^2\) du
= \(-\left(\frac{f}{u-f}\right)^2\) b .......................(iv)
-ve sign means that the image is longitudinally inverted
∴ size of image
(dv) = b\(\left(\frac{f}{u-f}\right)^2\)

(b) From eq. (iv)

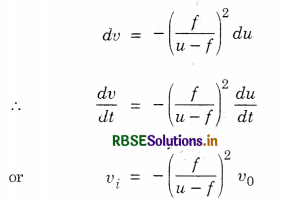
Question 2.
A ray of light falls on a transparent glass slab of refractive index 1.62. If the reflected ray and refracted rays are mutually perpendicular. What is the angle of incidence? Give calculations.
Answer:
Let a ray AO incident on the glass slab at O and is reflected along OB and refracted along OC having angle of incidence i and angle of refraction r as shown in the given figure 9.114.

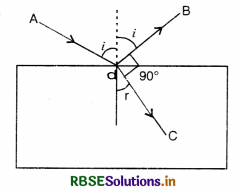
From the figure
i + 90° + r = 180°
or  i + r = 90°
or r = 90° - i
From Snell's law
µ = \(\frac{\sin i}{\sin r}=\frac{\sin i}{\sin (90-i)}=\frac{\sin i}{\cos i}\)
= tan i
or i = tan^-1 µ = tan ^-1 (1.62) = 59°19'

Question 3.
A motor car is fitted with a convex driving mirror of focal length 20 cm. A second motor car 2 m broad and 1.6 m high is 6 m away from the first car.
(i) Calculate the position and size of the image of the second car seen in the mirror of first.
(ii) If the second car is overtaking at a relative speed of 14 ms^-1, how fast will the image be moving and in what diection?
Answer:
(i) Here u = - 6m, f = 20 cm = 0.2 m
From mirror formula
\(\frac{1}{v}+\frac{1}{u}=\frac{1}{f}\) ................................(i)
∴ \(\frac{1}{v}=\frac{1}{f}-\frac{1}{u}=\frac{1}{0.2}-\frac{1}{6}\)
or v = \(\frac{6}{31}\) = 0.194 m = 19.4 cm
Linear magnification
m = \(\frac{\mathrm{I}}{\mathrm{O}}=\frac{v}{u}\) or I = \(\frac{v}{u}\) O
Breadth b = \(\frac{0.194}{6}\) x 2 = 0.064 m = 6.4 cm
Height h = \(\frac{0.194}{6}\) x 1.6 = 0.052 m = 5.2 cm

(ii) Differentiating both sides of eq.(i), we get
\(-\frac{1}{v^2} \frac{d v}{d t}-\frac{1}{u^2} \frac{d u}{d t}\) = 0 or \(\frac{d v}{d t}=-\frac{v^2}{u^2} \frac{d u}{d t}\)
∴ Speed of image
Vi = \(-\frac{v^2}{u^2}\) x speed of object
 = \(-\left(\frac{0.194}{6}\right)^2\) x 15 = 0.016 ms^-1
 = 1.6 km s^-1
 
Question 4.
A ray of light strikes a plane mirror at an angle of incidence 45° as shown in the figure 9.115. After reflection, the ray passes through a prism of refractive index 1.5 whose apex angle is 4°. Through what angle must the mirror be rotated if the total deviation of the ray be 90°?
Answer:
Deviation caused by mirror
δ₁ = 180° - 2i = 180° - 2 x 45° = 90°
Deviation caused by small angled prism
δ₂ = (µ - 1) α = (1.5 - 1) 4° = 2° (always)
Net deviation produced by the system
= δ₁ + δ₂ = 90° + 2° = 92° > 90°

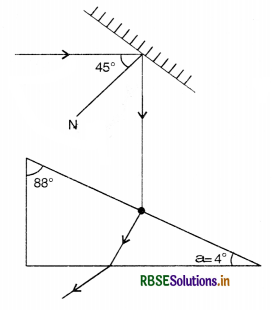
Greater is angle of incidence on mirror, smaller is the deviation.
Let the mirror be rotated clockwise by an angle to increase angle of incidence.
The deviation produced by the mirror
= 180° - 2 (45° + ß) = 90 - 2ß
Total deviation produced = 90 - 2ß + 2° = 92° - 2ß
∴ given 92°- 2ß = 90°
or ß = 1°

Question 5.
A glass sphere of radius 5 x 10 m has a small bubble 2 x 10^-2 m from its centre. The bubble is viewed along a diameter of the sphere, from the side on which it lies. How far from the sphere will it appear? Refractive index of glass 1.5.
Answer:
Since \(\frac{\mu_2}{v}-\frac{\mu_1}{u}=\frac{\mu_2-\mu_1}{\mathrm{R}}\)
Given µ₁ = 1.5, µ₂ = 1, u = 5 x 10^-2 - 2 x 10^-2 = 3 x 10^-2 m
R = 5 x 10^-2