RBSE Class 12 Physics Important Questions Chapter 8 वैद्युतचुंबकीय तरंगें

Rajasthan Board RBSE Class 12 Physics Important Questions Chapter 8 वैद्युतचुंबकीय तरंगें Important Questions and Answers.

RBSE Class 12 Physics Chapter 8 Important Questions वैद्युतचुंबकीय तरंगें

अति लघुत्तरीय प्रश्न

प्रश्न 1.
विद्युत चुम्बकीय तरंगों में विद्युत क्षेत्र \(\overrightarrow{\mathbf{E}}\) एवं चुम्बकीय, क्षेत्र \(\overrightarrow{\mathbf{B}}\) के मध्य (a) कोण एवम् (b) कलान्तर का मान लिखिए।
उत्तर:
(a) \(\overrightarrow{\mathbf{E}} व \overrightarrow{\mathbf{B}}\) के मध्य कोण \(\frac{\pi}{2}\)
(b) \(\overrightarrow{\mathbf{E}}\) व \(\overrightarrow{\mathbf{E}}\) के मध्य कलांतर शून्य

प्रश्न 2.
कोई दो मैक्सवेल समीकरणें लिखिए।
उत्तर:
(i) \(\oint \overrightarrow{\mathrm{E}} \cdot d \overrightarrow{\mathrm{S}}=\frac{q}{\varepsilon_0}\)
(ii) \(\oint \overrightarrow{\mathrm{E}} \cdot d \overrightarrow{\mathrm{S}}\) = 0

प्रश्न 3.
परा उच्च आवृत्ति (UHF) परिसर की आवृत्तियों का प्रसारण प्राय: किन तरंगों द्वारा होता है?
उत्तर:
रेडियो तरंगों द्वारा

प्रश्न 4.
रिमोट नियंत्रकों में कौन सी विद्युत चुम्बकीय तरंगों का उपयोग किया जाता है?
उत्तर:
अवरक्त तरंगें (Infrared waves)

प्रश्न 5.
संचार व्यवस्था के आवश्यक अवयवों के नाम लिखिए।
उत्तर:

• प्रेषित्र (Transmitter)
• संचार माध्यम (Communication Channel)
• अभिग्राही (Receiver)

प्रश्न 6.
निर्वात नलिका मैग्नेट्रॉन द्वारा उत्पन्न विद्युत चुम्बकीय तरंग का नाम लिखिए।
उत्तर:
सूक्ष्म तरंगें।

प्रश्न 7.
वेल्डिंग करते समय विशेष चश्मा या सीसे की खिड़की का मास्क विद्युत चम्बकीय विकिरण से आँखों को बचाने के लिए पहना जाता है। विकिरण का नाम और उसकी आवृत्ति परास लिखिए।
उत्तर:
पराबैंगनी किरणें
आवृत्ति परास - 10¹⁵ - 10¹⁶ Hz

प्रश्न 8.
विमान संचालन की रडार प्रणाली के लिए सूक्ष्म तरंगों को उपयुक्त क्यों माना जाता है?
उत्तर:
अपने लघु तरंगदैर्घ्य के कारण विमान संचालन में रडार प्रणाली के लिए सूक्ष्म तरंगें उपयुक्त है।

प्रश्न 9.
क्या विद्युत चुम्बकीय तरंगें ऊर्जा और संवेग वहन करती है?
उत्तर:
हाँ विद्युत चुम्बकीय तरंगें ऊर्जा और संवेग वहन करती है। क्योंकि जब ये किसी पृष्ठ पर आपतित होती हैं तो उस पर विकिरण दाब डालती है।

प्रश्न 10.
विद्युत और चुम्बकीय क्षेत्रों के आयामों के पदों में विद्युत चुम्बकीय तरंगों की चाल के लिए सम्बन्ध लिखिए।
उत्तर:
C = \(\frac{|\overrightarrow{\mathrm{E}}|}{|\overrightarrow{\mathrm{B}}|}\)

प्रश्न 11.
विद्युत और चुम्बकीय क्षेत्रों द्वारा निर्वांत में विद्युत चुम्बकीय तरंगों की चाल किस प्रकार निर्धारित की जाती है?
उत्तर:
विद्युत क्षेत्र सदिश \(|\overrightarrow{\mathrm{E}}| \) व चुम्बकीय क्षेत्र सदिश \(|\overrightarrow{\mathrm{B}}|\) के अनुपात के रूप में निर्धारित की जाती है।

प्रश्न 12.
(a) जल शोधन तथा 
(b) नेत्र शल्य चिकित्सा में उपयोग होने वाले विद्युत चुम्बकीय विकिरणों के नाम लिखिए।
उत्तर:
(a) पराबैंगनी किरणें, (b) पराबैगनी किरणे 

प्रश्न 13.
अवरक्त तरंगों को ऊष्मा तरंगें क्यों कहा जाता है?
उत्तर:
क्योंकि अधिकांश पदार्थों में विद्यमान जल के अणु अवरक्त तरंगों को तुरंत अवशोषित कर लेते हैं।

प्रश्न 14.
निम्नलिखित के लिए उपयोग किए जाने वाले विद्युत चुम्बकीय स्पेक्ट्रम के विकिरण का नाम लिखिए: 
(a) रडार 
(b) मानव शरीर के भीतरी भागों के फोटोग्राफ के लिए 
(c) रात्रि के समय और कूहाबन की स्थिति में आकाश का फोटोग्राफ लेने के लिए। प्रत्येक प्रकरण में आवृत्ति परिसर दीजिए।
उत्तर:
(a) सक्ष्म तरंगें
आवृत्ति परास - 10⁹ Hz - 10¹² Hz
(b) X किरणे
आवृत्ति परास - 10¹⁸ Hz - 10²⁰ Hz
(c) पराबैंगनी किरणें 
आवृत्ति परास - 10¹⁶ Hz - 10¹⁷ Hz

प्रश्न 15.
निम्नलिखित विद्युत चुम्बकीय तरंगों में से 
(a) न्यूनतम तरंगदैर्घ्य तथा 
(b) न्यूनतम आवृत्ति किसकी है? इन दोनों तरंगों में से प्रत्येक का एक उपयोग लिखिए।
उत्तर:
(a) न्यूनतम तरंगदैय की तरंग - गामा किरणें उपयोग - कैसंर कोशिकाओं को नष्ट करने में प्रयुक्त दवाओं में
(b) रेडियो तरंगें - रेडियो प्रसारण में

प्रश्न 16.
फोटो डायोड की उपयोग किसके संसूचन के लिए किया जाता है?
उत्तर:
प्रकाशिक सिग्नल 

लघु उत्तरीय प्रश्न

प्रश्न 1.
विद्युत चुम्बकीय तरंगों के कोई चार गुण लिखिए।
उत्तर:
विद्युत् - चुम्बकीय तरंगों के अभिलक्षण (Characteristics of Electromagnetic Waves)
(1) विद्युत् - चुम्बकीय तरंगें विद्युत् क्षेत्र एवं चुम्बकीय क्षेत्र के परस्पर लम्बवत् होती हैं।
(2) विधुत् - चुम्बकीय तरंगों के संचरण (propagation) के लिए माध्यम की आवश्यकता नहीं होती है।
(3) विद्युत् - चुम्बकीय तरंगें विद्युत् एवं चुम्बकीय क्षेत्रों से विक्षेपित नहीं होती क्योंकि ये उदासीन होती हैं अर्थात् इनमें कोई आवेशिव कण नहीं होते हैं।
(4) ये मुक्त आकाश में प्रकाश के वेग (c = 3 x 10⁸ ms^-1) से चलती हैं और इनकी चाल तरंगदैर्ध्य पर निर्भर नहीं करती है।
(5) ये त्वरित, दोलित एवं अवमंदित आवेशों के कारण उत्पन्न होती है।
(6) प्रकाश से सम्बन्धित समस्त घटनाओं के लिए विद्युत् क्षेत्र सदिश \((\vec{E})\) उत्तरदायी होता है, अत: इसे प्रकाश सदिश (light vector) भी कहते हैं।

(7) किसी माध्यम में विद्युत् - चुम्बकीय तरंगों की चाल
v = \(\frac{1}{\sqrt{\mu . \varepsilon}}\), जहाँ µ एवं ε क्रमश: माध्यम की निरपेक्ष चुम्बकशीलता (absolute permeability) एवं निरपेक्ष वैद्युतशीलता (absolute permitivity) हैं।
या v = \(\frac{1}{\sqrt{\mu_0 \mu_r \varepsilon_0 \cdot \varepsilon_r}}\), जहाँ µ_r व ε_r क्रमशः माध्यम की आपेक्षिक चुम्बकशीलता (relative permeability) व आपेक्षिक विद्युत्शीलता (relative permitivity) हैं।
या v = \(\frac{1}{\sqrt{\mu_r \cdot \varepsilon_r \cdot \mu_0 \cdot \varepsilon_0}}\)
= \(\frac{c}{\sqrt{\mu_r \cdot \varepsilon_r}}\), क्योंकि ε₀.µ₀ = \(\frac{1}{c^2}\)

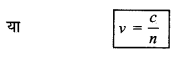
जहाँ; n = \(\sqrt{\mu_r \cdot \varepsilon_r}\) = माध्यम का अपवर्तनांक (refractive index) ...............(1)

(8) विद्युत् - चुम्बकीय तरंगों द्वारा ऊर्जा का स्थानान्तरण हो सकता है। विद्युत्-चुम्बकीय तरंगों द्वारा प्रति एकांक क्षेत्रफल से ऊर्जा स्थानान्तरण की दर (rate of energy transfer) को एक राशि से प्रदर्शित किया जाता है जिसे पॉइन्टिंग सदिश (Poynting vector) कहते हैं। इस सदिश को \(\overrightarrow{\mathrm{P}}\) द्वारा प्रदर्शित करते हैं। इसका मान,
\(\overrightarrow{\mathrm{P}}\) = \(\frac{\vec{E} \times \vec{B}}{\mu_0}\)
या \(\overrightarrow{\mathrm{P}}=\overrightarrow{\mathrm{E}} \times \overrightarrow{\mathrm{H}}\) ...............(2)
क्योंकि \(\frac{\overrightarrow{\mathrm{B}}}{\mu_0}\) = \(\overrightarrow{\mathrm{H}}\) चुम्बकन क्षेत्र की तीव्रता (Intensity of magnetising field)।

(9) विद्युत् - चुम्बकीय तरंग का औसत ऊर्जा घनत्व इस प्रकार दिया जाता है,
मुक्त आकाश में, स्थैतिक विद्युत क्षेत्र का ऊर्जा घनत्व
u_E = \(\frac{1}{2}\)ε₀E²
एवं मुक्त आकाश में स्थैतिक चुम्बकीय क्षेत्र का ऊर्जा घनत्व
u_B = \(\frac{1}{2 \mu_0}\)B²
दोनों का कुल ऊर्जा घनत्व
u = u_E + u_B
= \(\frac{1}{2}\)ε₀E² + \(\frac{1}{2 \mu_0}\)B²
परन्तु विद्युत चुम्बकीय तरंगों में \(\overrightarrow{\mathrm{E}}\) व \(\overrightarrow{\mathrm{B}}\) ज्यावक्रीय (sinusoidally) रूप से आकाश व समय में बदलते हैं।
अतः u = \(\frac{1}{2}\)ε₀E_rms² + \(\frac{1}{2 \mu_0}\)B_rms²
या u = \(\frac{1}{4}\)ε₀E_rms² + \(\frac{1}{4 \mu_0}\)B_rms² [∵ E_rms = \(\frac{E_0}{\sqrt{2}}\), B_rms = \(\frac{B_0}{\sqrt{2}}\)]
एवं E₀ = cB₀, और c² = \(\frac{1}{\mu_0 \varepsilon_0}\)
अतः u_E = \(\frac{1}{4}\) ε₀E₀² = \(\frac{1}{4} \)ε₀(cB₀)²
= \(\frac{1}{4}ε0\frac{\mathrm{B}_0^2}{\mu_0 \varepsilon_0}\) = \(\frac{1}{4 \mu_0}\) B₀² = u_B
अत: विद्युत चुम्बकीय तरंगों में E का औसत ऊर्जा घनत्व B के औसत ऊर्जा घनत्व के बराबर होता है एवं,

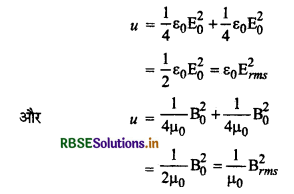
(10) विद्युत् - चुम्बकीय तरंगों की तीव्रता घनत्व पर निर्भर करती है।

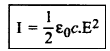
(11) विद्युत् - चुम्बकीय तरंगों के साथ संवेग भी सम्बद्ध है, अतः ये जिस सतह पर गिरती हैं उस पर दाब (pressure) डालती है। विद्युत्-चुम्बकीय तरंगों द्वारा डाले गये दाब को विकिरण दाब (radiation pressure) कहते हैं।

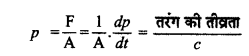
(12) विद्युत् - चुम्बकीय तरंगें परावर्तन, अपवर्तन, विवर्तन और व्यतिकरण की घटनाओं को प्रदर्शित करती हैं।
(13) विद्युत् - चुम्बकीय तरंगें अध्यारोपण के सिद्धान्त (principle of superposition) का अनुसरण करती हैं।

प्रश्न 2.
विस्थापन यारा की अवधारणा का समावेश मैक्सवेल ने क्यों किया? समझाइए।
उत्तर:
विस्थापन धारा की आवश्यकता (Need for Displacement Current)
ऐम्पियर के परिपथीय नियम के अनुसार, "किसी बन्द वक्र के परितः चुम्बकीय क्षेत्र की तीव्रता का रेखा - समाकलन उस बन्द वक्र द्वारा घिरे क्षेत्रफल में से गुजरने वाली कुल विद्युत धारा का µ₀ गुना होता है।" जहाँ µ₀ निर्वात की निरपेक्ष चुम्बकशीलता है।
गणितीय रूप में \(\oint \overrightarrow{\mathrm{B}} \cdot d \vec{l} \) = µ₀I
विद्युत धाराओं एवं चुम्बकीय क्षेत्रों के मध्य संबंध प्रदर्शित करने वाला यह नियम विद्युत परिपथों से संबंधित परिणामों को प्राप्त करने के लिए सुगमता से प्रयुक्त किया जा सकता है। लेकिन संधारित्र युक्त परिपथ में यह नियम लागू नहीं होता है। इस कठिनाई को दूर करने के लिए मैक्सवेल ने विस्थापन धारा की अवधारणा को प्रस्तुत किया तथा ऐम्पियर के परिपथीय नियम में संशोधन किया। विस्थापन धारा की आवश्यकता को समझने के लिए एक ऐसे विद्युत परिपथ की कल्पना कीजिए जिसमें एक आवेशित समान्तर प्लेट संघारित्र को एक प्रतिरोधक द्वारा अनावेशित किया जा रहा है। विद्युत धारा I संधारित्र की प्लेट A के बायें पृष्ठ से प्रारंभ होकर चालक तार में होकर प्रवाहित होगी और संधारित्र प्लेट B के दाएं पृष्ठ पर रुक जाती है। इसे चालन धारा (Conduction Current) कहते हैं।

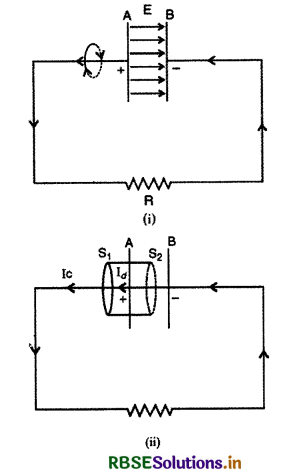
संघारित्र की प्लेटों A व B के बीच रिक्त स्थान में कोई भी धारा प्रवाहित नहीं हो सकती, लेकिन इस स्थान में एक विद्युत क्षेत्र E अवश्य विद्यमान रहता है। चालन धारा के कारण तारों के चारों ओर एक विद्युत चुम्बकीय क्षेत्र भी उत्पन्न हो जाता है।
ऐम्पियर के परिपथीय नियम की अपूर्णता को समझने के लिए संधारित्र की एक प्लेट A के परितः एक ही लूप के दो पृष्ठों S₁ व S₂ पर विचार कीजिए। लूप का पृष्ठ S₂ संधारित्र की दोनों प्लेटों A व B के बीच स्थित है, लेकिन यह पृष्ठ B को स्पर्श नहीं करता। चालन धारा I केवल लूप के पृष्ठ S₁ से गुजरती है। दोनों पृष्टये पर ऐम्पियर का परिपथीय नियम लगाने पर
लूप S₁ के लिए, \(\oint_{\mathrm{S}_{\mathrm{l}}} \overrightarrow{\mathrm{B}} \cdot d \vec{l}\) = µ₀I ...........(1)
लूप S₂ के लिए, \(\oint_{\mathrm{S}_2} \overrightarrow{\mathrm{B}} \cdot d \vec{l}\) = µ₀ x 0 ................(2)
क्योंकि लूप S₁ द्वारा धारा I घिरी है, और S₂ प्लेटों के अन्दर है जहाँ चालन धारा नहीं है।
∵ S₁ व S₂ अत्यन्त निकट है अत: यह अपेक्षा की जाती है कि
\(\oint_{\mathrm{S}_1} \overrightarrow{\mathrm{B}} \cdot d \vec{l}=\oint_{\mathrm{S}_2} \overrightarrow{\mathrm{B}} \cdot d \vec{l}\) .............(3)
समी. (2) व (3) परस्पर विरोधी है, अतः ऐम्पियर का परिपथीय नियम पूर्णतः लागू नहीं होता।
संघारित्र युक्त परिपथ में किरखॉफ के संधि - नियम का भी उल्लंघन पाया गया। A व B एक संधारित्र की प्लेटे हैं जिन्हें एक बैटरीद्वारा

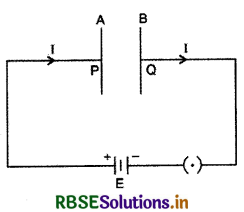
आवेशित किया जाता है। यदि किरखॉफ के सन्धि नियम को P व Q पर अलग - अलग लागू किया जाए तो इसका उल्लंघन होना प्रतीत होता है परन्तु किरखॉफ का नियम आवेश संरक्षण के नियम पर आधारित है, जो सदैव सत्य हैं। इसका अभिप्राय है कि दोनो प्लेटों के बीच कुछ - न - कुछ गायब है, यह गायब राशि विस्थापन धारा है। 

प्रश्न 3.
सिद्ध कीजिए कि विद्युत चुम्बकीय तरंगों की प्रकृति अनुप्रस्थ होती है?
उत्तर:
विद्युत् - चुम्बकीय तरंगों की अनुप्रस्थ प्रकृति (Transverse Nature of Electro - magnetic Waves)
विद्युत् - चुम्बकीय तरंगों में विद्युत् एवं चुम्बकीय क्षेत्र यदि परस्पर लम्बवत् रहते हुए तरंग संचरण (wave propagation) की दिशा के लम्बवत् कम्पन करते हैं, तो इसका अर्थ यह हुआ कि विद्युत् - चुम्बकीय तरंगें प्रकृति में अनुप्रस्थ (transverse) होती हैं। इस तथ्य का सत्यापन निम्नांकित तरीके से किया जा सकता है-
विद्युत् - चुम्बकीय तरंग के गमन में पहले विद्युत् क्षेत्र घटक पर विचार करते हैं। माना विद्युत् - चुम्बकीय तरंग 

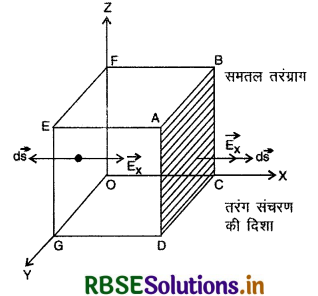
X - दिशा में गतिशील है। ABCD एक समतल तरंगान Y - Z तल में रहते हुए X - दिशा में गतिशील है। ABCD के बायीं ओर विद्युत् क्षेत्र तथा चुम्बकीय क्षेत्र के भाग x तथा t पर निर्भर होंगे, y और z पर नहीं क्योंकि विचाराधीन तरंग समतल तरंग है जिसका X - अक्ष की दिशा में संचरण हो रहा है।
गाउस के नियमानुसार समान्तर षटफलक ABCDOFEG से पारित कुल वैद्युत फ्लक्स शून्य होगा क्योंकि पृष्ठ से परिबद्ध आवेश शून्य है। अर्थात्
\(\oint_{\mathrm{s}} \overrightarrow{\mathrm{E}} \cdot \vec{d}\) = 0
या \(\int_{\mathrm{ABCD}} \overrightarrow{\mathrm{E}} \cdot \overrightarrow{d s}+\int_{\mathrm{OFEG}} \overrightarrow{\mathrm{E}} \cdot \overrightarrow{d s}+\int_{\mathrm{ADGE}} \overrightarrow{\mathrm{E}} \cdot \overrightarrow{d s}+ \int_{\mathrm{BCOF}} \overrightarrow{\mathrm{E}} \cdot \overrightarrow{d s}+\int_{\mathrm{OCDG}} \overrightarrow{\mathrm{E}} \cdot \overrightarrow{d s}+\int_{\mathrm{ABFE}} \overrightarrow{\mathrm{E}} \cdot \overrightarrow{d s}=0\) ................(1)
चूँकि विद्युत् क्षेत्र y तथा z पर निर्भर नहीं करता अतः y तथा z - अक्ष के अभिलम्ब तलों (normal planes) से आने वाले विद्युत् फ्लक्स युग्म में एक-दूसरे को निरस्त (cancel out) कर देंगे।

जहाँ पृष्ठ ABCD व OFEG का क्षेत्रफल S है।
∴ (E_x - E_x').S = 0
∵ S ≠ 0
∴ E_x - E_x' = 0
या E_x = E_x'
स्पष्ट है कि विद्युत् क्षेत्र का x - घटक समय 't' के अनुसार परिवर्तित नहीं होता है। दूसरे शब्दों में, हम कह सकते हैं कि X - अक्ष के अनुदिश विद्युत् क्षेत्र स्थिर होता है।
चूँकि स्थिर विद्युत् क्षेत्र तरंग का संचरण नहीं कर सकता, अत: विद्युत् क्षेत्र जो तरंग संचरण की दिशा के समान्तर है, शून्य है।
∴ E_x' = E_x = 0 
इसका अर्थ यह हुआ कि विद्युत् क्षेत्र तरंग संचरण (wave propagation) की दिशा के लम्बवत् होता है। इसी प्रकार यह सिद्ध किया जा सकता है कि चुम्बकीय क्षेत्र भी तरंग संचरण की दिशा के लम्बवत् होता है। स्पष्ट है कि विद्युत् एवं चुम्बकीय दोनों क्षेत्र तरंग संचरण की दिशा के लम्बवत् होते हैं, अतः विद्युत् - चुम्बकीय तरंगें अनुप्रस्थ होती हैं।

आंकिक प्रश्न

प्रश्न 1.
एक रेडियो 7.5 MHz से 12 MHz के बैण्ड के किसी स्टेशन से समस्वरित हो सकता है। संगत तरंगदैर्घ्य बैण्ड क्या होगा?
उत्तर:
ज्ञात है v₁ = 7.5 MHz = 7.5 x 10⁶ Hz
v₂ = 12 MHz = 12 x 10⁶ Hz
λ₁ = \(\frac{C}{v_1}=\frac{3 \times 10^8}{7.5 \times 10^6}\) = 40 m
2 = \(\frac{C}{v_2}=\frac{3 \times 10^8}{12\times 10^6}\) = 25 m
अत: तरंगदैर्ध्य परास 25 m से 40 m होगी।

प्रश्न 2.
(a) दिक्काल (मुक्त आकाश) में किसी बिन्दु पर विद्युत क्षेत्र सदिश (\(\overrightarrow{\mathbf{E}}\)) का परिमाण 9.3 V/m है। इस बिन्दु पर चुम्बकीय क्षेत्र सदिश (\(\overrightarrow{\mathbf{B}}\)) का परिमाण ज्ञात कीजिए।
(b) पराबैंगनी, अवरक्त तथा X किरणों में से किसकी तरंगदैर्घ्य अधिकतम होती है।
उत्तर:
(a) प्रकाश का वेग C = \(\frac{\overrightarrow{\mathrm{E}}}{\overrightarrow{\mathrm{B}}} \)
\(\overrightarrow{\mathrm{B}}=\frac{\overrightarrow{\mathrm{E}}}{\mathrm{C}}=\frac{9.3}{3 \times 10^8} \) = 3.1 x 10^-8 T
(b) अवरक्त तरंगे।

प्रश्न 3.
एक समतल विद्युत चुम्बकीय तरंग में दोलनी विद्युत क्षेत्र है-
E_y = 30 sin[2 x 10¹¹ t + 300 πx] Vm^-1 तो
(i) विद्युत चुम्बकीय तरंग की तरंगदैर्ध्य की गणना कीजिए।
(ii) दोलनी चुम्बकीय क्षेत्र का समीकरण बताइए।
उत्तर:
दिया है: E_y = 30 sin (2 x 10¹¹ t + 300 πx) Vm^-1
प्रमाणिक समीकरण E_y = E₀ sin (ωt + kx)
दोनों की तुलना करने पर
E₀ = 30Vm^-1 ω = 2 x 10¹¹ rad s^-1
K = 300 π radm^-1

(i) ∵ K = \(\frac{2 \pi}{\lambda}\)
λ = \(\frac{2 \pi}{K}=\frac{2 \pi}{300 \pi}=\frac{1}{150}\) = 6.67 x 10^-3 m
= 6.67 mm
(ii) B₀ = \(\frac{E_0}{C}=\frac{30}{3 \times 10^8}\) = 1 x 10^-7 T
चुम्बकीय क्षेत्र का समीकरण
B_z = 1 x 10^-7 sin (2 x 10¹¹ t + 300 πx).T 

प्रश्न 4.
निर्वात में 5 x 10¹⁹ Hz आवृत्ति की विद्युत चुम्बकीय तरंगों की तरंगदैर्ध्य की गणना कीजिए।
उत्तर:
यहाँ v = 5 x 10¹⁹ Hz, C = 3 x 10⁸ ms^-1, λ = ?
λ = \(\frac{C}{v}=\frac{3 \times 10^8}{5 \times 10^{19}}\) = 6 x 10^-12 m

प्रश्न 5.
25 MHz आवृत्ति की एक विद्युत चुम्बकीय तरंग निर्वात में X - दिशा में गतिमान है। किसी बिन्दु पर विद्युत वेक्टर \(\overrightarrow{\mathrm{E}}=6.3 \hat{j} \mathrm{~V}_{m^{-1}}\) है। इस बिन्दु पर \(\overrightarrow{\mathbf{B}}\) (चुम्बकीय क्षेत्र) का परिकलन कीजिए।
उत्तर:
दिया है: v = 25 MHz = 25 x 10⁶ Hz
X दिशा में गतिमान विद्युत चुम्बकीय तरंग का विद्युत क्षेत्र \(\overrightarrow{\mathrm{E}}=6.3 \hat{j}\) अर्थात् विद्युत क्षेत्र Y दिशा में है, अत: चुम्बकीय क्षेत्र सदिश z दिशा में होगा।
∵ B = \(\frac{E}{C}=\frac{6.3}{3 \times 10^8}\) = 2.1 x 10^-8 T
∴ \(\overrightarrow{\mathrm{B}}\) = (2.1 x 10^-8) \(\widehat{\mathrm{K}}\).T

प्रतियोनी परीक्षा संबंधी प्रश्न

प्रश्न 1.
एक विद्युत चुम्बकीय तरंग की तीव्रता विद्युत क्षेत्र में चुम्बकीय घटकों के अनुपात होगा: (C - विद्युत चुम्बकीय तरंगों की चाल)
(A) 1 : C
(B) 1 : C²
(C) C : 1
(D) 1 : 1
उत्तर:
(D) 1 : 1

प्रश्न 2.
एक समतल विद्युत चुम्बकीय तरंग का चुम्बकीय क्षेत्र \(\overline{\mathrm{B}}\) = 3 x 10^-8  sin (1.6 x 10³ x + 48 x 10¹⁰ t) T. से दर्शाया है। तब विद्युत क्षेत्र के लिए व्यंजक होगा-
(A) \(\overrightarrow{\mathrm{E}}\) = 3 x 10^-8 sin (1.6 x 10³ x + 48 x 10¹⁰t) \(\hat{i}\)V/m 
(B) \(\overrightarrow{\mathrm{E}}\) = 3 x 10^-8 sin (1.6 x 10³ x + 48 x 10¹⁰ t) \(\hat{j}\) V/m
(C) \(\overrightarrow{\mathrm{E}}\) = 60 sin (1.6 x 10³ x + 48 x 10¹⁰ t) \(\hat{k}\) V/m 
(D) \(\overrightarrow{\mathrm{E}}\) = 9 sin (1.6 x 10³ x + 48 x 10¹⁰t) \(\hat{k}\) V/m
उत्तर:
(D) \(\overrightarrow{\mathrm{E}}\) = 9 sin (1.6 x 10³ x + 48 x 10¹⁰t) \(\hat{k}\) V/m 

प्रश्न 3.
यदि एक विद्युत चुम्बकीय तरंग के लिए विद्युत क्षेत्र E = 6.3 x 10²⁷ वोल्ट/मी. है। तो चुम्बकीय क्षेत्र B का मान होगा-
(A) 5 x 10^-19 T 
(B) 2.1 x 10¹⁹ T
(C) 5 x 10^-20 T
(D) 2.1 x 10²⁰ T
उत्तर:
(B) 2.1 x 10¹⁹ T

प्रश्न 4.
एक विद्युत चुम्बकीय तरंग वायु से एक माध्यम में प्रवेश करती है। वायु में विद्युत क्षेत्र\( \overrightarrow{\mathbf{E}_1}=\mathbf{E}_{01} \hat{x} \cos \left[2 \pi v\left(\frac{z}{c}-t\right)\right]\) और माध्यम में विद्युत क्षेत्र \(\overrightarrow{\mathbf{E}_2}=\mathbf{E}_{02} \hat{x} \cos [k(2 z-c t]\) हैं। जहाँ k तरंग संख्या और v आवृत्ति है। माध्यम अचुम्बकीय है। यदि वायु और माध्यम की आपेक्षिक पारगम्यताऐं क्रमशः εr₁ और εr₂ हैं तब कौन सा विकल्प सही है?
(A) \(\frac{\varepsilon_{r_1}}{\varepsilon_{r_2}}=\frac{1}{4}\)
(B) \(\frac{\varepsilon_{r_1}}{\varepsilon_{r_2}}=\frac{1}{2}\)
(C) \(\frac{\varepsilon_{r_1}}{\varepsilon_{r_2}}=4\)
(D) \(\frac{\varepsilon_{r_1}}{\varepsilon_{r_2}}=2\)
उत्तर:
(A) \(\frac{\varepsilon_{r_1}}{\varepsilon_{r_2}}=\frac{1}{4}\)

प्रश्न 5.
निर्वात में विद्युत चुम्बकीय तरंग के विद्युत क्षेत्र का वर्गमाध्य मूल मान E_rms = 6 V/m है। चुम्बकीय क्षेत्र का शिखर मान-
(A) 1.41 x 10^-T
(B) 2.83 x 10^-8 T
(C) 0.70 x 10^-8 T
(D) 4.23 x 10^-8 T
उत्तर:
(B) 2.83 x 10^-8 T

प्रश्न 6.
आयाम मांडुलन में, ज्यावक्रीय वाहक आवृत्ति ω_c का प्रयोग किया गया है और संकेत आवृत्ति ω_m का मान इस प्रकार है कि ∆ω_m << ω_c से कौन - सी आवृत्ति विद्यमान नहीं है-
(A) ω_m + ω_c
(B) ω_c - ω_m
(C) ω_m
(D) ω_c
उत्तर:
(C) ω_m

प्रश्न 7.
एक लाल रंग का एक ई. डी. (प्रकाश उत्सर्जकन डायोड) 0.1 वाट पर एकसमान प्रकाश उत्सर्जित करता है। डायोड से 1m दूरी पर, इस प्रकाश के विद्युत क्षेत्र का आयाम होगा।
(A) 1.73 V/m
(B) 2.45 V/m
(C) 5.48 V/m
(D) 7.75 V/m.
उत्तर:
(B) 2.45 V/m

प्रश्न 8. 
सही कथन चुनिए-
(A) आवृत्ति मॉडुलन में उच्च आवृत्ति वाहक तरंग का आयाम श्रव्य संकेत की आवृत्ति के अनुरूप परिवर्तित की जाती है
(B) आयाम मॉडुलन में उच्च आवृत्ति वाहक तरंग का आयाम श्रव्य संकेत के आयाम के अनुरूप परिवर्तित किया जाता है।
(C) आयाम मॉडुलन में उच्च आवृत्ति वाहक तरंग की आवृत्ति श्रव्य संकेत के आयाम के अनुरूप परिवर्तित की जाती है।
(D) आवृत्ति मॉडुलन में उच्च आवृत्ति वाहक तरंग का आयाम श्रव्य संकेत के आयाम के अनुरूप परिवर्तित किया जाता है।
उत्तर:
(B) आयाम मॉडुलन में उच्च आवृत्ति वाहक तरंग का आयाम श्रव्य संकेत के आयाम के अनुरूप परिवर्तित किया जाता है।

प्रश्न 9.
निम्नलिखित विद्युत चुम्बकीय विकिरणों को प्रति क्वाण्टम ऊर्जा के बढ़ते क्रम में लिखिए-
(a) नीला प्रकाश
(b) पीला प्रकाश
(c) एक्स-रे
(d) रेडियो तरंगें।
(A) B, A, D, C
(B) D, B, A, C
(D) C,A, B, D
(C) A, B, D, C
(D) C,A, B, D
उत्तर:
(B) D, B, A, C