RBSE Class 12 Physics Important Questions Chapter 7 प्रत्यावर्ती धारा

Rajasthan Board RBSE Class 12 Physics Important Questions Chapter 7 प्रत्यावर्ती धारा Important Questions and Answers.

RBSE Class 12 Physics Chapter 7 Important Questions प्रत्यावर्ती धारा

अति लघुत्तरीय प्रश्न

प्रश्न 1.
प्रत्यावर्ती धारा के वर्ग माध्य मूल (rms) मान एवं शिखर मान में संबंध लिखित।
उत्तर:
I_rms = \(\frac{\mathrm{I}_0}{\sqrt{2}}\) जहाँ I_rms प्रत्यावर्ती धारा का वर्गमाध्य मूल मान व I₀ शिखर मान है।

प्रश्न 2.
दिए गए चित्र में अनुनादी अवस्था को दर्शाने वाला बिन्दु लिखिए।

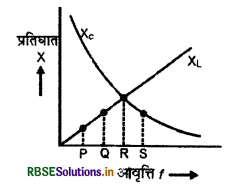
हल: 
अनुनादी अवस्था को दर्शने वाला बिन्दु R होगा।

प्रश्न 3.
श्रेणी LCR परिपथ मै अनुनाद के 'गुणता कारक' की परिभाषा लिखिए। इसका SI मात्र लिखिए।
उत्तर:
गुणता गुणांक को संधारित्र का प्रेरकत्व के सिरों पर विभवान्तर और प्रतिरोध के सिरों पर विभावान्तर के अनुपात के रूप में परिभाषित करते हैं। यह मात्रकहीन राशी है।

प्रश्न 4.
वॉटहीन धारा को परिभाषित कीजिए।
उत्तर:
परिपथ में बिना ऊर्जा क्षय के रहने वाली धारा को वॉटहीन धारा कहते हैं।

प्रश्न 5.
\(\sqrt{\mathrm{LC}}\) का विमीय सूत्र क्या हंगा?
उत्तर:
\(\sqrt{\mathrm{LC}}\) का विमीय सूत्र

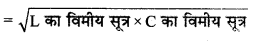
= \(\sqrt{\mathrm{M}^1 \mathrm{~L}^2 \mathrm{~T}^{-2} \mathrm{~A}^{-2} \times \mathrm{M}^{-1} \mathrm{~L}^{-2} \mathrm{~T}^{-4} \mathrm{~A}^2}\)
= \(\sqrt{\mathrm{M}^0 \mathrm{~L}^0 \mathrm{~T}^2 \mathrm{~A}^0}\)
= [T¹]

प्रश्न 6.
भारत में प्रत्यावर्ती धारा की आवृत्ति कितनी है? यह एक सेकण्ड में कितनी बार शून्य होती है?
उत्तर:
भारत में प्रत्यावर्ती धारा की आवृत्ति 50 Hz है। यह एक चक्र में दो बार शून्य होती है, अतः 1 सेकण्ड में 100 बार शून्य होती है।

प्रश्न 7.
धारा के वर्ग माध्य मूल मान को परिभाषित कीजिए। इसका शिखर मान से क्या संबंध है?
उत्तर:
प्रत्यावर्ती धारा का वर्ग माध्य मूल मान दिष्ट धारा के उस मान के बराबर है जिस पर प्रतिरोधक में समान ऊष्मा उत्पन्न होती है।
I_rms = \(\frac{\mathrm{I}_0}{\sqrt{2}}\)

प्रश्न 8.
एक संधारित्र को प्रत्यावर्ती स्रोत से जोड़ने पर औसत शक्ति का मान कितना होता है?
उत्तर:
शुद्ध प्रेरक युक्त परिपथ के लिए Φ = 90°  = π/2
∴ औसत शक्ति = 0

प्रश्न 9.
क्या चोक कुण्डली द्वारा दिष्ट धारा को नियंत्रित किया जा सकता है? कारण दीजिए।
उत्तर:
चोक कुण्डली द्वारा धारा के मार्ग में डाली गई रूकावट X_L = 2π/L
∵ दिष्ट धारा के लिए, f = 0 अत: X_L = 0
स्पष्ट है कि चोक कुण्डली दिष्ट धारा के मार्ग में कोई रुकावट नहीं डालेगी, अत: चोक कुण्डली द्वारा दिष्ट धारा का नियंत्रण संभव नहीं है।

प्रश्न 10.
प्रत्यावर्ती धारा LCR परिपथ में विशेषता गुणांक (Q) क्या प्रदर्शित करता है?
उत्तर:
विशेषता गुणांक (Q) LCR परिपथ द्वारा लगभग बराबर मान की विभिन्न आवृत्तियों में भेद करने की क्षमता का मापन करता है। यह अनुनाद बन की तीक्ष्णता के अनुक्रमानुपाती होता है।

प्रश्न 11.
प्रत्यावर्ती धारा परिपथ में वॉटहीन धारा का मान लिखो।
उत्तर:
वॉटहीन धारा (I) = I₀ sinΦ

प्रश्न 12.
अर्द्धशक्ति बिन्दु आवृत्तियाँ किसे कहते हैं? इन पर धारा का मान कितना होता है?
उत्तर:
अर्द्ध शक्ति बिन्दु आवृत्तेयाँ, श्रेणी LCR परिपथ के लिये खींचे गये अनुनाद वक्र पर आवृत्ति के वे मान हैं जिन पर परिपथ में शक्ति परिपथ की अधिकतम शक्ति की आधी रह जाती है तथा धारा का मान, धारा के शिखर मान का \(\frac{1}{\sqrt{2}}\) गुना रह जाता है।

प्रश्न 13.
दिष्ट धारा की तुलना में प्रत्यावर्ती धारा को प्राथमिकता क्यों दी जाती है?
उत्तर:
क्योंकि प्रत्यावर्ती धारा को आसानी से निम्न तथा उच्च वोल्टता में परिवर्तित किया जा सकता है तथा ऊष्या हानि को कम किया जा सकता है।

प्रश्न 14.
चोक कुण्डली किस सिद्धांत पर कार्य करती है?
उत्तर:
चौक कुण्डली वॉटहीन धारा के सिद्धांत पर कार्य करती है।

प्रश्न 15.
प्रत्यावर्ती धारा की अति उच्च आवृत्ति पर संघारित्र एक शुद्ध चालक की भाँति व्यवहार करता है क्यों?
उत्तर:
धारितीय प्रतिघात X_C = \(\frac{1}{2 \pi f C}\) से स्पष्ट है कि X_C ∝ \(\frac{1}{f}\)
अत: अति उच्च आवृत्ति के लिए X_C → 0
अतः संधारित्र शुद्ध चालक की भाँति व्यवहार करेगा।

लघु उत्तरीय प्रश्न

प्रश्न 1.
गणितीय रूप से सिद्ध कीजिए कि एक पूरे चक्र के लिए प्रत्यावर्ती धारा का औसत मान शून्य होगा।
उत्तर:
औसत मान (Average Value)
प्रत्यावर्ती धारा का परिमाण व दिशा दोनों ही आवर्त रूप से बदलते रहते हैं। एक पूरे चक्र में प्रत्यावर्ती धारा पहले आधे चक्र (first half cycle) में एक दिशा में एवं दूसरे अर्द्ध - चक्र (second half cycle) में विपरीत दिशा में अधिकतम मान को प्राप्त करती है। इस प्रकार एक पूरे चक्र के लिए प्रत्यावर्ती धारा का औसत मान शून्य होता है। इसीलिए जब एक चलकुण्डल धारामापी (moving cycle galvinometer) प्रत्यावर्ती धारा के मार्ग में जोड़ते हैं तो उसके संकेतक (pointer) में कोई विक्षेप उत्पन्न नहीं होता है। इसका कारण यह है कि चलकुण्डल धारामापी में उत्पन्न विक्षेप उसमें बहने वाली धारा के अनुक्रमानुपाती होता है।
प्रथम आधे चक्र के लिए धारा का औसत मान - यदि प्रत्यावर्ती धारा का शिखर मान I₀ है तो उसका तात्क्षणिक मान-
I = I_o sin ωt .................(1)
आधे चक्र के लिए धारा का औसत मान


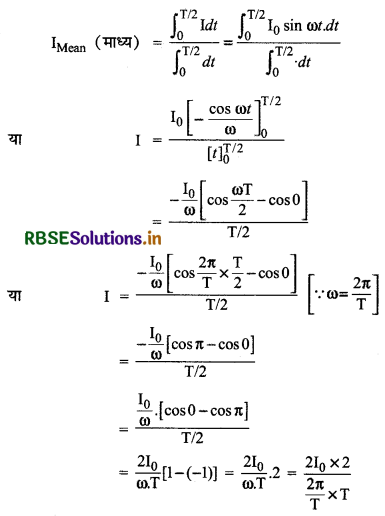
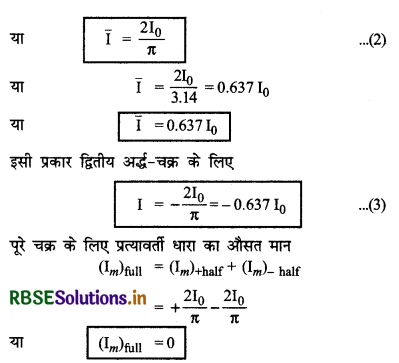
इसी प्रकार प्रत्यावर्ती वोल्टता का प्रथम अर्द्ध - चक्र के लिए औसत मान
\(\overline{\mathrm{V}} = \frac{2 \mathrm{~V}_0}{\pi}\) = 0.636 V₀
और द्वितीय अर्द्ध - चक्र के लिए
\(\overline{\mathrm{V}} = -\frac{2 \mathrm{~V}_0}{\pi}\) = -0.636 V₀
चूँकि धारा के चुम्बकीय व रासायनिक प्रभाव धारा के औसत मान पर निर्भर करते हैं और प्रत्यावर्ती धारा का औसत मान पूरे चक्र के लिए शून्य होता है, अतः प्रत्यावर्ती धारा चुम्बकीय एवं स्थायी रासायनिक प्रभाव (magnetic and stable chemical effect) प्रदर्शित नहीं करती है।

प्रश्न 2.
(a) किसी प्रत्यावर्ती धारा परिपथ में पद 'अनुनाद की तीक्ष्णता की व्याख्या कीजिए।
(b) किसी श्रेणी LCR पिरपथ में V_L = V_C ≠ V_R है। इस परिपथ के लिए शक्ति गुणांक का मान कितना है?
उत्तर:
(a) LCR परिपथ में यदि अनुनादी आवृत्ति f₀ के प्रत्येक ओर आवृत्ति के मान में थोड़ा - सा भी परिवर्तन करने पर धारा के मान में अत्यधिक कमी हो जाये, तो अनुनाद तीक्ष्ण कहलाता है। अनुनाद की तीक्ष्णता को एक विमाहीन राशि से व्यक्त करते हैं जिसे 'Q' गुणक कहते है।
(b) यदि LCR परिपथ में V_L = V_C है तो परिपथ का शक्ति गुणांक ∞ होगा।

प्रश्न 3.
V = V₀sin ωt वोल्टता के किसी स्रोत से श्रेणी में कोई प्रतिरोधक R और कोई प्रेरक L संयोजित है। कला में धारा से वोल्टता π/4 अग्र पायी जाती है। यदि प्रेरक को संधारित्र से प्रतिस्थापित कर दें तो वोल्टता कला में धारा से π/4 पश्च हो जाती है। यदि समान स्रोत से L, C और R को श्रेणी में संयाजित कर दें तो (i) औसत क्षयित शक्ति तथा (ii) परिपथ में ताक्षणिक धारा ज्ञात कीजिए।
उत्तर:
श्रेणीबद्ध (series) LCR परिपथ पर प्रयुक्त A.C. वोल्टता का विश्लेषणात्मक हल (analytical solution)
माना श्रेणी क्रम में जुड़े प्रेरकत्व (L), धारिता (C) व प्रतिरोध (R) के सिरों पर एक प्रत्यावर्ती विद्युत् वाहक बल V = V₀ sin ωt लगाया जाता है। माना किसी क्षण परिपथ के अलग - अलग भागों पर विद्युत् वाहक बल के मान निम्न हैं-

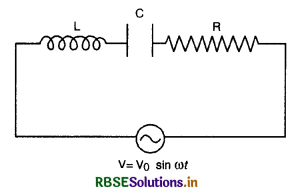
(i) प्रतिरोध के सिरों पर विभवान्तर
V_R = RI
(ii) संधारित्र के सिरों पर विभवान्तर
V_C = q/C
(iii) स्वप्रेरकत्व के कारण विद्युत् वाहक बल
V_L = \(L\frac{d \mathrm{I}}{d t}\)
अतः कुल विद्युत् वाहक का समीकरण
\(L\frac{d I}{d t} + RI + \frac{q}{\mathrm{C}}\) = V₀ sin ωt
अवकलन करने पर,
\(L\frac{d^2 \mathrm{I}}{d t^2} + R \frac{d \mathrm{I}}{d t} + \frac{1}{\mathrm{C}} \frac{d q}{d t}\) = ω V₀ cos ωt ......................(1)
∵ I = \(\frac{d q}{d t}\)
अत: समीकरण (1) से,
L\(\frac{d^2 \mathrm{I}}{d t^2} + R \frac{d \mathrm{I}}{d t} + \frac{1}{\mathrm{C}}.I\) = ω V₀ cos ωt .....................(2)
यदि समीकरण (2) का हल निम्न प्रकार है:
I = I_m sin(ωt - Φ) ........................(3)
जहाँ, Im तथा Φ नियतांक हैं जिनके मानों को ज्ञात करना है।
समीकरण (3) का अवकलन करने पर,
\(\frac{d \mathrm{I}}{d t}\) = I_m ω cos (ωt - Φ)
तथा \(\frac{d^2 \mathrm{I}}{d t^2}\) = -I_m ω² sin(ωt - Φ)


im का मान समीकरण (2) में रखने पर,
I = \(\frac{V_0}{\sqrt{R^2+\left(\omega L-\frac{1}{\omega C}\right)^2}} \sin (\omega t-\phi)\)
जहाँ Φ = tan^-1 \(\left[\frac{\left(\omega \mathrm{L}-\frac{1}{\omega \mathrm{C}}\right)}{\mathrm{R}}\right]\)

प्रत्यावर्ती परिपथों में औसत शक्ति (Average Power in A.C. Circuit)
किसी वैद्युत परिपथ में ऊर्जा व्यय की दर को 'शक्ति' (Power) अथवा 'सामर्थ्य' कहते हैं। दिष्ट धारा परिपथ में t सेकण्ड में व्यय ऊर्जा निम्न सूत्र से ज्ञात की जा सकती है-
W = VIt .........................(1)
स्पष्ट है कि दिष्ट धारा परिपथ में व्यय ऊर्जा परिपथ के विभवान्तर (V), धारा (I) एवं समय (t) पर निर्भर करती है, लेकिन प्रत्यावर्ती धारा परिपथ में व्यय ऊर्जा धारा एवं विभवान्तर के परिमाण के साथ - साथ उनके मध्य कलान्तर पर भी निर्भर करती है। प्रत्यावर्ती धारा परिपथ में धारा एवं विभवान्तर दोनों के मान समय के अनुसार बदलते हैं, अत: व्यय ऊर्जा ज्ञात करने के लिए समी. (1) का प्रयोग सीधे - सीधे नहीं कर सकते। माना प्रत्यावर्ती धारा परिपथ में धारा एवं विभवान्तर के मध्य कलान्तर Φ है और उन्हें निम्न समीकरणों से व्यक्त किया जाता है-
I = I₀ sin ωt .................(1)
V = V₀ sin (ωt + Φ) .................(2)
यदि किसी क्षण t पर समयान्तराल dt के लिए धारा एवं विभवान्तर को नियत मान ले तो इस समयान्तराल में व्यय ऊर्जा ज्ञात करने के लिए समी. (1) का उपयोग कर सकते हैं। अतः dt समयान्तराल में परिपथ में व्यय ऊर्जा dω = V.I.dt
अतः पूरे चक्र में व्यय ऊर्जा

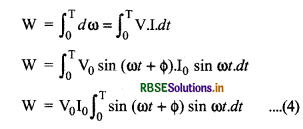
उक्त समाकलन को हल करने पर,

यदि विभवान्तर को V से व्यक्त करें, तो
P = V_rms.I_rms.cosΦ 
स्पष्ट है कि प्रत्यावर्ती धारा परिपथ में व्यय सामर्थ्य धारा एवं विभवान्तर के वर्ग माध्य मूल मान पर निर्भर करने के साथ - साथ उनके मध्य कलान्तर (Φ) पर भी निर्भर करती है। कलान्तर पर सामर्थ्य निम्न प्रकार निर्भर करती है-
(i) यदि प्रत्यावर्ती धारा परिपथ में केवल ओमीय प्रतिरोध (Ohmic resistance) है, तो Φ = 0
अतः P = V_rms I_rms cos 0°
P = V_rms.I_rms

(ii) यदि प्रत्यावर्ती धारा परिपथ में केवल शुद्ध प्रेरकत्व (Pure inductance) है, तो
Φ = + π/2 ∴ cos Φ = 0 
अतः P = 0 
अर्थात् परिपथ में व्यय शक्ति शून्य होगी।

(iii) यदि प्रत्यावर्ती धारा परिपथ में केवल शुद्ध संधारित्र हैं, तो
Φ = +\(\frac{\pi}{2}\) ∴ cos Φ = 0
अतः P = 0
अर्थात् परिपथ में व्यय सामर्थ्य शून्य होगी।

(iv) LCR परिपथ में cos Φ = \(\frac{\mathrm{R}}{\mathrm{Z}}\) अतः श्रेणी अनुनादी अवस्था में Φ = 0 अर्थात् धारा और वोल्टता एक ही कला में होते है अत: cos Φ = 1 अर्थात् अनुनादी अवस्था में परिपथ का शक्ति गुणांक अधिकतम होता है। विद्युत पंखे की मोटर में तार के कई फेरों के कारण स्वप्रेरकत्व L का मान बढ़ जाता है एवं शक्ति गुणांक बहुत कम हो जाता है। इस कला कोण को कम करने के लिए ही संधारित्र का उपयोग किया जाता है। यही कारण है कि कई बार घरों में पंखा धीमा चलने पर अक्सर इसका संघारित्र बदला गया है।

प्रश्न 4.
प्रेरणिक प्रतिघात तथा बारितीय प्रतिघात का आवृत्ति के साथ लेखाचित्र बनाइये।
उत्तर:

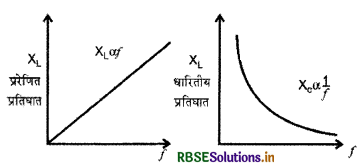
प्रश्न 5.
संघारित्र दिष्ट यारा का मार्ग अवरुद्ध करता है, जबकि प्रत्यावर्ती धारा को जाने देता है, क्यों?
उत्तर:
संघारित्र का प्रतिरोध RC = \(\frac{1}{\omega C}=\frac{1}{2 \pi f C}\)
दिष्ट धारा के लिये f = 0
∴ X_C = ∞ (अनन्त) अतः दिष्ट धारा के लिए संघारित अनन्त प्रतिरोध का कार्य करता है जिससे वह दिष्ट धारा को रोकता है।

प्रश्न 6.
विद्युत शक्ति संचरण में प्रयुक्त परिपथों के लिए शक्ति गुणांक कम होने का अर्थ है, अधिक शक्ति क्षय समझाइए।
उत्तर:
शक्ति क्षय P_av = I_rms V_rms cosΦ
Φ कम होने पर cos Φ का मान बढ़ता है। इसलिए शक्ति क्षय बढ़ता है।

प्रश्न 7.
प्रत्यावर्ती धारा परिपथ के लिए प्रतिरोध प्रतिघात एवं प्रतिबाधा में अन्तर स्पष्ट कीजिए।
उत्तर:
प्रतिरोध: किसी चालक द्वारा प्रत्यावर्ती धारा के मार्ग में अवरोध।
प्रतिघात: परेकत्व या संघारित्र द्वारा धारा के मार्ग में डाली गई रूकावट।
प्रतिबाधा: जब प्रत्ववर्ती धारा परिपथ में प्रतिरोध के साथ - साथ प्रतिघात भी होता है, तो पापथ की परिणामी रुकावट प्रतिबाधा कहलाती है।

दीर्घ उत्तरीय प्रश्न

प्रश्न 1.
प्रत्यावर्ती वोल्टता स्रोत से जुड़े एक श्रेणी RLC परिपथ के लिए सदिश चित्र (फेजर चित्र) बनाते हुए परिपथ की प्रतिबाधा का व्यंजक प्राप्त कीजिए।
उत्तर:
श्रेणीबद्ध (series) LCR परिपथ पर प्रयुक्त A.C. वोल्टता का विश्लेषणात्मक हल (analytical solution)
माना श्रेणी क्रम में जुड़े प्रेरकत्व (L), धारिता (C) व प्रतिरोध (R) के सिरों पर एक प्रत्यावर्ती विद्युत् वाहक बल V = V₀ sin ωt लगाया जाता है। माना किसी क्षण परिपथ के अलग - अलग भागों पर विद्युत् वाहक बल के मान निम्न हैं-

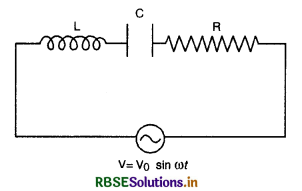
(i) प्रतिरोध के सिरों पर विभवान्तर
V_R = RI
(ii) संधारित्र के सिरों पर विभवान्तर
V_C = q/C
(iii) स्वप्रेरकत्व के कारण विद्युत् वाहक बल
V_L = L\(\frac{d \mathrm{I}}{d t}\)
अतः कुल विद्युत् वाहक का समीकरण
L\(\frac{d I}{d t}\) + RI + \(\frac{q}{\mathrm{C}}\) = V₀ sin ωt
अवकलन करने पर,
L\(\frac{d^2 \mathrm{I}}{d t^2}\) + R \(\frac{d \mathrm{I}}{d t}\) + \(\frac{1}{\mathrm{C}} \frac{d q}{d t}\) = ω V₀ cos ωt ......................(1)
∵ I = \(\frac{d q}{d t}\)
अत: समीकरण (1) से,
L\(\frac{d^2 \mathrm{I}}{d t^2}\) + R \(\frac{d \mathrm{I}}{d t}\) + \(\frac{1}{\mathrm{C}}\).I = ω V₀ cos ωt .....................(2)
यदि समीकरण (2) का हल निम्न प्रकार है:
I = Im sin(ωt - Φ) ........................(3)
जहाँ, Im तथा Φ नियतांक हैं जिनके मानों को ज्ञात करना है।
समीकरण (3) का अवकलन करने पर,
\(\frac{d \mathrm{I}}{d t}\) = I_m ω cos (ωt - Φ)
तथा \(\frac{d^2 \mathrm{I}}{d t^2}\) = -I_m ω² sin(ωt - Φ)


im का मान समीकरण (2) में रखने पर,
I = \(\frac{V_0}{\sqrt{R^2+\left(\omega L-\frac{1}{\omega C}\right)^2}} \sin (\omega t-\phi)\)
जहाँ Φ = tan^-1 \(\left[\frac{\left(\omega \mathrm{L}-\frac{1}{\omega \mathrm{C}}\right)}{\mathrm{R}}\right]\)

प्रश्न 2.
दिष्ट धारा की तुलना में प्रत्यावर्ती धारा की एक विशेषता एवं एक दोष लिखिए।
शुद्ध प्रेरकत्व युक्त प्रत्यावर्ती धारा परिपथ में निम्नलिखित के लिए व्यंजक ज्ञात कीजिए।
(i) धारा का तात्क्षणिक मान
(ii) परिपथ का प्रतिघात
(iii) धारा का शिखर मान शुद्ध प्रेरकत्व परिपथ के लिए शक्ति आरेख बनाइये।
उत्तर:
प्रत्यावर्ती धारा का वर्ग माध्य मूल मान (Root Mean Square Value of Alter - nating Current)
“एक पूरे चक्र के लिए प्रत्यावर्ती धारा के वर्ग के औसत मान के वर्गमूल को ही धारा का वर्ग माध्य मूल मान (r.m.s. value) कहते हैं।" इसे Irms से व्यक्त करते हैं। यदि पूरे चक्र में विभिन्न n समयों पर धारा के मान क्रमश: I₁, I₂, I₃, ..... In हों (चित्र 7.4), तो प्रत्यावर्ती धारा का वर्ग माध्य मूल मान

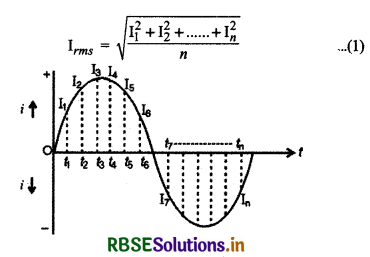
प्रत्यावर्ती धारा का समी.
I = I_m sin ωt
∵ ωt = θ
∴ I = I_m sinθ
अतः वर्ग माध्य मूल मान (root mean square value) की परिभाषानुसार,

या I_rms² = पूरे चक्र के लिए I² का औसत मान

क्योंकि पूरे चक्र (for full cycle) के लिए ज्या एवं कोज्या फलन का समाकलन शून्य होता है।
या I_rms² = \(\frac{\mathrm{I}_0^2}{2}\)

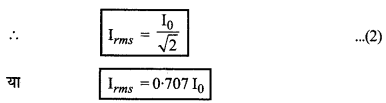
इसी प्रकार प्रत्यावर्ती वोल्टता का वर्ग माध्य मूल,

प्रत्यावर्ती धारा केवल ऊष्मीय प्रभाव (heating effect) प्रदर्शित करती है, क्योंकि ऊष्मीय प्रभाव धारा के वर्ग पर निर्भर करता है। यदि प्रतिरोध R में प्रत्यावर्ती धारा बह रही है तो ऊष्मा उत्पन्न होने की दर
P = i²R 
हम जानते हैं कि प्रत्यावर्ती धारा का मान आवर्त रूप (altemating) से बदलता रहता है, अत: ऊष्मा उत्पन्न होने की दर भी बदलती रहेगी। धारा के एक पूरे चक्र में ऊष्मा उत्पन्न होने की दर
\(\overline{\mathrm{P}}=\overline{\mathrm{I}_2} \mathrm{R}\)
यहाँ i^2 धारा के वर्ग i का एक पूरे चक्र के लिए औसत मान है।
∴ \(\overline{i^2}=\left(\mathrm{I}_{r m s}\right)^2\)
अतः \(\overline{\mathrm{P}}\) = (Irms)².R ......................(4)
समीकरण (4) से स्पष्ट है कि यदि प्रतिरोध R में Irms प्रबलता की दिष्ट धारा प्रवाहित करें तब भी ऊष्मा उत्पन्न होने की दर (Irms)² R ही होगी। अतः, "प्रत्यावर्ती धारा का वर्ग माध्य मूल मान स्थिर मान (constant value) की उस दिष्ट धारा (direct current) के मान के तुल्य है जो किसी प्रतिरोध में उसी दर से ऊष्मा उत्पन्न करती है जिस दर से वह प्रत्यावर्ती धारा उत्पन्न करती है।" इसीलिए प्रत्यावर्ती धारा के वर्ग माध्य मूल मान (I_rms) को धारा का 'प्रभावी मान' (Effective value) अथवा 'आभासी मान' (Virtual value) भी कहते हैं।

इसी प्रकार "प्रत्यावर्ती वोल्टेज का वर्ग माध्य मान उस दिष्ट वोल्टेज (direct voltage) के उस मान के बराबर है जो किसी प्रतिरोध के सिरों पर लगाने पर उसी दर से ऊष्मा उत्पन्न करता है जिस दर से उसी प्रतिरोध के सिरों पर वह प्रत्यावर्ती वोल्टेज लगाने पर उत्पन्न होती है।" धारा की भाँति ही V_rms को प्रत्यावर्ती वोल्टेज का प्रभावी मान (effective value) अथवा आभासी मान कहते हैं।
विशेष तथ्य: I_rms व I₀ के अनुपात को फॉर्म गुणक (form factor) कहते हैं। प्रत्यावर्ती धारा के लिए यह अनुपात 1.11 है।

प्रश्न 3.
अर्द्ध - शक्ति बिन्दु आवृत्तियों से क्या अभिप्राय हैं? एक LCR श्रेणी परिपथ के लिए बैण्ड चौड़ाई ज्ञात करने का व्यंजक प्राप्त कीजिए। प्रत्यावर्ती धारा व आवृत्ति के मध्य वक्र में अर्द्धशक्ति बिन्दु आवृत्तियों को दर्शाइए।
उत्तर:
अर्द्ध शक्ति बिन्दु या आवृत्तियाँ (HalrPower Frequencies)
L - C - R परिपथ में यदि अनुनादी आवृत्ति (f₀) के प्रत्येक ओर आवृत्ति के मान में थोड़ा - सा भी परिवर्तन करने पर धारा के मान में अत्यधिक कमी हो जाये, तो अनुनाद तीक्ष्ण (sharp) कहलाता है। अनुनाद की तीक्ष्णता (sharpness of resonance) को एक विमाहीन राशि (dimensionless quantity) से व्यक्त करते हैं जिसे Q - गुणक (Quality factor अथवा Q - Factor) कहते हैं।

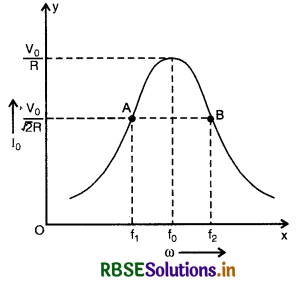
L - C - R परिपथ की अनुनादी आवृत्ति और उसके दोनों और की उन दो आवृत्तियों जिनके संगत धारा का आयाम अनुनादी धारा के आयाम का \(\frac{1}{\sqrt{2}}\) गुना होता है, के अन्तर के अनुपात को उस परिपथ का Q - गुणक कहते हैं। इसे से प्रदर्शित करते हैं। तथा परिपथ की शक्ति आधी रह जाती है इन्हें अर्द्धशक्ति बिन्दु या आवृत्तियाँ कहते है।

प्रश्न 4.
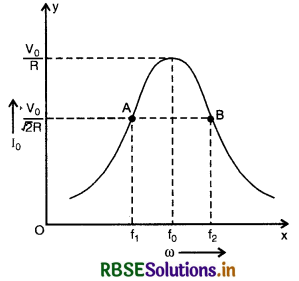
किसी बुक्ति X को किसी ac स्रोत V = V₀ sin ωt से संयोजित किया गया है। निम्नलिखित ग्राफ में दिखाए गए वक्र में वोल्टता, धारा और शक्ति के विचरण को दर्शाया गया है:

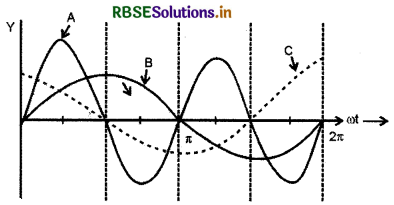
(a) युक्ति X को पहचानिए।
(b) इन वकों A, B और C में कौन वोल्टता, धारा और उपयुक्त शक्ति को परिपथ में निरुपित करते हैं? अपने उत्तर की पुष्टि कीजिए।
(c) ac स्रोत की आवृत्ति के साथ इसकी प्रतिबाधा किस प्रकार विचरण करती है? ग्राफ द्वारा दर्शाइए।
(a) परिपञ्च में धारा और ac वोल्टता में इसके कला सम्बन्ध के लिए व्यंजक प्राप्त कीजिए।
उत्तर:
(a) X प्रेरक कुण्डली है
(b) A शक्ति, B वोल्टता व C धारा है।
(c) हम जानते है Z = \(\sqrt{\mathrm{R}^2+(2 \pi \mathrm{L})^2}\)

प्रश्न 5.
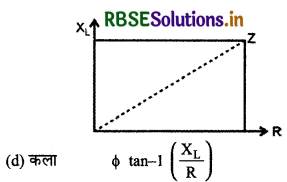
कोई युक्ति X किसी प्रत्यावर्ती धारा (ac) स्रोत V = V₀ sin wt वोल्टता से संयोजित है। X से प्रवाहित धारा I = I₀ sin (wt + \(\frac{\pi}{2}\)) है।
(a) युक्ति X को पहचानिए और इसके प्रतिघात के लिए व्यंजक लिखिए।
(b) X के लिए प्रत्यावर्ती धारा के एक चक्र में समय के साथ वोल्टता और धारा के विचरण को दर्शाने के लिए ग्राफ खींचिए।
(c) प्रत्यावर्ती धारा की आवृत्ति के साथ युक्ति X के प्रतिघात में किस प्रकार विचरण होता है? ग्राफ द्वारा इस विचरण को दर्शाइए।
(d) युक्ति X के लिए फेजर आरेख खींचिए।
उत्तर:
(a) X संघारित्र है।
परिपथ का प्रतिघात X_L = 2πfL

प्रश्न 6.
प्रत्यावर्ती धारा परिपथ में शक्ति का सूत्र स्थापित करो। प्रतिघात रहित एवं प्रतिरोध रहित परिपथ के लिए उपर्युक्त सूत्र में क्या परिवर्तन होता है? शक्ति गुणांक को भी परिभाषित कीजिये।
उत्तर:
प्रत्यावर्ती परिपथों में औसत शक्ति (Average Power in A.C. Circuit)
किसी वैद्युत परिपथ में ऊर्जा व्यय की दर को 'शक्ति' (Power) अथवा 'सामर्थ्य' कहते हैं। दिष्ट धारा परिपथ में t सेकण्ड में व्यय ऊर्जा निम्न सूत्र से ज्ञात की जा सकती है-
W = VIt .........................(1)
स्पष्ट है कि दिष्ट धारा परिपथ में व्यय ऊर्जा परिपथ के विभवान्तर (V), धारा (I) एवं समय (t) पर निर्भर करती है, लेकिन प्रत्यावर्ती धारा परिपथ में व्यय ऊर्जा धारा एवं विभवान्तर के परिमाण के साथ - साथ उनके मध्य कलान्तर पर भी निर्भर करती है। प्रत्यावर्ती धारा परिपथ में धारा एवं विभवान्तर दोनों के मान समय के अनुसार बदलते हैं, अत: व्यय ऊर्जा ज्ञात करने के लिए समी. (1) का प्रयोग सीधे - सीधे नहीं कर सकते। माना प्रत्यावर्ती धारा परिपथ में धारा एवं विभवान्तर के मध्य कलान्तर Φ है और उन्हें निम्न समीकरणों से व्यक्त किया जाता है-
I = I₀ sin ωt .................(1)
V = V₀ sin (ωt + Φ) .................(2)
यदि किसी क्षण t पर समयान्तराल dt के लिए धारा एवं विभवान्तर को नियत मान ले तो इस समयान्तराल में व्यय ऊर्जा ज्ञात करने के लिए समी. (1) का उपयोग कर सकते हैं। अतः dt समयान्तराल में परिपथ में व्यय ऊर्जा dω = V.I.dt
अतः पूरे चक्र में व्यय ऊर्जा

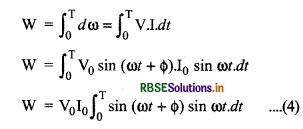
उक्त समाकलन को हल करने पर,

यदि विभवान्तर को V से व्यक्त करें, तो
P = V_rms.I_rms.cosΦ 
स्पष्ट है कि प्रत्यावर्ती धारा परिपथ में व्यय सामर्थ्य धारा एवं विभवान्तर के वर्ग माध्य मूल मान पर निर्भर करने के साथ - साथ उनके मध्य कलान्तर (Φ) पर भी निर्भर करती है। कलान्तर पर सामर्थ्य निम्न प्रकार निर्भर करती है-
(i) यदि प्रत्यावर्ती धारा परिपथ में केवल ओमीय प्रतिरोध (Ohmic resistance) है, तो Φ = 0
अतः P = V_rms I_rms cos 0°
P = V_rms.I_rms

(ii) यदि प्रत्यावर्ती धारा परिपथ में केवल शुद्ध प्रेरकत्व (Pure inductance) है, तो
Φ = + π/2 ∴ cos Φ = 0 
अतः P = 0 
अर्थात् परिपथ में व्यय शक्ति शून्य होगी।

(iii) यदि प्रत्यावर्ती धारा परिपथ में केवल शुद्ध संधारित्र हैं, तो
Φ = +\(\frac{\pi}{2}\) ∴ cos Φ = 0
अतः P = 0
अर्थात् परिपथ में व्यय सामर्थ्य शून्य होगी।

(iv) LCR परिपथ में cos Φ = \(\frac{\mathrm{R}}{\mathrm{Z}}\) अतः श्रेणी अनुनादी अवस्था में Φ = 0 अर्थात् धारा और वोल्टता एक ही कला में होते है अत: cos Φ = 1 अर्थात् अनुनादी अवस्था में परिपथ का शक्ति गुणांक अधिकतम होता है। विद्युत पंखे की मोटर में तार के कई फेरों के कारण स्वप्रेरकत्व L का मान बढ़ जाता है एवं शक्ति गुणांक बहुत कम हो जाता है। इस कला कोण को कम करने के लिए ही संधारित्र का उपयोग किया जाता है। यही कारण है कि कई बार घरों में पंखा धीमा चलने पर अक्सर इसका संघारित्र बदला गया है।

प्रश्न 7.
श्रेणी LCR परिपथ के लिए आवृत्ति एवं धारा के मध्य संबंध को ग्राफ द्वारा प्रदर्शित करो। अर्द्धशक्ति बिन्दु आवृत्तियों को दर्शाते हुए बैण्ड चौड़ाई के लिए आवश्यक सूत्र स्थापित करो।
उत्तर:
अर्द्ध शक्ति बिन्दु या आवृत्तियाँ (HalrPower Frequencies)
L - C - R परिपथ में यदि अनुनादी आवृत्ति (f₀) के प्रत्येक ओर आवृत्ति के मान में थोड़ा - सा भी परिवर्तन करने पर धारा के मान में अत्यधिक कमी हो जाये, तो अनुनाद तीक्ष्ण (sharp) कहलाता है। अनुनाद की तीक्ष्णता (sharpness of resonance) को एक विमाहीन राशि (dimensionless quantity) से व्यक्त करते हैं जिसे Q - गुणक (Quality factor अथवा Q - Factor) कहते हैं।

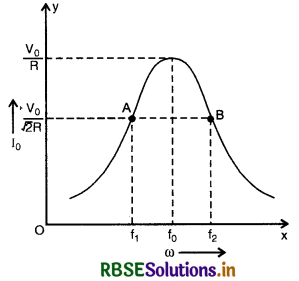
L - C - R परिपथ की अनुनादी आवृत्ति और उसके दोनों और की उन दो आवृत्तियों जिनके संगत धारा का आयाम अनुनादी धारा के आयाम का \(\frac{1}{\sqrt{2}}\) गुना होता है, के अन्तर के अनुपात को उस परिपथ का Q - गुणक कहते हैं। इसे से प्रदर्शित करते हैं। तथा परिपथ की शक्ति आधी रह जाती है इन्हें अर्द्धशक्ति बिन्दु या आवृत्तियाँ कहते है।

प्रश्न 8.
अनुनादी परिपथ से क्या तात्पर्य है? श्रेणी LCR अनुनादी परिपथ के लिए आवश्यक प्रतिबन्ध बताइए तथा अनुनादी आवृत्ति का व्यंजक स्थापित करो। इस परिपथ का कहाँ उपयोग होता है।
उत्तर:
श्रेणी L - C - R अनुनादी परिपथ (Series L - C - R Resonance Circuit)
श्रेणी अनुनादी परिपथ में प्रेरकत्व (L), संधारित्र (C) तथा प्रतिरोध (R) तीनों श्रेणी क्रम में एक प्रत्यावर्ती धारा स्रोत से जोड़ दिये जाते हैं। इस परिपथ की प्रतिबाधा
Z = \(\sqrt{\mathrm{R}^2+\left(\mathrm{X}_{\mathrm{L}} \sim \mathrm{X}_{\mathrm{C}}\right)^2}\)

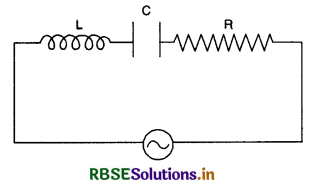
जब X_L = X_C तो (X_L ~ X_C) = 0
∴ Z = \(\sqrt{R^2+0}\) = R
या Z = R
जो कि प्रतिबाधा का न्यूनतम मान (minimum value) है, अतः परिपथ में प्रवाहित धारा \(\left(i=\frac{\mathrm{V}}{\mathrm{Z}}\right)\) का मान अधिकतम होगा। L - C - R परिपथ में यह अनुनाद की स्थिति है। जिस आवृत्ति पर परिपथ में धारा अधिकतम मिलती है; उसे अनुनादी आवृत्ति (resonant frequency) कहते हैं। इस प्रकार, "श्रेणीबद्ध (series) L - C - R परिपथ के लिए निश्चित प्रत्यावर्ती विभवान्तर की वह आवृत्ति जिसके लिए परिपथ में प्रवाहित धारा अधिकतम होती है, परिपथ की अनुनादी आवृत्ति (resonant frequency) कहलाती है।" इसे f₀ से व्यक्त करते हैं। 
∵ अनुनाद की स्थिति में,
X_L = X_C
∴ 2πf₀L = \(\frac{1}{2 \pi f_0 \mathrm{C}}\)

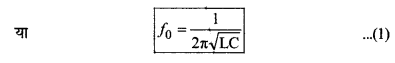
अनुनाद की दशा में X = X_L ~ X_C = 0 और Z = R
∴ tan Φ = \(\frac{X}{R}\) = 0
अतः Φ = 0
"अनुनाद की स्थिति में धारा एवं विभवान्तर समान कला (same phase) में होते हैं।" इस अवस्था में श्रेणी L - C - R परिपथ में प्रत्यावर्ती वोल्टता तथा धारा के फेजर आरेख चित्र 7.37 तथा प्रतिबाधा आरेख चित्र 7.37 में प्रदर्शित है।

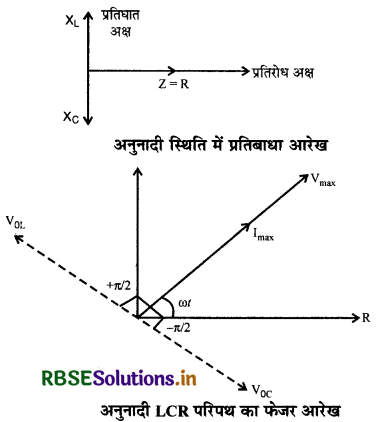
अनुनाद वक्र (Resonance Curve): अनुनाद की स्थिति में X_L = X_C होता है, तो परिपथ में बहने वाली धारा I अधिकतम होती है और जिस आवृत्ति पर यह स्थिति मिलती है, वह अनुनादी आवृत्ति fr होती है।
यदि X_L ≠ X_C तो (X_L ~ X_C) ≠ 0 
अत: (X_L ~ X_C)² > 0
अतः Z > R
अतः धारा I = \(\frac{\mathrm{V}}{\mathrm{Z}}\) का मान अनुनादी धारा (resonant current) से कम होगा। चाहे X_L > X_C हो अथवा X_L < X_C हो Z > R ही मिलेगा। इसी प्रकार आवृत्ति f का मान चाहे fr से अधिक हो अथवा कम हो, धारा का मान अनुनादी धारा से कम ही मिलेगा। f का मान fr से जितना दूर होगा, प्रतिबाधा उतनी ही अधिक होगी और फलस्वरूप धारा का मान उतना ही कम होगा। धारा का आवृत्ति के साथ परिवर्तन चित्र 7.39 में प्रदर्शित है। इसी वक्र को अनुनाद वक्र कहते है।

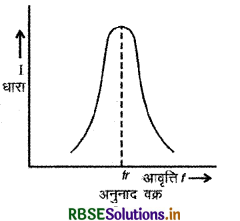
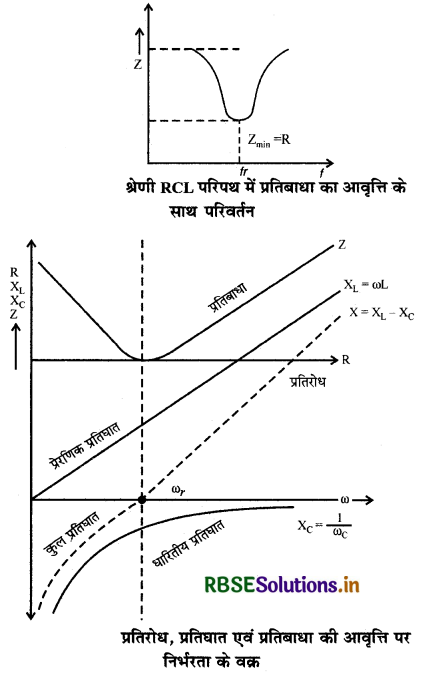
श्रेणीबद्ध RCL परिपथ में प्रतिबाधा का आवृत्ति के साथ परिवर्तन चित्र 7.40 में दिखाया गया है।

प्रश्न 9.
(i) अपचायी ट्रांसफार्मर का नामांकित आरेख खींचिए। इसकी क्रियाविधि के सिद्धांत का उल्लेख कीजिए।
(ii) वोल्टताओं को फेरा - अनुपात में व्यक्त कीजिए।
उत्तर:
ट्रान्सफॉर्मर (Transformer)
अन्योन्य प्रेरण (mutual inductance) के सिद्धान्त पर बना यह ऐसा उपकरण है जो प्रत्यावर्ती वोल्टता को बदलने के लिए उपयोग में लाया जाता है। इसकी सहायता से उच्च धारा की निम्न प्रत्यावर्ती वोल्टता (low alternating voltage of high current) को निम्न धारा की उच्च प्रत्यावर्ती वोल्टता में (high alternating voltage of low current) तथा निम्न धारा की उच्च प्रत्यावर्ती बोल्टता को उच्च धारा की निम्न प्रत्यावर्ती वोल्टता में बदला जा सकता है।
कार्य के अनुसार ट्रान्सफॉर्मर मुख्यत: दो प्रकार के होते हैं-
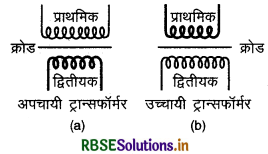
(i) उच्चायी ट्रान्सफॉर्मर (Step - up transformer): यह ट्रान्सफॉर्मर निम्न विभव वाली प्रबल प्रत्यावर्ती धारा (strong alternating current of low potential) को उच्च विभव वाली निर्बल प्रत्यावर्ती धारा (weak alternating current of high potential) में बदलने के काम आता है।

(ii) अपचायी ट्रान्सफॉर्मर (Step - down transformer): यह ट्रान्सफॉर्मर उच्च विभव वाली निर्बल प्रत्यावर्ती धारा (weak alternating current of high potential) को निम्न विभव वाली प्रबल प्रत्यावर्ती धारा (strong alternating current of low potential) में बदलने के काम आता है।

सिद्धान्त (Principle): यह अन्योन्य प्रेरण (mutual induction) के सिद्धान्त पर बनाया गया है। इस सिद्धान्त के अनुसार किसी परिपथ मैं धारा परिवर्तित होने पर निकट स्थित दूसरे परिपथ में प्रेरण उत्पन्न होता है।

रचना (Construction): ट्रान्सफॉर्मर की सैद्धान्तिक रचना चित्र 7.52 में दिखायी गई है। इसमें नर्म लोहे या सिलिकन स्टील

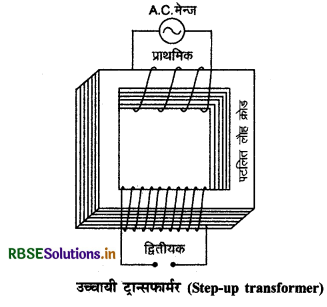
सिलिकन स्टील (silicon steel) का पटलित आयताकार क्रोड (laminated rectangular core) होता है भँवर धाराओं के प्रभाव को कम करने के उद्देश्य से क्रोड को पटलिन बनाया जाता है लौह क्रोड लेने का उद्देश्य यह है कि यह लौह चुम्बकीय पदार्थ ( ferromagnetic substance) है, अतः चुम्बकीय क्षेत्र रेखाओं को केन्द्रित करके ऊर्जा क्षय को कम करता है। क्रोड की एक भुजा पर ताँबे के तार लपेट कर प्राथमिक कुण्डली (primary coil) बनाते हैं और उसके सामने वाली भुजा पर ताँबे के तार लपेटकर द्वितीयक कुण्डली (secondary coil) बनाते हैं। जो वोल्टता हमें बदलनी होती है, उसे प्राथमिक कुण्डली के सिरों के मध्य आरोपित करते हैं। बदली हुई वोल्टता हमें द्वितीयक कुण्डली के सिरों के मध्य प्राप्त हो जाती है प्राथमिक कुण्डली में फेरों की संख्या N_p और द्वितीयक में फेरों की संख्या N_s से व्यक्त करते हैं। यदि N_s > N_p तो ट्रान्सफॉर्मर उच्चायी (step up) होगा और यदि N_s < N_p तो ट्रान्सफार्मर अपचायी (step down) होगा।

कार्यविधि (Working): जब ट्रान्सफॉर्मर की प्राथमिक कुण्डली के सिरों के मध्य प्रत्यावर्ती वोल्टता आरोपित करते हैं तो उसमें प्रत्यावर्ती धारा प्रवाहित होने लगती है और फलस्वरूप स्वप्रेरण के कारण एक वोल्टता e_p प्रेरित हो जाती है। यदि धारा परिवर्तन के कारण प्राथमिक कुण्डली में फ्लक्स परिवर्तन की दर \(\frac{\Delta \phi}{\Delta t}\) हो, तो
e_p = - N_p . \(\frac{\Delta \phi}{\Delta t}\) ...........................(1)
चूँकि क्रोड चुम्बकीय क्षेत्र रेखाओं के लिए बन्द एवं सुगम मार्ग प्रदान करता है; अतः चुम्बकीय फ्लक्स में विभिन्न प्रकार से होने वाली हानि को यदि नगण्य मान लें तो यह फ्लक्स परिवर्तन \(\left(\frac{\Delta \phi}{\Delta t}\right)\) द्वितीयक से भी होगा, अतः अन्योन्य प्रेरण के कारण द्वितीयक में उत्पन्न प्रेरित वि. वा. बल
es = - Ns. \(\frac{\Delta \phi}{\Delta t}\) ........................(2)
समी. (1) व (2) से,
\(\frac{e_s}{e_p}=\frac{\mathrm{N}_s}{\mathrm{~N}_p}\) ......................(3)
यदि प्राथमिक कुण्डली का प्रतिरोध नगण्य है और ऊर्जा में कोई क्षय नहीं है तो इसके सिरों पर उत्पन्न प्रेरित वि. वा. बल e_p इस पर आरोपित वोल्टता V_p के बराबर होगी। इसी प्रकार यदि द्वितीयक परिपथ खुला (open) है अर्थात् उसका प्रतिरोध अत्यधिक है तो इसके सिरों पर उत्पन्न अन्योन्य प्रेरित वोल्टता (mutual induced voltage) e_s का मान प्राप्त विभवान्तर V_s के बराबर होगा, अत:
\(\frac{\mathrm{V}_s}{\mathrm{~V}_p}=\frac{e_s}{e_p}=\frac{\mathrm{N}_s}{\mathrm{~N}_p}=r\) .......................(4)
जहाँ ट्रान्सफॉर्मर के लिए नियतांक है जिसे परिणमन अनुपात (transformation ratio) कहते हैं। उच्चायी ट्रान्सफॉर्मर के लिए r > 1 और अपचायी ट्रान्सफॉर्भर के लिए r < 1 होता है। 
समी. (4) से स्पष्ट है कि यदि ट्रान्सफॉर्मर उच्चायी है तो-
V_s > V_p ∴ N_s > N_p
अर्थात् द्वितीयक में फेरों की संख्या प्राथमिक में फेरों की संख्या से अधिक होगी।
इसी प्रकार यदि ट्रान्सफॉर्मर अपचायी है तो
V_s < V_p ∴ N_s < N_p
"अपचायी ट्रान्सफॉर्मर में द्वितीयक में फेरों की संख्या प्राथमिक के फेरों की संख्या से कम होगी।"
ट्रान्सफॉर्मर प्रत्यावर्ती बोल्टता में तो परिवर्तन करता है लेकिन शक्ति (power) में कोई परिवर्तन नहीं करता है अतः प्राथमिक कुण्डली के सिरों पर निवेशी शक्ति (input power) का मान द्वितीयक के सिरों पर निर्गत शक्ति (ouput power) के बराबर होता है अर्थात्
P_p = P_s
या V_p. I_p = V_s. I_s
या \(\frac{\mathrm{V}_p}{\mathrm{~V}_s}=\frac{\mathrm{I}_{\mathrm{S}}}{\mathrm{I}_{\mathrm{P}}}\) ............................(5)
इस समीकरण से स्पष्ट है कि उच्चायी ट्रान्सफॉर्मर के लिए,
∵ V_p < V_s ∴ I_s < I_p
अर्थात् उच्चायी ट्रान्सफॉर्मर वोल्टता तो बढ़ाता है लेकिन धारा को कम कर देता है। जिस अनुपात में वोल्टता बढ़ती है, उसी अनुपात में धारा कम हो जाती है। उदाहरण के लिए, यदि कोई उच्चायी ट्रान्सफॉर्मर वोल्टता को 5 गुना कर देता है तो द्वितीयक में धारा प्राथमिक में धारा की 1/5 गुनी रह जायेगी।
इसी प्रकार अपचायी ट्रान्सफॉर्मर के लिए
∵ V_p > V_s ∴ I_s > I_p
“अपचायी ट्रान्सफॉर्मर (step down transformer) वोल्टता को जिस अनुपात में कम करता है, धारा उसी अनुपात में बढ़ जाती है।"
ट्रान्सफॉर्मर की दक्षता (efficiency) निम्न सूत्र से प्राप्त की जा सकती है-
ट्रान्सफॉर्मर की दक्षता,

यदि किसी भी प्रकार ऊर्जा की हानि नहीं होती है, तो ट्रान्सफॉर्मर की दक्षता 100% होती है। अच्छे ट्रान्सफॉर्मर की दक्षता 98% तक होती है।
दान्सफॉर्मर में ऊर्जा की हानि: ट्रान्सफॉर्मर में ऊर्जा की हानि निम्न प्रकार से सम्भव है-

(i) तामिक हानि (Copper Loss): ट्रान्सफॉर्मर की कुण्डलियों में धारा बहने पर उनके ओमीय प्रतिरोध (ohmic resistance) के कारण ऊष्मा के रूप में कुछ ऊर्जा क्षय हो जाती है; इसी ऊर्जा क्षय को तानिक हानि कहते हैं। इस हानि को कम करने के लिए कुण्डलियों का प्रतिरोध कम रखने का प्रयास किया जाता है।

(ii) लौह हानि (Iron Loss): ट्रान्सफॉर्मर की क्रोड में मैंवर धाराओं (eddy currents) के कारण जो ऊर्जा क्षय हो जाती है, उसे लौह हानि कहते हैं। इसी हानि को कम करने के लिए क्रोड को पटलित (laminated) बनाया जाता है।

(iii) शैथिल्य हानि (Hysteresis Loss): ट्रान्सफॉर्मर की क्रोड प्रत्यावर्ती धारा के कारण बार - बार चुम्बकित एवं विचुम्बकित (magnetised and demagnetised) होती रहती है जिससे डोमेनों के बार-बार घूर्णन से आन्तरिक घर्षण (internal friction) के कारण क्रोड गर्म हो जाती है। इसी हानि को शैथिल्य हानि कहते हैं। इस हानि को कम करने के लिए क्रोड नर्म लोहे या सिलिकॉन स्टील की बनायी जाती है।

(iv) चुम्बकीय क्षरण (Magenetic Leakage): प्राथमिक कुण्डली में उत्पन्न चुम्बकीय फ्लक्स की कुछ क्षेत्र रेखाएँ क्रोड के बाहर वायु मार्ग से गुजर जाती हैं जिससे द्वितीयक के साथ सम्बद्ध चुम्बकीय फ्लक्स प्राथमिक की अपेक्षा कुछ कम हो जाता है। इससे ऊर्जा में होने वाली हानि को ही चुम्बकीय क्षरण (magnetic leakage) कहते हैं। इस हानि को कम करने के लिए क्रोड अधिक चुम्बकशीलता (more permeability) वाले पदार्थ को बनायी जाती है (जैसे- कच्चा लोहा, सिलिकॉन स्टील आदि)।

आंकिक प्रश्न

प्रश्न 1.
एक विद्युत बल्ब 220V आपूर्ति पर 100 W शक्ति देने के लिए बनाया गया है। स्रोत की शिखर वोल्टता ज्ञात कीजिए।
हल:
V_rms = \(\frac{\mathrm{V}_0}{\sqrt{2}}\)
V_o = V_rms \(\sqrt{2}\)
V_o = 220 x \(\sqrt{2} \) = 311 वोल्ट 

प्रश्न 2.
एक प्रत्यावर्ती वोल्टेज V = 70 sin 100 πt को 25 Ω के प्रतिरोधक से जोड़ा गया है। ज्ञात करो-
(i) स्रोत की आवृत्ति 
(ii) प्रतिरोधक में से प्रवाहित धारा।
हल: 
दिया है V = 70 sin 100 πt
मानक समीकरण V = V_o sin ωt से तुलना करने पर
V_o = 70 वोल्ट, ω = 100 π rad/s
ω = 2πf = 100π
(i) ∴ आवृत्ति f = 50 हर्ट्ज
(ii) V_rms = \(\frac{\mathrm{V}_0}{\sqrt{2}}=\frac{70}{\sqrt{2}}\)
I_rms = \(\frac{\mathrm{Vrms}}{\mathrm{R}}=\frac{70 / \sqrt{2}}{25}\)
I_rms = \(\frac{70}{1.414 \times 25}\)
I_rms = 1.98 ऐम्पियर 

प्रश्न 3.
150 वॉट का एक विद्युत बल्व 220 वोल्ट व 50 हज़ आवृत्ति की सप्लाई से जुड़ा है। गणना करो।
(i) बल्व का प्रतिरोध
(ii) बल्व से प्रवाहित वर्ग माध्य मूल धारा
हल: 
(i) दिया है P = 150 वॉट, V = 220 वोल्ट 
बल्व का प्रतिरोध R = \(\frac{\mathrm{V}^2}{\mathrm{P}}=\frac{(220)^2}{150}\) = 322.7 ओम
(ii) जैसा कि ज्ञात है
I_rms = \(\frac{\mathrm{Vrms}}{\mathrm{R}}=\frac{220}{322.7}\)
I_rms = 0.68 एम्पियर

प्रश्न 4.
एक प्रत्यावर्ती वोल्टेज V= 70 sin 100 πt को 25 π के प्रतिरोधक से जोड़ा गया है। ज्ञात करो-
(i) स्रोत की आवृत्ति 
(ii) प्रतिरोधक में से प्रवाहित धारा।
हल: 
दिया है V = 70 sin 100 πt 
मानक समीकरण V = V_o sin ωt से तुलना करने पर
V_o = 70 वोल्ट, ω = 100 π rad/s
(i) जैस कि ω = 2πf = 100π
∴ स्रोत की आवृत्ति f = 50 हज
(ii) V_rms = \(\frac{\mathrm{V}_0}{\sqrt{2}}=\frac{70}{\sqrt{2}}\)
I_rms = \(\frac{\mathrm{Vrms}}{\mathrm{R}}=\frac{70 / \sqrt{2}}{25}=\frac{70}{1.414 \times 25}\)
I_rms = 1.98 ऐम्पियर

प्रश्न 5.
एक कुण्डली 110 V - 50 Hz वाले प्रत्यावर्ती धारा स्रोत से 1.0 A की धारा तथा 100 W शक्ति लेती है। कुण्डली का प्रतिरोध तथा प्रेरकत्व ज्ञात कीजिए।
हल: 
दिया है, V_rms = 110V, f = 50 Hz
I_rms = 1.0 A,P = 100 W
कुण्डली द्वारा ली गई शक्ति केवल प्रतिरोध R के कारण होती है,
अत:
P = I_rms².R
∴ R = \(\frac{\mathrm{P}}{\mathrm{I}_{r m s}^2}=\frac{100}{(1.0)^2}\) = 100 Ω
परिपथ की प्रतिबाधा
Z = \(\frac{\mathrm{V}_{r m s}}{\mathrm{I}_{r m s}}=\frac{110}{1.0}\) = 110 Ω
परन्तु परिपथ की प्रतिबाधा
Z = \(\sqrt{\mathrm{R}^2+\mathrm{XC}_{\mathrm{L}}^2}\)
X_L² = Z² - R² = (Z + R) (Z - R)
= (110 + 100) (110 - 100)
= 210 x 10 = 2100Ω
X_L = \(\sqrt{2100}\) = 45.8 Ω
X_L = 2πfL
L = \(\frac{\mathrm{X}_{\mathrm{L}}}{2 \pi f}=\frac{45.8}{2 \times 3.18 \times 50}\)
L = 0.146 H

प्रश्न 6.
एक 15µF का संघारित्र 200V - 50 Hz के स्रोत से संबंधित किया जाता है। यारितीय प्रतिघात, धारा का वर्ग मध्य मूल मान तथा शिखर मान ज्ञात कीजिए।
हल: 
दिया है, C = 15µF = 15 x 10^-6 C,V_rms = 220V, f = 50 Hz
धारिता प्रतिघात
X_C = \(\frac{1}{2 \pi f C}=\frac{1}{2 \times 3.14 \times 50 \times 15 \times 10^{-6}}\)
X_C = \(\frac{1}{3.14 \times 15 \times 10^{-4}}\)
X_C = \(\frac{10^4}{3.14 \times 15}\) = 212.3 Ω
∴ धारा का वर्ग माध्यम मूल मान
I_rms = \(\frac{\mathrm{V}_{r m s}}{\mathrm{X}_{\mathrm{C}}}=\frac{220}{212.3}\) = 1.036 A
धारा का शिखर मान
I₀ = I_rms \(\sqrt{2}\)
= 1.036 x 1.414
I₀ = 1.465 A

प्रश्न 7.
100 µF धारिता के एक संघारित्र तथा 40Ω के एक प्रतिरोध का श्रेणीक्रम संयोजन 110 V, 60 Hz की प्रत्यावर्ती स्रोत से जुड़ा है। परिपथ में अधिकतम धारा का मान जत करो।
हल:
I_m = \(\frac{\mathrm{V}}{\sqrt{\mathrm{R}^2+\frac{1}{c^2 \omega^2}}}\)
दिया है V = 110V, C = 100µF = 100 x 10^-6 F
R = 10Ω, f = 60 Hz

प्रश्न 8.
प्रतिरोधक के सिरों पर विभवान्तर 160 V तथा प्रेरक के सिरों पर विभवान्तर 120 V है। अनुप्रयुक्त वोल्टता का प्रभावी मान ज्ञात कीजिए। यदि परिपथ में प्रभावी धारा 1.0 A है, तो परिपथ की कुल प्रतिबाधा परिकलित कीजिए।
हल:
दिया है- प्रतिरोधक के सिरों पर विभवान्तर V_R = 160 वोल्ट 
प्रेरक के सिरों पर विभवान्तर V_L = 120 वोल्ट
प्रभावी धारा I = 1.0 A
परिणामी वोल्टता VRL = \(\sqrt{\mathrm{V}_{\mathrm{R}}^2+\mathrm{V}_{\mathrm{L}}^2}\)
= \(\sqrt{(160)^2+(120)^2}\)
= 200 वोल्ट
परिपथ की प्रतिबाधा Z = \(\frac{\mathrm{V}_{\mathrm{RL}}}{\mathrm{I}}=\frac{200}{1}\) = 200Ω

प्रश्न 9.
किसी LCR प्रत्यावर्ती परिपथ में R = 10Ω, X_L = 100Ω एवं X_C = 100 Ω है। परिपथ की प्रतिबाधा का मान लिखिए।
हल:
दिया है R = 10Ω
तथा X_L = X_C = 10Ω
अतः प्रतिबाधा Z = R

प्रश्न 10.
एक प्रत्यावर्ती धारा परिपथ में वोल्टता V = 50 sin 314t वोल्ट तथा धारा I = 10 sin (314t + \(\frac{\pi}{4}\)) A है। ज्ञात कीजिए
(i) वॉटहीन धारा 
(ii) वर्ग माध्य मूल वोल्टता 
हल:
दिया है: V = 50 sin 314t वोल्ट
I = 10 sin (314t + \(\frac{\pi}{4}\) ) ऐम्पियर
स्पष्ट है f = \frac{\pi}{4}, V₀ = 50 वोल्ट I₀ = 10 ऐम्पियर

(i) वॉटहीन धारा = I_rms cosΦ
= \(\frac{\mathrm{I}_0}{\sqrt{2}} \cos \frac{\pi}{4}=\frac{10}{\sqrt{2}} \times \frac{1}{\sqrt{2}}\)
= 5 ऐम्पियर

(ii) वर्ग माध्य मूल वोल्टता V_rms = \(\frac{\mathrm{V}_0}{\sqrt{2}}=\frac{50}{\sqrt{2}}\)
= 50 x 1.414
= 70.7 वोल्ट

प्रश्न 11.
एक कुण्डली का 50 Hz आवृत्ति पर शक्ति गुणांक 0.707 है। यदि आवृत्ति दुगुनी कर दे तो कुण्डली का शक्ति गुणांक क्या होगा?
हल: 
कुण्डली का शक्ति गुणांक (cos Φ) = 0.707
आवृत्ति v₁ = 50 Hz
आवृत्ति v₂ = 100 Hz

प्रश्न 12.
कोई ac परिपथ दो परिपथ अवयवों X और Y के श्रेणी संयोजन से बना है। धारा कला में वोल्टता से \frac{\pi}{4} अग्र है। यदि अवयव X 100 Ω का शुद्ध प्रतिरोध है, तो
(a) परिपथ अवयव Y का नाम लिखिए।
(b) यदि वोल्टता का rms मान 141 वोल्ट है, तो धारा का rms मान परिकलित कीजिए।
(c) यदि ac स्रोत को dc स्रोत से प्रतिस्थापित किया जाए, तो क्या होगा?
हल: 
(a) परिपथ अवयव Y प्रेरक कुण्डली है।

(b) वोल्टता का rms मान V_rms = 141 वोल्ट
I_rms = \(\frac{\mathrm{V}_{\text {rms }}}{\mathrm{R}}=\frac{141}{100}\) = 1.41 ऐम्पियर

(c) ac स्रोत को dc से प्रतिस्थापित करने पर f = 0 तक X_L = 0 परिपथ में नियत स्थायी अधिकतम धारा प्रवाहित होगी।

प्रश्न 13.
अन्य कोई परिवर्तन किए बिना, संधारित्र C से पार्श्व में संयोजित किए जाने वाले उस अतिरिक्त संधारित्र C₁ का मान ज्ञात कीजिए। जिससे कि परिपथ का शक्ति गुणांक हो जाए।

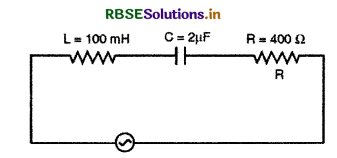
V=V₀ sin (1000t + Φ)
हल: 
दिया है-
L = 100 mH = 100 x 10^-3 H
C = 2µF = 2 x 10^-6 F
R = 400Ω
शक्ति गुणांक cosΦ = 1
∴ cosΦ = \(\frac{\mathrm{R}}{\sqrt{\mathrm{R}^2+\left(\mathrm{X}_{\mathrm{L}}-\mathrm{X}_{\mathrm{C}}\right)^2}}\)
1 = \(\frac{400}{\sqrt{(400)^2+\left(100-X_C\right)^2}}\)
(400)² + (100 - X_C)² = (400)²
(100 - X_C)² = 0
100 - X_C = 0
X_C = 100
X_C = \(\frac{1}{\omega C}\) = 100
दिया है V = V₀ (1000t + Φ)  अतः ω = 1000 रेडियन/से
\(\frac{1}{1000 \mathrm{C}}\) = 100
C = 10^-5 F = 10µF
अत: 8uF का संधारित्र पार्श्व में जोड़ने पर परिपथ का शक्ति गुणांक एकांक हो जाएगा।

प्रश्न 14.
एक ट्रांसफार्मर की प्राथमिक कुण्डली में 1 A की धारा प्रवाहित हो रही है। परिपथ की निवेशी शक्ति 4 KW तथा द्वितीयक कुण्डली में उत्पन्न वोल्टता 400 V होता है। यदि प्राथमिक कुण्डली में फेरों की संख्या 100 हो तो द्वितीयक कुण्डली में फेरों की संख्या ज्ञात करो।
हल:
P_m = I_pV_p
दिया है I_p = 1 Amp, P_in = 4000 W, V_S = 400V, N_p = 100
V_p = \(\frac{\mathrm{P}_{i n}}{\mathrm{I}_p}=\frac{4000}{1}\) = 4000 वॉट
\(\frac{V_S}{V_P}=\frac{N_S}{N_P}\)
N_s = \(\frac{400}{4000}\) x 100 = 10

प्रश्न 15.
उस ट्रांसफॉर्नर की प्राथमिक कुण्डली से प्रवाहित धारा की गणना करो जिसमें 20 ओम प्रतिरोध की युक्ति का वोल्टेज 200 V से 20 V किया जाता है। मान लीजिए ट्रांसफार्मर की दक्षता 80% है।
हल: 

80 = \(\frac{\mathrm{V}_{\mathrm{S}} \mathrm{I}_{\mathrm{S}}}{\mathrm{V}_{\mathrm{P}} \mathrm{I}_{\mathrm{P}}}\) x 100
4 V_p I_p = 5 V_s I_s
द्वितीयक में से प्रवाहित धारा
I_S = \(\frac{\mathrm{V}_{\mathrm{S}}}{\mathrm{R}}=\frac{20}{20}\) = 1 ऐम्पियर 
∴ 4 x 200 x I_p = 5 x 20 x 1
I_p = \(\frac{1}{8}\)
I_p = 0.125 A

प्रतियोनी परीक्षा संबंधी प्रश्न

प्रश्न 1.
एक प्रत्यावर्ती परिपथ की ताक्षणिका वि, वा, बल और धारा दिए गए है-
e = 100 sin 30t
i = 20 sin (30t - π/4)) 
प्रत्यावर्ती धारा के एक चक्र में परिपथ में व्ययित शक्ति एवं वॉटहीन धारा क्रमशः होगी-
(A) (50/\(\sqrt{2}\)),0
(B) 50, 0 
(C) 50,10
(D) 100/\(\sqrt{2}\), 10
उत्तर:
(D) 100/\(\sqrt{2}\), 10

प्रश्न 2. 
एक LCR परिपथ प्रत्यावर्ती धारा स्रोत से जुड़ा है। जब L को परिपथ से हटा देते है तो धारा और वोल्टता के बीच कलांतर π/3 हो जाता है। यदि इसके बजाय परिपथ से C को हटा दिया जाय तब भी धारा और वोल्टता के मध्य कलांतर π/3 ही रहता है। परिपथ का शक्ति गुणांक है-
(A) 1.0
(B) -1.0
(C) शून्य
(D) 0.5 
उत्तर:
(A) 1.0

प्रश्न 3.
एक ट्रांसफार्मर की दक्षता 90% है। यह 200 V व 3 KW की पावर सप्लाई पर काम कर रहा है। यदि, द्वितीयक कुण्डली में 6 A की धारा प्रवाहित हो रही है तो द्वितीयक कुण्डली के सिरों के बीच विभवान्तर तथा प्राथमिक कुण्डली में विद्युत धारा का मान क्रमशः होगा-
(A) 450V, 15 A
(B) 450 C, 13.5 A
(C) 600 V, 15 A
(D) 300 V, 15 A
उत्तर:
(A) 450 V, 15 A

प्रश्न 4.
यहाँ दर्शाए परिपथ में, बिन्दु 'C' बिन्दु 'A' से तब तक संयोजित है जब तक कि परिपथ में प्रवाहित धारा नियम नहीं। इसके बाद अचानक बिन्दु 'C' को बिन्दु A से विच्छेदित किया जाता है। t = L/R पर प्रतिरोध तथा प्रेरक के सिरों में वोल्टता का अनुपात होगा-

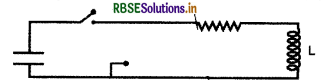
(A) \(\frac{e}{1-e}\)
(B) 1
(C)-1
(D) \(\frac{1 - e}{e}\)
उत्तर:
(C) -1

प्रश्न 5.
स्रोत जिसका emf (V) = 10sin 340t है से श्रेणी में 20 mH का प्रेरक, 50 µF का संधारित्र तथा 50Ω का प्रतिरोधक संयोजित है। इस प्रत्यावर्ती धारा परिपथ में शक्ति क्षय हैं।
(A) 0.51 W
(B) 0.67 W
(C) 0.76 W
(D) 0.89 W
उत्तर:
(A) 0.51 W

प्रश्न 6.
कोई लघु सिग्नल वोल्टता V(_f) = V₀ sin ωt किसी अदिश संघारित्र के सिरों पर अनुप्रयुक्त की गयी है-
(A) धारा (I_f) वोल्टता (V_f) से 90° पश्च है
(B) एक पूर्व चक्र में संघारित्र C वोल्टता स्रोत से कोई ऊर्जा उपयुक्त नहीं करता।
(C) धारा I_(f), वोल्टता V_(f) की कीला में है
(D) धारा I_(f), वोल्टता V_(f) से 180° अग्न है
उत्तर:
(B) एक पूर्व चक्र में संघारित्र C वोल्टता स्रोत से कोई ऊर्जा उपयुक्त नहीं करता।

प्रश्न 7.
किसी AC (एसी) स्रोत से जोड़ने पर एक प्रतिरोध 'R' द्वारा 'P' शक्ति ली जाती है। यदि इस प्रतिरोध के श्रेणीक्रम में एक प्रेरकत्व जोड़ने से परिपथ की प्रतिबाधा (Z) हो जाती है, तो ली गई शक्ति हो जायेगी-
(A) P\(\sqrt{\frac{R}{Z}}\)
(B)P (\(\sqrt{\frac{R}{Z}}\))
(C) 1P
(D) P (\(\sqrt{\frac{R}{Z}}\))²
उत्तर:
(D) P (\(\sqrt{\frac{R}{Z}}\))²

प्रश्न 8.
यदि एक विद्यार्थी L को दो विभिन्न मानों L₁ तथा L₂ (L₁ > L₂) के लिए समय (t) तथा संधारित्र पर अधिकतम आवेश के वर्ग (Q² max) के बीच दो ग्राफ बनाता है तो निम्नांकित में से कौन - सा ग्राफ सही है। (प्लॉट केवल अवस्था प्लॉट है तथा स्केल के अनुसार नहीं है)

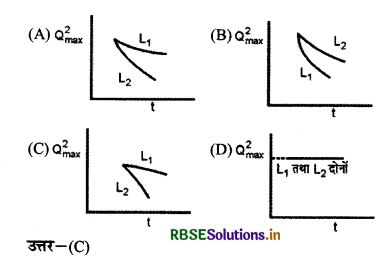
प्रश्न 9.
एक श्रेणी R - C परिपथ, किसी प्रत्यावतीं वोल्टेज के स्रोत से जुड़ा है। दो स्थितियों (a) तथा (b) पर विचार कीजिए-
(a) जब संधारित्र वायु से भरा है 
(b) जब संधारित्र माइका से भरा है इस परिपथ में प्रतिरोधक से प्रवाहित धारा 'I' है तथा संधारित्र के सिरों के बीच विभान्तर V हो तो-
(A)V_a > V_B
(B) I_a > I_b
(C) V_a = V_b
(D)V_a < V_b
उत्तर:
(A) V_a > V_B

प्रश्न 10.
एक कमरे की सप्लाई वोल्टता 120 V है। लीड के तारों का प्रतिरोध 6Ω है। एक 60 W बल्ब पहले से ही जल रहा है। इस बल्ब के समान्तर में 240 W का हीटर जलाने पर बल्ब की वोल्टता में कितनी कमी आयेगी-
(A) 2.9 वोल्ट
(B) 13.3 वोल्ट 
(C) 10.04 वोल्ट
(D) शून्य 
उत्तर:
(D) शून्य