RBSE Class 12 Physics Important Questions Chapter 5 Magnetism and Matter

Rajasthan Board RBSE Class 12 Physics Important Questions Chapter 5 Magnetism and Matter Important Questions and Answers.

RBSE Class 12 Physics Chapter 5 Important Questions Magnetism and Matter

Multiple Choice Questions

Question 1.
The SI unit of permeability is:
(A) Wb m^-1 A^-1
(B) Wb m A^-1
(C) Wb m^-1 A^-2
(D) Wb m A.
Answer:
(C) Wb m^-1 A-2

Question 2.
One tesla is equal to:
(A) 10⁷ gauss
(B) 10^-4 gauss
(C) 10⁴ gauss
(D) 10^-8 gauss.
Answer:
(C) 10⁴ gauss

Question 3.
Electric current through the straight horizontal part of a wire is flowing from east to west. The force experienced by this part of the wire due to earth’s magnetic field will be such as to pull it:
(A) in the north-south direction
(B) vertically upward
(C) vertically downward
(D) in the east-west direction.
Answer:
(C) vertically downward

Question 4.
A Cyclotron is used to accelerate:
(A) Electron
(B) Neutrons
(C) Positive ions
(D) None of these.
Answer:
(C) Positive ions

Question 5.
The area of B-H curve is an indication of:
(A) Susceptivity of the substance
(B) Retentivity of substance
(C) The energy dismissed per cycle
(D) The permeability of the medium.
Answer:
(C) The energy dismissed per cycle

Question 6.
If a long copper rod carries a direct current, the magnetic field associated with the current will be:
(A) inside the rod only
(B) outside the rod only
(C) both inside the outside the rod
(D) Neither a force nor a torque.
Answer:
(C) both inside the outside the rod

Question 7.
Magnetic meridian is a:
(A) point
(B) line along NS
(C) horizontal plane
(D) vertical plane along NS.
Answer:
(D) vertical plane along NS.

Question 8.
Magnetic dipole moment is a quantity directed from:
(A) south to north
(B) north to south
(C) east to west
(D) west to east.
Answer:
(A) south to north

Question 9.
The magnetic moment of a magnet is 0.1 amp x m². It is suspended in a magnetic field of intensity 3 x 10^-4 weber/m². The couple acting upon it when deflected by 30° from the magnetic field is:
(A) 1 x 10⁵ Nm
(B) 1.5 x 10^-5 Nm
(C) 2 x 10^-5 Nm
(D) 2.5 x 10^-5 Nm.
Answer:
(B) 1.5 x 10^-5 Nm

Question 10.
The S.I. unit of magnetic moment are:
(A) JT^-2
(B) TJ^-1
(C) Am²
(D) A^-1m².
Answer:
(C) Am²

Question 11.
The angle of dip at the magnetic equator is:
(A) 0°
(B) 45°
(C) 90°
(D) 30°.
Answer:
(A) 0°

Question 12.
At magnetic poles the angle of dip is:
(A) 45°
(B) 30°
(C) 90°
(D) zero.
Answer:
(C) 90°

Question 13.
The direction of force experienced by a current carrying conductor placed in a magnetic field is given by:
(A) Fleming’s left hand rule
(B) Fleming’s right hand rule
(C) Lenz’s rule
(D) Biot-Savart’s law.
Answer:
(A) Fleming’s left hand rul

Question 14.
Angle of dip is 90° at:
(A) poles
(B) equator
(C) Both (A) and (B)
(D) None of these.
Answer:
(A) poles

Question 15.
Tesla is the unit of:
(A) electric flux
(B) electric field
(C) magnetic induction
(D) magnetic flux.
Answer:
(C) magnetic induction

Question 16.
The magnetic moment of a diamagnetic atom is:
(A) equal to zero
(B) equal to one
(C) between zero and one
(D) much greater than one.
Answer:
(A) equal to zero

Question 17.
In which type of material the magnetic susceptibility does not depend on temperature?
(A) Diamagnetic
(B) Paramagnetic
(C) Ferromagnetic 
(D) Ferrite.
Answer:
(A) Diamagnetic

Question 18.
Above curie temperature:
(A) a paramagnetic substance becomes ferromagnetic
(B) a ferromagnetic substance becomes diamagnetic
(C) a paramagnetic substance becomes diamagnetic
(D) a ferromagnetic substance becomes paramagnetic.
Answer:
(D) a ferromagnetic substance becomes paramagnetic.

Question 19.
Domain formation is the necessary feature of:
(A) daimagnetism
(B) paramagnetism
(C) ferromagnetism
(D) All of these.
Answer:
(C) ferromagnetism

Question 20.
A bar of diamagnetic material is placed in a magnetic field with its length making an angle of 30° with the direction of the magnetic field. How will the bar behave?
(A) It will align itself perpendicular to the magnetic field
(B) It iwill align itself parallel to the magnetic field
(C) It wll remain as before
(D) Its behaviour can not be predicted.
Answer:
(A) It will align itself perpendicular to the magnetic field

Question 21.
Susceptibility is positive for:
(A) paramagnetic substances
(B) ferromagnetic substances
(C) non-magnetic substances
(D) diamagnetic substances.
Answer:
(B) ferromagnetic substances

Question 22.
The best material for the core of a transformer, is:
(A) stainless steel
(B) mild steel
(C) hard steel
(D) soft iron.
Answer:
(D) soft iron.

Question 23.
Lines of force, due to earth’s horizontal magnetic field, are:
(A) elliptical
(B) curved lines
(C) concentric circles
(D) parallel and straight.
Answer:
(D) parallel and straight.

Question 24.
Which of the following statements is not correct about the magnetic field?
(A) magnetic lines of force do not cut each other
(B) inside the manget, the lines go form north to south pole of the magnet
(C) the magnet lines form a closed loop
(D) tangents to the magnetic lines give the direction of the magnetic field.
Answer:
(B) inside the manget, the lines go form north to south pole of the magnet

Question 25.
If a diamagnetic substance is brought near north or south pole of a bar-magnet, it is:
(A) attracted by both poles
(B) repelled by both poles
(C) attracted by north pole and repelled by south pole
(D) repelled by north pole and attracted by south pole.
Answer:
(B) repelled by both poles

Fill in the blanks

Question 1.
Two magnetic lines ........................... cross each other.
Answer:
never.

Question 2.
Surface integral of     ........................... field over a closed surface is zero.
Answer:
magnetic.

Question 3.
Angle of dip is ........................... at the equator.
Answer:
zero.

Question 4.
Angle of dip is ........................... at the poles.
Answer:
90°.

Question 5.
The two ends of a magnet where attraction is maximum are called ........................... .
Answer:
poles.

Question 6.
Magnetic lines have no real existance and are purely ........................... .
Answer:
imaginary.

Question 7.
The value of µ₀ in free space is ........................... .
Answer:
4π x 10^-7 Hm^-1.

Question 8.
Bohr magneton µ_B =    ........................... .
Answer:
9.27 x 10^-24 Am².

Question 9.
A current loop behaves as a ........................... dipole.
Answer:
magnetic.

Question 10.
At ........................... temperature, a ferro-magnetic material passes over to para-magnetics.
Answer:
curie.

Very Short Type Questions

Question 1.
Magnetic field lines can be entirely confined within the core of a toroid, but not within a straight solenoid. Why?
Answer:
Magnetic field lines can be entirely confined to the core of a toroid because toroid has no ends. It can confine the field within its core. A straight solenoid has two ends. If the entire flux were confined between these ends, the flux throughout the cross-section at each end would be non-zero. This is not possible.

Question 2.
If magnetic monopoles existed, how would Gauss’s law of magnetism be modified.
Answer:
According to Gauss’s law, in magnetism, magnetic flux over any closed surface is always zero
i.e. \(\oint \overrightarrow{\mathrm{B}} \cdot \overrightarrow{d \mathrm{~S}}\) = 0
If monopoles existed, the magnetic flux would no longer be zero, but equal to the monopole, q_m enclosed by the surface.
\(\oint \overrightarrow{\mathrm{B}} \cdot \overrightarrow{d \mathrm{~S}}\) = q_m

Question 3.
The vertical component of earth’s magnetic field is \(\sqrt{3}\) times the horizontal component. What is the value of dip at this place?
Answer:
Since magnetic dip δ is given by
tan δ = \(\frac{\mathrm{V}}{\mathrm{H}}\)
Here V = \(\sqrt{3}\) H
tan δ = \(\frac{\sqrt{3} \mathrm{H}}{\mathrm{H}}=\sqrt{3}\)
or δ = 60°.

Question 4.
Two wires of equal lengths are bent in the form of two loops. One of the loops is a square shaped whereas the other loop is circular. These are suspended in a uniform magnetic field and the same current is passed through them. Which loop will experience greater torque? Give reasons.
Answer:
The torque depends upon the magnetic flux cutting the loops. Larger the area of the loop, more the magnetic flux cutting it and hence larger the value of torque.
Since for a given circumference, circle has maximum area hence the circular loop will experience maximum torque.

Question 5.
Write the S.I. unit of magnetic flux.
Answer:
S.I. unit of magnetic flux is weber and 1 Wb = 1 Tm².

Question 6.
Write S.I. unit of magnetic field \(\overrightarrow{\mathbf{B}}\).
Answer:
The S.I. unit of magnetic field B is tesla (T).

Question 7.
What is the value of horizontal component of the earth’s magnetic field at the magnetic poles?
Answer:
The value of H = 0 at the magnetic poles of earth.

Question 8.
Can you realise independent magnetic poles?
Answer:
No, independent magnetic poles don’t exist.

Question 9.
Define unit magnetic pole.
Answer:
Unit magnetic pole is defined as a pole of that much strength which when placed at a distance of 1 m from a similar and equal pole in free space, repels it with a force of \(\frac{\mu_0}{4 \pi}\) newton.

Question 10.
Write the value of Bohr’s magneton.
Answer:
9.27 x 10^-24 Am².

Question 11.
Does one part of a wire carrying current exert a force on another part of the same wire?
Answer:
No.

Question 12.
What is the unit of pole strength (m)?
Answer:
Am or NT^-1.

Question 13.
What is the unit of magnetic dipole moment (M)?
Answer:
AM² or JT^-1.

Question 14.
What is the direction of magnetic dipole moment?
Answer:
It is from S-pole to N-pole of the magnetic dipole.

Question 15.
What is the significance of Gauss’s law in magnetism?
Answer:
Magnetic poles exist in equal and opposite pairs.

Question 16.
A small magnet is pivoted to move freely in the magnetic meridian. At what place on the surface of earth, will the magnet be vertical?
Answer:
At the magnetic pole of earth.

Question 17.
Does earth’s magnetic field also change from time to time? If yes on what times scale does it change appreciably?
Answer:
Yes, it changes with time. The time period is few hundred years.

Question 18.
Explain why, besides the main magnetic N-S poles, there are several local poles on the earth’s surface oriented in different directions?
Answer:
Earth’s main field is due to magnetic dipole, while local fields might be due to magnetised mineral deposits.

Question 19.
What is in the ultimate source of earth’s magnetism?
Answer:
The electric currents circulating in the interior of the earth (whatever the reason/cause) is the ultimate source of earth’s magnetism.

Question 20.
Can a magnetic field line form a closed loop? Explain.
Answer:
Yes. The magnetic lines form closed oops inside the toroid and around a current carrying conductor.

Question 21.
What is the maximum and minimum value of dip?
Answer:
The maximum value of dip is 90° and it occurs at magnetic poles and the minimum value of dip is 0° at the equator of earth.

Question 22.
Does a bar magnet exert a torque on itself due to its own field?
Answer:
No, a bar magnet does not exert a force or a torque on itself due to its own field.

Question 23.
In which direction compass will point if located right to the geomagnetic north or south pole?
Answer:
Any direction. At poles, whole of the field is vertical. There is no component of field in horizontal direction. Hence in horizontal field free area, the horizontal needle may point in any direction.

Question 24.
What are magnetic elements of earth’s magnetic field?
Answer:
Magnetic elements are those properties of earth’s magnetic field which give us the complete knowledge of earth’s magnetic field. These are

• declination
• dip and
• horizontal component of earth’s magnetic field.

Question 25.
The electric currents in the outer conducting regions of earth’s core are thought to be responsible for earth’s magnetism. What might be the source of energy to sustain these currents?
Answer:
Radioactivity might be the source of energy, but the real cause is not exactly known.

Question 26.
The earth’s core is known to contain iron, yet geologists do not regard this as a source of earth’s magnetism. Why?
Answer:
The earth’s core contains molten iron and molten iron is not ferromagnetic.

Question 27.
The earth may have even reversed the direction of its field many times during its history of 4-5 billion years. How can geologists know about the earth’s field in such distant past?
Answer:
Earth’s magnetic field gets weakly recorded in certain rocks during solidification. Analysis of the magnetism of these rocks give us the clues of geomagnetic history.

Question 28.
What is the name of place where angle of dip is 0° and 90°?
Answer:
At the magnetic equator, the angle of dip is 0° and at magnetic poles, the angle of dip is 90°.

Question 29.
From where does the magnetic equator pass through India?
Answer:
Through Trivendrum.

Question 30.
What do you mean by magnetic maps?
Answer:
Maps giving values of magnetic elements are called magnetic maps.

Question 31.
What information does each magnetic element give about the earth’s magnetic field?
Answer:
Declination gives the plane.
Dip gives the direction.
Horizontal component of earth’s magnetic field gives the resultant intensity of earth’s magnetic field in the horizontal direction.

Question 32.
How does the knowledge of declination at a place help in navigation?
Answer:
Since declination at a place is the angle between the magnetic meridian and the geographical meridian, so knowing declination one can know the geographical meridian. Hence true north and south directions can be known which is essential for navigation.

Question 33.
Name the three commonly known ferromagnetic materials.
Answer:
Iron, Nickel and Cobalt are three commonly known ferromagnetic materials.

Question 34.
What is meant by non-magnetic material?
Answer:
Those materials which are not affected very much by strong magnetic field are called non-magnetic materials.

Question 35.
Why magnetic lines of force prefer to pass through ferromagnetic substances than through air?
Answer:
The relative permeability of a ferromagnetic material is µ_r >> 1, so magnetic lines of force prefer to pass through ferromagnetic substances than through air.

Question 36.
Magnetic field arises due to charge in motion. Can a system have a magnetic moment, even though its net charge is zero?
Answer:
Yes, the average of the charges on the system may be zero. Yet, the mean of the magnetic moments due to various currents may not be non-zero e.g. a neutron has zero charge, but non-zero magnetic moment.

Question 37.
How can a magnetised piece of iron be demagnetised?
Answer:
Either by heating the iron to its Curie point (770°C) or undergoing the iron piece through a succession of hysteresis loops of smaller size.

Question 38.
What do you infer from the large value of the susceptibility of the material? For example susceptibility of iron is more than that of copper. Explain.
Answer:
The susceptibility ✗ of a material is given by ✗_m = \(\frac{1}{\mathrm{H}}\)
So large value of the susceptibility of the material means large value of intensity of magnetisation i.e. the material can be magnetised more easily. So, greater value of susceptibility of iron means that it can be more easily magnetised than copper.

Question 39.
What is Curie point?
Answer:
It is the temperature for a ferromagnetic substance above which, it behaves as paramagnetic.

Question 40.
What happens if an iron bar magnet is melted. Does it retain its magnetism?
Answer:
The curie temperature of iron is 770°C. Iron melts at much higher temperature. Hence, iron will not behave as a ferromagnetic material and an iron bar magnet when melted, will not retain its magnetism.

Question 41.
Why is diamagnetism, in contrast, almost independent of temperature?
Answer:
In a diamagnetic sample, the magnetic moment of the sample on placing in a magnetic field is always opposite to the direction of field. It is not affected by the thermal motion of the dipoles.

Question 42.
If a toroid uses bismuth for its core, will the field in the core be (slightly) greater or (slightly) less than when the core is empty?
Answer:
Since bismuth is diamagnetic, the field in the core will be slightly less than when the core is empty.

Question 43.
Is the permeability of ferromagnetic material independent of the magnetic field? If not, is it more for lower or higher fields?
Answer:
No, permeability of a ferromagnetic material depends upon the applied magnetic field. It is more for lower value of applied field.

Question 44.
Why does a paramagnetic sample display greater magnetisation (for the same magnetisation field) when cooled?
Answer:
In paramagnetic substances, the atoms possess permanent magnetic dipole moment. When paramagnetic material is placed in magnetic field, these magnetic molecules are aligned in the direction of the field. The temperature disrupt this alignment. On decreasing the temperature, the thermal agitation trying to disrupt the alignment decreases thus making the sample display greater magnetisation.

Question 45.
What is a natural magnet?
Answer:
A natural magnet is a naturally occurring ore of iron; lodestone or magnetite or black iron oxide Fe₂O₃.
When a specimen of this ore is dipped in iron filings, the filings cling to the ore, especially at its ends.
This ore was originally found in Magnesia district in upper part of Greece. Hence this ore was said to form a natural magnet.

Question 46.
What is a magnet?
Answer:
Magnet. A material which can attract small pieces of iron, cobalt, nickel etc. towards it is called a magnet.
Artificial magnets are made by rubbing a bar of iron with a piece of lodestone (i.e. natural magnet). Artificial magnets are available in the form of bar magnet, horse-shoe magnet, magnetic needle, ball ended magnet, etc.

Question 47.
What is an electromagnet?
Answer:
The property of magnetism is achieved by passing current through a coil wound around a piece of iron. This arrangement is called an electromagnet.

Question 48.
What are magnetic and non-magnetic substances?
Answer:
The substances which can be attracted or repelled by a magnet are called magnetic substances. For example, iron, steel, cobalt, nickel etc. are all magnetic substances.
The substances like brass, paper, wood etc. which are not attracted by a magnet are called non-magnetic substances.

Question 49.
What kind of ferromagnetic material is used for coating magnetic tapes in a cassette player or for building ‘memory stores’ in a modern computer?
Answer:
Ferrites are used for coating magnetic tapes and for building memory stores in a computer because they possess insulating properties and exhibit ferromagnetism.

Question 50.
A certain region of space is to be shielded from magnetic fields. Suggest a method.
Answer:
The region of space to be shielded from magnetic fields is surrounded with soft iron rings. The magnetic field lines will be drawn into the ring, the enclosed region will become free of magnetic field.

Question 51.
Why are the magnetic poles of equal strength?
Answer:
Since the number of atomic north and south pole are equal, so the magnetic poles are of equal strength.

Question 52.
Write SI unit of magnetic flux. Is it a scalar or a vector quantity?
Answer:
Weber, scalar quantity.

Question 53.
How does dip angle change or one moves from magnetic equator to pole?
Answer:
The dip angle changes from 0° to 90° as we move from magnetic equator to pole.

Question 54.
Where on the earth’s surface is the value of angle of dip maximum?
Answer:
At the pole.

Question 55.
How does the (i) pole strength and (ii) magnetic moment of each part of a bar magnetic change if it is cut into two equal pieces along transverse length.
Answer:
The pole strength of each piece is the same but the magnetic moment becomes half of its previous value.

Question 56.
If the ratio of horizontal to the vertical component of earth’s magnetic field is 1/\(\sqrt{3}\) at a place, find angle of dip.
Or
The vertical component of earth’s magnetic field at a place is \(\sqrt{3}\) times the horizontal component. What is the angle of dip at this place.    
Answer:
Given, \(\frac{\mathrm{B}_{\mathrm{H}}}{\mathrm{B}_{\mathrm{V}}}=\frac{1}{\sqrt{3}}, so \frac{B_V}{B_H}=\frac{\sqrt{3}}{1}=\sqrt{3}\)
Since tan δ = \(\frac{\mathrm{B}_{\mathrm{V}}}{\mathrm{B}_{\mathrm{H}}}=\sqrt{3}\)
or δ = 60°.

Question 57. 
The permeability of a magnetic material is 0.9983. Name the type of magnetic material it represents.
Answer:
Since µ = 0.9983 < 1    .
So the material represents a diamagnetic substance.

Question 58.
Write SI unit of (i) magnetic pole strength
(ii) magnetic dipole moment of a bar magnet.
Answer:
(i) Am and
(ii) JT^-1 or Am².

Question 59.
How does the (i) pole strength and (ii) magnetic moment of each part of a bar magnet change if it is cut into two equal pieces along its length.    
Answer:
Pole strength as well as the magnetic moment will reduce to half of its initial value.

Question 60.
In what direction would a compass needle align if taken to geographic (i) North and (ii) South pole?
Answer:
At the poles, the horizontal component of earth’s magnetic field is zero, so the compass needle will align under the effect of vertical component.

Question 61.
Explain with the help of diagram the terms:
(i) magnetic declination and (ii) angle of dip at a given place.
Answer:
Magnetic declination (θ). At a place a shown in figure VSAQ 61 the angle between geographic meridian and the magnetic meridian as shown in figure VSAQ 61:

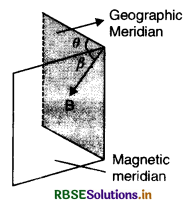
Angle of dip (δ). At a place is the angle made by the direction earth’s total magnetic field with the horizontal direction as shown in figure.

Question 62.
A small magnet is pivoted to move freely in a scalar meridian. At what place on the earth’s surface will the magnet be vertical.
Answer:
The magnet will be vertical at the magnetic pole of the earth.

Question 63.
Which direction would a compass point to, if located right on the geometrical north or south pole?
Answer:
On the geometrical north or south pole, the horizontal component of earth’s magnetic field is zero so the compass needle can point in any direction.

Question 64.
Which physical quantity has the unit Wb m^-2? Is it scalar or a vector quantity?
Answer:
Magnetic field induction and it is a vector quantity.

Question 65.
Where on the earth’s surface is the value of vertical component of earth’s magnetic field zero?
Answer:
At magnetic equator.

Question 66.
What should be orientation of a magnetic dipole in a uniform magnetic field so that its potential energy is maximum?
Answer:
Since potential energy U = - MB cos θ
So U will be maximum if θ = π.
i.e. the potential energy will be maximum when magnetic moment of the dipole is oriented opposite to the direction of magnetic field.

Question 67.
Define the term magnetic moment.
Answer:
The magnetic moment of a magnet (or a current loop) is defined on the maximum value of torque acting on a magnet when it is placed in a magnetic field of one tesla.

Question 68.
The magnetic lines of force prefer to pass through iron than air. Explain why.
Answer:
Because the permeability of iron is very large as compared to air.

Question 69.
Define intensity of magnetisation of a magnetic material. How does it vary with temperature of a paramagnetic material?
Answer:
Intensity of magnetisation of a magnetic material is defined as the magnetic moment developed per unit volume, when it is subjected to a magnetising field. It varies inversely proportional to its absolute temperature.

Question 70.
How does the magnetic induction of a paramagnetic material vary with temperature?
Answer:
It decreases with increase in temperature.

Question 71.
What type of magnetic material is used in making permanent magnets?
Answer:
For making permanent magnet, a material having high coercivity is used.

Question 72.
Write the S.I. unit of magnetic flux.
Answer:
S.I. unit of magnetic flux is weber and 1 Wb = 1 Tm².

Question 73.
Write S.I. unit of magnetic field \(\overrightarrow{\mathbf{B}}\).
Answer:
The S.I. unit of magnetic field B is tesla (T).

Question 74.
What is the value of horizontal component of the earth’s magnetic field at the magnetic poles?
Answer:
The value of H = 0 at the magnetic poles of earth.

Question 75.
Two wires of equal lengths are bent in the form of two loops. One of the loops is a square shaped whereas the other loop is circular. These are suspended in a uniform magnetic field and the same current is passed through them. Which loop will experience greater torque. Give reasons.
Answer:
The torque depends upon the magnetic flux cutting the loops. Larger the area of the loop, more the magnetic flux cutting it and hence larger the value of torque.
Since for a given circumference, circle has maximum area hence the circular loop will experience maximum torque.

Question 76.
An iron-cored solenoid has self inductance 2.8 H. When the core is removed, the self inductance become 2mH. What is the relative permeability of the core used?
Answer:
Given L = 2.8 H, L₀ = 2mH = 2 x 10^-3H, µ_r = ?
Since L = µ_r L₀
∴ µ_r = \(\frac{\mathrm{L}}{\mathrm{L}_0}=\frac{2.8}{2 \times 10^{-3}}\) = 1.4 x 10³ = 1400.

Short Answer Type Questions

Question 1.
What is induced magnetism? Discuss “Attraction is preceded by induction”.
Answer:
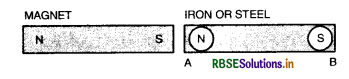
Induced magnetism
The magnetism acquired by a magnetic substance when kept near a magnet is called induced magnetism. When a piece of iron or steel AB is placed near in contact with a magnet it is found to be magnetised i.e. it acquires the property of attracting small iron filings if brought near its end B. If the magnet is now removed, all the iron filings fall down. Thus the steel piece behaves like a magnet so long as it is in the neighbourhood of the magnet.
A magnetic pole induces an opposite polarity on the nearer end of the iron piece and a similar polarity on the end far from it. In fact attraction on the iron piece is due to the induction by the magnet. Thus attraction is always preceded by induction.

Question 2.
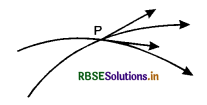
Why cannot two magnetic lines of forces due to a bar magnet cross each other?
Answer:
Because if they cross at any point (say P), there would be two tangents at point P and hence two directions of magnetic fields at the same point as shown in the figure, but magnetic field has only one direction.

Question 3.
A short bar magnet, placed with its axis making an angle θ with a uniform magnetic field \(\overrightarrow{\mathbf{B}}\), experiences a torque \(\vec{\tau}\). What is the magnetic moment of the magnet?
Answer:
The torque \(\vec{\tau}\) experienced by a bar magnet placed in a uniform magnetic field \(\overrightarrow{\mathbf{B}}\) is given by
\(\vec{\tau}\) = \(\vec{M}\) x \(\vec{B}\)
In magnitude
τ = MB sin θ
M = \(\frac{\tau}{\mathrm{B} \sin \theta}\)

Question 4.
Steel is preferred for making permanent magnets whereas soft iron is preferred for making electro magnets. Give one reason.    
Answer:
For permanent magnets. Permanent magnet should have high value of retentivity (to have large force of attraction for magnetic materials) and high value of coercivity (to reatin magnetism for long time), but coercivity is more important than the retentivity. Hence steel is preferred to iron.
For electromagnets. Electromagnets are used for lifting heavy materials and are continuously subjected to cyclic changes. Hence the material used for electromagnets must have high value of retentivity and small hysteresis loss. Hence soft iron is preferred to steel.

Question 5.
Define the terms magnetic dip and magnetic declination with the help of relevant diagram.
Answer:
Neutral point
A neutral point is that point where the field due to magnet is completely neutralised by the horizontal component of earth’s magnetic field. Thus, at the neutral point, if B is the magnetic field due to magnet and H, the horizontal component of earth’s magnetic field, then
B = H
Let us consider the position of the neutral point for the following two positions of a magnet:
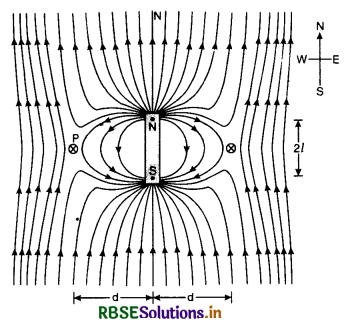
1. When magnet is placed with its north pole towards north of the earth.
Magnetic field due to a small bar magnet by placing its north pole towards north of the earth, then plot of magnetic field of the magnet is shown in Fig. LAQ 14 (a).

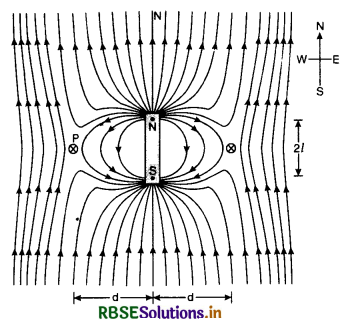
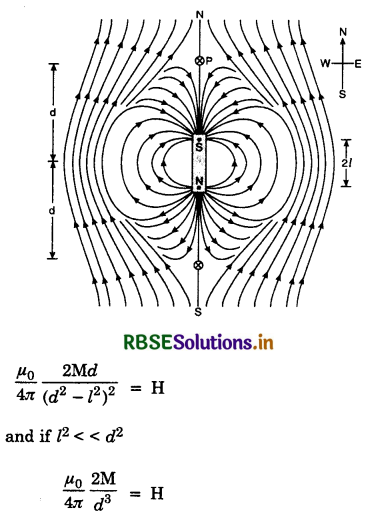
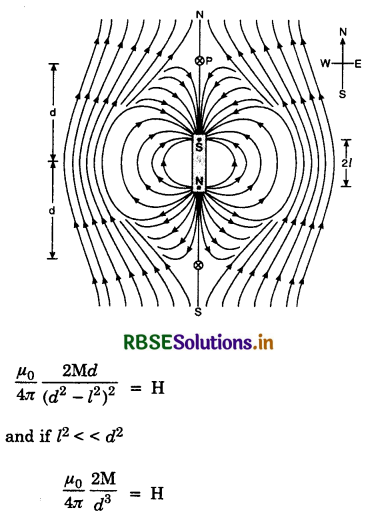
The magnetic field due to earth and that due to magnet cancel out at the two cross-marks on the equatorial line of the magnet. The normal bisector through the centre of the magnets and these positions are called neutral points. Let d be distance of each neutral point from the centre of the magnet. At neutral point, magnetic field due to the magnet is equal to magnetic field due to the earth.
∴ H = \(\frac{\mu_0}{4 \pi} \cdot \frac{\mathrm{M}}{\left(d^2+l^2\right)^{3 / 2}}\) .........................(1)
In case, the magnet is so small then l² can be neglected as compared to d², then
\(\frac{\mu_0}{4 \pi} \cdot \frac{\mathbf{M}}{d^3}\) = H .....................(2)
Knowing d and H the magnetic dipole moment of the bar can be calculated from equation.

2. When magnet is placed with its south pole towards north of the earth. The plot of magnetic field of the magnet in the case will be as shown in Fig. LAQ 14 (b).
The neutral points he on the axial line. At a neutral point, magnetic intensity due to magnet = magnetic field due to the earth.

Knowing d, H this equation can be used to find magnetic dipole of the magnet.

Question 6.
A magnetic needle suspended freely in uniform magnetic field experiences a torque but no net force. An iron nail near a bar magnet however experiences a force of attraction in addition to torque. Why?
Answer:
When a magnetic needle is suspended freely in uniform magnetic field, the two poles of the needle will experience equal and opposite forces hence net force is zero. On the other hand, when an iron nail is placed near a bar magnet, the magnetic field of bar magnet is non-uniform and the two poles of the iron nail will experience different force.

Question 7.
What are the uses of studying hysteresis curve of substance?
Or
What would be your consideration while making electromagnets?
Answer:
Uses of hysteresis curve. Fig. shows two hysteresis curves, one for steel and other for iron. We find that retentivity of soft iron is higher than steel and coercivity of steel is higher than soft iron. These properties are used for making permanent magnets, core of transformers and electromangets etc.

(i) For permanent magnets. Permanent magnet should have high value of retentivity (to have large force of attraction for magnetic materials) and coercivity (to remain magnetic for long time). But coercivity is more important than the retentivity. Hence steel is preferred to iron. Now some alloys like alnico, cobalt, steel are developed which have high value of retentivity and coercivity for making permanent magnets.


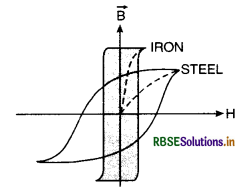
(ii) For electromagnets. Electromagnets are used for lifting heavy iron materials and are continuously subjected to cyclic changes. So the materials used for electromagnets must have high value of retentivity and small hysteresis loss. Hence soft iron is preferred to steel.

(iii) Core of transformer. The core of transformer (telephone diaphragms and chokes etc.) continuously undergo many cycles of magnetisation in one second. So we use the material which has less hysteresis loss. So soft iron is used for cores of transformers, chokes etc.

Question 8.
Why is ferromagnetism not found in liquids and gases?
Answer:
Because ferromagnetism is due to exchange interaction which exists only in those atoms which are lying very close to one another, but the atoms or molecules of liquids and gases are lying at a much larger distance as compared to atoms or molecules in solids. Thus the exchange interaction does not take place in liquids and gases, so ferromagnetism is not found in liquids and gases.

Question 9.
Why does paramagnetic substance move from weaker to stronger parts of non-uniform magnetic field?
Answer:
The atoms of paramagnetic substances possess permanent magnetic dipoles and these dipoles are randomly distributed in the absence of external magnetic field. But when the paramagnetic substance is subjected to a non-uniform magnetic field, each atom experiences a torque tendency to align its magnetic dipole moment along the direction of magnetic field, and thus a paramagnetic substance moves from weaker to stronger magnetic field.

Question 10.
Distinguish between diamagnetic, paramagnetic and ferromagnetic substances.
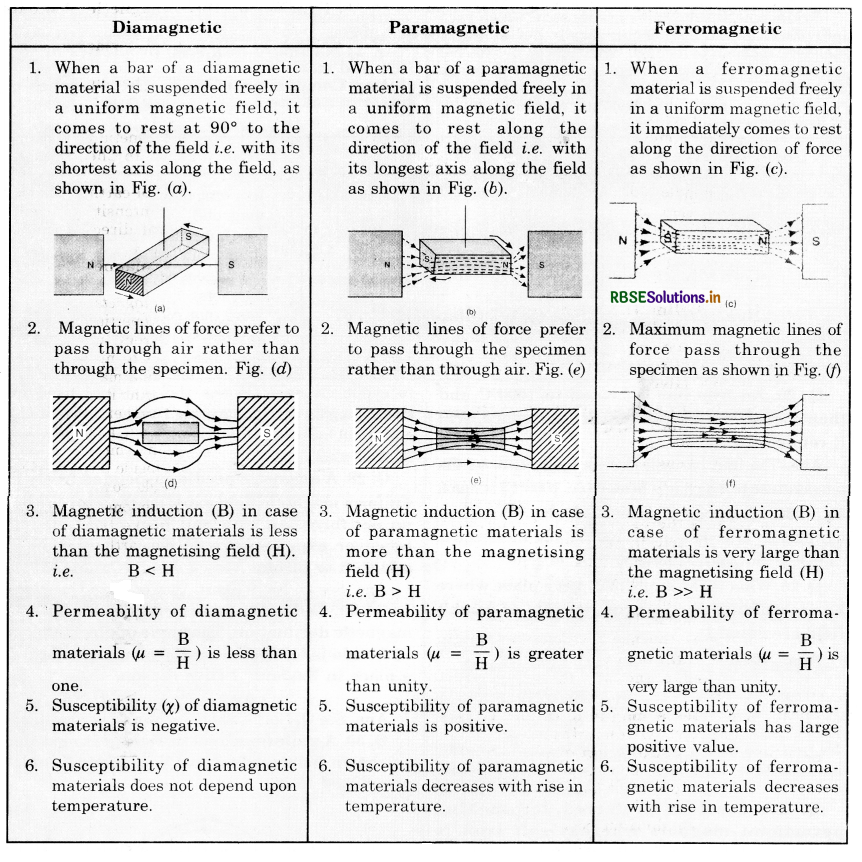
Answer:
Diamagnetic substances are those in which the individual molecule/atom/ion do not possess any net magnetic moment of their own. When placed in magnetic field they move from stronger part of the field to the weaker part of the field i.e., these are repelled by magnetic field.
Examples of diamagnetic substances are copper, antimony, bismuth, gold, quartz, mercury etc.

Paramagnetic substances are those in which the individual molecule/atom/ion has net non-zero magnetic moment its own. When a paramagnetic substance is placed in an external magnetic field induction B, it tends to align the individual dipole in the direction of the field.
Examples of paramagnetic substances are aluminium, platinum, chromium, chrome, glass etc.

Ferromagnetic substances are those in which each molecule/atom/ion has a non-zero magnetic moment. Individual magnetic moments interact with each other in such a way to align themselves, spontaneously in common direction. All molecular dipole moments in a domain are lined up resulting in some dipole moments.
When ferromagnetic substance is placed in external magnetic field, magnetic moment of different domains are aligned and the material gets strongly magnetised in the direction of field.
Some examples are iron, cobalt, nickel etc.

Question 11.
What is Hysteresis loop? Explain with the help of terms related to it.
Answer:
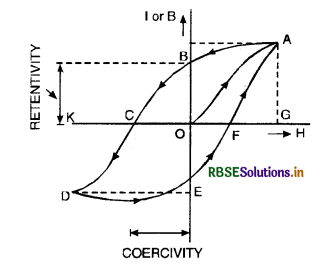
Consider a piece of magnetic material placed in variable magnetic field. When the applied field varies from O to G, the magnetic intensity follows a path OA. As the field is decreased from G to O, the magnetic intensity does not follow back the path AO but AB. As the field is gradually varied back from O to K, I follows path BD. Thus we find that I always lacks behind H and we get a graph like ABCDEFA.

Value of intensity of magnetisation of material when the magnetising field is reduced to zero is called Retentivity or residual magnetism. To reduce the residual magnetism to zero, we have to apply a magnetising field OC in opposite direction. This magnetising field is called coercivity. The phenomenon of lagging of I or B behind H when a specimen of magnetic material is subjected to a cycle of magnetisation is called hysteresis and the loop ABCDEFA is called hysteresis loop.

Question 12.
Why does a paramagnetic sample display greater magnetism when cooled?
Answer:
The paramagnetic material contains atoms possessing permanent magnetic dipole moment. When a paramagnetic material is placed in a magnetic field, these magnetic dipoles get aligned in the direction of magnetic field. The high temperature disrupts this alignment. When a paramagnetic material is cooled, the thermal agitation trying to disrupt the alignment decreases and thus sample displays greater magnetism.

Question 13.
Two identical iron bars A and B are given, one of which definitely known to be magnetised. How would you ascertain, whether or not both are magnetised? If only one is magnetised?
Answer:
Since repulsion is the sure test of magnetisation, because if bar A attracts the other bar B, then both may be magnets (i.e. their unlike poles are facing each other) or one bar may be a simple piece of iron, but if there is a force of repulsion between them, then both bars must be magnetised.

To know which one is magnetised, place the bar A on the table and bring one end of bar B near the two ends and at the middle of bar A. If there is force of attraction only at the ends of bar A, then bar A is magnetised and B is not magnetised and if there is force of attraction both at the ends as well as at the middle, then bar B is magnetised and A is unmagnetised.

Question 14.
Define the term angle of dip and magnetic declination. The angle of dip at a place in Kerala is 18°. Will its value be more or less at a place in; Kashmir? Give reason.
Answer:
Angle of dip and magnetic declination.
Neutral point
A neutral point is that point where the field due to magnet is completely neutralised by the horizontal component of earth’s magnetic field. Thus, at the neutral point, if B is the magnetic field due to magnet and H, the horizontal component of earth’s magnetic field, then
B = H
Let us consider the position of the neutral point for the following two positions of a magnet:
1. When magnet is placed with its north pole towards north of the earth.
Magnetic field due to a small bar magnet by placing its north pole towards north of the earth, then plot of magnetic field of the magnet is shown in Fig. LAQ 14 (a).

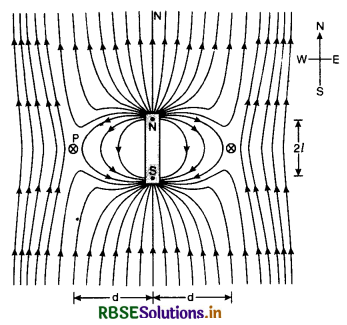
The magnetic field due to earth and that due to magnet cancel out at the two cross-marks on the equatorial line of the magnet. The normal bisector through the centre of the magnets and these positions are called neutral points. Let d be distance of each neutral point from the centre of the magnet. At neutral point, magnetic field due to the magnet is equal to magnetic field due to the earth.
∴ H = \(\frac{\mu_0}{4 \pi} \cdot \frac{\mathrm{M}}{\left(d^2+l^2\right)^{3 / 2}}\) .........................(1)
In case, the magnet is so small then l² can be neglected as compared to d², then
\(\frac{\mu_0}{4 \pi} \cdot \frac{\mathbf{M}}{d^3}\) = H .....................(2)
Knowing d and H the magnetic dipole moment of the bar can be calculated from equation.

2. When magnet is placed with its south pole towards north of the earth. The plot of magnetic field of the magnet in the case will be as shown in Fig. LAQ 14 (b).
The neutral points he on the axial line. At a neutral point, magnetic intensity due to magnet = magnetic field due to the earth.

Knowing d, H this equation can be used to find magnetic dipole of the magnet.
Kerala is closer to equator and at equator, the angle of dip is 0°. Thus as we move from Kerala to Kashmir, the dip angle increases. Hence, the dip angle is more in Kashmir.

Question 15.
What is the basic difference between magnetic and electric lines of force?
Answer:
The basic difference between magnetic and electric lines of force is that whereas magnetic lines of force are closed continuous curves, the electric lines of force are discontinuous. They start from the positive charge and end at the negative charge. On the contrary, magnetic lines of force exist even inside the body of the magnet and are therefore closed continuous curves.

Question 16.
Why does a magnetic dipole possess potential energy, when placed at some inclination with the direction of the field?
Answer:
When a magnetic dipole is placed in a uniform magnetic field, it aligns itself along the direction of the magnetic field in equilibrium. If a magnetic dipole is displaced from equilibrium position, a restoring torque acts on the dipole which bring it back. So if a dipole is placed at some inclination with the field, work has to be done against the restoring force. This work done is stored in the form of potential energy in the magnetic dipole.

Question 17.
A magnetic needle is placed on a cork floating on a still lake in the northern hemisphere. Does this needle together with the cork move towards the north of the lake?
Answer:
Since magnetic needle does not experience any net force, so the needle and the cork will not move towards the north of the lake. But, if the needle 
is inclined to the magnetic meridian, a torque will act on the needle and after a few oscillations, the needle will set itself along the magnetic meridian.

Question 18.
Expalin the three magnetic elements of earth at a place.
Answer:
Three elements of earth’s magnetic field are:

1. Declination at a place is the angle between magnetic and geographical meridian at that place.
2. Magnetic dip or inclination is the angle which the strength of earth’s magnetic field makes with its horizontal component in the magnetic meridian.
3. Horizontal component of earth’s magnetic field is the component of total intensity of earth’s magnetic field in the horizontal direction in the magnetic meridian.

Question 19. 
Why are permanent magnets made of steel and not of soft iron?
Answer:
The so-called permanent magnets are made of hard steel or special alloys. The properties of soft iron and of hard steel are quite different, i.e they have contrasting responses to attempts to make magnets out of them. It is not easy to make a magnet out of a steel rod. but it can be done by placing it in the North-South direction and repeatedly hammering it. Once it has become a magnet in this way, it retains this property unless heated to a high temperature. Our picture of what happens is this: inside the steel there are many small ’atomic’ magnets (like so many compass needles), initially all oriented in random direction; the repeated hammering tends to make them all align themselves in the direction of the earth’s field

On the other hand, filings (long thin pieces) of soft iron do easily become magnets themselves when placed in a magnetic field, for instance near a permanent magnet, but just as easily lose this property when removed. It is a case of "easy come easy go "!

Question 20.
Why should alkali halides be diamagnetic rather than paramagnetic?
Answer:
Paramagnetic substances should have permanent dipole moment. Since alkali halides do not exhibit permanent dipole moment due to their filled inner electron shells, hence they should be diamagnetic.

Question 21.
Distinguish between diamagnetic, paramagnetic and ferromagnetic substances.
Answer:

 
Question 22.
Derive relation between relative magnetic permeability and magnetic susceptibility.
Answer:
In SI units,
B = µ₀ (H + I)
Since I = ✗_m H
∴ B = µ₀ (H + ✗_m H)
B = µ₀H(l + ✗_m) 
Also B = µH
∴ µH = µ₀H (1 + ✗_m) 
or µ = µ₀ (1 + ✗_m)
or \(\frac{\mu}{\mu_0}\) = 1 + ✗_m
or µ_r = 1 + ✗_m
This is the required relation.

Question 23.
What are dia, para and ferromagnetic substances? Give one example of each.
Answer:
Diamagnetic substances are those in which the individual atoms/ions/molecules do not possess any net magnetic moment of their own when they are placed in a strong magnetic field, they are repelled and align itself in a direction at right angle to field. Bismuth, copper, quartz, mercury are some of diamagnetic substances.

Paramagnetic substances are those in which each individual atom/ion/molecule has a net non-zero magnetic moment of its own. When placed in external magnetic field, it tries to align itself in the direction of the field.
Aluminium, platinum, chromium are few examples of paramagnetic substances.

Ferromagnetic substances are those in which each individual atom/molecule/ion has non-zero magnetic moment and when placed in magnetic field it spontaneously aligns itself towards magnetic field.
Iron, cobalt, nickel are some ferromagnetic substances.

Question 24.
Compare magnetic properties of soft iron and steel.
Answer:
Comparison of magnetic properties of soft iron and steel.

Property	Soft Iron	Steel
1. Saturation magnetisation (Imax)	more (good for strong magnets)	less (not good for strong magnets)
2. Retentivity	more but unstable (good for electromagnets)	less but stable (good for permanent magnets)
3. Coercivity	less (not good for durable magnets)	more (good for durable magnets)
4.Hysteresis loss	less (good for transformer and choke cores and telephone diaphragms)	more (not good for repeated magnetisation)

Question 25.
An iron bar is heated to 1000°C and then cooled in a magnetic field free space. Will it retain magnetism?
Answer:
The iron bar will lose its magnetism as the temperature to which it is heated (i.e. 1000°C) is much above the curie point for iron (i.e. 770°C). So the iron bar magnet after hearing to 1000°C and then cooled, cannot retain its magnetism.

Question 26.
What is the angle of dip at a place where horizontal and vertical components of earth’s field are equal?
Answer:
Here BH = BV
Since tan δ = \(\frac{B_V}{B_H}=\frac{B_H}{B_H}=1\)
or tan δ = tan 45°
or δ = 45°.

Question 27.
Steel is preferred for making permanent magnets whereas soft iron is preferred for making electromagnets. Give one reason.
Answer:
For permanent magnets. Permanent magnets should have high value of retentivity (to have large force of attraction for magnetic materials) and high value of coercivity (to retain magnetism for long time), but coercivity is more important than the retentivity. Hence steel is preferred to iron.
For electromagnets. Electromagnets are used for lifting heavy materials and are continuously subjected to cyclic changes. Hence the material used for electromagnets must have high value of retentivity and small hysteresis loss. Hence soft iron is preferred than to steel.

Question 28.
A magnetic needle suspended freely in uniform magnetic field experiences a torque but no net force. An iron nail near a bar magnet however experience a force of attraction in addition to torque. Why?
Answer:
The atoms of paramagnetic substances possess permanent magnetic dipoles and these dipoles are randomly distributed in the absence of external magnetic field. But when the paramagnetic substance is subjected to a non-uniform magnetic field, each atom experiences a torque tendency to align its magnetic dipole moment along the direction of magnetic field, and thus a paramagnetic substance moves from weaker to stronger magnetic field.

Question 29.
Define the term angle of dip and magnetic declination. The angle of dip at a place in Kerala is 18°. Will its value be more or less at a place in Kashmi? Give reason.
Answer:
Angle of dip and magnetic declination.
Neutral point
A neutral point is that point where the field due to magnet is completely neutralised by the horizontal component of earth’s magnetic field. Thus, at the neutral point, if B is the magnetic field due to magnet and H, the horizontal component of earth’s magnetic field, then
B = H
Let us consider the position of the neutral point for the following two positions of a magnet:

(i) When magnet is placed with its north pole towards north of the earth.
Magnetic field due to a small bar magnet by placing its north pole towards north of the earth, then plot of magnetic field of the magnet is shown in Fig. LAQ 14 (a).

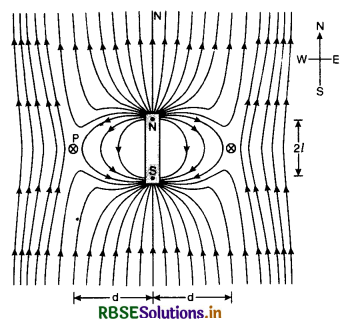
The magnetic field due to earth and that due to magnet cancel out at the two cross-marks on the equatorial line of the magnet. The normal bisector through the centre of the magnets and these positions are called neutral points. Let d be distance of each neutral point from the centre of the magnet. At neutral point, magnetic field due to the magnet is equal to magnetic field due to the earth.
∴ H = \(\frac{\mu_0}{4 \pi} \cdot \frac{\mathrm{M}}{\left(d^2+l^2\right)^{3 / 2}}\) .........................(1)
In case, the magnet is so small then l² can be neglected as compared to d², then
\(\frac{\mu_0}{4 \pi} \cdot \frac{\mathbf{M}}{d^3}\) = H .....................(2)
Knowing d and H the magnetic dipole moment of the bar can be calculated from equation.

(ii) When magnet is placed with its south pole towards north of the earth. The plot of magnetic field of the magnet in the case will be as shown in Fig. LAQ 14 (b).
The neutral points he on the axial line. At a neutral point, magnetic intensity due to magnet = magnetic field due to the earth.

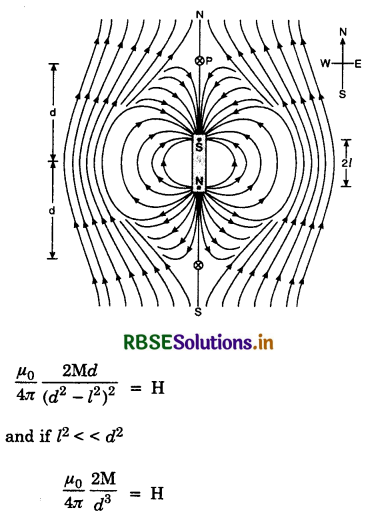
Knowing d, H this equation can be used to find magnetic dipole of the magnet.
Kerala is closer to equator and at equator, the angle of dip is 0°. Thus as we move from Kerala to Kashmir, the dip angle increases. Hence, the dip angle is more in Kashmir.

Question 30.
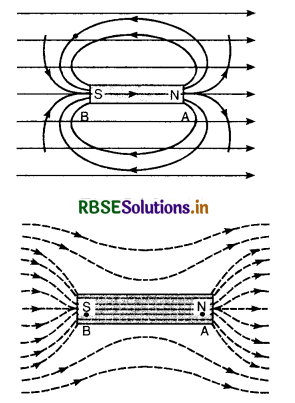
A uniform magnetic field gets modified as shown below, when two specimens X and Y are placed in it.

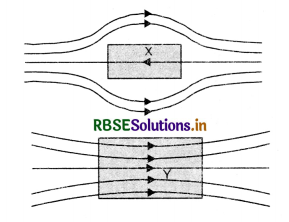
(i) Identify the two specimens X and Y.
(ii) State the reason for the behaviour of the field lines in X and Y.
Answer:
(i) The specimen X is a diamagnetic and Y is paramagnetic.
(ii) A diamagnetic substance when placed in a magnetic field acquire magnetism opposite to the direction of magnetising field and the magnetic lines avoid passing through it. On the other hand a paramagnetic substance acquire magnetism in the direction of magnetising field and the magnetic lines prefer to pass through the paramagnetic substance Y.

Question 31.
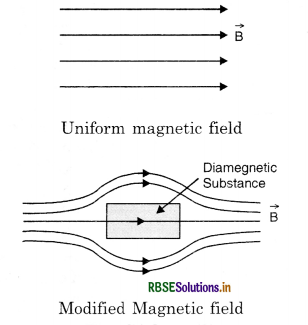
The susceptibility of a magnetic material is - 0.085. Identify the magnetic type of the material. A specimen of this material is placed in a uniform magnetic field. Draw the modified field pattern.
Answer:
Since susceptibility of the material is -ve, so it is a diamagnetic material.

Question 32.
Write three point of differences between para, dia and ferromagnetic substances giving one example of each.
Answer:

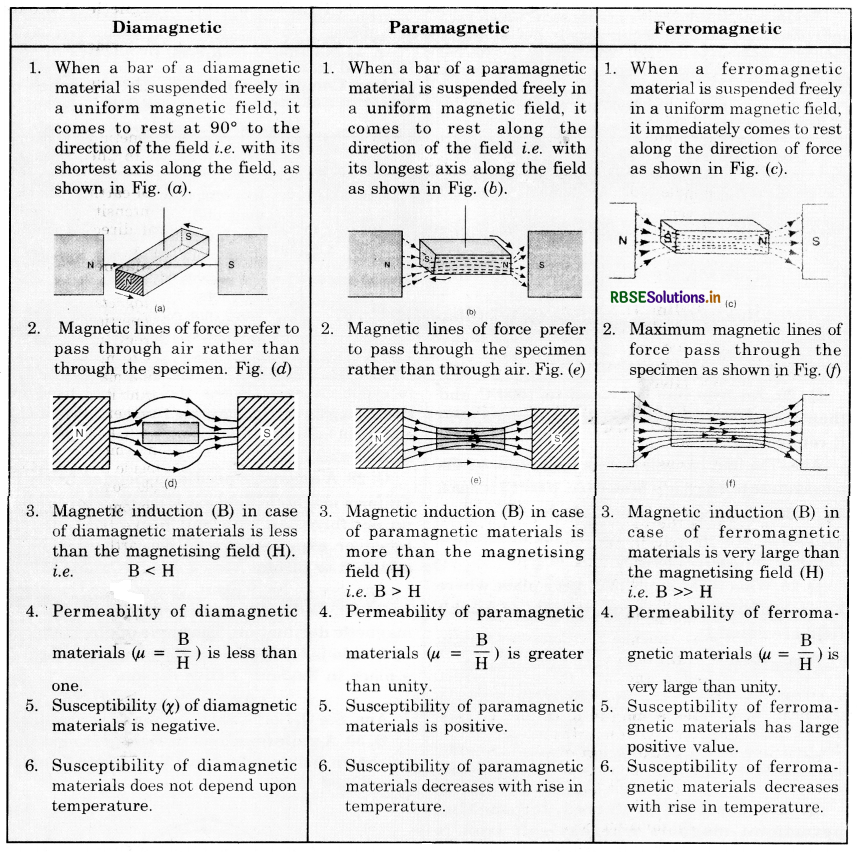
Question 33. 
A magnetic needle free to rotate in a vertical plane parallel to the magnetic meridian has its north tip dow n at 60° with the horizontal. The horizontal component of the earth's magnetic field at a place is known to be 0.4 G. Determine the magnitude of the earth’s magnetic field at the place.
Answer:
Here BH = 0.4 G, δ = 60°
Since BH = B cos θ
So B = \(\frac{\mathrm{B}_{\mathrm{H}}}{\cos \theta}=\frac{0.4}{\cos 60^{\circ}}=\frac{0.4}{\frac{1}{2}}\) = 0.8 G.

Question 34.
State and illustrate Curie law in magnetism.
Answer:
Curie law states that susceptibility of a material varies inversely with its temperature in kelvin.
According to Curie’s law, the intensity of magnetisation I of a para and ferromagnetic material is
(i) directly proportional to the magnetic induction,
i.e. I ∝ B
(ii) inversely proportional to the temperature.

This is Curie's law.
The graph between I and H/T is shown in Fig. SAQ 34 and it shows that as the external magnetic field is increased and T is decreased, the atomic dipoles get aligned more and more in the direction of applied magnetic field and after sometime saturation is reached.

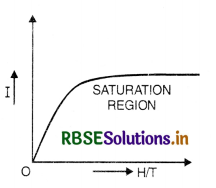
Question 35.
Write two properties of a material suitable for making (a) a permanent magnet, and (b) an electromagnet.
Answer:
For permanent magnet, we require a material having
(i) high coercivity, (ii) high retentivity
For electromagnet, we require a material having
(i) low coercivity, (ii) high permeability.

Question 36.
Distinguish between diamagnetic and ferromagnetic materials in respect of
(i) intensity of magnetisation
(ii) behaviour of non-uniform magnetic field and
(iii) Susceptibility.
Answer:

Property	Diamagnetic material	Ferromagnetic material
(i) Intensity of magnetisation	Small negative value	Large positive value
(ii) Behaviour of non-uniform magnetic field.	Weakly magnetised in a direction opposite to the magnetising field.	Strongly magnetised in the direction of magnetising field.
(iii) Susceptibility.	Small negative value.	Large positive value.

Question 37.
Derive expression for potential energy of a bar magnet when placed in a uniform magnetic field.
Answer:
Potential energy of a bar magnet. The torque \(\vec{\tau}\) acting on a magnetic dipole placed in a uniform magnetic field \(\overrightarrow{\mathrm{B}}\) is given by
\(\vec{\tau}=\overrightarrow{\mathrm{M}} \times \overrightarrow{\mathrm{B}}\)
[M = m 2l]
or τ = MB sin θ .........................(1)

This torque tends to align the magnetic dipole in the direction of \(\vec{B}\). If the dipole is rotated against the action of this torque, work has to be done, which is stored in the form of potential energy of the dipole.
Work done in rotating the dipole through an angle dθ against the torque is given by
dW = τ dθ - MB sin θ dθ
If the magnetic dipole is rotated from θ₁ to θ₂, total work done will be
W = ∫ dW = MB \(\int_{\theta_1}^{\theta_2}\) sin θ dθ
= - MB (cos θ₂ - cos θ₁)
This work done is the energy stored U
∴ U = - MB (cos θ₂ - cos θ₁)
If the dipole is rotated from θ₁ = 90° to θ₂ = θ then
U = - MB (cos θ - cos 90°)
U = -MB cos θ 
or U = -\(\overrightarrow{\mathrm{M}} \cdot \overrightarrow{\mathrm{B}}\).

Question 38.
Name three elements required to specify the earth’s magnetic field at a given place. Draw a labelled diagram to define these elements. Explain briefly how these elements are determined to find out the magnetic field at a given place on the surface of earth.
Answer:
Neutral point
A neutral point is that point where the field due to magnet is completely neutralised by the horizontal component of earth’s magnetic field. Thus, at the neutral point, if B is the magnetic field due to magnet and H, the horizontal component of earth’s magnetic field, then
B = H
Let us consider the position of the neutral point for the following two positions of a magnet:
(i) When magnet is placed with its north pole towards north of the earth.
Magnetic field due to a small bar magnet by placing its north pole towards north of the earth, then plot of magnetic field of the magnet is shown in Fig. LAQ 14 (a).

The magnetic field due to earth and that due to magnet cancel out at the two cross-marks on the equatorial line of the magnet. The normal bisector through the centre of the magnets and these positions are called neutral points. Let d be distance of each neutral point from the centre of the magnet. At neutral point, magnetic field due to the magnet is equal to magnetic field due to the earth.
∴ H = \(\frac{\mu_0}{4 \pi} \cdot \frac{\mathrm{M}}{\left(d^2+l^2\right)^{3 / 2}}\) .........................(1)
In case, the magnet is so small then l² can be neglected as compared to d², then
\(\frac{\mu_0}{4 \pi} \cdot \frac{\mathbf{M}}{d^3}\) = H .....................(2)
Knowing d and H the magnetic dipole moment of the bar can be calculated from equation.

(ii) When magnet is placed with its south pole towards north of the earth. The plot of magnetic field of the magnet in the case will be as shown in Fig. LAQ 14 (b).
The neutral points he on the axial line. At a neutral point, magnetic intensity due to magnet = magnetic field due to the earth.

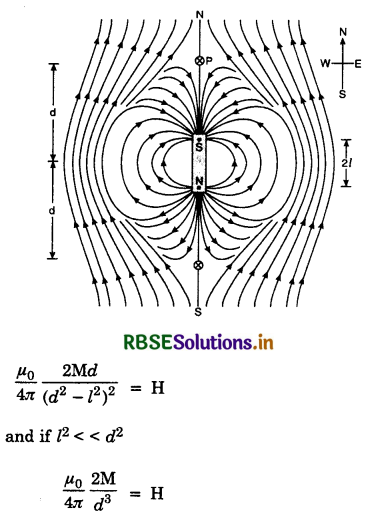
Knowing d, H this equation can be used to find magnetic dipole of the magnet.

Question 39.
(a) An iron ring of relative permeability µ_r has windings of insulated copper wire of n turns per metre. When the current in the windings is I, find the expression for the magnetic field in the ring.
(b) The susceptibility of magnetic material is 0.9853. Identify the type of magnetic material. Draw the modification of the field pattern on keeping a piece of this material in a uniform magnetic field.
Answer:
(a) From Ampere’s circuital law, we have

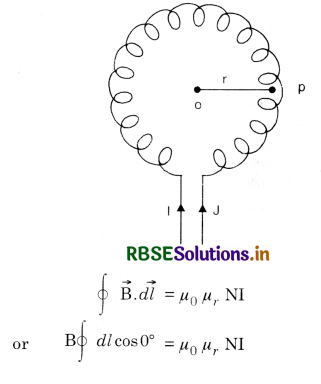
or B 2πr = µ₀µ_r NI
or B = µ₀µ_r\(\frac{\mathrm{N}}{2 \pi r}\).I
or B = µ₀ µ_r nI
where n = \(\frac{\mathrm{N}}{2 \pi r}\) is number of turns per unit length.
(b) Since susceptibility ✗ = 0.9853 < 1 and positive so the material is a paramagnetic substance and acquire weak magnetic field when placed in the magnetic field as shown in the figure.

Long Answer Type Questions

Question 1.
(a) Define Magnetic Field, Magnetic Intensity (or magnetic field at a point). What is the S.I. unit of magnetic intensity?
(b) Define uniform magnetic field. How is it represented geometrically?
Answer:
(a) Magnetic Field
The space around a magnet or a current carrying conductor in which the magnetic effect can be felt is called the maghetic field.
Magnetic Intensity
The strength of magnetic field or magnetic intensity at a point is the force experienced by a unit north pole placed at that point. The direction of the field is the direction in which this pole begins to move if free to do so.
Thus magnetic intensity is a vector quantity and has both magnitude and direction.
The S.I. unit of magnetic intensity is tesla or ampere metre.
If a magnetic pole of strength m units placed at a point where the magnetic intensity is \(\overrightarrow{\mathrm{B}}\) then it experiences a force of m \(\overrightarrow{\mathrm{B}}\).
(b) Uniform Magnetic Field
A magnetic field is said to be uniform if a unit isolated north pole placed at different points in the field experiences the same force in the same direction.

Graphically, a uniform magnetic field is represented by equidistant and mutually parallel lines.

Question 2.
(a) What are magnetic lines of force?
(b) Do the lines of force really exist?
(c) Mention important properties of magnetic lines of force.
Answer:
(a) Magnetic Lines of Force
(i) Imagine a small north magnetic pole is placed in the magnetic field created by a magnet, it will experience a force. The north pole will move under the influence of magnetic field. The path traced by a north pole free to move under the influence of magnetic field is called a magnetic line of force.
(ii) A line of force is a continuous curve in the magnetic field such that the tangent at any point of it gives the direction of the resultant field at that point.

The concept of magnetic lines of force is also used to represent the magnetic field in a region graphically.
(b) Actually the lines of force do not exist but are hypothetically considered to explain many phenomena in terms of lines of force.
(c) Properties of lines of force

1. They are closed and continuous curves.
2. They always start from the N-pole and terminate at the S-pole of the magnet.
3. The tangent at any point on a line of force gives the direction of magnetic field at the point. Fig. LAQ 2.
4. They never intersect one another because if two lines of force intersect, there would be two directions of magnetic field at that point which is impossible.
5. They are crowded near the poles where the magnetic field is strong and get separated where the magnetic field becomes weak.
6. Parallel and equidistant lines of force represent uniform magnetic field (such as the earth’s magentic field in a small region).
7. They behave like stretched elastic rubber strings.

Question 3.
Define magnetising field, magnetic induction, magnetic permeability, intensity of magnetisation and susceptibility.
Answer:
When a piece of a magnetic material is placed in a magnetic field, the magnetism so developed in the specimen is called induced magnetism. This phenomenon of inducing magnetism in a specimen is called magnetic induction. The field that induces magnetism is called the magnetising field.
The strength or intensity of magnetising field (H) at any point is defined as the force experienced by hypothetical unit north pole placed at that point. Its direction is the direction in which unit north pole tends to move if free to do so.
In terms of magnetic lines of force, strength or intensity of magnetising field at any point is the number of magnetic lines of force crossing unit area around that point, the area being held perpendicular to the lines of force.
The S.I. unit of H is weber/m² or tesla or (Wm²)

In Fig. LAQ 3 (a) a soft iron piece AB is placed in a uniform magnetising field. The piece gets magnetised with end B becoming S and end A becoming N. The magnetised specimen has its own field as shown. The resultant magnetic field is modified as shown in Fig. LAQ 3 (b).
The lines of force inside the magnetised specimen are called magnetic lines of induction.
Magnetic induction (B) at any point inside the magnetised specimen is defined as the number of magnetic lines of induction crossing unit area normally around this point. It is represented by B and is also called magnetic flux density. The units of B are the same as the units of H.
Intensity of Magnetisation (I) is defined as the magnetic moment developed per unit volume of the specimen.
I = \(\frac{\mathrm{M}}{\mathrm{V}}=\frac{m \times 2 l}{a \times 2 l}=\frac{m}{a}\)
where 2l is magnetic length; m is strength of each pole and a is area of cross-section of the specimen.
Therefore, intensity of magnetisation may also be defined as the pole strength developed per unit area of cross-section of the specimen.
The S.I. unit of I is ampere metre^-1 (Am^-1)
Magnetic Permeability (µ) is defined as the ratio of magnetic induction (B) developed in a specimen to the strength of magnetising field (H).
i.e. µ = \(\frac{\mathrm{B}}{\mathrm{H}}\) ......................(1)
It has no units.
Relative magnetic permeability (µ_r), of a material is the ratio of magnetic permeability (µ) to the permeability of free space (µ₀).
i.e. µ_r = \(\frac{\mu}{\mu_0}\)
Magnetic susceptibility (✗_m) is defined as the ratio of intensity of magnetisation (I) to the strength of magnetising field (H).
✗_m = \(\frac{\mathrm{I}}{\mathrm{H}}\) .......................(2)

Question 4.
Show that a circular loop carrying current acts as a dipole. What is dipole moment of this pole? What is its S.I. unit?
Or
A current loop is considered a magnetic dipole. Explain.
Answer:
When a current is passed through a circular coil (loop) of a conducting ware, the current loop acts as a dipole with one face as north and other as south pole. Therefore, a current loop behaves as a magnetic dipole. It has been experimentally found that magnetic dipole moment M of such a current loop is
(i) directly proportional to strength of current I.
i.e. M ∝ I
(ii) directly proportional to area of loop
∴ M ∝ A
Combining, M ∝ I A
or M = kIA
If    k = 1
∴ M = IA
or \(\overrightarrow{\mathrm{M}}=\overrightarrow{\mathrm{IA}}=\mathrm{IA} \vec{n}\)

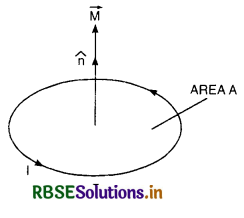
Proof. Let us consider a circular coil of radius R carrying a current I. We know that magnetic field at a point on its axis at a distance x from it is given by
B = \(\frac{\mu_0}{4 \pi} \frac{2 \pi \mathrm{IR}^2}{\left(\mathrm{R}^2+x^2\right)^{3 / 2}}\)
If the point lies at a distance very large as compared to the radius of the coil then
B = \(\frac{\mu_0}{4 \pi} \frac{2 \pi \mathrm{IR}^2}{x^3}\) [∵ x >> R]
Now, πR² = A, area of coil. Therefore,
B = \(\frac{\mu_0}{4 \pi} \frac{2 \text { IA }}{x^3}\) ..........................(1)
It can be shown that for a magnetic dipole, the magnetic field at a point on its axis and far away from its centre is given by
B = \(\frac{\mu_0}{4 \pi} \frac{2 \mathrm{M}}{x^3}\), ...........................(2)
When M is magnetic dipole moment of the magnetic dipole. From equations (1) and (2) it follows that a current loop behaves as magnetic dipole of magnetic dipole moment.
M = IA ..............................(3)
Units
In S.I., the unit of dipole M is ampere metre² (Am²).
It is defined as the magnetic moment of one turn loop of an area 1 m², when it carries a current of 1 A.
In vector form \(\overrightarrow{\mathrm{M}}\) = I A \(\hat{n}\).
The unit vector \(\hat{n}\) is perpendicular to the plane of the loop and its direction is fixed by the sense of flow of current I using the right hand rule.
Direction of \(\overrightarrow{\mathrm{M}}\): Curl the fingers of your right hand along the direction of current, thetr the direction of erected thumb gives the direction of magnetic dipole moment.

Question 5.
Discuss atom as a magnetic dipole. Hence define Bohr magneton.
Or
Obtain an expression for the magnetic moment of an electron in a circular orbit of radius r and moving with speed v. State the rule to find its direction. How does this magnetic moment change when the:
(i) Frequency of revolution is doubled.
(ii) Orbital radius is halved.
Answer:
Atom as a Magnetic Dipole
Every atom consists of a central part, called nucleus, where the entire mass and positive charge of the atom are concentrated. An equal number of negative charges (i.e. electrons) revolve around the nucleus in circular orbits.
The revolution of electron i.e., negative charge in anticlockwise direction is equivalent to conventional 

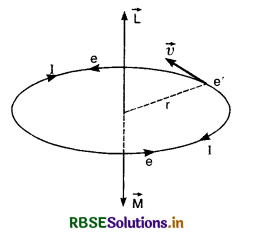
current I in the clockwise direction. The upper face with clockwise current acts as south pole and the lower face acts as north pole. Thus an electron revolving in an orbit is equivalent to a magnetic dipole.
Suppose e is the charge on an electron revolving in a circular orbit of radius r with a uniform angular velocity, ω. If T is the time period of revolution of the electron, then

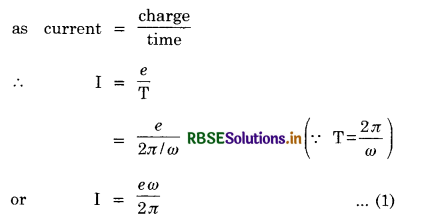
If M is the magnetic dipole moment of the magnetic dipole
M = IA
Using (1), and putting A = πr², we get
M =\( \frac{e \omega}{2 \pi}\) π r²
M = \(\frac{1}{2}\) e ωr² ............................(2)
Relation between orbital angular momentum and magnetic dipole momentum
Because of orbital motion, the revolving electron has an orbital angular momentum L given by
L = mvr = mrωr = mωr²
∴ From (2), M = \(\frac{1}{2} \frac{e}{m}\) = mωr²
M = \(\frac{1}{2} \frac{e}{m}\) L
In vector form, \(\overrightarrow{\mathrm{M}}=-\left(\frac{e}{2 m}\right) \overrightarrow{\mathrm{L}}\) ...............................(3)
This shows that like \(\overrightarrow{\mathrm{L}}\), magnetic dipole moment \(\overrightarrow{\mathrm{M}}\) of the atom is perpendicular to the plane of the orbit. Negative sign shows that direction of \(\overrightarrow{\mathrm{M}}\) is opposite to the direction of \(\overrightarrow{\mathrm{L}}\), as is clear from the figure.
According to Bohr’s theory, an electron cannot revolve in any orbit it likes. It can revolve only in those orbits for which the total angular momentum is an integral multiple of h/2π, where h is the Planck’s constant i.e.
Angular momentum of the electron

It is obvious that \(\frac{e h}{4 \pi m}\) is the least value of the magnetic moment. (µ_B = 9.27 x 10^-24 JT^-1 or Am²).
Bohr magneton
It is defined as the magnetic dipole moment associated with an electron due to its orbital motion in the first orbit of hydrogen atom.
From Eq. (2), we have
M = πevr² [∵ ω = 2πv]
So when
(i) v is doubled, M is also doubled
(ii) r is halved, M becomes l/4th.
Rule for direction is right hand rule i.e. if hold the fingers of our right hand in the direction of current, then perpendicular thumb gives the direction of magnetic field.

Question 6.
Define magnetic dipole and dipole moment. What are its units?
Answer:
Magnetic dipole
An arrangement of two magnetic poles of equal and opposite strength separated by a finite distance is said to constitute a magnetic dipole.
Common examples of magnetic dipoles are compass needle, a bar magnet, a current loop, an electron revolving in a circular or elliptical path etc.
Magnetic Dipole moment
Consider a magnetic dipole consisting of two poles N and S each having pole strength m as shown in the figure LAQ 6.

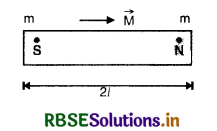
The distance between two poles is called magnetic length.
Magnetic dipole moment is the product of strength of either pole and the magnetic length.
i.e. \(\overrightarrow{\mathrm{M}}\) = m(2\(\overrightarrow{\mathrm{l}}\))
The direction of magnetic dipole moment is from south to north pole.
Unit: In SI. the unit of dipole moment is ampere metre² (A.m²)

Question 7.
Derive an expression for magnetic field strength at a point on the axial line of magnetic dipole (bar megnet).
Answer:
Consider a magnetic dipole (a bar magnet) of length 2l. Let us find magnetic field strength (B) at point P at a distance d from centre O of the magnetic dipole. Let m be the strength of each pole. Magnetic field strength at P due to N-pole.

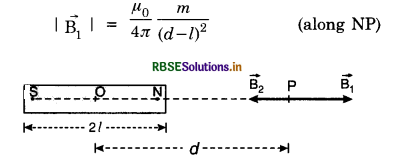
Magnetic field strength at P due to S-pole
\(\left|\overrightarrow{\mathrm{B}}_2\right|=\frac{\mu_0}{4 \pi} \frac{m}{(d+l)^2}\) (along PS)
Since \(\overrightarrow{\mathrm{B}}_1\) and \(\overrightarrow{\mathrm{B}}_2\) act along the same line and in opposite direction, so resultant magnetic field  at P will be:
B = \(\left|\overrightarrow{\mathrm{B}}_1\right|-\left|\overrightarrow{\mathrm{B}}_2\right|\)

Question 8.
Derive an expression for magnetic field strength at point on equitorial line of a magnetic dipole (bar magnet).
Answer:
Considera magnetic dipole (a bar magnet) of length 2l. Let us find magnetic field (B) at a point P at a distance d from centre O of the magnetic dipole.

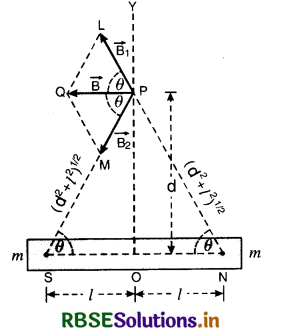
Let m be strength of each pole.
Magnetic field strength at P due to N-pole.
\(\left|\overrightarrow{\mathrm{B}}_1\right|=\frac{\mu_0}{4 \pi} \frac{m}{\left(d^2+l^2\right)}\) (along PL)
Magnetic field strength at P due to S-pole
\(\left|\overrightarrow{\mathrm{B}}_2\right|=\frac{\mu_0}{4 \pi} \frac{m}{\left(d^2+l^2\right)}\) (along PM)
Thus we find that \(\left|\overrightarrow{\mathrm{B}}_1\right|=\left|\overrightarrow{\mathrm{B}}_2\right|\) , so the components B₁ sin θ along OP and B₂ sin θ along PO cancel each other and the components, B₁ cos θ along PQ and B₂ cos θ along PQ get added.
∴ Resultant magnetic field strength at P will be
B = B₁ cos θ + B₂ cos θ
= 2B cos θ [along PQ]
B = \(\frac{\mu_0}{4 \pi} \frac{2 m \cos \theta}{\left(d^2+l^2\right)}\) (along PQ)

Question 9.
Derive an expression for the torque acting on a bar magnet placed in the uniform magnetic field.
Answer:
Consider a bar magnet N - S consisting of two equal and opposite poles N and S each of pole strength m and separated by a distance 2l, making
an angle θ with the magnetic field  as shown \(\overrightarrow{\mathrm{B}}\) in the figure.
Force acting on N-pole = mB (along the field \(\overrightarrow{\mathrm{B}}\)).
Force acting on S-pole = m B (opposite to the field \(\overrightarrow{\mathrm{B}}\))
Torque acting on the bar magnet
τ = (mB) (⊥ distance NA)
is τ = mB(NA)

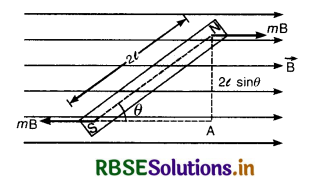
But NA = 2l sin θ
∴ τ = mB sin θ = 2ml B sin θ
or τ = MB sin θ
or \(\vec{\tau}=\overrightarrow{\mathrm{M}} \times \overrightarrow{\mathrm{B}}\)
\(\vec{\tau}\) is perpendicular to the plane containing \(\overrightarrow{\mathrm{M}}\) and \(\overrightarrow{\mathrm{B}}\).
If θ = 90° ; B = 1 then
τ = M x 1 x 1
or M = τ
Therefore magnetic dipole moment is defined as the torque experienced by the dipole placed perpendicular to uniform magnetic field of unit strength.
S.I. unit of  \(\overrightarrow{\mathrm{M}}\) is JT^-1 (joule per tesla).

Question 10.
(a) State and explain Gauss’s theorem in magnetism.
(b) Show that magnetic dipoles (more precisely electric currents) are most elementary sources of magnetic fields and that no individual poles exist.
Answer:
(a) Gauss’s law in magnetism. It states that for a closed surface
\(\oint \overrightarrow{\mathrm{B}} \cdot d \overrightarrow{\mathrm{S}}\) = 0
Proof
Consider a magnetic field produced by a bar magnet as shown in the figure. Let us consider a closed Gaussian surface enclosing the N-pole of this magnet is shown by dotted circle. We find that number of magnetic lines entering the Gaussian surface is equal to number of magnetic lines leaving it i.e. total normal flux for whole Gaussian surface is zero.

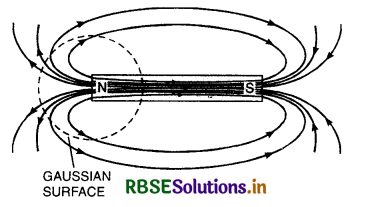
i.e. Φ_m = \(\oint_{\mathrm{S}} \overrightarrow{\mathrm{B}} \cdot d \overrightarrow{\mathrm{S}}\) = 0
This theorem implies that isolated magnetic poles do not exist.
or
Magnetic poles always exist in pairs.
(b) From electrostatics we have the Gauss’s theorem for any closed surface S enclosing a volume V in space, the surface integral of the electric field over S is proportional to the total electric charge inside V.
\(\oint_{\mathrm{S}} \overrightarrow{\mathrm{E}} \cdot d \overrightarrow{\mathrm{S}}=\frac{q}{\varepsilon_0}\)
The dipole consists of two equal and opposite charges near one another, so their total charge is zero. This is evidently also true if S does not enclose the origin, since we know directly that then there is no charge within S; so in all we can say that for any closed surface S,
\(\oint_{\mathrm{S}} \overrightarrow{\mathrm{E}}_{\text {dipole }} \cdot d \overrightarrow{\mathrm{S}}\) = 0
For any magnetic field \(\overrightarrow{\mathrm{B}}\) obtained by super position, Gauss’s theorem for magnetism
\(\oint_{\mathrm{S}} \overrightarrow{\mathrm{B}} \cdot d \overrightarrow{\mathrm{S}}=0\)
for all closed surface S ......................(1)
This is the precise expression of the absence of individual magnetic charges.
In the statement (1), we used a closed surface S. If S were an open surface, then the integral of a magnetic field B over it would generally be non-zero; It is called the flux of B through S.

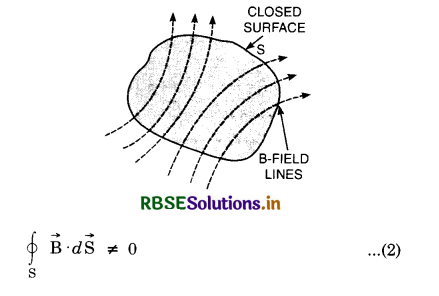
The main conclusion for equation (1) and (2) is that the absence of individual magnetic charges. The magnetic flux through any closed surface is always zero.
Unit of magnetic flux. The SI unit of magnetic flux is Weber (Wb), defined as follows:
The magnetic flux linked with a surface is said to be 1 weber, if a magnetic field of 1 tesla is associated with an area of 1 m².
∴ 1 Wb = 1 Tm²

Question 11.
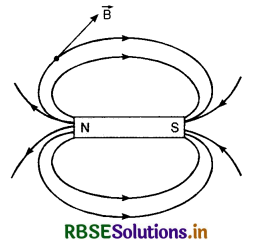
How is the magnetic field of a bar magnet mapped? Draw the field lines pattern around a bar magnet. Compare it with the field lines pattern around a current straight solenoid.
Answer:
For mapping the magnetic field of a bar magnet, place the bar magnet on a sheet of paper. Take a small compass needle. Place it close to one of the poles, say South. Mark by pencil dots, A and B, the positions, N, S of the ends of the compass needle. Shift the compass needle so that its n pole touches B. Mark the new position C of a S pole of the compass needle. Repeat this process to obtain a series of dots as shown in Fig. LAQ 11 (a) Join these points by a smooth curve. This is one magnetic line of force. Similarly, other magnetic lines of force can be drawn. Fig. LAQ 11 (b) shows the pattern of field lines around a bar magnet.

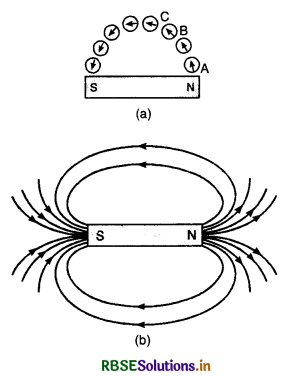
It should be clearly understood that the field lines exist in all the space around the magnet. In the figure, these lines are confined only in the plane of the paper.
Fig. LAQ 11 (c) shows the pattern of magnetic lines of force due to a straight solenoid carrying current. Comparison of the two field patterns shows that a current carrying solenoid behaves like a bar magnet. Looking at a face, if the current is anticlockwise, the face has north polarity and if the current is clockwise, the face has south polarity; Fig. LAQ 11 (d)

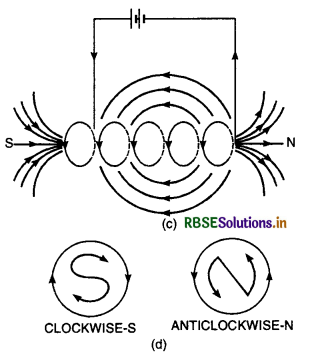
Thus a current carrying solenoid from outside resembles a bar magnet inside the solenoid, there is a strong magnetic field which can magnetise a specimen. Solenoid is hollow from inside whereas the bar magnet is solid.

Question 12.
(a) What is the evidence that the earth has magnetic field? What is the order of its magnitude?
(b) Define magnetic axis, geographic axis, magnetic meridian and geographical meridian.
Or
Describe the possible cause of earth magnetic field.
Answer:
(a) The earth itself behaves like a magnet. The direction and the magnitude of the earth’s magnetic field varies from place to place on the surface of earth. It is evident from the following experiments:
(i) If a magnet is suspended freely, it always rests pointing nearly in the geographic north-south direction. It is evident that the north pole of a magnet will point towards the geographic north only when there is a south pole of the earth’s magnet at the geographic north so as to attract the north pole of the magnet. Thus, in the geographic north, there must be the south pole of the earth’s magnet and in the geographic south, there must be the north pole of the earth’s magnet. Fig LAQ 12 (a). The typical value of earth’s magnetism is about 10^-4 Wb m^-2.

(ii) If we bury a soft iron bar in north-south direction under the earth’s surface, it is found that after some days it acquires the properties of a magnet.

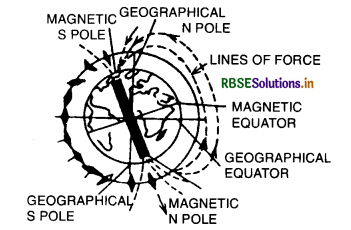
(iii) When we draw magnetic lines of a magnet, we come across neutral points. At these points the magnetic field due to earth is balanced by the magnetic field due to the magnet.

Possible causes of earth’s magnetism
(i) It is presumably due to circulating electric currents due to molten charged metallic fluid deep within the interior of the earth’s core of radius 3500 km (Compared to the earth’s radius 6400 km).

(ii) It may be due to rotation of earth about its own axis. Since every substance is made up of charged particles (p and e^-) so these rotating substances lead to circulating currents and are responsible for the magnetism of earth.

(iii) The gases in the atmosphere are in ionised state mainly due to cosmic rays, and as earth rotates, the strong electric currents are set up due to movement of ions. These currents might be magnetising the earth.

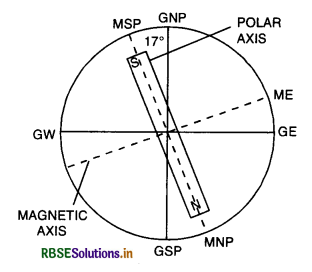
(b) (i) Magnetic axis
A line joining the north and south poles of a freely suspended magnet is called its magnetic axis.
(ii) Geographical axis
The axis of rotation of the earth is called its geographical axis or polar axis.
(iii) Magnetic meridian
The vertical plane passing through the axis of a freely suspended magnet is called magnetic meridian. The direction of earth’s magnetic field lies in the magnetic meridian.
(iv) Geographical meridian
The vertical plane passing through the true geographical north and south (or geographical axis of earth) is called geographical meridian.

Question 13.
(a) Define magnetic elements at a place.
(b) What are their mutual relations?
Answer:
(a) Elements of the earth’s magnetism
The quantities, which describe the magnetic field of the earth at a particular place, completed, in magnitude as well as in direction, are known as the magnetic elements of earth of that place.
These are:

• Declination
• Dip or Inclination
• Horizontal component of the earth’s field.

(i) Declination (θ)
It is defined as the angle between the magnetic meridian and the geographical meridian at a place.
In Fig. LAQ 13 (a) let PQRO represent the magnetic meridian and PQ'R'O represent the geographical merdian at the place P. Then angle θ between these two planes, by definition, is the angle of declination at the place P.

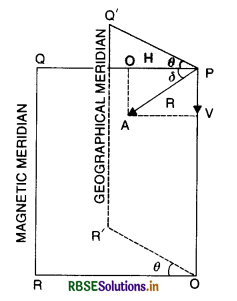
(ii) Dip or inclination (δ)
Dip at a place is defined as the angle between the direction of the total intensity of the earth’s magnetic field and a horizontal line in the magnetic meridian. 
In Fig. LAQ 13 (a) \(\overrightarrow{\mathrm{PA}}\) represents the total or resultant intensity of the earth’s magnetic field in magnitude as well as in direction. As P makes an angle 8 with PQ ( a horizontal line in the magnetic meridian PQRO), the angle of dip at the place P is δ.
(iii) Horizontal Component (H)
It is the component of earth’s magnetic field along the horizontal direction and denoted by H.

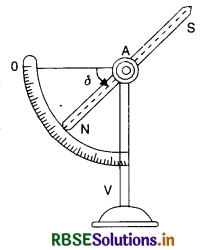
The total intensity of the earth’s magnetic field at any point can be resolved into two rectangular components, one along the horizontal and the other along the vertical direction.
The component of the resultant intensity of the earth’s magnetic field in the horizontal direction in magnetic meridian is called its horizontal component. It is denoted by H. The component of the resultant intensity of the earth’s magnetic field in the vertical direction in magnetic meridian is called its vertical component. It is denoted by V.
(b) Relation between magnetic elements
The resultant intensity, i.e. R along \(\overrightarrow{\mathrm{PA}}\) has been resolved into two rectangular components. Clearly, the horizontal component along PQ.
i.e. H = R cos δ .......................(1)
and the vertical component along PO
i.e., V = R sin δ ....................(2)
Dividing (2) by (1),. we get
\(\frac{\mathrm{V}}{\mathrm{H}}=\frac{\mathrm{R} \sin \delta}{\mathrm{R} \cos \delta}\) = tan δ ...........................(3)
Squaring (1) and (2) and adding, we get
H² + V² = R² cos² δ + R² sin² δ
= R² (cos² δ + sin² δ) = R²
∴ R = \(\sqrt{\mathrm{H}^2+\mathrm{V}^2}\) ..........................(4)

Question 14.
Define neutral point. How its location can be used to find the magnetic dipole moment of the magnet?
Answer:
Neutral point
A neutral point is that point where the field due to magnet is completely neutralised by the horizontal component of earth’s magnetic field. Thus, at the neutral point, if B is the magnetic field due to magnet and H, the horizontal component of earth’s magnetic field, then
B = H
Let us consider the position of the neutral point for the following two positions of a magnet:
(i) When magnet is placed with its north pole towards north of the earth.
Magnetic field due to a small bar magnet by placing its north pole towards north of the earth, then plot of magnetic field of the magnet is shown in Fig. LAQ 14 (a).

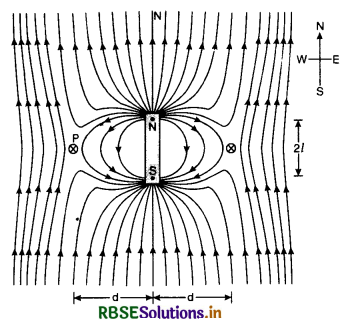
The magnetic field due to earth and that due to magnet cancel out at the two cross-marks on the equatorial line of the magnet. The normal bisector through the centre of the magnets and these positions are called neutral points. Let d be distance of each neutral point from the centre of the magnet. At neutral point, magnetic field due to the magnet is equal to magnetic field due to the earth.
∴ H = \(\frac{\mu_0}{4 \pi} \cdot \frac{\mathrm{M}}{\left(d^2+l^2\right)^{3 / 2}}\) .........................(1)
In case, the magnet is so small then l² can be neglected as compared to d², then
\(\frac{\mu_0}{4 \pi} \cdot \frac{\mathbf{M}}{d^3}\) = H .....................(2)
Knowing d and H the magnetic dipole moment of the bar can be calculated from equation.
(ii) When magnet is placed with its south pole towards north of the earth. The plot of magnetic field of the magnet in the case will be as shown in Fig. LAQ 14 (b).
The neutral points he on the axial line. At a neutral point, magnetic intensity due to magnet = magnetic field due to the earth.

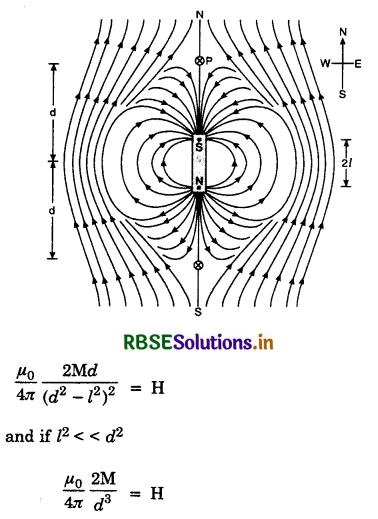
Knowing d, H this equation can be used to find magnetic dipole of the magnet.

Question 15.
How are materials classified according to their behaviour in magnetic field?
Answer:
On the basis of their behaviour in a magnetic field, the various materials can be classified in three classes.
(i) Diamagnetic. Those materials, which when placed in a magnetising field, are feebly magnetised in a direction opposite to the magnetising field are called diamagnetic substances. A few examples of diamagnetic materials are: copper, zinc, bismuth, water, sodium chloride, helium, argon etc.
When a diamagnetic substance is suspended in a magnetic field, it arranges itself in the direction of the magnetic field.

(ii) Paramagnetic. Those materials, which when placed in a magnetising field, are feebly magnetised in the direction of magnetic field, are called paramagnetic substances. A few examples of paramagnetic substances are: aluminium, sodium, antimony, platinum, copper chloride, liquid oxygen etc.
When a paramagnetic substance is suspended in a magnetic field it arranges itself to the direction of magnetic field.

(iii) Ferromagnetic. Those materials which when placed in a magnetising field are strongly magnetised in the direction of the magnetising field, are ferromagnetic substances. A few examples of ferromagnetic substances are iron, nickel, cobalt, alnico, mercury etc.

Question 16.
Briefly describe electron theory of magnetism. How para, dia and ferro magnetic behaviour are accounted for by the theory?
Answer:
Electron Theory of Magnetism. Each electron in an atom is revolving in an orbit around the nucleus. The revolving electron is equivalent to a tiny loop of current. Therefore, it possesses some orbital magnetic dipole moment 
\(\left|\overrightarrow{\mathrm{M}}_i\right|\) = current x area of the loop.
In addition to the orbital motion, every electron is assumed to have a spin motion around its axis. Therefore, another dipole magnetic moment called spin magnetic moment \(\overrightarrow{\mathbf{M}}_s\) is also associated with electron.
The vector sum of \(\overrightarrow{\mathrm{M}}_i\) and \(\overrightarrow{\mathrm{M}}_s\) provides the net dipole moment \(\overrightarrow{\mathrm{M}}\) to the electron.
(a) Diamagnetism. In a diamagnetic substance \(\overrightarrow{\mathrm{M}}_i\) and \(\overrightarrow{\mathrm{M}}_s\) cancel each other for every atom so that atom has no net magnetic dipole moment.
Therefore, motion of all the electrons in an atom of a diamagnetic material is assumed to be reduced to motion of two electrons revolving with the same angular velocity in a circular orbit of the same radius, but in opposite sense.

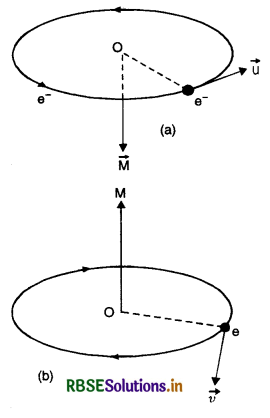
The magnetic moment of the two being equal and opposite, cancel each other (in the absence of any external magnetic field) so that net magnetic moment of each atom is zero. [Fig LAQ 16 (a) and (b)]
Let a uniform external magnetic field \(\overrightarrow{\mathrm{B}}\) be applied perpendicular to the plane of rotation of electron and directed away from the reader. Each electron experiences Lorentz force F = Bev. According to Fleming’s left hand rule,the Lorentz force F acts radially outwards on the electron revolving anticlockwise, tending to decrease the vel. of electron \( (\vec{v}-\overrightarrow{\Delta v})\). As a result of magnetic moment of electron decreases to \((\vec{M}-\overrightarrow{\Delta M})\). [Fig. LAQ 16 (a)]. On the electron revolving clockwise, the Lorentz force acts radially inwards tending to increase the velocity of electron to \((\vec{v}+\overrightarrow{\Delta v})\). Therefore, the magnetic moment of electron increases to \((\vec{M}+\overrightarrow{\Delta M})\). [Fig. LAQ 16 (b)] The vector addition magnetic moments gives rise to net dipole moment 2∆\(\overrightarrow{\mathrm{M}}\) directed towards the reader i.e opposite to external field \(\overrightarrow{\mathrm{B}}\).

The net magnetic moment 2∆\(\overrightarrow{\mathrm{M}}\) so developed is called induced magnetic moment. The magnetic moment induced in different atoms and vectorially to give a net magnetisation of the material in a direction opposite to \(\vec{B}\). This accounts for a diamagnetic behaviour of materials.
Further, as the appearance of induced magnetic moment in atoms is not affected by thermal motion of the atoms, therefore, magnetic susceptibility of such materials does not depend on temperature of the materials.

(b) Paramagnetism. In such materials, every atom has some permanent dipole moment. In the absence of an external magnetic field, the atomic dipoles are randomly oriented so that average magnetic moment per unit volume of the material is zero. Therefore a paramagnetism material does not behave as a magnet in the absence of an external magnetic field, Fig. LAQ 16 (e).

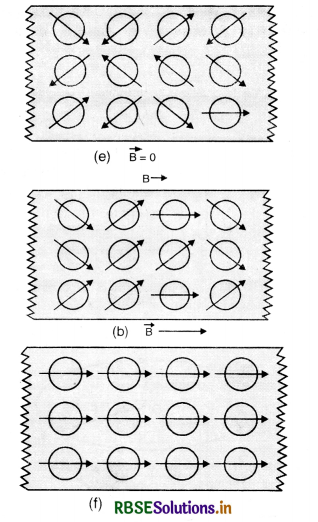
When external magnetic field \(\vec{B}\) is applied, it tries to aling the atomic dipole magnetic moments in the direction of the field. This is why the specimen gets magnetised in the direction of magnetising field. This is paramagnetism. Due to thermal motion the alignment is not complete Fig. LAQ 16 (f) but if the temperature of the specimen is lowered and strength of magnetic field is increased, complete alignment is also possible Fig. LAQ 16 (f).
When we raise the temperature of the material, the atomic dipoles acquire kinetic energy. This tends to disorient the dipoles. That is why magnetic susceptibility of the paramagnetic material decreases with rise in temperature.

(c) Ferromagnetism. This is explained by Weiss on the basis of domain theory in addition to electronic theory. Every atom of ferromagnetic substance is a tiny magnetic dipole having a permanent dipole moment. Atoms form very large number of small effective regions called domains. Each domain contains about 10¹⁰ atoms. A special interaction takes place in each domain and is called exchange coupling. This renders dipole moment of all atoms in a particular direction.
Each domain is a strong magnet without external field. Domains are randomly oriented so that their resultant magnetic moment in any direction is zero as given in figure LAQ 16 (g).

When external field is applied, it gets strongly magnetised which results in (i) Displacement of boundaries of domains [(Fig. LAQ 16 (h)]. (ii) Rotation of domains [(Fig. LAQ 16 (j)].
When a ferromagnetic material is heated above a certain temperature (called curie temperature), the exchange coupling suddenly disappears. The substance, therefore, starts behaving as paramagnetic. Curie temperature for iron is about 750°C.

Question 17.
(a) What do you mean by Hysteresis? Explain.
(b) Discuss some uses of the study of hysteresis studies.
Answer:
(a) Hysteresis. The lagging of intensity of magnetisation behind the magnetising field is called hysteresis. To explain term hysteresis, suppose a bar of iron is magnetised slowly. The intensity of magnetisation M increases with increase in the strength of magnetising field along OA [Fig. IAQ 17 (a)]. At A, any further increase in H does not produce any increase in M and therefore, corresponding to point A, the bar has acquired a state of magnetic saturation. If the magnetising field is now decreased slowly, the intensity of magnetisation also decreases but corresponding to point B when H becomes zero the intensity of magnetisation does not become zero.

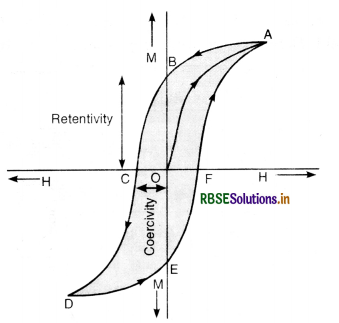
The value of intensity of magnetisation retained by the magnetic material, even when the magnetising field is reduced to zero is called its retentivity or remnant magnetism or residual magnetism.
Thus, OB represents the retentivity of the material under study. If now the direction of magnetising field is reversed, the intensity of magnetisation reduces along BC till it becomes zero at C. Thus to reduce the residual magnetism to zero, magnetising field equal to OC has to be applied in reverse direction.
The value of the reverse magnetising field which is to be applied to the magnetic material so as to reduce the residual magnetism to zero is called its coercivity.

When the magnetising field is further increased in reverse direction, the intensity of magnetisation increases along CD till corresponding to point B, it again acquires saturation value symmetrical to point A. On increasing the field again, the intensity of magnetisation follows the path DEFA, and the closed curve ABCDEFA is obtained for complete cycle of magnetisation.This closed curve is known as hysteresis loop. On repeating the process, the same closed curve is obtained again and again but portion OA is never obtained.
Corresponding to point B, H is zero but M has still some finite value and becomes zero after increasing H in reverse direction. Therefore, intensity of magnetisation does not become zero on making magnetising field zero but does so a little and this effect is called hysteresis.

(b) Uses. When a ferromagnetic substance is taken over a complete cycle of magnetisation, the energy spent per unit volume is numerically equal to the area of the hysteresis loop.
1. The shape of the hysteresis loop is characteristic of the magnetic materials. For example, for soft iron, the hysteresis loop is narrow and large in height, while that for steel, it is quite wide and small in height. [Fig. LAQ 17 (6)] The area of hysteresis loop for soft iron is found to be much smaller than for steel. Due to this, the loss of energy in case of soft iron bar will be very small as compared to that in case of steel, when both are taken over complete cycle of magnetisation. On account of this, soft iron is used to make the core of transformers and generators. Silicon, iron and mumetal (76% nickel. 17% iron and small percentage of copper and chromium) also possess narrow hysteresis loop and can be used to make the core of a transformer.

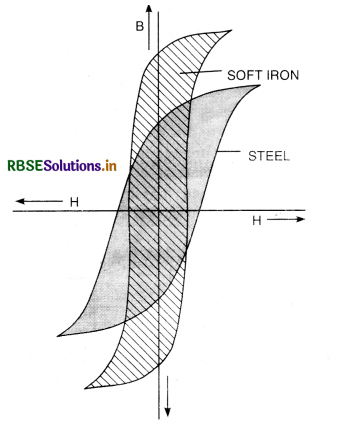
2. Due to high value of coercivity and fairly large value of retentivity, steel is used to make permanent magnets. The area of hysteresis loop is large for steel but it is of no consideration as a permanent magnet has never to be taken through a cycle of magnetisation. Materials suitable for making permanent magnets are cobalt steel (containing cobalt, tungsten and carbon) chromium, steel, tungsten steel. The alloy alnico (54% iron. 18% nickel. 10% aluminium, 12% cobalt, and 6% copper) is also very suitable for making permanent magnets. The only disadvantage is that alnico is brittle.
3.    For soft iron, coercivity is very small and area of hysteresis loop is very small. Because of these characteristics soft iron is an ideal material for making electromagnets.

Question 18.
What is magnet? What are its properties?
Answer:
Magnet. It is a piece of iron or some other material which can attract small pieces of iron, cobalt, nickel etc. A magnet may be natural or artificial. The word magnet has been derived from 'Magnesia' where the first known magnets (piece of lodestone) were found. This ore consists of Fe₂O₃ (magnetic oxide of iron). This ore is now known as a natural magnet, or simply magnet.
When the property of magnetism is achieved by passing current through a coil, the arrangement is called electromagnet.
Magnetic substances. The substances (such as iron, steel, cobalt, nickel) which can easily be attracted by a magnet, are called magnetic substances (more precisely ferromagnetic) while the substances (such as paper, wood, brass etc.) which are not attracted by a magnet are called non-magnetic.

Properties of a magnet. A magnet has the following properties:
(i) Attractive property. A magnet has the property of attracting small iron pieces towards it. If a magnet is brought near a layer of iron filings, it is found that the ends of this magnet attract more iron filings than the middle part of it. [Fig. LAQ 18 (a)] Thus, near the ends, there appears to be a point at which there is maximum attractive property.

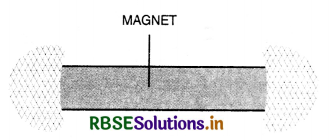
These points where the attraction appears to be maximum are called poles.
The poles are not exactly at the ends but are located slightly inside.


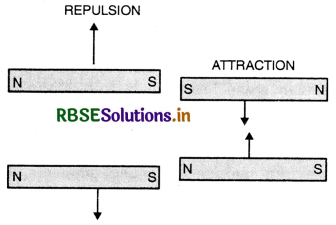
(ii) Like poles repel each other and unlike poles attract. Two like poles (both north poles or both south poles) repel each other and two unlike poles, (one north pole and other south pole) attract each other. [Fig. LAQ 18 (b)].
If the north poles (or the south poles) of two magnets are brought closer, two magnets repel each other. But if north pole of one magnet is brought near the south pole of another magnet, they attract each other.


(iii) Poles exist in pairs (no monopole exists).
If a magnet is broken into two parts from the middle, each part is found to be a magnet (i.e. has the attractive and directive property). If these pieces are broken again, each part is again found to retain magnetism [(Fig. LAQ 18 (c)] i.e. contains both poles. (N pole and S pole.)

(iv) A magnet always possesses a magnetic dipole moment.
(v) When suspended in a uniform magnetic field, magnet experiences torque and the magnetic field tries to align the magnet along its direction.
(vi) Directive property. If a magnet is suspended freely horizontally with a silk thread, it sets itself always pointing the earth’s north-south direction. The end which points towards the north, is called the north seeking pole (or simply north pole) and the end points towards the south, is called the south seeking pole which (or simply south pole).
(vii) A magnet moved with respect to a conductor produces electric current This property is electromagnetic induction.
(viii) Both the poles of a magnet are equally strong.
(ix) The field due to a magnet can deflect moving charged particle.
(x) The nature and extent of the magnetic property of a magnet is governed by electronic configuration of these elements.
(xi) Certain materials are repelled by magnets.
(xii) Magnetic property of a magnet is lost at high temperature.

Question 19.
Explain molecular theory of magnetism.
Answer:
Due to motion of charges of atoms of a substance there are magnetic properties associated with atoms and hence the molecules. Thus we have:
(i) Each molecule of magnetic substance, (whether magnetised or unmagnetised) is an independent magnet.
(ii) In an unmagnetised substance, these molecular magnets are randomly oriented and form closed chains.[Fig. LAQ 19 (a)] so they neutralise the effect of each other.
(iii) In a magnetised substance, these molecules are arranged such that the north pole of each molecular magnet points in one direction and the south pole in the opposite direction [Fig. LAQ 19 (b)]. It is obvious from the figure that near one end of the bar, there is north pole of each molecular magnet and therefore acts like a strong N pole, while near the other end, there is south pole of each molecular magnet and therefore acts like a strong S pole.
(iv) When a piece of iron is magnetised, the molecular magnets start setting themselves along straight chains and the magnetism of the piece increases.
(v) When all the molecular magnets are set along the direction of an externally applied magnetic field, the magnetic substance is said to be saturated with magnetism, and its magnetism cannot be further increased.
(vi) It also establishes that the strength of the two poles are equal.

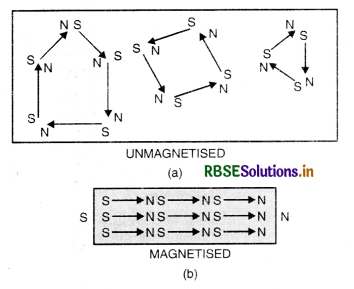
(vii) When a magnet is strongly heated or hammered, the kinetic energy of the molecules increases and, therefore, the molecular alignment gets disrupted and molecules go back to the closed chain arrangement due to thermal agitation and thus the magnet gets demagnetised.

Numerical Problems

Question 1.
A bar magnet of magnetic moment 6J/T is aligned at 60° with a uniform external magnetic field of 0.44 T. Calculate (a) the work done in turning the magnet to align its magnet moment.
(i) normal to the magnetic field,
(ii) opposite to the magnetic field and
(iii) the torque on the magnet in the final orientation in case (ii).
Answer:
Given M = 6 JT^-1, θ₁ = 60°, B = 0.44 T
Since W = MB (cos θ₁ - cos θ₂)
(a) (i) θ₂ = 90°
∴ W = 6 x 0.44 [cos 60° - cos 90°]
= 2.64(\(\frac{1}{2}\) - 0) = 1.34 J
(ii) θ₂ = 180°
∴ W = 6 x 0.44 [cos 60° - cos 80°]
= 2.64[\(\frac{1}{2}\) - 1] = 2.64 x \(\frac{3}{2}\)
= 3.9 J
(b) τ = MB sin π = MB.0 = 0.

Question 2.
A short bar magnet placed with its axis at 30° with a uniform external magnetic field of 0.16 T experiences a torque of magnitude 0.032 J.
(a) Estimate the magnetic moment of the magnet.
(b) If the bar were free to rotate, which orientations would correspond to its (i) stable, and (ii) unstable equilibrium? What is its potential energy in the field for cases (i) and (ii)?
Answer:
(a) The torque on a magnetic dipole of magnetic moment M in an external field B is
τ = MB sin θ
where θ is the angle between M and B
Here τ = 0.032 J, B = 0.16 T, θ = 30°
∴ M = \(\frac{0.032}{0.16 \times \frac{1}{2}}\) = 0.40 JT^-1.
The direction of M is from the south pole of the magnet to its north pole.
(b) Potential energy of a magnetic dipole in an external field B is given by U = - MB
(i) The bar is in stable equilibrium when its magnetic moment m is parallel to B (θ = 0); its potential energy then is minimum:
U = - MB = 0.40 x 0.16 = - 0 064 J
(ii) The bar is in unstable equilibrium when M is antiparallel to B (θ = 180°); its potential energy then is maximum.

Question 3.
What is the value of dip angle at the (i) magnetic equator (ii) at magnetic poles?
Answer:
(i) Zero, (ii) 90°.

Question 4.
A bar magnet 30 cm long is placed in the magnetic meridian with its north towards south of the earth. If the neutral point is obtained 30 cm from the magnet, find magnetic dipole moment and pole strength of the magnet.
Answer:
When magnet is placed with its north pole pointing south, neutral point is obtained on its axial line. Therefore, at neutral point
B_axia = B₀

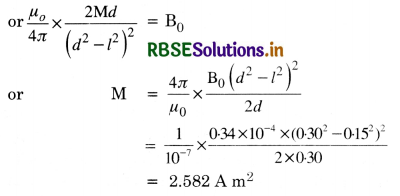
If m is pole strength of the magnet, then
m = \(\frac{\mathrm{M}}{2 l}=\frac{2.582}{0.30}\) = 8.606 Am.

Question 5.
A short bar magnet of magnetic moment 0.9 JT^-1 is placed with its axis at 45° to a uniform magnetic field. If it experiences a torque of 0.063 J.
(i) Calculate the magnitude of the magnetic field and
(ii) What orientation of the bar magnet corresponds to the stable equilibrium in the magnetic field?
Answer:
(i) Since τ = MB sin θ
∴ B = \(\frac{\tau}{\mathrm{B} \sin \theta}=\frac{0.063}{0.9 \times \sin 45^{\circ}}\)
= 0.009 T
(ii) For stable equilibrium, θ = 0°.

HOTS QUESTIONS

Question 1.
Work done in turning a magnet of magnetic moment M by an angle 90° from the meridian is n times the corresponding work done to turn it through an angle of 60°. Find the value of n.
Answer:
Work done in rotating a magnet from θ₁ to θ₂ in a magnetic field B is given by
W = MB (cos θ₁ - cos θ₂)
If W₁ is the work done to rotate the magnet from 0 to 90°, then
W₁ = MB (cos θ - cos 90°) = MB (1 - 0) = MB
If W₂ is the work done to rotate the magnet from 0 to 60°, then
W₂ = MB (cos 0° - cos 60°)
= MB (1 - 0.5) = \(\frac{\mathrm{MB}}{2}\)
∴ \(\frac{\mathrm{W}_1}{\mathrm{~W}_2}=\frac{2 \mathrm{MB}}{\mathrm{MB}}\) = 2
Given \(\frac{\mathrm{W}_1}{\mathrm{~W}_2}\) = n
∴ n = 2.

Question 2.
A long horizontal rigidly supported wire carries a current i_a of 100 A. Directed above it and parallel to it is a fine wire that carries a current i_b of 20 A and weighs 0.073 N/m. How far above the lower wire should the second wire be kept if we wish to support it by magnetic repulsion? Given permeability constant µ₀ = 4π x 10^-7 Wb A^-1 m^-1.
Answer:
If i_a and i_b are the antiparallel currents flowing in two parallel wires separated by a distance R, then the repulsion force experienced by unit length (1 m) of either wire is
F = \(\frac{\mu_0 i_a i_b}{2 \pi \mathrm{R}}\)
Weight per metre length of above wire = 0.073 Nm^-1
According to problem, the weight of lower wire is supported by upward magnetic repulsion, therefore
or R = \(\frac{\mu_0 i_a i_b}{2 \pi \times 0.073}\)
= \(\frac{4 \pi \times 10^{-7} \times 100 \times 20}{2 \pi \times 0.073}\)
= 4.4 x 10^-3 m = 4.48 mm.

Question 3.
A short bar magnet placed with its axis at 30° to a uniform magnetic field of 0.2T experiences a torque of 0.06 Nm.
(i) Calculate magnetic moment of the magnet and
(ii) Find out what orientation of the magnet corresponds to a stable equilibrium in the magnetic field.
Answer:
(i) Given B = 0.2T, θ = 30°, τ = 0.06 Nm
Since τ = MB sin θ
∴ M = \(\frac{\tau}{1 \sin \theta}=\frac{0.06}{0.2 \times \sin 60^{\circ}}\) = 0.06 Am²
Potential energy of magnetic dipole in a uniform magnetic field B is given by
U = - MB cos θ
In stable equilibrium, the potential energy is minimum i.e. cos θ = 1 or θ = 0°
So for stable equilibrium the magnet must be aligned with its magnetic moment parallel to the magnetic field.

Question 4.
A student records the following data for the magnitudes (B) of the magnetic field at axial points at different distances x from the centre of a circular coil of radius ‘a’ carrying a current I. Verify (for any two) that these observations are in good agreement with the expected theoretical variation of B with X.

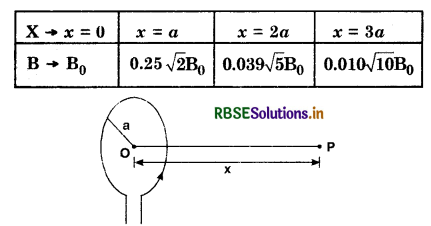
Answer:
The magnetic field at any point on the axis of a circular current carrying conductor is given by,
B = \(\frac{\mu_0}{4 \pi} \frac{2 \pi \mathrm{I} a^2}{\left(a^2+x^2\right)^{3 / 2}}\)
when x = 0, then

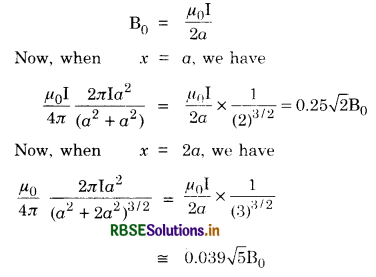
Question 5.
An iron sample having mass 8.4 kg is repeatedly taken over cycles of magnetisation and demagnetisation at a frequency of 50Hz. It is found that energy of 3.2 J is dissipated as heat in the sample in 30 minutes. If the density of iron is 7200 kg m^-3, calculate the value of energy dissipated per unit volume per cycle in the iron sample.
Answer:
Given m = 8.4 kg, v = 50 Hz, ρ = 7200 kg m^-3
∴ Volume = \(\frac{m}{\rho}=\frac{8.4}{7200}\) = 1.167 x 10^-3 m³
Energy dissipated in 30 minutes = 3.2 x 10⁴ J
∴ Energy dissipated/sec = \(\frac{3.2 \times 10^4}{30 \times 60}\) = 17.78 Js^-1
So energy dissipated/vol/cycle
= \(\frac{17.78}{1.167 \times 10^{-3} \times 50}\)
= 3047 Jm^-3 cycle^-1