RBSE Class 12 Physics Important Questions Chapter 4 गतिमान आवेश और चुंबकत्व

Rajasthan Board RBSE Class 12 Physics Important Questions Chapter 4 गतिमान आवेश और चुंबकत्व Important Questions and Answers.

RBSE Class 12 Physics Chapter 4 Important Questions गतिमान आवेश और चुंबकत्व

अति लघुत्तरीय प्रश्न

प्रश्न 1.
चुम्बकीय क्षेत्र में धारावाही चालक पर बल का सूत्र लिखिए।
उत्तर:
F =IB lsinθ

प्रश्न 2.
ऐम्पियर की अन्तर्राष्ट्रीय परिभाषा दीजिए।
उत्तर:
यदि 1 मीटर दूरी पर रखे दो समान्तर तारों में समान धारा प्रवाहित होने पर उनके मध्य 2 x 10^-7 न्यूटन/मी का बल कार्य करे तो तारों में बहने वाली समान धारा एक ऐम्पियर होगी।

प्रश्न 3.
चुम्बकीय क्षेत्र की दिशा ज्ञात करने के लिए कोई दो नियमों के नाम लिखिए।
उत्तर:

• मैक्सवेल का कॉक स्कू नियम 
• स्नो का नियम

प्रश्न 4.
समान्तर पथों पर गतिमान एक प्रोटॉन और एक इलेक्ट्रॉन किसी एक समान चुम्बकीय क्षेत्र, जो इनके गमनपथों के लम्बवत है, में प्रवेश करते हैं। इनमें से कौन सा उच्च आवृत्ति के वृत्तीय पथ में गति करेगा?
उत्तर:
आवृत्ति n = \(\frac{q B}{2 \pi m}\)
दोनों पर आवेश q समान है अत:
n ∝ \(\frac{1}{m}\)
अत: इलेक्ट्रॉन उच्च आवृत्ति के वृत्तीय पथ में गति करेगा।

प्रश्न 5.
किसी धारावाही कुण्डली का चुम्बकीय आघूर्ण किन कारकों पर निर्भर करता है?
उत्तर:
कुण्डली में फेरों की संख्या, कुण्डली की अनुप्रस्थ काट का क्षेत्रफल व कुण्डली में प्रवाहित धारा।

प्रश्न 6.
लम्बाई l की किसी चालक छड़ को किसी एकसमान चुम्बकीय क्षेत्र \(\overrightarrow{\mathbf{B}}\) के समान्तर रखा रखा गया है। इस छड़ को चुम्बकीय क्षेत्र के अनुदिश वेग \(\overrightarrow{\mathbf{v}}\) से गति करायी गयी है। इस चालक में प्रेरित वि. वा. बल का मान क्या होगा?
उत्तर:
F = I l B sinθ से 
F = 0 (∵θ = 0°) 

प्रश्न 7.
आरेख में दर्शाए अनुसार किसी लम्बे सीधे चालक, जिसे मध्य में त्रिज्या R के वृत्ताकार पाश में मोड़ा गया है, से कोई धारा I प्रवाहित हो रही है। बिन्दु 0 पर नेट चुम्बकीय क्षेत्र का परिमाण क्या होगा?

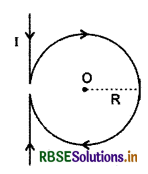
उत्तर:
सौधे तार के कारण R दूरी पर चुम्बकीय क्षेत्र
B₁ = \(\frac{\mu_0 I}{2 \pi R}\) ऊर्ध्वाधर नीचे की ओर 
वृत्तीय पाश के कारण चुम्बकीय क्षेत्र
B₂ = \(\frac{\mu_0 I}{2 R}\) अर्ध्वाधर ऊपर की ओर
अत: केन्द्र 0 पर परिणामी चुम्बकीय क्षेत्र

प्रश्न 8.
कोई आवेशित कण विभान्तर V से त्वरित होने के पश्चात किसी एक समान चुम्बकीय क्षेत्र में प्रवेश करता है और त्रिज्या r के वृत्त में गमन करता है। यदि विभवान्तर V को दोगुना कर दिया जाए तो वृत्त की त्रिज्या क्या होगी?

प्रश्न 9.
किसी चल कुण्डली गैल्वेनोमीटर की "धारा सुग्रहिता" की परिभाषा लिखिए।
उत्तर:
धारामापी में एकांक प्रबलता की धारा प्रवाहित होने पर धारामापी में उत्पन्न विक्षेप धारा सुग्राहिता कहलाती है।
धारा सुग्राहिता S_i = \(\frac{\phi}{I}\)

प्रश्न 10.
m₁ और m₂  द्रव्यमान के दो कणों पर समान आवेश है। इन्हें विराम से विभवान्तर V तक त्वरित करके फिर एक समान चुम्बकीय क्षेत्र \(\overrightarrow{\mathbf{B}}\) के क्षेत्र में प्रवेश कराया जाता है। यदि ये क्रमशः r₁ और r₂ त्रिज्याओं के वृत्तीय पथों पर गमन करते हैं। तो ज्ञात करो।
उत्तर:
हम जानते हैं r = \(\sqrt{\frac{2 m \mathrm{E}_k}{q \mathrm{~B}}}\)
विभवान्तर V अर्थात् ऊर्जा E_k, आवेश q व चुम्बकीय क्षेत्र B
नियत है। अतः r ∝ \(\sqrt{m}\)
m ∝ r₂
∴ \(\frac{m_1}{m_2}=\frac{r_1^2}{r_2^2}\)

प्रश्न 11.
चुम्बकीय क्षेत्र की विमाएँ एवं मात्रक लिखिए।
उत्तर:
विमाएँ - [M¹L⁰T^-2A^-1]
मात्रक - टेसला (T)

प्रश्न 12.
लारेन्ज बल कब अधिकतम होता है?
उत्तर:
जब आवेश चुम्बकीय क्षेत्र की दिशा के लम्बवत गतिशील होता है।

प्रश्न 13.
परिनालिका के अन्दर उत्पन्न चुम्बकीय बल रेखाएँ कैसी होती हैं?
उत्तर:
परिनालिका के अन्दर उत्पन्न चुम्बकीय बल रेखाएँ समान्तर एवं लम्बाई के अनुदिश होती हैं।

प्रश्न 14.
एक आवेशित कण, सम चुम्बकीय क्षेत्र के समान्तर गति करता है, तो कण का पथ कैसा होगा?
उत्तर:
समचुम्बकीय क्षेत्र के समान्तर गति करते कण का पथ ऋजुरेखीय होगा।

प्रश्न 15.
धारामापी के लिए दक्षतांक की परिभाषा दीजिए।
उत्तर:
धारामापी में एकांक विशेप के लिए आवश्यक धारा के मान को धारामापी का दक्षांक कहते हैं।

प्रश्न 16.
बारा सुग्राहिता का मात्रक लिखिए।
उत्तर:
डिग्री/ऐम्पियर

प्रश्न 17.
धारामापी की सुग्राहिता कैसे बढ़ाई जा सकती है?
उत्तर:
अधिक फेरे करके और अधिक क्षेत्रफल वाली कुण्डली में नरम लोहे का क्रोड लेकर धारामापी की सुग्राहिता बढ़ाई जा सकती है।

प्रश्न 18.
आप समचुम्बकीय क्षेत्र उत्पन्न करने के लिए किस युक्ति का चयन करेंगे?
उत्तर:
हेल्महोल्ट्ज कुण्डली

लघु उत्तरीय प्रश्न

प्रश्न 1.
(a) वह प्रतिबंध प्राप्त कीजिए जिसमें किसी चुम्बकीय क्षेत्र से गुजरते समय किसी इलेट्रॉन में कोई विचलन नहीं होता।
(b) समान चाल से गतिमान दो प्रोटॉन P और Q क्रमशः दो चुम्बकीय क्षेत्रों \(\overrightarrow{\mathbf{B}_1}\) और \(\overrightarrow{\mathbf{B}_2}\) से इन क्षेत्र दिशाओं के लम्बवत गति कर रहे हैं। यदि | \(\overrightarrow{\mathbf{B}_1}\) | > |\(\overrightarrow{\mathbf{B}_2} \)| है, तो इनमें से कौन-सा प्रोटॉन छोटी त्रिज्या के वृत्तीय पथ पर गमन करेगा? व्याख्या कीजिए।
उत्तर:
(a) चुम्बकीय क्षेत्र के समानान्तर आवेश प्रवेश करें।
(b) r ∝ \(\frac{1}{B}\)
प्रश्नानुसार | \(\overrightarrow{\mathbf{B}_1}\) | > |\(\overrightarrow{\mathbf{B}_2}\) | । अत: r₁ > r₂ अर्थात् छोटी त्रिज्या के पथ में गमन करेगा।

प्रश्न 2.
एक इलेक्ट्रॉन r त्रिज्या के वृत्तीय पथ पर समान कोणीय वेग ω से गति कर रहा है। धारावाही वृत्तीय चालक के केन्द्र पर उत्पन्न चुम्बकीय क्षेत्र के सूत्र की सहायता से इलेक्ट्रॉन के पथ के केन्द्र पर उत्पन्न चुम्बकीय क्षेत्र के लिए व्यंजक प्राप्त कीजिए।
उत्तर:
वृत्ताकार लूप के केन्द्र पर उत्पन्न चुम्बकीय क्षेत्र
B = \(\frac{\mu_0}{4 \pi} \frac{2 \pi \mathrm{I}}{r}\) ....................(i)
इलेक्ट्रॉन का कोणीय वेग ω है अतः इसके परिक्रमण का आवर्तकाल
T = \(\frac{2 \pi}{\omega}\)
∴ इलेक्ट्रॉन की कक्षा में तुल्य धारा
I = \(\frac{e}{\mathrm{~T}}=\frac{e}{2 \pi / \omega}=\frac{e \omega}{2 \pi}\)
समी. (i) से B = \(\frac{\mu_0}{2 \pi} \frac{e \omega}{\pi}\)

प्रश्न 3.
अमीटर व वोल्टमीटर में विभेद कीजिए। 
उत्तर:

अमीटर	वोल्टमीटर
(i) यह एक कम प्रतिरोध का उपकरण है जो परिपथ में प्रवाहित धारा के मापन हेतु प्रवाहित धारा के मापन हेतु प्रयुक्त होता है।	(i) यह उच्च प्रतिरोध का उपकरण है जो परिपथ के किसी भाग के विभवान्तर के मापन के लिए प्रयुक्त होता है।
(ii) इसे सदैव श्रेणीक्रम में जोड़ते हैं।	(ii) इसे समानान्तर क्रम में जोड़ते हैं

प्रश्न 4.
एक धारावाही परिनालिका एक छड़ चुम्बक की तरह कैसे व्यवहार करती है? समझाइए।
उत्तर:
परिनालिका चुंबक की भांति व्यवहार करती है। इसका एक सिरा उत्तर ध्रुव तथा दूसरा सिरा दक्षिण ध्रुव की तरह व्यवहार करता है। परिनालिका के भीतर चुंबकीय क्षेत्र रेखाएं समांतर सरल रेखाओं की भांति होती है। किसी छड़ चुंबक की सहायता से किसी विद्युत् धारावाही परिनालिका के दोनों ध्रुवों का निर्धारण किया जा सकता है। छड़ चुंबक के उत्तरी ध्रुव को परिनालिका के एक सिरे के निकट लाओ। यदि दोनों के बीच आकर्षण हो तो परिनालिका का वही सिरा, दक्षिण ध्रुव होगा। यदि उन दोनों में प्रतिकर्षण हो तो वह सिरा उत्तरी ध्रुव होगा।

प्रश्न 5. 
दो समानान्तर धारावाही चालक तारों के मध्य कार्यरत बल ज्ञात कीजिए। ऐम्पियर की सैद्धान्तिक परिभाषा इसके आधार पर लिखिए।
उत्तर:
दो समान्तर धारावाही चालक तारों के मध्य चुम्बकीय बल (Magnetic force between two parallel current carrying conducting wires):
हम अध्ययन कर चुके है कि किसी धारावाही चालक तार के चारों ओर एक चुम्बकीय क्षेत्र उत्पन्न हो जाता है, एवं चुम्बकीय क्षेत्र में स्थित धारावाही चालक पर बल कार्य करता है। अतः यदि एक धारावाही चालक तार के निकट कोई दूसरा धारावाही चालक तार रख दिया जाये तो वे दोनों चालक चुम्बकीय बल का अनुभव करेंगे।

जब दोनों में धारा की दिशा एक ही होती है तो इनके मध्य आकर्षण बल लगता है और जब धाराएँ विपरीत दिशा में होती हैं तो इनके मध्य प्रतिकर्षण बल लगता है। बायो - सावर्ट के नियम और लॉरंज बल को मिलाकर ऐम्पियर ने धारावाही चालकों के बीच लगने वाले बल की गणना की थी, इसीलिए इसे ऐम्पियर का नियम (Ampere's law) भी कहते हैं। इसे निम्न प्रकार समझाया गया है-

माना कि AB व CD दो लम्बे, समान्तर व ऋजु धारावाही चालक तार कागज के तल में स्थित हैं जिनमें क्रमशः I₁ व I₂ धाराएँ बह रही हैं और तारों के मध्य दूरी r है। चित्र 4.59 (a) में धाराएँ समान दिशा में और चित्र 4.59 (b) में धाराएँ विपरीत दिशा में बह रही हैं।

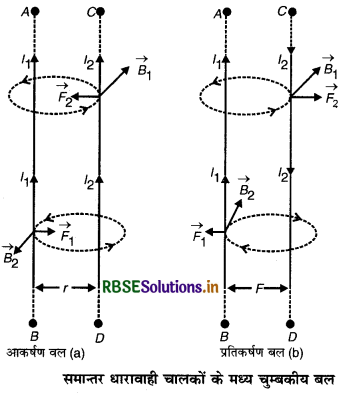
बायो - सावर्ट के नियमानुसार चालक AB के कारण चालक CD के किसी बिन्दु पर उत्पन्न चुम्बकीय क्षेत्र
B₁ = \(\frac{\mu_0}{2 \pi} \frac{\mathrm{I}_1}{r}\) NA^-1m^-1
दायें हाथ की हथेली के नियम नं. 1 (Right Hand Palm Rule Number 1) के अनुसार इस चुम्बकीय क्षेत्र की दिशा कागज के तल के लम्बवत् नीचे की ओर (perpendicular inward to the plane of paper) होगी। इस चुम्बकीय क्षेत्र में धारावाही चालक CD की l लम्बाई पर लगने वाला लॉरंज बल,
F₂ = I₂B₁ l sin 90°
= I₂ l B₁ = I₂ l \(\frac{\mu_0}{2 \pi} \frac{I_1}{r}\)

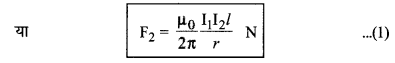
या F₂ = 2 x 10^-7 \(\frac{\mathrm{I}_1 \mathrm{I}_2 l}{r}\) N
अतः तार CD की एकांक लम्बाई पर लगने वाला बला,
f = \(\frac{F_2}{l}\) = 2 x 10^-7 \(\frac{\mathrm{I}_1 \mathrm{I}_2}{r}\) N - m^-1 ........................ (2) 
इसी प्रकार चालक CD में धारा प्रवाह के कारण चालक AB की एकांक लम्बाई पर लगने वाला बल

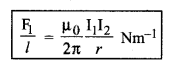
इस बल की दिशा फ्लेमिंग के बायें हाथ के नियम (Fleming's Left Hand Rule) से दी जाती है। यदि दोनों तारों में समान धारा बह रही हो (अर्थात् I₁ = I₂ = I) तो
F₁ = F₂ = F
\(\frac{\mathrm{F}}{l}=\frac{\mu_0}{2 \pi} \frac{\mathrm{I}^2}{r}\)
ऐम्पियर की परिभाषा: दो समान्तर सीधे धारावाही चालकों के मध्य लगने वाला बल
f = \(\frac{\mu_0}{2 \pi} \frac{\mathrm{I}_1 \mathrm{I}_2}{r}\) Nm^-1
= 2 x 10^-7 \(\frac{\mathrm{I}_1 \mathrm{I}_2}{r}\) Nm^-1
यदि I₁ = I₂ = 1A; r = 1m तो
F = 2 x 10^-7 Nm^-1
"यदि 1 m दूरी पर रखे दो समान्तर तारों में समान धारा बहने से उनके मध्य 2 x 10^-7 Nm^-1 का बल (आकर्षण या प्रतिकर्षण) कार्य करे तो तारों में बहने वाली प्रत्येक धारा 1A होगी।"

प्रश्न 6.
चल कुण्डल धारामापी में त्रिज्य चुम्बकीय क्षेत्र का क्या महत्व है?
उत्तर:
चम्बकीय क्षेत्र में लटकी हुई धारावाही कुण्डली पर लगने वाला बलयुग्म का आघूर्ण
τ =NIAB sinθ
जब त्रिज्य चुम्बकीय क्षेत्र में कुण्डली को लटकाया जाता है तो कुण्डली की प्रत्येक स्थिति में उसका तल किसी न किसी रेखा के अनुदिश होता है, अत: θ = 90°
∴ sinθ = 1
अत: τ = NIAB 
अतः τ ∝ I
अर्थात् कुण्डली पर बल आघूर्ण उसमें प्रवाहित धारा के अनुक्रमानुपाती होता है। इस प्रकार धारामापी स्केल को रेखीय बना सकते हैं।

प्रश्न 7.
स्पष्ट कीजिए कि बायो सेवर्ट नियम से, ऐम्पियर को परिपथीय नियम को समाकलन रूप में यथा \(\oint \overrightarrow{\mathrm{B}} \cdot d \vec{l}=\mu_0 \mathrm{U}\) के रूप में कैसे व्यक्त किया जा सकता है। जहाँ । उस पृष्ठसे गुजरने वाली कुल धारा है।
उत्तर:
ऐम्पियर का परिपथीय नियम (Ampere's Circuital Law) 
कथन: इस नियम के अनुसार, "किसी बन्द वक्र (closed curve) के परितः (around) चुम्बकीय क्षेत्र की तीव्रता का रेखीय समाकलन (linear integral) उस बन्द वक्र (closed curve) द्वारा घिरी आकृति (bound figure) में से गुजरने वाली कुल थारा कागुना होता है।"
गणितीय रूप में, Φ\(\overrightarrow{\mathrm{B}} \cdot d \vec{l}\) = µ₀ x [कुल धारा] 
या Φ\(\overrightarrow{\mathrm{B}} \cdot d \vec{l}\) = µ₀ΣI ..................(1)
जहाँ µ₀ - निर्वात् की निरपेक्ष चुम्बकशीलता (premiti - vity of free space)
उपपत्ति: ऐम्पियर के नियम की उपपत्ति दी जा सकती है, जब किसी भी आकृति के बन्द पथ से होकर धारा गुजरती है। किसी भी स्वेच्छगृहीत (arbitrary) बन्द पथ के लिए ऐम्पियर के नियम को सिद्ध करने से पूर्व एक विशेष स्थिति में अर्थात् किसी धारावाही चालक के परितः बन्द वृत्तीय पथ के लिए इसे सिद्ध करते हैं।

वृत्तीय पञ्च के लिए (For Circular Path): माना एक लम्बे तार XY में धारा I सिरे X से Y की ओर बह रही है। चालक में धारा बहने से इसके परितः चुम्बकीय क्षेत्र उत्पन्न होगा।

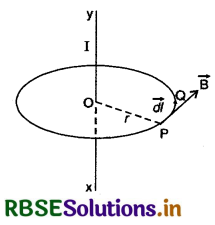
चालक को केन्द्र मानते हुए O केन्द्र वाले एवं r त्रिज्या वाले वृत्तीय पथ की कल्पना करते हैं। माना वृत्तीय पथ का एक अल्पांश \(\overrightarrow{\mathrm{PQ}}\) (= \(\overrightarrow{d l}\)) है और बिन्दु P पर चुम्बकीय क्षेत्र \(\overrightarrow{\mathrm{B}}\) है। दाहिने हाथ के नियमानुसार चुम्बकीय क्षेत्र की दिशा P पर वृत्तीय पथ की स्पर्श रेखा की दिशा (in the direction of tangent) में होगी। स्वाभाविक है कि \(\overrightarrow{\mathrm{B}}\) व अल्पांश \(\overrightarrow{\mathrm{dl}}\) एक ही दिशा में होंगे, अत: बन्द वृत्तीय पथ के लिए चुम्बकीय क्षेत्र का रेखीय समाकलन 
\(\oint_{\mathrm{B}}^{\vec{d} \cdot \vec{l}}=\oint \mathrm{B} d l \cos 0^{\circ}=\oint \mathrm{B} d l\) .................(2)
लम्बे एवं सीधै धारावाही चालक के कारण बिन्दु P पर उत्पन्न चुम्बकीय क्षेत्र,
B = \(\frac{\mu_0}{4 \pi} \frac{2 I}{r}\)
अत: समी. (2) से,

प्रश्न 8.
चल कुण्डली धारामापी का सिद्धांत लिखिए।
उत्तर:
निलम्बन कुण्डली धारामापी (Suspended Coil Galvanometer)
बनावट (Construction): इसमें एक अचुम्बकीय धातु ऐलुमिनियम के फ्रेम [non - magnetic metallic aluminium frame] पर पतले विद्युत्रोधी तौबे के तार के अनेक फेरों वाली आयताकार कुण्डली लिपटी (wound) रहती है। यह कुण्डली एक पतले फॉस्फर ब्रांज (Phosphor Bronze) के तार से, एक प्रबल स्थायी चुम्बक (strong magnet) के धुवखण्डों (N व S) के बीच लटकी रहती है। कुण्डली के बीच एक नर्म लोहे (soft iron) की बेलनाकार क्रोड (cylindrical core) रखी जाती है।

कुण्डली का एक सिरा निलम्बन (suspension) से बैंधा रहता है जो धारामापी के एक टर्मिनल (T₁) का कार्य करता है। कुण्डली का दूसरा सिरा एक ढीली कुण्डलित स्प्रिंग (loosely coiled spring) से जुड़ा रहता है, जो धारामापी के दूसरे टर्मिनल (T₂) का कार्य करता है। निलम्बन तार (suspension wire) का ऊपरी सिरा मरोड़ शीर्ष (torsion

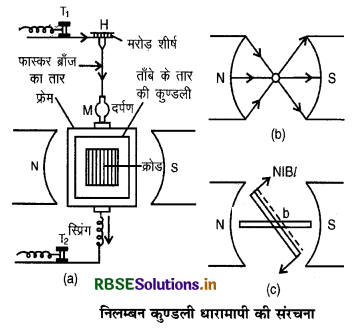
head) H से जुड़ा रहता है जिसमें कुण्डली को शून्य स्थिति (zero position) में लाने के लिए घुमाया जा सकता है। फॉस्फर ब्रांज के साथ एक समतल दर्पण M लगा रहता है जिसकी सहायता से लैम्म व स्केल व्यवस्था (lamp and scale arrangement) द्वारा कुण्डली का विक्षेप पढ़ा जा सकता है। यन्त्र के आधार (base) पर क्षैतिजकारी पेंच (horizontal screws) भी लगे रहते हैं। स्थायी चुम्बक के ध्रुव खण्ड (pole pieces) बेलनाकार रखे जाते हैं, ताकि कुण्डली की प्रत्येक स्थिति में चुम्बकीय क्षेत्र त्रिज्यीय (radial) रहे। ध्रुव खण्ड अवतल होते हैं और घोड़े की नाल चुम्बक से बने होते हैं।
सिद्धान्त (Principle): यदि धारावाही कुण्डली को समरूप चुम्बकीय क्षेत्र (uniform magnetic field) में रखा जाये तो उस पर लगने वाले बलयुग्म का आघूर्ण,
τ = nIAB sinθ
जहाँ n = कुण्डली में फेरों की संख्या (number of tums in coil); I = कुण्डली में प्रवाहित धारा; A = कुण्डली के तल का क्षेत्रफल; B = चुम्बकीय क्षेत्र की तीव्रता (intensity of magnetic field); θ = कुण्डली के तल पर खींचे गये अभिलम्ब एवं क्षेत्र रेखा के मध्य कोण (angle between normal drawn on plane of coil and field line)
यदि चुम्बकीय क्षेत्र त्रिज्य है तो।
θ = 90°; ∴ sinθ = 1
अत: τ = nIAB
इस बलयुग्म के प्रभाव में कुण्डली घूमने लगेगी, फलस्वरूप फॉस्फर ब्रांज के तार में ऐंठन (twist) लगने लगेगी। यदि यह ऐंठन Φ हो तो ऐंठन बलयुग्म का आघूर्ण
τ' = CΦ
जहाँ, C = एकांक ऐंठन के लिए बलयुग्म का आपूर्ण 
∵ सन्तुलन में τ = τ'
∴ nIAB = CΦ
या I = \(\left(\frac{\mathrm{C}}{n \mathrm{AB}}\right) \phi\) .........................(1)
या I = kΦ, जहाँ k = \(\frac{\mathrm{C}}{n \mathrm{AB}}\)
k को धारामापी का परिवर्तन गुणांक (torsion constant or reduction factor) कहते हैं।
∴ I ∝ Φ या Φ ∝ I
तार में उत्पन्न ऐंठन (अर्थात् धारामापी कुण्डली में उत्पन्न विक्षेप) प्रवाहित धारा के अनुक्रमानुपाती होती है। यही धारामापी का सिद्धान्त है।
धारा परिवर्तन गुणांक (Current Reduction Factor)-
समी. (1) से, I = \(\frac{\mathrm{C}}{n \mathrm{AB}} \phi\)
या I = kΦ .........................(2)
जिसमें k = \(\frac{\mathrm{C}}{n \mathrm{AB}}\) को ही धारामापी का धारा परिवर्तन गुणांक कहते हैं।
∵ धारा सुग्राहिता (Current Sensitivity): धारामापी की धारा सुग्राहिता कुण्डली में प्रति एकांक धारा के लिए उत्पन्न विक्षेप (deflection) से नापी जाती है अर्थात्
धारा सुग्राहिता S_i = \(\frac{\phi}{I}\)
= \(\frac{n \mathrm{AB}}{\mathrm{C}}\) .......................(3)
वोल्टेज सुग्राहिता (Voltage Sensitivity): यदि कुण्डली के सिरों के मध्य वोल्टेज V हो तो राशि \(\frac{\phi}{V}\) को वोल्टेज सुग्राहिता कहते हैं। यदि कुण्डली का प्रतिरोध R हो तो
V = RI
∴ वोल्टेज सुग्राहिता S_v = \(\frac{\phi}{\mathrm{V}}=\frac{\phi}{\mathrm{IR}}=\frac{n \mathrm{AB}}{\mathrm{CR}}\) .....................(4)
धारा सुग्राहिता एवं वोल्टेज सुनाहिता में सम्बन्ध (Relation between Current Sensitivity and Voltage Sensitivity)-
समी. (3) से, \(\frac{n \mathrm{AB}}{\mathrm{C}}=\frac{\phi}{\mathrm{I}}\),
यह मान समी. (4) में रखने पर,
वोल्टेज सुग्राहिता = \(\frac{\phi / I}{R}\)

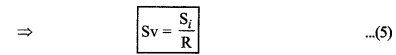
धारामापी की धारा सुग्राहिता को प्रभावित करने वाले कारक:
समी. (3) से स्पष्ट है कि धारामापी की धारा सुग्राहिता को निम्न प्रकार से बढ़ाया जा सकता है-

1. फेरों की संख्या (n) बढ़ाकर
2. कुण्डली का क्षेत्रफल (A) बढ़ाकर
3. चुम्बकीय क्षेत्र की प्रबलता (B) बढ़ाकर
4. मरोड़ी दृढ़ता (torsion rigidity) (C) घटाकर। 

प्रश्न 9.
साइक्लोट्रॉन का सिद्धान्त समझाइए। 
उत्तर:
साइक्लोट्रॉन एक ऐसी युक्ति है जिसका उपयोग प्रोटॉन जैसे आवेसो को त्वरित करने के लिए किया जाता है। ये त्वरित आवेस ही नाभिकीय अभिक्रिया को कराने में सहायक होते है। 
साइक्लोट्रॉन का सिद्धांत-
जब कोई आवेश चुंबकीय क्षेत्र में समकोण पर गति करता है तो यह वर्णन करता है कि वृत्ताकार पथ द्वारा दिया गया है-
r = \(\frac{M v}{B q}\)

प्रश्न 10.
यह दर्शाइए कि किस प्रकार छोटा धारावाही लूप एक दण्ड चुम्बक की तरह व्यवहार करता है?
उत्तर:

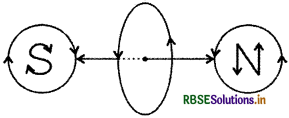
जब एक धारावाही लूप में धारा प्रवाहित होती है तो लूप एक चुम्बकीय द्विध्रुव या दण्ड चुम्बक की तरह व्यवहार करता है। अर्थात् एक फलक चुम्बकीय दक्षिणी ध्रुव S तथा दूसरा फलक उत्तरी ध्रुव N की भांति व्यवहार करने लगता है। "जिस फलक पर धारा वामावर्त (Anticlockwise) दिशा में प्रवाहित दिखायी देती है, वह फलक उत्तरी ध्रुव N एवं जिस फलक पर धारा दक्षिणावर्त (Clock wise) दिशा में प्रवाहित हुई प्रतीत होती है, वह फलक दक्षिणी ध्रुव की भाँति व्यवहार करता है।

प्रश्न 11.
ऐम्पियर के नियम से किसी धारावाही बेलनाकार चालक के अन्दर स्थित किसी बिन्दु पर चुम्बकीय क्षेत्र ज्ञात कीजिए।
उत्तर:
अलम्बे बेलनाकार धारावाही चालक के कारण चुम्बकीय क्षेत्र (Magnetic Field due to a current carrying long cylindrical conductor):
माना R त्रिज्या के एक बेलनाकार चालक में स्थायी धारा I प्रवाहित हो रही है जो इस चालक के सम्पूर्ण काट क्षेत्रफल में समान रूप से वितरित है। इस चालक से लम्बवत् r दूरी पर चुम्बकीय क्षेत्र ज्ञात करना है। धारा के सममित वितरण के कारण हम यह मान सकते हैं कि चुम्बकीय क्षेत्र \(\vec{B}\) की क्षेत्र रेखाएँ वृत्ताकार या संकेन्द्री वृत्त के आकार की होगी जिनके केन्द्र बेलन की अक्ष में होंगे।

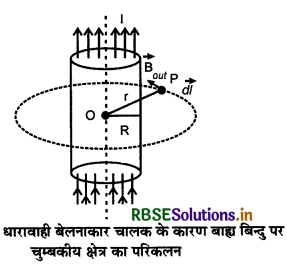
(i) जब बिन्दु बेलनाकार चालक के बाहर स्थित हो अर्थात् (r > R)- चित्र 4.49 के अनुसार r त्रिज्या के एक वृत्तीय बन्द पथ विचार करते हैं। इस पथ के प्रत्येक बिन्दु पर चुम्बकीय क्षेत्र का परिमाण नियत (समान) तथा दिशा पथ के अनुदिश होता है। ऐम्पीयर के नियम से,
\(\int \overrightarrow{\mathrm{B}_{\text {out }}} \cdot \overrightarrow{d l}=\mu_0 \Sigma \mathrm{I}\)
∫B_out dl cosθ = µ₀ΣI
यहाँ θ = 0°, cosθ = 1 तथा ΣI = I
∫ B dl = µ₀I
चूँकि ∫ dl = 2πr = वृत्तीय पथ की परिधि 
अतः B_out 2πr = µ₀I

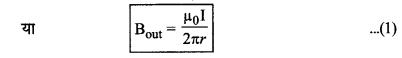
∴ B_out ∝ \(\frac{1}{r}\)
स्पष्ट है कि लम्बे बेलनाकार धारावाही चालक के कारण बाहरी बिन्दुओं पर चुम्बकीय क्षेत्र, दूरी के व्युत्क्रमानुपाती होता है।

(ii) जब बिन्दु बेलनाकार चालक के पृष्ठ पर हो अर्थात् r = R समीकरण (1) r = R रखने पर
B_s = \(\frac{\mu_0 I}{2 \pi R}\)

(iii) जब बिन्दु बेलनाकार धारावाही चालक के अन्दर स्थित हो (r < R)
चित्र 4.50 के अनुसार बेलनाकार चालक के अन्दर r त्रिज्या के वृत्ताकार बन्द पथ पर विचार करते हैं।
ऐम्पीयर के नियम से
\(\int \overrightarrow{\mathrm{B}} \cdot \overrightarrow{d l}=\mu_0 \Sigma \mathrm{I}\)
∫ B_in dl cosθ = µ₀ΣI
यहाँ θ= 0°, cosθ = 1

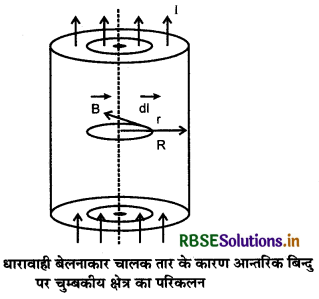
यहाँ ऐम्पियरियन लप में परिबद्ध धारा ΣI लूप के क्षेत्रफल πr² परिबद्ध धारा है। क्योंकि धारा एक समान वितरित है अतः r (r < R) त्रिज्या के वृत्ताकार पथ या परिबद्ध धारा इस वृत्त के क्षेत्रफल तथा चालक के काटक्षेत्र πR² का अनुपात होगी।
अर्थात्

स्पष्ट है कि बेलनाकार धारावाही चालक के अन्दर चुम्बकीय क्षेत्र, अक्ष से दूरी के समानुपाती होता है। यदि r = 0 तब B = 0
अर्थात् अक्ष पर चुम्बकीय क्षेत्र शून्य होता है तथा सतह पर अधिकतम होता है। इस प्रकरण में चुम्बकीय क्षेत्र का अक्ष से दूरी के साथ आलेख निम्न प्रकार होगा-

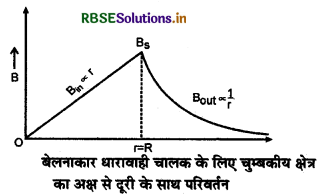
दीर्घ उत्तरीय प्रश्न

प्रश्न 1.
साइक्लोट्रॉन की क्रिया विधि लिखिए। दोनों डीज में त्वरित आवेशित कणों (आयनों) के पथ को प्रदर्शित करता साइक्लोट्रॉन का व्यवस्था आरेख बनाइये। साइक्लोट्रॉन के निम्न प्राचलों की व्युत्पत्ति कीजिए।
(i) साइक्लोट्रॉन की आवृत्ति
(ii) साइक्लोदॉन में आयनों की गतिज ऊर्जा
उत्तर:
साइक्लोट्रॉन आवृत्ति (Cyclotron frequency): साइक्लोट्रॉन की आवृत्ति यदि n है तो
n = \(\frac{1}{\mathrm{~T}}=\frac{q \mathrm{~B}}{2 \pi m}\)

और साइक्लोट्रॉन की कोणीय आवृत्ति (angular frequency)
ω = 2πn = 2π x \(\frac{q \mathrm{~B}}{2 \pi m}=\frac{q \mathrm{~B}}{m}\)

प्राप्त ऊर्जा (Energy gained): धनावेशित कण द्वारा प्राप्त ऊर्जा
E = \(\frac{1}{2}\)mv²
समी. (1) से, v = \(\frac{q \mathrm{~B} r}{m}\)
∴ E = \(\frac{1}{2} m \times \frac{q^2 B^2 r^2}{m^2}\)
या E = \(\frac{q^2 \mathrm{~B}^2 r^2}{2 m}\) ...................(6)
∴ धनावेशित कण द्वारा प्राप्त की गई अधिकतम ऊर्जा
E_max = \(\left(\frac{q^2 \mathrm{~B}^2}{2 m}\right) r_{\max }^2\)
अतः जब आवेशित कण अर्द्धचन्द्र की परिधि पर होगा (जहाँ त्रिज्या अधिकतम है) तो वह अधिकतम ऊर्जा ग्रहण कर चुका होगा।
यदि डीज के मध्य लगाया गया विभवान्तर (V) और दोनों डीज के मध्य माना N बार धनात्मक आवन अन्तराल (gap) को बाहर निकलने से पहले पार करता है।
∴ E_max = N(V_q)

प्रश्न 2.
ऐम्पियर का नियम लिखिए। एक अत्यधिक लम्बी परिनालिका के अक्ष पर चुम्बकीय क्षेत्र का व्यंजक प्राप्त कीजिए। आवश्यक चित्र बनाइये।
उत्तर:
ऐम्पियर का परिपथीय नियम (Ampere's Circuital Law) 
कथन: इस नियम के अनुसार, "किसी बन्द वक्र (closed curve) के परितः (around) चुम्बकीय क्षेत्र की तीव्रता का रेखीय समाकलन (linear integral) उस बन्द वक्र (closed curve) द्वारा घिरी आकृति (bound figure) में से गुजरने वाली कुल थारा कागुना होता है।"
गणितीय रूप में, Φ\(\overrightarrow{\mathrm{B}} \cdot d \vec{l}\) = µ₀ x [कुल धारा] 
या Φ\(\overrightarrow{\mathrm{B}} \cdot d \vec{l}\) = µ₀ΣI ..................(1)
जहाँ µ0 - निर्वात् की निरपेक्ष चुम्बकशीलता (premiti - vity of free space)
उपपत्ति: ऐम्पियर के नियम की उपपत्ति दी जा सकती है, जब किसी भी आकृति के बन्द पथ से होकर धारा गुजरती है। किसी भी स्वेच्छगृहीत (arbitrary) बन्द पथ के लिए ऐम्पियर के नियम को सिद्ध करने से पूर्व एक विशेष स्थिति में अर्थात् किसी धारावाही चालक के परितः बन्द वृत्तीय पथ के लिए इसे सिद्ध करते हैं।
(a) वृत्तीय पञ्च के लिए (For Circular Path): माना एक लम्बे तार XY में धारा I सिरे X से Y की ओर बह रही है। चालक में धारा बहने से इसके परितः चुम्बकीय क्षेत्र उत्पन्न होगा।

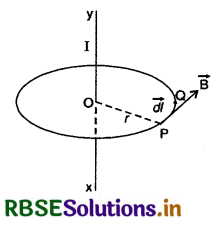
चालक को केन्द्र मानते हुए O केन्द्र वाले एवं r त्रिज्या वाले वृत्तीय पथ की कल्पना करते हैं। माना वृत्तीय पथ का एक अल्पांश \(\overrightarrow{\mathrm{PQ}}\) (= \(\overrightarrow{d l}\)) है और बिन्दु P पर चुम्बकीय क्षेत्र \(\overrightarrow{\mathrm{B}}\) है। दाहिने हाथ के नियमानुसार चुम्बकीय क्षेत्र की दिशा P पर वृत्तीय पथ की स्पर्श रेखा की दिशा (in the direction of tangent) में होगी। स्वाभाविक है कि \(\overrightarrow{\mathrm{B}}\) व अल्पांश \(\overrightarrow{\mathrm{dl}}\) एक ही दिशा में होंगे, अत: बन्द वृत्तीय पथ के लिए चुम्बकीय क्षेत्र का रेखीय समाकलन 
\(\oint_{\mathrm{B}}^{\vec{d} \cdot \vec{l}}=\oint \mathrm{B} d l \cos 0^{\circ}=\oint \mathrm{B} d l\) .................(2)
लम्बे एवं सीधै धारावाही चालक के कारण बिन्दु P पर उत्पन्न चुम्बकीय क्षेत्र,
B = \(\frac{\mu_0}{4 \pi} \frac{2 I}{r}\)
अत: समी. (2) से,

(b) किसी स्वेच्छाहीत पथ के लिए (ForArbitrary Path): एक लम्बे एवं सीधे धारावाही चालक XY के परितः किसी स्वेच्छाहीत बन्द पथ की कल्पना करते हैं। चालक में X से Y की ओर I धारा बह रही है। बन्द पथ को अनेक सूक्ष्म अल्पांशों \(\overrightarrow{\mathrm{AB}}\) (= \(\overrightarrow{d l_1}\) ), \(\overrightarrow{\mathrm{BC}}\) (= \(\overrightarrow{d l_2}\) ), \(\overrightarrow{\mathrm{CD}}\) (= \(\overrightarrow{d l_3}\) ),......... में बाँट लेते हैं। माना इन अल्पांशों से बिन्दु O, जहाँ से धारावाही चालक गुजरता है, पर अन्तरित कोण क्रमशः dθ₁, dθ₂, dθ₃, ....... हैं।
∴ dθ₁ + dθ₂ + dθ₃ + ............. = 2π .............(4)

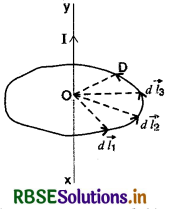
माना चाप अल्पांशों AB, BC, CD...... की त्रिज्याएँ क्रमशः r₁, r₂, r₃ ...... है। अत:
\(d \theta_1=\frac{d l_1}{r_1}, d \theta_2=\frac{d l_2}{r_2}, d \theta_3=\frac{d l_3}{r_3}, \ldots \ldots\) ..................(5)
यदि \(d \vec{l}_1 d \vec{l}_2, d \vec{l}_3, \ldots\) के अनुदिश चुम्बकीय क्षेत्रों की तीव्रताएँ क्रमश: \(\overrightarrow{\mathrm{B}_1}, \overrightarrow{\mathrm{B}_2}, \overrightarrow{\mathrm{B}_3}, \ldots \ldots\) हैं तो स्वेच्छग्रहीत बन्द पथ के लिए चुम्बकीय क्षेत्र \(\overrightarrow{\mathrm{B}}\) का रेखीय समाकलन

प्रश्न 3.
ऐम्पियर के परिपथीय नियम का उपयोग करते हुए अनन्त लम्बाई के धारावाही तार के कारण उत्पन चुम्बकीय क्षेत्र का परिमाण ज्ञात कीजिए।
उत्तर:
ऐम्पियर का परिपथीय नियम (Ampere's Circuital Law) 
कथन: इस नियम के अनुसार, "किसी बन्द वक्र (closed curve) के परितः (around) चुम्बकीय क्षेत्र की तीव्रता का रेखीय समाकलन (linear integral) उस बन्द वक्र (closed curve) द्वारा घिरी आकृति (bound figure) में से गुजरने वाली कुल थारा कागुना होता है।"
गणितीय रूप में, Φ\(\overrightarrow{\mathrm{B}} \cdot d \vec{l}\) = µ₀ x [कुल धारा] 
या Φ\(\overrightarrow{\mathrm{B}} \cdot d \vec{l}\) = µ₀ΣI ..................(1)
जहाँ µ₀ - निर्वात् की निरपेक्ष चुम्बकशीलता (premiti - vity of free space)
उपपत्ति: ऐम्पियर के नियम की उपपत्ति दी जा सकती है, जब किसी भी आकृति के बन्द पथ से होकर धारा गुजरती है। किसी भी स्वेच्छगृहीत (arbitrary) बन्द पथ के लिए ऐम्पियर के नियम को सिद्ध करने से पूर्व एक विशेष स्थिति में अर्थात् किसी धारावाही चालक के परितः बन्द वृत्तीय पथ के लिए इसे सिद्ध करते हैं।
(a) वृत्तीय पञ्च के लिए (For Circular Path): माना एक लम्बे तार XY में धारा I सिरे X से Y की ओर बह रही है। चालक में धारा बहने से इसके परितः चुम्बकीय क्षेत्र उत्पन्न होगा।

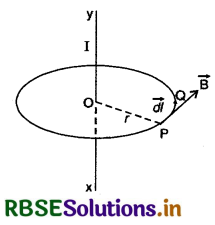
चालक को केन्द्र मानते हुए O केन्द्र वाले एवं r त्रिज्या वाले वृत्तीय पथ की कल्पना करते हैं। माना वृत्तीय पथ का एक अल्पांश \(\overrightarrow{\mathrm{PQ}}\) (= \(\overrightarrow{d l}\)) है और बिन्दु P पर चुम्बकीय क्षेत्र \(\overrightarrow{\mathrm{B}}\) है। दाहिने हाथ के नियमानुसार चुम्बकीय क्षेत्र की दिशा P पर वृत्तीय पथ की स्पर्श रेखा की दिशा (in the direction of tangent) में होगी। स्वाभाविक है कि \(\overrightarrow{\mathrm{B}}\) व अल्पांश \(\overrightarrow{\mathrm{dl}}\) एक ही दिशा में होंगे, अत: बन्द वृत्तीय पथ के लिए चुम्बकीय क्षेत्र का रेखीय समाकलन 
\(\oint_{\mathrm{B}}^{\vec{d} \cdot \vec{l}}=\oint \mathrm{B} d l \cos 0^{\circ}=\oint \mathrm{B} d l\) .................(2)
लम्बे एवं सीधै धारावाही चालक के कारण बिन्दु P पर उत्पन्न चुम्बकीय क्षेत्र,
B = \(\frac{\mu_0}{4 \pi} \frac{2 I}{r}\)
अत: समी. (2) से,

(b) किसी स्वेच्छाहीत पथ के लिए (ForArbitrary Path): एक लम्बे एवं सीधे धारावाही चालक XY के परितः किसी स्वेच्छाहीत बन्द पथ की कल्पना करते हैं। चालक में X से Y की ओर I धारा बह रही है। बन्द पथ को अनेक सूक्ष्म अल्पांशों \(\overrightarrow{\mathrm{AB}}\) (= \(\overrightarrow{d l_1}\) ), \(\overrightarrow{\mathrm{BC}}\) (= \(\overrightarrow{d l_2}\) ), \(\overrightarrow{\mathrm{CD}}\) (= \(\overrightarrow{d l_3} \)),......... में बाँट लेते हैं। माना इन अल्पांशों से बिन्दु O, जहाँ से धारावाही चालक गुजरता है, पर अन्तरित कोण क्रमशः dθ₁, dθ₂, dθ₃, ....... हैं।
∴ dθ₁ + dθ₂ + dθ₃ + ............. = 2π .............(4)

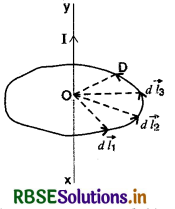
माना चाप अल्पांशों AB, BC, CD...... की त्रिज्याएँ क्रमशः r₁, r₂, r₃ ...... है। अत:
\(d \theta_1=\frac{d l_1}{r_1}, d \theta_2=\frac{d l_2}{r_2}, d \theta_3=\frac{d l_3}{r_3}, \ldots \ldots\) ..................(5)
यदि \(d \vec{l}_1 d \vec{l}_2, d \vec{l}_3, \ldots\) के अनुदिश चुम्बकीय क्षेत्रों की तीव्रताएँ क्रमश: \(\overrightarrow{\mathrm{B}_1}, \overrightarrow{\mathrm{B}_2}, \overrightarrow{\mathrm{B}_3}, \ldots \ldots\) हैं तो स्वेच्छग्रहीत बन्द पथ के लिए चुम्बकीय क्षेत्र \(\overrightarrow{\mathrm{B}}\) का रेखीय समाकलन

प्रश्न 4.
हेल्महोल्टज कुण्डलियाँ किसे कहते है? सिद्ध कीजिए कि हेल्महोल्टज कुण्डली में प्राप्त एक समान चुम्बकीय क्षेत्र का मान प्रत्येक कुण्डली द्वारा इसके केन्द्र पर उत्पन्न चुम्बकीय क्षेत्र का 1.4, 32 गुना होता है। आवश्यक आरेख भी बनाए।
उत्तर:
हेल्महोल्ट्ज कुण्डलियाँ (Helmholtz Coils):
दो समाक्षीय (Co - axial) तथा समान वृत्ताकार कुण्डलियाँ जिनमें समान परिमाण की विद्युत धारा समान दिशा में प्रवाहित हो रही हों तथा जिनके केन्द्रों के मध्य दूरी, उनकी त्रिज्या के समान हो, तो इस प्रकार के व्यवस्थित कुण्डलियों के युग्म को हेल्महोल्ट्ज कुण्डलियाँ कहते हैं।
हेल्महोल्ट्ज कुण्डलियों का उपयोग एक समान चुम्बकीय क्षेत्र उत्पन्न करने हेतु एक प्रायोगिक युक्ति है। क्योंकि इन कुण्डलियों के मध्य क्षेत्र में चुम्बकीय क्षेत्र का मान लगभग एक समान रहता है।

हेल्महोल्ट्ज कुण्डली एक उभयनिष्ठ फ्रेम पर इस प्रकार व्यवस्थित होती है कि इसकी दोनों कुण्डलियों के तल परस्पर समान्तर रहें। इसके अतिरिक्त दोनों कुण्डलियाँ श्रेणीक्रम में जुड़ी होती हैं जिससे दोनों में समान धारा एक ही दिशा में प्रवाहित हो सके। इसकी बनावट चित्र 4.36 में दर्शायी है। 


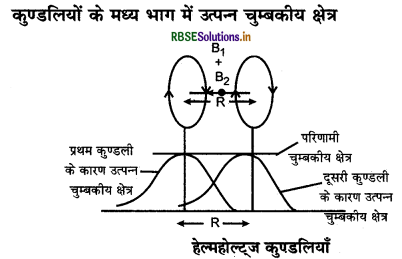
दोनों कुण्डलियों के मध्य भाग में चुम्बकीय क्षेत्र का परिणाम मान अलग - अलग दोनी कुण्डलियों द्वारा उत्पन्न चुम्बकीय क्षेत्रों का सदिश योग होता है। अत: दोनों कुण्डलियों के नति परिवर्तन बिन्दु के आस-पास भाग में एक समान चुम्बकीय क्षेत्र उत्पन्न हो जाता है।
यदि कुण्डलियों के मध्य भाग में एक कुण्डली के कारण उत्पन्न क्षेत्र B₁ हो तो
B₁ = \(\frac{4 \mu_0 \mathrm{NI}}{5 \sqrt{5} \mathrm{R}}\) (समी. 4 से) 
इसी प्रकार दूसरी कुण्डली द्वारा मध्य भाग में उत्पन्न चुम्बकीय क्षेत्र B₂ हो तो
B₂ = \(\frac{4 \mu_0 \mathrm{NI}}{5 \sqrt{5} \mathrm{R}}\)
तथा परिणामी चुम्बकीय क्षेत्र
B = B₁ + B₂ 
= 2B₁ (∵ \(\overrightarrow{\mathrm{B}}_1\) तथा \(\overrightarrow{\mathrm{B}}\) एक ही दिशा में है।)
∴ B = \(\frac{2 \times 4 \mu_0 \mathrm{NI}}{5 \sqrt{5} \mathrm{R}}\)
B = \(\frac{8}{5 \sqrt{5}} \frac{\mu_0 \mathrm{NI}}{\mathrm{R}}=0.716 \frac{\mu_0 \mathrm{NI}}{\mathrm{R}}\)
B = 1.432 \(\frac{\mu_0 \mathrm{NI}}{2 \mathrm{R}}\) .......................(7)

अर्थात् हेल्पहोल्ट्ज कुण्डली से प्राप्त एक समान चुम्बकीय क्षेत्र का मान प्रत्येक कुण्डली द्वारा इसके केन्द्र पर अपन चुम्बकीय क्षेत्र (अधिकतम चुम्बकीय क्षेत्र) का 1.432 गुना होता है।

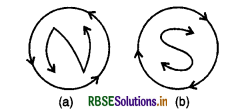
फलक पर बारा दक्षिणावर्त (clockwise) दिशा में बहती हुई प्रतीत होती है, वह फलक दक्षिणी ध्रुव की भाँति व्यवहार करता है।

प्रश्न 5.
बायो सेवर्ट का नियम का उपयोग करके R त्रिज्या के धारावाही पाश के अक्ष पर चुम्बकीय क्षेत्र के लिए व्यंजक व्युत्पन्न कीजिए। किसी वृत्ताकार तार, जिससे धारा I प्रवाहित हो रही है, के कारण क्षेत्र रेखाएँ खींचिए।
उत्तर:
वृत्ताकार धारावाही कुण्डली के अक्ष पर उत्पन्न चुम्बकीय क्षेत्र (Magnetic Field on the axis of a circular current loop) 
माना R त्रिज्या की एक वृत्ताकार कुण्डली में I धारा प्रवाहित हो रही है। कुण्डली में तार के N फेरे हैं। कुण्डली के केन्द्र O से x दूरी पर अक्षीय स्थिति (artial position) में एक बिन्दु P पर हमें चुम्बकीय क्षेत्र ज्ञात करना है। P पर कुण्डली द्वारा अन्तरित अर्द्ध - शीर्ष कोण (semivertical angle) θ है। पहले हम एक लूप पर विचार करते हैं। माना लूप के व्यास NM के बिन्दुओं N व M पर समान लम्बाई dl के दो अल्पांश (elements) हैं। इन अल्पांशों की बिन्दु P से दूरी यदि r हो तो N पर स्थित अल्पांश के कारण P पर उत्पन्न चुम्बकीय क्षेत्र

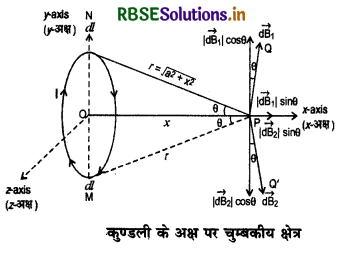
dB₁ = \(\frac{\mu_0}{4 \pi} \frac{\mathrm{I} d l \sin 90^{\circ}}{r^2}\)
= \(\frac{\mu_0}{4 \pi} \frac{\mathrm{I} d l}{r^2}\)
इसी प्रकार M पर स्थित समान लम्बाई के अल्पांश के कारण P पर उत्पन्न चुम्बकीय क्षेत्र
dB₂ = \(\frac{\mu_0}{4 \pi} \frac{\mathrm{I} d l \sin 90^{\circ}}{r^2}\)
= \(\frac{\mu_0}{4 \pi} \frac{\mathrm{I} d l}{r^2}\)
चित्र 4.34 से स्पष्ट है कि केन्द्र O के दोनों ओर सममिति (symmetry) में लिए गए समान लम्बाई (dl) के दो अल्पांशों द्वारा बिन्दु P पर समान परिमाण के चुम्बकीय क्षेत्र dB₁ व dB₂ उत्पन्न होते हैं। इन दोनों के निरक्षीय घटक dB₁ cosθ एवं dB₂ cosθ परिमाण में समान एवं दिशा में विपरीत होने के कारण एक - दूसरे को निष्प्रभावित कर देते हैं और अक्षीय घटक dB₁ sinθ एवं dB₂ sinθ जुड़कर चुम्बकीय क्षेत्र प्रदान करते हैं। इस प्रकार चुम्बकीय क्षेत्र केवल अक्षीय घटक dB sinθ के कारण ही मिलता है।
∴ बिन्दु P पर पूरे लूप के कारण उत्पन्न चुम्बकीय क्षेत्र
B = \(\int_0^{2 \pi R}\) dB sinθ
B = \(\int_0^{2 \pi \mathrm{R}} \frac{\mu_0}{4 \pi} \frac{\mathrm{I} d l}{r^2} \sin \theta\)
चित्र 4.34 से स्पष्ट है कि

सदिश रूप में

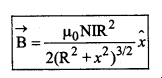
क्योंकि चित्र में दर्शाई धारा की दिशा के लिए \(\vec{B}\) की दिशा +\(\hat{x}\) दिशा में होगी। यदि धारा विपरीत दिशा में प्रवाहित हो तो \(\vec{B}\) की दिशा -\(\hat{x}\) दिशा में होगी।
विशेष स्थितियाँ-
(i) कुण्डली के केन्द्र पर चुम्बकीय क्षेत्र - केन्द्र पर चुम्बकीय क्षेत्र के लिए समी. (1) में x = 0 रखने पर

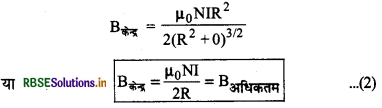
इस स्थिति में चुम्बकीय क्षेत्र की तीव्रता अधिकतम (Bmax) होती है।

(ii) यदि बिन्दु, कुण्डली की त्रिज्या R की तुलना में अत्यधिक दूरी पर स्थित हो, अर्थात् x >> R हो तो समीकरण (1) में R₂ को नगण्य मानते हुए
B = \(\frac{\mu_0 \text { NIR }^2}{2\left(0+x^2\right)^{3 / 2}}\)

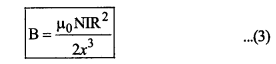
(iii) यदि अभीष्ट बिन्दु P, कुण्डली की अर्द्ध त्रिज्या R/2 के समान दूरी पर है (अर्थात् x = R/2) हैं; तो

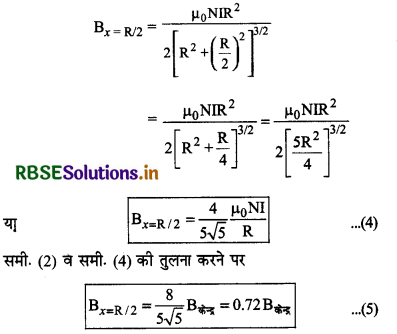
वृत्ताकार कुण्डली के अक्ष पर दूरी के साथ चुम्बकीय क्षेत्र में परिवर्तन: धारावाही वृत्ताकार कुण्डली के अक्ष पर चुम्बकीय क्षेत्र B का दूरी x के साथ परिवर्तन को चित्र 4.35 में दर्शाया गया है। चित्र से

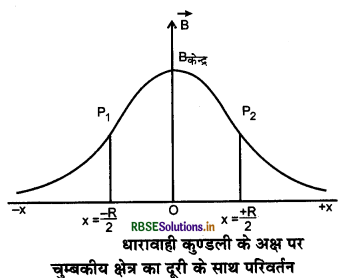
स्पष्ट है कि कुण्डली के केन्द्र पर चुम्बकीय क्षेत्र का मान अधिकतम होता है तथा अक्ष से दूरी बढ़ने के साथ चुम्बकीय क्षेत्र का मान घटता है। x = ∝ पर B का मान शून्य होता है। x = \(\pm \frac{\mathrm{R}}{2} \) पर आलेख की वक्रता शून्य होती है। इन बिन्दुओं को वक्र में P₁ व P₂ दर्शाया है। इन बिन्दुओं पर वक्रता में परिवर्तन होने के कारण इन बिन्दुओं को नति परिवर्तन बिन्दु (Point of Inflection) कहते हैं।
नति परिवर्तन बिन्दुओं के लिए-
(i) x < \(\frac{\mathrm{R}}{2} \) पर वक्रता धनात्मक होती है एवं x > \(\frac{\mathrm{R}}{2}\) पर वक्रता ऋणात्मक तथा x = \(\frac{\mathrm{R}}{2}\) पर वक्रता शून्य होती है।
(ii) \(\frac{d \mathrm{~B}}{d x}\) = नियत रहता है साथ \(\frac{d^2 \mathrm{~B}}{d^2 x}\) = 0 होता है।
(iii) नति परिवर्तन बिन्दुओं के मध्य दूरी कुण्डली की त्रिज्या के बराबर होती है।

प्रश्न 6.
किसी गैल्वेनोमीटर की आयताकार धारावाही कुण्डली पर कार्यरत बल - आघूर्ण के लिए व्यंजक व्युत्पन्न कीजिए। चुम्बकीय क्षेत्र को अरीह क्यों बनाया जाता है?
उत्तर:
निलम्बन कुण्डली धारामापी (Suspended Coil Galvanometer)
बनावट (Construction): इसमें एक अचुम्बकीय धातु ऐलुमिनियम के फ्रेम [non - magnetic metallic aluminium frame] पर पतले विद्युत्रोधी तौबे के तार के अनेक फेरों वाली आयताकार कुण्डली लिपटी (wound) रहती है। यह कुण्डली एक पतले फॉस्फर ब्रांज (Phosphor Bronze) के तार से, एक प्रबल स्थायी चुम्बक (strong magnet) के धुवखण्डों (N व S) के बीच लटकी रहती है। कुण्डली के बीच एक नर्म लोहे (soft iron) की बेलनाकार क्रोड (cylindrical core) रखी जाती है।

कुण्डली का एक सिरा निलम्बन (suspension) से बैंधा रहता है जो धारामापी के एक टर्मिनल (T₁) का कार्य करता है। कुण्डली का दूसरा सिरा एक ढीली कुण्डलित स्प्रिंग (loosely coiled spring) से जुड़ा रहता है, जो धारामापी के दूसरे टर्मिनल (T₂) का कार्य करता है। निलम्बन तार (suspension wire) का ऊपरी सिरा मरोड़ शीर्ष (torsion

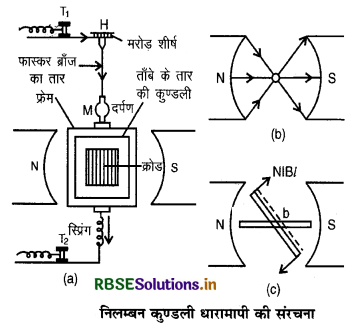
head) H से जुड़ा रहता है जिसमें कुण्डली को शून्य स्थिति (zero position) में लाने के लिए घुमाया जा सकता है। फॉस्फर ब्रांज के साथ एक समतल दर्पण M लगा रहता है जिसकी सहायता से लैम्म व स्केल व्यवस्था (lamp and scale arrangement) द्वारा कुण्डली का विक्षेप पढ़ा जा सकता है। यन्त्र के आधार (base) पर क्षैतिजकारी पेंच (horizontal screws) भी लगे रहते हैं। स्थायी चुम्बक के ध्रुव खण्ड (pole pieces) बेलनाकार रखे जाते हैं, ताकि कुण्डली की प्रत्येक स्थिति में चुम्बकीय क्षेत्र त्रिज्यीय (radial) रहे। ध्रुव खण्ड अवतल होते हैं और घोड़े की नाल चुम्बक से बने होते हैं।
सिद्धान्त (Principle): यदि धारावाही कुण्डली को समरूप चुम्बकीय क्षेत्र (uniform magnetic field) में रखा जाये तो उस पर लगने वाले बलयुग्म का आघूर्ण,
τ = nIAB sinθ
जहाँ n = कुण्डली में फेरों की संख्या (number of tums in coil); I = कुण्डली में प्रवाहित धारा; A = कुण्डली के तल का क्षेत्रफल; B = चुम्बकीय क्षेत्र की तीव्रता (intensity of magnetic field); θ = कुण्डली के तल पर खींचे गये अभिलम्ब एवं क्षेत्र रेखा के मध्य कोण (angle between normal drawn on plane of coil and field line)
यदि चुम्बकीय क्षेत्र त्रिज्य है तो।
θ = 90°; ∴ sinθ = 1
अत: τ = nIAB
इस बलयुग्म के प्रभाव में कुण्डली घूमने लगेगी, फलस्वरूप फॉस्फर ब्रांज के तार में ऐंठन (twist) लगने लगेगी। यदि यह ऐंठन Φ हो तो ऐंठन बलयुग्म का आघूर्ण
τ' = CΦ
जहाँ, C = एकांक ऐंठन के लिए बलयुग्म का आपूर्ण 
∵ सन्तुलन में τ = τ'
∴ nIAB = CΦ
या I = \(\left(\frac{\mathrm{C}}{n \mathrm{AB}}\right) \phi\) .........................(1)
या I = kΦ, जहाँ k = \(\frac{\mathrm{C}}{n \mathrm{AB}}\)
k को धारामापी का परिवर्तन गुणांक (torsion constant or reduction factor) कहते हैं।
∴ I ∝ Φ या Φ ∝ I
तार में उत्पन्न ऐंठन (अर्थात् धारामापी कुण्डली में उत्पन्न विक्षेप) प्रवाहित धारा के अनुक्रमानुपाती होती है। यही धारामापी का सिद्धान्त है।
धारा परिवर्तन गुणांक (Current Reduction Factor)-
समी. (1) से, I = \(\frac{\mathrm{C}}{n \mathrm{AB}} \phi\)
या I = kΦ .........................(2)
जिसमें k = \(\frac{\mathrm{C}}{n \mathrm{AB}}\) को ही धारामापी का धारा परिवर्तन गुणांक कहते हैं।
∵ धारा सुग्राहिता (Current Sensitivity): धारामापी की धारा सुग्राहिता कुण्डली में प्रति एकांक धारा के लिए उत्पन्न विक्षेप (deflection) से नापी जाती है अर्थात्
धारा सुग्राहिता S_i = \(\frac{\phi}{I}\)
= \(\frac{n \mathrm{AB}}{\mathrm{C}}\) .......................(3)
वोल्टेज सुग्राहिता (Voltage Sensitivity): यदि कुण्डली के सिरों के मध्य वोल्टेज V हो तो राशि \(\frac{\phi}{V}\) को वोल्टेज सुग्राहिता कहते हैं। यदि कुण्डली का प्रतिरोध R हो तो
V = RI
∴ वोल्टेज सुग्राहिता S_v = \(\frac{\phi}{\mathrm{V}}=\frac{\phi}{\mathrm{IR}}=\frac{n \mathrm{AB}}{\mathrm{CR}}\) .....................(4)
धारा सुग्राहिता एवं वोल्टेज सुनाहिता में सम्बन्ध (Relation between Current Sensitivity and Voltage Sensitivity)-
समी. (3) से, \(\frac{n \mathrm{AB}}{\mathrm{C}}=\frac{\phi}{\mathrm{I}},\)
यह मान समी. (4) में रखने पर,
वोल्टेज सुग्राहिता = \(\frac{\phi / I}{R}\)

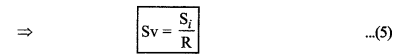
धारामापी की धारा सुग्राहिता को प्रभावित करने वाले कारक:
समी. (3) से स्पष्ट है कि धारामापी की धारा सुग्राहिता को निम्न प्रकार से बढ़ाया जा सकता है-

1. फेरों की संख्या (n) बढ़ाकर
2. कुण्डली का क्षेत्रफल (A) बढ़ाकर
3. चुम्बकीय क्षेत्र की प्रबलता (B) बढ़ाकर
4. मरोड़ी दृढ़ता (torsion rigidity) (C) घटाकर। 

प्रश्न 7.
टोरॉइड की संरचना कैसे होती है? किसी टोरॉइड के अन्दर चुम्बकीय क्षेत्र के लिए व्यंजक प्राप्त कीजिए, यदि टोराइड में r औसत त्रिज्या के N फेरे हैं और उनमें I धारा प्रवाहित हो रही है। दर्शाइए कि टोराइड के भीतर खुले क्षेत्र में तथा टोराइड के बाहर चुम्बकीय क्षेत्र शून्य होता है।
उत्तर:
धारावाही टोरॉइड के कारण चुम्बकीय क्षेत्र (Magnetie Field due to a Toroidal Solenoid)
एक लम्बी परिनालिका को मोड़कर जब वृत्ताकार रूप दे दिया जाता है तो उसे टोरॉइड कहते हैं। किसी आदर्श टोरॉइड जिससे फेरे साकर लिपटे होते हैं, के लिए टोरॉइड के भीतर चुम्बकीय क्षेत्र B नियत रहता है। आदर्श टोरॉइड में कुण्डलियाँ (coils) पूर्णत: वृत्ताकार होती हैं। वास्तव में टोरॉइड के फेरे सर्पिलाकार (helical) कुण्डली बनाते हैं तथा इसके बाहर सदैव ही एक क्षीण चुम्बकीय क्षेत्र पाया जाता है।

माना टोरॉइड की प्रति एकांक लम्बाई में n फेरे हैं तथा इसमें प्रवाहित धारा I है। धारा बहने के कारण टोरॉइड के फेरों के भीतर चुम्बकीय क्षेत्र उत्पन्न होता है। टोरोइड के भीतर चुम्बकीय बल रेखाएं संकेन्द्री वृत्तों (concentric circles) के रूप में होती हैं। सममिति (symmetry) से पथ के प्रत्येक बिन्दु पर चुम्बकीय क्षेत्र का मान समान रहता है तथा यह चुम्बकीय क्षेत्र प्रत्येक बिन्दु पर स्पर्श रेखा के अनुदिश है।

(i) टोरॉइड की कोड (core) के भीतर चुम्बकीय क्षेत्र: माना r त्रिज्या का एक वृत्ताकार पथ है जो टोरॉइड के फेरों के बीच के क्षेत्र में स्थित है। इस वृत्तीय पथ पर ऐम्पीयर के परिपथीय नियम से, 

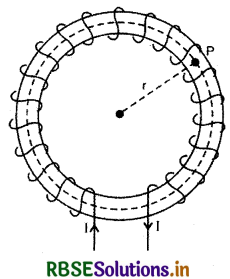
\(\oint \overrightarrow{\mathrm{B}} \cdot \overrightarrow{d l}\) = µ₀ x (बन्द परिपथ में बहने वाली कुल धारा) .....................(10)
बन्द परिपथ में बहने वाली कुल धारा
= टोरॉइड में फेरों की संख्या x प्रवाहित धारा
= n x 2πr x I
= 2πrnl
∴ समी. (8) से,
\(\oint \overrightarrow{\mathrm{B}} \cdot \overrightarrow{d l}\) = µ₀ x 2πrnl
∵ \(\overrightarrow{\mathrm{B}} \text { व } \overrightarrow{d l}\) एक ही दिशा में हैं, अत:

(ii) टोरॉइंड द्वारा घेरे गये रिक्त स्थान में: माना r₁ त्रिज्या का एक वृत्तीय पथ है जो टोरॉइड में प्रवाहित धारा से घिरे रिक्त स्थान में है तथा टोराइड के संकेन्द्रीय है। जब r₁ का मान r से छेटा है तो धारा शून्य होगी अर्थात्
I = 0
∴ ऐम्पीयर के परिपचीय नियम से,
\(\oint \overrightarrow{\mathrm{B}} \cdot \overrightarrow{d l}\) = µ₀ x (घिरे पथ द्वारा प्रवाहित धारा)

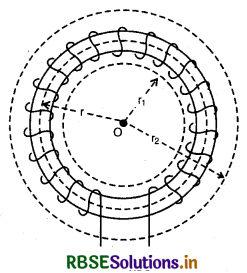
या ΦB. dl. cos0° = µ₀ x 0 = 0
या BΦdl = 0

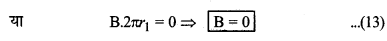
(iii) टोरॉइड के बाहर रिक्त स्थान में: माना r₂ त्रिज्या का एक वृत्तीय पथ है जो टोरॉइड द्वारा धेरे गये क्षेत्र के बाहर रिक्त स्थान में है। इस बन्द वृत्त से भी परिबद्ध (bound) नेट धारा शून्य होगी क्योंकि टोरॉइड का प्रत्येक फेरा r₂ त्रिज्या के वृत्त से परिबद्ध क्षेत्र से होकर दो बार गुजरता है, जबकि विद्युत धारा का मान समान परन्तु दिशाएँ विपरीत होती हैं। अत: वृत्त द्वारा परिबद्ध नेट धारा I = 0 
∴ ऐम्पीयर के परिपथीय नियम से,

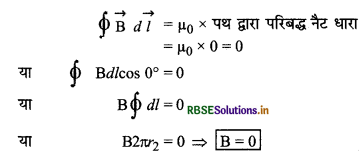
इस प्रकार टोरॉइड के कारण चुम्बकीय क्षेत्र

अर्थात् परिनालिका के सिरे पर उत्पन्न चुम्बकीय क्षेत्र परिनालिका के बीच के मध्य - बिन्दु पर उपस्थित चुम्बकीय क्षेत्र का आधा होता है।
विशेष: जब टोरॉइड की बाहरी एवं आन्तरिक त्रिज्याएँ दी गई हों तो प्रश्न हल करने के लिए उनका माध्य (mean) ले लेते हैं और सूत्र में r के स्थान पर इसी माध्य का प्रयोग करते हैं।
r = \(\frac{r_1+r_2}{2}\)

प्रश्न 8.
बायो सेवर्ट के नियम का कथन कीजिए। इसकी सहायता से किसी सीधे तथा परिमित लम्बाई के धारावाही चालक तार के कारण उत्पन्न चुम्बकीय क्षेत्र का व्यंजक प्राप्त कीजिए। दर्शाइए कि अनन्त लम्बाई के धारावाही तार के लम्बवत दूरी d पर चुम्बकीय क्षेत्र B = \(\frac{\mu_0 I}{2 \pi d}\) होता है।
उत्तर:
कुण्डली के केन्द्र पर चुम्बकीय क्षेत्र (Magnetic Field at the Centre of the Coil)
जब किसी वृत्ताकार धारावाही कुण्डली में धारा प्रवाहित की जाती है तो कुण्डली के चारों ओर चुम्बकीय क्षेत्र उत्पन्न हो जाता है। "वृत्ताकार कुण्डली के भीतर चुम्बकीय क्षेत्र लगभग समान होता है।" हमें कुण्डली के केन्द्र पर चुम्बकीय क्षेत्र का मान ज्ञात करना है। यदि कुण्डली कागज के तल में है तो उत्पन्न चुम्बकीय क्षेत्र की दिशा दाहिने हाथ के नियम से ज्ञात की जा सकती है। यदि धारा दक्षिणावर्त (Clockwise) दिशा में प्रवाहित हो तो चुम्बकीय क्षेत्र की दिशा कागज के तल के लम्बवत् नीचे की ओर होगी। यदि धारा वामावर्त (anticlockwise) दिशा में प्रवाहित हो तो चुम्बकीय क्षेत्र कागज के तल के लम्बवत् ऊपर की ओर होगी।

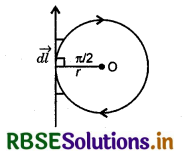
माना वृत्ताकार धारावाही कुण्डली का केन्द्र O है जिसकी त्रिज्या r है। इसमें I धारा दाक्षिणावर्त प्रवाहित है। इस कुण्डली में वृत्तीय लूपों के N फेरे हैं। चुम्बकीय क्षेत्र ज्ञात करने के लिए पहले एक वृत्ताकार लूप पर विचार करते है। इस लूप की परिधि को अनेक अल्पांशों में विभाजित मानते हैं। चित्र 4.3 1 में दर्शाए कुण्डली के अल्पांश dl के कारण केन्द्र O पर उत्पन्न चुम्बकीय क्षेत्र
dB = \(\frac{\mu_0}{4 \pi} \frac{\mathrm{I} d l \sin \theta}{r^2}\)
अल्पांश के मध्य बिन्दु से खींची गई स्पर्श रेखा त्रिज्या के साथ 90° का कोणं बनाती है, अतः
dB = \(\frac{\mu_0}{4 \pi} \frac{\mathrm{I} d l \sin 90^{\circ}}{r^2}\)
= \(\frac{\mu_0 \mathrm{I} d l}{4 \pi r^2}\)
∴ पूरे लूप के कारण O पर उत्पन्न चुम्बकीय क्षेत्र,
B = \(\int_0^{2 \pi r} d \mathrm{~B}\)

चुम्बकीय क्षेत्र की त्रिज्या पर निर्भरता-
समी. (1) से स्पष्ट है कि धारावाही वृत्ताकार कुण्डली के केन्द्र पर उत्पन्न चुम्बकीय क्षेत्र कुण्डली की त्रिज्या के व्युत्क्रमानुपाती होता है। अत: B का R के साथ आलेख अतिपरवलय होता है। B का 1/R के साथ आलेख सीधी रेखा प्राप्त होता है।

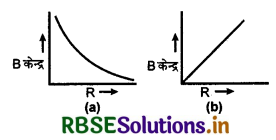
विशेष स्थिति-
किसी चाप (arc) के कारण केन्द्र पर उत्पन्नचुम्बकीय क्षेत्र: माना r त्रिज्या के धारावाही चाप AB के कारण उसके केन्द्र O पर उत्पन्न चुम्बकीय क्षेत्र ज्ञात करना है। बायो - सावर्ट के नियम से वृत्ताकार चाप के अल्पांश ab के कारण केन्द्र पर उत्पन्न चुम्बकीय क्षेत्र,

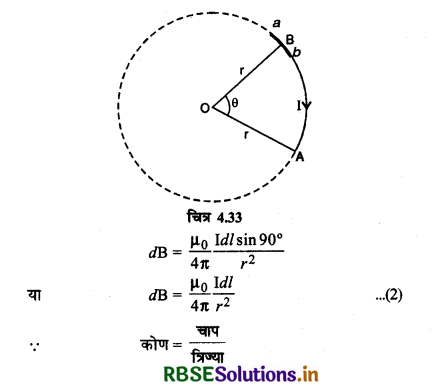
∴ चाप AB द्वारा केन्द्र पर अन्तरित कोण
θ = \(\frac{\mathrm{AB}}{r}\) ⇒ AB = rθ
अतः पूरे चाप AB के कारण O पर उत्पन्न चुम्बकीय क्षेत्र

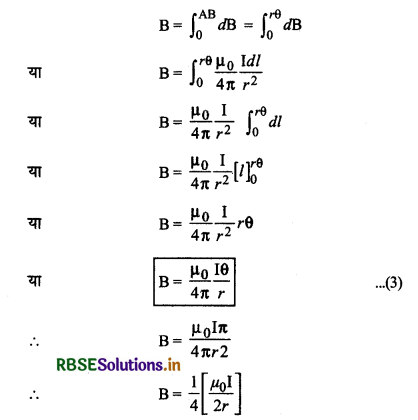
आंकिक प्रश्न

प्रश्न 1.
क्षैतिज तल में रखे एक लम्बे तथा सीधे तार में 50 A की धारा दक्षिण से उत्तर दिशा में प्रवाहित हो रही है। तार के पूर्व में 2.5 m दूरी पर स्थित किसी बिन्दु पर चुम्बकीय क्षेत्र का परिमाण एवं उसकी दिशा ज्ञात कीजिए।
उत्तर:

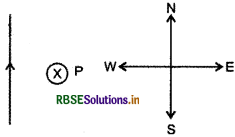
तार में प्रवाहित धारा I = 50 A
तार से बिन्दु P की दूरी d = 2.5 m
अत: P पर चुम्बकीय क्षेत्र की तीव्रता
B = \(\frac{\mu_0 \mathrm{I}}{2 \pi d}\)
= \(\frac{2 \times 10^{-7} \times 50}{2.5}\)
B = 4 x 10^-6 T

प्रश्न 2.
आरेख में दर्शाए अनुसार दो लम्बे सीधे, समान्तर तार A और B में, जो एक दूसरे से d दूरी पर स्थित हैं, से समान दिशा में समान धारा I प्रवाहित हो रही है।

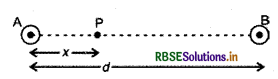
(a) इन तारों के बीच किसी एक तार से दूरी x पर स्थित किसी बिन्दु पर चुम्बकीय क्षेत्र ज्ञात कीजिए।
(b) दूरी के साथ 0 < x < d के लिए चुम्बकीय क्षेत्र में विचरण दर्शाने के लिए ग्राफ खींचिए।
उत्तर:
(a)

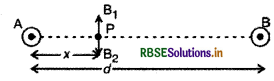
तार A के कारण बिन्दु P पर चुम्बकीय क्षेत्र
B₁ = \(\frac{\mu_0 I}{2 \pi x}\) ऊपर की ओर
तार B के कारण बिन्दु P पर चुम्बकीय क्षेत्र
B₂ = \(\frac{\mu_0 I}{2 \pi(d-x)}\) नीचे की ओर

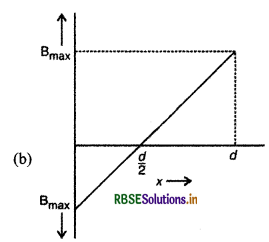
प्रश्न 3.
5 cm त्रिज्या एवं 100 फेरों वाली वृत्ताकार कुण्डली के केन्द्र पर उत्पन्न चुम्बकीय क्षेत्र 2 x 10^-5 T है। कुण्डली में प्रवाहित धारा ज्ञात कीजिए।
उत्तर:
दिया है r = 5cm = 5 x 10^-2 m
N = 100
B = 2 x 10^-5 T
∴ कुण्डली के केन्द्र पर उत्पन्न चुम्बकीय क्षेत्र
B = \(\frac{\mu_0}{4 \pi} \frac{2 \pi \mathrm{NI}}{r}=\frac{\mu_0 \mathrm{NI}}{2 r}\)
2 x 10^-5 = \(\frac{10^{-7} \times 10^{-2} \times I}{5 \times 10^{-2}}\)
I = 2 x 10^-2 A

प्रश्न 4.
दो सर्वसम पाश P और Q एजिनमें दोनों की त्रिज्या 5 cm हैं, चित्र में दर्शाए अनुसार लम्बवत तलों में इस प्रकार रखे है कि इनके केन्द्र उभयनिष्ठ हैं। यदि इनमें से क्रमशः 3 A और 4 A धाराएं प्रवाहित रही हैं, तो इन दोनों कुण्डलियों के उभयनिष्ठ केन्द्र पर नेट चुम्बकीय क्षेत्र का परिमाण और दिशा ज्ञात कीजिए।
उत्तर:
दिया है-
कुण्डलियों की त्रिज्या R = 5 cm = 5 x 10^-2 m
कुण्डली P में प्रवाहित धारा I₁ = 3 A
कुण्डली Q में प्रवाहित धारा I₂ = 4 A
कुण्डली P के कारण उत्पन्न चुम्बकीय क्षेत्र
B₁ = \(\frac{\mu_0 I_1}{2 r}=\frac{10^{-7} \times 3}{2 \times 5 \times 10^{-2}}\)
B = 3 x 10^-6 T
कुण्डली Q के कारण उत्पन्न चुम्बकीय क्षेत्र
B₂ = \(\frac{\mu_0 I_2}{2 r}=\frac{10^{-7} \times 4}{2 \times 5 \times 10^{-2}}\)
B₂ = 4 x 10^-6 T
\(\overrightarrow{\mathrm{B}_1}\) व \(\overrightarrow{\mathrm{B}_2}\) परस्पर लम्बवत होंगे अत: चुम्बकीय क्षेत्र का परिमाण

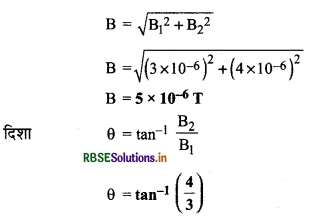
प्रश्न 5.
एक R त्रिज्या वाली धारावाही कुण्डली के अक्ष पर कितनी दूरी पर चुम्बकीय क्षेत्र का मान इसके केन्द्र पर चुम्बकीय क्षेत्र का 27 वाँ भाग होगा?
उत्तर:
धारावाही कुण्डली की अक्ष पर चुम्बकीय क्षेत्र
B = \(\frac{\mu_0 \mathrm{NIR}^2}{2\left(\mathrm{R}^2+x^2\right)^{3 / 2}}\)
कुण्डली के केन्द्र पर चुम्बकीय क्षेत्र
B_{केन्द्र} = \(\frac{\mu_0 \mathrm{NI}}{2 \mathrm{R}}\)
प्रश्नानुसार, B = \(\frac{1}{27}\) B_{केन्द्र}
या \(\frac{\mu_0 \mathrm{NIR}^2}{2\left(\mathrm{R}^2+x^2\right)^{3 / 2}}=\frac{1}{27} \frac{\mu_0 \mathrm{NI}}{2 \mathrm{R}}\)
(R² + x²)^3/2 = 3³ R³ = (3R)³
(R² + x²)^3/2 = 3R
R² + x² = 9R²
8R² = x
x = 2\(\sqrt{2}\) R

प्रश्न 6.
हेल्महोल्टज कुण्डलियों का व्यवस्था में प्रत्येक कुण्डली में 25 फेरे हैं तथा त्रिज्या 10 cm एवं प्रवाहित विद्युत धारा 0.1 A है। कुलियों के मध्य बिन्दु पर चुम्बकीय क्षेत्र ज्ञात कीजिए।
उत्तर:
दिया है-
फेरों की संख्या N = 25 
त्रिज्या R = 10 cm = 0.10 m 
प्रवाहित धारा I = 0.1 A
हेल्महोल्टज कुण्डलियों के मध्य क्षेत्र में चुम्बकीय क्षेत्र
B = \(\frac{8}{5 \sqrt{5}} \frac{\mu_0 \mathrm{NI}}{\mathrm{R}} \)
= \(\frac{8}{5 \sqrt{5}} \frac{4 \pi \times 10^{-7} \times 25 \times 0.1}{0.1}\)
= 2.25 x 10^-5 T

प्रश्न 7.
एक प्रोटॉन पुंज 8 x 10⁵ m/s के वेग से 0.6 T के समचुम्बकीय क्षेत्र की दिशा से 60° कोण पर प्रवेश करता है। प्रोटॉन के लिए
(i) पथ की त्रिज्या तथा
(ii) चूड़ी अन्तराल ज्ञात कीजिए।
उत्तर:
प्रोटॉन का \(\overrightarrow{\mathrm{B}}\) के अनुदिश वेग \(\overrightarrow{\mathrm{B}}\) के अनुर्दिश वेग
V cosθ = 8 x 10⁵ x cos 60°
= 8 x 10⁵ x \(\frac{1}{2}\) = 4 x 10⁵ m/s
प्रोटॉन का \(\overrightarrow{\mathrm{B}}\) के लम्बवत वेग
V sinθ = 8 x 10⁵ sin 60°
= 8 x 10⁵ x \(\sqrt{\frac{3}{2}}\)
= 4\(\sqrt{3}\) x 10⁵ m/s

(i) प्रोटॉन का पथ कुण्डलिनी प्रकार का है अत: पथ को त्रिज्या
r = \(\frac{m v \sin \theta}{q B}\)
r = \(\frac{1.67 \times 10^{-27} \times 4 \sqrt{3} \times 10^5}{1.6 \times 10^{-19} \times 0.6}\)
= 12 x 10^-5 m
= 1.2 µm

(ii) चुड़ी अन्तराल P = v cosθ T = v cosθ \(\frac{2 \pi m}{q B}\)
= \(\frac{4 \times 10^5 \times 2 \times 3.14 \times 1.67 \times 10^{-27}}{1.6 \times 10^{-19} \times 0.6}\)
= 43.7 x 10^-3 m = 4.37 mm.

प्रश्न 8.
किसी साइक्लोट्रॉन जिसकी डीज की त्रिज्या 40 cm है के द्वारा ट्रव्यमान 1.6 x 10^-27 kg और आवेश 1.6 x 10^-19 C के कणों को त्वरित किया गया है। इसमें 0.4 T के चुम्बकीय क्षेत्र का उपयोग किया गया है। इस त्वरक द्वारा कण पुंज को दी गयी गतिज ऊर्जा (MeV में) ज्ञात कीजिए।
उत्तर:
दिया है- 
डीज की त्रिज्या r = 40 cm = 0.40 m
आवेश q = 1.6 x 10^-19 C
आवेश का द्रव्यमान m = 1.6 x 10^-27 kg
चुम्बकीय क्षेत्र B = 0.4 T
पथ की त्रिज्या r = \(\frac{\sqrt{2 m \mathrm{E}_k}}{q \mathrm{~B}}\) से
गतिज ऊर्जा E_k = \(\frac{q^2 \mathrm{~B}^2 r^2}{2 m}\)
= \(\frac{\left(1.6 \times 10^{-19}\right)^2 \times(0.4)^2 \times(0.40)^2}{2 \times 1.67 \times 10^{-27}}\) जूल में
= \(\frac{\left(1.6 \times 10^{-19}\right)^2 \times(0.4)^2 \times(0.40)^2}{10^6 \times\left(1.6 \times 10^{-19}\right) \times 2 \times 1.67 \times 10^{-27}}\) MeV
= 0.023 x 10²
= 2.3 x 10² MeV ≈ 230 MeV

प्रश्न 9.
एक साइक्लोट्रॉन की dees की त्रिज्या 0.5 m है इसमें 1.7 T का अनुप्रस्थ चुम्बकीय क्षेत्र कार्यरत है। इसमें प्रोटॉन द्वारा अर्जित अधिकतम गतिज ऊर्जा ज्ञात कीजिए।
उत्तर:
दिया है- r = 0.5 m
T = 1.7 T
गतिज ऊर्जा E_k = \(\frac{q^2 B^2 r^2}{2 m}\)
= \(\frac{\left(1.6 \times 10^{-19}\right)^2 \times(1.7)^2 \times(0.5)^2}{2 \times 1.67 \times 10^{-27}}\) जल में
= \(\frac{\left(1.6 \times 10^{-19}\right)^2 \times(1.7)^2 \times(0.5)^2}{2 \times 1.67 \times 10^{-27} \times 1.6 \times 10^{-19} \times 10^6}\) MeV
Ek = 7 MeV

प्रश्न 10.
किसी ∝ - कण को 10 KV के विभवान्तर तक त्वरित किया गया है तथा यह x - अक्ष के अनुदिश गतिमान है। यह y - अक्ष के अनुदिश कार्यरत B = 2 x 10^-3 T के एक समान चुम्बकीय क्षेत्र में प्रवेश करता है। इसके पथ की त्रिज्या ज्ञात कीजिए। ( कण का द्रव्यमान = 6.4 x 10^-17 kg लिजिए)
उत्तर:
दिया है- 
त्वरक वोल्टता V = 10 KV = 10⁴ V
चुम्बकीय क्षेत्र B = 2 x 10^-3 T
∝ - कोण का द्रव्यमान m = 6.4 x 10^-7 kg
पथ की त्रिज्या r = \(\frac{\sqrt{2 m \mathrm{E} k}}{q \mathrm{~B}}=\frac{\sqrt{2 m e \mathrm{~V}}}{q \mathrm{~B}}\)
∝ कण पर आवेश = 2e = 2 x 1.6 x 10^-27
∴ r = \(\frac{\sqrt{2 m e \mathrm{~V}}}{2 e \mathrm{~B}}\)
r = \(\frac{\sqrt{2 \times 1.67 \times 10^{-27} \times 10^4 \times 1.6 \times 10^{-19}}}{2 \times 1.6 \times 10^{-19} \times 2 \times 10^{-3}}\)
r = 0.36 mm

प्रश्न 11.
एक 4 cm लम्बा तार एक परिनालिका के अन्दर उसके केन्द्र के पास परिनालिका की अक्ष से 60° के झुकाव पर रखा है और तार में 12 A की धारा प्रवाहित होती है तथा परिनालिका के कारण उत्पन्न चुम्बकीय क्षेत्र 0.25 T है तो तार पर लगने वाला बल ज्ञात कीजिए।
उत्तर:
दिया है l = 4 cm = 4 x 10^-2 m, θ = 60°
I = 12A, B = 0.25T 
F = IlB sinθ
= 12 x 0.25 x 4 x 10^-2 x sin 60°
= 0.12 x \(\frac{\sqrt{3}}{2}\)
= 0.06 x 1.732
= 0.10392 = 0.104N 

प्रश्न 12.
कोई परिनालिका जिसकी लम्बाई 0.5 m तथा त्रिज्या। cm है, में 500 फेरे हैं। इसमें 5 A विद्युत धारा प्रवाहित हो रही है। परिनालिका के भीतर चुम्बकीय क्षेत्र का मान ज्ञात कीजिए।
उत्तर:
प्रश्नानुसार l = 0.5 m, r = 1 cm = 0.01 m
N = 500 तथा I = 5 A
A = πR² = 3.14 x (10^-2)² = 3.14 x 10^-4 m²
l = 0.5 m स्पष्टत: A<<l
अतः परिनालिका की लम्बाई को अधिक मानते हुए
B = µ₀\(\frac{\mathrm{N}}{\mathrm{L}}\) I
B = 4π x 10^-7 x \(\frac{500}{0.5}\) x 5
B = 6.28 x 10^-3 T

प्रश्न 13.
10 सेमी औसत त्रिज्या के एक टोरॉइड में 1000 फेरे हैं। इसमें 0.1 ऐम्पियर की धारा प्रवाहित करने पर टोरॉइड की अक्ष पर चुम्बकीय क्षेत्र का मान ज्ञात कीजिए।
उत्तर:
प्रश्नानुसार, R = 10 सेमी, N = 1000 फेरे
I = 0.1 A
टोरॉइड की अक्ष पर चुम्बकीय क्षेत्र
B = \(\frac{\mu_0 \mathrm{NI}}{2 \pi \mathrm{R}}\)
B = \(\frac{4 \pi \times 10^{-7} \mathrm{NI}}{2 \pi R}=\frac{2 \times 10^{-7} \mathrm{NI}}{R}\)
B = \(\frac{2 \times 1000 \times 0.1 \times 10^{-7}}{0.1}\)
B = 2 x 10^-4 T

प्रश्न 14.
चित्र में दो लम्बे सीधे तारों A व C में धारा क्रमशः 100 A व 20 A बह रही हैं। उनके बीच 15 cm लम्बा तार B स्थित है, जिसमें 10 A की धारा बह रही है। B पर बल का मान ज्ञात कीजिए।

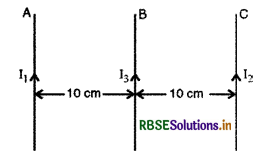
उत्तर:
दिया है; I₁ = 100 A, I₂ = 20 A
r₁ = r₂ = 10 cm = 0.10 m
I = 10 A
l = 15 cm = 0.15 m.
तार A में धारा I₁ के कारण तार B की स्थिति में चुम्बकीय क्षेत्र
B₁ = 2 x 10^-7 \(\frac{\mathrm{I}_1}{r_1}\) = 2 x 10^-7 x \(\frac{100}{0.10}\)
= 2 x 10^-4 T (कागज के लम्बवत अन्दर की ओर) 
तार C में धारा I₂ के कारण तार B की स्थिति में चुम्बकीय क्षेत्र
B₂ = 2 x 10^-7 \(\frac{\mathrm{I}_2}{r_2}\) = 2 x 10^-7 x \(\frac{20}{0.10}\)
B₂ = 0.4 x 10^-4 T (कागज के लम्बवत बाहर की ओर)
∴ तार B की स्थिति में परिणामी चुम्बकीय क्षेत्र
B = B₁ - B₂
= 2 x 10^-4 - 0.4 x 10^-4
= 1.6 x 10^-4 T
∴ तार B पर बल F = I l B sin 90°
= 10 x 1.6 x 10^-4 x 0.15 x 1
= 2.4 x 10^-4 N (तार A की ओर)

प्रश्न 15.
एक वर्गाकार कुण्डली जिसकी प्रत्येक भुजा 20 cm है, में 200 फेरे हैं और 2 A विद्युत धारा प्रवाहित हो रही है। कुण्डली ऊर्ध्वाधरतः लटकी हुई है और इसके तल पर खींचा गया अभिलम्ब 0.80 T के एक समान चुम्बकीय क्षेत्र की दिशा से 30° का कोण बनाता है। कुण्डली पर लगने वाले बल युग्म का परिमाण क्या है?
उत्तर:
दिया है: वर्गाकार कुण्डली की भुजा = 20 cm
कुण्डली का क्षेत्रफल A = (20)² = 400 cm²
= 4 x 10^-2 ms
प्रवाहित धारा I = 2 A
कुण्डली में फेरों की संख्या N = 200 
चुम्बकीय क्षेत्र B = 0.80 T
कोण θ  = 30°
अतः कुण्डली पर लगने वाला बलयुग्म
τ = NIAB sinθ
τ = 200 x 4 x 10^-2 x 2 x 0 x 0.80 x sin 30°
τ = 6.4 N - m

प्रश्न 16.
चलकुण्डली धारामापी की धारा सुग्राहिता को 50% बढ़ाने पर इसका प्रतिरोध दोगुना हो जाता है। इस धारामापी की वोल्टेज सुग्राहिता पर क्या प्रभाव पड़ेगा?
उत्तर:
धारा सुग्राहिता S_i = \(\frac{\mathrm{Q}}{\mathrm{I}}=\frac{\mathrm{nAB}}{\mathrm{C}} \)
वोल्टेज सुग्राहिता S_v = \(\frac{\mathrm{Si}}{\mathrm{R}}\) ................(i)
जब धारा सुगाहिता 50% बढ़ा दी जाती है तो उसका प्रतिरोध R' = 2R हो जाता है।
S'_i = S'_i + \(\frac{50}{100}\) = 1.5 S'_i
नई वोल्टेज सुग्राहिता
S'_v = \(\frac{1.5 \mathrm{~S}_i}{2 \mathrm{R}}\) ..................(ii)
सभी (i) व (ii) से स्पष्ट है कि S'_v <S_v अर्थात वोल्टेज सुग्राहिता घट जाती है।
∴वोल्टेज सुग्राहिता में प्रतिशत कमी
= \(\frac{\mathrm{S}_v-\mathrm{S}_v^{\prime}}{\mathrm{S}_v} \times 100 \)
= \(\frac{\frac{\mathrm{S}_i}{\mathrm{R}}-\frac{5 \mathrm{~S}_i}{2 \mathrm{R}} \times 1000}{\frac{\mathrm{S}_i}{\mathrm{R}}}\)
= 0.25 x 100 = 25% कम हो जाएगी।

प्रश्न 17.
30 Ω प्रतिरोध का एक धारामापी है। यह पूर्ण स्केल पर 2 mA की धारा देता है। इसे 0 ~ 0.3 A के अमीटर में रूपान्तरित करने के लिए आवश्यक प्रतिरोध के मान की गणना कीजिए।
उत्तर:
आवश्यक शण्ट तार का प्रतिरोध
S = \(\frac{\mathrm{Ig} \mathrm{G}}{\mathrm{I}-\mathrm{Ig}}\)
दिया है, Ig = 2 mA = 2 x 10^-3 A, G = 30 Ω
I = 0.3 A
∴ S = \(\frac{2 \times 10^{-3} \times 30}{0.3-2 \times 10^{-3}}=\frac{6 \times 10^{-2}}{0.298}\)
S = 0.2 Ω

प्रश्न 18.
एक धारामापी का प्रतिरोध 99 Ω है। इसके पूर्ण स्केल पर विक्षेप के लिए आवश्यक धारा 1 mA है। यदि धारामापी के साथ 1 Ω का शण्ट जोड़ दिया जाए तो धारामापी द्वारा मापी जा सकने वाली अधिकतम धारा का मान ज्ञात करो।
उत्तर:
दिया है- G = 99 Ω; Ig = 1 mA = 0.001 A
S = 1 Ω 
शण्ट तार का प्रतिरोध
S = \(\frac{\mathrm{Ig} \mathrm{G}}{\mathrm{I}-\mathrm{Ig}}\)
S = \(\frac{0.001 \times 99}{I-0.001}\) = 1
I - 0.001 = 0.001 x 99
I = 0.99 + 0.001
I = 1 A

प्रश्न 19.
एक धारामापी 0.5 mA धारा के लिए पूर्ण विक्षेप देता है। धारामापी का प्रतिरोध 20 Ω है। इसको 5 V परास के वोल्टमीटर में कैसे परिवर्तित करोगे?
उत्तर:
दिया है- Ig = 0.5 mA = 5 x 10^-4 A
G = 20 Ω, I = 5V
धारामापी को वोल्टमीटर में बदलने के लिए यदि R उच्च प्रतिरोध जोड़ा जाता है, तो R = \(\frac{\mathrm{V}}{\mathrm{Ig}}-\mathrm{G}=\frac{5}{5 \times 10^{-4}}-20\)
R = 10000 - 20 = 9980 Ω

प्रतियोनी परीक्षा संबंधी प्रश्न

प्रश्न 1.
0 बिन्दु पर चुम्बकीय क्षेत्र होगा-

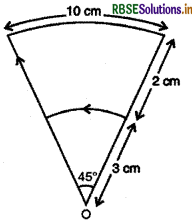
(A) 1.5 x 10^-5 T
(B) 10^-5 T
(C) 2 x 10^-5 T
(D) 10^-4 T 
उत्तर:
(B) 10^-5 T

प्रश्न 2.
R त्रिज्या के बेलनाकार चालक में स्थायी धारा प्रवाहित हो रही है। दूरी d के साथ चुम्बकीय क्षेत्र B के परिणाम का आरेख निम्न चित्र द्वारा प्रदर्शित होगा-

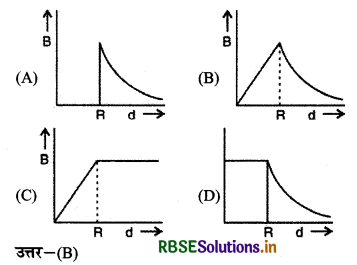
प्रश्न 3.
एक धारावाही लूप का द्विध्रुव आपूर्ण m है, जिसमें I धारा प्रवाहित है और लूप के केन्द्र पर चुम्बकीय क्षेत्र B, है। जब धारा को नियत रखते हुए द्विषुव आपूर्ण को दोगुना कर दिया जाता है तो लूप के केन्द्र पर चुम्बकीय क्षेत्र B₂ हो जाता है। B₁/B₂ का अनुपात है-
(A) \(\sqrt{2}\)
(B) \(1/\sqrt{2}\)
(C) 2
(D) \(\sqrt{3}\) 
उत्तर:
(A) \(\sqrt{2} \)

प्रश्न 4.
दो एकसमान तार A व B की प्रत्येक की लम्बाई l है, मेंसमानधारा I प्रवाहित है। A को मोड़कर R त्रिज्या का एक वृत्त और B को मोड़कर भुजा 'a' का एक वर्ग बनाया जाता है। यदि B_A और B_B क्रमशः वृत्त के केन्द्र पर चुम्बकीय क्षेत्र हैं, तब अनुपात \(\frac{\mathrm{B}_{\mathrm{A}}}{\mathrm{B}_{\mathrm{B}}}\) होगा-
(A) \(\frac{\pi^2}{16 \sqrt{2}}\)
(B) \(\frac{\pi^2}{16}\)
(C) \(\frac{\pi^2}{8 \sqrt{2}}\)
(D) \(\frac{\pi^2}{8}\)
उत्तर:
(C) \(\frac{\pi^2}{8 \sqrt{2}}\)

प्रश्न 5.
एक गैल्वेनोमीटर की कुण्डली का प्रतिरोध 100 Ω है। 1 mA धारा प्रवाहित करने पर इसमें पूर्ण विक्षेप आता हैं इस गैल्वेनोमीटर को 10 A के एमीटर से बदलने के लिए जो प्रतिरोध लगाना होगा वह है-
(A) 2 Ω
(B) 0.1 Ω 
(C) 3 Ω
(D) 0.01 Ω
उत्तर:
(D) 0.01 Ω

प्रश्न 6.
एक लम्बे धारावाही चालक तार में नियत धारा प्रवाहित है, को एक वृत्तीय लूप में मोड़ा गया है। लूप के केन्द्र पर चुम्बकीय क्षेत्र B है। तब इसे n फेनों के एक वृत्तीय कुण्डली के रूप में मोड़ा जाता है। n फेरों के कुण्डली के केन्द्र पर चुम्बकीय क्षेत्र होगा-
(A) 2nB
(B) 2n2B 
(C) nB
(D) n²B
उत्तर:
(D) n²B

प्रश्न 7.
एक समचुम्बकीय क्षेत्र में सूती धागे से एक छड़ चुम्बक को लटकाया गया है और यह सन्तुलन में है। इसे 60° घुमाने के लिए आवश्यक ऊर्जा का मान W हो तो इस नई स्थिति में चुम्बक को रखने के लिए आवश्यक बल आघूर्ण का मान होगा-
(A) \(\frac{\sqrt{3} W}{2}\)
(B) \(\frac{2 W}{\sqrt{3}}\)
(C) \(\frac{\mathrm{W}}{\sqrt{3}}\)
(D) \(\sqrt{3}\)
उत्तर:
(D) \(\sqrt{3}\) 

प्रश्न 8.
3.57 x 10^-2 T के लम्बवत् चुम्बकीय क्षेत्र के प्रभाव में एक वृत्तीय पथ पर एक इलेक्ट्रॉन परिक्रमा कर रहा है। यदि e/m का मान 1.76 x 10¹¹ C/kg है तो इलेक्ट्रॉन के परिक्रमण की आवृत्ति ज्ञात करो-
(A) 62.8 MHz
(B) 6.28MHz 
(C) 1 GHz
(D) 100 MHz 
उत्तर:
(C) 1 GHz

प्रश्न 9.
10 cm तथा 5 cm भुजाओं के एक आयतकार लूप (पाश) से एक विद्युतधारा I = 12 A प्रवाहित हो रही है। इस पाश को आरेख में दर्शाए गये अनुसार विभिन्न अभिविन्यासों में रखा गया है।

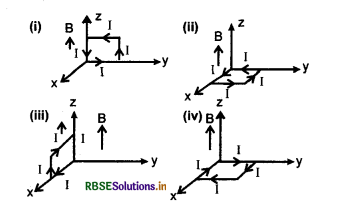
यदि वहाँ 0.3 T तीव्रता का कोई एक समान चुम्बकीय क्षेत्र, धनात्मक z दिशा में विद्यमान है तो दर्शाये गये किस अभिविन्यास में, यह पाश (लूप) (i) स्थायी सन्तुलन तथा (ii) अस्थायी सन्तुलन में होगा?
(A) क्रमश: (i) और (ii) में
(B) क्रमशः (i) और (iii) में
(C) क्रमशः (ii) और (iv) में
(D) क्रमशः (ii) और (iii) में।
उत्तर:
(C)  क्रमशः (ii) और (iv) में

प्रश्न 10.
दो समाक्षी परिनालिकाओं में, प्रत्येक से I धारा एक ही दिशा में प्रवाहित हो रही है। यदि बाहरी परिनालिका के कारण, भीतरी परिनालिका पर चुम्बकीय बल F तथा भीतरी परिनालिका के कारण, बाहरी परिनालिका पर चुम्बकीय बल हो तो
(A) \(\overrightarrow{\mathrm{F}_1} = \overrightarrow{\mathrm{F}_2}\) = 0 
(B) \(\overrightarrow{\mathrm{F}_1}\) भीतर की ओर व त्रिज्य है तथा \(\overrightarrow{\mathrm{F}_2}\) बाहर की ओर व त्रिज्य है
(C) \(\overrightarrow{\mathrm{F}_1}\) भीतर की ओर व त्रिज्य है तथा \(\overrightarrow{\mathrm{F}_2}\) = 0 है
(D) \(\overrightarrow{\mathrm{F}_1}\) बाहर की ओर व त्रिज्य है तथा \(\overrightarrow{\mathrm{F}_2}\) = 0 है।
उत्तर:
(A) \(\overrightarrow{\mathrm{F}_1}\) = \(\overrightarrow{\mathrm{F}_2}\) = 0 

प्रश्न 11.
एक छोटी चुम्बक जिससे निग्राहिता 3 x 10³ Am^-1 है की एक लौह चुम्बक विचुम्बकित हो जाती है। 10 cm लम्बी तथा 100 फेरों वाली परिनालिका में प्रवाहित धारा का मान होगा, जब इसमें रखी यह चुम्बक परिनालिका में चुम्बकित हो जाता है-
(A) 3 A
(B) 6 A 
(C) 30 mA
(D) 60 mA
उत्तर:
(A) 3 A