RBSE Class 12 Physics Important Questions Chapter 4 Moving Charges and Magnetism

Rajasthan Board RBSE Class 12 Physics Important Questions Chapter 4 Moving Charges and Magnetism Important Questions and Answers.

RBSE Class 12 Physics Chapter 4 Important Questions Moving Charges and Magnetism

Multiple Choice Questions

Question 1.
Two parallel wires carrying currents in the same direction attract each other because of:
(A) potential difference between them
(B) mutual induction between them
(C) electric forces between them
(D) magnetic forces between them.
Answer:
(D) magnetic forces between them.

Question 2.
An electric charge e moves with a constant velocity V parallel to the lines of force of a uniform magnetic field B, the force experienced by the charge is:
(A) Bev
(B) \(\frac{e v}{\mathrm{~B}}\)
(C) zero
(D) \(\frac{e}{\mathrm{~B} v}.\)
Answer:
(C) zero

Question 3.
What is the magnitude of force experienced by a stationary charge when placed in a uniform magnetic field?
(A) F = qvB sin θ
(B) F = qvB
(C) F = Zero
(D) None of these.
Answer:
(C) F = Zero

Question 4.
Two long parallel conductors carrying current in opposite direction:
(A) attract each other
(B) repel each other
(C) neither attract nor repel each other
(D) None of these.
Answer:
(B) repel each other

Question 5.
Resistance of ideal ammeter is:
(A) infinite
(B) zero
(C) 1Ω
(D) 10 Ω.
Answer:
(B) zero

Question 6.
To convert a galvanometer into a voltmeter.
(A) a high resistance is connected in parallel
(B) a low resistance is connected in series
(C) a low resistance is connected in parallel
(D) a high resistance is connected in series.
Answer:
(D) a high resistance is connected in series.

Question 7.
A charged particle enters in a magnetic field with some velocity parallel to the magnetic field. The nature of path followed by the charged particle will be:
(A) helical
(B) circular
(C) straight line
(D) parabolic.
Answer:
(C) straight line

Question 8.
The resistance of ideal voltmeter is:
(A) zero
(B) low
(C) high
(D) infinite.
Answer:
(D) infinite.

Question 9.
The basic instrument used to detect the current:
(A) Ammeter
(B) Voltmeter
(C) Galvanometer
(D) Voltameter.
Answer:
(C) Galvanometer

Question 10.
A charge q moves in a region, where electric field \(\overrightarrow{\mathbf{E}}\) and magnetic field \(\overrightarrow{\mathbf{B}}\) both exist, then the force on it is
(A) q (\(\overrightarrow{\mathbf{v}}\) x \(\overrightarrow{\mathbf{B}}\))
(B) q\(\overrightarrow{\mathbf{E}}\) + q(\(\overrightarrow{\mathbf{v}}\) x \(\overrightarrow{\mathbf{B}}\))
(C) q\(\overrightarrow{\mathbf{E}}\) + q(\(\overrightarrow{\mathbf{B}}\) x \(\overrightarrow{\mathbf{v}}\))
(D) q\(\overrightarrow{\mathbf{B}}\) + q(\(\overrightarrow{\mathbf{E}}\) x \(\overrightarrow{\mathbf{v}}\)).
Answer:
(B) q\(\overrightarrow{\mathbf{E}}\) + q(\(\overrightarrow{\mathbf{v}}\) x \(\overrightarrow{\mathbf{B}}\))

Question 11.
To convert a galvanometer into an ammeter, we connect:
(A) low resistance in parallel
(B) high resistance in series
(C) high resistance in parallel
(D) low resistance in series.
Answer:
(A) low resistance in parallel

Question 12.
A charged particle enters at 30° to the magnetic field. Its path becomes:
(A) circular
(B) helical
(C) elliptical
(D) straight line.
Answer:
(B) helical

Question 13.
A cyclotron is used to accelerate:
(A) Electron
(B) Neutrons
(C) Positive ions
(D) None of these
Answer:
(C) Positive ions

Question 14.
The sensitivity of a moving coil galva¬nometer increases with decrease is:
(A) number of turns
(B) area of coil
(C) magnetic field
(D) none of the above.
Answer:
(D) none of the above.

Question 15.
A magnetic field exerts no force on?
(A) stream of electrons
(B) stream of protons
(C) unmagnetised piece of iron
(D) stationary charge.
Answer:
(D) stationary charge.

Question 16.
In a cyclotron the angular frequency of the charged particle is independent of the:
(A) mass
(B) speed
(C) charge
(D) magnetic field.
Answer:
(B) speed

Question 17.
If a current is passed through a spring, then the spring will:
(A) expand
(B) compress
(C) remain same
(D) none of these.
Answer:
(B) compress

Question 18.
If electron and proton having same momenta enter normally to a magnetic field, then:
(A) Curved path of electron and proton will be same (ignoring sense of revolution)
(B) They will move undeflected
(C) Curved path of electron is more curved
(D) Path of proton is more curved.
Answer:
(A) Curved path of electron and proton will be same (ignoring sense of revolution)

Question 19.
The dimensions of E/B (electric field/ magnetic field) are same as that of:
(A) acceleration
(B) velocity
(C) charge
(D) current.
Answer:
(B) velocity

Question 20.
A charged particle enters a magnetic field at an angle of 90° with magnetic field. The path of the particle will be:
(A) a helix
(B) an ellipse
(C) a circle
(D) a straight line.
Answer:
(C) a circle

Fill in the blanks

Question 1.
........................... established in 1820 that a conductor carrying current produces a magnetic field around it.
Answer:
Oersted.

Question 2.
Unit of magnetic induction in S.I. is ...........................
Answer:
Tesla (T).

Question 3.
Charges at rest produce ........................... field.
Answer:
electrostatic.

Question 4.
........................... acts on the charge moving along the direction of magnetic field.
Answer:
No force.

Question 5.
........................... force is much smaller than the ........................... force.
Answer:
Magnetic, electric.

Question 6.
A charged particle follows a ........................... path in a uniform electric field.
Answer:
parabalic.

Question 7.
An ammeter is a ........................... resistance moving coil galvanometer.
Answer:
low.

Question 8.
A voltmeter is an ........................... resistance moving coil galvanometer.
Answer:
infinite.

Question 10.
An ammeter is always connected in ........................... in an electric circuit.
Answer:
series.

Very Short Answer Type Questions

Question 1.
A proton and an electron travelling along parallel path enters a region of uniform magnetic field, acting perpendicular to their paths. Which of them will move in a circular path with higher frequency.
Answer:
Electron will move with higher frequency, because angular frequency of a charged particle in perpendicular magnetic field is given by

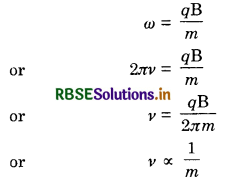
Since mass of electron is less than the mass of proton, so it will move with high frequency.

Question 2.
Describe SNOW rule for deflection of magnetic needle.
Answer:
The SNOW rule is, "when current flows in the conductor from South to North, over the needle, the north pole of the needle deflects towards west.

Question 3.
Describe the nature of the magnetic field as connected with nature of current.
Answer:
A straight current produces a circular magnetic field. A circular current produces a straight magnetic field.

Question 4.
A charged particle is moving away from you. If the direction of the magnetic field is clockwise, what is the charge on the particle?
Answer:
The charge on the particle is +ve.

Question 5.
A charged particle enters a uniform magnetic field experiences an upward force as indicated in the figure. What is the charge sign on the particle?

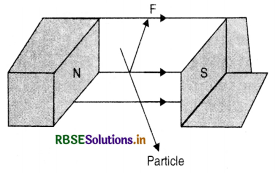
Answer:
Using Fleming’s left hand rule, the charge on the particle is positive moving normal to the magnetic field towards outwards and experience a force upwards.

Question 6.
Is the source a magnetic field analogue to the source of electric field?
Answer:
No, because, in electric field, the source of electric field is electric charge whereas in magnetic field, the source of magnetic field is not a magnetic charge.

Question 7. 
What is the value of constant \(\frac{\mu_0}{4 \pi}\)?
Answer:
\(\frac{\mu_0}{4 \pi}\) = 10^-7 TA^-1 m.

Question 8.
In the diagram below is shown a circular loop carrying current I. Show the direction of magnetic field with the help of lines of force.

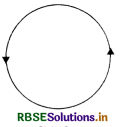
Answer:
Since the current is flowing in anticlockwise direction, so the loop will behave like north pole and the magnetic field \(\overrightarrow{\mathrm{B}}\) is perpendicular to the plane of paper and directed outward as shown in the figure VSAQ 8(b).

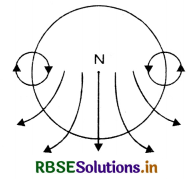
Question 9.
A current is set up in a long hollow copper conductor. Is there any magnetic field inside the conductor?
Answer:
From Ampere’s circuital law, we find that there will be no magnetic field inside the hollow conductor carrying current.

Question 10.
Why a solenoid tends to contract when a current is passed through it?
Answer:
In a solenoid, the turns of the coil are parallel to each other carrying current in the same direction, hence they attract each other which results in the form of contraction of the solenoid.

Question 11.
State any rule that relates the direction of electric current and the direction of accompaying magnetic field.
Answer:
Maxwell’s screw law.

Question 12.
Name the rule, relating direction of the current and the magnetic field.
Answer:
The rule is 'right hand rule'.

Question 13.
Write down the expression for Lorentz force.
Answer:
\(\overrightarrow{\mathrm{F}}=q(\overrightarrow{\mathrm{E}}+\vec{v} \times \overrightarrow{\mathrm{B}})\)

Question 14.
What is the force on a charge moving in magnetic field?
Answer:
The force \(\vec{F}\) on a charge q moving in a magnetic field \(\vec{B}\) with velocity \vec{v} is given by
\(\vec{F}\) = q (\(\vec{v}\) x \(\vec{B}\))

Question 15.
Under what condition is the force acting on a charge moving through a uniform magnetic field is maximum?
Answer:
The force acting on charge q moving in a magnetic field \(\vec{B}\) with velocity \(\vec{v}\) is given by
\(\vec{F}\) = q(\(\vec{v}\) x \(\vec{B}\))
Now \(\vec{F}\) will be maximum
If \(\vec{v}\) ⊥ \(\vec{B}\)
i.e. the direction of motion of the charge should be perpendicular to the direction of magnetic field.

Question 16.
An electron is moving along X-axis in a magnetic field acting along Y-axis. What is the direction of magnetic field acting on it?
Answer:
Negative Z-axis in accordance with Fleming's left hand rule.

Question 17.
What is the value of magnetic permeability of free space?
Answer:
It is µ₀ = 4π x 10^-7 TA^-1 m^-1.

Question 18.
What is the direction of force between two parallel conductors carrying current in (i) the same direction; (ii) opposite direction?
Answer:
(i) Force is acting inwards and hence is attractive.
(ii) Force is acting outwards and hence is repulsive.

Question 19.
The force \(\overrightarrow{\mathbf{F}}\) experienced by a particle of charge q moving with velocity \(\overrightarrow{\mathbf{v}}\) in a magnetic field \(\overrightarrow{\mathbf{B}}\) is given by \(\overrightarrow{\mathbf{F}}\) = q (\(\overrightarrow{\mathbf{v}}\) x \(\overrightarrow{\mathbf{B}}\) ), which pair of vectors are always at right angle to each other?
Answer:
\(\overrightarrow{\mathbf{v}}, \overrightarrow{\mathbf{F}} and \overrightarrow{\mathbf{B}} , \overrightarrow{\mathbf{F}}\) are two pairs ⊥ to each other.

Question 20.
What is S.I. unit of magnetic induction?
Answer:
Tesla or Wb m^-2.

Question 21.
A positive charge is moving vertically upwards when it enters a magnetic field directed to the earth. What is the direction of force on the charge?
Answer:
No force acts on the charge since v is parallel to field B.

Question 22.
Write expression for the Biot-Savart's law.
Answer:
The required expression is
dB = \(\frac{\mu_0}{4 \pi} \frac{\mathrm{I} d l \sin \theta}{r^2}\)

Question 24.
Give two factors by which voltage sensitivity of a moving coil galvanometer can be increased?
Answer:

• By increasing the number of turns of the coil.
• By increasing the area of cross-section of the coil.

Question 25.
Write expression for the magnetic flux density due to a circular current loop at a point (a) on the axis (b) at centre.
Answer:
The required expression is
(a) B = \(\frac{\mu_0 \mathrm{I} a^2 \mathrm{~N}}{2 x^3}\)
(b) B = \(\frac{\mu_0 \text { IN }}{2 a}\)

Question 26.
What is a solenoid?
Answer:
A solenoid is a straight cylindrical core on which a large number of turns of an insulated copper wire are wrapped.

Question 27.
Write expression for the magnetic flux density at inside point on the axis of a current carrying solenoid of finite length.
Answer:
The required expression is
B = \(\frac{\mu_0 \mathrm{I} n}{2}\left[\cos \phi_2-\cos \phi_1\right]\)

Question 28.
Write expression when solenoid has infinite length.
Answer:
The required expression is
(a) For point well inside, B = µ₀ In
(b) For point at the end, B = \(\frac{\mu_0 \mathrm{I} n}{2}\)

Question 29.
Write expression for the force on a current carrying conductor in a magnetic field.
Answer:
The required expression is dF = I dl B sin θ.

Question 30.
Write expression for the force between two short parallel wires carrying a current, when they are
(a) much separated (b) very close.
Answer:
The required expression is
(a) dF = \(\frac{\mu_0}{4 \pi} \frac{\mathrm{I}_1 \mathrm{I}_2 d l_1 d l_2}{r^2}\)
(b) dF = \(\frac{\mu_{\mathrm{o}} \mathrm{I}_1 \mathrm{I}_2}{2 \pi r}.\)

Question 31.
State Ampere's circuital law.
Answer:
The statement is, “The line integral of the magnetic field of induction round a closed curve is µ0 times the total current bounded by the curve”.

Question 32.
Give mathematical form of Ampere's circuital law.
Answer:
The required mathematical form is
\(\oint_{\mathrm{L}} \vec{B} \cdot \overrightarrow{d l}\) = µ₀I
In general, \(\oint_{\mathrm{L}} \vec{B} \cdot \overrightarrow{d l}\) = µ₀∑I.

Question 33.
Give mathematical form of Ampere’s circuital law in terms of current density of charge.
Answer:
The required form is
\(\oint_{\mathrm{L}} \overrightarrow{\mathrm{B}} \cdot \overrightarrow{d l}=\mu_0 \cdot \oint_{\mathrm{S}} \overrightarrow{\mathrm{J}} \cdot \overrightarrow{d \mathrm{~S}}\) .

Question 34.
What is a toroidal solenoid?
Answer:
A toroidal solenoid is a torus (ring of cylindrical cross-section) on which a large number of turns of an insulated copper wire are wrapped.

Question 35.
What is the effect of increasing the number of turns on magnetic field produced due to a circular coil?
Answer:
The magnetic field produced by a coil of n turns is n times the magnetic field produced by a coil of single turn.

Question 36.
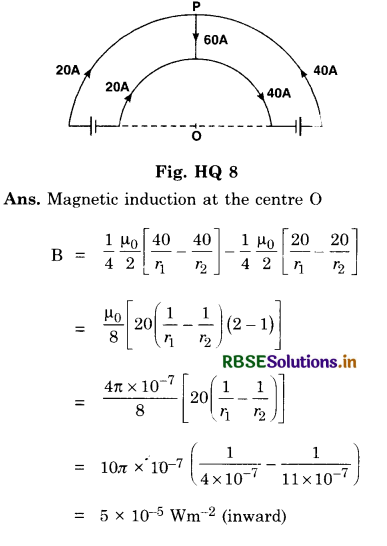
Consider the circuit as shown in Fig. VSAQ 36, where APB and AQB are semi-circles. What will be the magnetic field at the centre C of the circular loop?
Answer:
Refer to Fig. The magnetic field at point C will be zero.

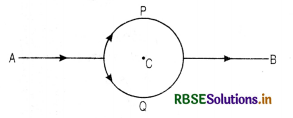
Question 37.
Why is the magnet of a moving coil galvanometer laminated?
Answer:
It provides a strong magnetic field.

Question 38.
Why has the magnet a horse-shoe shape?
Answer:
It provides a uniform magnetic field.

Question 39.
Why has the magnet concave pole faces?
Answer:
It provides a radial magnetic field.

Question 40.
Why is the coil wrapped on a conducting frame?
Answer:
Eddy currents in conducting copper frame help in stopping the coil soon.

Question 41.
What is the function of soft iron cylinder between the poles?
Answer:
It concentrates the magnetic field and reduces air resistance by reducing air gap.

Question 42.
Why do we use a mirror with the coil?
Answer:
It helps in measuring coil deflection by using lamp and scale arrangement.

Question 43.
What is the function of the radial magnetic field of the magnet?
Answer:
It keeps the arm of the couple and hence the torque on coil constant in all positions.

Question 44.
State the principle of moving coil galvanometer.
Answer:
It is based on the principle that when a current carrying conductor is placed in a magnetic field, it experiences a torque.

Question 45.
What is the nature of magnetic field in a moving coil golvanometer?
Answer:
It is radial in nature.

Question 46.
What is shunt? State its SI units.
Answer:
A small resistance connected in parallel to the coil of the galvanometer is called shunt. Its SI unit is ohm.

Question 47.
The current in a long straight wire is reversed. What is the effect on \overrightarrow{\mathbf{B}} at a particular point?
Answer:
The magnitude of magnetic field remains the same but its direction will be reversed.

Question 48.
Can a magnetic field act on electron at rest or in motion?
Answer:
No it cannot. Because, the magnetic field cannot change the kinetic energy on any charged particle, on which it acts.

Question 49.
Why does the picture on a T.V. screen become distorted when a magnet is brought near the screen?
Answer:
The magnet exerts a force on the beam of electrons and interferes with the force on them due to the incoming picture signal. Hence the picture of T.V. screen gets distorted.

Question 50.
What is meant by cyclotron frequency?
Answer:
The cyclotron frequency means the frequency of rotation of charged particles in their circular paths inside the dees and is given by:
v = \(\frac{q \mathrm{~B}}{2 \pi m}\)

Question 51.
What are the primary functions of electric field and magnetic field in a cyclotron?
Answer:

• The electric field is used to accelerate the charged particles and
• The magnetic field is used to bend the path of charged particles into the dees of the cyclotron and to adjust the frequency of their rotation.

Question 52.
Is the resistance of an ammeter greater than or less than that of the galvanometer of which it is formed?
Answer:
The resistance of an ammeter is always less than that of the galvanometer, of which it is formed.

Question 53.
How can a galvanometer be converted into an ammeter?
Answer:
A galvanometer can be converted into an ammeter by connecting a suitable small resistance in parallel to it.

Question 54.
Which of the two, an ammeter or a milliammeter, has a higher resistance and why?
Answer:
A milliammeter has a higher resistance than an ammeter because a very small current is to pass through a milliammeter as compared to an ammeter and hence millammeter has more resistance than an ammeter.

Question 55.
What is a dead beat galvanometer?
Answer:
The galvanometer whose coil comes to rest at once after the passage of current is called a dead beat galvanometer. Dead beat means non-oscillating.

Question 56.
By mistake a voltmeter is connected in series and an ammeter is connected in parallel, with a resistance in an electrical circuit. What will happen to the instruments?
Answer:
Since a voltmeter is a high resistance galvanometer, so it will decrease the current in the circuit to a very low value and will show reading between two points where it is connected and will not be damaged. Ammeter is a low resistance galvanometer and when connected in parallel, a very small current will flow through the ammeter and will show a deflection and will not be damaged.

Question 57.
How is an ammeter connected in an electric circuit?
Answer:
An ammeter is connected in series in an electric circuit.

Question 58.
Is the resistance of a voltmeter greater than or less than that of the galvanometer of which it is formed?
Answer:
The resistance of a voltmeter is always greater than that of the galvanometer, of which it is formed.

Question 59.
How is a voltmeter connected in an electric circuit?
Answer:
A voltmeter is connected in parallel in an electric circuit.

Question 60. 
What is the resistance of an ideal voltmeter and an ammeter?
Answer:
The resistance of an ideal voltmeter is infinite and that of an ammeter is zero.

Question 61.
Equal currents i, i are flowing through two infinitely long parallel wires. What will be the magnetic field at a mid-way when the current is flowing in the same direction?
Answer:
Zero, because the magnetic field produced by two conductors at the mid-point is equal and opposite.

Question 62.
Equal currents i, i are flowing through two infinitely long parallel wires. What will be the magnetic field at a mid-way, when the currents are flowing in opposite directions?
Answer:
The magnetic field at the mid-point will be twice the magnetic field due to one current carrying conductor because the magnetic fields are equal and in the same direction.
And B = 2\(\frac{\mu_0 I}{2 \pi r}=\frac{\mu_0 I}{\pi r}\)

Question 63.
What is the direction of force on a charged particle q moving with velocity \(\vec{v}\) in a uniform magnetic field \vec{B}?
Answer:
Since \(\vec{F}\) = q (\(\vec{v}\) x \(\vec{B}\))
So, the direction of force is perpendicular to both \(\vec{v}\) and \(\vec{B}\).

Question 64.
If a particle of charge q is moving with velocity v along x-axis and the magnetic field B is acting along Y-axis, use the expression \(\overrightarrow{\mathrm{F}}\) = q (\(\overrightarrow{\mathrm{v}}\) x \(\overrightarrow{\mathrm{B}}\)) to find the direction of force \(\overrightarrow{\mathrm{F}}\) acting on it.
Answer:
Given

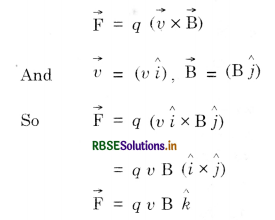
Thus the direction of force is along z-axis.

Question 65.
In the diagram below is shown a circular loop carrying current I. Show the direction of magnetic field with the help of lines of force.

Or
Sketch the magnetic field lines for a current carrying circular loop.
Answer:
The magnetic lines of force are as shown in the figure VSAQ 65 (a).

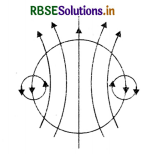
The direction of lines is inside the plane of paper.

Question 66.
An electron is moving along positive X-axis in the presence of uniform magnetic field along positive Y-axis. What is the direction of force acting on it?
Answer:
Since

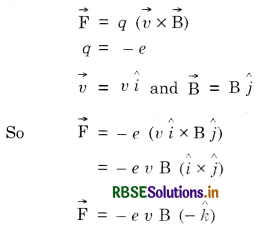
So the direction of magnetic force is along -ve z-axis.

Question 67.
Under what condition is the force acting on a charge moving through a uniform magnetic field is minimum?
Answer:
Since F = q v B sin θ
So F will be minimum, if sin θ = 0, i.e. θ = 0 or 180°.
So force will be minimum if the charged particle moves parallel or antiparallel to the field.

Question 68.
Under what condition an electron moving through a magnetic field experiences the maximum force?
Answer:
Since F = q v B sin θ
So F will be maximum, if sin θ = 0 or θ = 90°.
So force will be maximum if the charged particle moves perpendicular to the field.

Question 69.
An electron and a proton moving parallel to each other in the same direction with equal momenta enter into a uniform magnetic field which is at right angles to their velocities. Trace their trajectories in the magnetic field.
Answer:
Since \(\frac{m v^2}{r}\) = q v B
∴ r = \(\frac{m v}{q \mathrm{~B}}\)
Both will have circular trajectories but in opposite directions.

Question 70.
An electron is moving along (+) x-axis in the presence of uniform magnetic field along (+) y-axis. What is the direction of force acting on it?
Answer:
From Fleming L.H. Rule, the direction of force is along (-) z-axis.

Question 71.
In a certain arrangement a proton does not get deflected while passing through a magnetic field region. Under what condition is this possible?
Answer:
Since force acting on a proton of charge q in a magnetic field B is
F = q uB sin θ
If    θ = 0° or 180°, F = 0.

Question 72.
What will be the path of a charged particle moving along the direction of a uniform magnetic field?
Answer:
The path will be a straight line, because no force is experienced by a charged particle in a magnetic field, if v | | B.

Question 73.
State two properties of the material of the wire used for the suspension of the coil in a moving coil galvanometer.
Answer:

• Its tensile strength should be high, so that it does not break due to the weight of the coil.
• Its restoring torque per unit twist should be low.

Question 74.
Give two factors by which the current sensitivity of the moving coil galvanometer can be increased.
Answer:
Since current sensitivity = \(\frac{n \mathrm{BA}}{k}\).
So to increase current sensitivity, we have to increase magnetic field (B) and decrease k.

Question 75.
An ammeter and a milliammeter are converted from the same galvanometer. Out of two, which current measuring instrument has higher resistance?
Answer:
Milliammeter has higher resistance because an ammeter requires a shunt of smaller resistance.

Question 76.
How can a galvanometer be converted into voltmeter?
Answer:
A galvanometer can be converted into a voltmeter by connecting a suitable high resistance in series to its coil.

Question 77.
How can a galvanometer be converted into an ammeter?
Answer:
A galvanometer can be converted into an ammeter by connecting a suitable low resistance in parallel to its coil.

Question 78.
Write an expression for the force experienced by a charged particle moving in a uniform magnetic field B.
Answer:
F = q v B sin θ.

Question 79.
What is the nature of the magnetic field in moving coil galvanometer?
Answer:
The magnetic field in the moving coil galvanometer is radial i.e. always parallel to the plane of the coil.

Question 80.
How will the magnetic field intensity at the centre of a circular coil carrying current change, if the current through the coil is doubled and the radius of the coil is halved?
Answer:
In first case. At the centre of circular coil
B = \(\frac{\mu_0 \mathrm{I}}{2 r}\)
In second case I' → 2I and r' = r/2
So B' = \(\frac{\mu_0 \mathrm{I}^{\prime}}{2 r^{\prime}}=\frac{\mu_0 2 \mathrm{I}}{2 \frac{r}{2}}=4\left(\frac{\mu_0 \mathrm{I}}{2 r}\right)\)
or B' = 4B.

Question 81.
A charged particle enters into a uniform magnetic field experiences an upward force as indicated in the figure. What is the charge sign on the particle?

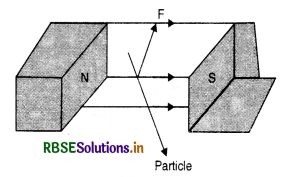
Answer:
Using Fleming’s left hand rule, the charge on the particle is positive moving normal to the magnetic field towards outwards and experience a force upwards.

Question 82.
The force \(\overrightarrow{\mathrm{F}}\) experienced by a particle of charge q moving with velocity \(\overrightarrow{\mathrm{v}}\) in a magnetic field \overrightarrow{\mathrm{B}} is given by \(\overrightarrow{\mathrm{F}} \)= q(\(\overrightarrow{\mathrm{v}}\) x \(\overrightarrow{\mathrm{B}}\)), which pair of vectors are always at right angle to each other?
Answer:
\(\overrightarrow{\mathbf{v}}\), \(\overrightarrow{\mathbf{F}}\) and \(\overrightarrow{\mathbf{B}}\) , \(\overrightarrow{\mathbf{F}}\) are two pairs ⊥ to each other.

Question 83.
Which of the two, an ammeter or a milliameter, has a higher resistance and why?
Answer:
A milliammeter has a higher resistance than an ammeter because a very small current is to pass through a milliammeter as compared to an ammeter and hence millammeter has more resistance than an ammeter.

Question 84.
An electron beam is projected along +ve x-axis, experiences a force due to magnetic field along y-axis. What is the direction of magnetic field?
Answer:
As given by Fleming’s Left Hand Rule, the direction of magnetic field is along -ve z-axis.

Short Answer Type Questions

Question 1.
Define tesla. In what other ways can it be written?
Answer:
We know
F = q v B sin θ
B = \(\frac{\mathrm{F}}{q v \sin \theta}\)
If q = 1 C; v = 1 ms^-1; θ = 90°; sin 90° = 1; F = IN,
Then B = \(\frac{1}{1 \times 1 \times 1}\) = 1 tesla.
Thus magnetic induction is said to be 1 tesla if a charge of 1C moving at right angles to it with a velocity of 1 ms^-1 experiences a force of IN. Other ways of writing tesla
(i) 1 tesla = 1 Wb m^-2
(ii) 1 tesla = \(\frac{1 \mathrm{~N}}{1 \mathrm{C} \times 1 \mathrm{~ms}^{-1}}=\frac{1 \mathrm{~N}}{1 \mathrm{Cs}^{-1} \times 1 \mathrm{~m}}\)
or 1 T = \(\frac{1 N}{1 \mathrm{~A} \times 1 \mathrm{~m}}\) = 1 N A^-1 m^-1

Question 2.
Is there a magnetic force exerted by a magnetic field on a stationary electric charge?
Answer:
No, because force \(\overrightarrow{\mathrm{F}}\) exerted by magnetic field \(\overrightarrow{\mathrm{B}}\) on a charge q is
\(\overrightarrow{\mathrm{F}}\) = q(\(\overrightarrow{\mathrm{v}}\) x \(\overrightarrow{\mathrm{B}}\))
For stationary charge
\(\overrightarrow{\mathrm{v}}\) = 0 ∴ \(\overrightarrow{\mathrm{F}}\) = 0 

Question 3.
Is any work done by magnetic field on moving charge perpendicular to the magnetic field?
Answer:
No. Because force on a moving charge is
\(\overrightarrow{\mathrm{F}}\) = q (\(\overrightarrow{\mathrm{v}}\) x \(\overrightarrow{\mathrm{B}}\))
The direction of \(\overrightarrow{\mathrm{F}}\) is perpendicular to \(\overrightarrow{\mathrm{v}}\) and \(\overrightarrow{\mathrm{B}}\).
Since W = \(\overrightarrow{\mathrm{F}}\).\(\overrightarrow{\mathrm{S}}\)
= F S cos θ
= FS cos 90° [∵ angle between F & S is 90°]
= 0
i.e. No work is done

Question 4.
An electron is not deflected while moving through a certain region of space. Can we say that there is no magnetic field in the region?
Answer:
No. Since force acting on a charged particle q moving with velocity v is
\(\overrightarrow{\mathrm{F}}\) = q (\(\overrightarrow{\mathrm{v}}\) x \(\overrightarrow{\mathrm{B}}\))
or F = q v B sin θ
For charge moving parallel to magnetic field
θ = 0
∴ F = 0
Thus when a charged particle is moving parallel to the magnetic field, it will not be deflected.

Question 5.
A magnetic field that varies in magnitude from point to point but has a constant direction (east to west) is set up in a chamber. A charged particle enters the chamber and travels undeflected along a straight path with constant speed. What can you say about the initial velocity of the particle?
Answer:
The force on a charged particle moving inside magnetic field is given by
\(\overrightarrow{\mathrm{F}_m}=q(\vec{v} \times \overrightarrow{\mathrm{B}})\)
The force on particle will be zero (will remain undeflected), if \(\overrightarrow{\mathrm{v}}\) x \(\overrightarrow{\mathrm{B}}\) is equal to zero i.e. if initial velocity v is either parallel or antiparallel to magnetic field B.

Question 6.
An electron travelling west to east enters a chamber having a uniform magnetic field in a north to south direction. Specify the direction in which a uniform magnetic field should be set up to prevent the electron deflecting from its straight line path.
Answer:
Under the action of electrostatic field, the electron will be deflected towards north (towards positive plate). It will remain undeflected, if force due to magnetic field is towards south. For \(\overrightarrow{\mathrm{v}}\) velocity from west to east, the expression for magnetic Lorentz force
\(\overrightarrow{\mathrm{F}_m}=-e(\vec{v} \times \overrightarrow{\mathrm{B}})\)
or Fleming left hand rule tells that \(\overrightarrow{\mathrm{B}}\) should be applied along vertical and in downward direction.

Question 7.
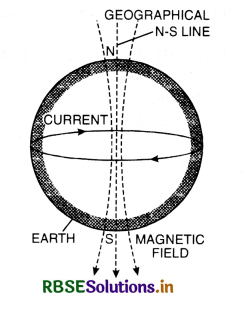
Assuming that the earth's magnetic field is due to large circular loop of current in the interior of the earth, what is the plane of the loop and what is the direction of current around it?
Answer:
The direction of magnetic field at the centre of the earth is from north to south. (It is on the surface of earth that the magnetic field is from south to north). The magnetic field will be produced along the NS direction, if the circular loop is held in equatorial plane and the current flows in clockwise direction, when seen from north of the earth.

Question 8.
An electron and a proton, moving parallel to each other in the same direction with equal momenta, enter a uniform magnetic field which is at right angles to their velocities. Trace their projectory in the magnetic field.
Answer:
Let mass of electron = m_e
Mass of proton = m_p
Vel. of electron = v_e
Vel. of proton = v_p
Magnitude of charge of electron = magnitude of charge of proton = q.
If the magnetic field is B, then
For electron
\(\frac{m_e v_e^2}{r}\) = B q v_e
or r =\( \frac{m_e v_e}{\mathrm{~B} q}\) ..............................(i)
For proton
\(\frac{m_p v_p^2}{\mathrm{R}}\) = B q v_p
or R = \(\frac{m_p v_p}{\mathrm{~B} q}\) ..........................(ii)
∴ Given m_ev_e = m_pv_p
So from (i) and (ii)
R = r

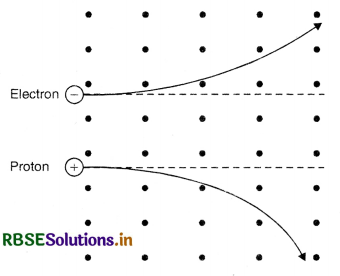
If the direction of magnetic field is perpendicular to the plane of paper in upward direction, then the trajectory of electron will be upwards and that of proton is downward in accordance with Fleming’s left hand rule as shown in figure.

Question 9.
Free electrons always keep on moving in a conductor. Even then, no magnetic force acts on them in a magnetic field unless a current is passed through it. Why?
Answer:
When no electric current is passed in a conductor and the conductor is placed in a magnetic field, no magnetic force will act on the electrons because the motion of electrons in the conductor is random motion and their average velocity is zero. And when current is passed in the conductor, the free electrons acquire drift velocity in a definite direction and hence magnetic force acts on them.

Question 10.
Two long parallel straight wires X and Y separated by a distance of 5 cm in air carry current of 10 A and 5 A respectively in opposite directions. Calculate the magnitude and direction of the force on a 20 cm length of the wire Y.

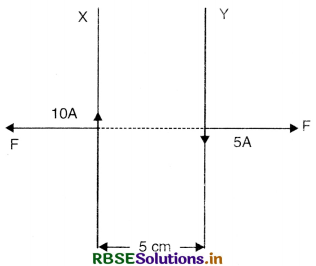
Answer:
Here r = 5 cm = 0.05 m, I₁ = 10 A, I₂ = 5A, l = 20 cm = 0.2 m, F = ?
Since F = \(\frac{\mu_0}{4 \pi} \frac{2 \mathrm{I}_1 \mathrm{I}_2}{r}\) l
∴ F = \(\frac{10^{-7} \times 2 \times 10 \times 5 \times 0.2}{0.05}\)
or F = 4 x 10^-5 N
The direction of F acting on conductor Y is in the plane of the paper, perpendicular to Y and is directed away from conductor X.

Question 11.
A neutron, a proton, an electron and an alpha particle enter a region of constant magnetic field with equal velocities. The magnetic field is along the inward normal to the plane of paper. The tracks of the particles are labeled in Fig. SAQ 11. Which of the tracks show the path of the electron and α-particle?

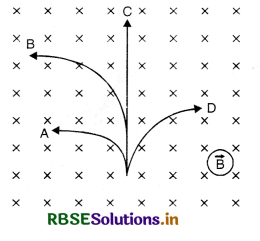
Answer:
Since neutron is a neutral particle hence it does not experience any force in \(\vec{B}\). Hence its track is given by path C.
Applying Fleming’s left hand rule, we find that the electron will be deflected towards right. Hence the track D represents the path of electron. And proton and α-particles are deflected towards left.
Since radius of a charged particle in magnetic field B is given by

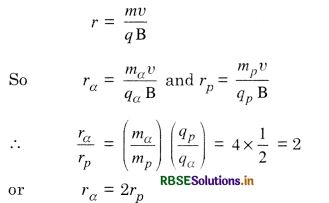
i.e. the track of α-particle is less curved than that of proton.
Hence, the track A is the path of proton and track B represents the path of α-particle.

Question 12.
A charge q moving in a straight line is accelerated by a potential difference V. It enters a uniform magnetic field B perpendicular to its path. Deduce in terms of V an expression for the radius of the circular path in which they travel.
Answer:
Let v be the velocity acquired by the electron when accelerated under a potential difference of V.
∴ eV = \(\frac{1}{2}\) mv²
or v = \(\sqrt{\frac{2 e \mathrm{~V}}{m}}\)
Since electron describes circular path of radius r in the magnetic field, therefore

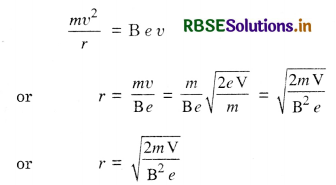
Question 13.
A proton and an alpha particle of the same velocity enter in turn a region of uniform magnetic field acting in a plane perpendicular to the magnetic field. Deduce the ratio of the radii of the circular paths described by the particles. Explain why kinetic energy of the particle after emerging from the magnetic field remains unaltered.
Answer:
For proton:
q_p = q; r_p = ?; m_p = m and 
For α-particle:
q_α = 2q; r_α = ?; m_α = 4m

1 = \(\frac{r_\alpha}{2 r_p}\)
or r_α = 2 r_p
K.E. of the particle remains the same since the angle between centripetal force and direction of motion is 90°. No work is done in rotation of the particle since W = FS cos 90° = 0. Hence K.E. remains constant.

Question 14.
A proton and an α-particle enter a uniform magnetic field perpendicularly with the same speed. How many times is the time period of α-particle than that of proton? Deduce an expression for the ratio of the radii of the circular paths of two particles.
Answer:
Since time period of a charged particle q of mass m in a magnetic field B is given by:

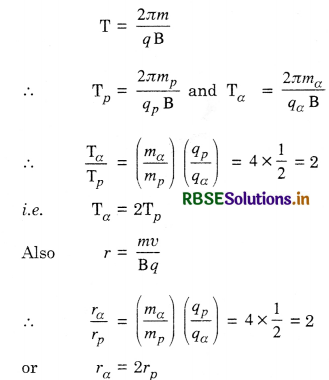
Question 15.
An electron revolves in a circular orbit of radius r with uniform angular speed w . From the expression for magnetic field due to current carrying circular conductor, deduce the expression for magnetic field at the centre of electron orbit.
Answer:
Magnetic field at the centre of a circular conductor of radius r carrying current I is
B = \(\frac{\mu_0}{4 \pi} \frac{2 \pi \mathrm{I}}{r}\) ...........................(i)
The equivalent current due to motion of electron in circular orbit is given by:
I = \(\frac{e}{T}=\frac{e}{2 \pi / \omega}\) (∵ T = \(\frac{2 \pi}{\omega}\))
or I = \(\frac{e \omega}{2 \pi}\)
So equation (i) becomes
B = \(\frac{\mu_0}{4 \pi} \frac{2 \pi}{r} \cdot \frac{e \omega}{2 \pi}\)
or B = \(\frac{\mu_0 e \omega}{4 \pi r}\)

Question 16.
Both the electric and magnetic fields can deflect a moving electron. What is the difference between these deflections?
Answer:
In electric field. The force acts on the electron in a direction opposite the electric field and the deflection produced is in the plane of the electric field and the acceleration is produced in the electron \(\left[a=\frac{e \mathrm{E}}{m}\right]\).
Hence the speed and therefore, the kinetic energy of the electron changes.

In a magnetic field. The force (\(\overrightarrow{\mathrm{F}}=q(\vec{v} \times \overrightarrow{\mathrm{B}})\)) acts nomral to the plane of direction of motion and magnetic field and the deflection produced to the electron beam is perpendicular to the plane of \(\overrightarrow{\mathrm{B}}\), hence work done by the magnetic field is zero. Hence the kinetic energy of moving electron remains unchanged.

Question 17.
In what way is an electric field different from a magnetic field?
Answer:
A charged particle always experiences force due to an electric field. It does not matter; whether the charged particle is at rest or is in motion. However, due to magnetic field, force on a charged particle acts only, when it moves inside the magnetic field and its motion is not along the direction of the magnetic field. Further, when electric field acts, the kinetic energy of the charged particle is affected. However, there is no effect on the kinetic energy of a charged particle due to its motion inside the magnetic field.

Question 18. 
In what respect does a wire carrying a current differ from a wire, which carries no current?
Answer:
A current carrying wire produces magnetic field. It is because, when current flows through a wire, electrons move inside it along a definite direction. On the other hand, in a wire which carries no current, electrons are in motion in random directions. Such a wire does not produce any magnetic field.

Question 19.
Two parallel wires carrying current in the same direction attract each other, while two beams of electrons travelling in the same direction repel each other. Why?
Answer:
When current flows through two parallel wires in the same direction, the force F_m experienced by one wire is due to the magnetic field produced by the other wire and is attractive in nature.
In case of two beams of electrons moving in the same direction, in addition to F_m another force F_e (electrical and repulsive for two electrons) also acts.
Since F_m < F_e.
In fact F_m = 10^-27 F_e, the electrons experience a strong repulsive force only.
 
Question 20.
Explain with reason, in which direction does the current loop KLMN move when kept near an infinitely long straight wire carrying current as shown in figure.

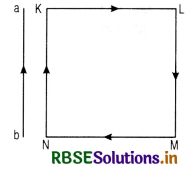
Answer:
Due to interaction of current in ab and KN there will be a force of repulsion (current in opposite directions) given by
F₁ = \(\frac{\mu_0}{4 \pi} \times \frac{2 \mathrm{I}_1 l_2}{r_1}\)
and due to interaction between ab and LM there will be a force of attraction (currents in same direction) and given by

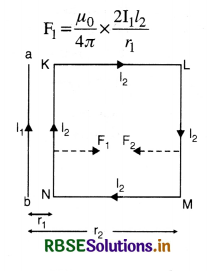
Clearly force of attraction F₂ is lesser than force of repulsion F₂ . Hence the coil will be repelled away from ab.
Forces on NM and KL will be equal and opposite and acting in the same plane therefore they will cancel each other.
Net repulsive force is
F₁ - F₂ = \(\frac{\mu_0 \mathrm{I}_2 \mathrm{I}_2}{4 \pi}\left[\frac{1}{r_1}-\frac{1}{r_2}\right]\)

Question 21.
Why an electron cannot be accelerated in a cyclotron?
Answer:
A cyclotron cannot accelerate electrons because owing to their small mass even a comparatively small increase in energy of the electrons gives them a very high velocity because of which the mass starts increasing and they go out of step with the oscillating electric field.

Question 22.
Find the expression for maximum energy of a charged particle accelerated by a cyclotron.
Answer:
Let r₀ = Maximum radius of circular path followed by charged particle (Equal to the radius of the Dees)
v₀ = Maximum velocity
Since the necessary centripetal force is provided by the Lorentz magnetic force, therefore,

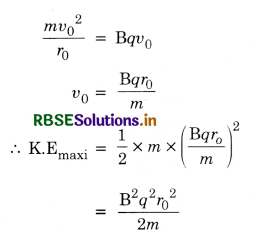
This is the required result.

Question 23.
What is the effect of charged particle in magnetic and electric field acting perpendicular to each other?
Answer:
Consider a charged particle moving with velocity v in an electric field of strength \(\overrightarrow{\mathrm{E}}\) and magnetic field \(\overrightarrow{\mathrm{B}}\). It is supposed, that electric field \(\overrightarrow{\mathrm{E}}\) and magnetic field \(\overrightarrow{\mathrm{B}}\) act mutually perpendicular to each other and charged particle moves perpedicular to magnetic field \(\overrightarrow{\mathrm{B}}\).

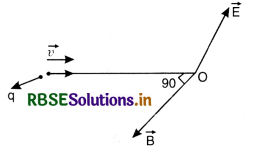
Force acting on the charged particle due to electric field
\(\overrightarrow{\mathrm{F}}_e=q \overrightarrow{\mathrm{E}}\)
Force acting on the charged particle due to magnetic field
\(\overrightarrow{\mathrm{F}}_m=q(\vec{v} \times \overrightarrow{\mathrm{B}})\)
This force will act perpendicular to the plane containing \(\overrightarrow{\mathrm{v}}\) and \(\overrightarrow{\mathrm{B}}\) i.e. in the direction of \(\overrightarrow{\mathrm{E}}\).
∴ Total force acting on the charged particle due to electric and magnetic field will be
\(\overrightarrow{\mathrm{F}}=\overrightarrow{\mathrm{F}}_e+\overrightarrow{\mathrm{F}}_m\)
= q \(\overrightarrow{\mathrm{E}}+q(\vec{v} \times \overrightarrow{\mathrm{B}})\)
or \(\overrightarrow{\mathrm{F}}=q[\overrightarrow{\mathrm{E}}+(\vec{v} \times \overrightarrow{\mathrm{B}})]\)
or F = q [E + vB sin 90°]
or F = q [E + vB]
If the direction of magnetic field is so adjusted that force exerted by electric field is opposite to the force exerted by magnetic field, therefore, the electron then travels unaffected from the original direction of motion.

Question 24.
An electron beam passes through a region of crossed electric and magnetic fields of strength E and B respectively. For what value of electron speed the beam will remain undeflected?
Answer:
Since electric force on the electron beam, F_e = eE.
And magnetic force on the electron beam, F_m = e v B.
So the electron beam will pass undeflected, if
F_e = F_m
or e E = e v B
or v = \(\frac{E}{B}\).

Question 25.
An electron and a proton, moving parallel to each other in the same direction with equal momenta, enter a uniform magnetic field which is at right angles to their velocities. Trace their projectory in the magnetic field.
Answer:
Let mass of electron = m_e
Mass of proton = m_p
Vel. of electron = v_e
Vel. of proton = v_p
Magnitude of charge of electron = magnitude of charge of proton = q.
If the magnetic field is B, then
For electron
\(\frac{m_e v_e^2}{r}\) = B q v_e
or r = \(\frac{m_e v_e}{\mathrm{~B} q}\) ..............................(i)
For proton
\(\frac{m_p v_p^2}{\mathrm{R}}\) = B q v_p
or R = \(\frac{m_p v_p}{\mathrm{~B} q}\) ..........................(ii)
∴ Given m_ev_e = m_pv_p
So from (i) and (ii)
R = r

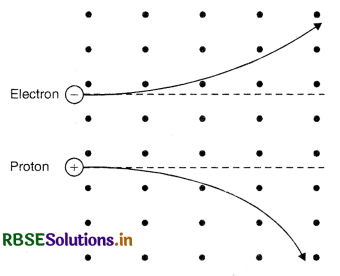
If the direction of magnetic field is perpendicular to the plane of paper in upward direction, then the trajectory of electron will be upwards and that of proton is downward in accordance with Fleming’s left hand rule as shown in figure.

Question 26.
Explain why two long parallel straight conductors carrying current in opposite directions in air repel?
Answer:
When two long parallel straight conductors PQ and RS carrying currents I₁ and I₂ in opposite directions, each conductor experiences force due to
the magnetic field of other conductors. Using Fleming Left Hand Rule, the forces \(\overrightarrow{\mathrm{F}}_1\) and \(\overrightarrow{\mathrm{F}}_2\) experienced

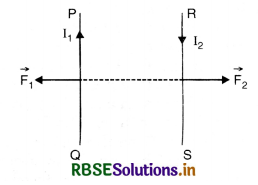
by the conductors are away from each other i.e. they repel each other. 

Question 27.
Write a relation for the force \(\overrightarrow{\mathbf{F}}\) acting on a charge carrier q moving with velocity \(\overrightarrow{\mathbf{v}}\) through the magnetic field \(\overrightarrow{\mathbf{B}}\) in vector notation. Using this relation, deduce the conditions under which this force will be (i) maximum (ii) minimum.
Answer:
The magnetic force \(\overrightarrow{\mathbf{F}}\) is given by
\(\overrightarrow{\mathbf{F}}\) = q(\(\overrightarrow{\mathbf{v}}\) x \(\overrightarrow{\mathbf{B}}\))
or F = q v B sin θ
where θ is the angle between \(\overrightarrow{\mathbf{v}}\) and \(\overrightarrow{\mathbf{B}}\)
(i) For maximum, sin θ = 1 or θ = \(\frac{\pi}{2}\)
And F_max = q v B
(ii) For minimum, sin θ = 0 or θ = 0° or π
And F_min = 0.

Question 28.
A charge q moving in a straight line is i accelerated by a potential difference V. It enters a uniform magnetic field B perpendicular to its path. Deduce in terms of V an expression for the radius of the circular path in which they travel.
Answer:
Let v be the velocity acquired by the electron when accelerated under a potential difference of V.
∴ eV = \(\frac{1}{2}\) mv²
or v = \(\sqrt{\frac{2 e \mathrm{~V}}{m}}\)
Since electron describes circular path of radius r in the magnetic field, therefore

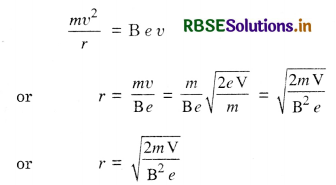
Question 29.
A proton and an alpha particle of the same velocity enter in turn a region of uniform magnetic field acting in a plane perpendicular to the magnetic field. Deduce the ratio of the radii of the circular paths described by the particles. Explain why kinetic energy of the particle after emerging from the magnetic field remains unaltered.
Answer:
For proton:
q_p = q; r_p = ?; m_p = m and 
For α-particle:
q_α = 2q; r_α = ?; m_α = 4m

1 = \(\frac{r_\alpha}{2 r_p}\)
or r_α = 2 r_p
K.E. of the particle remains the same since the angle between centripetal force and direction of motion is 90°. No work is done in rotation of the particle since W = FS cos 90° = 0. Hence K.E. remains constant.

Question 30.
What do you mean by current sensitivity of a moving coil galvanometer? On what factors does it depend?
Answer:
Current Sensitivity of a galvanometer is defined as the deflection produced in the galvanometer on passing unit current through its coil.
Current sensitivity depends upon

1. Number of turns of the coil
2. Area of the coil
3. Torsional rigidity of the suspension wire
4. Strength of the magnetic field produced by the magnet.

Question 31.
You are given a low resistance R₁, a high resistance R₂ and a moving coil galvanometer. Suggest how would you use these to have an instrument that will be able to measure (i) current (ii) potential difference?
Answer:

• To measure current, the low resistance R₁ will be connected in parallel with the coil of the galvanometer. This arrangement is called Ammeter.
• To measure potential difference, high resistance R₂ will be connected in series with the coil of the galvanometer. This arrangement is called voltmeter.

Question 32.
A particle of mass m, with charge q moving with a uniform speed v, normal to a uniform magnetic field B, describes a circular path of radius r. Derive expression for the (i) time period of revolution and (ii) kinetic energy of the particle.
Answer:
(i) When the charge is moving normal to the uniform magnetic field, the centripital force is provided by the magnetic field

Question 33.
A deuteron and an alpha particle having same momentum are in turn allowed to pass through a magnetic field B, acting normal to the direction of motion of the particles. Calculate the ratio of the radii of the circular paths described by them.
Answer:
pd = pα
Now r = \(\frac{m v}{B q}=\frac{p}{B q}\) ⇒ r ∝ \(\frac{1}{q}\)
Therefore, \(\frac{r_d}{r_\alpha}=\frac{q_\alpha}{q_d}=\frac{2 e}{e}\) = 2

Question 34.
How will you convert galvanometer into an ammeter? Why is an ammeter always connected in series?
Answer:
Magnetic field at the centre of a circular conductor of radius r carrying current I is
B = \(\frac{\mu_0}{4 \pi} \frac{2 \pi \mathrm{I}}{r}\) ...........................(i)
The equivalent current due to motion of electron in circular orbit is given by:
I = \(\frac{e}{T}=\frac{e}{2 \pi / \omega}\) (∵ T = \(\frac{2 \pi}{\omega}\))
or I = \(\frac{e \omega}{2 \pi}\)
So equation (i) becomes
B = \(\frac{\mu_0}{4 \pi} \frac{2 \pi}{r} \cdot \frac{e \omega}{2 \pi}\)
or B = \(\frac{\mu_0 e \omega}{4 \pi r}\)

Question 35.
A charge q of mass m moving with velocity v, at right angles to a uniform magnetic field B. Deduce the expression for the radius of the circular path it describes.
Answer:
A current carrying wire produces magnetic field. It is because, when current flows through a wire, electrons move inside it along a definite direction. On the other hand, in a wire which carries no current, electrons are in motion in random directions. Such a wire does not produce any magnetic field.
i.e. r = \(\frac{m v}{q \mathrm{~B}}\).

Long Answer Type Questions

Question 1.
Define magnetic field. Write an expression for force on a charge q moving with velocity \(\overrightarrow{\mathbf{v}}\) in a region having uniform magnetic field strength\( \overrightarrow{\mathbf{B}}\). How does the speed change as the charge moves? Under what circumstances the force \(\overrightarrow{\mathbf{F}}\) will be zero and maximum? Also obtain S.I. unit of the strength of magnetic field. Also give dimensional formula of B.
Answer:
Magnetic field. A magnetic field is the space around a magnet or around a current carrying conductor in which magnetic influence can be felt.
In general, a moving charge is a source of magnetic field. Thus the strength of magnetic field B can be defined by deriving an expression for the force acting on a moving charge in a magnetic field.
Expression for force on a charge moving in a uniform magnetic field (or Magnetic Lorentz force)
Let a charge +q be moving inside a magnetic field of strength \(\overrightarrow{\mathbf{B}}\) with velocity \(\overrightarrow{\mathbf{v}}\) making an angle θ with \(\overrightarrow{\mathbf{B}}\) as shown in the figure LAQ 1. The charge q will experience a force \(\overrightarrow{\mathbf{F}}\) along X-axis called Lorentz

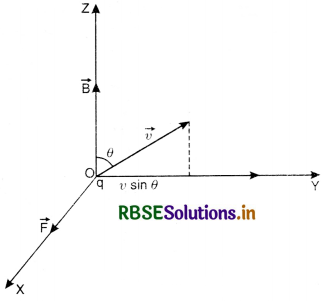
It is found that, the magnitude of the force is
(i) directly proportational to the magnitude of the strenght of magnetic field
i.e. F ∝ B
(ii) directly proportational to the magnitude of charge q
i.e. F ∝ q
(iii) directly proportational to the component of velocity along a direction perpendicular to the direction of magnetic field
i.e. F ∝ v sin θ
Combining all the above factors, we get
F ∝ q B v sin θ
or F = kq B v sin θ
where k is constant of proportionality and in S.I., its value is found to be 1.
∴ F = q B v sin θ .......................(1)
In vector form
\(\overrightarrow{\mathrm{F}}=q(\vec{v} \times \overrightarrow{\mathrm{B}})\) ..................................(2)
This is called Lorentz magnetic force acting on a moving charge inside a magnetic field.

Effect of magnetic field on speed of the charge
Since force \(\vec{F}\) is perpendicular to both \(\vec{v}\) and \(\vec{B}\), so it is centripetal force. Hence the speed of charge does not change as it moves inside the magnetic field.

Condition for force to be zero: F = 0 for following two cases:
(i) If θ = 0° or 180°
Then from Eqn. (1), we have
F = qv B. 0 = 0 [∵ sin 0° = sin 180° = 0]
i.e. charged particle moving parallel or antiparallel to the magnetic field experiences no force.
(ii) If v = 0 i.e. the charged particle is at rest.
Then from Ezn. (1), we have
F = q.0. B sin θ = 0
i.e. if a charged particle is at rest in a magnetic field, it will experience no force.

Condition for force to be maximum
If    θ = 90°, then from equation (1), we have
F = q.B sin 90° = qvB
i.e. a charged particle will experience a maximum force when moving perpendicular to the magnetic field.

Definition of \(\vec{B}\)
From eq. (1)
B = \(\frac{\mathrm{F}}{q v \sin \theta}\)
In S.I. if F = 1N, q = 1 C, v = 1 ms^-1, then B = 1 tesla (T)
So strength of magnetic field is said to be I T, if 1C charge is moving with velocity of 1 ms^-1 at right angle to a magnetic field experiences a force of 1N.
So 1 T = \(\frac{1 \mathrm{~N}}{1 \mathrm{C} .1 \mathrm{~ms}^{-1}}=\frac{1 \mathrm{~N}}{1 \mathrm{As} .1 \mathrm{~ms}^{-1}}\)
= NA^-1m^-1    [∵ 1C = 1A.1S]

Dimensional formula of B
B = \( \frac{\mathrm{F}}{q v \sin \theta}=\frac{\left[\mathrm{M} \mathrm{L} \mathrm{T}^{-2}\right]}{[\mathrm{AT}]\left[\mathrm{LT}^{-1}\right]}\)
= [MA^-1T^-2]

Question 2.
(a) Discuss Oersted’s experiment to establish that magnetic field is produced due to current in a wire.
(b) Give the arrangement of magnetic field round a straight wire and state the rule to find the direction of magnetic field.
Answer:
(a) Oersted’s Experiment. A Danish science teacher Hans Oersted observed that when a wire was arranged above and parallel to a compass needle and current was passed through it as shown in Fig. LAQ 2 (a) the N-pole of the needle was deflected towards west to a position that was no longer parallel to the wire. On reversing the direction of current, the N-pole was deflected towards east.

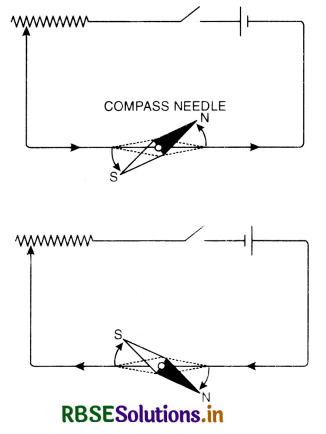
A magnetic needle can be deflected only by another magnetic field. The current in the wire, therefore, must be producing a magnetic field. Magnetism produced by current is called electromagnetism.
The above direction of magnetic needle can be summarised by Snow Rule.
Snow Rule. Current from S to N, in a wire placed over a magnetic needle, the north of the needle is deflected towards west.

(b) Magnetic field round a straight wire Set up vertically a large rectangular coil of about 10 turns of thick insulated copper wire and pass one of its sides through a hole in a piece of cardboard. Connect it in series with a rheostat, a switch, an ammeter and a battery as shown in Fig. LAQ 2 (c).

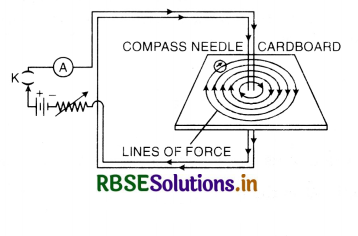
Close the key and adjust the rheostat so that a current of 2-3 amperes passes through the coil. Map the field around the wire either using iron filings or a compass needle. It is found that the lines of force are concentric circles with the wire as centre. The direction of the lines of force can be worked out by Maxwell’s right hand grip rule. Imagine the wire gripped in the right hand with the thumb pointing along the wire in the direction of the current. Then the direction of the fingers will give the direction of lines of force (Fig. LAQ 2 (d))

On reversing the direction of current by interchanging the connections of the battery, the N-pole of the compass needle is found to point in the opposite direction i.e. the direction of field is reversed.

Question 3.
Explain Biot-Savart’s law for the magnetic field produced at a point due to the current flowing in a current element. How will you determine the direction of the field?
Answer:
Biot-Savart's law
This law is used to find the magnetic field intensity at a point due to a current carrying conductor.
Let us consider a small element XY (of length dl) of a conductor PQ through which a current 1 is flowing.
If dB is the magnetic field induction at a distance r from dl at a point P, according to this law
dB ∝ I (strength of current) ...................(1)

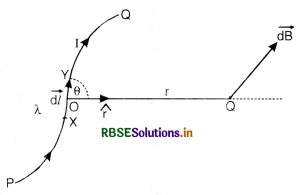
dB ∝ dl (Length of current element) ...................(2)
dB ∝ sin θ (θ is Angle between \(\vec{r}\) and \(\overrightarrow{d l})\) ....................(3)
dB ∝ \(\frac{1}{r^2} \)..................(4)
Combining (1), (2), (3) and (4)
dB ∝ \(\frac{\mathrm{I} d l \sin \theta}{r^2}\)
∴ dB = k.\(\frac{\mathrm{I} d l \sin \theta}{r^2}\) ..............................(5)
In SI Units
k = \(\frac{\mu_0}{4 \pi}\) ...........................(6)
where µ₀ is called the absolute permeability of free space
and µ₀ = 4π x 10^-7 Wb A^-1 m^-1
∴ dB = \(\frac{\mu_0}{4 \pi} \cdot \frac{\mathrm{I} d l \sin \theta}{r^2}\) ...................................(7)
Vector form
If we denote the distance of the element from Q by the displacement vector \( \vec{r}\) and the length of the element \(\overrightarrow{d l}\), then

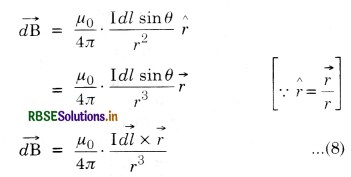
Direction of \(\overrightarrow{d B}\). Applying the right hand rule for the vector product of two vectors, we find that \(\overrightarrow{d B}\) is perpendicular to the plane containing \(\overrightarrow{d B}\) and \(\overrightarrow{r}\) and is directed inwards. The direction of magnetic field is also given by Right Hand Rule.
Imagine the current element to be grasped in the right hand so that the extended thumb points in the direction of the current. The direction of the field lines is then given by the fingers encircling the element.

Question 4.
Derive an expression for the intensity of magnetic field at the centre of a circular coil carrying current.
Or
State the Biot-Savart’s law for the magnetic field due to a current carrying element. Use this law to obtain a formula for magnetic field at the centre of circular loop of radius r carrying steady current I. Sketch the magnetic field lines for a current loop clearly indicating the direction of the field.
Answer:
Biot-Savart’s law. It states that the magnetic field induction dB at point P due to a current element\( \mathrm{I} \overrightarrow{d l}\) is given as
(i) dB ∝ I
(ii) dB ∝ dl
(iii) dB ∝ sin θ
(iv) dB ∝ \(\frac{1}{r^2}\)
Combining these factors, we get

dB ∝ \(\frac{\mathrm{I} d l \sin \theta}{r^2}=\frac{\mu_0}{4 \pi} \frac{\mathrm{I} d l \sin \theta}{r^2}\)
In vector form
d \(\overrightarrow{\mathrm{B}} = \frac{\mu_0}{4 \pi} \mathrm{I} \frac{\overrightarrow{d l} \times \vec{r}}{r^3}\)
The direction of d \(\overrightarrow{\mathrm{B}}\) is perpendicular to the plane of paper and directed inwards.

Intensity of magnetic field at the centre of a circular coil carrying current. Consider a conductor bent into the form of the loop of a circle and carrying current I as shown in Fig. LAQ 4 (b). Let us determine the intensity of the magnetic field at the centre of the circle O.
Consider an element AB = d \(\overrightarrow{\mathrm{l}}\) of the circular loop. The magnetic field at the centre O due to this current element is given by
\(\overrightarrow{d \mathbf{B}}=\frac{\mu_0}{4 \pi} \cdot \frac{\mathrm{I} d \vec{l} \times \vec{r}}{r^3}\)
where \(\vec{r}\) is the vector from current element of length \(\overrightarrow{d l}\) to the point O. 

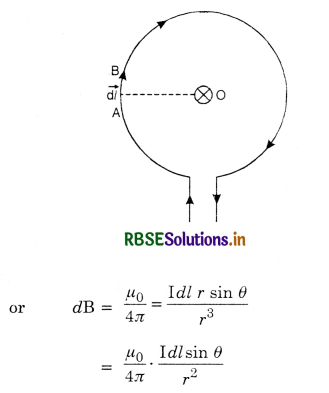
Since the angle θ between dl and r is 90°, we have
dB = \(\frac{\mu_0}{4 \pi} \cdot \frac{\mathrm{I} d l}{r^2}\) ......................(1)
The direction of this field is perpendicular to the plane of the loop and directed away from the reader and is shown by the sign of a cross in a circle (resembling the tail of an arrow).
The loop can be divided into a large number of such current elements. The magnitude of the field due to each current element is the same as that given by Eqn. (1) and is perpendicular to the plane of the loop directed away from the reader.
The total magnetic field at O is given by

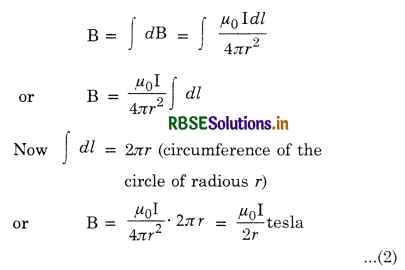
If the coil consists of n turns wound one over the other, we have
B = \(\frac{\mu_0 n \mathrm{I}}{2 r}tesla\). ............................(3)
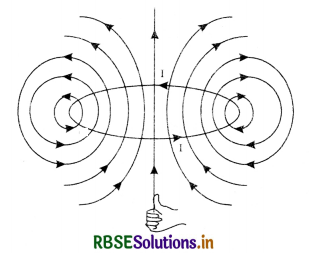
Magnetic field lines of circular current loop
The magnetic field lines due to circular wire form a closed loop are shown in Fig. LAQ 4 (c) and the direction of magnetic field is given by right hand thumb rule.

Question 5.
Derive an expression for the magnetic field intensity due to current flowing in a long straight conductor.
Answer:
Magnetic field due to a long straight conductor
Consider a long straight conductor XY through which current I is flowing from end X to Y as shown in Fig. LAQ 5. According to Biot-Savart’s law, strength of magnetic field at point P due to small element AB is given by
\(\overrightarrow{d \mathrm{~B}}=\frac{\mu_0}{4 \pi} \cdot \frac{\mathrm{I} \overrightarrow{d l} \times \vec{r}}{r^3}.\)
where \(\mathrm{I} \overrightarrow{d l}\) is a vector in the direction of flow of current and \(\vec{r}\) is a vector from A to P.

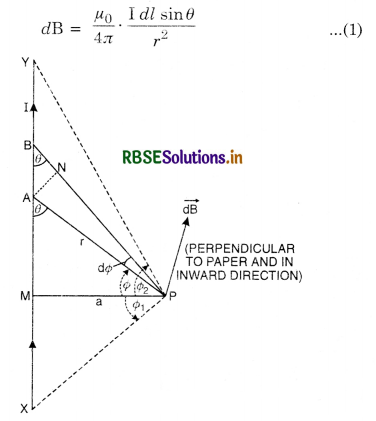
Since AB = dl is infinitesimally small, ∠ABP will also be equal to θ. If we drop AN perpendicular to BP, then from right angled triangle ABN, we have
dl sin θ = AN
substituting for dl sin θ in equation(1), we have
dB = \(\frac{\mu_0}{4 \pi} \cdot \frac{\mathrm{I}(\mathrm{AN})}{r^2}\) ................................(2)
Let ∠APM = Φ and ∠APB = dΦ. Then,
AN = rdΦ
Substituting for AN in equation (2), we have
dB = \(\frac{\mu_0}{4 \pi} \cdot \frac{\mathrm{I}(r d \phi)}{r^2}\)
or dB = \(\frac{\mu_0}{4 \pi} \cdot \frac{\mathrm{I} d \phi}{r}\) ..........................(3)
From right angled triangle AMP, we have
cos Φ = \(\frac{a}{r}\)
or r = \(\frac{a}{\cos \phi}\)
Substituting for r in equation (3), we have
dB = \(\frac{\mu_0}{4 \pi} \cdot \frac{I \cos \phi d \phi}{a}\) .............................(4)
Join PX and PY. Let ∠XPM = Φ₁ (in anticlockwise direction) and ∠YPM = Φ₂ (in clockwise direction). Then, magnetic field due to the whole length of the conductor can be found by the integrating dB given by equation (4) in limits - Φ₁ to Φ₂. Thus, magnetic field due to current flowing through whole conductor XY is given by

For infinitely long conductor,
Φ₁ - Φ₂ =\( \frac{\pi}{2}\)
sin Φ₁ = sin Φ₂ = 1
∴ B = \(\frac{\mu_0}{4 \pi} \frac{2 \mathrm{I}}{a}=\frac{\mu_0 \mathrm{I}}{2 \pi a}\)
The direction of the magnetic field is given by Right hand thumb rule or Maxwell’s cork screw rule.
Right hand thumb rule
According to this rule, if we grasp the conductor in the palm of the right hand so that the thumb points in the direction of the flow of curren t, then the direction in which the fingers curl, gives the direction of magnetic lines of force.
Maxwell’s cork screw' rule. If a right handed cork screw is rotated, so that it moves in the direction of flow of current through the conductor, then the direction of the rotation of the thumb gives the direction of magnetic lines of force.

Question 6.
State Biot-Savart’s law'. Using this law. derive the expression for the magnetic field due to a current carrying circular loop of radius ‘R’ at a point which is at a distance ‘x’ from its centre along the axis of the loop.
Answer:
Biot-Savart’s law. It states that the magnetic field dB at a point P due to a curren t element Idl is given by
dB ∝ \(\frac{I d l \sin \theta}{r^2}\)
or dB = \(\frac{\mu_0}{4 \pi} \frac{\mathrm{Idl} \sin \theta}{r^2}\)
Magnetic Field at a Point on the Axis of a Circular Coil
I = Current length the coil
Let, O be the centre of coil
R = Radius of the circular coil
x = Distance of point P on the axis from the centre of the coil
AB = an element of the coil
dl = Length of the element AB
CP = r
According to Biot-Savart’s law, magnetic field dB at the point P due to element\( \overrightarrow{d l}\) is given by

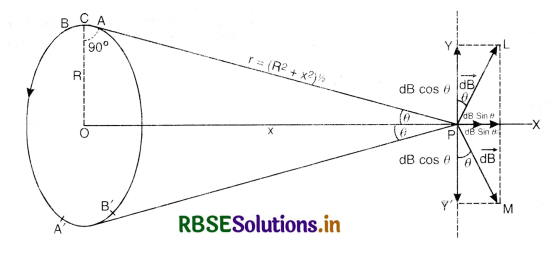
\(\overrightarrow{d \mathrm{~B}}=\frac{\mu_0}{4 \pi} \frac{\mathrm{I} \overrightarrow{d l} \times \vec{r}}{r^3}\)
The direction \(\overrightarrow{d \mathrm{~B}}\) at point P will be along PL i.e. perpendicular to CP and in the plane of paper. As angle between \(\mathrm{I} \overrightarrow{d l}\) and \(\vec{r} \)is 90°, the magnitude of magnetic field due to small element at point P is given by
dB = \(\frac{\mu_0}{4 \pi} \cdot \frac{\mathrm{I} d l}{r^2}\) ................................(1)
If we calculate the magnitude \(\overrightarrow{d \mathrm{~B}}\) due to an equal current element A'B' lying just opposite to the current element AB, it will be found that the magnitude of the magnetic field in this case also is the same as given by equation (1) but it acts along PM. The components of two magnetic fields along YY' will cancel out as they are equal in magnitude and opposite in direction. Same will happen for the current element taken in similar pairs.
Therefore, component of magnetic field due to a current element along PX is dB sin θ. The magnetic field due to the whole coil at P is obtained by integrating dB sin θ over the circumference of the coil i.e.
Magnetic field at P due to the circular coil is given by
B = ∫dB sin θ
= ∫\(\frac{\mu_0}{4 \pi} \cdot \frac{\mathrm{I} d l}{r^2}\) sin θ
= \(\frac{\mu_0}{4 \pi} \cdot \frac{\mathrm{I}}{r^2}\) sin θ ∫dl
Now, ∫ dl = circumference of the coil of radius R, = 2πR

The direction of magnetic field is along PX.
If the coil consists of n turns, then strength of magnetic field at point P due to the coil will become n times that given by equation (2) i.e.
B =\( \frac{\mu_0}{4 \pi} \cdot \frac{2 \pi n \mathrm{IR}^2}{\left(\mathrm{R}^2+x^2\right)^{3 / 2}}\)
Special cases
1. Magnetic field at the centre of the coil.
When point P lies at the centre of the coil, x = 0.
Then, setting x = 0 in equation (2). we have
B = \(\frac{\mu_0}{4 \pi} \cdot \frac{2 \pi \mathrm{I}}{\mathrm{R}}\) ...............................(3)
For a coil of n turns, the expression will be
B = \(\frac{\mu_0}{4 \pi} \cdot \frac{2 \pi n \mathrm{I}}{\mathrm{R}}\) ...............................(4)
2. When observation point lies far away from the centre of the coil. In case, observation point P lies at a distance very large as compared to the radius of the coil i.e. if x >> R. then R² can be neglected as compared to x² in equations (2) and (3).
Therefore, for a coil of single turn,
B = \(\frac{\mu_0}{4 \pi} \times \frac{2 \pi \mathrm{I} R^2}{x^2}\) .............................(5)
But πR² = A, the area of coil, Therefore.
B = \(\frac{\mu_0}{4 \pi} \times \frac{2 \mathrm{IA}}{x^3}\) ..............................(6)

Question 7.
Derive an expression for the force acting on a current carrying conductor placed in a magnetic field.
Or
Derive an expression for the maximum force experienced by a straight conductor of length l, carrying current I and kept in a uniform magnetic field B.
Answer:
Consider a conductor PQ carrying current I placed in a uniform magnetic field B. The magnetic field is acting along x-axis and conductor is placed along x-axis.
Let
n = no. of electrons per unit volume
A = area of cross-section of conductor
v_d = drift velocity of electrons
∴ I = n A e v_d ........................(1)
Since each electron is moving in uniform magnetic field, therefore, each electron will experience Lorentz force.

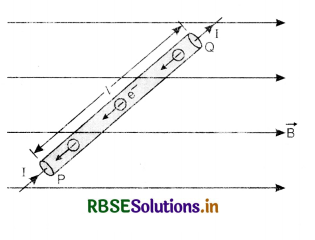
Let l be length of conductor PQ
∴ No. of electrons in the conductor = nA.l
Force acting on each electron = - \(\left(\vec{v}_d \times \overrightarrow{\mathrm{B}}\right)\)
Force experienced by electrons in the conductor

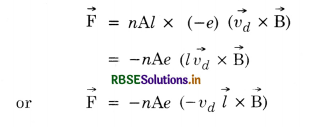
(∵ the direction of\( \vec{l}\) is in the direction of I i.e. from P to Q whereas the direction of \(\vec{v}_d\) is from Q to P. So l\(\vec{v}_d\) = -\(\vec{l}\) vd )
or\( \overrightarrow{\mathrm{F}}\) = n Ae v_d(\(\vec{l} \times \overrightarrow{\mathrm{B}}\))
Using Eq. (1), we get
\(\overrightarrow{\mathrm{F}} = I(\vec{l} \times \vec{B})\) ....................(2)
In magnitude    
F = IlB sin θ
or F = BIl sin θ .....................(3)
Special Cases
(i) When the conductor is held parallel to the magnetic field
i.e. θ = 0°
So F = BIl sin 0° = 0
i.e. if the current carrying conductor is placed parallel to the magnetic field it will experience no force.
(ii) If the conductor is held perpendicular to the magnetic field
i.e. θ = 90°
∴F = BIl sin 90° = BIl
i.e. if the current carrying conductor is placed perpendicular to the magnetic field, it will experience maximum force.

Question 8.
Find the force between two infinitely long straight conductors carrying current in (i) the same direction and (ii) in opposite direction and hence define one ampere.
Or
Write the expression for the magnitude of force per unit length between two infinitely long parallel straight conductors. Hence define the SI unit of current.
Or
Derive a mathematical expression for the force per unit length experienced by each of the two long current carrying conductors placed parallel to each other in air. Hence define one ampere of current. Explain why two parallel straight conductors carrying current in the opposite direction kept near each other in air repel?
Answer:
(i) Force between two Parallel Wires Carrying Current in the same direction
When two parallel wires carrying current are held side by side, each wire is in the magnetic field produced by the other. Therefore, each wire experiences a force. When current through the two wires flows in the same direction there is a mutual force of attraction between them. The reverse is also true.
Let AB and CD be two parallel wires carrying currents I₁ and I₂ and held parallel to each other at a distance r. Fig. LAQ 8 (a) shows the case when currents in the two wires are in the same direction.
At any point P magnetic field intensity due to current I₂ in CD is
B₂ = \(\frac{\mu_0 I_2}{2 \pi r}\) ...............................(1)
Its direction is perpendicular to the plane of the paper and upwards.

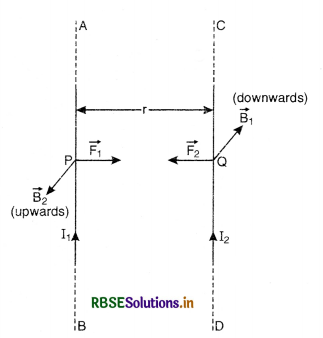
Force per unit length experienced by conductor AB is given by:
F₁ = B₂I₁
Using Eq. (1), we get
F₁ = \(\frac{\mu_0 \mathrm{I}_1 \mathrm{I}_2}{2 \pi r}\) ..............................(2)
Using Fleming's Left Hand Rule, this force F₁ acts on the conductor AB is in the plane of the paper, perpendicular to AB and directed towards CD.
Similarly, we can prove that the force experienced by conductor CD will also act on the plane of the paper and perpendicular to CD and directed towards AB.
Thus two parallel conductors carrying current in the same direction attract each other.

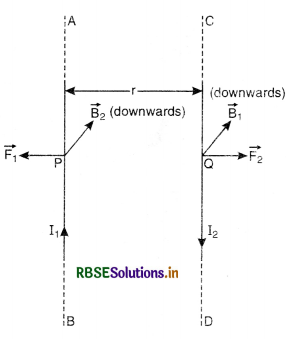
(ii) When current is flowing in opposite directions
Let the currents I₁ and I₂ be flowing in conductors AB and CD in opposite directions as shown in Fig. LAQ 4 (b).
Again by applying Fleming's Left Hand Rule, we find that the direction of magnetic field intensity \(\overrightarrow{\mathrm{B}}_1\) and \(\overrightarrow{\mathrm{B}}_2\) are directed inwards and the forces \(\overrightarrow{\mathrm{F}}_1\) and \(\overrightarrow{\mathrm{F}}_2\) are acting in opposite direction, so the conductors AB and CD will repel each other.
Thus two parallel conductors carrying current in opposite directions repel each other.

Definition of one ampere
The force per unit length between two parallel current carrying straight conductors is given by:
F = \(\frac{\mu_0}{4 \pi} \frac{2 \mathrm{I}_1 \mathrm{I}_2}{r}\)
If I₁ = I₂ = 1 ampere
F = \(\frac{4 \pi \times 10^{-7}}{4 \pi} \times \frac{2 \times 1 \times 1}{1}\)
= 2 x 10^-7 Nm^-1
So, one ampere of current is that much current which while flowing in two long parallel wires one metre apart in vacuum produces between them a force of 2 X 10^-7 Nm^-1.

Question 9.
Discuss relative strengths of electrical and magnetic forces.
Answer:
Consider two charges q₁ and q₂ placed at a distance |r₁₂| apart in air. The force between two charges
\(\left|\overrightarrow{\mathrm{F}}_e\right|=\frac{q_1 q_2}{4 \pi \varepsilon_0} \frac{1}{\left|r_{12}\right|^2}\) ...................................(1)
Again consider two electrically neutral parallel current carrying elements of lengths dl₁ and dl₂ carrying currents I₁ and I₂.
∴ Magnetic force between two current elements

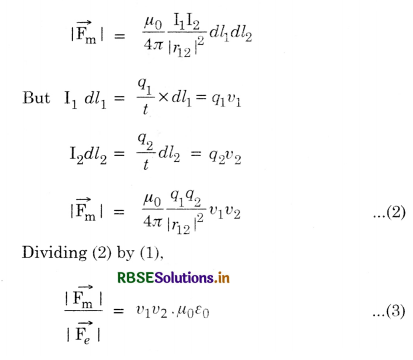
Since L.H.S, is a dimensionless quantity therefore, the quantity µ₀ ε₀ must have dimensions of (velocity)² as numerator has dimensions of (velocity)² as v₁ and v₂ are the drift velocities of electrons in current elements.
∴ v₁v₂ = 10^-5 x 10^-5
= 10^-10 m²s^-2
where µ₀ε₀ = 1 /c², where c is the velocity of light. (c² = 9 x 10¹⁶ m²s^-2)
From (3)

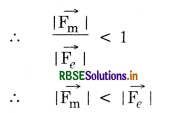
Question 10.
(a) State and prove Ampere's circuital law for straight conductor.
(b) Generalise Ampere's circuital law from a closed plane surface.
Answer:
(a) Ampere circuital law. It states that the line integral of magnetic field. B around any closed circuit is equal to µ₀ times the total current passing through the closed circuit.
\(\oint \overrightarrow{\mathrm{B}} \cdot \overrightarrow{d l}\) = µ₀I
Proof. Consider a long straight conductor carrying current I. The magnetic field produced at point P distance r from the conductor is:

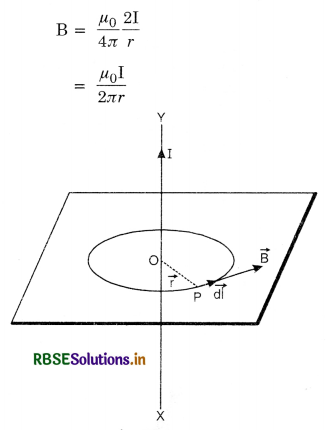
This magnetic field is along circumference of the circle of radius r, with the wire as centre.
Consider a line of constant magnetic induction of radius 'r'. The field \(\overrightarrow{\mathrm{B}}\) at any point P of this line has a magnitude \(\frac{\mu_0 I}{2 \pi r}\) and is directed tangentially in the anticlockwise as seen in this particular case.
Let us evaluate the line integral \(\oint \overrightarrow{\mathrm{B}} \cdot \overrightarrow{d l}\) along the circle in the anticlockwise direction.
\(\vec{B}\) and \(\overrightarrow{d l}\) always have the same direction where dl is a line element along the circle. 

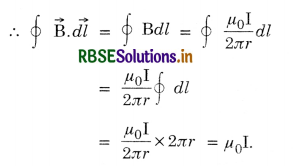
This means that irrespective of the radius 'r' of the circle, the closed integral of \(\vec{B}\) is µ₀I i.e. it depends upon the current through the circle.

(b) Generalisation of Ampere's circuital law Consider a closed path of any arbitrary shape which encloses the wire. Let P be any observation point at a distance r from the wire [Fig. LAQ 10 (b)]. The magnetic induction \(\vec{B}\) at P has a magnitude µ₀I/ 2πr and is perpendicular to r. Now the displacement vector \(\overrightarrow{d l}\) is inclined to \(\vec{B}\) at angle θ.

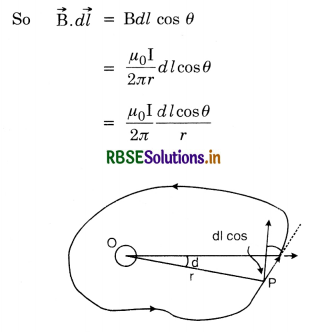
Now dl cos θ is the component of \(\overrightarrow{d l}\) in the direction of \(\vec{B}\) and, as is clear from Fig.LAQ 10(b), \(\frac{d l \cos \theta}{r}\) = dΩ, the angle subtended by \(\overrightarrow{d l}\) at O i.e. the cross-section of the wire. Thus

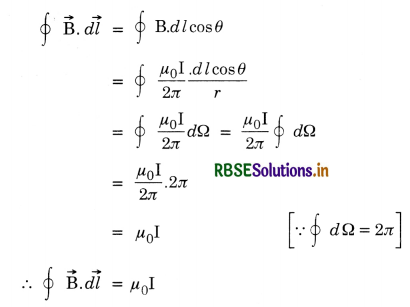
Question 11.
Applying Ampere’s circuital law, find magnetic field
(i) due to toroidal solenoid
(ii) due to a straight long solenoid
Or
Using Ampere’s circuital law, derive an expression for the magnetic field along the axis of a toroidal solenoid.
(iii) due to an infinitely long wire carrying current.
Answer:
(i) Magnetic Induction due to current in a toroidal solenoid A toroidal solenoid in an anchor ring (torus) around which a large number of turns of a wire are wrapped as shown in the Fig. LAQ 11 (a).

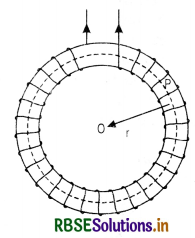
Let n be the number of turns of wire of per unit length of the toroid and I be the current flowing through it. Let us find the magnetic flux density (or field) B at a point P inside the turns of the toroid, where distance of P from the centre of the toroid is r. From symmetry, the magnetic flux density at all points distant r from 0 is the same. Thus magnetic lines of induction inside the solenoid are concentric circles.
The line integral of the magnetic field along the circular path of radius r is
\(x = {-b \pm \sqrt{b^2-4ac} \over 2a}\oint \overrightarrow{\mathrm{B}} \cdot \overrightarrow{d l}\) = µ₀ x Total current in the circle
= µ₀(2πnI),
Since current passes in the same direction.
∴ \(\oint \mathrm{B} d l \cos 0^{\circ}\) = µ₀ (2πrnI)
or B 2πr = µ₀ (2πrnI)
or B = µ₀ nI
The field B is independent of r, depending only on the current and number of turns per unit length. The field inside is constant in magnitude and is always tangential. Fig. LAQ 11 (b).

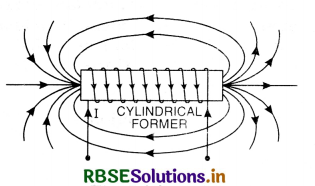
(ii) Magnetic field due to a straight long solenoid. A straight long solenoid is as shown in Fig. LAQ 11. (c). In fact, if the radius of the circle into which the axis of toroidal solenoid is bent made large and large, then a small portion of it will appear straight. Obviously, the magnetic field inside a straight solenoid will be same as that inside a toroidal solenoid i.e.
B = µ₀ nI, .....................(1)
where n is number of turns per unit length and 1 is current passed through it. However, it may be pointed out that in case of a straight long solenoid, magnetic field is not uniform throughout the conductor.
Proof. Consider a long ideal solenoid (for ideal solenoid \(\overrightarrow{\mathrm{B}}\) inside is uniform and outside is zero) carrying current I and having n number of turns per unit length.

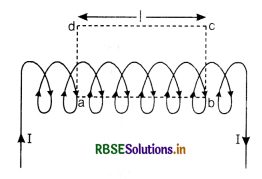
Consider a rectangular path abed of length l.
From Ampere's circuital law, we have

However it may be pointed out that in case of a straight long solenoid, magnetic field is given by the above formula only at a point well inside the solenoid. At points near to its ends, the magnetic field is found to be µ₀nI/2. Figure (b) also shows the magnetic field produced due to a solenoid, when current is passed through it. The field is just as due to a permanent bar magnet.
(iii) Magnetic field due to a long wire carrying current
Consider an infinitely long wire XY carrying current I as shown in figure LAQ 11 (d). Let us find magnetic field B at point P at a distance r from the wire. Draw a circle of radius r passing through point P, such that the wire, XY is normal to the plane of the circle and passing through its centre. 

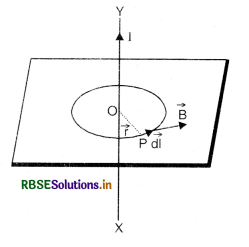
Let \(\overrightarrow{\mathrm{B}}\) be magnetic field at P due to the wire XY carrying current and \(d \vec{l}\) be a small element of the circle drawn around the wire.
From Ampere’s circuital law, we have
\(\oint \overrightarrow{\mathrm{B}} \cdot \overrightarrow{d l}=\mu_0 \mathrm{I}\)
or \(\oint \)Bdl cos 0° = µ₀I
or B \(\oint\) dl = µ₀I
or B. 2πr = µ₀I
or B = \(\frac{\mu_0 \mathrm{I}}{2 \pi r}\) ..............................(i)
The above equation gives the strength of megnetic field at a distance r from an infinitely long current carrying wire.

Question 12.
Obtain an expression for torque acting in a rectangular current loop, when placed inclined at an angle θ with the direction of magnetic field \(\overrightarrow{\mathrm{B}}\).
Answer:
Consider a rectangular loop PQRS with sides PQ = l and PS = b. Let I be the current flowing in the loop placed in a uniform magnetic field \(\overrightarrow{\mathrm{B}}\) as shown in the figure.
Let θ be angle made by the plane of the coil with magnetic field \(\overrightarrow{\mathrm{B}}\). Let \(\overrightarrow{\mathrm{F}}_1\), \(\overrightarrow{\mathrm{F}}_2\), \(\overrightarrow{\mathrm{F}}_3 \)and \(\overrightarrow{\mathrm{F}}_4 \)be forces acting on the arms PQ, QR, RS and SP respectively of the coil.
Force on arm SP
\(\vec{F}_4=\mathrm{I}(\vec{b} \times \vec{B})\)
or F₄ = IbB sin (180° - θ)
or F₄ = BIb sin θ .............................(1) [upwards]
Force on arm QR

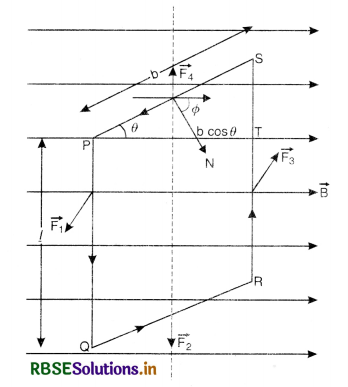
\(\vec{F}_2=\mathrm{I}(\vec{b} \times \vec{B})\)
or F₂ = I bB sin θ
or F₂ = BIb sin θ ................................(2) [downwards]
Since the forces \(\vec{F}_4\) and \(\vec{F}_2 \)are equal in magnitude and acting in opposite direction along the same straight line, so they cancel each other's effect. Hence produce no torque i.e. resultant torque is zero.
Force on arm PQ
\(\vec{F}_1 = \mathrm{I}(\vec{b} \times \vec{B})\)
or F₁ = IlB sin 90°
or F₁ = BIl ......................(3) (towards the reader)
Force on arm RS
\(\vec{F}_3 = \mathrm{I}(\vec{b} \times \vec{B})\)
or F₃ = IlB sin 90°
or F₃ = BIl .........................(4) (away from the reader)
These two parallel, equal and opposite forces acting along different lines of action, so they form a couple. The moment of the couple i.e. torque τ is given by
τ = Either force x ⊥ distance between the forces
= BIl (PT)
= BIl b cos θ
τ = BIA cos θ ................(5)
(where A = l x b is the area of the rectangular coil)
If the coil has n turns, then
τ = nBIA cos θ ..................(6)
If normal to the plane of the coil, makes an angle Φ with B, then θ = 90 - Φ.
So τ = nBIA cos (90 - Φ) = nBIA sin Φ.

Question 13.
(a) What, is a galvanometer?
(b) With the help of labelled diagram, explain the principle and working of a moving coil galvanometer.
Or
With the help of a neat and labelled diagram, explain the underlying principle and working of a moving coil galvanometer. What is the function of (i) uniform radial field (ii) soft iron core in such a device?
Answer:
(a) Galvanometer. It is an electrical instrument which is used to detect and measure small currents.
(b) Moving coil galvanometer Principle. When a conductor carrying current is placed in a magnetic field, it experiences a mechanical force given by Fleming's left hand rule.

Construction. It consists of a narrow coil ABCD, having a large number of turns of thin insulated copper wire wound on a light non-magnetic metallic frame. The coil is suspended by means of a fine phosphor bronze strip S or a quartz fibre from a movable torsion head in between the pole pieces N and S of a strong permanent horse-shoe magnet [Fig. FAQ 13 (a)]. A hair spring of phosphor bronze, having only a few turns, is attached to lower end of the coil. The other end of the spring is connected to the binding screw T₂ whereas the torsion head is connected to the binding screw T₁. Thus, the current enters through the torsion head, and after passing through the suspension fibre and the coil leaves through the hair spring. A small light mirror is attached to the lower portion of the suspension fibre so that reading can be taken by a lamp and scale arrangement. In this way, small deflections can be read.

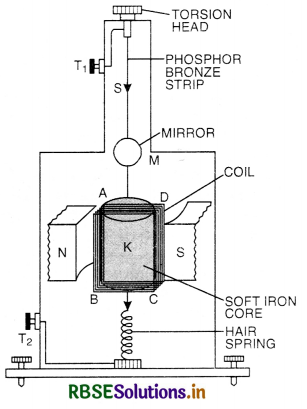
A cylindrical soft iron piece. K called the core, is placed symmetrically between the pole pieces of the magnet. Besides, the pole pieces are given a cylindrical shape.
Need of cylindrical poles. The iron core helps to concentrate the magnetic field so that the direction of the line of force in the small air gap between the pole pieces and the core almost coincides with the radii of the cylindrical pole pieces [Fig. LAQ 13 (b)]. Such a field is called radial field Evidently in such a field, the plane of the coil in all its positions is always parallel to the magnetic field.

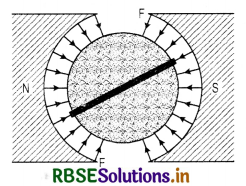
Theory. Let a current be passed through the coil along ABCD as indicated. The limb AB experiences a force normal to it and directed outwards i.e. towards the reader as in Fig. LA.Q 13 (c). Radial magnetic field, can easily be verified by applying Fleming's left hand rule. Similarly, the limb CD experiences a force equal and parallel to that on AB but opposite in sense, i.e.. directed away from the reader. Since the plane of the coil remains parallel to the magnetic field in all the positions of the coil, the forces on the limbs AB and CD always remain perpendicular to the plane of the coil (Fig. LAQ c, d). No forces act on the sides AD and BC as they are parallel to the field.

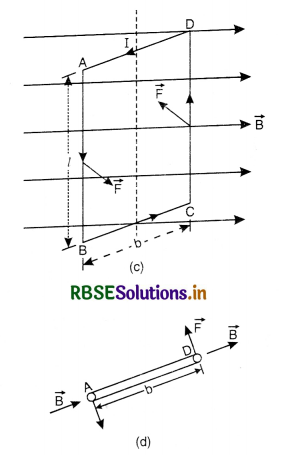
Now let I = Strength of the current flowing through the coil.
B = Magnetic field supposed to be uniform and always parallel to the coil.
l = Length of the coil = AB = CD
b = breadth of the coil = AD = BC
A = Area of the coil = l x b
n = Number of turns in the coil.
Now the coil carrying current placed in a magnetic field as above is subject to torque whose magnitude is given by
τ = nBIA cos α
For radial field α = 0
∴ Deflecting torque, τ = n.BIA .....................(1)
Restoring couple. Under the action of this deflecting couple, the coil rotates in the anti-clockwise direction. Due to elastic forces, a restoring couple is produced in the suspension coil. The couple is proportional to the twist produced in the wire. As soon as restoring couple becomes equal to the deflecting couple, equilibrium is established. The coil does not rotate further.
Let θ = Angle through which the coil rotates till it reaches the equilibrium position
k = Restoring couple per unit twist
∴ Restoring couple = k θ
I = \(\frac{k \theta}{n \mathrm{BA}}\)
I = G θ
where G = \(\frac{k}{n \mathrm{AB}}\) is constant for instrument and is called galvanometer constant.
∴ I ∝ θ
Thus deflection of coil is proportional to the current passing through it.
Working. The levelling screws are adjusted for levelling the instrument. The torsion head is set so that the coil hangs freely without touching the poles of the soft iron core. Pass the current and measure the deflection by using a lamp and scale arrangement. As the mirror gets deflected, a bright circular spot moves over the scale graduated in cms. Thus, the deflection of the coil can be measured.

Question 14.
Discuss the sensitivity of a moving coil galvanometer.
Answer:
A galvanometer is said to be sensitive, if it gives a large deflection, even when a small current is passed through it or a small voltage is applied across its coil.
Current sensitivity. It is defined as the deflection produced in the galvanometer on passing unit current through its coil. Therefore,
Current sensitivity =\( \frac{\theta}{\mathrm{I}}=\frac{n \mathrm{BA}}{k}\)
Voltage sensitivity. It is defined as the deflection produced in the galvanometer when a unit voltage is applied across its coil. Therefore, if θ is deflection produced on applying voltage V, then
Voltage sensitivity = \(\frac{\theta}{\mathrm{V}}\)
If R is resistance of coil and I is current that passes through coil on applying voltage V, then V = IR
∴ Voltage sensitivity = \(\frac{\theta}{\mathrm{IR}}=\frac{n \mathrm{BA}}{k \mathrm{R}}\).
Thus, a galvanometer will be highly sensitive, if (i) n is large; (ii) B is large; (iii) A is large; (iv) R is small and (v) k is small.
However, n and A cannot be increased beyond certain limit otherwise, the size of the galvanometer and the resistance of the instrument will become large. Therefore. B is made as large as possible and k is made as small as possible. To increase B, a very strong permanent magnet is used. The suspension wire is made of phosphor bronze, as for this material, k is very small. The value of k further decreases, if the wire is hammered into flat strip. In very sensitive galvanometers, quartz fibre is used for suspension of the coil as for quartz, k, is still smaller.

Question 15.
What is an Ammeter? How a galvanometer is converted into an ammeter? Why is ammeter connected in series in a circuit?
Or
How do you convert galvanometer into an ammeter? Why is an ammeter always connected in series?
Answer:
Ammeter. An ammeter is an instrument to measure current flowing in a circuit.
Conversion of a galvanometer into an ammeter
It can be done by connecting a shunt resistance S (a resistance of low value in parallel) to galvanometer such that a very small current Ig flows through the galvanometer as shown in the figure LAQ 15.

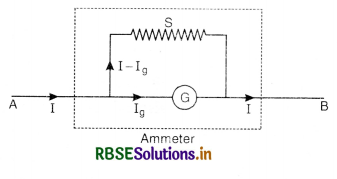
Let G = resistance of the galvanometer
S = Shunt resistance (S << G)
I_g = Small current which produces full scale deflection in the galvanometer
I = current in the main circuit
∴ I - I_g = current passing through the shunt.
From Fig., we have
P.D. across the galvanometer = P.D. across the shunt.
I_g G = S (I - Ig)
or S = \(\frac{I_g G}{I-I_g}\)
where G is the resistance galvanometer and I is the range of galvanometer.

Why ammeter is connected in series?
Since an ammeter is a low resistance galvanometer and is used to measure the current flowing in the circuit, so entire current should flow through it, hence it is connected in series.

Question 16.
What is a voltmeter? How a galvanometer is converted into a voltmeter? Why is a voltmeter connected in parallel in a circuit?
Answer:
Voltmeter. It is a high resistance galvanometer used for measuring potential difference across the two ends of a conductor carrying current.
Conversion of a galvanometer into a voltmeter
It can be done by connecting a high resistance in series with a galvanometer, so that a small current I_g flows through the galvanometer.

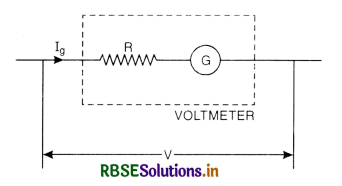
Let G = Resistance of the galvanometer.
Ig = The current which produces full scale deflection in the galvanometer.
R = A high resistance joined in series with the galvanometer.
V = Potential difference to be measured by the voltmeter
∴ R + G = total resistance of the voltmeter.
From the figure, we have
I_g = \(\frac{\mathrm{V}}{\mathrm{R}+\mathrm{G}}\) [using ohm's law]
or I_g R + I_g G = V
or I_gR = V - I_g G
or R = \(\frac{\mathrm{V}-\mathrm{I}_{\mathrm{g}} \mathrm{G}}{\mathrm{I}_{\mathrm{g}}}=\frac{\mathrm{V}}{\mathrm{I}_{\mathrm{g}}}-\mathrm{G} \)
∴ R = \(\frac{\mathrm{V}}{\mathrm{I}_{\mathrm{g}}}\) - G
Thus a voltmeter is a galvanometer in which a high resistance is connected in series.

Why voltmeter is connected in parallel?
Because voltmeter has high resistance and is used to find the potential difference between two points, so it is connected in parallel to the circuit. Hence it draws minimum current from the circuit.

Question 17.
Show that the path followed by a charged particle moving in a direction perpendicular to the electric field is parabolic.
Answer:
Motion of a charged particle in an electric field
Let us consider that a charged particle having charge q and mass m is moving with velocity v along x-axis. When there is no electric field, the charge +q reaches at point C on the screen.
If an electric field \(\overrightarrow{\mathrm{E}}\) is applied perpendicular to the charge from o to a distance x, then the charged particle will experience a force \(\overrightarrow{\mathrm{F}}\) given by

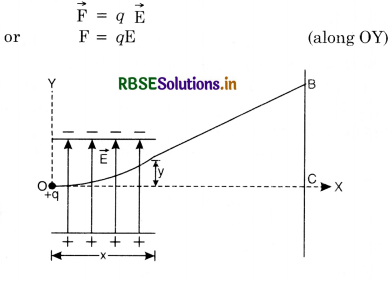
∴ Acceleration to the charged particle along OY will be
a = \(\frac{\mathrm{F}}{m}=\frac{q \mathrm{E}}{m}\) .............................(1)
As this acceleration (or force) is acting perpendicular to the motion of the charged particle, so the speed of the particle will not change, but its direction of motion will be changed.
If t is the time taken by the particle inside the electric field, then
t = \(\frac{x}{v}\) ..........................(2)
If y is the displacement of the charged particle along OY direction, then

i.e. the path followed by the charged particle is a parabola.
Hence inside the electric field, the charged particle moves in a parabolic path.

Question 18.
Discuss the motion of a charged particle when subjected to a uniform magnetic field when
(i) The direction of motion of charged particle is perpendicular to the magnetic field.
(ii) The direction of motion of the charged particle makes an angle with the direction of magnetic field.
Answer:
When a moving charged particle is subjected to a uniform magnetic field, it experiences a force \(\vec{F}\) which is perpendicular to its velocity \(\vec{v} \)and magnetic field \(\vec{B}\).
(i) When the direction of motion of charged particle is perpendicular to the magnetic field.
Let \(\vec{B}\) be a uniform magnetic field (represented by ⊗ and directed towards the reader). Let a charged particle of charge +q and mass m be moving with velocity \(\vec{v}\) right angle to the field (i.e. in the plane of the paper) then magnetic force acting on the charge q will be
\(\overrightarrow{\mathrm{F}}=q(\vec{v} \times \overrightarrow{\mathrm{B}})\)
or F = qv B sin 90°
or F = qv B .................(1)
As this force acts at right angle to the velocity \(\vec{v}\) of the charged particle, so it is unable to change the velocity but can make the charged particle to move in a circular path.
If r is the radius of the circle, then the centripetal force required by the charged particle will be

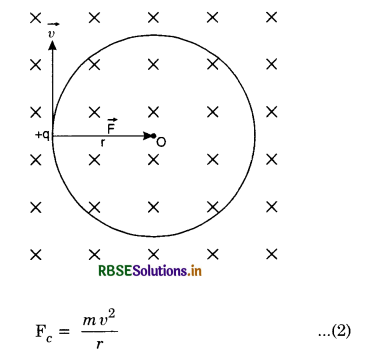
This centripetal force is provided by the magnetic force acting on the charged particle.
i.e. F_c = F
or \(\frac{m v^2}{r}\) = q v B
or r = \(\frac{m v}{q \mathrm{~B}}\) ............................(3)
i.e. r ∝ m, r ∝ v
The time period of the charged particle will be

(ii) When the direction of charged particle makes an angle with the direction of magnetic field.
If the charged particle of charge q and mass m moving with velocity \(\vec{v}\) inside a uniform magnetic field \(\vec{B}\) making an angle θ with the direction of magnetic field an shown in figure, (b) then, the velocity \(\vec{v}\) can be resolved into two rectangular components.
(i) v cos θ ( = v₁) in the direction of magnetic field.
(ii) v sin θ (= v₂) in the direction perpendicular to the magnetic field.

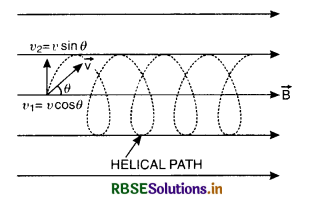
For perpendicular component
The force acting on the charged particle due to magnetic field for component \(\overrightarrow{v_2}\) is given by
\(\overrightarrow{\mathrm{F}}=q\left(\overrightarrow{v_2} \times \overrightarrow{\mathrm{B}}\right)\)
or F = q v₂ B sin 90° = q v₂ B
or F = q (v sin θ) B ...........................(6)
As this force is acting perpendicular to the plane of \(\overrightarrow{v_2}\) and \(\overrightarrow{B}\), so it will simply move the particle in a circle and provides the necessary centripetal force.
If r is the radius of the circular path, then

For parallel component
The force acting on charged particle due to the magnetic field for component is \(\overrightarrow{v_1}\) given by
\(\overrightarrow{\mathrm{F}}_1=q\left(\overrightarrow{v_1} \times \overrightarrow{\mathrm{B}}\right)\)
or F₁ = q v₁ B sin 0°
or F₁ = 0
Thus, no force is acting on the charged particle in the magnetic field. Hence, the charged particle will cover the linear distance in the direction of magnetic field with the same speed v cos θ ( = v₁)
Hence, the charged particle under the combined effect of the two components of velocities, will cover linear as well as circular path i.e. helical path whose axis is parallel to the magnetic field as shown in figure LAQ 19 (b).

Question 19.
Explain with the help of a labelled diagram the underlying principle, construction and working of a cyclotron.
Or
Draw a neat and labelled diagram of a cyclotron. State the underlying principle and explain how charged particle gets accelerated in this machine? How mathematically that the cyclotron frequency does not depend upon the speed of the particle?

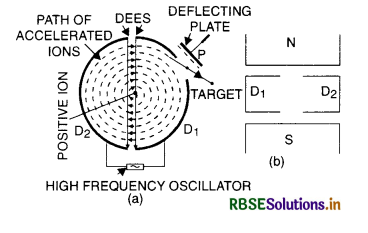
Answer:
Principle. It is based upon the principle that a charged particle moving at right angles to a uniform magnetic field is acted upon by a force perpendicular to its direction of motion and follow a circular path.
Construction. It consists of two semicircular hollow metal boxes D₁ and D₂ called dees. D's are separated by a small gap and are connected to terminals of high frequency oscillator providing alternating potential of nearly 10,000 V and millions hertz frequency. Whole of the apparatus is placed in a metal box containing gas at low pressure and placed between the poles of a strong electromagnetic field perpendicular to the plane of D's.
Working
Let a positive ion (₁H¹, ₁H², ₂He³ or ₂He⁴) be located in the gap when D₁ is negatively and D₂ positively charged, the positive ion will get accelerated towards D₁. Since magnetic field is uniform and acting at right angle to the plane of D’s, the ions traverse a circular path in When the ion emerges out into the gap after completing a semicircle in D₁. If during the time taken to cover semicircle, the electric field gets reversed, the ions further get accelerated towards D₂. It enters D₂ with greater speed and moves in D₂ in a bigger semicircle. The process is repeated time and again and each time ions get an additional kick in the proper direction. The ion becomes faster and faster until it reaches the periphery of the D's where it is brought out of the chamber by means of deflecting plate P charged to a very high negative potential and is made for bombarding the target.
Theory
Let m = mass of the ion to be accelerated,
B = flux density of the magnetic field,
r = radius of the semicircular path in which the ion moves,
q = charge on the ion,
v = velocity with which the ion moves in the semicircle
Force acting on the charged particle
F = Bqv sin 90°
or F = B qv
This force provides the necessary centripetal force because it moves along circular path
∴ \(\frac{m v^2}{r}\) = Bqv
∴ v = \(\frac{\mathrm{B} q r}{m}\)
Time taken by charged particle to complete half circle,
t = \(\frac{\text { half circumference }}{\text { velocity }}=\frac{\pi r}{v}\)
= \(\frac{\pi r}{\mathrm{~B} q r / m}=\frac{\pi m}{\mathrm{~B} q r}\)
As m, B, q are constant,
∴ t is constant.
This clearly shows that time taken by the charged particle to complete a semicircle is independent of its speed and the radius of circle in which it moves.
Let T = time period of oscillator
∴ T = 2t = \(\frac{2 \pi m}{\mathrm{~B} q}\)
Frequency of oscillator field
v = \(\frac{1}{\mathrm{~T}}=\frac{\mathrm{B} q}{2 \pi m}\)
This frequency is constant and is independent of velocity (or energy) of the particle and radius of the circular path in which it moves.
Limitations.
1. The cyclotron is unable to accelerate the ions beyond a certain limit since mass will increase according to equation
m= \(\frac{m_0}{\sqrt{1-\frac{v^2}{c^2}}}\), whenever v²/c² are not negligible.
Hence required frequency will now be
v = \(\frac{\mathrm{B} q \sqrt{1-v^2 / c^2}}{2 \pi m_0}\)
Since we are unable to change the frequency in short duration, hence ion will get out of phase with high frequency accelerating field and thus lose energy instead of gaining.
2. Electrons cannot be accelerated with cyclotron.
3. Neutrons cannot be accelerated with cyclotron.

Question 20.
Find the expression for maximum energy of a charged particle accelerated by a cyclotron.
Answer:
Let r₀ = Maximum radius of circular path followed by charged particle (Equal to the radius of the Dees)
v₀ = Maximum velocity
Since the necessary centripetal force is provided by the Lorentz magnetic force, therefore,
\(\frac{m v_0^2}{r_0}\) = Bqv₀
v₀ = \(\frac{\mathrm{B} q r_0}{m}\)
∴ K.E_maxi = \(\frac{1}{2} \times m \times\left(\frac{\mathrm{B} q r_o}{m}\right)^2=\frac{\mathrm{B}^2 q^2 r_0^2}{2 m}\)
This is the required result.

Question 21.
State Biot-Savart’s law. Using this law, derive the expression for the magnetic field due to a current carrying circular loop of radius ‘R’ at a point which is at a distance V from its centre along the axis of the loop.
Answer:
Biot-Savart’s law. It states that the magnetic field dB at a point P due to a current element Idl is given by
dB ∝ \(\frac{I d l \sin \theta}{r^2}\)
or dB = \(\frac{\mu_0}{4 \pi} \frac{\mathrm{Idl} \sin \theta}{r^2}\)
Magnetic Field at a Point on the Axis of a Circular Coil
I = Current length the coil
Let, O be the centre of coil
R = Radius of the circular coil
x = Distance of point P on the axis from the centre of the coil
AB = an element of the coil
dl = Length of the element AB
CP = r
According to Biot-Savart’s law, magnetic field dB at the point P due to element \(\overrightarrow{d l}\) is given by

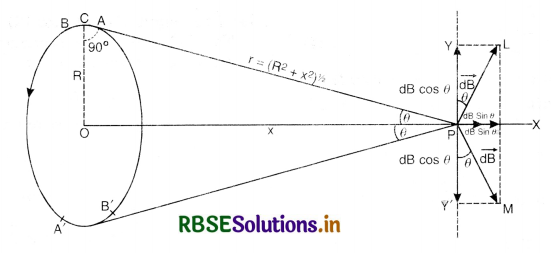
\(\overrightarrow{d \mathrm{~B}}=\frac{\mu_0}{4 \pi} \frac{\mathrm{I} \overrightarrow{d l} \times \vec{r}}{r^3}\)
The direction \(\overrightarrow{d \mathrm{~B}}\) at point P will be along PL i.e. perpendicular to CP and in the plane of paper. As angle between \(\mathrm{I} \overrightarrow{d l}\) and \(\vec{r}\) is 90°, the magnitude of magnetic field due to small element at point P is given by
dB = \(\frac{\mu_0}{4 \pi} \cdot \frac{\mathrm{I} d l}{r^2}\) ................................(1)
If we calculate the magnitude \(\overrightarrow{d \mathrm{~B}}\) due to an equal current element A'B' lying just opposite to the current element AB, it will be found that the magnitude of the magnetic field in this case also is the same as given by equation (1) but it acts along PM. The components of two magnetic fields along YY' will cancel out as they are equal in magnitude and opposite in direction. Same will happen for the current element taken in similar pairs.
Therefore, component of magnetic field due to a current element along PX is dB sin θ. The magnetic field due to the whole coil at P is obtained by integrating dB sin θ over the circumference of the coil i.e.
Magnetic field at P due to the circular coil is given by
B = ∫dB sin θ
= ∫\(\frac{\mu_0}{4 \pi} \cdot \frac{\mathrm{I} d l}{r^2}\) sin θ
= \(\frac{\mu_0}{4 \pi} \cdot \frac{\mathrm{I}}{r^2}\) sin θ ∫dl
Now, ∫ dl = circumference of the coil of radius R, = 2πR

The direction of magnetic field is along PX.
If the coil consists of n turns, then strength of magnetic field at point P due to the coil will become n times that given by equation (2) i.e.
B = \(\frac{\mu_0}{4 \pi} \cdot \frac{2 \pi n \mathrm{IR}^2}{\left(\mathrm{R}^2+x^2\right)^{3 / 2}}\)
Special cases
1. Magnetic field at the centre of the coil.
When point P lies at the centre of the coil, x = 0.
Then, setting x = 0 in equation (2). we have
B = \(\frac{\mu_0}{4 \pi} \cdot \frac{2 \pi \mathrm{I}}{\mathrm{R}}\) ...............................(3)
For a coil of n turns, the expression will be
B = \(\frac{\mu_0}{4 \pi} \cdot \frac{2 \pi n \mathrm{I}}{\mathrm{R}}\) ...............................(4)
2. When observation point lies far away from the centre of the coil. In case, observation point P lies at a distance very large as compared to the radius of the coil i.e. if x >> R. then R² can be neglected as compared to x² in equations (2) and (3).
Therefore, for a coil of single turn,
B = \(\frac{\mu_0}{4 \pi} \times \frac{2 \pi \mathrm{I} R^2}{x^2}\) .............................(5)
But πR² = A, the area of coil, Therefore.
B = \(\frac{\mu_0}{4 \pi} \times \frac{2 \mathrm{IA}}{x^3}\) ..............................(6)

Question 22.
Derive an expression for the maximum force experienced by a straight conductor of length l, carrying current I and kept in a uniform magnetic field B.
Answer:
Consider a conductor PQ carrying current I placed in a uniform magnetic field B. The magnetic field is acting along x-axis and conductor is placed along x-axis.
Let
n = no. of electrons per unit volume
A = area of cross-section of conductor
v_d = drift velocity of electrons
∴ I = n A e v_d ........................(1)
Since each electron is moving in uniform magnetic field, therefore, each electron will experience Lorentz force.

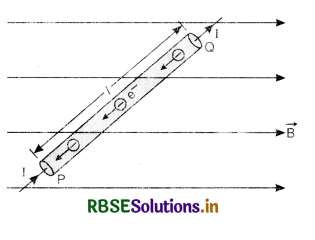
Let l be length of conductor PQ
∴ No. of electrons in the conductor = nA.l
Force acting on each electron = - \(\left(\vec{v}_d \times \overrightarrow{\mathrm{B}}\right)\)
Force experienced by electrons in the conductor

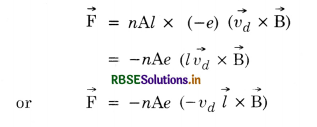
(∵ the direction of \(\vec{l}\) is in the direction of I i.e. from P to Q whereas the direction of \(\vec{v}_d\) is from Q to P. So l\(\vec{v}_d\) = -\(\vec{l}\) vd )
or \(\overrightarrow{\mathrm{F}}\) = n Ae v_d(\(\vec{l} \times \overrightarrow{\mathrm{B}}\))
Using Eq. (1), we get
\(\overrightarrow{\mathrm{F}} = I(\vec{l} \times \vec{B})\) ....................(2)
In magnitude    
F = IlB sin θ
or F = BIl sin θ .....................(3)
Special Cases
(i) When the conductor is held parallel to the magnetic field
i.e. θ = 0°
So F = BIl sin 0° = 0
i.e. if the current carrying conductor is placed parallel to the magnetic field it will experience no force.
(ii) If the conductor is held perpendicular to the magnetic field
i.e. θ = 90°
∴F = BIl sin 90° = BIl
i.e. if the current carrying conductor is placed perpendicular to the magnetic field, it will experience maximum force.

Question 23.
State the Biot-Savart’s law for magnetic field due to a current carrying element. Use this law to obtain a formula for magnetic field at the centre of circular loop of radius r carrying steady current I. Sketch the magnetic field lines for a current loop clearly indicating the direction of the field.
Answer:
Biot-Savart’s law. It states that the magnetic field induction dB at point P due to a current element \(\mathrm{I} \overrightarrow{d l}\) is given as
(i) dB ∝ I
(ii) dB ∝ dl
(iii) dB ∝ sin θ
(iv) dB ∝ \(\frac{1}{r^2}\)
Combining these factors, we get

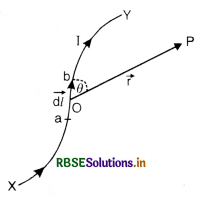
dB ∝ \(\frac{\mathrm{I} d l \sin \theta}{r^2}=\frac{\mu_0}{4 \pi} \frac{\mathrm{I} d l \sin \theta}{r^2}\)
In vector form
\(d \overrightarrow{\mathrm{B}} = \frac{\mu_0}{4 \pi} \mathrm{I} \frac{\overrightarrow{d l} \times \vec{r}}{r^3}\)
The direction of \(d \overrightarrow{\mathrm{B}}\) is perpendicular to the plane of paper and directed inwards.

Intensity of magnetic field at the centre of a circular coil carrying current. Consider a conductor bent into the form of the loop of a circle and carrying current I as shown in Fig. LAQ 4 (b). Let us determine the intensity of the magnetic field at the centre of the circle O.
Consider an element AB = \(d \overrightarrow{\mathrm{l}}\) of the circular loop. The magnetic field at the centre O due to this current element is given by
\(\overrightarrow{d \mathbf{B}}=\frac{\mu_0}{4 \pi} \cdot \frac{\mathrm{I} d \vec{l} \times \vec{r}}{r^3}\)
where \(\vec{r}\) is the vector from current element of length \(\overrightarrow{d l}\) to the point O. 

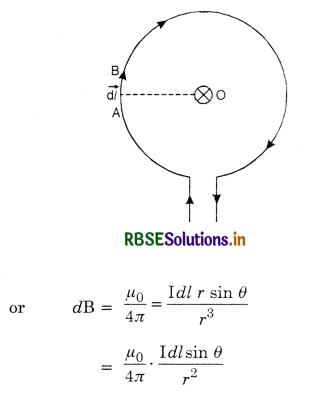
Since the angle θ between dl and r is 90°, we have
dB = \(\frac{\mu_0}{4 \pi} \cdot \frac{\mathrm{I} d l}{r^2}\) ......................(1)
The direction of this field is perpendicular to the plane of the loop and directed away from the reader and is shown by the sign of a cross in a circle (resembling the tail of an arrow).
The loop can be divided into a large number of such current elements. The magnitude of the field due to each current element is the same as that given by Eqn. (1) and is perpendicular to the plane of the loop directed away from the reader.
The total magnetic field at O is given by

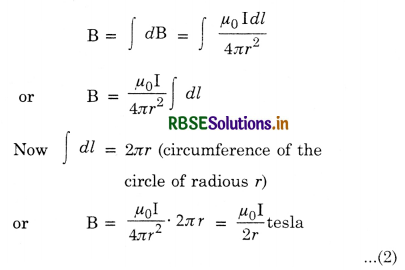
If the coil consists of n turns wound one over the other, we have
B = \(\frac{\mu_0 n \mathrm{I}}{2 r}\)tesla. ............................(3)
Magnetic field lines of circular current loop
The magnetic field lines due to circular wire form a closed loop are shown in Fig. LAQ 4 (c) and the direction of magnetic field is given by right hand thumb rule.

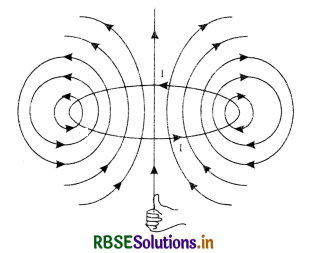
Question 24.
State Biot-Savart’s law, giving the mathematical expression for it. Use this law to derive the expression for the magnetic field due to a circular coil carrying current at a point along its axis. How does a circular loop carrying current behave as a magnet?
Answer:
Biot-Savart’s law. It states that the magnetic field induction dB at point P due to a current element \(\mathrm{I} \overrightarrow{d l}\) is given as
(i) dB ∝ I
(ii) dB ∝ dl
(iii) dB ∝ sin θ
(iv) dB ∝ \(\frac{1}{r^2}\)
Combining these factors, we get

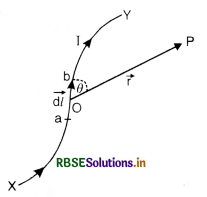
dB ∝ \(\frac{\mathrm{I} d l \sin \theta}{r^2}=\frac{\mu_0}{4 \pi} \frac{\mathrm{I} d l \sin \theta}{r^2}\)
In vector form
\(d \overrightarrow{\mathrm{B}} = \frac{\mu_0}{4 \pi} \mathrm{I} \frac{\overrightarrow{d l} \times \vec{r}}{r^3}\)
The direction of \(d \overrightarrow{\mathrm{B}}\) is perpendicular to the plane of paper and directed inwards.

Intensity of magnetic field at the centre of a circular coil carrying current. Consider a conductor bent into the form of the loop of a circle and carrying current I as shown in Fig. LAQ 4 (b). Let us determine the intensity of the magnetic field at the centre of the circle O.
Consider an element AB = \(d \overrightarrow{\mathrm{l}}\) of the circular loop. The magnetic field at the centre O due to this current element is given by
\(\overrightarrow{d \mathbf{B}}=\frac{\mu_0}{4 \pi} \cdot \frac{\mathrm{I} d \vec{l} \times \vec{r}}{r^3}\)
where \(\vec{r}\) is the vector from current element of length \(\overrightarrow{d l}\) to the point O. 

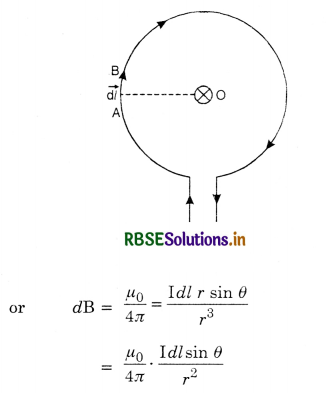
Since the angle θ between dl and r is 90°, we have
dB = \(\frac{\mu_0}{4 \pi} \cdot \frac{\mathrm{I} d l}{r^2}\) ......................(1)
The direction of this field is perpendicular to the plane of the loop and directed away from the reader and is shown by the sign of a cross in a circle (resembling the tail of an arrow).
The loop can be divided into a large number of such current elements. The magnitude of the field due to each current element is the same as that given by Eqn. (1) and is perpendicular to the plane of the loop directed away from the reader.
The total magnetic field at O is given by

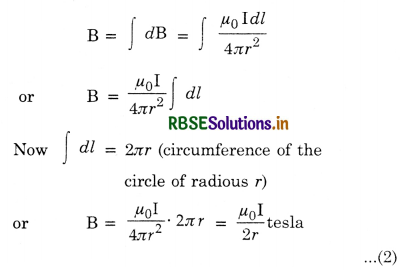
If the coil consists of n turns wound one over the other, we have
B = \(\frac{\mu_0 n \mathrm{I}}{2 r}\)tesla. ............................(3)
Magnetic field lines of circular current loop
The magnetic field lines due to circular wire form a closed loop are shown in Fig. LAQ 4 (c) and the direction of magnetic field is given by right hand thumb rule.

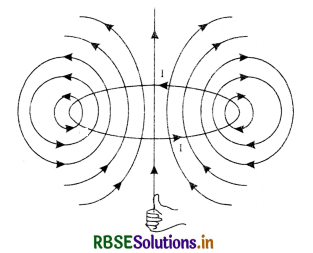
A current carrying circular loop has magnetic field around it and its magnetic moment is IA, hence it behaves like a magnet.

Question 25.
With the help of a labelled diagram, state the underlying principle of a cyclotron. Explain clearly how it works to accelerate the charged particles. Show that cyclotron frequency is independent of energy of the particle. Is there an upper limit on the energy acquired by the particle? Give reason.
Answer:
Principle. It is based upon the principle that a charged particle moving at right angles to a uniform magnetic field is acted upon by a force perpendicular to its direction of motion and follow a circular path.
Construction. It consists of two semicircular hollow metal boxes D₁ and D₂ called dees. D's are separated by a small gap and are connected to terminals of high frequency oscillator providing alternating potential of nearly 10,000 V and millions hertz frequency. Whole of the apparatus is placed in a metal box containing gas at low pressure and placed between the poles of a strong electromagnetic field perpendicular to the plane of D's.
Working
Let a positive ion (₁H¹, ₁H², ₂He³ or ₂He⁴) be located in the gap when D₁ is negatively and D₂ positively charged, the positive ion will get accelerated towards D₁. Since magnetic field is uniform and acting at right angle to the plane of D’s, the ions traverse a circular path in When the ion emerges out into the gap after completing a semicircle in D₁. If during the time taken to cover semicircle, the electric field gets reversed, the ions further get accelerated towards D₂. It enters D₂ with greater speed and moves in D₂ in a bigger semicircle. The process is repeated time and again and each time ions get an additional kick in the proper direction. The ion becomes faster and faster until it reaches the periphery of the D's where it is brought out of the chamber by means of deflecting plate P charged to a very high negative potential and is made for bombarding the target.
Theory
Let m = mass of the ion to be accelerated,
B = flux density of the magnetic field,
r = radius of the semicircular path in which the ion moves,
q = charge on the ion,
v = velocity with which the ion moves in the semicircle
Force acting on the charged particle
F = Bqv sin 90°
or F = B qv
This force provides the necessary centripetal force because it moves along circular path
∴ \(\frac{m v^2}{r}\) = Bqv
∴ v = \(\frac{\mathrm{B} q r}{m}\)
Time taken by charged particle to complete half circle,
t = \(\frac{\text { half circumference }}{\text { velocity }}=\frac{\pi r}{v}\)
= \(\frac{\pi r}{\mathrm{~B} q r / m}=\frac{\pi m}{\mathrm{~B} q r}\)
As m, B, q are constant,
∴ t is constant.
This clearly shows that time taken by the charged particle to complete a semicircle is independent of its speed and the radius of circle in which it moves.
Let T = time period of oscillator
∴ T = 2t = \(\frac{2 \pi m}{\mathrm{~B} q}\)
Frequency of oscillator field
v = \(\frac{1}{\mathrm{~T}}=\frac{\mathrm{B} q}{2 \pi m}\)
This frequency is constant and is independent of velocity (or energy) of the particle and radius of the circular path in which it moves.
Limitations.
1. The cyclotron is unable to accelerate the ions beyond a certain limit since mass will increase according to equation
m= \(\frac{m_0}{\sqrt{1-\frac{v^2}{c^2}}}\), whenever v²/c² are not negligible.
Hence required frequency will now be
v = \(\frac{\mathrm{B} q \sqrt{1-v^2 / c^2}}{2 \pi m_0}\)
Since we are unable to change the frequency in short duration, hence ion will get out of phase with high frequency accelerating field and thus lose energy instead of gaining.
2. Electrons cannot be accelerated with cyclotron.
3. Neutrons cannot be accelerated with cyclotron.
A rotating charged particle is always accelerated and radiate electromagnetic energy.

Question 26.
(a) A particle of charge q is moving with velocity v in the presence of crossed electric field E and magnetic field B as shown. Write the condition under which the particle will continue moving along x-axis. How would the trajectory of the particle be affected if the electric field is switched off?

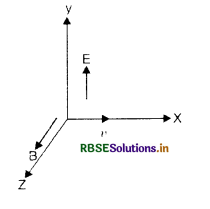
(b) A horizontal wire AB of length 'l' and mass ‘m’ carries a steady current I₁, free to move in vertical plane is in equilibrium at a height of 'h’ over another parallel long wire CD carrying a steady current I₂, which is fixed in a horizontal plane as shown. Derive the expression for the force acting per unit length on the wire AB and write the condition for which wire AB is in equilibrium.

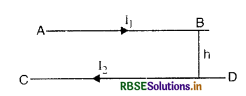
Answer:
(a) The condition for particle to continue along x-axis is:
qE = q vB sin 90°
or v = \(\frac{E}{B}\)
When the electric field is switched off, the trajectory of the charge will become helical about the direction of the magnetic field.

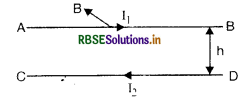
(b) At any point P magnetic field intensity due to current I₂ in CD
B = \(\frac{\mu_0 \mathrm{I}_2}{2 \pi r}\)
Its direction is perpendicular to the plane of the paper and downwards.
Force per unit length experienced by conductor AB is given by
\(\frac{\mathrm{F}}{\mathrm{h}} \) = B, I₁ = \(\frac{\mu_0 I_1 I_2}{2 \pi r}\)
At equilibrium
\(\frac{\mu_0 I_1 I_2}{2 \pi r} = \frac{m g}{h}\).

Question 27.
(i) Derive the expression for the torque acting on a current carrying loop placed in a magnetic field.
(ii) Explain the significance of a radial magnetic field when a current carrying coil is kept in it.
Answer:
(i) Torque on current carrying loop in a magnetic field
Consider a rectangular loop PQRS with sides PQ = l and PS = b. Let I be the current flowing in the loop placed in a uniform magnetic field \(\overrightarrow{\mathrm{B}}\) as shown in the figure.
Let θ be angle made by the plane of the coil with magnetic field \(\overrightarrow{\mathrm{B}}\). Let \(\overrightarrow{\mathrm{F}}_1\), \(\overrightarrow{\mathrm{F}}_2\), \(\overrightarrow{\mathrm{F}}_3\) and \(\overrightarrow{\mathrm{F}}_4\) be forces acting on the arms PQ, QR, RS and SP respectively of the coil.
Force on arm SP
\(\vec{F}_4=\mathrm{I}(\vec{b} \times \vec{B})\)
or F₄ = IbB sin (180° - θ)
or F₄ = BIb sin θ .............................(1) [upwards]
Force on arm QR

\(\vec{F}_2=\mathrm{I}(\vec{b} \times \vec{B})\)
or F₂ = I bB sin θ
or F₂ = BIb sin θ ................................(2) [downwards]
Since the forces \(\vec{F}_4\) and \(\vec{F}_2\) are equal in magnitude and acting in opposite direction along the same straight line, so they cancel each other's effect. Hence produce no torque i.e. resultant torque is zero.
Force on arm PQ
\(\vec{F}_1 = \mathrm{I}(\vec{b} \times \vec{B})\)
or F₁ = IlB sin 90°
or F₁ = BIl ......................(3) (towards the reader)
Force on arm RS
\(\vec{F}_3 = \mathrm{I}(\vec{b} \times \vec{B})\)
or F₃ = IlB sin 90°
or F₃ = BIl .........................(4) (away from the reader)
These two parallel, equal and opposite forces acting along different lines of action, so they form a couple. The moment of the couple i.e. torque τ is given by
τ = Either force x ⊥ distance between the forces
= BIl (PT)
= BIl b cos θ
τ = BIA cos θ ................(5)
(where A = l x b is the area of the rectangular coil)
If the coil has n turns, then
τ = nBIA cos θ ..................(6)
If normal to the plane of the coil, makes an angle Φ with B, then θ = 90 - Φ.
So τ = nBIA cos (90 - Φ) = nBIA sin Φ.
(ii) A radial field is always perpendicular to the plane of the coil, hence moving coil galvanometer has linear scale. 

HOTS QUESTIONS

Question 1.
A current I flows in a conductor placed perpendicular to the plane of paper. Indicate the direction of the magnetic field due to a small element d \vec{l} at point P situated at a distance \vec{r} from the element as shown in the figure HQT.

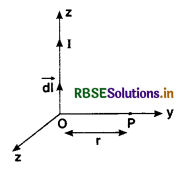
Answer:
From Biot-Savart law, we have

i.e. magnetic field at P is directed along negative x-direction.

Question 2.
To increase the current sensitivity of a moving coil galvanometer by 50%, its resistance is increased so that the new resistance becomes twice its initial resistance. By what factor does its voltage sensitivity change?
Answer:
Given I'_s = I_s + \(\frac{50}{100}\)Is = 1.5 I_s
And R' = 2R
Initial voltage sensitivity, V'_s = \(\frac{\mathrm{I}_{\mathrm{s}}}{\mathrm{R}}\)
New, voltage sensitivity, V'_s = \(\frac{\mathrm{I}_s^{\prime}}{2 \mathrm{R}}\)
= 1.5\(\frac{I_s}{2 \mathrm{R}}\) = 0.75 V_s
∴ % decrease in voltage sensitivity
= \(\frac{\mathrm{V}_{\mathrm{s}}-\mathrm{V}_s^{\prime}}{\mathrm{V}_s}\) x 100 = \(\frac{\mathrm{V}_s-0.75 \mathrm{~V}_s}{\mathrm{~V}_s}\) x 100 = 25%

Question 3.
A galvanometer can be converted into a voltmeter to measure upto
(i) V volts by connecting a resistance R₁ in series with coil.
(ii) \(\frac{V}{2}\) volts by connecting a resistance R₂ in series with its coil.
Find the resistance R, in terms of R₁ and R₂ required to convert it into a voltmeter that can read upto 2V volts.
Answer:
For conversion of a galvanometer into a voltmeter of range 2V,

For conversion of galvanometer into a voltmeter of range 2V, we have

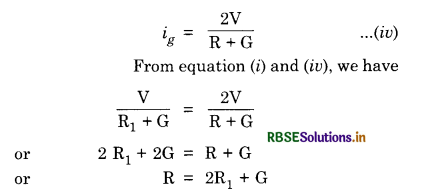
Putting the value of G from equation (iii), we get
R = 2R₁ + R₁ - 2R₂
or R = 3R₁ - 2R₂

Question 4.
Find the total magnetic induction at point O due to current through curved portion and straight portion.

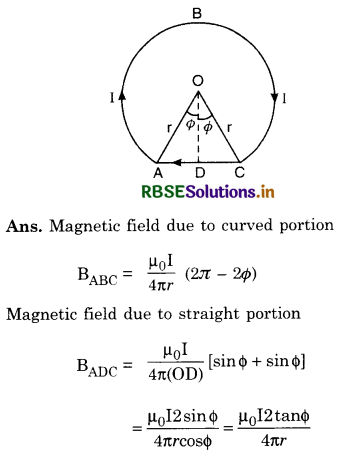
∴ Total magnetic induction at O
B₀ = \(\frac{\mu_0 I}{4 \pi r}(2 \pi-2 \phi)+\frac{\mu_0 I}{4 \pi r} 2 \tan \phi\)
= \(\frac{\mu_0 \mathrm{I}}{2 \pi r}\)[π - Φ + tanΦ]

Question 5.
A galvanometer having 30 divisions has a current sensitivity of 20µA per division. It has a resistance of 25Ω. How will you convert it into an ammeter measuring upto I_A? How will you convert this ammeter into a voltmeter reading upto IV?
Answer:
Given, current sensitivity
I_s = 20µA div^-1 = 20 x 10^-6 A div^-1
The galvanometer has 30 divisions, so current for full scale deflection, I_g = 30 x 20 x 10^-6 A = 6 x 10^-4 A
When the galvanometer is to be converted into an ammeter, thus the value of shunt required
S = \(\frac{\mathrm{I}_g}{\mathrm{I}-\mathrm{I}_g} \mathrm{G}=\frac{6 \times 10^{-7}}{1-6 \times 10^{-4}} \times 25\)
= 0.015 Ω (in parallel)
When the galvanometer is to be converted into a voltmeter, then the value of resistance R is given by
R = \(\frac{\mathrm{V}}{\mathrm{I}}\) - RA
= \(\frac{1}{1}-\frac{\mathrm{GS}}{\mathrm{G}+\mathrm{S}}=1-\frac{25 \times 0.015}{25+0.015}\)
= 1 - 0.015 = 0.985 Ω (in series)

Question 6.
A 5 MeV proton moves vertically downward through a magnetic field of induction 1.5 Wbm^-2 pointing horizontally from south to north. Calculate the force acting on the proton, mass of proton = 1.6 x 10^-27 kg. 

= 3.1 x 10⁷ ms^-1
The magnetic field is horizontal from south to north and velocity \(\vec{v}\) vertically downward i.e. angle between \(\vec{v}\) and \(\vec{B}\) = 90°.
∴ Force on proton, F = q v B sin 90°
= q v B = e v B.
= 1.6 x 10^-19 x 3.1 x 10⁷ x 1.5 = 7.44 x 10^-12 N.

Question 7.
Use Biot Savart law to obtain an expression for the magnetic field at the centre of a coil in the form of a square of sides 2a carrying a current I.
Answer:
Let O be the centre of a square ABCD of sides 2a as shown in the figure
Magnetic field at O due to side AB 

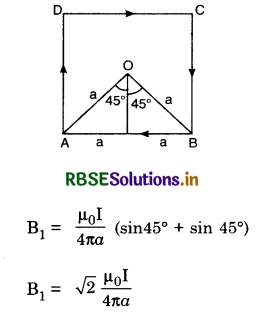
By symmetry, magnetic field will be same for each side
∴ Total magnetic field at O
B = 4B₁ = \(\frac{4 \sqrt{2} \mu_0 I}{4 \pi a}=\frac{\sqrt{2} \mu_0 I}{\pi a}\)

Question 8.
Two concentric coplanner semi-circular conductors form part of two current loops as shown in the figure. If their radii are 11 cm and 4 cm. Calculate the magnetic induction at the centre.