RBSE Class 12 Physics Important Questions Chapter 3 विद्युत धारा

Rajasthan Board RBSE Class 12 Physics Important Questions Chapter 3 विद्युत धारा Important Questions and Answers.

RBSE Class 12 Physics Chapter 3 Important Questions विद्युत धारा

अति लघुत्तरीय प्रश्न

प्रश्न 1.
किसी धारावाही चालक में किसी बिन्दु पर विद्युत क्षेत्र और धारा धनत्व का अनुपात क्या कहलाता है?
उत्तर:
प्रतिरोधकता

प्रश्न 2.
किसी बाह्य प्रतिरोध R से संबोजित आंतरिक प्रतिरोध। का कोई सेल अधिकतम धारा की आपूर्ति कब कर सकता है?
उत्तर:
जब प्रतिरोध R = 0 हो।

प्रश्न 3.
आन्तरिक प्रतिरोध r तथा emf(E) का कोई सेल किसी परिवर्ती बाह्य प्रतिरोध R के सिरो से संयोजित है। R के फलन के रूप में टर्मिनल विभवान्तर V का ग्राफ कैसा होगा?
उत्तर:

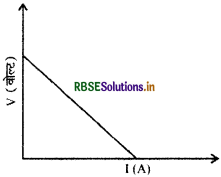
प्रश्न 4.
किसी दिए गए चालक के सिरों पर अनुप्रयुक्त विभवान्तर दुगुना कर दिया जाता है। चालक में इलेक्ट्रानों की गतिशीलता पर क्या प्रभाव होगा?
उत्तर:
गतिशीलाता, µ = \(\frac{q z}{m}\) अर्थात् गतिशीलता, विश्रांतिकाल पर निर्भर करती है। अत: विभवान्तर का मान द्गुना करने पर भी गतिशीलता अपरिवर्तित रहती है।

प्रश्न 5.
एक आवेशित कण आवेशित समांतर पट्टिका संधारित्र की पट्टिकाओं के बीच रखा है। यह किसी बल F का अनुभव करता है। यदि किसी एक पट्टिका को हटा दिया जाए तो आवेशित कण पर बल का मान क्या होगा?
उत्तर:
आवेशित समांतर पट्टिका के बीच रखे आवेश q पर आरोपित 
बल, F = E_q = \(\frac{\sigma}{\varepsilon_0} q\)
दोनों पट्टिकाओं द्वारा आरोपित बल एक ही दिशा में अर्थात +ve प्लेट से - ve की ओर होंगे। कोई एक पट्टिका हटा देने पर बल।

प्रश्न 6.
V वोल्ट की किसी बैटरी से किसी समान्तर पट्टिका संधारित्र को आवेशित किया गया है। इस बैटरी को हटाकर पद्रिकाओं के बीच पृथकन को आधा कर दिया जाता है। इस संधारित्र के सिरों पर नया विभवान्तर क्या होगा?
उत्तर:
पृथकन आधा होने पर विभवान्तर भी आधा हो जाएगा।

प्रश्न 7.
m²V-¹s-¹ किसका SI मात्रक हैं?
उत्तर:
गतिशीलता।

प्रश्न 8.
आरेख में किसी कार्बन प्रतिरोधक को दर्शाया गया है? वर्ण कोड का उपयोग करके इस प्रतिरोध का मान लिखिए।

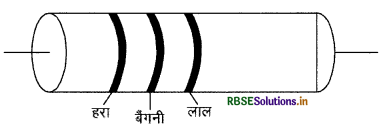
उत्तर:
प्रतिरोध का प्रथम सार्थक अंक - 5 (हरा)
प्रतिरोध का दूसरा सार्थक अंक - 7 (बैगनी)
तथा गुणक - 10² (लाल) 
अतः प्रतिरोध का मान - 57 x 10² ओम
= 5.7 किलो ओम

प्रश्न 9.
समान लम्बाई और समान त्रिज्या के निक्रोम और ताँबे के तार श्रेणीक्रम में संयोजित हैं। इनमें से धारा I प्रवाहित कराई गई है। कौन - सा तार अधिक तप्त होगा? अपने उत्तर की पुष्टि कीजिए।
उत्तर:
समान लम्बाई और समान त्रिज्या के लिए, तार का प्रतिरोध
R ∝ P 
जैसा कि ρ नाइक्रोम > ρ ताँया
अत: नाइक्रोम का प्रतिरोध अधिक होगा। श्रेणीक्रम में दोनों भागों में से समान धारा प्रवाहित होती है और उत्पन्न ऊष्मा = I²Rt होगी। इसीलिए नाइक्रोम भाग के तार में अधिक ऊष्मा उत्पन्न होती है।

प्रश्न 10.
मीटर सेतु में सन्तुलन बिन्दु प्राय: मध्य भाग में क्यों प्राप्त करते हैं?
उत्तर:
शून्य विक्षेप की स्थिति तार के मध्य में होने पर मीटर सेतु की सुग्राहिता अधिकतम होती है।

प्रश्न 11.
चित्र में दशाए कार्बन प्रतिरोध का मान 22 x 10⁵ Ω ± 5% है। प्रथम वलय A का रंग लिखिए।

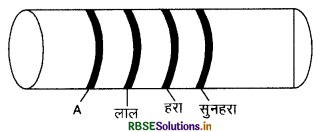
उत्तर:
प्रतिरोध 22 x 10⁵ Ω ±5% का प्रथम सार्थक अंक 2 है अतः A का रंग - लाल होगा।

प्रश्न 12.
अति चालकता को परिभाषित कीजिए।
उत्तर:
कम ताप पर किसी पदार्थ की प्रतिरोधकता के शून्य हो जाने की घटना को अति - चालकता कहते हैं। जिन पदार्थों में यह घटना होती है, उन्हें अति - चालक कहते हैं।

प्रश्न 13.
किसी चालक में इलेक्ट्रॉनों के अपवाह वेग को परिभाषित करो।
उत्तर:
किसी चालक में इलेक्ट्रॉनो के विद्युत क्षेत्र के प्रभाव में एक नियम औसत वेग से एक दिशा में प्रवाहित होते हैं। इस नियम औसत एक दिशीय वेग को अनुगमन वेग कहते हैं। इसे v_d से प्रदर्शित करते हैं।

प्रश्न 14.
ऐसे दो पदार्थों के नाम लिखिए, जिनकी प्रतिरोधकता ताप बढ़ाने पर घटती है।
उत्तर:

• सिलिकॉन
• जर्मेनियम

प्रश्न 15.
सेल का विद्युत वाहक बल हमेशा टर्मिनल वोल्टेज से अधिक होता है, क्यों? कारण दीजिए।
उत्तर:
क्योंकि विभव का कुछ भाग सेल के अत्य आन्तरिक प्रतिरोध में व्यय हो जाता है।

प्रश्न 16.
आयनिक गतिशीलता को परिभाषित कीजिए।
उत्तर:
आयनिक गतिशीलता (Ionic Mobility): एकांक विद्युत क्षेत्र आरोपित करने पर आयन का अनुगमन वेग आयनिक गतिशीलता कहलाती है।

प्रश्न 17.
धारा घनत्व का SI मात्रक लिखिए।
उत्तर:
ऐम्पियर/मी²

लघु उत्तरीय प्रश्न

प्रश्न 1.
किसी धारावाही चालक में पद आवेशवाहकों की 'गतिशीलता' की परिभाषा लिखिए। विश्रान्तिकाल के पदों में गतिशीलता के लिए संबंध प्राप्त कीजिए।
उत्तर:
गतिशीलता (Mobility):
हम जानते हैं कि चालकता गतिमान आवेश वाहकों से उत्पन्न होती है। धातुओं में ये गतिमान आवेश वाहक इलेक्ट्रॉन होते हैं, आयनित गैस में ये इलेक्ट्रॉन तथा धनावेशित आवन होते है, विद्युत् अपघट्य में वे धनायन तथा ऋणायन दोनों हो सकते हैं।
एक महत्वपूर्ण राशि गतिशीलता (mobility) है जिसे प्रति एकांक विद्युत् क्षेत्र के अनुगमन वेग के परिमाण के रूप में परिभाषित करते हैं।
∴ µ = \(\frac{\left|\overrightarrow{v_d}\right|}{\mathrm{E}}=\frac{v_d}{\mathrm{E}}\) ...............(1)
∵ v_d = \(\frac{e \tau}{m} \mathrm{E}\)
या \(\frac{v_d}{\mathrm{E}}=\frac{e \tau}{m}\)

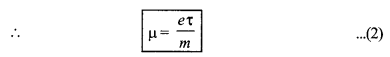
∴ इलेक्ट्रॉन को गतिशीलता
µ_e = \(\frac{e \tau_e}{m_e}\)
मात्रक - चूँकि µ = \(\frac{v_d}{\mathrm{E}}\)
∴ µ का मात्रक = \(\frac{\mathrm{ms}^{-1}}{\mathrm{Vm}^{-1}}\) = m²s^-1V^-1
या µ का मात्रक = \(\frac{\mathrm{ms}^{-1}}{\mathrm{NC}^{-1}}\) = mCs^-1N^-1
विद्युत् धारा एवं गतिशीलता में सम्बन्ध
I = e_nA v_d
परन्तु v_d = µ_eE

किसी अर्द्धचालक के लिए विद्युत् धारा एवं गतिशीलता में सम्बन्ध-
अर्द्धचालक में इलेक्ट्रॉन व होल दोनों के कारण चालकता होती है, 
अतः
I = I_e + I_h
= en_eAv_e + e.n_hAv_h
= en_eAµ_eE + e.n_hAµ_hE

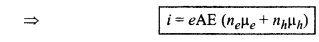
प्रश्न 2.
किसी धारावाही चालक में पद इलेक्ट्रॉनों के 'अपवाह वेग' की परिभाषा लिखिए। धारा धनत्व और इलेक्ट्रॉनों के अपवाह वेग के बीच संबंध प्राप्त कीजिए।
उत्तर:
अनुगमन वेग (Drift Velocity)
जब किसी चालक के सिरों के मध्य विभवान्तर लगाया जाता है तो चालक के अन्दर एक विद्युत् क्षेत्र (धन सिरे से ऋण सिरे की ओर) \(\overrightarrow{\mathrm{E}}\) उत्पन्न हो जाता है और प्रत्येक मुक्त इलेक्ट्रॉन पर एक वैद्युत बल (F = - E.e) लगने लगता है। इस बल के प्रभाव में इलेक्ट्रॉन त्वरित \(\left(a=\frac{\mathrm{F}}{m}\right)\) होता है और वह चालक के धनात्मक सिरे की ओर गति करने लगता है। गति के दौरान वह अन्य इलेक्ट्रॉनों एवं चालक के धन आयनों से टकराता हुआ वेग में परिवर्तन करता हुआ चलता है। इलेक्ट्रॉन की इस गति को अनुगमन गति (Drift motion) कहते हैं और दो उत्तरोत्तर टक्करों (Successive collisions) के मध्य इलेक्ट्रॉन के औसत वेग को अनुगमन वेग (Drift velocity) कहते हैं। इसे से v_d व्यक्त करते हैं।

अर्थात् आरोपित विद्युत् क्षेत्र (imposed electric field) के कारण इलेक्ट्रॉनों द्वारा प्राप्त अधिकतम वेग (drift velocity) जिससे इलेक्ट्रॉन अन्य आयनों से टकराते हैं उसे अनुगमन वेग कहते हैं। टकराने में लगे समय को श्रांतिकाल कहते हैं। अधिकतर चालकों के लिए श्रांतिकाल 10^-14 s कोटि का होता है।

किसी आयन से टकराने के ठीक पहले इलेक्ट्रॉनों का वेग अधिकतम (maximum) तथा टकराने के ठीक बाद क्षण भर के लिए वेग शून्य हो जाता है। पुनः इलेक्ट्रॉन विद्युत् क्षेत्र में त्वरित होता है और आयनों से टकराने वाली पूर्व स्थिति (previous position) को दोहराता है। "इस प्रकार बैटरी का विभवान्तर इलेक्ट्रॉनों को त्वरित (accelerated) गति प्रदान नहीं कर पाता है बल्कि यह उन्हें चालक की लम्बाई के अनुदिश (along) एक छोटा नियत वेग ही दे पाता है जो कि इलेक्ट्रॉनों की अनियमित गति के ऊपर आरोपित रहता है। इलेक्ट्रॉनों के इस नियत वेग को ही अनुगमन वेग कहते हैं।" अनुगमन वेग का कोटि मान 10^-4 ms^-1 होता है।

अनुगमन वेग के कम होने का कारण: चित्र 3.5 में विद्युत् क्षेत्र आरोपित करने पर मुक्त इलेक्ट्रॉनों की अनियमित गति (मोटी रेखा) के साथ उसका अनुगमन (बिन्दुवत्) भी दिखाया गया है। चित्र से स्पष्ट है कि विद्युत् क्षेत्र की अनुपस्थिति में इलेक्ट्रॉन 8 टक्करों के पश्चात् स्थिति 1 से X तक अनियमित गति करता हुआ पहुँचता है, जबकि वैद्युत क्षेत्र आरोपित करने पर इलेक्ट्रॉन की अन्तिम स्थिति X के बजाय X' हो जाती है। इस प्रकार विद्युत् क्षेत्र द्वारा नैट विस्थापन XX' हो जाता है जिसका मान काफी कम होता है। इसीलिए अनुगमन वेग भी कम होता है।


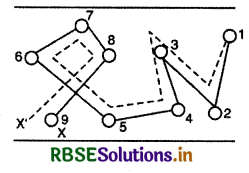
श्रांतिकाल (Relaxation Time): "मुक्त इलेक्ट्रॉन की धातु के परमाणुओं से हुई दो क्रमागत टक्करों के बीच लगे औसत समय को श्रान्तिकाल कहते हैं।" इसे τ से व्यक्त करते हैं। यदि दो उत्तरोत्तर टक्करों के बीच औसत दूरी अर्थात् माध्य मुक्त पथ (mean free path) λ हो तथा उसकी औसत चाल या वर्ग माध्य मूल चाल (root mean square speed) v_r हो तो

λ का मान 10^-9 m तथा τ का मान 10^-14 सेकण्ड की कोटि का होता है।

प्रश्न 3.
(a) 47 kΩ ± 10% कार्बन प्रतिरोधक पर पाए जाने वाले वर्ण बैण्डों का क्रम बताइए।
(b) मैंगनिन के वे दो गुणधर्म लिखिए जो इसे मानक प्रतिरोधक बनाने के लिए उपयुक्त पदार्थ बनाते हैं।
उत्तर:
(a) पीला, बैंगनी, नारंगी, चाँदी सा
(b) प्रतिरोधकता अधिक होती है तथा प्रतिरोध ताप गुणांक कम होता है।

प्रश्न 4.
(अ) किरॉफ का नियम लिखिए।
(ब) विभवमापी की सहायता से दो प्राथमिक सेलों की तुलना करने का परिपथ चित्र बनाइए।
उत्तर:
(अ) किरखोफ के नियम (Kirchhoff's Laws):
ओम का नियम केवल सरल विद्युत परिपर्थों के लिए ही उपयोगी है। ऐसे परिपथ जिनमें एक से अधिक विद्युत वाहक स्रोत जुड़े है, उनमें ओम के नियम के प्रयोग में कठिनाई होती है। सन् 1842 में जटिल वैद्युत परिपथों के लिए दो नियमों का प्रतिपादन गुस्ताव रॉबर्ट किरखोफ ने किया। किरखोफ के नियमों को समझने से पूर्व हम कुछ शब्दावली को परिभाषित करेंगे।

संधि (Juction): किसी विद्युत परिपथ में जिस बिन्दु पर तीन या तीन से अधिक धारावाही शाखाएँ (Branchs) मिलती है, उसे संधि कहते है।

शाखा (Branch): किसी विद्युत परिपथ के जाल (network) का वह भाग जिसमें विद्युत धारा नियत रहती है, शाखा कहलाती है।

लूप या पाश (Loop): विभिन्न चालकों, प्रतिरोधों एवं अन्य अवयवों से मिलकर बना विद्युत परिपथ, लूप या पाश कहलाता है।

किरखॉफ का प्रथम नियम या संधि नियम (Kirchhoff's First Law or Junction Law) 
प्रथम नियम - "किसी वैद्युत परिपथ में किसी संधि पर मिलने वाली समस्त धाराओं का बीजगणितीय योग (algebraic sum) शून्य होता है।" अर्थात्
Σi = 0 ................(1)
किसी संधि की ओर आने वाली (incoming) धाराओं को धनात्मक एवं संधि से दूर जाने वाली (outgoing) धाराओं को ऋणात्मक मान लिया जाता है। संधि O पर मिलने वाली धाराओं के लिए,

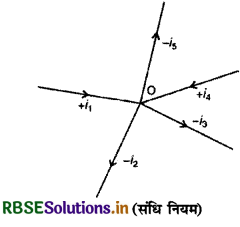
i₁ - i₂ - i₃ + i₄ - i₅ = 0
या i₁ + i₄ = i₂ + i₃ + i₅
या संधि की ओर आने वाली धाराओं का योग
= संधि से दूर जाने वाली धाराओं का योग इस प्रकार किरखॉफ के प्रथम नियम को इस प्रकार भी कह सकते हैं, "किसी परिपथ में किसी संथि की ओर आने वाली धाराओं का योग संधि से दर जाने वाली धाराओं के योग के बराबर होता है।" किरखॉफ का प्रथम नियम आवेश संरक्षण (law of Conservation of Charge) के सिद्धान्त पर आधारित है।

किरखॉफ का द्वितीय नियम या लूप नियम (Kirchhoff's Second Law or Loop Law)
द्वितीय नियम - "किसी बन्द परिपथ में परिपथ का परिणामी विद्युत वाहक बल परिपथ के विभिन्न अवयवों (elements) के सिरों पर उत्पन्न विभवान्तरों के योग के बराबर होता है।" किरखॉफ का यह नियम ऊर्जा संरक्षण (Law of Conservation of Energy) के सिद्धांत पर आधारित होता है अर्थात्
ΣE = ΣV = ΣiR .................(2)
उदाहरण के लिए, चित्र 3.27 में किरखॉफ के नियम लगाते हैं-

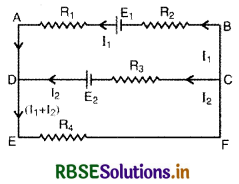
उपर्युक्त नियमों के आधार पर,
A से B की दिशा में E₁= -
B से A की दिशा में E₁ = + 
D से C की दिशा में E₂ = -
C से D की दिशा में E₂ = +
बन्द पाश ABCDA में,
ΣE = ΣiR
बन्द पाश का रास्ता A→ B → C →D →A
-E₁ + E₂ = -i₁R₁ - i₁R₂ + i₂R₃
⇒ E₂ - E₁ = i₂R₃ - i₁(R₁ + R₂) ..............(3)
बन्द पाश DCFED में,
बन्द पाश का रास्ता D → C → F → E →D
ΣE = Σi.R
-E₂ = -i₂.R₃ - (i₁ + i₂)R₄
या E₂ = i₂R₃ + (i₁ + i₂)R₄ ...............(4)

(ब) विभवमापी के उपयोग (Uses of Potentiometer)
1. दो सेलों के विद्युत् वाहक बलों की तुलना करना: जिन सेलों के विद्युत् वाहक बलों E₁ व E₂ की तुलना करनी है, उन्हें चित्र 3.36 के अनुसार द्विमार्गी कुंजी (two way key) एवं धारामापी के द्वारा विभवमापी से जोड़ देते हैं। प्राथमिक परिपथ में एक बैटरी E_p, एक कुंजी K एवं परिवर्ती प्रतिरोध (variable resistance) Rh भी चित्र की भाँति जोड़ देते है।
एक प्रतिरोधक बॉक्स से (R.B) एक उच्च प्रतिरोध R को लगाया जाता है ताकि धारामापी से होकर उच्च धाराएँ ना जाएँ।


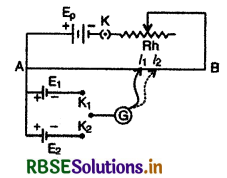
प्रयोग विधि:
(1) पहले कुंजी K को दबाकर विभवमापी तार AB के सिरों के मध्य विभवान्तर स्थापित कर लेते हैं। अब कुंजी K₁ व K₂ को बारी - बारी से लगाकर धारा नियन्त्रक (rheostat) को इस प्रकार व्यवस्थित (adjust) करते है कि जॉकी को तार के सिरों A व B के मध्य स्पर्श (touch) कराने पर धारामापी में विक्षेप दोनों ओर प्राप्त हो जाये। माना इस स्थिति में तार की विभव प्रवणता है।

(ii) अव द्विमार्गी कुंजी की कुंजी K₂ को खुला रखकर K₁ को लगाकर सेल E₁ को द्वितीयक परिपथ में जोड़ते हैं और धारामापी में अविक्षेप स्थिति (no deflection position) ज्ञात करके तार की लम्बाई " ज्ञात कर लेते हैं, अतः।
E₁ = kl₁ ................(1)
(iii) अब K₁ को खुला रखकर K₂ को लगाकर E₂ को द्वितीयक परिपथ में जोड़ते है और शून्य विक्षेप (zero deflection) की स्थिति में l₂ ज्ञात कर लेते हैं, अतः
E₂ = kl₂ .............(2)
समी. (i) व (ii) से,
\(\frac{\mathrm{E}_1}{\mathrm{E}_2}=\frac{l_1}{l_2}\) .......................(3)
यदि दोनों सेलों में कोई एक प्रमाणिक सेल (standard cell) है तो दूसरे सेल का विद्युत् वाहक बल भी ज्ञात कर सकते हैं।

विभवमापी व वोल्टमीटर में अन्तर:
(1) वोल्टमीटर द्वारा विद्युत् बाहक बल नापने के लिए वोल्टमीटर में विक्षेप पढ़ना पड़ता है। विक्षेप के पढ़ने में त्रुटि (error) रह जाती है, जबकि विभवमापी द्वारा विद्युत् वाहक बल अविक्षेप (null) विधि से नापा जाता है, इसे तार पर शून्य विक्षेप स्थिति पढ़ना कहते हैं। अतः विभवमापी को आदर्श वोल्टमीटर (ideal voltmeter) भी कहते हैं।

(2) विभवमापी द्वारा सेल का विद्युत् वाहक बल नापते (measurement) समय शून्य विक्षेप स्थिति में सेल के परिपथ में कोई धारा प्रवाहित नहीं होती है अर्थात् सेल खुले परिपथ (open circuit) पर होता है। अत: सेल के विद्युत् वाहक बल का वास्तविक मान प्राप्त होता है। इस प्रकार विभवमापी अनन्त प्रतिरोध (infinite resistance) के आदर्श (ideal) वोल्टमीटर के समान कार्य करता है।

2. सेल का आन्तरिक प्रतिरोध ज्ञात करना - बैटरी, कुंजी एवं धारा नियन्त्रक को संयोजक पेंचों A व B से जोड़कर प्राथमिक परिपथ तैयार कर लेते हैं। अब जिस सेल का आन्तरिक प्रतिरोध ज्ञात करना है उसे और एक प्रतिरोध बॉक्स को चित्र 3.37 की तरह पेंच A व द्विमार्गी कुंजी (two way key) से जोड़ते हैं तथा द्विमार्गी कुंजी को धारामापी एवं जॉकी से जोड़कर द्वितीयक परिपथ (secondary circuit) तैयार करते हैं।


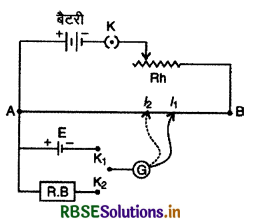
प्रयोग विधि:
(i) कुंजी K को बन्द करके तार AB में विभवान्तर (potential difference) स्थापित कर लेते हैं। अब धारा नियन्त्रक को इस प्रकार व्यवस्थित करते हैं कि जॉकी को तार के सिरों A व B के बीच स्पर्श कराने पर धारामापी में विक्षेप दोनों ओर प्राप्त हो जाये। माना इस स्थिति में तार की विभव प्रवणता में है।

(ii) कुंजी K₂ को खुला (open) रखकर K₁ को बन्द करके सेल को द्वितीयक परिपथ में डालते हैं और जॉकी से शून्य विक्षेप की स्थिति में तार की लम्बाई l₁ ज्ञात कर लेते हैं, अत:
E = kl₁ ........................(4)

(iii) अब K₁ को बन्द (close) रखते हुए K₂ को बन्द करते हैं और प्रतिरोध बॉक्स में कोई समुचित प्रतिरोध (Proper resistance) R लगाकर पुनः अविक्षेप स्थिति में तार की लम्बाई l₂ ज्ञात कर लेते हैं। यह सेल के टर्मिनल विभवान्तर के सन्तुलन के संगत है, अतः
V = kl₂......................(5)
माना सेल का आन्तरिक प्रतिरोध r है यदि सेल को R ओम के प्रतिरोध से शंट करने पर सेल में i धारा बहती है, तो ओम के नियम से
E = i(R + r)
एवं V = iR
⇒ 1+ \(\frac{r}{\mathrm{R}}=\frac{l_1}{l_2} \)
⇒ \(\frac{r}{\mathrm{R}}=\frac{l_1-l_2}{l_2}\)
अत: आन्तरिक प्रतिरोध r = \(\mathrm{R}\left[\frac{l_1-l_2}{l_2}\right]\) ...........................(6)

प्रश्न 5.
किरखॉफ के नियम का उपयोग करते हुए व्हीटस्टोन सेतु की सन्तुलन अवस्था के लिए आवश्यक प्रतिबन्ध प्राप्त कीजिए। आवश्यक परिपथ चित्र बनाइये।
उत्तर:
हीटस्टोन सेतु (Wheatstone's Bridge):
इंग्लैण्ड के वैज्ञानिक प्रोफेसर सी. एफ. द्वीटस्टोन (C.F. Wheatstone) ने चार प्रतिरोधों, एक धारामापी एवं एक सेल को जोड़कर एक विशेष प्रकार का परिपथ तैयार किया जो हीटस्टोन सेतु के नाम से जाना गया। इसकी सहायता से हम अज्ञात (unknown) प्रतिरोध ज्ञात कर सकते हैं।
रचना: द्वीटस्टोन सेतु की सैद्धान्तिक रचना चित्र 3.28 में दिखाई गई है। चार प्रतिरोधों P, Q, R, S को जोड़कर एक चतुर्भुज ABCD बनाते हैं। बिन्दुओं A व C के मध्य एक सेल जोड़ देते हैं। बिन्दुओं B व D के मध्य एक धारामापी जोड़ दिया जाता है। K₁ बैटरी कुंजी है और K₂ धारामापी कुंजी है। यदि कुंजी K₁ को हम पहले बन्द (close) करें और फिर K₂ को, तब यदि धारामापी में कोई विक्षेप (deflection) न दें तब इस अवस्था में,

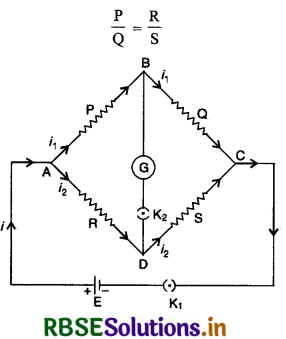
सिद्धान्त: जब बैटरी कुंजी (battery key) K₁ को दबाते हैं तो परिपथ में मुख्य धारा i बहती है। इस धारा को A बिन्दु पर दो मार्ग मिलने से यह दो भागों i₁ व i₂ में बँट जाती है। i₁ को B बिन्दु पर और i₂ को D बिन्दु पर पुनः दो मार्ग मिलते हैं। B व D पर, i₁ व i₂ के विभाजन की निग्न तीन स्थितियाँ सम्भव हैं-
(i) जब V_B> B_D तो B बिन्दु पर i₁ का एक भाग धारामापी से गुजर कर उसमें एक दिशा में विक्षेप उत्पन्न करता है और शेष भाग (remaining part) प्रतिरोध Q से होकर गुजरता है। बिन्दु D पर धारा का कोई बँटवारा (distribution) नहीं होता है।

(ii) जब V_B < V_D होता है तो B पर धारा का विभाजन नहीं होता है, बल्कि D पर धारा i₂ का एक भाग धारामापी से गुजरकर पहले की विपरीत दिशा में विक्षेप उत्पन्न करेगा और शेष भाग प्रतिरोध से गुजरता है।

(iii) V_B = B_D तो धारामापी वाली भुजा में कोई धारा न बहने से उसमें शून्य विक्षेप (zero deflection) की स्थिति रहती है। यही सेतु के सन्तुलन की स्थिति कहलाती है। स्पष्ट है कि परिपथ में तो धारा बहती है, लेकिन धारामापी वाली भुजा पर इस धारा का कोई प्रभाव नहीं पड़ता है। यह घटना ठीक उसी प्रकार की है कि नदी की धारा का सेतु पर कोई प्रभाव नहीं पड़ता है। इसीलिए इसे सेतु परिपथ कहते हैं। इस प्रकार सेतु के सन्तुलन की स्थिति में,
V_B = V_D
अतः V_A - V_B = V_A - V_D
या i₁P = i₂R ...........(1)
और V_B - V_C = V_D - V_C
या i₁Q = i₂S
समीकरण (1) व (2) से,
या \(\frac{\mathrm{P}}{\mathrm{Q}}=\frac{\mathrm{R}}{\mathrm{S}}\) .............(3)
अतः स्पष्ट है कि "जब सेतु सन्तुलित होता है तो चतुर्भुज ABCD की किन्हीं भी दो संलग्न (corresponding) भुजाओं के प्रतिरोधों का अनुपात शेष दो संलग्न भुजाओं के प्रतिरोधों के अनुपात (ratio) के बराबर होता है।"
समी. (3) से, S = \(\frac{Q}{P}\) x R
अतः सेतु के सन्तुलन की स्थिति ज्ञात करके हम S का मान उक्त सूत्र से ज्ञात कर सकते है। P और Q वाली भुजाओं को हम अनुपातिक भुजाएँ (ratio arms), R वाली भुजा को प्रामाणिक भुजा (standard arms) और S भुजा को अज्ञात भुजा कहते हैं।

वैकल्पिक विधि (Alternative Method) - किरखॉफ के नियम से, कुंजी K₁ को दबाने पर परिपथ में मुख्य धारा i बिन्दु A पर दो भागों में बँट जाती है। धारा i₁ प्रतिरोध P से होकर और (i - i₁) प्रतिरोध R से होकर गुजरती है। चित्र 3.29 में धाराओं की स्थिति यह मानकर दिखाई गई है कि V_B > V_D धारा ig धारामापी वाली भुजा से गुजरती है और बिन्दु D पर R से होकर आने वाली धारा (i - i₁) के साथ जुड़ जाती है और प्रतिरोध S में होकर निकलती है। बिन्दु C पर पुनः सभी धाराएँ मिल जाती हैं।
जब सेतु सन्तुलित होता है तो धारामापी वाली भुजा से कोई धारा नहीं बहती है अर्थात्

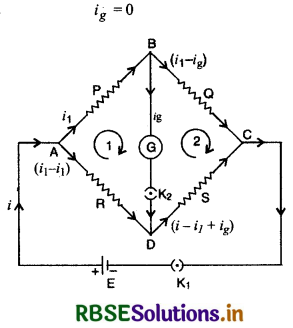
धारामापी का प्रतिरोध G मान लेते हैं। 
बन्द पाश ABDA में किरखॉफ के द्वितीय नियम से,
i₁P + i_g.G - (i - i₁)R = 0 
∵ सन्तुलनावस्था में, i_g = 0
∴ i₁P + 0 - (i - i₁)R = 0
या i₁P = (i - i₁)R 
या \(\frac{i_1}{\left(i-i_1\right)}=\frac{\mathrm{R}}{\mathrm{P}}\) ................(4)
इसी प्रकार बन्द पाश BCDB में किरखॉफ के द्वितीय नियम से,
(i₁ - i_g) Q - i_g.G - (i - i₁ + i_g)S = 0
पुनः सन्तुलनावस्था में,
i_g = 0
∴ (i₁ - 0)Q - 0 - (i - i₁ + 0)S = 0
या i₁Q - (i - i₁)S = 0
या i₁Q = (i - i₁)S
या \(\frac{i_1}{\left(i-i_1\right)}=\frac{\mathrm{S}}{\mathrm{Q}}\) ................(5)
समी. (4) व (5) से,
\(\frac{R}{P}=\frac{S}{Q}\)

प्रश्न 6.
ओम का नियम क्या है? इस नियम की कोई दो सीमाएँ लिखिए।
उत्तर:
ओम का नियम (Ohm's Law):
सन् 1828 में जर्मन वैज्ञानिक डॉ. जॉर्ज साइमन ओम (George Simon Ohm) ने वैद्युत धारा के सम्बन्ध में एक मूल नियम प्रस्तुत किया जिसे ओम का नियम कहते हैं। इस नियम के अनुसार, "यदि किसी चालक की भौतिक अवस्था (physical conditions) (जैसे- ताप, लम्बाई, क्षेत्रफल आदि) न बदलें तो उसके सिरों पर लगाये गये विभवान्तर एवं उसमें बहने वाली धारा का अनुपात नियत रहता है।" माना यदि चालक के सिरों पर V विभवान्तर लगाने पर उसमें i धारा बहे तो ओम के नियम से,
\(\frac{\mathrm{V}}{i}\) = नियतांक
इस नियतांक को चालक का वैद्युत प्रतिरोध (Electric Resistance) कहते हैं और इसे R से व्यक्त करते हैं।
अत: \(\frac{\mathrm{V}}{i}\) = R
इस सूत्र से, V = Ri .......................(1)
या V ∝ i या i ∝V
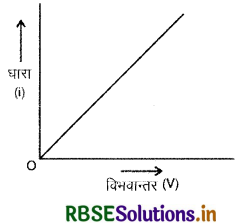
अर्थात् किसी चालक में बहने वाली धारा चालक पर लगाये गये विभवान्तर के समानुपाती (propotional) होती है, यदि चालक की भौतिक अवस्थाएँ न बदली जायें।
चूँकि V ∝ i या i ∝ V 
अत: V एवं । के मध्य खींचा गया ग्राफ एक सरल रेखा होगी।

प्रश्न 7.
विभवमापी के मानकीकरण से क्या अभिप्राय है? समझाइए।
उत्तर:
द्वितीयक परिपथ में मानक सेल का प्रयोग कर विभव प्रवणता का मानक प्राप्त करना विभवमापी का मानकीकरण कहलाता है।

प्रश्न 8.
सेल की टर्मिनल वोल्टता और विद्युत वाहक बल में क्या अन्तर है? इनमें आपस में किस तरह से संबंध है?
उत्तर:
सेल का विद्युत् वाहक बल (Electromotive Force or e.m.f.)
"इकाई धनावेश को परिपथ में प्रवाहित करने में सेल द्वारा जितना कार्य किया जाता है अर्थात् एकांक आवेश को परिपथ में बहने के लिए सेल द्वारा जितनी ऊर्जा दी जाती है, उसे ही सेल का विद्युत् वाहक बल कहते हैं। इसे E से व्यक्त करते हैं; अत: सेल का वि. वा. बल
E = \(\frac{\mathrm{W}}{q}\) ....................(1)
जहाँ W सेल द्वारा q आवेश को प्रवाहित करने में किया गया कार्य है।
∴ E का मात्रक = \(\frac{\mathrm{J}}{\mathrm{C}}\) = वोल्ट 
यदि W = 1 J, q = 1C तो E = 1 JC^-1 या वोस्ट
अर्थात् यदि 1 C आवेश को परिपथ में प्रवाहित करने में सेल द्वारा 1 J कार्य किया जाता है तो सेल का वि. वा. बल 1 JC^-1 या 1 वोल्ट होगा।
वि. वा. बल का मान एक सेल के लिए नियत होता है और विभिन्न सेलों के लिए भिन्न - भिन्न होता है। उदाहरण के लिए, वोल्टीय सेल का वि. वा. बल 1.08 वोल्ट; डेनियल सेल का वि. वा. बल 1.08 वोल्ट; लेक्लांशी एवं शुष्क सेल के लिए वि. वा. बल 1.5 वोल्ट होता है।

टर्मिनल विभवान्तर (Terminal Potential Difference)
"इकाई धनावेश को एक टर्मिनल से दूसरे टर्मिनल तक बाहरी परिपथ में प्रवाहित करने में सेल द्वारा जितना कार्य किया जाता है अर्थात् सेल जितनी ऊर्जा देता है; वह टर्मिनल विभवान्तर के तुल्य होता है।" यदि बाहा प्रतिरोध (R) में q आवेश प्रवाहित करने में सेल West कार्य करता है तो टर्मिनल विभवान्तर
V =  \(\frac{\mathrm{W}_{\mathrm{ext}}}{q}\)  वोल्ट ............................(2)
यदि बाह्य प्रतिरोध में बहने वाली धारा i हो तो
V = \(\frac{\mathrm{W}_{\mathrm{ext}}}{q}\) = IR (ओम के नियम से) 
इसी प्रकार आन्तरिक प्रतिरोध (r) के कारण व्यय ऊर्जा अर्थात् विभव - पतन (potential drop)
V= Ir 
∴ विद्युत् वाहक बल की परिभाषानुसार, विद्युत् वाहक बल
E = (बाह्य कार्य + आन्तरिक कार्य)
एकांक आवेश को प्रवाहित करने में 
या E = V + v 
या E = IR + Ir = I(R+r)

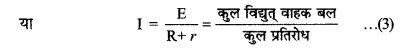
पुनः E = V + Ir
∴ टर्मिनल विभवान्तर
V = E - Ir ................(4)
इस समीकरण से यह भी स्पष्ट है कि यदि
I = 0 तो V = E
"खुले परिपथ में किसी सेल का टर्मिनल विभवान्तर ही उसके विद्युत् वाहक बल के तुल्य होता है।"
समी. (4) से स्पष्ट है:
Ir = E - V
∴ r = \(\frac{E-V}{I} \)...............(5)
∵ V = IR  ∴ I = \(\frac{\mathrm{V}}{\mathrm{R}}\)
∴ r = \(\frac{E-V}{V / R}\) या r = \(\frac{(E-V) R}{V}\) ....................(5)
समीकरण (5) व (6) की सहायता से सेल का आन्तरिक प्रतिरोध ज्ञात किया जा सकता है।

प्रश्न 9.
विभव प्रवणता से आप क्या समझते हैं? यह किन कारकों पर निर्भर करती है?
उत्तर:
विभवमापी (Potentiometer)
विभवमापी एक ऐसा उपकरण (instrument) है जिसकी सहायता से हम किसी विभवान्तर या विद्युत् वाहक बल की शुद्धता (accurately) से माप कर सकते हैं।
यह यन्त्र परिपथ से कोई धारा न लेकर विभवान्तर को मापता है। परिपथ में बहने वाली धारा वास्तविक मान से कुछ कम होती है जिसके कारण वोल्टमीटर की तुलना में विभवमापी विभवान्तर को अधिक शुद्धता से मापती है। अतएव हम कह सकते हैं कि विभवमापी विभव मापन का वोल्टमीटर की तुलना में आदर्श उपकरण हैं।

सिद्धान्त: माना L लम्बाई का कोई AB प्रतिरोध तार है जिसके सिरों पर E विद्युत् वाहक बल एवं नगण्य (neglegible) आन्तरिक प्रतिरोध वाला सेल जोड़ा जाता है, अतः तार AB के सिरों पर E विभवान्तर उत्पन्न हो जायेगा क्योंकि आन्तरिक प्रतिरोध नगण्य है। तार की प्रति इकाई लम्बाई में विभव पतन (potential drop) को विभव प्रवणता (potential gradient) कहते हैं। अत: तार में उत्पन्न विभव प्रवणता
k = \(\frac{\mathrm{E}}{\mathrm{L}}\) ...................(1)

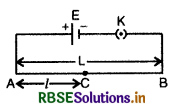
अब यदि तार AB पर कोई बिन्दु C ले लें तो A व C के मध्य विभवान्तर V_AC,  दूरी AC अर्थात् l पर निर्भर करेगा। बिन्दु C को बिन्दु B की ओर खिसकाने पर V_AC का मान बढ़ेगा और A की ओर खिसकाने (sliding) पर घटेगा। यदि A से C की दूरी है तो विभवान्तर
V_AC = k.l ...................(2)
अब यदि चित्र 3.32 की भाँति A व C के मध्य एक अज्ञात विद्युत् वाहक बल E' की एक सेल एक धारामापी

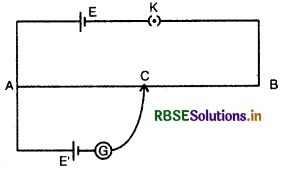
द्वारा जोड़ दें तो धारामापी में उत्पन्न विक्षेप इस बात पर निर्भर करेगा कि V_AC व E' में कौन बड़ा है। सुविधा के लिए (for convenient) A व C के मध्य तुल्य परिपथ चित्र 3.33 के अनुसार दिखा सकते हैं। चित्र में V_AC को परिवर्तनशील (variable) दिखाया गया है क्योंकि इसका मान बिन्दु C की स्थिति पर निर्भर करता है। चित्र के अनुसार E' व V_AC इस प्रकार जुड़े (combined) है कि वे एक - दूसरे को प्रतिरोध करते हैं। इस परिपथ का परिणामी विद्युत् वाहक बल (E' ~ V_AC) होगा, अतः स्पष्ट है कि जब V_AC = E' होगा तो परिणामी विद्युत् वाहक बल (resultant electro - motive force) शून्य होगा और परिपथ में कोई धारा नहीं बहेगी, फलस्वरूप धारामापी में अविक्षेप (no deflection) की स्थिति होगी।

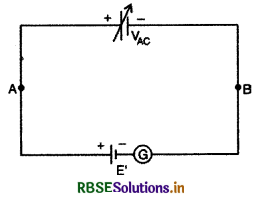
उक्त विवेचना से स्पष्ट है कि यदि किसी अज्ञात विद्युत् वाहक बल E' को धारामापी द्वारा चित्र 3.33 की भाँति जोड़कर C की स्थिति तार AB पर इस प्रकार ज्ञात कर लें कि धारामापी शून्य विक्षेप (zero deflection) की स्थिति प्रदर्शित करे तो अज्ञात विद्युत् वाहक बल E' का मान V_AC के बराबर होगा, अतः
E' = V_AC = kl ..................(3)
इस प्रकार सूत्र (3) की सहायता से l का मान ज्ञात करके अज्ञात विद्युत् वाहक बल E' की माप की जा सकती है। यही विभवमापी का सिद्धान्त है।
विभव प्रवणता पैदा करने वाले सेल E एवं AB से बना परिपथ प्राथमिक परिपथ (primary circuit) और अज्ञात विद्युत् वाहक बल E' वाले सेल तथा धारामापी से AC के मध्य तैयार परिपथ को द्वितीयक परिपथ (secondary circuit) कहते हैं।

विभवमापी की रचना: विभवमापी में मुख्यतः उच्च विशिष्ट प्रतिरोध (high specific resistance) व निम्न प्रतिरोध ताप गुणांक (low temperature coefficient) की मिश्र धातु (alloys) (जैसे- कॉन्स्टेन्टन या मैगनिन आदि) का 4 से 12 मीटर लम्बा एक समान व्यास (diameter) का एक तार होता है जो चित्र 3.34 की भाँति एक - एक मीटर के फेरों (turms) के रूप में धातु की पिरनियों (pulleys) से होकर गुजरता है अथवा एक - एक मीटर लम्बे टुकड़े ताँबे की पत्तियों द्वारा सिरों पर जुड़े होते हैं। प्रारंभिक एवं अंतिम सिरे A व B संयोजक पेंचों से जोड़ दिये जाते हैं। तारों की लम्बाई के समान्तर एक मीटर पैमाना लगा रहता है जिसके द्वारा जॉकी की सहायता से पाठ्यांक (reading) लिया जाता है।

प्रश्न 10.
विभवमापी के तार में लम्बे समय तक विद्युत धारा क्यों नहीं प्रवाहित की जानी चाहिए।
उत्तर:
क्योंकि अधिक समय तक धारा प्रवाहित करने पर जूल के तापन नियम के अनुसार ताप बढ़ने पर प्रतिरोध बढ़ जाता है जिससे विभव प्रवणता प्रभावित हो जाती है।

प्रश्न 11.
किसी सेल का वि. वा. बल या किसी प्रतिरोधक पर विभवान्तर का यथार्थ मान बोल्टमीटर से ज्ञात नहीं किया जा सकता क्यों? विभवमापी से यथार्थ मापन कैसे सम्भव है?
उत्तर:
वोल्टमीटर से यथार्थ मापन ज्ञात नहीं किया जा सकता क्योंकि विद्युत धारा वास्तविक मान से कम प्रवाहित होती है। जबकि विभवमापी परिपथ से बिना धारा लिये लम्बाई के अनुसार विभवान्तर का मापन करता है।

प्रश्न 12.
व्हीटस्टोन सेतु, के प्रयोगों में पहले बैटरी कुंजी तथा फिर धारामापी कुंजी को क्यों दबाया जाता है?
उत्तर:
प्रेरण प्रभाव (Induction effect) से बचने के लिए हमेशा बैटरी कुन्जी (K₁) पहले दबाई जाती है फिर धारामापी कुन्जी (K₂) दबाई जाती है।

दीर्घ उत्तरीय प्रश्न

प्रश्न 1.
(i) अपवाह वेग की परिभाषा लिखिए।
(ii) इलेक्ट्रॉन - अपवाह के आधार पर मुक्त इलेक्ट्रॉनों की घनत्व संख्या और विश्रांतिकाल के पदों में किसी चालक की प्रतिरोधकता के लिए व्यंजक व्युत्पन्न कीजिए। किसी चालक की प्रतिरोधकता किन कारकों पर निर्भर करती है?
(iii) मानक प्रतिरोधकों के निर्माण में कांस्टेन्टन और मैंगनिन जैसे मिश्रधातुओं का उपयोग क्यों किया जाता है?
उत्तर:
(i) अनुगमन वेग (Drift Velocity)
जब किसी चालक के सिरों के मध्य विभवान्तर लगाया जाता है तो चालक के अन्दर एक विद्युत् क्षेत्र (धन सिरे से ऋण सिरे की ओर) \(\overrightarrow{\mathrm{E}}\) उत्पन्न हो जाता है और प्रत्येक मुक्त इलेक्ट्रॉन पर एक वैद्युत बल (F = - E.e) लगने लगता है। इस बल के प्रभाव में इलेक्ट्रॉन त्वरित \(\left(a=\frac{\mathrm{F}}{m}\right)\) होता है और वह चालक के धनात्मक सिरे की ओर गति करने लगता है। गति के दौरान वह अन्य इलेक्ट्रॉनों एवं चालक के धन आयनों से टकराता हुआ वेग में परिवर्तन करता हुआ चलता है। इलेक्ट्रॉन की इस गति को अनुगमन गति (Drift motion) कहते हैं और दो उत्तरोत्तर टक्करों (Successive collisions) के मध्य इलेक्ट्रॉन के औसत वेग को अनुगमन वेग (Drift velocity) कहते हैं। इसे से v_d व्यक्त करते हैं।

अर्थात् आरोपित विद्युत् क्षेत्र (imposed electric field) के कारण इलेक्ट्रॉनों द्वारा प्राप्त अधिकतम वेग (drift velocity) जिससे इलेक्ट्रॉन अन्य आयनों से टकराते हैं उसे अनुगमन वेग कहते हैं। टकराने में लगे समय को श्रांतिकाल कहते हैं। अधिकतर चालकों के लिए श्रांतिकाल 10^-14 s कोटि का होता है।
किसी आयन से टकराने के ठीक पहले इलेक्ट्रॉनों का वेग अधिकतम (maximum) तथा टकराने के ठीक बाद क्षण भर के लिए वेग शून्य हो जाता है। पुनः इलेक्ट्रॉन विद्युत् क्षेत्र में त्वरित होता है और आयनों से टकराने वाली पूर्व स्थिति (previous position) को दोहराता है। "इस प्रकार बैटरी का विभवान्तर इलेक्ट्रॉनों को त्वरित (accelerated) गति प्रदान नहीं कर पाता है बल्कि यह उन्हें चालक की लम्बाई के अनुदिश (along) एक छोटा नियत वेग ही दे पाता है जो कि इलेक्ट्रॉनों की अनियमित गति के ऊपर आरोपित रहता है। इलेक्ट्रॉनों के इस नियत वेग को ही अनुगमन वेग कहते हैं।" अनुगमन वेग का कोटि मान 10^-4 ms^-1 होता है।

अनुगमन वेग के कम होने का कारण: चित्र 3.5 में विद्युत् क्षेत्र आरोपित करने पर मुक्त इलेक्ट्रॉनों की अनियमित गति (मोटी रेखा) के साथ उसका अनुगमन (बिन्दुवत्) भी दिखाया गया है। चित्र से स्पष्ट है कि विद्युत् क्षेत्र की अनुपस्थिति में इलेक्ट्रॉन 8 टक्करों के पश्चात् स्थिति 1 से X तक अनियमित गति करता हुआ पहुँचता है, जबकि वैद्युत क्षेत्र आरोपित करने पर इलेक्ट्रॉन की अन्तिम स्थिति X के बजाय X' हो जाती है। इस प्रकार विद्युत् क्षेत्र द्वारा नैट विस्थापन XX' हो जाता है जिसका मान काफी कम होता है। इसीलिए अनुगमन वेग भी कम होता है।

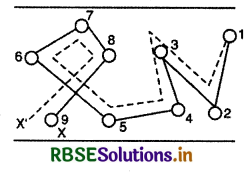
श्रांतिकाल (Relaxation Time): "मुक्त इलेक्ट्रॉन की धातु के परमाणुओं से हुई दो क्रमागत टक्करों के बीच लगे औसत समय को श्रान्तिकाल कहते हैं।" इसे τ से व्यक्त करते हैं। यदि दो उत्तरोत्तर टक्करों के बीच औसत दूरी अर्थात् माध्य मुक्त पथ (mean free path) λ हो तथा उसकी औसत चाल या वर्ग माध्य मूल चाल (root mean square speed) v_r हो तो

λ का मान 10^-9 m तथा τ का मान 10^-14 सेकण्ड की कोटि का होता है।

(ii) गतिशीलता (Mobility):
हम जानते हैं कि चालकता गतिमान आवेश वाहकों से उत्पन्न होती है। धातुओं में ये गतिमान आवेश वाहक इलेक्ट्रॉन होते हैं, आयनित गैस में ये इलेक्ट्रॉन तथा धनावेशित आवन होते है, विद्युत् अपघट्य में वे धनायन तथा ऋणायन दोनों हो सकते हैं।
एक महत्वपूर्ण राशि गतिशीलता (mobility) है जिसे प्रति एकांक विद्युत् क्षेत्र के अनुगमन वेग के परिमाण के रूप में परिभाषित करते हैं।
∴ µ = \(\frac{\left|\overrightarrow{v_d}\right|}{\mathrm{E}}=\frac{v_d}{\mathrm{E}}\) ...............(1)
∵ v_d = \(\frac{e \tau}{m} \mathrm{E}\)
या \(\frac{v_d}{\mathrm{E}}=\frac{e \tau}{m}\)

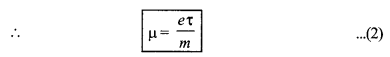
∴ इलेक्ट्रॉन को गतिशीलता
µ_e = \(\frac{e \tau_e}{m_e}\)
मात्रक - चूँकि µ = \(\frac{v_d}{\mathrm{E}}\)
∴ µ का मात्रक = \(\frac{\mathrm{ms}^{-1}}{\mathrm{Vm}^{-1}}\) = m²s^-1V^-1
या µ का मात्रक = \(\frac{\mathrm{ms}^{-1}}{\mathrm{NC}^{-1}}\) = mCs^-1N^-1
विद्युत् धारा एवं गतिशीलता में सम्बन्ध
I = e_nA v_d
परन्तु v_d = µ_eE

किसी अर्द्धचालक के लिए विद्युत् धारा एवं गतिशीलता में सम्बन्ध-
अर्द्धचालक में इलेक्ट्रॉन व होल दोनों के कारण चालकता होती है, 
अतः
I = I_e + I_h
= en_eAv_e + e.n_hAv_h
= en_eAµ_eE + e.n_hAµ_hE

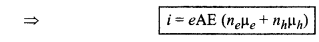
(iii) क्योंकि इन पदार्थों की प्रतिरोधकता पर ताप का प्रभाव अपेक्षाकृत नगण्य होता है।

प्रश्न 2.
पोटैशियोमीटर का कार्यकारी सिद्धान्त लिखिए।
उत्तर:
विभवमापी (Potentiometer)
विभवमापी एक ऐसा उपकरण (instrument) है जिसकी सहायता से हम किसी विभवान्तर या विद्युत् वाहक बल की शुद्धता (accurately) से माप कर सकते हैं।
यह यन्त्र परिपथ से कोई धारा न लेकर विभवान्तर को मापता है। परिपथ में बहने वाली धारा वास्तविक मान से कुछ कम होती है जिसके कारण वोल्टमीटर की तुलना में विभवमापी विभवान्तर को अधिक शुद्धता से मापती है। अतएव हम कह सकते हैं कि विभवमापी विभव मापन का वोल्टमीटर की तुलना में आदर्श उपकरण हैं।
सिद्धान्त: माना L लम्बाई का कोई AB प्रतिरोध तार है जिसके सिरों पर E विद्युत् वाहक बल एवं नगण्य (neglegible) आन्तरिक प्रतिरोध वाला सेल जोड़ा जाता है, अतः तार AB के सिरों पर E विभवान्तर उत्पन्न हो जायेगा क्योंकि आन्तरिक प्रतिरोध नगण्य है। तार की प्रति इकाई लम्बाई में विभव पतन (potential drop) को विभव प्रवणता (potential gradient) कहते हैं। अत: तार में उत्पन्न विभव प्रवणता
k = \(\frac{\mathrm{E}}{\mathrm{L}}\) ...................(1)

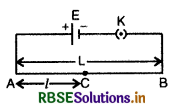
अब यदि तार AB पर कोई बिन्दु C ले लें तो A व C के मध्य विभवान्तर V_AC,  दूरी AC अर्थात् l पर निर्भर करेगा। बिन्दु C को बिन्दु B की ओर खिसकाने पर V_AC का मान बढ़ेगा और A की ओर खिसकाने (sliding) पर घटेगा। यदि A से C की दूरी है तो विभवान्तर
V_AC = k.l ...................(2)
अब यदि चित्र 3.32 की भाँति A व C के मध्य एक अज्ञात विद्युत् वाहक बल E' की एक सेल एक धारामापी

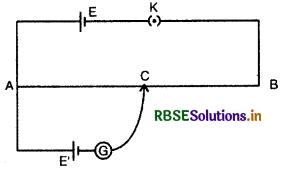
द्वारा जोड़ दें तो धारामापी में उत्पन्न विक्षेप इस बात पर निर्भर करेगा कि V_AC व E' में कौन बड़ा है। सुविधा के लिए (for convenient) A व C के मध्य तुल्य परिपथ चित्र 3.33 के अनुसार दिखा सकते हैं। चित्र में V_AC को परिवर्तनशील (variable) दिखाया गया है क्योंकि इसका मान बिन्दु C की स्थिति पर निर्भर करता है। चित्र के अनुसार E' व V_AC इस प्रकार जुड़े (combined) है कि वे एक - दूसरे को प्रतिरोध करते हैं। इस परिपथ का परिणामी विद्युत् वाहक बल (E' ~ V_AC) होगा, अतः स्पष्ट है कि जब V_AC = E' होगा तो परिणामी विद्युत् वाहक बल (resultant electro - motive force) शून्य होगा और परिपथ में कोई धारा नहीं बहेगी, फलस्वरूप धारामापी में अविक्षेप (no deflection) की स्थिति होगी।

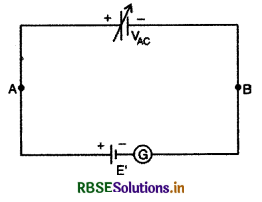
उक्त विवेचना से स्पष्ट है कि यदि किसी अज्ञात विद्युत् वाहक बल E' को धारामापी द्वारा चित्र 3.33 की भाँति जोड़कर C की स्थिति तार AB पर इस प्रकार ज्ञात कर लें कि धारामापी शून्य विक्षेप (zero deflection) की स्थिति प्रदर्शित करे तो अज्ञात विद्युत् वाहक बल E' का मान V_AC के बराबर होगा, अतः
E' = V_AC = kl ..................(3)
इस प्रकार सूत्र (3) की सहायता से l का मान ज्ञात करके अज्ञात विद्युत् वाहक बल E' की माप की जा सकती है। यही विभवमापी का सिद्धान्त है।
विभव प्रवणता पैदा करने वाले सेल E एवं AB से बना परिपथ प्राथमिक परिपथ (primary circuit) और अज्ञात विद्युत् वाहक बल E' वाले सेल तथा धारामापी से AC के मध्य तैयार परिपथ को द्वितीयक परिपथ (secondary circuit) कहते हैं।

विभवमापी की रचना: विभवमापी में मुख्यतः उच्च विशिष्ट प्रतिरोध (high specific resistance) व निम्न प्रतिरोध ताप गुणांक (low temperature coefficient) की मिश्र धातु (alloys) (जैसे- कॉन्स्टेन्टन या मैगनिन आदि) का 4 से 12 मीटर लम्बा एक समान व्यास (diameter) का एक तार होता है जो चित्र 3.34 की भाँति एक - एक मीटर के फेरों (turms) के रूप में धातु की पिरनियों (pulleys) से होकर गुजरता है अथवा एक - एक मीटर लम्बे टुकड़े ताँबे की पत्तियों द्वारा सिरों पर जुड़े होते हैं। प्रारंभिक एवं अंतिम सिरे A व B संयोजक पेंचों से जोड़ दिये जाते हैं। तारों की लम्बाई के समान्तर एक मीटर पैमाना लगा रहता है जिसके द्वारा जॉकी की सहायता से पाठ्यांक (reading) लिया जाता है।

प्रश्न 3.
(i) किसी चालकमेंइलेक्ट्रॉनों के अपवाहवेगकेलिएव्यंजक व्युत्पन्न कीजिए। इस प्रकार ओम के नियम की उत्पत्ति कीजिए।
(ii) कोई तार जिसकी अनुप्रस्थ काट में एक सिरे से दूसरे सिरे तक रेखिकतः वृद्धि हो रही है किसी V बोल्ट की बैटरी से संयोजित है। तार में निम्नलिखित में से कौन सी राशियाँ नियत रहती हैं?
(a) अपवाह वेग 
(b) धारा धनत्व
उत्तर:
(i) इलेक्ट्रॉन का अपवाह (Driff Motion of Electron)
किसी विलगित (isolated) धात्वीय चालक में मुक्त इलेक्ट्रॉनों की गति वैसी ही होती है जैसी कि किसी बर्तन में भरे गैस - अणुओं की होती है। इसीलिए धातु में मुक्त इलेक्ट्रॉनों के समूह को 'इलेक्ट्रॉन गैस' (electron gas) भी कहते हैं। गैस अणुओं की भाँति मुक्त इलेक्ट्रॉनों की गति भी अनियमित होती है। ये धातु के स्थिर आयनों के खाली स्थान में अनियमित गति करते हुए उनसे टकराते (collide) रहते हैं जिससे उनका वेग निरन्तर बदलता रहता है। यह गति केवल ऊष्मीय ऊर्जा (thermal energy) के कारण होती है। कमरे के ताप पर इनका वेग लगभग 10⁵ ms^-1 की कोटि (order) का होता है, परन्तु यह वेग सभी दिशाओं में अनियमित रूप से वितरित रहता है; किसी विशेष दिशा (specific direction) में कोई नेट गति नहीं होती है। इस गति को चित्र 3.4 में दिखाया गया है। यदि धातु में n इलेक्ट्रॉन हों तथा उनके अलग - अलग वेग क्रमशः \(\overrightarrow{u_1}\), \(\overrightarrow{u_2}\), \(\overrightarrow{u_3}, \ldots\), \(\overrightarrow{u_n}\) हों तो इलेक्ट्रॉनों का औसत वेग

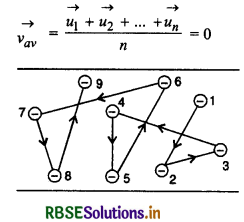
अतः आवेश का किसी भी दिशा में नैट प्रवाह नहीं होता है।

(ii) अपवाह वेग नियत रहेगा। जबकि धारा धनत्व का मान अनुप्रस्थ काट क्षेत्रफल की रैखिक वृद्धि के साथ घटता है।

प्रश्न 4.
(a) किसी मीटर सेतु का कार्यकारी सिद्धांत लिखिए।
(b) किसी मीटर सेतु में,आरेख में दर्शाए अनुसार, प्रतिरोध R और S के साथ दूरी l, पर प्रतिरोध के पार्श्व में किसी अज्ञात प्रतिरोध X को संयोजित करने पर अब संतुलन बिन्दु दूरी l₂ पर प्राप्त होता है। l₁ और S के पदों में X के लिए सूत्र प्राप्त कीजिए।
उत्तर:
मीटर सेतु (Meter Bridge)
हीटस्टोन सेतु के सिद्धान्त पर आधारित यह एक ऐसा उपकरण है जिसकी सहायता से अज्ञात प्रतिरोध (unknown resistance) ज्ञात किया जा सकता है।
सिद्धान्त: मीटर सेतु ऐसा उपकरण है जो व्हीटस्टोन सेतु के सिद्धान्त पर कार्य करता है।
रचना: मीटर सेतु की रचना चित्र 3.30 में दिखायी गई है। इसमें समान परिच्छेद (uniform cross - section) का 1 मीटर कॉन्स्टेन्टन या मैंगनिन का तार होता है जो एक लकड़ी के बोर्ड पर एक मीटर पैमाने के सहारे कसा रहता है। तार के सिरों A व C पर ताँबे की दो के आकार की पत्तियाँ (L - shaped thick copper strips) जुड़ी रहती हैं जिनके ऊपर संयोजक पेंच लगे रहते हैं। इन पत्तियों के बीच एक और ताँबे की पत्ती चित्र के अनुसार लगी होती है जिस पर तीन संयोजक पेंच लगे होते हैं। चित्र में अंकित बिन्दु A, B,C व D क्रमश: व्हीटस्टोन सेतु से संगत (corres - ponding) चारों बिन्दुओं को व्यक्त (represent) करते हैं। इस पत्ती के मध्य में लगे पेंच D से एक सुग्राही (sensitive) धारामापी जुड़ा होता है जिसका दूसरा सिरा सी कुंजी (jockey) से जुड़ा होता है। सी कुंजी तार AC के सहारे खिसक सकती है। सौ कुंजी की स्थिति (position) ही तार AC पर बिन्दु B को व्यक्त करती है।

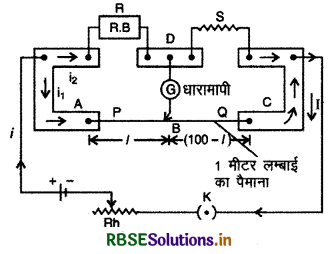
प्रयोग विधि: परिपथ व्यवस्था चित्र 3.30 के अनुसार करते हैं। संयोजक पेंचों A व D के मध्य प्रतिरोध बॉक्स (resistance box) एवं D व C के मध्य अज्ञात प्रतिरोध S को जोड़ देते हैं। A व C के मध्य एक सेल व एक धारा नियन्त्रक (rheostat) को कुंजी K के द्वारा जोड़ देते हैं। अनुपात भुजाएँ (ratio arms) P व Q तार AC के दो भागों से प्राप्त होती है जो जॉकी द्वारा निर्धारित बिन्दु से विभक्त (divide) होते हैं।

प्रतिरोध बॉक्स में कोई समुचित (suitable) प्रतिरोध (R) लगाकर कुंजी K को बन्द करते हैं और सी कुंजी को तार AC पर दायें या बायें खिसकाकर (moved) बिन्दु B की वह स्थिति ज्ञात कर लेते हैं जब धारामापी में शून्य विक्षेप होता है। यह सेतु के सन्तुलन की स्थिति है (जब V_B = B_D)। इस स्थिति में मीटर पैमाने पर बिन्दु B की स्थिति पढ़कर तार के दोनों भागों AB व BC की लम्बाइयाँ सेमी में ज्ञात कर लेते है। यदि AB की लम्बाई l सेमी है तो BC की लम्बाई (100 - l) सेमी होगी।
∵ प्रतिरोध ∝ लम्बाई 
अतः P ∝ l
तथा Q ∝ (100 - l)
∴ \(\frac{\mathrm{P}}{\mathrm{Q}}=\frac{l}{(100-l)} \)
सेतु सन्तुलन की स्थिति में,
\(\frac{\mathrm{P}}{\mathrm{Q}}=\frac{\mathrm{R}}{\mathrm{S}}\)
∴ \(\frac{l}{(100-l)}=\frac{\mathrm{R}}{\mathrm{S}}\)
∴ S = \(\frac{\mathrm{R}(100-l)}{l}\) .....................(1)
यहाँ R प्रतिरोध बॉक्स में लगाया गया प्रतिरोध है। इसी सूत्र की सहायता से अज्ञात प्रतिरोध S का मान ज्ञात किया जा सकता है।

प्रश्न 5.
किसी व्हीटस्टोन सेतु के कार्यकारी सिद्धांत का उल्लेख कीजिए। परिपथ आरेख की सहायता से व्याख्या कीजिए कि मीटर सेतु का उपयोग करके किसी तार के पदार्थ के विशिष्ट प्रतिरोध के निर्धारण में इस सिद्धांत का उपयोग किस प्रकार किया जा सकता है?
उत्तर:
हीटस्टोन सेतु (Wheatstone's Bridge):
इंग्लैण्ड के वैज्ञानिक प्रोफेसर सी. एफ. द्वीटस्टोन (C.F. Wheatstone) ने चार प्रतिरोधों, एक धारामापी एवं एक सेल को जोड़कर एक विशेष प्रकार का परिपथ तैयार किया जो हीटस्टोन सेतु के नाम से जाना गया। इसकी सहायता से हम अज्ञात (unknown) प्रतिरोध ज्ञात कर सकते हैं।
रचना: द्वीटस्टोन सेतु की सैद्धान्तिक रचना चित्र 3.28 में दिखाई गई है। चार प्रतिरोधों P, Q, R, S को जोड़कर एक चतुर्भुज ABCD बनाते हैं। बिन्दुओं A व C के मध्य एक सेल जोड़ देते हैं। बिन्दुओं B व D के मध्य एक धारामापी जोड़ दिया जाता है। K₁ बैटरी कुंजी है और K₂ धारामापी कुंजी है। यदि कुंजी K₁ को हम पहले बन्द (close) करें और फिर K₂ को, तब यदि धारामापी में कोई विक्षेप (deflection) न दें तब इस अवस्था में,

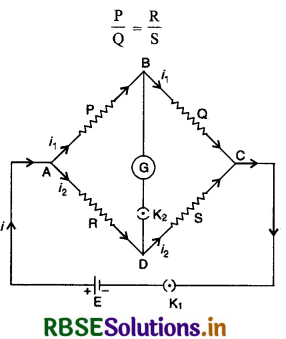
सिद्धान्त: जब बैटरी कुंजी (battery key) K₁ को दबाते हैं तो परिपथ में मुख्य धारा i बहती है। इस धारा को A बिन्दु पर दो मार्ग मिलने से यह दो भागों i₁ व i₂ में बँट जाती है। i₁ को B बिन्दु पर और i₂ को D बिन्दु पर पुनः दो मार्ग मिलते हैं। B व D पर, i₁ व i₂ के विभाजन की निग्न तीन स्थितियाँ सम्भव हैं-
(i) जब V_B> B_D तो B बिन्दु पर i₁ का एक भाग धारामापी से गुजर कर उसमें एक दिशा में विक्षेप उत्पन्न करता है और शेष भाग (remaining part) प्रतिरोध Q से होकर गुजरता है। बिन्दु D पर धारा का कोई बँटवारा (distribution) नहीं होता है।

(ii) जब V_B < V_D होता है तो B पर धारा का विभाजन नहीं होता है, बल्कि D पर धारा i₂ का एक भाग धारामापी से गुजरकर पहले की विपरीत दिशा में विक्षेप उत्पन्न करेगा और शेष भाग प्रतिरोध से गुजरता है।

(iii) V_B = B_D तो धारामापी वाली भुजा में कोई धारा न बहने से उसमें शून्य विक्षेप (zero deflection) की स्थिति रहती है। यही सेतु के सन्तुलन की स्थिति कहलाती है। स्पष्ट है कि परिपथ में तो धारा बहती है, लेकिन धारामापी वाली भुजा पर इस धारा का कोई प्रभाव नहीं पड़ता है। यह घटना ठीक उसी प्रकार की है कि नदी की धारा का सेतु पर कोई प्रभाव नहीं पड़ता है। इसीलिए इसे सेतु परिपथ कहते हैं। इस प्रकार सेतु के सन्तुलन की स्थिति में,
V_B = V_D
अतः V_A - V_B = V_A - V_D
या i₁P = i₂R ...........(1)
और V_B - V_C = V_D - V_C
या i₁Q = i₂S
समीकरण (1) व (2) से,
या \(\frac{\mathrm{P}}{\mathrm{Q}}=\frac{\mathrm{R}}{\mathrm{S}}\) .............(3)
अतः स्पष्ट है कि "जब सेतु सन्तुलित होता है तो चतुर्भुज ABCD की किन्हीं भी दो संलग्न (corresponding) भुजाओं के प्रतिरोधों का अनुपात शेष दो संलग्न भुजाओं के प्रतिरोधों के अनुपात (ratio) के बराबर होता है।"
समी. (3) से, S = \(\frac{Q}{P}\) x R
अतः सेतु के सन्तुलन की स्थिति ज्ञात करके हम S का मान उक्त सूत्र से ज्ञात कर सकते है। P और Q वाली भुजाओं को हम अनुपातिक भुजाएँ (ratio arms), R वाली भुजा को प्रामाणिक भुजा (standard arms) और S भुजा को अज्ञात भुजा कहते हैं।

वैकल्पिक विधि (Alternative Method) - किरखॉफ के नियम से, कुंजी K₁ को दबाने पर परिपथ में मुख्य धारा i बिन्दु A पर दो भागों में बँट जाती है। धारा i₁ प्रतिरोध P से होकर और (i - i₁) प्रतिरोध R से होकर गुजरती है। चित्र 3.29 में धाराओं की स्थिति यह मानकर दिखाई गई है कि V_B > V_D धारा i_g धारामापी वाली भुजा से गुजरती है और बिन्दु D पर R से होकर आने वाली धारा (i - i₁) के साथ जुड़ जाती है और प्रतिरोध S में होकर निकलती है। बिन्दु C पर पुनः सभी धाराएँ मिल जाती हैं।
जब सेतु सन्तुलित होता है तो धारामापी वाली भुजा से कोई धारा नहीं बहती है अर्थात्

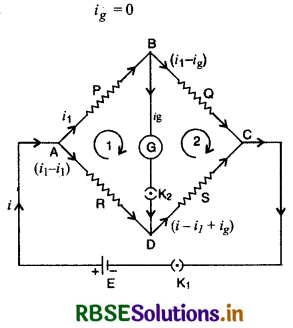
धारामापी का प्रतिरोध G मान लेते हैं। 
बन्द पाश ABDA में किरखॉफ के द्वितीय नियम से,
i₁P + i_g.G - (i - i₁)R = 0 
∵ सन्तुलनावस्था में, i_g = 0
∴ i₁P + 0 - (i - i₁)R = 0
या i₁P = (i - i₁)R 
या \(\frac{i_1}{\left(i-i_1\right)}=\frac{\mathrm{R}}{\mathrm{P}}\) ................(4)
इसी प्रकार बन्द पाश BCDB में किरखॉफ के द्वितीय नियम से,
(i₁ - i_g) Q - i_g.G - (i - i₁ + i_g)S = 0
पुनः सन्तुलनावस्था में,
i_g = 0
∴ (i₁ - 0)Q - 0 - (i - i₁ + 0)S = 0
या i₁Q - (i - i₁)S = 0
या i₁Q = (i - i₁)S
या \(\frac{i_1}{\left(i-i_1\right)}=\frac{\mathrm{S}}{\mathrm{Q}}\) ................(5)
समी. (4) व (5) से,
\(\frac{R}{P}=\frac{S}{Q}\)

मीटर सेतु (Meter Bridge)
हीटस्टोन सेतु के सिद्धान्त पर आधारित यह एक ऐसा उपकरण है जिसकी सहायता से अज्ञात प्रतिरोध (unknown resistance) ज्ञात किया जा सकता है।
सिद्धान्त: मीटर सेतु ऐसा उपकरण है जो व्हीटस्टोन सेतु के सिद्धान्त पर कार्य करता है।
रचना: मीटर सेतु की रचना चित्र 3.30 में दिखायी गई है। इसमें समान परिच्छेद (uniform cross - section) का 1 मीटर कॉन्स्टेन्टन या मैंगनिन का तार होता है जो एक लकड़ी के बोर्ड पर एक मीटर पैमाने के सहारे कसा रहता है। तार के सिरों A व C पर ताँबे की दो के आकार की पत्तियाँ (L - shaped thick copper strips) जुड़ी रहती हैं जिनके ऊपर संयोजक पेंच लगे रहते हैं। इन पत्तियों के बीच एक और ताँबे की पत्ती चित्र के अनुसार लगी होती है जिस पर तीन संयोजक पेंच लगे होते हैं। चित्र में अंकित बिन्दु A, B,C व D क्रमश: व्हीटस्टोन सेतु से संगत (corres - ponding) चारों बिन्दुओं को व्यक्त (represent) करते हैं। इस पत्ती के मध्य में लगे पेंच D से एक सुग्राही (sensitive) धारामापी जुड़ा होता है जिसका दूसरा सिरा सी कुंजी (jockey) से जुड़ा होता है। सी कुंजी तार AC के सहारे खिसक सकती है। सौ कुंजी की स्थिति (position) ही तार AC पर बिन्दु B को व्यक्त करती है।

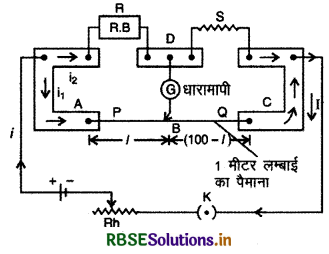
प्रयोग विधि: परिपथ व्यवस्था चित्र 3.30 के अनुसार करते हैं। संयोजक पेंचों A व D के मध्य प्रतिरोध बॉक्स (resistance box) एवं D व C के मध्य अज्ञात प्रतिरोध S को जोड़ देते हैं। A व C के मध्य एक सेल व एक धारा नियन्त्रक (rheostat) को कुंजी K के द्वारा जोड़ देते हैं। अनुपात भुजाएँ (ratio arms) P व Q तार AC के दो भागों से प्राप्त होती है जो जॉकी द्वारा निर्धारित बिन्दु से विभक्त (divide) होते हैं।

प्रतिरोध बॉक्स में कोई समुचित (suitable) प्रतिरोध (R) लगाकर कुंजी K को बन्द करते हैं और सी कुंजी को तार AC पर दायें या बायें खिसकाकर (moved) बिन्दु B की वह स्थिति ज्ञात कर लेते हैं जब धारामापी में शून्य विक्षेप होता है। यह सेतु के सन्तुलन की स्थिति है (जब V_B = B_D)। इस स्थिति में मीटर पैमाने पर बिन्दु B की स्थिति पढ़कर तार के दोनों भागों AB व BC की लम्बाइयाँ सेमी में ज्ञात कर लेते है। यदि AB की लम्बाई l सेमी है तो BC की लम्बाई (100 - l) सेमी होगी।
∵ प्रतिरोध ∝ लम्बाई 
अतः P ∝ l
तथा Q ∝ (100 - l)
∴ \(\frac{\mathrm{P}}{\mathrm{Q}}=\frac{l}{(100-l)}\) 
सेतु सन्तुलन की स्थिति में,
\(\frac{\mathrm{P}}{\mathrm{Q}}=\frac{\mathrm{R}}{\mathrm{S}}\)
∴ \(\frac{l}{(100-l)}=\frac{\mathrm{R}}{\mathrm{S}}\)
∴ S = \(\frac{\mathrm{R}(100-l)}{l}\) .....................(1)
यहाँ R प्रतिरोध बॉक्स में लगाया गया प्रतिरोध है। इसी सूत्र की सहायता से अज्ञात प्रतिरोध S का मान ज्ञात किया जा सकता है।

प्रश्न 6.
(a) परिपथ आरेख की सहायता से किसी सेल के आंतरिक प्रतिरोध को मापने की विधि का संक्षिप्त में वर्णन कीजिए।
(b) कारण दीजिए कि किसी सेल के वि. वा, बल (emf) की माप के लिए वोल्टमीटर की तुलना में पोटेशियोमीटर के उपयोगको वरीयता दी जाती है।
अथवा
विभवमापी की सहायता से प्राथमिक सेल का आंतरिक प्रतिरोध ज्ञात करने का सूत्र व्युत्पन्न कीजिए। परिपथ चित्र बनाइए।
उत्तर:
सेल का आन्तरिक प्रतिरोध ज्ञात करना - बैटरी, कुंजी एवं धारा नियन्त्रक को संयोजक पेंचों A व B से जोड़कर प्राथमिक परिपथ तैयार कर लेते हैं। अब जिस सेल का आन्तरिक प्रतिरोध ज्ञात करना है उसे और एक प्रतिरोध बॉक्स को चित्र 3.37 की तरह पेंच A व द्विमार्गी कुंजी (two way key) से जोड़ते हैं तथा द्विमार्गी कुंजी को धारामापी एवं जॉकी से जोड़कर द्वितीयक परिपथ (secondary circuit) तैयार करते हैं।

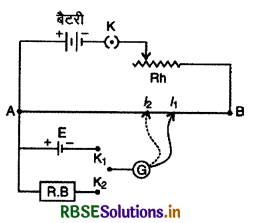
प्रयोग विधि:
(i) कुंजी K को बन्द करके तार AB में विभवान्तर (potential difference) स्थापित कर लेते हैं। अब धारा नियन्त्रक को इस प्रकार व्यवस्थित करते हैं कि जॉकी को तार के सिरों A व B के बीच स्पर्श कराने पर धारामापी में विक्षेप दोनों ओर प्राप्त हो जाये। माना इस स्थिति में तार की विभव प्रवणता में है।
(ii) कुंजी K₂ को खुला (open) रखकर K₁ को बन्द करके सेल को द्वितीयक परिपथ में डालते हैं और जॉकी से शून्य विक्षेप की स्थिति में तार की लम्बाई l₁ ज्ञात कर लेते हैं, अत:
E = kl₁ ........................(4)
(iii) अब K₁ को बन्द (close) रखते हुए K₂ को बन्द करते हैं और प्रतिरोध बॉक्स में कोई समुचित प्रतिरोध (Proper resistance) R लगाकर पुनः अविक्षेप स्थिति में तार की लम्बाई l₂ ज्ञात कर लेते हैं। यह सेल के टर्मिनल विभवान्तर के सन्तुलन के संगत है, अतः
V = kl₂......................(5)
माना सेल का आन्तरिक प्रतिरोध r है यदि सेल को R ओम के प्रतिरोध से शंट करने पर सेल में i धारा बहती है, तो ओम के नियम से
E = i(R + r)
एवं V = iR
⇒ 1 + \(\frac{r}{\mathrm{R}}=\frac{l_1}{l_2}\) 
⇒ \(\frac{r}{\mathrm{R}}=\frac{l_1-l_2}{l_2}\)
अत: आन्तरिक प्रतिरोध r = \(\mathrm{R}\left[\frac{l_1-l_2}{l_2}\right]\) ...........................(6)

प्रश्न 7.
विभिन्न वि, वा, बल (emf) और आंतरिक प्रतिरोधों के दो सेल एक दूसरे के साथ पार्श्व में संयोजित हैं। इस संयोजन के तुल्य वि. वा. बल (emf) और तुल्य आन्तरिक प्रतिरोध के लिए व्यंजक व्युत्पन्न कीजिए।
उत्तर:
जब सेल भिन्न विद्युत् वाहक बल एवं भिन्न आन्तरिक प्रतिरोध के हों: चित्र 3.21 में E₁ व E₂ विद्युत् वाहक बलों एवं आन्तरिक प्रतिरोधों r₁ व r₂ के दो सेलों का श्रेणीक्रम संयोजन दिखाया गया है और यह संयोजन R प्रतिरोध में धारा भेजता है। यदि परिपथ में प्रवाहित धारा i हो तो पहली सेल की टर्मिनल वोल्टता
V₁ = सेल का वि. वा. बल - आन्तरिक प्रतिरोध के सिरों पर विभव - पतन

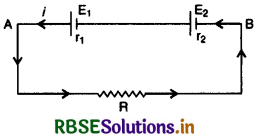
या V₁ = E₁ - ir₁
इसी प्रकार दूसरे सेल की टर्मिनल वोल्टता
V₂ = E₂ - ir₂ 
यदि परिपथ के बिन्दुओं A व B के मध्य विभवान्तर V हो तो
V = V₁ + V₂
= (E₁ - ir₁) + (E₂ - ir₂)
या V = (E₁ + E₂) - i(r₁ + r₂) ...................(2)
यदि प्रभावी विद्युत् वाहक बल E हो एवं प्रभावी आन्तरिक प्रतिरोध r हो तो
V = E - ir .....................(3)
समी. (2) व (3) की तुलना करने पर,
E = E₁ + E₂ ....................(4)
एवं r₁ + r₂ .......................(5)
∵ सेलों का श्रेणीक्रम संयोजन प्रतिरोध R में धारा भेज रहा है, अत:
i = \(\frac{\mathrm{E}}{\mathrm{R}+r}\)
या i = \(\frac{\mathrm{E}_1+\mathrm{E}_2}{\mathrm{R}+\left(\eta_1+r_2\right)}\) .....................(6)
यदि सेलों का संयोजन इस प्रकार है कि वे एक-दूसरे का विरोध कर रहे हों तो
E = E₁ ~ E₂ .................(7)
अत: I = \(\frac{\mathrm{E}_1 \sim \mathrm{E}_2}{\mathrm{R}+\left(r_1+r_2\right)}\) ...................(8)

प्रश्न 8.
मीटर सेतु द्वारा अज्ञात प्रतिरोध ज्ञात करने की विधि समझाइये। परिपथ चित्र बनाइये।
उत्तर:
मीटर सेतु (Meter Bridge)
हीटस्टोन सेतु के सिद्धान्त पर आधारित यह एक ऐसा उपकरण है जिसकी सहायता से अज्ञात प्रतिरोध (unknown resistance) ज्ञात किया जा सकता है।
सिद्धान्त: मीटर सेतु ऐसा उपकरण है जो व्हीटस्टोन सेतु के सिद्धान्त पर कार्य करता है।
रचना: मीटर सेतु की रचना चित्र 3.30 में दिखायी गई है। इसमें समान परिच्छेद (uniform cross - section) का 1 मीटर कॉन्स्टेन्टन या मैंगनिन का तार होता है जो एक लकड़ी के बोर्ड पर एक मीटर पैमाने के सहारे कसा रहता है। तार के सिरों A व C पर ताँबे की दो के आकार की पत्तियाँ (L - shaped thick copper strips) जुड़ी रहती हैं जिनके ऊपर संयोजक पेंच लगे रहते हैं। इन पत्तियों के बीच एक और ताँबे की पत्ती चित्र के अनुसार लगी होती है जिस पर तीन संयोजक पेंच लगे होते हैं। चित्र में अंकित बिन्दु A, B,C व D क्रमश: व्हीटस्टोन सेतु से संगत (corres - ponding) चारों बिन्दुओं को व्यक्त (represent) करते हैं। इस पत्ती के मध्य में लगे पेंच D से एक सुग्राही (sensitive) धारामापी जुड़ा होता है जिसका दूसरा सिरा सी कुंजी (jockey) से जुड़ा होता है। सी कुंजी तार AC के सहारे खिसक सकती है। सौ कुंजी की स्थिति (position) ही तार AC पर बिन्दु B को व्यक्त करती है।

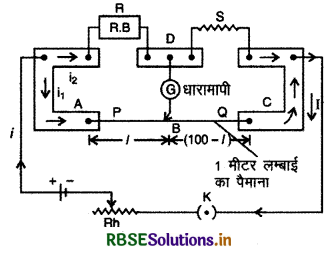
प्रयोग विधि: परिपथ व्यवस्था चित्र 3.30 के अनुसार करते हैं। संयोजक पेंचों A व D के मध्य प्रतिरोध बॉक्स (resistance box) एवं D व C के मध्य अज्ञात प्रतिरोध S को जोड़ देते हैं। A व C के मध्य एक सेल व एक धारा नियन्त्रक (rheostat) को कुंजी K के द्वारा जोड़ देते हैं। अनुपात भुजाएँ (ratio arms) P व Q तार AC के दो भागों से प्राप्त होती है जो जॉकी द्वारा निर्धारित बिन्दु से विभक्त (divide) होते हैं।

प्रतिरोध बॉक्स में कोई समुचित (suitable) प्रतिरोध (R) लगाकर कुंजी K को बन्द करते हैं और सी कुंजी को तार AC पर दायें या बायें खिसकाकर (moved) बिन्दु B की वह स्थिति ज्ञात कर लेते हैं जब धारामापी में शून्य विक्षेप होता है। यह सेतु के सन्तुलन की स्थिति है (जब V_B = B_D)। इस स्थिति में मीटर पैमाने पर बिन्दु B की स्थिति पढ़कर तार के दोनों भागों AB व BC की लम्बाइयाँ सेमी में ज्ञात कर लेते है। यदि AB की लम्बाई l सेमी है तो BC की लम्बाई (100 - l) सेमी होगी।
∵ प्रतिरोध ∝ लम्बाई 
अतः P ∝ l
तथा Q ∝ (100 - l)
∴ \(\frac{\mathrm{P}}{\mathrm{Q}}=\frac{l}{(100-l)}\) 
सेतु सन्तुलन की स्थिति में,
\(\frac{\mathrm{P}}{\mathrm{Q}}=\frac{\mathrm{R}}{\mathrm{S}}\)
∴ \(\frac{l}{(100-l)}=\frac{\mathrm{R}}{\mathrm{S}}\)
∴ S = \(\frac{\mathrm{R}(100-l)}{l}\) .....................(1)
यहाँ R प्रतिरोध बॉक्स में लगाया गया प्रतिरोध है। इसी सूत्र की सहायता से अज्ञात प्रतिरोध S का मान ज्ञात किया जा सकता है।

प्रश्न 9.
सेल के विद्युत वाहक बल से क्या अभिप्राय है? यह किन - किनकारकों पर निर्भर करता है? विद्युत वाहक बलाएवंटर्मिनल विभवान्तर V में संबंध स्थापित कीजिए। सिद्धकीजिए कि विद्युत वाहक बल टर्मिनल वोल्टता से अधिक होता है।
उत्तर:
सेल का विद्युत् वाहक बल (Electromotive Force or e.m.f.)
"इकाई धनावेश को परिपथ में प्रवाहित करने में सेल द्वारा जितना कार्य किया जाता है अर्थात् एकांक आवेश को परिपथ में बहने के लिए सेल द्वारा जितनी ऊर्जा दी जाती है, उसे ही सेल का विद्युत् वाहक बल कहते हैं। इसे E से व्यक्त करते हैं; अत: सेल का वि. वा. बल
E = \(\frac{\mathrm{W}}{q}\) ....................(1)
जहाँ W सेल द्वारा q आवेश को प्रवाहित करने में किया गया कार्य है।
∴ E का मात्रक = \(\frac{\mathrm{J}}{\mathrm{C}}\) = वोल्ट 
यदि W = 1 J, q = 1C तो E = 1 JC^-1 या वोस्ट
अर्थात् यदि 1 C आवेश को परिपथ में प्रवाहित करने में सेल द्वारा 1 J कार्य किया जाता है तो सेल का वि. वा. बल 1 JC^-1 या 1 वोल्ट होगा।
वि. वा. बल का मान एक सेल के लिए नियत होता है और विभिन्न सेलों के लिए भिन्न - भिन्न होता है। उदाहरण के लिए, वोल्टीय सेल का वि. वा. बल 1.08 वोल्ट; डेनियल सेल का वि. वा. बल 1.08 वोल्ट; लेक्लांशी एवं शुष्क सेल के लिए वि. वा. बल 1.5 वोल्ट होता है।

टर्मिनल विभवान्तर (Terminal Potential Difference)
"इकाई धनावेश को एक टर्मिनल से दूसरे टर्मिनल तक बाहरी परिपथ में प्रवाहित करने में सेल द्वारा जितना कार्य किया जाता है अर्थात् सेल जितनी ऊर्जा देता है; वह टर्मिनल विभवान्तर के तुल्य होता है।" यदि बाहा प्रतिरोध (R) में q आवेश प्रवाहित करने में सेल West कार्य करता है तो टर्मिनल विभवान्तर
V =  \(\frac{\mathrm{W}_{\mathrm{ext}}}{q}\)  वोल्ट ............................(2)
यदि बाह्य प्रतिरोध में बहने वाली धारा i हो तो
V = \(\frac{\mathrm{W}_{\mathrm{ext}}}{q}\) = IR (ओम के नियम से) 
इसी प्रकार आन्तरिक प्रतिरोध (r) के कारण व्यय ऊर्जा अर्थात् विभव - पतन (potential drop)
V= Ir 
∴ विद्युत् वाहक बल की परिभाषानुसार, विद्युत् वाहक बल
E = (बाह्य कार्य + आन्तरिक कार्य)
एकांक आवेश को प्रवाहित करने में 
या E = V + v 
या E = IR + Ir = I(R+r)

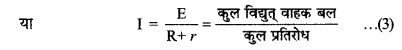
पुनः E = V + Ir
∴ टर्मिनल विभवान्तर
V = E - Ir ................(4)
इस समीकरण से यह भी स्पष्ट है कि यदि
I = 0 तो V = E
"खुले परिपथ में किसी सेल का टर्मिनल विभवान्तर ही उसके विद्युत् वाहक बल के तुल्य होता है।"
समी. (4) से स्पष्ट है:
Ir = E - V
∴ r = \(\frac{E-V}{I}\) ...............(5)
∵ V = IR  ∴ I = \(\frac{\mathrm{V}}{\mathrm{R}}\)
∴ r = \(\frac{E-V}{V / R}\) या r = \(\frac{(E-V) R}{V}\) ....................(5)
समीकरण (5) व (6) की सहायता से सेल का आन्तरिक प्रतिरोध ज्ञात किया जा सकता है।

आंकिक प्रश्न

प्रश्न 1.
ताँबे के तार की अनुप्रस्थ काट का क्षेत्रफल 3 mm² है। यदि ताँबे के प्रति एकांक आयतन में मुक्त इलेक्ट्रॉनों की संख्या 8.5 x 10²⁸ m^-3 हो तथा दिवे गये तार में 6A की धारा बहे तो ज्ञात कीजिए
(i) तार के किसी परिच्छेद से। घण्टे में प्रवाहित सम्पूर्ण आवेश 
(ii) धारा धनत्व 
(iii) इलेक्दानों का अपवाह वेग। 
उत्तर:
प्रश्नानुसार, अनुप्रस्थ काट क्षेत्रफल A= 3 mm² = 3 x 10^-6 m²
इलेक्ट्रॉन संख्या धनत्व n = 8.5 x 10²⁸ m^-3
प्रवाहित धारा I = 6A तथा समय t = 1 घंटा 
(i) आवेश, q = It = 6 x 3600 C
= 21600 C = 21.16 x 10⁴ C
(ii) धारा धनत्व J = \(\frac{I}{A}=\frac{6}{3 \times 10^{-6}}\) = 2 x 10⁶ A/m²

प्रश्न 2.
वृत्तीय अनुप्रस्थ परिच्छेद वाले एक तार में मुक्त इलेक्ट्रॉनों के अपवाह वेग V_d के कारण धारा i बहती है। समान पदार्थ एवं दोगुनी त्रिज्या के दूसरे चालक में धारा 2i बह रही है तो अपवाह वेग क्या होगा?
उत्तर:
अपवाह वैग V_d = \(\frac{\mathrm{I}}{\text { neA }}\) = V
और दूसरे तार में V_d = \(\frac{2 i}{n(4 \mathrm{Ae})}\) (क्योंकि त्रिज्या दोगुनी)
∴ V_d = \(\frac{V}{2}\)
ओम के नियम, प्रतिरोधकता एवं चालकता पर आधारित

प्रश्न 3.
दिए गए V - I ग्राफ से प्रतिरोधक के प्रतिरोध का मान ज्ञात कीजिए।

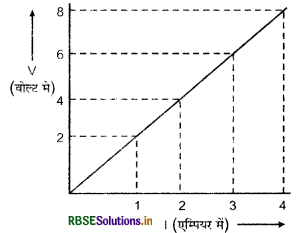
उत्तर:
चित्रानुसार V = 2 वोल्ट के संगत धारा I = 1 ऐम्पियर 
अतः प्रतिरोध R = \(\frac{\mathrm{V}}{\mathrm{I}}=\frac{2}{1}\) = 2 ओम

प्रश्न 4.
0°C ताप पर एक चालक का प्रतिरोध x Ω है। वह ताप ज्ञात कीजिए जिस पर चालक का प्रतिरोध 3x हो जाता है। चालक का प्रतिरोध ताप गुणांक नियत है जिसका मान 0.4 x 10^-2 °C^-1 है।
उत्तर:
0° C पर चालक का प्रतिरोध R₀ = xΩ
किसी ताप t पर चालक का प्रतिरोध R_τ = 3x 
प्रतिरोध ताप गुणांक ∝ = 0.4 x 10^-2°C^-1
R_t = R₀ (1 + α.t) से
3x = x(1 + 0.4 x 10^-2t) 
3 = 1 + 0.4 x 10^-2t
t = \(\frac{2}{0.4 \times 10}\)
t = 500°C

प्रश्न 5.
एक तार का प्रतिरोध 1Ω है। इसे खींचकर इसकी लम्बाई दोगुनी कर दी जाती है। नया प्रतिरोध क्या होगा?
उत्तर:
खींचने से पूर्व तार की लम्बाई l व अनुप्रस्थ परिच्छेद क्षेत्रफल A हो तो खींचने के बाद लम्बाई 2l हो जाती है और अनुप्रस्थ परिच्छेद A2 हो जाता है।
l₁A₁ = l₂A₂
l.A = 2lA₂
A₂ = \(\frac{\mathrm{A}}{2}\)
हम जानते हैं प्रतिरोध R ∝ \(\frac{l}{\mathrm{~A}}\)

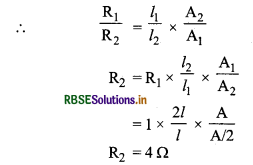
वैकल्पिक विधि : लम्बाई खींचकर दोगुनी करने पर नया प्रतिरोध
R₁ = n₂R
= 22R
= 4 x 1 = 4Ω

प्रश्न 6. 
एक कार्बन प्रतिरोधक पर क्रमशः लाल, काली, नारंगी एवं चांदी रंग की पद्रियाँ है। प्रतिरोधक का प्रतिरोध एवं सहयता क्या है?
उत्तर:
प्रथम पट्टी का रंग - लाल - वर्णकोड 2 
दूसरी पट्टी का रंग - काला - वर्णकोड 0 
तीसरी पट्टी का रंग - नारंगी - गुणक वर्ण कोर्ड 10³ 
चौथी पट्टी का रंग - चाँदी सा - सह्यता 10% 
कार्बन प्रतिरोधक का प्रतिरोध = 20 x 10³Ω ± 10%
= 20k Ω ±10% 

प्रश्न 7.
47xΩ ± 10% कार्बन प्रतिरोधक पर पाए जाने वाले वर्ण बैण्डों का क्रम लिखिए।
उत्तर:
दिए गए कार्वन प्रतिरोध के लिए, 
प्रथम सार्थक अंक 4 का वर्ण - पीला 
दूसरे सार्थक अंक 7 का वर्ण - बैंगनी
गुणक 10³ का वर्ण - नारंगी 
सहयता 10% का वर्ण - चांदी सा 

प्रश्न 8.
तीन प्रतिरोध समान्तर क्रम में जुड़े हैं। इस संयोजन में 30V की बैटरी से 7.5 A की विद्युत धारा प्रवाहित की जाती है। यदि दो प्रतिरोधों के मान 10Ω एवं 12Ω हो तो तीसरे प्रतिरोध का मान ज्ञात कीजिए।
उत्तर:
दिया है-संयोजित बैटरी का टर्मिनल बोल्टता V = 30 V
प्रवाहित धारा I = 7.5 A 
∴ संयोजन का तुल्य प्रतिरोध = \(\frac{\mathrm{V}}{\mathrm{I}}=\frac{30}{7.5}\) = 4Ω
तीन प्रतिरोध समान्तर क्रम में संयोजित हैं तब तुल्य प्रतिरोध
\(\frac{1}{\mathrm{R}}=\frac{1}{\mathrm{R}_1}+\frac{1}{\mathrm{R}_2}+\frac{1}{\mathrm{R}_3}\)
दिया है,
R₁ = 10Ω व R₂ = 12Ω

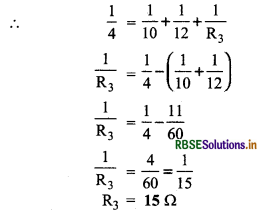
प्रश्न 9.
चित्र में प्रदर्शित नेटवर्क में बिन्दुओं A व B के मध्य विभवान्तर (V_B - V_D) ज्ञात कीजिए।

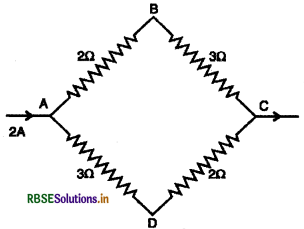
उत्तर:
प्रश्नानुसार ABC भाग का प्रतिरोध
R_ABC = 2 + 3 = 5Ω 
और ADC भाग का प्रतिरोध
R_ADC = 3 + 2 = 5Ω 
∴ R_ABC  = R_ADC 
अत: बिन्दु A से धारा दो समान भागों में विभाजित होती है।
i = \(\frac{2}{2}\) = 1A
∴ V_A - V_B = 2 x 1 = 2 वोल्ट ...........................(1)
तथा  V_A - V_D = 3 x 1 = 3 वोल्ट ...........................(2)
समो. (2) में से (1) को घटाने पर
V_B - V_D = 1 वोल्ट 

प्रश्न 10.
चित्र में प्रदर्शित नेटवर्क का बिन्दुओं A व B के मध्य तुल्य प्रतिरोध ज्ञात कीजिए।

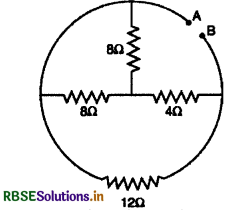
उत्तर:

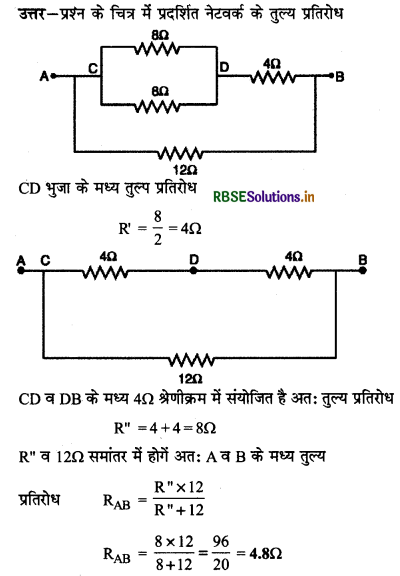
प्रश्न 11.
आन्तरिक प्रतिरोध 4Ω और वि. वा. बल (emf) 12 वोल्ट की कोई बैटरी किसी बाहय प्रतिरोध R से संयोजित है। यदि प्रतिरोध से प्रवाहित धारा 0.5 A है, तो (a) R तथा (b) बैटरी की टर्मिनल वोल्टता का मान परिकलित कीजिए।
उत्तर:
(a) प्रश्नानुसार, दिया है सेल का आंतरिक प्रतिरोध R = 4Ω
वि. वा. बल R = 12 वोल्ट 
परिपथ में प्रवाहित धारा I = 0.5A
I = \(\frac{\mathrm{E}}{\mathrm{R}+r}\)
I(R + r) = E
= \(\frac{E}{I}\) - r
= \(\frac{12}{0.5}\) - 4 = 20Ω

(b) टर्मिलन विभवान्तर V = IR
V = 0.5 x 20 = 10 वोल्ट 

प्रश्न 12.
998Ω प्रतिरोध का वोल्टमीटर 2V वि, वा, बल और 2Ω आन्तरिक प्रतिरोध के किसी सेल के सिरों से संयोजित है। वोल्टमीटर के सिरों के बीच तथा सेल के टर्मिनलों के बीच भी विभवान्तर ज्ञात कीजिए। वोल्टमीटर के पाठयांक में त्रुटि का आंकलन कीजिए।
उत्तर:
परिपथ का कुल प्रतिरोध Req = 998 + 2 = 1000Ω
वि. वा. बल E_eq = 2V 
तब परिपथ में प्रवाहित धारा I = \(\frac{\mathrm{Eeq}}{\operatorname{Req}}=\frac{2}{1000}\)
= 2 x 10^-3 A
वोल्टमीटर के सिरों के बीच विभवान्तर V = IR
= 2 x 10^-3 x 998
V = 1.996 वोल्ट
सेल के टर्मिनल के बीच विभवान्तर V₁ = IR
= 2 x 10^-3 x 2 
= 0.004 वोल्ट
या V = 4 मिली वोल्ट 
वोल्टमीटर के पाठयांक में त्रुटि ∆V = 4 मिलीवोल्ट

प्रश्न 13.
आरेख में दर्शाए अनुसार वि.वा.बल (emf) E₁ = 2V और आन्तरिक प्रतिरोध r₁ = 1Ω के किसी सेल को वि.वा.बल (emf) E₂ = 8V और आन्तरिक प्रतिरोध r₂ = 2Ω के किसी अन्य सेल से 4Ω के बाहय प्रतिरोध से होकर संयोजित किया गया है। बिन्दुओं A और C के बीच विभवान्तर ज्ञात कीजिए।

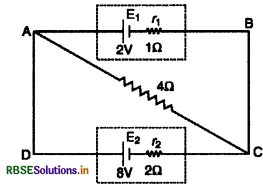
उत्तर:
दिवा है: E₁ = 2V, E₂ = 8V
r₁ = 1Ω, r₂ = 2Ω, R = 4Ω
तुल्य वि.वा.बल E = \(\frac{\mathrm{E}_1 r_2+\mathrm{E}_2 r_1}{r_1+r_2}\)
= \(\frac{2 \times 2+8 \times 1}{1+2}\)
= 4 वोल्ट
तुल्य आंतरिक प्रतिरोध r = \(\frac{r_1 r_2}{r_1+r_2}\)
= \(\frac{1 \times 2}{1+2}=\frac{2}{3} \Omega\)
∴ बाह्य प्रतिरोध में प्रवाहित धारा
i = \(\frac{\mathrm{E}}{\mathrm{R}+r}\)
i = \(\frac{4}{4+\frac{2}{3}}=\frac{12}{14}=\frac{6}{7}\) = Amp
∴ A व C के बीच विभवान्तर V = iR
V = \(\frac{6}{7} \times 4\)
V = \(\frac{24}{7}\) = 3.11 बोल्ट 

प्रश्न 14.
12 V वि.वा. बल तथा 2Ω आंतरिक प्रतिरोध की एक बैटरी किसी प्रतिरोधक से संयोजित है। यदि इसमें 0.5 A की विद्युत प्रवाहित हो तो प्रतिरोधक का प्रतिरोध ज्ञात कीजिए। यदि परिपथ बन्द हो तो सेल की टर्मिनल वोल्टता क्या होगी?
उत्तर:
प्रश्नानुसार, वि. वा. बल E = 12V
आंतरिक प्रतिरोधा r = 2Ω
परिपथ में प्रवाहित धारा I = 0.5 A 
टर्मिनल विभवान्तर V = E - Ir
= 12 - 0.5 x 2
= 12 - 1 = 11 वोल्ट

प्रश्न 15.
10 V तथा नगण्य आन्तरिक प्रतिरोध की बैटरी एक घनीय परिपच जाल के विकर्णतः सम्मुख कोनों से जुड़ी है। परिपथ जाल में 2Ω प्रतिरोध के 12 प्रतिरोधक है। परिपथ जाल का समतुल्य प्रतिरोध ज्ञात कीजिए।

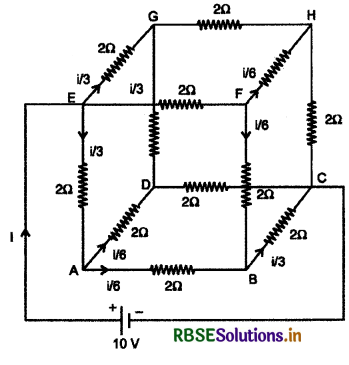
उत्तर:
बन्द लूप EABC में किरचॉक के द्वितीय नियम से
i/3 x 2 + i/6 x 2 + i/3 x 2 = 10
\(\frac{5}{6} i\) x 2 = 10
i = 6 Amp
अत: तुल्य प्रतिरोध R_eq = \(\frac{10}{6}=\frac{5}{3} \Omega\)

प्रश्न 16.
किरखॉफ के नियमों का उपयोग करके चित्र में प्रदर्शित नेटवर्क में धारा I1 का मान ज्ञात कीजिए।

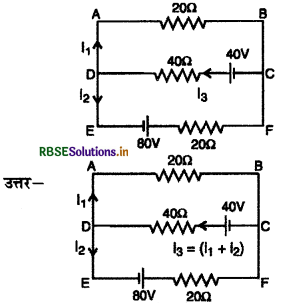
20I₁ + 40(I₁ + I₂) = 40
या 20I₁ + 40I₁ + 40 I₂ = 40
या 60I₁ + 40I₂ = 40
या 3I₁ + 2I₂ = 2 .................(i)
इसी प्रकार, बन्द पाश CDEFC किरचॉफ के द्वितीय नियम से,
20I₂ + 40(I₁ + I₂) = 80 + 40
या 20I₂ + 40I₁ + 40I₂ = 120 
या 40I₁ + 60I₂ = 120
या 2I₁ + 3I₂ = 6 .................(ii)
समी. (i) व (ii) को हल करने पर
I₁ = \frac{-6}{5} = - 1.2A 

प्रश्न 17.

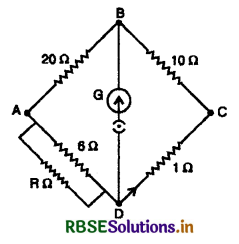
चित्र में यदि कीटस्टोन सेतु संतुलन अवस्था में हैतो अज्ञात प्रतिरोध R की गणना कीजिए।
उत्तर:
संतुलन अवस्था

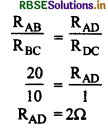
R_AD, R व 6Ω का तुल्य प्रतिरोध है जो समान्तर क्रम में संयोजित है।
R_AD = \(\frac{R \times 6}{R+6}\) = 2
6R = 2R + 12
4R = 12
R = 3Ω

प्रश्न 18.
किसी मीटर सेतु की दो भुजाओं में क्रमश: R = 5Ω और 5 प्रतिरोध है तब प्रतिरोध को समान प्रतिरोध द्वारा शंट (पावं पथ) कर दिया जाता है। तो नया संतुलन बिन्दु 1.5 l₁ पर पाया जाता है। आरंभिक सन्तुलन लम्बाई का मान परिकलित कीजिए। S का मान परिकलित कीजिए।

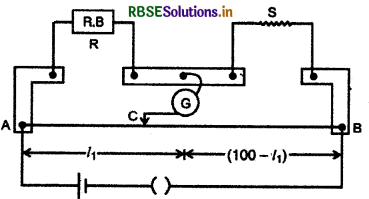
उत्तर:
आंरभिक अवस्था में

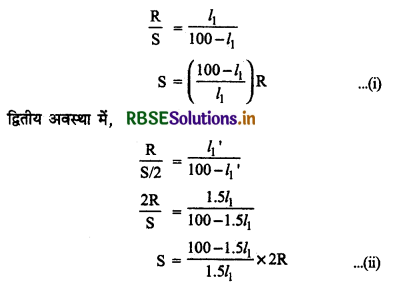
समी. (i) व (ii) की तुलना करने पर
\(\left(\frac{100-l_1}{l_1}\right) \mathrm{R}=\left(\frac{100-1.5 l_1}{1.5 l_1}\right) \times 2 \mathrm{R}\)

प्रश्न 19.
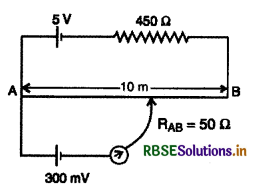
नीचे दिये गये पोटेशियोमीटर परिपथ में संतुलन लम्बाई l परिकलित कीजिए। कारण देकर स्पष्ट कीजिए। कि सभी अन्य कारकों को अपरिवर्तित करते हुए 5V वि.वा, बल (emf) के परिचालक सेल को 2V के सेल के द्वारा प्रतिस्थापित कर दिया जाए, तो यह परिपथ कार्य करेगा अथवा नहीं।

उत्तर:
तार AB का प्रतिरोध R_AB = 50Ω
तार की लम्बाई l = 10m
∴ एकांका लम्बाई का प्रतिरोध ρ = \(\frac{\mathrm{R}_{\mathrm{AB}}}{l}\)
= \(\frac{50}{10}\) = 5Ω
विभवमापी के प्राथमिक परिपथ में जुड़े सेल का विद्युत वाहक बल
E_p = 5V
परिपथ का तुल्य प्रतिरोध R = 450 + 50 = 500Ω
अतः विभवमापी के तार में प्रवाहित धारा
I = \(\frac{\mathrm{E}_p}{\mathrm{R}}=\frac{5}{500}\) = 0.01 Amp
संतुलन लम्बाई के तुल्य विभवान्तर V = 300 mV (किरखॉफ के द्वितीय नियम से
ε = Iρl
300 mV = 0.01 x 5l
l = \(\frac{300 \times 10^{-3}}{5 \times 0.01}\)
l = 60 x 10^-1 = 6 सेमी.

प्रश्न 20.
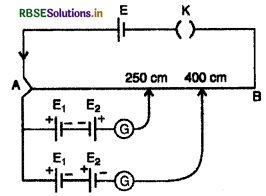
E₁ व E₂ विद्युत वाहक बलों वाले दो प्राथमिक सेल वियवमापी तार AB से चित्र की भाँति जुड़े हैं। दो भिन्न संयोजनों की संतुलन लम्बाइयाँ 250 cm व 400 cm हैं। E₁ व E₂ का अनुपात ज्ञात कीजिए।

उत्तर:
यदि तार AB की विभव प्रवणता K वोल्ट/सेमी हो तो
E₁ - E₂ = K x 250 ...................(i)
और E₁ + E₂ = K x 400 ...................(ii)
समी. (i) व (ii) को जोड़ने पर
2E₁ = 650K
E₁ = 325K 
समी. (ii) में से (i) को घटाने पर
E₂ = 75K
\(\frac{E_1}{E_2}=\frac{325}{75}\)
\(\frac{\mathrm{E}_1}{\mathrm{E}_2}=\frac{13}{7}\)

प्रतियोनी परीक्षा संबंधी प्रश्न

प्रश्न 1.
मीटर ब्रिज के बाएँ रिक्त स्थान में एक प्रतिरोधक तार जुड़ा है जो दाँयी ओर के रिक्त स्थान में जुड़े 10Ω के प्रतिरोध को सेतु तार के उस बिन्दु पर संतुलित करता है जो तार को 3 : 2 में विभाजित करता है। यदि प्रतिरोध तार की लम्बाई 1.5m हो तो 1Ω के तार की लम्बाई होगी-
(A) 1.5 x 10^-1 m
(B) 1.5 x 10^-2 m
(C) 1.0 x 10^-2 m 
(D) 1.0 x 10^-1 m
उत्तर:
(D) 1.0 x 10^-1 m

प्रश्न 2. 
3 x 10^-10 V/m के विद्युत क्षेत्र में 7.5 x 10^-4 मी.से.^-1 के अपवाह वेग से गतिशील आवेशित कण की गतिशीलता m²V^-1S^-1 में होगी-
(A) 2.5 x 10^-6
(B) 2.25 x 10^-15
(C) 2.25 x 10¹⁵ 
(D) 2.5 x 10⁶
उत्तर:
(D) 2.5 x 10⁶

प्रश्न 3.
एक प्रतिरोधक का वर्णकोड निम्न चित्र में दर्शाया है-

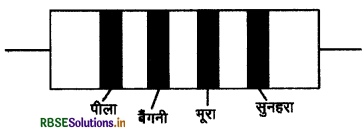
प्रतिरोध के मान एवं सहयता क्रमशः है-
(A) 4.7kΩ, 5% 
(B) 470Ω, 5% 
(C) 470kΩ, 5%
(D) 47kΩ, 10% 
उत्तर:
(B) 470Ω, 5%

प्रश्न 4. 
यदि 8 x 10²⁸ मी³ मुक्त इलेक्ट्रॉन प्रति एकांक आयतन तथ 5 mm2 अनुप्रस्थ काट क्षेत्रफल के धारावाही तार में 1.5 A धारा प्रवाहित है। इलेक्ट्रॉनों का अपवाह वेग होगा-
(A) 0.02 mm/s
(B) 2 mm/s 
(C) 0.2 mm/s
(C) इनमें से कोई नहीं
उत्तर:
(A) 0.02 mm/s

प्रश्न 5.
आयतन को नियत रखते हुए किसी प्रतिरोधक तार की लम्बाई में 0.5% वृद्धि की जाती है तो प्रतिरोध में कितना परिवर्तन होगा-
(A) 0%
(B) 1%
(C) 0.5%
(D) 2%
उत्तर:
(B) 1%

प्रश्न 6.
10Ω के लोड प्रतिरोधक के समान्तर क्रम में जुड़ी दो बैटरियों के वि.वा.बल 12V व 13V हैं। इन दोनों बैटरियों के आन्तरिक प्रतिरोध क्रमशः 1Ω व 2Ω हैं। लोड के सिरो के मध्य विभवान्तर होगा-
(A) 11.4V और 11.5V
(B) 11.7V और 11.8V 
(C) 11.6V और 11.7V
(D) 11.5V और 11.6V
उत्तर:
(D) 11.5V और 11.6V

प्रश्न 7.
किसी प्रतिरोध R से प्रवाहित आवेश का समय t के साथ विचरण Q = at - bt² के रूप में होता है, जहाँ a और b अनात्मक नियतांक हैं। R में उत्पन्न कुल ऊष्मा है-

प्रश्न 8.
किसी विभवमापी के तार की लम्बाई 4m है और इसका प्रतिरोध 8Ω है। इस श्रेणीक्रम में, 2V विद्युत वाहक बल का एक संचायक सेल तथा एक प्रतिरोधक जोड़ा गया है। अत: इस तार पर प्रति सेंटीमीटर 1 mV विभव प्रवणता प्राप्त होगी-
(A) 40Ω
(B) 44Ω
(C) 48Ω
(D) 32Ω
उत्तर:
(D) 32Ω

प्रश्न 9. 
L लम्बाई के एक विभवमापी तार तथा एक प्रतिरोधी (r) को श्रेणीक्रम में E₀ (ई० एम० एफ०) की बैटरी तथा प्रतिरोध r₁ से जोड़ा गया है। इस विभवमापी की l लम्बाई पर किसी अज्ञात E के लिये संतुलन बिन्दु प्राप्त होता है तो E का मान है-

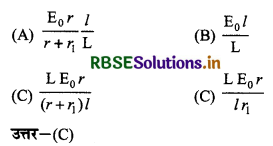
प्रश्न 10.
असमान परिच्छेद (मोटाई) के धातु चालक के सिरों के बीच एक स्थिर विभवान्तर आरोपित किया जाता हैं। इस चालक के अनुदिश जो राशि अपरिवर्तित रहे वह है-
(A) धारा
(B) अपवाह वेग 
(C) विद्युत क्षेत्र
(D) धारा घनत्व। 
उत्तर:
(A) धारा