RBSE Class 12 Physics Important Questions Chapter 3 Current Electricity

Rajasthan Board RBSE Class 12 Physics Important Questions Chapter 3 Current Electricity Important Questions and Answers.

RBSE Class 12 Physics Chapter 3 Important Questions Current Electricity

Multiple Choice Questions

Question 1.
The ratio of drift velocity to that of thermal velocity of an electron in a conductor is:
(A) 10^-5
(B) 10^-6
(C) 10^-8
(D) 10^-10.
Answer:
(D) 10^-10

Question 2.
The speed at which current travels in a conductor is nearly:
(A) 3 x 10^-4 ms^-1
(B) 3 x 10^-5 ms^-1
(C) 4 x 10^-6 ms^-1
(D) 3 x 10^-8 ms^-1.
Answer:
(D) 3 x 10^-8 ms^-1.

Question 3.
When current I is made to flow in a wire of radius r, the drift velocity is v_d. If the same current is passed through a wire of radius 2r, then drift velocity will be:
(A) 4vd
(B) 2vd
(C) \(\frac{v_d}{2}\)
(D) \(\frac{v_d}{4}\).
Answer:
(D) \(\frac{v_d}{4}\).

Question 4.
Which one of the following is best material for making connecting wires?
(A) Maganin
(B) Constantan
(C) Copper
(D) Nichrome.
Answer:
(C) Copper

Question 5.
Constantan and maganin are used to make standard resistances because:
(A) Their resistances are high
(B) Their resistances are low
(C) Their temperature coefficient of resistance is high
(D) Their temperature coefficient of resistance is low.
Answer:
(D) Their temperature coefficient of resistance is low.

Question 6.
A wire of resistivity ρ is stretched to double its length. Then its new resistivity will:
(A) be half
(B) be double
(C) be four times
(D) not change.
Answer:
(D) not change.

Question 7.
Dimensions of electrical resistance is
(A) [ML²T^-3A^-2]
(B) [ML²T^-3A^-1]
(C) [ML³T^-3A^-2]
(D) [ML²T^-3A]
Answer:
(A) [ML²T^-3A^-2]

Question 8.
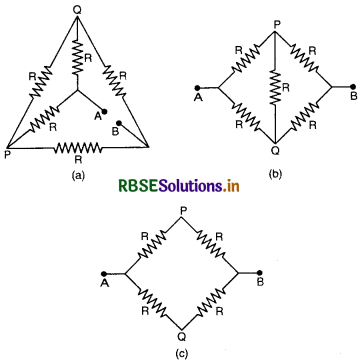
Eight resistances each of 4Ω are connected in the circuit as shown in the fig. The equivalent resistance between A and B is:
(A) \(\frac{8}{3}\) Ω
(B) \(\frac{32}{3}\) Ω
(C) \(\frac{32}{15}\) Ω
(D) \(\frac{32}{11}\) Ω
Answer:
(C) \(\frac{32}{15}\) Ω

Question 9.
1 kW h is equal to:
(A) 36 x 10³ J
(B) 36 x 10⁵ J
(C) 36 x 10^-15 J
(D) 36 x 10^-3 J.
Answer:
(B) 36 x 10⁵ J

Question 10.
n cells each of emf E are connected in parallel. The effective emf of the parallel combination is:
(A) E
(B) \(\frac{\mathrm{E}}{n}\)
(C) E + n
(D) nE.
Answer:
(A) E

Question 11.
A heater coil is cut into two equal parts and only one part is now used in the heater: The heat generated will now be:
(A) one fourth
(B) halved
(C) doubled
(D) four times.
Answer:
(C) doubled

Question 12.
As shown in figure, the current flowing in the resistor 2R (in ohm) is:
(A) \(\frac{2 E}{R}\)
(B) \(\frac{3E}{7R}\)
(C) \(\frac{E}{7R}\)
(D) \(\frac{E}{R}\)
Answer:
(B) \(\frac{3E}{7R}\)

Question 13.
The heat produced by a 100 W heater in 2 minutes is equal to:
(A) 4 x 10³ J
(B) 6 x 10³ J
(C) 10 x 10³ J
(D) 12 x 10³ J.
Answer:
(D) 12 x 10³ J.

Question 14.
Two cells X and Y are connected to a resistance of 10 Q as shown in figure. The terminal voltage of cell Y is:
(A) zero
(B) 2V
(C) 4V
(D) 10V.
Answer:
(A) zero

Question 15.
Dimensional formula for potential difference is:
(A) [M⁰L²T^-3A^-1]
(B) [ML²T^-2A^-1]
(C) [ML²T^-3A^-1]
(D) [MLT^-2A]
Answer:
(C) [ML²T^-3A^-1]

Question 16.
The unit of electric power is:
(A) Volt
(B) Joule
(C) Watt    
(D) kWh.
Answer:
(C) Watt    

Question 17.
The S.I. unit of electrical resistivity is:
(A) ohm
(B) ohm-metre
(C) ohm-metre^-1
(D) mho-metre^-1.
Answer:
(B) ohm-metre

Question 18.
Ohm’s law is not obeyed by:
(A) Electrolytes
(B) discharge tubes
(C) Vacuum tubes
(D) All of these.
Answer:
(D) All of these.

Question 19.
The basic instrument used to detect the current is:
(A) Ammeter
(B) Voltmeter
(C) Galvanometer
(D) Voltameter.
Answer:
(C) Galvanometer

Question 20.
Resistivity of a conducting wire:
(A) varies with its length
(B) varies with its mass
(C) varies with its cross-section
(D) is independent of its dimensions.
Answer:
(D) is independent of its dimensions.

Question 21.
A carbon resistance is having coding Green, Orange, Black and Gold. The resistance of the resistor is:
(A) 53 x 10⁰ ± 5% Ω
(B) 54 x 10⁰ ± 10% Ω
(C) 53 x 10¹ ± 5% Ω
(D) 53 x 10⁰ ± 10% Ω
Answer:
(A) 53 x 10⁰ ± 5% Ω

Question 22.
Kirchhoffs first and second laws are respectively based on law of conservation.
(A) Momentum and energy
(B) Charge and energy
(C) Mass and energy
(D) None of these.
Answer:
(B) Charge and energy

Question 23.
The instrument for the accurate measurement of the e.m.f. of a cell is:
(A) a voltmeter
(B) an ammeter
(C) a potentiometer
(D) slide wire bridge.
Answer:
(C) a potentiometer

Question 24.
A wire of length L is drawn to a length 2L, then its resistance will:
(A) Increase four times
(B) Decrease to \(\frac{1}{4} \text { th }\) of the original
(C) Increase two times
(D) Not change.
Answer:
(A) Increase four times

Question 25.
Wheat stone bridge is used to measure:
(A) E.m.f.
(B) Potential
(C) Resistance
(D) Current
Answer:
(C) Resistance

Question 26.
Resistance of a conductor increases with the rise of temperature, because,
(A) relaxation time decrease
(B) relaxation time increases
(C) electron density decreases
(D) electron density increases.
Answer:
(A) relaxation time decrease

Question 27.
What is the unit of specific resistance?
(A) ohm cm²
(B) ohm cm^-1
(C) ohm - cm
(D) ohm - cm^-2.
Answer:
(C) ohm-cm

Question 28.
Which of the following characteristics is immaterial for the fuse wire?
(A) Resistivity
(B) Radius
(C) Length
(D) None of them.
Answer:
(C) Length

Question 29.
SI unit of current is:
(A) milli ampere
(B) micro ampere
(C) ampere
(D) none of these.
Answer:
(C) ampere

Question 30.
Calculate the current through a lamp of 60 W operating at 220 V.
(A) 2.73 A
(B) 27.3 A
(C) 0.372 A
(D) 0.273 A.
Answer:
(D) 0.273 A.

Fill in the blanks

Question 1.
The motion of electric charge constitute ............................ current.
Answer:
electric.

Question 2.
Direction of current is taken as the direction of motion of ............................ charge.
Answer:
positive.

Question 3.
Resistance of a conductor is due to ............................ of free electrons with the ions (or atoms) of the conductor.
Answer:
collision.

Question 4.
Conductivity is the ............................ of resistivity.
Answer:
reciprocal.

Question 5.
Relaxation time is of the order of ............................ second.
Answer:
10^-14.

Question 6.
Ohm's law is not a ............................ law.
Answer:
fundamental.

Question 7.
............................ of metals increases with rise of temperature.
Answer:
Resistance.

Question 8.
Kirchhoffs second law is also called ............................ rule.
Answer:
loop.

Question 9.
A slide wire bridge is also called as ............................ bridge.
Answer:
meter.

Question 10.
A ............................ is used to compare e.m.f.s of two cells.
Answer:
potentiometer.

Question 11.
Kirchhoffs first law is based on the law of conservation of ............................
Answer:
charge.

Question 12.
Kirchhoffs second law is based on the law of conservation of ............................         
Answer:
energy.

Question 13.
Kirchhoffs second law holds for a ............................ circuit only.
Answer:
closed.

Very Short Answer Type Questions

Question 1.
Name the charge carriers of electricity.
Answer:
The charge carriers of electric current are electrons. They move from lower potential towards higher potential.

Question 2.
What is drift velocity?
Answer:
The velocity with which the electrons are drifted from lower potential end to higher potential end of the conductor under the influence of an external field. Its value varies from 0.1 to 1.0 cm s^-1.

Question 3.
Explain why bending a wire does not affect electrical resistance.
Answer:
The electrons have little inertia of motion and therefore, are able to go around the bends easily.

Question 4.
Is a wire carrying current charged?
Answer:
No, because no chemical potential energy is stored in the wire carrying current.

Question 5.
What is dangerous to human body, current or voltage?
Answer:
Due to passage of current, there takes place a chemical and heating effect in the body and current is more dangerous.

Question 6.
How does resistance of a wire I depend on the temperature?
Answer:
The resistance of a wire goes on increasing with increase in temperature and decreases with decrease in its temperature. For low temperature, the increase is almost linear, but as temperature increases, the resistance starts increasing at much higher rate.

Question 7.
Why is it that drift velocity is different from the velocity of electrons between collisions?
Answer:
When an electron moves, it suffers so many collision that its forward movement is very slow-it, however, may be moving at a high speed between two collisions.

Question 8.
What is the difference between resistance and resistor?
Answer:
Resistance. It is the property of a material due to which it opposes the flow of current passing through it.
Resistor. A material which offers some resistance to electric current is called a resistor.

 
Question 9.
If high current is to be drawn from a low-voltage source, it must have low internal resistance. Why?
Answer:
Since I_max = \(\frac{\mathrm{E}}{r}\) i.e. Maximum current drawn r from a source is inversely proportional to its internal resistance. So lower the internal resistance of the source, higher the maximum current that can be drawn from it.

Question 10.
V-I graph for a metallic wire at two different temperatures T₁ and T₂ is as shown in the following figure. Which of the two temperatures T₁ and T₂ is higher and why?

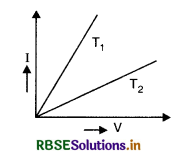
Answer:
T₂ > T₁ because
Resistance = \(\frac{1}{\text { Slope of the curve }}\)
Hence the resistance of wire is more at temperature T₂. So T₂ > T₁.

Question 11.
How does the resistance of an ohmic conductor depend upon the applied voltage?
Answer:
Resistance is independent of applied voltage.

Question 12.
Is internal resistance a defect of a cell?
Answer:
Yes, because a part of chemical energy obtained from the cell is spent in the cell itself due to internal resistance.

Question 13.
Why do we prefer potentiometer of longer length for sensitive measurements?
Answer:
The longer the length of potentiometer wire - more sensitive it is. If, for example, we have 2 volt battery across a potentiometer of 100 cm then its each centimere measures 1/50 volt - if the length is 1000 cm then its each centimetre measures 1/500 volt.

Question 14.
How many free electrons flowing per second will constitute 1A current?
Answer:
I = \(\frac{q}{t}=\frac{n e}{t}\) = 1
So n = \(\frac{\mathrm{I} t}{e}=\frac{1 \times 1}{1.6 \times 10^{-19}}\)
or n = 6.25 x 10¹⁸ electrons

Question 15.
On what factors the resistance of a conductor depends?
Answer:
The resistance of a conductor depends on:

• the nature of conductor
• temperature of the conductor
• dimensions of the conductor.

Question 16.
Name the alloys/metals used to make standard resistors.
Answer:
Manganin, constantan, nichrome, eureka.

Question 17.
Why conducting wires are made of copper?
Answer:
Copper is used for making conducting wires because:

• conductivity of copper is very high
• it is a diamagnetic hence it doesn’t get magnetised when current is passed through it and hence doesn’t disturb current in the circuit.

Question 18.
A high tension (H.T.) supply of it is 6 kV have a very large internal resistance, why?
Answer:
It is required, to protect the high tension supply, otherwise if the supply is short-circuited accidentally, the current drawn will exceed safety limit and H.T., supply will get damaged.

Question 19.
What is the order of magnitude of the resistance of a (dry) human body?
Answer:
The resistance of a dry human body is about 10 kΩ.

Question 20.
Currents of the order of 0.1 A, through the human body are fatal. What causes the death: heating of the body due to electric current or something else?
Answer:
The cause of death of a person cannot be heating. The person may receive burns if the currents are too large. The cause of death is the interference caused by external currents with the nerve processes related to our heart beating, which is basically electrical in nature. Beyond a certain point, this interference is fatal.
 
Question 21.
A nerve fibre contains a membrane separating two conducting fields maintained at a potential difference. What is the order of this potential difference?
Answer:
Approximately 0.1 V.

Question 22.
Why do we prefer a potentiometer to measure e.m.f. of a cell rather than a voltmeter?
Answer:
Potentiometer does not draw any current from the cell whose e.m.f. is to be determined, whereas a voltmeter always draws some current. Therefore, measures the lesser value of e.m.f. of a cell.

Question 23.
Using irieter bridge, it is advised to obtain the null point in the middle of the wire. Why?
Answer:
It is advised to obtain the maximum accuracy. In this case the ratio arms are nearly equal and end resistances of copper string also produce the least effect. Hence the bridge is most sensitive.

Question 24.
A steady current flows in a metallic conductor of non-uniform cross-section. Which of the following quantities, current, current density and drift speed are constant along the conductors?
Answer:
Only current is constant.

Question 25.
Out of two bulbs marked 25 W and 100 W which one has higher resistance?
Answer:
Since P = \(\frac{\mathrm{V}^2}{\mathrm{R}}\)
R = \(\frac{\mathrm{V}^2}{\mathrm{P}}\) or R ∝ \(\frac{1}{P}\)
So 25 W bulb has more resistance.

Question 26.
Why one experiences fatal shock when accidentally touches a line wire of 220 V supply?
Answer:
Resistance of human body
R = 10 kΩ = 10⁴ Ω
∴ I = \(\frac{E}{R}=\frac{220}{10^4}\) = 22 mA
Our nervous system is very sensitive and fails temporarily even to small currents like this.

Question 27.
What is the effect of temperature on relaxation time in a metal?
Answer:
The relaxation time decreases with rise in temperature.

Question 28.
What is the effect of heating of a conductor on the drift velocity of free electron?
Or
Will the drift speed of free electrons in a metallic conductor increase or decrease with the increase in its temperature?
Answer:
Since drift velocity of free electrons is:
v_d = \(\frac{e \mathbf{E}}{m} \tau\)
So as the temperature is increased, τ decreases and hence drift velocity decreases.

Question 29.
If p.d. V applied across a conductor is increased to 2V, how will the drift velocity of the electron change?
Answer:
Since v_d = \(\frac{e \mathrm{E}}{m} \tau=\frac{e \mathrm{~V}}{m l} \tau \)So as V is made 2V, v_d will become 2v_d i.e. drift velocity is doubled.

Question 30.
Explain the variation of conductivity of a metallic conductor with temperature.
Answer:
The conductivity of a metallic conductor decreases with increase in temperature and vice versa.

Question 31.
Define conductance of a material. Give its S.I. unit.
Answer:
The conductance of a material is reciprocal of the resistance of the material.
S.I. unit of conductance is (Ω^-1) or mho.

Question 32.
Define conductivity of a conductor. Give its S.I. unit.
Answer:
Conductivity of a conductor is reciprocal of resistivity of the conductor.
S.I. unit of conductivity is (S m^-1) or siemen per metre.

Question 33.
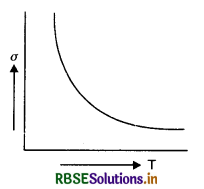
Explain with the help of a graph, the variation of conductivity with temperature for a metallic conductor?
Answer:
The graph between a and T is as shown in Fig. VSAQ 33.

Question 34.
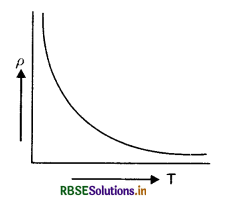
Sketch a graph showing variation of resistivity of carbon with temperature.
Answer:
Since resistivity of carbon decreases with temperature, so the graph between ρ and T is shown in figure VSAQ 34.

Question 35.
How does the mobility of electrons in a conductor change, if the potential difference applied across the conductor is doubled. Keeping the length and temperature of the conductor constant.
Answer:
No change, because mobility is independent of applied potential difference.

Question 36.
The metallic conductor is at temperature θ₁. The temperature of metallic conductor is increased to θ₂. How will the product of its resistivity and conductivity change?
Answer:
Since ρ = \(\frac{1}{\sigma}\)
∴ ρ.σ = 1
Thus the product is independent of temperature.

Question 37.
A resistance R is connected across a cell of emf ε and internal resistance r. A potentiometer now measures the potential difference between the terminals of the cell as V. Write the expression for 'r' in terms of ε, V and R.
Answer:
The relation between ε, V and R is
r = R\([\frac{\varepsilon-\mathrm{V}}{\mathrm{V}}]\)

Question 38.
Explain how does resistivity of a conductor depend upon (i) number density n of free electron and (ii) relaxation time τ.
Answer:
Since ρ = \(\frac{m}{n e^2 \tau}\)
So ρ ∝ \(\frac{1}{n}\) and ρ = \(\frac{1}{\tau}\).

Question 39.
How does the conductance of a semiconducting material change with rise in temperature?
Answer:
The conductance of a semi-conducting material increases with rise in temperature.

Question 40.
Two wires of equal length, one of copper and other of manganin, have the same resistance. Which wire is thicker?
Answer:

i.e. manganin wire is thicker than copper wire.

Question 41.
Resistivity of copper, silver and manganin are 1.7 x 10^-8 Ωm, 1.0 x 10^-8 Ωm and 44 x 10^-8 Ωm respectively. Which of these is the best conductor?
Answer:
Since R = \(\frac{\rho l}{\mathrm{~A}}\)
For the given length and area of cross-section
R ∝ ρ
Since the value of ρ is the least for silver, so it is the best conductor of the three given conductors.

Question 42.
What happens to the power dissipation if the value of electric current passing through a conductor of a constant resistance is doubled?
Answer:
Since power dissipated, P = I²Rt
or P ∝ I²
So if current is doubled, the power dissipated becomes four times.

Question 43.
The variation of potential difference V with length l in the case of two potentiometers, P and Q is as shown in the figure VSAQ 43. Which of these two will you prefer for comparing the emfs of the two primary cells?

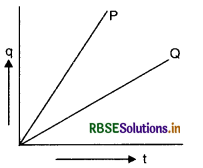
Answer:
The potential preferred for comparing emfs of two primary cells is that which have lesser potential difference per unit length. Since the slope of Q (potential gradient) is lesser than that of P, hence the potentiometer Q will be preferred.

Question 44.
Two bulbs are rated (P₁, V) and (P₂, V). If they are connected (i) in series and (ii) in parallel across a supply V, find the power dissipated in the two combinations in terms of P₁ and P₂.
Answer:
Resistances of the two bulbs R₁ = \(\frac{\mathrm{V}^2}{\mathrm{P}_1}\) and R₂ = \(\frac{\mathrm{V}^2}{\mathrm{P}_2}\)
(i) Net resistance in series
R_s = R₁ + R₂ = \(\frac{\mathrm{V}^2}{\mathrm{P}_1}+\frac{\mathrm{V}^2}{\mathrm{P}_2}=\mathrm{V}^2\left(\frac{\mathrm{P}_1+\mathrm{P}_2}{\mathrm{P}_1 \mathrm{P}_2}\right)\)
(ii) Net resistance in parallel

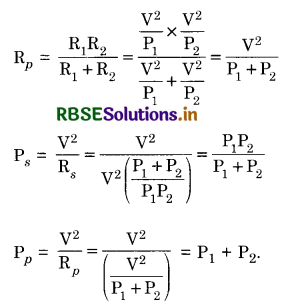
Question 45.
(a) You are required to select a carbon resistor of resistance of 56 kΩ ± 10% from a shopkeeper. What would be the sequence of colour bands required to code the desired resistor?
(b) Write two characteristic properties of the material of a metre bridge wire.
(c) What precautions do you take to minimise the error in finding the unknown resistance of the given wire?
Answer:
(a) Number 5 corresponds to green, No. 6 corresponds to blue, 103 corresponds to orange and 10% corresponds to silver.
∴ Sequence of Colours is
Green, blue, orange, silver

(b) Metre bridge wire must have

• High resistivity
• Low-temperature coefficient of resistivity

(c) To minimise the error in determining the resistance of a wire, the

• Wire should be of uniform thickness
• The balance point should be near the midpoint of the wire.

Question 46.
Name the device used for measuring the internal resistance of a secondary cell.
Answer:
Potentiometer.

Question 47.
A wire of resistivity ρ is stretched to double its length. What will be its new resistivity?
Answer:
Resistivity is independent of the dimensions of the conductor, so there will be no change in ρ.

Question 48.
A copper wire of resistivity ρ is stretched to reduce its diameter to half of its original value. What will be its new resistivity?
Answer:
There will be no change in ρ.

Question 49.
If the length of a wire conductor is doubled by stretching it, keeping the p.d. across it constant by what factor does the drift speed of electrons change?
Answer:
Since v_d = \(\frac{e \mathrm{~V}}{m l} \tau\)
or v_d ∝ \(\frac{1}{l}\)
So as the length is doubled, the speed is reduced by half.

Question 50.
(a) Define the terms ‘drift velocity’ and ‘relaxation time’ giving their physical significance.
(b) A conductor of length L is connected across a dc source of emf E. If the conductor is replaced by another of the same material and area of cross-section but of length 5L, by what factor will the drift velocity change?
Answer:
(a) Drift Velocity: It is the average velocity of the free electrons with which they get drifted towards the positive terminal under the influence of the external field.
Significance: The net current flowing through any cross-section is controlled by drift velocity and there is no transport of charges in a direction perpendicular to the applied field.
Relaxation Time (τ): The average time between successive collisions of electrons or ions in a conductor is called relaxation time.
Significance: It determines the drift velocity acquired by the electrons under the given applied electric force and also determines the electrical conductivity of a conductor at different temperatures.

(b) In first case:
v_d = \(\frac{e \mathrm{~V}}{m \mathrm{~L}} \tau\)
In second case:
v'_d = \(\frac{e \mathrm{~V} \tau}{m 5 \mathrm{~L}}\)
v'_d = \(\frac{1}{5}\left(\frac{e \mathrm{~V}}{m \mathrm{~L}} \tau\right)=\frac{v_d}{5}\)
Thus we find that the drift velocity becomes \(\frac{1}{5}\) of its original value.

Question 51.
What will be the change in the resistance of a circular wire when its radius is halved and length is reduced by \(\frac{1}{4} t h\) of its original length? Answer:
In first case,
R = \(\frac{\rho l}{\mathrm{~A}}=\frac{\rho l}{\pi r^2}\)
In second case,
R' = \(\frac{\rho \frac{l}{4}}{\pi\left(\frac{r}{2}\right)^2}=\frac{\rho l}{\pi r^2}=\mathrm{R}\).
So there is no change in the resistance.

Question 52.
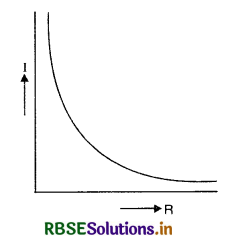
Plot a graph showing the variation of current ‘I’ versus resistance ‘R’, connected to a cell of emf E and internal resistance 'r'.
Answer:
Since current in the circuit is given as
I = \(\frac{\mathrm{E}}{\mathrm{R}+r}\)
So the graph between I and R is as shown in Fig. VSAQ 52.

Question 53.
Nichrome and copper wires of same length and same radius are connected in series. Current I is passed through them. Which wire gets heated up more? Justify your answer.
Answer:
Heat produced
H = I² Rt = I² \(\frac{\rho l}{\mathrm{~A}} t\)
When l and A are the same.
H ∝ ρ
Since    ρ_nichrome > ρ_copper
∴ H_nichrome H_copper

Question 54.
What are superconductors?
Answer:
Superconductors are the materials having zero resistance (at very low temperatures).

Question 55.
The sequence of bands marked on carbon resistance are red, red, red, silver. Write the value of the resistance with tolerance.
Answer:

Question 56.
A carbon resistor is marked in colour band of red, black, orange and silver. What is the resistance and tolerance value of the resistance?
Answer:

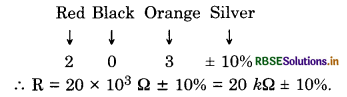
Question 57.
A voltage of 30V is applied across certain carbon resistor with first, second and third rings of blue, black and yellow colours respectively. Find the value of current through the resistor.
Answer:
1st ring → blue → 6
2nd ring → black → 0
3rd ring → yellow → 10⁴
∴ Values of resistance, R = 60 x 10⁴ Ω
So I = \(\frac{\mathrm{E}}{\mathrm{R}}=\frac{30}{60 \times 10^4}\) = 5 x 10^-5 A

Question 58.
Two identical slabs, of a given metal, are joined together in two different ways, as shown in figures (i) and (ii). What is the ratio of the resistance of these two combinations?

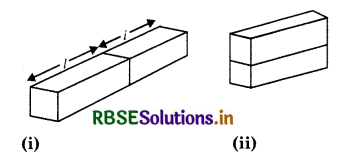
Answer:
(i) The resistance is R₁ = \(\frac{\rho 2 \mathrm{l}}{2 \mathrm{lt}}=\frac{\rho}{\mathrm{t}}\)
(ii) The resistance is R₂ = \(\frac{\rho l}{1 \times 2 t}=\frac{\rho}{2 t}\)
∴ \(\frac{\mathrm{R}_1}{\mathrm{R}_2}\) = 2

Question 59.
In a meter bridge, two unknown resistances R and S when connected in two gaps, give a null point at 40 cm from one end. What is the ratio of R and S?
Answer:
Here l = 40 cms
∴ \(\frac{\mathrm{R}}{\mathrm{S}}=\frac{l}{100-l}=\frac{40}{100-40}=\frac{40}{60}=\frac{2}{3}\)

Short Answer Type Questions

Question 1.
What do you understand by
(i) steady current
(ii) varying current and
(iii) alternating current?
Answer:
(i) Steady Current. The current whose magnitude does not change with time is called steady current. If we plot a graph between current (I) and time (t) it will be straight line parallel to t-axis Fig. SAQ (i) (a)

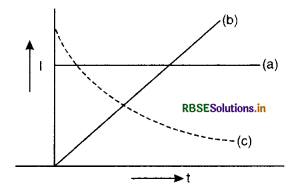
(ii) Varying Current. The current whose magnitude changes with time is called varying current. The graph may or may not be a straight line, Fig. SAQ 1 (i) (b) and (c).
(iii) The current whose magnitude changes, continuously and direction changes periodically is called

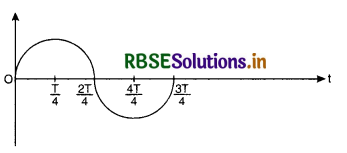
alternating current. Such a current is represented by a sine curve or cosine curve. Fig. SAQ 1 (ii)

Question 2.
When drift velocity is so small, how is it that an electric bulb lights up as soon as we turn the switch on?
Answer:
A particular electron does not have to reach the electric bulb to make current flow in the bulb. As soon as the switch is turned on, the potential difference becomes applied at the ends of the terminals of the bulb and an electric field is set up. Changes occur at the initial state of setting of electric field which give rise to a changing magnetic field. The changing magnetic field gives rise to another changing electric field and so on. This electromagnetic phenomenon takes place at the speed of electromagnetic waves which is the same as velocity of light 3 x 10⁸ ms^-1. The set electric field make current flow through the bulb instantly.

Question 3.
A large number of free electrons are present in metals. Why is there no current in the absence of electric field across it?
Answer:
The current is due to flow of charge in a definite direction. In a metal, the free electrons move in all directions haphazardly, in the absence of electric field; the average thermal velocity of electrons is zero. Therefore, there is no current in metal in the absence of electric field. In the presence of electric field, each free electron experiences a force opposite to the direction of field due to which the electrons acquire a drift velocity and there is a net flow of charge in a definite direction which constitutes the current.

Question 4.
Since drift velocity of electrons is very small, how then is current established almost the instant a circuit is closed?
Answer:
When the circuit is closed, the electric field is established almost instantaneously with the speed of light, however, it does take a little while for the current to reach its steady state.

Question 5.
If the electron drift speed is so small and the electron’s charge is small, how can we still obtain large amount of current in a conductor?
Answer:
Current in a conductor is proportional to electron number density (Number of free electrons per unit volume), and the electron number density is ~ 10²⁹ m^-3. So a large amount of current is obtained in a conductor.

Question 6.
Distinguish between resistance and specific resistance.
Answer:

Resistance	Specific resistance
1. It is the ratio of the P.D. across the conductor to the two ends of a conductor to the current flowing i.e. R = \(\frac{\mathrm{V}}{\mathrm{I}}\)	1. It is the resistance of conductor of unit length and unit area of cross-section and is given by ρ = \(\frac{\mathrm{RA}}{l}\)
2. It depends upon the length, area of cross-section and nature of material.	2. It is independent of length and area of cross-section of the material and depends only on the nature of the material.
3. Unit of resistance in SI is ohm (Ω).	3. Unit of specific resistance in SI is ohm-metre (Ωm)

Question 7.
Distinguish between e.m.f. of a cell and potential difference.
Answer:

E.M.F. of a cell	Potential difference
1. The e.m.f. of a cell is the maximum potential difference between the two electrodes of a cell when the cell is in the open circuit.	1. The potential difference between the two points is the difference of potential between those two points in a closed circuit.
2. It is independent of the resistance of the circuit and depends upon the nature of electrodes and the nature of electrolyte of cell.	2. It depends upon the resistance between the two points of the circuit and current flowing in the circuit.
3. The term e.m.f. is used or the source of electric current of the electric circuit.	3. The potential difference is measured between any two points.
4. It is a cause.	4. It is an effect.

Question 8.
Define average relaxation time. Find the expression of drift velocity in terms of average relaxation time.
Answer:
Average relaxation time (τ). It is the time interval which a free electron, on the average, spends between two successive collisions.
Relation between average relaxation time and drift velocity
In the absence of electric field, the free electrons in a conductor are always moving in all directions. So average velocity at any instant is zero and hence, cannot constitute an electric current.
When an electric field is applied in the conductor, the electrons get accelerated opposite to the electric field. The force on an electron of charge -e is given by

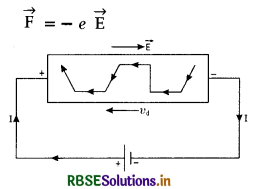
If m is the mass of the electron, then acceleration produced in the electron
\(\vec{a}=\frac{\overrightarrow{\mathrm{F}}}{m}=-\frac{e \overrightarrow{\mathrm{E}}}{m}\) .........................(1)
Due to this acceleration, the free electrons gain extra velocity i.e. energy. But this energy is destroyed at each collision against the positive ion, in the conductor. The average time for which each electron is accelerated before suffering a collision is called average relaxation time τ.
If \(\overrightarrow{v_d}\) is the average velocity of all the electrons called drift velocity, then
\(\overrightarrow{v_d}\) = 0 + \(\overrightarrow{A}\) τ
Using eqn. (1), we get
\(\overrightarrow{v_d} = -\frac{e \overrightarrow{\mathrm{E}} \tau}{m}\)
-ve sign means that the direction of \overrightarrow{v_d} is opposite to \overrightarrow{E}.
In magnitude,
v_d = \(\frac{e \mathrm{E} \tau}{m}\) ...........................(2)
This is the required relation between drift velocity and average relaxation time.

 
Question 9.
State and explain Ohm’s law.
Answer:
Ohm’s law. It states that current flowing through a conductor is proportional to the potential difference across its two ends provided the physical conditions (temperature, mechanical strain etc.) of the conductor remain unchanged.
If V is the potential difference between two ends of a conductor and I is the current flowing through it, then
V ∝ I
or V = RI ...................(1)
where R is the constant of proportionality and is called the resistance of the conductor. Its value depends upon
(i) Shape of conductor
(ii) Length of conductor
(iii) Nature of the material.

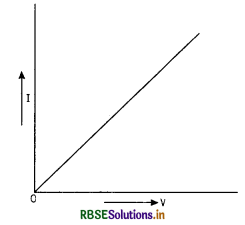
If a graph is plotted between V and I, the graph will be a straight line passing through the origin as shown in Fig.
Note: Conductors obeying Ohm’s law are called ohmic conductors and those which do not obey Ohm’s law are called non-ohmic conductors.

Question 10.
Define resistance and give its units.
Answer:
Resistance. Resistance is the property of a material by virtue of which it opposes the flow of current through it and quantitatively it is given by,
R = \(\frac{V}{I}\)
= \(\frac{\text { Potential difference }}{\text { Current }}\)
The S.I. unit of resistance is ohm (Ω). It is a practical unit of resistance.
Definition of ohm
If    V = 1 volt; I = 1 ampere
then R = 1 ohm.
Hence a conductor has a resistance of one ohm if a current of one ampere flows through it when a potential difference of one volt is maintained across its two ends.
1 ohm = \(\frac{1 \text { volt }}{1 \text { ampere }}\) or 1 Ω
= 1 VA^-1

Question 11.
What are the factors on which resistance of a conductor depend? Hence define, specific resistance (or resistivity).
Answer:
Following are the factors on which the resistance K of a conductor depends:
(i) Length 'l'. Resistance of a conductor is directly proportional to its length.
i.e. R ∝ l
Thus, longer conductors offer more resistance. This is due to the reason that the electrons going from one end to the other suffer more collisions due to the larger length.

(ii) Area of cross-section ‘A’. Resistance of a conductor varies inversely as the area of cross-section of the conductor.
i.e R ∝ \(\frac{1}{A}\)
Therefore, a thin wire offers more resistance as compared to a thick wire of the same length. This is due to the reason that less number of electrons per unit length are available in the case of a thin wire than that in the case of a thick wire.
Combining the above factor, R ∝ \(\frac{l}{A}\)
or R = ρ\(\frac{l}{\mathrm{~A}}\) ........................(1)
where ‘ρ’ is a constant of proportionality. This constant is known as the resistivity or specific resistance.

Question 12.
Define conductance and conductivity.
Or
Define electrical conductivity of a conductor and give its S.I. unit.
Answer:
Conductance. The reciprocal of resistance is called conductance. It is denoted by G. The unit of conductance is ohm-1 or mho or siemen (S).
G = \(\frac{1}{\mathrm{R}}\)
Conductivity. It is a measure of ease with which the current flows through a conductor. R is defined as the reciprocal resistivity. It is denoted by σ.
σ = \(\frac{1}{\rho}\)
The unit of σ is mho m^-1 or Sm^-1.

Question 13.
Discuss the effect of temperature on the resistance of a conductor. Hence define the temperature coefficient of resistance. What is the unit of the temperature coefficient of resistance?
Answer:
For moderate range of temperature θ°C, the resistance R of a conductor is given by R = R₀ (1 + α θ),
where R₀ is the resistance of the conductor at 0° C and α is the temperature coefficient of resistance for the material which depends upon the nature of material. From the above expression, we have
α = \(\frac{\mathrm{R}-\mathrm{R}_0}{\mathrm{R}_0 \theta}\)
Thus, the temperature coefficient of resistance is defined as the change in resistance per unit resistance at 0°C per degree rise of temperature.
SI. unit of α is \(\frac{\text { ohm }}{\text { ohm } \times \text { kelvin }}\) = kelvin^-1 or K^-1
Value of ‘α’ for different materials. For copper, the value of a is 0.004 per °C and for pure platinum, the temperature coefficient is \(\frac{1}{273}\) per °C, the same as that for a perfect gas. Hence, platinum resistance thermometer gives nearly the same temperature as a perfect gas thermometer.

In the case of alloy, the rate at which the resistance changes with temperature is much less e.g. manganin which is an alloy of copper, nickel, iron and manganese has a resistance which is thirty to forty times as that of pure copper for the same dimensions but its temperature coefficient is very small i.e. 0.00001 per degree Celsius. For this reason, it is an excellent substance to be used for the construction of a standard resistance coil. The resistance of Indian rubber, carbon, mica decreases with temperature, then a is negative.

Question 14.
(a) Define electric power, electric energy and give their units.
(b) What is relation between kWh and joule?
Answer:
(a) Electric Power. Let a current ‘I’ be flowing through a conductor having a potential difference ‘V’ across its ends. The work W done in sending the current for time 't' is given by W = VIt
But power P of the circuit is given by,

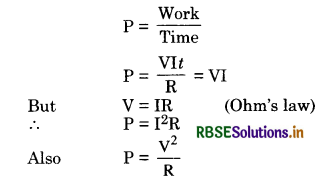
If ‘V' is measured in volt and ‘I’ in ampere, the power will be in ‘watt’.
∴ 1 watt = 1 volt x 1 ampere
Thus, the power of an electric circuit is said to be one watt if a current of one ampere passes through it when a potential difference of one volt is applied to its ends.
A bigger unit of power called ‘kilowatt’ is also commonly used.
1 kilowatt = 1000 watt
Electric energy. Electric energy is the total amount of work done by the current in a given time.
Let a current of 1 ampere passes through a conductor in t seconds when a potential difference of V volt is applied to its ends. Then the energy consumed or the work done can be written as,
W = V It joule
In S.I. units,
1 joule = 1 volt x 1 ampere x 1 second
or 1 joule = 1 watt x 1 second
A bigger unit of electric energy is watt-hour.
Definition of Watt hour. Electric energy of an electric circuit is said to be one watt hour if one ampere current flows under a pot. diff. of 1 volt for 1 hour.

(b) 1 kWh = 1000 x 60 x 60 Ws
= 3.6 x 10⁶
or 1 kWh = 3.6 x 10⁶ J

Question 15.
On what factors does the internal resistance of the cell depend?
Answer:
The internal resistance of a cell depends upon the following factors:

• Distance between the plates.
• Area of the plates immersed in the electrolyte. If area increases, the internal resistance decreases.
• The nature of the electrolyte.
• The nature of the electrodes.
• Temperature of electrolyte.

Question 16.
Using Ohm’s law, calculate the resistance of combination of few resistances joined in series.
Answer:
(a) Resistance in series. Resistances are said to be connected in series if they are joined end to end and the same (i.e. total) current flows through each one of them. Since there is a single path for giving charge, the same current must flow through each resistor. (Fig. SAQ 16)

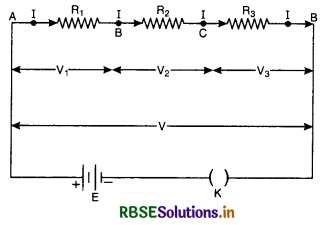
Let R₁, R₂ and R₃ = three resistances connected in series
I = current flowing through R₁, R₂ and R₃
V = potential difference across A and B
V₁, V₂ and V₃ = potential differences across R₁, R₂ and R₃ respectively.
It is clear that
V = V₁ + V₂ + V₃ ...................(1)
According to Ohm’s law,
V₁ = IR₁, V₂ = IR₂ and V₃ = IR₃ ....................(2)
Let R_s be the combined resultant resistance. Obviously, when such a resistance is connected between A and B and a potential difference V is applied across its ends, it allows a current I through it.
∴ V = I R_s ...................(3)
Substituting respective values in (3),
IR_s = IR₁ + IR₂ + IR₃
IR_s = I (R₁ + R₂ + R₃)
or R_s = R₁ + R₂ + R₃ ......................(4)
Hence when a number of resistances are connected in series, the total or resultant resistance is equal to the sum of the individual resistances.
If there are n resistances and each is equal to R and if they are connected in series, then their resultant is given by
R_s = R + R + R + R ........ n times
or R_s = nR ..................(5)
i.e. R_s = number of resistances x value of each resistance
Thus effective resistance increases.

Question 17.
Using Ohm’s law, calculate the resistance of combination of few resistances joined in parallel.
Answer:
Resistance in parallel. Resistances are said to be connected in parallel if one end of each resistance is connected at one point and the other end is connected to another point so that the potential difference across each resistance is the same. However, current passing through each resistance is a part of the total current.

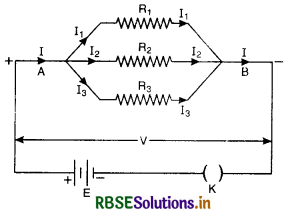
As shown in Fig. SAQ 17 let R₁, R₂ and R₃ be three resistances connected in parallel I₁, I₂ and I₃ be currents flowing through R₁, R₂ and R₃ respectively
I = total current flowing between A and B
V    = potential difference across A and B.
It is clear that
I = I₁ + I₂ + I₃ ...................(1)
Since the potential difference across R₁, R₂ and R₃ is the same i.e. V, according to Ohm’s law,
V    = I₁ R₁, V = I₂ R₂ and V = I₃ R₃
∴ I₁ = \(\frac{\mathrm{V}}{\mathrm{R}_1}\), I₂ = \(\frac{\mathrm{V}}{\mathrm{R}_2}\) and I₃ = \(\frac{\mathrm{V}}{\mathrm{R}_3}\) .......................(2)
Let Rp the be resultant resistance. Obviously, when such a resistance is connected betwen A and B and a potential difference V is applied across its ends, it allows a current I through it.
∴ I = \(\frac{\mathrm{V}}{\mathrm{R}_p}\) ....................(3)
From (1), (2) and (3), we get

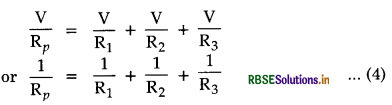
Hence when a number of resistances are connected in parallel, the reciprocal of the resultant resistance is equal to sum of the reciprocals of individual resistances.
If there are n resistances each equal to ‘R’ and if these are in parallel, then resultant is given by:

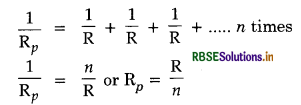
Thus effective resistance decreases.

Question 18.
What do you mean by internal resistance, e.m.f. (electromotive force) and terminal potential difference of a cell?
Answer:
Internal Resistance. The resistance offered by the electrolyte to the flow of electric current through it is called the internal resistance of the cell.
Electromative force. The potential difference between the two poles of a cell in an open circuit (when no current is drawn from the cell), is called the e.m.f. of the cell.
Due to its e.m.f., a cell drives the charge round the circuit. Therefore, e.m.f. of a cell is also defined as the energy supplied by the cell to drive a unit charge round the complete circuit. It is denoted by E.
In S.I., the unit of e.m.f is volt (V) or joule per coulomb (J C^-1).
The e.m.f. of a cell is called one volt, if 1 joule of work is performed by the cell to drive one coulomb of charge round the circuit.
When the current flows through the cell, its electrolyte offers resistance to the flow of current.
Terminal Potential Difference of a Cell
The potential difference between the two poles of a cell in a closed circuit (when current is drawn from the cell) is called the terminal potential difference of the cell. It is denoted by V. When current flows through the circuit, there is fall of potential across the internal resistance of the cell. The potential difference between the two poles of the cell is less than the e.m.f. of the cell by an amount equal to potential drop across the internal resistance. Therefore, the terminal potential difference of a cell is always less than its e.m.f.

Question 19. 
Derive a relation between internal resistance, e.m.f. and terminal potential difference of a cell.
Or
Derive the expression for internal resistance of a cell.
Answer:
Consider the circuit as shown in Fig. SAQ 19. Insert the key K₁ and read the voltmeter. It gives the e.m.f. E of the cell. Now insert some resistance in circuit with the help of the resistance box and also close the key K₂ so that the circuit becomes closed. Again read the voltmeter. It gives the potential difference between the ends of the external resistance and let it be V. The value of V is smaller than E due to the fall of potential inside the cell.

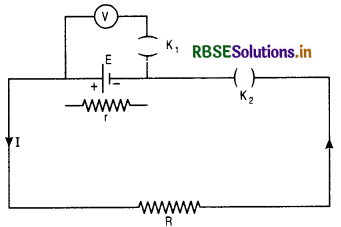
Let r be the internal resistance of the cell and I the current flowing through the circuit when K₂ is closed. Now
I = \(\frac{\mathrm{E}}{\mathrm{R}+r}\)
or E = (R + r) I ................................(1)
Fall of potential in the external circuit is given by
V= IR .........................(2)
Dividing (1) and (2),

Thus knowing the values of E, V and R, the internal resistance r can be determined.

Question 20.
A wire of resistance 1 Ω is stretched to double its length. What is the new resistance?
Answer:
If l is the length and A is area of cross-section of a wire having resistivity ρ, then
Resistance of the wire, R = ρ\(\frac{l}{\mathrm{~A}}\)
when its length is doubled, its area of cross-section reduces to half of its initial area of cross-section.
∴ New Resistance,
R₁ = \(\frac{\rho 2 l}{\mathrm{~A} / 2}\) = 4\(\frac{\rho l}{\mathrm{~A}}\) = 4R
Given R = 1Ω
∴ R₁ = 4 x 1 = 4Ω

Question 21.
When electric field is applied in a conductor, it should cause acceleration, why then do the electrons acquire a steady average drift velocity?
Answer:
When electric field is applied in a conductor it increases the drift velocity of the electrons but on collision of these electrons with the ions of the metal, the electrons lose its drift speed. Again the electric field starts to accelerate and increase its drift velocity and again the electrons suffer collision with the ions of the metal and this process continues and the electrons acquire steady average drift velocity and not the acceleration.

Question 22.
Define resistivity of a material and discuss the factors on which it depends.
Answer:
Resistivity (specific resistance) (ρ). If the material of a conductor is defined as the resistance of unit length and unit area of cross-section of the conductor.
And ρ = \(\frac{m}{n e^2 \tau}\)
Thus resistivity of the material of a conductor depends upon
(i) ρ ∝ \(\frac{1}{n}\) i.e. resisitivity is inversely proportional to the number density of electrons (number of electons per unit volume) inside the conductor.
(ii) ρ ∝ \(\frac{1}{\tau}\) i.e. resistivity is inversely proportional to the average relaxation time of the free electrons in the conductor.
The value of n depends upon the nature of conductor and τ depends upon the temperature of the conductor.

Question 23.
Differentiate ohmic and non- ohmic conductors.
Answer:
Differences between ohmic and non-ohmic 

Ohmic conductors	Non-ohmic conductors
1. They obey Ohm’s law.	1. They do not obey Ohm’s law.
2. The graph between V and I is a straight lipe passing through the origin.	2. Graph between V and I is not a straight line.
3. The value of resistance is constant and is independent of V and I.	3. The value of resistance is not constant and changes when voltage is applied.
4. At constant temperature all metals are ohmic conductors.	4. Vacuum tubes, semiconductors, transistors, electrolytes etc, are non-ohmic conductors.

Question 24.
A given wire having resistance R is stretched so as to reduce its diameter to half of its previous value. What will be its new resistance?
Answer:
If l is the length of a wire and A is its area of cross-section, then resistance of the wire.
R = ρ\(\frac{l}{\mathrm{~A}}\)
When its diameter is reduced to half, its area of cross-section becomes \(\frac{A}{4}\)
i.e. A₁ = \(\frac{A}{4}\)
If l₁ is the new length, then
l₁A₁ = lA
or l₁\(\frac{A}{4}\) = lA
or l₁ = 4l
∴ New resistance,
R₁ = \(\frac{\rho 4 l}{\mathrm{~A} / 4}=16\left(\rho \frac{l}{\mathrm{~A}}\right)\) = 16R
or R₁ = 16R.

Question 25.
Give relation between drift velocity and electric field.
Answer:
The current density (J), electrical conductivity (σ) and electric field (E) are related by a relation.
J = σE

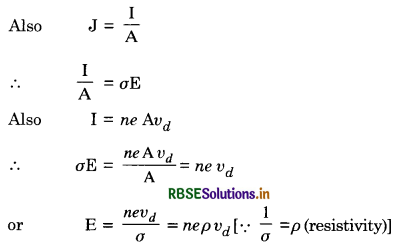
Question 26.
What is cause of heat produced in a conductor when current flows through it?
Answer:
When electrons travel through a conductor, they collide with the positive ions in the crystal lattice. Due to these collisions, energy is transferred from the electrons to the ions. As a result of this, the amplitude of thermal vibrations of the lattice increases and consequently the temperature of the crystal rises.

Question 27.
The filament of a bulb glows when current flows through it but the wires connected to it do not. Explain.
Answer:
According to Joule’s law,
Heat produced, H = \(\frac{\mathrm{I}^2 \mathrm{R} t}{4.2}\) calories
or H ∝ R when I and t are constants.
The resistance of the filament of a bulb is very high. Hence heat produced will be large when a current passes through the filament of a bulb and it glows. On the other hand, the connecting wires are made of copper whose resistance is very small and hence no production of heat occurs when current flows through them.

Question 28.
Two bulbs are 50 W and 30 W and are in series. They are rated 220 volt and 220 volt main put across them. Shall they work correctly?
Answer:
Although the potential difference applied is the same for which they are rated - but since they are placed in series the potential 220 volt gets divided depending on their resistances. So none of the two will work properly.

Question 29.
Two electric bulbs have tungsten filaments of the same length. If one of them is rated 60 watt and the other 100 watt then which one has thicker filament wire?
Answer:
The bulb marked 100 watt has lesser resistance than one marked 60 watt. Since the lengths are the same, the former has thicker wire.

Question 30.
A toaster produces more heat than a light bulb when they are connected in parallel. Which has the greater resistance?
Answer:
The light bulb has large resistance. In the parallel arrangement of toaster and fight bulb since the same potential difference will exist between their terminals, therefore, by Joule’s law,
Heat produced, H = \(\frac{\mathrm{Vl} t}{4.2}\) calories.
or H ∝ I when V and t are constants.
The currents in the toaster and the fight bulb are inversely proportional to their resistances. Hence more current flows through the toaster than the fight bulb, more heat will be produced in the toaster.

Question 31.
A 50 W bulb is connected in (i) series; (ii) parallel with a room heater, is connected across that mains. If 50 W bulb is now replaced by 150 W bulb in each of the two cases, will the heat produced by heater by smaller, remain the same or be larger?
Answer:
(i) In series, the output of heater will increase.
(ii) In parallel, output of heater will remain the same.

Question 32.
Two bulbs are 100 W and 50 W and are in series. Each bulb is rated 200 V and the series combination is put across 220 V mains. Comment upon the result.
Answer:
P.D. of 220 V will be divided across the two bulbs i.e., each will have a P.D. less than 220 V. Hence each will give lesser fight.

Question 33.
What is electric power? Give its unit.
Answer:
Electric power is the rate at which the work is done by the source ofe.m.f. in maintaining the current in electric circuit.
We know W = VIt joule
Power, P = \(\frac{\mathrm{W}}{t}=\frac{\mathrm{VI} t}{t}\) joule/second
or P = VI
Unit of power is watt.
P = 1 watt if V = 1 volt and 1 = 1 ampere.
i.e., Power of an electric circuit is said 1 W if 1A of current flows in it against a P.D. of 1 volt.
Power is also measured in kW (= 1,000 W) and MW (= 106 W)

Question 34.
Define junction and loop. State Kirchhoff's laws.
Answer:
(a) Junction. It is a point where two or more conductors are connected to source and current gets distributed at that point.
Loop. Loop is a closed path of an electric circuit.

(b) Kirchhoff's First Law or Junction Rule It states that the algebraic sum of currents meeting at a point is zero.
This law is also called Kirchhoff’s current law. Kirchhoff's Second Law or Loop Rule It states that in a closed electric circuit, the algebraic sum of e.m.f.’s is equal to the algebraic sum of the products of the resistance and the currents flowing through them.
This law may be called Kirchhoff’s Voltage Law.

Question 35.
What is electric energy? Give its practical unit. How is it related to joule?
Answer:
Electric energy is the total work done or energy supplied by the source e.m.f. in maintaining the current in an electric circuit for a given time. Electric energy = W = Pt = VIt
SI unit of energy is joule
1 joule = 1 volt x ampere x second
= 1 watt x 1 second
Practical or bigger unit is kWh or B.O.T.
I kWh = 1 kW x 1 hour
or 1 kWh = 1,000 W x 1 hour
1 kWh = 1000\(\frac{J}{s}\) x 3600 s
or 1 kWh = 3.6 x 10⁶ J
Electric energy consumed = \(\frac{\text { watt } \times \text { hour }}{1,000}\) kWh or  B.O.T.

Question 36.
Which lamp has greater resistance, a 60 W or 100 W lamp, when connected to the same supply?
Answer:
Since electric power P is given by
P = VI = V.\(\frac{\mathrm{V}}{\mathrm{R}}=\frac{\mathrm{V}^2}{\mathrm{R}}\)
or P ∝ \(\frac{1}{\mathrm{R}}\)
or P ∝ \(\frac{1}{\mathrm{P}}\)
So resistance is inversely proportional to the power of the lamp. Hence 60 W lamp has more resistance than 100 W lamp.

Question 37.
What are the characteristics and functions of fuse wire?
Answer:
A fuse wire should have (i) high resistance and (ii) low melting point so that when such a wire is put in series with electrical installations, under strong current, the wire melts away avoiding damage to the main installations.

Question 38.
A 25 W and a 100 W bulbs are joined in parallel and connected to A.C. mains. Which will glow brighter?
Answer:
We know that P = V²/R or R = V²/P.
\(\frac{R_{25}}{R_{100}}=\frac{P_{100}}{P_{25}}=\frac{100}{25}=4\)
Power dissipated,
\(\frac{\mathrm{P}_{25}^{\prime}}{\mathrm{P}_{100}^{\prime}}=\frac{\mathrm{I}^2 \mathrm{R}_{25}}{\mathrm{I}^2 \mathrm{R}_{100}}=\frac{\mathrm{R}_{25}}{\mathrm{R}_{100}}=4\)
Bulb of 25 W will glow brighter and will consume power 4 times more than 100 W bulb.

Question 39.
A 25 W and a 100 W bulbs are joined in parallel and connected to A.C. mains. Which one will glow brighter and why?
Answer:
\(\frac{\mathrm{R}_{25}}{\mathrm{R}_{100}}=\frac{\mathrm{P}_{100}}{\mathrm{P}_{25}}=\frac{100}{25}=4\)
P.D. across both the bulbs when joined in parallel is equal, ratio of power dissipated is:
\(\frac{\mathrm{P}_{100}^{\prime}}{\mathrm{P}_{25}^{\prime}}=\frac{\mathrm{V}^2 / \mathrm{R}_{100}}{\mathrm{~V}^2 / \mathrm{R}_{25}}=\frac{\mathrm{R}_{25}}{\mathrm{R}_{100}}=4\)
∴ P'₁₀₀ = 4 P'₂₅
Hence 100 W will glow brighter.

Question 40.
Two electric bulbs P and Q have their resistances in the ratio of 1 : 2. They are connected in series across a battery. Find the ratio of the power dissipation in these bulbs.
Answer:
When bulbs are connected in series same current I flows in both the bulbs, so power dissipation
P= I²R
or P ∝ R
∴ \(\frac{\mathrm{P}_1}{\mathrm{P}_2}=\frac{\mathrm{R}_1}{\mathrm{R}_2}=\frac{1}{2}.\)

Question 41.
The diagram shows a piece of pure semiconductor S, in series with a variable resistor R and a source of constant voltage V. Would you increase or decrease the value of R to keep the reading of ammeter (A) constant, when semiconductor S is heated? Give reason.

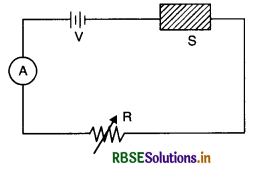
Answer:
The value of R should be increased to keep the reading of ammeter A constant because when semiconductor is heated its resistance is decreased, hence the value of R should be increased to keep the current constant hence the ammeter reading constant.

Question 42.
Is Ohm’s law universally applicable for all conducting elements? If not give examples of elements, which do not obey Ohm’s law.
Answer:
No, the elements which do not obey Ohm’s law are vacuum diode, semiconductor diode, thyrister and disordered conductors etc.

Question 43.
Explain the significance of Kirehhoff's law.
Answer:
Ohm’s law can be used only to analyse simple electrical circuits. When the circuit contains more than one source of e.m.f. and the distribution of current in various branches of the circuit is quite complicated, then one is unable to analyse such a circuit by making use of Ohm’s law. In such a case, Kirchhoff's laws are used to analyse the circuit.

Question 44.
If each of the resistance in the network shown below is R, what is the resistance between terminals A and B?
Answer:
The network is given in Fig. SAQ 44 (a).
Its equivalent circuit is given in Fig. SAQ 44 (b).
It is a balanced Wheatstone bridge in which resistance R between P and Q carries no current. Hence we have effective circuit as shown in Fig. SAQ 44 (c).
Terminals A and B have two resistances of values 2R in parallel.
Hence, total resistance
RT = \(\frac{2 R \times 2 R}{2 R+2 R}\) = R

 
Question 45.
Prove that electric current density of a metallic conductor is directly proportional to the drift speed of electrons.
Answer:
Consider that a wire of length l and area of cross-section A be subjected to an electric field of strength E.
If V = Potential difference applied across the end of the wire,
∴ E = \(\frac{\mathrm{V}}{l}\) or V = El

Let n = number of free electrons per unit volume of the conductor,
vd = Drift velocity of electrons
∴ Charge flowing through the conductor wire,
q = n Ale
Time taken by the electrons to cross the conductor,
t = \(\frac{\text { Distance }}{\text { Velocity }}=\frac{l}{v_d}\)
Current I = \(\frac{\text { Charge }}{\text { Time }}=\frac{n \mathrm{Ale}}{\frac{l}{v_d}}\)
I = n v_d Ae ........................(1)
This is the required relation between current and drift velocity.
Since n, A and e are constants,
∴ I ∝ v_d
Hence, the current flowing through a conductor is directly proportional to the drift velocity. The small value of drift velocity (is 10^-3 ms^-1) produces a large amount of electric current, due to the presence of extremely large number of free electrons in a conductor.
I = nv_d eA 
∴ Current density,
J = \(\frac{\mathrm{I}}{\mathrm{A}}\) = nev_d
or J ∝ v_d.

Question 46.
How does drift velocity of electrons in a metallic conductor vary with the rise of temperature?
Answer:
The drift velocity of free electrons is given by
v_d = \(\frac{e \mathrm{E}}{m} \tau\),
where E is the applied electric field and r is average relaxation time. As the temperature of the conductor is increased, the rate of collision of electrons with the atoms of the conductor also increases and the average relaxation time (τ) decreases. Thus the drift velocity (v_d) also decreases with rise in temperature.

Question 47.
You are given n-resistors each of resistance r. These are first connected to get minimum possible resistance. In second case again connected to the maximum possible resistance. Compare the ratio between the minimum and maximum value of resistance so obtained.
Answer:
To get minimum possible resistance, the n resistors are connected in parallel.
∴ \(\frac{1}{\mathrm{R}_p}=\frac{1}{r}+\frac{1}{r}+\ldots \ldots \ldots n \text { times }=\frac{n}{r}\)
or R_p = \(\frac{r}{n}\) ........................(i)
To get maximum possible resistance, the n resistors are connected in series.
∴ R_s = r + r + .................. n times = nr ..................(ii)
So, \(\frac{\text { minimum resistance }}{\text { maximum resistance }}=\frac{\mathrm{R}_p}{\mathrm{R}_s} = \frac{r}{n} \times \frac{1}{n r}=\frac{1}{n^2}.\)

Question 48.
Define the term current density of a metallic conductor. Deduce the relation connecting current density (J) and conductivity (σ) of the conductor, when electric field, E, is applied to it.
Answer:
Current density (J). The current density in a conductor at a point is defined as the amount of current flowing per unit area of the conductor around the point, provided area is held normal to the direction of current.
If I is the current passing through a conductor having area of cross-section A, then magnitude of current density is given by:
J = \(\frac{\mathrm{I}}{\mathrm{A}}\) .............................(1)
J is a vector quantity having direction in which the positive charge is moving.
Relation between J, σ and E
We know that current density J is given by

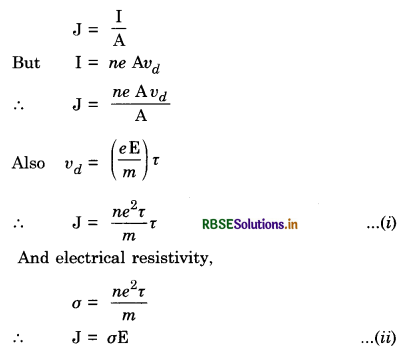
Question 49.
Write the mathematical relation for the resistivity of a material in terms of relaxation time, number density, mass and charge carriers in it. Explain using this relation, why the resistivity of a metal increases and that of semiconductor decreases with rise in temperature.
Answer:
The resistivity of a material is given by

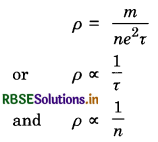
where m is mass, n is number density of electrons, e charge, on charge carriers and τ is relaxation time.
For a metallic conductor. The rate of collision with the atoms of the conductor increases and τ decreases so the resistivity of the material increases with rise in temperature.
For a semiconductor. In a semi-conductor, with the increase in temperature, more covalent bonds break and the charge carriers which are electrons and holes also increases and thus n increases, so resistivity decreases.
 
Question 50.
(a) Define the term ‘conductivity’ of a metallic wire. Write its SI unit.
(b) Using the concept of free electrons in a conductor, derive the expression for the conductivity of a wire in terms of number density and relaxition time. Hence obtain the relation between current density and the applied electric field E.
Answer:
(a) Conductivity of a conductor is reciprocal of resistivity of the conductor.
S.I. unit of conductivity is (S m-1) or siemen per metre.
(b) Relation between J, σ and E
We know that current density J is given by

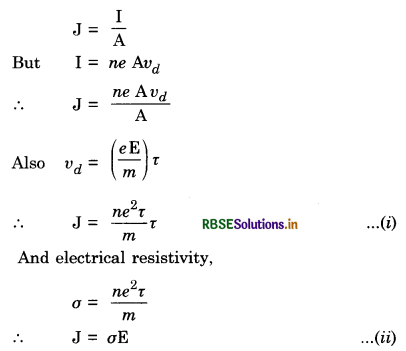
Question 51.
Length of a conductor is increased to three times. What is the effect on (i) drift speed of electrons (ii) resistance and (iii) resistivity if potential across the conductor is kept constant.
Answer:
(i) Drift speed of electrons,
V_d = \(\frac{e \mathrm{E}}{m} \tau=\frac{e \mathrm{~V}}{m l} \tau\)
So when length is increased three times, the drift speed is decreased to \(\frac{1}{3}rd\) of its initial speed.

(ii) Resistance of the conductor,
R = \(\frac{\rho l}{\mathrm{~A}}\)
As the length is increased 3 times, the area of cross-section becomes one-third.
So R' = \(\frac{\rho 3 l}{\mathrm{~A} / 3}=\rho \frac{9 l}{\mathrm{~A}} = 9R\)
So resistance becomes nine times.

(iii) Resistivity is independent of length of the conductor and depends only on the nature of the material, hence remains unchanged.

Question 52.
What is meant by drift velocity of free electrons? Derive Ohm’s law on the basis of theory of electron drift.
Or
Explain how does the resistivity of a conductor depend upon (i) number density ‘n’ of free electrons, and (ii) relaxation time τ.
Or
Define the term resistivity and write its S.I. unit. Derive the expression for the resistivity in terms of number density of free electrons and relaxation time.
Or
Show that the resistance of a conductor is given by:
R = \(\frac{m l}{n e^2 \tau \mathrm{A}}\)
Answer:
Drift Velocity is defined as the velocity of free electrons with which they get drifted towards the positive terminal under the influence of the external field.
Resistivity (specific resistance) (ρ). If the material of a conductor is defined as the resistance of unit length and unit area of cross-section of the conductor.
And ρ = \(\frac{m}{n e^2 \tau}\)
Thus resistivity of the material of a conductor depends upon
(i) ρ ∝ \(\frac{1}{n}\) i.e. resisitivity is inversely proportional to the number density of electrons (number of electons per unit volume) inside the conductor.
(ii) ρ ∝ \(\frac{1}{\tau}\) i.e. resistivity is inversely proportional to the average relaxation time of the free electrons in the conductor.
The value of n depends upon the nature of conductor and τ depends upon the temperature of the conductor.
Ohm’s law from drift velocity of electrons.
Since drift velocity v_d and current I flowing in a conductor are related by the relation:
v_d = \(\frac{\mathrm{I}}{n e \mathrm{~A}} \).........................(1)
Also drift velocity in terms of average relaxation time r is given by

This is Ohm’s law.
But \(\frac{\mathrm{V}}{\mathrm{I}}\) = R, the resistance of the conductor
So Eq. (3) becomes

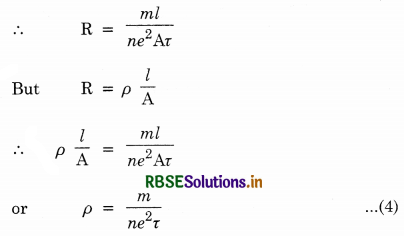
Question 53.
Derive condition of a balanced Wheatstone’s bridge.
Or
Draw the diagram of Wheatstone bridge. Why does no current flow through the galvanometer when the bridge is balanced?
Or
What is Wheatstone bridge? Deduce the condition for which Wheatstone bridge is balanced.
Answer:
Wheatstone Bridge. Wheatstone bridge is an electrical arrangement which forms the basis of the instruments used to determine an unknown resistance.
Principle of Wheatstone bridge. If four resistances P, Q, R and S are arranged as shown in figure LAQ 18, if the galvanometer does not show any defection, then
\(\frac{\mathrm{P}}{\mathrm{Q}}=\frac{\mathrm{R}}{\mathrm{S}}\)
Derivation
Wheatstone bridge consists of four resistances P, Q, R and S arranged as shown in Fig. LAQ 18 with a cell E between the points A and C and a galvanometer G between B and D.
Let I be the total current given out by the cell which on reaching the point A divides itself into two parts : (a) I₁ flowing through P and (b) (I - I₁) through R. The current I₁, on reaching the point B, divides itself into two parts : (a) Ig through the galvanometer G and (b) (I₁ - I_g) through Q. The current Ig through the arm BD and (I - I₁) through AD combine at D to send a current (I - I₁ + I_g) through S. On reaching the point C, the current (I₁ - I_g) through BC and (I - I₁ + I_g) through DC combine to give the total current I, thus completing the circuit. (The values of the currents at a junction can be verified by applying Kirchhoffs first law at the junction).

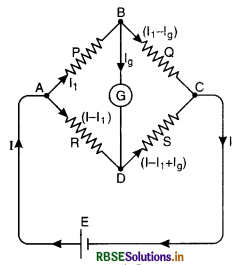
Applying Kirchhoffs second law to the closed mesh ABDA, we get
I₁P + I_gG - (I - I₁) R = 0. ...................(1)
where G is the resistance of the galvanometer.
Again applying Kirchhoffs second law to the closed mesh BCDB we get,
(I - I_g) Q - (I - I₁ + I_g) S - I_gG = 0 ...........................(2)
The value of R is so adjusted that the points B and D are at the same potential and as such no current flows in the arm BD i.e. I_g = 0. This is indicated by zero deflection in the galvanometer G. In this position, the bridge is said to be balanced. Putting I_g = 0 in equations (1) and (2), we get 
I₁P  - (I - I₁) R = 0
or  I₁P = (I - I₁)R .......................(3)
and I₁ Q - (I - I₁) S = 0
i.e. I₁ Q = (I - I₁) S ........................(4) 
Dividing (3) by (4), we get
\(\frac{\mathrm{I}_1 \mathrm{P}}{\mathrm{I}_1 \mathrm{Q}}=\frac{\left(\mathrm{I}-\mathrm{I}_1\right) \mathrm{R}}{\left(\mathrm{I}-\mathrm{I}_1\right) \mathrm{S}}\)
or \(\frac{\mathrm{P}}{\mathrm{Q}}=\frac{\mathrm{R}}{\mathrm{S}}\)

Question 54.
Explain the principle on which the working of a potentiometer is based. Why is the use of potentiometer prferred over that of a voltmeter for measuring the e.m.f. of a cell.
Answer:
Principle. The potentiometer is based upon the principle that when a constant current is passed through a wire of uniform area of cross-section, the potential drop across any portion of wire is directly proportional to the length of that portion.
Let V be potential difference across certain portion of wire whose resistance is R. If I is the current through the wire, then
V = IR
We know that R = ρ\(\frac{l}{\mathrm{~A}}\)
where l, A and ρ are length, area of cross-section and specific resistance of the material of wire respectively.
∴ V = Iρ\(\frac{l}{\mathrm{~A}}\)
If constant current is passed through the wire of uniform area of cross-section, then ρ, I and A are constants and we have
V    = (constant) l
or V ∝ l
Hence, if a constant current flows through a wire of uniform area of cross-section, then potential drop along the wire is directly proportional to the length of the wire.

Or

Why potentiometer is preferred over voltmeter?
Answer:
(a) Drift Velocity: It is the average velocity of the free electrons with which they get drifted towards the positive terminal under the influence of the external field.
Significance: The net current flowing through any cross-section is controlled by drift velocity and there is no transport of charges in a direction perpendicular to the applied field.
Relaxation Time (τ): The average time between successive collisions of electrons or ions in a conductor is called relaxation time.
Significance: It determines the drift velocity acquired by the electrons under the given applied electric force and also determines the electrical conductivity of a conductor at different temperatures.
(b) In first case:
v_d = \(\frac{e \mathrm{~V}}{m \mathrm{~L}} \tau\)
In second case:
v'_d = \(\frac{e \mathrm{~V} \tau}{m 5 \mathrm{~L}}\)
v'_d = \(\frac{1}{5}\left(\frac{e \mathrm{~V}}{m \mathrm{~L}} \tau\right)=\frac{v_d}{5}\)
Thus we find that the drift velocity becomes \(\frac{1}{5}\) of its original value.

Question 55.
Define ‘relaxation time’ in a conductor. Explain how it varies with increase in temperature of a conductor. State the relation between resistivity and relaxation time.
Answer:
Relaxation time (τ). It is the time interval which a free electron, on the average, spends between two successive collisions between electrons and ions in the lattice of a conductor.
Relaxation time,
τ = \(\frac{\text { mean free path }}{\text { r.m.s. velocity of electron }}\)
or τ = \(\frac{\lambda}{v_{\mathrm{rms}}}\)
As the temperature of the conductor is increased, the r.m.s. velocity v_rms is also increased and hence τ is decreased.
Relation between ρ and τ
ρ = \(\frac{m}{n e^2 \tau}\),
where m is the mass of electron, n is number density of electrons and e is the charge on an electron.

Question 56.
Explain how does resistivity of a conductor depend upon (i) number density n of free electron and (ii) relaxation time λ?
Answer:
The resistivity of a conductor ρ is related to relaxation time λ by the following relation
ρ = \(\frac{m}{n e^2 \tau}\)
So ρ ∝ \(\frac{1}{n}\) and ρ ∝ \(\frac{1}{\tau}\).

Question 57.
With the help of a circuit diagram, explain how would you compare the e.m.f. of the primary cells using a potentiometer?
Answer:
(b) (i) Comparison of e.m.f.s of two cells
The circuit diagram for the comparison of e.m.f.s. of two cells is shown in Fig. The auxiliary circuit consists of a battery, an ammeter, rheostat Rh and key K. The positive terminals of two cells E₁ and E₂ whose e.m.f. is to be compared are connected to end A. The negative terminals are connected to two way key. The common terminal of the key is connected to jockey through galvanometer. 

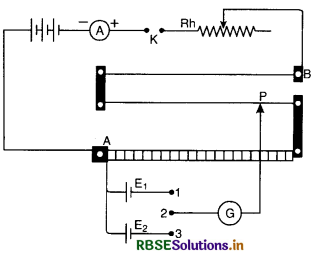
The +ve terminal of auxiliary battery is connected to zero end of the scale. Insert key between 1 and 2 so that cell E₁ is in circuit. Press the jockey and slide it on the wire and find a point P such that galvanometer gives no deflection.
This will happen when potential difference between A and P is equal to e.m.f. of cell. Note length AP = l₁ using principle of potentiometer.
E₁ ∝ l₁ ......................(i)
Remove the plug from 1 and 2, insert it between 2 and 3. Again slide the jockey to get a balance point. If l₂ be the length of wire giving the balance point with the cell of e.m.f. E₂.
∴ E₂ ∝ l₂ ..................(ii)
Dividing (i) by (ii) , we get
\(\frac{E_1}{E_2}=\frac{l_1}{l_2}\)
∴ E₁ and E₂ can be compared
(ii) Determination of internal resistance of a cell.
The internal resistance of a cell is given by
r = \(\mathrm{R} \frac{(\mathrm{E}-\mathrm{V})}{\mathrm{V}}\) ..........................(iii)
when E = e.m.f. of cell
V = Potential difference
R = External resistance of circuit
The values of E and V can be determined with the help of a potentiometer circuit as shown in Fig LAQ 20 (c). When the key K₁ in the auxiliary circuit is closed, a constant current flows through the wire AB of the potentiometer

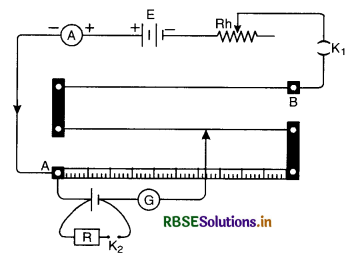
Keep the key K₂ open, the jockey J is slided along the wire to get a balance point. Let l₁ be length of wire giving balance point P.
Using principle of potentiometer
E = kl₁
where k is the fall of potential per unit length of the wire AB. Close the key K₂ and take out some resistance R from the resistance box. The jockey is again slided along the potentiometer wire to get balance point.
Let l₂ be length of wire giving the balance point in this case. The potential difference V across the terminals of the cell is given by,
V = kl₂
Substituting for E and V in equation (i), we get

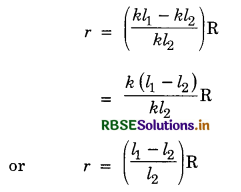
Knowing the values of R, l₁ and l₂ the value of r can be obtained.

Question 58.
Write mathematical relation between mobility and drift velocity of charge carriers in a conductor. Name the mobile charge carriers responsible for conduction of electric current in (i) an electrolyte and (ii) an ionised gas.
Answer:
If E is applied electric field across the two ends to a conductor and v_d is drift velocity of charge carriers in a conductor and µ is mobility, then
v_d = µE
(i) In an electrolyte the charge carriers are positive and negative ions.
(ii) In ionised gas the charge carriers are free electrons and positive ions.

Question 59.
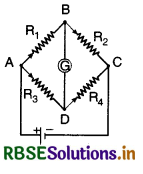
The given figure shows the network of resistances R₁, R₂, R₃ and R₄. Using Kirchhoff s laws, establish the balanced condition for the network.
Answer:
When the bridge is balanced, no current will flow through galvanometer G.
Now using the Kirchhoff's junction law the currents are distributed in the four arms of the Wheatstone bridge as shown in figure. 
Applying Kirchhoff's voltage law
for loop ABDA, i₁P - i₂R = 0 ⇒ \(\frac{i_1}{i_2}=\frac{R}{P}\) ........................(1) 
and  for loop BCDB, i₁Q - i₂S = 0  ⇒ \(\frac{i_1}{i_2}=\frac{S}{Q}\) ..........................(2)
From (1) and (2), \(\frac{P}{R} = \frac{Q}{S}\), this is the balanced condition for the bridge. 

Question 60.
Write the principle of working of a potentiometer. Describe briefly, with the help of a circuit diagram, how a potentiometer is used to determine the internal resistance of a given cell.
Answer:
(a) Potentiometer. An instrument which is used for measuring e.m.f. or potential difference accurately is called potentiometer.

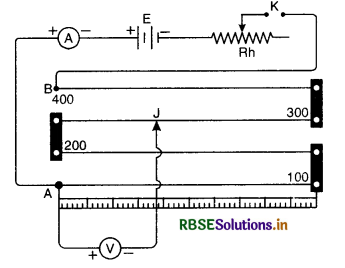
A potentiometer consists of a number of segments of wire of uniform area of cross-section stretched on a wooden board between two thick copperstrips. Each segment of wire is 100 cm long. The wire is usually of constantan or magnanin. A metre rod is fixed parallel to its length [Fig. LAQ 20 (a)] a battery connected across the two end terminals sends a current through the wire which is kept constant by using a rheostat. strips. Each segment of wire is 100 cm long. The wire is usually of constantan or magnanin. A metre rod is fixed parallel to its length [Fig. LAQ 20 (a)] a battery connected across the two end terminals sends a current through the wire which is kept constant by using a rheostat.

Principle. The potentiometer is based upon the principle that when a constant current is passed through a wire of uniform area of cross-section, the potential drop across any portion of wire is directly proportional to the length of that portion.
Let V be potential difference across certain portion of wire whose resistance is R. If I is the current through the wire, then
V = IR
We know that
R = ρ\(\frac{l}{\mathrm{~A}}\)
where l, A and ρ are length, area of cross-section and specific resistance of the material of wire respectively.
∴ V = Iρ\(\frac{l}{\mathrm{~A}}\)
If constant current is passed through the wire of uniform area of cross-section, then ρ, I and A are constants and we have
V = (constant) l
or V ∝ l
Hence, if a constant current flows through a wire of uniform area of cross-section, then potential drop along the wire is directly proportional to the length of the wire.

(b) (i) Comparison of e.m.f.s of two cells
The circuit diagram for the comparison of e.m.f.s. of two cells is shown in Fig. The auxiliary circuit consists of a battery, an ammeter, rheostat Rh and key K. The positive terminals of two cells E₁ and E₂ whose e.m.f. is to be compared are connected to end A. The negative terminals are connected to two way key. The common terminal of the key is connected to jockey through galvanometer. 

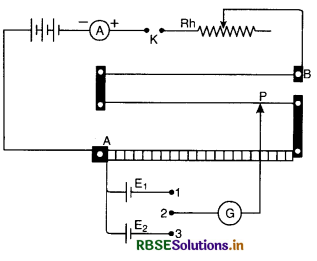
The +ve terminal of auxiliary battery is connected to zero end of the scale. Insert key between 1 and 2 so that cell E₁ is in circuit. Press the jockey and slide it on the wire and find a point P such that galvanometer gives no deflection.
This will happen when potential difference between A and P is equal to e.m.f. of cell. Note length AP = l₁ using principle of potentiometer.
E₁ ∝ l₁ ......................(i)
Remove the plug from 1 and 2, insert it between 2 and 3. Again slide the jockey to get a balance point. If l₂ be the length of wire giving the balance point with the cell of e.m.f. E₂.
∴ E₂ ∝ l₂ ..................(ii)
Dividing (i) by (ii) , we get
\(\frac{E_1}{E_2}=\frac{l_1}{l_2}\)
∴ E₁ and E₂ can be compared
(ii) Determination of internal resistance of a cell.
The internal resistance of a cell is given by
r = \(\mathrm{R} \frac{(\mathrm{E}-\mathrm{V})}{\mathrm{V}}\) ..........................(iii)
when E = e.m.f. of cell
V = Potential difference
R = External resistance of circuit
The values of E and V can be determined with the help of a potentiometer circuit as shown in Fig LAQ 20 (c). When the key K₁ in the auxiliary circuit is closed, a constant current flows through the wire AB of the potentiometer

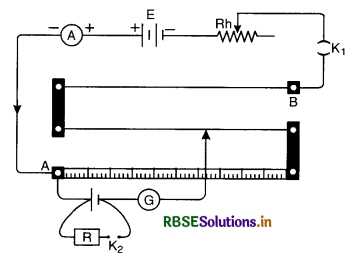
Keep the key K₂ open, the jockey J is slided along the wire to get a balance point. Let l₁ be length of wire giving balance point P.
Using principle of potentiometer
E = kl₁
where k is the fall of potential per unit length of the wire AB. Close the key K₂ and take out some resistance R from the resistance box. The jockey is again slided along the potentiometer wire to get balance point.
Let l₂ be length of wire giving the balance point in this case. The potential difference V across the terminals of the cell is given by,
V = kl₂
Substituting for E and V in equation (i), we get

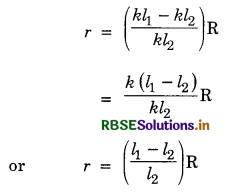
Knowing the values of R, l₁ and l₂ the value of r can be obtained.

Question 61.
What happens to the drift velocity (v_d) of electrons and to the resistance (R), if the length of a conductor is doubled (keeping potential difference unchanged)?
Answer:
Drift velocity of free electron is given by

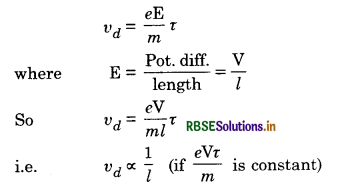
It means if l is doubled (keeping pot. diff. unchanged), the drift velocity will become half of the original value.
We know, resistance R ∝ l (length of the conductor)
Therefore, the resistance of the conductor becomes double of the original value when length of the conductor is doubled.

Question 62.
Define electrical conductivity of a conductor and give its S.I. unit.
Answer:
P.D. of 220 V will be divided across the two bulbs i.e., each will have a P.D. less than 220 V. Hence each will give lesser fight.

Question 63.
The following table gives the length of three copper wires, their diameters, and the applied potential difference across their ends. Arrange the wires in increasing order according to the following:
(а) The magnitude of the electric field within them,
(b) The drift speed of electrons through them, and
(c) The current density within them.

Wire no.	Length	Diameter	Potential Difference
1	L	3d	V
2	2L	d	V
3	3L	2d	2V

Answer:
(a) E₁ = \(\frac{\mathrm{V}}{\mathrm{L}}\), E₂ = \(\frac{\mathrm{V}}{2 \mathrm{~L}}\) = 0.5 E₁, E₃ = \(\frac{2 \mathrm{~V}}{3 \mathrm{~L}}\) = 0.67 E₁
So E₂ < E₃ < E₁
(b) Since v_d = \(\frac{e \mathrm{E} \tau}{m}\)
or v_d ∝ E
∴ (v_d)₂ < (v_d)₃ < (v_d)₁
(c) As I = ne A v_d
∴ J = \(\frac{\mathrm{I}}{\mathrm{A}}\) = ne v_d
∴ J₂ < J₃ < J₁.

Question 64.
A 10 V cell of negligible internal resistance is connected in parallel across a battery of emf 200 V and internal resistance 38 Ω as shown in the figure. Find the value of current in the circuit.

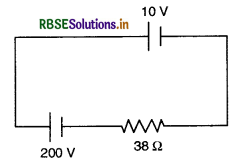
Answer:
The direction of current I in the circuit is as shown below.

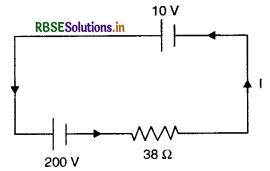
Using kirchhoff s law, we get
-10 + 200 + 38 I = 0
or 38 I = 190
or  I =\( \frac{190}{38}\) = 5 A.

Question 65.
In a potentiometer arrangement for determining the emf of a cell, the balance point of the cell in open circuit is 350 cm. When resistance of 9 Ω is used in the external circuit of the cell, the balance point shifts to 300 cm. Determine the internal resistance of the cell.
Answer:
Given l₁ = 350 cm, l₂ = 300 cm, R = 9 Ω, r = ?

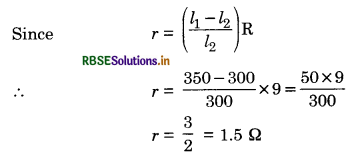
Long Answer Type Questions

Question 1.
(a) Define electric current. What is its S.I. unit? Is it a scalar or a vector quantity? What is the direction of electric current?
(b) How many electrons flowing per second should flow to produce a current of 1A?
Answer:
(a) Electric current. The flow of charge in a definite direction constitutes the electric current and the rate of flow of charge through any cross-section of a conductor is the measure of current i.e.,
= \(\frac{\text { Total charge flowing }(q)}{\text { Time taken }(t)}\)
If dq charge is flowing through a section of a conductor in time dt, the electric current is given by
I = \(\frac{d q}{d t}\) ..........................(1)
Unit of electric current. S.I. unit of current is ampere. It is also called practical unit of current. It is denoted by A,

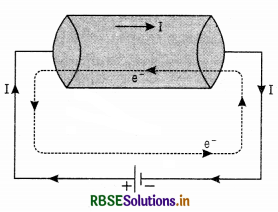
1 ampere (A) = \(\frac{1 \text { Coulomb }}{1 \text { second }}\) = 1 C s^-1
Thus the current through a wire is said to be 1 ampere if one Coulomb of charge is flowing per second through a section of the wire.
Current is a scalar quantity, the direction of flow of positive charges is considered as conventional direction of current.
In solids, positive charges being heavy do not move and current is due to free electrons, therefore, conventional direction of current is opposite to electronic current.

(b) I = \(\frac{q}{t}=\frac{n e}{t}\)
n = \(\frac{\mathrm{I} t}{e}=\frac{1 \times 1}{1.6 \times 10^{-19}}\)
= 6.25 x 10¹⁸ electrons per second.
 
Question 2.
(a) State Ohm's law.
(b) Define resistance. Give its SI unit.
Answer:
(a) Ohm's law. It states that current flowing through a conductor is proportional to the potential difference across its two ends provided the physical conditions (temperature, mechanical strain etc.) of the conductor remain unchanged.
If V is the potential difference between two ends of a conductor and I is the current flowing through it, then
V ∝ I
or V = RI ...................(1)
where R is the constant of proportionality and is called the resistance of the conductor. Its value depends upon
(i) Shape of conductor
(ii) Length of conductor
(iii) Nature of the material

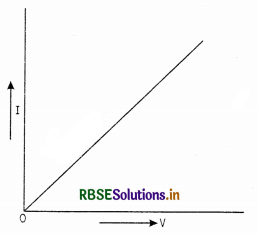
If a graph is plotted between V and I, the graph will be a straight line passing through the origin as shown in Fig.
Note: Conductors obeying Ohm's law are called ohmic conductors and those which do not obey Ohm's law are called non-ohmic conductors.

(b) Resistance. Resistance is the property of a material by virtue of which it opposes the flow of current through it and quantitatively it is given by,
R = \(\frac{\mathrm{V}}{\mathrm{I}}\)
= \(\frac{\text { Potential difference }}{\text { Current }} \)
The S.I. LTnit of resistance is ohm (Ω). It is a practical unit of resistance.
Definition of ohm
If V = 1 volt ; I = 1 ampere
then R = 1 ohm.
Hence a conductor has a resistance of one ohm if a current of one ampere flows through it when a potential difference of one volt is maintained across its two ends.
1 ohm = \(\frac{1 \text { volt }}{1 \text { ampere }}\) or 1Ω
= IV A^-1

Question 3.
What are the factors on which resistance of a conductor depend? Hence define specific resistance (or resistivity).
Answer:
Following are the factors on which the resistance R of a conductor depends:
(i) Length. 'l'. Resistance of a conductor is directly proportional to its length.
i.e. R ∝ l
Thus, longer conductors offer more resistance. This is due to the reason that the electrons going from one end to the other suffer more collisions due to the larger length.
(ii) Area of cross-section ‘A’ Resistance of a conductor varies inversely as the area of cross-section of the conductor.
i.e. R ∝ \(\frac{1}{\mathrm{~A}}\)
Therefore, a thin wire offers more resistance as compared to a thick wire of the same length. This is due to the reason that less number of electrons per unit length are available in the case of a thin wire than that in the case of a thick wire.
Combining the above factor,
R ∝ \(\frac{l}{\mathrm{~A}}\)
or R = ρ\(\frac{l}{\mathrm{~A}} \)..........................(1)
where 'ρ' is a constant of proportionality. This constant is known as the resistivity or specific resistance of the material. Its value depends upon the nature of the material of the conductor.
Definition of Resistivity
If l = 1 and A = 1, then R = ρ, or ρ = R
Therefore, specific resistance of a material is defined as the resistance of wire, made up of that material, having unit length and unit area of cross-section.
Units
Since ρ = \(\frac{\text { R.A }}{l}\)
∴ S I. units of
ρ = \(\frac{\Omega m^2}{m}\) = Ω m (ohm metre)
Resistivity depends on number density of electrons (n) and temperature of the conductor.

Question 4.
Illustrate failures of Ohm's law with examples.
Answer:
Ohm's law is not a fundamental law of nature. It is a common property of certain substances.
In many cases, the relation V ∝ I does not hold good. Following cases may arise that:

(1) V depends upon I (non-linearly).
Illustration. When current flowing through a conductor is increased, heat is produced. Due to increased temperature, the resistance increases. The curve between V and I which is linear for low current becomes non-linear for strong current. This is as shown in Fig. LAQ 4 (a).

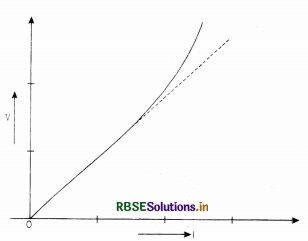
The dashed line represents the linear Ohm's law. The solid line is the voltage V verses current I graph for a good conductor.

(2) The relation between V and I depends on the sign of V for the same absolute value of V.
For a semiconductor diode or pn junction, the variation of current is different, when the sign of potential difference applied across is changed. When positive terminal of a battery is connected to p- section and negative terminal to the n-section (forward bias), the variation of current with potential difference is much more rapid than what it is when applied in opposite manner (reverse bias) as shown in Fig. LAQ 4 (b).

It may be noted that in case of a semiconductor, the variation of current with potential difference is non-linear in addition to the fact that magnitude of variation depends upon the sign of potential difference applied across it.

(3) The relation between V and I is not unique.
This property is illustrated by a device called Thyristor.
The characteristic of variation of voltage with current is as shown in Fig. LAQ 4 (c).

Here V is not proportional to I. In the region AB, current increases with decrease in voltage.

(4) Ohm's law fails in case of certain conductor at 4K or at low temperatures.

Question 5.
How will you establish that electrons carry current?
Answer:
To establish that electrons carry current in a conductor, the \(\left(\frac{e}{m}\right)\) of charge is measured from its angular momentum.
Let r = radius of circular loop
n = no. of electrons per unit length
I = strength of current flowing through the loop
Let v = drift velocity of charge flowing in the conductor
No. of charges flowing per unit length of the loop = (nv)
If e = charge on each charged particle or current carrier
Total charge flowing per sec through any cross-section
= (nv) e
This is called current I = (nv) e
When charged particle goes along a circular loop its angular momentum is given by
L= mvr
Total angular momentum due to all current carriers is
L = (mvr)n = m (nv) r
L = m x \(\frac{\mathrm{I}}{e}\)r
L = I\(\left(\frac{m}{e}\right)\)r
\(\left(\frac{m}{e}\right)\) can be measured by meaning L, I and r.

The angular momentum is measured by relating it to the twist produced in a suspension from which loop is hung. On reversing the direction of current, a twist is produced in suspension due to sudden change in angular momentum.
The value of twist depends upon the angular momentum.
It was found that \(\left(\frac{e}{m}\right)\) determined by this experiment corresponds to electron from other experiment.
It is thus experimentally established that current in metal is carried by negatively charged ions.

Question 6.
Give an elementary description of current flow in a conductor and define drift velocity.
Answer:
Elementary description of current in a conductor. In metallic conductor the electrons in the outermost orbits of the atoms are loosely held by the nucleus and become easily free. These electrons do not remain attached to a particular atom of conductor but wander freely throughout the body of the conductor. The free electrons move about with different speeds in different directions.

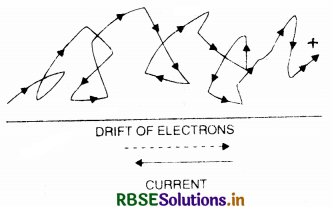
As the electrons are very light, even at normal temperature they have large speeds of the order of 10⁶ ms^-1. They rush around inside the metal, collide with positive metal ions a large number of times per second and change direction at each collision. Thus the atoms move at random in all directions so that there is no net flow of electrons through the wire one way or another.

When the ends of the wire are connected to the two terminals of a cell, an electric field is set up along the length of the wire from the positive to the negative terminal. Under the influence of this field, the electrons flow continuously from the negative terminal through the wire to the positive terminal and then through the battery to the negative terminal. As they move, they suffer frequent collisions, with the copper atoms. During the short time between the collisions, an electron accelerates and gains an extra velocity towards the positive terminal. But this extra velocity is destroyed at each collision. The net result is that the electrons, in addition to their random motion in all directions at huge speeds, acquire a slow drift velocity vd towards the positive terminal, ranging from 0.1 to 1.0 cm s^-1. We may thus imagine an electron moving at random with high velocity and often colliding with copper atoms and suffering change in direction but at the same time drifting slowly towards the positive terminal.

Thus drift velocity is defined as the velocity of the free electron with which they get drifted towards the positive terminal under the influence of the external field.

Question 7.
Establish the relation between current and drift velocity.
Or
Establish the relation between drift velocity of electrons and the electric field applied to the conductor.
Answer:
Consider that a wire of length l and area of cross-section A be subjected to an electric field of strength E.
If V = Potential difference applied across the end of the wire,
∴ E = \(\frac{\mathrm{V}}{l}\) or V = El

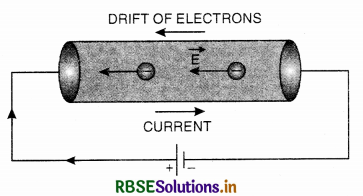
Let n = number of free electrons per unit volume of the conductor,
v_d = Drift velocity of electrons
∴ Charge flowing through the conductor wire,
q = n Ale
Time taken by the electrons to cross the conductor,
t = \(\frac{\text { Distance }}{\text { Velocity }}=\frac{l}{v_d}\)
Current I = \(\frac{\text { Charge }}{\text { Time }}=\frac{n \mathrm{Ale}}{\frac{l}{v_d}}\)
I = n v_d Ae ........................(1)
This is the required relation between current and drift velocity.
Since n, A and e are constants,
∴ I ∝ v_d
Hence, the current flowing through a conductor is directly proportional to the drift velocity. The small value of drift velocity (is 10^-3 ms^-1) produces a large amount of electric current, due to the presence of extremely large number of free electrons in a conductor.

Question 8.
Deduce Ohm’s law from the concept of drift velocity.
Or
Show that the resistance of a conductor is given by
R = \(\frac{m l}{n e^2 \mathrm{~A} \tau}\)
Or
Show that the resistivity of a conductor is given by
ρ = \( \frac{m \mathrm{I}}{n \mathrm{e}^2 \tau}\)
Or
Explain how does the resistivity of a conductor depend upon (t) number density ‘n’ of free electrons, and (ii) relaxation time τ?
Or
Define the term resistivity and write its S.I. unit. Derive the expression for the resistivity in terms of number density of free electrons and relaxation time.
Answer:
Since drift velocity v_d and current I flowing in a conductor are related by the relation:
v_d = \(\frac{\mathrm{I}}{n e \mathrm{~A}}\) .........................(1)
Also drift velocity in terms of average relaxation time r is given by

This is Ohm’s law.
But \(\frac{\mathrm{V}}{\mathrm{I}}\) = R, the resistance of the conductor
So Eq. (3) becomes

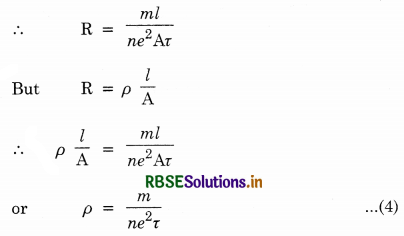
Question 9.
Discuss the effect of temperature on resistivity of metals.
Or
How does the resistivity of (i) a conductor and (ii) a semiconductor vary with temperature? Give reason for each case.
Answer:
Variation of Resistivity with temperature
Resistivity is given by,
ρ = \(\frac{m}{n e^2} \frac{1}{\tau}\)
∴ ρ ∝ \(\frac{1}{\tau} \)
The resistivity varies with relaxation time. The relaxation time changes with collision. It will decrease with increase in amplitude of vibration. Since with the increase in temperature, the amplitude of vibration increases, relaxation time decreases and hence resistivity increases.

(i) In many metals, or conductors at room temperature resistivity increases with increase in temperature. At low temperature, resistivity increases at a higher power of T. This is shown in Fig. LAQ 9 (a). The graph is a straight line over a limited range of temperature. Point corresponds to 273 K is taken as reference point having resistivity ρ0.


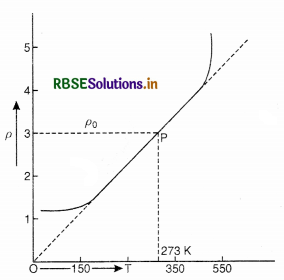
(ii) Alloys in general are poor conductors of electricity. But Nichrome has very high resistivity. This is because in nichrome Ni ions and Cr ions are of different sizes and possess random locations relative to each other, though their crystalline lattice are regular. Therefore, an electron, passes through a very random medium and is very frequently deflected. The variation of resistivity with temperature in case of nichrome is as shown in Fig. LAQ 9 (b)


(iii) In case of insulators, the resistivity increases nearly exponentially with decrease in temperature. The number of electrons in thermodynamic equilibrium at a temperature T is given by
n = n₀ e^-Eg/kT .....................(1)
where k is Boltzmann’s constant, n₀ is of the order of 10²⁸ m^-3 and E_g is called energy gap.
Also ρ = \(\frac{m}{n e^2 \tau} \)...........................(2)
Putting eqn. (1) in (2) we get
∴ ρ = \(\frac{m}{n_0 e^2 \tau e^{-\mathrm{E}_g / k \mathrm{~T}}}\)
or ρ = ρ₀ e^Eg/kT
Where, ρ₀ = \(\frac{m}{n_0 e^2 \tau}\) is a factor which depends weakly on temperature. The value of factor kT is about 0.03 eV at room temperature. The value of E_g can vary from nearly zero to several electron volt. The materials, for which E_g ≤ 1 eV, resistivity at room temperature will not be very high. Such materials are called semiconductors.
The materials, for which E_g > 1 eV, the resistivity at room temperature will be very high and such substances are called insulators.

Question 10.
Discuss the effect of temperature on the resistance of a conductor. Hence define the temperature coefficient of resistance. What is the unit of the temperature coefficient of resistance?
Answer:
For moderate range of temperature θ°C, the resistance R of a conductor is given by R = R₀ (1 + α θ),
where R0 is the resistance of the conductor at 0°C and α is the temperature coefficient of resistance for the material which depends upon the nature of material. From the above expression, we have
α = \(\frac{\mathrm{R}-\mathrm{R}_0}{\mathrm{R}_0 \boldsymbol{\theta}}\)
Thus, the temperature coefficient of resistance is defined as the change in resistance per unit resistance at 0°C per degree rise of temperature.
SI. unit of α is
\(\frac{\text { ohm }}{\text { ohm } \times \text { kelvin }}\) = kelvin^-1 or K^-1
Value of ‘α’ for different materials. For copper, the value of a is 0.004 per °C and for pure platinum, the temperature coefficient is \(\frac{1}{273}\) per °C, the same as that for a perfect gas. Hence, platinum resistance thermometer gives nearly the same temperature as a perfect gas thermometer. In the case of alloy, the rate at which the resistance changes with temperature is much less e.g. manganin which is an alloy of copper, nickel, iron and manganese has a resistance which is thirty to forty times as that of pure copper for the same dimensions but its temperature coefficient is very small i.e. 0.00001 per degree Celsius. For this reason, it is an excellent substance to be used for the construction of a standard resistance coil. The resistance of Indian rubber, carbon, mica decreases with temperature, then α is -ve

Question 11.
What is colour coding of resistor? Explain with examples to find the resistance.
Answer:
A colour code is used to indicate the resistance value and its percentage reliability.

The resistor has a set of concentric rings A, B, C, D (Fig. LAQ 3.11) on it with their significant value as in Table
To read the value of carbon resistance, the following sentence is found to be of great help:
B B ROY Great Britain Very Good Wife
The bold face letters in the above sentence correspond to the colour Black, Brown, Red, Orange, Yellow, Green, Blue, Violet, Grey and White respectively. The colours of first two bands A and B corresponds to figures 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 and the colour of the third band corresponds to multipliers 10⁰, 10¹, 10², 10³, 10⁴, 10⁵, 10⁶, 10⁷, 10⁸ and 10⁹ respectively. If the colour of the fourth band is gold, the tolerance is 5%, in case the colour is silver, the tolerance is 10%. In case, there is no fourth band, then its tolerance is 20%.

Colour	Number	Multiplier		Tolerance
Black	0	1	Gold	5%
Brown	1	101	Silver	10%
Red	2	102	No Colour	20%
Orange	3	I03
Yellow	4	104
Green	5	105
Blue	6	106
Violet	7	107
Grey	8	108
White	9	109

Therefore to assess the value of resistance
1. First two bands from the end indicate the first two significant figures of resistance in ohm.
2. The third band indicates the decimal multiplier.
3. The last band stands for the tolerance in per cent.
Illustration
1. 1st band → Red - 2
2nd band → Red - 2
3rd band → Red - 10²
4th band → Silver → 10%
∴ Value of resistance 22 x 10² Ω ± 10% variation

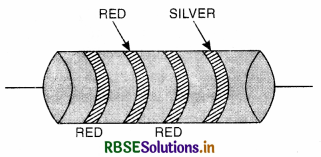
2. 1st band → Yellow → 4
2nd band → Violet → 7
3rd band → Brown → 1
4th band → Gold → 5%
∴ Value of resistance is
47 x 10¹ Ω ± 5% variation
470 Ω ± 5% variation

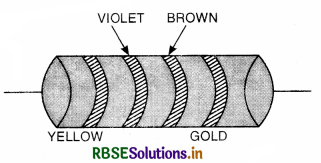
3. If D band is used as third colour, they indicate a multiplier value of 10^-1 for gold and 10^-2 for Ag band as shown is Fig. LAQ 11 (c).

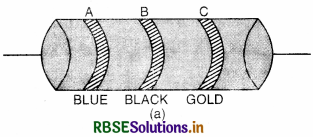
(a) 60 x 10^-1 = 6 Ω
(b) 54 x 10^-2 = 0.54 Ω

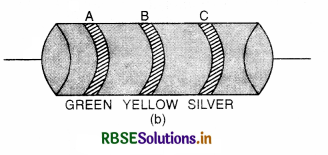
Question 12.
(a) Derive an expression for heat produced in a conductor for the flow of an electric current through it.
(b) What is the cause of heat produced?
Answer:
(a) Consider a conductor of resistance R and let V be the potential difference applied across the ends of AB. If I is the current flowing in the conductor for time t, then the total charge flowing from A to B in time t is:
q = It
Work done in carrying a charge q across P.D. of V is
W = Vq
But q = It
∴ W = VIt
But V = IR
W = (IR) It
W = I2 Rt. .........................(i)
Again I = V/Rt
∴ W = V\(\frac{\mathrm{V}}{\mathrm{R}}t\)
∴ W = \(\frac{\mathrm{V}^2}{\mathrm{R}}t\) .............................(ii)
If entire work is dissipated as heat, then the heat produced is given by
H = W = I² Rt joule
= \(\frac{\mathrm{I}^2 \mathrm{R} t}{4.2}\) calorie.
which is Joule’s law.
The law states that the amount of heat produced in a conductor when a constant current flows through it is.
(i) directly proportional to the square of the current H ∝ I²
(ii) directly proportional to resistance H ∝ R
(iii) directly proportional to time. H ∝ t
(b) Cause of heat produced in a conductor when current flows through it. When the electrons travel through a conductor, they collide with the positive ions in the crystal lattice. Due to these collisions, energy is transferred from the electrons to the ions. As a result of this, the amplitude of thermal vibrations of the lattice increases and consequently the temperature of the crystal rises.

Question 13.
(a) Define electric power, I electric energy and give their units.
(b) What is relation between kWh and joule?
Answer:
(a) Electric Power. Let a current 'I' be flowing through a conductor having a potential difference ‘V’ across its ends. The work W done in sending the current for time ‘t’ is given by
W = VI t
But power P of the circuit is given by,
P = \(\frac{\text { Work }}{\text { Time }}\)
P = \(\frac{\mathrm{VI} t}{t}\) = VI
But V = IR (Ohm's law)
∴ P = I²R
Also P = \(\frac{\mathrm{V}^2}{\mathrm{R}} \)
If ‘V’ is measured in volt and T in ampere, the power will be in ‘watt’.
∴ 1 watt = 1 volt x 1 ampere
Thus, the power of an electric circuit is said to be one watt if a current of one ampere passes through it when a potential difference of one volt is applied to its ends.
A bigger unit of power called ‘kilowatt’ is also commonly used.
1 kilowatt = 1000 watt
Electric Energy. Electric energy is the total amount of work done by the current in a given time. Let a current of 1 ampere passes through a conductor in t seconds when a potential difference of V volt is applied to its ends. Then the energy consumed or the work done can be written as,
W = V It joule
In S.I. units,
1 joule = 1 volt x 1 ampere x 1 second
or 1 joule = 1 watt x 1 second
A bigger unit of electric energy is watt-hour. Definition of Watt hour. Electric energy of an electric circuit is said to be one watt hour if one ampere current flows under a pot. diff. of 1 volt for 1 hour.
1 watt-hour = 1 watt x 1 hour
= 1 volt x 1 ampere x 1 hour
In practice, however, still bigger unit of electric energy called kilowatt hour (kWh) is used.
1 kilowatt-hour = 1000 watt hour
This is also called Board of Trade unit or unit of electricity.
Note. No. of units consumed
= No. of kWh
= \(\frac{\text { watts } \times \text { hours }}{1000}\)
(b) 1 kilowatt-hour
= 1000 x 60 x 60
= 3.6 x 10⁶ joule

Question 14.
Explain how the cells are grouped in series? Obtain the condition for maximum current through an external resistor.
Answer:
Cells in series. The cells are said to be connected in series, if we can proceed from one point to another through one path. Fig. LAQ 14 shows the series combination of n cells. Here n cells, each of e.m.f. E and internal resistance r are connected to an external resistance R.
In series combination, the total e.m.f. of the cells is equal to the sum of the e.m.fs. of the individual cells.
∴ Total e.m.f. of the cells = n E
Since internal resistance of all the cells are also connected in series.
∴ Total internal resistance of the cells = nr

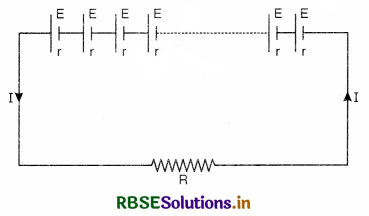
So current flowing through the circuit.
I = \(\frac{n \mathrm{E}}{\mathrm{R}+n r}\)
Case 1. If R << nr, So R + nr ≃ nr
∴ I = \(\frac{n \mathrm{E}}{n r}=\frac{\mathrm{E}}{r}\)
= current due to single cell.
Case 2. If R >> nr, so R + nr ≃ R
∴ I = \(\frac{n \mathrm{E}}{\mathrm{R}}\) = n x current due to single cell.
Thus in series combination of cells, to have maximum current, the total internal resistance of the cells should be negligible as compared to the external resistance of the circuit.

Question 15.
Explain how the cells are grouped in parallel. Obtain the condition for maximum current through an external resistor.
Answer:
Cells in parallel. The cells are said to be connected in parallel, if we can proceed from one point to another through different paths. Fig. LAQ 15 shows 
the parallel combination of m cells. Here m cells, each of e.m.f. E and internal resistance r are connected to an external resistance R.
In parallel combination, the total e.m.f. of the cells is equal to the e.m.f. of a single cell.
∴ Total e.m.f. of the cells = E
Since internal resistances of all the cells are connected in parallel,
∴ Total internal resistance of the cells is given by

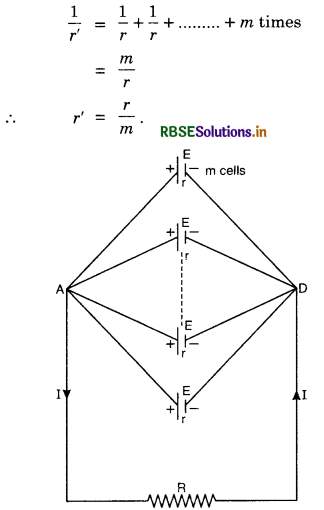
So current flowing through the circuit
I = \(-\frac{\mathrm{E}}{\mathrm{R}+\frac{r}{m}}\)
Case 1. If R >> \(\frac{r}{m}\), then R + \(\frac{r}{m}\) ≃ R
∴ I = \(\frac{E}{R}\) = current due to single cell.
Case 2. If R << \(\frac{r}{m}\), then R + \(\frac{r}{m}\) ≃ \(\frac{r}{m}\)
∴ I = \(\frac{\mathrm{E}}{\frac{r}{m}}=\frac{m \mathrm{E}}{r}\)
or I = m x current due to single cell.
Thus in parallel combination of cells, to have maximum current, the total external resistance of the circuit should be negligible as compared to the total internal resistance of the cells.

Question 16.
Explain how cells are mixed grouped? Obtain the condition for maximum current through an external resistor.
Answer:
Cells in mixed grouping
Fig. LAQ 16 shows n cells in series in one row and m rows of cells in parallel. Let each cell be of e.m.f. E and internal resistance r. This series-parallel combination of the cells are connected to an external resistance R. Here n cells are connected in series in a row.
∴ Total internal resistance of cells in a row = nr
Total e.m.f. of the cells in a row = n E.
Also in rows cells are in parallel, and each row has internal resistance nr,

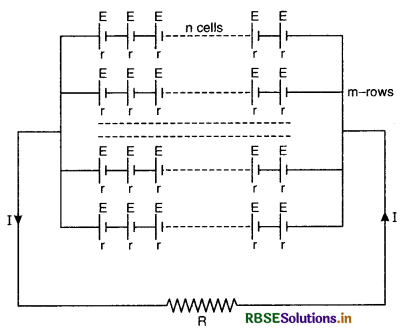
∴ Total internal resistance of all the cells is given by

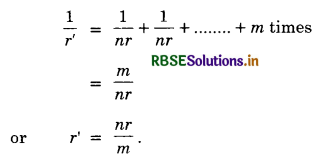
∴ Total resistance of the circuit = R + \(\frac{n r}{m}\)
Hence current flowing through the circuit
I = \(\frac{\mathrm{E} r}{\mathrm{R}+\frac{n r}{m}}=\frac{m n \mathrm{E}}{m \mathrm{R}+n r}\)
Condition for maximum current in the circuit
I will be maximum,
If (mR + nr) = minimum

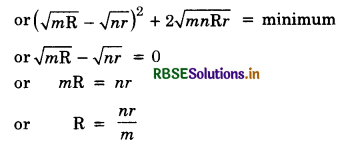
= total internal resistance
Thus in mixed grouping of cells, the current in the circuit will be maximum, if the value of external resistance is equal to the total internal resistance of all the cells.

Question 17.
(a) Define junction and loop.
(b) State and explain Kirchhoff's law.
Answer:
(a) Junction. It is a point where two or more conductors are connected to source and current gets distributed at that point.
Loop. Loop is a closed path of an electric circuit.
(b) Kirchhoff's First Law or Junction Rule
It states that the algebraic sum of currents meeting at a point is zero.
This law is also called Kirchhoffs current law.
To explain this law, consider a number of wires connected at a point P. Current i₁, i₂, i₃, i₄ and i₅ flow through these wires in the directions as shown in Figure LAQ 17.

Sign conventions
(i) The current approaching the point P be taken as positive.
(ii) Current flowing away from it be taken as negative.
According to Kirchhoff's first law
i₁ + i₂ - i₃ - i₄ - i₅ = 0
or Σi = 0 
The most evident conclusion of this law is that the current entering a point must be the same as that leaving it. Hence there cannot be any accumulation of current at any point in a conductor.
Kirchhoff's Second Law or Loop Rule
It states that in a closed electric circuit, the algebraic sum of e.m.f.’s is equal to the algebraic sum of the products of the resistance and the currents flowing through them.
This law may be called Kirchhoff's voltage law.
Sign Conventions
Select any point on the loop and traverse the loop once in any direction clockwise or anticlockwise.
(i) If the direction of flow of current in a resistance is the same as that of traversing the loop, the product of the resistance and the current flowing through it is taken as positive and vice versa.
(ii) While traversing the loop, if -ve pole of a cell is encountred first then its e.m.f. is as +ve, otherwise negative.
The resistance of a conductor has no sign. The sign of the product of the current and resistance will, therefore, be decided by the sign of electric current.

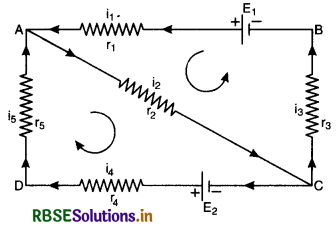
Considering circuit ABCA, we have
E₁ = i₁ r₁ + i₂ r₂ + i₃ r₃
In circuit ABCDA, we have
E₁ - E₂ = i₁ r₁ - i₅ r₅ - i₄ r₄ + i₃ r₃

Question 18.
State and derive the principle of Wheatstone bridge using Kirchhoff's law.
Or
What is Wheatstone bridge? Deduce the condition for which Wheatstone bridge is balanced.
Answer:
Wheatstone Bridge. Wheatstone bridge is an electrical arrangement which forms the basis of the instruments used to determine an unknown resistance.
Principle of Wheatstone bridge. If four resistances P, Q, R and S are arranged as shown in figure LAQ 18, if the galvanometer does not show any defection, then
\(\frac{\mathrm{P}}{\mathrm{Q}}=\frac{\mathrm{R}}{\mathrm{S}}\)
Derivation
Wheatstone bridge consists of four resistances P, Q, R and S arranged as shown in Fig. LAQ 18 with a cell E between the points A and C and a galvanometer G between B and D.
Let I be the total current given out by the cell which on reaching the point A divides itself into two parts : (a) I₁ flowing through P and (b) (I - I₁) through R. The current I₁, on reaching the point B, divides itself into two parts : (a) Ig through the galvanometer G and (b) (I₁ - I_g) through Q. The current Ig through the arm BD and (I - I₁) through AD combine at D to send a current (I - I₁ + I_g) through S. On reaching the point C, the current (I₁ - I_g) through BC and (I - I₁ + I_g) through DC combine to give the total current I, thus completing the circuit. (The values of the currents at a junction can be verified by applying Kirchhoffs first law at the junction).

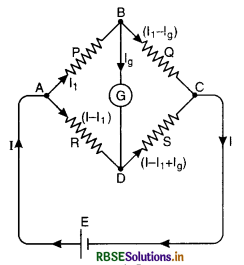
Applying Kirchhoffs second law to the closed mesh ABDA, we get
I₁P + I_gG - (I - I₁) R = 0. ...................(1)
where G is the resistance of the galvanometer.
Again applying Kirchhoffs second law to the closed mesh BCDB we get,
(I - I_g) Q - (I - I₁ + I_g) S - I_gG = 0 ...........................(2)
The value of R is so adjusted that the points B and D are at the same potential and as such no current flows in the arm BD i.e. I_g = 0. This is indicated by zero deflection in the galvanometer G. In this position, the bridge is said to be balanced. Putting I_g = 0 in equations (1) and (2), we get 
I₁P  - (I - I₁) R = 0
or  I₁P = (I - I₁)R .......................(3)
and I₁ Q - (I - I₁) S = 0
i.e. I₁ Q = (I - I₁) S ........................(4) 
Dividing (3) by (4), we get
\(\frac{\mathrm{I}_1 \mathrm{P}}{\mathrm{I}_1 \mathrm{Q}}=\frac{\left(\mathrm{I}-\mathrm{I}_1\right) \mathrm{R}}{\left(\mathrm{I}-\mathrm{I}_1\right) \mathrm{S}}\)
or \(\frac{\mathrm{P}}{\mathrm{Q}}=\frac{\mathrm{R}}{\mathrm{S}}\)

Question 19.
Discuss a practical form of a Wheatstone’s Bridge to find an unknown resistance.
Or
Discuss slide wire bridge method for finding resistances.
Or
Draw a circuit diagram of a meter bridge and write the necessary mathematical relation used to determine the value of unknown resistance. Why cannot such arrangement be used for measuring very low resistances?
Answer:
The practical form of Wheatstone’s bridge is slide wire bridge.
Slide wire bridge. It consists of uniform wire AC, usually one metre long, soldered to the ends of two thick rectangular strips of copper A and C, fixed on a wooden base.

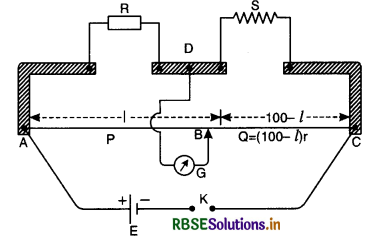
A sliding contact B, called the jockey, can be moved along a graduated scale. By pressing a small key mounted on the jockey, contact can be made at any point along the length of the wire.
If the length of the wire is 1 metre, it is called meter bridge. The unknown resistance is placed across the gap DC and a known resistor R is placed across the gap AD. The two resistances P and Q are obtained from the wire AC by moving the jockey B connceted to the strip D through a galvanometer G.
Working. The key K in the cell circuit is inserted and the jockey is moved along the wire till, for a certain position B, that galvanometer shows no deflection. The bridge is then said to be balanced, if P and Q are the resistances of the parts AB and BC of the wire, we have
\(\frac{\mathrm{P}}{\mathrm{Q}}=\frac{\mathrm{R}}{\mathrm{S}}\)
If the slide wire is of uniform cross-section, the resistance, of AB and BC shall be proportional to their lengths, say l and (100 - l) respectively. If r is the resistance per cm length of the wire, we have
\(\frac{\mathrm{P}}{\mathrm{Q}}=\frac{l r}{(100-l) r}=\frac{l}{100-l}\)
Substituting in the above equation, we have
\(\frac{l}{100-l}=\frac{\mathrm{R}}{\mathrm{S}}\)
or S = \(\frac{100-l}{l}\)R
Knowing l and R; S can be calculated.
This arrangement cannot be used for determining very low resistance because this apparatus is most sensitive only when all the resistances of all arms [P, Q, R and S] are comparable i.e. neither too large, nor too small.
Advantage. It is a null method and therefore it is accurate.

Question 20.
(a) What is potentiometer? What is its principle?
(b) How will you use potentiometer
(i) to compare e.m.f. s of two cells?
(ii) to determine internal resistance of a cell?
Or
State the working principle of a potentiometer. Explain with the help of a circuit diagram how the e.m.f. of two primary cells are compared by using a potentiometer.
Answer:
(a) Potentiometer. An instrument which is used for measuring e.m.f. or potential difference accurately is called potentiometer.

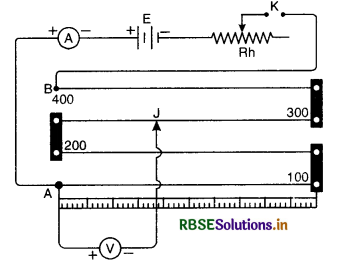
A potentiometer consists of a number of segments of wire of uniform area of cross-section stretched on a wooden board between two thick copperstrips. Each segment of wire is 100 cm long. The wire is usually of constantan or magnanin. A metre rod is fixed parallel to its length [Fig. LAQ 20 (a)] a battery connected across the two end terminals sends a current through the wire which is kept constant by using a rheostat. strips. Each segment of wire is 100 cm long. The wire is usually of constantan or magnanin. A metre rod is fixed parallel to its length [Fig. LAQ 20 (a)] a battery connected across the two end terminals sends a current through the wire which is kept constant by using a rheostat.

Principle. The potentiometer is based upon the principle that when a constant current is passed through a wire of uniform area of cross-section, the potential drop across any portion of wire is directly proportional to the length of that portion.
Let V be potential difference across certain portion of wire whose resistance is R. If I is the current through the wire, then
V = IR
We know that
R = ρ\(\frac{l}{\mathrm{~A}}\)
where l, A and ρ are length, area of cross-section and specific resistance of the material of wire respectively.
∴ V = Iρ\(​​\)
If constant current is passed through the wire of uniform area of cross-section, then ρ, I and A are constants and we have
V = (constant) l
or V ∝ l
Hence, if a constant current flows through a wire of uniform area of cross-section, then potential drop along the wire is directly proportional to the length of the wire.

(b) (i) Comparison of e.m.f.s of two cells
The circuit diagram for the comparison of e.m.f.s. of two cells is shown in Fig. The auxiliary circuit consists of a battery, an ammeter, rheostat Rh and key K. The positive terminals of two cells E₁ and E₂ whose e.m.f. is to be compared are connected to end A. The negative terminals are connected to two way key. The common terminal of the key is connected to jockey through galvanometer. 

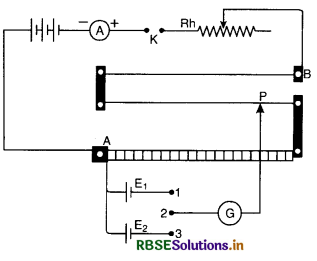
The +ve terminal of auxiliary battery is connected to zero end of the scale. Insert key between 1 and 2 so that cell E₁ is in circuit. Press the jockey and slide it on the wire and find a point P such that galvanometer gives no deflection.
This will happen when potential difference between A and P is equal to e.m.f. of cell. Note length AP = l₁ using principle of potentiometer.
E₁ ∝ l₁ ......................(i)
Remove the plug from 1 and 2, insert it between 2 and 3. Again slide the jockey to get a balance point. If l₂ be the length of wire giving the balance point with the cell of e.m.f. E₂.
∴ E₂ ∝ l₂ ..................(ii)
Dividing (i) by (ii) , we get
\(\frac{E_1}{E_2}=\frac{l_1}{l_2}\)
∴ E₁ and E₂ can be compared
(ii) Determination of internal resistance of a cell.
The internal resistance of a cell is given by
r = \(\mathrm{R} \frac{(\mathrm{E}-\mathrm{V})}{\mathrm{V}}\) ..........................(iii)
when E = e.m.f. of cell
V = Potential difference
R = External resistance of circuit
The values of E and V can be determined with the help of a potentiometer circuit as shown in Fig LAQ 20 (c). When the key K₁ in the auxiliary circuit is closed, a constant current flows through the wire AB of the potentiometer

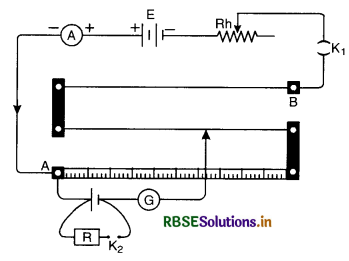
Keep the key K₂ open, the jockey J is slided along the wire to get a balance point. Let l₁ be length of wire giving balance point P.
Using principle of potentiometer
E = kl₁
where k is the fall of potential per unit length of the wire AB. Close the key K₂ and take out some resistance R from the resistance box. The jockey is again slided along the potentiometer wire to get balance point.
Let l₂ be length of wire giving the balance point in this case. The potential difference V across the terminals of the cell is given by,
V = kl₂
Substituting for E and V in equation (i), we get

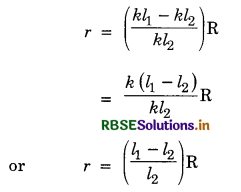
Knowing the values of R, l₁ and l₂ the value of r can be obtained.

Question 21.
(a) Use Kirhhoffs rules to obtain the balance condition in a Wheatstone bridge.
(b) Draw a circuit diagram for determining the unknown resistance R using meter bridge. Explain brefly its working, giving the necessary formula used.
Answer:
Wheatstone Bridge. Wheatstone bridge is an electrical arrangement which forms the basis of the instruments used to determine an unknown resistance.
Principle of Wheatstone bridge. If four resistances P, Q, R and S are arranged as shown in figure LAQ 18, if the galvanometer does not show any defection, then
\(\frac{\mathrm{P}}{\mathrm{Q}}=\frac{\mathrm{R}}{\mathrm{S}}\)
Derivation
Wheatstone bridge consists of four resistances P, Q, R and S arranged as shown in Fig. LAQ 18 with a cell E between the points A and C and a galvanometer G between B and D.
Let I be the total current given out by the cell which on reaching the point A divides itself into two parts : (a) I₁ flowing through P and (b) (I - I₁) through R. The current I₁, on reaching the point B, divides itself into two parts : (a) I_g through the galvanometer G and (b) (I₁ - I_g) through Q. The current I_g through the arm BD and (I - I₁) through AD combine at D to send a current (I - I₁ + I_g) through S. On reaching the point C, the current (I₁ - I_g) through BC and (I - I₁ + I_g) through DC combine to give the total current I, thus completing the circuit. (The values of the currents at a junction can be verified by applying Kirchhoffs first law at the junction).

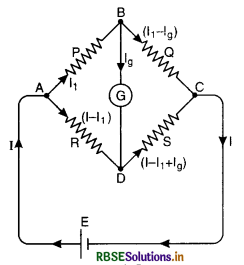
Applying Kirchhoffs second law to the closed mesh ABDA, we get
I₁P + I_gG - (I - I₁) R = 0. ...................(1)
where G is the resistance of the galvanometer.
Again applying Kirchhoffs second law to the closed mesh BCDB we get,
(I - I_g) Q - (I - I₁ + I_g) S - I_gG = 0 ...........................(2)
The value of R is so adjusted that the points B and D are at the same potential and as such no current flows in the arm BD i.e. I_g = 0. This is indicated by zero deflection in the galvanometer G. In this position, the bridge is said to be balanced. Putting I_g = 0 in equations (1) and (2), we get 
I₁P  - (I - I₁) R = 0
or  I₁P = (I - I₁)R .......................(3)
and I₁ Q - (I - I₁) S = 0
i.e. I₁ Q = (I - I₁) S ........................(4) 
Dividing (3) by (4), we get
\(\frac{\mathrm{I}_1 \mathrm{P}}{\mathrm{I}_1 \mathrm{Q}}=\frac{\left(\mathrm{I}-\mathrm{I}_1\right) \mathrm{R}}{\left(\mathrm{I}-\mathrm{I}_1\right) \mathrm{S}}\)
or \(\frac{\mathrm{P}}{\mathrm{Q}}=\frac{\mathrm{R}}{\mathrm{S}}\)

The practical form of Wheatstone’s bridge is slide wire bridge.
Slide wire bridge. It consists of uniform wire AC, usually one metre long, soldered to the ends of two thick rectangular strips of copper A and C, fixed on a wooden base.

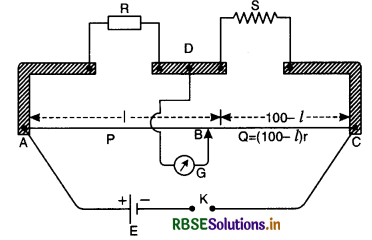
A sliding contact B, called the jockey, can be moved along a graduated scale. By pressing a small key mounted on the jockey, contact can be made at any point along the length of the wire.

If the length of the wire is 1 metre, it is called meter bridge. The unknown resistance is placed across the gap DC and a known resistor R is placed across the gap AD. The two resistances P and Q are obtained from the wire AC by moving the jockey B connceted to the strip D through a galvanometer G.

Working. The key K in the cell circuit is inserted and the jockey is moved along the wire till, for a certain position B, that galvanometer shows no deflection. The bridge is then said to be balanced, if P and Q are the resistances of the parts AB and BC of the wire, we have
\(\frac{\mathrm{P}}{\mathrm{Q}}=\frac{\mathrm{R}}{\mathrm{S}}\)
If the slide wire is of uniform cross-section, the resistance, of AB and BC shall be proportional to their lengths, say l and (100 - l) respectively. If r is the resistance per cm length of the wire, we have
\(\frac{\mathrm{P}}{\mathrm{Q}}=\frac{l r}{(100-l) r}=\frac{l}{100-l}\)
Substituting in the above equation, we have
\(\frac{l}{100-l}=\frac{\mathrm{R}}{\mathrm{S}}\)
or S = \(\frac{100-l}{l}R\)
Knowing l and R; S can be calculated.
This arrangement cannot be used for determining very low resistance because this apparatus is most sensitive only when all the resistances of all arms [P, Q, R and S] are comparable i.e. neither too large, nor too small.
Advantage. It is a null method and therefore it is accurate.

Numerical Problems
Question 1.
A voltage of 30 V is applied across a carbon resistor with first, second and third rings of blue, black and yellow colours respectively. Calculate the value of current in mA, through the resistor.
Answer:
Blue - 6
Black - 0
Yellow - 10⁴
∴ R = 60 x 10⁴ Ω
V = 30 volt
So I = \( \frac{\mathrm{V}}{\mathrm{R}}=\frac{30}{60 \times 10^4}\)
= 0.5 x 10^-4 = 0.05 mA.

Question 2.
Find the value of unknown resistance X in the following circuit, if no current flows through the section AD. Also calculate the current drawn by the circuit from the battery of emf 6 V and negligible internal resistance.

Answer:
Since no current flows through AD. so the given circuit is a balanced Wheatstone bridge.
∴ The condition of balanced Wheatstone bridge is
\(\frac{P}{Q}=\frac{R}{S}\)
or \(\frac{2}{4}=\frac{3}{x}\)
or X = 6 Ω

In the circuit ABDC, the resistances P and Q are in series and R and X are in series and both are in parallel.
So equivalent resistance,

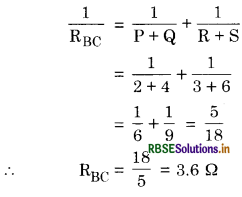
∴ Current drawn by the circuit,
I = \(\frac{\mathrm{E}}{3.6+2.4}=\frac{6}{6}\) = 1 A.

Question 3.
Calculate the current shown by ammeter A in the circuit diagram given below.

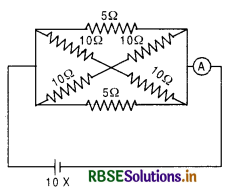
Answer:
The equivalent circuit is shown in the Fig. NP 3 (b). The resistance of branch PQ is
R₁ = \(\frac{10 \times 10}{10+10}+\frac{10 \times 10}{10+10}\)
or R₁ = 5 + 5 = 10 Ω
Now the resistances AB, PQ and CD are in parallel, so their equivalent resistance is

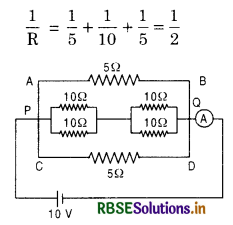
or R = 2
So current, I = \(\frac{\mathrm{E}}{\mathrm{R}}=\frac{10}{2}\) = 5 A.

Question 4.
Find the current drawn from a cell of emf 1 V and internal resistance \(\frac{2}{3}\) Ω connected to the network given adjoint.

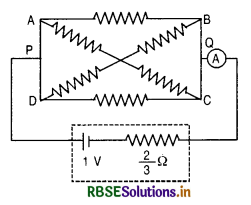
Answer:
The equivalent circuit is shown in the Fig. NP 3 (b). The resistance of branch PQ is
R₁ = \(\frac{10 \times 10}{10+10}+\frac{10 \times 10}{10+10}\)
or R₁ = 5 + 5 = 10 Ω
Now the resistances AB, PQ and CD are in parallel, so their equivalent resistance is

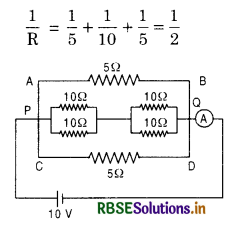
or R = 2
So current, I = \(\frac{\mathrm{E}}{\mathrm{R}}=\frac{10}{2} \)= 5 A.
The value of equivalent resistance is
R = \(\frac{1}{3}\) Ω
∴ I = \(\frac{\mathrm{E}}{\mathrm{R}+r}=\frac{1}{\frac{1}{3}+\frac{2}{3}}\) = 1 A.

Question 5.
How many electrons pass through a wire in 2 minutes, if the current passing through wire is 300 mA?
Answer:
Let n electrons pass through wire in 2 minutes when a current of 300 mA or 0.3 A pass for 2 minutes (120 s).
Charge passing = I dt = 0.3 x 120 = 36 C
Also charge with n electrons
= n x 1.6 x 10^-19 C
∴ n 1.6 x 10^-9 = 36
or n = \(\frac{36}{1.6 \times 10^{-19}}\)
= \(\frac{360}{16}\) x 10¹⁹
or n = 22.5 x 10¹⁹ electrons.

HOTS QUESTIONS 

Question 1.
A steady current flows in a metallic conductor of non-uniform cross-section. Which of the following quantities is constant along the conductor; (a) current, (b) current density, (c) electric field (d) drift speed? Justify:
Answer:
It is already stated that current is constant current density, electric field and drift speed are directly proportional to the area of cross-section.

Question 2.
Two primary cells of e.m.fs. E₁ and E₂ (E₁ > E₂) are connected to the potentiometer wire AB as shown in the figure HQ 2.

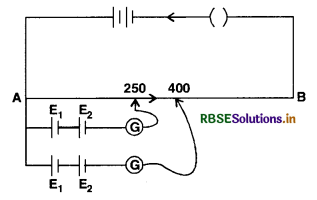
If the balancing lengths for the two combinations of the cells are 250 cm and 400 cm, find the ratio of E₁ and E₂.
Answer:
Given E₁ > E₂
So the balancing condition is
\(\frac{\mathrm{E}_1-\mathrm{E}_2}{\mathrm{E}_1+\mathrm{E}_2}=\frac{250}{400}=\frac{5}{8}\)
or 8E₁ - 8E₂ = 5E₁ + 5E₂
or 3E₁ = 13E₂
or \(\frac{\mathrm{E}_1}{\mathrm{E}_2}=\frac{13}{3}\)

Question 3.
An electric motor runs on a dc source of emf E and internal resistance r. Show that the power output of the source, is maximum when the current drawn by the motor is\( \frac{E}{2 r}\).
Answer:
Input power, P_i = EI
Power consumed by internal resistance, P = I²r
∴ Output power, P₀ = P_i - P = EI - I²r
For output to be maximum \(\frac{d \mathrm{P}_0}{d t}\) = E - 2Ir = 0
or I = \(\frac{\mathrm{E}}{2 r}\)

Question 4.
The following circuit shows the use of potentiometer to measure the internal resistance of a cell.
(i) When the key K is open, how does the balance point change, if the current from the driver cell decreases?
(ii) When the key K is closed, how does the balance point change if R is increased keeping current from the driver cell constant?

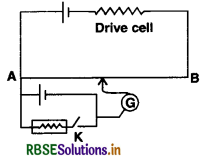
Answer:
(i) When the key K is open and the current from the driver cell decreases, the potential gradient of the potentiometer wire decreases and the balancing length l =\( \frac{\mathrm{E}}{k}\) (k potential gradient) increases and hence the balance point is shifted towards right.

(ii) When the key k is closed and R increases the terminal potential difference across the cell E increases and the balancing length l = \(\frac{\mathrm{V}}{k}\) increases so the balancing point is shifted towards right.
 
Question 5.
The circuit shown in the diagram contains battery B, a rheostat Rh. and identical lamps P and Q. What will happen to the brightness of the lamps, if the resistance through the rheostat is increased? Give reasons.

Answer:
On increasing the resistance through the rheostat, the resistance of the circuit increases and current in the main circuit decreases, hence the potential difference across P decreases and that across Q increases. So the brightness of bulb P decreases and that of Q increases.

Question 6.
In a Wheatstone bridge experiment, a student by mistake, connects key (K) in place of galvanometer and galvanometer (G) in place of key (K). How will be the test for the balance of the bridge?

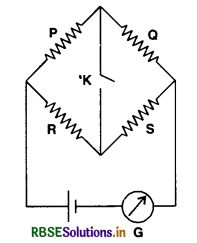
Answer:
In balanced position of the bridge no current will flow in key (K) and hence a constant current will flow in the galvanometer and it will show a constant deflection even when the key K is pressed. 

Question 7.
The voltage current variation of two metallic wires X and Y at constant temperature are a shown in the figure HQ 7. Assuming that the wires have the same length and the same diameter explain which of two wires will have larger resistivity.

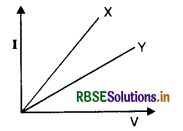
Answer:
In the given diagram we find that the slope of graph of X is more than the slope of graph of Y. It means that conductance of X is more than that or Y. In other words resistane of Y is more than that of X. So for same value of l and diameter (i.e. area of cross-section A), wire Y will have larger resistivity.