RBSE Class 12 Physics Important Questions Chapter 2 स्थिर वैद्युत विभव तथा धारिता

Rajasthan Board RBSE Class 12 Physics Important Questions Chapter 2 स्थिर वैद्युत विभव तथा धारिता Important Questions and Answers.

RBSE Class 12 Physics Chapter 2 Important Questions स्थिर वैद्युत विभव तथा धारिता

अति लघुत्तरीय प्रश्न

प्रश्न 1.
उस भौतिक राशि का नाम लिखिए जिसका मात्रक JC^-1 होता है। यह राशि सदिश है अथवा अदिश?
उत्तर:
JC^-1 विद्युत विभव का मात्रक है। यह सदिश राशि है।

प्रश्न 2.
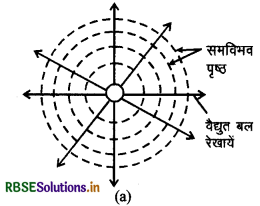
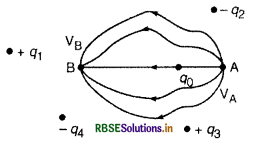
किसी वियुक्त बिन्दु आवेश (-q) के कारण समविभव पृष्ठ खींचिए तथा इसकी विद्युत क्षेत्र रेखाएँ चित्रित कीजिए।
उत्तर:

प्रश्न 3.
किसी एक समान विद्युत क्षेत्र में दो बिन्दुओं के बीच किसी आवेशित कण को गति कराने में किया गया कार्य कण के गमन पथ पर निर्भर नहीं करता। क्यों?
उत्तर:
क्योंकि विद्युत बल एक संरक्षी बल है। 

प्रश्न 4.
किसी वैद्युत द्विधुव का समविभव पृष्ठ खींचिए।
उत्तर:

प्रश्न 5.
किसी आवेशित चालक खोल के भीतर इसके समस्त आयतन में स्थिर वैद्युत विभव नियत क्यों रहता है?
उत्तर:
आवेशित चालक खोल के भीतर विद्युत क्षेत्र \(\overrightarrow{\mathrm{E}}\) शून्य होता है अत: dv = E.dr = 0 होगा। अतः समस्त आयतन में स्थिर विद्युत विभव नियत रहता है।

प्रश्न 6.
किसी आवेश 'q' का द्विध्रुव आघूर्ण 'p' के किसी द्विषुव के ऊपर स्थिर किसी बिन्दु A से द्विध्रुव के नीचे स्थित किसी बिन्दु B पर विषुवतीय तल में बिना किसी त्वरण के ले जाया जाता है। इस प्रक्रिया में किया गया कार्य ज्ञात कीजिए।

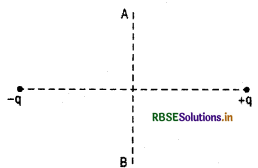
उत्तर:
विद्युत द्विध्रुव की निरक्षीय स्थिति में किसी बिन्दु पर विभव V = 0
अत: A से B तक आवेश q को लाने में किया गयश कार्य शून्य होगा।
W = v_q = 0

प्रश्न 7.
संधारित्र का मूल उपयोग क्या है?
उत्तर:
विद्युत आवेश तथा विद्युत ऊर्जा की बड़ी मात्रा को संचित करने के लिए।

प्रश्न 8.
विद्युत बल रेखा के अनुदिश विद्युत विभव बढ़ता है अथवा घटता है?
उत्तर:
विद्युत बल रेखाएँ उच्च विभव से निम्न विभव की ओर चलती है, अत: बल रेखा के अनुदिश विद्युत विभव घटता है।

प्रश्न 9.
समविभव पृष्ठ को परिभाषित कीजिए।
उत्तर:
किसी वैद्युत क्षेत्र में खींचा गया वह पृष्ठ जिस पर स्थित सभी बिन्दुओं पर वैद्युत विभव बराबर हों, समविभव पृष्ठ कहलाता है। दूसरे शब्दों में, समविभव पृष्ठ पर किन्हीं दो बिन्दुओं के बीच वैद्युत विभवान्तर शून्य होता है। अत: किसी आवेश को समविभव पृष्ठ के एक बिन्दु से दूसरे बिन्दु तक ले जाने में कोई कार्य नहीं करना पड़ेगा। परन्तु यह तभी सम्भव है जबकि वैद्युत आवेश को वैद्युत क्षेत्र के लम्बवत् ले जाया जाये।

प्रश्न 10.
क्या दो समविभव पृष्ठ एक - दूसरे को काट सकते हैं?
उत्तर:
नहीं, क्योंकि यदि ऐसा होगा तो कयान बिन्दु पर विद्युत विभव के दो मान होंगे जो सम्भव नहीं है।

प्रश्न 11.
क्या किसी बिन्दु पर विद्युत क्षेत्र शून्य हो सकता है जबकि उस बिन्दु पर विभव शून्य न हो। उदाहरण दीजिए।
उत्तर:
हां सम्भव है। आवेशित गोलीय कोश व आवेशित चालक के अन्दर विद्युत क्षेत्र शून्य होता है परन्तु विद्युत विभव नहीं।

प्रश्न 12.
जब कोई विद्युत द्विधुव किसी विद्युत क्षेत्र के समान्तर रखा जाता है तो इसकी विद्युत स्थितिज ऊर्जा क्या होगी?
उत्तर:
U = - PE sinθ
∴ θ = 0°, cosθ = 1
∴ U = -pE

प्रश्न 13.
क्या निर्वात में किसी बिन्दु पर विद्युत विभव शून्य हो सकता है जबकि उस बिन्दु पर विद्युत क्षेत्र शून्य नहीं है? उदाहरण दीजिए।
उत्तर:
हाँ सम्भव है। विद्युत द्विध्रुव को मिलाने वाली रेखा के मध्य बिन्दु से गुजरने वाली निरक्ष रेखा पर।

प्रश्न 14.
समविभव पृष्ठ विद्युत बल रेखाओं के लम्बवत् होते हैं, क्यों?
उत्तर:
समविभव पृष्ठ पर एक बिन्दु से दूसरे बिन्दु तक किसी आवेश को ले जाने में कोई नहीं करना पड़ता है, अतः समविभव पृष्ठ के अनुदिश विद्युत क्षेत्र की तीव्रता का घटक शून्य होना चाहिए, यह तभी संभव है जब विद्युत क्षेत्र पृष्ठ के लम्बवत हो।

प्रश्न 15.
किसी चालक की धारिता का मान किन कारकों पर निर्भर करता है?
उत्तर:
किसी चालक की धारिता का मान चालक के अनुप्रस्थ काट के क्षेत्रफल तथा उसके चारों ओर के माध्यम पर निर्भर करता है।

प्रश्न 16.
माध्यम के परावैद्युतांक की परिभाषा लिखिए।
उत्तर:
किसी संधारित्र की प्लेटों के मध्य भरे पदार्थ का परावैद्युतांक उस संधारित्र की धारिता तथा समान वायु संधारित्र की धारिता के अनुपात के बराबर होता है।

लघु उत्तरीय प्रश्न

प्रश्न 1.
सिद्ध कीजिये कि किसी बिन्दु आवेश के चारों ओर परावैद्युत माध्यम होने पर उसके कारण विद्युत विभव निर्वात की तुलना में 1/ε_r गुना कम होता है।
उत्तर:
यदि बिन्दु आवेश निर्वात में स्थित है तो +q आवेश r दूरी पर विद्युत विभव
V = \(\frac{1}{4 \pi \varepsilon_0} \frac{q}{r}\)
यदि बिन्दु आवेश के चारों और ε_r परावैद्युतांक का परावैद्युत माध्यम है तो P पर विद्युत विभव
V = \(\frac{1}{4 \pi \varepsilon_0 \varepsilon_r} \frac{q}{r}\)
V' = \(\frac{1}{\varepsilon_r}\left[\frac{1}{4 \pi \varepsilon_0}-\frac{q}{r}\right]\)
V' = \(\frac{\mathrm{V}}{\varepsilon_r}\)

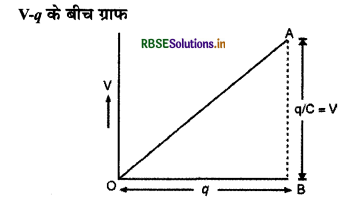
प्रश्न 2.
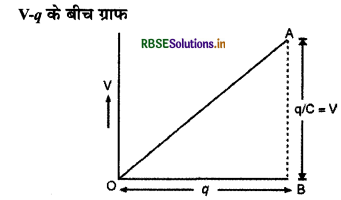
C धारिता के संधारित्र पर मौजूद आवेश एवं विभवान्तर के मध्य ग्राफ खींचिए।
उत्तर:
संधारित्र पर संचित आवेश उसकी प्लेटों के विभवान्तर के अनुक्रमानुपाती होता है अर्थात् q ∝ V
अतः q व V के मध्य खींचा गया ग्राफ सरल रेखा प्राप्त होगी

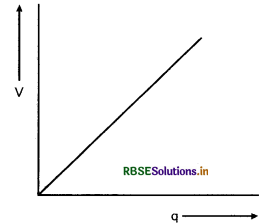
प्रश्न 3.
दो बिन्दु आवेश q₁ और q₂ वायु में r₁₂ दूरी पर स्थित हैं। इस निकाय की स्थिर विद्युत स्थितिज ऊर्जा के लिए व्यंजक स्थापित कीजिए।
उत्तर:
आवेश समूह की वैद्युत स्थितिज ऊर्जा (Electric Potential Energy of a System of Charges):
किन्हीं दो अथवा दो से अधिक आवेशों को अनन्त से एक - दूसरे के समीप लाकर निकाय की रचना करने में किया गया कार्य उन आवेशों से बने निकाय (system) में स्थितिज ऊर्जा के रूप में एकत्र हो जाता है। इस संचित (stored) ऊर्जा को ही निकाय की वैधुत स्थितिज ऊर्जा कहते हैं। इसे U से व्यक्त करते हैं।
अत: "दो या दो से अधिक बिन्दु आवेशों के किसी निकाय की वैद्युत स्थितिज ऊर्जा उस कार्य के बराबर होती है जो उन आवेशों को अनन्त से परस्पर निकट लाकर निकाय की रचना करने में किया जाता
है।"
(a) दो आवेशों के निकाय की वैधुत स्थितिज ऊर्जा: माना दो आवेशों के निकाय में q₁ व q₂ आवेश r दूरी पर क्रमश: A व B पर स्थित हैं।
+q₁ के कारण बिन्दु B पर उत्पन्न विभव

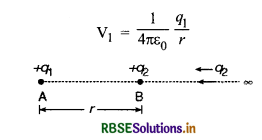
चूँकि किसी बिन्दु पर विद्युत् विभव उस कार्य के बराबर होता है जो एकांक धनावेश को अनन्त से उस बिन्दु तक लाने में करना पड़ता हैं।
अत: +q₂ आवेश को अनन्त से B बिन्दु तक लाने में किया गया कार्य अर्थात् दोनों आवेशों के निकाय की वैद्युत स्थितिज ऊर्जा
U = W = V₁q₂
= \(\frac{1}{4 \pi \varepsilon_0} \frac{q_1}{r} \times\) q₂
या U = \(\frac{1}{4 \pi \varepsilon_0} \frac{q_1 q_2}{r}\) .............(1)
यदि दोनों आवेश समान प्रकृति (equal nature) के हैं, तो U का मान धनात्मक होगा और यदि एक आवेश धनात्मक एवं दूसरा ऋणात्मक है, तो U का मान ऋणात्मक होगा, अतः U का मान निकालते समय आवेशों के मान चिह्न सहित (proper sign) रखने चाहिए।

(b) दो से अधिक आवेशों के निकाय की वैद्युत स्थितिज ऊर्जा: n आवेशों के निकाय को वैद्युत स्थितिज ऊर्जा उस कार्य के बराबर होती है जो निकाय के सभी आवेशों को अनन्त से उनकी स्थिति तक लाने में करना पड़ता है। पहले आवेश q₁ को अनन्त से उसकी स्थिति P₁\(\left(\overrightarrow{r_1}\right)\) तक लाने में कोई कार्य नहीं करना पड़ेगा क्योंकि शेष सभी आवेश अनन्त पर होंगे, अत: पहले आवेश के आने का विरोध नहीं होगा।
∴ W₁ = 0
जब दूसरा आवेश q₂ उसकी स्थिति P₂\( \left(\overrightarrow{r_2}\right)\) तक लाते हैं, तो पहला आवेश q₁ उसके आने का विरोध करेगा। अतः q₂ को लाने में कृत कार्य
W₂ = (q₂ के कारण P₂ स्थिति में विभव) x q₂
= \(\frac{1}{4 \pi \varepsilon_0} \frac{q_1}{r_{12}} \cdot q_2 = \frac{1}{4 \pi \varepsilon_0} \frac{q_1 q_2}{r_{12}}\)
जब तीसरा आवेश q₃ अनन्त से P₃\(\overrightarrow{\left(r_3\right)}\) तक लाते हैं, तो कृत कार्य
W₃ = (q₁ व q₂ के कारण P₃ पर विभव) x q₃
= \(\left[\frac{1}{4 \pi \varepsilon_0} \frac{q_1}{r_{13}}+\frac{1}{4 \pi \varepsilon_0} \frac{q_2}{r_{23}}\right] \times q_3\)
= \(\frac{1}{4 \pi \varepsilon_0}\left[\frac{q_1 q_3}{r_{13}}+\frac{q_2 q_3}{r_{23}}\right]\)
इसी प्रकार चौथे आवेश q₄ को P₄\(\left(\overrightarrow{r_4}\right)\) स्थिति तक लाने में कृत कार्य
W₄ = \(\frac{1}{4 \pi \varepsilon_0}\left[\frac{q_1 q_4}{r_{14}}+\frac{q_2 q_4}{r_{24}}+\frac{q_3 q_4}{r_{34}}\right]\)
∴ चारों आवेशों के निकाय की वैद्युत स्थितिज ऊर्जा
U = W₁ + W₂ + W₃ + W₄

इसी प्रकार अन्य आवेशों को लाने में कृत कार्य ज्ञात करके उन्हें जोड़ने पर,

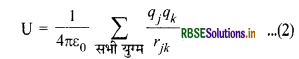
इस योग को ज्ञात करने में हमें आवेशों के प्रत्येक युग्म का एक बार ही प्रयोग करना पड़ता है अत: अत समीकरण को निम्न प्रकार लिख सकते हैं-
U =\( \frac{1}{2} \sum_{\substack{j=1 \\ j=1 \\ j \neq k}}^n \sum_{\substack{n=1}}^n \frac{1}{4 \pi \varepsilon_0} \cdot \frac{q_j}{q_{k k}} \)..........(3)
यहाँ \frac{1}{2} का गुणा इसलिए करना पड़ रहा है क्योंकि इस योग में आवेशों के प्रत्येक युग्म को दो बार लेते हैं। उदाहरण के लिए जब j = 1, k = 2 और j = 2, k = 1, लेने पर आवेशों का एक ही युग्म दो आर (q₁q₂ और q₂q₁) आता है। हमें एक युग्म केवल एक ही बार प्रयोग करना है, अतः \(\frac{1}{2}\) का प्रयोग अत्यन्त आवश्यक है।

प्रश्न 4.
समविभव पृष्ठों के दो महत्त्वपूर्ण लक्षण लिखिए। 
उत्तर:
समविभव पृष्ठ (Equi - potential Surface):
"ऐसा पृष्ठ जिसके प्रत्येक बिन्दु पर विद्युत् विभव समान होता है, समविभव पृष्ठ कहलाता है।"
समविभव पृष्ठ की विशेषताएँ: विभवान्तर की परिभाषा के अनुसार किन्हीं दो बिन्दुओं के मध्य विभवान्तर उस कार्य के बराबर होता है जो एकांक धनावेश को निम्न विभव के बिन्दु से उच्च विभव के बिन्दु तक ले जाने में करना पड़ता है अर्थात् A व B बिन्दुओं के मध्य विभवान्तर
V_B - V_A = W_AB 
यदि A व B दोनों बिन्दु एक समविभव पृष्ठ पर स्थित हैं,
तो V_B = V_A
∴ W_AB  = V_B - V_A = 0 
अर्थात् "समविभव पृष्ठ पर किन्हीं दो बिन्दुओं के मध्य परीक्षण आवेश को एक बिन्दु से दूसरे बिन्दु तक ले जाने में कोई कार्य नहीं किया जाता है।" समविभव पृष्ठ के किन्हीं भी दो बिन्दुओं के बीच कोई विभवान्तर नहीं होता।
एकांक धनावेश को किसी समविभव पृष्ठ पर एक सूक्ष्म विस्थापन dl देने में किया गया कार्य
dw = \(\overrightarrow{\mathrm{E}} \cdot d \vec{l}\) = E dl cosθ = 0 
∴ cos θ = 0 ⇒ θ = 90° अर्थात् \(\overrightarrow{\mathrm{E}} \perp d \vec{l}\)
स्पष्ट है कि विद्युत् क्षेत्र सदैव समविभव पृष्ठ के लम्बवत् होता है। एक बिन्दु आवेश के कारण इससे r दूरी पर उत्पन्न विभव
V = \(\frac{1}{4 \pi \varepsilon_0} \frac{q}{r}\) ...............(1)
स्पष्ट है कि यदि का मान नियत हो जाये, तो एका मान भी नियत (constant) हो जायेगा।

प्रश्न 5.
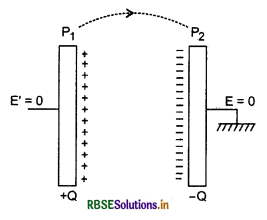
संक्षेप में व्याख्या कीजिए कि जब समान्तर पट्टिका संधारित्र को किसी dc स्रोत से संयोजित किया जाता है, तो वह संघारित्र किस प्रकार आवेशित हो जाता है?
उत्तर:
जब समान्तर पट्टिका संधारित्र की प्लेट P, को किसी dc स्रोत से Q आवेश प्रदान किया जाता है। प्लेट P₂ का बाध्य पृष्ठ भूसम्पर्कित होने के कारण इस पर स्थित मुक्त आवेश पृथ्वी में चला जाता है।
परन्तु अन्तः पृष्ठ पर विपरीत प्रकृति का - Q आवेश प्लेट P₁ पर +Q आवेश से बध्द होने के कारण वहीं बना रहता है। इस प्रकार इन प्लेटों पर समान परन्तु विपरीत प्रकृति के आवेश होते हैं। यदि प्लेटों के मध्य दूरी अल्प है तो इस प्रभाग में एक समान विद्युत क्षेत्र उत्पन्न हो जाता है।

प्रश्न 6.
धारिता C के किसी समान्तर पट्टिका संधारित्र को किसी बैटरी द्वारा 'V' वोल्ट तक आवेशित किया गया है। कुछ समय पश्चात् बैटरी को हटा लिया जाता है और पट्टिकाओं के बीच की दूरी दोगुनी कर दी जाती है। जब इस पट्टिकाओं के बीच के रिक्त स्थान में परावैद्युतांक 1 < K < 2 को कोई गुटका रख दिया जाता है। इसका निम्नलिखित पर क्या प्रभाव होगा?
(i) संधारित्र की पट्टिकराओं के बीच विद्युत - क्षेत्र 
(ii) संधारित्र में संचित ऊर्जा।
उत्तर:
(i) संधारित्र की पट्टिकाओं के बीच विद्युत क्षेत्र \(\frac{E_0}{\mathrm{~K}}\) हो जाएगा। अर्थात् विद्युत क्षेत्र का मान घट जाएगा।
(ii) संधारित्र की नई धारिता C = \(\frac{\varepsilon_0 \varepsilon_r A}{2 \mathrm{~d}}\)
ε_r का मान 2 से कम हैं अतः धारिता C घट जाएगी जबकि विभवान्तर V नियत है तब संचित ऊर्जा का मान कम हो जाता है।

प्रश्न 7.
जब किसी परावैद्युत प्लेट को बाहरी विद्युत क्षेत्र में रखते हैं तो परावैधुत प्लेट के अन्दर विद्युत क्षेत्र कम क्यों हो जाता है?
उत्तर:
परावैधुत गुटके को बाहरी विद्युत क्षेत्र में रखने पर इसके अणुओं का ध्रुवण हो जाता है, फलस्वरूप इसके अन्दर बाहरी क्षेत्र की विपरीत दिशा में एक विद्युत क्षेत्र प्रेरित हो जाता है। इसीलिए बाहरी क्षेत्र में रखने पर परावैद्युत प्लेट के अन्दर विद्युत क्षेत्र घट जाता है।

प्रश्न 8.
a त्रिज्या के किसी गोलीय कोश को Q आवेश दिया जाता है और इसकी त्रिज्या b तक बढ़ा दी जाती है। इस प्रक्रिया में कृत कार्य का मान ज्ञात कीजिए।
उत्तर:
C = 4πε₀ R और U = \(\frac{1}{2} \frac{\mathrm{Q}^2}{\mathrm{C}}\)
∴ कोश की त्रिज्या बढ़ाने में कृत कार्य
W = U₁ - U₂ = \(\frac{\mathrm{Q}^2}{4 \pi \varepsilon_0 \alpha}-\frac{1}{2} \frac{\mathrm{Q}^2}{4 \pi \varepsilon_0 b}\)
W = \(\frac{\mathrm{Q}^2}{8 \pi \varepsilon_0}\left[\frac{1}{a}-\frac{1}{b}\right]\)

प्रश्न 9.
एक विद्युत क्षेत्र के लिए समविभव पृष्ठ चित्र में दर्शाए गए हैं। यह दिया गया है कि V₁ > V₂। इस पैटर्न के लिए संगत बल रेखाएँ खींचिए। यह भी बताइए कि किस क्षेत्र में विद्युत क्षेत्र तीव्रता उच्च है।

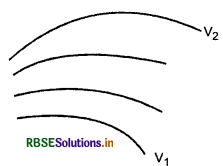
उत्तर:
नीचे दिये गये चित्र में बल रेखाएँ, समविभव पृष्ठ के लम्बवत हैं और वे उच विभव से निम्न विभव की ओर दिष्ट हैं। विद्युत क्षेत्र की तीव्रता नीचे की ओर बाएँ क्षेत्र में अधिकतम है जहाँ समविभव पृष्ठ आपस में आप - पास है।

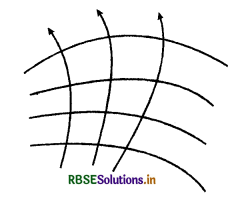
प्रश्न 10.
विभव प्रवणता तथा विद्युत क्षेत्र की तीव्रता में संबंध स्थापित कीजिए।
उत्तर:
विद्युत प्रवणता के रूप में विद्युत् क्षेत्र (Electric Field as a Gradient of Electric) 
माना एक बिन्दु आवेश +q बिन्दु O पर रखा है और इससे r दूरी पर बिन्दु P पर विद्युत् विभव V एवं (r - dr) दूरी पर स्थित बिन्दु Q पर विभव (v + dv) है।

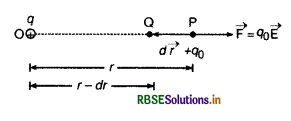
यदि एक अत्यन्त सूक्ष्म परीक्षण आवेश (very small test charge) q₀ को P से Q तक ले जाने में कृत कार्य dW है, तो
(V + dV) - V = \(\frac{d \mathrm{~W}}{q_0}\)
या dV = \(\frac{d \mathrm{~W}}{q_0}\) ................(1)
P बिन्दु पर स्थित +q₀ आवेश पर लगने वाला बल
\(\overrightarrow{\mathrm{F}}=q_0 \overrightarrow{\mathrm{E}}\) (OP दिशा में)
∴ इस बल के विरुद्ध (against) \(d \vec{r}\) विस्थापन (displacement) देने में अर्थात् P से Q तक q₀ आवेश को ले जाने में कृत कार्य
dW = \( \overrightarrow{\mathrm{F}} \cdot \overrightarrow{d r}\)
= F.dr.cos180° = -F.dr
परन्तु F = q₀E
∴ dW = -q₀E.dr
या \(\frac{d \mathrm{~W}}{q_0}\) = -E.dr ................(2)
समी. (1) व (2) से, dV = -E.dr

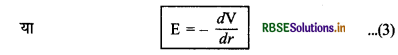
"अर्थात् किसी बिन्दु पर विद्युत् क्षेत्र की तीव्रता (electric field intensity) उस बिन्दु पर ऋणात्मक विभव प्रवणता (potential gradient) के बराबर होती है।" ऋण चिह्न यह दर्शाता है कि विद्युत् क्षेत्र \(\overrightarrow{\mathrm{E}}\) को दिशा सदैव उच्च (higher) विभव से निम्न (lower) विभव की ओर अर्थात् विभव के घटने की दिशा में (in decreasing directon) होती है। विभव प्रवणता एक सदिश राशि है जिसकी दिशा विद्युत् क्षेत्र \(\overrightarrow{\mathrm{E}}\) की विपरीत दिशा में अर्थात् विभव बढ़ने (increasing potential) की दिशा में होती है।
विद्युत् क्षेत्र व विद्युत् विभव में सम्बन्ध
∵ \(\overrightarrow{\mathrm{E}} = -\frac{d \mathrm{~V}}{\overrightarrow{d r}}\)
या dV = \(-\overrightarrow{\mathrm{E}} \cdot \vec{d}\)
उपरोक्त समीकरण को बिन्दु \(\overrightarrow{r_1} \text { व } \overrightarrow{r_2}\) के मध्य समाकलन करने पर,

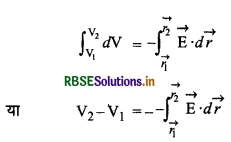
जहाँ, बिन्दु \(\overrightarrow{r_1} \text { व } \overrightarrow{r_2}\) पर विद्युत् विभव क्रमश: V₁ व V₂ है। यदि हम बिन्दु \(\overrightarrow{r_1}\) को अनन्त पर मानें, तो V₁ = 0 और \(\overrightarrow{r_2}=\vec{r}\) लेने पर
\(\mathrm{V}(\vec{r})=-\int_{\infty}^{\overrightarrow{ }} \overrightarrow{\mathrm{E}} \cdot \overrightarrow{d r}\)

प्रश्न 11.
निम्नलिखित कथनों की व्याख्या कीजिए-
(i) चालक के अन्दर विद्युत क्षेत्र शून्य होता है।
(ii) आवेशित चालक के पृष्ठ पर प्रत्येक बिन्दु पर स्थिर वैद्युत क्षेत्र अभिलम्बवत होना चाहिए।
उत्तर:
चालक स्थिर - वैद्युतिकी (Electrostatics of Conductors)
चालक (conductors) वे पदार्थ है जिनसे होकर धारा का प्रवाह (flow of charge) अर्थात् आवेश का प्रवाह हो जाता है। सभी धात्विक पदार्थ चालक होते हैं। इनकी चालकता (conductivity) का कारण यह है कि सभी चालकों में आवेश वाहकों अर्थात् मुक्त इलेक्ट्रॉनों (free electrons) की बड़ी संख्या मौजूद रहती है। चालक स्थिर - वैद्युतिकी के कुछ महत्वपूर्ण तथ्य निम्नलिखित हैं-
चालक के अन्दर विद्युत् क्षेत्र शून्य होता है: माना एक चालक ABCD किसी बाह्य विद्युत् क्षेत्र \(\overrightarrow{\mathrm{E}_{\text {ext }}}\) में रखा है। चालक के मुक्त इलेक्ट्रॉनों पर बाहा क्षेत्र 

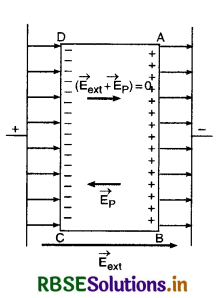
की विपरीत दिशा में E_ext, बल लगेगा अतः वे चालक के पृष्ठ AB से CD को और गति करने लगेंगे और CD किनारे पर एकत्र (collect) हो जायेंगे। फलस्वरूप AB किनारा समान परिमाण से धनावेशित हो जायेगा। इन आवेशों को प्रेस्ति आवेश (induced charges) कहते हैं। ये प्रेरित आवेश चालक के अन्दर एक वैद्युत क्षेत्र \(\overrightarrow{\mathrm{E}}_{\mathrm{P}}\) उत्पन्न करते हैं जो बाह्य क्षेत्र \(\overrightarrow{\mathrm{E}}_{\mathrm{ext}}\) का विरोध करता है और इलेक्ट्रॉनों की गति का भी विरोध करता है, अत: इलेक्ट्रॉनों का प्रवाह तुरन्त रुक जाता है, जैसे ही \(\overrightarrow{\mathrm{E}}_{\mathrm{P}}\) का परिमाण \(\overrightarrow{\mathrm{E}}_{\mathrm{ext}}\) के परिमाण के बराबर हो जाता है, चालक के अन्दर नेट विद्युत् क्षेत्र \(\left(\vec{E}_{\text {ext }}+\vec{E}_{\mathrm{P}}\right)\) = 0 हो जाता है। अर्थात् E_ext - E_p = 0, क्योंकि \(\vec{E}_{e x t} \text { व } \vec{E}_P\) की दिशाएँ विपरीत हैं।

आवेशित चालक के पृष्ठ पर प्रत्येक बिन्दु पर स्थिर - वैधुत क्षेत्र अभिलम्बवत् होना चाहिए: स्थिर - वैद्युत स्थितियों के अन्तर्गत चालक के पृष्ठ पर आवेश का पुनर्वितरण (redistribution of charges) हो जाता है इसलिए आवेश का प्रवाह रुक जाता है। अतः पृष्ठ के अनुदिश (along) विद्युत् क्षेत्र का घटक (component) शून्य होना चाहिए अर्थात्

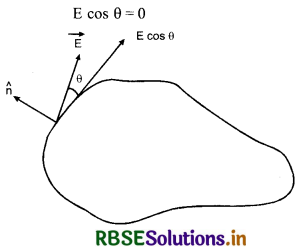
जहाँ θ पृष्ठ पर स्पर्शी (tangent) एवं विद्युत् क्षेत्र के मध्य कोण है।
चूंकि E ≠ 0 अत: cosθ = 0 
या θ = 90°
अर्थात् विद्युत् क्षेत्र \(\overrightarrow{\mathrm{E}}\) चालक के पृष्ठ के लम्बवत् होना चाहिए।

दीर्घ उत्तरीय प्रश्न

प्रश्न 1.
संघारित्र किसे कहते हैं? गोलीय संघारित्र की धारिता का व्यंजक व्युत्पन्न कीजिए।
उत्तर:
संधारित्र एवं उसका सिद्धान्त (Capacitor and its Principle)
"वह युक्ति (device) जिसमें चालक के आकार को बिना बदले उसकी बारिता बढ़ायी जा सकती है, संधारित्र कहलाती है।"
किसी चालक को q आवेश देने पर यदि उसका विभव V हो जाता है, तो उसकी धारिता
C = \(\frac{q}{\mathrm{~V}}\)
स्पष्ट है कि यदि किसी प्रकार आवेश q के लिए विभव का मान V से कम हो जाये, तो चालक की धारिता C बढ़ जायेगी। इसी विचार से संधारित्र की खोज हुई। संधारित्र का सिद्धान्त (principle) निम्नलिखित तीन पदों में समझा जा सकता है-
(i) माना किसी चालक A को q आवेश देने पर उसका विभव V हो जाता है, तो उसकी धारिता
C = \(\frac{q}{V}\) ............(1)
(ii) अब यदि चालक A के पास इसी प्रकार का दूसरा अनावेशित चालक B लाया जाये, तो प्रेरण (induction) द्वारा उसका आवेशन (charging) चित्र 2.36 (b) की भाँति होगा।


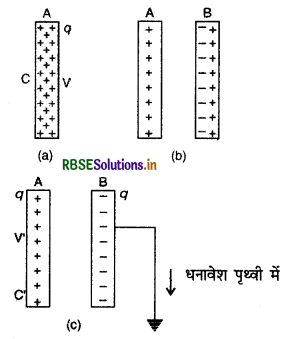
(ii) अब यदि चालक B को पृथ्वी से सम्बन्धित कर दिया जाये, तो उसका समस्त धनादेश पृथ्वी में चला जायेगा। इस नवीन स्थिति में यदि चालक A का विभव V' हो, तो A की धारिता
C' = \(\frac{q}{V^{\prime}} \)..............(2)
समीकरण (1) व (2) से,
\(\frac{\mathrm{C}^{\prime}}{\mathrm{C}}=\frac{q / \mathrm{V}^{\prime}}{q / \mathrm{V}}=\frac{\mathrm{V}}{\mathrm{V}}\)
या \(\frac{\mathrm{C}^{\prime}}{\mathrm{C}}=\frac{\mathrm{V}}{\mathrm{V}^{\prime}}\) ............(3)
परन्तु V' = चालक A के आवेश के कारण विभव + चालक B के आवेश के कारण उत्पन्न विभव 
या V' = V - V"
इसी समीकरण से स्पष्ट है कि
V > V'
∴ समी. (3) से, C' > C
अर्थात् "जब एक आवेशित चालक के पास दूसरा अनावेशित एवं पृथ्वी से सम्बन्धित चालक लाया जाता है तो पहले चालक की धारिता बढ़ जाती है।" यही संधारित्र का सिद्धान्त है। इस प्रकार उक्त सिद्धान्त से स्पष्ट है कि संधारित्र में दो पृथक्कित धात्वीय प्लेटें (separated metallic plates) होती है जिसमें एक को आवेश दिया जाता है और दूसरी को भूसम्पर्कित कर देते हैं। जब प्लेटों के मध्य किसी परावैद्युत माध्यम की जगह वायु होती है तो उसे वायु संधारित्र कहते हैं।

गोलाकार संधारित्र की धारिता (Capacity of Spherical Capacitor) 
गोलाकार संधारित्र की रचना चित्र 2.37 में दिखायी गई है। इसमें दो समकेन्द्रीय (concentric) गोलीय प्लेटें A व B होती है। बाहरी प्लेट B को पृथ्वी से सम्बन्धित किया जाता है और भीतरी प्लेट A को +q आवेश दिया जाता है। बाहरी गोले पर प्रेरण द्वारा उत्पन्न धनात्मक आवेश पृथ्वी में चला जाता है और केवल ऋणात्मक आवेश रह जाता है। अत:

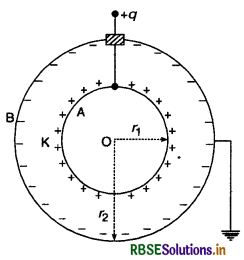
भीतरी गोले पर उत्पन्न विभव
V = V₁ + V₂
जहाँ V₁ = भीतरी गोले के +q आवेश के कारण उत्पन्न विभव
= \(+\frac{1}{4 \pi \varepsilon_0 \mathrm{~K}} \frac{q}{r_1}\)
और V₂ = बाहरी गोले के -q आवेश के कारण उत्पन्न विभव
= \(-\frac{1}{4 \pi \varepsilon_0 \mathrm{~K}} \cdot \frac{q}{r_2}\)

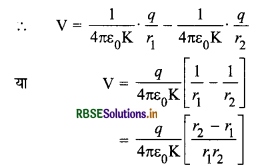
चूंकि बाहरी गोला पृथ्वी से सम्बन्धित है अतः इसका विभव शून्य होगा।
∴ दोनों गोलों के मध्य विभवान्तर
= V - 0 = V
∴ संधारित्र की धारिता

समीकरण (1) से स्पष्ट है कि गोलाकार संधारित्र को धारिता निम्न प्रकार बढ़ायी जा सकती है-
(i) गोलों की त्रिज्याएँ r₁ व r₂ बड़ाकर, लेकिन यह संधारित्र के सिद्धान्त के विरुद्ध है, अत: त्रिज्याएँ बढ़ाकर धारिता नहीं बढ़ायी जाती है।
(ii) C ∝ K अर्थात् दोनों गोलों के मध्य अधिक परावैद्युतांक (dielectric constant) वाला परावैद्युत माध्यम (dielectric medium) रखकर धारिता बढ़ायी जा सकती है।
(iii) C ∝ \(\frac{1}{\left(r_2-r_1\right)}\) अर्थात् दोनों गोलों के मध्य दूरी घटाकर धारिता बढ़ाई जा सकती है।

प्रश्न 2.
विभव को परिभाषित कीजिए। विद्युत द्विध्रुव के कारण किसी बिन्दु (r, Q) पर विद्युत विभव का व्यंजक प्राप्त कीजिए। आवश्यक चित्र बनाइए।
उत्तर:
स्थिर वैद्युत विभव (Electrostatic Potential)
"विद्युत् विभव वह कारण है जो आवेश के प्रवाह की दिशा निर्धारित करता है अर्थात् विद्युत् विभव किसी आवेशित वस्तु के वैद्युत तल (plane) को व्यक्त करता है।" जिस प्रकार द्रवों का प्रवाह सदैव उच्च गुरुत्वीय तल (gravity plane) से निम्न तल की ओर होता है, ऊष्मा का प्रवाह उच्च ताप को वस्तु से निम्न ताप की वस्तु की ओर होता है, ठीक उसी प्रकार आवेश (धनात्मक) का प्रवाह भी उच्च विभव से निम्न विभव की ओर होता है। विद्युत् विभव एक अदिश राशि है। इसे V से व्यक्त करते हैं।
चित्र 2.2 में दिखाया गया है कि आवेशों के एक विन्यास के कारण उत्पन्न विद्युत् क्षेत्र में किसी परीक्षण आवेश (+q₀) को बिन्दु A से B

तक ले जाने में कृत कार्य केवल प्रारम्भिक एवं अन्तिम बिन्दुओं की स्थिति पर निर्भर करता है, इस बात पर नहीं कि परीक्षण आवेश को किस मार्ग से ले जाया गया है अर्थात् कृत कार्य मार्ग पर निर्भर नहीं करता है। यदि बिन्दुओं A व B पर विद्युत् विभव क्रमश: V_A व V_B हों, तो उनके मध्य विभवान्तर की परिभाषा निम्न प्रकार से की जायेगी-
V_B - V_A = \(\frac{\mathrm{W}_{\mathrm{AB}}}{q_0}\) ...............(1)
जहाँ W_AB = +q₀ आवेश को A से B तक ले जाने में किया गया कार्य अनु. 2.2 के समीकरण (2) के आधार पर,
W_AB = U_B - U_A = ∆U
∴ V_B - V_A = \(\frac{\mathrm{U}_{\mathrm{B}}-\mathrm{U}_{\mathrm{A}}}{q_0}=\frac{\mathrm{W}_{\mathrm{AB}}}{q_0}\) ...............(2)
समी. (1) में यदि q₀ = +1 C, तो
V_B - V_A = W_AB
"अर्थात् किन्हीं दो बिन्दुओं के मध्य विभवान्तर (potential difference) उस कार्य के तुल्य है जो एकांक धनावेश को निम्न विभव (lower potential) के बिन्दु से उच्च विभव (higher potential) के बिन्दु तक ले जाने में करना पड़ता है।"
समी. (1) से विभवान्तर (V_B - V_A) का मात्रक

"अर्थात् एकांक धनावेश (unit positive charge) को यदि एक बिन्दु से दूसरे बिन्दु तक ले जाने में कृत कार्य 1 J, हो, तो उन बिन्दुओं के मध्य विभवान्तर 1 V होगा।" यदि बिन्दु A को बिन्दु B से दूर करते जावे तो VA का मान घटता जायेगा और अनन्त पर शून्य हो जायेगा। अत: यदि बिन्दु A अनन्त पर है, तो
V_A = 0
∴ समी. (2) से,
V_B - 0 = \(\frac{\mathrm{W}_{\infty \mathrm{B}}}{q_0}\)
या V_B = \(\frac{\mathrm{W}_{\infty \mathrm{B}}}{q_0}\)
या किसी भी बिन्दु के लिए व्यापक रूप से,
V = \(\frac{\mathrm{W}}{q_0}\)
यदि q₀ = +1 C, तो V = W
"अर्थात् किसी बिन्दु पर विद्युत् विभव उस कार्य के तुल्य है जो +1 C आवेश को अनन्त से उस बिन्दु तक लाने में करना पड़ता है।"
मात्रक एवं विमीय सूत्र-किसी बिन्दु पर विद्युत् विभव

यदि q₀ = +1 C, W = 1 J, तो V = 1 वोल्ट
"अर्थात् यदि +1 C आवेश को अनन्त से किसी बिन्दु तक लाने में 1 J कार्य करना पड़ता है, तो उस बिन्दु पर विद्युत् विभव 1 वोल्ट होगा।"
पुनः V = \(\frac{\mathrm{W}}{q_0}\)

=\(\frac{\left[\mathrm{M}^1 \mathrm{~L}^2 \mathrm{~T}^{-2}\right]}{\left[\mathrm{A}^1 \mathrm{~T}^1\right]} \)
= [M¹L²T^-3A^-1]

वैद्युत द्विधुव के कारण किसी बिन्दु पर विद्युत विभव (Potential at a Point due to electric dipole) 
माना 2l लम्बाई के एक वैद्युत द्विध्रुव के मध्य - विन्दु O से r दूरी पर स्थिति बिन्दु P पर विभव ज्ञात करना है।
वैद्युत द्विध्रुव आघूर्ण ।\(\overrightarrow{\mathrm{P}}\)। = q x 2l
या P = q x 2l

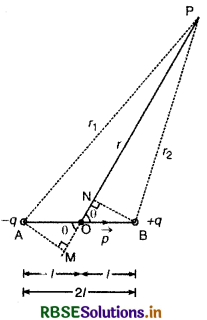
चित्र 2.10 में,
cosθ = \(\frac{\mathrm{OM}}{\mathrm{OA}}=\frac{\mathrm{OM}}{l}\)
∴ OM = l cosθ
∴ दूरी MP = OM + OP
= OP + OM = r + lcosθ
दूरी r₁ = AP ≈ MP = (r + lcosθ)
इसी प्रकार, r₂ = BP ≈ NP = (r - lcosθ) 
∴ -q आवेश के कारण P पर उत्पन्न विभव
V₁ = \(-\frac{1}{4 \pi \varepsilon_0} \frac{q}{r_1}\)
और +q के कारण P पर उत्पन्न विभव
V₂ = \(+ \frac{1}{4 \pi \varepsilon_0} \frac{q}{r_2}\)
P पर परिणामी विभव
V = V₁ + V₂
= \(-\frac{1}{4 \pi \varepsilon_0} \frac{q}{r_1}+\frac{1}{4 \pi \varepsilon_0} \frac{q}{r_2}\)
= \(\frac{q}{4 \pi \varepsilon_0}\left[\frac{1}{r_2}-\frac{1}{r_1}\right]\)

(i) यदि बिन्दु P अक्षीय (axial) स्थिति में है, तो
θ = 0 ∴ cosθ = 1
अतः \(\mathrm{V}=\frac{1}{4 \pi \varepsilon_0} \frac{p}{\left(r^2-l^2\right)}\) ..............(2)
दीर्घ दूरियों के लिए r >> l ∴ r₂ >>> l₂
अत: l₂ को r₂ की तुलना में छोड़ने पर,

(ii) यदि बिन्दु P निरधीय (equatorial) स्थिति में स्थित है, तो
θ = 90° ∴ cosθ = 0 

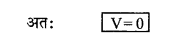
अर्थात् वैद्युत द्विध्रुव की निरक्षीय (equatorial) स्थिति में विद्युत् विभव शून्य होता है।

प्रश्न 3.
संघारित्र को परिभाषित कीजिए। परिपथ चित्र बनाकर तीन संघारित्रों के चुंगी संयोजन के लिए संबंध ज्ञात कीजिए।
उत्तर:
संधारित्र एवं उसका सिद्धान्त (Capacitor and its Principle)
"वह युक्ति (device) जिसमें चालक के आकार को बिना बदले उसकी बारिता बढ़ायी जा सकती है, संधारित्र कहलाती है।"
किसी चालक को q आवेश देने पर यदि उसका विभव V हो जाता है, तो उसकी धारिता
C = \(\frac{q}{\mathrm{~V}}\)
स्पष्ट है कि यदि किसी प्रकार आवेश q के लिए विभव का मान V से कम हो जाये, तो चालक की धारिता C बढ़ जायेगी। इसी विचार से संधारित्र की खोज हुई। संधारित्र का सिद्धान्त (principle) निम्नलिखित तीन पदों में समझा जा सकता है-
(i) माना किसी चालक A को q आवेश देने पर उसका विभव V हो जाता है, तो उसकी धारिता
C = \(\frac{q}{V}\) ............(1)
(ii) अब यदि चालक A के पास इसी प्रकार का दूसरा अनावेशित चालक B लाया जाये, तो प्रेरण (induction) द्वारा उसका आवेशन (charging) चित्र 2.36 (b) की भाँति होगा।

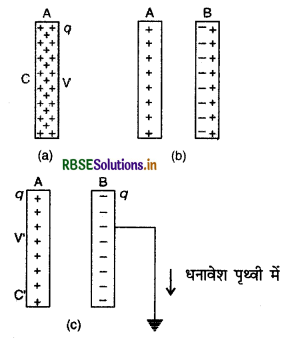
(ii) अब यदि चालक B को पृथ्वी से सम्बन्धित कर दिया जाये, तो उसका समस्त धनादेश पृथ्वी में चला जायेगा। इस नवीन स्थिति में यदि चालक A का विभव V' हो, तो A की धारिता
C' = \(\frac{q}{V^{\prime}}\) ..............(2)
समीकरण (1) व (2) से,
\(\frac{\mathrm{C}^{\prime}}{\mathrm{C}}=\frac{q / \mathrm{V}^{\prime}}{q / \mathrm{V}}=\frac{\mathrm{V}}{\mathrm{V}}\)
या \(\frac{\mathrm{C}^{\prime}}{\mathrm{C}}=\frac{\mathrm{V}}{\mathrm{V}^{\prime}}\) ............(3)
परन्तु V' = चालक A के आवेश के कारण विभव + चालक B के आवेश के कारण उत्पन्न विभव 
या V' = V - V"
इसी समीकरण से स्पष्ट है कि
V > V'
∴ समी. (3) से, C' > C
अर्थात् "जब एक आवेशित चालक के पास दूसरा अनावेशित एवं पृथ्वी से सम्बन्धित चालक लाया जाता है तो पहले चालक की धारिता बढ़ जाती है।" यही संधारित्र का सिद्धान्त है। इस प्रकार उक्त सिद्धान्त से स्पष्ट है कि संधारित्र में दो पृथक्कित धात्वीय प्लेटें (separated metallic plates) होती है जिसमें एक को आवेश दिया जाता है और दूसरी को भूसम्पर्कित कर देते हैं। जब प्लेटों के मध्य किसी परावैद्युत माध्यम की जगह वायु होती है तो उसे वायु संधारित्र कहते हैं।

प्रश्न 4.
किसी समान्तर पट्टिका संधारित्र जिसकी धारिता C और जिसे वोल्टता V तक आवेशित किया गया है, में संचित ऊर्जा के लिए व्यंजक व्युत्पन्न कीजिए। संधारित्र में यह ऊर्जा किस प्रकार संचित होती है?
उत्तर:
संधारित्र में संचित ऊर्जा (Stored Energy in Capacitor):
संधारित्र को आवेशित करने में किया गया कार्य ही आवेशित संधारित्र की ऊर्जा कहलाती है। यदि आवेशित संधारित्र की एक प्लेट के आवेश को दूसरी प्लेट तक ले जाया जाये तो संधारित्र अनाविष्ट (uncharged) हो जायेगा। इस क्रिया में जितनी ऊर्जा प्राप्त होगी, वही आवेशित संधारित्र की ऊर्जा होगी।
माना कि संधारित्र का प्रारम्भिक विभवान्तर V है और अनाविष्ट होने पर इसका अन्तिम विभवान्तर शून्य होगा। उक्त क्रिया में संधारित्र का औसत विभवान्तर
= \(\frac{0+V}{2}=\frac{V}{2}\)
यदि संधारित्र पर आवेश q हो तो इस आवेश को एक प्लेट से दूसरी प्लेट तक ले जाने में किया गया कार्य अर्थात् संधारित्र की ऊर्जा
U = W = आवेश x औसत विभवान्तर
= q x \(\frac{\mathrm{V}}{2}\)
या U = \(\frac{1}{2}\) qV
∴ q = CV
∴ U = \(\frac{1}{2} CV.V = \frac{1}{2}\)CV²
या U = \(\frac{1}{2}C\left(\frac{q}{C}\right)^2 = \frac{1}{2} \frac{q^2}{\mathrm{C}}\), क्योंकि V = \(\frac{q}{C}\)

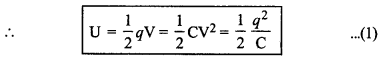
चूँकि वायु संधारित्र (air capacitor) की धारिता
C = \(\frac{\mathrm{A} \varepsilon_0}{d}\)
और विद्युत् क्षेत्र की तीव्रता

चूंकि संधारित्र का आयतन
= प्लेटों का क्षेत्रफल x उनके मध्य दूरी
= A.d
∴\( \frac{\mathrm{U}}{\mathrm{Ad}}=\frac{1}{2} \varepsilon_0 \mathrm{E}^2\)
या संधारित्र के प्रति एकांक आयतन में संचित ऊर्जा
= \(\frac{1}{2} \varepsilon_0 E^2\)

u को ऊर्जा घनत्व भी कहते हैं।

संधारित्र की प्लेटों के बीच परावैद्युत पदार्थ की पट्टी प्रवेश करायी जाने पर संघारित्र की ऊर्जा में परिवर्तन: वायु संधारित्र के लिए जिसकी धारिता C₀, आवेश q₀ तथा प्लेटों के बीच विभवान्तर V₀ है, तब संधारित्र की ऊर्जा
U₀ = \(\frac{1}{2}\)C₀V₀² = \(\frac{1}{2} \frac{q_0^2}{\mathrm{C}_0}\)
(i) माना संधारित्र को आवेशित करने के पश्चात् उसकी प्लेटों के बीच बैटरी जुड़ी रहती है। तब प्लेटों के बीच विभवान्तर V₀ नियत रहता है। अब प्लेटों के बीच परावैद्युत पदार्थ रखने पर संधारित्र की धारिता C₀ से बढ़कर KC₀ हो जाती है, अत: संधारित्र द्वारा संचित ऊर्जा
U₀ = \(\frac{1}{2}\)C₀V₀² = \(\frac{1}{2}\left(\mathrm{KC}_0\right) \mathrm{V}_0^2\) = KU₀
अर्थात् संधारित्र की ऊर्जा बढ़ जाती है।

(ii) यदि संधारित्र को आवेशित करने के पश्चात् बैटरी हटा दी जाती है तब K परावैधुतांक वाले पदार्थ की पट्टी प्लेटों के बीच रखी जाती है, तब संधारित्र पर संचित आवेश q₀ ही बना रहता है। इस दशा में संधारित्र की ऊर्जा
U₀ = \(\frac{1}{2} \frac{q_0^2}{\mathrm{C}}=\frac{1}{2} \frac{q_0^2}{\mathrm{KC} \mathrm{C}_0}=\frac{\mathrm{U}_0}{\mathrm{~K}}\)
अर्थात् संधारित्र की ऊर्जा घट जाती है।

प्रश्न 5.
वायु में पृथकन 'd' पर स्थित क्षेत्रफल 'A' की धातु की दो समान्तर पट्टिकाओं के किसी निकाय पर विचार कीजिए। इस समान्तर पट्टिका संघारित्र की धारिता के लिए व्यंजक व्युत्पन्न कीजिए।
उत्तर:
प्लेटों के मध्य आंशिक रूप से परावैद्युत माध्यम होने पर समान्तर प्लेट संधारित्र की बारिता (Capacitance of Parallel Plate Capacitor when Partially Filled with Dielectric Substance):
माना समान्तर प्लेट संधारित्र की प्लेटों के मध्य दूरी d है और उनके मध्य K परावैद्युतांक (dielectric constant) एवं t मोटाई (thickness) का परावैद्युत माध्यम आंशिक (partially) रूप से रखा है। प्लेटों के मध्य वायु वाले क्षेत्र में विद्युत् क्षेत्र की तीव्रता \(\overrightarrow{\mathrm{E}}_0\) एवं परावैद्युत माध्यम में \(\overrightarrow{\mathrm{E}}\) है। दोनों प्लेटों पर आवेश का पृष्ठ घनत्व

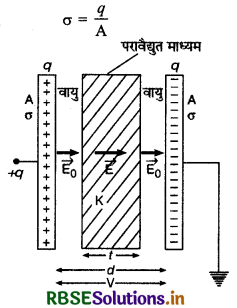
यदि प्लेटों के मध्य दूरी उनके विस्तार की तुलना (comparison to their extent) में नगण्य हो तो
E₀ = \(\frac{\sigma}{\varepsilon_0}\) और E = \(\frac{\sigma}{\varepsilon_0 \mathrm{~K}}\)
विभवान्तर की परिभाषा से प्लेटों के मध्य विभवान्तर V = +1 C आवेश को ऋण प्लेट से धन प्लेट तक ले जाने में किया गया कार्य
= +1 C आवेश को (d - t) दूरी वायु (air) में +t दूरी परावैद्युत माध्यम (dielectric medium) में ले जाने में कृत कार्य
= E₀ (d - t) + E.t

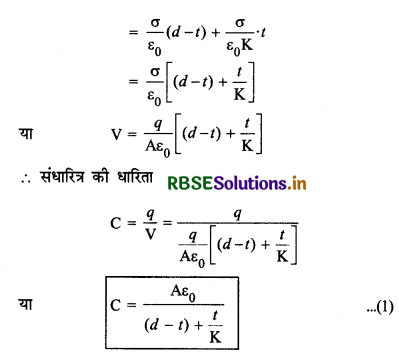
विशेष स्थितियाँ: (i) यदि प्लेटों के मध्य केवल वायु है तो t = 0
∴ C₀ = \(\frac{A \varepsilon_0}{(d-0)+0}\)
या C₀ = \(\frac{\mathrm{A} \varepsilon_0}{d}\)
(ii) यदि प्लेटों के मध्य केवल परावैद्युत माध्यम है तो t = d
∴ C = \(\frac{\mathrm{A} \varepsilon_0}{(d-d)+\frac{d}{\mathrm{~K}}}=\frac{\mathrm{A} \varepsilon_0}{\frac{d}{\mathrm{~K}}}=\frac{\mathrm{KA} \varepsilon_0}{d}\)
या C = \(\frac{\mathrm{KA} \varepsilon_0}{d}\)

(iii) यदि प्लेटों के मध्य भिन्न - भिन्न (different) परावैद्युतांकों के n माध्यम रखे हों जिनकी मोटाइयाँ क्रमशः t₁,t₂,......t_n हो तो
d = (t₁ + t₂ +.......+ t_n)

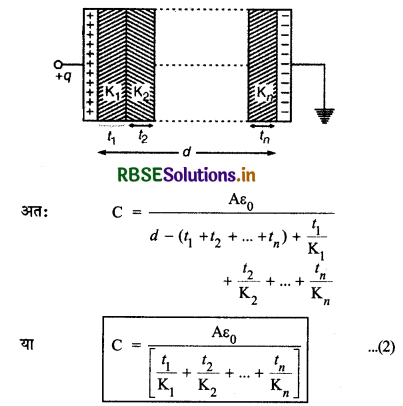
(iv) जब प्लेटों के बीच t मोटाई की धातु की कोई पट्टी हो तो
K = ∞
अत: समीकरण (1) से,
C = \(\frac{\mathrm{A} \varepsilon_0}{(d-t)+\frac{t}{\infty}}=\frac{\mathrm{A} \varepsilon_0}{d-t}\)

प्रश्न 6.
संघारित्रों के समान्तर क्रम संयोजन की तुल्य धारिता धारिता के लिए व्यंजक प्राप्त कीजिए।
उत्तर:
संधारित्रों का पार्यक्रम संयोजन (Parallel Combination of Capacitors)
इस संयोजन में सभी संधारित्रों की पहली प्लेटें एक संधि A व दूसरी प्लेटें दूसरी संधि B के मध्य जोड़ दी जाती हैं। पहली संधि A को +q आवेश दिया जाता है और संधि B को भूसम्पकिंत कर दिया जाता है। चूँकि सभी संधारित्र संधियों A व B के मध्य जुड़े होते हैं अतः सबका विभवान्तर (V) समान होता है। संधि A को दिया गया आवेश +q धारिताओं के अनुसार तीनों संधारित्रों में बँट जाता है।
∴ q = q₁ + q₂ + q₃ ...............(1)

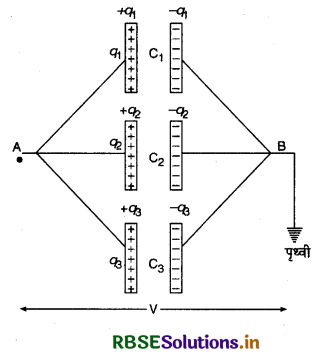
चूँकि सभी संधारित्रों का विभवान्तर समान (V) है। अतः
q₁ = C₁V, q₂ = C₂V, q₃ =C₃V
यदि संयोजन की तुल्य धारिता C हो तो
q = CV 
∴  समी. (1) में आवेशों के मान रखने पर,
CV = C₁V + C₂V + C₃V 
या C = C₁ + C₂ + C₃
इसी प्रकार अन्य सभी धारिताएँ जुड़ जायेंगी।

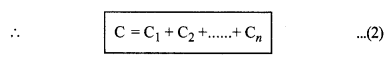
प्रश्न 7.
संधारित्र की संचित ऊर्जा से क्या तात्पर्य है? सिद्ध कीजिए-"दो आवेशित चालकों को जोड़ने पर उनके विभव में पविर्तनों का अनुपात चालकों की धारिताओं के व्युत्क्रमानुपाती होता है।"
उत्तर:
संधारित्र में संचित ऊर्जा (Stored Energy in Capacitor):
संधारित्र को आवेशित करने में किया गया कार्य ही आवेशित संधारित्र की ऊर्जा कहलाती है। यदि आवेशित संधारित्र की एक प्लेट के आवेश को दूसरी प्लेट तक ले जाया जाये तो संधारित्र अनाविष्ट (uncharged) हो जायेगा। इस क्रिया में जितनी ऊर्जा प्राप्त होगी, वही आवेशित संधारित्र की ऊर्जा होगी।
माना कि संधारित्र का प्रारम्भिक विभवान्तर V है और अनाविष्ट होने पर इसका अन्तिम विभवान्तर शून्य होगा। उक्त क्रिया में संधारित्र का औसत विभवान्तर
= \(\frac{0+V}{2}=\frac{V}{2}\)
यदि संधारित्र पर आवेश q हो तो इस आवेश को एक प्लेट से दूसरी प्लेट तक ले जाने में किया गया कार्य अर्थात् संधारित्र की ऊर्जा
U = W = आवेश x औसत विभवान्तर
= q x \(\frac{\mathrm{V}}{2}\)
या U = \(\frac{1}{2}\) qV
∴ q = CV
∴ U = \(\frac{1}{2}\) CV.V = \(\frac{1}{2}\)CV²
या U = \(\frac{1}{2}C\left(\frac{q}{C}\right)^2 = \frac{1}{2} \frac{q^2}{\mathrm{C}}\), क्योंकि V = \(\frac{q}{C}\)

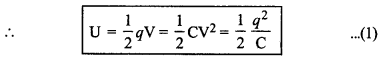
चूँकि वायु संधारित्र (air capacitor) की धारिता
C = \(\frac{\mathrm{A} \varepsilon_0}{d}\)
और विद्युत् क्षेत्र की तीव्रता

चूंकि संधारित्र का आयतन
= प्लेटों का क्षेत्रफल x उनके मध्य दूरी
= A.d
∴ \(\frac{\mathrm{U}}{\mathrm{Ad}}=\frac{1}{2} \varepsilon_0 \mathrm{E}^2\)
या संधारित्र के प्रति एकांक आयतन में संचित ऊर्जा
= \(\frac{1}{2} \varepsilon_0 E^2\)

u को ऊर्जा घनत्व भी कहते हैं।

संधारित्र की प्लेटों के बीच परावैद्युत पदार्थ की पट्टी प्रवेश करायी जाने पर संघारित्र की ऊर्जा में परिवर्तन: वायु संधारित्र के लिए जिसकी धारिता C₀, आवेश q₀ तथा प्लेटों के बीच विभवान्तर V₀ है, तब संधारित्र की ऊर्जा
U₀ = \(\frac{1}{2}\)C₀V₀² = \(\frac{1}{2} \frac{q_0^2}{\mathrm{C}_0}\)
(i) माना संधारित्र को आवेशित करने के पश्चात् उसकी प्लेटों के बीच बैटरी जुड़ी रहती है। तब प्लेटों के बीच विभवान्तर V₀ नियत रहता है। अब प्लेटों के बीच परावैद्युत पदार्थ रखने पर संधारित्र की धारिता C₀ से बढ़कर KC₀ हो जाती है, अत: संधारित्र द्वारा संचित ऊर्जा
U₀ = \(\frac{1}{2}\)C₀V₀² = \(\frac{1}{2}\left(\mathrm{KC}_0\right) \mathrm{V}_0^2\) = KU₀
अर्थात् संधारित्र की ऊर्जा बढ़ जाती है।

(ii) यदि संधारित्र को आवेशित करने के पश्चात् बैटरी हटा दी जाती है तब K परावैधुतांक वाले पदार्थ की पट्टी प्लेटों के बीच रखी जाती है, तब संधारित्र पर संचित आवेश q₀ ही बना रहता है। इस दशा में संधारित्र की ऊर्जा
U₀ = \(\frac{1}{2} \frac{q_0^2}{\mathrm{C}}=\frac{1}{2} \frac{q_0^2}{\mathrm{KC} \mathrm{C}_0}=\frac{\mathrm{U}_0}{\mathrm{~K}}\)
अर्थात् संधारित्र की ऊर्जा घट जाती है।

आंकिक प्रश्न

प्रश्न 1.
10^-9 कूलॉम के बिन्दु आवेश के कारण 1 m दूर बिन्दु पर विद्युत विभव की गणना करो।
हल: 
दिया है: q = 10^-9 C, r = 1m
∴ विद्युत विभव V = \(\frac{k q}{r}=\frac{9 \times 10^9 \times 10^{-9}}{1}\)
V = 9 वोल्ट

प्रश्न 2.
\(\sqrt{2}\) m भुजा के वर्ग के कोनों पर 100 µC, -50 µC, 20 µC तथा -60 µC के चार आवेश क्रमशः रखे हैं। वर्ग के केन्द्र पर विद्युत विभव ज्ञात करो।
हल: 
चित्रानुसार

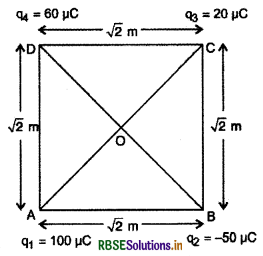
q₁ = 100 µC, q₂ = 50 µC 
AC = BD = AD\(\sqrt{2}\) = \(\sqrt{2}\).\(\sqrt{2}\) = 2 m
∴ A0 = BO = CO = DO =\(\frac{A C}{2}\) = 1 m
वर्ग के केन्द्र पर विभव
V₀ = \(\frac{K q_1}{A O}+\frac{K q_2}{B O}+\frac{K q_3}{C O}+\frac{K q_4}{D O}\)
V₀ = \(\frac{K}{1}\) [q₁ + q₂ + q₃ + q₄]
V₀ = 9 x 109 [100 + -50] + 20 + (-60)] x 10^-6
V₀ = 9 x 109 x 10 x 10^-6
V₀ = 9 x 104 वोल्ट

प्रश्न 3.
दो आवेश +q तथा -q चित्रानुसार व्यवस्थित हैं तथा B के मध्य बिन्दुओं पर विभव क्रमशः V_A तथा V_B  हैं, तब V_A - V_B ज्ञात करो।

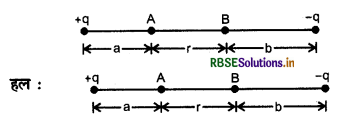
बिन्दु A पर नेट विभव 
V_A = +q  के कारण विभव + (-q) के कारण विभव
V_A = \(\frac{q}{4 \pi \varepsilon_0 a}+\frac{1}{4 \pi \varepsilon_0} \frac{(-q)}{a+r}\)
बिन्दु B पर नेट विभव 
V_B = (+q) के कारण विभव + (-q) के कारण विभव

प्रश्न 4.
30 µC का आवेश xy निर्देश तंत्र के मूल बिन्दु पर स्थित है। \((\frac{a}{\sqrt{2}}, \frac{a}{\sqrt{2}})\) तथा (a, 0) बिन्दुओं के मध्य विभवान्तर ज्ञात करो।
हल: 

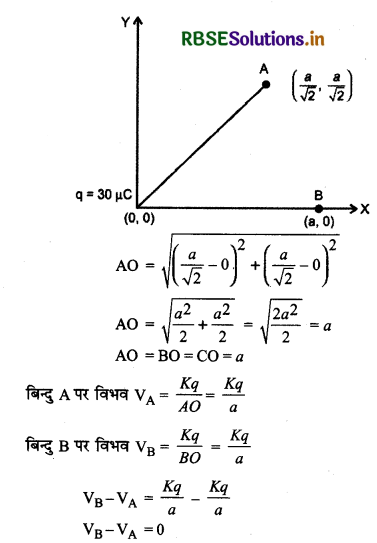
प्रश्न 5.
तीन आवेश -q, +q तथा +q क्रमशः xy तल में (0,a) (0,0) तथा (0,-a) बिन्दुओं पर स्थित है। अक्ष से कोण बनाने वाली रेखा पर r दूरी पर सिद्ध कीजिये कि विभव निम्न होगा-
\(\mathrm{V}=\frac{1}{4 \pi \varepsilon_0}\left[\frac{q}{r}+\frac{2 q a \cos \theta}{r^2}\right]\) r>>a
हल:

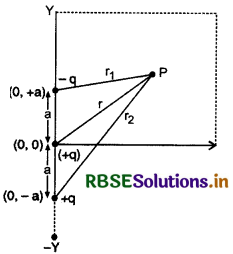
यहाँ (0,a) तथा (0, -a) पर स्थित आवेश क्रमशः -q तथा +q आवेश विद्युत द्विध्रुव का निर्माण करते है जिनके मध्य दूरी 2a है। अतः P बिन्दु पर इस विद्युत द्विध्रुव के कारण विद्युत विभव
V₁ = \(\frac{1}{4 \pi \varepsilon_0} \frac{q \cdot 2 a \cos \theta}{r^2}\)
(0,0) पर स्थित q आवेश के कारण बिन्दु P पर विभव
V₂ = \(\frac{1}{4 \pi \varepsilon_0} \frac{q}{r}\)
अत: P बिन्दु पर परिणामी विद्युत विभव
V = V₁ + V₂
\(=\frac{1}{4 \pi \varepsilon_0} \frac{2 q a \cos \theta}{r^2}+\frac{1}{4 \pi \varepsilon_0} \frac{q}{r}\)
V = \(\frac{1}{4 \pi \varepsilon_0}\left[\frac{q}{r}+\frac{2 q a \cos \theta}{r^2}\right]\)

प्रश्न 6.
एक विद्युत द्विध्रुव के आवेशों -1 µC तथा +1 µC के मध्य दूरी 4 x 10^-14 m है। द्विध्रुव के केन्द्र से 2 x 10^-6 m दूरी पर स्थित किसी अक्षीय बिन्दु पर विभव ज्ञात करो। 
हल: 

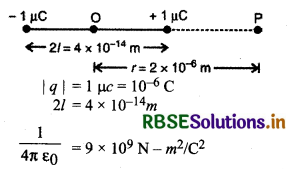
यहाँ r² >>> l²
द्विध्रुव की अक्ष पर विद्युत विभव

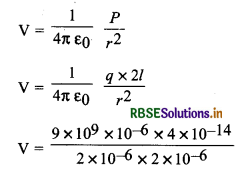
V= 90 वोल्ट 

प्रश्न 7.
दो बिन्दु आवेश क्रमशः 8 x 10^-19 C तथा -8 x 10^-19 C परस्पर 2 x 10^-10 m दूरी पर स्थित हैं। इस द्विध्रुव से 4 x 10^-6 m दूरी पर स्थित बिन्दु पर विभव ज्ञात करो जब बिन्दु (अ) द्विधुव की अक्ष पर हो (ब) द्विध्रुव निरक्ष पर हो (स) द्विषुव से 60° पर स्थित
हल:

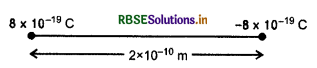
(अ) द्विधुव अक्ष पर विद्युत विभव
अक्ष पर θ = 0
cos0° = 1
P = |q| x 2l
= 8 x 10^-19 x 2 x10^-10
= 16 x 10^-29 cm
r = 4 x 10^-6 m
V = \(\frac{1}{4 \pi \varepsilon_0} \frac{\mathrm{P} \cos \theta}{r^2}\)
V = \(\frac{9 \times 10^9 \times 16 \times 10^{-29}}{\left(4 \times 10^{-6}\right)^2}\)
V = 9 x 10^-8 वोल्ट

(ब) निरक्ष पर θ = 90°, cos 90° = 0
V = 0 

(स) θ = 60° cos 60° = \(\frac{1}{2}\)

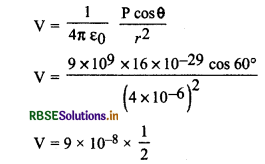
V = 4.5 x 10% वोल्ट

प्रश्न 8.
किसी विद्युत क्षेत्र में (x,y) बिन्दु पर विद्युत विभव का मान निम्न है-
V = 6xy + y² - x²
इस बिन्दु पर विद्युत क्षेत्र के मान का परिकलन कीजिये।

प्रश्न 9.
किसी विद्युत क्षेत्र में विद्युत विभव निम्न सूत्र से दिया जाता है:
V = \(\frac{343}{r}\) वोल्ट। स्थिति सदिश \(\vec{r}=3 \hat{i}+2 \hat{j}-6 \hat{k}\) पर विद्युत क्षेत्र ज्ञात करो।
हल:
V = \(\frac{343}{r}\)
\(\stackrel{\wedge}{r}=\frac{\vec{r}}{r}\)

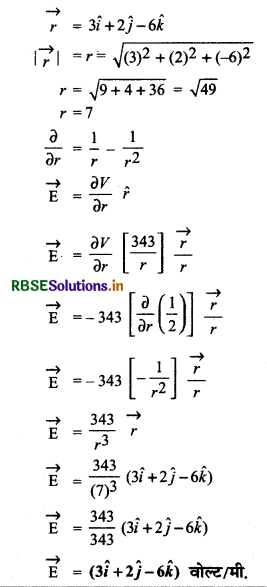
प्रश्न 10.
आवेशों +q, +2q तथा +4q को a मीटर भुजा वाले समबाहु त्रिभुज के कोनों पर रखने पर कितना कार्य करना पड़ेगा?
हल:

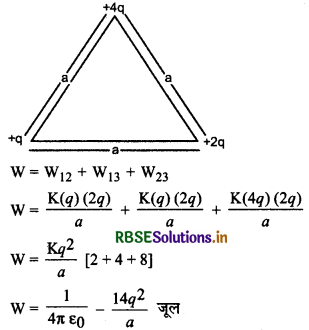
प्रश्न 11.
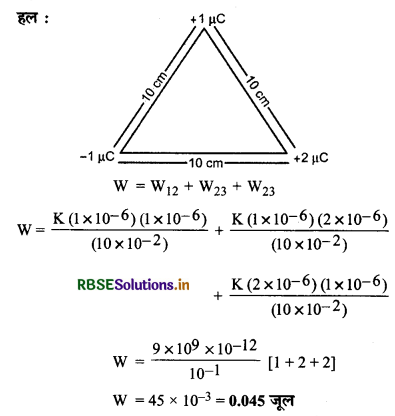
+1 µC, -1 µC और +2 µC के तीन बिन्दु आवेश आरम्भ में एक - दूसरे से अनन्त दूरी पर हैं। इन सभी आवेशों को 10 cm भुजा के किसी समबाहु त्रिभुज के शीर्षों पर स्थापित करने में किया गया कुल कार्य परिकालित कीजिए।

प्रश्न 12.
(अ) दो आवेशों +7 µC तथा -2 µC जो क्रमशः (-9 cm, 0,0) तथा (+9 cm, 0,0) पर स्थित है, के निकाय पर कोई बात य क्षेत्र आरोपित नहीं है। इस निकाय की स्थिर विद्युत स्थितिज ऊर्जा ज्ञात करो।
(ब) दोनों आवेशों को परस्पर अनन्त दूरी तक अलग करने के लिए कितना कार्य करना होगा?
हल: 
चित्र 
अत: (अ) q1 +7 µC = 7 x 10^-6 C
q2 = -2 µC = -2 x 10^-6 C
r = 18 cm = 18 x 10^-2 m
U = \(\frac{1}{4 \pi \varepsilon}-\frac{q_1 q_2}{r}\)
U = \(\frac{9 \times 10^9 \times\left(+7 \times 10^{-6}\right) \times\left(-2 \times 10^{-6}\right)}{18 \times 10^{-2}}\)
U = -0.7 J

(ब) अनन्त पर स्थितिज ऊर्जा
U₂ = 0
दी गई स्थिति में स्थितिज ऊजाँ
U₁ = -0.7 J
दोनों आवेशों को परस्पर अनन्त दूरी तक अलग करने के लिए कृत कार्य
W = U₂ - U₁
= 0 - (-0.7)
W = 0.7 J

प्रश्न 13.
किसी समान्तर पट्टिका संधारित्र की पट्टिकाओं के बीच के रिक्त स्थान को दो ढंगों से पूर्णतः भरा गया है। इसे परावैद्युतांक K के गुटके से भरा गया है। दूसरे प्रकरण में, इसे आरेख में दर्शाए अनुसार समान मोटाई के दो गुटकों, जिनके परावैधुतांक क्रमश: K₁ और K₂ हैं, से भरा गया है। दोनों ही प्रकरणों में संधारित्र की धारिता समान है। K, K₁ और K₂ में संबंध प्राप्त कीजिए।

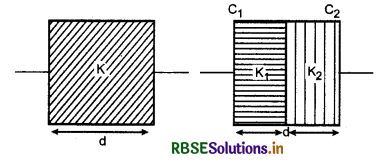
हल: 
प्रकरण (i) में-
संधारित्र की धारिता C₁ = \(\frac{K \varepsilon_0 A}{d}\)
प्रकरण (ii) में-
संधारित्र दो संधारित्रों जिनमें K₁ व K₂ परावैद्युतांक का माध्यम भरा है जो श्रेणी क्रम में संयोजित है अतः तुल्य धारिता

दोनों ही प्रकरणों में धारिता समान है। अत:
C₂ = C₁

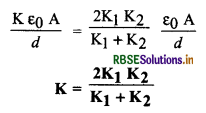
प्रश्न 14.
नीचे दिए गए आरेख में ज्ञात कीजिए
(a) नेटवर्क के बिन्दु A और B के बीच तुल्य धारिता। दिया गया है: C₁ = C₅ = 8 µF, C₂ = C₃ = C₄ = 4 µF
(b) बैटरी द्वारा आपूर्त अधिकतम आवेश, और 
(c) नेटवर्क में संचित कुल ऊर्जा

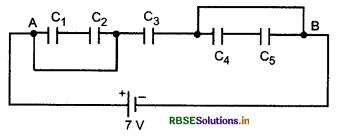
हल: 
दिया है: C₁ = 8 µF, C₂ = 4 µF, C₃ = 8 µF
C₄ = 4 µF, C₅ = 8 µF 
(a) नेटवर्क के बिन्दु A और B के बीच C₁, C₂, C₄ व C₅ लघुपथित हैं।
अत: तुल्य धारिता C = C₄ = 4 µF 

(b) आवेश Q = CV
= 4 x 7 µc
= 28 µc
 
(c) संचित ऊर्जा U =\(\frac{1}{2} \mathrm{CV}^2 \)
= \(\frac{1}{2}\) x 4 x 10^-6 x 7 x 7
= 98 x 10^-6 J

प्रश्न 15.
V वोल्ट की किसी बैटरी से किसी समान्तर पट्टिका संधारित्र को आवेशित किया गया है। इस बैटरी को हटाकर पट्टिकाओं के बीच पृथकन को आधा कर दिया जाता है। इस संधारित्र के सिरों पर नया विभवान्तर क्या होगा?
हल: 
पृथकन आधा होने पर संधारित की धारिता
C₁ = \(\frac{\varepsilon_0 \mathrm{~A}}{d / 2}=\frac{2 \varepsilon_0 \mathrm{~A}}{d}\)
C₁ = 2C 
जबकि Q = CV नियत है तब
Q = C₁V₁
V₁ = \(\frac{\mathrm{Q}}{\mathrm{C}^1}=\frac{\mathrm{CV}}{2 \mathrm{C}}=\frac{\mathrm{V}}{2}\)

प्रश्न 16.
1 µF धारिता के किसी संघारित्र को उपेक्षणीय आंतरिक प्रतिरोध तथा 10 V वि. वा. की किसी बैटरी के सिरों से संयोजित कर आवेशित किया गया है। इस संधारित्र को पूर्ण रूप से आवेशित करने में बैटरी द्वारा आपूर्त किए गए आवेश की मात्रा का परिकलन कीजिए।
हल: 
दिए है; C = 1 µF = 10^-6 F
V = 10V 
Q = CV
= 10^-6 x 10
= 10^-5 C

प्रश्न 17.

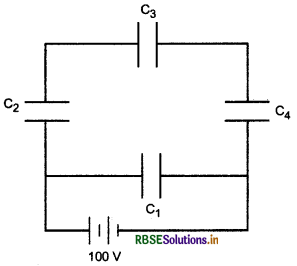
आरेख में दर्शाए चित्रानुसार, चार संधारित्रों के नेटवर्क जिनमें प्रत्येक की धारिता 12 µF है, की किसी बैटरी से संयोजित किया गया है। नेटवर्क में एकत्रित कुल आवेश ज्ञात कीजिए।
हल: 
C₂, C₃ व C₄ श्रेणीक्रम में संयोजित है अत: इनका तुल्य 
धारिता C₁ = \(\frac{C_1}{3}=\frac{12}{3} \mu \mathrm{F}\) (∵ C₁ = C₂ = C₃)
C₁ = 4 µF
C₁ व C₁ समानान्तर क्रम में हैं अत: नेटवर्क की तुल्य धारिता
C_eq = C₁ + C₁
= 4 + 12 = 16 µF 
नेटवर्क में एकत्रित कुल आवेश
Q = C_eq V
= 16 x 10^-6 x 100
Q = 16 x 10^-4 कूलॉम

प्रश्न 18.
किसी समान्तर पट्टिका संधारित्र को विभवान्तर V तक आवेशित किया गया है। इसे स्रोत से वियोजित करके समान धारिता के किसी अन्य अनावेशित संधारित्र के साथ संयोजित किया गया। इस संयोजन में संचित ऊर्जा और आरम्भ में एकल संधारित्र में संचित ऊर्जा का अनुपात परिकलित कीजिए।
हल: 
एकल संधारित्र में संचित ऊर्जा
U₁ = \(\frac{1}{2}\) C.V²
अनावेशित संधारित्र V = 0 के संधारित्र से जोड़ने पर उभयनिष्ठ विभव
V = \(\frac{\mathrm{C}_1 \mathrm{~V}_1+\mathrm{C}_2 \mathrm{~V}_2}{\mathrm{C}_1+\mathrm{C}_2}=\frac{\mathrm{CV}+0}{\mathrm{C}+\mathrm{C}}\)
V = \(\frac{\mathrm{V}}{2}\)
संयोजन कौ तुल्य ऊर्जा

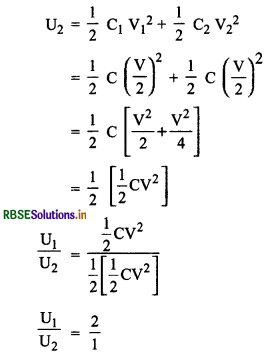
प्रतियोनी परीक्षा संबंधी प्रश्न

प्रश्न 1.
0.2 m3 आयतन के निर्वातित क्षेत्र में विद्युत विभव 5 V है तो इस क्षेत्र में विद्युत क्षेत्र का मान होगा-
(A) 1 N/C
(B) 5 N/C 
(C) शून्य
(D) 0.5 N/C 
उत्तर:
(C) शून्य

प्रश्न 2. 
एक लघु विद्युत द्विधुव का द्विध्रुव आघूर्ण 16 x 10^-9 Cm है। द्विध्रुव के अक्ष के साथ 60° का कोण बनाते हुए रेखा पर जोडे के अक्ष से 0.6 m दूरी पर स्थित बिन्दु पर द्विधुव के कारण विद्युत विभव होगा-
(A) 400 C
(B) शून्य 
(C) 50V
(D) 200 V
उत्तर:
(D) 200 V

प्रश्न 3.
एक वायु समान्तर प्लेट संधारित्र की धारिता 6 µF है। किसी परावैद्युत माध्यम की उपस्थिति में धारिता 30 µF हो जाती है। माध्यम का विद्युतशीलता होगा-
(εr = 8.85 x 10^-12 C² N^-1 m^-2) 
(A) 0.44 x 10^-10 C² N^-1 m^-2 
(B) 5.00 C² N^-1 m^-2
(C) 0.44 x 10^-13 C²N^-1 m^-2
(D) 1.77 x 10-12 C²N^-1m^-2
उत्तर:
(A) 0.44 x 10^-10 C² N^-1 m^-2  

प्रश्न 4. 
दो वर्गाकार धात्विक प्लेटों से बने संघारित्र के मध्य पृथकन d है। चित्र में दर्शाए अनुसार K परावैद्युतांक का माध्यम भरा है। तुल्य धारिता है-

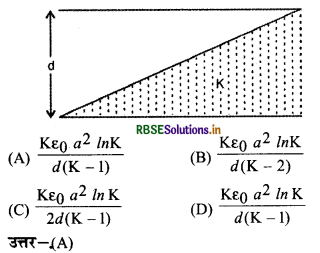
प्रश्न 5. 
एक इलेक्ट्रॉन विरामावस्था से h ऊँचाई से जांघर विद्युत क्षेत्र E में गिरता है। अब विद्युत क्षेत्र की दिशा उलट जाती है, इसका परिमाण समान रहता है। एक प्रोटॉन को विराम से कध्वं दूरी से गिरने दिया जाता है। इलेक्ट्रॉन के गिरने में लगा। प्रोटॉन के गिरने में लगा समय तुलना में-
(A) 10 गुना अधिक होगा 
(B) 5 गुना अधिक होगा 
(C) कम होगा
(D) बराबर होगा
उत्तर:
(C) कम होगा

प्रश्न 6.
90 pF धारिता के समान्तर प्लेट संघारित्र को 20V वि. वा. बल की बैटरी से जोड़ा गया है। यदि इनके मध्य K= 5/3 परावैद्युतांक के परावैद्युत पदार्थ की प्लेट को डाल दिया जाता है, तो प्रेरित आवेश का परिमाण होगा।
(A) 0.4 nC
(B) 0.9 nC 
(C) 1.2 nC
(D) 0.3 nC 
उत्तर:
(C) 1.2 nC

प्रश्न 7.
संधारित्रों से बने एक परिपथ को चित्र में दिखाया गया है। एक बिन्दु - आवेश Q (जिसका मान 4 µF तथा 9 µF वाले संधारित्रों के कुल आवेशों के बराबर है) के द्वारा 30m दूरी पर वैद्युत - क्षेत्र का परिमाण होगा।

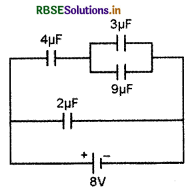
(A) 360 N/C
(B) 420 N/C 
(C) 480 N/C
(D) 240 N/C
उत्तर:
(B) 420 N/C

प्रश्न 8. 
आरेख में दर्शाए अनुसार 2 µF धारिता के किसी संधारित्रका आवेशन किया गया है। जब स्विच s को स्थिति 2 पर घुमाया जाता है, तो इसमें संचित ऊर्जा का प्रतिशत क्षय होगा।

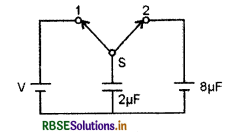
(A) 0%
(B) 20%
(C) 75%
(D) 80% 
उत्तर:
(D) 80%

प्रश्न 9. 
एक समान्तर - पट्टिका वायु संधारित्र की धारिता C है। इसे पहले V विद्युत वाहक बल के सेल से जोड़ा जाता है और फिर सेल को हटा लिया जाता है। इसके पश्चात् संधारित्र की दो पट्टिकाओं (प्लेटों) के बीच के स्थान को, एक परावैद्युत पदार्थ के स्लैब (पट्ट) से पूरा भर दिया जाता है। इस पदार्थ का परावैद्युतांक K है। इस संधारित्र के लिये निम्नलिखित में से कौन - सा कथन सही नहीं है-
(A) संधारित्र में संचित ऊर्जा K गुना कम हो जाती है
(B) संचित ऊर्जा में परिवर्तन \(\frac{1}{2} \mathrm{CV}^2\left(\frac{1}{\mathrm{~K}}-1\right)\) होता है
(C) संधारित्र पर आवेश का संरक्षण नहीं होता है 
(D) दो प्लेटों (पट्टिकाओं) के बीच विभवान्तर K गुना कम हो जाता है।
उत्तर:
(A) संधारित्र में संचित ऊर्जा K गुना कम हो जाती है

प्रश्न 10.
आरेख में दर्शाये गये अनुसार चार प्लेटों को इस प्रकार रखा गया है, कि एक प्लेट से अगली प्लेट d दूरी पर है। प्रथम तथा अंतिम (चतुर्थ) प्लेट आपस में एक तार द्वारा जुड़ी है। भीतरी दो प्लेटों के बीच V विभवान्तर है, तो प्लेट 1 तथा 2 के बीच विद्युत् क्षेत्र E का मान होगा-

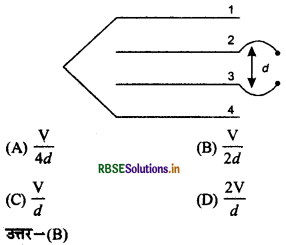
प्रश्न 11. 
R त्रिज्या के किसी एकसमान आवेशित ठोस गोले के पृष्ठ का विभव V0 है। (∞ के सापेक्ष मापा गया) यदि इस गोले के लिये \(\frac{3 \mathrm{~V}_0}{2}\), \(\frac{5 \mathrm{~V}_0}{4}\), \(\frac{3 \mathrm{~V}_0}{4}\) तथा \(\frac{V_0}{4}\) विभवों वाले समविभवी पृष्ठों की त्रिज्याएँ क्रमशः R₁, R₂, R₃ तथा R₄ है तो-
(A) R₁ =0R₂ > (R₄ - R₃)
(B) R₁ = 0 तथा (R₂ - R₁) > R₂ (R₄ - R₃) 
(C) R₁ = 0 तथा R₂ (R₄ - R₃)
(D) 2P < R₄
उत्तर:
(C) R₁ = 0 तथा R₂ (R₄ - R₃)

प्रश्न 12.
धातु के एक गोले को 10⁶ वोल्ट विभव तक आवेशित किया जाता है। वायु के आयतन को रोकने के लिए विद्युत क्षेत्र की तीव्रता को 3 x 10⁶ वोल्ट मी से अधिक नहीं होने दिया गया है। गोले पर न्यूनतम आवेश होगा-
(A) 37.1 µC
(B) 33.3 µC 
(C) 50.0 µC
(D) 73.3 µC, 
उत्तर:
(A) 37.1 µC

प्रश्न 13.
चार समान आवेश Q, जो प्रत्येक एक वर्ग जिसकी भुजा a है के कोनों पर रखे गए हैं। किसी आवेश -q को वर्ग के केन्द्र से अनन्त तक ले जाने में किया गया कार्य होगा-
(A) शून्य
(B) \(\frac{\sqrt{2} q}{\pi \varepsilon_o \mathrm{a}}\)
(C) \(\frac{q^2}{2 \pi \varepsilon_o a}\)
(D) \(\frac{\sqrt{2} q^2}{\pi \varepsilon_o a}\)
उत्तर:
(D) \(\frac{\sqrt{2} q^2}{\pi \varepsilon_o a}\)

प्रश्न 14. 
माना त्रिविम में एक विद्युत क्षेत्र\( \vec{E}=30 x^2 \hat{i}\) है। तब विभवान्तर V_A - V₀, जहाँ V₀ मूल बिन्दु पर विभव तथा V_A, x = 2m पर विभव है, है-
(A) 120 J
(B) -120 J
(C) -80 J
(D) 80 J
उत्तर:
(C) -80 J