RBSE Class 12 Physics Important Questions Chapter 2 Electrostatic Potential and Capacitance

Rajasthan Board RBSE Class 12 Physics Important Questions Chapter 2 Electrostatic Potential and Capacitance Important Questions and Answers.

RBSE Class 12 Physics Chapter 2 Important Questions Electrostatic Potential and Capacitance

Multiple Choice Questions

Question 1.
A circle of radius ‘r’ is drawn with charge ‘+q' at the center. A charge q₀ is brought from the point B to C. Then work done is:

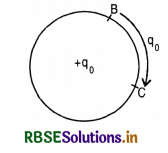
(A) positive
(B) negative
(C) infinite
(D) zero.
Answer:
(D) zero.

Question 2.
Angle between equipotential surface and electric field line is:
(A) zero
(B) 180°
(C) 90°
(D) 45°.
Answer:
(C) 90°

Question 3.
What is the dimensional formula of capacitance?
(A) [M^-1L^-2T⁴A²]
(B) [M^-1L^-2T⁴A^-2]
(C) [M^-1L^-2T^-4A²]
(D) [M^-1L^-2T^-4A^-2].
Answer:
(A) [M^-1L^-2T⁴A²]

Question 4.
The work done in moving a positive charge on an equipotential surface is:
(A) Negative
(B) Positive
(C) Zero
(D) Infinite.
Answer:
(C) Zero

Question 5.
If n capacitors are connected in parallel to a V-volt source, then total energy of the system is:
(A) CV
(B) \(\frac{1}{2}\)CV²
(C) \(\frac{1}{2}\)nCV²
(D) \(\frac{1}{2 n}\)CV²
Answer:
(C) \(\frac{1}{2}n\)CV²

Question 6.
What is the dimensional formula of electric potential?
(A) [M²L²T^-3A^-1]
(B) [ML²T^-3A^-1]
(C) [ML²T^-2A^-1]
(D) [ML²T^-2A¹]
Answer:
(A) [M²L²T^-3A^-1]

Question 7.
The SI unit of potential gradient is:
(A) Vm^-1
(B) Vm
(C) Cm
(D) Wb.
Answer:
(A) Vm^-1

Question 8.
Dimensional formula for potential difference is:
(A) M⁰L²T^-2A^-1
(B) ML²T^-2A^-1
(C) ML²T^-3A^-1
(D) MLT^-2A.
Answer:
(C) ML²T^-3A^-1

Question 9.
Dimensional formula of dielectric strength is:
(A) [MLT³A]
(B) [ML³TA^-1]
(C) [MLT^-3A^-1]
(D) [MLT^-3A].
Answer:
(C) [MLT^-3A^-1]

Question 10.
On what factors the capacitance of a capacitor depends?
(A) Nature of dielectric
(B) Area of plate
(C) Distance between plates
(D) All.
Answer:
(D) All.

Question 11.
Electric potential at a point in an electric field:
(A) energy
(B) work done
(C) force
(D) work done per unit charge.
Answer:
(D) work done per unit charge.

Question 12.
Capacitance of earth is considered to be:
(A) 711 µF
(B) 0
(C) ∝
(D) uncertain.
Answer:
(A) 711 µF

Question 13.
Energy per unit volume for a capacitor having area A and separation d kept at a potential difference V is given by
(A) \(\frac{1}{2} \varepsilon_0 \frac{\mathrm{V}^2}{d^2}\)
(B) \(\frac{1 \mathrm{~V}^2}{2 \varepsilon_0 d^2}\)
(C) \(\frac{1}{2} \mathrm{CV}^2\)
(D) \(\frac{\mathrm{Q}^2}{2 \mathrm{C}}\)
Answer:
(A) \(\frac{1}{2} \varepsilon_0 \frac{\mathrm{V}^2}{d^2}\)

Question 14.
Relation between dielectric constant ‘K’ and electric susceptibility ✗_e is:
(A) ✗_e = 1 + k
(B) ✗_e = k - 1
(C) ✗_e = \(\frac{1}{1+k}\)
(D) k = \(\frac{1}{1+\chi_e}\)
Answer:
(B) ✗_e = k - 1

Question 15.
What will be the resultant capacitance of capacitor connected as shown in the figure between A and B?

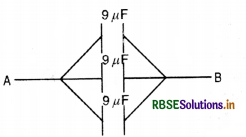
(A) \(\frac{1}{3}\) µF
(B) 27 µF
(C) \(\frac{9}{3}\) µF
(D) \(\frac{27}{3}\) µF.
Answer:
(B) 27 µF

Question 16.
What will be the resultant capacitance of capacitors connected as shown in figure between A and B?

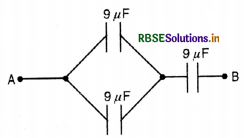
(A) 6 µF
(B) 2 µF
(C) 27 µF
(D) 4 µF.
Answer:
(A) 6 µF

Question 17.
Can a body have charge and still be at zero potential?
(A) yes, always
(B) yes, but not always
(C) never
(D) depends on nature of the charge.
Answer:
(B) yes, but not always

Question 18.
For a point charge located in space, equipotential surfaces are:
(A) concentric circles
(B) concentric spheres
(C) parallel plates
(D) parallel linear lines.
Answer:
(B) concentric spheres

Question 19.
A charge of 10 µC experiences a force of 5 N in an electric field. The potential gradient at that point is:
(A) 2 x 10⁶ NC ^-1
(B) 2 x 10^-6 NC^-1
(C) 0.5 x 10^-6 NC^-1
(D) 0.5 x 10⁶ NC^-1
Answer:
(D) 0.5 x 10⁶ NC^-1

Question 20.
The electric potential ah the surface of an atomic nucleus (Z = 50) of radius 9.0 x 10^-15 m is:
(A) 80 V
(B) 8 x 10⁶ V
(C) 9 V
(D) 9 x 10⁵ V.
Answer:
(B) 8 x 10⁶ V

Question 21.
Which of the following is a volt?
(A) joule per coulomb
(B) erg per ampere
(C) erg per cm
(D) newton/(coulomb x metre²).
Answer:
(A) joule per coulomb

Question 22.
Two charges are placed a finite distance apart. If a glass slab is placed between them, force between them will:
(A) be zero
(B) increase
(C) decrease
(D) remains the same.
Answer:
(C) decrease

Question 23.
An alpha particle is accelerated through a potential difference of 10⁴ V. The gain in K.E. of the alpha particle is:
(A) 2 x 10⁴ eV
(B) 2 x 10^-4 eV
(C) 2 x 10⁴ J
(D) 2 x 10⁴ erg.
Answer:
(A) 2 x 10⁴ eV

Question 24.
If charge on the capacitor is doubled, the value of its capacitance will be:
(A) doubled
(B) halved
(C) remains same
(D) None of these.
Answer:
(C) remains same

Question 25.
When a thick plate of a dielectric is placed in the air space of a parallel plate capacitor, then:
(A) capacitance decreases
(B) capacitance increases
(C) capacitance remains unchanged
(D) capacitance becomes zero.
Answer:
(B) capacitance increases

Question 26.
A very-very thin sheet of aluminium is placed in between the plates of the capacitor, the capacitance will
(A) increase
(B) decrease
(C) remains same
(D) may increase or decrease.
Answer:
(C) remains same

Question 27.
Capacitor of capacity 1 µF is charged with a charge 40 µC. The energy stored in the condenser is:
(A) 180 x 10^-6 J
(B) 1800 J
(C) 800 x 10^-6 J
(D) 16000 J
Answer:
(C) 800 x 10^-6 J

Fill in the blanks

Question 1.
.............................. is the degree of electrification.
Answer:
Electric potential.

Question 2.
Potential is a .............................. quantity.
Answer:
scalar.

Question 3.
Two different equipotential surfaces .............................. intersect each other.
Answer:
cannot.

Question 4.
The basic use of a capacitor is to    .............................. charge and energy.
Answer:
store.

Question 5.
Physical quantity having unit JC^-1 is ..............................
Answer:
Electric potential.

Question 6. 
A dielectric is used in a capacitor to .............................. its capacitance.
Answer:
increase.

Question 7.
Water has very .............................. dielectric constant.
Answer:
high.

Question 8.
Line integral of electric field is    .............................. of the path followed.
Answer:
independent.

Question 9.
Electric potential .............................. only on the distance from the source charge.
Answer:
depends.

Question 10.
A .............................. is a material in which all the electrons are tightly bound to the nuclei of atoms.
Answer:
dielectric.

Very Short Answer Type Questions

Question 1.
What is the work done by the field of a nucleus in a complete circular orbit of the electron? What if the orbit is elliptical?
Answer:
Since we know work done in moving a charge along a closed orbit is zero so no work is done by the field of a nucleus in a complete circular orbit of the electron. As work done is zero for a closed path, so elliptical orbit or circular orbit have the same meaning.

Question 2.
Is it possible to produce high voltage on the human body without getting a shock?
Answer:
Yes. If the body is perfectly insulated from the ground. Since there is no potential difference acting on the body, so no current will pass through the body and the human body will not receive any shock.

Question 3.
Would electrons move from higher potential to lower potential or vice versa?
Answer:
Since positive charge moves from higher to lower potential, so the electrons being negatively charged move from lower to higher potential.

Question 4.
A small test charge is released at rest at a point in the electrostatic field configuration. Will it travel along the line of force at that point?
Answer:
Not necessarily. It is true only if the line of force is a straight line. The line of force gives the direction of acceleration and not that of velocity, in general.

Question 5.
Is potential difference more basic or potential?
Answer:
Potential difference is more basic, because the potential at a point can be called the potential difference between the given point and at infinity.

Question 6.
What is the condition required to choose potential at infinity to be zero?
Answer:
The distribution of charge must be finite.

Question 7.
Define the term “dielectric constant” of a medium in terms of capacitance of a capacitor.
Answer:
Since capacitance of a capacitor with vacuum as a medium is given by
C_v = \(\frac{\varepsilon_0 \mathrm{~A}}{d}\)
And capacitance of a capacitor with dielectric of dielectric constant K as medium between the plates is
C_m = \(\frac{\mathrm{K} \varepsilon_0 \mathrm{~A}}{d}\)
∴ \(\frac{C_m}{C_v}\) = K
Thus dielectric constant of a medium is defined as the ratio of the capacitance of a capacitor with medium as dielectric to the capacitance of the capacitor with medium as vacuum (or air).

Question 8.
Define the unit of electric potential.
Answer:
The unit of electric potential is volt. The electric potential at a point in an electric field is said to be one volt, if 1 J of work is done in bringing 1 C charge from infinity to that point against the electrostatic force.

Question 9.
The electric potential is constant in a region. What can you say about electric field there?
Answer:
Since electric field intensity
E = -\(\frac{d \mathrm{~V}}{d r}\)
So, when V is constant, \(\frac{d \mathrm{~V}}{d r}\) = 0
or E = 0
Hence, if electric potential is constant, electric field is zero. 

Question 10.
Are we free to call the potential of our reference point as + 100 V instead of zero?
Answer:
Yes. The potential of the reference point can be assigned any value whatsoever as per the requirements of the situation.

Question 11.
Why do we often regard the potential of the earth to be zero?
Answer:
The earth behaves as a very big conductor for our general point of view, and addition and removal of small charge from earth does not make any significant change, hence the potential of earth remains constant for all practical purposes. So due to this constancy of potential, we consider the potential of earth as zero for our convenience for all practical purposes.

Question 12.
What is resultant electric field intensity inside a conductor kept in an electrostatic field?
Answer:
The resultant electric field intensity is zero inside a conductor kept in an electrostatic field.

Question 13.
What is electric field intensity inside a cavity of a conductor kept in an electric field?
Answer:
Electric field intensity is zero inside a cavity of a conductor kept in an electrostatic field.

Question 14.
What is effect of dielectric on the capacitance of a capacitor?
Answer:
A dielectric increases the capacitance of a capacitor in proportion with its dielectric constant.

Question 15.
Write expression for the capacitance of the series combination of n capacitors.
Answer:
The required expression is,
\(\frac{1}{\mathrm{C}_s}=\frac{1}{\mathrm{C}_1}+\frac{1}{\mathrm{C}_2}+\ldots \ldots \ldots .+\frac{1}{\mathrm{C}_n} \)

Question 16.
How can the energy of a capacitor be decreased by keeping the charge on the capacitor unchanged?
Answer:
Energy U = \(\frac{q^2}{2 \mathrm{C}}\)
As q is constant
∴ U ∝ \(\frac{1}{\mathrm{C}}\)
But C ∝ dielectric.
So U can be decreased by increasing the dielectric constant of the medium.

Question 17.
What is the value of potential at any point on the equatorial line of an electric dipole?
Answer:
Zero.

Question 18.
Is the electrostatic potential necessarily zero at a point where the electric field strength is zero? Give an example to illustrate your answer.
Answer:
No. Since E = -\(\frac{d \mathrm{~V}}{d r}\)
So, if E = 0, \(\frac{d \mathrm{~V}}{d r}\) = 0 or V = constant
For example, the electric field inside a charged hollow spherical shell is zero and potential is constant and has the same value as the potential on the surface of the spherical shell.

Question 19.
Does the positive or negative nature of electric potential depend upon the nature of test charge?
Answer:
No, the positive or negative nature of electric potential is independent of the (+ve or - ve) nature of test charge. But it depends upon the nature of source charge.

Question 20.
The electric potential at a point in the electric field is V. What is the electric potential energy of a charge q0 placed at that point?
Answer:
Potential energy U = q₀V.

Question 21.
What is the physical significance of the line integral of electric field strength?
Answer:
The line integral of electric field strength gives the amount of work done in displacing a unit test positive charge between the limits of integration.

Question 22.
What is the unit and dimensions of electrostatic potential?
Answer:
Unit of potential in S.I. is volt.
Dimensional formula of potential
= \(\frac{\mathrm{W}}{q_0}=\frac{\left[\mathrm{ML}^2 \mathrm{~T}^{-2}\right]}{[\mathrm{AT}]}=\left[\mathrm{ML}^2 \mathrm{~T}^{-3} \mathrm{~A}^{-1}\right]\)

Question 23.
Name the physical quantity which has its unit joule/coulomb [JC^-1]. Is it scalar or vector?
Answer:
The physical quantity having unit JC^-1 (= volt) is potential or potential difference and it is a scalar quantity.

Question 24.
What is the work done in moving a charge of 10 nC between two points on an equipotential surface?
Answer:
On an equipotential surface, the potential difference between two points is zero i.e.
V = 0
∴ Work done,
W = V.q
= 0 x 10 n
or W = 0

Question 25.
What is the shape of the equipotential surfaces for a given point charge?
Answer:
For a point charge, the equipotential surfaces are co-centric spheres centered at the locations of the point charge itself.

Question 26.
State whether the direction of an electrostatic field is along that of rise or fall of electrostatic potential?
Answer:
The direction of an electrostatic field is from higher potential to lower potential i.e. it is along the fall of potential.

Question 27.
What is a capacitor?
Answer:
A capacitor is a system of two conductors having equal and opposite charges (+q & -q) and separated by a small distance, by an insulator or dielectric.

Question 28.
When a dielectric is inserted in between the plates of a capacitor how does the capacitance change?
Answer:
The capacitance of the capacitor increases by a factor K (K is dielectric constant of the dielectric).

Question 29.
Where does the energy of a capacitor reside?
Answer:
The energy of a capacitor resides within the dielectric medium separating the two plates.

Question 30.
Is there any conductor which can be given unlimited charge?
Answer:
Yes, earth is one such conductor.

Question 31.
What is meant by dielectric strength of a medium?
Answer:
The dielectric strength of a medium is the maximum line of electric field strength that can be set-up in the dielectric without causing electric breakdown.

Question 32.
What is the basic use of a capacitor?
Answer:
The basic use of a capacitor is to store charge and energy.

Question 33.
Can there be a potential difference between two conductors of the same volume carrying equal positive charges?
Answer:
Yes. Because two conductors having the same volume may have different shapes hence their capacitances may be different and there can be a potential difference between them.

Question 34.
What are the dimensions of capacitance?
Answer:
Dimensions of capacitance

Question 35.
What is the net charge on a charged capacitor?
Answer:
Zero. Because the two plates of charged capacitor carry equal and opposite charges. Hence net charge is zero.

Question 36.
Can a metal sphere of radius 1 cm hold a charge of 1 C?
Answer:
No, because the potential of a metal sphere will become
V = \(\frac{1}{4 \pi \varepsilon_0} \frac{q}{r}\)
= 9 x 10⁹ x \(\frac{1}{10^{-2}}\)
= 9 x 10¹¹ V
This potential is much greater than required to ionise the air and the charge leaks to surrounding air.

Question 37.
When a potential difference is applied across the ends of a conductor, how is the drift velocity of the electrons related to the relaxation time?
Answer:
Drift velocity is directly proportional to the relaxation time.
v_d = \(\frac{e \mathrm{E}}{m} \tau\)

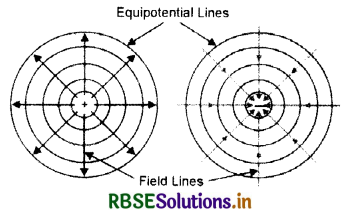
Question 38.
Draw the equipotential surfaces due to an isolated point charge.
Answer:
These are as shown in Fig. VSAQ 38.

Question 39.
A 500 µC charge is at the center of a square of side 10 cm. Find the work done in moving the charge of 10 µC between two diagonally opposite points on the square.
Answer:
Two diagonally opposite points on a square are equidistant from the center of square where the source charge 500 µC is located. Hence the potential on the two points is the same.
∴ Work done in moving q₀ = 10 µC from one point to another is
W = q₀(V - V) = 0.

Question 40.
A uniform electric field exists between two charged plates as shown in the figure VSAQ 40. What should be the work done in moving a charge q along the closed rectangular path ABCDA?

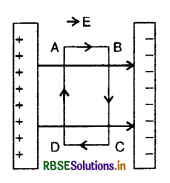
Answer:
The work done in moving charge q along closed rectangular ABCDA is zero.
Because W = q (VA - VA) = 0.

Question 41.
A point charge Q is placed at point O as shown in the figure VSAQ 41. Is the potential difference V_A - V_B positive, negative or zero, if Q is (i) positive (it) negative.

Answer:
V_A - V_B is + ve, if Q is positive, and V_A - V_B is - ve, if Q is negative.

Question 42.
Define electric potential at a point in an electric field.
Answer:
V_A - V_B is + ve, if Q is positive, and V_A - V_B is - ve, if Q is negative.

Question 43.
A and B are two conducting spheres of the same radii. A being solid and B hollow. Both are charged to the same potential. What will be the relation between the charges on the two spheres?
Answer:
Since spheres A and B are of the same radii, hence their capacitance is the same and both have the same charges.

Question 44.
Why does the electric field inside a dielectric decrease when it is placed in an external field?
Or
How does the electric field inside a dielectric decrease when it is placed in an external electric field.
Answer:
The electric field inside the dielectric decreases because the polarisation of dielectric set up an electric field opposite to the applied electric field.

Question 45.
Two protons A and B are placed between two parallel plates having a potential difference V as shown in the figure VSAQ 45. Will these protons experience equal or unequal force?

Answer:
Since the electric field is uniform throughout the parallel plates, so both the protons will experience the same force.

Question 46.
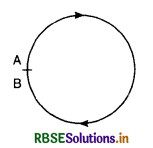
What would be the work done if a point charge +q is taken from a point A to the point B on the circumference of a circle with another point charge +q at the center?

Answer:
Since the circumference of the circle is an equipotential surface, hence work done from A to B is zero.

Question 47.
What is an equipotential surface?
Answer:
Equipotential surface. Any surface, which has the same electrostatic potential at every point is called an equipotential surface.

Question 48.
Draw an equipotential surface in a uniform electric field.
Answer:

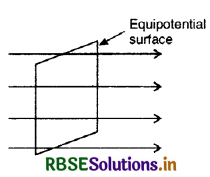
Question 49.
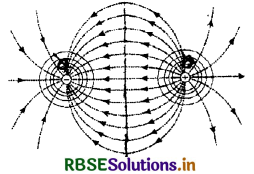
Draw an equipotential surface for a system consisting of two charges Q, -Q separated by a distance r in air.
Answer:
The equipotential surfaces are shown by solid lines.

Question 50.
If a point charge +q is taken first from A to C and then from C to B of a circle drawn with another point charge +q as center as shown in the figure, then along which path more work will be done.

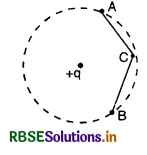
Answer:
Points A and B are on the circle and have the same potential so V_C - V_A = V_C - V_B
So work done in taking a point charge from A to C is equal to the work done in taking a point charge from C to B.

Question 51.
Give the dependence of electrostatic potential due to a small electric dipole at a far-off point lying on (i) the axial line and (ii) the equatorial line.
Answer:
(i) For small electric dipole, on the axis line
V ∝ \(\frac{1}{r^2}\)
(ii) On the equatorial line.
V    =    0.

Question 52.
What is the shape of equipotential surface for a given point charge?
Answer:
The equipotential surface for a given point charge co-centric spherical shells, whose centers are located at the given point charge.

Question 53.
How much work is done in moving a 500 µC charge between two points on an equipotential surface?
Answer:
No work is done in moving a charge from one point to another on an equipotential surface.

Question 54.
Define capacitance of a capacitor.
Answer:
The capacitance of a capacitor is defined as the ratio of charge on either plate and the potential difference between the plate i.e. C = Q/V.

Question 55.
What is the function of a dielectric in a capacitor?
Answer:
The dielectric introduced between the plates of a capacitor increases the capacitance of the capacitor.

Question 56.
Sketch a graph to show how the charge Q acquired by a capacitance C varies with increase in potential difference between its plates.
Answer:
The graph between Q and V is as shown in the figure.
The slope of Q-V graph gives the capacitance of the capacitor.

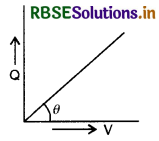
i.e. Slope = tan θ = \(\frac{\mathrm{Q}}{\mathrm{V}}\) = C

Question 57.
In an electric field an electron is kept freely. If a proton replaces this electron, what will be the relationship between the forces experienced by them?
Answer:
F_proton = F_electron.

Question 58.
The distance of the field point on the equatorial plane of a small electric dipole is halved. By what factor does the electric field due to the dipole change?
Answer:
For a small electric dipole
E_equi = \(\frac{1}{4 \pi \varepsilon_0} \frac{q}{r^3}\)
or E_equi ∝ \(\frac{1}{r^3}\)
So when r is made \(\frac{r}{2}\), the electric field intensity will increase 2³ = 8 times the original field.

Question 59.
Name the dielectric whose molecules have:
(i) non-zero and (ii) zero dipole moment.
Answer:
(i) Water has non-zero dipole moment.
(ii) Diamond has zero dipole moment.

Question 60.
Define dielectric constant of a medium in terms of capacitance of a capacitor.
Answer:
Dielectric constant of a medium is defined as the ratio of the capacitance of the capacitor, when the dielectric as medium to the capacitance of the same capacitor with air as medium.

Question 61.
What are the factors on which capacitance of a parallel plate capacitor depends? Also give the formula.
Answer:
The capacitance of a parallel plate capacitor depends upon:

• Relative permittivity of the medium.
• Area of the plate and
• Distance between the plates.

C = \(\frac{\mathrm{K} \varepsilon_0 \mathrm{~A}}{d}\)

Question 62.
In the given figure VSAQ 62 charge Q is placed at the center of a dotted circle. Work done in taking another charge +q from A to B is W₁ and from B to C is W₂. Which one of the following is correct W₁ > W₂, W₁ = W₂ and W₁ < W₂.

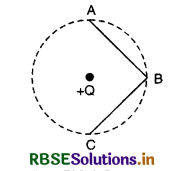
Answer:
As W = Q (q₁ - q₂)
V_A - V_B = V_B - V_C
∴ W₁ = W₂

Short Answer Type Questions

Question 1.
Show that the work done in moving a unit charge along a closed path is zero.
Answer:
The work done in moving a unit charge from A to B along l₁ is:

Hence no work is done in moving a unit positive test charge over a closed path in an electric field.

Question 2.
How can a positively charged body be at zero or negative potential?
Answer:
If a positively charged body B is moved gradually towards a small positively charged body A, at a particular distance, the -ve charge induced on A due to B will become equal to +ve charge initially present on body A. Hence the body A will be at zero potential. If body B is further moved towards A, -ve charge will be induced on body A. Hence body A will be +vely charged but at -ve potential. So a positively charged body can be at zero or negative potential.

Question 3.
Discuss that potential is spherically symmetric for a point charge. Define eV, MeV, meV.
Answer:
It means that the potential does not depend on the direction of the point w.r.t. charge but it depends upon the distance of the charge.
It is +ve for q > 0 and -ve for q < 0.

Electron volt is defined as the amount of energy gained when an electron falls under a potential difference of 1 volt.
If the work done in moving a charge ‘q’ from one point to the other, then potential difference is 
V = \(\frac{\mathrm{W}}{q}\)
W = qV
or q = 1e = 1.6 x 10^-19 C
V = 1 volt
Then W = 1 eV
1 eV = 1.6 x 10^-19 C x 1 V
= 1.6 x 10^-19 CV
1 eV = 1.6 x 10^-19 J [∵ 1 CV = 1 J]
1 keV = 10³ x 1.6 x 10^-19 J
=    1.6 x 10^-16 J
1 MeV = 10⁶ x 1.6 x 10^-19 J
=    1.6 x 10^-13 J
1GeV = 10⁹ eV
=    10⁹ x 1.6 x 10^-19 J
=    1.6 x 10^-10 J
1 meV = 10^-3 x 1.6 x 10^-19
=    1.6 x 10^-22 J

Question 4.
State and define S.I. units of potential. Derive dimensional formula of potential difference.
Answer:
The S.I. unit of potential is 1 volt or 1 joule/C.
The electrostatic potential at a point is said to be one volt if one joule of work is done in moving a charge of 1 Coulomb from ∞ to that point against the electrostatic forces.
Pot.difference = \(\frac{\text { Work }}{\text { Charge }}\)
∴ V = \(\frac{\left[\mathrm{ML}^2 \mathrm{~T}^{-2}\right]}{[\mathrm{A} . \mathrm{T}]}=\left[\mathrm{ML}^2 \mathrm{~T}^{-3} \mathrm{~A}^{-1}\right]\)

Question 5.
Give the physical meaning of electrostatic potential.
Answer:
Level of water determines the direction of flow of water. Similarly, temperature of a body determines the direction of flow of heat from or towards the body when it is brought in contact with another body. Exactly on these lines electrostatic potential of a body represents its state of electrification/charging which determines the direction of flow of charge when this body is kept in contact with another charged body. The charge always flows from a body at higher potential to the one at lower potential. The flow continues till their potentials are equal. Earth is supposed to: be at zero potential. When a charged body is held in Contact with earth, and charge flows from body to earth, the potential of body must be greater than the potential of earth. Hence the potential of the body must be positive (>zero). On the contrary, if charge flows from earth to body the potential of the body is said to be negative (< zero).

Question 6.
Show that electrostatic forces are conservative in nature.
Answer:
We know that work done against electrostatic force in moving a unit positive test charge from a point A to another point, B in electric field is
W = \(V(\overrightarrow{r_A}) - V(\overrightarrow{r_B})\)
This work done is independent of the path followed. If we have a closed loop, i.e. B coincides with A, then W = 0 i.e. no net work is done in carrying a unit positive test charge (or any other charge for that purpose) around a closed loop in an electrostatic field.

This means if some work is done by us in moving a charge in one part of the closed loop, we shall recover the same amount of work in moving the charge in the other part of the loop. This establishes that electrostatic forces are conservative in nature.

Question 7.
Show that electric potential = \(\frac{\text { Potential Energy }(\mathbf{U})}{\text { Charge }(q)}\).
Answer:
The potential energy U of a system of two charges q and q0 separated by a distance r is given by
U = \(\frac{1}{4 \pi \varepsilon_0} \frac{q q_0}{r}\) .......................(1)
The potential V at a distance r from charge q0 is given by
V = \(\frac{1}{4 \pi \varepsilon_0} \frac{q_0}{r}\) .........................(2)
Dividing eq.(2) by (1), we get
\(\frac{\mathrm{V}}{\mathrm{U}}=\frac{1}{q}\)
or V = \(\frac{\mathrm{U}}{q}\)
i.e. Electric potential = \(\frac{\text { Potential Energy }(\mathbf{U})}{\text { Charge }(q)}\)

Question 8.
What is the importance of equipotential surfaces?
Answer:
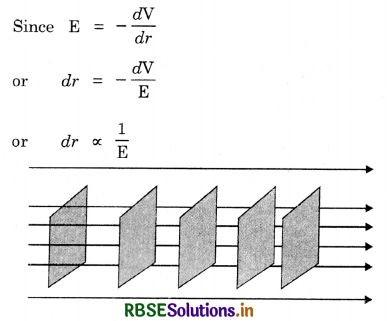
The drawings of equipotential surfaces give us a visual picture of both the magnitude as well as direction of electric field intensity in region of space.
In the region of strong electric fields, equipotential surfaces are close together. The reverse is also true. This follows from
E = -\(\frac{d \mathrm{~V}}{d r}\) i.e. dr = -\(\frac{d \mathrm{~V}}{\mathrm{E}}\) or dr ∝ \(\frac{1}{\mathrm{E}}\)

Question 9.
Define conductors and insulators. Why conductors were called non-electrics and insulators were called dielectrics? Describe two types of dielectrics.
Answer:
Conductors and Insulators. A substance, which allows an electric current to flow through itself, is called a conductor. It has free electrons inside itself. Examples are metals, human body, earth etc.
A substance, which does not allow an electric current to flow through itself, is called an insulator. It does not have free electrons inside itself. Examples are ebonite, glass, quartz, rubber, plastic etc.
Non-electric and Dielectric. When a conductor was rubbed, electric charge produced on it was conducted away through body to earth. As no charge was found present on the rubbed conductor, it was supposed to have no charge. Hence it was called non-electric.
On the other hand, charge stays in an insulator when it is rubbed. It was supposed to have charge. Hence it was called dielectric.
Types of dielectric. Dielectrics are of two types- polar and non-polar.

• Polar dielectrics. Their atoms have separate centers of positive and negative charges. These separated centers are called poles and the atoms are called dipoles.
• Non-polar dielectrics. Their atoms do not have separate centers of positive and negative charges in normal conditions. But inside an electric field, they develop poles.

Question 10.
Two copper spheres of radii r₁ and r₂ having charges q₁ and q₂ are connected by means of a wire. What is the electrical condition that no charge flows between them?
Answer:
In Fig. SAQ 10 we have two copper spheres A and B of radii r₁ and r₂ having charges q₁ and q₂ respectively.
Potential of A
V₁ = \(\frac{1}{4 \pi \varepsilon_0} \frac{q_1}{r_1}\)

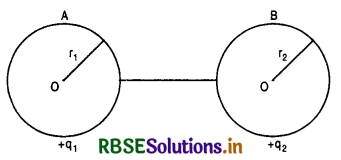
Potential of B
V₂ = \(\frac{1}{4 \pi \varepsilon_0} \frac{q_2}{r_2}\)
On connecting these two spheres by a wire, the charge will flow from a body at higher potential to the body at low potential, till the potential of both spheres becomes equal.
So the electrical condition that no charge flows between them is that when
Potential of sphere A = Potential of sphere B
or \(\frac{1}{4 \pi \varepsilon_0} \frac{q_1}{r_1} = \frac{1}{4 \pi \varepsilon_0} \frac{q_2}{r_2}\)
or q₁r₂ = q₂r₁
This is the condition when flow of charge will stop.

Question 11.
Two point charges 4 µC and - 2 µC are separated by a distance of 1 m in air. At what point on the line joining the charges is electric potential zero?
Answer:
Let the potential at P at a distance x meter from A be zero.

Question 12.
Discuss the variation of electric field strength and electric potential due to a charged spherical conducting shell when we move from infinity to the center of the shell. 
Answer:
The electric field E and electric potential V due to a charged spherical shell of charge q at a distance r (outside the shell) are given as
E = \(\frac{q}{4 \pi \varepsilon_0 r^2}\) and
V = \(\frac{q}{4 \pi \varepsilon_0 r}\)
At infinity r = ∞, so E = V = 0.
Now as we move from infinity towards the sphere, both E and V start increasing in magnitude, but the rate of increase of V is higher than that of E.
At the surface of the shell, both E and V acquire the maximum value. As we move inside the shell, E becomes zero but V remains constant, equal to that on the surface of the shell.

Question 13.
Calculate the electric potential at the surface of a gold nucleus. Given radius of nucleus = 6.6 x 10^-15 m and atomic weight of gold is 79.
Answer:
Here charge on the nucleus
q = Ze = 79 x 1.6 x 10^-19 C
Radius of nucleus r = 6.6 x 10^-15 m
∴ Electric potential V = \(\frac{1}{4 \pi \varepsilon_0} \frac{q}{r}\)
or V = 9 x 10⁹\(\frac{79 \times 1.6 \times 10^{-19}}{6.6 \times 10^{-15}}\)
= 1.66 x 10⁷ volt.

Question 14.
A cube of side b has a charge q at each of its vertices. Determine the potential and electric field due to this charge at the center of the cube.
Answer:
Let r = distance of each charge at vertex from the center of cube.

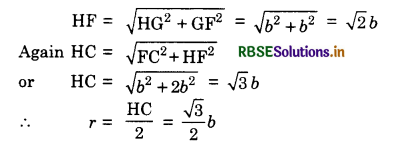
Potential at the centre O = Potential due to each of 8 charges

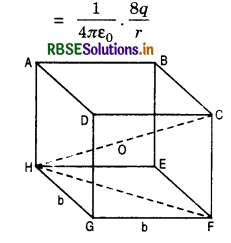
∴ Potential at O, V = \(\frac{1}{4 \pi \varepsilon_0} \times \frac{8 q \times 2}{\sqrt{3} b}\)
= \(\frac{4 q}{\sqrt{3} \pi \varepsilon_0 b}\)
However, electric field inside a symmetrically shaped surface is zero since fields will mutually cancel each other.

Question 15.
A charge q is distributed over two concentric hollow spheres of radii r and R such that the surface densities are equal. Find the potential at the common center.
Answer:
Let q₁ and q₂ be charges on two hollow spheres having radii r and R respectively.
So q = q₁ + q₂
As the surface densities of two hollow spheres are equal
 

Question 16.
A point charge q is placed at O as shown in the figure.
Is V_P - V_Q positive or negative when (i) q > 0 and (ii) q < 0? Justify your answer.

Answer:
Let OP = r_P and OQ = r_Q

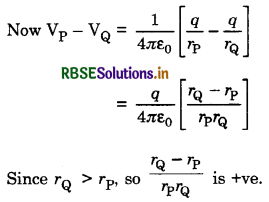
∴ (i) If q is positive, V_P - V_Q = positive
(ii) If q is negative, V_P - V_Q = negative.

Question 17. 
Two small charged bodies interact in air with a force F. What will be the force of interaction between these bodies be after they are placed in a dielectric of permittivity K, if their potentials are kept the same as they were in air?
Answer:
The force of interaction between two bodies having charges q₁ and q₂ and separated by a distance r in air is given by
F = \(\frac{1}{4 \pi \varepsilon_0} \frac{q_1 q_2}{r^2}\)
When these charged bodies are placed in a dielectric of permittivity K, the potential of each charged body will decrease by a factor K So to keep the potential the same, the charges of the two bodies must be made K q₁ and K q₂
Hence the force of interaction between these two charged bodies in a medium having dielectric of permittivity K will be
F₁ = \(\frac{1}{4 \pi \varepsilon_0 \mathrm{~K}} \frac{\left(\mathrm{K} q_1\right)\left(\mathrm{K} q_2\right)}{r^2}\)
= K\(\left[\frac{1}{4 \pi \varepsilon_0} \frac{q_1 q_2}{r^2}\right]\)
or F₁ = KF
i.e. the force of interaction will become K-times.

Question 18.
Show that the potential is constant within and at the surface of a charged conductor.
Answer:
Since the electric field is equal to -ve of potential gradient 
i.e E = -\(\frac{d \mathrm{~V}}{d x}\)
Inside the conductor, E = 0
∴ \(\frac{d \mathrm{~V}}{d x}\) = 0
or V = constant
Hence the potential within and at the surface of a charge conductor is constant i.e. surface of a conductor is an equipotential surface.

Question 19.
What is electrostatic shielding? What is its importance?
Answer:
The phenomenon in which a certain region of space is protected from the electric field is called electrostatic shielding. Consider a conductor of any shape having a cavity inside it as shown in the figure. Let +q be the charge on the conductor. Draw a Gaussian surface just around the cavity inside the conductor as shown by dotted closed lines.

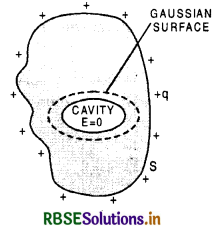
From Gauss's theorem
\(\oint \overrightarrow{\mathbf{E}} \cdot d \overrightarrow{\mathbf{S}}=\frac{q}{\varepsilon_0}\)
Since charge inside the conductor is zero i.e. q = 0
∴ \(\oint \overrightarrow{\mathbf{E}} \cdot d \overrightarrow{\mathbf{S}}\) = 0
or \(\overrightarrow{\mathrm{E}}\) = 0
or E = 0
i.e. electric field inside the cavity of a conductor is always zero.
Importance
(i) In a thunderstorm accompanied by lightning, it is safer to be inside a car or a bus rather than near a tree or on the open ground.
(ii) In electronic devices, certain circuits or components are shielded by covering them with metal shields.

Question 20.
During lightning you are safer inside a house than under a tree. Why?
Answer:
When we stand under a tree, we provide an easy path for the lightning to pass through our body. But when we are in the house, discharge due to lightning may be conducted to the ground through iron pipes/walls etc. Therefore, we are safer.

Question 21.
The safest way to save yourself from lightning is to be inside a car. Comment.
Answer:
The body of the car is metallic. It provides electrostatic shielding to the person in the car, because electric field inside the car is zero. The discharge due to lightning passes to the ground through the metallic body of the car.

Question 22.
A slab of a material of dielectric constant K has the same area as the plates of a parallel plate capacitor, but has a thickness \(\frac{3}{4}\) d, where d is the separation between the plates. How is the capacitance changed when the slab is inserted between the plates?
Answer:
The capacitance of a capacitor with vacuum (or free space) or medium having distance between the plates d is:
C = \(\frac{\varepsilon_0 \mathrm{~A}}{d}\) .............................(1)
We know that, a dielectric of dielectric constant K and thickness t is equivalent to thickness \(\frac{t}{\mathrm{~K}}\) for vacuum of free space.
So total equivalent vacuum separation of the plates of the capacitor will be:

Question 23.
Why water has very high dielectric constant?
Answer:
Due to unsymmetric placement of the atoms of water molecule, it possesses permanent electric dipole moment which is about 0.6 x 10^-20 Cm. This magnitude of dipole moment is about 10 times more than the induced dipole moment acquired by the molecule. Hence due to this large value of permanent dipole moment, the dielectric constant of water molecules is very high.

Question 24.
Show that the capacitance of an insulated spherical conductor is directly proportional to the radius of the spherical conductor.
Answer:
Consider an isolated spherical conductor of radius r having charge +q, which resides at its surface only. The charge behaves as if it is concentrated at its center O. If V is the potential at the surface of the spherical conductor, then

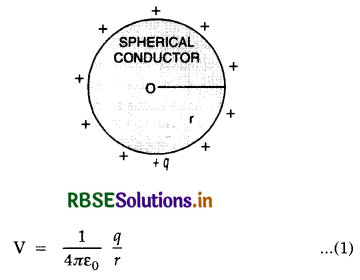
∴ Capacitance of the spherical conductor is given by
C = \(\frac{q}{\mathrm{~V}}=\frac{q \cdot 4 \pi \varepsilon_0 r}{q}\) = 4πε₀r
or C ∝ r

Question 25.
What is the capacitance of earth?
Answer:
Since earth is a spherical conductor of radius r = 6.4 x 10⁶ m
∴ Capacitance of earth
C = 4πε₀r = \(\frac{1}{9 \times 10^9}\) x 6.4 x 10⁶
or C = 711 x 10^-6 Fs
or C = 711 µF

Question 26.
Show that the capacitance of spherical capacitor is more than that of a spherical conductor.
Answer:
The capacitance of a spherical conductor of radius 'a' is given by
C = 4πε₀a .................(1)
The capacitance of a spherical capacitor of inner radius a and outer radius b is given by
C' = 4πε₀\(\left(\frac{a b}{b-a}\right)\) .....................(2)
Dividing eqns. (2) by (1), we get

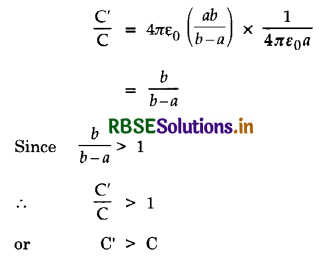
Question 27.
Find the radius of a sphere of capacitance 1 F. Hence discuss if it is possible to have a sphere of capacitance 1F.
Answer:
C = 4πε₀r
∴ r = \(\frac{\mathrm{C}}{4 \pi \varepsilon_0}\) = 9 x 10⁹ x 1 m
r = 9000 km
It is too a large value, hence an isolated sphere of 1F capacitance cannot be had in practice.

Question 28.
Show that the line integral of electric Held (or work done in moving a unit charge) along a closed path in the electric Held is always zero.
Answer:
The line integral of electric field \(\overrightarrow{\mathrm{E}}\) from point A to B is given by:
\(\int_{\mathrm{A}}^{\mathrm{B}} \overrightarrow{\mathrm{E}} \cdot \overrightarrow{d l}=\frac{q}{4 \pi \varepsilon_0}\left(\frac{1}{r_{\mathrm{A}}}-\frac{1}{r_{\mathrm{B}}}\right)\) .....................(i)
Similarly, the line integral of electric field from point B to A is given by:
\(\int_{\mathrm{B}}^{\mathrm{A}} \overrightarrow{\mathrm{E}}, \overrightarrow{d l}=-\frac{q}{4 \pi \varepsilon_0}\left(\frac{1}{r_{\mathrm{B}}}-\frac{1}{r_{\mathrm{A}}}\right)\)

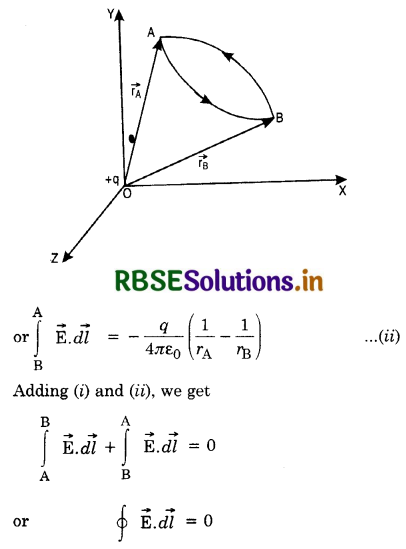
i.e. line integral of electric field along a closed path in the electric field is zero.

Question 29.
Show that the electric field intensity at a point in an electric field is equal to the -ve of the potential gradient of the field at that point.
i.e. E = -\(\frac{d V}{d r}\).
Answer:
Let P and Q be two points situated at a very small distance dr from each other in the electric field \(\overrightarrow{\mathrm{E}}\) of source charge +q lying at O Fig. SAQ 29. The points P and Q and so close that the electric field \(\overrightarrow{\mathrm{E}}\) between P and Q is almost uniform as shown in Fig.

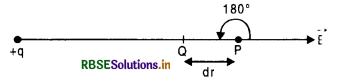
Let potential difference between P and Q = dV
By definition,
Potential difference between P and Q = Work done in moving a unit test charge from P to Q.
If a small positive test charge q₀ is moved from point P to Q, then

Question 30.
Define an equipotential surface. What are its characteristics? Give examples for (i) A point charge (ii) Uniform electric field (iii) for a pair of two equal and opposite charges?
Answer:
A surface on which the potential is the same everywhere is called equipotential surface.
Characteristics of equipotential surfaces
1. No work is done in moving a test charge over an equipotential surface,
Since potential difference = \(\frac{\text { Work done }}{\text { Charge }} \)
For an equipotential surface,
potential difference = 0
∴ \(\frac{\text { Work done }}{\text { Charge }}\) = 0
or Work done = 0

2. Electric field intensity \(\overrightarrow{\mathrm{E}}\) ⊥ to the equipotential surface.
Since potential difference between two points A and B = -line integral of electric field
i.e. dV = -\(\int_{\mathrm{A}}^{\mathrm{B}} \overrightarrow{\mathrm{E}} \cdot \overrightarrow{d l}\)
Since for an equipotential surface, dV = 0 B
∴ \(\int_{\mathrm{A}}^{\mathrm{B}} \overrightarrow{\mathrm{E}} \cdot \overrightarrow{d l}\) = 0 ......................(i)
i.e. line integral of electric field between any two points on equipotential surface is zero. 
From eq. (i), \(\overrightarrow{\mathrm{E}} \cdot \overrightarrow{d l}\) = 0
or \(\overrightarrow{\mathrm{E}} \perp \overrightarrow{d l}\)

3. Equipotential surface helps us to distinguish regions of strong fields from those of weak fields.

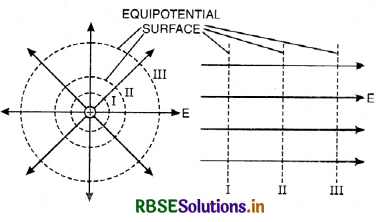
So equipotential surfaces are closer together, where the electric field is stronger and vice versa as shown in Fig. SAQ 2.30 (a).
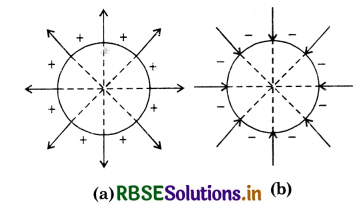
Examples
(i) In the case of an isolated point charge, all points equidistant from the charge are at the same potential. Thus, for a point charge, equipotential surfaces will be a series of concentric spherical shells with the charges at center [Fig SAQ 30 (b)] . The potential at each of the spherical surfaces (I, II and III) is different but for all points on any one surface, it is the same. Since,
E = -\(\frac{d \mathrm{~V}}{d r}\) (for constant dV)
dr ∝ \(\frac{1}{\mathrm{E}}\).
It follows that for the same charge in potential, distance between equipotential surfaces increases with decrease in electric field.
(ii) For a uniform electric field, the equipotential surfaces are at right angles to the field lines [Fig. SAQ 30 (c)].

(iii) Fig. SAQ 30 (c) and SAQ 30 (d) show respectively the equipotential surfaces and electric lines of force for two equal positive charges and a pair of equal and opposite charges. The dotted lines

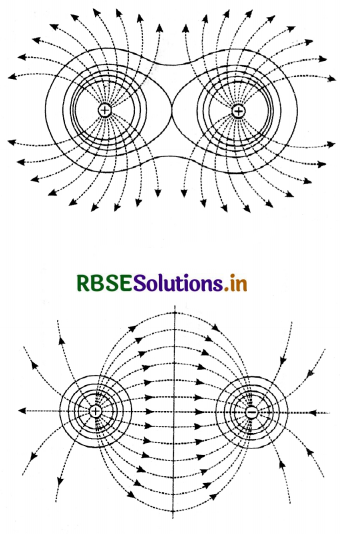
represent electric lines of force. The thick circles around the charges represent equipotential surfaces due to individual charges. The equipotential surfaces due to charges is obtained by adding potentials at a point due to two charges algebraically. They have been represented by thick curves or lines.

Question 31.
What is capacitor? Explain its principle.
Answer:
Capacitor. A capacitor is a device used for storing electric charge and electrical energy. It is an arrangement of conductors in which the capacitance of the system can be increased without increasing the size.
Principle of a Capacitor. It is based on the principle that when an earthed conductor is based in the neighborhood of a charged conductor, the capacitance of the system increases considerably.
Explanation
When an uncharged conductor B is placed near a charged conductor A, due to induction, negative charge will be induced on the nearer face of B and positive charge on its farther side as shown in Fig. SAQ 31. The induced negative charge on B lowers the potential of A, while the induced positive charge raises its potential. As the induced negative charge is nearer to conductor A than the induced positive charge, the potential of conductor A on the whole is lowered. Therefore, capacitance of a conductor increases by a small amount, when another uncharged conductor is placed near it.

Now connect the conductor B to the earth as shown in Fig. The induced positive charge on B will immediately flow to the earth. However, the induced negative charge on B will stay on it. The potential of A will get lowered by a large amount. Thus, it follows that the capacitance of a conductor is greatly increased, when an earth-connected conductor is placed near it. It forms the principle of a capacitor.

Question 32.
Distinguish between electric potential and electric potential energy and state the relation between them.
Answer:

Electric Potential	Electric Potential Energy
1. Electric potential at a point in an electric field is the amount of work done in moving a unit positive test charge from infinity to that point against the electrostatic force.	1. Electric potential energy of a system of charges is the amount of work done in moving these charges from infinity to their respective positions.
2. Electric Pot. V = \(\frac{1}{4 \pi \varepsilon_0} \frac{q}{r}\)	2. Electric Pot. energy U = \(\frac{1}{4 \pi \varepsilon_0} \frac{q q_0}{r}\)

Relation between V and U
Since U = \(\frac{1}{4 \pi \varepsilon_0} \frac{q q_0}{r}\)
And V = \( \frac{1}{4 \pi \varepsilon_0} \frac{q}{r}\)
∴ U = q₀V.

Question 33.
What do you mean by electrical capacitance? Define its S.I. unit. Show that capacitance of spherical conductor is directly proportional to its radius.
Answer:
Electrical Capacitance. If a charge q is given to an isolated conductor, its potential rises. It is found that the potential V is proportional to the charge q
i.e. q ∝ V
or q = CV
where C is the constant of proportionality and is called the capacitance of the conductor.
or C = \(\frac{q}{V}\) .........................(i)
So the capacitance of a conductor is defined as the ratio of charge on the conductor to its potential.
Unit of Capacitance
In S.I., the unit of capacitance is farad (F).
If q = 1C, V = 1 volt, then C = 1 farad
Capacitance of a conductor is said to be one farad, when a charge of one coulomb raises its potential through 1 volt.
Capacitance of spherical conductor
Consider an isolated spherical conductor of radius r having charge q, which resides at its surface only. (Fig. SAQ 33). The charge behaves as if it is concentrated at its centre.

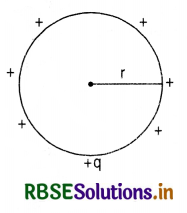
If V is the potential on the surface of the sphere, then
V = \(\frac{1}{4 \pi \varepsilon_0} \frac{q}{r}\) ...........................(ii)
Capacitance of the spherical conductor is given by
C = \(\frac{q}{\mathrm{~V}}\)
Using Eq.(ii), we get
C = \(\frac{q 4 \pi \varepsilon_0 r}{q}\) = 4πε₀r
C ∝ r

Question 34.
Calculate the total capacitance of a number of capacitors connected in series.
Answer:
Capacitors in Series. Capacitors are said to be connected in series if the second plate of one is connected with the first plate of the next and so on. This leaves the first plate of first capacitor and the second plate of the last capacitor as free plates. These free plates are connected to the terminals A and B. The terminal B is earthed while the connected between A and B (Fig. SAQ 34).

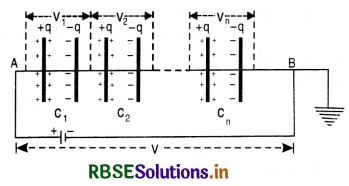
In a series combination, each capacitor is charged with the same charge while they will be raised through different potentials in accordance with their capacities. If V₁, V₂, ......................., V_n are potential differences across various capacitors of capacities C₁, C₂, ....................., C_n respectively, then
V = V₁ + V₂ + ....................+ V_n .......................(1)
where V is the potential difference between A and B.

Further V = \(\frac{q}{\mathrm{C}}\)
where C is the resultant capacity of the combination. Substituting for V₁, V₂, ..................... V_n and V in the equation (1), we get:

Thus the reciprocal of the resultant capacity of a number of capacitors connected in series is equal to the sum of the recoprocals of their individual capacities.

Question 35.
Calculate the total capacitance of a number of capacitors connected in parallel.
Or
If you are provided with capcaitors of smaller capacities, how can you obtain a large capcity from them? Explain.
Answer:
We will use parallel combination of the given capacitors.
Capacitors in parallel. Capcaitors are said to be connected in parallel if the 'positively charged' plates of all the capacitors are connected together at a point. A while the 'earthed' plates are connected together at another point B. The point B is also connected to earth while the source of charge is connected between the points A and B.

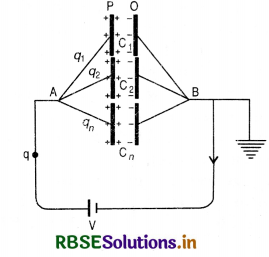
Capacitors having capacities C₁, C₂, ......................., C_n draw charges q₁, q₂, .................., q_n in accordance with their capacities. If q is the total charge drawn from the source, then
q = q₁ + q₂ + ..........................+ q_n .........................(1)
Since all the capacitors are connected between two common points A and B therefore, the potential difference across each of them is the same i.e. V. This is also the potential difference across the two terminals of the source of charge.

If 'C' is the capacity of the combination, then
V = \(\frac{q}{\mathrm{C}}\)
or q = CV
Substituting for q and q₁, q₂, ................, q_n in equation (1), we get
CV = C₁V + C₂V + C₃V + .....................+ C_nV
or CV = (C₁ + C₂ + ................+ C_n) V
or C = C₁ + C₂ + ..................+ C_n
Thus the resultant capacity of a number of capacitors connected in parallel is equal to the sum of their individual capacitites.

Question 36.
Define the term 'electric field intensity. Electric field inside a conductor is zero. Explain.
Answer:
The electric field intensity at any point in the electric field is the force experienced by a unit positive charge placed at that point.
Electric field inside a conductor is zero. When a conductor is placed inside an electric field, the free electrons in the conductor start drifting under the influence of electric field. The free electrons move towards the positive plate. The redistribution of charges will create its own electric field due to induced charges till the electric field due to induced charges become equal to external field. Hence net electric field inside the conductor is zero.

Question 37.
Derive an expression for electric potential at a point along the axial line of an electric dipole.
Answer:
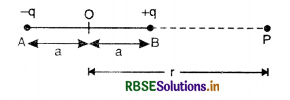
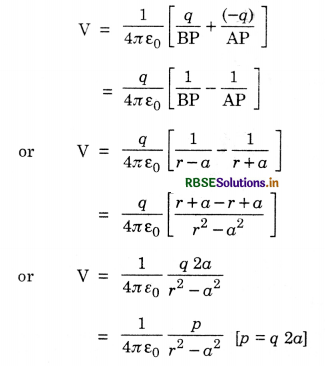
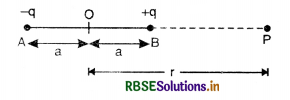
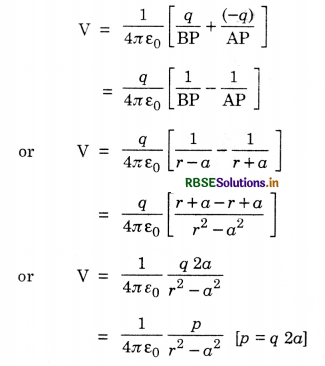
Let an electric dipole consist of two charges -q and +q separated by a distance 2a as shown in the figure SAQ 37. Let us find electric potential at point P, at a distance r from the mid-point of the dipole.

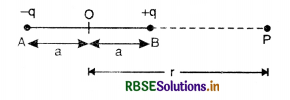
The electric potential of OP due to the dipole is given by

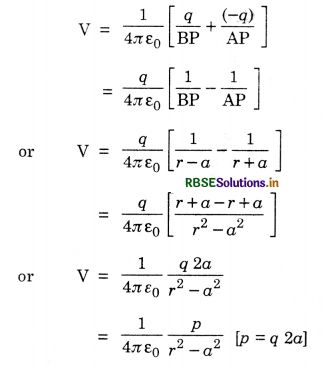
For a short dipole: r >> a, so r² - a² ≃ r²
So V = \(\frac{1}{4 \pi \varepsilon_o} \frac{p}{r^2}\).

Question 38.
Deduce an expression for electric potential due to an electric dipole at any point on its axis. Mention one contrasting feature of electric potential of dipole at a point as compared to that due to a single charge.
Answer:
For electric on the axial line,
Let an electric dipole consist of two charges -q and +q separated by a distance 2a as shown in the figure SAQ 37. Let us find electric potential at point P, at a distance r from the mid-point of the dipole.

The electric potential of OP due to the dipole is given by

For a short dipole: r >> a, so r² - a² ≃ r²
So V = \(\frac{1}{4 \pi \varepsilon_o} \frac{p}{r^2}.\)
So for a dipole
V ∝ \(\frac{1}{r^2}\)
And for a monopole (or a single charge)
V ∝ \(\frac{1}{r}\).

Question 39.
Figure shows two identical capacitors C₁ and C₂ each of 1 µF capacitance connected to a battery of 6 V. Initially switch S is closed. After some time S is left open and dielectric slab of dielectric constant k = 3 are inserted to fill

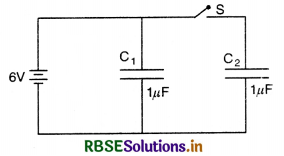
completely the space between the plates of the two capacitors. How will the (i) charge and (ii) potential difference between the plates of the capacitors be affected after the slabs are inserted.
Answer:
In C₁
charge qd = C dV = KCV
i.e. it increases K-times
Potential V remains the same as 6 V.
In C₂
charge qd = C dV remains constant
And Potential
Vd = \(\frac{\mathrm{V}}{\mathrm{K}}\)
i.e. it decreases K-times.

Question 40. 
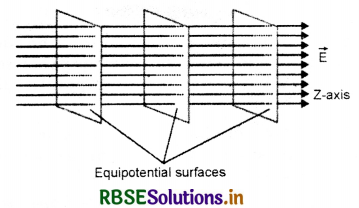
(i) Draw the equipotential surfaces corresponding to a uniform electric field in the z-direction.
(ii) Derive an expression for the electric potential at any point along the axial line of an electric dipole.
Answer:
(i) The equipotential surfaces are as shown in Fig. SAQ 40.

(ii) Electric potential on the axial line of an electric dipole.
Answer:
Let an electric dipole consist of two charges -q and +q separated by a distance 2a as shown in the figure SAQ 37. Let us find electric potential at point P, at a distance r from the mid-point of the dipole.

The electric potential of OP due to the dipole is given by

For a short dipole: r >> a, so r² - a² ≃ r²
So V = \(\frac{1}{4 \pi \varepsilon_o} \frac{p}{r^2}.\)

Question 41.
Draw the electric field lines due to a uniformly charged thin sphereical shell when charge on the shell is (i) positive and (ii) negative.
Answer:
The electric field lines due to a uniformly charged thin spherical shell when the shell is positive all directed radially in outward direction as shown in Fig. SAQ 2.41(a) and all directed radically in inward direction as shown in Fig. SAQ 41(b).

Question 42.
A parallel plate capaciotr, each with plate area A and swparation d is charged to a potential difference V. The battery used to charge it is then disconnected. A dielectric slab of thickness d and dielectric constant K is now placed between the plates. What change, if any will take place in (i) charge on plates (ii) electric field intensity between the plates (iii) capacitance.
Answer:
(i) Once the battery is disconnected, the charge on the plates remains the same.
(ii) Electric field intensity between the plates decreases due to polarisation of dielectric.
(iii)The capacitance of capacitor increases K times.

Questin 43.
Two dielectric slabs of dielectric constants K₁ and K₂ are filled in between two plates each of area A, of a parallel plate capacitor. Find net capacitance.

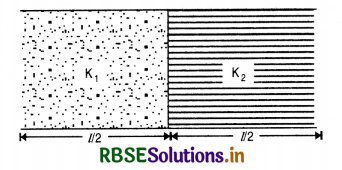
Answer:
In the given figure 2.66 we find that there are two capacitors having dielectric of dielectric constants K₁ and K₂ and are connected in parallel.
So total capacitance of the equivalent capacitor is C = C₁ + C₂
= \(\frac{\mathrm{K}_1 \mathrm{E}_0 \mathrm{~A}}{l / 2}+\frac{\mathrm{K}_2 \mathrm{~F}_0 \mathrm{~A}}{l / 2}\)
= \(\frac{2 \mathrm{E} \varepsilon_0 \mathrm{~A}}{l}[K1 + K2]\).

Question 44.
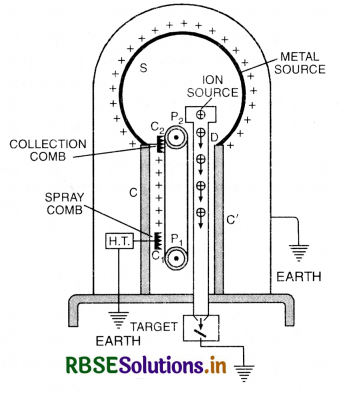
Draw a labelled diagram of Van de Graaff generator. State its principle of working.
Answer:
Principle. It is based on the following two facts:
(i) If a charged conductor is in internal contact with another hollow conductor accepts all available charge on the charged condutor irrespective of its own potential.
(ii) The electric discharge takes place in air or gases readily at pointed conductors.

Question 45.
The given graph shows the variation of charge q versus potential difference V for capacitors C₁ and C₂. The two capacitors have the same plate separation, but the plate area of C₂ is double that of C₁. Which of the lines in the graph corresponds to C₁ and C₂ and why?
Answer:
Let A be area of each plate of the capacitor, d is the distance between the plates, then

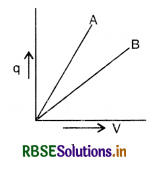
The capacitance of the parallel plate capacitor
C = \(\frac{\varepsilon_0 \mathrm{~A}}{d}\)
or C ∝ A (∵ d is the same for both capacitors)
Since area of C₂ is double than C₁
So C₂ = 2C₁
Slope of the q-V graph gives the capacitance.
i.e. Slope = \(\frac{q}{\mathrm{~V}}\) = C
Since slope of A is more than the slope of B so line A corresponds to C₂ and B corresponds to C₁.

Question 46.
A parallel plate capacitor with air between the plates has a capacitance of 8 pF. The separation between the plates is now reduced by half and the space between them is filled with a medium of dielectric constants. Calculate the value of the capacitance of the capacitor in the second case.
Answer:
In first case,
The capacitance of the capacitor with air as medium is given by
C₁ = \(\frac{\varepsilon_0 \mathrm{~A}}{d}\) = 8 pF ........................(i)
In 2nd case
The distance is reduced to half i.e. d/2 and K = 5.
So C₂ = \(\frac{\mathrm{K} \varepsilon_0 \mathrm{~A}}{d / 2}=2 \mathrm{~K}\left(\frac{\varepsilon_0 \mathrm{~A}}{d}\right)\)
Using Eq. (i) we get
C₂ = 2K x 8 = 2 x 5 x 8 = 80 pF.

Question 47.
(a) How many electrons must be added to one plate and removed from the other so as to store 25.0 J of energy in a 5.0 nF parallel plate capacitor?
(b) How would you modify this capacitor so that it can store 50.0 J of energy without changing the charge on its plates?
Answer:
Given U = 25.0 J, C = 5.0 nF = 5 x 10^-9 F, n = ?
(a) Since U = \(\frac{\mathrm{Q}^2}{2 \mathrm{C}}\)
or Q² = U x 2C = 25 x 2 x 5 x 10^-9
= 25 x 10^-8
So Q = 5 x 10^-4 C
or ne = 5 x 10^-4
or n = \(\frac{5 \times 10^{-4}}{e}=\frac{5 \times 10^{-4}}{1.6 \times 10^{-19}}\)
= 3.125 x 10¹⁵

(b) Since C = \(\frac{\varepsilon_0 \mathrm{~A}}{d}\)
Now U can be made double by making C half. This can be done
(i) by doubling the plate separation or
(ii) by decreasing the area of the plates by \(\frac{1}{2}\).

Question 48.
A point charge +Q is placed at the center O of an uncharged hollow spherical conductor of inner radius 'a' and outer radius 'b'. Find the following:
(a) The magnitiude and sign of the charge induced on the inner and outer surface of the conducting shell.
(b) The magnitude of electric field vector at a distance
(i) r =\( \frac{a}{2}\), and
(ii) r = 2b, from the center of the shell.

Answer:
(a) The charge on the inner durface of the conducting shell = -Q
The charge on the outer surface of the conducting shell = +Q

(b) (i) For r = \(\frac{a}{2}\)
E = \(\frac{1}{4 \pi \varepsilon_0} \frac{\mathrm{Q}}{r^2}=\frac{1}{4 \pi \varepsilon_0} \frac{4 \mathrm{Q}}{a^2}\)
(ii) For r = 2b
E = \(\frac{1}{4 \pi \varepsilon_0} \frac{\mathrm{Q}}{r^2}=\frac{1}{4 \pi \varepsilon_0} \frac{\mathrm{Q}}{4 b^2}\)

Long Answer Type Questions

Question 1.
What is the significance of the line integral of an electrostatic field \(\overrightarrow{\mathbf{E}}\).
Or
Show that the work done in displacing an electric charge in an electric field is given by the product of magnitude of the charge and the line integral of electric field.
i.e. W = q₀\(\int_{\mathbf{A}}^{\mathbf{B}} \overrightarrow{\mathbf{E}} \cdot \overrightarrow{d l}\)
Answer:
Let a source charge +q be placed at the origin O and \(\overrightarrow{\mathbf{E}}\) be the electric field produced by this charge at P. Let us move a test charge q₀ in this electric field from point A to point B. Let us move q₀ from point P to Q through very small displacement \(\overrightarrow{d l}\).

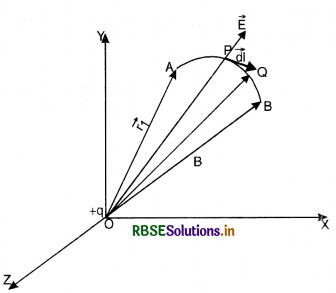
Small work done
dW = \(\overrightarrow{\mathrm{F}} \cdot d \vec{l}=-q_0 \overrightarrow{\mathrm{E}} \cdot d \vec{l}\)
where \(\overrightarrow{\mathrm{F}}\) = -q₀\(\overrightarrow{\mathrm{E}}\).
-ve sign shows that in order to keep the charge q₀ in equilibrium an equal and opposite force is required.
Total work done in moving the test charge q₀ from A to B will be

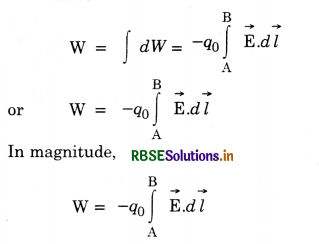
i.e. work done in displacing the charge is the product of magnitude of charge and line integral of electric field.
Work done by the field per unit charge
\(\frac{\mathrm{W}}{q_0}=\int_{\mathrm{A}}^{\mathrm{B}} \overrightarrow{\mathrm{E}} \cdot d \vec{l}\)
In other words, the line integral of an electrostatic field from point A to point B gives the work done by the field when a unit positive charge moves from a to B under the effect of the field.

Question 2.
Show that the line integral of electric field is independent of the path followed.
Or
Show that work done in moving an electric charge is independent of the path followed.
Or
Show that the electric field due to a point charge is conservative.
Answer:
Consider a point source charge +q located at the origin 0 as shown in Fig LAQ 2. Let A and B be two points in the electric field having position vectors \(\vec{r}_{\mathrm{A}}\) and \(\vec{r}_{\mathrm{B}}\) respectively. Connect A and B through any curve. Let P be a point where electric field due to

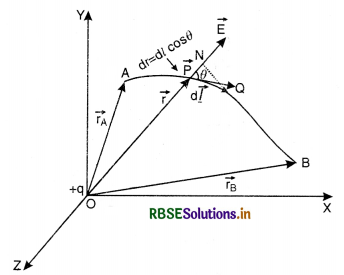
charge +q be \(\overrightarrow{\mathrm{E}}\) and let \(\overrightarrow{\mathrm{OP}}=\vec{r}\) and \(\overrightarrow{\mathrm{PQ}}=d\overrightarrow{\mathrm{l}}\) (infinitesimally small displacement along the path AB)
Since \(\overrightarrow{\mathrm{E}} \cdot d \vec{l}\) = Edl cos θ ........................(i)
(where θ is the angle between the direction of\( \overrightarrow{\mathrm{E}}\) and \(d\overrightarrow{\mathrm{l}}\))
In rt ∠∆ PNQ
\(\frac{\mathrm{PN}}{\mathrm{PQ}}\) = cos θ
or PN = PQ cos θ
or dr = dl cos θ
or dl cos θ = dr
So equation (i) becomes
\(\overrightarrow{\mathrm{E}} \cdot d \vec{l}\) = Edr ...........................(ii)
The electric field \(\overrightarrow{\mathrm{E}}\) at point P is given by
\(\overrightarrow{\mathrm{E}}=\frac{1}{4 \pi \varepsilon_0} \frac{q}{r^2} \hat{r}\)
or E = \(\frac{1}{4 \pi \varepsilon_0} \frac{q}{r^2}\) ........................(iii)
Putting equation (iii) in (ii), we get
\(\overrightarrow{\mathrm{E}} \cdot \overrightarrow{d l}=\frac{1}{4 \pi \varepsilon_0} \frac{q}{r^2} d r\)
∴ Line integral of electric field between A and B is 
\(\int_{\mathrm{A}}^{\mathrm{B}} \overrightarrow{\mathrm{E}} \cdot \overrightarrow{d l}=\frac{q}{4 \pi \varepsilon_0} \int_{r_{\mathrm{A}}}^{r_{\mathrm{B}}} \frac{1}{r^2} d r\)
or \(\int_{\mathrm{A}}^{\mathrm{B}} \overrightarrow{\mathrm{E}} \cdot \overrightarrow{d l}=\frac{q}{4 \pi \varepsilon_0}\left[-\frac{1}{r}\right]_{r_{\mathrm{A}}}^{r_{\mathrm{B}}}\)
=\( \frac{q}{4 \pi \varepsilon_0}\left[\frac{1}{r_{\mathrm{A}}}-\frac{1}{r_{\mathrm{B}}}\right]\) .......................(iv)
Eq.(iv) shows that the line integral of electric field between two points is independent of the path follwed between the two points.
Since work done in moving a test charge q0 in the electric field \(\overrightarrow{\mathrm{E}}_{\mathrm{B}}\) from point A to B is given by

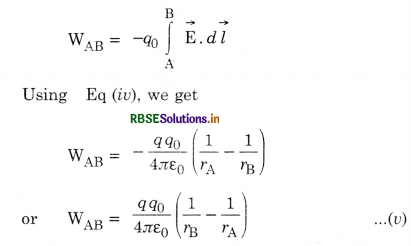
Thus we find that the work done in moving an electric charge is independent of the path followed. Since a conservative field is that in which the work done (or line integral) is independent of the path. From eqns. (iv) and (v) we find that electric field is conservative.

Question 3.
Define electrostatic potential at a point in an electric field in terms of line integral of the field. Drive its general expression for single charge.
Answer:
The expression for the line integral of electrostatic field is given by
\(\int_{\mathrm{A}}^{\mathrm{B}} \overrightarrow{\mathrm{E}} \cdot \overrightarrow{d l}=\frac{q}{4 \pi \varepsilon_0}\left(\frac{1}{r_{\mathrm{A}}}-\frac{1}{r_{\mathrm{B}}}\right)\)
This can be further written as
\(\int_{\mathrm{A}}^{\mathrm{B}} \overrightarrow{\mathrm{E}} \cdot \vec{d} l=\left(\frac{1}{4 \pi \varepsilon_0} \frac{q}{r_{\mathrm{A}}}\right)-\left(\frac{1}{4 \pi \varepsilon_0} \cdot \frac{q}{r_{\mathrm{B}}}\right)\)
The R.H.S. of the equation is the difference of two values of the same scalar function at two endpoints of the path A and B. The scalar function \(\left(\frac{1}{4 \pi \varepsilon_0} \frac{1}{r}\right)\) is called electrostatic potential function, and is denoted by V.

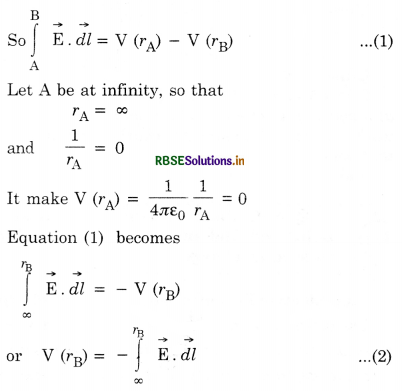
Definition of Potential. The electric potential at a point in an electrostatic field is negative of the line integral of that field taken along continuous curve from a point at infinity (outside the field where its intensity is zero), to that point.
Expression for potential 
For convenience, if we write V(r_B) = V_B, then Eq. (2) can be written as
V_B = -\(x = {-b \pm \sqrt{b^2-4ac} \over 2a}\int_{-\infty}^{\mathrm{B}} \overrightarrow{\mathrm{E}} \cdot \overrightarrow{d l}\)
or V_B = \(\frac{\mathrm{W}_{\infty} \mathrm{B}}{q_0} \quad\left[\because \mathrm{W}_{\mathrm{AB}}=-q \int_{\mathrm{A}}^{\mathrm{B}} \overrightarrow{\mathrm{E}} d \vec{l}\right]\)
Thus electric potential at a point in the electric field may be defined as the amount of work done in bringing a unit positive test charge from infinity to that point against the electric field.
Since W_∞B = \(x = {-b \pm \sqrt{b^2-4ac} \over 2a}\frac{q q_0}{4 \pi \varepsilon_0}\left(\frac{1}{r_{\mathrm{B}}}-\frac{1}{\infty}\right)\)
⇒ or \(\frac{\mathrm{W}_{\alpha \mathrm{B}}}{q_0}=\frac{2}{4 \pi \varepsilon_0}\left[\frac{1}{r_\beta}-\frac{1}{\alpha}\right]=\frac{q q_0}{4 \pi \varepsilon_0 r_{\mathrm{B}}}\)
∴ V_B = \(\frac{1}{4 \pi \varepsilon_0} \frac{q}{r_{\mathrm{B}}}\)
Dimensional formula of V
Since V = \(\frac{\mathrm{W}}{q_0}=\frac{\left[\mathrm{ML}^2 \mathrm{~T}^{-2}\right]}{[\mathrm{AT}]}\)
= [M¹L²T^-3A^-1]
Units of V
If W = 1 J, q₀ = 1 C, V = 1 volt. So potential at a point in an electric field is said to be 1 V, if 1 J work is done in bringing 1 C charge from infinity to that point.
And 1 V = 1 J C^-1

Question 4.
Define electric potential at a point and find an expresion for it due to a point charge.
Answer:
Electric Potential due to a point charge.
The potential at a point in an electric field may be defined as the amount of work done in moving a unit +ve charge from infinity to the point against the electrostatic forces.
Expression. Consider a point P in an electric field of an isolated charge +q at point O. To find the potential at point P, consider that at any instant the unit +ve charge is at pt. A such that OA = x.

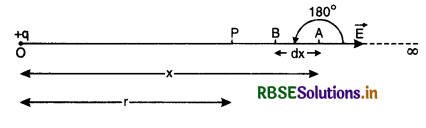
∴ Force experienced by unit +ve charge,
F = \(\frac{1}{4 \pi \varepsilon_0} \frac{q}{x^2}\)
Suppose unit + ve charge be given a small displacement dx from A to B against the electrostatic force.
∴ Small amount of work done in moving the +ve charge from A to B.
dW = \(\overrightarrow{\mathrm{F}} \cdot \overrightarrow{d x}\) = F dxs cos 180°
= - F dx
dW = -\(\frac{1}{4 \pi \varepsilon_0} \frac{q}{x^2}\) dx
Total work done in moving the unit +ve charge from ∞ to P is

This work done in moving the unit +ve charge from ∞ to P is called potential at point P.
V = \(\frac{1}{4 \pi \varepsilon_0} \frac{q}{r}\)
Again, if the source charge is located at a point whose position vector is \(\overrightarrow{r^{\prime}}\) the potential at the point whose position vector is \(\vec{r}\) is
V = \( \frac{1}{4 \pi \varepsilon_0} \frac{q}{\left|\vec{r}-\overrightarrow{r^{\prime}}\right|}\)
This is the required result.
Characteristics of Potential V
(i) Potential is a scalar quantity.
(ii) Its value at infinity is zero.
(iii) It depends only on the distance from the source charge.
(iv) Potential is +ve if q > 0 and -ve if q < 0.

Question 5.
Find the potential at a point due to two-point charges. Discuss the result for a general charge distribution.
Answer:
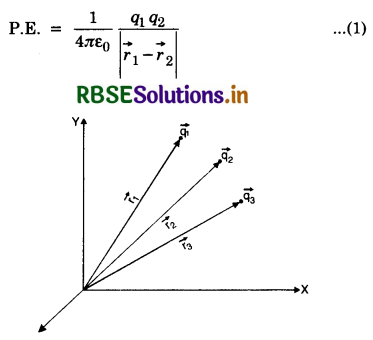
Potential at a point due to two-point charges.
Let charges q₁, q₂ be positioned at position vectors r₁, r₂ respectively and \(\vec{r}\) is position vector at which potential has to be calculated.

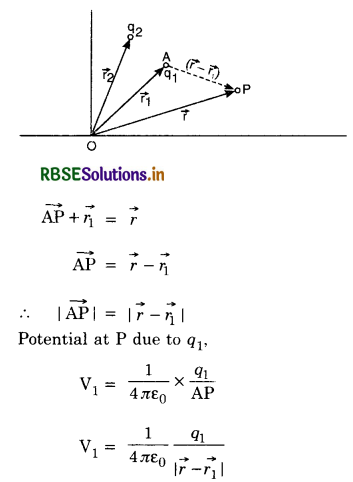
Similarly, Potential at P due to q₂
V₂ = \(\frac{1}{4 \pi \varepsilon_0} \frac{q_2}{\left|\vec{r}-\vec{r}_2\right|}\)
Because potential is scalar, therefore, total potential at any point due to two charges is also scalar. Total potential at P
V = V₁ + V₂
= \(\frac{1}{4 \pi \varepsilon_0}\left[\frac{q_1}{\left|\vec{r}-\vec{r}_1\right|}+\frac{q_2}{\left|\vec{r}-\vec{r}_2\right|}\right]\)
General Case
Potential due to a general charge distribution is given by:
V(r) = \(\begin{aligned} \frac{1}{4 \pi \varepsilon_0} \times & {\left[\int_l \frac{\lambda\left(\vec{r}^{\prime}\right) d l}{\left|\vec{r}-\vec{r}^{\prime}\right|}+\int_{\mathrm{S}} \frac{\sigma\left(\vec{r}^{\prime}\right) d s}{\left|\vec{r}-\vec{r}^{\prime}\right|}\right.} \\ &\left.+\int_{\mathrm{V}} \frac{\rho\left(\vec{r}^{\prime}\right) d \mathrm{~V}}{\left|\vec{r}-\vec{r}^{\prime}\right|}+\sum_{\text {all pt.charges }} \frac{q_i}{\left|\vec{r}-\vec{r}_i\right|}\right] \end{aligned}\)

Question 6.
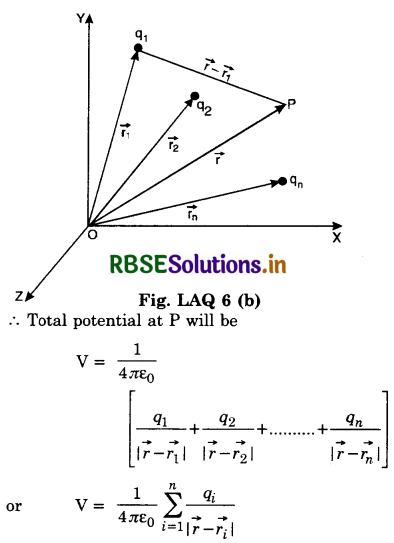
Derive an expression for potential at a point due to a group of point charges.
Answer:
It states that the total potential at any point due to a number of point charges is the algebraic sum of the potential due to different charges.
Let us find electric potential at point P due to n charges namely q₁, q₂, .............., q_n lying at distances r₁, r₂, ............, r_n respectively from point P.

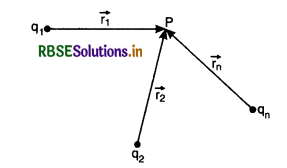
Potential at P due to q₁ (assuming other charges to be absent)
V₁ = \(\frac{1}{4 \pi \varepsilon_0} \frac{q_1}{r_1}\)
Similarly, potential due to other charges are 

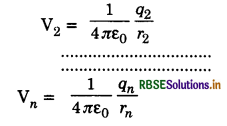
∴ Total potential at P₁ due to all charges
V = V₁ + V₂ + ........................... + V_n
or V = \(\frac{1}{4 \pi \varepsilon_0}\left[\frac{q_1}{r_1}+\frac{q_2}{r_2}+\ldots \ldots \ldots+\frac{q_n}{r_n}\right]\)
or V = \(\frac{1}{4 \pi \varepsilon_0} \sum_{i=1}^n \frac{q_i}{r_i}\) ..............................(i)
In terms of position vectors
If the n charges q₁, q₂, ................, q_n are having position vectors \(\vec{r}_1, \vec{r}_2, \ldots \ldots \ldots, \vec{r}_n\) respectively from origin O and ponit of observation P has positive vector \(\vec{r}\), then

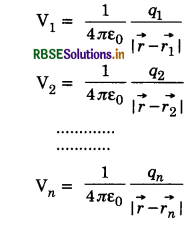
Question 7.
Define potential difference between two points in an electrostatic field. Find an expression for it. Define its SI unit.
Answer:
Potential difference between two points
The potential difference between two points in an electric field may be defined as the amount of work done in moving a unit positive test charge from one point to the other (without acceleration) against the electrostatic force.

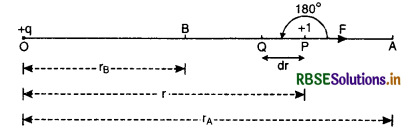
Expression. Consider two points A and B in the electric field of an isolated charge +q placed at point O (Fig. LAQ 7). Let OA = r_A and OB = r_B.
In order to find work done in moving the unit positive test charge from A to B, consider that at any instant, the test charge is at point P such that OP = r. The force experienced by the unit positive test charge at point P is equal to electric field at this point i.e.
F = \(\frac{1}{4 \pi \varepsilon_0} \frac{q}{r^2}\) (along PA)
Suppose the test charge is moved through an infinitesimally small distance PQ = dr towards point B against the electrostatic force of repulsion. Then, small work done in moving the test charge from P to Q is given by
W = \(\overrightarrow{\mathrm{F}} \cdot \overrightarrow{d r}\) = F dr cos 180°
= - Fdr
= -\(\frac{1}{4 \pi \varepsilon_0} \frac{q}{r^2}dr\)
The negative sign shows that the test charge is displaced in a direction opposite to that of the force acting on it. Therefore, work done in moving the unit positive test charge from A to B is given by

SI unit of potential difference is volt.
The potential difference between two points is said to be one volt if 1 J of work is done in bringing a charge of 1 C from one point to another against electrostatic forces.
1 V = 1 JC^-1

Question 8.
Derive an expression for electric potential at a point due to electric dipole. Hence find its value on (i) axial line and (ii) equatorial line.
Or
Derive an expression for the electric potential at a point along the axial line of an electric dipole.
Answer:
Let us calculate the electric potential at any point P due to an electric dipole, consisting of two charges -q and +q at A and B respectively separated from each other by a distance 2a from each other. Let 'r' be the distance of the point P from the center O of the dipole and r₁ and r₂ be the distances of P from the centers of charges +q and -q respectively.

In ∆OBP,
r₁ = BP = MP = OP - OM
= r - a cos θ
In ∆ANP,
r₂ = PN = NO + OP = OP + NO
= r + a cos θ
So Eq. (i) becomes

(ii) At equatorial line,
θ = 90°
V = \(\frac{p \cos 90^{\circ}}{r^2}\) = 0

Question 9.
Obtain an expression for potential energy of the configuration of (i) two charges and (ii) three charges. Hence generalise the result for a system of n point charges.
Answer:
Potential energy. The potential energy of the system of charges is the amount of work done in bringing the charges from infinity to the given configuration of charges.
Expression for the P.E. of two-point charges
Let q₁ and q₂ be two charges positioned at positions \(\overrightarrow{r_1}, \overrightarrow{r_2}\) and in the configuration where P.E. is to be calculated.

Step I. Move the charge q₁ and bring it to the location\( \overrightarrow{r_1}\). Since charge is not being moved against any electrostatic forces, therefore, no work has to be done.

Step II. Potential at point B due to charge q₁
V_B =\( \frac{1}{4 \pi \varepsilon_0} \frac{q_1}{\left|\vec{r}_1-\vec{r}_2\right|}\)
∴ Work done in bringing charge q₂ = Electric potential at pt. B x q₂
So W = \(\frac{1}{4 \pi \varepsilon_0} \frac{q_1 q_2}{\left|\vec{r}_1-\vec{r}_2\right|}\)
This work done is stored as P.E. of the system of two point charges.
∴ P.E. = \(\frac{1}{4 \pi \varepsilon_0} \frac{q_1 q_2}{\left|\vec{r}_1-\vec{r}_2\right|}\)
Potential Energy Due to Three Charges
Suppose \(\overrightarrow{r_1}, \overrightarrow{r_2}, \overrightarrow{r_3}\) are the position vectors of charges q₁, q₂, q₃ respectively. We suppose that q₁ is positioned at \(\vec{r}_1\) and q₂ is brought from infinity to \(\vec{r}_2\). Then P.E. stored in system of q₁ and q₂.


Step III. Suppose q₃ is brought from infinity to position vector \(\overrightarrow{r_3}\). It interacts with q₁, q₂.
∴ the work done in bringing q₃ from infinity to that position, will be stored as potintial energy.
P.E. = \(\frac{1}{4 \pi \varepsilon_0}\left[\frac{q_1 q_3}{\left|\overrightarrow{r_1}-\overrightarrow{r_3}\right|}+\frac{q_2 q_3}{\left|\overrightarrow{r_2}-\overrightarrow{r_3}\right|}\right]\) ..................(2)
Total P.E. of the system is the scalar sum of the expressions (1) and (2)
P.E. = \(\frac{1}{4 \pi \varepsilon_0}\left[\frac{q_1 q_2}{\left|\overrightarrow{r_1}-\vec{r}_2\right|}+\frac{q_1 q_3}{\left|\overrightarrow{r_1}-\overrightarrow{r_3}\right|}+\frac{q_2 q_3}{\left|\overrightarrow{r_2}-\vec{r}_3\right|}\right]\)
This can be written as,

Additional factor \(\left(\frac{1}{2}\right)\) connected to the terms like q1, q3 will be the same as q₃ q₁.
Generalization. If there are n charged particles q₁, q₂, ...................., q_n at position vectors\( \overrightarrow{r_1}, \overrightarrow{r_2}, \overrightarrow{r_3} \ldots \ldots \ldots \ldots \overrightarrow{r_n}.\)
P.E. = \(\frac{1}{2} \frac{1}{4 \pi \varepsilon_0} \sum_{\substack{i \\ i \neq j}}^n \sum_j^n \frac{q_i q_j}{\left|\vec{r}_i-\vec{r}_j\right|}\)
Units of Potential energy. The unit of P.E. is eV and other related units are meV, keV, MeV, GeV

Question 10.
Derive the expression for the potential energy of the electric dipole when placed in a uniform electric field. 
Answer:
The torque acting on an electric dipole when placed in a uniform electric field \(\overrightarrow{\mathrm{E}}\) is given by:
\(\vec{\tau}=\vec{p} \times \overrightarrow{\mathrm{E}}\)
or τ = pE sin θ .................(i)
where θ is the angle made by the dipole with electric field \(\overrightarrow{\mathrm{E}}\).

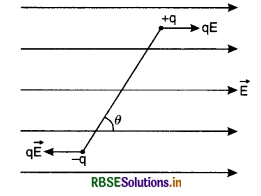
If the dipole is rotated through a small angle dθ against the torque, work has to be done.
Small work done, dW = τ dθ
= p E sin θ dθ
∴ Total work done in rotating the dipole from θ₁ to θ₂ against the torque is given by
W = ∫ dW = pE \(\int_{\theta_1}^{\theta_2} \sin \theta d \theta\)
= pE [-cos θ]_θ2^θ1
or W = - p E (cos θ₂ - cos θ₁)
This work done is stored in the form of its potential energy, U
U =  -p E (cos θ₂ - cos θ₁)
If the dipole is initially perpendicular to the electric field, then work done in rotating the dipole through an angle θ will be U = - pE (cos θ - cos 90°)
= -p E cos θ
or U = -\(\vec{p} \cdot \vec{E}\)

Question 11.
What do you mean by conductors, insulators and dielectrics? Discuss briefly the behaviour of conductors in electrostatic fields.
Answer:
Conductors. Those substances which allow electric current to pass through them are called conductors e.g. metals, aqueous solution of salts, ionized gases, human body etc. In conductors, there are free electrons which account for their ability to conduct current through them.
Insulators. Those substances which do not allow electric current to pass through them are called insulators e.g. glass, mica, pure water, all gases etc. In insulators, the electrons are strongly bound to their atoms.
Dielectrics. Insulators are also called dielectrics. They do not conduct electricity but on applying electric field, induced charges are produced on their faces. Thus dielectrics may be defined as the insulating materials which transmit electric effect without conducting.

Behaviour of a conductor inside the electric field
When a conductor is placed inside an electric field, the free electrons in the conductor start drifting under the influence of electric field. The free electrons move towards the positive side. As the electrons leave the atom, it makes the atom +vely charged. The atom cannot change its position in the solid, but due to the drift of electrons the positive charges on the atom goes on shifting towards the -ve side. Finally +ve and -ve charges appear on the surface of the conductor which are equal in magnitude and are called induced charges. These induced charges produce their own electric field inside the conductor. The drift of electrons stops, when the internal electric field due to induced charges become equal to external field. Hence net electric field inside the conductor is zero.

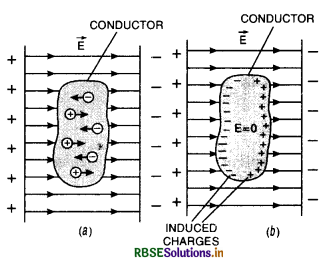
Question 12.
Explain the term capacitance (or capacity) of a conductor. What are its S.I. units? Why is this unit so large? Name other units of capacitance.
Answer:
Capacitance of a conductor. The electrical capacitance of a conductor is the ability of the conductor to store charge in it.
When a charge is given to a conductor, its potential rises. The actual rise of potential due to this charge will depend upon the size of the conductor and on its position relative to any neighboring conductors. It will also depend upon whether the neighboring conductor is insulated or earthed.
The potential V of the conductor is directly proportional to the charge q given to it.
i.e. q ∝ V
or q = CV
where C is the constant of proportionality and is called the capacitance of the conductor and its value depends on the shape and dimensions of the conductor.
And    C = \(\frac{q}{\mathrm{~V}}\)
Thus capacitance of a conductor may be defined as the ratio of the charge on the conductor to its potential.
If    V = 1, then C = q
i.e. capacitance of a conductor is the amount of charge required to raise its potential by unity.
Units
In S.I., the unit of capacitance is farad,
Since C = \(\frac{q}{\mathrm{~V}}\)
So, if q = 1 coulomb, V = 1 volt, then C = 1 farad.
Hence, the capacitance of a conductor is said to be 1 farad, if 1 coulomb charge raises its electrical potential by 1 volt 
∴ 1 farad = \(\frac{1 \text { coulomb }}{1 \text { volt }}\)
or 1F = \(\frac{1 \mathrm{C}}{1 \mathrm{~V}}\) = 1 CV^-1
Why farad is very large?
One farad = \(\frac{1 \mathrm{C}}{1 \mathrm{~V}}=\frac{\mathrm{C}^2}{\mathrm{~J}} \quad\left[\because \mathrm{V}=\frac{\mathrm{J}}{\mathrm{C}}\right]\)
J is a convenient unit of energy but coulomb is a very big unit of charge.
Other unit of capacitance is microfarad (µF),
1 µF = 10^-6 F
Still smaller unit of capacitance is picofarad (pF),
1 pF = 10^-12 F.

Question 13.
(a) What is a parallel plate capacitor? Derive an expression for the capacitance of a parallel plate capacitor.
(b) Define dielectric constant of a medium.
Answer:
(a) Parallel plate capacitor. A parallel plate capacitor is a combination of two conducting plates held parallel to each other at suitable distance having some dielectric in between them. One of the plate is positively charged and the other is earthed.
Expression for capacitance of parallel plate capacitor

Let a parallel plate capacitor consist of two thin conducting plates A and B held parallel to each other at a certain distance d apart. Medium between plates is given to be vacuum. Plate A is insulated and B is earthed.
When charge +q is given to A, it induces -q on the nearer face of B and +q on the farther face of the plate B. Free +ve charge on B flows to the earth.

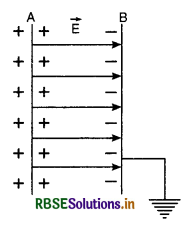
Electric field intensity between the plate is
E = \(\frac{\sigma}{\varepsilon_0}\)
where σ is the charge density and equal to q/A.
Also E = \(\frac{\mathrm{V}}{d}\), where V is the P.D. between plates.
V = Ed = \(\frac{\sigma}{\varepsilon_0} d=\frac{q d}{\mathrm{~A} \varepsilon_0} \quad\left[\because \sigma=\frac{q}{\mathrm{~A}}\right]\)
If C is the capacitance of the parallel plate capacitor, then
C = \(\frac{q}{\mathrm{~V}}=\frac{q}{\frac{q d}{\mathrm{~A} \varepsilon_0}}=\frac{\mathrm{A} \varepsilon_0}{d}\)
or C = \(\frac{\mathrm{A} \varepsilon_0}{d}\)
This is the expression for the capacitance when the medium is air or vacuum.
If A is in m², d is in m, then C is taken in farad. If medium between plates is other than air, capacitance of capacitor is given by
C = \(\frac{\varepsilon_0 \mathrm{KA}}{d}\)
where K is dielectric constant.

(b) Definition of dielectric constant
In vacuum the capacitance of capacitor,
C₁ = \(\frac{\varepsilon_0 \mathrm{~A}}{d}\) .........................(i)
In dielectric medium, the capacitance of capacitor
C₂ = \(\frac{\varepsilon_0 \mathrm{KA}}{d}\) ..........................(ii)
Dividing (i) and (ii), we get
\(\frac{\mathrm{C}_2}{\mathrm{C}_1}=\frac{\varepsilon_0 \mathrm{KA}}{d} \times \frac{d}{\varepsilon_0 \mathrm{~A}}\) = K
∴ Dielectric constant of a medium is defined as the ratio of capacitance of capacitor with dielectric as medium to the capacitance of the same capacitor with air as medium.

Question 14.
What is spherical capacitor? Derive expression for its capacitance.
Answer:
Spherical capacitor. A spherical capacitor consists of two concentric spherical conducting shells separated by a certain dielectric. One spherical shell is earthed and other is used to store charge on it.
Expression for capacitance of a spherical capacitor

Let P and Q be two spherical conducting shells of a spherical capacitor as shown in Fig. LAQ 14 Let a and b be their respective radii. Let a charge + q be given to inner shell P, so -q charge will be induced on the inner surface of shell Q, whose outer surface is earthed.

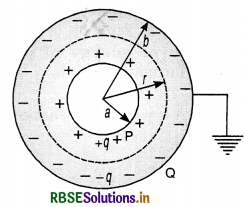
The electric field intensity E on gaussian spherical shell (as shown by dotted lines) of radius r is given by
E = \(\frac{1}{4 \pi \varepsilon_0} \frac{q}{r^2}\) .......................(1)
The potential difference between two spherical shells P and Q is given by

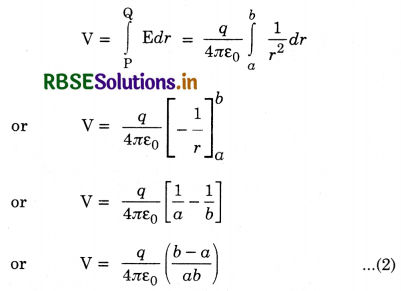
If C is the capacitance of the spherical capacitor, then

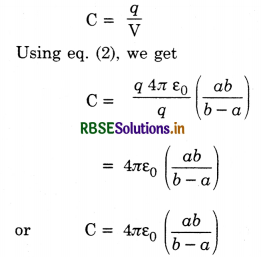
Question 15.
What is a cylindrical capacitor? Derive expressions for its capacitance?
Answer:
Cylindrical Capacitor. A cylindrical capacitor consists of two coaxial conducting cylindrical shells separated by a certain dielectric. One cylindrical shell is earthed and other is used to store charge on it.
Expression for capacitance of a cylindrical capacitor

Let P and Q be two conducting cylindrical shells of a cylindrical capacitor of radii a and b as shown in Fig. LAQ 15.

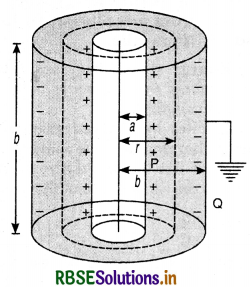
Let a charge +q be given to cylinder P, so negative charge will be induced on the inner surface of cylinder Q, whose outer surface is earthed.
Let λ be linear charge density. The electric field intensity E on Gaussian cylinder (as shown by dotted lines) of radius r is given by
E = \(\frac{1}{2 \pi \varepsilon_0} \frac{\lambda}{r}\)
The potential difference of cylindrical shells P and Q is given by

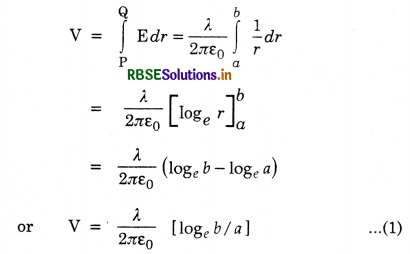
Total charge on the cylinder, q = λl .................(2)
If C is the capacitance of the cylindrical capacitor, then
C = \(\frac{q}{V}\)
Using eq. (1) & (2), we get
C = \( \frac{\lambda l 2 \pi \varepsilon_0}{\lambda \log _e b / a}=\frac{2 \pi \varepsilon_0 l}{\log _e b / a}\)
or C = \(\frac{2 \pi \varepsilon_0 l}{2 \cdot 303 \log _{10} b / a}\)

Question 16. 
(a) Calculate the energy stored in a capacitor.
(b) What is the energy when number of capacitors are placed (i) in series and (ii) in parallel?
Answer:
(a) Energy stored in a capacitor.
The energy stored in a capacitor is the amount of work done in charging it.
Let a capacitor be charged gradually. At any instant during charging, let q be charge and V be the potential difference between the plates of the capacitor. If C is the capacitance of the capacitor, then
V = \(\frac{q}{\mathrm{C}}\)
Let an additional charge dq be transferred to the capacitor.
Work done in transferring the charge dq
dW = Vdq = \(\frac{q}{\mathrm{C}}dq\)
Total work done in delivering charge q to capacitor is given by
W = \(\int_0^q \frac{q}{\mathrm{C}} d q=\frac{1}{\mathrm{C}} \int_0^q q d q\)
= \(\frac{1}{\mathrm{C}}\left[\frac{q^2}{2}\right]_0^q\)
This work done is stored in the form of electric potential energy U:

If C is measured in farad, V is measured in volt then U is expressed in joule.
Another form of energy of parallel plate capacitor. If the conductor is a parallel plate capacitor, then
q = A σ where σ = charge density

The factor A d is called volume of capacitor between two plates.
∴ Energy of capacitor per unit volume
=\( \frac{1}{2} \varepsilon_0 \mathrm{E}^2\)
Energy per unit volume is called energy density.

(b) (i) When capacitors are connected in series.

Total energy of capacitors connected in series is equal to sum of energies of each capacitor.
(ii) When capacitors are connected in parallel.
U = \(\frac{1}{2}\) CV²
For capacitors in parallel
∴ C = C₁ + C₂ + C₃ + ..............................
So U =\( \frac{1}{2}\)(C₁ + C₂ + C₃ + ...................)V²
or U = \(\frac{1}{2}\)C₁V² + \(\frac{1}{2}\)C₂V² +\( \frac{1}{2}\) C₃V² + ..........................
∴ U = U₁ + U₂ + U₃ + .......................
Total energy of capacitors connected in parallel is equal to sum of energies of each capacitor.

Question 17.
(a) What is a dielectric?
(b) What are polar and non-polar molecules, give examples.
(c) Define atomic polarisability.
Answer:
(a) Dielectric. A dielectric is a material in which all the electrons are tightly bound to the nuclei of atoms, so that there are no free electrons to carry current. In other words, a dielectric is a substance that does not conduct electric current through it. When an electric charge is given to a dielectric, it remains localised or fixed in the region of their initial distribution or application in contrast to conductors where the charge immediately spread on the surface.
The molecules or atoms of a dielectric can be classified as either (i) polar or (ii) non-polar.
Polar molecules. A polar molecule is one in which the centre of gravity of the positi ve charges (i.e. protons ) does not coincide with the centre of gravity of the negative charges (i.e. electrons). Due to finite separation between the positive and negative charges, polar molecules are permanent electric dipoles and have permanent electric dipole moments, e.g. HCl, NH₃, H₂O, CO₂ are polar molecules. In the absence of electric field, the dipole moment of these polar molecules point in random directions and arrange themselves in closed chains and net dipole moment is zero.

Effect of applied Electric field on polar molecules. An applied electric field merely aligns the polar molecules parallel to itself. Because the molecules are in constant thermal agitation, the alignment is not complete as shown in Fig. LAQ 17 (b). However, the alignment increases as the applied electric field is increased or as the temperature is decreased. The dipole moment may also be increased by the applied electric field.

Non-polar molecules. A non-polar molecule is one, in which the center of gravity of the positive charges (i.e. protons) coincides with the center of gravity of the negative charges (i.e. electrons). Thus in these molecules, there is no separation between the centers of positive and negative charges and so they have no permanent electric dipole moments.

Some common non-polar molecules are oxygen (O₂), nitrogen (N₂), hydrogen (H₂) etc.
Effect of applied electric field on non-polar molecules. When a non-polar molecule is placed in an electric field, the center of positive charge moves in the direction of field and center of gravity of the negative charge in an opposite direction. This separation of +ve and -ve charges continues till the force on either of them due to external field is completely balanced by the internal forces arising due to relative displacements. The molecule develops a dipole moment called induced moment. Such a molecule is said to be polarized.

The induced dipole moment disappears as the electric field is removed.
Atomic polarisability. If \(d \vec{l}\) is the separation between centers of positive and negative charge.
q = positive or negative charge on the atom.
Atomic dipole moment \(\vec{p} =d \vec{l}\).
The net induced electric dipole moment for an atom is proportional to the strength of applied electric field \(\overrightarrow{\mathrm{E}}\) and its direction is parallel \(\overrightarrow{\mathrm{E}}\).
\(\overrightarrow{\mathrm{p}}\) ∝  ε₀ \(​​\)
or \(\overrightarrow{\mathrm{p}}\) = α ε₀ \(\overrightarrow{\mathrm{E}}\)
where α is called proportionality constant or atomic polarisability. Atomic polarisability is defined as the electric dipole moment induced in the atom by an electric field of unit strength.
Dimensions of α
= \(\frac{\text { Dimensions of } p}{\text { Dim. of } \varepsilon_0 E}\)
=\( \frac{\mathrm{Cm}}{\left(\mathrm{C}^2 \mathrm{~N}^{-1} \mathrm{~m}^{-2}\right)\left(\mathrm{NC}^{-1}\right)}\)
or Dimension of α = m³
∴ α has dimensions of volume.

Question 18.
(a) Discuss the polarisation of dielectric slab placed in an electric field. What happens to the applied electric field?
(b) Define dielectric constant in reference to applied and reduced electric field.
(c) Define polarisation density. Show that it is equal to reduced surface charge density.
(d) Define electric susceptibility and prove that
(i) K = 1 + ✗, (ii) K = 1 + N α.
Answer:
(a) Polarisation of a dielectric slab
Consider a charged parallel plate capacitor with vacuum between the two plates such that E₀ is the electric field between the plates
E₀ = \(\frac{\sigma}{\varepsilon_0}\) ............................(i)
where σ is the magnitude of surface charge densities on each plate.
Suppose a dielectric slab of non-polar atom is introduced between the plates. The polarization of the slab takes place. On the left face, a net negative charge -qi and on the right face, a positive charge +qi appears. There is no net charge in the interior of the dielectric marked by dotted boundary in the Fig. 2.88 (b). The charge -qi and +qi on the two surfaces of the dielectric slab are called induced charges. The induced charges set up an electric field E_p inside the dielectric. It is called electric field due to polarisation. The direction of electric field due to polarisation is from positive surface to the negative surface of the slab i.e. along a direction opposite to the direction of applied electric field E₀. Therefore, the resultant electric field is given by
E = E₀ - E_p

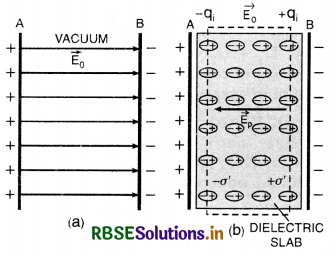
Since, magnitude of E is less than E₀, E is called the reduced value of electric field. In other words, on placing a dielectric slab inside an electric field, the strength of the electric field gets reduced. It can be understood in another way also. If -σ' and +σ' are surface charge densities of the left and right faces of the dielectric slab (due to induced charges developed), then electric field between the two plates of the capacitor will be
E = \(\frac{\sigma}{\varepsilon_0}+\left(\frac{-\sigma^{\prime}}{\varepsilon_0}\right)\)
or E = \(\frac{\sigma-\sigma^{\prime}}{\varepsilon_0}\) ...........................(2)
Obviously, the value of E is less than E₀.

(b) Dielectric constant. The ratio of the strength of applied electric field to the strength of reduced value of electric field on placing the dielectric between the plates of the capacitor is called the dielectric constant of the dielectric medium.
It is also known as relative permittivity or specific inductive capacity and is denoted by K (or ε_r). Therefore, dielectric constant of a dielectric is given by
K = \(\frac{\mathrm{E}_0}{\mathrm{E}}\) .........................(3)
The value of K is always greater than 1.

(c) Polarisation density. The induced dipole moment development per unit volume in a dielectric slab on placing it inside the electric field is called polarisation density. It is denoted by P. If p is induced dipole moment of an atom acquired by the dielectric and N is number of atoms per unit volume, then
P = Np ........................(4)
Since, p = α ε₀ E,
∴ P = N α ε₀ E, ............................(5)
If A is the area of each plate of the capacitor and d, the distance between them, then the volume of the dielectric slab = Ad. Since induced charges -qi and +qi are developed on the two faces of the dielectric, the slab possesses total dipole moment equal to qid. Therefore, from definition of polarisation density,
P = \(\frac{q_i d}{\mathrm{Ad} d}=\frac{q_i}{\mathrm{~A}}\)
Since \(\frac{q_i}{\mathrm{~A}}\) = σ', induced surface charge density, we have
P = σ' ..................... (6)
Therefore, reduced value of electric field on placing dielectric between the two plates, a capacitor may be expressed as:
E = \(\frac{\sigma-\sigma^{\prime}}{\varepsilon_0}=\frac{\sigma}{\varepsilon_0}-\frac{\sigma^{\prime}}{\varepsilon_0}\)
or E = E₀ - \(\frac{\mathrm{P}}{\varepsilon_0}\) ................................(7)
(d) Electric susceptibility. The polarisation density of a dielectric slab is directly proportional to the reduced value of the electric field and may be expressed asP ∝ ε₀ E
P = ✗ε₀E ....................(8)
The constant of proportionality ✗ is called electric susceptibility of the dielectric slab. It is a dimensionless constant.
Setting the value of P in equation (7), we have
E = E₀ - \(\frac{\chi \varepsilon_0 E}{\varepsilon_0}\) = E₀ - ✗_E
or E₀ = E (1 + ✗) .....................(9)
or \(\frac{\mathrm{E}_0}{\mathrm{E}}\) = 1 + ✗ ...............................(10)
From equation (3) and (10), we have
K = 1 + ✗ ........................(11)
Also, from equations (5) and (8), we have
✗ ε₀E = Naε₀E
or ✗ = Na
and K = 1 + Na

Question 19.
Explain how does capacitance of a ‘parallel plate capacitor change on introducing a ‘dielectric slab’.
Answer:
Capacitance of a parallel plate capacitor with dielectric slab between the plates.
Consider a parallel plate capacitor having each plate of area A and separated by distance d. When there is vacuum between the two plates, the capacitance of the parallel plate capacitor is given by
C₀ = \(\frac{\varepsilon_0 \mathrm{~A}}{d}\) ............................(1)
If electric field between the two plates is E₀, potential difference between the plates is given by
V₀ = \(\frac{q}{\mathrm{C}_0}=\frac{q d}{\varepsilon_0 \mathrm{~A}}\)
Suppose a dielectric slab of thickness t (t < d) is introduced between the two plates of the capacitor (Fig. LAQ 19). Then electric field inside the slab will be reduced to
E = E₀ - \(\frac{\mathrm{P}}{\varepsilon_0}\)
The potential difference between the plates when dielectric of thickness 't' is introduced is V (say).
V = Pot. diff. between plate + Pot. diff. between dielectric
V = E₀ (d - t) + Et

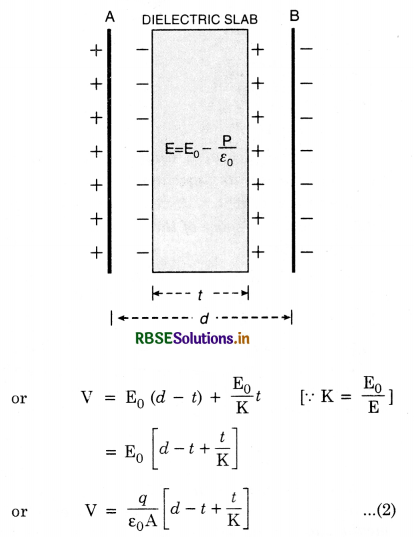
So, the capacitance of the capacitor with dielectric partially filling the space between the plates of the capacitor is given by
C = \(\frac{q}{\mathrm{~V}}\)

i.e. the presence of a dielectric slab inside a capacitor increases its capacitance.
Special case. If t = d, i.e. the dielectric is filled between the whole space of the capacitor plates.
From eq. (5),
C = \(\frac{d \mathrm{C}_0}{d+\frac{d}{\mathrm{~K}}-d}=\frac{d \mathrm{C}_0 \mathrm{~K}}{d}=\mathrm{C}_0 \mathrm{~K}\)
or C = KC₀
i.e. the capacitance of the capacitor increases K times, when dielectric of dielectric constant K is introduced between its plates
or K = \(​​\) ......................(6)
Hence relative permittivity K is defined as the ratio of capacitance of capacitor with dielectric between the medium to the capacitance of the capacitor with air as medium.

Question 20.
Explain how does capacity of parallel plate capacitor change on introducing a conducting slab.
Answer:
Let q = charge on the plate A.
A = area of plate.
d = distance between the plates 
When a slab of a conductor is introduced between the plates of parallel plate capacitor, a negative induced charge density develops on the upper side and a positive induced charge density on its lower side due to polarisation thereby reducing the field to zero in the interior of the slab.

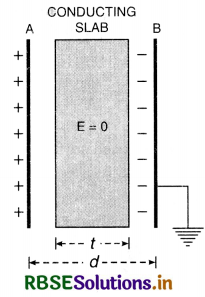
The capacitance of the capacitor when there is vacuum between its two plates.
C₀ = \(\frac{\varepsilon_0 \mathrm{~A}}{d}\) .........................(1)
On introducing the conducting slab the field will last long for distance (d - t) instead of d
∴ Potential difference between the capacitor plates

∴ C > C₀
i.e. the presence of a conducting slab increases the capacitance of the capacitor.
Special Case, If t = d and the conductor is kept insulated with the plates of the capacitor
From Eq. (3),
C = \(\frac{d}{d-d} \mathrm{C}_0=\frac{d}{0}=\infty\)
i.e. the capacitance of the capacitor becomes infinite.

Question 21.
(a) Derive an expression for common potential when two capacitors at different potentials touch each other.
(b) Two capacitors at different potentials touch each other. Show that there is always loss of energy.
Answer:
(a) Let two capacitors of capacities C₁, C₂ and potentials V₁ and V₂ touch each other. If their common potential is V, then the sum of charges
Before sharing = C₁V₁ + C₂V₂
And after sharing = C₁V + C₂V
= V (C₁ + C₂)
Since charges are conserved, therefore
V(C₁ + C₂) = C₁V₁ + C₂V₂
or V = \(\frac{\mathrm{C}_1 \mathrm{~V}_1+\mathrm{C}_2 \mathrm{~V}_2}{\mathrm{C}_1+\mathrm{C}_2}\)

(b) Sum of energies before sharing is
E₁ = \(\frac{1}{2}\) C₁V₁² + \(\frac{1}{2}\) C₂V₂²
and sum of energies after sharing is

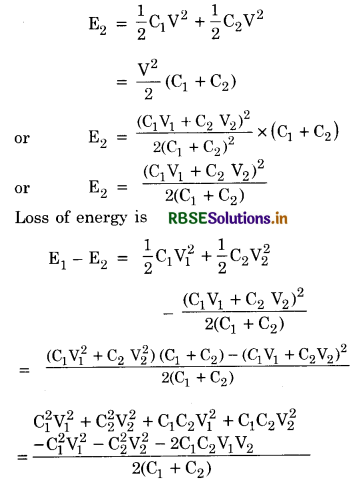
E₁ - E₂ = \(\frac{\mathrm{C}_1 \mathrm{C}_2\left(\mathrm{~V}_1^2+\mathrm{V}_2^2-2 \mathrm{~V}_1 \mathrm{~V}_2\right)}{2\left(\mathrm{C}_1+\mathrm{C}_2\right)}\)
= \(\frac{\mathrm{C}_1 \mathrm{C}_2\left(\mathrm{~V}_1-\mathrm{V}_2\right)^2}{2\left(\mathrm{C}_1+\mathrm{C}_2\right)}\)
= a positive quantity.
Hence there is always a loss of energy when two capcaitors share the charges.

Question 22.
Draw a labelled diagram of Van de Graaff generator. State its principle of working.
Answer:
Principle. It is based on the following two facts:
(i) If a charged conductor is in internal contact with another hollow conductor, the hollow conductor accepts all available charge on the charged conductor irrespective of its own potential.

(ii) The electric discharge takes place in air or gases readily at pointed conductors.
Construction. A large hollow metallic sphere S is mounted on two. insulating columns CC' as shown in Fig. LAQ 22. An endless belt of an insulating material is made to run on two pulleys P₁ and P₂ with the help of an electric motor. The metal comb C₁, called spray comb is held near the lower end of the belt. When it is maintained say at high positive potential with the help of H. T. source (≈ 10⁴V), it produces ions in its vicinity. The positive ions get sprayed on the belt due to the repulsive action of comb C₁, which are carried upward by the moving belt. A comb C₂ called collection comb is positioned near the upper end of the belt such that the pointed end touch the belt and the other end is in contact with the inner surface of the metallic sphere S.

Working. The comb C₂ collects the positive ions and transfers them to the metallic sphere. The charge transferred by the comb C₂ immediately moves on to the outer surface of the hollow sphere. As the belt goes on revolving continuously the accumulation of positive charge on the sphere also keeps on taking place and its potential rises considerably. With the increase of charge on the sphere, its leakage due to ionisation of surrounding air also becomes faster. The maximum potential to which the sphere can be raised is reached, when the rate of loss of charge due to leakage becomes equal to the rate at which the charge is transferred to the sphere. To prevent the leakage of charge from the sphere, the generator is completely enclosed inside an earth-connected steel tank which is filled with air under pressure.

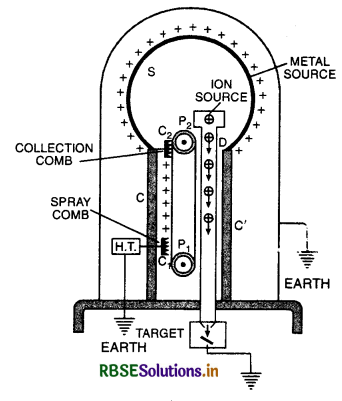
If the projectiles such as protons, deuterons etc. are now generated in the discharge tube D with lower end earthed and upper end inside the hollow sphere, they get accelerated down the tube due to the high potential difference. On leaving the discharge tube at the other end, they hit the target with large kinetic energy and bring about nuclear disintegration.

Question 23.
What is dielectric? Why does the capacitance of a parallel plate capacitor increase on introduction of a dielectric between its two plates? Derive an expression for the capacitance of such a capacitor having two identical plates each of area A and separated by distance x. The space between the plates has a medium of dielectric constant K.
Answer:
Dielectric is an insulting medium which transmits electric current without conducting.
When a dielectric is introduced between the plates of a charged capacitor the dielectric gets polarised and opposite electric field is developed in the dielectric due to polarisation. Thus the net electric field inside the dielectric decreases without bringing any change in the charge. Some charge and decrease in electric field produces decrease in electric potential and hence increase in capacity of the capacitor \(\left(\mathrm{C}=\frac{q}{\mathrm{~V}}\right)\):
Capacitance of a parallel plate capacitor

(a) Parallel plate capacitor. A parallel plate capacitor is a combination of two conducting plates held parallel to each other at suitable distance having some dielectric in between them. One of the plate is positively charged and the other is earthed.
Expression for capacitance of parallel plate capacitor

Let a parallel plate capacitor consist of two thin conducting plates A and B held parallel to each other at a certain distance d apart. Medium between plates is given to be vacuum. Plate A is insulated and B is earthed.
When charge +q is given to A, it induces -q on the nearer face of B and +q on the farther face of the plate B. Free +ve charge on B flows to the earth.

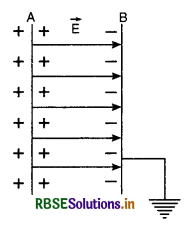
Electric field intensity between the plate is
E = \(\frac{\sigma}{\varepsilon_0}\)
where σ is the charge density and equal to q/A.
Also E = \(\frac{\mathrm{V}}{d}\), where V is the P.D. between plates.
V = Ed = \(\frac{\sigma}{\varepsilon_0} d=\frac{q d}{\mathrm{~A} \varepsilon_0} \quad\left[\because \sigma=\frac{q}{\mathrm{~A}}\right]\)
If C is the capacitance of the parallel plate capacitor, then
C = \(\frac{q}{\mathrm{~V}}=\frac{q}{\frac{q d}{\mathrm{~A} \varepsilon_0}}=\frac{\mathrm{A} \varepsilon_0}{d}\)
or C = \(\frac{\mathrm{A} \varepsilon_0}{d}\)
This is the expression for the capacitance when the medium is air or vacuum.
If A is in m², d is in m, then C is taken in farad. If medium between plates is other than air, capacitance of capacitor is given by
C = \(\frac{\varepsilon_0 \mathrm{KA}}{d}\)
where K is dielectric constant.
(b) Definition of dielectric constant
In vacuum the capacitance of capacitor,
C₁ = \(\frac{\varepsilon_0 \mathrm{~A}}{d}\) .........................(i)
In dielectric medium, the capacitance of capacitor
C₂ = \(\frac{\varepsilon_0 \mathrm{KA}}{d}\) ..........................(ii)
Dividing (i) and (ii), we get
\(\frac{\mathrm{C}_2}{\mathrm{C}_1}=\frac{\varepsilon_0 \mathrm{KA}}{d} \times \frac{d}{\varepsilon_0 \mathrm{~A}}\) = K
∴ Dielectric constant of a medium is defined as the ratio of capacitance of capacitor with dielectric as medium to the capacitance of the same capacitor with air as medium.

Question 24.
Four point Charges Q, q, Q and q are placed at the corners of a square of side ‘a’ as shown in the figure.

Find the
(a) resultant electric force on a charge Q, and
(b) potential energy of this system.
Answer:
(a) Force at Q due to q
F₁ = k \(\frac{\mathrm{Qq}}{a^2}=k \frac{\mathrm{Q} q}{a^2}\) where k = \(\frac{1}{4 \pi \varepsilon_0}\)
Force at Q due to Q

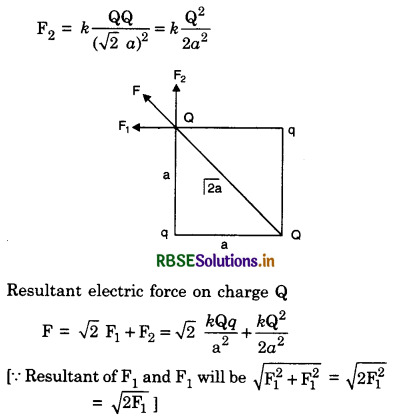
(b) Since potential of two charges q₁ and q₂ at distance r is

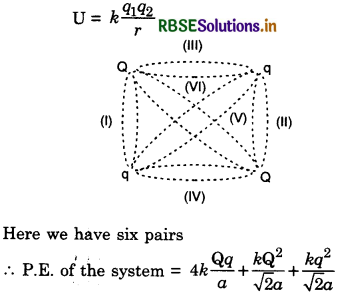
HOTS QUESTIONS

Question 1.
Two charged conducting spheres A and B having radii a and b are connected to each other by a copper wire. Find the ratio of the electric Held at the surfaces of the two spheres.
Answer:
Let q_A and q_B be charge on sphere A and B respectively, then
V_A = \(\frac{1}{4 \pi \varepsilon_0} \frac{q_{\mathrm{A}}}{a}\)
and V_B = \(\frac{1}{4 \pi \varepsilon_0} \frac{q_{\mathrm{B}}}{b}\)
When the two charged spheres are connected by a copper rod, their potential will become equal i.e.
\(\frac{1}{4 \pi \varepsilon_0} \frac{q_{\mathrm{A}}}{a}=\frac{1}{4 \pi \varepsilon_0} \frac{q_{\mathrm{B}}}{b} \quad \text { or } \quad \frac{q_{\mathrm{A}}}{q_{\mathrm{B}}}=\frac{a}{b}\) ...............................(i)
The electric field at the surfaces of two spheres

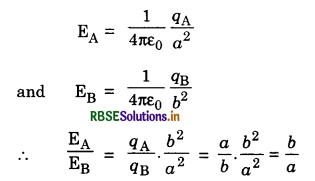
Question 2.
A uniform electric field E exists between two charged plates as shown in Fig. HQ 2. What would be the work done in moving a charge q along the closed rectangular path ABCDA?

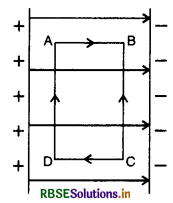
Answer:
Zero. Since electric field is conservative field and work done for describing a closed path in the conservative field is always zero.

Question 3.
The graphs shows the variation of voltage V across the plates of two capacitors A and B versus increase of charge Q stored on them. Which of the two capacitors has higher capacitance? Give reason for your anwer.

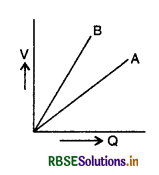
Answer:
Capacitance A has higher capacitance. Since capacitance C = \(\frac{Q}{V}\) and here the slope of the graph is given by \(\frac{V}{Q} \left(\text { i.e. } \frac{1}{\mathrm{C}}\right)\). Hence capacitance is given by reciprocal of slope V - Q graph. As slope of capacitor A is less than that of capacitor B. Hence the capacitance of capacitor A is higher.

Question 4.
The given graph shows the variation of charge q versus potential difference V for two capacitors C₁ and C₂. The two capacitors have the same plate separation but the plate area of C₂ is double than that of C₁. Which of the lines in the graph correspond to C₁ and C₂ and why?

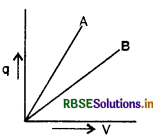
Answer:
Since capacitance of a capacitor is given by
C = \(\frac{\varepsilon_0 \mathrm{~A}}{d}\)
Here d is the same for both the capacitors.
So C ∝ A
As area of C₂ = 2 x Area of C₁
∴ C₂ = 2 C₁
Also C = \(\frac{q}{\mathrm{~V}}\). Thus the slope of q -V graph gives the value of capacitance. Here slope for A is greater than B, hence graph A corresponds to C₂ and graph B corresponds to C₁.

Question 5.
Show that the plates of a parallel plate capacitor attract each other with a force given by
F = \(\frac{\mathbf{Q}^2}{2 \varepsilon_0 \mathbf{A}}\)
The symbols have their usual meanings.
Answer:
If r is the separation between the plates of the capacitor, the energy stored U is given by
U = \(\frac{\mathrm{Q}^2}{2 \mathrm{C}}=\frac{\mathrm{Q}^2}{2\left(\varepsilon_0 \frac{\mathrm{A}}{r}\right)}=\frac{\mathrm{Q}^2 r}{2 \varepsilon_0 \mathrm{~A}} ...........................(i) [∵ C = \frac{\varepsilon_0 \mathrm{~A}}{d}]\)
If the plate separation is increased to r + dr, the energy stored is given by
U' = \(\frac{\mathrm{Q}^2(r+d r)}{2 \varepsilon_0 \mathrm{~A}}\) ..........................(ii)
Therefore, the work done to increase the plate separation by dr is
dW = U' - U = \(\frac{\mathrm{Q}^2 d r}{2 \varepsilon_0 \mathrm{~A}}\) ..........................(iii)
If F is the force between the plates of the capacitor, then work done dW is also given by
dW = Fdr .......................(iv)
From eq. (iii) and eq. (iv), we have
F dr = \(\frac{\mathrm{Q}^2 d r}{2 \varepsilon_0 \mathrm{~A}}\)
or F = \(\frac{\mathrm{Q}^2}{2 \varepsilon_0 \mathrm{~A}}\)

Question 6.
Two identical plane metallic surfaces A and B are kept parallel to each other in air separated by a distance of 1.0 cm as shown in Fig. HQ 6. Surface A is given a positive potential of 10 V and outer surface of B is earthed.

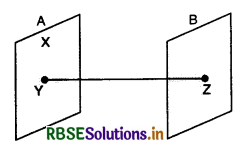
(i) What is the magnitude and direction of uniform electric field between points Y and Z?
(ii) What is the work done in moving a charge of 20 pC from point X to Y. Where X is situated on surface A?
Answer:
(i) Magnitude of electric field
E = \(\frac{d \mathrm{~V}}{d r}=\frac{10}{1.0 \times 10^{-2}}\) = 10³ Vm-1
Direction of \(\vec{E}\) is from plate B to plate A
(ii) Surface A is equipotential surface, so potential difference between X and Y is zero
i.e. ∆V= 0
∴ work done = q ∆V = 0
Thus, no work is done in moving a charge from X to Y.

Question 7.
A circuit has a section AB as shown in Fig. HQ 7. The emf of, the source equals E = 10V, the capacitor capacitances are equal to C₁ = 1.0 µF and C₂ = 2.0 µF and the potential difference V_A - V_B = 5.0 V. Find the voltage across each capacitor.

Answer:
Potential difference between A and B is:

Question 8.
A capacitor of 5 µF is charged to 1C by using a constant voltage supply. If one of the plates of charged capacitor is earthed after disconnecting it from external voltage supply, find the new
(a) Capacitance
(b) Voltage across the capacitor
(c) Charge on the capacitor.

Answer:
(a) Capacitance of the capacitor
C =\( \frac{\varepsilon_0 \mathrm{~A}}{d}\)
Since capacitance of capacitor does not depend on the charge of the capacitor, hence it will remain the same Fig. 2.107 (a).
(b) Voltage across the' capacitor plates when charged capacitor is earthed V' =\( \frac{\mathrm{V}}{2}\) i.e. voltage across the plates will be halved Fig. 2.107 (b).
(c) Since q = CV 
∴ q' = \(\mathrm{C}\left(\frac{\mathrm{V}}{2}\right)=\frac{1}{2}(\mathrm{CV})=\frac{q}{2}\)
Hence, charge will reduce to half the original value.