RBSE Class 12 Physics Important Questions Chapter 13 नाभिक

Rajasthan Board RBSE Class 12 Physics Important Questions Chapter 13 नाभिक Important Questions and Answers.

RBSE Class 12 Physics Chapter 13 Important Questions नाभिक

अति लघुत्तरीय प्रश्न

प्रश्न 1.
नाभिकीय भट्टी में प्रयुक्त शीतलक का कार्य लिखिए।
उत्तर:
नाभिकीय भट्टी में प्रयुक्त शीतलक नाभिकीय विखण्डन में उत्पन्न ऊष्मा से विस्फोट की आशंका से बचाने का कार्य करता है।

प्रश्न 2.
एक समान दर से चलने वाली श्रृंखला अभिक्रिया के लिए न्यूट्रॉन गुणांक का मान कितना होगा?
उत्तर:
एक समान दर से चलने वाली श्रृंखला अभिक्रिया के लिए न्यूट्रॉन गुणांक का मान K = 1 होना चाहिए।

प्रश्न 3.
किसी तत्व के चार नाभिक संलयित होकर कोई भारी नाभिक बनाते हैं जिसमें ऊर्जा का स्मोच होता है। जनक अथवा संतति नाभिकों में से किसकी बंधन ऊर्जा प्रति न्यूक्लिऑन अधिक झेगी।
उत्तर:
नाभिकीय संलयन के उपरांत संतति नाभिक अधिक स्थायी होते हैं अतः संतति की बंधन ऊर्जा प्रति न्यूक्लिऑन अधिक होगी।

प्रश्न 4.
नाभिक की द्रव्यमान क्षति से क्या अभिप्राय है?
उत्तर:
नाभिक के सम्भावित द्रव्यमान (गणना द्वारा प्राप्त द्रव्यमान m_c) एवं वास्तविक द्रव्यमान (m_a) के अन्तर को द्रव्यमान क्षति कहते है। इसे ∆m से व्यक्त करते हैं।
∴ ∆m = m_c - m_a
या ∆m = [Z m_p + (A - Z) m_n] - m

प्रश्न 5.
एक रेडियोएक्टिव तत्व का क्षय स्थिरांक 0.693 प्रति मिनट है। इसकी अर्द्ध - आयु तथा औसत-आयु क्या होगी?
उत्तर:
क्षय स्थिरांक λ = 0.693 प्रति मिनट
अर्द्ध - आयु T = \(\frac{0.693}{\lambda}\) = 1 मिनट
औसत - आयु Ta = 1.44 T = 1.44 मिनट

प्रश्न 6.
रेडियोएक्टिव पदार्थ की सक्रियता को परिभाषित कीजिए। इसका SI मात्रक लिखिए।
उत्तर:
रेडियोएक्टिव प्रतिदर्श की कुल क्षय दर प्रतिदर्श की रेडियोएक्टिवता कहलाती है। इसका SI मात्रक बेकुरल (Bq) है।

प्रश्न 7.
न्यूक्लियर रिएक्टर में प्रयुक्त दो मंदको के नाम लिखिए।
उत्तर:

• भारी जल D₂O
• ग्रेफाइट

प्रश्न 8.
त्वचा रोग के उपचार के लिए किस रेडियोएक्टिव समस्थानिक का उपयोग किया जाता है?
उत्तर:
स्ट्रांशियम - 90 का उपयोग

प्रश्न 9.
नाभिकीय बल के दो अभिलाक्षणिक गुण लिखिए।
उत्तर:

• अल्प परास का बल है।
• प्रकृति में सबसे मजबूत आकर्षण बल है।

प्रश्न 10.
नाभिकीय क्षय में न्यूट्रिनो का प्रायोगिक संसूचन कठिन क्यों है?
उत्तर:
न्यूट्रिनो का संसूचन करना कठिन है क्योंकि ये द्रव्यमान एवं आवेशरहित होते हैं और न्यूक्लिऑन के साथ अन्योन्य क्रिया नहीं करते हैं।

प्रश्न 11.
दो न्यूक्लिऑनों युग्मो के मध्य दूरी के साथ स्थितिज ऊर्जा में परिवर्तन को दर्शाते हुए ग्राफ खींचिए। नाभिकीय बल की (i) आकर्षण (ii) प्रतिकर्षण प्रकृति को दर्शाइए।
उत्तर:

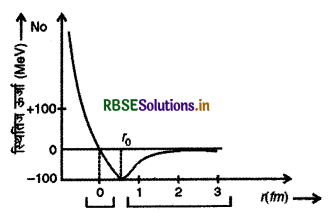
लघु उत्तरीय प्रश्न

प्रश्न 1.
एक रेडियोएक्टिव नाभिक D निम्न प्रकार क्षयित हो रहा है-

प्रश्न 2.
रेडियोएक्टिव क्षयता का नियम लिखिए। एक रेडियोएक्टिव नाभिक का क्षय निम्न प्रकार से होता है। अन्तिम उत्पाद की द्रव्यमान संख्या एवं परमाणु क्रमांक ज्ञात कीजिए जबकि प्रारंभिक नाभिक की द्रव्यमान संख्या A = 238 एवं परमाणु क्रमांक Z = 92 है।

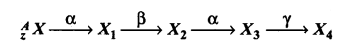
उत्तर:
रेडियोएक्टिव क्षयता का नियम: किसी क्षण रेडियोएक्टिव परमाणु के क्षय होने की दर उस क्षण उपस्थित अविघटित परमाणुओं की संख्या के अनुक्रमानुपाती होती है।
\(\left(\frac{-d N}{d t}\right)\) ∝ N
\(\frac{-d N}{d t}\) = λN
जहाँ λ क्षय स्थिरांक है जिसका मात्रक विघटन प्रति सेकण्ड है। दिया गया भय इस प्रकार होगा।

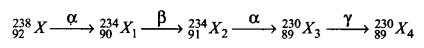
X₄ नाभिक का परमाणु क्रमांक 89 तथा द्रव्यमान संख्या 230 होगी।

प्रश्न 3.
नाभिक में इलेक्ट्रॉन नहीं होते हैं फिर भी ß - कण नाभिक से निकलते हैं, कैसे?
उत्तर:
नाभिक से ß - कण का उत्सर्जन केवल तभी होता है जब एक न्यूट्रॉन एक प्रोटॉन, एक ß - कण एवं एक एन्टीन्यूट्रिनों में टूटता है। यही इलेक्ट्रॉन ß - कण के रूप में उत्सर्जित होता है। अभिक्रिया निम्न प्रकार प्रदर्शित कर सकते हैं।

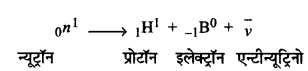
प्रश्न 4. निम्नलिखित नाभिकीय अभिक्रियाओं को पूर्ण करो-
(i) ¹⁰₅B + ¹₀n → ⁴₂He + ............
(ii) ⁹⁴₄₂Mo + ²₁H → ⁹⁵₄₃Te + .............
उत्तर:
(i) ₁₀₅B + ¹₀n → ⁴₂He + ⁷₃Li
(ii) ⁹⁴₄₂Mo + ²₁H → ⁹⁵₄₃Te + ¹₀n

प्रश्न 5.
निम्नलिखित नाभिकीय अभिक्रियों को पूरा करो-
(a) ²⁰⁸₈4Po → ²⁰⁴₈₂Pb + ............. 
(b) ³²₁₅P → ³²₁₆S + ...........
उत्तर:
(a) ²⁰⁸₈₄Po → ²⁰⁴₈₂Pb + ⁴₂He
(b) 32 15P → 32 16S + ⁰_-1B

प्रश्न 6.
नाभिकीय शृंखला अभिक्रिया में क्रांतिक द्रव्यमान से क्या आशय है?
उत्तर:
नाभिकीय विखण्डन में उत्पन्न सभी न्यूट्रॉन विखण्डन में भाग नहीं लेते हैं। यहाँ न्यूट्रॉन की उत्पत्ति की दर पिण्ड के आयतन \(\left(\frac{4}{3} \pi r^3\right)\) पर निर्भर होती है; जबकि पृष्ठ से क्षरण की दर पृष्ठीय क्षेत्रफल (4πr²) पर निर्भर करती है। इस प्रकार

स्पष्ट है पिण्ड का आकार छोटा होने पर क्षरण पर उत्पत्ति दर के सापेक्ष अधिक होगी, जबकि पिण्ड का आकार अधिक होगा तो क्षरण दर की अपेक्षा उत्पत्ति दर अधिक होगी व शृंखला अभिक्रिया की सम्भावना अधिक होगी। उपरोक्त व्याख्या से स्पष्ट है भारी नाभिक (यूरेनियम) का वह न्यूनतम द्रव्यमान (आकार) जिसमें नाभिकीय विखण्डन श्रृंखला अभिक्रिया सम्भव होती है उसे क्रांतिक द्रव्यमान कहते हैं।

प्रश्न 7.
भारी जल नाभिकीय भट्टी में उपयुक्त मंदक है क्यों?
उत्तर:
जब समान द्रव्यमान के दो कणों के बीच प्रत्यास्थ टक्कर होती है तो उनके वेग आपस में बदल जाते हैं अतः जब तीव्र वेग वाला न्यूट्रॉन समान द्रव्यमान वाले हाइड्रोजनी पदार्थ जैसे भारी जल से टकराता है तो टक्कर के पश्चात न्यूट्रॉन के वेग में अधिकतम ह्यस होता है।

प्रश्न 8.
नाभिकीय विखण्डन एवं नाभिकीय संलयन में एक असमानता एवं एक समानता बताइये।
उत्तर:
असमानता: नाभिकीय विखण्डन में भारी नाभिक दो हल्के नाभिकों में टूटता है जबकि नाभिकीय संलयन में दो हल्के नाभिक मिलकर भारी नाभिक बनाते हैं।
समानता: दोनों अभिक्रियाओं में द्रव्यमान क्षति होती है जो ऊर्जा के रूप में बदलकर मुक्त होती हैं।

प्रश्न 9.
नाभिकीय बल की आवेश अनिर्भर प्रकृति से क्या अभिप्राय है?
उत्तर:
नाभिकीय बल न्यूक्लिआनों के आवेश पर निर्भर नहीं करता है। अत: यह p - p युग्म, p - n युग्म एवं n - n युग्म के लिए समान होता हैं।

प्रश्न 10.
रेडियोएक्टिव क्षय की प्रक्रिया में सभी तत्व अन्त में सीसे (pb) में क्यों बदल जाते है?
उत्तर:
सीसा (Z = 82) से भारी सभी तत्व अस्थायी होते हैं और स्थायित्व प्राप्त करने के लिए वे रेडियोएक्टिव किरणें उत्सर्जित करके अपने द्रव्यमान में कमी उत्पन्न करते रहते हैं। इसीलिए सभी भारी तत्व अन्ततः स्थायी तत्व सीसे में बदल जाते हैं।

प्रश्न 11.
ß - कणों का ऊर्जा वितरण सतत क्यों होता है?
उत्तर:
ß - कणों का कर्जा वितरण सतत होता है क्योंकि ß - कण उत्सर्जित होने के साथ \(\bar{v}\) (एन्टीन्यूट्रिनो) भी उत्सर्जित होता है अतः ß - उत्सर्जन की कुल ऊर्जा दोनों में बंट जाती है लेकिन दोनों की कुल ऊर्जा नियत होती है। कणों के मध्य अन्योन्य क्रिया के कारण ऊर्जा का बँटवारा हो जाता है। इसीलिए ß - कणों का ऊर्जा वितरण सतत होता है।

प्रश्न 12.
ß - उत्सर्जन की प्रक्रिया में संवेग संरक्षण के सिद्धांत का पालन किस प्रकार होता है?
उत्तर:
हम जानते हैं कि जब नाभिक के अन्दर एक न्यूट्रॉन, एक प्रोटॉन एवं एक न्यूट्रिनों में टूटता है तो एन्टीन्यूट्रिनो के साथ ß कण का उत्सर्जन होता है। इस उत्सर्जन से पूर्व नाभिक का संवेग शून्य होता है। ß - कण के साथ एन्टीन्यूट्रिनो इतने संवेग से उत्सर्जित होता है कि इसके तथा ß - कण के साथ नये नाभिक के संवेगों का वेक्टर योग शून्य हो जाता है।

दीर्घ उत्तरीय प्रश्न

प्रश्न 1.
किसी रेडियोएक्टिव तत्व की अर्द्ध - आयु को परिभाषित कीजिए तथा अर्द्ध - आयु का निम्न के साथ सम्बन्ध लिखिए-
(a) रेडियोएक्टिव क्षय स्थिरांक
(b) रेडियोएक्टिव तत्व की औसत आयु
उत्तर:
अर्द्ध - आयु की संकल्पना (Concept of Half - life)
हम जानते हैं कि रेडियोएक्टिव तत्वों का सदैव विघटन होता रहता है और जैसे - जैसे समय बीतता जाता है, अविघटित नाभिकों की संख्या घटती जाती है। "वह समय जिसमें किसी रेडियोएक्टिव पदार्थ के अविघटित नाभिकों (undecayed nuclei) की संख्या घटकर आधी रह जाती है, उस तत्व की अर्द्ध - आयु कहलाती है।" इसे T से व्यक्त करते हैं। एक तत्व के लिए इसका मान नियत एवं विभिन्न तत्वों के लिए भिन्न - भिन्न होता है। अर्द्ध - आयु का मान लिये गये पदार्थ की मात्रा पर निर्भर नहीं करता है। इसे भौतिक एवं रासायनिक प्रभावों द्वारा बदला नहीं जा सकता है। कुछ तत्वों की अर्द्ध - आयु नीचे दी जा रही है-

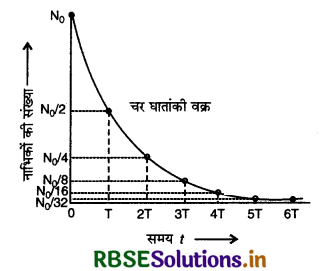
यदि किसी रेडियोएक्टिव तत्व की अर्द्ध - आयु T है तो T समय पश्चात् वह अपनी प्रारम्भिक मात्रा का 50%, 2T समय बाद 25%, 3T समय बाद 12.5, 4T समय बाद 6.25% शेष रह जायेगा। यदि पदार्थ के नाभिकों की संख्या को समय के साथ ग्राफ कर प्लॉट करें तो चित्र 13.15 की तरह चरघातांकी वक्र प्राप्त होगा।
माना प्रारम्भ में किसी पदार्थ के नाभिकों की संख्या N₀ है अर्थात् t = 0 पर N = N₀ तो एक अर्द्ध - आयु (अर्थात् t = T) के बाद शेष नाभिकों की संख्या
N₁ = \(\frac{\mathrm{N}_0}{2}\)
या N₁ = N₀ \(\left(\frac{1}{2}\right)^1\)
दो अर्द्ध - आयुओं के पश्चात् अर्थात् t = 2T के बाद शेष नाभिक

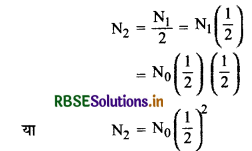
इसी प्रकार तीन अर्द्ध - आयुओं के बाद (t = 3T) शेष नाभिक
N₃ = \(\frac{\mathrm{N}_2}{2} = N0 \left(\frac{1}{2}\right)^2\left(\frac{1}{2}\right)\)
या N₃ = N₀\(\left(\frac{1}{2}\right)^3\)
इसी प्रकार n अर्द्ध - आयुओं के पश्चात् (t = nT) शेष नाभिक
N_n = N₀\(\left(\frac{1}{2}\right)^n\)
या व्यापक रूप से । अर्द्ध - आयुओं के पश्चात् शेष नाभिकों की
संख्या -
N = N₀\(\left(\frac{1}{2}\right)^n\) .......................(1)
∵ t = n.t
∴ n = \(\frac{t}{T}\) की सहायता से n का मान ज्ञात कर सकते हैं।
अर्द्ध - आयु तथा क्षय नियतांक में सम्बन्ध: यदि प्रारम्भ में (अर्थात् t = 0) नाभिकों की संख्या N₀ हो तो t समय के बाद शेष नाभिकों की संख्या
N = N₀e^-λt
जब t = T तो N = \(\frac{\mathrm{N}_0}{2}\)
∴ \(\frac{\mathrm{N}_0}{2}\) = N₀e^-λt
या \(\frac{1}{2}\) = e^-λT = \(\frac{1}{e^{\lambda T}}\)
या 2 = e^λT
दोनों ओर का लघुगणक लेने पर
log_e2 = log_ee^λT = λT log_ee = λT
या λT = log_e2
या T= \(\frac{\log _e 2}{\lambda}\) ...............(2)
इस समीकरण की सहायता से λ ज्ञात होने पर T का मान ज्ञात कर सकते है और T ज्ञात होने पर λ का मान ज्ञात कर सकते हैं।
∵     log_e2 = 0.6931
∴ T = \(\frac{0.6931}{\lambda}\) ..................(3)
या λ = \(\frac{0.6931}{T}\) ...................(4)

रेडियोएक्टिव पदार्थ की माध्य - आयु (Average Life of a Radioactive Substance)
जैसा कि हम पढ़ चुके हैं, रेडियोएक्टिव विघटन की प्रकृति सांख्यिकीय (statistical) होती है अर्थात् यह नहीं कहा जा सकता है कि कौन - सा नाभिक कब विघटित होगा और विघटित होकर किस प्रकार का कण उत्सर्जित करेगा। किसी भी नाभिक के विघटन का समय शून्य से अनन्त के मध्य कुछ भी हो सकता है। सभी नाभिकों की आय के औसत को ही माध्य - आयु (Average life) कहते हैं। इसे τ से प्रकट करते हैं। गणितीय रूप से यह सिद्ध किया जा सकता है कि किसी रेडियोएक्टिव पदार्थ की माध्य आयु क्षय नियतांक (λ) के व्युत्क्रम के बराबर होती है अर्थात्

या τ = \(\frac{1}{\lambda}\)
माध्य - आयु का व्यंजक (Expression for Mean or Average Life)
रदरफोर्ड एवं सोडी के नियम से
\(\frac{d \mathrm{~N}}{d t}\) = -λN
केवल परिमाण लेने पर-
या \(\left|\frac{d \mathrm{~N}}{d t}\right|\) = λN ....................(1)
अतः समय t व (t + dt) के मध्य विघटित नाभिकों की संख्या
dN = λNdt ...................(2)
या t = 0 पर अविघटित नाभिकों की संख्या N₀ हो तो

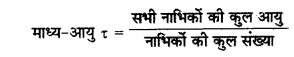
= \(\frac{\Sigma t d \mathrm{~N}}{\mathrm{~N}_0}\)
समीकरण (2) से
या τ = \(\frac{\Sigma t \lambda \mathrm{N} d t}{\mathrm{~N}_0}\)
∵ N = N₀e^-λt 
या τ = \(\frac{\Sigma t \lambda\left(\mathrm{N}_0 e^{-\lambda t}\right) d t}{\mathrm{~N}_0}\)
= Σtλe^-λt dt
चूँकि नाभिक लगातार अनन्त काल तक विघटित होते रहते हैं। अत: Σ को t = 0 से t = 0 के निश्चित समाकलन के रूप में लिख सकते है।

प्रश्न 2.
रदरफोर्ड - सोडी का रेडियोएक्टिव क्षय का नियम लिखिए तथा संबंधित समीकरण को व्युत्पन्न कीजिए। रेडियोएक्टिव तत्व का क्षय वन बनाइये। किसी रेडियोएक्टिव तत्व की अर्द्ध - आयु एवं माध्य - आयु का अनुपात लिखिए।
उत्तर:
रेडियोएक्टिव क्षय सम्बन्ध में रदरफोर्ड तथा सोडी के नियम (Rutherford and Soddy's Laws about Radioactivity)
सन् 1902 में रदरफोर्ड एवं सोडी ने अनेक रेडियोएक्टिव पदार्थों के स्वतः विघटन का प्रायोगिक अध्ययन किया और रेडियोएक्टिव क्षय के सम्बन्ध में निम्नांकित निष्कर्ष निकाले जो रदरफोर्ड एवं सोडी के नियमों के रूप में जाने गये। इनके अनुसार-

1. रेडियोएक्टिवता एक नाभिकीय घटना है तथा रेडियोएक्टिव किरणों के उत्सर्जन की दर को भौतिक या रासायनिक कारण द्वारा नियन्त्रित नहीं किया जा सकता है अर्थात् न तो इसे बढ़ाया जा सकता है और न ही घटाया जा सकता है।

2. रेडियोएक्टिव पदार्थों के विघटन की प्रकृति सांख्यिकीय (statistical) है अर्थात् यह कहना कठिन है कि कौन - सा नाभिक कब विघटित होगा और विघटित होकर कौन - सा कण उत्सर्जित करेगा? किसी नमूने से निश्चित समय में उत्सर्जित कणों की संख्या निश्चित होती है। विघटन की प्रक्रिया में α, ß, γ किरणों के उत्सर्जन के साथ एक तत्व दूसरे नये तत्व में बदलता रहता है जिसके रासायनिक एवं रेडियोएक्टिव गुण बिल्कुल नये होते हैं।

3. किसी भी क्षण रेडियोएक्टिव परमाणुओं के क्षय (decay) होने की दर उस क्षण उपस्थित परमाणुओं की संख्या के अनुक्रमानुपाती होती हैं। माना किसी समय t पर उपस्थित परमाणुओं की संख्या N है तथा, समय t + ∆t पर यह संख्या घट कर अपने मान की N - ∆N रह जाती है तो परमाणुओं के क्षय होने की दर -\(\frac{\Delta \mathrm{N}}{\Delta t}\) होगी। अतः रदरफोर्ड व सोडी के नियमानुसार
यदि ∆t समय में ∆N नाभिक विघटित हो जाते हैं तो विघटन की दर
-\(\frac{\Delta \mathrm{N}}{\Delta t}\) ∝ N (उस समय मौजूद नाभिकों की संख्या गणित की भाषा में विघटन की दर)
-\(\frac{d \mathrm{~N}}{d t}\) ∝ N
या \(\frac{d \mathrm{~N}}{d t}\) = -λN .................(1)

जहाँ λ एक नियतांक है, जिसे शव नियतांक (decay constant or disintegration constant) कहते हैं। समी. (1) में ऋणात्मक चिह्न यह दर्शाता है कि समय बढ़ने पर विघटन की दर घटती है। λ का मात्रक सेकण्ड^-1 है। λ का मान एक दिये गये पदार्थ के लिए तो नियत रहता है परन्तु भिन्न - भिन्न पदार्थों के लिए भिन्न - भिन्न होता है।
समी. (1) को निम्न प्रकार भी लिख सकते हैं-
\(\frac{d \mathrm{~N}}{d t}\) = -λdt ...............(2)
इसका समाकलन करने पर
log_eN = -λt + C ..................(3)
जहाँ C, समाकलन नियतांक है।
जब t = 0 तो N = N₀ 
∴ log_eN₀ = 0 + C या C = log_eN₀
∴ समी. (3) से
log_eN = -λt + log_eN₀ 
या log_eN - log_eN₀ = -λt
या log_e\(\frac{\mathrm{N}}{\mathrm{N}_0}\) = -λt
प्रति लघुगणक (Anti - log) लेने पर-
\(\frac{\mathrm{N}}{\mathrm{N}_0}\) = e^-λt
या N = N₀e^-λt .................(4)
समी. (4) से स्पष्ट है कि N का मान पहले तेजी से और बाद में धीरे - धीरे घटता है अर्थात् रेडियोएक्टिव पदार्थ का क्षय पहले तेजी से और फिर धीरे - धीरे होता है। इस नियम को चरघातांकी नियम (exponential law) कहते हैं। समी. (4) से यह भी स्पष्ट है कि रेडियोएक्टिव पदार्थ को पूर्णतः क्षयित (completely decay) होने में अनन्त समय लगेगा।
क्षय नियतांक (Decay Constant)
समी. (4) में t = \(\frac{1}{\lambda}\) रखने पर
N = N₀e^-1 या N = N₀\(\left(\frac{1}{e}\right)\) ...................(5)

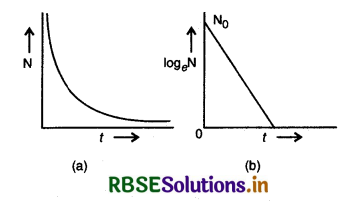
"अतः क्षय नियतांक उस समय का व्युत्क्रम है जिसमें अविघटित नाभिकों की संख्या अपने प्रारम्भिक मान की \(\left(\frac{1}{e}\right)\) गुनी रह जाती है।" इस प्रकार समीकरण (4) के अनुसार N का मान पहले तेजी से और बाद में धीरे - धीरे घटता है अर्थात् रेडियोएक्टिव पदार्थ का क्षय पहले तेजी से और फिर धीरे - धीरे होता है। इस नियम को क्षय चरघातांकी नियम कहते हैं। अविघटित नाभिकों की संख्या N तथा समय t के मध्य ग्राफ चित्र 13.14 (a) में प्रदर्शित है जबकि log_eN तथा समय t के मध्य परिवर्तन चित्र 13.14 (b) में दिखाया गया है।

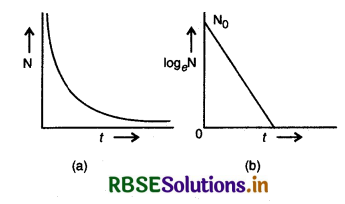
हम जानते है कि रेडियोएक्टिव तत्व की अर्द्ध - आयु
T = \(\frac{0.693}{\lambda}\)
तथा रेडियोएक्टिव तत्व की माध्य - आयु
τ = \(\frac{1}{\lambda}\)
∴ \(\frac{T}{\tau}=\frac{0.693}{\lambda} / \frac{1}{\lambda}\)
T : τ = 0.693 : 1

प्रश्न 3.
द्रव्यमान क्षति से क्या तात्पर्य है? द्रव्यमान क्षति एवं नाभिकीय बंधन ऊर्जा में संबंध स्थापित कीजिए तथा इससे प्रति न्यूक्लिऑन बंधन ऊर्जा का व्यंजक भी लिखिए।
उत्तर:
द्रव्यमान क्षति तथा नाभिकीय बन्धन ऊर्जा (Mass Defect and Nuclear Binding Energy)
हम पढ़ चुके हैं कि परमाणु का समस्त द्रव्यमान तथा धन आवेश नाभिक में केन्द्रित होता है और नाभिक प्रोटॉनों एवं न्यूट्रॉनों से मिलकर बना है। हम यह भी जानते हैं कि अमुक नाभिक में कितने प्रोटॉन एवं कितने न्यूट्रॉन होते हैं, अतः गणना द्वारा किसी नाभिक का सम्भावित दव्यमान (expected mass) ज्ञात किया जा सकता है। द्रव्यमान स्पेक्ट्राग्राफ (mass spectrograph) द्वारा किसी नाभिक का वास्तविक द्रव्यमान (actual mass) भी ज्ञात किया जा सकता है। यह पाया जाता है कि किसी नाभिक का वास्तविक द्रव्यमान उसके न्यूक्लिऑनों से गणना द्वारा प्राप्त सम्भावित द्रव्यमान से सदैव कम होता है, द्रव्यमान के इसी अन्तर को द्रव्यमान क्षति (mass defect) कहते हैं। इस प्रकार,
द्रव्यमान क्षति = गणना द्वारा प्राप्त नाभिक का द्रव्यमान - नाभिक का वास्तविक द्रव्यमान
या ∆m = m_c - m_a
यहाँ पर calculated mass को संक्षेप में m_c व actual mass को m_a से व्यक्त किया गया है।
∴ ∆m = [प्रोटॉनों का द्रव्यमान + न्यूट्रॉनों का द्रव्यमान] - नाभिक का वास्तविक दव्यमान
या ∆m = [Z.m_p + (A - Z)m_n] - m ................(1)
जहाँ Z, परमाणु क्रमांक, A द्रव्यमान क्रमांक, प्रोटॉन का द्रव्यमान, m_p, m_n न्यूट्रॉन का द्रव्यमान एवं m, नाभिक का वास्तविक द्रव्यमान है। आइन्स्टीन के अनुसार यह द्रव्यमान (∆m) कर्जा में बदल जाता है, इसी कर्जा को नाभिक की बन्धन ऊर्जा कहते हैं। यही ऊर्जा नाभिक के समस्त न्यूक्लिऑनों को नाभिक के रूप में बाँधे रहती है। ∆m का अर्थ है कि जब प्रोटॉन तथा न्यूट्रॉन मिलकर नाभिक का निर्माण करते है तो ∆m द्रव्यमान लुप्त हो जाता है तथा उसके तुल्य ऊर्जा (∆m)c² मुक्त (liberate) हो जाती है। इस ऊर्जा के कारण ही प्रोटॉन व न्यूट्रॉन नाभिक से बंधे रहते हैं। स्पष्ट है कि नाभिक के प्रोटॉनो तथा न्यूट्रॉनों को तोड़ने के लिए इतनी ही बाह्य ऊर्जा की आवश्यकता होगी। इस प्रकार यह स्पष्ट हो जाता है कि जब प्रोटॉन एवं न्यूट्रॉन मिलकर नाभिक बनाते हैं तो इस क्रिया में कुछ ऊर्जा निकलती है, जिसे 'नाभिक की बन्धन अर्जा' कहते हैं। इस तथ्य से यह भी स्पष्ट है कि यदि इतनी ही ऊर्जा (बन्धन ऊर्जा के बराबर) नाभिक को दे दी जाये तो उसके समस्त न्यूक्लिऑन बन्धन मुक्त (unbound) हो जायेंगे। अतः बन्धन ऊर्जा की परिभाषा इस प्रकार भी कर सकते हैं, "किसी नाभिक की बन्धन ऊर्जा, ऊर्जा की वह मात्रा है जो नाभिक को दे देने पर उसके समस्त न्यूक्लिऑनों को बन्धन मुक्त कर दे।" अतः नाभिक की बन्धन ऊर्जा

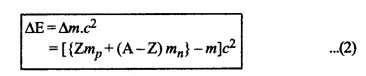
यदि नाभिक को बन्धन ऊर्जा में न्यूक्लिऑनों की संख्या का भाग दें तो हमें नाभिक की 'बन्धन ऊर्जा प्रतिन्यूक्लिऑन' (binding energy per nucleon) प्राप्त होगी। बन्धन ऊर्जा नाभिक के स्थायित्व (stability) को प्रदर्शित करती है।

संकुलन गुणांक (Packing Coefficient): इसे द्रव्यमान क्षति प्रति न्यूक्लिऑनों के रूप में परिभाषित किया जाता है।

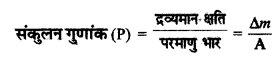
उदाहरण α - कण की बन्धन ऊर्जा-
α - कण हीलियम (₂He⁴) का नाभिक होता है। इसमें 2 प्रोटॉन एवं 2 न्यूट्रॉन होते हैं। इसका वास्तविक द्रव्यमान 4.00389 amu होता है।
∴ α - कण के लिए
m_a = 4.00389 amu
गणना द्वारा प्राप्त द्रव्यमान
m_c = [2m_p + 2m_n] = 2 [m_p + m_n]
= 2 [1.00813 + 1.00893] amu
= 2[2.01706] = 4.03412 amu
∴ द्रव्यमान क्षति
∆m = m_c - m_a = (4.03412 - 4.00389) amu
या ∆m = 0.03023 amu
∴ α - कण की बन्धन ऊर्जा
∆E = 0.03023 x 931 MeV
या ∆E = 28.14 MeV
स्पष्ट है कि α - कण के बनने में 28.14 MeV कर्जा मुक्त होती है, अत: α - कण के न्यूक्लिऑनों को बन्धन मुक्त करने के लिए 28.14 MeV ऊर्जा की आवश्यकता होगी। α - कण के नाभिक में चार न्यूक्लिऑन होते हैं अतः α - कण की
प्रति न्यूक्लियॉन बन्धन ऊर्जा = \(\frac{\Delta E}{A}=\frac{28 \cdot 14}{4}\)
= 7.03 MeV
इसी प्रकार हम ड्यूट्रॉन की बन्धन कर्जा ज्ञात कर सकते हैं। परिणाम इस प्रकार होंगे-
ड्यूट्रॉन की बन्धन ऊर्जा = 2.17 MeV
और प्रति न्यूक्लिऑन बन्धन ऊर्जा = 1.08 MeV
इस प्रकार स्पष्ट है कि α - कण को विखण्डित करने में ड्यूट्रॉन की तुलना में बहुत अधिक ऊर्जा की आवश्यकता होती है। अत: α - कण, ड्यूट्रॉन की तुलना में अधिक स्थायी है। ड्यूट्रॉन की बन्धन ऊर्जा तथा प्रतिन्यूक्लिऑन बन्धन ऊर्जा की पुष्टि आंकिक उदाहरणों तथा प्रश्नों में हो जाती है।

प्रश्न 4.
नाभिकीय विखण्डन से क्या तात्पर्य है? विखण्डन की क्रिया स्वयं श्रृंखला बद्ध क्यों नहीं होती है? समझाइये कि श्रृंखला अभिक्रिया प्राप्त करने के लिये क्या करना होगा?
उत्तर:
नाभिकीय विखण्डन (Nuclear Fission)
"किसी भारी नाभिक (heavy nucleus) के दो या दो से अधिक हल्के नाभिकों (light nuclei) में टूटने की प्रक्रिया को 'नाभिकीय विखण्डन' कहते हैं।" इस घटना की खोज सन् 1939 में जर्मन के दो वैज्ञानिकों ओटोझन (Otto Hann) एवं स्ट्रास्मान (Strassmann) ने की थी। उन्होंने यूरेनियम - 238 के नाभिक पर जब लगभग 106 eV ऊर्जा वाले न्यूट्रॉनों की बमबारी की तो पाया कि ₉₂U²³⁸ का नाभिक दो लगभग बराबर हल्के नाभिकर्को बेरियम (₅₆Ba¹⁴⁸) एवं क्रिप्टॉन (₃₆Kr⁸⁸) में टूट जाता है और एक विखण्डन में 3 न्यूट्रॉनों के साथ अपार ऊर्जा मुक्त होती है। प्रक्रिया निम्न समीकरण से व्यक्त होती है-

नाभिकीय विखण्डन की इस घटना में अत्यधिक परिमाण में ऊर्जा भी उत्पन्न होती है। इसका कारण यह है कि इस प्रक्रिया में प्राप्त नाभिकों के द्रव्यमानों का योग प्रयुक्त नाभिक के द्रव्यमान से कुछ कम होता है अर्थात् इस प्रक्रिया में कुछ द्रव्यमान लुप्त हो जाता है जो आइन्स्टीन के द्रव्यमान - ऊर्जा सम्बन्ध (∆E = ∆m.c²) के अनुसार ऊर्जा में बदल जाता है। इसी ऊर्जा को 'नाभिकीय ऊर्जा' (nuclear energy) कहते हैं। प्राकृतिक यूरेनियम (natural uranium) में दो आइसोटोप ₉₂U²³⁵ व ₉₂U²³⁸ पाये जाते हैं। इनका अनुपात 1 : 145 होता है। इस प्राकृतिक यूरेनियन में 99.3% यूरेनियम - 238 तथा केवल 0.7% यूरेनियम - 235 होता है। यूरेनियम के ये दोनों आइसोटोप विखण्डनीय (fissionable) हैं। प्रयोगों द्वारा यह पता चलता है कि यूरेनियम - 238 का विखण्डन केवल तीव्रगामी (fast moving) न्यूट्रॉनों (10⁶ eV ऊर्जा वाले) द्वारा ही सम्भव है जबकि यूरेनियम - 235 का विखण्डन मन्दगामी (Slow moving) न्यूट्रॉनों (1 eV से भी कम ऊर्जा वाले) से जैसे ऊष्मीय न्यूट्रानों (0.03 eV ऊर्जा) से भी सम्भव है। इस प्रकार स्पष्ट है कि यूरेनियम - 235 विखण्डन के लिए अधिक उपयोगी है। परमाणु बम में यूरेनियम - 235 प्रयोग में लाया जाता है।


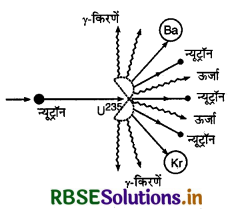
यूरेनियम - 235 का विखण्डन: जब मन्दगामी न्यूट्रॉन यूरेनियम - 235 के नाभिक से टकराता है तो वह उसमें अवशोषित (absorbed) हो जाता है तथा यूरेनियम का अन्य आइसोटोप यूरेनियम - 236 अस्थायी रूप से बनता है। चूँकि ₉₂U²³⁶ अस्थायी है अतः यह तुरन्त ही दो नाभिकों में टूट जाता है तथा तीन नये न्यूट्रॉन व अपार ऊर्जा उत्सर्जित करता है। प्रक्रिया निम्न समीकरण द्वारा व्यक्त की जाती है-
₉₂U²³⁵ +₀n¹ → ₉₂U²³⁶ → ₅₆Ba¹⁴⁴ +₃₆Kr⁸⁹ + 3.₀n¹ + ऊर्जा 

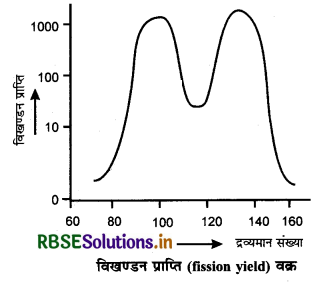
यह आवश्यक नहीं है कि यूरेनियम - 235 के विखण्डन में सदैव बेरियम एवं क्रिप्टन के ही नाभिक प्राप्त हों, बल्कि इसमें 20 से भी अधिक भिन्न - भिन्न तत्वों के 100 से भी अधिक आइसोटोप प्राप्त होते है जिनकी द्रव्यमान संख्या 75 से 160 तक होती है। उदाहरण के लिए - एक अन्य अभिक्रिया निम्न प्रकार है-
₉₂U²³⁵ + ₀n¹ → (₉₂U²³⁶) → ₅₄Xe¹⁴⁰ + ₃₈Sr⁹⁴ +2 ₀n¹ + ऊर्जा
यूरेनियम के प्रत्येक विखण्डन में लगभग 200 MeV ऊर्जा प्राप्त होती है। इस ऊर्जा का अधिकांश भाग विखण्डन से प्राप्त खण्डों की गतिज ऊर्जा के रूप में प्राप्त होता है। शेष भाग उत्सर्जित न्यूट्रॉनों की गतिज ऊर्जा, किरणों तथा ऊष्मा व प्रकाश विकिरणों (heat and light radiations) के रूपों में प्राप्त होता है।
1 ग्राम यूरेनियम के विखण्डन से मुमा ऊर्जा: यूरेनियम - 235 के एक ग्राम परमाणु (235 g) में परमाणुओं की संख्या एवोगैडो संख्या (6 x 10²³) के बराबर होती है। अतः 
1 ग्राम यूरेनियम में परमाणुओं की संख्या = \(\frac{6 \times 10^{23}}{235}\)
एक यूरेनियम परमाणु विखण्डन में लगभग 200 MeV ऊर्जा मुक्त होती है। अत: 1 g यूरेनियम के विखण्डन से
मुक्त ऊर्जा = \(\frac{6 \times 10^{23}}{235}\) x 200 MeV
= 5 x 10²³ MeV
इस प्रकार हम देखते हैं कि 1 ग्राम यूरेनियम के विखण्डन होने पर 5 x 10²³ MeV ऊर्जा उत्पन्न होती है जो 20 टन IN.T. (Trinitrotoluene) में विस्फोट करने से उत्पन्न होती है। इस कर्जा से 2 x 10⁴ किलोवॉट घण्टा (kWh) विद्युत ऊर्जा उत्पन्न हो सकती है।

प्रश्न 5.
नाभिकीय संलयन से क्या तात्पर्य है? यह क्रिया नाभिकीय विखण्डन से किस प्रकार भिन्न है? प्रकृति में नाभिकीय संलयन का उदाहरण दीजिए।
उत्तर:
नाभिकीय संकलन (Nuclear Fusion)
"वह प्रक्रिया, जिसमें दो हल्के नाभिक परस्पर संयुक्त होकर एक भारी नाभिक की रचना करते हैं, नाभिकीय संलयन कहलाती है।" इस प्रक्रिया में प्राप्त भारी नाभिक का द्रव्यमान, संयोग करने वाले दोनों नाभिकों के द्रव्यमान के योग से कम होता है। द्रव्यमान की यह क्षति आइन्सटीन के द्रव्यमान ऊर्जा संम्बन्ध (∆E = ∆mc²) के अनुसार ऊर्जा में रूपान्तरित हो जाती है।
उदाहरण के लिए, भारी हाइड्रोजन अर्थात् ड्यूटीरियम के दो नाभिक संयोग करते हैं, तो ट्राइटियम प्राप्त होता है।

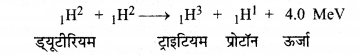
नाभिकीय अभिक्रिया एक कठिन प्रक्रिया है तथा यह साधारण ताप व दाब पर संभव नहीं होती है। इसका कारण यह है कि संलयित होने वाले नाभिक धनावेशित होते हैं। अतः जब वे एक - दूसरे के निकट आते हैं तो उनके मध्य वैद्युत प्रतिकर्षण बल कार्य करने लगता है। इस प्रतिकर्षण बल के विरुद्ध संलवित होने के लिए नाभिकों की गतिज ऊर्जा बहुत अधिक (10⁵ eV) होनी चाहिए। इसके लिए अति उच्च ताप (10⁸K) तथा अति उच्च दाब की आवश्यकता होती है। इतना अधिक ताप सूर्य पर ही सम्भव होता है। पृथ्वी पर इतना अधिक ताप नाभिकीय विखण्डन के द्वारा ही उत्पन्न किया जा सकता है। अत: पृथ्वी पर नाभिकीय संलयन नाभिकीय विखण्डन के बाद ही संभव है। इसी आधार पर 'संलयन बम' अथवा 'हाइड्रोजन बम' बनाया गया है। चूंकि संलयन अति उच्च ताप पर होता है अतः इसे 'ताप नाभिकीय अभिक्रिया' (Thermo nuclear) भी कहते हैं।

प्रश्न 6.
नाभिकीय भट्ठी का सरल रेखाचित्र बनाते हुए इसकी प्रक्रिया स्पष्ट कीजिए।
उत्तर:
सौर ऊर्जा का स्रोत (Source of Solar Energy)
सूर्य की अपार ऊर्जा के सम्बन्ध में समय - समय पर विभिन्न मत व्यक्त किये गये हैं। आधुनिक मतानुसार, सूर्य की अपार ऊर्जा (huge energy) का स्रोत हल्के नाभिकों का संलयन है। सूर्य का लगभग 90% भाग हाइड्रोजन तथा होलियम से बना है तथा शेष 10% भाग में अन्य तत्व हैं जिनमें से अधिकांश हल्के तत्व हैं। सूर्य के भीतरी भाग का ताप लगभग 2 x 10⁷ K है। इतने ऊँचे ताप पर सूर्य में उपस्थित सभी तत्वों के परमाणुओं से इलेक्ट्रॉन अलग हो जाते हैं जिससे हाइड्रोजन, हीलियम आदि तत्वों के परमाणु प्लाज्मा (Plasma) अवस्था में आ जाते हैं (पदार्थ की वह अवस्था जिसमें पदार्थ के धनात्मक आयन अर्थात् नाभिक तथा इलेक्ट्रॉन अत्यधिक संख्या में उपस्थित हों, पदार्थ की प्लाज्मा अवस्था कहलाती है।) अर्थात् ये तत्व नाभिकीय अवस्था में होते हैं। अत्यधिक ताप के कारण जब चार प्रोटॉन (हाइड्रोजन नाभिक) संलयित होकर एक α - कण (हीलियम नाभिक) का निर्माण करते हैं तो इस अभिक्रिया में अत्यधिक ऊर्जा उत्पन्न होती है। इस प्रकार संलयन से उत्पन्न ऊर्जा ही सुर्य की अपार ऊजा का स्रोत है।
हाइड्रोजन नाभिकों का हीलियम नाभिक में संलयन निम्न दो प्रकार से हो सकता है-
(i) कार्बन - नाइट्रोजन चक्र (C - N Cyele): अमेरिकी वैज्ञानिक बेथे (Bethe) के मतानुसार, सूर्य एवं तारों के अन्दर चार हाइड्रोजन नाभिकों का एक हीलियम नाभिक में संलयन सीधे न होकर कई ताप नाभिकीय अभिक्रियाओं के एक चक्र के द्वारा होता है। ये ताप नाभिकीय अभिक्रियाएँ बड़ी तेजी के साथ होती रहती हैं। इन अभिक्रियाओं में कार्बन एक उत्प्रेरक (Catalyst) की भाँति प्रयुक्त होता है।
अभिक्रियाएँ निम्न प्रकार हैं-
₁H¹ + ₆C¹² → ₇N¹³ + γ (ऊर्जा)
₇N¹³ → ₆C¹³ + ₊₁ß⁰ + v (न्यूट्रिनो)
₁H¹ + ₆C¹³ → ₇N¹⁴ + γ (ऊर्जा)
₁H¹ + ₇N¹⁴ → ₈O¹⁵ + γ (ऊर्जा)
₈O¹⁵ → ₇N¹⁵ + ₊₁ß⁰ + v
₁H¹ + ₇N¹⁵ → ₆C¹² + ₂He⁴
उक्त सभी समीकरणों को जोड़ने पर
₁H¹ + ₁H¹ + ₁H¹ + ₁H¹ → ₂He⁴ + 2 +₁ß⁰ + 2v + γ (ऊर्जा)
एक प्रकार एक C - N चक्र में चार हाइड्रोजन के नाभिक संलवित होकर एक हीलियम नाभिक की रचना करते हैं तथा 2 पॉजिट्रॉन (₊₁ß⁰) व 24.7 MeV ऊर्जा मुक्त होती है। ये पॉजिट्रॉन दो इलेक्ट्रॉनों से मिलकर विनाशित (Annihilate) हो जाते हैं तथा 2 MeV ऊर्जा मुक्त करते हैं। इस प्रकार एक C - N चक्र में 26.7 MeV ऊर्जा मुक्त होती है। वह ऊर्जा सूर्य का ताप स्थिर बनाये रखने में सहायक होती है। चूँकि सूर्य के द्रव्य के 1 ग्राम में लगभग 2 x 10²³ प्रोटॉन होते हैं, अतः सूर्य के 1 ग्राम द्रव्य से अपार ऊर्जा (≈ 313.35 x 10²³ MeV) उत्पन्न होती है। इसके अतिरिक्त नाभिकीय संलयन में प्राप्त ß - किरणें सूर्य से छनती (Filter) हुई पराबैंगनी, दृश्य प्रकाश तथा अवरक्त किरणों के रूप में लगातार सूर्य से विकिरित होती रहती है।

(ii) प्रोटॉन - प्रोटॉन चक्र (p - pCycle): वर्तमान अनुसन्धानों के अनुसार बेथे का सिद्धान्त केवल उच्च ताप वाले तारों के लिए अधिक सत्य होता है। सूर्य के लिए, जो उन तारों की अपेक्षा कम ताप पर होते हैं, कार्बन - नाइट्रोजन चक्र की अपेक्षा एक अन्य चक्र की अधिक सम्भावना होती है जिसे 'प्रोटॉन - प्रोटॉन चक्र' कहते हैं। इस चक्र में भी कई ताप नाभिकीय अभिक्रियाओं के द्वारा चार हाइड्रोजन नाभिक संलवित होकर हीलियम के नाभिक की रचना करते हैं। अभिक्रियाएँ निम्न प्रकार है-
¹₁H + ¹₁H → ¹₂H + ₊₁⁰ß + v + 0.42 MeV ................(i)
₊₁ß⁰ + _-1ß⁰ → γ + γ + 1.02 MeV .................(ii)
¹₂H + ₁¹H → ₃²He + γ + 5.49 MeV .....................(iii)
³₂H + ³₂H → ⁴₂He + ₁¹H + ₁¹H + 12.86 MeV ..................(iv)
इन अभिक्रियाओं में चौथी अभिक्रिया होने के लिए यह आवश्यक है कि पहली तीन अभिक्रियाएँ दो - दो बार हों और दो हल्के (light) हीलियम नाभिक मिलकर सामान्य हीलियम का एक नाभिक बनाएँ। अत: समीकरण (i), (ii) व (iii) में 2 की गुणा करके चौथी समीकरण में जोड़ने पर अर्थात् 2(i) + 2(ii) + 2(iii) + (iv) से
4 ₁¹H + 2 _-1⁰ß → ₂⁴He + 2v + 6γ + 26.7 + MeV
या 
(4 ₁¹H + 4 _-1⁰ß) → (₂⁴He + 2 _-1⁰ß) + 6γ + 26.7 + MeV
अत: यह निष्कर्ष निकलता है कि चार हाइड्रोजन परमाणु मिलकर एक ₂⁴He परमाणु बनाते हैं और इस प्रक्रिया में 26.7 MeV ऊर्जा मुक्त होती है।
इस प्रकार स्पष्ट है कि इस चक्र का भी नेट परिणाम वही है जो C - N चक्र का है। इस चक्र में उत्पन्न ऊर्जा सूर्य के ताप को स्थिर बनाये रखने में सहायक होती है तथा γ - किरणों का विकिरण, दृश्य प्रकाश, पराबैगनी किरणों तथा अवरक्त किरणों के रूप में होता है।

सूर्य लगभग प्रति सेकण्ड 3.8 x 10²⁶ जूल ऊर्जा विकिरत करता है। समीकरण ∆E = ∆m.c² के अनुसार प्रति सेकण्ड इतनी ऊर्जा देने के लिए सूर्य का द्रव्यमान प्रति सेकण्ड लगभग 4.1 x 10⁹ kg कम हो जाता है। इस प्रकार सूर्य तीव्र गति से नष्ट हो रहा है। सूर्य का कुल द्रव्यमान 2 x 10³⁰ kg है, अतः नष्ट होने वाला द्रव्यमान इसकी तुलना में बहुत कम है। उपरोक्त आँकड़ों से सूर्य के जीवन की गणना की जा सकती है। ऐसा अनुमान है कि सूर्य अभी अगले एक हजार करोड़ वर्षों तक (10¹¹ वर्षों तक) इसी दर से ऊर्जा उत्सर्जित करता रहेगा।

प्रश्न 7.
रेडियोएक्टिव विकिरण संबंधी रदरफोर्ड तथा सोडा का नियम क्या है? इसकी सहायता से सिद्ध कीजिए कि किसी क्षण पदार्थ में अवशेष नाभिकों की संख्या N = N₀e^-λt होती है।
उत्तर:
रेडियोएक्टिव क्षय सम्बन्ध में रदरफोर्ड तथा सोडी के नियम (Rutherford and Soddy's Laws about Radioactivity)
सन् 1902 में रदरफोर्ड एवं सोडी ने अनेक रेडियोएक्टिव पदार्थों के स्वतः विघटन का प्रायोगिक अध्ययन किया और रेडियोएक्टिव क्षय के सम्बन्ध में निम्नांकित निष्कर्ष निकाले जो रदरफोर्ड एवं सोडी के नियमों के रूप में जाने गये। इनके अनुसार-

1. रेडियोएक्टिवता एक नाभिकीय घटना है तथा रेडियोएक्टिव किरणों के उत्सर्जन की दर को भौतिक या रासायनिक कारण द्वारा नियन्त्रित नहीं किया जा सकता है अर्थात् न तो इसे बढ़ाया जा सकता है और न ही घटाया जा सकता है।

2. रेडियोएक्टिव पदार्थों के विघटन की प्रकृति सांख्यिकीय (statistical) है अर्थात् यह कहना कठिन है कि कौन - सा नाभिक कब विघटित होगा और विघटित होकर कौन - सा कण उत्सर्जित करेगा? किसी नमूने से निश्चित समय में उत्सर्जित कणों की संख्या निश्चित होती है। विघटन की प्रक्रिया में α, ß, γ किरणों के उत्सर्जन के साथ एक तत्व दूसरे नये तत्व में बदलता रहता है जिसके रासायनिक एवं रेडियोएक्टिव गुण बिल्कुल नये होते हैं।
(3) किसी भी क्षण रेडियोएक्टिव परमाणुओं के क्षय (decay) होने की दर उस क्षण उपस्थित परमाणुओं की संख्या के अनुक्रमानुपाती होती हैं। माना किसी समय t पर उपस्थित परमाणुओं की संख्या N है तथा, समय t + ∆t पर यह संख्या घट कर अपने मान की N - ∆N रह जाती है तो परमाणुओं के क्षय होने की दर -\(\frac{\Delta \mathrm{N}}{\Delta t}\) होगी। अतः रदरफोर्ड व सोडी के नियमानुसार
यदि ∆t समय में ∆N नाभिक विघटित हो जाते हैं तो विघटन की दर
-\(\frac{\Delta \mathrm{N}}{\Delta t}\) ∝ N (उस समय मौजूद नाभिकों की संख्या गणित की भाषा में विघटन की दर)
-\(\frac{d \mathrm{~N}}{d t}\) ∝ N
या \(\frac{d \mathrm{~N}}{d t}\) = -λN .................(1)

जहाँ λ एक नियतांक है, जिसे शव नियतांक (decay constant or disintegration constant) कहते हैं। समी. (1) में ऋणात्मक चिह्न यह दर्शाता है कि समय बढ़ने पर विघटन की दर घटती है। λ का मात्रक सेकण्ड^-1 है। λ का मान एक दिये गये पदार्थ के लिए तो नियत रहता है परन्तु भिन्न - भिन्न पदार्थों के लिए भिन्न - भिन्न होता है।
समी. (1) को निम्न प्रकार भी लिख सकते हैं-
\(\frac{d \mathrm{~N}}{d t}\) = -λdt ...............(2)
इसका समाकलन करने पर
log_eN = -λt + C ..................(3)
जहाँ C, समाकलन नियतांक है।
जब t = 0 तो N = N₀ 
∴ log_eN₀ = 0 + C या C = log_eN₀
∴ समी. (3) से
log_eN = -λt + log_eN₀ 
या log_eN - log_eN₀ = -λt
या log_e\(\frac{\mathrm{N}}{\mathrm{N}_0}\) = -λt
प्रति लघुगणक (Anti - log) लेने पर-
\(\frac{\mathrm{N}}{\mathrm{N}_0}\) = e^-λt
या N = N₀e^-λt .................(4)

समी. (4) से स्पष्ट है कि N का मान पहले तेजी से और बाद में धीरे - धीरे घटता है अर्थात् रेडियोएक्टिव पदार्थ का क्षय पहले तेजी से और फिर धीरे - धीरे होता है। इस नियम को चरघातांकी नियम (exponential law) कहते हैं। समी. (4) से यह भी स्पष्ट है कि रेडियोएक्टिव पदार्थ को पूर्णतः क्षयित (completely decay) होने में अनन्त समय लगेगा।
क्षय नियतांक (Decay Constant)
समी. (4) में t = \(\frac{1}{\lambda}\) रखने पर
N = N₀e^-1 या N = N₀\(\left(\frac{1}{e}\right)\) ...................(5)

"अतः क्षय नियतांक उस समय का व्युत्क्रम है जिसमें अविघटित नाभिकों की संख्या अपने प्रारम्भिक मान की \(\left(\frac{1}{e}\right)\) गुनी रह जाती है।" इस प्रकार समीकरण (4) के अनुसार N का मान पहले तेजी से और बाद में धीरे - धीरे घटता है अर्थात् रेडियोएक्टिव पदार्थ का क्षय पहले तेजी से और फिर धीरे - धीरे होता है। इस नियम को क्षय चरघातांकी नियम कहते हैं। अविघटित नाभिकों की संख्या N तथा समय t के मध्य ग्राफ चित्र 13.14 (a) में प्रदर्शित है जबकि log_eN तथा समय t के मध्य परिवर्तन चित्र 13.14 (b) में दिखाया गया है।

हम जानते है कि रेडियोएक्टिव तत्व की अर्द्ध - आयु
T = \(\frac{0.693}{\lambda}\)
तथा रेडियोएक्टिव तत्व की माध्य - आयु
τ = \(\frac{1}{\lambda}\)
∴ \(\frac{T}{\tau}=\frac{0.693}{\lambda} / \frac{1}{\lambda}\)
T : τ = 0.693 : 1

आंकिक प्रश्न

प्रश्न 1.
²⁷₁₃Al की नाभिकीय त्रिज्या 3.6 फर्मी है। ⁶⁴₂₉Cu की नाभिकीय त्रिज्या ज्ञात कीजिए।
हल:
R ∝ Al^1/3 से
\(\frac{R_1}{R_2}=\left(\frac{A_1}{A_2}\right)^{1 / 3}\)
दिया है-
R₁ = 3.6 फर्मी, A₁ = 27, A₂ = 64

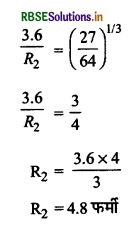
प्रश्न 2.
¹⁶₈O के नाभिक की त्रिज्या 3 x 10^-15 m है। ²⁰⁵₈₂Pb के नाभिक की त्रिज्या ज्ञात कीजिए।
हल:
¹⁶₈O के लिए त्रिज्या R₁ = 3 x 10^-15 m, A₁ = 16
²⁰⁵₈₂Pb के लिए त्रिज्या R₂ = ? A₂ = 205
∵ R ∝ Al^1/3
∴ \(\frac{R_2}{R_1}=\left(\frac{A_2}{A_1}\right)^{1 / 3}=\left(\frac{205}{16}\right)^{1 / 3}\)
\(\frac{R_2}{R_1}\) = 2.33
R₂ = R₁ x 2.33
R₂ = 3 x 10^-15 x 2.33
R₂ = 7.01 x 10^-15 m

प्रश्न 3.
द्रव्यमान संख्या A = 240 तथा बन्धन ऊर्जा प्रति न्यूक्लिऑन BE/A = 7.6 MeV का कोई नाभिक दो टुकड़ों में विखण्डित होता है जिनमें प्रत्येक के लिए A = 120 और BE/A = 8.5 MeV है। मुक्त ऊर्जा परिकलित कीजिए।
हल:
विखण्डन से पूर्व बंधन ऊर्जा B₁ = 240 x 7.6 = 1824 MeV
विखण्डन के पश्चात बंधन ऊर्जा B₂ = 2 x 120 x 8.5 = 2040 MeV
मुक्त ऊर्जा ∆E = (-1824) - (-2040)
∆E = 216 MeV

प्रश्न 4.
¹²₆C कार्बन नाभिक को बन्धन ऊर्जा MeV में ज्ञात कीजिए।
हल:
¹²₆C में 6 प्रोटॉन तथा 6 न्यूट्रॉन हैं अत: कार्बन के नाभिक का मापित द्रव्यमान
m_c = Z m_p + (A - Z) m_n
= 6 x 1.007825 + (12 - 6) x 1.008665
= 6 (1/007825 + 1.008665)
= 6 x 2.016590
m_c = 12.09894 amu
¹²₆C नाभिक का द्रव्यमान (m_a) = 12 amu
अतः द्रव्यमान क्षति ∆m = m_c - m_a
= 12.09894 - 12
= 0.09894 amu
¹²₆C नाभिक की बंधन ऊर्जा = 0.09894 x 931 MeV
= 92.11 MeV

प्रश्न 5.
₂₆Fe⁵⁶ की बन्धन ऊर्जा प्रति न्यूक्लिऑन ज्ञात कीजिए। दिया है: m_p = 1.007825 amu, m_n = 1.008665 amu एवं m(₂₆Fe⁵⁴) = 55.934939 amu
हल:
दिया है: ₂₆Fe⁵⁶ के लिए - प्रोटॉनों की संख्या Z = 26
न्यूट्रॉनों की संख्या (A - Z) = 56 - 26 = 30
m_p = 1.007825 amu
m_p = 1.008665 amu
m = 55.934939 amu
∆m = [Z m_p + (A - Z)m_n] - m
= [26 x 1.007825 + 30 x 1.008665] -55.934939
∆m = 0.528461 amu
∴ बंधन ऊर्जा
∆E = 0.528461 x 931 MeV
= 491.997191 MeV
∴ बंधन ऊर्जा प्रति न्यूक्लियॉन
E_b = \(\frac{\Delta E}{A}=\frac{491: 9971}{56}\)
E_b = 8.786 MeV प्रति म्यूक्लियॉन 

प्रश्न 6.
किसी रेडियोएक्टिव तत्व का क्षयांक 10^-3 प्रतिवर्ष है। इसकी अर्द्ध - आयु का मान वर्ष में ज्ञात कीजिए।
हल:
दिया है क्षयांक λ = 10^-3 प्रतिवर्ष
∴ अर्द्ध - आयु T_1/2 = \(\frac{0.693}{\lambda}=\frac{0.693}{10^{-3}}\)
T_1/2 = 693 वर्ष 

प्रश्न 7.
किसी रेडियोएक्टिव तत्व की सक्रियता 10^-3 विघटन/वर्ष है। इसकी अर्द्ध - आयु व औसत - आयु का अनुपात ज्ञात कीजिए।
हल:
सक्रियता A = λN
A = \(\frac{0.693}{T_{1 / 2}}\) N ..............(1)
A = \(\frac{1}{\tau}\) N ...................(2)
समी. (1) में समी. (2) का भाग देने पर

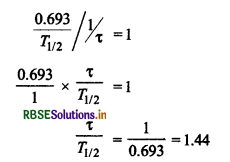
प्रश्न 8.
एक रेडियोएक्टिव प्रतिदर्श की सक्रियता 3200 वर्ष में अपने प्रारम्भिक मान की 1/4 हो जाती है। प्रतिदर्श की माध्यम - आयु की गणना कीजिए।
हल:
A = \(\frac{A_0}{4}=\frac{A_0}{2^2}\)
समी. (1) की A = \(\frac{A_0}{2^n}\) से तुलना करने पर
n = 2
समय t = nT_1/2
∴ t = 2 x T_1/2
दिया है
T_1/2 = 1600 वर्ष
T_1/2 = \(\frac{0.693}{\lambda}\)
अतः माध्य - आयु
τ = 1.44 x T_1/2
= 1.44 x 1600
= 2284 वर्ष 

प्रश्न 9.
थोरियम - 227 की औसत - आयु 2.74 वर्ष एवं सक्रियता 37 रदरफोर्ड है। थोरियम की मात्रा ज्ञात कीजिए।
हल:
प्रश्नानुसार, R = 37 रदरफोर्ड
= 37 x 10⁶ विघटन/सेकण्ड
औसत - आयु τ = 2.74 वर्ष
∴ अर्द्ध - आयु T_1/2 = 0.693 τ = 0.693 x 2.74
T_1/2 = 1.8988 वर्ष
= 1.8988 x 365 x 24 x 3600 सेकेंड
सक्रियता A = λN
यदि Th²⁹⁷ की आपेक्षिक मात्रा से ग्राम है। तब इसमें सक्रिय परमाणुओं की संख्या N = \(\frac{6.02 \times 10^{23}}{227}\) x m
∴ A = λN
37 x 10⁶ = \(\frac{0.693}{T_{1 / 2}}\) N
37 x 10⁶ = \(\frac{0.693}{1.8988 \times 365 \times 24 \times 3600} \times \frac{6.02 \times 10^{23}}{227}\) x m
m = \(\frac{37 \times 10^6 \times 1.8988 \times 365 \times 24 \times 3600 \times 227}{0.693 \times 6.02 \times 10^{23}}\)
m = 1.206 x 10^-6 gm
m = 1.206 µg

प्रश्न 10.
एक रेडियोएक्टिव प्रतिदर्श में सक्रिय नाभिकों की संख्या 6 घण्टे में अपने प्रारम्भिक मान की 6.25% रह जाती है। रेडियोएक्टिव प्रतिदर्श की अर्द्ध - आयु ज्ञात कीजिए।
हल:
दिया है- t = 6 घंटे
\(\frac{N}{N_0}=\frac{6.25}{100}=\frac{1}{16}\)
N = N₀\(\left(\frac{1}{2}\right)^n\) से
\(\frac{N}{N_0}=\frac{1}{16}=\left(\frac{1}{2}\right)^4\)
n = 4
अतः अर्द्ध - आयु T_1/2 = \(\frac{t}{n}=\frac{6}{4}\)
T_1/2 = 1.5 घण्टे

प्रश्न 11.
₈₈Ra²²⁶ के नाभिक से एक α कण उत्सर्जित होता है। यदि α कण की ऊर्जा 4.662 MeV है तो इस क्षव में कुल मुक्त ऊर्जा कितनी है?
हल:
²²⁶₈₈Ra के लिए, Z = 88, A = 226
E_α = 4.662 MeV

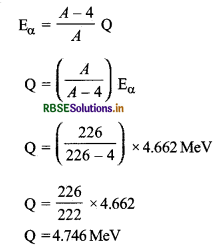
प्रश्न 12.
नाभिक X¹⁷⁶ ß क्षय कर नाभिक Y¹⁷⁶ में क्षयित है यदि X तथा Y के परमाण्वीय दव्यमान क्रमश: 175.942694 u है तथा 175.941426 u है तो असर्जित ß कण की अधिकतम ऊर्जा जात करो।
हलः
X¹⁷⁶ → Y¹⁷⁹ + _-ß⁰
द्रव्यमान क्षति ∆m = [175.94294 - 175.941426] u
∆m = 0.001268 u
ß कण को अधिकतम गतिज ऊर्जा
E_K = ∆mc²
1 u = 931 \(\frac{\mathrm{MeV}}{\mathrm{C}^2}\)
E_K = 0.001268 x 931 \(\frac{\mathrm{MeV}}{\mathrm{C}^2}\) C²
E_K = 1.18 MeV

प्रश्न 13.
नाभिकीय संलयन ²₁H + ³₁H → ⁴₂He + ¹₀n में मुक्त ऊर्जा की मात्रा MeV में गणना करो। दिया है: m (²₁He) = 2.014102 u, m(³₁H) = 3.016049 u, m(⁴₂He)  = 4.002603 u, m_n = 1.00867 u, 1 u = 931 MeV
हल:
दिया है : संलयन क्रिया
²₁H + ³₁H → ⁴₂He + ¹₀n
अभिक्रिया से पूर्व नाभिकों का कुल द्रव्यमान
m_i = 2.014102 + 3.016049
m_i  = 5.030151 u 
अभिक्रिया के पश्चात उत्पाद नाभिकों का कुल द्रव्यमान
m_f = 4.002603 + 1.00867
= 5.011273 u
द्रव्यमान क्षति ∆m = 5.030151 - 5.011273
= 0.018878 u 
मुक्त कर्जा E =  ∆m x 931.5 MeV
E = 0.018878 x 913.5
E = 17584857 MeV

प्रश्न 14.
अभिक्रिया ²³⁵₉₂U + ¹₀n → ¹⁴⁰₅₄Xe + ⁹⁴₃₈Sr + 2 ¹₀n + Q के लिए Q का मान ज्ञात कीजिए। दिया है-
²³⁵₉₂U का द्रव्यमान = 235.04352 u
¹⁴⁰₅₄Xe का द्रव्यमान = 139.9054 u 
⁹⁴₃₈Sr का द्रव्यमान = 93.9063 u
¹₀n का द्रव्यमान = 1.00867 u
हल:
द्रव्यमान क्षति
∆m = [M(²³⁵₉₂U) + M(¹₀n) - M(¹⁴⁰₅₄Xe) - M(⁹⁴₃₈Sr) - M(2 ¹₀n)]
∆m = [(235.0435 + 1.00867) - (139.9054 + 93.9063 + 2 x 1.00867)]
∆m = [236.05217 - 235.82904] u
∆m = 0.22313 u
Q = ∆mc²
Q = 02313 x 931 \(\frac{\mathrm{MeV}}{\mathrm{C}^2}\) C² (∵ 1u = 931 \(\frac{\mathrm{MeV}}{C^2}\))
Q = 207.73 MeV

प्रतियोनी परीक्षा संबंधी प्रश्न

प्रश्न 1.
जब एक यूरेनियम समस्थानिक ²³⁵₉₂U पर एक न्यूट्रॉन की बमबारी की जाती है तो ⁸⁹₃₆Kr, तीन न्यूट्रॉन और ...... उत्पन्न होते हैं-
(A) ¹⁰₃₆Kr
(B) ¹⁰³₃₆Kr
(C) ¹⁴⁴₃₆Ba
(D) ⁹¹₄₀Kr
उत्तर:
(C) ¹⁴⁴₃₆Ba

प्रश्न 2.
दो रेडियोएक्टिव तत्व A और B की प्रारंभिक सक्रियताएँ 10 क्यूरी और 20 क्यूरी हैं। यदि A पर मोलों की संख्या B से दोगुनी है। क्षय नियतांक λ_A और λ_B के मान होंगे-
(A) (10,5)
(B) (5,20)
(C) (20,10)
(D) (50,100)
उत्तर:
(B) (5,20)

प्रश्न 3.
एक रेडियोएक्टिव पदार्थ के लिए, अर्द्ध - आयु 10 मिनट है। यदि प्रारंभ में 600 नाभिक हैं, 450 नाभिकों के विघटन में लगा समय (मिनट में) होगा-
(A) 30
(B) 10
(C) 20
(D) 15
उत्तर:
(C) 20

प्रश्न 4. 
दो रेडियोधर्मी तत्व A तथा B की अद्ध - आयु क्रमशः 10 min तथा 40 min है। प्रारम्भ में दोनों के नमूनों में नाभिकों की संख्या बराबर है। 80 min के उपरान्त A तथा B के क्षय हुए नाभिकों की संख्या का अनुपात होगा-
(A) 1 : 16
(B) 4 : 1
(C) 1 : 4
(D) 5 : 4
उत्तर:
(C) 1 : 4

प्रश्न 5.
एक गाँव को विद्युत ऊर्जा प्रदान करने वाले नाभिकीय संयन्त्र में एका वर्ष अर्द्ध - आयु के रेडियोधर्मी पदार्थ को ईंधन के रूप में प्रयोग किया जा रहा है। प्रारम्भ में ईधन की मात्रा इतनी है कि गाँव की सम्पूर्ण विद्युत शक्ति की आवश्यकताएँ उस समय उपलव्य विद्युत शक्ति की 12.5% है। यदि वह संयंत्र गाँव की सम्पूर्ण ऊर्जा आवश्यकताओं को अधिकतम nT वर्षों के लिये पूरा कर सकता है तब का मान है-
(A) 3
(B) 4
(C) 5
(D) 6
उत्तर:
(A) 3

प्रश्न 6.
₃Li⁷ + ₁H¹ → ₂He⁴+ Q
₃Li⁷ तथा ₂He⁴ की प्रतिन्यूक्लिऑन बन्धन ऊर्जाएँ क्रमश: 5.60 MeV तथा 7.06 MeV है तो उपरोक्त नाभिकीय अभिक्रिया में मुक्त ऊर्जा ए का क्या मान होगा?
(A) 19.6 MeV
(B) 2.4 MeV
(C) -2.4 MeV
(D) 17.3 MeV
उत्तर:
(D) 17.3 MeV

प्रश्न 7.
एक तुरन्त तैयार किया हुआ रेडियो आइसोटोप प्रतिदर्श जिसकी अर्द्ध - आयु 1386 सेकण्ड है की सक्रियता 10³ विघटन प्रति से, है। यदि log_e = 0.693 है, तब प्रथम 80 सेकण्ड में विघटित नाभिकों व प्रारम्भिक की संख्याओं का अनुपात (प्रतिशत निकट पूर्णांक में) कितना है?
(A) 4
(B) 8 
(C) 12
(D) 16
उत्तर:
(A) 4 

प्रश्न 8.
यह मान लें कि एक न्यूट्रॉन, एक प्रोटॉन और एक इलेक्ट्रॉन में टूटता है। इस प्रक्रिया में निर्गत ऊर्जा है (न्यूट्रॉन का द्रव्यमान = 1.6750 x 10^-27 किग्रा, प्रोटॉन का द्रव्यमान = 1.6725 x 10^-27 किग्रा, इलेक्ट्रॉन का द्रव्यमान = 9 x 10^-31 किग्रा)
(A) 0.73 MeV
(B) 7.10 MeV
(C) 6.30 MeV
(D) 5.4 MeV
उत्तर:
(A) 0.73 MeV

प्रश्न 9.
यदि ²⁷Al की नाभिकीय त्रिज्या 3.6 फी है तो ⁶⁴Cu की नाभिकीय त्रिज्या फर्मी में लगभग होगी-
(A) 2.4
(B) 12
(C) 4.8
(D) 3.6
उत्तर:
(C) 4.8

प्रश्न 10.
एक मिश्रण में दो रेडियोएक्टिव पदार्थ A₁ और A₂ की अर्द्ध आयु क्रमशः 20 सेकण्ड तथा 10 सेकण्ड है। प्रारम्भ में मिश्रण में A₁ और A₂ की मात्राएँ क्रमशः 40 ग्राम तथा 160 ग्राम हैं, तब कितने समय पश्चात् मिश्रण में दोनों की मात्रा समान हो जाएगी?
(A) 60 सेकण्ड
(B) 80 सेकण्ड
(C) 20 सेकण्ड
(D) 40 सेकण्ड।
उत्तर:
(D) 40 सेकण्ड

प्रश्न 11.
किसी रेडियोएक्टिव नाभिक की अर्द्ध - आयु 50 दिन है तो इसके 1/2 भाग के क्षयित होने के समय t₂, तथा 1/3 भाग के क्षयित होने के समय t₁, का समय अन्तराल (t₂ - t₁) होगा-
(A) 30 दिन
(B) 50 दिन
(C) 60 दिन
(D) 15 दिन।
उत्तर:
(D) 15 दिन