RBSE Class 12 Physics Important Questions Chapter 13 Nuclei

Rajasthan Board RBSE Class 12 Physics Important Questions Chapter 13 Nuclei Important Questions and Answers.

RBSE Class 12 Physics Chapter 13 Important Questions Nuclei

Multiple Choice Questions

Question 1.
The energy released in a typical nuclear fusion reaction is approximately:
(A) 25 MeV
(B) 200 MeV
(C) 800 MeV
(D) 1050 MeV.
Answer:
(A) 25 MeV

Question 2.
A radioactive element has half life period 800 years. After 6400 years what amount will remain?
(A) \(\frac{1}{2}\)
(B) \(\frac{1}{16}\)
(C) \(\frac{1}{8}\)
(D) \(\frac{1}{256}.\)
Answer:
(D) \(\frac{1}{256}.\)

Question 3.
A positron has same mass as:
(A) proton
(B) α-particle
(C) α-neutron
(D) electron.
Answer:
(D) electron.

Question 4.
₁H¹ + ₁H¹ + ₁H² → X + ₁e⁰ + energy.
The emitted particle is:
(A) Neutron
(B) Proton
(C) α-particle
(D) Neutrion.
Answer:
(C) α-particle

Question 5.
Which of the following isotopes is used for treatment of cancer?
(A) K⁴⁰
(B) Co⁶⁰
(C) Sr⁹⁰
(D) I¹³¹.
Answer:
(B) Co⁶⁰

Question 6.
Electron net (eV) is a unit of:
(A) Energy
(B) Potential
(C) Current
(D) Charge.
Answer:
(A) Energy

Question 7.
The Binding energy per nucleon is maximum in case of:
(A) ₂He⁴
(B) ₂₆Fe⁵⁶
(C) ₅₆Ba¹⁴¹
(D) ₉₅U²³⁵.
Answer:
(B) ₂₆Fe⁵⁶

Question 8.
N¹⁴ is bombarded with ₂He⁴. The resulting nucleus is ₈O¹⁷ with the emission of:
(A) Neutrino
(B) Antineutrino
(C) Proton
(D) Neutron
Answer:
(C) Proton

Question 9.
A radioactive element ₉₀X²³⁸ decays into ₉₁Y²³⁸. The number of ß-particles emitted are:
(A) 4
(B) 6
(C) 2
(D) 1.
Answer:
(D) 1.

Question 10.
In the following nuclear reaction:
₆C¹¹ → ₅B¹¹ + ß+ + X
what does X stands for:
(A) A neutron
(B) A neutrino
(C) An electron
(D) A proton.
Answer:
(B) A neutrino

Question 11.
The volume occupied by an atom is greater than the volume of the nucleus by a factor of about:
(A) 10¹
(B) 10⁵
(C) 10¹¹
(D) 10¹⁵.
Answer:
(D) 10¹⁵.

Question 12.
What percentage of original radioactive atom is left after four half lives:
(A) 20%
(B) 10%
(C) 5%
(D) 6%.
Answer:
(D) 6%.

Question 13.
In fusion, the percentage of mass converted into energy is about:
(A) 0.01%
(B) 0.1%
(C) 1%
(D) 10%.
Answer:
(C) 1%

Question 14.
Half life of radium is 1600 years. Its average life is:
(A) 3200 years
(B) 4800 years
(C) 2309 years
(D) 4217 years.
Answer:
(C) 2309 years

Question 15.
Which of the following is used as modulator in nuclear reactor?
(A) Uranium
(B) Heavy Water
(C) Cadmium
(D) Plutonium.
Answer:
(B) Heavy Water

Question 16.
Hydrogen bomb is based on the principle of:
(A) Nuclear fusion
(B) Nuclear fission
(C) ß-decay    
(D) None of these.
Answer:
(A) Nuclear fusion

Question 17.
Energy generated in stars is mainly due to:
(A) Nuclear fusion
(B) Nuclear fission
(C) Gravitational pull
(D) Chemical reaction.
Answer:
(A) Nuclear fusion

Question 18.
A chain reaction is continuous due to:
(A) Large mass defect
(B) Large energy
(C) Production of more neutrons in fission reaction
(D) None of these.
Answer:
(C) Production of more neutrons in fission reaction

Question 19.
The energy equivalent of one atomic mass unit is:
(A) 1.6 x 10^-19 J
(B) 6.02 x 10²³ J
(C) 9.31 MeV
(D) 931 MeV.
Answer:
(D) 931 MeV.

Question 20.
The average binding energy per nucleon of a nuclear inside an atomic nucleus is about:
(A) 8 MeV
(B) 8 MeV
(C) 8 joule
(D) 8 erg.
Answer:
(C) 8 joule

Question 21.
An atom bomb works on the principle of:
(A) Alpha-decay
(B) Beta-decay
(C) Nuclear fission
(D) Nuclear fusion.
Answer:
(C) Nuclear fission

Question 22.
The penetrating power is maximum for:
(A) α-rays
(B) ß-rays
(C) γ-rays
(D) None of these.
Answer:
(C) γ-rays

Question 23.
A nucleus of ₁₁N²³ contains:
(A) 12 electrons
(B) 12 protons
(C) 12 neutrons
(D) 11 neutrons.
Answer:
(C) 12 neutrons

Question 24.
A nucleus _nX^m emit one α-particle and two ß-particles the resulting nucleus is:
(A) _n-2Y^m-4
(B) _n-4Z^m-6
(C) _nZ^m-6
(D) _nX^m-4
Answer:
(D) _nX^m-4

Question 25.
In a nuclear reactor, there is conservation of:
(A) Momentum
(B) Charge
(C) Energy 
(D) All of these.
Answer:
(B) Charge

Question 26.
When ₃Li⁷ nuclei are bombarded by protons, the resultant nuclei are ₄Be⁸. The particles emitted will be:
(A) alpha particles
(B) beta particles
(C) gamma particles
(D) neutron.
Answer:
(C) gamma particles

Fill in the blanks

Question 1.
Electron volt is the unit of ...........................
Answer:
energy.

Question 2.
Atoms having same number of neutrons are called ...........................
Answer:
isotones.

Question 3.
The average binding energy required to extract one nucleon from the nucleus is called ...........................
Answer:
binding energy per nucleon.

Question 4.
The ........................... decay law can be expressed as N = N₀ e^-λt.
Answer:
radioactive.

Question 5.
Both neutrino (v) and antineutrino (\(\bar{v}\)) have almost ........................... mass and are ........................... particles.
Answer:
zero, neutral.

Question 6.
One atomic mass unit = ...........................
Answer:
1.67 x 10^-31 kg.

Question 7.
The relation between nuclear radius and mass number ...........................
Answer:
R = R₀ A^1/3.

Question 8.
The ratio of size of atom and size of the nucleus is ...........................
Answer:
≃ 10⁵.

Question 9.
During radioactivity, the electrons are emitted from the ........................... of atom.
Answer:
nucleus.

Question 10.
Half life of radioactive element depends upon ...........................
Answer:
nature of element.

Very Short Answer Type Questions

Question 1.
Give the value of nuclear density.
Answer:
Nuclear density = 2.9 x 10¹⁷ kg m^-3.

Question 2.
What is impact parameters for scattering by 180°?
Answer:
Impact parameter is zero.

Question 3.
Define impact parameter.
Answer:
It is the perpendicular distance of velocity vector of α-particles from the central line of nucleus when the particle is far away from the nucleus of the atom.

Question 4.
Define atomic mass unit.
Answer:
It is defined as 1/12th of the mass of carbon atom C¹².

Question 5.
Give value of atomic mass unit.
Answer:
1 atomic mass unit = 1.66 x 10^-27 kg.

Question 6.
Define electron volt.
Answer:
It is the energy gained by an electron when accelerated by one volt.

Question 7.
Give relation between a.m.u. and electron volt.
Answer:
1 a.m.u. = 931.5 x 10⁶ eV = 931.5 MeV.

Question 8.
Give value of electron volt.
Answer:
1 electron volt = 1.6 x 10^-19 J.

Question 9.
Define nucleons.
Answer:
Protons and neutrons constituting a nucleus are called nucleons.

Question 10.
Define atomic number.
Answer:
The number of protons in a nucleus, is called atomic number. It is represented by the symbol Z.

Question 11.
How many Joules are there in 1 MeV?
Answer:
1 MeV = 1.6 x 10^-13 J.

Question 12.
Define isotones.
Answer:
Isotones are the atoms having the same number of neutrons.

Question 13.
Define isotopes.
Answer:
Isotopes. The atoms which have the same atomic number Z, but different mass number A, are called isotopes.

Question 14.
Define isobars.
Answer:
Isobars. The atoms which have the same mass number A, but different atomic number Z, are called isobars.

Question 15.
Define mass number.
Answer:
The number of nucleons in a nucleus, is called mass number. It is represented by the symbol A.

Question 16.
What is the approxinate density of nucleus?
Answer:
Of the order of 10¹⁷ kg m^-3.

Question 17.
What is the ratio of gravitational, electric and nuclear interaction?
Answer:
F_g : F_e : F_n : 1 : 10³⁶ : 10³⁸.

Question 18.
What is mass defect?
Answer:
It is the difference between the masses of nucleons constituting a nucleus and the rest mass of the nucleus.

Question 19.
Write expression for mass defect.
Answer:
D_m = ZM_p + (A - Z) M_n - M_nucleus

Question 20.
What is the relation between nuclear radius and mass number?
Answer:
R = R₀ A^1/3
or R ∝ A^1/3
However volume ∝ A.

Question 21.
Give an equation representing the decay of a free electron.
Answer:
₀n¹ → ₁p¹ + _-1e⁰ + \(\bar{v}\)
where \(\bar{v}\) is antineutrino having zero mass. Half life period of neutron is 10.8 minute.

Question 22.
Which one has higher binding energy per nucleon: ₉₂U²³⁵ or ₈O¹⁶?
Answer:
₈O¹⁶.

Question 23.
Define half life of a radioactive substance.
Answer:
Half life of a radioactive substance is the time in which half of the radioactive substance disintegrates. If T is the half life period and λ is the disintegration constant, then T = \(\frac{0.693}{\lambda}\).

Question 24.
A certian radioacitve substance has a half life period of 30 days. What is disintegration constant?
Answer:
λ = \(\frac{0.693}{\mathrm{~T}}=\frac{0.693}{30 \times 24 \times 60 \times 60}\)
or λ = 2.6736 x 10^-7 s^-1

Question 25.
Give the relation between half life and disintegration constant of a radioactive material.
Answer:
Half life T and disintegration constant λ are related by the relation.
T = \(\frac{0.693}{\lambda}\)

Question 26.
Define radioactive decay constant.
Answer:
It is defined as reciprocal of the time after which the number of atoms of a radioactive substance decreases to (1/2.7183) or 36.8% of their number present initially.

Question 27.
Define curie.
Answer:
Curie. It is the radioactivity of 1 gram of radium. One gram of radium gives only 3.7 x 10¹⁰ disintegrations per second. Therefore, the radioactivity of a smaple is said to be 1 curie if it undergoes 3.7 X 10¹⁰ disintegrations per second.
1 ci = 3.7 x 10¹⁰ disintegrations/s and 1 µ ci = 3.7 X 10⁴ disintegrations/s.

Question 28.
What are secondary neutrons?
Answer:
Neutrons produced in fission, are called secondary neutrons.

Question 29.
Write expression for the rate of decay.
Answer:
The required expression is, R = λN.

Question 30.
Give units of rate of decay.
Answer:
The unit are:

• curie = 3.7 x 10¹⁰ disintegrations per sec.
• rutherford = 10⁶ disintegrations per sec.

Question 31.
Define rate of decay or activity.
Answer:
The number of nuclei disintegrating per second, is called rate of decay. It is also called activity. It is represented by symbol R.

Question 32.
In which atom model electrons in the ground state are in stable equilibrium?
Answer:
Thomson atom model.

Question 33.
In which atom model electrons in the ground state are not in stable equilibrium?
Answer:
Rutherford’s model of atom.

Question 34.
In Rutherford’s atom model an atom has a highly non-uniform mass distribution. Explain.
Answer:
In Rutherford’s atom model, all the positive charge and almost whole mass is concentrated at the centre of the atom called nucleus hence the distribution of mass is highly non-uniform.

Question 35.
Draw the graph showing the variation of binding energy per nucleon with mass number. Explain using the graph, why heavy nuclei can undergo fission?
Answer:

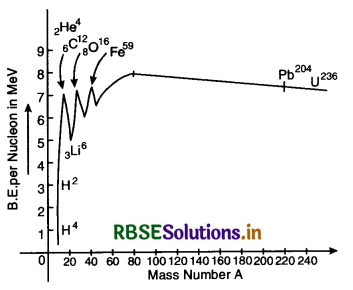
The binding energy per nucleon of heavy nuclei is quite low due to Coulomb’s repulsion between the protons and it is easy to break such nuclei.

Question 36.
Name the reaction which takes place when a slow neutron beam strikes ²³⁵₉₂U nuclei. Write the nuclear reaction involved.
Answer:
The reaction is
¹₀n + ²³⁵₉₂U → ²³⁶₉₂U → ⁹²₃₆Kr + ¹⁴¹₅₆Ba + 3 ¹₀n
The reaction is nuclear fission.

Question 37.
In the series of radioactive disintegration of ^Z_AX first an alpha-particle and then a beta particle is emitted. What is the atomic number and mass number of the new nucleus formed by these successive disintegrations?
Answer:
The reaction, during alpha decay is
^Z_AX → ⁴₂He + ^Z-4_A-2Y
Here has A protons and (Z - A) neutrons and ^Z-4_A-2Y has (A - Z) protons and (Z - 4) - (A - 2) = (Z - A - 2) neutrons.
The reaction during beta decay is
^Z-4_A-2Y → ⁰_-1e + ^Z-4_A-1Z

Question 38.
Does the ratio of neutrons to protons in a nucleus increase, decrease or remain the same after the emission of
(i) α-particle
(ii) ß-particle.
Answer:
(i) Increase, because only heavy elements emit α-particle.
(ii) Decreases, because only light elements emit ß- particle.

Question 39.
You are given two nuclides ₃X⁷ and ₃X⁴:
(i) Are they isotope of the same element? Why?
(ii) Which one of the two is likely to be more stable?
Answer:
(i) Yes, they are isotope of the same element because both have the same atomic number 3.
(ii) Since ₃X⁴ has less number of neutrons, so it is more stable.

Question 40.
What is the ratio of the nuclear densities of the two nuelei having mass numbers in the ratio 1 : 4?
Answer:
The ratio is 1 : 1 as nuclear density is independent of mass number.

Question 41.
Which one of ⁷₃X and ⁴₃Y is likely to be more stable? Give reason.
Answer:
⁷₃X will be more stable than ⁴₃Y. Because the odd even pair is more stable than odd-odd pair.

Question 42.
Some scientists have predicted that a global nuclear war would be followed by nuclear winter. What would cause the nuclear winter?
Answer:
Because after the nuclear war the radioactive waste will hang in the atmosphere and will abstract the light radiation to reach the surface of earth and will cause the nuclear winter.

Question 43.
Why is the gold foil preferred as scattering object in Rutherford’s experiment?
Answer:
Because gold is a heavy substance having atomic number 79 and can be stretched into very thin foil.

Question 44.
What is self-sustained nuclear reaction?
Answer:
The nuclear reaction which once initiated keeps on ‘going on’, without any further need of any external ‘missiles’.

Question 45.
Why is heavy water used as moderator?
Answer:
It is used to slow down neutrons so that the fission reaction gets under control.

Question 46.
Complete the following nuclear reaction:
₅B¹⁰ + (?)₃ = Li⁷ + ₂He⁴.
Answer:
Let the unknown particle be represented on
∴ 10 + A = 7 + 4 or A = 1
And 5 + Z = 3 + 2 or Z = 0
∴ The unknown particle is ₀n¹ i.e. neutron.

Question 47.
What is a nuclear fission reaction?
Answer:
The splitting of a higher atomic mass nucleus to lower atomic mass nuclei with emission of energy is called nuclear fission.
₉₂U²³⁵ + ₀n¹ → ₉₂U²³⁶ → ₃₆Kr⁹² + ₅₆Ba¹⁴¹ + 3 ₀n¹ + energy is one of fission reaction.

Question 48.
Define the principle of hydrogen bomb.
Answer:
Nuclear fusion is the principle of hydrogen bomb. Atoms of lower atomic mass fuse into heavier atom with emission of energy. One of such reaction is
₁H² + ₁H² → ₂He⁴ + 24 MeV.

Question 49.
What is the role of a moderator in a nuclear reactor?
Answer:
A moderator slows down the neutrons and hence the nuclear reaction.

Question 50.
Define critical mass of nuclear mass of nuclear chain reaction.
Answer:
When the chained nuclear reaction is sustained or steady, i.e., the rate of production of neutrons is equal to the rate of loss of neutrons, the size of the fissionable matter is said to be critical and its mass is called critical mass.

Question 51.
Define nuclear fission and fusion.
Answer:
Nuclear fission is a process in which heavy nucleus disintegrates into lighter nuclei. Nuclear fusion is a process in which nuclei of fighter atoms are fused together into heavy atom with the release of enormous energy.

Question 52.
Name the material used as ‘control rods’ in a nuclear reactor.
Answer:
Cadmium.

Question 53.
What is a thermonuclear reaction?
Answer:
The nuclear fusion of two fight nuclei takes place at very high temperature (≃10⁷K). This is called thermonuclear reaction.

Question 54.
At what temperature the nuclear fusion is possible?
Answer:
About 5000 K to 6000 K.

Question 55.
Can fusion reaction be controlled in a sustained manner?
Answer:
No.

Question 56.
What are the types of damage caused by radiation?
Answer:
Two types of damage is caused by radiation:
1. Pathological damage
2. Genetical damage.

Question 57.
What is the source of solar energy?
Answer:
Solar energy is due to nuclear fusion taking place inside the sun.
4 ₁H¹ → ₂He⁴ + Q
where Q is the energy released when 4 protons fuse to a helium atom.

Question 58.
State the reason, why heavy water is generally used as a moderator in a nuclear reactor.
Answer:
The moderator helps to slow down the neutrons so that the fission reaction gets under control.

Question 59.
Name the absorbing material used to control the reaction rate of neutrons in a nuclear reactor.
Answer:
Cadmium and boron.

Question 60.
What is the nuclear radius of ¹²⁵Fe, if that of ²⁷Al is 3.6 fermi?
Answer:
Since R = R₀A^1/3
or R ∝ A^1/3

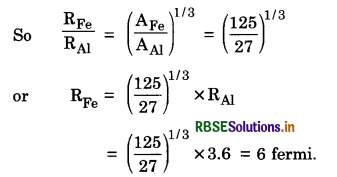
Question 61.
Out of the two characteristics the mass number (A) and the atomic number (Z) of a nucleus, which one does not change during ß- decay.
Answer:
Mass number (A) does not change during ß-decay, because during ß-decay, we get
^A_ZX → ^A_Z+1Y + _-1e⁰.

Question 62.
Four nuclei of an element undergo fusion to form a heavier nucleus with release of energy, which of the two-the parent or the daughter nucleus would have-higher binding energy/nucleon?
Answer:
The daughter nuclei will have higher binding energy per nucleon as release in energy is accompanied by an increase of binding energy.

Question 63.
Name the reaction which takes place when a slow neutron beam strikes ²³⁵₉₂U nuclei. Write the nuclear reaction involved.
Answer:
The reaction is
¹₀n + ²³⁵₉₂U → ²³⁶₉₂U → ⁹²₃₆Kr + ¹⁴¹₅₆Ba + 3 ¹₀n
The reaction is nuclear fission.

Question 64.
In the series of radioactive disintegration of ^Z_AX first an alpha particle and then a beta particle is emitted. What is the atomic number and mass number of the new nucleus formed by these successive disintegrations?
Answer:
The reaction, during alpha decay is
^Z_AX → ⁴₂He + ^Z-4_A-2Y
Here ^Z_AX has A protons and (Z - A) neutrons and ^Z-4_A-2Y has (A - Z) protons and (Z - 4) - (A - 2) = (Z - A - 2) neutrons. The reaction during beta decay is
^Z_AX → ⁴₂He + ^Z-4_A-2Y → _-1e⁰ + _Z-4A-1Z.

Question 65.
Compare the radii of the two nuclei with mass number 1 and 27 respectively.
Answer:
Since r ∝ A^1/3
∴ \(\frac{r_1}{r_2}=\left(\frac{\mathrm{A}_1}{\mathrm{A}_2}\right)^{\frac{1}{3}}=\left(\frac{1}{27}\right)^{\frac{1}{3}}=\frac{1}{3}.\)

Question 66.
You are given two nuclides ₃X⁷ and ₃X⁴:
(i) Are they isotopes of the same element? Why?
(ii) Which one of the two is likely to be more stable?
Answer:
(i) Yes, they are isotope of the same element because both have the same atomic number 3.
(ii) Since ₃X⁴ has less number of neutrons, so it is more stable.

Question 67.
Which property of nuclear force explains the approximate constancy of binding energy per nucleon with mass number A for nuclei in the range 30 < A < 170?
Answer:
Short range nature of nuclear force. 

Question 68.
What percentage of a given mass of radioactive substance will be left undecayed after four half periods?
Answer:
The percentage of mass undecayed
= \(\left(\frac{1}{2}\right)^4\) x 100 = \(\frac{100}{16}\) = 6.25%.

Question 69.
State the conditions for controlled chain reaction in a nuclear reactor.
Answer:
Since in a nuclear fission, three neutrons are realeased, so if on the average one neutron causes further fission, the chain reaction is said to be controlled.

Question 70.
Give the mass number and atomic number of elements on the right-hand side of the decay process ²²⁰₈₆Ru → Po + He.
Answer:
The complete equation is ²²⁰₈₆Ru → ²¹⁶₈₄Po + ⁴₂He
So for Po, Z = 84, A = 216
for He, Z = 2, A = 4.

Question 71.
Which has greater ionising power α-particle or ß-particle.
Answer:
α-particle has greater ionising power than ß-particle.

Question 72.
Why do α-particles have a high ionising power?
Answer:
Because a particle has large mass and large nuclear cross-section.

Question 73.
What will be the ratio of the radii of two nuclei of mass number A₁ and A₂?
Answer:
Since R ∝ A^1/3
∴ \(\frac{\mathrm{R}_1}{\mathrm{R}_2}=\left(\frac{\mathrm{A}_1}{\mathrm{~A}_2}\right)^{1 / 3}\)

Question 74.
Name two radioactive elements, which are not found in observable quantity in nature, why is it so?
Answer:
Plutonium and tritium are not found in observable quantity in nature because of their very small values of half state.

Question 75.
A nucleus of mass number A, has a mass defect ∆m. Give the formula, for the binding energy per nucleon of this nucleus.
Answer:
B.E. Per nucleon = \(\frac{\text { Total binding energy }}{\text { Number of nucleons }}\)
= \(\frac{\Delta m c^2}{\mathrm{~A}}\).

Question 76.
What is the difference between an electron and a ß-particle?
Answer:
Basically there is no difference between an electron and a ß-particle. The electron of nuclear origin is called a ß-particle.

Question 77.
Write any one equation representing nuclear fusion reaction.
Answer:
The equation of a nuclear fission is
₁H² + ₁H² → ₂He⁴ + 24MeV.

Question 78.
The radioactive isotope D decays according to the sequence 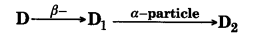. If the mass number and atomic number of D₂ are 176 and 71 respectively, what is (i) the mass number and (ii) atomic number of D?
Answer:

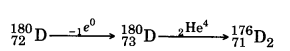
So Mass no = 180 and atomic number = 72.

Question 79.
Write the nuclear decay process for ß-decay of ³²₁₅P.
Answer:
³²₁₅P → ³²₁₆S + _-1e⁰.

Question 80.
What is the source of solar energy?
Answer:
Nuclear fusion reaction taking place in the sun.

Question 81.
Two nuclei have mass numbers in the ratio 1 : 3. What is the ratio of their nuclear densities?
Answer:
The ratio is 1 : 1 as nuclear density is independent of mass number.

Short Answer Type Questions

Question 1.
What are isotopes? Give examples.
Answer:
Isotopes of an element are the atoms of the element which have the same atomic number but different atomic weights. For example ₁H¹, ₁H², ₁H³ are the isotopes of hydrogen. As isotopes of an element have the same atomic number, they contain the same number of protons and the same number of electrons. But as their atomic weights are different they contain different number of neutrons. Isotopes of an element have identical chemical properties. Their physical properties, however, differ. All the known elements have one or more isotopes. The relative abundance of different isotopes differs from element to element.

Question 2.
What are isobars?
Answer:
Isobars are the atoms of different elements which have the same atomic weight, but different atomic numbers. Isobars contain different number of protons, different number of electrons and also different number of neutrons. Only the total number of nucleons in them is the same.

For example ₁₁Na²² and ₁₀Ne²² are isobars. Similarly, ₂₀Ca⁴⁰ and ₁₈Ar⁴⁰ are isobars ₁₇C¹³⁷ and ₁₆S³⁷ are also isobars. The chemical properties of isobars are widely different. Their physical properties may be identical. Isobars occupy different places in the periodic table.

Question 3.
What is meant by B.E. per nucleon and packing fraction?
Answer:
Average Binding-Energy per nucleon of a nucleus is the average energy we have to spend to remove a nucleon from the nucleus to infinite distance. It is given by the total binding energy divided by the mass number of the nucleus.
i.e. Average B.E./nucleon = \(\frac{\text { Total B.E. }}{\text { Mass number }}\)

Packing fraction of a nucleus is defined as the mass defect per nucleon of the nucleus. Thus
Packing friction = \(\frac{\text { Mass defect }}{\text { Mass number }}\)
= \(\frac{\Delta m}{\mathrm{~A}}\)

Question 4.
Is the rest mass of proton exactly equal to the rest mass of a neutron?
Answer:
No, the rest mass of proton and neutron are not exactly equal. They are only approximately equal.
m_n = 1.00866 a.m.u.;
m_p = 1.00782 a.m.u.

Question 5.
Is free neutron a stable particle?
Answer:
No, a free neutron is not a stable particle. It decays spontaneously into a proton, an electron and antineutrino
₀n¹ → ₁H¹ + _-1e⁰ + \(\bar{v}\)

Question 6.
What is alpha decay, beta decay and gamma decay?
Answer:
During alpha decay, an alpha particle is emitted resulting in decrease of mass number by 4 and atomic number by 2.
₉₂U²³⁸ → ₂He⁴ + ₉₀Th²³⁴
During beta decay, a neutron of the nucleus disintegrates to give rise to proton, electron and antineutrino.
₀n¹ → _-1p¹ + _-1e⁰ + \(\bar{v}\)
Reaction for emission of beta particle results in increase of atomic number by 1 whereas the mass number remains constant.
₉₀Th²³⁴ → _-1ß⁰ + ₉₁Pa²³⁴
Gamma decay usually follows alpha decay. During alpha particle emission, the nucleus is left in an excited state.
To return to normal stage, it emits a single γ-ray of large energy or γ-rays are emitted in steps. However, during γ-decay, atomic number and mass number remain the same.

Question 7.
A radioactive nucleus A decays as follows:

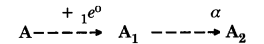
If the mass number and atomic number of A₂ are 176 and 71 respectively, what are the mass number and atomic numbers of A₁ and A? Which of these three elements are isobars?
Answer:
Writing atomic and mass numbers of A as x and y,
_xA^y → +₁e⁰ + _x-1A₁^y
_x-1A₁^y → ₂He⁴ + _x-3A₂^y-4
Now in A₂, x-3 = 71 or x = 74
and y-4 = 176
or y = 180
∴ Complete reaction is
₇₄A¹⁸⁰ → ₊₁e⁰ + ₇₃A₁¹⁸⁰
₇₃A₁¹⁸⁰ → ₂He⁴ + ₇₁A₂¹⁷⁶
A and A₁ are isobars since mass number of each is 180.

Question 8.
What are radio isotopes? What are their applications?
Answer:
The radioactive elements which are chemically identical but differ in their mass number are called radio isotopes. These are also called radio isotopes or radio-nuclides. Five most important radio-isotopes are iodine-131, phosphorus-33, sulphur-35, carbon-14 and sodium-24.
Applications

1. In medicine, these are used for treatment of diseases. Malignant cells are more sensitive to radiations than a healthy cell and can be killed by controlled doses of radiation.
2. Radioactive gold is used for treatment of syphilis.
3. Radioactive bismuth is used in treatment of blood cancer.
4. Radioactive iodine can be used to treat diabetes and heart trouble.
5. Radio isotopes used as tracers are used for location of tumours.
6. Radioactive chromium is used to study blood processes and blood diseases.
7. Iron-59 helps us to determine the rate of formation of R.B.C. in the blood.
8. Cobalt is used to detect flaws in metal structures.

Question 9.
Explain with the help of nuclear reaction in each of the following cases, how the neutron-to-proton ratio changes during (i) alpha decay; (ii) beta decay?
Answer:
For alpha decay, let us consider a nuclear reaction:
₉₂U²³⁸ → ₂He⁴ + ₉₀Th²³⁴
Initial neutron-proton ratio
= \(\frac{238-92}{92}=\frac{146}{92}\) = 1.59
Final neutron-proton ratio
= \(\frac{238-90}{90}=\frac{144}{90}\) = 1.57
∴ Neutron-proton ratio decrease during ß-decay.

Question 10.
Define the term half life period and decay constant of a radioactive substance. Write their SI unit. Establish a relation between them.
Answer:
Half life period (T). It is the time during which the number of atoms of a radioactive material reduces to half of the original number.
Decay constant (λ). Decay constant of a radioactive element is the time after which the number of radioactive atoms reduces to \(\frac{1}{e}\) times the original number of atoms in the sample.

Relation between T and λ
Half life period. It is the time during which the number of atoms of a radioactive material reduces to half of the original number.
Let N₀ = number of atoms at t = 0 (at the start of the observation)
N = number of atoms after time t
So, N = N₀e^-λt ..........................(1)
where λ is constant called disintegration constant
Let T = half life period
So, when t = T, N = N₀/2.
Substituing in Eq.(1), we have
\(\frac{\mathrm{N}_0}{2}\) = N₀e^-λt
eλt = 2
λT = log_e2 = 2.303 log₁₀2
= 0.693
or T = \(\frac{0.693}{\lambda}\)

Question 11.
A neutron is absorbed by ⁶₃Li nucleus with the subsequent emission of an α-particle.
(i) Write down the corresponding reaction.
(ii) Calculate the energy released in MeV in this reaction given ⁶₃Li = 6.01516 u; mass (neutron) = 1.0086654 u mass (α) = 4.0026044 u and mass (triton) = 3.0100000 u. Take 1u = 931 MeV/c².
Answer:
(i) The nuclear reaction is:
¹₀n + ⁶₃Li → ⁴₂α + ³₁T

(ii) Decrease in mass = m (neutron) + m (Li) - m (α) - m (T)
∴ BE = [m (neutron) + m (Li) - m (α) - m (T)]c²
= [1.0086654 + 6.015126 - 4.0026044 - 3.0100000] uc²
= 0.0111870 uc²
= 0.0111870 x 931
= 1.0415097 MeV.

Question 12.
(a) Show that decay rate R of a sample of a radio-nuclide is related to the number of radioactive nuclei N at that instant by the expression R = λN.
(b) The half life of ²³⁸₉₂U against α-decay is 1.5 x 10¹⁷ s. What is the activity of a sample of ²³⁸₉₂U having 25 x 10²⁰ atoms?
Answer:
(a) The decay rate R is equal to the number of radioactive disintegration in the sample taking place per second.
i.e. R = \(-\frac{d \mathrm{~N}}{d t}\) ..........................(i)
From the law of radioactive disintegration, the rate of disintegration \(\left[-\frac{d \mathrm{~N}}{d t}\right]\) is proportional to number of atoms present at that instant i.e.
\(-\frac{d \mathrm{~N}}{d t}\) ∝ N
or \(-\frac{d \mathrm{~N}}{d t}\) = λN
Using Eq. (i), we get:
R = λN

(b) Here T = 1.5 x 10¹⁷ s
Since λ =\( \frac{0.693}{T}=\frac{0.693}{1.5 \times 10^{-17}}\) s^-1
∴ R = λN
= \(\frac{0.693}{1.5 \times 10^{-17}}\) x 25 x 10²⁰ dis s^-1
= \(\frac{693 \times 25}{1.5}\) = 11550 atoms/s

Question 13.
(a) Draw the energy level diagram showing the emission of ß-particle followed by γ-rays by a ⁶⁰₂₇Co nucleus.
(b) Plot the distribution of kinetic energy of ß-particles and state why energy spectrum is continuous?
Answer:
(a) The energy spectrum of b-particles is continuous because an antineutrino is simultaneously emitted in β-decay: the total energy released in b-decay is shared by b-particle and the antineutrino so that momentum of the system may remain conserved.

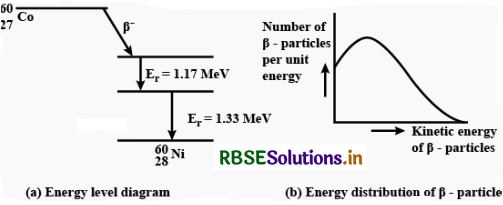
(b) Beta decay. The emission of electron ß-particle) from the nucleus of an atom is called ß-decay. It is believed that emission of an electron by the nucleus is due to transformation of a neutron into a proton and an electron. When a neutron changes into a proton, a ß-particle is ejected whereas a proton remains in the nucleus. The emission of ß-partic1e, therefore:

• increases the atomic number by one and
• keeps the mass number unaffected.

Question 14.
Half life of ²³⁸₉₂U against α-decay is 4.5 x 10⁹ years. Calculate activity of 1 g of sample ²³⁸₉₂U.
Answer:
Number of atoms in 238 g of Uranium = 6.023 x 10²³
∴ Number of atoms in 1 g

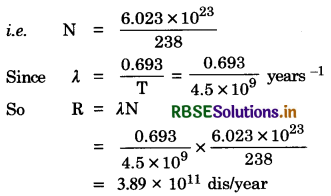
Question 15.
Write the nuclear reactions for the following:
(i) α-decay of ²⁰⁴₈₄Po
(ii) ß-decay of ³²₁₅P
(iii) ß+ - decay to ¹¹₆C
Answer:
(i) ²⁰⁴₈₄Po → ⁴₂He + ²⁰⁰₈₂Hg
(ii) ³²₁₅P → _-1e⁰ + ³²₁₆S
(iii) ¹¹₆C → _-1e⁰ + ¹¹₅B

Question 16.
Calculate the binding energy per nucleon (in MeV) of the nucleus 5626Fe.
[Given: mass of ¹₁H = 1.00783 u, mass of ¹₀n = 1.00867 u, mass of ⁵⁶₂₆Fe = 55.934939 u. 1u = 931 MeV/c².
Answer:
B.E. of ⁵⁶₂₆Fe
= [^Z_mH+^{(A - Z)}_mN - m(^A_ZX)] 931.5
= [{26 x 1.007825 + (56 - 26) x 1.008665} - 55.934939] 931.5
= [{26.20345 + 30.25995} - 55.934939] 931.5
= 492.26 MeV

B.E. of 20983Bi
= [{83 x 1.007825 + (209 - 83) x 1.008665} - 208.980388] 931.5
= [{83.64975 + 127.09179 - 208.980388] 931.5
= 1640.1 MeV.
B.E. per nucleon = \(\frac{1640.1}{209}\) = 7.84 MeV
Fe56 has greater binding energy per nucleon.

Question 17.
Give the mass number and atomic number of elements on the right hand side of the decay process:
²²⁰₈₆Rn → Po + He.

The graph shows how the activity of a sample of radon-220 changes with time. Use the graph to determine its half-life. Calculate the value of decay constant of radon-220.
Answer:
The given reaction is
²²⁰₈₆Rn → ²¹⁶₈₄Po + ⁴₂He
Mass number of Po = 216, He = 4
Atomic number of Po = 84, He = 2

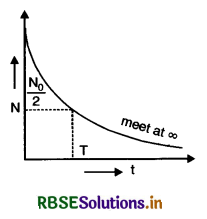
Half life
From the graph of decay of Rn - 220, we find that at t = 0, number of nuclei present = N₀ and at t = ∞, N₀ → 0
Since N = N₀ e^-λt ...................(i)
As at t = T, N = \(\frac{\mathrm{N}_0}{2}\)
∴ \(\frac{\mathrm{N}_0}{2}\) = N₀e^-λt
or λT = log_e2 = 2.303 log₁₀ 2
or T = \(\frac{2.303 \times 0.3010}{\lambda}=\frac{0.693}{\lambda}\)
From Eq. (i)
It t = \(\frac{1}{\lambda}\), then
N = N₀ e^{-λ.\(\frac{1}{\lambda}\)} = \(\frac{\mathrm{N}_0}{e}\)
So decay constant is the time after which the number of radioactive elements reduces to \(\frac{1}{e}\) times the initial number of atoms.

Question 18.
With the help of an example, explain how the neutron to proton ratio changes during alpha decay of a nucleus.
Answer:
For alpha decay, let us consider a nuclear reaction:
₉₂U²³⁸ → ₂He⁴ + ₉₀Th²³⁴
Initial neutron-proton ratio
= \(\frac{238-92}{92}=\frac{146}{92}\) = 1.59
Final neutron-proton ratio
= \(\frac{238-90}{90}=\frac{144}{90}\) = 1.57
∴ Neutron-proton ratio decrease during ß-decay.

Question 19.
When a deuteron of mass 2.0141u and negligible kinetic energy is absorbed by lithium (⁶₃Li) of nucleus of mass 6.0155 u, the compound nucleus disintegrates spontaneously into two alpha particles, each of mass 4.0026 u.
Calculate the energy in joules carried by each alpha particle. (1 u = 1.66 x 10^-27 kg).
Answer:
The reaction is:
²₁H + ⁶₃Li → ⁸₄Be → 2[⁴₂He]
∴ Mass defect, ∆m
= m (²₁H) + m (⁶₃Li) - 2m (⁴₂He)
= [2.0141 + 6.0155 - 2 x 4.0026] u
= 0.0244 u
= 0.0244 x 1.66 x 10^-27 kg
= 0.0405 x 10^-27 kg
∴ Binding energy Q = ∆mc²
= 0.0405 x 10^-27 x 9 x 10¹⁶
= 0.3645 x 10^-11 J
= 36.45 x 10^-13 J
This energy is equally shared by both the alpha particles.
∴ Energy carried by each alpha particle
= \(\frac{1}{2}\)[36.45 x 10^-13] = 18.225 x 10^-13 J

Question 20.
The ionising power of ß-particles is less compared to α-particles, but their penetrating power is more,why?
Answer:
The velocity of ß-particles emitted by a radioactive element is very large as compared to the velocity of a particles. They take very little time near the atoms of the medium. Thus the probability of ionising the atom is comparatively less. On the other hand, the loss of energy is very slow and hence they can penetrate the medium through a sufficient depth.

Question 21.
Natural radioactivity is found in heavy elements only. Explain.
Answer:
A heavy nucleus contains a large number of protons and neutrons. The protons inside the nucleus repel each other with coulomb's force, and in heavy nucleus the electrical repulsive forces become effective.

Question 22.
What is natural radioactivity? How does it vary with external parameters like temperature, pressure etc?
Answer:
The process of spontaneous disintegration of an unstable nucleus with the emission of high energy rays like α-rays, ß-rays and γ-rays is called natural radioactivity. This phenomenon is predominant in elements with high atomic number. Generally, trans-uranium elements (elements with atomic number Z > 92) exhibit this phenomenon. Natural radioactive decay does not depend on temperature, pressure etc.

Question 23.
A certain radioactive element disintegrates for an interval of time equal to its mean life. What fraction of the element has disintegrated?
Answer:
Here t = τ
Number of atoms left in the sample after time t = τ is given by
N = N₀ e^-λτ = N₀ e^{-λ.\(\frac{1}{\lambda}\)} [∵ τ = \(\frac{1}{\lambda}\)]
or N = N₀ e^-1 = \(\frac{\mathrm{N}_0}{e}\)
or N = \(\frac{\mathrm{N}_0}{2.718}\) = 0.368 N₀
So fraction of element disintegrated
= N₀ - 0.368 N₀ = 0.632 N₀.
Hence the fraction of the element disintegrated in time equal to its mean life is 0.632.

Question 24.
What are the characteristic properties of radioactive elements?
Answer:
Following are characteristic properties of radioactive elements:

1. Radioacitive decay does not depend on temperature, light, pressure etc.
2. Radioactive elements emit three types of radiations namely, α-rays, ß-rays and γ-rays
3. Radioactivity is an irreversible process.
4. Radioactive substances do not show any abnormality in their chemical and physical properties.

Question 25.
What is meant by electron capture?
Answer:
In case of an unstable nuclei having more number of protons, the coulomb barrier prevents any emission of positron to make the nucleus stable. So in that case, an orbital electron is captured by the nucleus which helps in transforming a proton into a neutron thereby reducing the atomic number of the nucleus.

Question 26.
What is the concept of compound nucleus?
Answer:
The theory of formation of a compound nucleus was put forward by Neil Bohr in 1936 and is a useful tool for explaining a nuclear reaction. According to this theory, when an incident particle hits target nucleus, it is captured by the target nucleus resulting in the formation of an unstable nucleus called compound nucleus, which in turn disintegrate to give a new particle and a new nucleus.
(i) Incident particle + target nucleus → compound nucleus.
(ii) Compound nucleus → product nucleus + emitted particle.

Question 27.
Uranium ₉₂U²³⁸ is not suitable for chain reaction. Why?
Answer:
₉₂U²³⁸ is found in the form of three isotopes i.e. U²³³, U²³⁵ and U²³⁸. But the percentage of U²³³ and U²³⁵ nuclei are very small. The incident slow neutron of energy 0.025 eV can cause fission in U²³⁵ but not in nuclei U²³⁸ because for fission of U²³⁸ neutron of energy more than 1 MeV is required. Also the secondary neutrons get slowed down on colliding with U²³⁸ nuclei and are unable to cause further fission of U²³⁸. Thus U²³⁸ is not suitable for chain reaction.

Question 28.
What is nuclear fission? Give an example to illustrate it. What is the importance of fission phenomenon?
Answer:
Nuclear fission. A process in which a heavy nucleus disintegrates into two lighter nuclei of nearly same masses is called nuclear fission.
e.g. When slow neutron is bombarded on a heavy nucleus of ₉₂U²³⁵ yielding two daughter nuclei Ba and Kr and tremendous amount of energy, the nuclear reaction can be represented as:
₉₂U²³⁵ + ₀n¹ → ₉₂U²³⁶ → ₅₆Ba¹⁴¹ + ₃₆Kr⁹² + 3₀n¹+ ∆Q

Importance of nuclear fission
1. Controlled nuclear fission is used in number of yields e.g.
(а) to prepare isotopes.
(b) to generate power for propulsion of ships, submarine and aircrafts.
(c) to produce plutonium for explosive purpose.
2. Uncontrolled nuclear fission is used in atom bomb.

Question 29.
Distinguish between controlled and uncontrolled chain reactions.
Answer:
Controlled chain reaction. In controlled chian reaction neutrons are absorbed by using cadmium rods and on an average one neutron remains available for exciting further fission.

Uncontrolled chain reaction. If the fissionable material is having mass greater than critical mass and the reaction is started it will accelerate at a rapid rate and whole material explodes and a tremendous amount of energy is released.

Question 30.
Distinguish between nuclear fission and nuclear fusion.
Answer:
Distinction between Nuclear fission and Nuclear fusion:
Nuclear fission

• A bigger nucleus is split into two or more smaller nuclei.
• It produces huge energy.
• Nuclear reaction can be controlled.
• It is the principle of atom or fission bomb.

Nuclear fusion

• Two light nuclei combine to form a heavier nucleus.
• It also produces huge energy.
• Nuclear reaction can be controlled.
• It is the principle of hydrogen or fusion bomb.

Question 31.
Explain nuclear holocaust. Describe its sources.
Answer:
Nuclear holocaust
Definition. Nucleus is a source of huge amount of energy. Uncontrolled release of large nuclear energy, is called atomic explosion. The situation caused by such atomic explosion, is called nuclear holocaust.

Sources. Its sources are
(1) atom bomb
(2) hydrogen bomb,
(i) Atom bomb. It works on the phenomenon of uncontrolled nuclear fission chain reaction. Uranium (U235) is used as fission material.
(ii) Hydrogen bomb. It works on phenomenon of fusion of hydrogen nuclei to form helium nucleus.The high temperature needed for fusion is produced by fission bomb.

Question 32.
Describe the nucleus as a source of nuclear energy.
Answer:
Nucleus as a source of Nuclear Energy.
Binding energy curve shows that average binding energy is 8.5 MeV per nucleon for moderate nuclei with mass number 40 to 120. It is less than this for lighter nuclei with A < 40 and also for heavy nuclei with A > 120. It means that light and heavy nuclei are less tightly bound. Whenever nuclei of less average binding energy per nucleon are converted into those of more average binding energy, some mass is converted into energy.

From this situation, it is expected that energy will be evolved if heavy nuclei be split into moderate nuclei or light nuclei be joined (fused) to form a less light nuclei. The former process is known as nuclear fission and the latter as nuclear fusion. Both these processes become source of nuclear energy.

Question 33.
A nucleus ²³₁₀Ne undergoes ß-decay and becomes ²³₁₁Ne. Calculate the maximum kinetic energy of electrons emitted assuming that the daughter nucleus anti-neutrino carry negligible kinetic energy.
(mass of ²³₁₀Ne = 22.994466 u, mass ²³₁₁Ne = 22.989770 u, 1u = 931.5 MeV/c²)
Answer:
The decay scheme is
²³₁₀Ne → ²³₁₁Ne + _-1e⁰ + Q
So mass defect,
∆m = 22.994466 u - [22.989770 + Negligible mass]
= 0.004696 u
∴ Energy released = 0.004696 x 931.5
= 4.374 MeV.

Question 34.
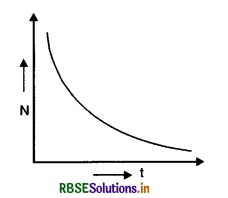
State the law of radioactive decay. If N₀ is the number of radioactive nuclei in the sample at same initial time, find out the relation to determine the number N present at a subsequent time. Draw a plot of N as a function of time.
Answer:
Law of radioactive decay
The number of atoms disintegrated per second is directly proportional to the number of radioactive atoms actually present at that instant and is independent of all physical conditions like temperature, pressure humidity, chemical composition etc.
Let at t = 0,
N₀ = number of atoms present
N = number of atoms left after time t.
dN = number of atoms disintegrated in time dt.
i.e. -\(\frac{d \mathrm{~N}}{d t}\) ∝ N
or -\(\frac{d \mathrm{~N}}{d t}\) = λN, ..........................(i)
where λ is a constant called disintegration constant and depends upon the nature of the radioactive substance.
Now from, (i), we have
\(\frac{1}{N}\) dN = -λdt
or ∫\(\frac{1}{N}\) dN = λ∫dt
or log_eN = λt + C ................(ii)
where C is constant of integration. To determine its value,
since N = N₀ initially
i.e. when t = 0, N = N₀
log_e N₀ = 0 + C
Substituting the value of C in (ii), we have
log_eN = -λt + log_eN₀
or log_eN - log_eN₀ = -λt
log_e \(\frac{\mathrm{N}}{\mathrm{N}_0}\) = -λt
or \(\frac{\mathrm{N}}{\mathrm{N}_0}\) = e^-λt
or N = N₀e^-λt ..................(iii)
which is the required equation.
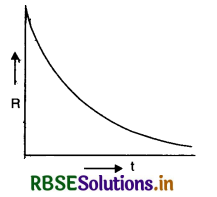
Eq. (iii) shows that the radioactive decay occurs according to exponential law and the number of radioactive atoms decreases exponentially. Since N shall become zero only when t becomes infinity, it shows that time taken by a radioactive element to disintegrate completely is infinitely long.

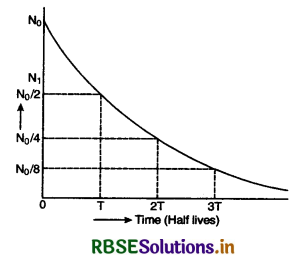
The curve in Fig. SAQ 34 shows the exponential decay of radioactive substance.

Question 35.
Draw a plot of the binding energy per nucleon as a function of mass number for a large number of nuclei. Explain the energy release in the process of nuclear fission from the above plot. Write a typical reaction in which a large amount of energy is released in the process of nuclear fission.
Or
Draw a graph showing the variation of binding energy per nucleon verses the mass number. Explain with the help of this graph the release of energy in the process of nuclear fission and fusion.
Or
Explain the processes of nuclear fission and nuclear fusion by using the plot of binding energy per nucleon (BE/A) versus the mass number A.
Answer:
Plot of binding energy per nucleon is shown in fig. SAQ 35.

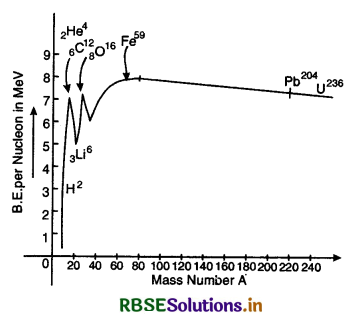
From the graph we find that
1. The binding energy per nucleon increases gradually from mass number A = 20 to mass number A = 40.

2. The curve is almost flat between mass number 40 and 120. This means that the variation in binding energy per nucleon in the range is small (about 10%). The average binding energy per nucleon in this region is about 8.5 MeV. It is maximum for iron (⁵⁹₂₆Fe) and has a value 8.8 MeV.

3. The binding energy per nucleon decreases slowly and continuously from A = 120 to A = 240. It reaches a value of 7.6 MeV at A = 238. Thus we find that if any nucleon with A = 240 breaks into two nuclei, nucleons get more lightly bound, so energy would be released in the process. This process is called nuclear fission.

4. When two light nuclei (A < 10) are join to form a heavier nucleus, the binding per nucleon of the fused heavier nuclei is more than the binding energy per nucleon of the lighter nuclei. Hence we find that the final system is more tightly bound than the initial system, and the energy released in this process is called nuclear fusion.
A typical nuclear fission reaction is
²³⁵₉₂U + ¹₀n → ²³⁶₉₂U → ¹⁴⁴₅₆Ba + ⁸⁹₃₆Kr + 3¹₀n + 200 MeV

Question 36.
Distinguish between isotopes and isobars. Give one example for each of the species. A radioactive isotope has half life of 5 years. How long will it take the activity to reduce to 3.125%.
Answer:
Isotopes are elements having same atoms number but different mass number e.g. ²³⁸₉₂U and ²³⁵₉₂U are isotopes of U.
Isobars are elements having the same mass number but different atomic numbers, e.g. ⁴⁰₁₈Ar and ⁴⁰₂₀Ca.
Given \(\frac{\mathrm{A}}{\mathrm{A}_0}\) = 3.125% = \(\frac{1}{32}\),
t1/2 = 5 years, t = ?
Since \(\frac{\mathrm{A}}{\mathrm{A}_0} = (\frac{\mathrm{A}}{\mathrm{A}_0})\)ⁿ
So (\(\frac{1}{32}\)) = (\(\frac{1}{2}\))^t/5 or (\(\frac{1}{2}\))⁵ = (\(\frac{1}{2}\))^t/5
or \(\frac{t}{5}\) = 5 or t = 25 years.

Question 37.
Explain with the help of nuclear reaction in each of the following cases, how the neutron-to-proton ratio changes during (i) alpha decay; (ii) beta decay?
Answer:
For alpha decay, let us consider a nuclear reaction:
₉₂U²³⁸ → ₂He⁴ + ₉₀Th²³⁴
Initial neutron-proton ratio
= \(\frac{238-92}{92}=\frac{146}{92}\) = 1.59
Final neutron-proton ratio
= \(\frac{238-90}{90}=\frac{144}{90}\) = 1.57
∴ Neutron-proton ratio decrease during ß-decay.

Question 38.
Define the term half life period and decay constant of a radioactive substance. Write their SI unit. Establish a relation between them.
Answer:
Half life period (T). It is the time during which the number of atoms of a radioactive material reduces to half of the original number.
Decay constant (λ). Decay constant of a radioactive element is the time after which the number of radioactive atoms reduces to \(\frac{1}{e}\) times the original number of atoms in the sample.

Relation between T and λ
Half life period. It is the time during which the number of atoms of a radioactive material reduces to half of the original number.
Let N₀ = number of atoms at t = 0 (at the start of the observation)
N = number of atoms after time t
So, N = N₀e^-λt ..........................(1)
where λ is constant called disintegration constant
Let T = half life period
So, when t = T, N = N₀/2.
Substituing in Eq.(1), we have
\(\frac{\mathrm{N}_0}{2}\) = N₀e^-λt
e^λt = 2
λT = log_e2 = 2.303 log₁₀2
= 0.693
or T = \(\frac{0.693}{\lambda}\)

Question 39.
A neutron is absorbed by ⁶₃Li nucleus with the subsequent emission of an α-particle.
(i) Write down the correspondihg reaction.
(ii) Calculate the energy relased in MeV in this reaction given ⁶₃Li = 6.01516 u; mass (neutron) = 1.0086654 u mass (α) = 4.0026044 u and mass (triton) = 3.0100000 u. Take 1u = 931 MeV/c².
Answer:
(i) The nuclear reaction is:
¹₀n + ⁶₃Li → ⁴₂α + ³₁T

(ii) Decrease in mass = m (neutron) + m (Li) - m (α) - m (T)
∴ BE = [m (neutron) + m (Li) - m (α) - m (T)]c²
= [1.0086654 + 6.015126 - 4.0026044 - 3.0100000] uc²
= 0.0111870 uc²
= 0.0111870 x 931
= 1.0415097 MeV.

Question 40.
(a) Show that decay rate R of a sample of a radio nuclide is related to the number of radioactive nuclei N at that instant by the expression R = λN.
(b) The half life of ²³⁸₉₂U against α-decay is 1.5 x 10¹⁷ s. What is the activity of a sample of ²³⁸₉₂U having 25 x 10²⁰ atoms?
Answer:
(a) The decay rate R is equal to the number of radioactive disintegration in the sample taking place per second.
i.e. R = -\(\frac{d \mathrm{~N}}{d t}\) ..........................(i)
From the law of radioactive disintegration, the rate of disintegration \(\left[-\frac{d \mathrm{~N}}{d t}\right]\) is proportional to number of atoms present at that instant i.e.
\(-\frac{d \mathrm{~N}}{d t}\) ∝ N
or \(-\frac{d \mathrm{~N}}{d t}\) = λN
Using Eq. (i), we get:
R = λN

(b) Here T = 1.5 x 10¹⁷ s
Since λ = \(\frac{0.693}{T}=\frac{0.693}{1.5 \times 10^{-17}}\) s^-1
∴ R = λN
= \(\frac{0.693}{1.5 \times 10^{-17}}\) x 25 x 10²⁰ dis s^-1
= \(\frac{693 \times 25}{1.5}\) = 11550 atoms/s

Question 41.
(a) Draw the energy level diagram showing the emission of ß-particle followed by γ-rays by a ⁶⁰₂₇Co nucleus.
(b) Plot the distribution of kinetic energy of ß-particles and state why energy spectrum is continuous?
Answer:
(a) The energy spectrum of b-particles is continuous because an antineutrino is simultaneously emitted in β-decay: the total energy released in b-decay is shared by b-particle and the antineutrino so that momentum of the system may remain conserved.

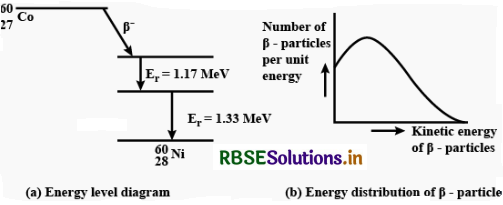
(b) Beta decay. The emission of electron ß-particle) from the nucleus of an atom is called ß-decay. It is believed that emission of an electron by the nucleus is due to transformation of a neutron into a proton and an electron. When a neutron changes into a proton, a ß-particle is ejected whereas a proton remains in the nucleus. The emission of ß-partic1e, therefore:

• increases the atomic number by one and
• keeps the mass number unaffected.

Question 42.
Estimate the ratio of the wavelength associated with the electron orbiting around the nucleus in the ground and first excited state of hydrogen atom.    
Answer:
Since de-Broglie hypothesis is related to Bohr’s atomic model as
nλ = 2πr
Since r ∝ n²
∴ r = a₀n²
So nλ = 2πa₀n²
Hence λ = 2πa₀n
∴ \(\frac{\lambda_1}{\lambda_2}=\frac{2 \pi a_0 1}{2 \pi a_0 2}=\frac{1}{2}\)

Question 43.
Write the nuclear reactions for the following:
(i) α-decay of ²⁰⁴₈₄Po
(ii) ß-decay of ³²₁₅P
(iii) ß+- decay to
Answer:
(i) ²⁰⁴₈₄Po → ⁴₂He + ²⁰⁰₈₂Hg
(ii) ³²₁₅P → _-1e⁰ + ³²₁₆S
(iii) ¹¹₆C → _-1e⁰ + ¹¹₅B

Question 44.
Calculate the binding energy per nucleon (in MeV) of the nucleus ⁵⁶₂₆Fe.
[Given: mass of ¹₁H = 1.00783 u, mass of ¹₀n = 1.00867 u, mass of ⁵⁶₂₆Fe = 55.934939 u. 1u = 931 MeV/c².
Answer:
B.E. of ⁵⁶₂₆Fe
= [^Z_mH+^{(A - Z)}_mN - m(^A_ZX)] 931.5
= [{26 x 1.007825 + (56 - 26) x 1.008665} - 55.934939] 931.5
= [{26.20345 + 30.25995} - 55.934939] 931.5
= 492.26 MeV

B.E. of 20983Bi
= [{83 x 1.007825 + (209 - 83) x 1.008665} - 208.980388] 931.5
= [{83.64975 + 127.09179 - 208.980388] 931.5
= 1640.1 MeV.
B.E. per nucleon = \(\frac{1640.1}{209}\) = 7.84 MeV
Fe⁵⁶ has greater binding energy per nucleon.

Question 45.
Give the mass number and atomic number of elements on the right hand side of the decay process:
²²⁰₈₆Rn → Po + He.

The graph shows how the activity of a sample of radon-220 changes with time. Use the graph to determine its half-life. Calculate the value of decay constant of radon-220.
Answer:
The given reaction is
²²⁰₈₆Rn → ²¹⁶₈₄Po + ⁴₂He
Mass number of Po = 216, He = 4
Atomic number of Po = 84, He = 2

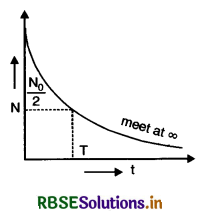
Half life
From the graph of decay of Rn - 220, we find that at t = 0, number of nuclei present = N₀ and at t = ∞, N₀ → 0
Since N = N₀ e^-λt ...................(i)
As at t = T, N = \(\frac{\mathrm{N}_0}{2}\)
∴ \(\frac{\mathrm{N}_0}{2}\) = N₀e^-λt
or λT = log_e2 = 2.303 log₁₀2
or T = \(\frac{2.303 \times 0.3010}{\lambda}=\frac{0.693}{\lambda}\)
From Eq. (i)
It t = \(\frac{1}{\lambda}\), then
N = N₀ e^{-λ.\(\frac{1}{\lambda}\)} = \(\frac{\mathrm{N}_0}{e}\)
So decay constant is the time after which the number of radioactive elements reduces to \(\frac{1}{e}\) times the initial number of atoms.

Question 46.
With the help of an example, explain how the neutron to proton ratio changes during alpha decay of a nucleus.
Answer:
For alpha decay, let us consider a nuclear reaction:
₉₂U²³⁸ → ₂He⁴ + ₉₀Th²³⁴
Initial neutron-proton ratio
= \(\frac{238-92}{92}=\frac{146}{92}\) = 1.59
Final neutron-proton ratio
= \(\frac{238-90}{90}=\frac{144}{90}\) = 1.57
∴ Neutron-proton ratio decrease during ß-decay.

Question 47.
When a deuteron of mass 2.0141 u and negligible kinetic energy is absorbed by lithium (⁶₃Li) of nucleus of mass 6.0155 u, the compound nucleus disintegrates spontaneously into two alpha particles, each of mass 4.0026 u. Calculate the energy in joules carried by each alpha particle. (1 u = 1.66 x 10^-27 kg).
Answer:
The reaction is:
²₁H + ⁶₃Li → ⁸₄Be → 2[⁴₂He]
∴ Mass defect, ∆m
= m (²₁H) + m (⁶₃Li) - 2m (⁴₂He)
= [2.0141 + 6.0155 - 2 x 4.0026] u
= 0.0244 u
= 0.0244 x 1.66 x 10^-27 kg
= 0.0405 x 10^-27 kg
∴ Binding energy Q = ∆mc²
= 0.0405 x 10^-27 x 9 x 10¹⁶
= 0.3645 x 10^-11 J
= 36.45 x 10^-13 J
This energy is equally shared by both the alpha particles.
∴ Energy carried by each alpha particle
= \(\frac{1}{2}\)[36.45 x 10^-13] = 18.225 x 10^-13 J

Question 48.
A radioactive nucleus ‘A’ undergoes a series of decays according to the following scheme:

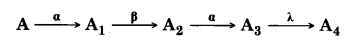
The mass number and atomic number of A are 180 and 72 respectively. What are these numbers for A₄.
Answer:
An α-particle is ₂He⁴, ß-particle is _-1e⁰ and α-particle makes no change in Z and A. Hence the given reaction proceed as:

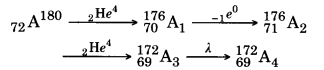
So the mass number A₄ is 172 and atomic number is 69.

Question 49.
(i) Define ‘activity’ of a radioactive material and write its S.I. unit.
(ii) Plot a graph showing variation of activity of a given radioactive sample with time.
(iii) The sequence of stepwise decay of a radioactive nucleus is:

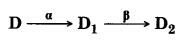
If the atomic number and mass number of D₂ are 71 and 176 respectively, what are their corresponding values for D?
Answer:
(i) The activity of a radioactive substance is defined as the rate at which the nuclei of its atoms in the sample disintegrate.
i.e. R = \(-\frac{d \mathrm{~N}}{d t}\)
The S.I. unit of activity is curie (i)
(ii) Graph between variation of activity of a given radioactive sample with time is shown in Fig SAQ 49.

(iii) The sequence of stepwise decay is as follow

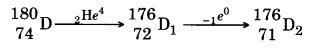
So atomic number and'mass number of D is 74 and 180 respectively.

Question 50.
What is the basic mechanism for the emission of ß^- or ß⁺ particles in a nucleide? Give an example by writing explicitly a decay process for ß^- emission. Is (a) the energy of the emitted ß-particles continuous or discrete; (b) the daughter nucleus obtained through ß-decay, an isotope or an isobar of the parent nucleus?
Answer:
Mechanism for emission of ß^-
Beta decay. The emission of electron ß-particle) from the nucleus of an atom is called ß-decay. It is believed that emission of an electron by the nucleus is due to transformation of a neutron into a proton and an electron. When a neutron changes into a proton, a ß-particle is ejected whereas a proton remains in the nucleus. The emission of ß-particle, therefore:
(i) increases the atomic number by one and
(ii) keeps the mass number unaffected.
The energy of ß-disintegration is provided by the difference between the mass of the parent nucleus and the sum of the masses by the daughter nucleus and ß-particles. The ß-disintegration energy is thus given by:
E_ß = _ZM_n^A - [_z+1M_n^A + m_e] ......................(1)
where
M_n = mass of nucleus
m_e = mass of electron
(A, Z) and (A, Z+ 1) mass number of atom i.e. number of parent and daughter nuclei.
i.e. n = p + \(\bar{e}\) + v (neutrino)
The ß⁺ emission
The atomic number decreases by one and the mass number remains unaffected
i.e. _zX^A → _z-1Y^A + ₁e⁰ + Q
i.e. p → n+ e⁺ +\(\bar{v}\) (antineutrino)
Example of ß^- decay
_zX^A → _z+1Y^A + _-1e⁰ + Q
i.e. ₉₀Th²³⁴ → ₉₁Pa²³⁴ + _-1e⁰. (ß^- -particle)
(a) Energy emitted through ß-decay is continuous.
(b) The daughter nucleus is isobar of the parent nucleus.

Long Answer Type Questions

Question 1.
Define the terms nucleus, nucleons, atomic number, mass number, nuclide, isotopes, isobars, isotones and isomers.
Answer:
Nucleus. A nucleus consists of protons and neutrons and the size of nucleus is about 10^-14 m. The protons and neutrons inside the nucleus go on interchanging to each other and hence called nucleons (i.e. protons or neutrons).

Nucleons. Protons and neutrons inside the nucleus of an atom are called nucleons.

Atomic number (Z). The number of protons in the nucleus is called atomic number of the element.

Mass number (A). Total number of nucleons in the nucleus is called mass number i.e. A = Z + N, so number of neutrons in the nucleus N = A - Z.

Nuclide. A nuclide is a specific nucleus of an atom characterised by its atomic number Z and mass number A Symbolically, nuclide is represented by _ZX^A

Isotopes. The atoms of an element which have same atomic number but different mass number are called isotopes, e.g. ₈O¹⁶, ₈O¹⁷,₈O¹⁸ are three isotopes of oxygen and ₁₇Cl³⁵, ₁₇Cl³⁷ are two isotopes of chlorine.

Isobars. The atoms having the same mass number but different atomic number are called isobars e g. ₁₈Ar⁴⁰, ₂₀Ca⁴⁰ and ₁H³, ₂H³. Isobars have the same numbers of nucleons.

Isotones. Atoms whose nuclei have the same number of neutrons are called isotones e.g. ₁₇Cl³⁷ and ₁₉Cl³⁹.

Isomers. The nuclei have the same atomic number and same mass number but in different energy states are called isomers e.g. a nucleus in its ground state and the identical nucleus in metastable excited state are isomers.

Question 2.
Define electron volt and atomic mass unit and find relation between them. Express atomic mass unit in MeV (or eV).
Answer:
Electron volt. It is the unit of energy. It is defined as the energy acquired by an electron when it is accelerated through a potential difference of one volt.
∴ 1eV = 1.6 x 10^-19 C x 1 V
1 eV = 1.6 x 10^-19 J
A unit, called million electron volt (MeV) is often used in atomic physics.
1 MeV = 10⁶ eV = 1.6 x 10^-13 J

Atomic mass unit. The atomic mass unit (written as amu) is 1/12th the actual mass of carbon ₆C¹².
As we know, 1 gram atom of an element contains 6.023 x 10²³ atom (Avogadro's number).
Thus 6.023 x 10²³ atoms of carbon weigh = 12 g
1 atom of carbon weighs = \(\frac{12 \times 10^{-3}}{6.023 \times 10^{23}}\) kg
Hence 1 amu = \(\frac{1}{12} \times \frac{12 \times 10^{-3}}{6.023 \times 10^{23}}\) kg
= 1.66 x 10^-27 kg

Relation between amu and MeV (or Energy equivalence of 1 amu.)
From Emstein's mass energy relation, we have E = m₀c².
where E is the energy equivalent of rest mass m₀ and c is the velocity of light. Thus,
1 amu = 1.66 x 10^-27 x (3 x 10⁸)² J
= \(\frac{1.66 \times 9 \times 10^{-11}}{1.6 \times 10^{-19}}\) (∵ 1 eV = 1.6 x 10^-19 J)
= 931 x 10⁶ eV
= 931 MeV.

Question 3.
(a) Write a note on the structure of the nucleus.
(b) Explain the properties of nucleus as regards nuclear charge, nuclear mass, nuclear size and density.
Answer:
(a) Strcture of nucleus. Rutherford's experiments on the scattering of α-particles by atoms led to the discovery of a positively charged heavy central core, called nucleus, of radius of the order of 10^-15 m.
1. The entire positive charge and almost the entire mass of the atom is concentrated in the nucleus.

2. Nucleus contains protons and neutrons called nucleons. A proton carries a unit positive charge and mass 1836 times that of an electron. The neutron is electrically neutral and has mass 1836.6 times that of an electron. The number of protons in the nucleus is called atomic number (Z) whereas the total number of neutrons and protons is called mass number (A).

3. Negatively charged electrons round the nucleus revolve in various orbits. The negative charge on the electron is of the same magnitude as the positive charge on the proton. The number of electrons revolving round the nucleus is equal to that of protons so that an atom is normally electrically neutral.

(b) Nuclear charge. The positive charge of the nucleus is due to the presence of protons. The charge on a proton is equal to 1.6 x 10^-19 C. If Z be the atomic number, then nuclear charge = Z x 1.6 x 10^-19 C.
The mass of the nucleus is equal to the sum of the masses of all protons and neutrons minus the mass defect.
Let Z = atomic number
A = mass number
Mn = mass of neutron
and ∆m = mass defect
Then the number of neutrons = (A - Z)
∴ Mass of the nucleus = ZM_p + (A - Z) M_n - ∆m.

Nuclear size. The distance of the closest approach of α-particle from. the nucleus is the measure of radius of nucleus or size of nucleus. For metals its value is about 10^-14 m.
The dimensiohs of nucleus have been measured by several experiments involving the scattering of n,p,e, etc. Every time it is found that the volume of nucleus is directly proportional to the number of nucleons (A) in the nucleus.
If R is the radius of the nucleus having mass number A, then
\(\frac{4}{3}\)π R³ ∝ A
or R³ ∝ A
or R ∝ A^1/3
or R = R₀A^1/3
where R₀ = 1.2 x 10^-15 m = 1.2 fm. It shows that greater the mass number, greater the nuclear radius.

Density of nucleus (ρ) It is defined as the nuclear mass per unit volume.

Thus the nuclear density is of the order of 10¹⁷ kgm^-3 and is independent of its mass number. Therefore, all nuclei have the same approximate density.

Question 4.
State and explain mass defect and packing fraction.
Answer:
Mass defect. It is found that the mass of a stable nucleus is always less than the sum of masses of its constituent protons and neutrons in their free state. The difference between the sum of the masses of nucleons constituting it and the rest mass of the nucleus is called mass defect.
Let
M_p = mass of protons in the nucleus
M_n = mass of neutrons in the nucleus
M = mass of nucleus
N = number of neutrons
Z = number of protons
A = total number of nucleous
∴ The mass defect
∆m = ZM_p + (A - Z) M_n - M.

Packing fraction (f). Though the atomic masses are considered to be whole numbers, yet they differ from the integers by small amount. This variation of atomic masses from whole numbers is considered to be due to some deviations of the mass of the nucleus from the mass of the constituents of the nucleus (i.e. protons and neutrons). The term packing fraction is defined as the mass defect per nucleon.
∴ f = \(\frac{\text { mass defect }}{\text { mass number }}=\frac{\Delta m}{\mathrm{~A}}=\frac{\mathrm{M}-\mathrm{A}}{\mathrm{A}}\)
where M is the atomic mass, A is the mass number (i.e. number of protons and neutrons in a.m.u.)
Thus f can be +ve, -ve or zero accordingly as M > A, M < A, M = A.
Packing fraction is a fundamental characteristic of the nucleus and is directly related to the availability of the energy of the nucleus and its stability. A negative packing fraction which will also correspond to a negative mass defect will mean that the atomic mass of the nucleus is less than the nearest whole number which will correspond to some conversion of mass into energy during the formation of the nucleus. Also, negative packing fraction will imply that the nucleus is exceptionally stable because we have to supply more energy to break the nucleus into its constituent nucleons while a positive packing fraction will indicate the nucleus to be less stable.

Question 5.
State and explain binding energy of a nucleus.
Answer:
Binding energy. The binding energy of a nucleus may be defined as the energy required to break up a nucleus into its constituent protons and neutrons at infinite distance apart.
Or
Binding energy in terms of mass defect can be defined as the energy equivalent to the mass defect, is called binding energy of the nucleus.
If ∆m is the mass defect, then
Binding energy, B.E. = ∆m c² (in joule)
If mass defect is in a.m.u. then
B.E. = (∆m x 931.5) M eV.

Expression for binding energy. The mass defect (∆m) of a nucleus containing Z protons and (A - Z) neutrons is given by

Expression for binding energy. The mass defect (∆m) of a nucleus containing Z protons and (A - Z) neutrons is given by
∆m = Zm_p + (A - Z) M_n - M ..........................(1)
where M is mass of the nucleus.
so M = (Zm_p + (A - Z) M_n) - ∆m ..........................(2)
Since mass of atom m _ZX^A is given by
M = m_N + ZM_e
Using the value of mN from Eq. (2), we get
M = [ZM_p + (A - Z) M_n] - ∆m + ZM_e
or Mass defect,
∆m = Z (M_p + M_e) + (A - Z) M_n - M
or ∆m = ZM_H + (A - Z) M_n - M
∴ B.E. = ∆Mmc²
or B.E. = [ZM_H + (A - Z) M_n - M] c²

Question 6.
Define binding energy per nucleon. Draw a curve between binding energy per nucleon and the mass number. From the curve state, which portion of the curve indicates possibilities of release of energy and by what process?
Answer:
Binding energy per nucleon. Binding energy per nucleon is the average energy required to extract one nucleon from the nucleus.
∴ B.E. per nucleon = \(\frac{\mathrm{B} \cdot \mathrm{E}}{\mathrm{A}}=\frac{\Delta m c^2}{\mathrm{~A}}\)

Binding Energy Curve. The graph between the binding energy per nucleon and the mass number A is called binding energy curve and is shown in Fig. LAQ 6.

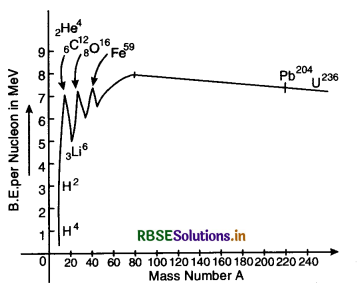
Conclusions
1. The binding energy per nucleon is very low for light nuclei such as deuteron (₁H²), helium (₂He³) etc.

2. The binding energy per nucleon rises rapidly with increasing volume of A upto A ≅ 20.

3. There exists peaks in the curve corresponding to mass numbers A = 4, 12, 16, 20. The nuclei corresponding to those mass numbers are ₂He⁴, ₆C¹²,₈O¹⁶, ₁₀N²⁰. The peaks indicate that these nuclei have more binding energy per nuejeon than their immediate neighbours. So they are more stable nuclei.

4. The binding energy per nucleon increases gradually hum mass number A = 20 to mass number A = 40.

5. The curve is almost flat between mass number 40 and 120. This means that the variation in binding energy per nucleon in the range is small (about 10%). The average binding energy per nucleon in this region is about 8.5 MeV. It is maximum for iron (₂₆Fe⁵⁹) and has a value 8.8 MeV.

6. The binding energy per nucleon decreases slowly and continuously from A = 120 to A = 240. It reaches a value of 7.6 MeV at A = 238. This decrease is due to the increased coulomb potential energy of protons in the nucleus.

7. Binding energy per nucleon is smaller for light and heavier nuclei i.e. light and heavier nuclei are less stable than middle one. In ordier to attain higher value of binding energy per nucleon, the heavier nuclei may split into lighter nuclei (process of fission) and lighter nuclei may unite to form heavier nuclei (process of fusion). In both these nuclear processes, a large amount of energy is released.

Question 7.
Describe how neutron was discovered.
Answer:
Discovery of Neutron

Various experiments
1. In 1930, Bothe and Becker, found that when Beryllium was bombarded by α - particles, no protons were ejected as expected. Instead, a highly penetrating type of radiation was emitted. They assumed this radiation to be γ-rays and gave the following nuclear reaction:
₄Be⁹ + ₂He⁴ → (₆C¹³) → (₆C¹³) + hv (7MeV)

2. In 1932, Joliot and Curie found that these radiations could knock out protons from paraffin wax. Energy measurement showed that for ejection of protons incident radiation must have energy of 55 MeV and not just 7 MeV.


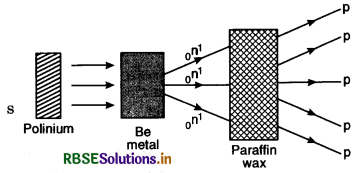
3. In 1932, Chadwick performed an experiment in which α-particle emitted from polinium source were made to bombard on Be metal. Highly penetrating radiations were found to come out of Be metal and when these radiations were made to fall on hydrocarban like 'paraffin wax', high energy protons were knocked out from the paraffin wax as shown in Fig. LAQ 7. Chadwick concluded that these penetrating radiations consisted of neutral particles having mass nearly that of protons. These particles were called neutrons.
The nuclear reaction may be written as
₄Be⁹ + ₂He⁴ → (₆C¹³) → ₆C¹² + ₀n¹
where 0n1 represents the neutron with mass 1 u and no charge.

Properties of neutron.

1. Neutron is elementary particle having mass equal to 1.6748 x 10^-27 kg.
2. It is an uncharged particle and hence the electric and magnetic fields have no influence on it.
3. It possesses very high penetrating power due to its neutral character.
4. It possesses very low ionising power (again due to its neutral character).
5. The neutrons can be slowed down by passing them through heavy water, paraffin wax, graphite etc. This happens due to the scattering of the neutrons. The scatterers are commonly known as moderators.
6. The slow neutrons, also known as thermal neutrons are found to be more efficient in causing nuclear reactions.
7. Neutron is a stable particle within the nucleus. However, outside the nucleus, the neutron is an unstable particle. Its half life period is about 12 minutes. It decays according to the following scheme:
   ₀n¹ → ₁H¹ + _-1e⁰ + \(\bar{v}\),
   where \(\bar{v}\) is called antineutrino.

Question 8.
Describe forces which keep nucleons bound together giving their definitions, properties and theory.
Answer:
The forces that keep the nucleons bound together in a nucleus, are called nuclear forces.

Nuclear force. We know that inside the nucleus there are protons and neutrons and the coulomb's force of repulsion is about 10³⁶ times as large as the gravitational force of attraction between two protons. Hence the nucleus should not be stable, but we find that the nucleus is very stable, it means that there must be a third type of force which is stronger than the coulomb's force and exist in the nucleus which is responsible for binding the nucleons together in the nucleus. This force is called nuclear force and it is about 100 times stronger than the coulomb's force.

Properties.

1. They are strong attractive forces and exist between two protons, between two neutrons and between a proton and a neutron.
2. They are charge independent. Force between two protons = force between two neutrons = force between a proton and neutron.
3. They are spin dependent. It is more between nucleons having spin in the same direction and less between those having spin in opposite directions.
4. They are short range forces. It is effective only upto a distance of 10 x 10^-15 m (10 fermi) and zero beyond it. Hence it is not extended from one nucleon to all nucleons of the nucleus.
5. They vary with distance. They start acting only when distance between nucleons becomes 10 fermi. As distance decreases, force increases. Increase is slow upto 5 fermi and then rapid. Force is maximum at distance 15 fermi (Fig. LAQ 8)

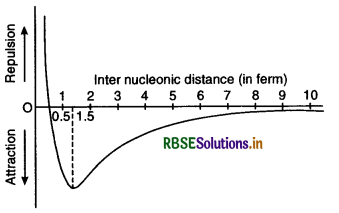
At lesser distances, repulsive forces start acting, decreasing the attractive force.

Question 9.
What is radioactivity? What is the difference between natural and induced radioactivities? Give the properties of different types of rays emitted by radioactive substances.
Answer:
Radioactivity. The phenomenon of spontaneous disintegration of the nucleus of an atom with the emission of some radiations is called radioactivity. There are a number of heavy elements occurring in nature whose nuclei are unstable and undergo spontaneous disintegration with emission of some radiations. The rate of emission or intensity of radiations is not influenced by any external agency such as the temperature or pressure. The substances having this property are called radioactive substances.

Natural and induced (or artificial) radioactivities. The radioactivity exhibited by some naturally occurring elements is called natural radioactivity. All elements with atomic number greater than 82 are radioactive. It is, however, possible to induce radioactivity in the elements with atomic number less that 83 by artificial means. This type of radioactivity is called induced or artificial radioactivity.

Properties of α-rays

1. The α-rays are shot out from the radioactive material with large velocities ranging from 1.4 x 10⁷ to 2.3 x 10⁷ ms^-1.
2. They produce ionisation in the gas through which they pass. The ionising power is 100 times greater than that of ß-rays and 10,000 times greater than that of γ-rays.
3. They affect a photographic plate. The effect is very-very feeble.
4. They produce fluorescence in substances like zinc sulphide, barium platinocyanide etc.
5. The α-rays are scattered when they pass through thin sheets of mica, gold foil etc. The angle of divergence of α-particles from its straight path is 2 to 3 degrees. Geiger and Marsaden found that a few particles, sometimes, were deflected by more than 20°. This was explained by Rutherford to be due to the repulsion between α-particle and the positively charged nucleus of the atom.
6. The α-rays are deflected by electric and magnetic fields showing that they are charged particles as shown in in Fig. LAQ 9.
7. They produce a heating effect. A quantity of radium always maintains itself at a temperature higher than that of the surroundings. The evolution of heat is due to the stoppage of α, ß and γ rays by the radioactive substance.
8. The body suffers incurable burns when exposed to α-rays.

Properties of ß-rays

1. ß-rays are shot out from radioactive elements with very high velocities ranging from 1% to 99% of the velocity of light. The velocity of all ß-particles given out by an element is not the same.
2. They produce ionisation in air but the number of ions produced is very less than those of α-rays. Although their velocity is very large they possess a comparatively small mass than that of α-particle and hence they have small kinetic energy. As ß-particles are slowed down by collision with the atoms of the gas and change their path, their tracks in a Wilson Cloud Chamber are scattered and not continuous as those of α-particles.
3. They affect a photographic plate and their effect is greater than those of α-rays.
4. ß-rays produce fluorescence in barium, platinocyanide, calcium, tungsten, willemite etc.
5. Because of their small mass, they can penetrate through large thickness of matter, e.g., they can easily pass through 1 cm of thick aluminium sheet.
6. They are more easily scattered when they pass through matter, because their mass is very small as compared to the mass of the atomic nuclei.

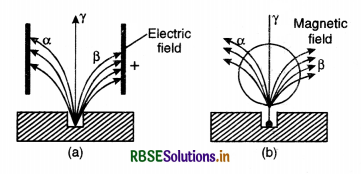
Properties of γ-rays

1. The velocity of γ-rays is the same as that of , light i.e. 3 x 10⁸ ms^-1.
2. They produce ionisation in gases through which they pass but their effect is very small as compared to that of α-rays and ß-rays. This is due to the fact that their mass is very small as compared to that of α and ß-ray particles.
3. They affect photographic plate and their effect is greater than those for ß-rays.
4. They produce fluorescence in barium, platinocyanide, etc.
5. They are more penetrating that even ß-rays and can pass very easily through 30 cm thickness of iron.
6. They are diffracted from crystals in a way similar to X-ray diffraction.
7. They are not affected by electric and magnetic fields. This shows that they are neutral particles; further experiments have shown that they are similar to e.m. rays.
8. γ-rays can be absorbed by the matter.

Question 10.
Write down the laws of radioactive disintegration and deduce an expression for the decay law. Hence define disintegration constant.
Or
State the laws of radioactive decay and hence derive the relation N = N₀e^-λt where the letters have their usual meanings.
Answer:
Laws of Radioactive disintegration

1. Radioactivity is spontaneous process which does not depend upon external factors.
2. During disintegration either α or ß-particle is emitted. Both are never emitted simultaneously.
3. Emission of α-particle decreases atomic number by two and mass number by 4.
4. Emission of ß-particle increases atomic number by one but mass number remains the same.
5. Emission of γ-ray does not change atomic or mass number.
6. The number of atoms disintegrated per second is directly proportional to the number of radioactive atoms actually present at that instant. This law is called radioactive decay law.

Let at t = 0
N₀ = number of atoms present
N = number of atom left after time t.
dN = number of atoms disintegrated in time dt.
i.e. \(-\frac{d \mathrm{~N}}{d t}\) ∝ N
or \(-\frac{d \mathrm{~N}}{d t}\) = λN, ............................(i)
where λ is a constant called disintegration constant and depends upon the nature of the radioactive substance.
Now from, (i), we have
\(\frac{1}{N}\)dN = -λ dt
or ∫\(\frac{1}{N}\) dN = -λ∫ dt
or log_eN = λt + C, ................................(ii)
where C is constant of integration. To determine its value,
since N = N₀ initially,
i.e. when t = 0, N = N₀
log_eN₀ = 0 + C
Substituting the value of C in (ii), we have
log_eN = -λt + log_eN₀
or log_eN - log_eN₀ = -λt
log_e\(\frac{\mathrm{N}}{\mathrm{N}_0}\) = -λt
or \(\frac{\mathrm{N}}{\mathrm{N}_0}\) = e^-λt
or N = N₀ e^-λt ...........................(iii)
which is the required equation.
Eq. (iii) shows that the radioactive decay occurs according to exponential law and the number of radioactive atoms decreases exponentially. Since N shall become zero only when t becomes infinity, it shows that time taken by a radioactive element to disintegrate completely is infinitely long.
The curve in Fig. LAQ 10. shows the exponential decay radioactive substance.

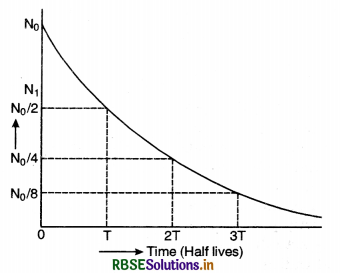
Disintegration constant
In Eq. (iii), if t = 1/λ
Then N = N₀ e^{-λx\(\frac{1}{\lambda}\)} = N₀e^-1 = \(\frac{\mathrm{N}_0}{e}\)
Thus disintegration constant is defined as the time after which the number of radioactive atoms reduce to 1/e times the original number of atoms.

Question 11.
What is meant by (i) half life Band (ii) average life of a radioactive substance? Derive expression for them. What is relation between average life and half life.
Answer:
(i) Half life period. It is the time during which the number of atoms of a radioactive material reduces to half of the original number.
Let N₀ = number of atoms at t = 0 (at the start of the observation)
N = number of atoms after time t
So, N = N₀e^-λt ........................(1)
where λ is constant called disintegration constant
Let T = half life period
So, when t = T, N = -N₀/2.
Substituting in Eq, (1), we have
\(\frac{\mathrm{N}_0}{2}\) = N₀e^-λt
e^λt = 2
λt = log_e2 = 2.303 log₁₀2
= 0.693
or T = \(\frac{0.693}{\lambda}\)

(ii) Average life. The atoms of a radioactive substance are constantly disintegrating and thus the life of every atom is different.
So average life of a radioactive substance is the ratio of sum of lives of all the atoms to the total number of atoms.
Average life =

Suppose dN atoms disintegrate in a time dt, t seconds after the separation of the substance, when the actual number of atoms present is N.
Then \(\frac{d \mathrm{~N}}{d t}\) = -λN
dN = -λNdt = -λN₀e^-λt dt
where N₀ is the number of atoms in the beginning of time. Each of these dN atoms disintegrate between the time t and t + dt i.e these atoms had a life of t seconds.
∴ Total life of dN atoms = t dN
Hence total life time of all the atoms

Hence average life τ_a of the atom is the reciprocal of the radioactive disintegration constant λ.

Relation between average life and half life
Since average life of a radioactive element is given by
τ_a = \(\frac{1}{\lambda}\) ...........................(i)
and half life of a radioactive element is given by
T = \(\frac{0.693}{\lambda}\)
Using Eq. (i), we get
T = 0.693 τ_a.

Question 12.
What is meant by the Alpha decay? Estimate the velocity or energy of α-particle.
Answer:
Alpha decay
Alpha decay is a process involving the emission of a fast-moving helium nucleus (an alpha-particle) by nuclei which generally contain 210 or more nucleons.
Since ₂He⁴ contains two protons and two neutrons, after an alpha emission the parent nucleus is transformed into a daughter nucleus which has (i) an atomic number smaller by two and (ii) mass number smaller by four.
Transformation of the _ZX^A nucleus into the _Z-2X^A-4 nucleus by an alpha decay can be expressed by the equation.
_ZX^A = _Z-2Y^A-4 + ₂He⁴ ...........................(1)

Energy released. The energy Q, released in this process, can be obtained from Einstein's mass energy relation.
It is given by the expression
Q = (M_X - M_Y - M_α) c²
This energy is shared by the daughter nucleus, _Z-2Y^A-4 and the alpha-paraticle, ₂He⁴.
As the parent nucleus _ZX^A is at rest before it undergoes alpha-decay, alpha-particles are emitted with fixed energy, which can be calculated by applying the principle of conservation of energy and momentum.
Let v_α and v_y be the velocities of the alpha-particles and the daughter nucleus, _Z-2Y^A-4. According to the principle of conservation of momentum,
M_Y. v_Y = M_α. v_α ..................(2)
By equating the sum of kinetic energies of the nucleus Y and the alpha particle of the released in the alpha-decay, we have another equation.
\(\frac{1}{2}\) M_α.v_α² + \(\frac{1}{2}\) M_Yv² = Q .........................(3)
By substituting for v_y from Eq. (2) in Eq. (3), we can easily obtain

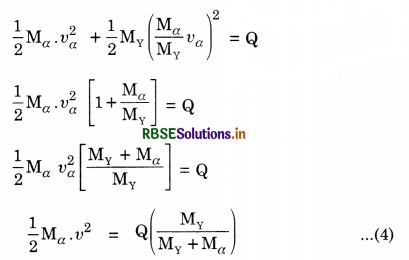
If we substitute M_y = A - 4 amu and M_α = 4 amu in Eq. (4) the kinetic energy carried by the alpha-particle can be approximated by the relation.
[K.E.]_α = Q\(\frac{(\mathrm{A}-4)}{\mathrm{A}}\) .......................(5)

Question 13.
What is beta decay? Write a brief account of ß-particle spectrum.
Answer:
Beta decay. The emission of electron (ß-particle) from the nucleus of an atom is called ß-decay. It is believed that emission of an electron by the nucleus is due to transformation of a neutron into a proton and an electron. When a neutron changes into a proton, a ß-particle is ejected whereas a proton remains in the nucleus. The emission of ß-particle, therefore:

• increases the atomic number by one and
• keeps the mass number unaffected.

The energy of ß-disintegration is provided by the difference between the mass of the parent nucleus and the sum of the masses by the daughter nucleus and ß-particles. The ß-disintegration energy is thus given by:
E_ß = _ZM_n^A - [_Z+1M_n^A + m_e] ........................(1)
where
M_n = mass of nucleus
m_e = mass of electron
(A, Z) and (A, Z + l) = mass number of atom i.e. number of parent and daughter nuclei.

Theory of ß-particle Spectra
According to Eq. (1) the same mass disappears during the emission of a ß-particle and all ß-particles must be emitted with the same energy. But actually it is found that
(1) ß-particle emitted by a radioactive substance has a continuous energy range, extending from zero to a certain maximum. The upper energy level is called the end point energy and is the characteristic of nature of ß-emitter Fig. LAQ 13 shows the spectrum of the ß-particles emitted with end point energy 1.17 MeV.
(2) Every ß-particle energy distribution curve has a well defined maximum whose height and position depend upon the nature of ß-emitter.

Pauli suggested that in ß-particle disintegration, another particle neutrino was simultaneously emitted along with ß-particle. The neutrino is supposed to be fundamental particle having:
(i) zero charge
(ii) zero rest mass, and
(iii) a spin of \(\frac{1}{2} \cdot \frac{h}{2 \pi}\)

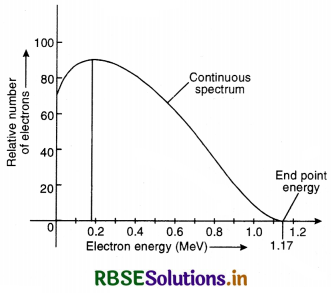
A ß-decay can thus be represented as
n → p + e^- + v (neutrino)
Under neutrino hypothesis, each ß-decay is accompanied by discrete energy E_ß which corresponds to the end point energy in the continuous ß-particles spectrum. The disintegration energy is shared by ß-particle, neutrino and the recoil nucleus in a continuous range of different ways. The neutrino may take any amount of the available ß-disintegration energy so that the energy left at the disposal of the ß-particle will be different for each disintegration. Thus ß-particles of all possible energies extending from zero to a certain maximum (end point energy) shall be emitted. Thus Pauli's neutrino hypothesis satisfactorily explains the continuous energy range of ß-particle spectrum.

It was found late that ß-decay is accompanied by two kinds of neutrinos, the neutrino (v) and antineutrino (\(\bar{v}\)). In ordinary ß-decay, it is an antineutrino that is emitted.
n → p + e^- + \(\bar{v}\)

Question 14.
What is gamma decay? Write a short note on the energy distribution in gamma ray spectrum.
Answer:
Gamma decay. The emission of high energy photons, also called gamma rays, by a radioactive substance is called gamma decay.

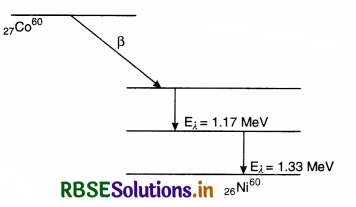
The emission of an alpha or beta particle by a radioactive nucleus often leaves the product nucleus in an excited state. The excited nuclei return to their ground state by emitting γ-rays whose energies correspond to the energy differences between the various excited states and the ground state. The γ-rays emitted by the nuclei have an energy range upto several MeV. The γ-rays emitted by a source thus possess discrete, though different energies and gamma ray energy spectrum consists of sharp lines of definite wavelength.
γ-rays are uncharged, they suffer weak interaction with matter and are not easily detected.
A well known example of such a process is decay of ₂₇Co⁶⁰. By beta-emission, the ₂₇Co⁶⁰ nucleus is first transformed into the excited ₂₈Ni⁶⁰ nucleus, which in turn reaches the ground state by emitting photons of energies 1.17 MeV and 1.33 MeV. In Fig. 13.20 this process has been shown through an energy-level diagram.

Question 15.
What is rate of decay? What are the units of measuring radioactivity?
Answer:
Rate of Decay (R). It is equal to the number of radioactive disintegrations in the sample taking place per second. Mathematically, it is represented as:
R (t) = \(\frac{d \mathrm{~N}}{d t}\) = λN (t) ....................(1)

Unit of measuring radioactivity
Radioactivity is measured by the number of radioactive nuclei that decay per second. The two units of radioactivity are curie (ci) and rutherford (rd).
(i) Curie. It is the radioactivity of 1 gram of radium. One gram of radium gives only 3.7 x 10¹⁰ disintegrations per second. Therefore, the radioactivity of a sample is said to be 1 curie if it undergoes 3.7 x 10¹⁰ disintegrations per second.
∴ 1 ci = 3.7 x 10¹⁰ disintegrations, and 1µ ci= 3.7 x 10⁴ disintegrations.

(ii) Rutherford (rd). The radioactivity of a material is said to be 1 rutherford if it undergoes 106 disintegrations per second. Thus
1 rd = 10⁶ disintegrations
∴ 1 µ ci = 3.7 x 10⁴ rd and 1 m ci = 37 rd.

Question 16.
What do you mean by nuclear reaction? What quantities are conserved in nuclear reaction? What is Q-value of nuclear reaction?
Answer:
Nuclear Reaction
The conversion of the nucleus of an element into a nucleus of another element is called a nuclear reaction. This is generally caused by bombarding the target nucleus by high energy particle.

For example, if an incident projectile ‘a’ hits the target nucleus X, a nuclear reaction takes place and as a result there is a new nucleus Y and an outgoing particle ‘b’ are produced.
i.e. a + X → Y + b
In short form, this reaction can be written as X (a,b) Y.
In 1919, Rutherford observed that when α-particles, from a polonium source were made to hit nitrogen atom, protons were given off in the reaction. The nuclear reaction for this process can be written as
₇N¹⁴ + ₂He⁴ → ₈O¹⁷ + H¹
The above reaction can also be written as ₇N¹⁴ (α,p) ₈O¹⁷. 
Following quantities remain conserved during a nuclear reaction.

1. Conservation of charge. Total charge of the reactant is conserved.
2. Conservation of nucleons. Total number of nucleons before and after the reaction remains constant.
3.  Mass and energy conservation. In a nuclear reaction mass and energy are not separately conserved. However, their total is always conserved i.e. the energy equivalent of mass is liberated as can be understood in the Q-value of the nuclear reactions.
4. Conservation of linear momentum. It is a fundamental law and is always conserved in nuclear reactions also.
5. Conservation of angular momentum. Total angular momentum J is composed of orbital angular momentum L and spin angular momentum S. Vector sum of the total angular momentum is conserved in a nuclear reaction.

Q-Value of a nuclear reaction
Consider a nuclear reaction represented by the equation
a + x → y + b
where target nucleus ‘x’ is supposed to be at rest initially. Since the total energy of the system is to be conserved. Let the mass of projectile ‘a’, target nucleus x, product nucleus y and product particle ‘b' be represented as m_a, M_x, M_y and m_a respectively. Then from the law of conservation of total energy, we have
(E_a + m_ac²) + M_xc² = (E_y + M_yc²) + (E_b + m_p c²) .......................(1)
Where E’s correspond to the kinetic energies. Let us introduce a quantity called Q-value of the nuclear reaction, which represents the difference of energy of the products and the reactants.
i.e. Q = E_y + E_b - E_a
So Eq. (1) may take the form
(m_a + M_x - M_y - m_b) c² 
= E_y + E_b - E_a = Q
or Q = [(m_a +M_x) - (M_y + m_b)] c²
Thus Q-value of a nuclear reaction is defined as the energy available from the difference in mass of the projectile plus the target and the product nucleus and the product particle.
If (m_a + M_x) > (M_y + m_b), then Q > 0 and the reaction releases energy called exoergic reaction. If (m_a + M_x) < (m_y + m_b), then Q < 0 and the reaction absorb energy and called endoergic reaction.

Question 17. 
What is nuclear fission? Discuss the source of energy released during fission.
Answer:
Nuclear fission. A process in which a heavy nucleus disintegrates into two lighter nuclei of nearly equal masses, is called nuclear fission

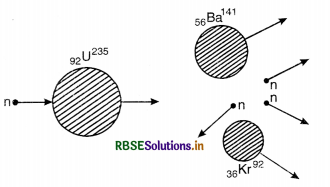
Slow neutrons were bombarded on a heavy nucleus of ₉₂U²³⁵ yielding two lighter nuclei of barium (₅₆Ba¹⁴¹) are krypton (₃₆Kr⁹²) along with three neutrons and tremendous amount of energy (Fig. LAQ 17). The nuclear reaction can be represented as follows:
₉₂U²³⁵ + ₀n¹ → ₅₆Ba¹⁴¹ + ₃₆Kr⁹² + 3 ₀n¹ + Q
Energy released in fission. This huge energy is provided by the difference of mass of the nuclei before and after fission.
Before fission:
Mass of ₉₂U²³⁵ = 235.0439 a.m.u.
Mass of one ₀n¹ = 1.0087 a.m.u.
Total mass of reactants = 236.0526 a.m.u.
After fission. Mass of ₅₆Ba¹⁴¹ = 140.9139 a.m.u.
Mass of ₃₆Kr⁹² = 91.8973 a.m.u.
Mass of 3 neutrons = 3.0261 a.m.u
Total mass of reaction products = 235.8373 a.m.u.
Mass lost in fission = 236.0526 - 235.8373 = 0.2153 a.m.u.
This mass is converted into energy in the fission process. Thus, energy released in a single fission = 2153 x 931 = 200 MeV
This energy appears mainly in the form of kinetic energy of fission fragments and secondary neutrons. It may be subsequently converted into heat. The nuclear fission is important reaction for two reasons.

• A large amount of energy about 200 MeV is released in fission of each nucleus.
• The reaction is accompanied by emission of secondary neutrons.

Theory. Bohr and Wheeler gave the explanation of the nuclear fission based on the liquid drop model of the nucleus. The nucleus is considered to be spherical in shape and is acted upon by two kinds of forces.

• The surface tension force (maintaining its spherical shape)
• The coulomb's repulsive force (tending to deform the shape).

When these spherical nuclei are bombarded by slow neutrons, results in its capture and form a compound nucleus and sets oscillations in the nucleus tending to deform its shape and the surface tension forces try to keep it spherical, but if the effect of coulomb’s force is increased, the nucleus ultimately splits into two parts of comparable masses and few neutrons. The sequence of steps leading to fission is as shown in Fig LAQ 17 (a).

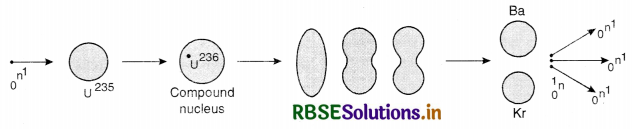
Question 18.
Explain the meaning of ‘chain reaction’ and controlled ‘chain reaction’.
Answer:
Nuclear chain reaction. In fission reaction, on the average three neutrons are emitted. These three neutrons can further produce fission of three more uranium nuclei and so on. This can lead to a chain reaction and within no time a large number of uranium can undergo fission resulting in the enormous amount of energy.

It is also possible that one or more neutrons produced during fission may escape out of uranium piece or may be absorbed and get lost. The chain reaction can be sustained only if, on the average, more than one neutron per fission are available to cause further fission as shown in Fig. LAQ 18. The escape of neutrons which do not cause further fission depends upon following factors.

1. Leakage of neutrons from the system. If the size of the fissionable material is small, then the incident neutrons escape and the chain reaction will not be sustained. So for a sustained nuclear chain reaction, the number of neutrons lost must be equal to the number of neutrons produced and the system is said to be critical. For a material to be of critical size, its linear dimension, should be of the order of mean free path of the neutrons.

2. Presence of non-fissionable material in the system. The non-fissionable material present in the sample of U²³⁵ can slow down the incident neutrons and they get absorbed without causing further fission. Thus to have sustained chain reaction, the fissionable material should be free from such impurities.

3. Absorption of neutrons by U²³⁸. In a sample of uranium, there are three isotopes namely U²³³, U²³⁵ and U²³⁸ having abundance of 0.006%, 0.714% and 99.28%. If neutrons are made to bombard on such a material, they are slowed down by collision with U²³⁸ and are thus absorbed. U²³⁸ is also fissionable but require the energy of incident neutrons more than 1 MeV, where as U²³⁵ is fissionable with neutrons having energy of the order of 0.025 eV. Thus for self-sustained chain reaction to take place either U²³⁸ is seprated from U²³⁵ (this is called enriched uranium) or moderators be used to slow down the neutrons to energy about 0.025 eV to cause fission in U²³⁵.

Question 19.
Explain the process of release of energy in a nuclear reactor. Draw a labelled diagram of a nuclear reactor and write down the function of each part.
Or
What is controlled nuclear chain reaction? Describe a nuclear reactor and the function of each component.
Answer:
Nuclear Reactor. Uncontrolled chain reaction causes a lot of damage. If the chain reaction is controlled in such a way that on the average, one neutron from each fission is left to excite further fission, the number of fissions occurring per second thus remains constant. In such cases, energy will not get out of control. Such a system in which the arrangement for absorption of desired number of neutrons is provided so that the chain reaction may proceed in a controlled manner, is called a nuclear reactor. Thus nuclear reactor is a device in which a controlled chain reaction produces radioactive isotopes and energy.
A nuclear reactor consists of following parts:

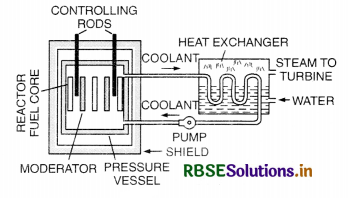
1. Nuclear Fuel. Nuclear fuel is a material such as U²³⁵, U²³³, Pu²³⁹ which is fissionable by thermal neutrons. Out of these materials only U²³⁵ is available in nature mixed with U²³⁸. Nuclear fuel is fabricator of the form of rods which are sealed in aluminium containers. The containing nuclear fuel are called fuel elements.

2. Moderator. The fuel elements are placed parallel to each other separated by some material known as moderator as shown in Fig. LAQ 19 (b). The purpose of a moderator is to slow down the fast neutrons emitted in fission. Most of these neutrons have energies in the range 1 MeV to 2 MeV. The energy of fast neutrons is reduced to thermal value (0.25 eV) as a result of many collisions with the atoms of the moderator. The material of the moderator should:

• have low mass number.
• not absorb neutrons
• be physically and chemically stable in the high temperature conditions in the reactor.

Graphite and heavy water fulfil these conditions and are mostly used as moderators.

3. Control rods. The chain reaction is controlled by means of control rods. The control rods are made of materials which intensely absorb neutrons. These rods can be inserted into the core partially or completely.
The part of reactor which contains fuel elements moderator and control rod is called core. The chain reaction takes place in the core and hence the energy is liberated in it.

4. Coolant. The cooling fluid which removes heat is called coolant. These are water, CO₂ and liquid metal. The heat carried away by the coolant is used to generate steam which in turn operates generators.

5. Shielding. To prevent the escape of high energy radiation from the core, it is surrounded by a layer of thick concrete containing a high proportion of light and high thick elements.

• They are used to produce electric energy.
• They are used to prepare radio isotopes.
• It can generate power for propulsion of ships, submarine and aircrafts.
• It produces plutonium for explosive purpose.

Working. Neutrons produced by the action of α-particles on polonium or beryllium are slowed down and are used initially to bring about fission of say U²³⁵ nuclei. The emitted neutrons are slowed down by the passage through the moderator to split further U²³⁵ nucleus. The chain reaction is said to be steady so that effective multiplication factor K_e is 1.
K_e = \(\frac{\text { Rate of emission of neutrons }}{\text { Rate of loss of neutrons }}\)
Some lost neutrons are absorbed by ₉₂U²³⁸ present in enriched uranium which gives rise to ₉₂U²³⁹.
₀n¹ + ₉₂U²³⁸ → ₉₂U²³⁹ → _-1ß⁰ + ₉₃Np²³⁹
₉₃Np²³⁹ → _-1ß⁰ + ₉₄Pu²³⁹ → ₉₂U²³⁵ + ₂He⁴
₉₄Pu²³⁹ is produced as a bye product and can be used for fission purpose. India used ₉₄Pu²³⁹ in nuclear device which was exploded on 18th May 1974 and later on May 11 & 13, 1998 at Pokhran.

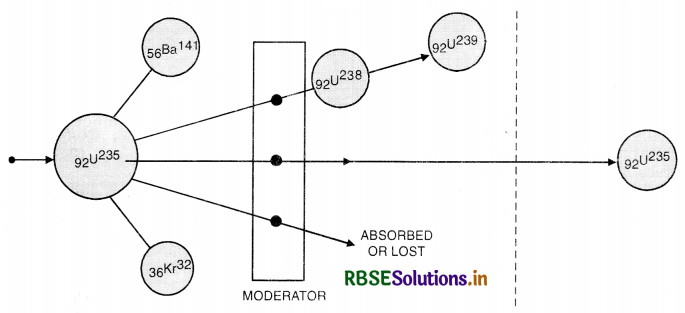
Uses. A nuclear reactor is used for generation of electricity, preparation of radio isotopes. Most of energy set free is in form of heat which through heat exchange is made to furnish steam to operate conventional turbines and electric generators.

Question 20.
(a) Explain nuclear fusion. What are the conditions for fusion?
(b) What are the sources of energy in sun and stars?
Answer:
(a) Nuclear fusion. Nuclear fusion is process in which lighter nuclei (like ₁H¹) are fused together into heavier atom (like ₂He⁴), with the release of enormous amoun t of energy. The energy thus released is known as thermonuclear energy and the reaction is called thermonuclear reaction. The cause of energy is again mass defect. Nuclear fusion takes place at very high temperature and very high density.
e.g. two deuterons can fuse together to form a medium nucleus and release energy of about 24 MeV.
i.e., ₁H² + ₁H² → ₂He⁴ + 24 MeV.
Some other examples of such reactions are
₁H¹ + ₁H¹ → ₁H² + ₊₁e⁰ + 0.42 MeV
4 ₁H¹ → ₂He⁴ + 2 ₊₁e⁰ + 26.7 MeV
₁H³ + ₁H² → ₂He⁴ + ₀n¹ + 17.6 MeV
₃Li⁷ + ₁H¹ → ₂He⁴ + ₂He⁴ + 17.3 MeV.
Nuclear fusion reactions take place in the presence of very high temperature (about 10⁷ K), so they are called thermonuclear reactions. All these reactions are exoergic and release huge energies. The energy comes from conversion of mass of final stage nucleus formed as a result of fusion is always less than that of the individual light nuclei.
The temperature of the order of 10⁷ K is very difficult to obtain. The mechanism involved for producing high temperature is a self-sustained fission explosion. When an atom bomb containing U²³⁵ explodes, very high temperature ( ≃ 10⁷ K) is produced. Thus atomic explosion acts as trigger and release tremendous amount of energy.

Conditions for Fusion
(1) Either the reacting nuclei should be given large amount of kinetic energy to overcome the mutual repulsion between them.
(2) Or a very higher temperature should be produced. Such high temperature exists in the territory of stars. Therefore, thermal fission is possible in stars.

(b) Source of energy in sun and stars.
The temperature of the core of the sun is about 20 million degrees. At this high temperature, proton-proton cycle takes place with the release of large amount of energy. The reactions are:
₁H¹ + ₁H¹ → ₁H² + ₁e⁰ + 0.41 MeV
₁H¹ + ₁H² → ₂He³ + 5.51 MeV
₂He³ + ₂He³ → ₂He⁴ + 2(₁H¹) + 12.98 MeV
Adding these reactions, we get
4(₁H¹) → ₂He⁴ + (₁e⁰) + 24.7 MeV
Hence, fusion of 4 hydrogen nuclei results one helium nucleus, two positrons (₁e⁰) and liberation of 24.7 M eV of energy. Estimation of hydrogen in the sun reveals that it can continue proton-proton cycle going for about 30 billion years. A similar thermonuclear reaction takes place in some stars also.
But in stars, whose core is much more hot than that of sun, another type of thermonuclear reactions take place. These are called carbon nitrogen cycle.

Carbon-Nitrogen Cycle
₆C¹² + ₁H¹ → ₇N¹³ + hv (energy)
₇N¹³ → ₆C¹³ + +1^e (positron)
₆C¹³ + ₁H¹ → ₇N¹⁴ + hv (energy)
₇N¹⁴ + ₁H¹ → ₈O¹⁵ + hv (energy)
₈O¹⁶ → ₇N¹⁵ + 1^e (positron)
₇N¹⁴ + ₁H¹ → ₈O¹⁶ + hv (energy)
₈O¹⁶ → ₆C¹² + 2He⁴
Adding, 4 ₁H¹ → ₂He⁴ + 2^e+ + 26.7 MeV
Hydrogen bombs make use of fusion reactions. Hence, they are called fusion bombs.

Question 21.
State the laws of radioactive decay. Deduce the relation N = N₀e^-λt. Sketch a graph to illustrate radioactive decay. Define hlf life.
Answer:
Laws of Radioactive disintegration

1. Radioactivity is spontaneous process which does not depend upon external factors.
2. During disintegration either α or ß-particle is emitted. Both are never emitted simultaneously.
3. Emission of α-particle decreases atomic number by two and mass number by 4.
4. Emission of ß-particle increases atomic number by one but mass number remains the same.
5. Emission of γ-ray does not change atomic or mass number.
6. The number of atoms disintegrated per second is directly proportional to the number of radioactive atoms actually present at that instant. This law is called radioactive decay law.

Let at t = 0
N₀ = number of atoms present
N = number of atom left after time t.
dN = number of atoms disintegrated in time dt.
i.e. \(-\frac{d \mathrm{~N}}{d t}\) ∝ N
or \(-\frac{d \mathrm{~N}}{d t}\) = λN, ............................(i)
where λ is a constant called disintegration constant and depends upon the nature of the radioactive substance.
Now from, (i), we have
\(\frac{1}{N}\)dN = -λ dt
or ∫\(\frac{1}{N}\) dN = -λ∫ dt
or log_eN = λt + C, ................................(ii)
where C is constant of integration. To determine its value,
since N = N₀ initially,
i.e. when t = 0, N = N₀
log_eN₀ = 0 + C
Substituting the value of C in (ii), we have
log_eN = -λt + log_eN₀
or log_eN - log_eN₀ = -λt
log_e\(\frac{\mathrm{N}}{\mathrm{N}_0}\) = -λt
or \(\frac{\mathrm{N}}{\mathrm{N}_0}\) = e^-λt
or N = N₀ e^-λt ...........................(iii)
which is the required equation.
Eq. (iii) shows that the radioactive decay occurs according to exponential law and the number of radioactive atoms decreases exponentially. Since N shall become zero only when t becomes infinity, it shows that time taken by a radioactive element to disintegrate completely is infinitely long.
The curve in Fig. LAQ 10. shows the exponential decay radioactive substance.

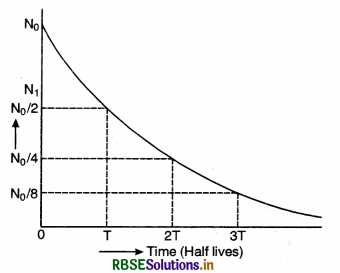
Disintegration constant
In Eq. (iii), if t = 1/λ
Then N = N₀ e^-λx\(\frac{1}{\lambda} \)= N₀e^-1 = \(\frac{\mathrm{N}_0}{e}\)
Thus disintegration constant is defined as the time after which the number of radioactive atoms reduce to 1/e times the original number of atoms.

(i) Half life period. It is the time during which the number of atoms of a radioactive material reduces to half of the original number.
Let N₀ = number of atoms at t = 0 (at the start of the observation)
N = number of atoms after time t
So, N = N₀e^-λt ........................(1)
where λ is constant called disintegration constant
Let T = half life period
So, when t = T, N = -N₀/2.
Substituting in Eq, (1), we have
\(\frac{\mathrm{N}_0}{2}\) = N₀e^-λt
e^λt = 2
λt = log_e2 = 2.303 log₁₀2
= 0.693
or T = \(\frac{0.693}{\lambda}\)

(ii) Average life. The atoms of a radioactive substance are constantly disintegrating and thus the life of every atom is different.
So average life of a radioactive substance is the ratio of sum of lives of all the atoms to the total number of atoms.
Average life =

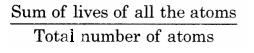
Suppose dN atoms disintegrate in a time dt, t seconds after the separation of the substance, when the actual number of atoms present is N.
Then \(\frac{d \mathrm{~N}}{d t}\) = -λN
dN = -λNdt = -λN₀e^-λt dt
where N0 is the number of atoms in the beginning of time. Each of these dN atoms disintegrate between the time t and t + dt i.e these atoms had a life of t seconds.
∴ Total life of dN atoms = t dN
Hence total life time of all the atoms

Hence average life τ_a of the atom is the reciprocal of the radioactive disintegration constant λ.

Relation between average life and half life
Since average life of a radioactive element is given by
τ_a = \(\frac{1}{\lambda}\) ...........................(i)
and half life of a radioactive element is given by
T = \(\frac{0.693}{\lambda}\)
Using Eq. (i), we get
T = 0.693 τ_a.

Question 22.
State three properties of nuclear forces. Show that the density of nuclear matter is independent of mass number A.
Answer:
(a) Strcture of nucleus. Rutherford's experiments on the scattering of α-particles by atoms led to the discovery of a positively charged heavy central core, called nucleus, of radius of the order of 10^-15 m.
1. The entire positive charge and almost the entire mass of the atom is concentrated in the nucleus.

2. Nucleus contains protons and neutrons called nucleons. A proton carries a unit positive charge and mass 1836 times that of an electron. The neutron is electrically neutral and has mass 1836.6 times that of an electron. The number of protons in the nucleus is called atomic number (Z) whereas the total number of neutrons and protons is called mass number (A).

3. Negatively charged electrons round the nucleus revolve in various orbits. The negative charge on the electron is of the same magnitude as the positive charge on the proton. The number of electrons revolving round the nucleus is equal to that of protons so that an atom is normally electrically neutral.

(b) Nuclear charge. The positive charge of the nucleus is due to the presence of protons. The charge on a proton is equal to 1.6 x 10^-19 C. If Z be the atomic number, then nuclear charge = Z x 1.6 x 10^-19 C.
The mass of the nucleus is equal to the sum of the masses of all protons and neutrons minus the mass defect.
Let Z = atomic number
A = mass number
M_n = mass of neutron
and ∆m = mass defect
Then the number of neutrons = (A - Z)
∴ Mass of the nucleus = ZM_p + (A - Z) M_n - ∆m.

Nuclear size. The distance of the closest approach of α-particle from. the nucleus is the measure of radius of nucleus or size of nucleus. For metals its value is about 10^-14 m.
The dimensiohs of nucleus have been measured by several experiments involving the scattering of n,p,e, etc. Every time it is found that the volume of nucleus is directly proportional to the number of nucleons (A) in the nucleus.
If R is the radius of the nucleus having mass number A, then
\(\frac{4}{3}\)π R³ ∝ A
or R³ ∝ A
or R ∝ A^1/3
or R = R₀A^1/3
where R₀ = 1.2 x 10^-15 m = 1.2 fm. It shows that greater the mass number, greater the nuclear radius.

Density of nucleus (ρ) It is defined as the nuclear mass per unit volume.

Thus the nuclear density is of the order of 10¹⁷ kgm^-3 and is independent of its mass number. Therefore, all nuclei have the same approximate density.

Mass defect. It is found that the mass of a stable nucleus is always less than the sum of masses of its constituent protons and neutrons in their free state. The difference between the sum of the masses of nucleons constituting it and the rest mass of the nucleus is called mass defect.
Let
M_p = mass of protons in the nucleus
M_n = mass of neutrons in the nucleus
M = mass of nucleus
N = number of neutrons
Z = number of protons
A = total number of nucleous
∴ The mass defect
∆m = ZM_p + (A - Z) M_n - M.

Packing fraction (f). Though the atomic masses are considered to be whole numbers, yet they differ from the integers by small amount. This variation of atomic masses from whole numbers is considered to be due to some deviations of the mass of the nucleus from the mass of the constituents of the nucleus (i.e. protons and neutrons). The term packing fraction is defined as the mass defect per nucleon.
∴ f = \(\frac{\text { mass defect }}{\text { mass number }}=\frac{\Delta m}{\mathrm{~A}}=\frac{\mathrm{M}-\mathrm{A}}{\mathrm{A}}\)
where M is the atomic mass, A is the mass number (i.e. number of protons and neutrons in a.m.u.)
Thus f can be +ve, -ve or zero accordingly as M > A, M < A, M = A.
Packing fraction is a fundamental characteristic of the nucleus and is directly related to the availability of the energy of the nucleus and its stability. A negative packing fraction which will also correspond to a negative mass defect will mean that the atomic mass of the nucleus is less than the nearest whole number which will correspond to some conversion of mass into energy during the formation of the nucleus. Also, negative packing fraction will imply that the nucleus is exceptionally stable because we have to supply more energy to break the nucleus into its constituent nucleons while a positive packing fraction will indicate the nucleus to be less stable.

HOTS QUESTIONS

Question 1.
How many electrons, protons and neutrons are there in 12 g of ₆C¹² and in 14 g of ₆C¹⁴?
Answer:
12 g of ₆C¹² has number of atoms = 6 x 10²³
∴ the number of electrons in 12 g of ₆C¹²
= 6 x 6 x 10²³ = 36 x 10²³
The number of protons in 12 g of ₆C¹² = 36 x 10²³
The number of neutrons in 12 g of ₆C¹² = (A - Z) x 6 x 10²³ = 6 x 6 x 10²³ = 36 x 10²³
Similarly
No. of electrons in 14 g of ₆C¹⁴ = 36 x 10²³
No. of protons in 14 g of ₆C¹⁴ = 36 x 10²³
No. of neutrons in 14 g of ₆C¹⁴ = (A - Z) x 6 x 10²³
= (14 - 6) x 6 x 10²³
= 48 x 10²³.

Question 2.
At any instant, the ratio of the amount of radioactive substance is 2 : 1. If their half lives be respectively 12 and 16 hours, then after two days what will be the ratio of the substances?
Answer:
No. of half lives, N₁ =\( \frac{48}{12}\) = 4 and N₂ = \(\frac{48}{16}\) = 3 [∵ n = \(\frac{t}{\mathrm{~T}}\)]

Question 3.
Radioactive element A are being produced at a cbnstant rate α. The element has a decay constant λ. At time t = 0, there are N0 nuclei of the element.
(a) Calculate the number of nuclei A at time t.
(b) If α = 2 N₀λ, calculate the number of nuclei of A after one half life of A and also limiting value of N as t → ∞.
Answer:
(a) Rate of production of radioactive nuclei = λN
Rate of decay of radioactive nuclei = λN
∴ \(\frac{d \mathrm{~N}}{d t}\) = α - λN
or \(\frac{d \mathrm{~N}}{\alpha-\lambda \mathrm{N}}\) = dt ............................(i)
Since at t = 0, N = N₀ and at t = 1, N = N₁
So integrating eq. (i) within these limits, we get

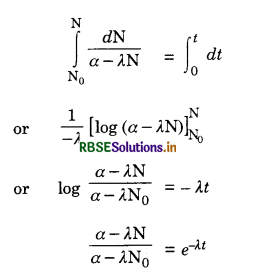
or α - λN = (α - λN₀)e^-λt
or λN = α - (α - λN₀)e^-λt
= (1 - e-λt) + λN₀e^-λt
or N = \(\frac{\alpha\left(1-e^{-\lambda t}\right)}{\lambda}\) + N₀e^-λt

(b) Given α = 2N₀λ and t = \(\frac{0.693}{\lambda}\)
So N = \(\frac{2 \mathrm{~N}_0 \lambda}{\lambda}\) (1 - e^-0.693) + N₀e^-0.693
= 2N₀ - 2N₀e^-0.693 + N0e^-0.693
or N = 2N₀ - N₀e^-0.693
= N₀ (2 - e^-0.693)
= N₀ [2 - \(\frac{1}{2}\)] = N₀ \(\frac{3}{2}\)
or N = 1.5 N₀

(c) At t → ∞
N = \(\frac{\alpha}{\lambda}=\frac{2 \mathrm{~N}_0 \lambda}{\lambda}\) = 2 N₀.

Question 4.
Calculate the energy liberated in kWh,where 100 g of ₃Li⁷ are converted into ₂He⁴ by proton bombbardment. Given mass of ₃Li⁷ = 7.0183 u, mass of ₂He⁴ = 4.0040 u and mass of ₁H¹ = 1.0081 u.
Answer:
The given reaction is
₃Li⁷ + ₂He⁴ → 2(₂He⁴)+ Q
Total mass before reaction = 7.0183 + 1.0081
= 8.0264 u
Total mass after reaction = 2 x 4.0040 = 8.0080 u
Mass defect
∆m = 8.0264 - 8.0080 = 0.0184 u
Loss of mass for 8.0183g of ₃Li⁷ = 0.0184g
Loss of mass for 100g of ₃Li⁷ = \(\frac{0.0184}{8.0183}\) x 100
∴ Energy librated
Q = ∆mc² = \(\frac{0.0184 \times 100 \times 10^{-3}}{7.0183}\) x 9 x 10¹⁶ J
Q = \(\frac{0.0184 \times 1000 \times 10^{-3}}{7.0183 \times 3.6 \times 10^6}\) x 9 x 10¹⁶ kWh
= 5.53 x 10⁵ kWh.

Question 5.
There are two radioactive substances A and B. Decay constant of B is two times that of A. Initially both have equal number of nuclei. After n half lives of A, rate of disintegration of both are equal. Find the value of n.
Answer:
Let λ_A = A, So λ_B = 2λ
If total number of atoms in A and B at t = 0 is N₀
Then, initial rate of disintegration of A = λN₀
Initial rate of disintegration of B = 2λN
Since λ_B = 2λ_A
∴ T_B = \(\frac{\mathrm{TA}}{2}\)
So after one half life of A
\(-\frac{d \mathrm{~N}}{d t}=\frac{\lambda \mathrm{N}_0}{2}\)
And after two half lives of B
\(-\frac{d \mathrm{~N}}{d t}=\frac{2 \lambda \mathrm{N}_0}{4}=\frac{\lambda \mathrm{N}_0}{2}\)
So \(\left(-\frac{d \mathrm{~N}}{d t}\right)_{\mathrm{A}}=\left(-\frac{d \mathrm{~N}}{d t}\right)_{\mathrm{B}}\)
After n = 1 i.e. one half life of A.