RBSE Class 12 Physics Important Questions Chapter 12 परमाणु

Rajasthan Board RBSE Class 12 Physics Important Questions Chapter 12 परमाणु Important Questions and Answers.

RBSE Class 12 Physics Chapter 12 Important Questions परमाणु

अति लघुत्तरीय प्रश्न

प्रश्न 1.
कोई इलेक्ट्रॉन उच्च ऊर्जा स्तर n₂ = 2, 3, 5, ...... से मूल ऊर्जा स्तर n₁ = 1 में संक्रमण करता है तो प्राप्त हाइड्रोजन स्पेक्ट्रम की श्रेणी का नाम लिखिए।
उत्तर:
लाइमन श्रेणी।

प्रश्न 2.
हाइड्रोजन परमाणु के स्पेक्ट्रम के लिए रिडवर्ग का सूत्र लिखिए।
उत्तर:
किसी ऊर्जा स्तर में इलेक्ट्रॉन की ऊर्जा
E_n = -Rch\(\frac{\mathrm{Z}^2}{n^2}\)

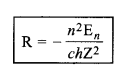
प्रश्न 3.
हाइड्रोजन परमाणु को निम्नतम अवस्था से दूसरी उत्तेजित अवस्था तक उत्तेजित करने के लिए आवश्यक ऊर्जा कितनी होगी?
उत्तर:
निम्नतम अवस्था में ऊर्जा E₁ = -13.6 eV 
दूसरी उत्तेजित अवस्था में कर्जा E₃ = -1.85 eV
आवश्यक ऊर्जा ∆E = E₃ - E₁
= (-1.85 eV) - (-13.6 eV)
∆E = 11.75 eV

प्रश्न 4.
हाइड्रोजन परमाणु की निम्नतम अवस्था में ऊर्जा (-) X eV है। इस अवस्था में इलेक्ट्रॉन की गतिज ऊर्जा कितनी होगी?
उत्तर:
हाइड्रोजन परमाणु की निम्नतम अवस्था में ऊजाँ
T.E = \(\frac{-\mathrm{KZ} e^2}{2 r_n}=(-) \times \mathrm{eV}\)
इलेक्ट्रॉन की गतिज ऊर्जा
E_k = \(\frac{\mathrm{K} \mathrm{Z} e^2}{2 r_n}\)
E_k = (+) x eV

प्रश्न 5.
हाइड्रोजन स्पेक्ट्रम की कौन - सी श्रेणी स्पेक्ट्रम के दृश्य क्षेत्र में होता है?
उत्तर:
बॉमर श्रेणी।

प्रश्न 6.
आयनन ऊर्जा की परिभाषा लिखिए।
उत्तर:
आयनन ऊर्जा: "वह न्यूनतम ऊर्जा जिसे अवशोषित करके परमाणु आयनित हो जायें अर्थात् इलेक्ट्रॉन अपनी मूल अवस्था में सदैव के लिए अलग हो जाये, उस परमाणु की आयनन ऊर्जा कहलाती है।"

प्रश्न 7.
बोर का आवृत्ति प्रतिबंध क्या है?
उत्तर:
जब कोई इलेक्ट्रॉन उच्च ऊर्जा अवस्था E₂ से निम्न ऊर्जा अवस्था E₁ में संक्रमण करता है तो उत्सर्जित फोटॉन की आवृत्ति निम्न सूत्र से मिलेगी-
hv = E₂ - E₁

प्रश्न 8.
संघट्ट प्रांचल (Impact Parameter) की परिभाषा दीजिए।
उत्तर:
जब α - कण नाभिक से अधिक दूर होता है तो इसके वेग सदिश की नाभिक से लम्बवत दूरी को संघट्ट प्रांचल कहते हैं। इसे b से व्यक्त करते है। इसका मान
b = \(\frac{1}{4 \pi \varepsilon_0} \frac{Z e^2 \cot \left(\frac{\theta}{2}\right)}{E_k}\)
जहाँ θ प्रकीर्णन कोण और E_k, α - कण की गतिज ऊर्जा है।

प्रश्न 9.
किसी नाभिक से प्रकीर्णित α - कण का मार्ग कैसा होता है?
उत्तर:
अतिपरवलयाकार (hyperbolic)

प्रश्न 10.
पूर्णत: पराबैंगनी क्षेत्र में आने वाली हाइड्रोजन स्पेक्ट्रम की श्रेणी का नाम लिखिए।
उत्तर:
लाइमन श्रेणी

प्रश्न 11.
हाइड्रोजन स्पेक्ट्रम की उन श्रेणियों के नाम लिखिए जो अवरक्त क्षेत्र में आती हैं।
उत्तर:
अवरक्त क्षेत्र में आने वाली श्रेणियाँ हैं- पाश्चन श्रेणी, ब्रेकेट श्रेणी, फुण्ड श्रेणी आदि।

प्रश्न 12.
हाइड्रोजन स्पेक्ट्रम की उस - श्रेणी का नाम लिखिए जो विद्युत चुम्बकीय तरंगों के स्पेक्ट्रम के दृश्य क्षेत्र में आती हैं?
उत्तर:
बॉमर श्रेणी की प्रथम चार रेखाएँ H_α, H_ß,  H_γ  व H_δ तरंगों के स्पेक्ट्रम के दृश्य क्षेत्र में आती हैं।

प्रश्न 13.
यदि परमाणु में इलेक्ट्रॉन स्थिर होता तो क्या होता?
उत्तर:
यदि परमाणु में इलेक्ट्रॉन स्थिर होता तो वह नाभिक द्वारा वैद्युत आकर्षण बल द्वारा खींच लिया जाता और परमाणु स्थायी न रहता।

प्रश्न 14.
हाइड्रोजन परमाणु की विभिन्न कक्षाओं की त्रिज्याओं का अनुपात क्या होता है?
उत्तर:
r_n = \(\frac{\varepsilon_0 h^2}{\pi m Z e^2} n^2\)
r_n = n²r₁
∴ r₁ : r₂ : r₃ = (1)² : (2)² : (3)² : ...............
r₁ : r₂ : r₃ = 1 : 4 : 9 

लघु उत्तरीय प्रश्न

प्रश्न 1.
परमाणु के रदरफोर्ड मॉडल की दो कमियाँ लिखिए।
उत्तर:

• रेखीय वर्णक्रम की व्याख्या करने में असफल
• परमाणु के स्थायित्व की व्याख्या करने में असफल

प्रश्न 2.
हाइड्रोजन परमाणु के लिए नील्स बोर के कोई दो अभिगृहीत लिखिए।
उत्तर:
(i) बोर की प्रथम अभिगृहीत:
(i) परमाणु में इलेक्ट्रॉन निश्चित त्रिज्याओं की कक्षाओं में नाभिक के चारों ओर परिक्रमण करते हैं, इन कक्षाओं में परिक्रमण करते समय इलेक्ट्रॉन विद्युत चुम्बकीय विकिरण उत्सर्जित नहीं करते हैं। ये विशिष्ट कक्षाएँ 'स्थायी कक्षाएँ' कहलाती हैं।
(ii) इलेक्ट्रॉन नाभिक के चारों ओर केवल उन्हीं कक्षाओं में रह सकता है जिनके लिए कोणीय संवेग का मान \(\frac{h}{2 \pi}\) का पूर्ण गुणज होता हैं।

प्रश्न 3.
बोर मॉडल की दो सीमाएं लिखिए।
उत्तर:
बोर मॉडल की दो सीमाएँ-

• इस सिद्धांत द्वारा केवल एक इलेक्ट्रॉन वाले परमाणु जैसे - हाइड्रोजन, आयनित हीलियम आदि की ही व्याख्या की जा सकती हैं।
• यह सिद्धांत परमाणु में इलेक्ट्रॉन वितरण संबंधी कोई सूचना नहीं देता है।

प्रश्न 4.
बोर के क्वांटीकरण के द्वितीय अभिगृहीत का कथन लिखिए। हाइड्रोजन स्पेक्ट्रम में लाइमन श्रेणी की प्रथम रेखा के संगत तरंगदैर्ध्य को ज्ञात कीजिए।
उत्तर:
बोर के क्वांटीकरण का द्वितीय अभिगृहीत:
हाइड्रोजन परमाणु एवं हाइड्रोजन सदृश्य आयनों के लिए बोर मॉडल (Bohr Model for Hydrogen Atom and Hydrogen like Ions)
वैज्ञानिक नील्स बोर ने चिरसम्मत भौतिकी एवं प्रारंभिक क्वांटम संकल्पनाओं को संयुक्त करके हाइड्रोजन एवं हाइड्रोजन सदृश्य आयनों जैसे He⁺, Li⁺⁺ जिनमें एकपक्षीय इलेक्ट्रॉन होते हैं को समझाते हुए निम्नलिखित तीन अभिगृहीत प्रस्तुत किये। (i) परमाणु में इलेक्ट्रॉन निश्चित त्रिज्याओं की कक्षाओं में नाभिक के चारों ओर परिक्रमण करते हैं, इन कक्षाओं में परिक्रमण करते समय इलेक्ट्रॉन विद्युत चुम्बकीय विकिरण उत्सर्जित नहीं करते हैं। ये विशिष्ट कक्षाएँ स्थायी कक्षाएँ (Stationary) कहलाती हैं। जब ये इलेक्ट्रॉन इन कक्षाओं में परिक्रमण करते हैं तो इलेक्ट्रॉन व नाभिक के मध्य कार्य करने वाला कूलॉम (आकर्षण) बल इलेक्ट्रॉनों को परिक्रमण के लिए आवश्यक अभिकेन्द्रीय बल प्रदान करता है।

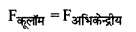
यदि एक इलेक्ट्रॉन Ze आवेश के नाभिक के चारों ओर n वीं स्थायी कक्षा में परिक्रमा करता है तो
\(\frac{\mathrm{K}(\mathrm{Ze}) e}{r_n^2}=\frac{m v_n^2}{r_n}\) .................(i)
जहाँ r_n, n वीं स्थायी कक्षा की त्रिज्या तथा V_n, n वीं कक्षा में इलेक्ट्रॉन का वेग है। अत:
\(\frac{\mathrm{KZ \textrm {Ze } ^ { 2 }}}{r_n^2}=\frac{m v_n^2}{r_n}\) ..................(i)

(ii) इलेक्ट्रॉन नाभिक के चारों ओर केवल उन्हीं कक्षाओं में रह सकता है जिनके लिए कोणीय संवेग का मान \(\frac{h}{2 \pi}\) का पूर्ण गुणज (Integral multiple) होता है, जहाँ h प्लांक नियतांक है। इन कक्षाओं को स्थायी कक्षाएँ (Stable Orbits) कहते हैं।
यदि इलेक्ट्रॉन का द्रव्यमान m, कक्षीय वेग V एवं कक्षा की त्रिज्या r हो तो
∵ कोणीय संवेग = n x \(\frac{h}{2 \pi}\)
mvr = \(\frac{n h}{2 \pi}\) ...............(2)

(iii) स्थायी कक्षाओं में रहते हुए इलेक्ट्रॉन ऊर्जा का उत्सर्जन नहीं करते हैं और इस प्रकार परमाणु का स्थायित्व बना रहता है। जब इलेक्ट्रॉन को बाहर से ऊर्जा दी जाती है तो वह उसका अवशोषण करता है और निम्न ऊर्जा की कक्षा से उच्च ऊर्जा की कक्षा में चला जाता है। इसके विपरीत जब इलेक्ट्रॉन उच्च ऊर्जा की कक्षा से निम्न कर्जा की कक्षा में जाता है तो वह ऊर्जा का उत्सर्जन करता है। यह उत्सर्जित ऊर्जा फोटॉन के रूप में होती है। यदि इलेक्ट्रॉन उच्च ऊर्जा E₂ वाली कक्षा से निम्न ऊर्जा E₁ वाली कक्षा में जाता है तो उत्सर्जित फोटॉन की ऊर्जा

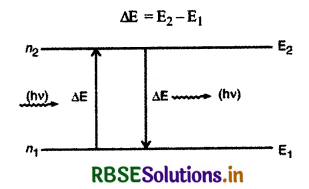
परन्तु प्लांक के सिद्धांत से ∆E = hv, जहाँ v उत्सर्जित फोटॉन की आवृत्ति है।
hv = E₂ - E₁
हाइड्रोजन स्पेक्ट्रम में लाइमन श्रेणी की संगत प्रथम - रेखा के संगत तरंगदैर्ध्य
\(\frac{1}{\lambda}=R\left[\frac{1}{1^2}-\frac{1}{n^2}\right]\)
प्रथम रेखा के लिए n = 2

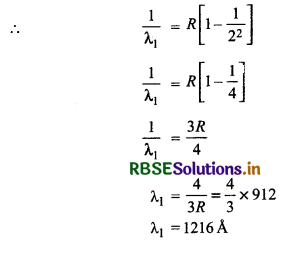
प्रश्न 5.
हाइड्रोजन परमाणु में प्रथम उत्तेजित अवस्था में परिक्रमण करते इलेक्ट्रॉन की तरंगदैथ्य ज्ञात करो।
उत्तर:
प्रथम उत्तेजित अवस्था में इलेक्ट्रॉन के लिए n = 2 
इसीलिए यदि डी - ब्रॉग्ली तरंगदैर्ध्य λ हो तो
nλ = 2πr_n
जहाँ r_n द्वितीय कक्षा की त्रिज्या है।
r_n = n²r₁ से
r₂ = (2)² x 0.529 Å
∴ 2λ = 2 x π x (2)² x 0.529    
λ = 2π x 2 x 0.529
λ = 6.28 Å

प्रश्न 6.
हाइड्रोजन परमाणु में केवल एक इलेक्ट्रॉन है, परन्तु उसके उत्सर्जन स्पेक्ट्रम में कई रेखाएं होती हैं। ऐसा कैसे होता है, संक्षेप में समझाइए।
उत्तर:
प्रत्येक परमाणु के कुछ निश्चित ऊर्जा स्तर होते हैं। सामान्यतया हाइड्रोजन परमाणु का इलेक्ट्रॉन निम्नतम कर्जा स्तर में रहता है। जब परमाणु को बाहरी स्रोत से ऊर्जा प्राप्त होती है, तो यह इलेक्ट्रॉन निम्न कर्जा स्तर से उच्च ऊर्जा स्तर में संक्रमण कर जाता है अर्थात परमाणु उजित हो जाता है। लगभग 10^-8 सेकण्ड रुककर इलेक्ट्रॉन ऊर्जा स्तर छोड़ देता है तथा यहाँ दो संभावनाएँ होती हैं-

• इलेक्ट्रॉन सीधे उच्च ऊर्जा स्तर से निम्न ऊर्जा स्तर में संक्रमण कर जाय।
• इलेक्ट्रॉन उच्च ऊर्जा स्तर से अन्य निम्न ऊर्जा स्तरों से होते हुए निम्नतम ऊर्जा स्तर में लौट सकता है।

चूँकि प्रकाश स्रोत जैसे - हाइड्रोजन लैम्प में असंख्य परमाणु होते हैं, अत: स्रोत में सभी सम्भव संक्रमण होने लगते हैं तथा स्पेक्ट्रम में अनेक रेखाएँ दिखाई देती हैं।

प्रश्न 7.
बोर सिद्धांत के अनुसार इलेक्ट्रॉन की स्थायी कक्षा से क्या आशय है तथा इसके लिए शर्त क्या है?
उत्तर:
बोर के अनुसार इलेक्ट्रॉन की स्थायी कक्षा वह होती है, जिसमें घूमते हुए इलेक्ट्रॉन ऊर्जा उत्सर्जित नहीं करता।
शर्तं: इन कक्षाओं में घूमते इलेक्ट्रॉन का कोणीय संवेग \(\frac{h}{2 \pi}\) का पूर्ण गुणज होता है। जहाँ h प्लांक नियतांक हैं। इसे क्वाण्टम प्रतिबंध कहते हैं।

प्रश्न 8.
प्रयोगशाला में हाइड्रोजन परमाणु के अवशोषण स्पेक्ट्रम में बामर श्रेणी को प्राप्त नहीं किया जा सकता है परन्तु सूर्य के अवशोषण स्पेक्ट्रम में इसे देखा जा सकता है क्यों?
उत्तर:
सूर्य में हाइड्रोजन के परमाणु उपस्थित है। अत: सूर्य के अवशोषण स्पेक्ट्रम में हाइड्रोजन की स्पेक्ट्रम श्रेणियाँ पाई जाती हैं। सूर्य में उपस्थित हाइड्रोजन के परमाणु बहुत ऊँचे ताप पर होते हैं जिससे कि अनेक परमाणु उच्च ऊर्जा स्तरों (जैसे - n = 2) में भी रहते हैं। अतः वहाँ n = 2 ऊर्जा स्तर से भी अवशोषण स्पेक्ट्रम प्राप्त हो सकता है। जिसमें आमर श्रेणी प्राप्त हो जाती है।

प्रश्न 9.
किसी परमाणु के ऊर्जा स्तर A, B, तथा C क्रमशः E_A, E_B तथा E_C है तथा E_A < E_B < E_C हैं। यदि C से B में, B से A तथा C से A में संक्रमण से तरंगदैर्ध्य क्रमशः λ₁, λ₂ व λ₃  उत्सर्जित होती है तो सिद्ध तो सिद्ध कीजिए कि λ₃ = \(\frac{\lambda_1 \lambda_2}{\lambda_1+\lambda_2}\)
उत्तर:

 
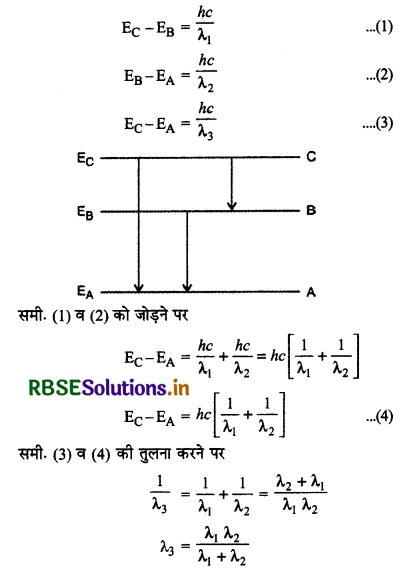
प्रश्न 10.
बोर के परमाणु मॉडल का उपयोग करके, हाइड्रोजन परमाणु की वीं कक्षा में परिक्रमा करते हुए इलेक्ट्रॉन की त्रिज्या के लिए व्युत्पन्न कीजिए।
उत्तर:
हाइड्रोजन परमाणु एवं हाइड्रोजन सदृश्य आयनों के लिए बोर मॉडल (Bohr Model for Hydrogen Atom and Hydrogen like Ions)
वैज्ञानिक नील्स बोर ने चिरसम्मत भौतिकी एवं प्रारंभिक क्वांटम संकल्पनाओं को संयुक्त करके हाइड्रोजन एवं हाइड्रोजन सदृश्य आयनों जैसे He⁺, Li⁺⁺ जिनमें एकपक्षीय इलेक्ट्रॉन होते हैं को समझाते हुए निम्नलिखित तीन अभिगृहीत प्रस्तुत किये। (i) परमाणु में इलेक्ट्रॉन निश्चित त्रिज्याओं की कक्षाओं में नाभिक के चारों ओर परिक्रमण करते हैं, इन कक्षाओं में परिक्रमण करते समय इलेक्ट्रॉन विद्युत चुम्बकीय विकिरण उत्सर्जित नहीं करते हैं। ये विशिष्ट कक्षाएँ स्थायी कक्षाएँ (Stationary) कहलाती हैं। जब ये इलेक्ट्रॉन इन कक्षाओं में परिक्रमण करते हैं तो इलेक्ट्रॉन व नाभिक के मध्य कार्य करने वाला कूलॉम (आकर्षण) बल इलेक्ट्रॉनों को परिक्रमण के लिए आवश्यक अभिकेन्द्रीय बल प्रदान करता है।

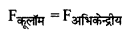
यदि एक इलेक्ट्रॉन Ze आवेश के नाभिक के चारों ओर n वीं स्थायी कक्षा में परिक्रमा करता है तो
\(\frac{\mathrm{K}(\mathrm{Ze}) e}{r_n^2}=\frac{m v_n^2}{r_n}\) .................(i)
जहाँ r_n, n वीं स्थायी कक्षा की त्रिज्या तथा V_n, n वीं कक्षा में इलेक्ट्रॉन का वेग है। अत:
\(\frac{\mathrm{KZ \textrm {Ze } ^ { 2 }}}{r_n^2}=\frac{m v_n^2}{r_n}\) ..................(i)

(ii) इलेक्ट्रॉन नाभिक के चारों ओर केवल उन्हीं कक्षाओं में रह सकता है जिनके लिए कोणीय संवेग का मान \(\frac{h}{2 \pi}\) का पूर्ण गुणज (Integral multiple) होता है, जहाँ h प्लांक नियतांक है। इन कक्षाओं को स्थायी कक्षाएँ (Stable Orbits) कहते हैं।
यदि इलेक्ट्रॉन का द्रव्यमान m, कक्षीय वेग V एवं कक्षा की त्रिज्या r हो तो
∵ कोणीय संवेग = n x \(\frac{h}{2 \pi}\)
mvr = \(\frac{n h}{2 \pi}\) ...............(2)

(iii) स्थायी कक्षाओं में रहते हुए इलेक्ट्रॉन ऊर्जा का उत्सर्जन नहीं करते हैं और इस प्रकार परमाणु का स्थायित्व बना रहता है। जब इलेक्ट्रॉन को बाहर से ऊर्जा दी जाती है तो वह उसका अवशोषण करता है और निम्न ऊर्जा की कक्षा से उच्च ऊर्जा की कक्षा में चला जाता है। इसके विपरीत जब इलेक्ट्रॉन उच्च ऊर्जा की कक्षा से निम्न कर्जा की कक्षा में जाता है तो वह ऊर्जा का उत्सर्जन करता है। यह उत्सर्जित ऊर्जा फोटॉन के रूप में होती है। यदि इलेक्ट्रॉन उच्च ऊर्जा E₂ वाली कक्षा से निम्न ऊर्जा E₁ वाली कक्षा में जाता है तो उत्सर्जित फोटॉन की ऊर्जा

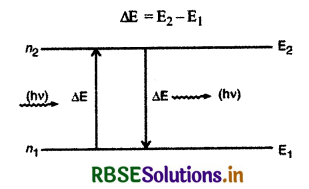
परन्तु प्लांक के सिद्धांत से ∆E = hv, जहाँ v उत्सर्जित फोटॉन की आवृत्ति है।
hv = E₂ - E₁

दीर्घ उत्तरीय प्रश्न

प्रश्न 1.
हाइड्रोजन परमाणु में स्थायी कक्षों की परिभाषा के लिए बोर के अभिगृहीत का उल्लेख कीजिए। डी - ब्रॉग्ली की परिकल्पना किस प्रकार इन कक्षों के स्थायित्व की व्याख्या करती है?
उत्तर:
हाइड्रोजन परमाणु एवं हाइड्रोजन सदृश्य आयनों के लिए बोर मॉडल (Bohr Model for Hydrogen Atom and Hydrogen like Ions)
वैज्ञानिक नील्स बोर ने चिरसम्मत भौतिकी एवं प्रारंभिक क्वांटम संकल्पनाओं को संयुक्त करके हाइड्रोजन एवं हाइड्रोजन सदृश्य आयनों जैसे He⁺, Li⁺⁺ जिनमें एकपक्षीय इलेक्ट्रॉन होते हैं को समझाते हुए निम्नलिखित तीन अभिगृहीत प्रस्तुत किये। (i) परमाणु में इलेक्ट्रॉन निश्चित त्रिज्याओं की कक्षाओं में नाभिक के चारों ओर परिक्रमण करते हैं, इन कक्षाओं में परिक्रमण करते समय इलेक्ट्रॉन विद्युत चुम्बकीय विकिरण उत्सर्जित नहीं करते हैं। ये विशिष्ट कक्षाएँ स्थायी कक्षाएँ (Stationary) कहलाती हैं। जब ये इलेक्ट्रॉन इन कक्षाओं में परिक्रमण करते हैं तो इलेक्ट्रॉन व नाभिक के मध्य कार्य करने वाला कूलॉम (आकर्षण) बल इलेक्ट्रॉनों को परिक्रमण के लिए आवश्यक अभिकेन्द्रीय बल प्रदान करता है।

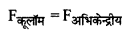
यदि एक इलेक्ट्रॉन Ze आवेश के नाभिक के चारों ओर n वीं स्थायी कक्षा में परिक्रमा करता है तो
\(\frac{\mathrm{K}(\mathrm{Ze}) e}{r_n^2}=\frac{m v_n^2}{r_n}\) .................(i)
जहाँ r_n, n वीं स्थायी कक्षा की त्रिज्या तथा V_n, n वीं कक्षा में इलेक्ट्रॉन का वेग है। अत:
\(\frac{\mathrm{KZ \textrm {Ze } ^ { 2 }}}{r_n^2}=\frac{m v_n^2}{r_n}\) ..................(i)

(ii) इलेक्ट्रॉन नाभिक के चारों ओर केवल उन्हीं कक्षाओं में रह सकता है जिनके लिए कोणीय संवेग का मान \(\frac{h}{2 \pi}\) का पूर्ण गुणज (Integral multiple) होता है, जहाँ h प्लांक नियतांक है। इन कक्षाओं को स्थायी कक्षाएँ (Stable Orbits) कहते हैं।
यदि इलेक्ट्रॉन का द्रव्यमान m, कक्षीय वेग V एवं कक्षा की त्रिज्या r हो तो
∵ कोणीय संवेग = n x \(\frac{h}{2 \pi}\)
mvr = \(\frac{n h}{2 \pi}\) ...............(2)

(iii) स्थायी कक्षाओं में रहते हुए इलेक्ट्रॉन ऊर्जा का उत्सर्जन नहीं करते हैं और इस प्रकार परमाणु का स्थायित्व बना रहता है। जब इलेक्ट्रॉन को बाहर से ऊर्जा दी जाती है तो वह उसका अवशोषण करता है और निम्न ऊर्जा की कक्षा से उच्च ऊर्जा की कक्षा में चला जाता है। इसके विपरीत जब इलेक्ट्रॉन उच्च ऊर्जा की कक्षा से निम्न कर्जा की कक्षा में जाता है तो वह ऊर्जा का उत्सर्जन करता है। यह उत्सर्जित ऊर्जा फोटॉन के रूप में होती है। यदि इलेक्ट्रॉन उच्च ऊर्जा E₂ वाली कक्षा से निम्न ऊर्जा E₁ वाली कक्षा में जाता है तो उत्सर्जित फोटॉन की ऊर्जा

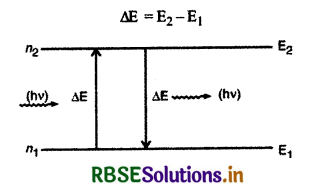
परन्तु प्लांक के सिद्धांत से ∆E = hv, जहाँ v उत्सर्जित फोटॉन की आवृत्ति है।
hv = E₂ - E₁

बोर के क्वाण्टमीकरण के द्वितीय अभिगृहीत का डी - ब्रॉग्ली द्वारा स्पष्टीकरण (De - Broglie Pic ture of Bohr's second Postulate)
बोर के परमाण मॉडल में तीन अभिगृहीत (postulates) हैं जिनमें दूसरे अभिगृहीत के अनुसार, "नाभिक के परितः इलेक्ट्रॉन केवल उन्हीं कक्षाओं में नाभिक की परिक्रमा कर सकते हैं जिनके लिए कोणीय संवेग का मान \(\frac{h}{2 \pi}\) का पूर्ण गुणज (whole multiple) होता है।" अर्थात्
कोणीय संवेग = n x \(\frac{h}{2 \pi}\) जहाँ n = 1, 2, 3, 4 ...........

इस अभिगृहीत में समस्या यह है कि कोणीय संवेग का मान \(\frac{h}{2 \pi}\) का ही पूर्ण गुणज क्यों होता है? सन् 1923 में फ्रांसीसी भौतिकविद् लुईस डी - ब्रॉग्ली ने इस समस्या का समाधान प्रस्तुत किया। डी - ब्रॉग्ली ने तर्क दिया कि इलेक्ट्रॉन को बोर द्वारा प्रस्तावित कक्षा में कण तरंग के रूप में देखा जाना चाहिए। जिस प्रकार डोरियों में उत्पन्न तरंगें अनुनादी अवस्था में अप्रगामी तरंगें उत्पन्न करती हैं उसी प्रकार कण तरंगें (particle waves) भी अनुनादी अवस्थाओं में अप्रगामी तरंगें उत्पन्न कर सकती हैं। किसी डोरी में अप्रगामी तरंगें तभी बनेंगी जब तरंग द्वारा डोरी में एक ओर जाने में तथा वापस आने में तय की गई कुल दूरी,

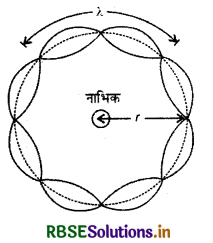
एक तरंगदैर्ध्य, दो तरंगदैर्ध्य अथवा कोई भी पूर्णाक संख्या की तरंगदैर्ध्य के बराबर हो। अन्य स्थितियों में (तरंगदैर्ध्य के अन्य गुणांकों) परावर्तन के पश्चात् अध्यारोपण (superposition) होता है और उनके आयाम शून्य हो जाते हैं। यदि कक्षा की त्रिज्या r_n है तो n वीं कक्षा में इलेक्ट्रॉन द्वारा कक्षा की परिधि में तय की गई कुल दूरी 2πr_n होगी। अतः
2πr_n = nλ, जहाँ n = 1,2,3,....  .............(1)
चित्र 12.15 में किसी वृत्ताकार कक्षा पर, जिसके लिए n = 4 है, एक अप्रगामी कण - तरंग प्रदर्शित की गई है। इस प्रकार
2πr_n = 4λ
जहाँ λ, n वीं कक्षा में इलेक्ट्रॉन की डी - ब्रॉग्ली तरंगदैर्ध्य है।
परन्तु λ = \(\frac{h}{p}=\frac{h}{m v_n}\), जहाँ V_n, n वीं कक्षा में इलेक्ट्रॉन की चाल है।
अत: समी. (1) से,
2πr_n = n x \(\frac{h}{m v_n}\)

यही बोर के परमाणु मॉडल का द्वितीय अभिगृहीत है। इस प्रकार डी - ब्रॉग्ली की परिकल्पना (hypothesis) परिक्रमी इलेक्ट्रॉन के कोणीय संवेग के क्वाण्टमीकरण की बोहर द्वारा प्रस्तावित द्वितीय अभिगृहीत के लिए व्याख्या प्रस्तुत करती है। इलेक्ट्रॉन की क्याण्टित कक्षाएँ (Quantised states) तथा ऊर्जा स्थितियाँ, इलेक्ट्रॉन की तरंग प्रकृति के कारण हैं और केवल अनुनादी अप्रगामी तरंगें ही अवस्थित रह सकती हैं।

प्रश्न 2.
डी - ब्रॉग्ली परिकल्पना में बोर के द्वितीय अभिगृहीत की व्याख्या कीजिए। कक्षा n = 3 के लिए इलेक्ट्रॉन का अप्रगामी तरंग प्रतिरूप बनाइए।
उत्तर:
बोर के क्वाण्टमीकरण के द्वितीय अभिगृहीत का डी - ब्रॉग्ली द्वारा स्पष्टीकरण (De - Broglie Pic ture of Bohr's second Postulate)
बोर के परमाण मॉडल में तीन अभिगृहीत (postulates) हैं जिनमें दूसरे अभिगृहीत के अनुसार, "नाभिक के परितः इलेक्ट्रॉन केवल उन्हीं कक्षाओं में नाभिक की परिक्रमा कर सकते हैं जिनके लिए कोणीय संवेग का मान \(\frac{h}{2 \pi}\) का पूर्ण गुणज (whole multiple) होता है।" अर्थात्
कोणीय संवेग = n x \(\frac{h}{2 \pi}\) जहाँ n = 1, 2, 3, 4 ...........

इस अभिगृहीत में समस्या यह है कि कोणीय संवेग का मान \(\frac{h}{2 \pi}\) का ही पूर्ण गुणज क्यों होता है? सन् 1923 में फ्रांसीसी भौतिकविद् लुईस डी - ब्रॉग्ली ने इस समस्या का समाधान प्रस्तुत किया। डी - ब्रॉग्ली ने तर्क दिया कि इलेक्ट्रॉन को बोर द्वारा प्रस्तावित कक्षा में कण तरंग के रूप में देखा जाना चाहिए। जिस प्रकार डोरियों में उत्पन्न तरंगें अनुनादी अवस्था में अप्रगामी तरंगें उत्पन्न करती हैं उसी प्रकार कण तरंगें (particle waves) भी अनुनादी अवस्थाओं में अप्रगामी तरंगें उत्पन्न कर सकती हैं।

एक तरंगदैर्ध्य, दो तरंगदैर्ध्य अथवा कोई भी पूर्णाक संख्या की तरंगदैर्ध्य के बराबर हो। अन्य स्थितियों में (तरंगदैर्ध्य के अन्य गुणांकों) परावर्तन के पश्चात् अध्यारोपण (superposition) होता है और उनके आयाम शून्य हो जाते हैं। यदि कक्षा की त्रिज्या r_n है तो n वीं कक्षा में इलेक्ट्रॉन द्वारा कक्षा की परिधि में तय की गई कुल दूरी 2πr_n होगी। अतः
2πr_n = nλ, जहाँ n = 1,2,3,....  .............(1)
चित्र 12.15 में किसी वृत्ताकार कक्षा पर, जिसके लिए n = 4 है, एक अप्रगामी कण - तरंग प्रदर्शित की गई है। इस प्रकार
2πr_n = 4λ
जहाँ λ, n वीं कक्षा में इलेक्ट्रॉन की डी - ब्रॉग्ली तरंगदैर्ध्य है।
परन्तु λ = \(\frac{h}{p}=\frac{h}{m v_n}\), जहाँ V_n, n वीं कक्षा में इलेक्ट्रॉन की चाल है।
अत: समी. (1) से,
2πr_n = n x \(\frac{h}{m v_n}\)

यही बोर के परमाणु मॉडल का द्वितीय अभिगृहीत है। इस प्रकार डी - ब्रॉग्ली की परिकल्पना (hypothesis) परिक्रमी इलेक्ट्रॉन के कोणीय संवेग के क्वाण्टमीकरण की बोहर द्वारा प्रस्तावित द्वितीय अभिगृहीत के लिए व्याख्या प्रस्तुत करती है। इलेक्ट्रॉन की क्याण्टित कक्षाएँ (Quantised states) तथा ऊर्जा स्थितियाँ, इलेक्ट्रॉन की तरंग प्रकृति के कारण हैं और केवल अनुनादी अप्रगामी तरंगें ही अवस्थित रह सकती हैं।
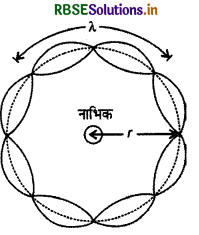
n = 3 के लिए इलेक्ट्रॉन का अप्रगामी तरंग प्रतिरूप
3λ = 2πr

प्रश्न 3.
हाइड्रोजन परमाणु के लिए बोर सिद्धांत के अभिग्रहीत लिखिए। इसकी n वीं कक्षा में इलेक्ट्रॉन की कुल ऊर्जा के लिए सूत्र स्थापित करो।
उत्तर:
n वीं कक्षा में इलेक्ट्रॉन की कुल ऊर्जा (Total Energy of Electron in nth Orbit)
किसी भी स्थायी कक्षा में कुल ऊर्जा (E), गतिज ऊर्जा तथा स्थितिज ऊर्जा के योग के बराबर होती है।
इलेक्ट्रॉन की गतिज ऊर्जा
K_n = \(\frac{1}{2}\)mv²
बोर की प्रथम अभिग्रहीत से

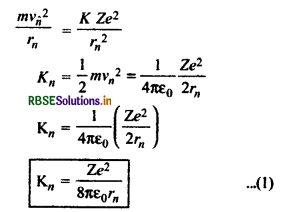
इलेक्ट्रॉन की स्थितिज ऊर्जा

∴ इलेक्ट्रॉन की कुल ऊर्जा
E_n = K_n + U
= \(\frac{Z e^2}{8 \varepsilon_0 \pi r_n}-\frac{Z e^2}{4 \varepsilon_0 \pi r_n}\)
E_n = -\(\frac{Z e^2}{8 \pi \varepsilon_0 r_n}\) .................(3)
समी. (3) में rn का मान रखने पर
E_n = -\(\frac{Z e^2}{8 \pi \varepsilon_0\left[\frac{\varepsilon_0 n^2 h^2}{\pi m Z e^2}\right]}\)
E_n = -\(\frac{Z^2}{n^2}\left[\frac{m e^4}{8 \varepsilon_0^2 h^2}\right]\) .................(4)
समी. (4) में समी मान रखने पर
E_n = -\(\frac{Z^2}{n^2}\left[\frac{9.1 \times 10^{-31} \times\left(1.6 \times 10^{-19}\right)^4}{8 \times\left(8.86 \times 10^{-12}\right)^2\left(6.62 \times 10^{-34}\right)^2}\right]\)

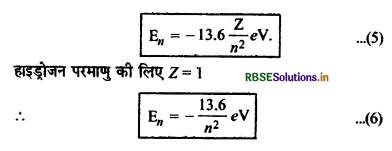
प्रश्न 4.
बोर परमाणु मॉडल की प्रथम व द्वितीय परिकल्पनाएँ लिखिए। इलेक्ट्रॉन के स्थायी कक्षा के लिए त्रिज्या एवं वेग के लिए व्यंजक प्राप्त कीजिए।
उत्तर:
हाइड्रोजन परमाणु एवं हाइड्रोजन सदृश्य आयनों के लिए बोर मॉडल (Bohr Model for Hydrogen Atom and Hydrogen like Ions)
वैज्ञानिक नील्स बोर ने चिरसम्मत भौतिकी एवं प्रारंभिक क्वांटम संकल्पनाओं को संयुक्त करके हाइड्रोजन एवं हाइड्रोजन सदृश्य आयनों जैसे He⁺, Li⁺⁺ जिनमें एकपक्षीय इलेक्ट्रॉन होते हैं को समझाते हुए निम्नलिखित तीन अभिगृहीत प्रस्तुत किये। (i) परमाणु में इलेक्ट्रॉन निश्चित त्रिज्याओं की कक्षाओं में नाभिक के चारों ओर परिक्रमण करते हैं, इन कक्षाओं में परिक्रमण करते समय इलेक्ट्रॉन विद्युत चुम्बकीय विकिरण उत्सर्जित नहीं करते हैं। ये विशिष्ट कक्षाएँ स्थायी कक्षाएँ (Stationary) कहलाती हैं। जब ये इलेक्ट्रॉन इन कक्षाओं में परिक्रमण करते हैं तो इलेक्ट्रॉन व नाभिक के मध्य कार्य करने वाला कूलॉम (आकर्षण) बल इलेक्ट्रॉनों को परिक्रमण के लिए आवश्यक अभिकेन्द्रीय बल प्रदान करता है।

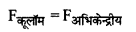
यदि एक इलेक्ट्रॉन Ze आवेश के नाभिक के चारों ओर n वीं स्थायी कक्षा में परिक्रमा करता है तो
\(\frac{\mathrm{K}(\mathrm{Ze}) e}{r_n^2}=\frac{m v_n^2}{r_n}\) .................(i)
जहाँ r_n, n वीं स्थायी कक्षा की त्रिज्या तथा V_n, n वीं कक्षा में इलेक्ट्रॉन का वेग है। अत:
\(\frac{\mathrm{KZ \textrm {Ze } ^ { 2 }}}{r_n^2}=\frac{m v_n^2}{r_n}\) ..................(i)

(ii) इलेक्ट्रॉन नाभिक के चारों ओर केवल उन्हीं कक्षाओं में रह सकता है जिनके लिए कोणीय संवेग का मान \(\frac{h}{2 \pi}\) का पूर्ण गुणज (Integral multiple) होता है, जहाँ h प्लांक नियतांक है। इन कक्षाओं को स्थायी कक्षाएँ (Stable Orbits) कहते हैं।
यदि इलेक्ट्रॉन का द्रव्यमान m, कक्षीय वेग V एवं कक्षा की त्रिज्या r हो तो
∵ कोणीय संवेग = n x \(\frac{h}{2 \pi}\)
mvr = \(\frac{n h}{2 \pi}\) ...............(2)

(iii) स्थायी कक्षाओं में रहते हुए इलेक्ट्रॉन ऊर्जा का उत्सर्जन नहीं करते हैं और इस प्रकार परमाणु का स्थायित्व बना रहता है। जब इलेक्ट्रॉन को बाहर से ऊर्जा दी जाती है तो वह उसका अवशोषण करता है और निम्न ऊर्जा की कक्षा से उच्च ऊर्जा की कक्षा में चला जाता है। इसके विपरीत जब इलेक्ट्रॉन उच्च ऊर्जा की कक्षा से निम्न कर्जा की कक्षा में जाता है तो वह ऊर्जा का उत्सर्जन करता है। यह उत्सर्जित ऊर्जा फोटॉन के रूप में होती है। यदि इलेक्ट्रॉन उच्च ऊर्जा E₂ वाली कक्षा से निम्न ऊर्जा E₁ वाली कक्षा में जाता है तो उत्सर्जित फोटॉन की ऊर्जा

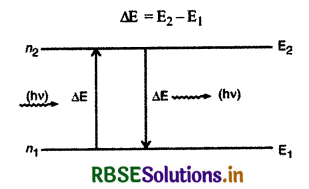
परन्तु प्लांक के सिद्धांत से ∆E = hv, जहाँ v उत्सर्जित फोटॉन की आवृत्ति है।
hv = E₂ - E₁

स्थायी बोर कक्षाओं की त्रिज्याएँ (Radii of Stable Orbits)
माना किसी परमाणु की n वीं कक्षा की त्रिज्या rn है और इसमें एक इलेक्ट्रॉन v_n वेग से गति कर रहा है। यदि इलेक्ट्रॉन का द्रव्यमान m हो तो बोर की द्वितीय अभिगृहीत से

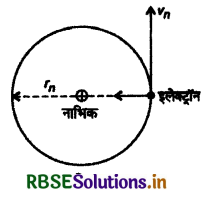
mv_nr_n = \(\frac{n h}{2 \pi}\) ...............(1)
बोर की प्रथम अभिगृहीत से
\(\frac{K Z e^2}{r_n^2}=\frac{m v_n^2}{r_n}\) ....................(2)
समी. (1) से v_n = \(\frac{n h}{2 \pi m r_n} \)
समी. (2) में v_n व k का मान रखने घर

∴ हाइड्रोजन की प्रथम कक्षा (बोर कक्षा) के लिए-
Z = 1, n = 1
r₁ = \(\frac{\varepsilon_0 h^2}{\pi m e^2}\) ...................(4)
समी. (4) में सभी नियतांको के मान रखने पर
r₁ = \(\frac{8.86 \times 10^{-12} \times\left(6.62 \times 10^{-34}\right)^2}{3.14 \times 9.1 \times 10^{-31} \times\left(1.6 \times 10^{-19}\right)^2}\)
r₁ = 0.528 x 10^-10 मी.

अतः हाइड्रोजन की n वीं कक्षा के लिए
r_n = \(\left(\frac{\varepsilon_0 h^2}{\pi m e^2}\right) n^2\)

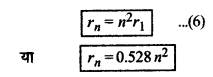
इलेक्ट्रॉन की कक्षीय चाल (Orbital speed of Electron)
∵ v_n = \(\frac{n h}{2 \pi m r_n}\)
उपरोक्त समीकरण में r_n = \(\frac{\varepsilon_0 h^2 n^2}{\pi m Z e^2}\) रखने पर

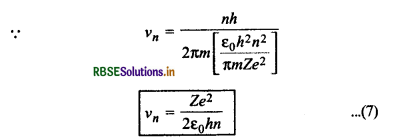
हाइड्रोजन परमाणु की प्रथम कक्षा के लिए
v_n = \(\frac{e^2}{2 \varepsilon_0 h}\) (∵ Z = 1, n = 1)
v_n = \(\frac{1.6 \times 10^{-19}}{2 \times 8.86 \times 10^{-12} \times 6.62 \times 10^{-34}}\)
v_n = 2.18 x 10⁶ मी/से.
∴ समी परमाणुओं के लिए
v_n = \(\frac{Z}{n} v_1\)
या v_n = \(\frac{Z}{n}\) x 2.18 x 10⁶ मी/से 

प्रश्न 5.
बोर की परिकल्पनों का उल्लेख कीजिए। इन परिकल्पनाओं का उपयोग कर हाइड्रोजन परमाणु की। वीं कक्षा में एक इलेक्ट्रॉन की कुल ऊर्जा का व्यंजक लिखिए। हाइड्रोजन के ऊर्जा स्तरों को प्रदर्शित करने वाला चित्र बनाइए।
उत्तर:
हाइड्रोजन परमाणु एवं हाइड्रोजन सदृश्य आयनों के लिए बोर मॉडल (Bohr Model for Hydrogen Atom and Hydrogen like Ions)
वैज्ञानिक नील्स बोर ने चिरसम्मत भौतिकी एवं प्रारंभिक क्वांटम संकल्पनाओं को संयुक्त करके हाइड्रोजन एवं हाइड्रोजन सदृश्य आयनों जैसे He⁺, Li⁺⁺ जिनमें एकपक्षीय इलेक्ट्रॉन होते हैं को समझाते हुए निम्नलिखित तीन अभिगृहीत प्रस्तुत किये। (i) परमाणु में इलेक्ट्रॉन निश्चित त्रिज्याओं की कक्षाओं में नाभिक के चारों ओर परिक्रमण करते हैं, इन कक्षाओं में परिक्रमण करते समय इलेक्ट्रॉन विद्युत चुम्बकीय विकिरण उत्सर्जित नहीं करते हैं। ये विशिष्ट कक्षाएँ स्थायी कक्षाएँ (Stationary) कहलाती हैं। जब ये इलेक्ट्रॉन इन कक्षाओं में परिक्रमण करते हैं तो इलेक्ट्रॉन व नाभिक के मध्य कार्य करने वाला कूलॉम (आकर्षण) बल इलेक्ट्रॉनों को परिक्रमण के लिए आवश्यक अभिकेन्द्रीय बल प्रदान करता है।

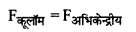
यदि एक इलेक्ट्रॉन Ze आवेश के नाभिक के चारों ओर n वीं स्थायी कक्षा में परिक्रमा करता है तो
\(\frac{\mathrm{K}(\mathrm{Ze}) e}{r_n^2}=\frac{m v_n^2}{r_n}\) .................(i)
जहाँ r_n, n वीं स्थायी कक्षा की त्रिज्या तथा V_n, n वीं कक्षा में इलेक्ट्रॉन का वेग है। अत:
\(\frac{\mathrm{KZ \textrm {Ze } ^ { 2 }}}{r_n^2}=\frac{m v_n^2}{r_n}\) ..................(i)

(ii) इलेक्ट्रॉन नाभिक के चारों ओर केवल उन्हीं कक्षाओं में रह सकता है जिनके लिए कोणीय संवेग का मान \(\frac{h}{2 \pi}\) का पूर्ण गुणज (Integral multiple) होता है, जहाँ h प्लांक नियतांक है। इन कक्षाओं को स्थायी कक्षाएँ (Stable Orbits) कहते हैं।
यदि इलेक्ट्रॉन का द्रव्यमान m, कक्षीय वेग V एवं कक्षा की त्रिज्या r हो तो
∵ कोणीय संवेग = n x \(\frac{h}{2 \pi}\)
mvr = \(\frac{n h}{2 \pi}\) ...............(2)

(iii) स्थायी कक्षाओं में रहते हुए इलेक्ट्रॉन ऊर्जा का उत्सर्जन नहीं करते हैं और इस प्रकार परमाणु का स्थायित्व बना रहता है। जब इलेक्ट्रॉन को बाहर से ऊर्जा दी जाती है तो वह उसका अवशोषण करता है और निम्न ऊर्जा की कक्षा से उच्च ऊर्जा की कक्षा में चला जाता है। इसके विपरीत जब इलेक्ट्रॉन उच्च ऊर्जा की कक्षा से निम्न कर्जा की कक्षा में जाता है तो वह ऊर्जा का उत्सर्जन करता है। यह उत्सर्जित ऊर्जा फोटॉन के रूप में होती है। यदि इलेक्ट्रॉन उच्च ऊर्जा E₂ वाली कक्षा से निम्न ऊर्जा E₁ वाली कक्षा में जाता है तो उत्सर्जित फोटॉन की ऊर्जा

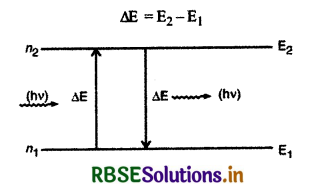
परन्तु प्लांक के सिद्धांत से ∆E = hv, जहाँ v उत्सर्जित फोटॉन की आवृत्ति है।
hv = E₂ - E₁

n वीं कक्षा में इलेक्ट्रॉन की कुल ऊर्जा (Total Energy of Electron in nth Orbit)
किसी भी स्थायी कक्षा में कुल ऊर्जा (E), गतिज ऊर्जा तथा स्थितिज ऊर्जा के योग के बराबर होती है।
इलेक्ट्रॉन की गतिज ऊर्जा
K_n = \(\frac{1}{2}\)mv²
बोर की प्रथम अभिग्रहीत से

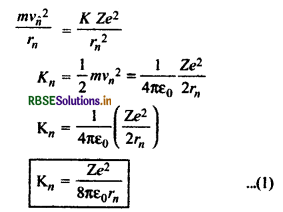
इलेक्ट्रॉन की स्थितिज ऊर्जा

∴ इलेक्ट्रॉन की कुल ऊर्जा
E_n = K_n + U
= \(\frac{Z e^2}{8 \varepsilon_0 \pi r_n}-\frac{Z e^2}{4 \varepsilon_0 \pi r_n}\)
E_n = - \(\frac{Z e^2}{8 \pi \varepsilon_0 r_n}\) .................(3)
समी. (3) में rn का मान रखने पर
E_n = -\(\frac{Z e^2}{8 \pi \varepsilon_0\left[\frac{\varepsilon_0 n^2 h^2}{\pi m Z e^2}\right]}\)
E_n = -\(\frac{Z^2}{n^2}\left[\frac{m e^4}{8 \varepsilon_0^2 h^2}\right]\) .................(4)
समी. (4) में समी मान रखने पर
E_n = -\(\frac{Z^2}{n^2}\left[\frac{9.1 \times 10^{-31} \times\left(1.6 \times 10^{-19}\right)^4}{8 \times\left(8.86 \times 10^{-12}\right)^2\left(6.62 \times 10^{-34}\right)^2}\right]\)

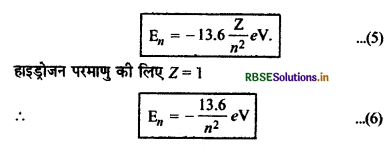
स्पेक्ट्रमी श्रेणी (Spectrum Series)
हाइड्रोजन एक सरलतम परमाणु है और इसलिए इसका स्पेक्ट्रम सरलतम होता है। हाइड्रोजन के स्पेक्ट्रम का विधिवत अध्ययन 1885 में स्वीडन के एक स्कूल अध्यापक जान जेकब बामर (John Jeqab Balrmer) ने किया था। इस स्पेक्ट्रम में काली पृष्ठ भूमि पर बहुत सी पृथक-पृथक चमकीली रेखाएँ प्राप्त होती हैं। इन रेखाओं को H_α, H_ß, H_γ, H_δ....... कहते हैं। इनकी यह विशेषता है कि स्पेक्ट्रम के एक सिरे से दूसरे सिरे की ओर जाने पर रेखाओं की चमक तथा उनके बीच की दूरी नियमित रूप से घटती जाती हैं। इस प्रकार ये रेखाएँ एक श्रेणी की सदस्य हैं जिसे 'बॉमर श्रेणी' (Balmer Series) कहते हैं।

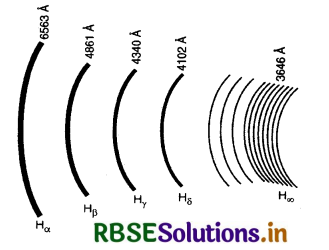
बामर ने यह ज्ञात किया कि बामर श्रेणी की सभी रेखाओं की तरंगदैर्ध्य (α) निम्न समीकरण के द्वारा व्यक्त की जा सकती हैं-
\(\frac{1}{\lambda}=R\left[\frac{1}{2^2}-\frac{1}{n^2}\right]\) .....................(i)
जहाँ n = 3, 4, 5, ...........
जहाँ λ तरंगदैर्घ्य तथा R एक नियतांक है जिसे रिडवर्ग नियतांक कहते हैं। जहाँ n के पूर्णाक मान 3, 4, 5 इत्यादि हो सकते हैं। R का मान 1.097 x 10⁷ m^-1 है। इस समीकरण को बामर सूत्र कहते हैं।
समीकरण: (1) में n = 3 मानकर रेखा Hα की तरंगदैर्ध्य प्राप्त कर सकते है-
\(\frac{1}{\lambda}\) = 1.097 x 10⁷ \(\left[\frac{1}{2^2}-\frac{1}{3^2}\right]\) m^-1
= 1.522 x 10⁶ m^-1
अर्थात्
λ = 656.3 nm
हाइड्रोजन के लिए स्पेक्ट्रम की अन्य श्रेणियाँ भी खोजी जा चुकी हैं। इस समीकरण से हाइड्रोजन के स्पेक्ट्रम में प्राप्त होने वाली सभी श्रेणियों की व्याख्या की जा सकती है-

(i) लाइमन श्रेणी (Lyman Series): जब हाइड्रोजन का परमाणु किसी उच्च ऊर्जा स्तर से प्रथम ऊर्जा स्तर (मूल स्तर) में आता है (अर्थात् n₁ = 1 तथा n₂ = 2, 3, 4, 5...) तब उत्सर्जित स्पेक्ट्रम की रेखाएँ स्पेक्ट्रम के पराबैंगनी (Ultraviolet) भाग में मिलती हैं। इन रेखाओं की तरंगदैर्घ्य निम्न प्रकार ज्ञात कर सकते है-
\(\frac{1}{\lambda}=R\left[\frac{1}{1^2}-\frac{1}{n^2}\right]\)
यहाँ n = 2, 3, 4 ........ 
हाइड्रोजन स्पेक्ट्रम की लाइमन श्रेणी की रेखाओं को लाइमन ने सन् 1916 में फोटोग्राफ किया था। इस श्रेणी की सबसे बड़ी तरंगदैर्घ्य (n = 2 के लिए) 1216 Å तथा सबसे छोटी तरंगदैर्घ्य (n = ∞) के लिए 912 Å हैं।

(ii) बॉमर श्रेणी (Balmer Series): जब हाइड्रोजन परमाणु किसी उच्च ऊर्जा स्तर से द्वितीय ऊर्जा स्तर में आता है (n₁ = 2 तथा n₂ = 3,4, 5....) तो उत्सर्जित स्पेक्ट्रम की रेखाएं स्पेक्ट्रम के दृश्य भाग में प्राप्त होती है। इन रेखाओं की तरंगदैर्ध्य निम्न समीकरण से ज्ञात की सकते हैं-
\(\frac{1}{\lambda}=R\left[\frac{1}{2^2}-\frac{1}{n^2}\right]\)
जहाँ n = 3, 4, 5, ...........
इन रेखाओं को सर्वप्रथम सन् 1885 में ऑमर ने देखा। इस श्रेणी की सबसे बड़ी तरंगदैर्ध्य (n = 3 के लिए) 6563 Å तथा सबसे छोटी तरंगदैर्ध्य (n = ∞ के लिए) 3636 Å है।
इस श्रेणी की प्रथम 4 रेखाएँ स्पेक्ट्रम की दृश्य क्षेत्र में प्राप्त होती हैं तथा शेष अदृश्य पराबैंगनी क्षेत्र में। दृश्य क्षेत्र में पाई जाने वाली रेखाओं के नाम- H_α(λ = 6563 Å), H_ß (λ = 4861 Å) H_γ (λ = 4340 Å) तथा H_δ (λ = 4102 Å)।

(iii) पाश्चन श्रेणी (Paschan Series): जब हाइड्रोजन का परमाणु किसी उच्च ऊर्जा स्तर से तृतीय ऊर्जा स्तर में आता है (n₁ = 3 तथा n₂ = 4, 5, 6.......) तो उत्सर्जित रेखाएँ स्पेक्ट्रम के अवरक्त (Infrared) भाग में प्राप्त होती हैं। इन रेखाओं की तरंगदैर्ध्य निम्न समीकरण से ज्ञात कर सकते हैं।
\(\frac{1}{\lambda}=R\left[\frac{1}{3^2}-\frac{1}{n^2}\right]\)
जहाँ n = 4, 5, 6, 7 ..........

(iv) पैकेट श्रेणी (Brackett Series): जब हाइड्रोजन का परमाणु किसी उच्च ऊर्जा स्तर से चतुर्थ ऊर्जा स्तर में आता है (n₁ = 4 तथा n₂ = 5, 6, 7, 8 ....) तो उत्सर्जित रेखाएँ स्पेक्ट्रम में अवरक्त (Infrared) भाग में प्राप्त होती है। इन रेखाओं की तरंगदैर्ध्य अग्र समीकरण से ज्ञात कर सकते हैं।
\(\frac{1}{\lambda}=R\left[\frac{1}{4^2}-\frac{1}{n^2}\right]\)
जहाँ n = 5, 6, 7, 8, ................

(v) फुण्ड श्रेणी (Pfund Series): जब हाइड्रोजन का परमाणु किसी उच्च ऊर्जा स्तर से पंचम ऊर्जा स्तर में आता है (n₁ = 5 तथा n₂ = 6, 7, 8, 9.....) तो फुण्ड श्रेणी की रेखाएँ प्राप्त होती है। ये रेखाएँ स्पेक्ट्रम के दूर अवरक्त भाग में प्राप्त होती हैं। इन रेखाओं की तरंगदैर्ध्य निम्न समीकरण से ज्ञात कर सकते हैं-
\(\frac{1}{\lambda}=R\left[\frac{1}{5^2}-\frac{1}{n^2}\right]\)
यहाँ n = 6, 7, 8, 9, ......................
उपरोक्त समीकरणों के सरल सूत्रों से केवल कुछ तत्वों (हाइड्रोजन एकधा आवनित होलियम और द्वित आयनित लीथियम) के स्पेक्ट्रमों को ही निरूपित किया जा सकता है।

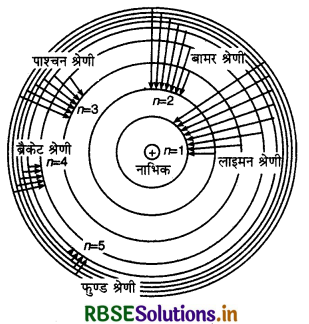
आंकिक प्रश्न

प्रश्न 1.
गीगर - मार्सडन प्रयोग में, जब 8 MeV ऊर्जा का α - कण, Z = 80 नाभिक से सीधा टकराता है, तो क्षण - भर के लिए विरामावस्था में आने तथा दिशा प्रतिलोमन से पूर्व उसके समीपतम पहुंचने की दूरी का परिकलन कीजिए।
हल:
K = \(\frac{1}{4 \pi \varepsilon_0} \frac{(Z e)(2 e)}{r_0}\)
r₀ = \(\frac{2 Z e^2}{4 \pi \varepsilon 0 K}\)
= \(\frac{9 \times 10^9 \times 2 \times 80 \times\left(1.6 \times 10^{-19}\right)^2}{8 \times 10^6 \times\left(1.6 \times 10^{-19}\right)}\)
r₀ = 2.88 x 10^-14 m

प्रश्न 2.
हाइड्रोजन परमाणु की सबसे आंतरिक इलेक्ट्रॉन कक्षा की त्रिज्या 5.3 x 10^-11 m है। इसकी द्वितीय उत्तेजित अवस्था में कक्षा की त्रिज्या क्या होगी?
हल:
दिया है r₁ = 5 .3 x 10^-11 मी.
हम जानते हैं r_n = n²r₁
द्वितीय उत्तेजित अवस्था के लिएn = 3
∴ r₃ = (3)²r₁
r₃ = 9 x 5.3 x 10^-11
r₃ = 47.7 x 10^-11 m
r₃ = 4.77 x 10^-10 m

प्रश्न 3.
एक दी गई बोर कक्षा में इलेक्ट्रॉन की कुल ऊर्जा - 1.5 eV हैं। गणना कीजिए- (i) गतिज ऊर्जा (ii) स्थितिज ऊर्जा।
हलः
(i) कुल कर्जा के ऋणात्मक मान के तुल्य किसी कक्षा में इलेक्ट्रॉन की गतिज ऊर्जा होती है। अत:
E_K = -(-1.5 eV)
E_K = 1.5 eV
(ii) कुल ऊर्जा का दोगुनी इलेक्ट्रॉन की स्थितिज ऊर्जा होती है।
E_P = 2 E_K
E_P = -1.5 x 2 = -3 eV

प्रश्न 4.
पहली बोर कक्षा में इलेक्ट्रॉन की ऊर्जा -13.6 eV है। गणना कीजिए- (i) रिडवर्ग नियतांक (ii) तीसरी कक्षा में इलेक्ट्रॉन की ऊर्जा।
हल:
प्रथम बोर कक्षा में इलेक्ट्रॉन की ऊर्जा
E₁ = -13.6 eV
= -13.6 x 1.6 x 10^-19 J
(i) रिडवर्ग नियतांक के पर्दो में ऊर्जा
E_n = -\(\frac{R c h}{n^2} \)
E₁ = -Rch
∴ R = -\(\frac{E_1}{C h}\)
R = -\(\frac{\left(-13.6 \times 1.6 \times 10^{-19}\right)}{3 \times 10^8 \times 6.62 \times 10^{-34}}\)
R = 1.097 x 10⁷ प्रति मी.
(ii) समी (1) से n = 3 के लिए
E_n = \(\frac{-13.6}{3^2}\) eV
E_n = \(\frac{-13.6}{9}\) eV
E_n = -1.51 eV

प्रश्न 5.
एकल आयनित हीलियम (He⁺) की तीसरी कक्षा (n = 3) में इलेक्ट्रॉन की चाल की गणना कीजिए।
हल:
हाइड्रोजन सम - परमाणु में इलेक्ट्रॉन की चाल
V_n = \(\frac{1}{4 \pi \varepsilon_0} \frac{2 \pi Z e^2}{n h}\)
He⁺ के लिए Z = 2 तथा n = 3
V₃ = \(\frac{9 \times 10^9 \times 2 \times 3.14 \times 2 \times\left(1.6 \times 10^{-19}\right)^2}{3 \times 6.62 \times 10^{-34}}\)
V₃ = 1.46 x 10⁶ मी/से.

प्रश्न 6.
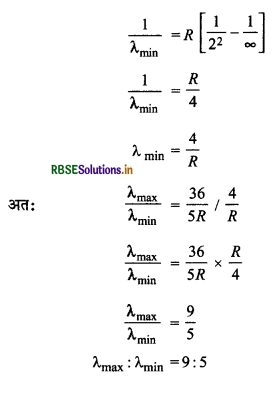
हाइड्रोजन स्पेक्ट्रम में बॉमर श्रेणी की रेखाओं के अधिकतम तरंगदैर्ध्य एवं न्यूनतम तरंगदैर्ध्य का अनुपात ज्ञात कीजिए।
हल:
बॉमर श्रेणी के रेखाओं की अधिकतम तरंगदैध्य के लिए
n₁ = 2 व n₂ = 3

बॉमर श्रेणी के रेखाओं की न्यूनतम तरंगदैर्ध्य के लिए
n₁ = 2, n₂ = ∞

प्रश्न 7.
हाइड्रोजन परमाणु की निम्नतम अवस्था ऊर्जा - 13.6 eV है। यदि एक इलेक्ट्रॉन -0.85 eV ऊर्जा स्तर से -3.4 eV ऊर्जा स्तर को संक्रमण करे तो उत्सर्जित स्पेक्ट्रमी रेखा की तरंगदैर्य का परिकलन कीजिए। यह तरंगदैर्ध्य हाइड्रोजन स्पेक्ट्रम की किस श्रेणी में होगी?
हल:
∆E = hv = \(\frac{h c}{\lambda}\) = E₂ - E₁
λ = \(\frac{h c}{E_2-E_1}\)
= \(\frac{6.63 \times 10^{-34} \times 3 \times 10^8}{\left[-0.85-(-3.4) \times 1.6 \times 10^{-19}\right]}\)
= 4.87 x 10^-7 m
= 4870 Å
यह बॉमर श्रेणी की होगी।

प्रश्न 8.
हाइड्रोजन स्पेक्ट्रम में लाइमन श्रेणी की प्रथम एवं तृतीय रेखाओं के संगत तरंग संख्याओं का अनुपात ज्ञात कीजिए।
हल:
तरंग संख्या \(\bar{v}=\frac{1}{\lambda}=R\left[\frac{1}{n_1^2}-\frac{1}{n_2^2}\right]\)
लाइमन श्रेणी की प्रथम रेखा के लिए
\(\overline{\mathrm{v}_1}=\mathrm{R}\left[\frac{1}{1^2}-\frac{1}{2^2}\right]=\frac{3 R}{4}\)
लाइमन श्रेणी की तृतीय रेखा के लिए
\(\frac{\overline{v_1}}{\overline{v_3}}=\frac{3 R}{4} / \frac{16}{15 R}=\frac{4}{5}\)

प्रश्न 9.
बॉमर श्रेणी में उत्सर्जित स्पेक्ट्रमी रेखाओं की लघुत्तम तरंगदैर्ध्य परिकलित कीजिए।
हल:
बॉमर श्रेणी के लिए n₁ = 2
बॉमर श्रेणी के लिए लघुत्तम तरंगदैर्ध्य
λ_min = \(\frac{n_1^2}{R}=\frac{2^2}{1.097 \times 10^7}\)
λ_min = \(\frac{4}{1.097 \times 10^7}\)
λ_min = 3639.7 Å

प्रश्न 10.
आरंभ में निम्नतम अवस्था में कोई हाइड्रोजन परमाणु किसी फोटोंन को अवशोषित करता है, जो उसे n = 4 स्तर तक उत्तेजित कर देता है। फोटॉन की आवृत्ति का अनुमान लगाइए।
हल:
प्रश्नानुसार n₁ = 1, n₂ = 4
∴ उत्सर्जित फोटॉन की तरंगदैर्ध्य λ हो तो

फोटॉन की आवृत्ति v = \(\frac{c}{\lambda}\)
v = \(\frac{R_C \times 15}{16}\)
v = \(\frac{15}{16}\) x 1.097 x 10⁷ x 3 x 10⁸
v = 3.08 x 10¹⁵ Hz

प्रश्न 11.
निम्नलिखित चित्र में एक परमाणु के ऊर्जा स्तरों को दर्शाया गया है। कौन से संक्रमण से 275 nm तरंगदैर्घ्य के फोटॉन का उत्सर्जन होगा?

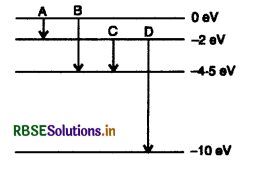
तरंगदैर्ध्य λ तथा फोटॉन की ऊर्जा में संबंध
E = \(\frac{h c}{\lambda}\)
E = \(\frac{1242 \mathrm{nmeV}}{275 \mathrm{~nm}}\)
E = 4.5 eV
इस ऊर्जा का फोटॉन संक्रमण B में उत्सर्जित होगा।

प्रतियोनी परीक्षा संबंधी प्रश्न

प्रश्न 1.
यदि लाइमन श्रेणी की श्रेणी सीमा आवृत्ति v_L है तो फुण्ड श्रेणी की श्रेणी सीमा आवृत्ति होगी-
(A) \(\frac{v_L}{16}\)
(B) \(\frac{v_L}{25}\)
(C) 25 v_L
(D) 16 v_L 
उत्तर:
(B) \(\frac{v_L}{25}\) 

प्रश्न 2.
एक इलेक्ट्रॉन हाइड्रोजन परमाणु की विभिन्न उत्तेजित अवस्थाओं से मूल अवस्था आते समय विकिरण उत्सर्जित करता है। माना n वीं अवस्था और मूल अवस्था में इलेक्ट्रॉन की डी - ब्रॉग्ली तरंगदैध्य क्रमशः λ_n व λ_g हैं। माना n वीं उत्तेजन अवस्था से मूल अवस्था में संक्रमण के दौरान अत्सर्जित फोटॉन की तरंगदैर्ध्य An है, तब n होगी (A और B नियतांक है)
(A)An² = A + Bλ_nⁿ
(B) An² = λ
(C) An = A + (B/λ_n²)
(D) An = A + Bλ_n
उत्तर:
(C) An = A + (B/λ_n²)

प्रश्न 3.
हाइड्रोजन परमाणु की बोर कक्षा में इलेक्ट्रॉन की गतिज ऊर्जा और कुल ऊर्जा का अनुपात होगा-
(A) 2 : -1
(B) 1 : -1
(C) 1 : 1
(D) 1 : -2
उत्तर:
(B) 1 : -1

प्रश्न 4.
निम्नलिखित में से किसके लिए, बोर मॉडल उपर्युक्त नहीं है?
(A) ड्यूटेरॉन परमाणु
(B) एकल आयनित निऑन परमाणु (Ne⁺)
(C) हॉइड्रोजन परमाणु
(D) एकल आयनित हीलियम परमाणु (He⁺)
उत्तर:
(B) एकल आयनित निऑन परमाणु (Ne⁺)

प्रश्न 5.
हाइड्रोजन परमाणु में इसकी मूल अवस्था में इलेक्ट्रॉन का परिक्रमण काल 1.6 x 10^-16 सेकण्ड है। प्रथम उत्तेजित अवस्था में इलेक्ट्रॉन की परिक्रमण आवृत्ति होगी-
(A) 6.2 x 10¹⁵
(B) 1.6 x 10¹⁴
(C) 7.8 x 10¹⁴
(D) 5.6 x 10¹² 
उत्तर:
(C) 7.8  x 10¹⁴

प्रश्न 6.
किसी अचल हाइड्रोजन परमाणु का एक इलेक्ट्रॉन पाचवें अवस्था से न्यूनतम स्तर को गमन करता है, तो फोटॉन उत्सर्जन के परिणामस्वरूप परमाणु द्वारा प्राप्त वेग होगा-
(A) \(\frac{24 h \mathrm{R}}{25 m}\)
(B) \(\frac{24 h \mathrm{R}}{25 m}\)
(C) \(\frac{25 m}{24 m \mathrm{R}}\)
(D) \(\frac{24 m}{24 m \mathrm{R}}\)
(जहाँ, m इलेक्ट्रॉन का द्रव्यमान, R रिडबर्ग नियतांक और h प्लांक नियतांक है)
उत्तर:
(A) \(\frac{24 h \mathrm{R}}{25 m}\)

प्रश्न 7.
हाइड्रोजन के समान किसी परमाणु में, n = 3 अवस्था से n = 1 अवस्था में संक्रमण से पराबैंगनी विकिरणों का उत्सर्जन होता है। तो, इसी परमाणु में अवरक्त किरणों का उत्सर्जन होगा, यदि संक्रमण हो-
(A) 2 → 1 में
(B) 3 → 2 में
(C) 4 → 2 में
(D) 4 → 3 में
उत्तर:
(D) 4 → 3 में

प्रश्न 8.
एक हाइड्रोजन समान परमाणु में इलेक्ट्रॉन क्वाण्टम संख्या n के ऊर्जा स्तर से एक दूसरे क्वाण्टम संख्या (n - 1) के ऊर्जा स्तर पर संक्रमण करता है। यदि n >>1 तब उत्सर्जित विकिरण की आवृत्ति किसके समानुपाती है?
(A) \(\frac{1}{n}\)
(B) \(\frac{1}{n^2}\)
(C) \(\frac{1}{n^2 / 2}\)
(D) \(\frac{1}{n^3}\)
उत्तर:
(D) \(\frac{1}{n^3} \)

प्रश्न 9.
हाइड्रोजन (₁H¹), इयूटेरियम (₁H²), एकल आयनित हीलियम (₂HC⁴)⁺ और द्वि - आयनित लीथियम (₃H⁶)²⁺ सभी में नाभिक के चारों ओर एक इलेक्ट्रॉन है। n = 2 से n = 1 के इलेक्ट्रॉन संक्रमण पर विचार कीजिये। यदि उत्सर्जित विकिरण की तरंगदैर्ध्य क्रमशः λ₁, λ₂, λ₃ एवं λ₄ है तब निम्नलिखित में कौन - सा लगभग सही है?
(A) 4λ₁ = 2λ₂ = 2λ₃ = λ₄
(B) λ₁ = 2λ₂ = 2λ₃ = λ₄
(C) λ₁ = λ₂ = 4λ₃ = 9λ₄
(D) λ₁ = 2λ₂ = 3λ₃ = 4λ₄
उत्तर:
(C) λ₁ = λ₂ = 4λ₃ = 9λ₄

प्रश्न 10.
जब कोई इलेक्ट्रॉन, हाइड्रोजन जैसे परमाणु/आयन की उत्तेजित अवस्था से न्यूनतम ऊर्जा अवस्था में संक्रमण करता है, तो उसकी।
(A) गतिज ऊर्जा से वृद्धि तथा स्थितिज ऊर्जा व कुल कर्जा में कमी होती है। 
(B) गतिज ऊर्जा, स्थितिज ऊर्जा तथा कुल ऊर्जा में कमी हो जाती है
(C) गतिज ऊर्जा कम होती है, स्थितिज ऊर्जा बढ़ती है और कल ऊर्जा वही रहती है
(D) गतिज ऊर्जा व कुल ऊर्जा कम हो जाती है किन्तु स्थितिज ऊर्जा बढ़ गयी है।
उत्तर:
(A) गतिज ऊर्जा से वृद्धि तथा स्थितिज ऊर्जा व कुल कर्जा में कमी होती है।