RBSE Class 12 Physics Important Questions Chapter 12 Atoms

Rajasthan Board RBSE Class 12 Physics Important Questions Chapter 12 Atoms Important Questions and Answers.

RBSE Class 12 Physics Chapter 12 Important Questions Atoms

Multiple Choice Questions

Question 1.
In Rutherford scattering experiment, what will be correct angle for α-scattering for an impact parameter b = 0?
(A) 90°
(B) 270°
(C) 0°
(D) 180°.
Answer:
(D) 180°.

Question 2.
The nuclear model of atom was proposed by:
(A) J. J. Thomson
(B) E. Rutherford
(C) Niel Bohr
(D) Sommerfield.
Answer:
(B) E. Rutherford

Question 3.
The angular momentum of the orbital electron is integral multiple of:
(A) h
(B) 2πh
(C) \(\frac{h}{2 \pi}\)
(D)None of these.
Answer:
(C) \(\frac{h}{2 \pi}\)

Question 4.
If 13.6 eV energy is required to ionise the hydrogen atom, then energy required to remove an electron from n = 2 is:
(A) 10.2 eV
(B) 0eV
(C) 3.4 eV
(D) 6.0 eV.
Answer:
(C) 3.4 eV

Question 5.
The Bohr model of atoms:
(A) Assumes that the angular momentum of electron in quantised
(B) Predicts continuous emission spectra for atoms
(C) Predicts the same emission spectra for all types of atoms
(D) Einstein photoelectric effect.
Answer:
(A) Assumes that the angular momentum of electron in quantised

Question 6.
In which of the following system will the radius of first orbit be minimum?
(A) hydrogen atom
(B) deuterium atom
(C) singly ionised helium
(D) doubly ionised lithium
Answer:
(D) doubly ionised lithium

Question 7.
When hydrogen atom is in first excited level, its radius is:
(A) same
(B) half
(C) twice
(D) fourtimes.
Answer:
(D) fourtimes.

Question 8.
The wavelengths involved in the spectrum of deuterium (₁H²) are slightly different from that of hydrogen spectrum, because:
(A) sizes of the two nuclei are different
(B) masses of the two nuclei are different
(C) attraction, between the electron and the nucleus is different in the two cases
(D) nuclear forces are different in the two cases
Answer:
(B) masses of the two nuclei are different

Question 9.
What would happen, if the electron, in an atom were stationary?
(A) nothing
(B) it will fuse with nucleus
(C) it will move away from nucleus
(D) None of these.
Answer:
(B) it will fuse with nucleus

Question 10.
Name the series of hydrogen specturm lying in the ultraviolet region.
(A) Lyman
(B) Balmer
(C) Paschen
(D) Pfund.
Answer:
(A) Lyman

Fill in the blanks

Question 1.
J.J. Thomson suggested ............................. model of atom.
Answer:
plum pudding.

Question 2.
Rutherford model successfully explained the ............................. scattering.
Answer:
alpha ray.

Question 3.
According to Bohr model, orbital angular momentum is integral multiple of .............................
Answer:
\(\frac{h}{2 \pi}\)

Question 4.
The radius of first orbit of hydrogen atom is called ............................. radius.
Answer:
Bohr.

Question 5.
The distance of closest approach give an estimate of size of the .............................
Answer:
nucleus.

Question 6.
The size of atom in Thomson’s model is the ............................. as the atomic size in Rutherford’s model.
Answer:
same.

Question 7.
The size of the atom is about ............................. m.
Answer:
10^-10.

Question 8.
............................. series has the least wavelength.
Answer:
Lyman.

Question 9.
The total energy possessed by an electron in hydrogen atom in ground state is .............................
Answer:
-13.6 eV.

Question 10.
According to Rutherford’s model, atom has a lot of ............................. space.
Answer:
empty.

Very Short Answer Type Questions

Question 1.
Is the size of the atom in Thomson’s model, the same as the atomic size in Rutherford’s model?
Answer:
Yes.

Question 2.
What are α-particles?
Answer:
Alpha particles are helium nuclei i.e. helium atom from which the two electrons have been removed.

Question 3.
What is the size of atom?
Answer:
About 10^-10 m.

Question 4.
What are stationary orbits?
Answer:
These are special orbits. An electron in a stationary orbit does not lose any energy i.e. electron in stationary orbit does not obey the laws of electromagnetic theory of radiation.

Question 5.
What would happen if the electrons in an atom were stationary?
Answer:
In that case, the electron would fall into the nucleus due to electrostatic attraction and the atom would be unstable.

Question 6.
What is the ionisation energy of hydrogen in eV?
Answer:
13.6 eV.

Question 7.
What is Bohr’s radius?
Answer:
The radius of first permitted orbit in hydrogen atom is called Bohr’s radius.

Question 8.
In which series of hydrogen spectra, the big transitions involve the largest changes of energy?
Answer:
Lyman series. 

Question 9.
What is meant by the model of an atom?
Answer:
The model which describes how the constituents of atom are distributed in space is called atomic model.

Question 10.
Why is gold foil preferred on scattering object in Rutherford’s experiment?
Answer:
Because gold is a heavy substance (Z = 79) and can be stretched into very thin foil.

Question 11.
In Rutherford’s atom model an atom has a highly non-uniform mass distribution. Explain.
Answer:
Because in Rutherford’s atomic model all the positive charge of the atom is supposed to be concentrated at the centre called nucleus.

Question 12.
In which atom model electrons in the ground state are in stable equilibrium?
Answer:
In Thomson’s model of atom.

Question 13.
Which model of atom has a nearly continuous mass distribution in it?
Answer:
In Thomson’s model of atom.

Question 14.
What is the energy possessed by an electron in the orbit n → ∞?
Answer:
Since E = -\(\frac{13.6}{n^2}\) eV
So, when n → ∞
E = 0

Question 15.
Name the series of hydrogen spectrum which has the least wavelength.
Answer:
Lyman Series.

Question 16.
In which series of hydrogen spectra, the transitions involve the largest change of energy?
Answer:
In Lyman Series.

Question 17.
What is the ratio of size of atom and the size of the nucleus?
Answer:
≅ 105.

Question 18.
In what respect do the atoms of different elements differ from each other?
Answer:
The atoms of different elements:

• have different mass number.
• have different charge.

Question 19.
What are expectations from a model of the atom?
Answer:

1. Atom as a whole neutral.
2. Most of the atoms are stable.
3. It should explain the line spectrum of the atom.

Question 20.
Which atom model, Rutherford’s atom model or Thomson’s atom model suggests that most of the mass of the atom is due to positively charged part?
Answer:
Both the models suggest the same idea.

Question 21.
What is the difference between an atom and an ion?
Answer:
An ion is the atom from which the outermost orbit, one or more electrons have been removed.

Question 22.
What is atomic number and atomic mass number?
Answer:
Atomic number is the number of protons in the atom and atomic mass number is the number of protons and neutrons in the atom.

Question 23.
A classical atom based on Rutherford’s model is doomed to collapse. Explain.
Answer:
Classically, an orbiting electron around the nucleus is always accelerated and hence continuously radiate energy and fall towards the nucleus and ultimately collapse.

Question 24.
What is the order of velocity of electron in a hydrogen atom in ground state?
Answer:
10⁶ ms^-1.

Question 25.
What is the value of Rydberg constant?
Answer:
1.097 x 10⁷ m^-1.

Question 26.
What is the Bohr quantisation condition for the angular momentum of an electron in the second orbit?
Answer:
Bohr’s quantisation condition is
Angular momentum = mvr = \(\frac{n h}{2 \pi}\)
For second orbit, n = 2,
So mvr = \(\frac{2 h}{2 \pi}=\frac{h}{\pi}.\)

Question 27.
Calculate the ratio of energies of photons produced due to transition of electron of hydrogen atom from its,
(i) Second permitted energy level to the first level, and
(ii) The highest permitted energy level to the second permitted level.
Answer:
E₁ = -3.4- (-13.6) = 10.2 eV
E₂ = 0 - (-3.4) = 3.4 eV
∴ \(\frac{\mathrm{E}_1}{\mathrm{E}_2}=\frac{10.2}{3.4}\) = 3

Question 28.
An electron revolves in a circular orbit around a nucleus of charge Ze. How is the electron velocity related to the radius of its orbit?
Answer:
Since mvr = \(\frac{n h}{2 \pi}\)
∴ v = \(\frac{n h}{2 \pi m r}\)
where r is given by r = 4πε₀\(\frac{n^2 h^2}{4 \pi^2 m e^2}\).

Question 29.
Can a hydrogen atom absorb a photon whose energy exceeds its energy?
Answer:
Yes, it can absorb.

Question 30.
Name the series of hydrogen spectrum which lies in the visible region of electro-magnetic spectrum.
Answer:
Balmer series.

Question 31.
The wavelengths of some of the spectral lines obtained in hydrogen spectrum are 9546 Å, 6463Å and 1216Å, which one of these wavelengths belong to Lyman series?
Answer:
Wavelength 1216 Å belongs to Lyman series because Lyman series has the least wavelength.

Question 32.
Name the series of hydrogen spectrum which has least wavelength.
Answer:
Lyman series.

Question 33.
The total energy of an electron in the first excited state of the hydrogen atom is about -3.4 eV. What is the kinetic energy of the electron in this state? Answer:
Kinetic energy of the electron in the orbit is equal to negative of its total energy.
i.e. E_k = -E = -(-3.4) = 3.4 eV.

Question 34.
The total energy of an electron in the first excited state of the hydrogen atom is about -3.4 eV. What is the potential energy of the electron in this state?
Answer:
Potential energy of the electron in an orbit is equal to twice its total energy.
i.e. E_p = 2E = -3.4 x 2 = -6.8 eV.

Question 35.
What is the ratio of radii of the orbits corresponding to first excited state and ground state in a hydrogen atom?
Answer:
Since rn ∝ n²
For 1st excited state n = 2 and for ground state n = 1
∴ \(\frac{r_1}{r_0}=\frac{2^2}{1^2}=\frac{4}{1}\) = 4 : 1

Question 36.
Find the wavelength of the electron orbiting in the ground state of hydrogen atom.
Answer:
At ground state, the energy of electron,
E = 13.6 eV
Since E = \(\frac{h c}{\lambda}\)
∴ λ = \(\frac{h c}{\mathrm{E}}=\frac{6.67 \times 10^{-34} \times 3 \times 10^8}{13.6 \times 1.6 \times 10^{-19}}\) = 91.2 x 10^-9
or λ = 91.2 Nm

Short Answer Type Questions

Question 1.
Though hydrogen atom contains only one electron, yet its emission spectrum consists of iriarty lines. Give reason.
Answer:
The source of hydrogen spectrum (i.e. a hydrogen lamp) has a large number of hydrogen atoms. Each atom, has one electron but the atom can exist in various stationary states. Therefore, all possible electron transitions from higher to lower energy states may occur. This would give rise to a larger number of spectral lines.

Question 2.
Why do not the negatively charged electrons fall into the positively charged nucleus?
Answer:
Because the electrons are not stationary but are revolving around the nucleus in circular orbits. The electrostatic force of attraction between the nucleus and electrons provides the necessary centripetal force which does not allow the electron to fall into the nucleus.

Question 3.
Nuclear atom model is required to explain the results of Rutherford experiment. Why?
Answer:
In Rutherford experiment, a few α-particles are scattered through large angles. Therefore, massive and positive part of atom should be concentrated in a small space in the atom. This small positive part having atom entire mass of the atom was called nucleus.

Question 4.
Explain the meaning of ground state and excited state of an atom.
Answer:
Ground state. The most stable energy state of a nucleus, atom or molecule. When an atom is in the ground state, its extra nuclear electrons move in shells such that the energy of the atom is minimum.

Excited state. When the atom is in any of the states with quantum number n greater than one, it is said to be in the excited state. The excitation energy is the difference in energy between the ground state and the excited state. As value of quantum number n increases, corresponding energy level approach closer and closer to zero. When n becomes infinite, the energy becomes zero and the electron is no more bound to the nucleus.

Question 5.
What is Bohr’s quantum condition?
Answer:
According to Bohr’s quantum condition, the permitted orbits are those in which the angular momentum of the electron is integral multiple of h/2π, where h is Planck’s constant
i.e. m v r = nh/2π (when n = 1, 1, .................. called principal quantum number).

Question 6.
Rutherford’s α-particles scattering experiment shows that most of the α-particles pass through almost unscattered while some are scattered through large angles. What information does it give about the structure of the atom?
Answer:
(i) Since a large number of α-particles pass through almost unscattered, it means that major portion of atom is empty space.
(ii) The scattering of α-particles through large angles showed that these α-particles experience a very strong electric force of repulsion. This indicates that the entire positive charge of atom is confined in a small part of the volume of atom called nucleus.

Question 7.
When impact parameter of α-particle is zero, the α-particle travelling directly towards the centre of the nucleus retraces its path. Explain why?
Answer:
Since impact parameter is given by:
b = \(\frac{Z e^2 \cot \frac{\theta}{2}}{4 \pi \varepsilon_0 \mathrm{E}}\)
where b = 0, cot \(\frac{\theta}{2}\) = 0
or \(\frac{\theta}{2}\) = 90°
or θ = 180°
i.e. α-particle retraces its path as its angle of scattering is 180°.

Question 8.
What is distance of the closest approach?
Answer:
When an α-particle is at a very large distance from the nucleus, its potential energy is zero. As it moves towards the nucleus, its kinetic energy decreases and appears as potential energy. After reaching a certain distance r0 from the nucleus, its whole kinetic energy appears as potential energy. This minimum distance to which the α-particle moves upto nucleus, is called distance of the closest approach.

Question 9.
In Rutherford’s model r₁ and v₁ denote the radius and speed of an electron around the nucleus in an orbit. If r₂ and v₂ are the corresponding values for another orbit and r₂ > r₁. What is the value of \(\frac{v_1}{v_2}\)? Give reasons in support of your answer.
Answer:
Since r and v represents the radius and speed of electron around the nucleus.
So r²v = constant
or r₁v₁² = r₂v₂²
or \(\frac{v_1}{v_2}=\sqrt{\frac{r_2}{r_1}}\)
As r₂ > r₁ so \(\frac{r_2}{r_1}\) > 1
so \(\frac{v_1}{v_2}\) > 1.

Question 10.
Calculate the speed of the electron revolving around the nucleus of a hydrogen atom in order that it may not be pulled into the nucleus by electrostatic attraction.
Answer:
In order that an electron revolving around the nucleus may not be pulled into the nucleus by electrostatic attraction, the centripetal force should be equal to electrostatic force of attraction.

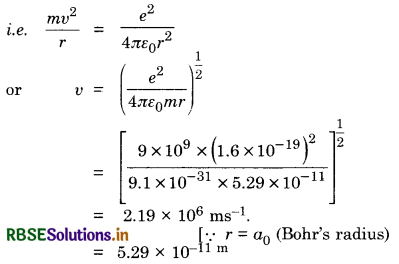
Question 11.
Show that the velocity of the electron in the first orbit is time the velocity of light.
Answer:
The velocity of electron in nth orbit is given by
v_n = \(\frac{2 \pi \mathrm{Z} e^2}{4 \pi \varepsilon_0 n h}\)
For hydrogen Z = 1 and in the first orbit n = 1

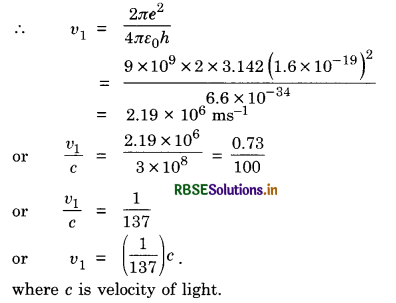
Question 12.
The energy level of an atom of an element X are shown in Fig. SAQ 12.12. A photon of wavelength 620 nm is emitted. This corresponds to which of the transitions; A, B, C, D or E?

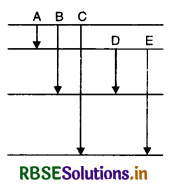
Answer:
The energy of photon
E = hv = h\(\frac{c}{\lambda}=\frac{6.6 \times 10^{-34} \times 3 \times 10^8}{620 \times 10^{-9}}\) J
or E = 3.2 x 10^-19 J
= \(\frac{3.2 \times 10^{-19}}{1.6 \times 10^{-19}}\) = 2eV
Thus only D transition is possible.

Question 13.
What is Bohr’s frequency condition?
Answer:
Whenever an electron jumps from higher energy orbit E_n2 to lower energy orbit E_n1, the frequency of the radiation emitted is given by
hv = E_n2 - E_n1
It is called Bohr’s frequency condition.

Question 14.
What is the interpretation of negative energy of an orbiting electron?
Answer:
Negative sign associated with energy of orbital electron indicates that the electron is bound to the nucleus by attractive forces so that a definite amount of energy must be supplied to the electron to separate it completely from the nucleus.

Question 15.
How do you justify the assumption that nucleus is at rest while treating the motion of an electron around it?
Answer:
As the mass of electron is very small as compared to mass of nucleus, so the radius of orbit of nucleus about the centre of mass is very small. Hence we can assume the nucleus to be stationary.

Question 16.
The energy level diagram of an element is given below. Identify by doing necessary calculations, which transition corresponds to the emission of a spectral line of wavelength 102.7 nm.

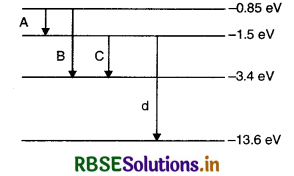
Answer:
Given λ = 102.7 nm = 102.7 x 10^-19 m.
Since E₁ - E₂ = \(\frac{h c}{\lambda}\)
= \(\frac{6.626 \times 10^{-34} \times 3 \times 10^8}{102.7 \times 10^{-9} \times 1.6 \times 10^{-19}}\) eV
= 12.1 eV
Here For D - line, we have
E₁ - E₂ = - 1.5 - (-13.6) = 12.1 eV.

Question 17.
State Bohr postulates for hydrogen atom.
Answer:
Bohr’s Postulates
In order to explain the stability of the atom and its line spectra, Bohr gave a set of postulates.
1. An electron in an atom revolves in a circular orbit around the nucleus. The force of attraction between the electron and the nucleus provides the necessary centripetal force for the circular motion.

2. The electron can revolve in those orbits for which its orbital angular momentum is an integral multiple of h/2π. The allowed orbits are given by
mvr = \(\frac{n h}{2 \pi}\) ..........................(1)
where n is an integer and h is Planck’s constant. The integer n is known as the principal number and can take any integral value 1, 2, 3, .... The numerical value of h is 6.624 x 10^-34 Js. This postulate is known as quantization of the angular momentum.

3. The electron moving in an allowed orbit does not radiate energy. Therefore, the total energy of the electron remains constant in an allowed orbit.

4. Electromagnetic radiation is emitted when the electron jumps from a higher orbit having energy. E_n1 to a lower orbit having E_n2 The frequency v of the emitted radiation is given as
v = \(\frac{\mathrm{E}_{n_2}-\mathrm{E}_{n_1}}{h}\) ................................(2)
Eq. (2) represents the Bohr’s frequency condition.

Question 18.
State two postulates of Bohr’s theory of hydrogen atom.
Answer:
Bohr’s Postulates
In order to explain the stability of the atom and its line spectra, Bohr gave a set of postulates.
1. An electron in an atom revolves in a circular orbit around the nucleus. The force of attraction between the electron and the nucleus provides the necessary centripetal force for the circular motion.

2. The electron can revolve in those orbits for which its orbital angular momentum is an integral multiple of h/2π. The allowed orbits are given by
mvr = \(\frac{n h}{2 \pi}\) ..........................(1)
where n is an integer and h is Planck’s constant. The integer n is known as the principal number and can take any integral value 1, 2, 3, .... The numerical value of h is 6.624 x 10^-34 Js. This postulate is known as quantization of the angular momentum.

3. The electron moving in an allowed orbit does not radiate energy. Therefore, the total energy of the electron remains constant in an allowed orbit.

4. Electromagnetic radiation is emitted when the electron jumps from a higher orbit having energy. E_n1 to a lower orbit having E_n2 The frequency v of the emitted radiation is given as
v = \(\frac{\mathrm{E}_{n_2}-\mathrm{E}_{n_1}}{h}\) ................................(2)
Eq. (2) represents the Bohr’s frequency condition.

Question 19.
Explain Rutherford’s experiment on the scattering of α-particles and state the significance of the results.
Answer:
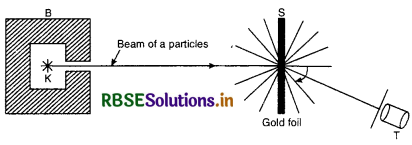
Experimental arrangement
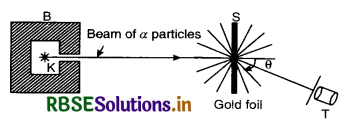
The schematic diagram of scattering of α-particles is shown in Fig. SAQ 19 (a).
B is a block of lead having a thin tunnel. This tunnel terminates into a hole H inside the block. The radium source emits α-particles in all directions. Most of α-particles are absorbed by the lead block. A thin pencil of a rays comes out of the tunnel and falls on a gold foil.The gold atoms scatter the α-particles. When scattered α-particles fall on a screen S coated with zinc sulphide (ZnS), they produce flashes. These flashes are observed through the telescope T. Particles scattered through different angles can be observed by rotating the ZnS screen along with the telescope.


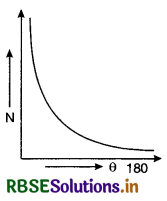
Observations

1. Most of the α-particles were scattered by small angles of the order of a few degrees.
2. Some α-particles were scattered in the back-ward direction i.e. by angles more than 90°.
3. A few of α-particles were reflected nearly straight back.

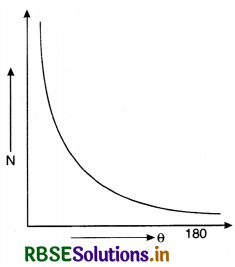
The graph between the total number of α-particles (N) scattered and scattering angle (θ) was as shown in Fig. SAQ 19 (b). 


Conclusion.

1. Since a large number of α-particles suffer practically no deviation, it means that major portion of atom is empty space.
2. The scattering of α-particles through large angle showed that these α-particles experienced a very strong electric force repulsion. This indicates that the entire +ve charges of atom is confined in a small part of the volume of atom.
3. The backward scattering α-particles shows that most of the mass of atom is concentrated in a small portion of the volume of the atom.

Question 20.
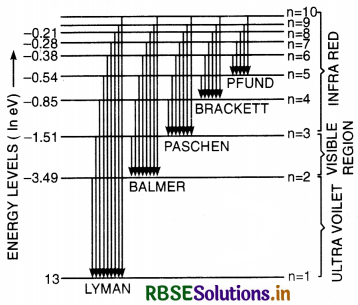
Sketch the energy level diagram for hydrogen atom. Mark the transition corresponding Lyman and Balmer series.
Answer:
Energy level diagram for Hydrogen atom.

Question 21.
Explain how Rutherford’s experiment on scattering of α-particles led to the estimation of the size of the nucleus.
Answer:
In Rutherford’s experiment most of α-particles were scattered by small angles of the order of a few degrees. A few α-particles about 1 in 8000, get deflected through 90° or more. To explain this, Rutherford concluded that all the positive charge and the mass of the atom is concentrated in a very small central region called the nucleus of the atom and the size of the nucleus was observed to be \(\frac{1}{10,000}\) the size of the atom.

Question 22.
In the given figure for the stationary orbits of the hydrogen atom, mark the transition representing the Balmer and Lyman series.

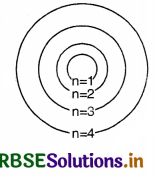
Answer:
The transitions representing the Balmer and Lyman series are shown in Fig. SAQ 22 (b).

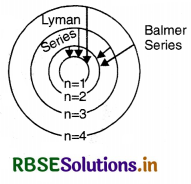
Question 23.
Derive an expression for the total energy of an electron in any orbit of a hydrogen atom according to Bohr atomic model.
Answer:
The force of attraction between the nucleus and the electron provides the necessary centripetal force for the revolving electron

Question 24.
State Bohr’s quantisation condition of angular momentum. Calculate the shortest wavelength of the Brackett series and state to which part of the electromagnetic spectrum does it belong.
Answer:
Bohr’s quantisation condition: Only those orbits are permitted in which the angular momentum of the electron is an integral multiple of h/2π.
For Brackett Series.
Shortest wavelength is for the transition of electrons from
n₁ = ∞ to n_f = 4
Using the equation

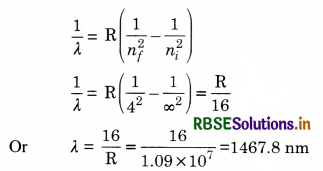
Question 25.
The energy levels of an atom of element X are shown in the diagram. Which one of the level transitions will result in the emission of photons of wavelength 620 nm? Support your answer with mathematical calculations.

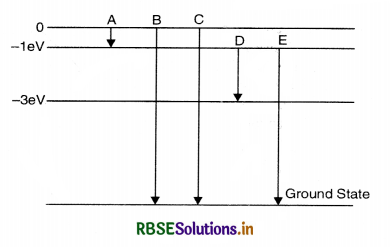
Answer:
Since E = hv = \(\frac{h c}{\lambda}\)
or λ = 620 nm = 620 x 10^-9 m
E = \(\frac{6.6 \times 10^{-34} \times 3 \times 10^8}{620 \times 10^{-9}}\) = 3.2 x 10^-19 J
E = \(\frac{3.2 \times 10^{-19}}{1.6 \times 10^{-19}}\) = 2 eV
In transition D, E = [-1 -(-2)] = 2 eV
So D transition will take place.

Question 26.
(a) State Bohr’s postulate to define stable orbits in hydrogen atom. How does de-Broglie’s hypothesis explain the stability of these orbits?
(b) A hydrogen atom initially in the ground state absorbs a photon which excites it to the n = 4 level. Estimate the frequency of the photon.
Answer:
(a) According to Bohr postulate, the electron can revolve around the nucleus in those orbits for which the orbital angular momentum is integral multiple of h/2π. These orbits are called non-radiating or stationary orbits.

Bohr suggested that stationary orbits are those in which orbital circumference (2πr) is an integral multiple of de-Broglie wavelength λ i.e., stationary orbits for an electron are those which contain the complete waves of electron. So we have
2πr = nλ,
where n = 1, 2, 3, ..................... ................(ii)
Also λ = \(\frac{h}{m v}\)
∴ 2πr = n\(\frac{h}{m v}\)
or m v r = \(\frac{h}{2 \pi}\) .........................(iii)
mvr is the angular momentum of the electron as particle. The equation (iii) corresponds to the Bohr's 2nd postulate, i.e, the total angular momentum of the moving electron is an integral multiple of ω. So the new concept of de-Broglie confirms Bohr's postulate.

(b) Given n₁ = 1 and n₂ = 4
Since \(\frac{1}{\lambda}=\mathrm{R}_{\mathrm{H}}\left[\frac{1}{n_1^2}-\frac{1}{n_2^2}\right]=\mathrm{R}_{\mathrm{H}}\left[\frac{1}{1}-\frac{1}{16}\right]=\frac{15}{16} \mathrm{R}_{\mathrm{H}}\)
As c = vλ
∴ \(\frac{c}{\lambda}\) = v
or v = c x \(\frac{15}{16}\) x R_H
= 3 x 10⁸ x \(\frac{15}{16}\) x 1.09 x 10⁷
or v = 3 x 10¹⁵ Hz.

Question 27.
Calculate the orbital period of the electron in the first excited state of hydrogen atom.
Answer:
First excited state n = 2, T = ?
T = \(\frac{2 \pi r}{v}=\frac{n^3 h^3}{4 \pi^2 m e^4 k^2}\), where k = \(\frac{1}{4 \pi \varepsilon_0}\)
Substituting the values, we have
T = \(\begin{array}{r} \frac{(2)^3\left(6.6 \times 10^{-34}\right)^3}{4 \times(3.14)^2 \times 9.1 \times 10^{-31} \times\left(1.6 \times 10^{-19}\right)^4} \\ \times\left(9 \times 10^9\right)^2 \end{array}\)
T = 1.22 x 10^-15 s.

Long Answer Type Questions

Question 1.
Give a brief account of Rutherford’s theory of scattering of alpha particles. What results did it have to the structure of an atom?
Answer:
Rutherford’s theory of scattering of α-particles when bombarded on a thin foil of a material becomes more and more diffused or scattered. The diffusion increases with thickness and atomic weight of the material of the foil. This phenomenon is called as Scattering.

Experimental arrangement
The schematic diagram of scattering of α-particles is shown in Fig. LAQ 1 (a).
B is a block of lead having a thin tunnel. This tunnel terminates into a hole H inside the block. The radium source emits α-particles in all directions. Most of α-particles are absorbed by the lead block. A thin pencil of α-rays comes out of the tunnel and falls on a gold foil. The gold atoms scatter the α-particles. When scattered α-particles fall on a screen S coated with zinc sulphide (Zn S), they produce flashes. These flashes are observed through the telescope T. Particles scattered through different angles can be observed by rotating the ZnS screen along with the telescope.


Observations.

• Most of the α-particles were scattered by small angles of the order of a few degrees.
• Some α-particles were scattered in the backward direction i.e. by angles more than 90°.
• A few of α-particles were reflected nearly straight back.

The graph between the total number of α-particles (N) scattered and scattering angle (O) was as shown in Fig. LAQ 1 (b).

Conclusion.

1. Since a large number of α-particles suffer practically no deviation, it means that major portion of atom is empty space.
2. The scattering of α-particles through large angles showed that these α-particles experienced a very strong electric force of repulsion. This indicates that the entire +ve charge of atom is confined in a small part of the volume of the atom.
3. The backward scattering of α-particles shows that most of the mass of atom is concentrated in a small portion of the volume of the atom.

Rutherford proposed the following model for the atom.
1. All positive charge and almost the entire mass of an atom is concentrated in a very small volume at the centre of atom. This concentrated positive charge and its mass is called the nucleus. The nucleus has a diameter of about 10^-14 m.
2. The nucleus is surrounded by the electrons to make the atom electrically neutral.
3. The electrons revolve about the nucleus in various circular orbits.

Rutherford pointed out that if the electrons inside the atom are not stationary for if they were at rest, they will be pulled into the positive nucleus due to strong electrostatic force of attraction between the nucleus and the elgctrons. He assumed that the electrons are revolving around the nucleus in the circular orbits, the necessary centripetal force is provided to them by the electrostatic force of attraction.

Question 2.
What is impact Explain.
Answer:
Impact Parameter
Suppose an α-particle is incident on a nucleus N along AB from large distance as shown in Fig. LAQ 2. The line drawn through the nucleus N and parallel to the direction of motion of the α-particle is called the head-on collision line. The perpendicular distance between the fine AB and this fine is called the impact parameter. It is denoted by b. The impact parameter of α-particles is defined as the perpendicular distance of the velocity vector of α-particle from the centre of the nucleus, when it is far away from the atom.

Path of an alpha particle in the Coulomb field of heavy nucleus. The impact parameter b and the scattering angle θ are defined as shown in the diagram and is given by

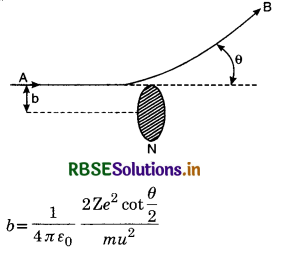
or b = \(\frac{1}{4 \pi \varepsilon_0} \frac{\mathrm{Z} e^2 \cot \frac{\theta}{2}}{\mathrm{E}_\alpha}\) [∵ E_α = \(\frac{1}{2}\) mv²]
For large impact parameter, an α-particle will go undeviated and for small impact parameter, α-particle will suffer large scattering because force experienced by α-particle obeys inverse square law. For head-on collision, the impact parameter b = 0 and the α-particle will be rebound because
for b = 0, cot\(\frac{\theta}{2}\) = 0
or \(\frac{\theta}{2}\) = 90° or θ = 180°
The scattering experiment provides us a method to know the nature of force between the nucleus and scattering particle.

Question 3.
What is distance of the closest approach? Derive an expression for it.
Answer:
Distance of the closest approach (r₀). It is the minimum distance upto which an α-particle travelling directly towards the centre of the nucleus can move before coming to rest and then retrace its path.

Expression for r₀
Let an α-particle of kinetic energy be approaching the nucleus from infinity along the head-on collision line Fig. 12.10. Let the collision between α-particle and the nucleus be elastic and the mass of nucleus is very large as compared to the mass of α-particle and both the α-particle and the nucleus are considered to be point charges. Let α-particle turn back from point P at a distance r₀ where its kinetic energy converts into electrostatic potential energy.
If m is the mass and u is the initial velocity of α-particle then
E_α = \(\frac{1}{2}\) mu²
If Ze is the charge on the nucleus and (2e) is the charge on α-particle.
Then, P.E. of α-particle at P,
E_p = \(\frac{1}{4 \pi \varepsilon_0} \frac{(\mathrm{Z} e)(2 e)}{r_0}=\frac{2 \mathrm{Z} e^2}{4 \pi \varepsilon_0 r_0}\) ..............................(1)
This is equal to the kinetic energy of α-particle. Thus
E_α = E_p = \(\frac{2 Z e^2}{4 \pi \varepsilon_0 r_0}\) ............................(2)

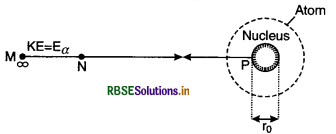
The minimum distance of the closest approach is
r₀ = \(\frac{2 Z e^2}{4 \pi \varepsilon_0 \mathrm{E}_\alpha}\) .............................(3)
or r₀ = \(\frac{1}{4 \pi \varepsilon_0} \frac{2 Z e^2}{\left(\frac{1}{2} m u^2\right)}\)
or r₀ = \(\frac{1}{4 \pi \varepsilon_0} \frac{4 Z e^2}{m u^2}\) .........................(4)
The distance of the closest approach is approximately equal to the radius of the nucleus of the atom.

Drawbacks of Rutherford’s Model
The electrons must revolve around the nucleus in order to prevent them from falling into the nucleus due to electrostatic force.
Rutherford atomic model offered serious difficulties as regards the utility of the atom. The drawbacks of this atom model are discussd below:
1. The electrons revolving round the nucleus are continuously accelerated towards the centre. According to Lorentz an accelerated charged particle should continuously radiate energy. Therefore, in an atom also, revolving electron should continuously emit energy and hence the radius of its path should go on decreasing and ultimately it should fall into the nucleus as shown in Fig. LAQ 3 (b). Therefore, Rutherford’s atomic model cannot explain the stability of the atom.


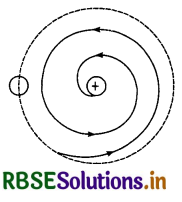
2. As such, electron can revolve in all possible radii on the basis of Rutherford’s atomic model and hence it should be able to emit continuous energy spectrum. However, an atom like hydrogen has line spectrum.

Question 4.
Discuss Quantization of energy on the basis of wave nature of particle.
Answer:
Energy quantization
In a wave motion particles come to rest after a distance on half wavelength \(\left(\frac{\lambda}{2}\right)\). The two ends of this distance must represent a rest position.
When, motion of a particle of mass m is confined to a line of length L, the ends of this length must represent rest position
Hence, L = n.\(\frac{\lambda}{2}\) here n = 1, 2, 3, ...................    
or λ = \(\frac{2 \mathrm{~L}}{n}\)
Thus wavelength is quantized.

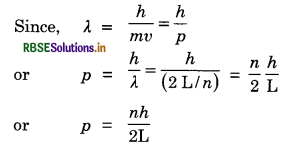
Thus momentum is also quantized.
Further, E =\( \frac{1}{2} m v^2=\frac{m^2 v^2}{2 m}=\frac{p^2}{2 m} \mathrm{E}=\frac{p^2}{2 m}\)
Thus energy is also quantized.

The quantized value of E is given by
E_n = \(\frac{(n h / 2 \mathrm{~L})^2}{2 m}\)
E_n = \(\frac{n^2 h^2}{8 m \mathrm{~L}^2}\), n = 1, 2, 3, ................
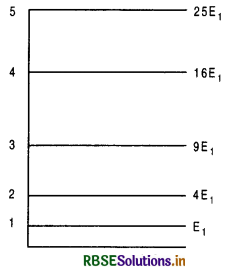
The parameter n which takes the integer values 1,2, 3, ............... labels the stationary states in ascending (increasing) order of energy (i.e. as n increases, E increases).
Hence, the energy of free particle of mass m, having motion confined to a line of length L can be only of the following values:
E₁ = \(\frac{h^2}{8 m L^2}\),
E₂ = \(\frac{4 h^2}{8 m L^2}\),
E₃ = \(\frac{9 h^2}{8 m L^2}\), ..................
E₄ = \(\frac{n^2 h^2}{8 m L^2}\),
and not any real number between zero and infinite as expected by classical mechanics.
The stationary state with the least energy E₁ = \(\frac{h^2}{8 m L^2}\), is called the ground state of quantum system.
Fig. LAQ 4 shows the energy level diagram for first five stationary states of a particle of mass m moving freely along a fine of length L.

Question 5.
State and explain Bohr’s postulates for the structure of the hydrogen atom. Obtain the expression for
(i) Radii of permitted orbits
(ii) The energy of an electron in the nth orbit.
(iii) Frequency of radiation emitted by hydrogen atom
(iv) Rydberg constant
Answer:
Bohr’s Postulates
In order to explain the stability of the atom and its line spectra, Bohr gave a set of postulates. 
1. An electron in an atom revolves in a circular orbit around the nucleus. The force of attraction between the electron and the nucleus provides the necessary centripetal force for the circular motion.

2. The electron can revolve in those orbits for which its orbital angular momentum is an integral multiple of h/2π. The allowed orbits are given by
mvr = \(\frac{n h}{2 \pi}\) .................... (1)
where n is an integer and h is Planck’s constant. The integer n is known as the principal number and can take any integral value 1, 2, 3, ........... .The numerical value of h is 6.624 x 10^-24 Js. This postulate is known as quantization of the angular momentum.

3. The electron moving in an allowed orbit does not radiate energy. Therefore, the total energy of the electron remains constant in an allowed orbit.

4.    Electromagnetic radiation is emitted when the electron jumps from a higher orbit having energy E_n1 to a lower orbit having E_n2. The frequency v of the emitted radiation is given as
v = \(\frac{\mathrm{E}_{n_2}-\mathrm{E}_{n_1}}{h}\) ...............................(2)
Eq. (2) represents the Bohr’s frequency condition.

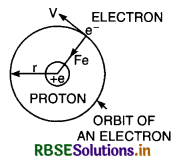
Bohr’s Theory of hydrogen atom
Hydrogen atom consists of nucleus proton carrying a positive charge +e. A single electron of charge -e is revolving around the nucleus in a circular orbit. Let r be the radius of the orbit. The force of attraction between the nucleus and the electron is
Fe = \(\frac{1}{4 \pi \varepsilon_0} \cdot \frac{e . e}{r^2}=\frac{e^2}{4 \pi \varepsilon_0 r^2}\) .............................(1)
where ε0 is the absolute permittivity of free space. This force provides the centripetal force for the revolving electron.
∴ \(\frac{e^2}{4 \pi \varepsilon_0 r^2}=\frac{m v^2}{r}\) .............................(2)
where v is the speed of the electron in the orbit and m is the mass.
Rewriting Eq. (2), we get mv² = \(\frac{e^2}{4 \pi \varepsilon_0 r}\) ............................(3)
According to Bohr’s second postulate,
mvr = \(\frac{n h}{2 \pi}\)
or v = \(\frac{n h}{2 \pi m r}\) ...........................(4)
Substituting this value of v in Eq. (2), we obtain
\(\frac{e^2}{4 \pi \varepsilon_0 r^2}=\frac{m}{r} \cdot \frac{n^2 h^2}{4 \pi^2 m^2 r^2} \quad \text { or } r=\frac{n^2 h^2 4 \pi \varepsilon_0}{4 \pi^2 m e^2}\) .........................(5)
The equation gives the radius of nth orbit out of the allowed orbits.
Thus for n = 1
r₁ = \(\frac{h^2 4 \pi \varepsilon_0}{4 \pi^2 m e^2}\) ............................(6)
Substituting the various values, we get
r₁ = \(\frac{\left(6.624 \times 10^{-34}\right)^2}{4 \times 9 \times 10^9 \times(3.142)^2 \times 9 \times 10^{-31} \times\left(1.6 \times 10^{-19}\right)^2}\)
or r₁ = 0.53 x 10^-10 m
= 0.53 Å .......................(7)
Energy of electron in hydrogen atom. The electron revolving around the nucleus possesses a kinetic energy. This kinetic energy is given by
K.E. = \(\frac{1}{2}\) mv²
Substituting the value of mv², from eq. (3)
K.E. = \(\frac{1}{2}\left(\frac{e^2}{4 \pi \varepsilon_o r}\right)\) ...........................(8)
The potential energy of the electron in the field of nucleus is
P.E. = \(\frac{(e)(-e)}{4 \pi \varepsilon_o r}=\frac{-e^2}{4 \pi \varepsilon_o r}\) .............................(9)
The total energy of E of electron is sum of the kinetic and potential energies of the electron. Thus
E = \(\frac{1}{2} \frac{e^2}{4 \pi \varepsilon_o r}-\frac{e^2}{4 \pi \varepsilon_o r}\)
E = \(\frac{e^2}{8 \pi \varepsilon_o r}\) ...............................(10)
Substituing the allowed values of r from Eq. (5), we obtain the allowed values of the energy hydrogen atom as
E = -\(\frac{e^2}{8 \pi \varepsilon_o} \frac{4 \pi^2 m e^2}{4 \pi \varepsilon_o n^2 h^2}\)
E = -\(\frac{m e^4}{8 \varepsilon_o^2 n^2 h^2}\) ..........................(11)
It must be noted that the total energy of hydrogen atom is negative and varies inversely as the square of principal quantum number n.
Thus, En = -\(\frac{m e^4}{8 \varepsilon_o^2 n^2 h^2}\) ..............................(12)
The allowed values of energy are called the energy levels of the hydrogen atom.

Frequencies of Radiations and Wave Number
Suppose an electron jumps from a higher orbit having quantum number n₂ to lower orbit having quantum number n₁. Let E_n1 and E_n2 be the energies of the states n₂ and n₁ respectively. Then,

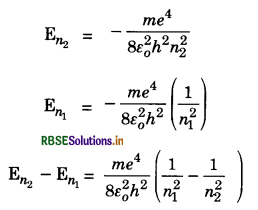
This difference in energy is emitted as radiations. The frequencies of emitted radiation according to fourth postulate is

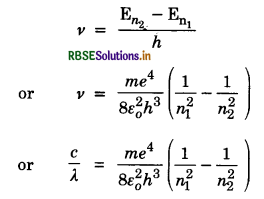
where λ is wavelength of radiation emitted and c is the velocity of light.
The above equation can be written as

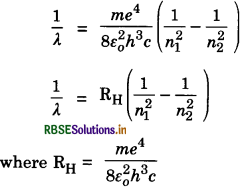
= 1.0974 x 10⁷ m^-1
R_H is called Rydberg constant for hydrogen atom. The quantity 1/λ represents the number of waves in a unit length. It is known as wave number and denoted by \(\bar{v}\).
∴ \(\bar{v}\) = R_H\(\left(\frac{1}{n_1^2}-\frac{1}{n_2^2}\right) \)
When the radiation emitted by a hydrogen atom are analysed in prism, or grating a spectrograph each transmission appears as a line. Therefore, the spectrum of hydrogen atom is a line spectrum.

Question 6.
(a) Explain various series of spectral lines of spectrum of hydrogen atom and draw energy level diagram.
(b) What are limitations of Bohr’s theory?
Answer:
(a) According to the equation
\(\bar{v}\) = R_H\(\left(\frac{1}{n_1^2}-\frac{1}{n_2^2}\right)\)
where n₂ = 2, 3, 4, ......................
1. Lyman series. When an electron jumps from any higher orbit to the first orbit, i.e. if n₁ = 1, and n₂ = 2, 3, 4, .................., the series obtained is called Lyman series. It is given by
\(\bar{v}\) = R_H\(\left(\frac{1}{1^2}-\frac{1}{n_2^2}\right)\)
It lies in the ultraviolet region.

2. Balmer series. When an electron jumps from any higher orbit to the second orbit, i.e. if n₁ = 2, and n₂ = 3, 4, 5 ............, the series obtained is called Balmer series. It is given by
\(\bar{v}\) = R_H\(\left(\frac{1}{2^2}-\frac{1}{n_2^2}\right)\),
It lies in the visible region.

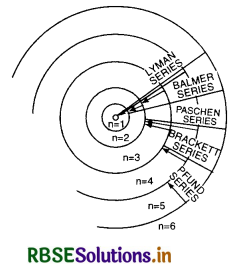
3. Paschen series. When an electron jumps from any higher orbit to the 3rd orbit, i.e. if n₁ = 3, and n₂ = 4, 5, 6, ......................., the series obtained is called Paschen series. It is given by
\(\bar{v}\) = R_H\(\left(\frac{1}{3^2}-\frac{1}{n_2^2}\right)\)
It lies in the infrared region.

4. Brackett series. When an electron jumps from any higher orbit to the 4th orbit, i.e. if n₁ = 4, and n₂ = 5, 6, 7, ........................, the series obtained is called Brackett series. It is given by
\(\bar{v}\) = R_H\(\left(\frac{1}{4^2}-\frac{1}{n_2^2}\right)\)
It lies in the infrared region.

5. Pfund series. When an electron jumps from any higher orbit to the 5th orbit, i.e. if n₁ = 5, and n₂ = 6, 7, 8, ........................, the series obtained is called Pfund series. It is given by
\(\bar{v}\) = R_H\(\left(\frac{1}{5^2}-\frac{1}{n_2^2}\right) \)
It lies in the infrared region.

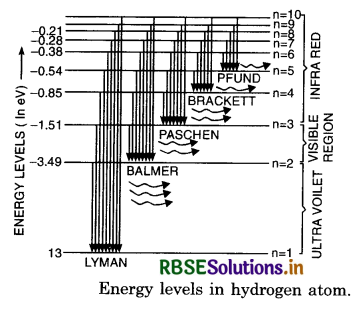
Energy Level Diagram of H-atom
The energy level diagram of various permitted stationary orbit is as shown in Fig. LAQ 6 (b). It is called Gossel's diagram.
The total energy of an electron in the nth orbit of hydrogen atom is

The energy of H-atom is the lowest when principal quantum number n = 1.
E₁ = -\(\frac{13.6}{(1)^2}\) eV

It is called ground state energy of H-atom. The state of the hydrogen when n = 1 is called normal or ground state.
The higher energy values of H-atom corresponding to n = 2, 3, ...................... are called excited state energies. The state corresponding to n = 2 is called first excited state.
The energy of 1st excited state
E₂ = \(\frac{-13.6}{(2)^2}\) eV = -3.4 eV
The state corresponding to n = 3 is called second excited state.
E₃ = \(\frac{-13.6}{32}\) eV = -1.51 eV
The energies of 3rd, 4th, .................. excited states of H-atom are -85 eV, -54 eV ..........................

(b) Limitations of Bohr theory
(a) When Bohr's theory is applied to atom with more than one electron, the predictions do not agree with experiments entirely. Certain perdicted lines are not observed at all.

(b) When the spectral lines are studied with a high resolution spectrograph, each line is found to consist of a group of several lines very close together. This is called fine structure of hydrogen lines. Bohr's theory does not explain this structure.

(c) It is observed experimentally that some spectral lines are stronger and others are weaker in intensity. Bohr's theory does not predict anything about the relative intensity of spectral lines.

(d) Bohr's postulates look arbitrary. There is no reason for assuming the orbit to be circular and having an angular momentum equal to integral multiple of h/2π.

HOTS QUESTIONS

Question 1.
A proton moves with speed of 7.45 x 10⁵ ms^-1 directly towards a free proton originally at rest. Find the distance of the closest approach for the two protons (m_p = 1.66 x 10^-27 kg).
Answer:
Let initial speed of proton = v
Let distance of the closest approach = r
If v₁ be the speed of two protons after attaining distance r, then
From law of conservation of momentum
mv + 0 = mv₁ + mv₂
or v₁ = \(\frac{v}{2}\) .............................(i)
From law of conservation of energy

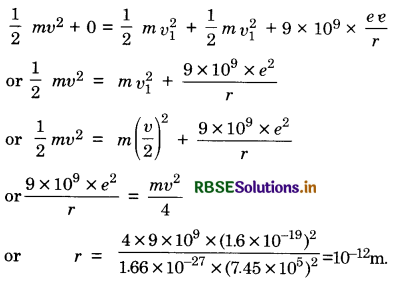
Question 2.
Calculate the radius of third orbit of hydrogen atom. Compare it with the radius of second Bohr orbit of singly ionised helium atom.
Answer:
We know that Bohr radius r₀ = 5.3 x 10^-11 m
For hydrogen atom,
rn = n²r₀ ......................(i)
∴ Radius of third orbit
r₃ = 3² x 5.3 x 10^-11 = 4.77 x 10^-10 m = 4.77 Å
For comparison of radii, the nth Bohr's orbit of singly ionised helium atom is
[r_n]_He + \(\frac{1}{Z} r_n=\frac{1}{Z}\left(n^2 r_0\right)\)
For He+, n = 2 and Z = 2
∴ (r₂)_He+ = \(\frac{1}{2}\) (4 x r₀) = 2r₀ = 2 x 0.53 Å
= 1.60 Å
∴ \(\frac{r_3}{\left[r_3\right]_{\mathrm{He}^{+}}}=\frac{4.77}{1.06}\) = 4.5.

Question 3.
The energy of an electron in an excited hydrogen atom is -3.4 eV. Calculate the angular momentum of the electron according to Bohr’s theory.
(Given Rydberg’s constant R = 1.09737 x 10^-7 m^-1, h = 6.626176 x 10^-34 Js, c = 3 x 10⁸ ms^-1)
Answer:
Energy of electron in nth orbit of hydrogen atom

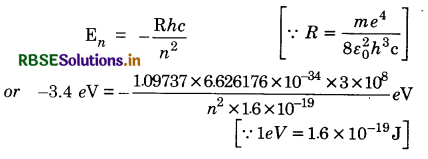
or n² = \(\frac{13.6}{3.4}\) = 4
or n = 2
For Bohr's quatum condition, angular momentum
mvr = \(\frac{n h}{2 \pi}\)
or = \(\frac{2 \times 6.626176 \times 10^{-34}}{2 \times 3.142}\)
= 2.1102 x 10^-34 Js.

Question 4.
The wavelength of first member of Balmer series in the hydrogen spectrum is 6563 Å.
(i) Calculate the wavelength of second member of Balmer series
(ii) The wavelength of first member of Lyman series in the same spectrum.
Answer:
For Balmer series, we have
\(\frac{1}{\lambda}=\mathrm{R}\left[\frac{1}{2^2}-\frac{1}{n_i^2}\right]\), ni = 3, 4, 5 ................
For 1st member of Balmer series, n = 3
∴ \(\frac{1}{\lambda}=\mathrm{R}\left[\frac{1}{2^2}-\frac{1}{3^2}\right] = \frac{5 \mathrm{R}}{36}\) .....................(i)

(i) For 2nd member of Balmer series, n = 4
∴ \(\frac{1}{\lambda}=\mathrm{R}\left[\frac{1}{2^2}-\frac{1}{4^2}\right] = \frac{3 \mathrm{R}}{16}\) .....................(ii)
∴ \(\frac{\lambda_1}{\lambda}=\frac{5 \mathrm{R} / 36}{3 \mathrm{R} / 16}=\frac{20}{27}\)
or λ₁ = \(\frac{20}{27}\) λ = \(\frac{20}{27}\) x 6563 Å = 4861 Å

(ii) For Lyman series, we have
\(\frac{1}{\lambda}=\mathrm{R}\left[\frac{1}{2^2}-\frac{1}{n_i^2}\right]\), ni = 2, 3, 4, ................
For 1st member of Lyman series ni = 2
∴\(\frac{1}{\lambda_2}=\mathrm{R}\left[\frac{1}{1^2}-\frac{1}{2^2}\right]=\frac{3 \mathrm{R}}{4}\) ........................(iii)
From (i) and (iii), we have
\(\frac{\lambda_2}{\lambda}=\frac{5 R / 36}{3 R / 4}=\frac{5}{27}\)
or λ₂ = \(\frac{5}{27}\) x λ = \(\frac{5}{27}\) x 6563 = 1215 Å

Question 5.
An α-particle of 10 MeV collides head-on with a copper nucleus (Z = 29) and returns on its original path. What conclusion would you draw about the size of the nucleus?
Answer:
Here Eα = 10 MeV = 10 x 1.6 x 10^-13 J
= 16 x 10^-13 J

or R = 8.4 x 10^-15 m