RBSE Class 12 Physics Important Questions Chapter 11 Dual Nature of Radiation and Matter

Rajasthan Board RBSE Class 12 Physics Important Questions Chapter 11 Dual Nature of Radiation and Matter Important Questions and Answers.

RBSE Class 12 Physics Chapter 11 Important Questions Dual Nature of Radiation and Matter

Multiple Choice Questions

Question 1.
Work function of a metal surface is 4.2 eV. The maximum wavelength which can eject electrons from this metal surface is:
(A) 3076 Å
(B) 4116 Å
(C) 2956 Å
(D) 5088 Å.
Answer:
(C) 2956 Å

Question 2.
The threshold wavelength of sodium metal is 6800 Å. The work function is:
(A) 1.82 eV
(B) 3.64 eV
(C) 0.91 eV
(D) 2.73 eV.
Answer:
(A) 1.82 eV

Question 3.
Photo electric current can be increased by using:
(A) higher frequency radiations
(B) higher intensity radiations
(C) higher work function metal plates
(D) none of these.
Answer:
(B) higher intensity radiations

Question 4.
A proton and α-particle are accelerated through the same potential difference. The ratio of their de-Broglie wavelength will be:
(A) 1 : 1
(B) 1 : 2
(C) 2 : 1
(D) 2 : 1.
Answer:
(D) 2 : 1.

Question 5.
The wavelength of an electron of energy 10 keV will be:
(A) 0.12 Å
(B) 1.2 Å
(C) 12 Å
(D) 120 Å.
Answer:
(A) 0.12 Å

Question 6.
If photon and an electron have same de-Broglie wavelength then:
(A) both have same kinetic energy
(B) proton has more K.E. than electron 
(C) electron has more K.E. than proton
(D) both have same velocity.
Answer:
(C) electron has more K.E. than proton

Question 7.
If we consider electrons and photons of same wave length, then they will have the same:
(A) velocity
(B) angular momentum
(C) energy
(D) momentum.
Answer:
(D) momentum.

Question 8.
The mass of photon at rest is:
(A) 1
(B) Infinite
(C) zero
(D) None of these
Answer:
(C) zero

Question 9.
When an electron is accelerated with 1V potential difference, then its kinetic energy is:
(A) \(\frac{1}{1840}\) eV
(B) 1840 eV
(C) 1eV
(D) 1840 c² eV.
Answer:
(C) 1eV

Question 10.
1 million electron volt is:
(A) 1.6 x 10^-19 J
(B) 1.6 x 10^-16 eV
(C) 1.6 x 10^-13 J
(D) 1.6 x 10^-11 eV.
Answer:
(C) 1.6 x 10^-13 J

Question 11.
Energy equivalent to mass of an electron is:
(A) 0.511 MeV
(B) 5.11 MeV
(C) 51.1 MeV
(D) 511 MeV.
Answer:
(A) 0.511 MeV

Question 12.
Electron volt (eV) is the unit of:
(A) Energy
(B) Potential
(C) Current
(D) Charge.
Answer:
(A) Energy

Question 13.
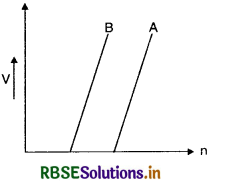
According to Einstein's photoelectric equation, the graph between K.E. of photoelectron ejected and frequency V of incident radiation is:

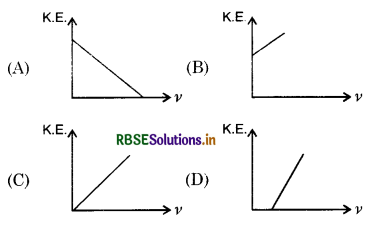
Answer:

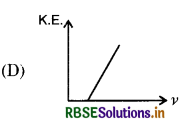
Question 14.
1 MeV is equal to:
(A) 10^-3 J
(B) 1.6 x 10^-13 J
(C) 1.6 x 10^-19 J
(D) 6.25 x 10¹⁸ J.
Answer:
(B) 1.6 x 10^-13 J

Question 15.
The momentum of a photon of frequency v is:
(A) \(\frac{h v}{c}\)
(B) \(\frac{h c}{v}\)
(C) Zero
(D) None of these.
Answer:
(A) \(\frac{h v}{c}\)

Fill in the blanks

Question 1.
Photon is not a ............................... particle.
Answer:
material.

Question 2.
Photoelectric effect demonstrate ............................... nature of radiations.
Answer:
particle.

Question 3.
Bright light means more photons, not more ............................... photons.
Answer:
energetic.

Question 4.
According to de-Broglie hypothesis matter has ............................... nature.
Answer:
wave.

Question 5.
A particle momentum associated with de-Broglie wave of wavelength λ is = ...............................
Answer:
\(\frac{h}{m v}\)

Question 6.
The wavelength of a photon and its de-Broglie wavelength are ...............................
Answer:
equal.

Question 7.
A moving particle is associated with a ............................... packet, rather than a wave.
Answer:
wave.

Question 8.
de-Broglie waves are ............................... from e.m. waves.
Answer:
different.

Question 9.
A photocell converts ............................... energy into electric energy.
Answer:
light.

Question 10.
The work function of alkali metals is ............................... low.
Answer:
very.

Very Short Answer Type Questions

Question 1.
What is rest mass of a photon?
Answer:
Zero.

Question 2.
Name different processes involved in electron emission.
Answer:
The processes are:

• thermionic emission
• field emission
• photoelectric emission
• secondary emission.

Question 3.
Define a photon.
Answer:
It is an energy particle (or packet) emitted by a source of radiation.

Question 4.
Define work function.
Answer:
It is the minimum energy required by a free electron to come out of the metal surface.

Question 5.
Give principle of a photocell.
Answer:
It works on phenomenon of photoelectric effect.

Question 6.
What is the momentum of a photon of frequency v?
Answer:
Momentum, p = \(\frac{h}{\lambda}\)
p = \(\frac{h}{c / v}=\frac{h v}{c}\)

Question 7.
Calculate momentum of electron, if their wavelength is 2 Å. given, Planck’s constant h = 6.626 x 10^-34 Js; mass of electron m = 9.1 x 10^-31 kg.
Answer:
Momentum, p = \(\frac{6.626 \times 10^{-34}}{2 \times 10^{-10}}\)
= 3.31 x 10^-24 kg ms^-1

Question 8.
What function does a photocell perform?
Answer:
It converts light energy into electric energy.

Question 9.
Light from a bulb is falling on a wooden table but no photoelectrons are emitted. Why?
Answer:
Since wood is a bad conductor (insulator) so it has no free electrons.

Question 10.
Why are alkali metals most suited as photosensitive materials?
Answer:
The work function of alkali metals is very low, so light of low frequency can also emit electrons from them.

Question 11.
Do all photoelectrons emitted from a metal surface possess the same energy?
Answer:
No. The energy range is from zero to certain maximum value [ = h (v - v₀)].

Question 12.
What determines the strength of photo-electric current?
Answer:
With the increase in intensity of incident radiation, the strength of photoelectric current increases.

Question 13.
Does the threshold frequency depend on intensity of light?
Answer:
No.

Question 14.
Is photoelectric emission possible at all frequencies?
Answer:
No, photoelectric emission takes place only if the frequency of incident light is more than threshold frequency.

Question 15.
What determines the maximum velocity of photoelectrons?
Answer:
The frequency of the incident radiations and work function of the metallic surface.

Question 16.
On what factor the retarding potential of photocell depends?
Answer:
Frequency of incident radiations.

Question 17.
What determines the maximum velocity of the photoelectrons?
Answer:
It depends upon (i) frequency of incident light and (ii) work function of the metallic surface.

Question 18.
How many electron volt make one joule?
Answer:
1 J = \(\frac{1}{1.6 \times 10^{-19}}\) eV = 6.25 x 10^-18 eV.

Question 19.
Which phenomenon illustrates the particle nature of light?
Answer:
Photoelectric effect.

Question 20.
Is matter wave an electromagnetic wave?
Answer:
No.

Question 21.
What information is derived from electron diffraction experiments?
Answer:
A particle possesses wave nature also.

Question 22.
With what purpose was famous Davisson Germer experiment with electrons performed?
Answer:
This experiment was performed to show wave nature of electrons.

Question 23.
The de-Broglie wavelength associated with an electron accelerated through a potential difference V is λ. What will be wavelength when accelerating potential is increased to 4 V?
Answer:
In first case.
λ = \(\frac{h}{\sqrt{2 m e \mathrm{~V}}}\)
In second case
λ' = \(\frac{h}{\sqrt{2 m e(4 \mathrm{~V})}}\)
∴ \(\frac{\lambda^{\prime}}{\lambda}\) = 2 or λ' = 2λ

Question 24.
How will the photoelectric current change on decreasing the wavelength of incident radiation for a given photosensitive material?
Answer:
Photelectric current will not change with decrease in wavelength of incident radiations.

Question 25.
Electrons are emitted from a photosensitive surface when it is illuminated by green light but electron emission does not take place by yellow light. Will the electrons be emitted when surface is illuminated by (i) red light, (ii) blue light?
Answer:
The energy of emitted photons E = hv
i.e. E ∝ v
And v_b > v_g > v_y > v_r
So E_b > E_g > E_y > E_r

• Since photoelectrons are not emitted by yellow light, so electrons will not be emitted by red light.
• Since green light is able to emit electrons so blue light will emit electrons with large velocity.

Question 26.
Ultraviolet light is incident on two photosensitive materials, having work functions W₁ and W₂, where W₁ > W₂. In which case will the kinetic energy of the emitted electrons be greater? Why?
Answer:
The kinetic energy will be more for substance having work function W₂.    [∵ W₂ < W₁]
Because, KE = hv - W.
So smaller the work function, more will be the KE of the emitted electrons.

Question 27. 
What is the de-Broglie wavelength of an atom of mass m, moving at absolute temperature T K?
Answer:
Since de-Broglie wavelength is given by
\(\lambda=\frac{h}{\sqrt{2 m \mathrm{~K}}}=\frac{h}{\sqrt{2 m\left(\frac{3}{2} k \mathrm{~T}\right)}}=\frac{h}{\sqrt{3 m k \mathrm{~T}}}\)
where k is Boltzmann constant.

Question 28.
Two metals A and B have work functions, 2 eV and 5 eV respectively. Which metal has lower threshold wavelength?
Answer:
Since work function,

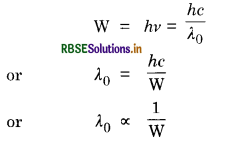
So larger the work function, smaller will the threshold wavelength. Hence metal B has lower threshold wavelength.

Question 29.
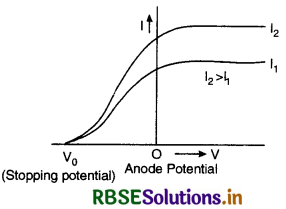
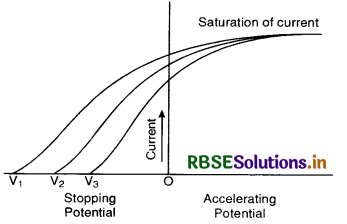
The figure VSAQ 29 shows a plot of three curves a, b,c showing the variation of photocurrent in collector plate potential for three different intensities I₁, I₂ and I₃ having frequencies v₁, v₂ and v₃ respectively incident on a photosensitive

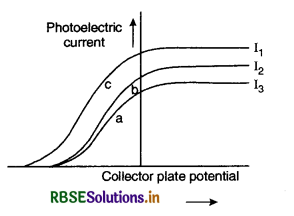
surface. Point out the two curves for which the incident radiations have the same frequency but different intensities.
Answer:
The curves a and b have the same frequency and different intensities I₃ and I₂. as the stopping potential for curves a & b is the same.

Question 30.
What is the stopping potential of a photocell, in which electrons with a maximum kinetic energy of 6 eV are emitted.
Answer:
eV₀ = KE
or eV₀ = 6 eV
or V₀ = 6 V.

Question 31.
How does the stopping potential applied to a photocell change, if the distance between the light source and the cathode of the cell is doubled?
Answer:
Stopping potential remains unchanged. Because on increasing the distance between the photocells and the source, the intensity of incident radiation decreases but stopping potential is independent of the intensity of incident radiations.

Question 32.
An electron and alpha particle have the same de-Broglie wavelength associated with them. How are their kinetic energies related to each other?    
Answer:
Since λ = \(\frac{h}{\sqrt{2 m \mathrm{E}}}\)
Since λ_e = λ_a

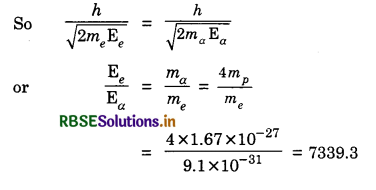
Question 33.
An electron and alpha particle have the same kinetic energy. How are the de-Broglie wavelengths associated with them related?
Answer:

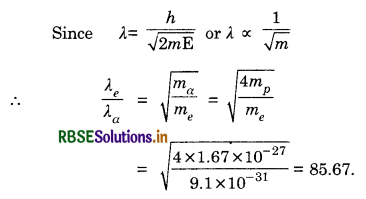
Question 34.
An electron and a proton have the same kinetic energy. Which one of two has larger wavelength and why?
Answer:
Electron has the larger wavelength
∴ \(\frac{\lambda_e}{\lambda_p}=\sqrt{\frac{m_p}{m_e}}=\sqrt{\frac{1.67 \times 10^{-27}}{9.1 \times 10^{-31}}}\)
= 42.83.

Question 35.
What is photon?
Answer:
A photon is a packet of energy of electromagnetic wave, and E = hv.

Question 36.
Define work function for a given metallic surface.
Answer:
Work function of a metallic surface is the minimum amount of energy required to eject an electron out of the metal surface.

Question 37.
How will photoelectric current change on decreasing the wavelength of incident radiation for a given photosensitive material?
Answer:
Photoelectric current will not change with decrease in wavelength of incident radiations.

Question 38.
Estimate the frequency associated with a photon of energy 2 eV.
Answer:
Since E = hv
∴ v = \(\frac{\mathrm{E}}{h}=\frac{2 e \mathrm{~V}}{6.63 \times 10^{-34} \mathrm{Js}}=\frac{2 \times 1.6 \times 10^{-19}}{6.63 \times 10^{-34}}\) Hz
or v = 4.8 x 10¹⁴ Hz.

Question 39.
In photoelectric effect, does the photoelectric current depend on the intensity of incident radiation? Give reasons.
Answer:
Yes, the photoelectric current depends on the intensity of incident radiations.
Reason:
When intensity of incident radiation is increased, there is an increase in number of photons falling on the surface of photosensitive material and hence photoelectric current inreases with increase in intensity of radiations.

Question 40.
In an experiment on photoelectric effect, the following graphs were obtained between the photoelectric current I and anode potential V. Name the characteristics of the incident radiation that was kept constant in this experiment.

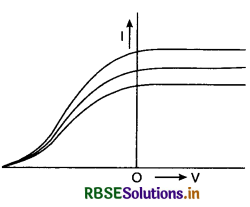
Answer:
Since stopping potential was the same for all the characteristics, it means that the frequency (or wavelength) of incident radiation was kept constant.

Question 41.
Two metals A and B have work functions, 2 eV and 5eV respectively. Which metal has lower threshold wavelength?
Answer:
Since work function,

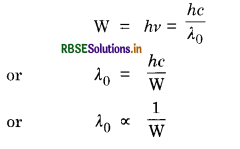
So larger the work function, smaller will the threshold wavelength. Hence metal B has lower threshold wavelength.

Question 42.
Does the ‘stopping potential’ in a photoelectric emission depend upon:
(i) intensity of incident radiation in a photo cell?
(ii) the frequency is incident radiation?
Answer:
Stopping potential depends upon the frequency of incident radiation and independent of intensity of radiation.

Question 43.
Draw graphs showing variation of photoelectric current with applied voltage for two incident radiations of equal frequency and different intensities mark the graph for the radiation of higher E intensity.
Answer:
The graph is as shown in figure VSAQ 43.

Question 44.
The frequency (v) of incident radiation is greater than threshold frequency (v₀) in a photocell. How will the stopping potential vary if frequency (v) is increased, keeping other factors constant.
Answer:
From Einstein’s photoelectric equation, we have
K.E. = hv - hv₀
or eV₀ = hv - hv₀
or V₀ = \(\frac{h}{e}\) (v - v₀)
Since v > v₀, so with the increase in v, the stopping potential increases.

Question 45.
If the intensity of radiation in a photocell is increased, how does the stopping potential vary?
Answer:
Stopping potential is independent of intensity of incident radiation, hence the stopping potential will remain unchanged.

Question 46.
How does the maximum kinetic energy of electrons emitted vary with the work function of the metal?
Answer:
The maximum kinetic energy of emitted electrons decreases, as the work function of the metal increases.

Question 47.
Express de-Broglie wavelength associated with electron in terms of the accelerating voltage V.
Answer:
The wavelength of electron is given by
λ = \(\frac{12.27}{\sqrt{\mathrm{V}}}\) Å

Question 48.
With what purpose was famous Davisson Germer experiment with electrons performed?
Answer:
Davisson-Germer experiment was performed to prove experimentally the wave nature of electrons.

Question 49.
de-Broglie wavelength associated with an electron accelerated through a potential difference V is λ. What will be the de-Broglie wavelength when the accelerating potential is increased to 4V.
Answer:
In 1st case
λ = \(\frac{h}{\sqrt{2 m e V}}\)
In 2nd case

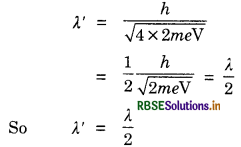
Question 50.
What is the de-Broglie wavelength (in Å) associated with an electron accelerated through a potential of 100 V?
Answer:
Since λ = \(\frac{12.27}{\sqrt{V}}\) Å
For V = 100 volt
λ = \(\frac{12.27}{\sqrt{100}}\) Å = 1.227 Å

Question 51.
A photon has velocity c and frequency v. Write the expression for its wavelength.
Answer:
Since c = vλ
So λ = \(\frac{c}{v}\)

Question 52.
Show graphically how the stopping potential for a given photosensitive surface varies with frequency of the incident radiation.
Answer:
The graph is as given in Fig. VSAQ 52.

Question 53.
Show graphically, the variation of the de-Broglie wavelength (λ) with the potential (V) through which an electron is accelerated from rest.
Answer:
The graph is as shown below.

Question 54.
In the wave picture of light, intensity of light is determined by square of the amplitude of wave. What determines the intensity of light in the photon picture of light?
Answer:
In photo picture, the intensity of light is given by number of photons crossing per unit time.

Question 55.
Name the phenomenon which shows the quantum nature of electromagnetic radiation.
Answer:
The quantum nature of electromagnetic radiation is shown by photoelectric effect.

Question 56.
State one factor which determines the intensity of light in the photon picture of light.
Answer:
Intensity of light is determined by number of photons emitted per second.
 
Short Answer Type Questions

Question 1.
Every metal has a definite work function. Why do photeloectrons not come-out all with same energy if incident radiation is monochromatic? Why is there an energy distribution of photoelectrons?
Answer:
Work function merely indicates the minimum energy required for the electron in the highest level of the conduction band to get out of the metal. Not all electrons in the metal belong to this level. They occupy a continuous bands of level. Consequently, for the same incident radiation, electrons knocked off from different levels come out with different energies.

Question 2.
Does every photon incident on photocathode cause emission of an electron?
Answer:
No, some of the photons may be absorbed by the photocathode. As this probability of absorption is also existing, so all the photons may not cause electron-emission.

Question 3.
Why is it important for photoelectric emission that the metal surface should be clean?
Answer:
In case the metal surface is not clean, then some impurity layer may be present on the metal surface. In order to eject an electron, the incident photon will have to have more work function to cross the impurity layer. So an incident photon may not be able to eject an electron if there is impurity layer on the surface of metal.

Question 4.
Explain two ways of emission of electrons from metal surfaces.
Answer:
Electrons can be emitted from metal surface by two ways:

• Photoelectric emission. If radiations of frequency above certain minimum frequency called threshold frequency is incident on the surface, electrons are emitted. Such electrons are called photoelectrons and the phenomenon is called photoelectric effect.
• Thermoelectric emission is the process of emission of electrons when metal surface is strongly heated. Such electrons are called thermoelectrons.

Question 5.
Define work function of a metal and photoelectric effect.
Answer:
Photoelectric effect is the phenomenon of emission of electrons from the surface of metals when light radiations of suitable frequency fall on them.

Work function of a metal is the minimum amount of the energy required to take away an electron from the metal when electromagnetic wave is incident on it.

Question 6.
State the relation between work function and threshold frequency.
Answer:
Work function W₀ is the minimum energy required to eject an electron from the surface with zero velocity. If v₀ is the frequency of light required for this purpose, then
W₀ = hv₀
v₀ is called threshold frequency.

Question 7.
Can visible light be able to emit an electron bound in a metal having binding energy of 4eV?
Answer:
Photoelectric emission takes place when the energy of incident photon is more than the work function of the metal. A photon of visible light carries energies between 0.81 eV to 3 eV, which is less than 4eV, so photoelectric emission will not take place in this case.

Question 8.
Work function of aluminium is 4.2 eV. If two photons each of energy 3eV strike an electron of aluminium, will the emission of electron be possible?
Answer:
No, the electron will not be emitted by the aluminium, because for the emission of electron the energy of each photon should be more than the work function of the surface (i.e. E > 4.2 eV)

Question 9.
State the dependence of work function on kinetic energy of electrons emitted in a photocell. If the intensity of the incident radiation is doubled, what changes occur in the stopping potential and photoelectric current?
Answer:
For a given frequency v of the incident radiation, the stopping potential V₀ is related to the maximum K.E. of the photoelectron which has been just stopped from reaching the collecting plate.
Maximum K.E. of the electron
= \(\frac{1}{2}\) mv²_max,
where m is the mass of the electron and v_max, the maximum velocity of the emitted electron. If e is the charge on electron then
eV₀ = \(\frac{1}{2}\) mv²_max
If the intensity of radiation is doubled, the number of photons available will be doubled and hence photoelectric current will be doubled but since v_max remains the same even on doubling the intensity, hence stopping potential will remain constant.

Question 10.
State the laws of photoelectric emission.
Or
What is photoelectric effect? State and explain the laws relating to this effect.
Answer:
Law of photoelectric emission are four definitions of photoelctric effect:

1. The velocity of electrons emitted is independent of the intensity of light and depend only upon the frequency (or wavelength) of the incident light.
2. Photoelectric current (or the number of photoelectrons ejected per second) is proportional to intensity of incident light. 
3. For a given metal, there exists a certain minimum frequency below which the emission of electrons stops completely. This frequency is called the threshold frequency.
4. Photoelectric emission is an instantaneous process.

Question 11.
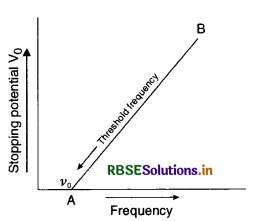
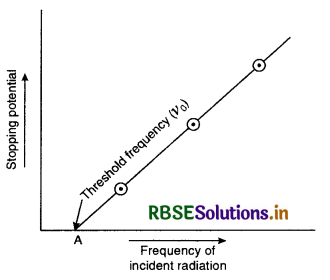
Draw a graph showing the variation of stopping potential with frequency of incident radiations in relation to photoelectric effect. Deduce an expression for the slope of this graph using Einstein's photoelectric equation.
Answer:
Graph between stopping potential V₀ and frequency v is as shown in figure.
According to Einstein photoelectric equation
eV = hv - W₀ .............................(1)
where W₀ is the work function and is constant for a substance.
Differentiating equation (i) partially, we get

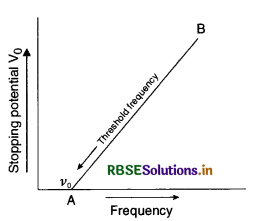
e ∆V = h ∆v - 0
or \(\frac{\Delta \mathrm{V}}{\Delta v}=\frac{h}{e}\)
But \(\frac{\Delta \mathrm{V}}{\Delta v}\) is the slope of line AB
∴ Slope of AB = \(\frac{h}{e}\), where h is the Planck's constant.

Question 12.
For photoelectric effect in a metal, the figure shows the plot of cut off voltage versus frequency of incident radiations. Calculate
(i) the threshold frequency;
(ii) the work function for given metal.

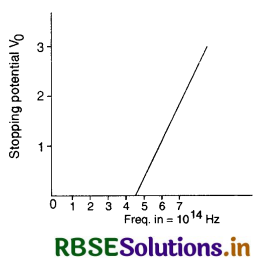
Answer:
The intercept made by the graph on frequency axis gives the threshold frequency.
∴ v₀ = 4.5 x 10¹⁴ Hz
Work function of the metal,
W₀ = hv₀
= 6.62 x 10^-34 x 4.5 x 10¹⁴ J
= 2.98 x 10^-19 J
or W₀ = \(\frac{2.98 \times 10^{-19}}{1.6 \times 10^{-19}}\) eV = 1.8625 eV.

Question 13.
Two metals X and Y have work functions 2 eV and 5 eV respectively. Which metal will emit electrons, when it is irradiated with light of wavelength 400 nm and why?
Answer:
Given λ = 400 nm = 400 x 10^-9 m
= 4 x 10^-7 m
∴ Energy of incident light

Hence metal-X will emit electrons.

Question 14.
Discuss dual nature of radiations.
Answer:
Dual Nature of Radiation
According to the wave theory, the radiant energy spreads out continuously in the form of waves but according to the quantum theory, the radiant energy spreads out in discrete packets (or quanta) each having the energy hv, where v is the frequency of the radiation and h is the Planck's constant. Its value is 6.624 x 10^-34 Js. These two theories are apparently contradictory. Some of the experimental observations can be explained on the basis of one theory and some other observations can be explained by the second theory. Therefore, one theory could not be rejected in favour of the other. With the development of quantum mechanics and experimental observations, the dual nature of radiation has been established. In other words, radiation behaves sometimes as waves and sometimes as particles. Thus, it is said to have dual nature.

Question 15.
Define the term threshold frequency and stopping potential in relation to phenomenon of photoelectric effect. How is the photoelectric current affected on increasing the (i) frequency
(ii) intensity of incident radiation and why?
Answer:
Threshold frequency. The minimum value of frequency of incident radiation below which photoelectric emission stops altogether is called Threshold frequency.

Stopping potential. The value of retarding potential at which the photoelectric current becomes zero is called stopping potential for the given frequency of incident radiations.

• When the frequency of incident radiation is increased (at constant intensity of radiation), the photoelectric current remains constant.
• When intensity of incident radiation is increased, there is an increase in number of photons falling on the surface of photosensitive material and hence photoelectric current increases with intensity of radiation.

Question 16.
Sketch a graph between frequency of incident radiations and stopping potential for a given photosensitive material. What information can be obtained from the value of the intercept of potential axis?
A source of light of frequency of greater than the threshold frequency is placed at a distance of 1 m from the cathode of a photocell. The stopping potential is found to be V. If the distance of the light source from the cathode is reduced, explain giving reasons, what change will you observe in the:
(i) Photoelectric current,
(ii) Stopping potential?
Answer:
For first part:
Graph between stopping potential V₀ and frequency v is as shown in figure.
According to Einstein photoelectric equation
eV = hv - W₀ .............................(1)
where W₀ is the work function and is constant for a substance.
Differentiating equation (i) partially, we get

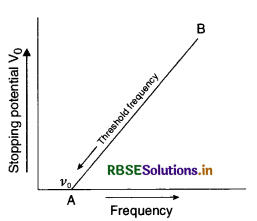
e ∆V = h ∆v - 0
or \(\frac{\Delta \mathrm{V}}{\Delta v}=\frac{h}{e}\)
But \(\frac{\Delta \mathrm{V}}{\Delta v}\) is the slope of line AB
∴ Slope of AB = \(\frac{h}{e}\), where h is the Planck's constant.

It is given that stopping potential is V and v > v₀.
(i) Photoelectric current will increase as the distance between source from the cathode is decreased.
(ii) Stopping potential will remain the same, till the frequency of incident radiation remains the same.

Question 17.
Sketch the graphs showing the variation of stopping potential with frequency of incident radiations for two photosensitive materials A and B having threshold frequencies v₀ > v₀' respectively?
(i) Which of the two metals, A or B has higher work function?
(ii) What information do you get from the slope of the graphs?
(iii) What does the value of the intercept of graph ‘A’ on the potential axis represent?
Answer:
Graph between variation of stopping potential and frequency of incident radiation.

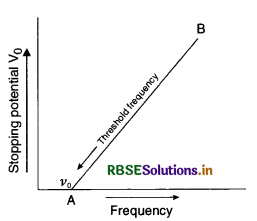
(i) Since work function, W₀ ∝ v₀.
So metal B has higher work function than metal A.
(ii) The slope of the graph helps to find the Planck’s constant.
(iii) Intercept of the graph A on the potential axis gives threshold frequency v₀.

Question 18.
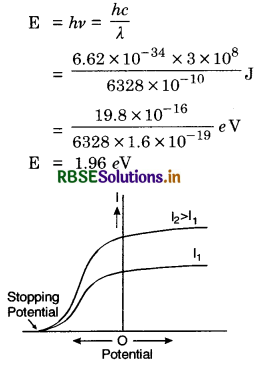
Ultraviolet light of wave-length 2271 Å from a 100 W mercury source radiates a photocell made of molybednum metal. If the stopping potential is 1.3 V, estimate the work function of the metal. How would the photocell respond to high intensity (10⁸ W m^-2) red light of wavelength 6328 Å produced by a He-Ne laser?
Plot a graph showing the variation of photoelectric current with anode potential for two light beams of the same wavelength but different intensity.
Answer:
Stopping potental of molybednum = 1.3 V
∴ Work function of molybednum = 1.3 eV
Energy of photon of red light,

As E is more than the work function of molybednum, hence it will emit electrons.
Since wavelength of two sources is the same but intensity is different, so stopping potential is the same and saturation current will be more for more intense light as shown in Fig. SAQ 18.

Question 19.
Mention the significance of Davisson and Germer’s experiment. An α-particle and a proton are accelerated from rest through the same potential difference V. Find the ratio of de-Broglie wavelength associated with them.
Answer:
The significance of Davisson and Germer’s experiment is that it confirms the wave nature of moving electrons.
Since E = qV = \(\frac{1}{2}\) mv²
∴ m²v² = 2qmV
or mv = \(\sqrt{2 q m \mathrm{~V}}\)
So λ = \(\frac{h}{m v}=\frac{h}{\sqrt{2 q m \mathrm{~V}}}\)
For proton, M = m, q = e & λ = λ_p
So λ_p = \(\frac{h}{\sqrt{2 e m \mathrm{~V}}}\)
For α-particle 
M = 4 m, q = 2e and λ = λ_α

Question 20.
Red light, however bright, it cannot produce the emission of electrons from a clean tine surface, but even weak ultraviolet radiation can do so, why?
X-rays of wavelength λ fall on a photosensitive surface, emitting electrons. Assuming the work function of the surface can be neglected, prove that the de-Broglie wavelength of electrons emitted will be \(\sqrt{\frac{h \lambda}{2 m c}}\)
Answer:
Because the work function of zinc surface is more than red light and less than the energy of ultraviolet light.
To prove that de-Broglie wavelength = \(\sqrt{\frac{h \lambda}{2 m c}}\)
From Einstein's photoelectric equation,

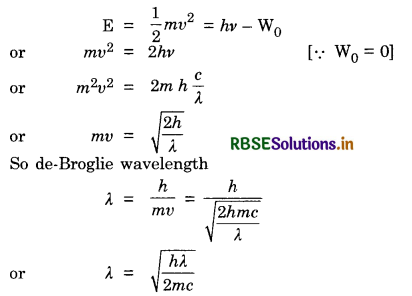
Question 21.
Define the term work function of a metal. The threshold frequency of a metal is f₀ when the light of frequency 2f₀ is incident on the metal plate, the maximum velocity of electrons emitted is v₁. When the frequency of the incident radiation is increased to 5f₀, the maximum velocity of electrons emitted is v₂. Find the ratio of to v₂.
Answer:
Work function (W₀). The minimum energy required in order to remove the electrons from the metal surface so as to overcome the surface barrier is called the work function of the metal.
From Einstein’s photoelectric equation,

Question 22.
A photon and an electron have got the same de-Broglie wavelength. Which has greater total energy? Explain.
Answer:
Energy, E₁ = hv = \(\frac{h c}{\lambda}\) .............................(i)
For an electron, moving with velocity v and effective mass m, the de-Broglie wavelength is given by
λ = \(\frac{h}{m v}\) or m = \(\frac{h}{\lambda v}\)
Total energy of the electron,
E₂ = mc² = \(\left(\frac{h}{\lambda v}\right)\)c² ............................(ii)
From (i) and (ii), we have
\(\frac{\mathbf{E}_2}{\mathbf{E}_1}=\left(\frac{h}{\lambda v}\right) c^2 \times \frac{\lambda}{h c}=\frac{c}{v}>1\)
∴ E₂ > E₁ thus electron has total energy greater than that of photon.

Question 23.
The de-Broglie wavelength of a photon is the same as the wavelength of electron. Show that kinetic energy of photon is \(\frac{2 \mathrm{mc} \lambda}{\mathrm{h}}\) times the kinetic energy of electron, where m is the mass of electron and c is the velocity of light.
Answer:
Given λ_ph = λ_e = λ = \(\frac{h}{m v}\)
K.E. of photon, E_ph = hv = \(\frac{h c}{\lambda}\) ..............................(i)
K.E. of electron,

Question 24.
Show that de-Broglie hypothesis of matter wave supports the Bohr's concept of stationary orbit.
Answer:
According to de-Broglie hypothesis, the wavelength of the wave associated with electron while moving with velocity v is given by
λ = \(\frac{h}{m v}\) ........................(i)
According to de-Broglie, stationary orbit is that orbit whose circumference is integral multiple of wavelength of wave associated with electron in that orbit.
If λ is the de-Broglie wavelength of electron while revolving in an orbit of radius r, then
2 πr = nλ
or λ = \(\frac{2 \pi r}{n}\) ...........................(ii)
From (i) and (ii)
\(\frac{2 \pi r}{n}=\frac{h}{m v}\)
or mvr = \(\frac{n h}{2 \pi}\)
i. e. Total angular momentum = n\(\left(\frac{h}{2 \pi}\right)\)
This is what is stated by Bohr about his stationary orbit.

Question 25.
Why is the wave nature of matter not apparent in our daily observations?
Answer:
The value of de-Broglie wavelength associated with a moving particle is given by
λ = \(\frac{h}{m v}\)
Consider a particle of mass 1 kg moving with velocity v = 1ms^-1, then wavelength of de-Broglie wave associated with the particle will be
λ = \(\frac{6.62 \times 10^{-34}}{1 \times 1}\)
= 6.62 x 10^-34 m
This value of λ is of the order of 10^-34 m and is very small as compared to the size of the particle of 1 kg would possess and hence λ cannot be detected by any instrument. So wave nature of matter is not apparent in our daily observations.

Question 26.
An electromagnetic wave of length λ is incident on a photosensitive surface of negligible work function. If the photoelectrons emitted from the surface have the same de-Broglie wavelength λ, prove that λ = \(\left(\frac{2 m c}{h}\right) \lambda_1^2\).
Answer:
Kinetic energy of electromagnetic wave is
E = \(\frac{h c}{\lambda}\) .......................(1)
de-Broglie wavelength

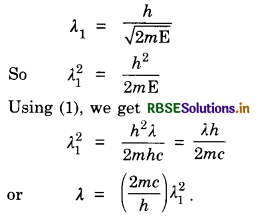
Question 27.
Show that Bohr’s second postulate ‘the electron revolves around the nucleus only in certain fixed orbits without radiating energy can be explained on the basis of de-Broglie hypothesis of wave nature of electron.
Answer:
According to de-Broglie hypothesis, the wavelength of the wave associated with electron while moving with velocity v is given by
λ = \(\frac{h}{m v}\) ..........................(i)
According to de-Broglie, stationary orbit is that orbit whose circumference is integral multiple of wavelength of wave associated with electron on that orbit.
If λ is the de-Broglie wavelength of electron while revolving in an orbit of radius r, then
2 πr = nλ
or λ = \(\frac{2 \pi r}{n}\) ...........................(ii)
From (i) and (ii),
\(\frac{2 \pi r}{n}=\frac{h}{m v}\)
or mvr = \(\frac{n h}{2 \pi}\)
i.e. Total angular momentum = n \(\left(\frac{h}{2 \pi}\right)\)
This is stated by Bohr about his stationary orbits.

Question 28.
In Davisson and Germer experiment, states the observation which led to (i) show the wave nature of electrons and (ii) confirm the de-Broglie relation.
Answer:
1. A fine beam of accelerated electrons is made to fall on nickel crystal and the intensity of electron beam scattered in the given direction is detected for different values of Φ. Graphs are plotted between I and Φ and a bump is observed at accelerating voltage 54 V and Φ = 50°. This bump is due to constructive interference of electrons scattered from different layers of regularly spaced atoms of the crystal. This establishes wave nature of electron.

2. From Bragg’s law for first order diffraction 2d sin θ = λ
For Ni crystal d = 0.91 Å and θ = 65°
so λ = 2 x 0.91 x sin 65° = 1.65 Å
According to de-Broglie hypothesis, the wavelength of electron in a p.d. 54 V is
λ = \(\frac{12.27}{\sqrt{54}}\) Å = 1.66 Å
So there is close agreement with the estimated value of de-Broglie wavelength and the experimental value given by Davisson-Germer method. This confirms the de-Broglie relation for electrons in motion.

Question 29.
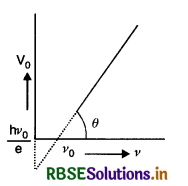
Write Einstein’s photoelectric equation in terms of the stopping potential and the threshold frequency for a given photosensitive material. Draw a plot showing the variation of stopping potential vs the frequency of incident radiation.
Answer:
From Einstein’s photoelectric equation, we have
(K.E.)_max = hv - W ....................(1)
If V₀ is stopping potential and v₀ is threshold frequency, then
[K.E.]_max = eV₀ and W = hv₀
So eq. (1) becomes eV₀ = hv - hv₀ = h (v - v₀)

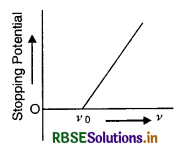
This is Einstein’s photoelectron equation in terms of the stopping potential and the threshold frequency graph between stopping potential and the frequency of incident radiation v is given in Fig.

Question 30.
Define the term work function of a metal. The threshold frequency of a metal is f₀ when the light of frequency 2f₀ is incident on the metal plate, the maximum velocity of electrons emitted is v₁. When the frequency of the incident radiation is increased to 5f₀, the maximum velocity of electrons emitted is v₂. Find the ratio of v₁ to v₂.
Answer:
Work function (W₀). The minimum energy required in order to remove the electrons from the metal surface so as to overcome the surface barrier is called the work function of the metal.
From Einstein’s photoelectric equation,

Question 31.
State the dependence of work function on kinetic energy of electrons emitted in a photocell. If the intensity of the incident radiation is doubled, what changes occur in the stopping potential and photoelectric current?
Answer:
For a given frequency v of the incident radiation, the stopping potential V₀ is related to the maximum K.E. of the photoelectron which has been just stopped from reaching the collecting plate.
Maximum K.E. of the electron
= \(\frac{1}{2}\) mv²_max,
where m is the mass of the electron and v_max, the maximum velocity of the emitted electron. If e is the charge on electron then
eV₀ = \(\frac{1}{2}\) mv²_max
If the intensity of radiation is doubled, the number of photons available will be doubled and hence photoelectric current will be doubled but since v_max remains the same even on doubling the intensity, hence stopping potential will remain constant.

Question 32.
Define the term threshold frequency and stopping potential in relation to phenomenon of photoelectric effect. How is the photoelectric current affected on increasing the (i) frequency (ii) intensity of incident radiation and why?
Answer:
Threshold frequency. The minimum value of frequency of incident radiation below which photoelectric emission stops altogether is called Threshold frequency.

Stopping potential. The value of retarding potential at which the photoelectric current becomes zero is called stopping potential for the given frequency of incident radiations.
(i) When the frequency of incident radiation is increased (at constant intensity of radiation), the photoelectric current remains constant.
(ii) When intensity of incident radiation is increased, there is an increase in number of photons falling on the surface of photosensitive material and hence photoelectric current increases with intensity of radiation.

Question 33.
Sketch a graph between frequency of incident radiations and stopping potential for a given photosensitive material. What information can be obtained from the value of the intercept of potential axis?
A source of light of frequency of greater than the threshold frequency is placed at a distance of 1 m from the cathode of a photocell. The stopping potential is found to be V. If the distance of the light source from the cathode is reduced, explain giving reasons, what change will you observe in the:
(i) Photoelectric current,
(ii) Stopping potential?
Answer:
For first part:
Graph between stopping potential V₀ and frequency v is as shown in figure.
According to Einstein photoelectric equation
eV = hv - W₀ .............................(1)
where W₀ is the work function and is constant for a substance.
Differentiating equation (i) partially, we get

e ∆V = h ∆v - 0
or \(\frac{\Delta \mathrm{V}}{\Delta v}=\frac{h}{e}\)
But \(\frac{\Delta \mathrm{V}}{\Delta v}\) is the slope of line AB
∴ Slope of AB = \(\frac{h}{e}\), where h is the Planck's constant.

It is given that stopping potential is V and v > v₀.
(i) Photoelectric current will increase as the distance between source from the cathode is decreased.
(ii) Stopping potential will remain the same, till the frequency of incident radiation remains the same.

Question 34.
Sketch the graphs showing the variation of stopping potential with frequency of incident radiations for two photosensitive materials A and B having Threshold frequencies v₀ > v₀' respectively?
(i) Which of the two metals, A or B has higher work function?
(ii) What information do you get from the slope of the graphs?
(iii) What does the value of the intercept of graph ‘A’ on the potential axis represent?
Answer:
Graph between variation of stopping potential and frequency of incident radiation.

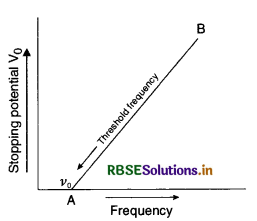
(i) Since work function, W₀ ∝ v₀.
So metal B has higher work function than metal A.
(ii) The slope of the graph helps to find the Planck’s constant.
(iii) Intercept of the graph A on the potential axis gives threshold frequency v₀.

Question 35.
Why is wave theory of electromagnetic radiation not able to explain photoelectric effect? How does photon picture resolve this problem?
Answer:
According to the wave theory, more intense a beam, more is the kinetic energy it will impart to the photoelectron. This does not agree with the experimental observations (max K.E. of emitted photoelectron is independent of intensity) on the photoelectric effect. Also according to the wave theory photoemission can occur at all frequencies.

The photon picture resolves this problem by saying that light in interaction with matter behaves as if it is made of quanta or packets of energy, each of energy hv. This picture enables us to get a correct explanation of all the observed experimental features of photoelectric effect.

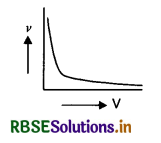
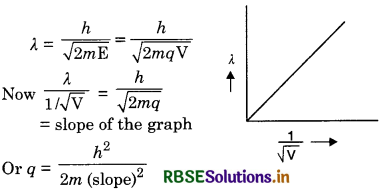
Question 36.
Plot a graph showing variation of de Broglie wavelength (λ) associated with a charged particle of mass m, versus V is the potential difference through which the particle is accelerated. How does this graph give us the information regarding the magnitude of the charge of the particle?
Answer:
The plot is as shown Fig. SAQ 36.
We know that

Question 37.
Red light, however bright, it cannot produce the emission of electrons from a clean zinc surface, but even weak ultraviolet radiation can do so, why?
X-rays of wavelength A fall on a photosensitive surface, emitting electrons. Assuming the work function of the surface can be neglected, prove that the de-Broglie wavelength of electrons emitted will be \(\sqrt{\frac{h \lambda}{2 m c}}\)
Answer:
Because the work function of zinc surface is more than red light and less than the energy of ultraviolet light.
To prove that de-Broglie wavelength = \(\sqrt{\frac{h \lambda}{2 m c}}\)
From Einstein's photoelectric equation,

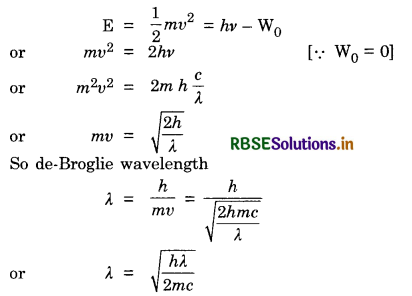
Question 38.
A electron is accelerated through a potential difference of 10V. What is the de- Broglie wavelength associated with it? To which part of the electromagnetic spectrum does this value of wavelength correspond?
Answer:
The de-Broglie wavelength of electron
λ = \(\frac{12.27}{\sqrt{\mathrm{V}}}\) Å = \(\frac{12.27}{\sqrt{100}}\) = 1.227 Å
or λ = 1.227 x 10^-10 m
This wavelength belongs to X-lays.

Question 39.
Plot a graph showing the variation of stopping potential with the frequency of incident radiation for two different photosensitive materials having work functions and W₂ (W₁ > W₂). On what factors does the (i) slope and (ii) intercept of the lines depends?
Answer:
The graph between variation of stopping potential and frequency is shown is Fig. SAQ 39.

Since work function W = hv₀
Let W₁ be work function of photosensitive material A and W₂ is that of B, then the threshold frequency for material A will be greater than that of B.
The slope of the line = \(\frac{V}{\lambda}\) i.e. the slope of the line is ratio of stopping potential and frequency which is constant for all metals. The intercept of the line depends upon the threshold frequency and larger the work function, more will be the threshold frequency.

Question 40.
(i) Name the experiment which confirms the existence of wave nature of electrons. Derive the expression for de-Broglie wavelength of an electron moving under a potential difference of V volts.
(ii) An electron and a proton have the same kinetic energy. Which of these particles has the shorter de-Broglie wavelength?
Answer:
(i) The name of experiment is: Davisson - Germer experiment.
Expression for de-Broglie wavelength of an electron moving in a potential difference of V volts.
And λ = \(\frac{h}{\sqrt{2 m e \mathrm{~V}}}=\frac{12.27}{\sqrt{\mathrm{V}}}\) Å

(ii) λ = \(\frac{h}{\sqrt{2 m e \mathrm{~V}}}\)
or λ ∝ \(\frac{1}{\sqrt{m}}\)
We know that mass of proton is more than mass of electron.
So λ_p < λ_e

Question 41.
Using photon picture of light, show how Einstein’s photoelectric equation can be established. Write two features of photoelectric effect which cannot be explained by wave theory.
Answer:
Einstein’s photoelectric equation

1. Radiation with frequency ν consists of a stream of discrete quanta or photons, with energy hν, where h is Planck’s constant. Photons travel at the speed of light through space.
2. When photons and electrons in the emitter’s atoms collide when radiation of frequency ν is incident on a photosensitive surface. During such a collision, the photon’s whole energy is transmitted to the electron with no time lag.

A photon is not a material particle but quanta of energy. The incident photon’s absorbed energy hv by an electron is utilized in two ways. The electron uses some of its energy to break free from the atom. The minimum energy required to free-electron from a given surface is called photoelectric work function φ₀ of the material of the surface.
(i) Wave theory could not explain instantaneous emission of photons.
(ii) Wave theory could not explain the concept of threshold frequency.

Question 42.
If light of wavelength 412.5 nm is incident on each of the metals given below, which one will show photoelectric emission and why?

Metal	Work function (eV)
Na	1.92
K	2.15
Ca	3.20
Mg	4.17

Answer:
Na and K. Because
E = \(\frac{h c}{\lambda}=\frac{6.67 \times 10^{-34} \times 3 \times 10^8}{412.5 \times 10^{-9}}\) = 0.048 x 10^-7 J
= \(\frac{0.048 \times 10^{-7}}{1.6 \times 10^{-19}}\) eV
E = 3 eV
So metals having work function less than 3 eV will show photoelectric effect. Hence both Na and K will show photoelectric effect.

Long Answer Type Questions

Question 1.
(a) What do you mean by "free electrons” in metals? Define work function.
(b) What is electron emission? What are various types of electron emission?
Answer:
(a) Free electrons in metals
Within a solid piece of a substance like lithium, atoms are closely packed and, therefore, the loosely bound electrons of each atom are easily moved from the influence of their nucleus to that of their neighbour. Such loosely bound (actually unbounded) electrons are called free electrons.

Work function
The minimum energy required in order to remove the electrons from the metal surface so as to overcome the surface barrier is called the work function of the metal.
It is measured in electron volt (eV). The work function of a metal depends upon its nature and condition of its surface.

(b) Electron emission
The phenomenon of the emission of electrons from the surface of a metal is known as electron emission.
There are four ways of getting it done:
1. Thermionic emission. When a metal filament is sufficiently heated by passing electric current through it so as to overcome the work function (Φ) of the metal electrons are ejected from its surface. This process of emission of electrons from a metal surface at high temperature is called thermionic emission.

2. Photoelectric emission. When electromagnetic radiation of suitable energy is allowed to fall on a photosensitive material, electrons may be emitted from its surface. This effect is called photoelectric effect and the emitted electrons are called photoelectrons.

3. Field emission. When a very strong electric field (-10⁹ volts/m) is applied on the metal, it emits electrons. The type of emission is called field emission. This method is difficult and dangerous. So this method is not used in domestic electronic devices.

4. Secondary emission. When fast moving electrons strike with the surface of a metal, electrons are emitted from the metallic surface. These electrons are called secondary electrons and the phenomenon is known as secondary emission. This method is of limited applications.

Question 2.
What are photons? State their properties?
Answer:
Photon. A photon is a quantum or packet of energy which has zero rest mass and energy equal to product of the frequency of the radiation and Planck’s constant.
i.e. E = hv

Features.
1. Photon always travel in straight lines.
2. Energy of photon, E = hv
3. Wavelength of photon λ = \(\frac{c}{v}\)
4. Mass of photon = \(\frac{h v}{c^2}\)
5. Momentum of photon = \(\frac{h v}{c^2} \cdot c=\frac{h v}{c}\left(\text { or } \frac{h}{\lambda}\right)\)
Since mass depends upon frequency, so is not the same for all photons of different frequency.
6. Rest mass of photon is zero
Since mass of moving particle is given by
m = \(\frac{m_0}{\sqrt{1-\frac{v^2}{c^2}}}\)
where m₀ is rest mass of the particle, v is the velocity of particle and c is the velocity of light
∴ m₀ = m\(\sqrt{1-\frac{v^2}{c^2}}\)
For photon, v = c
∴ Rest mass of photon, m₀ = m\(\sqrt{1-\frac{c^2}{c^2}}\) = 0 
7. Photons are electrically neutral.
8. They cannot be deflected by electrical or magnetic field.

Question 3.
(a) What is photoelectric effect? Give experiments to show the variation of current with intensity of radiation, effect of potential and frequency of incident radiation on photoelectric current.
(b) Hence deduce the laws of photoelectric emisson.
Answer:
(a) Photoelectric effect
In 1887, Hallwachs discovered that an insulated Zn-plate, negatively charged, lost its charge if exposed to ultraviolet light. Hertz had previously noticed that a spark passed more easily across the gap of an induction coil when the negative metal terminal was exposed to sun light. Afterwards, it was discovered that alkali metals like Li, Na, K, Rb and Cs eject electrons when illuminated by visible light. Thus, the surface atoms absorb the energy of radiations falling on them and emit electrons. This is called photoelectric effect.

The phenomenon of ejection of electrons from a metal surface when illuminated by light, or any other radiations of suitable wavelength (or frequency) is called photoelectric effect. The emitted electrons are called photoelectrons because they are liberated by means of light.

Experimental study of photoelectric effect Photoelectric phenomenon can be studied by a simple device as shown in Fig. It consists of a simple quartz tube T with photosensitive plate P called emitting electrode and the other electrode C called collecting electrode. This tube with electrodes is called photo tube. Ultraviolet light can be made to enter the tube through a window W.

A H.T. battery B is connected to a resistance R the mid point of which is earthed so that the plate P is at zero potential. Collector C can be maintained at a desired positive or negative potential w.r.t. P. The potential difference between the electrodes P and C can be measured by a voltmeter V and current flowing in the circuit by microammeter (µA).

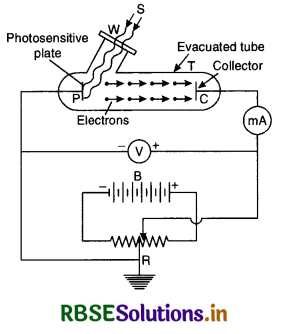
In the absence of any radiations there is no flow of the electrons in the circuit and microammeter shows no deflection. When ultraviolet light is made to fall on photosensitive plate P, it emits photoelectrons which are collected by the collecting plate C and the current flows in the circuit as indicated by microammeter.

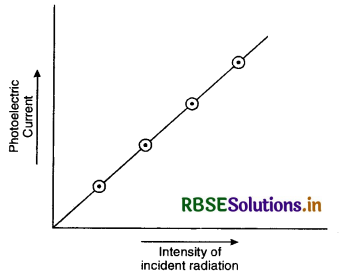
I. Effect-of intensity of light on photoelectric current
The radiations of fixed frequency are made to fall on plate P, keeping the accelerated potential constant. Now intensity of incident radiations is varied and the photoelectric current is noted each time. It is found that the photoelectric current increases linearly with increase in intensity of incident radiations. If a graph is plotted between the intensity of incident radiations and photoelectric current, the graph is a straight line passing through the origin as shown in Fig. LAQ 3 (b). It means that the number of photoelectrons emitted per second from the photosensitive plate is directly proportional'to the intensity of incident radiations.

II. Effect of potential on photoelectric current
Apply some positive potential to the collector and allow light of fixed intensity I₁, and fixed frequency to fall upon the plate P. Increase the positive potential of C gradually and measure the photoelectric current each time. It is found that photoelectric current increases with the increase in accelerating potential till, for certain positive potential of C, the current becomes maximum beyond which it does not increase further for any increase in accelerating potential.

The maximum value of photoelectric current at a given fixed frequency and intensity is called saturation current. At this stage all the electrons emitted by photosensitive plate P are collected by plate C (Fig. LAQ 13 (c)).

When the plate C is made negative w.r.t. the plate P and increase its magnitude gradually the photoelectric current decreases and becomes zero for certain negative potential (V₀) of plate C.

The value of retarding potential at which the photoelectric current becomes zero is called cut off or stopping potential for the given frequency of incident radiations. The stopping potential is just sufficient to stop the fastest photoelectron emitted by the plate P.

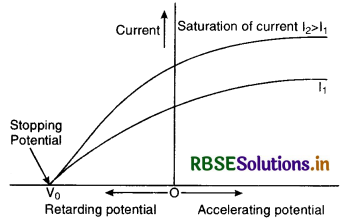
If the same experiment is repeated with radiations of the same frequency and higher intensity I₂ (I₂ > I₁), then saturation current will be higher but stopping potential is the same. It means that stopping potential is independent of intensity of incident radiations.

If the plate C is given small negative potential, the photoelectric current does not immediately drop to zero. It means that when plate P is illuminated by radiations of certain frequency, the photoelectrons of different energies are emitted. But when retarding potential becomes equal to the stopping potential V₀, the current drops to zero. It means that the work done by the retarding potential on the fastest electrons must be equal to their kinetic energy.
i.e. \(\frac{1}{2}\) mv²_max = eV₀

III. Effect of frequency of incident radiations on photoelectric current
The intensity of incident radiations at various frequencies is suitably adjusted so as to get the same saturation current each time when collector C is made positive w.r.t. P. Now, if the potential is reduced to zero and then to negative till stopping potential is reached in each case, it is found that the stopping potential increases with the increase in frequency i.e. for frequencies of incident radiations v₁ > v₂ > v₃, the corresponding potentials are of the order
V₁ > V₂ > V₃ (Fig.(d)).

It means that an increase in the frequency of the incident light increases the velocity and hence kinetic energy of the emitted electrons so that greater retarding potential is required to stop them completely.

IV. Threshold frequency
If a graph is plotted between the frequency of incident radiations and stopping potential, the graph is a straight line not passing through the origin but from point A, as shown in Fig. LAQ 3 (e). It means that there is certain frequency v0 for which the stopping potential is zero. This is called threshold frequency.

The minimum value of frequency of incident radiations below which the photoelectric emission stops altogether is called threshold frequency.

(b) Laws of photoelectric emission
The results of the experimental studies of photoelectric effect are regarded as the laws of photoelectric effect, as mentioned below:

1. For a given metallic surface, there is a minimum value of frequency of the incident radiations called threshold frequency below which there is no photoelectric emission, whatsoever, may be intensity of the incident radiations.
2. Above the threshold frequency the number of photoelectrons emitted per second is directly proportional to the intensity of incident radiations.
3. Above the threshold frequency the maximum kinetic energy of emitted photoelectron is independent of intensity of incident radiations, but depends upon the frequency of incident radiations.
4. The photoelectric emission is an instantaneous process. The time taken by the incident radiations and emission of photoelectrons is very small, even less than 10^-9 second (above threshold frequency).

Question 4.
Why Classical Theory (i.e. Wave theory) fails to explain the phenomenon of photoelectric emission? What is Einstein's photoelectric equation and how it explains the laws of photoelectric effect?
Answer:
Failure of Classical or Wave Theory
Laws of photoelectric emission cannot be explained on the basis of the wave nature of light.

• On the basis of nature of light it cannot be explained that why light of high intensity but of frequency less than threshold frequency cannot produce photoelectric emission, whereas light of low intensity but higher frequency cannot produce photoelectric emission.
• It cannot explain the result that kinetic energy of emitted electrons is independent of intensity of incident light.
• Instantaneous emission of photoelectron could not be explained by classical theory.

Einstein’s photoelectric equation
In 1905, Einstein suggested that the experimental results in photoelectricity could be explained by applying Planck’s quantum theory i.e. light radiation consists of tiny packets of energy called a photon having energy E = hv where h is Planck’s constant and v is the frequency of incident radiation.

Einstein assumed that one incident' photon can eject only one electron. The photon energy is utilised in two ways:
(i) A part of energy of a photon is used for electron free from the atom and away from the metal surface. This energy is called photoelectric work function W₀.
(ii) The balance of the photon energy is used up in giving the electron a kinetic energy \(\frac{1}{2}\)mv².
∴ Energy of incident photon = Work function + K.E. of electron
or hv = W₀ + \(\frac{1}{2}\)mv² ......................... (i)
If v₀ is the threshold frequency which is just sufficient to eject an electron with zero velocity,
Then W₀ = hv₀ ............................(ii)
Putting (ii) in (i) we get
hv = hv₀ + \(\frac{1}{2}\)mv²
or \(\frac{1}{2}\)mv² = h (v - v₀) R. ............................(iii)

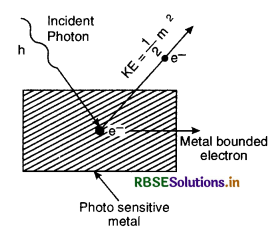
Equation (iii) is called Einstein photoelectric equation. 

Explanation of photoelectric effect from Einstein equation
1. From equation (iii), if v < v₀, kinetic energy is negative and no photoelectrons are emitted. It shows that if the frequency of incident radiations is less than threshold frequency no electron emission can take place.

2. If v > v₀, the maximum velocity v_max of photoelectrons depends only on the kinetic energy of incident radiations and independent of its intensity.

3. When intensity of incident radiation is increased, the number of photons falling on photo cathode increases. As a result of it, electrons emitted by photocathode increases. This explains the increase in photoelectric current with the increase in intensity of incident radiations.

4. According to Einstein’s theory, the incident light is in the fofm of packets of energy (or photons) and the photons strike the surface of photocathode and these photons are immediately absorbed by some atom and immediate emission of photoelectrons starts. Hence photoelectric effect is instantaneous process. Thus, Einstein’s equation of photoelectric emission explains all the laws of photoelectric emission.

Question 5.
What is a photocell? Explain different types of photocells.
Answer:
Photocell or Photoelectric cell
Photoelectric cell is a device for converting light energy into electrical energy. It is based on photoelectric effect. Photoelectric cells are mainly of three types.
I. Photoemissive cell
II. Photovoltaic cell
III. Photoconductive cell

I. Photoemissive cell
Photoemissive cells are of two types:
(a) Vacuum type
(b) Gas filled type.

(а) Vacuum type Cell
Principle. Photoemissive is based on the principle that electrons are emitted from the cathode when illuminated by radiations of suitable frequency.

Construction. It consists of an evacuated glass bulb fitted with two metallic electrodes i.e. a cathode and an anode as shown in Fig. LAQ 5 (a). Cathode C is semi-cylindrical metal coated with a photosensitive material and connected to the negative terminal of the battery B. Anode A is in the form of a straight wire so placed that it does not obstruct the light falling on cathode.

Working. When visible U.V. light is made to fall on the photosensitive cathode, electrons are emitted which are attracted by the positive anode. The magnitude of current is directly proportional to the intensity of incident radiations though the magnitude of current is small.

(b) Gas filled type cell. To increase the magnitude of the current the cell is filled with an inert gas like argon or neon. When cathode C is illuminated by radiations of suitable frequency, the emitted electrons from the cathode ionise the gas, hence large number of electrons are produced. These electrons are attracted by the anode, so a large current is produced by this cell. In these cells, the magnitude of the photoelectric current is not proportional to the intensity of incident radiations.


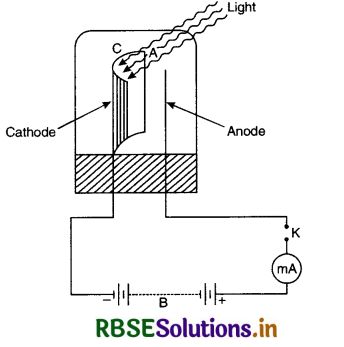
Uses

1. They are used for sound reproduction from a motion-picture film.
2. In television
3. As burglar’s alarm.
4. In photometry
5. To control the temperature of furnaces.

II. Photovoltaic cell
It is self-generating cell which employs semiconductor contacts against metals. When light is incident on the semiconductor, it generates an e.m.f. and can therefore, provide a current without a battery.

Principle. It is based on the principle that when light or any radiations are ms e.m.f. which is proportional to the radiant energy incident on it.

Construction. The most commonly used photovoltaic cells are of the barrier layer type iron-selenium cells. A thin layer of selenium (semiconducting material) is placed on an iron disc. The surface film is a translucent layer of silver or platinum to act as a front electrode. The barrier layer is formed by cathode sputtering process. A contact ring on the silver layer acts as one electrode and the iron base as the other.

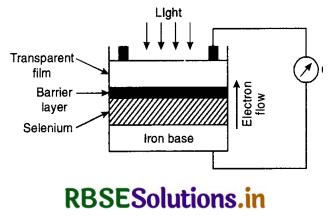
Working. When light is made to fall on the semiconductor i.e. selenium, it ejects electrons which travel from selenium to the front silver electrode through the barrier layer. The barrier layer does not allow the electrons to go in opposite direction because it acts as a rectifier. The e.m.f. generated between silver electrode and selenium is almost proportional to the intensity of incident light. The main advantage of this cell is that it requires no external battery for its own operation i.e. it is self-generating.

Uses. Since the internal e.m.f. and hence current generated by it is large enough to be measured by a pointer type galvanometer, so they are used in photographic exposure meters, direct reading illumination meters and photometers.

III. Photoconductive Cell
Principle. It is based on the principle that the resistance of semiconductor like selenium (Se), Cd S, Pb etc. decreases when radiations are made to fall on them.

Construction. The simplest form of photo-conductive cell using selenium is as shown in Fig. LAQ 5 (c). It consists of a pair of interlocking comb-like electrodes made of gold deposited on glass. Over these a thin film of selenium is deposited. Actually the selenium forms a large number of strips, electrically in parallel because Se has very high resistivity (700 Qm in the dark). The commonly used Cd S cell is shown in Fig. LAQ 5 (d). It has a light sensitivity than Se.

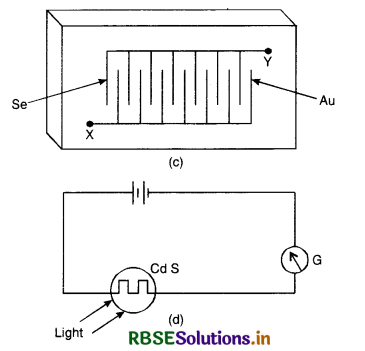
Working. When no light is falling on the cell (dark), its resistance is very high hence current is low. When the cell is illuminated, its resistance decreases and circuit current becomes large. The resistance between their terminals XY, falls from about 10⁷ Ω in the dark to about 10⁶ Ω in bright light.

Uses. Photoconductive cells have been used for detecting ships and aircrafts by the radiations given out by their exhausts or funnels and for telephony by modulated infrared light.

Question 6.
What are the important applications of photocell?
Answer:
The photoelectric cells have been the following important applications:
1. Modern Talkies or Cinematography. In sound motion pictures or modern talkies, now so commonly use, a sound track is provided at the edges of the picture film.

2. Television. Television is the process of transmission and reproduction of moving figures at a distance and this method is similar in many respects to the transmission of pictures. In television, the pictures already contained on a photographic film are reproduced, while in transmission of pictures an actual moving figure, say the face of the actor, is reproduced. The process of television involves the following essential points:

• Scanning of the object which is to be televised. It consists in dissecting the object into large number of elements by making a narrow and intense beam of light more rapidly back and forth over a limited portion of the object.
• Conversion of light impulses received from the scanned object into electric impulses, for which the photoelectric cell is used.
• Reconversion of the electric impulses back to light impulses in such a way as to reconstruct the original object. The first two points are attended to by a television transmitter while the third by a television receiver.

3. Burglar Alarm. Infrared light is invisible to the eye. When a beam of infrared light is projected across the room in which photoelectric cell is fitted in a closed circuit. When the burglar walks in that room he cuts the incident light and stops the photoelectric current momentarily. This actuates an electric relay which causes another electric circuit to be completed, thereby ringing the bell.

In the above case, the photoelectric cell is continuously working. In another arrangement i.e. in the open circuit the cell is actuated only when another source of light e.g. the light of the intruder torch, when the photoelectric current produced actuates a relay which closes the electric bell circuit, thereby ringing the bell.

4. Micro photometers. These are the instruments for measuring the intensity of light and studying the final structure of a spectral line. These use photoelectric cells.

5. Foot-candle Meter. This instrument is used for measuring the intensity of illumination at a given place directly. It consists of a photovoltaic cell and a galvanometer. In this an iron plate P covered with thin layer of Selenium S on which is deposited a very thin semi-transparent film of gold. A metal ring R in contact with the gold film forms the negative terminal of the cell and the iron plate act as the positive terminal.

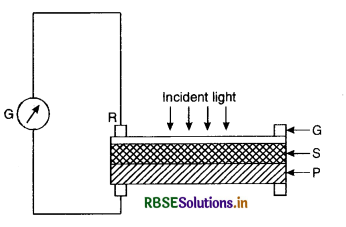
When a beam of incident light falls over the gold-film, it is transmitted through it and on falling on selenium, it derives the electrons into the gold film which becomes negative. The electrons cannot pass as easily to the iron plate as to the gold-film. The electrical current producd is proportional to the incident fight radiations and hence the galvanometer G can be directly calibrated to read the intensity of illumination in foot-candles. Such devices have replaced the older type of photometers for measuring Candle Powers, and are now used by photographers as illumination meters or exposure meters.
Intensity of illumination (I) =\( \frac{\text { Illuminating power }(\mathrm{Q})}{\text { Square of distance }\left(\mathrm{R}^2\right)}\)
∴ Illuminating power (Q) = Intensity of illumination (I) x square of distance (R²)
i.e.Candle power = foot candles x ft²

6. Fire Alarms. To protect a building from fire, gas filled photoelectric cells are used at various places in the building. Whenever there is a flame, the fight falls on the cell and photoelectric current is produced which after suitable amplification causes a bell to ring.

7. Counting Machines. An important example of counting machines is met with on docks where it is used to count the number of packages or bags loaded in a ship. A beam of fight falls on a photoelectric cells (gas filled) and the current after amplification starts a counting machine. As soon as the path of the beam is cut off by the package, the current stops for a while and the counting machine advances by one.

8. Automatic Switching of Street Lighting Circuit. A photoelectrical cell is also used in the street lighting circuit. The sunlight falls on it and the current generated keeps the circuit open. As soon as the intensity of sunlight falls below a certain value (e.g. in the evening) the photoelectric current becomes very feeble and the street light circuit is closed. This method has the advantage that the time of street light is automatically adjusted in summer and winter.

9. Exposure Meters in Photographs. An exposure meter is a device to calculate the correct time of exposure. The photoelectric cell in the instrument produces a current proportional to the intensity of light falling on it. The current operates a galvanometer, the scale of which is calibrated to read the time of exposure.

10. Complexion Meters. The light reflected from the face of a person falls on a photoelectric cell when the current produced is proportional to the intensity of the reflected light and such measures the complexion of the person.

11. Day light Recorders. Photoelectric cells find use in meteorology to record day light. The current produced in a photoelectric cell with day light is coupled with clock system and a current time graph is plotted giving a measure of day light.

12. These cells are also used in traffic signals, colour identification etc.

Question 7.
What led de-Broglie to put forward, the duality hypothesis for matter?
Answer:
Following observations led him to the duality hypothesis for matter.
(i) In this universe the whole energy is in the form of matter and electromagnetic radiation.
(ii) Nature love symmetry, as the radiations have got dual nature, matter should also possess dual nature:
Derivation of de-Broglie wavelength
For photon
Energy of a photon can be written as
E = hv = \(\frac{h c}{\lambda}\) ..............................(1)
If a photon possesses some mass (which is by virtue of its motion i.e. its rest mass would be zero) its energy according to the theory of relativity energy of photon E = (mass of photon)c²
Using Eq. (1), we get
\(\frac{h c}{\lambda}\) = (mass of photon)c²
∴ mass of photon = \(\frac{h c}{\lambda c^2}=\frac{h}{\lambda c}\)
So Momentum of photon, p = (mass of photon) c

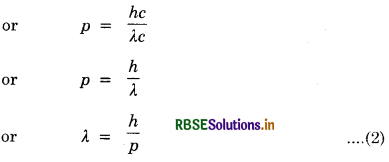
For a material particle
If instead of photon, we consider a material particle of mass m moving with velocity v then momentum of material particle
p = mv
∴ Wavelength associated with the material particle,
λ = \(\frac{h}{p}=\frac{h}{m v}\) ............................(3)
This wavelength is called de-Broglie wavelength and the wave is called de-Broglie wave or matter wave. From de-Broglie wave equation (3) we find that

1. The wavelength of moving particle is inversely proportional to its momentum i.e.
   λ ∝ \(\frac{1}{p}\).
2. The wavelength of moving particle is independent of the charge of matter.
3. de-Broglie waves are not .electromagnetic waves, because electromagnetic waves are only associated with accelerated charged particles.
4. Lighter the particle, greater the wavelength
   i.e. λ ∝ \(\frac{1}{m}\).

Question 8.
Derive the expression of de-Broglie wavelength in term of energy and temperature.
Answer:
In terms of energy
The kinetic energy of a material particle of mass m moving with velocity v is given by
E = \(\frac{1}{2} m v^2=\frac{m^2 v^2}{2 m}=\frac{p^2}{2 m}\)
or p = \(\sqrt{2 m \mathrm{E}}\) ...........................(1)
Since de-Broglie wavelength λ is given by
λ = \(\frac{h}{p}\)
Using Eq. (1), we get
λ = \(\frac{h}{\sqrt{2 m \mathrm{E}}}\) ...............................(2)

In terms of temperature
From kinetic theory of gases, the average kinetic energy of a material particle is given by:
E = \(\frac{3}{2}\) kT
So Eq. (2) can be written as:
λ = \(\frac{h}{\sqrt{2 m \cdot \frac{3}{2} k^{\prime} \mathrm{T}}}\)
or λ = \(\frac{h}{\sqrt{3 m k \mathrm{~T}}}\).

Question 9.
Derive the expression for de-Broglie wavelength associated with an electron in a potential difference of V volts.
Answer:
Let an electron having charge V and mass m be accelerated through a potential V volts, and attains a velocity v.
∴ Kinetic energy of electron,
E = \(\frac{1}{2}\) mv² ............................(i)
Also, kinetic energy of electron is given by
E = eV ...........................(ii)
From (i) and (ii), we have
\(\frac{1}{2}\) mv² = eV
or mv² = 2eV
or m²v² = 2 meV
or mv = \(\sqrt{2 m e \mathrm{~V}}\)
de-Broglie wavelength of electron,

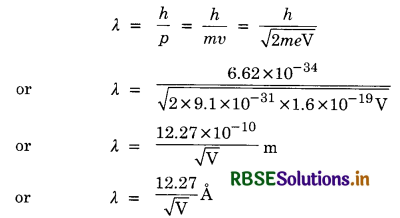
Question 10.
Show that the velocity of de-Broglie wave is more than the velocity of particle associated with it.
Answer:
We associate de-Broglie wave with a moving particle, so it is reasonable to expect that this wave travels with the same velocity as that of the particle. If we call the de-Broglie wave velocity as w, we may apply the usual formula W = vλ to determine the value of W. The wavelength λ is the de-Broglie wavelength given by
λ = \(\frac{h}{m v}\)
Now from the Planck's law,
E = hv or v = \(\frac{E}{h}\) ..............................(1)
Also from mass energy relation
E = mc² .............................(2)
From Eq. (1) & (2), we have
v = \(\frac{m c^2}{h}\)
de-Broglie wave velocity is, therefore, given by
W = vλ = \(\frac{m c^2}{h} \times \frac{h}{m v}=\frac{c^2}{v}\)
Since the particle velocity v, must be less than the velocity of light c, (i.e. c > v)
So, w > c
Thus the de-Broglie wave travels faster than the velocity of light associated with it.

Question 11.
What is the physical meaning of wave packet?
Answer:
Wave packet
de-Broglie wave associated with a material particle has velocity more than the velocity of the particle. So it was difficult to conceive as to how the de-Broglie wave was associated with the particle. Schrodinger postulated that a moving particle is not associated with one wave but a group of waves called wave-packet; and each wave has slightly different speed and wavelength. The wave packet is the result of a superposition of individual waves whose interference with one another results in the variation of amplitude that defines the group shape. Since the wave speed varies with wavelength, hence the different individual waves do not proceed together and the wave packet has speed different from that of the waves which compose it. The amplitude of each wave is so chosen that they interfere constructively over a small region of space as shown in Fig. LAQ 11. The velocity of wave packet when calculated comes out to be equal to velocity of the material particle with which it is associated.

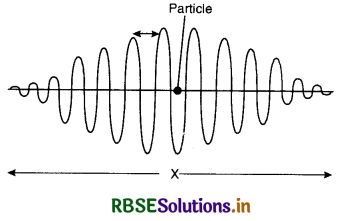
Thus wave packet is a type of wave motion in which amplitude of the wave is very large in a small region and negligibly small in the rest of space. The probability of finding the particle is maximum, where amplitude of the waves is large and probability is minimum where amplitude of the wave is small.

Question 12.
Describe an experiment which shows the wave nature of electron.
Or
Describe experimental verification of de-Broglie wave equation.
Answer:
Davisson and Germer Experiment
The first experimental proof of the wave nature of particles was proved in 1927 by C.J. Davisson and L.H. Germer.

Principle. Electrons accelerated by a known potential are diffracted from a crystal and their wavelength is measured by optical formula.

Construction. The experimental arrangement used by Davisson and Germer is as shown in Fig. (a). The electrons from hot tungsten cathode are accelerated by a potential difference V between the cathode C and anode A. This arrangement is called electron gun. A Ni crystal is placed such that the electrons strike on it at an angle O. The detector D can move along an arc scale with its centre O as shown in the figure.

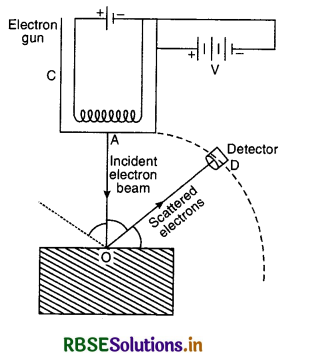
Working. A fine beam of electrons is allowed to strike the Ni target. The intensity of scattered electrons in a given direction is determined by a detector. The intensity of scattered beam is measured at different values osf Φ and a graph is plotted between Φ and intensity of scattered beam. Such graphs are plotted at different accelerating voltages as shown in 

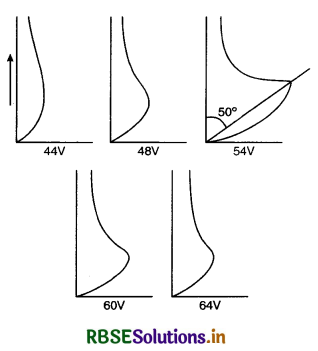
Fig. From these graphs we find that the scattered electron beam of 54 V has diffraction peak at angle Φ = 50°. This appearance of bump at a particular direction is due to the interference of electrons scattered from different layers of regularly spaced atoms of the crystal. This established wave nature of electrons.
It is found that the maxima in the diffraction pattern occurs, when Bragg's condition is satisfied. i.e. 2d sin θ = nλ .......................(1)
where d is the distance between atomic planes, λ is the wavelength of the electron and n is the order of spectrum.
From the we have
θ + Φ + 0 = 180°
∴ 2 θ = 180° - Φ = 180° - 50°
= 130°
∴ θ = 65°
For n = 1, Eq. (1) becomes
λ = 2 d sin θ 
For Ni crystal d = 0.91 Å = 0.91 x 10^-10 m
∴ λ= 2 x 0.91 x 10^-10 x sin 65°
λ = 1.65 Å
Also for 54 V, the de-Broglie wavelength of electron is given by (theoretically)
λ = \(\frac{12.27}{\sqrt{54}}\) Å = 1.67 Å
Thus the two results are in close agreement with each other. So Davisson and Germer experiment provides direct verification of de-Broglie hypothesis of wave nature of moving particles.

HOTS QUESTIONS

Question 1.
Find the frequency of light which ejects electrons from a metal surface, fully stopped by a retarding potential of 3V. The photoelectric effect begins in this metal at a frequency of 6 x 10¹⁴ Hg. Find the work function for this metal (Given h = 6.63 x 10^-34 Js)
Answer:
Here c = 1.6 x 10^-19 C, V = 3V and v₀ = 6 x 10⁺¹⁴ Hz
From Einstein’s photoelectric equation
\(\frac{1}{2}\) mv² = hv - W₀
or eV₀ = hv - hv₀
or hv = eV₀ + hv₀
or v = \(\frac{e \mathrm{~V}_0}{h}\) + v₀
= \(\frac{1.6 \times 10^{-19} \times 3}{6.63 \times 10^{-34}}\) + 6 x 10¹⁴
= 7.24 x 10¹⁴ + 6 x 10¹⁴ = 13.24 x 10¹⁴
or v = 1.324 x 10¹⁵ Hz.

Question 2.
Find the number of photons emitted per second by a 25W source of monochromatic light of wavelength 6000Å.
Answer:
Energy of photon

E = hv = \(\frac{h c}{\lambda}=\frac{6.6 \times 10^{-34} \times 3 \times 10^8}{6000 \times 10^{-10}} \)   
= 3.3 x 10^-19 J
So number of photons emitted per second by 25W source
n = \(\frac{25 \mathrm{~W} \times 1 s}{3.3 \times 10^{-19} \mathrm{~J}}\)
or n = 7.57 x 10¹⁹.

Question 3.
Radiation of wavelength 180 nm ejects photoelectrons from a plate whose work function is 2.0 eV. If uniform magnetic field of flux density 5.0 x 10^-5 T is applied parallel to the plate, what should be the radius of the path followed by electrons ejected normally from the plate with maximum energy.
Answer:
Here λ = 180 nm = 180 x 10^-9 m,
W0 = 2.0 eV = 2 x 1.6 x 10^-19 J
From Einstein’s equation
\(\frac{1}{2}\)mv² = hv - W₀ = \(\frac{h c}{\lambda}\) - W₀
= \(\frac{6.63 \times 10^{-34} \times 3 \times 10^8}{180 \times 10^{-9}}\) - 2 x 1.6 x 10^-19
= 7.8 x 10^-19 J
or v = \(\sqrt{\frac{2 \times 7.8 \times 10^{-19}}{9.1 \times 10^{-31}}}\) = 1.31 x 10⁶ ms^-1
Since Bev = \(\frac{m v^2}{r}\)
∴ r = \(\frac{m v}{e \mathrm{~B}}=\frac{9.1 \times 10^{-31} \times 1.31 \times 10^6}{1.6 \times 10^{-19} \times 5 \times 10^{-5}}\) = 0.149 m.

Question 4.
Radiation of wavelength 5000Å and of intensity 2 x 10^-3 w cm^-2 falls on a photosensitive surface. Assuming that every absorbed photon results in the ejection of photoelectron, find how many photoelectrons are produced per cm² per sec.
Answer:
Here I = 2 x 10^-3 W cm^-2, λ = 5000Å = 5 x 10^-7 m
Energy of one photon
E = hv = \(\frac{h c}{\lambda}\)
or E = \(\frac{6.62 \times 10^{-34} \times 3 \times 10^8}{5 \times 10^{-7}}\) = 4 x 10^-19 J
Number of photons incident per unit area per sec.
n = \(\frac{\mathrm{I}}{\mathrm{E}}=\frac{2 \times 10^{-3}}{4 \times 10^{-19}}\) = 5 x 10¹⁵

Question 5.
Find de-Broglie wavelength associated with an electron moving with velocity 0.6 C. Given, rest mass of electron = 9.1 x 10^-31 kg; h = 6.63 x 10^-34 Js
Answer:
Here v = 0.6 C, m = 9.1 x 10^-31 kg, h = 6.63 x 10^-34 Js
de-Broglie wavelength
λ = \(\frac{h}{m v}=\frac{h \sqrt{1-\frac{v^2}{c^2}}}{m_0 v}\)
= \(\frac{6.63 \times 10^{-34} \sqrt{1-(0.6)^2}}{9.1 \times 10^{-31} \times 0.6 \times 3 \times 10^8}\)
= 3.24 x 10^-12 m.

Question 6.
The kinetic energy of an electron is equal to the energy of photon. Show that de-Broglie wavelength of this electron is less than the wavelength associated with a photon.
Answer:
Given KE of electron E_e = Energy of photon E_p
i.e. E_e = E_p ............................(i)
For electron