RBSE Class 12 Physics Important Questions Chapter 10 तरंग-प्रकाशिकी

Rajasthan Board RBSE Class 12 Physics Important Questions Chapter 10 तरंग-प्रकाशिकी Important Questions and Answers.

RBSE Class 12 Physics Chapter 10 Important Questions तरंग-प्रकाशिकी

अति लघुत्तरीय प्रश्न

प्रश्न 1.
(i) बिन्दु स्रोत एवं 
(ii) सुदूर प्रकाश स्रोत से किस प्रकार का तरंगाग्र बनता है?
उत्तर:
(i) गोलीय तरंगाग्र
(ii) समतल तरंगाग्न

प्रश्न 2.
दो तरंगों के आयामों का अनुपात a₁ : a₂ है तो इनकी तीव्रताओं का अनुपात क्या होगा?
उत्तर:
हम जानते हैं तीव्रता ∝ आयाम²
I ∝ a²
\(\frac{\mathrm{I}_1}{\mathrm{I}_2}=\frac{a_1^2}{a_2^2}\)

प्रश्न 3.
अघुवित प्रकाश विरल माध्यम से सघन माध्यम में गमन करता है। यदि परावर्तित और अपवर्तित किरणें एक - दूसरे के लम्बवत हैं तो परावर्तित प्रकाश की दिशा बताइए।
उत्तर:
परावर्तित प्रकाश आपतन के तल के लम्बवत रैखिकतः धूवित होता है।

प्रश्न 4.
दीर्घवृत्तीय थुवित प्रकाश को समझाइए।
उत्तर:
ऐसा प्रकाश जिसमें प्रकाश सदिश का आयाम दीर्घवृत्तीय पथ पर घूर्णन करता है, दीर्घवृत्तीय ध्रुवित प्रकाश कहलाता है।

प्रश्न 5.
तरंगाग्र एवं किरण में भिन्नता बताइए।
उत्तर:
समान कला में दोलन करने वाले कणों की निधि तरंगान कहलाती है और तरंगान पर खींची गई लम्बवत रेखा तरंग संचरण की दिशा व्यक्त करती है, इसी को किरण कहते हैं।

प्रश्न 6.
मैलस का नियम लिखिए।
उत्तर:
मैलस का नियम: जब अधुवित प्रकाश दो पोलेराइडों की व्यवस्था, विश्लेषक व धुवक दोनों से गुजरता है तो निर्गत प्रकाश की तीव्रता I धुवक एवं विश्लेषक के अक्षों के बीच अंतरित कोण की कोज्या के वर्ग cos2θ के अनुक्रमानुपाती होती है। 
अर्थात् I ∝ cos²θ
I = I₀ cos²θ
जहाँ I₀ निर्गत प्रकाश की तीव्रता का अधिकतम मान है।

प्रश्न 7.
किसी उत्तल लेंस से निर्गत तरंगान को चित्रित करो, जब इसके फोकस पर प्रकाश का बिन्दु स्रोत रखा हो।
उत्तर:

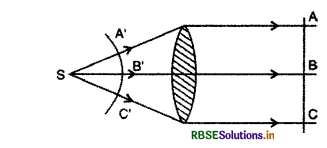
प्रश्न 8.
प्रकाश के तरंग सिद्धांत की कमियाँ बताइए।
उत्तर:
प्रकाश के तरंग सिद्धान्त में काल्पनिक माध्यम ईथर की सर्वत्र कल्पना की गई थी लेकिन माइकेल्सन एवं मोरले प्रयोग से यह सिद्ध हुआ कि ईथर नाम का कोई माध्यम नहीं होता है। इस प्रकार प्रकाश का तरंग सिद्धांत असफल प्रतीत होता है।

प्रश्न 9.
प्रकाश के विवर्तन के हाइगेन्स का कथन लिखिए।
उत्तर:
फ्रेस्नेल ने हाइगेन्स के तरंग सिद्धांत के आधार पर विवर्तन की व्याख्या करते हुए कहा, विवर्तन उन द्वितीयक तरंगिकाओं के अध्यारोपण में होने वाले व्यतिकरण का परिणाम है जो एक तरंगाग्न के उस भाग से चलती है जो अवरोध द्वारा रोका नहीं जाता है।

प्रश्न 10.
दो तरंगों के द्वारा व्यतिकरण प्राप्त करने की शर्त क्या है?
उत्तर:
दोनों स्रोत कला सम्बद्ध होने चाहिए।

प्रश्न 11.
उन दो भौतिक घटनाओं का उल्लेख कीजिए जिनसे प्रकाश के तरंग स्वरूप की पुष्टि होती है?
उत्तर:
व्यतिकरण, ध्रुवण

प्रश्न 12.
एक पोलेरॉइड से आंशिक रेखीय घुवित प्रकाश को गुजार जाता है। पोलेरॉइड के घूर्णन कोण के सापेक्ष निर्गत प्रकाश की तीव्रता को ग्राफ द्वारा दिखाइए।
उत्तर:

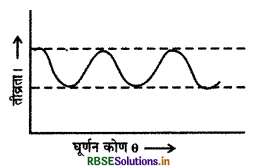
प्रश्न 13.
फ्रेस्नेल दूरी किस कहते हैं?
उत्तर:
रेखा - छिद्र से पर्दे की वह दूरी जिस पर विवर्तन के कारण पर्दे पर प्रकाश के केन्द्र से फैलाव रेखा - छिद्र के आकार के बराबर हो जाता है, फ्रेनेल दूरी कहलाती है। इसे ZF से प्रदशित करते हैं।

प्रश्न 14.
निम्नलिखित तरंगों में कौन - सी शुवित हो सकती है-
(i) ऊष्मीय तरंगें 
(ii) ध्वनि तरंगें? अपने उत्तर के समर्थन में तर्क दीजिए।
उत्तर:
ऊष्मीय तरंगें ध्रुवित हो सकती हैं क्योंकि ऊष्मीय तरंगें अनुप्रस्थ तरंगें है। जबकि ध्वनि तरंगें ध्रुवित नहीं हो सकती क्योंकि ध्वनि तरंगें अनुदैर्ध्य तरंगें हैं।

लघु उत्तरीय प्रश्न

प्रश्न 1.
प्रकाश के व्यतिकरण और विवर्तन में कोई दो अन्तर लिखिए।
उत्तर:

व्यतिकरण	विवर्तन
1. जब दो समान आवृत्ति की कला संबद्ध तरंगें परस्पर अध्यारोपित होती हैं तब व्यतिकरण की घटना होती हैं।	1. एक ही तरंगाग्र की द्वितीयक तरंगिकाओं के परस्पर अध्यारोपण से विवर्तन होता है।
2. समान आयाम की तरंगें होने पर अदीप्त फ्रिन्ज की तीव्रता शून्य होती है।	2. अदीप्त फ्रिन्ज की तीव्रता शून्य नहीं होती, लगभग शून्य होती है।

प्रश्न 2.
एकल स्लिट द्वारा विवर्तन में तीव्रता वितरण का वक्र बनाइए।
उत्तर:

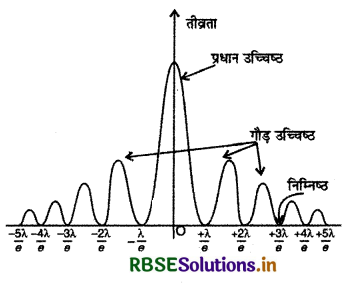
प्रश्न 3.
फ्रेनेल विवर्तन और फ्रॉनहॉफर विवर्तन में विभेद कीजिए।
उत्तर:
फ्रेनेल विवर्तन और फ्रॉनहॉफर विवर्तन में अन्तर

फ्रेनेल विवर्तन	फ्रॉनहॉफर विवर्तन
1. प्रकाश स्रोत एवं पर्दा दोनों विवर्तक से सीमित दूरी पर होते हैं।	1. प्रकाश - स्रोत एवं पर्दा दोनों प्रभावी विवर्तक से अनन्त दूरी पर होते हैं।
2. इसमें आपतित एवं विवर्तित तरंगान गोलीय व बेलनाकार होते हैं।	2. इसमें आपतित एवं विवर्तित तरंगान समतल होते हैं।
3. इस विवर्तन में स्रोत एवं पर्दे की विवर्तक से दरियाँ महत्वपूर्ण होती है।	3. इस विवर्तन में तरंगानों का विवर्तक पर झुकाव महत्त्वपूर्ण होता है।

प्रश्न 4.
कला सम्बद्ध स्रोत क्या है? व्यतिकरण प्रारूप प्राप्त करने के लिए ये क्यों आवश्यक हैं? यंग के द्विस्लिट प्रयोग में दो कला सम्बद्ध स्रोत कैसे प्राप्त करोगे?
उत्तर:
“यदि दो प्रकाश - स्रोतों के मध्य कलान्तर समय के साथ नियत रहता है तो दोनों कला संबद्ध स्रोत कहलाते हैं। दूसरे शब्दों में, कह सकते हैं कि ऐसे स्रोत जिनके मध्य या तो कलान्तर होना नहीं चाहिए और यदि है तो उसे समय के साथ नियत रहना चाहिए, कला सम्बद्ध स्रोत कहलाते हैं। दो भिन्न स्रोतों का कला सम्बद्ध होना लगभग असंभव है। एक ही स्रोत से उत्पन्न दो वास्तविक या काल्पनिक स्रोत कला सम्बन्ध होते हैं। ऐसे स्रोतों से उत्सर्जित तरंगें अपने पथ में रखे पर्दे पर स्थायी व्यतिकरण प्रतिरूप बनाती हैं।

प्रश्न 5.
कथन "प्रकाश को प्रकाश में जोड़ने पर अन्धकार उत्पन्न हो सकता है।" इस कथन की व्याख्या कीजिए।
उत्तर:
जब दो कला सम्बद्ध स्रोतों से चलकर दो तरंगें अध्यारोपण करती हैं और अध्यारोपण के क्षेत्र में जब एक तरंग का शीर्ष दूसरी तरंग के गर्त पर पड़ता है अथवा पहली तरंग का गर्त दूरी तरंग के शीर्ष पर पड़ता है तो परिणामी आयाम (A = a ~ b) शून्य होता है, जिसके फलस्वरूप वहाँ पर अदीप्त फ्रिन्ज बनती है। इस प्रकार स्पष्ट है कि दिया गया कथन सत्य है।

प्रश्न 6.
सूक्ष्मदर्शी की विभेदन क्षमता किस प्रकार बदलती है-
(i) तरंगदैर्ध्य घटाने पर
(ii) अभिदृश्यक लेन्स का द्वारक घटाने पर?
उत्तर:

अतः (i) तरंगदैर्ध्य λ का मान घटाने पर सूक्ष्मदर्शी की विभेदन क्षमता बढ़ जाती है।
(ii) अभिदृश्यक का द्वारक घटाने पर शंकु कोण का मान कम हो जायेगा, अतः विभेदन क्षमता कम हो जायेगी।

प्रश्न 7.
एकल रेखा छिद्र विवर्तन प्रतिरूप में कौन - से दो प्रमुख परिवर्तन आप देखेंगे जब एकवर्णी प्रकाश स्रोत को श्वेत प्रकाश स्रोत से प्रतिस्थापित कर दिया जाता है?
उत्तर:

• प्रत्येक विवर्तन क्रम में स्लिट का विवर्तित प्रतिबिम्ब श्वेत प्रकाश के अवयवी रंगों में विक्षेपित हो जाता है।
• उच्च क्रम में विक्षेपण अधिक होता है, अतः विभिन्न रंगों में अतिव्यापन हो जाता है।

प्रश्न 8.
पोलोरॉइड किस सिद्धांत पर आधारित होते हैं? पोलेरॉइड बनाने की विधि लिखिए।
उत्तर:
समतल भूवित प्रकाश की उत्पत्ति (Production of Plane Polarised Light)
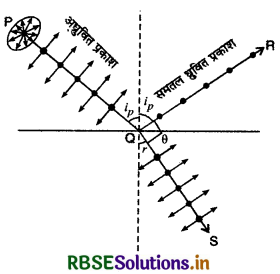
1. परावर्तन द्वारा (Polarisation by Reflection): सन् 1808 में फ्रांसीसी इंजीनियर मैलस' (Malus) ने यह ज्ञात किया कि जब साधारण प्रकाश किसी पारदर्शी माध्यम (जैसे - काँच) के पृष्ठ से परावर्तित होता है, तो वह आंशिक रूप (partially) से समतल धूवित हो जाता है। सन् 1811 में 'बूस्टर' (Brewster) ने इसका विस्तार से अध्ययन किया और यह बताया कि परावर्तित प्रकाश में ध्रुवित प्रकाश की मात्रा आपतन कोण पर निर्भर करती है। आपतन कोण बदलने पर एक ऐसा विशेष आपतन कोण आता है जिस पर परावर्तित प्रकाश पूर्णत: समतल भूवित (plane polarised) होता है तथा इसके कम्पन आपतन तल के लम्बवत् होते हैं। आपतन कोण के इस विशेष मान को 'बूस्टर कोण' (Brewster's angle) अथवा 'घुवण कोण' (Angle of polarisation) कहते हैं और इसे प्रायः i_p से प्रदर्शित करते हैं। पानी के लिए इसका मान लगभग 53° और काँच के लिए 57° होता है। यदि पारदर्शी माध्यम का अपवर्तनांक µ हो तो बूस्टर के अनुसार µ एवं i_p में निम्नलिखित सम्बन्ध होता है-

इस सूत्र को 'बूस्टर का नियम' कहते हैं।
ध्रुवण कोण पर परावर्तित तथा अपवर्तित किरणे QR व QS परस्पर लम्बवत् होती हैं। इस तथ्य को निम्न प्रकार सिद्ध किया जा सकता है-
माना अपवर्तन कोण r है।
तब स्नेल के नियम से,
µ = \(\frac{\sin i_{\mathrm{P}}}{\sin r}\) ..................(2)
परन्तु बूस्टर के नियम से,
µ = tan i_p = \(\frac{\sin i_{\mathrm{P}}}{\cos i_{\mathrm{P}}}\) .................(3)

समी. (2) व (3) से
\(\frac{\sin i_{\mathrm{P}}}{\sin r}=\frac{\sin i_{\mathrm{P}}}{\cos i_{\mathrm{P}}}\)
या sin r = cos i_p
या cos (90° - r) = cos i_p
या 90° - r = ip
या i_p + r = 90° ...................(4)
अब चित्र 10.33 से,
i_p + θ + r = 180°
या θ + 90° = 180° [समी. (4) से]
या θ = 180° - 90° 
या θ = 90° ...................(5)
अर्थात् परावर्तित एवं अपवर्तित किरणें परस्पर लम्बवत् होती है। यदि यह दिया गया हो कि
i_p + r = 90°
तो ip व µ में सम्बन्ध निम्न प्रकार स्थापित होगा,
∵ µ = \(\frac{\sin i_{\mathrm{P}}}{\sin r}\)
और r = 90° - i_p
∴ µ = \(\frac{\sin i_{\mathrm{P}}}{\sin \left(90^{\circ}-i_{\mathrm{P}}\right)}\)
= \(\frac{\sin i_{\mathrm{P}}}{\cos i_{\mathrm{P}}}\)
या µ = tan i_p
यही बूस्टर का नियम है।

(2) प्रकीर्णन द्वारा ग्रुवण (Polarisation by Scatter - ing): जब कोई प्रकाश पुंज ऐसे माध्यम से होकर गुजरता है जिसमें मौजूद कणों का आकार प्रकाश के तरंगदैर्ध्य की कोटि का होता है तो प्रकाश का प्रकीर्णन हो जाता है। जब प्रकीर्णित प्रकाश को उसकी आपतन दिशा की लम्बवत् दिशा में देखते हैं तो प्रकाश समतल भूवित दिखाई देता है जिसकी पुष्टि विश्लेषक द्वारा हो जाती है। इस घटना को प्रकीर्णन द्वारा प्रकाश का ध्रुवण कहते हैं।

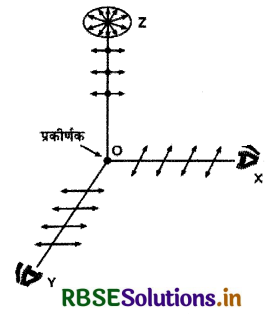
चित्र 10.33 में अधुवित प्रकाश का पुंज Z - दिशा के अनुदिश एक प्रकीर्णक (scatter) पर आपतित हो रहा है। कि प्रकाश - तरंगों की प्रकृति अनुप्रस्थ होती है, अत: प्रकाश वेक्टर के कम्पन XY तल में होंगे। जब हम X - अक्ष के अनुदिश देखते हैं तो प्रकाश की अनुप्रस्थ प्रकृति के कारण हम केवल Y - अक्ष के समान्तर ही दोलन देख पाते हैं। इसी प्रकार जब Y - अक्ष के अनुदिश देखते हैं तो केवल X - अक्ष के समान्तर ही दोलन देख पाते है। इस प्रकार आपतन दिशा के लम्बवत् प्रकीर्णित प्रकाश समतल ध्रुवित होता है।

(3) द्वि - अपवर्तन द्वारा धुवण (Polarisation by Double Refraction): कुछ क्रिस्टल; जैसे - कैल्साइट, क्वार्ट्ज ऐसे क्रिस्टल होते हैं कि जब उन पर कोई प्रकाश किरण आपतित होती है तो वह किरण क्रिस्टल में दो अपवर्तित किरणों में विभाजित हो जाती है। इस घटना को द्वि - अपवर्तन कहते हैं। इनमें से एक किरण अपवर्तन के नियमों का पालन करती है। इसे

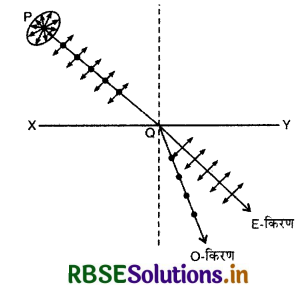
साधारण किरण (Ordinary ray) या O - किरण कहते हैं। दूसरी अपवर्तित किरण अपवर्तन के नियमों का पालन नहीं करती है, इसे असाधारण किरण (extraordinary Tay) या E - किरण कहते हैं। ये दोनों किरणे परस्पर लम्बवत् तलों में समतल धुवित होती हैं। साधारण किरण में कम्पन, आपतन तल के लम्बवत् तल में और असाधारण किरण में कम्पन आपतन तल में होते हैं। व्यवहार में इन दोनों अपवर्तित समतल धुवित किरणों में से एक को किसी विधि द्वारा अलग कर दिया जाता है जिससे कि क्रिस्टल में से समतल धूवित प्रकाश निकल सके।

द्वि - वर्णता (Dichroism): टूमलीन क्रिस्टल पर आपतित साधारण प्रकाश की किरण क्रिस्टल के भीतर दो ध्रुवित अपवर्तित किरणों में

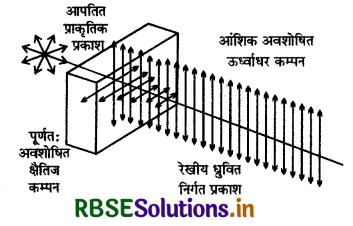
बैंट जाती है। इनमें से एक किरण क्रिस्टल द्वारा अवशोषित कर ली जाती है। टूर्मेलीन क्रिस्टल द्वारा वरणात्मक अवशोषण (selective absorption) को इस प्रक्रिया को द्वि - वर्णता कहते हैं।

पूर्ण पारगमन के लिए प्रयोग: यदि किसी सतह पर आपतित होने वाला एकवर्णीय प्रकाश का किरण पुंज पूर्ण रूप से पारगमित हो जाए और कोई परावर्तन न हो, ऐसा करने के लिए एक लेसर किरण का पुंज, एक ध्रुवक, एक प्रिज्म तथा एक पदों लेते हैं। लेसर स्रोत से उत्सर्जित प्रकाश को ध्रुवक से गुजारते हैं फिर यह एक प्रिज्म की सतह पर बूस्टर कोण से आपतित करते हैं। ध्रुवक को घुमाने पर हम देखते हैं कि एक विशेष सरेखन (alignment) के लिए प्रिज्म पर आपतित होने वाला प्रकाश पूर्ण रूप से पारगमित हो जाता है तथा प्रिज्म के पृष्ठ से कोई प्रकाश परावर्तित नहीं होता है।

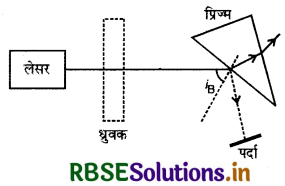
प्रश्न 9.
प्रकाश के विवर्तन से आप क्या समझते हो? प्रकाश तरंगों की अपेक्षा ध्वनि तरंगों में विवर्तन अधिक सरलता से क्यों प्रेक्षित होता है?
उत्तर:
प्रकाश का विवर्तन (Diffraction of Light)
"प्रकाश के मार्ग में मौजूद किसी रुकावट (obstacle) के किनारों से प्रकाश - तरंगों की रुकावट का ज्यामितीय छाया की ओर मुड़ जाना ही प्रकाश का विवर्तन कहलाता है।" इस प्रकार रुकावट के कारण प्रकाश अपने ऋजुरेखीव गमन (rectilinear path) से विचलित हो जाता है। इस विचलन का मान जैसे - जैसे बढ़ता जाता है वैसे - वैसे रुकावट का आकार छोटा होता जाता है। जिस समय रुकावट का आकार प्रकाश के तरंगदैध्य के क्रम का होता है तो प्रकाश का विवर्तन सबसे अधिक होता है। चित्र 10.15 में प्रदर्शित विवर्तन की तीन स्थितियों में सबसे अच्छा विवर्तन अर्थात् सुपरिभाषित विवर्तन तब होता है जब स्लिट की चौड़ाई न्यूनतम (a = 1.5λ) होती है।
चित्र 10.15 मे स्पष्ट है कि जैसे - जैसे स्लिट की चौड़ाई घटती जाती है, वैसे - वैसे विवर्तन का फैलाव बढ़ता जाता है।

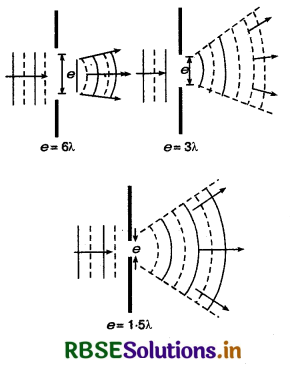
इस प्रकार निष्कर्ष यह निकलता है कि विवर्तन के लिए सबसे महत्वपूर्ण शर्त यह है कि रुकावट का आकार तरंगों के तरंगदैर्ध्य के क्रम का होना चाहिए। चूँकि विवर्तन भी तरंग गति का लक्षण है, अत: यह सभी प्रकार की तरंगों के साथ परिलक्षित होता है। ध्वनि - तरंगों की तरंगदैर्ध्य काफी बड़ी होती हैं। अतः इनका विवर्तन व्यावहारिक जीवन में आसानी से अनुभव किया जा सकता है। जैसे - दरवाजों, खिड़कियों आदि के किनारों से ध्वनि तरंगों का विवर्तन हो जाता है लेकिन प्रकाश - तरंगों की तरंगदैर्ध्य बहुत छोटी होती है। अत: इनका विवर्तन देखने के लिए प्रयोगशाला में विशेष प्रबन्ध करना पड़ता है।

प्रश्न 10.
यंग के द्विस्लिट प्रयोग में व्यतिकरण प्रारूप किस प्रकार प्रभावित होगा, जब
(i) स्लिट S₁ और S₂ के मध्य दूरी घटा दी जाये।
(ii) पूरी व्यवस्था को जल में डुबो दिया जाये। प्रत्येक स्थिति में अपने उत्तर को स्पष्ट कीजिए।
उत्तर:
(i) SS₁ के मध्य दूरी घटाने से फ्रिज की चौड़ाई बढ़ जाएगी क्योंकि ß ∝ \(\frac{1}{d}\)
(ii) फ्रिज की चौड़ाई घट जाएगी क्योंकि जल में प्रकाश की तरंगदैर्ध्य कम हो जाएगी। ß ∝ λ

दीर्घ उत्तरीय प्रश्न

प्रश्न 1.
तरंगान किसे कहते हैं? हाइगेन्स के तरंग सिद्धान्त के आधार पर प्रकाश के अपवर्तन नियमों की व्याख्या कीजिए। आवश्यक किरण चित्र बनाइए।
उत्तर:
समतल तरंगों का अपवर्तन (Reflection of Plane Waves)
चित्र 10.5 में XX' दो माध्यमों की सीमा रेखा (boundary line) है। पहले माध्यम में तरंग की चाल v₁ है और दूसरे माध्यम में तरंग की

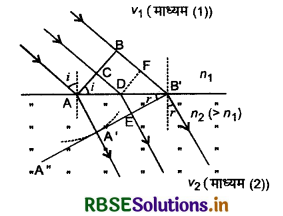
चाल v₂ है। माना कोई समतल तरंगाग्र AB पहले माध्यम में v₁ वेग से चलकर दूसरे माध्यम के पृष्ठ पर आपतन कोण i पर आपतित होता है। जैसे ही तरंगान का बिन्दु A दूसरे माध्यम के पृष्ठ पर पहुँचता है, द्वितीयक तरंगिकाएँ बननी शुरू हो जाती हैं जो दूसरे माध्यम में v₂ वेग से आगे बढ़ती हैं। जैसे - जैसे तरंगान के शेष बिन्दु दूसरे माध्यम के पृष्ठ पर टकराते जाते हैं द्वितीयक तरंगिकाएँ बननी आरम्भ हो जाती हैं और जब B बिन्दु B' तक पहुँचता है तब तक A पर बनने वाली तरंगिकाएँ A' तक पहुंच जाती हैं। इस प्रकार A'B' अपवर्तित तरंगान प्राप्त होता है। यदि B को B' तक या A को A' तक पहुँचने में लगा समय τ हो तो 
BB' = v₁τ [∵ दूरी = चाल x समय]
और AA' = v₂τ
चित्र से,
∆ ABB' में sin i = \(\frac{\mathrm{BB}^{\prime}}{\mathrm{AB}^{\prime}}\)
तथा ∆AA'B' में
sin r = \(\frac{\mathrm{AA}^{\prime}}{\mathrm{AB}^{\prime}}\)
∴ \(\frac{\sin i}{\sin r}=\frac{\frac{\mathrm{BB}^{\prime}}{\mathrm{AB}^{\prime}}}{\frac{\mathrm{AA}^{\prime}}{\mathrm{AB}^{\prime}}}=\frac{\mathrm{BB}^{\prime}}{\mathrm{AA}^{\prime}}=\frac{v_1 \tau}{v_2 \tau}=\frac{v_1}{v_2}\)
या \(\frac{\sin i}{\sin r}=\frac{v_1}{v_2}\) = नियतांक 
इस प्रकार-

• आपतित किरण, अपवर्तित किरण एवं अभिलम्ब तीनों एक बिन्दुगामी हैं और एक ही तल में हैं।
• आपतन कोण की ज्या एवं अपवर्तन कोण की ज्या में एक निश्चित अनुपात है। यही स्नेल का नियम है।

स्नेल ने प्रकाश का प्रायोगिक अध्ययन करके यह बताया था कि

जहाँ n₂₁ = प्रथम माध्यम के सापेक्ष द्वितीय माध्यम का अपवर्तनांक इस प्रकार यदि हाइगेन्स एवं स्नेल के नियमों को सम्बन्धित कर दें 

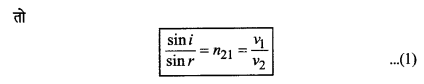
यदि प्रथम व द्वितीय माध्यमों के निरपेक्ष अपवर्तनांक क्रमशः n₁ व n₂ हों तो
n₂₁ = \(\frac{n_2}{n_1}\)
अत: समी. (1) को निम्न प्रकार दिखा सकते हैं-

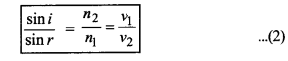
प्रश्न 2.
व्यतिकरण के लिए आवश्यक कोई दो शर्ते लिखिए। यंग के द्विस्लिट प्रयोग में व्यतिकरण फ्रिन्जों की चौड़ाई ज्ञात करने में व्यंजक प्राप्त कीजिए। यंग के द्विस्लिट प्रयोग में व्यतिकरण प्रारूप में तीव्रता वितरण का आरेख खींचिए।
उत्तर:
यंग का प्रयोग (Young's Experiment)
प्रकाश के व्यतिकरण का प्रायोगिक अध्ययन सर्वप्रथम सन् 1801 में वैज्ञानिक टॉमस बंग (Thomas Young) ने किया था। उन्होंने अपने मूल प्रयोग में सूर्य के प्रकाश का उपयोग किया था। उनके प्रयोग का सैद्धान्तिक आरेख चित्र 10.9 में प्रदर्शित है।

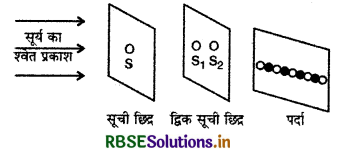
उन्होंने सूर्य के प्रकाश को एक सूची छिद्र (narrow slit) (S) पर डाला और इससे निर्गत प्रकाश को कुछ दूरी पर स्थित समदूरस्थ दो एक - दूसरे के अतिनिकटस्थ (very near) सूची छिद्रों S₁ व S₂ पर डाला तथा द्विक् सूची छिद्रों से निर्गत प्रकाश को एक पर्दे पर हाला। S₁ व S₂ से निर्गत प्रकाश तरंगें अध्यारोपित (superimpose) होकर पर्दे पर क्रमशः दीप्त एवं अदीप्त बिन्दु उत्पन्न करती हैं। जिन बिन्दुओं पर प्रकाश तरंगें समान कला में मिलती हैं, उन बिन्दुओं पर अधिकतम तीव्रता प्राप्त होती है और जिन बिन्दुओं पर तरंगें परस्पर विपरीत कला में मिलती है, उन पर न्यूनतम तीव्रता प्राप्त होती है।

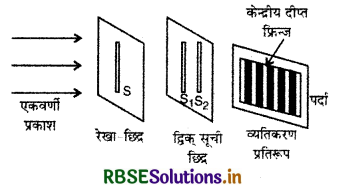
पर्दे पर प्राप्त इन दीप्त एवं अदीप्त बिन्दुओं की तीव्रता बढ़ाने के लिए सूची छिद्रों के स्थान पर रेखा - छिद्रों का प्रयोग किया तथा इनकी संख्या बढ़ाने के लिए सूर्य के प्रकाश के स्थान पर एकवर्णी प्रकाश स्रोत प्रयुक्त किया। S₁ व S₂ से निकलने वाली प्रकाश - तरंगों के अध्यारोपण के फलस्वरूप पर्दे पर समान चौड़ाई की दीप्त तथा अदीप्त पट्टियाँ (Bright and dark bands) एकान्तर क्रम में प्राप्त होती हैं। इन पट्टियों को 'फ्रिन्जे' (Fringes) कहते हैं। फ्रिन्जों के इस समूह को द्विक् रेखा - छिद्र का 'व्यतिकरण प्रतिरूप' (Interference patterm) कहते हैं।

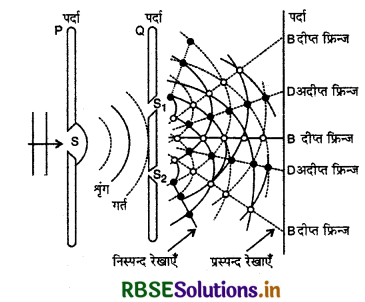
प्रयोग की व्याख्या (Explanation of the Experi - ment): यंग के द्विक रेखा - छिद्र प्रयोग (Young's double slit experiment) की व्याख्या हाइगेन्स के तरंग सिद्धान्त के आधार पर चित्र 10.11 के अनुसार की गई। रेखा - छिद्र S पर एकवर्णी प्रकाश का एक समतल तरंगाग्र आपतित होता है तो S से एक तरंगाग्र निर्गत होता है जो S₁ व S₂ पर आपतित होता है। चूंकि S₁ व S₂ स्लिट S से समान दूरी पर हैं अत: S₁ व S₂ दोनों एक ही तरंगान पर स्थित होंगे। जैसे ही S से चलने वाला तरंगाग्र S₁ व S₂ पर पहुँचता है तो हाइगेन्स के तरंग सिद्धान्त के अनुसार S₁ व S₂ नये प्रकाश - स्रोत का कार्य करने लगते हैं। तथा इनसे द्वितीयक तरंगिकाएँ निकलने लगती हैं चूँकि रेखाछिद्र S₁ व S₂ रेखाछिद्र S से समान दूरियों पर हैं। अतः रेखाछिद S से चलने वाली प्रकाश तरंगें रेखाछिद्र S₁ व S₂ पर एक ही कला में पहुँचती है। रेखाछिद S₁ व S₂ से चलने वाली द्वितीयक तरंगिकाएँ (secondary wavelets) एक - दूसरे पर अध्यारोपण करती हुई पर्दे पर पहुंचती हैं। S₁ व S₂ को केन्द्र मानकर अविच्छिन्न (continuous) तथा विच्छिन (dotted) चाप खींचते हैं। अविच्छिन्न चाप तरंगिकाओं के शृंगों (crests) को तथा विच्छिन्न चाप गौ (troughs) को प्रदर्शित करते हैं। जिन स्थानों पर एक तरंगिका का श्रृंग दूसरी तरंगिका के श्रृंग से अथवा एक तरंगिका का गर्त दूसरी तगिका के गर्त से मिलता है अर्थात् तरंगिकाएं एक ही कला में मिलती हैं। उन स्थानों पर संपोषी या रचनात्मक व्यतिकरण होता है। अतः परिणामी आयाम दोनों तरंगिकाओं के आयामों के योग के बराबर होता है और प्रकाश की तीव्रता अधिकतम होती है। चित्र में इन स्थानों की खाली वृत्तों (O) द्वारा दिखाया गया है। इन्हें मिलाने वाली रेखाएँ प्रस्पंद रेखाएँ (anti nodal lines) कहलाती हैं।

इसके विपरीत जिन स्थानों पर एक तरंगिका का श्रृंग, दूसरी तरंगिका के गर्त से मिलता है अर्थात् तरंगिकाएँ विपरीत कला में मिलती हैं उन स्थानों पर विनाशी व्यतिकरण होता है अतः परिणामी आयाम दोनों तरंगिकाओं के आयामों के अन्तर के बराबर होता है। यदि तरंगिकाओं के आयाम एक - दूसरे के बराबर हैं तो उन बिन्दुओं पर परिणामी शून्य होता है अर्थात् वहाँ प्रकाश की तीव्रता शुन्य होती है। चित्र में इन स्थानों को काले बिन्दुओं (O) द्वारा दिखाया गया है। इन्हें मिलाने वाली रेखाएँ निस्पंद रेखाएँ (nodal lines) कहलाती हैं। इस प्रकार पर्दे पर दीप्त एवं अदीप्त फ्रिजें एकान्तर क्रम में दिखाई पड़ती है।

S₁ व S₂ से समान दूरी पर स्थित पर्दे पर स्थित बिन्दु O पर दोनों स्रोतों से तरंगों के मध्य पधान्तर शून्य होता है, अत: वहाँ पर दीप्त फ्रिन्जे बनती हैं। इसे केन्द्रीय दीप्त फ्रिन्ज कहते हैं। इस फ्रिज के दोनों ओर एकान्तर क्रम में समान चौड़ाई की अदीप्त एवं दीप्त फ्रिजें प्राप्त होती हैं। चित्र 10.11 में इन फिन्जों को नामांकित किया गया है। यदि रेखा - छिद्र S पर भिन्न - भिन्न रंगों का प्रकाश डालें तो दीप्त एवं अदीप्त पट्टियाँ उसी रंग की प्राप्त होती है जिस रंग का प्रकाश पर डाला जाता है। साथ ही साथ प्रकाश की तरंगदैर्ध्य बदलने के कारण इन पट्टियों की चौड़ाइयाँ भी भिन्न - भिन्न हो जाती हैं। सबसे अधिक चौड़ाई लाल प्रकाश के लिए प्राप्त होती है और तरंगदैर्ध्य घटने के साथ चौड़ाई घटती जाती है।

दीप्त एवं अदीप्ति फ्रिन्जों की स्थितियाँ एवं फ्रिन्ज की चौड़ाई (Positions of Bright & Dark Fringes and Fringe Width)
माना यंग के प्रयोग में स्लिटों S₁ व S₂ के मध्य दूरी 2d है और इनसे पर्दे की दूरी D है। S₁S₂ की लम्बार्द्धक (perpendicular bisector) रेखा पर्दे के O बिन्दु पर मिलती है, अत: O पर ही केन्द्रीय

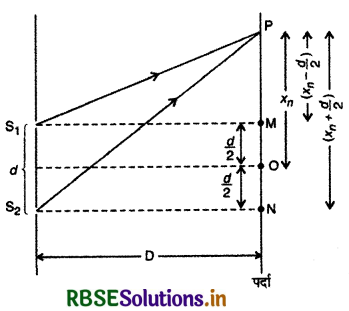
दीप्त फ्रिज बनेगी। पर्दे पर O से xn दूरी पर स्थित बिन्दु P है, जहाँ पर बनने वाली फ्रिन्ज का प्रकार (दीप्त या अदीप्त) इस बात पर निर्भर करेगा कि S₁ व S₂ से P पर पहुँचने वाली तरंगों में पचान्तर कितना है। अतः सर्वप्रथम हम पथान्तर ज्ञात करते हैं।
समकोण ∆S2PN से,
S₂P² = S₂N² + PN² = D² + \(\left(x_n+\frac{d}{2}\right)^2\)
इसी प्रकार समकोण ∆S1PM से,
S₁P² = S₁M² + PM² = D² + \(\left(x_n+\frac{d}{2}\right)^2\)
∴ (S₂P² - S₁P²) = D² + \(\left(x_n+\frac{d}{2}\right)^2\) - D² - \(\left(x_n+\frac{d}{2}\right)^2\)
या (S₂P + S₁P) (S₂P - S₁P) = x_n² + \(\frac{d^2}{4}\) + 2x_n.\(\frac{d}{2}\) - x_n² - \(\frac{d^2}{4}\) + 2x_n.\(\frac{d}{2}\)
या (S₂P + S₁P) (S₂P - S₁P) = 2x_n.d
यदि बिन्दु P बिन्दु O से अधिक दूर नहीं है तो
S₁P ≈ S₂P ≈ D 
∴ (S₂P + S₁P) ≈ D + D = 2D 
अत: 2D.(S₂P - S₁P) = 2x_n.d 
या S₂P - S₁P = \(\frac{x_n \cdot d}{\mathrm{D}}\) ......................(1)
अदीप्त फ्रिन्ज की चौड़ाई एवं दीप्त फ्रिन्जों की स्थितियाँ-
यदि P बिन्दु पर n वीं दीप्त फ्रिन्ज बनती है तो पथान्तर
S₂P - S₁P = nλ .................(2)
समी. (1) व (2) की तुलना करने पर,
\(\frac{x_n \cdot d}{\mathrm{D}}\) = nλ 

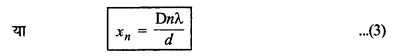
इस समीकरण की सहायता से केन्द्रीय दीप्त फ्रिज से दीप्त फ्रिजों की स्थितियाँ ज्ञात की जा सकती हैं।
इसी प्रकार x_{n + 1} = \(\frac{\mathrm{D}(n+1) \lambda}{d}\)
चूँकि दो क्रमागत (continuous) दीप्त फ्रिजों के मध्य अदीप्त फ्रिज होती है। अतः अदीप्त फ्रिज की चौड़ाई
ß = x_{n + 1} - x_n
= \(\frac{\mathrm{D}(n+1) \lambda}{d}-\frac{\mathrm{D} n \lambda}{d}\)
या ß = \(\frac{\mathrm{D} n \lambda}{d}+\frac{\mathrm{D} \lambda}{d}-\frac{\mathrm{D} n \lambda}{d}\)

इस सूत्र से अदीप्त फ्रिज की चौड़ाई ज्ञात कर सकते हैं।
पुनः समी. (3) से,
x_n = \(\frac{\mathrm{D} n \lambda}{d}=\frac{\mathrm{D} \lambda}{d} \cdot n=\beta n\)

इस सूत्र की सहायता से केन्द्र फ्रिज से दीप्त फ्रिजों की स्थितियाँ ज्ञात कर सकते हैं, यदि हमें फ्रिज की चौड़ाई ß ज्ञात हो।

दीप्त फ्रिज की चौड़ाई एवं अदीप्त फ्रिन्जों की स्थितियाँ: यदि P बिन्दु पर n वीं अदीप्त फ्रिन्ज बनती है तो पथान्तर
S₂P - S₁P = (2n - 1) λ/2 = \(\left(n-\frac{1}{2}\right)\)λ
या S₂P - S₁P = \(\left(n-\frac{1}{2}\right) \lambda\) ...............(6)
अब समो. (1) व (6) की तुलना करने पर,
\(\frac{x_n \cdot d}{\mathrm{D}}=\left(n-\frac{1}{2}\right) \lambda\)

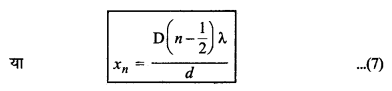
इस सूत्र की सहायता से केन्द्रीय दीप्त फ्रिज से अदीप्त फ्रिन्जों की दूरियाँ ज्ञात कर सकते हैं।
इसी प्रकार
x_{n + 1} = \(\frac{\mathrm{D}\left(n+1-\frac{1}{2}\right) \lambda}{d}=\frac{\mathrm{D}\left(n+\frac{1}{2}\right) \lambda}{d}\)
या x_{n + 1} = \(\frac{\mathrm{D}\left(n+\frac{1}{2}\right) \lambda}{d}\)
चूँकि दो अदीप्त फ्रिजों के मध्य दीप्त फ्रिज होती है, अत: दीप्त फ्रिज की चौड़ाई
ß = x_{n + 1} - x_n
= \(\frac{\mathrm{D}\left(n+\frac{1}{2}\right) \lambda}{d}-\frac{\mathrm{D}\left(n-\frac{1}{2}\right) \lambda}{d}\)
= \(\frac{\mathrm{D} \lambda}{d}\left(n+\frac{1}{2}-n+\frac{1}{2}\right)\)

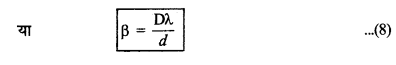
पुन: समी. (7) से,
x_n = \(\frac{\mathrm{D} \lambda}{d}\left(n-\frac{1}{2}\right)\)

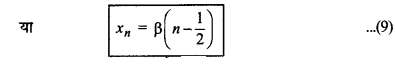
समी. (4) व (8) से स्पष्ट है कि दीप्त एवं अदीप्त फ्रिन्जों की चौड़ाई समान होती है।

प्रश्न 3.
व्यतिकरण फ्रिज प्रतिरूप प्राप्त करने के लिए बंग स्लिट प्रयोग का किरण चित्र बनाइए। प्रदीप्त फिन्जों के लिए फ्रिज चौड़ाई का व्यंजक व्युत्पन्न कीजिए।
उत्तर:
दीप्त एवं अदीप्ति फ्रिन्जों की स्थितियाँ एवं फ्रिन्ज की चौड़ाई (Positions of Bright & Dark Fringes and Fringe Width)
माना यंग के प्रयोग में स्लिटों S₁ व S₂ के मध्य दूरी 2d है और इनसे पर्दे की दूरी D है। S₁S₂ की लम्बार्द्धक (perpendicular bisector) रेखा पर्दे के O बिन्दु पर मिलती है, अत: O पर ही केन्द्रीय

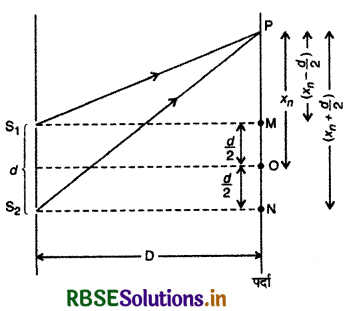
दीप्त फ्रिज बनेगी। पर्दे पर O से x_n दूरी पर स्थित बिन्दु P है, जहाँ पर बनने वाली फ्रिन्ज का प्रकार (दीप्त या अदीप्त) इस बात पर निर्भर करेगा कि S₁ व S₂ से P पर पहुँचने वाली तरंगों में पचान्तर कितना है। अतः सर्वप्रथम हम पथान्तर ज्ञात करते हैं।
समकोण ∆S₂PN से,
S₂P² = S₂N² + PN² = D² + \(\left(x_n+\frac{d}{2}\right)^2\)
इसी प्रकार समकोण ∆S₁PM से,
S₁P² = S₁M² + PM² = D² + \(\left(x_n+\frac{d}{2}\right)^2\)
∴ (S₂P² - S₁P²) = D² + \(\left(x_n+\frac{d}{2}\right)^2\) - D² - \(\left(x_n+\frac{d}{2}\right)^2\)
या (S₂P + S₁P) (S₂P - S₁P) = x_n² + \(\frac{d^2}{4}\) + 2x_n.\(\frac{d}{2}\) - x_n² - \(\frac{d^2}{4}\) + 2x_n.\(\frac{d}{2}\)
या (S₂P + S₁P) (S₂P - S₁P) = 2x_n.d
यदि बिन्दु P बिन्दु O से अधिक दूर नहीं है तो
S₁P ≈ S₂P ≈ D 
∴ (S₂P + S₁P) ≈ D + D = 2D 
अत: 2D.(S₂P - S₁P) = 2x_n.d 
या S₂P - S₁P = \(\frac{x_n \cdot d}{\mathrm{D}}\) ......................(1)
अदीप्त फ्रिन्ज की चौड़ाई एवं दीप्त फ्रिन्जों की स्थितियाँ-
यदि P बिन्दु पर n वीं दीप्त फ्रिन्ज बनती है तो पथान्तर
S₂P - S₁P = nλ .................(2)
समी. (1) व (2) की तुलना करने पर,
\(\frac{x_n \cdot d}{\mathrm{D}}\) = nλ 

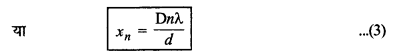
इस समीकरण की सहायता से केन्द्रीय दीप्त फ्रिज से दीप्त फ्रिजों की स्थितियाँ ज्ञात की जा सकती हैं।
इसी प्रकार x_{n + 1} = \(\frac{\mathrm{D}(n+1) \lambda}{d}\)
चूँकि दो क्रमागत (continuous) दीप्त फ्रिजों के मध्य अदीप्त फ्रिज होती है। अतः अदीप्त फ्रिज की चौड़ाई
ß = x_{n + 1} - x_n
= \(\frac{\mathrm{D}(n+1) \lambda}{d}-\frac{\mathrm{D} n \lambda}{d}\)
या ß = \(\frac{\mathrm{D} n \lambda}{d}+\frac{\mathrm{D} \lambda}{d}-\frac{\mathrm{D} n \lambda}{d}\)

इस सूत्र से अदीप्त फ्रिज की चौड़ाई ज्ञात कर सकते हैं।
पुनः समी. (3) से,
x_n = \(\frac{\mathrm{D} n \lambda}{d}=\frac{\mathrm{D} \lambda}{d} \cdot n=\beta n\)

इस सूत्र की सहायता से केन्द्र फ्रिज से दीप्त फ्रिजों की स्थितियाँ ज्ञात कर सकते हैं, यदि हमें फ्रिज की चौड़ाई ß ज्ञात हो।

दीप्त फ्रिज की चौड़ाई एवं अदीप्त फ्रिन्जों की स्थितियाँ: यदि P बिन्दु पर n वीं अदीप्त फ्रिन्ज बनती है तो पथान्तर
S₂P - S₁P = (2n - 1) λ/2 = \(\left(n-\frac{1}{2}\right)\)λ
या S₂P - S₁P = \(\left(n-\frac{1}{2}\right) \lambda\) ...............(6)
अब समो. (1) व (6) की तुलना करने पर,
\(\frac{x_n \cdot d}{\mathrm{D}}=\left(n-\frac{1}{2}\right) \lambda\)

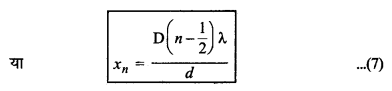
इस सूत्र की सहायता से केन्द्रीय दीप्त फ्रिज से अदीप्त फ्रिन्जों की दूरियाँ ज्ञात कर सकते हैं।
इसी प्रकार
x_{n + 1} = \(\frac{\mathrm{D}\left(n+1-\frac{1}{2}\right) \lambda}{d}=\frac{\mathrm{D}\left(n+\frac{1}{2}\right) \lambda}{d}\)
या x_{n + 1} = \(\frac{\mathrm{D}\left(n+\frac{1}{2}\right) \lambda}{d}\)
चूँकि दो अदीप्त फ्रिजों के मध्य दीप्त फ्रिज होती है, अत: दीप्त फ्रिज की चौड़ाई
ß = x_{n + 1} - x_n
= \(\frac{\mathrm{D}\left(n+\frac{1}{2}\right) \lambda}{d}-\frac{\mathrm{D}\left(n-\frac{1}{2}\right) \lambda}{d}\)
= \(\frac{\mathrm{D} \lambda}{d}\left(n+\frac{1}{2}-n+\frac{1}{2}\right)\)

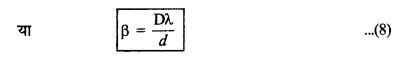
पुन: समी. (7) से,
x_n = \(\frac{\mathrm{D} \lambda}{d}\left(n-\frac{1}{2}\right)\)

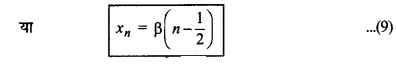
समी. (4) व (8) से स्पष्ट है कि दीप्त एवं अदीप्त फ्रिन्जों की चौड़ाई समान होती है।

प्रश्न 4.
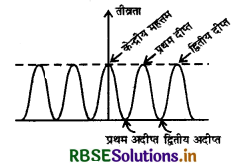
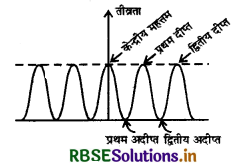
एकल झिरी द्वारा विवर्तन प्रतिरूप में उत्पन्न फ्रिन्जों की तीव्रता वितरण का तुलनात्मक ग्राफ खींचिए। केन्द्रीय उच्चिष्ठ की चौड़ाई का व्यंजक प्राप्त कीजिए।
उत्तर:
एकल रेखा - छिद्र द्वारा प्रकाश का विवर्तन (Diffraction of Light at a Single Slit)
चित्र 10.16 (a) में एकल रेखा - छिद्र (single slit) से विवर्तन प्रतिरूप देखने की व्यवस्था एवं चित्र 10.16(b) में दिखाई देने वाला विवर्तन प्रतिरूप दिखाया गया है। रेखा - छिद्र प्राप्त करने के लिए काले पेंट से रंगी हुई काँच की प्लेट पर ब्लेड की तीक्ष्ण धार से एक पतली रेखा खींच लेते हैं। यही रेखा, रेखा - छिद्र का कार्य करती है। इस स्लिट युक्त प्लेट को एक सीधे एवं ऊर्ध्वाधर तन्तु वाले लैम्प से कुछ मीटर की दूरी पर चित्र 10.16 (a) की भाँति रखते हैं। स्लिट से लैम्प की अधिक दूरी इसलिए रखी जाती है ताकि स्लिट पर समान्तर किरण पुंज आपतित हो। स्लिट के पीछे की तरफ से स्लिट को देखने पर हमें चित्र 10.16 (b) की भाँति 'विवर्तन प्रतिरूप' दिखाई देता है अर्थात् हमें एक तन्तु (fliament) दिखाई न देकर बीच में एक श्वेत चौड़ी पट्टी (white broad band) दिखाई देती है जिसके दोनों ओर तीन-चार रंगीन परन्तु कम चौड़ी पट्टियाँ दिखाई देती हैं। इन पट्टियों की तीव्रताएँ क्रमशः घटती जाती है।

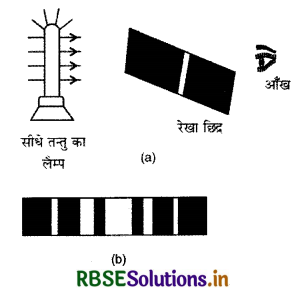
इन रंगीन पट्टियों के मध्य बढ़ती चौड़ाई की अदीप्त पट्टियाँ होती हैं। रेखा-छिद्र जितना बारीक होता है, 'विवर्तन प्रतिरूप' (Diffraction pattern) उतना ही अधिक फैला हुआ होता है तथा बीच की दीप्त पट्टी भी उतनी ही अधिक फैली होती है। विवर्तन प्रतिरूप का बनना यह प्रदर्शित करता है कि जब प्रकाश रेखा - छिद्र से होकर गुजरता है तो रेखा - छिद्र के किनारों पर थोड़ा - सा मुड़ (bend away) जाता है। यदि रेखा - छिद्र को चौड़ा करते जायें तो विवर्तन प्रतिरूप का फैलाव कम होता जाता है और धीरे - धीरे एक निश्चित स्लिट चौड़ाई के बाद रंगीन पट्टियों का दिखाई देना बन्द हो जाता है और एक पतली रेखा दिखाई देने लगती है अर्थात् स्लिट से होकर प्रकाश संचरण (propagation) ऋजुरेखीय हो जाता है। स्पष्ट है कि विवर्तन का होना आपतित प्रकाश की तरंगदैर्ध्य के सापेक्ष रेखा - छिद्र की चौड़ाई पर निर्भर करता है। यदि रेखा - छिद्र की चौड़ाई आपतित प्रकाश की तरंगदैर्घ्य की कोटि (order) की है तो विवर्तन होगा अन्यथा विवर्तन उपेक्षणीय (negligible) होगा। महत्वपूर्ण निष्कर्ष - विवर्तन प्रारूप में एकवर्णी प्रकाश - स्रोत को श्वेत प्रकाश से बदलने पर विवर्तन प्रारूप रंगीन हो जाता है लेकिन केन्द्रीय उच्चिष्ठ श्वेत ही रहता है।

प्रश्न 5.
हाइगेन्स के द्वितीयक तरंगिका सिद्धांत के आधार पर परावर्तन की व्याख्या कैसे करोगे?
उत्तर:
समतल तरंगों का परावर्तन (Reflection of Plane Waves)
माना AB एक समतल तरंगान है जो आपतन कोण i पर परावर्तक पृष्ठ पर आपतित होता है। तरंगान की चाल v है। सबसे पहले तरंगान का A बिन्दु परावर्तक (reflector) पर पहुँचता है। जैसे ही A बिन्दु परावर्तक पर पहुँचता है, द्वितीयक तरंगिकाएँ बननी आरम्भ हो जाती हैं और तरंगान की चाल (v) से ही आगे बढ़ती हैं। इसके बाद तरंगाग्र AB के शेष बिन्दु परावर्तक पर पहुँचते रहते हैं और द्वितीयक तरंगिकाएँ बनती रहती हैं। जब तरंगाग्र का बिन्दु B परावर्तक के B' तक पहुँचता है तब तक A पर बनने वाली तरंगिकाएँ A' तक पहुँच जाती हैं। इस प्रकार A'B' परावर्तित तरंगाग्र (reflected wavefront) प्राप्त होता है।

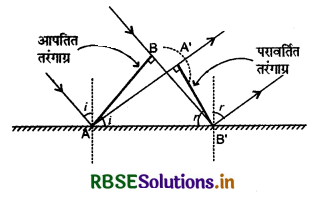
यदि B को B' या A को A' तक पहुँचने में लगा समय t हो तो
BB' = AA' = चाल x समय = v x t
अब ∆ABB' व ∆AA'B' से,
∠ABB' = ∠AA'B' (प्रत्येक समकोण है)
भुजा BB' = AA' सिद्ध कर चुके हैं।
भुजा AB' दोनों में उभयनिष्ठ (common) है।
∴ ∆ABB' = ∆AA'B'
∴ ∠BAB' = ∠A'B'A
या ∠i = ∠r 
या आपतन कोण = परावर्तन कोण
इस प्रकार-

• आपतित किरण, परावर्तित किरण एवं अभिलम्ब तीनों एक ही तल में हैं, क्योंकि तीनों कागज के तल में हैं।
• आपतन कोण परावर्तन कोण के बराबर है। यही परावर्तन के नियम हैं।

आंकिक प्रश्न

प्रश्न 1.
दो कला सम्बद्ध प्रकाश तरंगों के आयाम 3 : 1 हैं। इन तरंगों से प्राप्त व्यतिकरण प्रारूप में अधिकतम एवं न्यूनतम तीव्रताओं का अनुपात ज्ञात करो।
हल:
प्रश्नानुसार, a₁ : a₂ = 3 : 1
\(\frac{\mathrm{I}_{\max }}{\mathrm{I}_{\min }}=\frac{\left(\frac{a_1}{a_2}+1\right)^2}{\left(\frac{a_1}{a_2}-1\right)^2}=\frac{\left(\frac{3}{1}+1\right)^2}{\left(\frac{3}{1}-1\right)^2}\)
\(\frac{I_{\max }}{I_{\min }}=\left(\frac{4}{2}\right)^2=\left(\frac{2}{1}\right)^2=\frac{4}{1}\)
I_max : I_min = 4 : 1

प्रश्न 2.
यंग के द्विस्लिट प्रयोग में दो स्लिटों की चौड़ाईयों का अनुपात 4 : 1 है। व्यतिकरण प्रारूप में अधिकतम एवं न्यूनतम तीव्रताओं का अनुपात ज्ञात करो।
हल:
स्लिट से निर्गत प्रकाश की तीव्रता स्लिट की चौड़ाई के अनुक्रमानुपाती होती है।

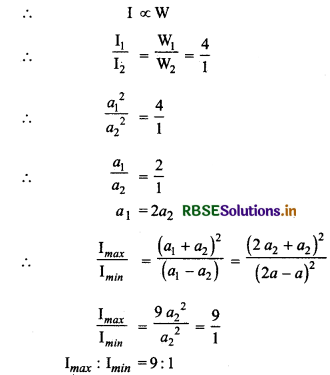
प्रश्न 3.
यंग के द्विस्लिट प्रयोग में 400 nm तरंगदैर्घ्य का प्रकाश प्रयोग करने पर फ्रिन्जों की चौड़ाई X प्राप्त होती है। तरंगदैर्घ्य बढ़ाकर 600 nm कर दी जाती है और स्लिटों के बीच के दूरी घटाकर आधी कर दी जाती है। यदि पर्दे पर फ्रिजों की चौड़ाई पूर्व की चौड़ाई के बराबर अर्थात् X ही रहे तो पहली और दूरी स्थितियों में पदें एवं स्लिटों के मध्य दूरियों का अनुपात क्या होगा?
हल:
प्रथम स्थिति में फिन्जों की चौड़ाई
X = \(\frac{\mathrm{D}_1 \lambda_1}{2 d}\)
द्वितीय स्थिति में जब स्लिटों के मध्य दूरी आधी अर्थात् d कर दी जाती है और फिन्जों की चौड़ाई X ही रहती है। अत:
X = \(\frac{\mathrm{D}_2 \lambda_2}{ d}\)
समी. (1) व (2) से
\(\frac{\mathrm{D}_1 \lambda_1}{2 d} = \frac{\mathrm{D}_2 \lambda_2}{ d}\)
या \(\frac{D_1}{D_2} = 2 x \frac{\lambda_2}{\lambda_1}\)
दिया है: λ₁ = 400 nm = 400 x 10^-9 m
λ₂ = 600 nm = 600 x 10^-9 m
∴ \(\frac{\mathrm{D}_1}{\mathrm{D}_2}=\frac{2 \times 600 \mathrm{~nm}}{400 \mathrm{~nm}}\) = 3
∴ D₁ : D₂ = 3 : 1

प्रश्न 4.
द्विस्लिट पर 630 nm तरंगदैर्ध्य का लेसर प्रकाश आपतित करने पर व्यतिकरण प्रारूप बनता है जिसमें फ्रिन्ज की चौड़ाई 7.2 nm है। इस दूसरे लेसर प्रकाश के स्रोत की तरंगदैर्ध्य की गणना करो जिसे स्लिटों के युग्म पर आपतित करने पर उत्पन्न व्यतिकरण प्रारूप में फ्रिन्ज चौड़ाई करने पर उत्पन्न व्यतिकरण प्रारूप में फ्रिज चौड़ाई 8.1 mm होती है।
हल:
फ्रिज की चौड़ाई ß = \(\frac{\lambda \mathrm{D}}{d}\)
जहाँ λ - तरंगदैर्घ्य, D - स्लिट और पर्दे के मध्य दूरी
d - स्लिटों के मध्य दूरी है।
D और d समान है, अत
\(\frac{\beta_1}{\beta_2}=\frac{\lambda_1}{\lambda_2}\)
यहाँ ß₁ = 7.2 x 10^-3 m,
ß₂ = 8.1 x 10^-3 m
λ₁ = 630 x 10^-9 m
लेसर प्रकाश के दूसरे स्रोत से उत्सर्जित प्रकाश की तरंगदैर्घ्य
λ₁ = \(\frac{\beta_2}{\beta_1}\) x λ₁
λ₂ = \(\frac{8.1 \times 10^{-3}}{7.2 \times 10^{-3}}\) x 630 x 10^-9
λ₂ = 708.75 x 10^-9 m
λ₂ = 708.75 nm

प्रश्न 5.
वंग के द्विस्लिट प्रयोग में 1.4 m दूर रखे पर्दे पर व्यतिकरण प्रारूप बनाने के लिए 800 nm और 600 nm तरंगदैथ्यों के प्रकाश पुंज प्रयुक्त किये जाते हैं। यदि दोनों स्लिटों के मध्य पृथक्कन 0.28 nm हैं तो दोनों तरंगदैथ्यों के संयुग्मन से बनी दीप्त फ्रिन्ज की केन्द्रीय फ्रिज से दूरी ज्ञात करो।
हल:
दिया है,
λ₁ = 800 nm, λ₂ = 600 nm, D = 1.4 m और d = 0.28 mm
= 2.8 x 10^-4 m
λ तरंगदैर्ध्य की n वी फ्रिज की चौड़ाई = 800 nm के साथ 600 nm की (n+ 1) वीं फ्रिज की तरंगदैर्ध्य
\(\frac{\mathrm{D} n \lambda_1}{d}=\frac{\mathrm{D}(n+1) \lambda_2}{d}\)
nλ₁ = (n + 1)λ
n x 800 x 10-9 = (n + 1) x 600 x 10^-9
\(\frac{n+1}{n}=\frac{4}{3}\)
\(\frac{1}{n}=\frac{4}{3}-1=\frac{1}{3}\)
n = 3
∴ केन्द्रीय फ्रिज से न्यूनतम दूरी
y_n = \(\frac{D_n \lambda_1}{d}\)
y_n = \(\frac{1.4 \times 3 \times 800 \times 10^{-9}}{2.8 \times 10^{-4}}\)
y_n = 12 x 10^-3 m
y_n = 12 mm

प्रश्न 6.
यंग के द्विस्लिट प्रयोग में स्लिटों के एक युग्म को 630 nm तरंगदैर्ध्य के एकवर्णी प्रकाश से प्रकाशित किया जाता है। 8.1 mm के पृथक्कन पर दीप्त फ्रिन्जें व्यतिकरण प्रारूप में बनती है। दूसरे एकवर्णी प्रकाश स्रोत से प्रकाशित करने पर दो क्रमागत फ्रिन्जों के बीच दूरी 7.2 mm होती है। दूसरे स्रोत से प्राप्त प्रकाश की तरंगदैर्घ्य ज्ञात करो।
हल:
हम जानते हैं फ्रिज चौड़ाई B = \(\frac{\mathrm{D} \lambda}{d}\)
दिये गये यंग द्विस्लिट प्रयोग के लिए, D और d निवत है-
\(\frac{\beta_1}{\beta_2}=\frac{\lambda_1}{\lambda_2}\)
जबकि \(\frac{\mathrm{D}}{d}\) = निवतांक
यहाँ ß₁ = 8.1 x 10^-3 m
λ₁ = 630 nm
= 6.3 x 10^-7 m
ß₂ = 7.2 x 10^-3 m
∴ λ₂ = \(\frac{\beta_2}{\beta_1} \times \lambda_1\)
= \(\frac{7 \cdot 2 \times 10^{-3} \mathrm{~m}}{8.1 \times 10^{-3}}\) x 6.3 x 10^-1
= 5.6 x 10^-7 m
λ₂ = 560 nm

प्रश्न 7.
एक संकीर्ण स्लिट पर 500 nm तरंगदैर्ध्य का समतल प्रकाश पुंज आपतित होता है जिससे 1 m दूर रखे पर्दे पर विवर्तन प्रारूप बनता है। इसमें यह प्रेक्षित किया जाता है कि पर्दे के मध्य में 2.5 mm दूरी पर प्रथम निनिष्ठ बनाता है। स्लिट की चौड़ाई ज्ञात कीजिए।
हल:
पर्दे के केन्द्र से वें निम्नष्ठि की दूरी
x_n = \(\frac{n \mathrm{D} \lambda}{d}\)
जहाँ D - स्लिट से पर्दे की दूरी, λ - प्रकाश की तरंगदैर्ध्य, d - प्रथम निम्निष्ठ के लिए स्लिट की चौड़ाई
n = 1
x_n = 2.5 mm
= 2.5 x 10^-3 m, D = 1 m
λ = 500 nm
= 500 x 10^-9 m
∴ 2.5 x 10^-3 = \(\frac{1 \times 1 \times 500 \times 10^{-9}}{d}\)
d = 2 x 10^-4
= 0.2 mm

प्रश्न 8.
600 nm तरंगदैर्ध्य की एक समान्तर प्रकाश किरण पुंज एक पतली झिरी पर आपतित होती है और परिणामी विवर्तन पैटर्न का, 2 m दूर स्थित एक पर्दे पर अवलोकन किया जाता है। यह प्रेक्षित किया जाता है कि प्रथम निम्निष्ठ पर्दे के केन्द्र से 3 mm दूरी पर है। झिरी की चौड़ाई का परिकलन कीजिए।
हुल:
झिरी की चौड़ाई
d = \(\frac{\mathrm{D} \lambda}{y}\)
यहाँ λ = 600 nm
= 600 x 10^-9 m
D = 1.2 m
y = 3 mm = 3 x 10^-3 m
d = \(\frac{1.2 \times 600 \times 10^{-9}}{3 \times 10^{-3}}\)
d = 2.4 x 10^-4 मी

प्रश्न 9.
2 x 10^-6 m द्वारक की एकल झिरी द्वारा होने वाले विवर्तन का अध्ययन करने के लिए बारी - बारी से सोडियम के प्रकाश की 590 nm और 596 nm को दो तरंगदैथ्यों का उपयोग किया गया है। झिरी और पर्दे के बीच की दूरी 1.5 मी. है। दोनों प्रकरणों में प्राप्त विवर्तन पैटर्न में पहले उच्चिष्ठ की स्थितियों के बीच पृथक्करण परिकलित कीजिए।
हल:
पहले प्रकरण में पहले उच्चिष्ठ की स्थिति
X₁ = \(\frac{3 \mathrm{D} \lambda_2}{2 d}\)
दूसरे प्रकरण में पहले उच्चिष्ठ की स्थिति
X₂ = \(\frac{3 \mathrm{D} \lambda_2}{2 d}\)
λ₁ = 590 nm,
λ₂ = 596 nm
उच्चिष्ठों के बीच पृथक्करण
∆X = X₂ - X₁
= \(\frac{3 \mathrm{D}}{2 d}\left[\lambda_2-\lambda_1\right]\)
∆X = \(\frac{3 \times 1.5}{2 \times 2 \times 10^{-6}}[596-590] \times 10^{-9}\)
∆X = 6.75 x 10^-3 मी
= 6.75 मिमी. 

प्रश्न 10.
0.1 mm दूरी में पृथक दो बिन्दु एक सूक्ष्मदर्शी से बस देखें जा सकते हैं। जब 6000 A° तरंगदैर्ध्य का प्रकाश काम में लिया जा रहा है। यदि 4800 A°का प्रकाश काम में लिया लाए तो विभेदन सीमा क्या झेगी?
हल:
एक सूक्ष्मदर्शी के लिए विभेदन सीमा
S = \(\frac{1.22 \lambda y}{D}\) x α
अत: S₂ = S₁\(\frac{\lambda_1}{\lambda}\)
= 0.1 x \(\frac{4800}{6000}\)
= 0.8 mm

प्रश्न 11.
यदि 0.2 m द्वारक वाले अभिदृश्यक वाली दूरदर्शी का उपयोग दो तारों को देखने के लिए किया जाता है तो तारों के मध्य न्यूनतम कोणीय दूरी क्या होगी? प्रयुक्त प्रकाश की तरंगदैर्घ्य 5900 Å है।
हल:
न्यूनतम कोणीय अन्तराल जो दूरदर्शी द्वारा विभेदित किया जा सकता है-
dθ = \(\frac{1 \cdot 22 \lambda}{D}\)
= \(\frac{1.22 \times 5900 \times 10^{-10}}{0.2}\)
= 3.6 x 10^-6 rad

प्रश्न 12.
यदि युवक और विश्लेषक के मध्य कोण 45° है। तो मूल प्रकाश और पारगमित प्रकाश की तीव्रताओं में अनुपात ज्ञात करो।
हल:
ध्रुवक से पारगमित प्रकाश की तीव्रता आपतित प्रकाश की तीव्रता की आधी रह जाती है।
धुवक से पारगमित प्रकाश की तीव्रता = \(\frac{\mathrm{I}_0}{2}\)
विश्लेषक से पारगमित प्रकाश की तीव्रता जब ध्रुवक और विश्लेषक के बीच कोण 45° है।
अतः I = \(\left(\frac{\mathrm{I}_0}{2}\right)\) cos2 45° = \(\frac{\mathrm{I}_0}{2} \times \frac{1}{2}\)
I = \(\frac{\mathrm{I}_0}{4}\)
या I = \(\frac{\mathrm{I}_0}{4}\)
\(\frac{\mathrm{I}}{\mathrm{I}_0}=\frac{1}{4}\)

प्रश्न 13.
जब किसी पदार्थ पर आपतित प्रकाश से संगत आपतन कोण 60° हो तो परावर्तित प्रकाश पूर्णतया धुवित हो जाता है। माध्यम में अपवर्तित प्रकाश का वेग ज्ञात कीजिए।
हल: 
60° पर आपतित प्रकाश पूर्णतया भूवित हो जाता है अतः पदार्थ का ध्रुवण कोण ip = 60°
बूस्टर के नियम से माध्यम का अपवर्तनांक
n = tan ip
n = tan 60°
= \(\sqrt{3}\)
जबकि माध्यम का अपर्वनांक

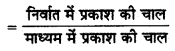
v = \(\frac{C}{V}\)
v = \(\frac{C}{n}\)
v = \(\frac{3 \times 10^8}{\sqrt{3}}\)
v = 1.732 x 10⁸ m/s

प्रतियोनी परीक्षा संबंधी प्रश्न

प्रश्न 1.
एक धुवक - विश्लेषक के सेट के विश्लेषण से निर्गत प्रकाश की तीव्रता मूल तीव्रता की 10% है। मानिए कि घुवक - विश्लेषण सेट प्रकाश का कोई भाग अवशोषित नहीं करता है, निर्गत तीव्रता शून्य करने के लिए विश्लेषक को किस कोण से घुमाना होगा-
(A) 45°
(B) 71.6°
(C) 90°
(D) 18.4°
उत्तर:
(A) 45°

प्रश्न 2.
मानिए कि एक तारे से आने वाले प्रकाश की तरंगदैर्ध्य 600 nm है। तो 2 m व्यास के दूरदर्शक की विभेदन सीमा होगी-
(A) 7.32 x 10^-7 rad 
(B) 6.00 x 10^-7 rad
(C) 3.66 x 10^-7 rad
(D) 1.83 x 10^-7 rad 
उत्तर:
(C) 3.66 x 10^-7 rad

प्रश्न 3.
I₁ व I₂ तीव्रताओं के दो कलासंबन्ध स्रोत है। यदि \(\frac{\mathbf{I}_{1 \mathbf{m a x}}}{\mathbf{I}_{\min }}\) अनुपात 6 : 1 तो \(\frac{I_1}{I_2}\) ज्ञात करो-
(A) \(\frac{16}{9}\)
(B) \(\frac{9}{16}\)
(C) \(\frac{4}{1}\)
(D) \(\frac{25}{9}\)
उत्तर:
(D) \(\frac{25}{9} \)

प्रश्न 4.
एक आदर्श धुवक A में से होकर I तीव्रता का घुवित प्रकाश गुजरता है। एक दूसरा धुवक B उसके पीछे रखा है। B के बाद प्रकाश की तीव्रता I/2 हो जाती है। A और B के बीच में अन्य प्रारुपित ध्रुवक रखा है। अब B के बाद प्रकाश की तीव्रता 1/8 प्राप्त होती है। A व C युवकों के बीच कोण है
(A) 45°
(B) 60° 
(C) 0°
(D) 30°
उत्तर:
(A) 45° 

प्रश्न 5.
µ अपर्वनांक के एक पदार्थ के समतल पृष्ठ पर वायु से अघुवित प्रकाश आपतित है। एक आपतन कोण i पर, परावर्तित किरण और आपतित किरण परस्पर लम्बवत प्राप्त होती है। इस स्थिति में कौन सा विकल्प सही है-
(A) i = sin^-1\(\left(\frac{1}{\mu}\right)\)
(B) परावर्तित प्रकाश का आपतन तल के लम्बवत विद्युत सदिश होता है।
(C) परावर्तित प्रकाश आपतन तल के समान्तर विद्युत सदिश के भूवित होता है।
(D) i = tan^-1\(\left(\frac{1}{\mu}\right)\)
उत्तर:
(A) i = sin^-1\(\left(\frac{1}{\mu}\right)\)

प्रश्न 6.
यंग के किसी द्विझरी प्रयोग में, दो झिरियों की चौड़ाईयों में अनुपात 1 : 25 है। तो व्यक्तिकरण पैटर्न में उच्चिष्ठतथा निम्नष्ठ की तीव्रताओं का अनुपात \(\frac{\mathbf{I}_{\max }}{\mathbf{I}_{\operatorname{mim}}}\) होगा।
(A) \(\frac{121}{49}\)
(B) \(\frac{49}{121}\)
(C) \(\frac{4}{9}\)
(D) \(\frac{9}{4}\)
उत्तर:
(D) \(\frac{9}{4} \)

प्रश्न 7.
यंग के द्वि - छिद्र प्रयोग में S₁ एवं S₂ स्लिटों से आने वाली तरंगों के बीच बिन्दु P एवं Q पर पश्चान्तर क्रमशः शून्य एवं \(\frac{\lambda}{4}\) है। P व Q पर तीव्रताओं का अनुपात होगा-
(A) 2 : 1
(B) 12 : 1
(C) 4 : 1
(D) 3 : 4
उत्तर:
(A) 2 : 1

प्रश्न 8.
यंग के द्वि - छिद्र प्रयोग में, दोनों स्लिटें एक समान आयाम A, और तरंगदैर्ध्य λ की तरंगों के कला सम्बद्ध स्रोत की भाँति कार्य करती हैं। इसी व्यवस्था (arrangement) से एक दूसरे प्रयोग में दोनों स्लिटों को उसी आयाम और तरंगदैर्घ्य के कला - असम्बद्ध स्रोतों की भाँति कार्य कराया जाता है। यदि पहली स्थिति में पर्दे के मध्य बिन्दु पर तीव्रता I₁ और दूसरी स्थिति में I₂ हो तो अनुपात \(\frac{I_1}{I_2}\) हैं-
(A) 2
(B) 1
(C) 0.5
(D) 4 
उत्तर:
(A) 2

प्रश्न 9. 
'E' ऊर्जा का विकिरण किसी पूर्णतः परावर्तक पृष्ठ पर अभिलम्बवत् आपतित होता है। यदि प्रकाश का वेग C हो तो, इस पृष्ठ का स्थानान्तरित संवेग होगा-
(A) \(\frac{2 \mathrm{E}}{c}\)
(B) \(\frac{2 \mathrm{E}}{c^2}\)
(C) \(\frac{E}{c^2}\)
(D) \(\frac{\mathrm{E}}{c}\)
उत्तर:
(B) \(\frac{2 \mathrm{E}}{c^2}\)

प्रश्न 10.
दो संबद्ध प्रकाश स्रोत प्रकाश उत्सर्जित करते हैं-
(A) समान तीव्रता
(B) समान पिच
(C) नियत परन्तु अलग - अलग तरंगदैर्ध्य
(D) समान आवृत्ति परन्तु नियत कलान्तर।
उत्तर:
(D) समान आवृत्ति परन्तु नियत कलान्तर।

प्रश्न 11.
यदि एकल पट्टी द्वारा फ्रॉनहॉफर विवर्तन में, पट्टी की चौड़ाई बढ़ती है, केन्द्रीय उच्चतम की चौड़ाई होगी-
(A) बढ़ेगी
(B) घटेगी
(C) अपरिवर्तित रहेगी
(D) प्रयुक्त प्रकाश की तरंगदैर्ध्य पर निर्भर करेगी।
उत्तर:
(B) घटेगी 

प्रश्न 12.
यदि व्यतिकरण के लिए प्रयोग में लाए गये यंग के द्वि - स्लिट उपकरण को वायु से पानी में विस्थापित कर दिया जाए, तो फ्रिज की चौड़ाई-
(A) बढ़ जाएगी
(B) घट जाएगी
(C) अनन्त हो जाएगी
(D) कोई बदलाव न होगा।
उत्तर:
(B) घट जाएगी