RBSE Class 12 Physics Important Questions Chapter 1 वैद्युत आवेश तथा क्षेत्र

Rajasthan Board RBSE Class 12 Physics Important Questions Chapter 1 वैद्युत आवेश तथा क्षेत्र Important Questions and Answers.

RBSE Class 12 Physics Chapter 1 Important Questions वैद्युत आवेश तथा क्षेत्र

अतिलघु उत्तरीय प्रश्न

प्रश्न 1. 
एक क्वाण्टम आवेश का मान लिखिए। 
उत्तर:
एक क्वाण्टम आवेश q = 1.6 x 10^-19 C.

प्रश्न 2. 
उस प्रयोग का नाम लिखिए जिससे विद्युत आवेश की क्वाण्टम प्रकृति की स्थापना हुई।
उत्तर:
मिलिकन तेल बूंद प्रयोग।

प्रश्न 3. 
यदि किसी बन्द पृष्ठ से गुजरने वाला नेट विद्युत फ्लक्स शून्य है, तो इससे क्या निष्कर्ष निकलता है?
उत्तर:
इस पृष्ठ से कोई नेट आवेश परिबद्ध नहीं हैं। 

प्रश्न 4. 
विद्युत द्विधुव आघूर्ण की परिभाषा लिखिए।
उत्तर:
"जब परिमाण में समान किन्तु प्रकृति में विपरीत (equal in magnitude but differ in nature) दो आवेश किसी अल्प दूरी (small distance) पर रखे होते हैं तो वे वैद्युत द्विधूव की रचना करते हैं। किसी आवेश एवं दोनों आवेशों के मध्य दूरी का गुणनफल वैद्युत द्विषुव आपूर्ण (electric dipole moment) कहलाता है।" इसे P से व्यक्त करते हैं। यह सदिश राशि है जिसकी दिशा ऋण आवेश से धन आवेश की ओर होती है।
माना कि वैद्युत द्विधूव के आवेश -q व +q कूलॉम है तथा उनके बीच की अल्प दूरी 2l हो तो वैद्युत द्विध्रुव आघूर्ण
p = q x 2l ................(1)
वैधुत द्विध्रुव आघूर्ण का मात्रक = Cm 
तथा वैद्युत द्विध्रुव आघूर्ण का विमीय सूत्र
= [A¹T¹L¹]
= [M⁰L¹T¹A¹]

प्रश्न 5.
किसी बंद पृष्ठ से गुजरने वाला विद्युत पलक्स किस पर निर्भर करता है?
उत्तर:
नेट परिबद्ध आवेश तथा माध्यम की विद्युतशीलता।

प्रश्न 6. 
यदि किसी बंद पृष्ठ में प्रवेश करने और बाहर निकलने वाले विद्युत फलक्स का Φ₁ और Φ₂ हैं तो इस पृष्ठ में परिबद्ध नेट विद्युत आवेश होगा।
उत्तर:
ε₀(Φ₂ - Φ₁)

प्रश्न 7. 
आप एक धातु के गोले को बिना स्पर्श कराये कैसे आवेशित कर सकते हैं?
उत्तर:
प्रेरण द्वारा आवेशित करके। 

प्रश्न 8. 
आदर्श वैद्युत द्विध्रुव किसे कहते हैं?
उत्तर:
यदि वैद्युत द्विध्रुव के दोनों आवेश काफी बड़े हों और उनके मध्य दूरी अत्यन्त कम हो, तो वह आदर्श वैद्युत द्विध्रुव कहलाता है।

प्रश्न 9. 
किसी बिन्दु आवेश को किसी खोखले चालक गोले ft I d hf = T; k'r' तथा बाहरी त्रिज्या '2r' है, के केन्द्र पर रखा गया है। इस गोले के भीतरी पृष्ठ पर पृष्ठीय आवेश घनत्व तथा बाहरी पृष्ठ पर पृष्ठीय आवेश घनत्व का अनुपात क्या होगा?
उत्तर:
भीतरी पृष्ठ पर पृष्ठीय आवेश घनत्व
σ₁ = \(\frac{q}{4 \pi r^2}\)
बाहरी पृष्ठ पर पृष्ठीय आवेश घनत्व
σ₂ = \(\frac{q}{4 \pi(2 r)^2}=\frac{q}{4\left(4 \pi r^2\right)}\)
∴ \(\frac{\sigma_1}{\sigma_2}=\frac{4}{1}\)
σ₁ : σ₂ = 4 : 1

प्रश्न 10. 
विद्युतरोधी आधारों पर रखे दो धात्विक गोले A और B एक दूसरे के सम्पर्क में हैं। आरेख में दर्शाए अनुसार कोई धनावेशित छड़ P गोले A के निकट लाई गई है। इन दोनों गोलों को एक - दूसरे से पृथक् करके छड़ P को हटा दिया गया है। गोले A और B पर आवेशों की प्रकृति क्या होगी?

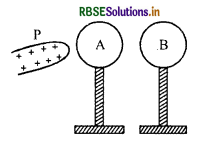
उत्तर:
A पर ऋणावेश व B पर धनावेश।

प्रश्न 11. 
कोई धात्विक गोला किसी विद्युत रोधी आधार पर रखा है। किसी त्राणावेशित छड़ को इस गोले के निकट लाकर, दर्शाए अनुसार गोले को भूसम्पर्कित कर दिया गया है। भूसम्पर्कण को हटाने और ऋणावेशित छड़ को दूर ले जाने पर गोले पर आवेश की प्रकृति क्या होगी? अपने उत्तर के लिए कारण दीजिए।

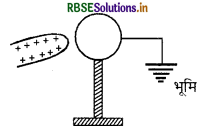
उत्तर:
गोले पर आवेश की प्रकृति ऋणात्मक होगी। प्रेरण के प्रभाव से इलेक्ट्रॉन छड़ की ओर आकर्षित होंगे।

प्रश्न 12. 
दो सर्वसम चालक गेंदों A और B पर क्रमशः - Q और 3Q आवेश हैं। इन्हें एक - दूसरे के सम्पर्क में लाकर फिर एक - दूसरे से दूरी पर पृथक् कर दिया गया। इसके बीच कूलॉमी बल की प्रकृति ज्ञात कीजिए।
उत्तर:
संपर्क में लाकर दूर करने पर दोनों गेंदों पर समान प्रकृति का आवेश q =\(\frac{-\mathrm{Q}+3 \mathrm{Q}}{2}=\mathrm{Q}\) होगा : अतः कूलॉमी बल की प्रकृति प्रतिकर्षणात्मक होगी।

प्रश्न 13. 
किसी धातु के गोले को दिया गया आवेश क्या इस पर निर्भर करता है कि गोला ठोस है अथवा खोखला? अपने उत्तर के लिए कारण दीजिए?
उत्तर:
नहीं, क्योंकि दोनों ही स्थितियों में आवेश केवल पृष्ठ पर ही वितरित होगा।

प्रश्न 14. 
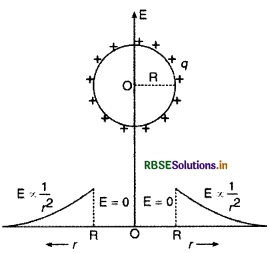
यदि किसी गोलीय गाउसीय पृष्ठ की त्रिज्या में वृद्धि कर दी जाए तो उसमें परिबद्ध किसी बिन्दुकित आवेश के कारण विद्युत क्षेत्र में क्या परिवर्तन होगा?
उत्तर:
विद्युत फ्लक्स नियत रहेगा, तब E ∝\(\frac{1}{r^2}\)
अतः विद्युत क्षेत्र घट जाएगा। 

प्रश्न 15. 
विद्युत फ्लक्स का मात्रक एवं विमीय सूत्र लिखिए। 
उत्तर:
मात्रक - Nm²C^-1
वियि सूत्र - [M¹L³T^-3A^-1] 

प्रश्न 16. 
समरूप वैद्युत क्षेत्र में स्थायी संतुलन की अवस्था में द्विध्रुव विद्युत क्षेत्र के साथ किस स्थिति में होता है? 
उत्तर:
द्विध्रुव पर लगने वाले बलयुग्म का आपूर्ण
τ = PE sinθ
यदि θ = 0 तो sinθ = 0
∴ τ = 0
यही स्थायी साम्यावस्था होती है अर्थात् वैद्युत द्विध्रुव क्षेत्र के अनुदिश होना चाहिए।

प्रश्न 17. 
एक समरूप आवेशित चालक गोले के कारण उसके केन्द्र पर विद्युत क्षेत्र की तीव्रता का मान कितना होता है?
उत्तर:
विद्युत फ्लक्स का मान आवेश की मात्रा पर निर्भर करता है। चूँकि चालक गोले के अन्दर आवेश शून्य है अत: विद्युत क्षेत्र की तीव्रता शून्य होगी।

लघु उत्तरीय प्रश्न

प्रश्न 1.
कूलॉम के नियम का महत्त्व समझाइए।
उत्तर:
कूलॉम का नियम बहुत बड़ी दूरियों से लेकर बहुत छोटी दूरियों के लिए सत्य है। इस नियम से उन बलों की व्याख्या करने में सहायता मिलती है, जिनके कारण-

• किसी परमाणु के इलेक्ट्रॉन उसके नामिक के साथ बैंधकर परमाणु की रचना करते हैं।
• दो या दो से अधिक परमाणु परस्पर संयुक्त होकर एक अणु की रचना करते हैं।
• अनेक परमाणु अथवा अणु परस्पर मिलकर ठोस तथा द्रवों की रचना करते हैं।

प्रश्न 2.
किसी बिन्दु पर विद्युत क्षेत्र की तीव्रता की परिभाषा निम्न प्रकार की जाती है।
E = \(\lim _{q_0 \rightarrow 0} \frac{E}{q_0}\)
जहाँ q₀ परीक्षण आवेश है और F इस पर लगने वाला बल है। इस सूत्र में \(\lim _{q_0 \rightarrow 0}\) का भौतिक महत्त्व क्या है?
उत्तर:
\(\lim _{q_0 \rightarrow 0}\) का विचार लेने का कारण यह है कि परीक्षण आवेश को प्रेक्षण बिन्दु पर रखने पर स्रोत आवेश (q) प्रभावित नहीं होना चाहिए। यदि धन परीक्षण आवेश +q₀ अति सूक्ष्म नहीं होगा तो इसका अपना स्वयं का विद्युत क्षेत्र उत्पन्न होगा और फलस्वरुप मापित विद्युत क्षेत्र की तीव्रता वास्तविक विद्युत क्षेत्र से अधिक होगी।

प्रश्न 3. 
यदि वैद्युत द्विध्रुव की अदीय स्थिति में प्रेक्षण बिन्दु की दूरी आधी कर दी जाए तो प्रेक्षण बिन्दु पर विद्युत क्षेत्र की तीव्रता पर क्या प्रभाव पड़ेगा?
उत्तर:
अक्षीय स्थिति में
E = \(\frac{1}{4 \pi \varepsilon_0} \frac{2 \mathrm{P}}{\mathrm{r}^3}\)
अतः E ∝\(\frac{1}{r^3}\)
स्पष्ट है कि यदि दूरी r के स्थान पर \(\frac{r}{2}\) कर दी जाये तो विद्युत क्षेत्र की तीव्रता 8 गुना हो जाएगी।

प्रश्न 4. 
किसी धात्विक गोलीय खोल की आन्तरिक त्रिज्या R₁ और बाहरी त्रिज्या R₂ है। इस खोल के केन्द्र पर कोई आवेश Q स्थित है। इस खोल के (i) भीतरी पृष्ठ, और (ii) बाहरी पृष्ठ पर पृष्ठीय आवेश घनत्व क्या होगा?
उत्तर:
धात्विक गोलीय खोल के आन्तरिक पृष्ठ पर - Q आवेश प्रेरित हो जाएगा और बाहरी पृष्ठ पर + Q आवेश प्रेरित हो जाएगा।
आन्तरिक पृष्ठ पर आवेश का पृष्ठ धनत्व
\(=\frac{-Q}{4 \pi R_1^2}\)
 बाहरी पृष्ठ पर आवेश का पृष्ठ घनत्व
\( =\frac{Q}{4 \pi R_2^2}\)

प्रश्न 5. 
यदि किसी पृष्ठ से बद्ध आवेश शून्य है तो इसका क्या यह तात्पर्य है कि समस्त पृष्ठ पर हर जगह विद्युत क्षेत्र शून्य है? इसके व्युत्क्रम यदि हर जगह किसी पृष्ठ पर विद्युत क्षेत्र शून्य है तो क्या इसका तात्पर्य है कि आन्दर आवेश शून्य है? 
उत्तर:
∵ q = 0, अतः गाउस की प्रमेय से,
Φ_E = \(\int \overrightarrow{\mathrm{E}} \cdot d \overrightarrow{\mathrm{S}}\) = 0
यह समीकरण यह नहीं बताता है कि \(\overrightarrow{\mathrm{E}}\) का मान अवश्य ही गाउसीय पृष्ठ पर शून्य होगा। यह भी सम्भव है कि \(\overrightarrow{\mathrm{E}}\) शून्य न हो, परन्तु पृष्ठ पर यह हर बिन्दु पर d\(\overrightarrow{\mathrm{S}}\) के लम्बवत् हो, तब समाकलन \(\phi \overrightarrow{\mathrm{E}}\) , d\(\overrightarrow{\mathrm{S}}\) शून्य होगा।
इसका व्युत्क्रम सही है यदि गाउसीय पृष्ठ के सभी बिन्दुओं पर \(\overrightarrow{\mathrm{E}}\) शून्य है, तब गाउस की प्रमेय से,
\(\phi \varepsilon=\int \overrightarrow{\mathrm{E}} \cdot d \overrightarrow{\mathrm{S}}=\frac{q}{\varepsilon_0}\)
⇒ q = 0
अत: गाउसीय पृष्ठ से बद्ध कोई आवेश नहीं है।

प्रश्न 6. 
किसी एकसमान विद्युत क्षेत्र में रखे किसी विद्युत द्विध्रुव पर लगने वाले बल आघूर्ण के लिए व्यंजक व्युत्पन्न कीजिए। इस विद्युत क्षेत्र में द्विधुव के उस अभिविन्यास की पहचान कीजिए जिसमें यह स्थायी संतुलन प्राप्त कर लेता है।
उत्तर:
एकसमान बाह्य क्षेत्र में द्विधुव (Dipole in a Uniform External Field) 
(a) समरूप विद्युत् क्षेत्र में द्विधुव पर लगने वाले बलयुग्म का आघूर्ण: चित्र 1.39 में एक समरूप विद्युत् क्षेत्र में एक वैद्युत द्विध्रुव

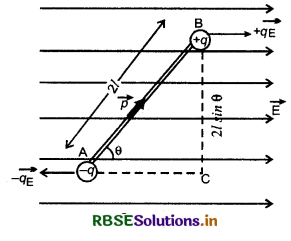
θ विक्षेप (deflection) की स्थिति में दिखाया गया है। द्विधुव के आवेशों (+q) व (-q) पर लगने वाले वैद्युत बल (qE) परिमाण में समान एवं दिशा में विपरीत हैं तथा दोनों की क्रिया रेखाएँ (line of action) भिन (different) हैं। अत: ये दोनों बल बलयुम बनाते हैं। इस बल युग्म का आघूर्ण
τ = बल x बलों की क्रिया रेखाओं के मध्य दूरी 
या τ = qE x BC 
चित्र से, \(\frac{\mathrm{BC}}{\mathrm{AB}}\) = sinθ
या BC = AB. sinθ 
या BC = 2l.sinθ
अतः τ = qE x 2l sinθ
= q2l. E sinθ

चित्र 1.40 की सहायता से सदिश रूप (veeter form) में बलयुग्म के आपूर्ण को निम्न प्रकार लिख सकते हैं-

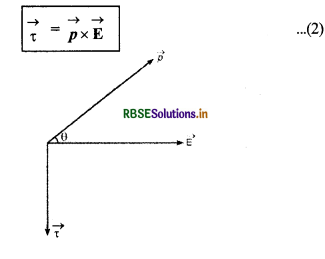
सदिश राशि बल आघूर्ण \(\vec{τ}\) को दिशा दक्षिणावर्त पेंच के नियमानुसार (according to right handed crew rule) \(\vec{p}\) व \(\vec{E}\) के तल के लम्बवत् होती है।
(i) जब θ = 0 तो sinθ = 0
अत: τ = pE sinθ = 0 
या τ = 0
यही स्थायी सन्तुलन (stable equilibrium) की अवस्था है।

(ii) यदि θ = 90° तो sinθ = 1 
τ_max = pE 

(iii) ∵ τ = pE sinθ
यदि E = 1 NC^-1, sinθ = 1 अर्थात् θ = 90°
तो τ = p
अर्थात् "वैद्युत द्विध्रुव आघूर्ण उस बलयुग्म के आघूर्ण (torque) के तुल्य है जो द्विघुव पर तब कार्य करता है जब वह एकांक तीव्रता के समरूप (uniform) वैद्युत क्षेत्र में क्षेत्र के लम्बवत् रखा होता है।"

(b) जब वैद्युत द्विध्रुव असमान (non - uniform) विद्युत् क्षेत्र में होता है-
(i) जब विद्युत् क्षेत्र \(\vec{p}\) की दिशा में बड़ता है: इस दशा में यदि (-q) आवेश की स्थिति में विद्युत् क्षेत्र E₁ और (+q) की स्थिति में E₂  है और E₂ > E₁ अत: (-q) पर बल qE₁ आवेश (+q) पर बल qE₂ से कम होगा और फलस्वरूप नेट बल = qE₂ - qE₁ होगा।

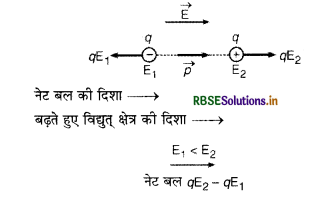
(ii) जब विद्युत् क्षेत्र \(\vec{p}\) की विपरीत दिशा में बढ़ता है: इस दशा में (-q) पर लगने वाला बल qE₁ आवेश (+q) पर लगने वाले बल qE₂ से अधिक होगा क्योंकि E₁ > E₂ अत: नेट बल = qE₁ - qE₂ होगा।    

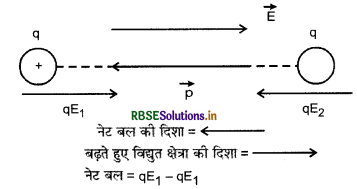
उक्त दोनों स्थितियों में द्विध्रुव पर नेट बल युग्म का आघूर्ण τ = pE sinθ = 0 होगा क्योंकि θ = 0°।

प्रश्न 7. 
दो विशाल समान्तर समतल चादरों के एकसमान आवेश घनत्व + σ तथा - σ हैं। (i) इन चादरों के बीच तथा (ii) इन चादरों के बाहर विद्युत क्षेत्र निर्धारित कीजिए।
उत्तर:

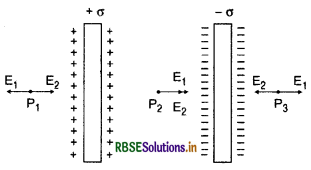
प्रत्येक प्लेट के कारण उसके निकट स्थित किसी बिन्दु पर विद्युत क्षेत्र की तीव्रता E₁ = E₂ = \(\frac{\sigma}{2 \varepsilon_0}\)
(i) इन चादरों के बीच बिन्दु P₂ पर विद्युत क्षेत्र की तीव्रता

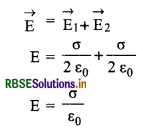
(ii) इन चादरों के बाहर P₁ या P₃ बिन्दु पर E = \(\overrightarrow{\mathrm{E}}_1 \sim \overrightarrow{\mathrm{E}}_2\) = 0

प्रश्न 8. 
गाउस नियम का अनुप्रयोग यह दर्शाने के लिए कीजिए कि किसी आवेशित गोलीय खोल के लिए खोल के बाहर विद्युत क्षेत्र इस प्रकार का होता है कि जैसे समस्त आवेश उसके केन्द्र पर संकेन्द्रित (सांदित) है।
उत्तर:
एकसमान आवेशित गोलीय कोश के कारण विद्युत् क्षेत्र की तीव्रता (Electric Field Intensity Due to a Uniformly Charged Spherical Shell)
माना R त्रिज्या का एक गोलीय कोश है जिस पर +q आवेश समान रूप से वितरित है। कोश के केन्द्र O से r दूरी पर स्थित बिन्दु P पर वैद्युत क्षेत्र की तीव्रता \(\vec{E}\) ज्ञात करनी है। बिन्दु P की निम्न स्थितियाँ ली जा सकती हैं-

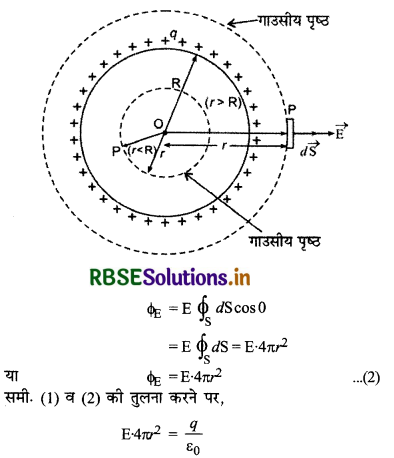
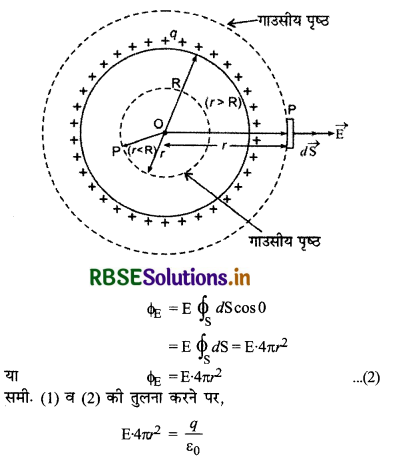
(i) जब बिन्दु P गोलीय कोश के बाहर (Outside Spherical Shell) स्थित है(r > R): इस दशा में कोश के केन्द्र O को केन्द्र मानकर r त्रिज्या के गोलीय गाउसीय पृष्ठ की कल्पना करते हैं। इस पृष्ठ में परिबद्ध आवेश q होगा तथा बिन्दु P इस पृष्ठ पर होगा। अत: गाउस प्रमेय से इस गाउसीय पृष्ठ का निर्गत कुल वैद्युत फ्लक्स
\(\phi_{\mathrm{E}}=\frac{q}{\varepsilon_0}\) .............(1)
गाउसीय पृष्ठ के प्रत्येक बिन्दु पर विद्युत् क्षेत्र की तीव्रता समान होगी और त्रिज्या की दिशा बाहर की और होगी। बिन्दु P पर एक लघु क्षेत्रफल अवयव (element) dS लें तो इससे गुजरने वाला वैद्युत फ्लक्स
\(\phi_{\mathrm{E}}=\overrightarrow{\mathrm{E}} \cdot \overrightarrow{\mathrm{S}}\)
अतः सम्पूर्ण पृष्ठ (whole surface) से निर्गत (exit) वैद्युत फ्लक्स
\(\phi_{\mathrm{E}}=\oint_{\mathrm{S}} \overrightarrow{\mathrm{E}} \cdot d \overrightarrow{\mathrm{S}}=\oint_{\mathrm{S}} \mathrm{E} \cdot d \mathrm{~S} \cos \theta\)
∵ गोलाकार गाउसीय पृष्ठ के प्रत्येक बिन्दु पर E नियत रहता है और θ = 0°, अत:

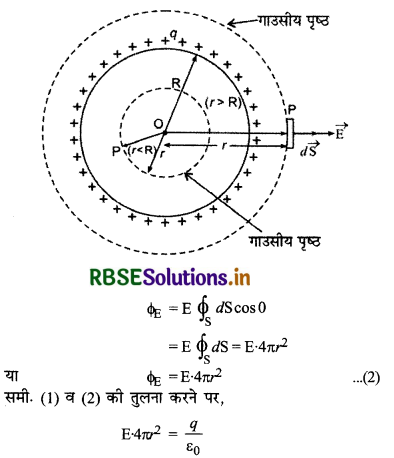
∴ E = \(\frac{1}{4 \pi \varepsilon_0} \cdot \frac{q}{r^2}\) ............(3)
सदिश रूप में,
\(\overrightarrow{\mathrm{E}}=\frac{1}{4 \pi \varepsilon_0} \cdot \frac{q}{r^2} \cdot \hat{r}\) ...............(4)
जहाँ \(\hat{r}\) = OP दिशा में एकांक (unit) वेक्टर। यदि कोश पर आवेश का पृष्ठ घनत्व (surface density) σ हो, तो
q = 4πR²σ
अतः समीकरण (4) से,
E = \( \frac{\sigma}{\varepsilon_0} \frac{\mathrm{R}^2}{r^2}\) ...............(5)

(ii) जबबिन्दुगोलीय कोश के पृष्ठपर स्थित है (On the Surface of Spherical Shell) (r = R): इस स्थिति में गाउसीय पृष्ठ की त्रिज्या R होने पर भी परिबद्ध आवेश q ही रहेगा अतः समी- (3) में r = R रखने पर,
E = \(\frac{1}{4 \pi \varepsilon_0} \frac{q}{\mathrm{R}^2}\) .........................(6)
सदिश रूप में (vectorially),
\(\overrightarrow{\mathrm{E}}=\frac{1}{4 \pi \varepsilon_0} \frac{q}{\mathrm{R}^2} \hat{r}\) .........................(7)
अर्थात् E का मान नियत होता है और यह अधिकतम मान होता है।

(iii) जब बिन्दु P गोलीय कोश के अन्दर (Inside the spherical Shell) स्थित है (r < R): चूँक गोलीय कोश को दिया गया समस्त आवेश कोश के पृष्ठ पर समान रूप से वितरित होता है तथा कोश के अन्दर कोई आवेश मौजूद नहीं होता है, अत: यदि O को केन्द्र मानकर r त्रिज्या (r < R) का कोई गाउसीय पृष्ठ खाँचें तो इस पृष्ठ से परिबद्ध आवेश शून्य होगा, अर्थात् गाउसीय पृष्ठ से निर्गत फ्लक्स

अर्थात् गोलीय कोश के अन्दर प्रत्येक बिन्दु पर विद्युत् क्षेत्र की तीव्रता शून्य होगी।

आवेशित गोलीय कोश के कारण उत्पन्न विद्युत् क्षेत्र की तीव्रता E कोश के केन्द्र O से दूरी r पर चित्र 1.60 की भाँति निर्भर करती है।

प्रश्न 9. 
विद्युत बल रेखाओं को परिभाषित कीजिए। विद्युत बल रेखाओं के कोई तीन गुण लिखिए।
उत्तर:
वैद्युत क्षेत्र रेखाएँ (Electric Lines of Field)
"वैद्युत क्षेत्र में स्वतन्त्रतापूर्वक (freely) छोड़ा गया धन परीक्षण आवेश जिस मार्ग का अनुसरण (follow) करता है, उसे उस क्षेत्र की वैद्युत क्षेत्र - रेखा या विद्युत बल रेखा कहते हैं।" वैद्युत क्षेत्र रेखाओं की निम्नलिखित विशेषताएँ (characteristics) होती हैं-
(i) वैद्युत क्षेत्र रेखा के किसी बिन्दु पर खींची गई स्पर्श रेखा उस बिन्दु पर परिणामी विद्युत् क्षेत्र की दिशा व्यक्त करती है।
(ii) वैद्युत क्षेत्र रेखाएँ धन आवेश से ऋण आवेश की ओर चलती है।
(iii) दो क्षेत्र रेखाएँ कभी एक - दूसरे को नहीं काटती (intersect) हैं क्योंकि यदि वे काटेंगी तो कटान बिन्दु (point of intersection) पर दोनों वक्रों पर खींची गई स्पर्श रेखाएँ दो परिणामी विद्युत् क्षेत्र व्यक्त करेंगी जो कि सम्भव नहीं है। अत: क्षेत्र रेखाओं का काटना भी सम्भव नहीं है।

(iv) वैद्युत क्षेत्र रेखाएँ खुले वक्र (open curves) के रूप में होती हैं क्योंकि ये धनावेश से चलकर ऋणावेश पर समाप्त हो जाती हैं।
(v) वैद्युत क्षेत्र रेखाएँ किसी पृष्ठ से लम्बवत् बाहर निकलती है और पृष्ठ पर लम्बवत क्षेत्र ही समाप्त होती है।
(vi) किसी स्थान पर वैद्युत बल रेखाओं का पृष्ठ घनत्व (surface density) (एकांक क्षेत्रफल से गुजरने वाली क्षेत्र रेखाओं की संख्या) उस स्थान पर 'वैद्युत' क्षेत्र की तीव्रता के अनुपात में होता है अर्थात् क्षेत्र रेखाएँ जितनी सघन (dense) होंगी, वहाँ विद्युत् क्षेत्र उतना ही प्रबल (strong) होगा। क्षेत्र रेखाओं की संख्या के पदों में विद्युत् क्षेत्र की तीव्रता की परिभाषा निम्न प्रकार की जा सकती है-
"किसी स्थान पर क्षेत्र रेखाओं की दिशा के लम्बवत् एकांक क्षेत्रफल (unit area) से गुजरने वाली क्षेत्र रेखाओं की संख्या, उस स्थान पर विद्युत् क्षेत्र की तीव्रता के तुल्य होती है।"

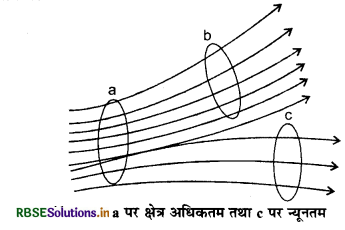
(vii) ये खिची हुई लचकदार डोरी (flexible string) की तरह लम्बाई में सिकुड़ने (contract) का प्रयत्न करती हैं। इसी कारण विपरीत आवेशों में आकर्षण होता है।
(viii) ये अपनी लम्बाई की लम्ब दिशा में एक - दूसरे से दूर रहने (for apart) का प्रयास करती हैं। इसलिए समान आवेशों के मध्य प्रतिकर्षण होता है।

प्रश्न 10. 
बिन्दु आवेशों (i) q > 0  (ii) q < 0 के लिए वैद्युत बल रेखाएँ खींचिए।
उत्तर:

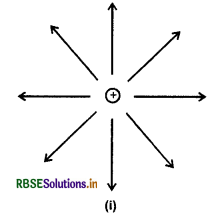
प्रश्न 11. 
विद्युत विषव की अक्षीय रेखा पर स्थित किसी बिन्दु पर विद्युत क्षेत्र की तीव्रता ज्ञात कीजिए।
उत्तर:
वैद्युत द्विध्रुव (इलेक्ट्रिक डाइपोल) वह निकाय (सिस्टम) है जिसमे दो बराबर परन्तु विपरीत प्रकार के बिन्दु आवेश एक - दूसरे से अल्प दूरी पर स्थित होते हैं। किसी एक आवेश तथा दोनो आवेशों के बीच की दूरी के गुणनफल को वैद्युत द्विध्रुव आघूर्ण (electric dipole moment) p कहते हैं। वास्तव में वैद्युत द्विध्रुव आघूर्ण उस निकाय में हुए आवेशों के ध्रुवीकरण को मापता है और अन्तर्राष्ट्रीय इकाई प्रणाली में इसकी इकाई कूलम्ब - मीटर है।

प्रकृति मे विभिन्न स्थितियों मे वैद्युत द्विध्रुव प्रकट होता है। दोनो आवेशो को मिलाने वाली रेखा को द्विध्रुव की अक्ष कहते हैं। यदि वैद्युत द्विध्रुव के दोनो आवेश -q तथा +q कूलॉम हों तथा उनके बीच की दूरी 2l मीटर हो तब वैद्युत द्विध्रुव का आघूर्ण ( p = q.2l) होता है। वैद्युत द्विध्रुव आघूर्ण एक सदिश है जिसकी दिशा प्रायः ऋणात्मक आवेश से धनात्मक आवेश की तरफ लिया जाता है।

यदि दो बराबर के बिन्दु आवेश (चार्ज) हों - एक ऋणात्मक और दूसरा धनात्मक - जिन्हें +q और −q लिखा जाये और उन दोनों के बीच का (ऋणात्मक से धनात्मक दिशा में जाता हुआ) विस्थापन सदिश (डिसप्लेसमेंट वेक्टर) d हो, तो अगर विद्युत द्विध्रुव आघूर्ण को p द्वारा दिखाया जाये तो वह इस प्रकार होगा:
p = qd
इसमें p की दिशा भी ऋणात्मक से धनात्मक की ओर होगी।
यदि बहुत से बिन्दु आवेश हों तो उनका विद्युत द्विध्रुवाघूर्ण निम्नलिखित तरीके से परिभाषित किया जाता है-
p = ∑_iq_ir_i,
जहाँ r_i , आवेश q_i का स्थिति सदिश है।
विद्युत क्षेत्र E में रखे द्विध्रुव पर लगने वाला बलाघूर्ण
M = p x E

दीर्घ उत्तरीय प्रश्न

प्रश्न 1. 
विद्युत क्षेत्र की तीव्रता की परिभाषा लिखिए। एक आवेशित चालक की सतह पर विद्युत बल एवं विद्युत दाब के लिए व्यंजक प्राप्त कीजिए। आवश्यक चित्र बनाइए।
उत्तर:
संधारित्र में संचित ऊर्जा से क्या तात्पर्य है? सिद्ध कीजिए- "दो आवेशित चालकों को जोड़ने पर उनके विभव में परिवर्तनों का अनुपात चालकों की धारिताओं के व्युत्क्रमानुपाती होता है।" समरूप आवेशित अचालक गोले के कारण विद्युत क्षेत्र व दूरी के मध्य आरेख बनाइये।
आवेशित चालक की सतह पर बल-
माना एक चालक की सतह पर पृष्ठ आवेश धनत्व σ है। हम चालक के बाहर एवं ठीक अन्दर चालक के सापेक्ष दो सममित बिन्दुओं क्रमश : P₁ व P₂ पर विचार करेंगे।
चूँकि किसी आवेशित चालक पृष्ठ के ठीक बाहर विद्युत क्षेत्र σ /ε₀  होता है अतः बिन्दु P₁ पर विद्युत क्षेत्र

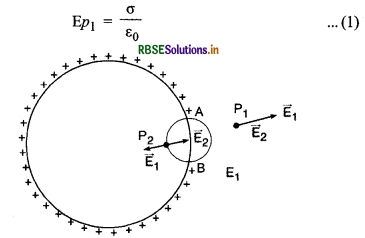
चूँकि चालक के भीतर विद्युत क्षेत्र शून्य होता है। अत: बिन्दु P₂ पर विद्युत क्षेत्र
Ep₂ = 0 ..............(2)
अब हम चालक के दो भागों (i) अल्पांश AB जिसका क्षेत्रफल ds है तथा (ii) चालक के बचे हुए भाग ACB में विभक्त कर सकते हैं। यदि अल्पांश AB के कारण निकट स्थित बिन्दुओं पर उत्पन्न विद्युत क्षेत्र की तीव्रता \(\overrightarrow{\mathrm{E}}_1\) एवं भाग ACB के कारण \(\overrightarrow{\mathrm{E}}_2\) है, तो
Ep₁ =E₁ + E₂ ..................(3)
(बिन्दु P₁ पर E₁ व E₂ समान दिशा में हैं)
तथा, Ep₂ = E₁ - E₂ ...............(4)
(बिन्दु P₂ पर E₁ व E₂ परस्पर विपरीत हैं)
समी- (2) व (4) से,
E₁ - E₂ = 0 
अर्थात्, E₁ = E₂ .............(5)
समीकरण (1) व (3) से,
E₁ + E₂ = \(\frac{\sigma}{\varepsilon_0}\)
E₂ = \(\frac{\sigma}{2 \varepsilon_0}\)  (∵ E₁ = E₂) 
यदि अल्पांश AB पर कुल आवेश dq है तो अल्पांश पर बल,

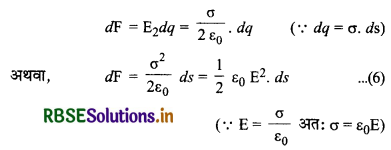
सम्पूर्ण पृष्ठ पर लगने वाला बल
E = \(\int \frac{\sigma^2}{\mathrm{~S} 2 \varepsilon_0} d s=\int \frac{\varepsilon_0 \mathrm{E}^2}{2} d s\) ............(7)
तथा पृष्ठ के एकांक क्षेत्रफल पर बल या दाब
P = \(\frac{d \mathrm{~F}}{d \mathrm{~S}}=\frac{\sigma 2}{2 \varepsilon_0}=\frac{1}{2} \varepsilon_0 \mathrm{E}^2\)
इसी दाब को विद्युत दाब कहते हैं।

प्रश्न 2.
गाउस नियम का उपयोग करते हुए R त्रिज्या के एकसमान आवेश वितरण σ के गोलीय खोल के कारण इसके केन्द्र से दूरी x के किसी बिन्दु पर विद्युत क्षेत्र के लिए व्यंजक व्युत्पन्न कीजिए, जबकि
(i) 0 < x < R, और 
(ii) x > R
उत्तर:
जब बिन्दु P गोलीय कोश के बाहर (Outside Spherical Shell) स्थित है(r > R): इस दशा में कोश के केन्द्र O को केन्द्र मानकर r त्रिज्या के गोलीय गाउसीय पृष्ठ की कल्पना करते हैं। इस पृष्ठ में परिबद्ध आवेश q होगा तथा बिन्दु P इस पृष्ठ पर होगा। अत: गाउस प्रमेय से इस गाउसीय पृष्ठ का निर्गत कुल वैद्युत फ्लक्स
\(\phi_{\mathrm{E}}=\frac{q}{\varepsilon_0}\) .............(1)
गाउसीय पृष्ठ के प्रत्येक बिन्दु पर विद्युत् क्षेत्र की तीव्रता समान होगी और त्रिज्या की दिशा बाहर की और होगी। बिन्दु P पर एक लघु क्षेत्रफल अवयव (element) dS लें तो इससे गुजरने वाला वैद्युत फ्लक्स
\(\phi_{\mathrm{E}}=\overrightarrow{\mathrm{E}} \cdot \overrightarrow{\mathrm{S}}\)
अतः सम्पूर्ण पृष्ठ (whole surface) से निर्गत (exit) वैद्युत फ्लक्स
\(\phi_{\mathrm{E}}=\oint_{\mathrm{S}} \overrightarrow{\mathrm{E}} \cdot d \overrightarrow{\mathrm{S}}=\oint_{\mathrm{S}} \mathrm{E} \cdot d \mathrm{~S} \cos \theta\)
∵ गोलाकार गाउसीय पृष्ठ के प्रत्येक बिन्दु पर E नियत रहता है और θ = 0°, अत:

∴ E = \(\frac{1}{4 \pi \varepsilon_0} \cdot \frac{q}{r^2}\) ............(3)
सदिश रूप में,
\(\overrightarrow{\mathrm{E}}=\frac{1}{4 \pi \varepsilon_0} \cdot \frac{q}{r^2} \cdot \hat{r}\) ...............(4)
जहाँ \(\hat{r}\) = OP दिशा में एकांक (unit) वेक्टर। यदि कोश पर आवेश का पृष्ठ घनत्व (surface density) σ हो, तो
q = 4πR²σ
अतः समीकरण (4) से,
E = \(\frac{\sigma}{\varepsilon_0} \frac{\mathrm{R}^2}{r^2} \) ...............(5)

जब बिन्दु P गोलीय कोश के अन्दर (Inside the spherical Shell) स्थित है (r < R): चूँक गोलीय कोश को दिया गया समस्त आवेश कोश के पृष्ठ पर समान रूप से वितरित होता है तथा कोश के अन्दर कोई आवेश मौजूद नहीं होता है, अत: यदि O को केन्द्र मानकर r त्रिज्या (r < R) का कोई गाउसीय पृष्ठ खाँचें तो इस पृष्ठ से परिबद्ध आवेश शून्य होगा, अर्थात् गाउसीय पृष्ठ से निर्गत फ्लक्स

अर्थात् गोलीय कोश के अन्दर प्रत्येक बिन्दु पर विद्युत् क्षेत्र की तीव्रता शून्य होगी।

आवेशित गोलीय कोश के कारण उत्पन्न विद्युत् क्षेत्र की तीव्रता E कोश के केन्द्र O से दूरी r पर चित्र 1.60 की भाँति निर्भर करती है।

प्रश्न 3. 
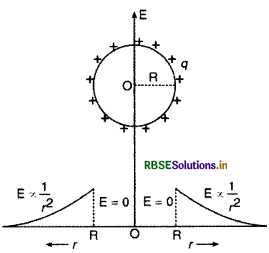
यह दर्शाने के लिए गाउस के नियम का उपयोग कीजिए कि त्रिज्या R के एकसमान आवेशित किसी गोलीय खोल के बाहर खोल के केन्द्र से r दूरी पर स्थित किसी बिन्दु पर विद्युत क्षेत्र का मानकर सना ही होता है, जितना कि केन्द्र पर सम्पूर्ण आवेश को सांद्रित मानर इसी बिन्दु पर होता। दूरी r के साथ, r < R और r ≥ R के लिए विद्युत क्षेत्र के विचरण को दर्शाने के लिए ग्राफ भी खींचिए।
उत्तर:
(i) जब बिन्दु P गोलीय कोश के बाहर (Outside Spherical Shell) स्थित है(r > R): इस दशा में कोश के केन्द्र O को केन्द्र मानकर r त्रिज्या के गोलीय गाउसीय पृष्ठ की कल्पना करते हैं। इस पृष्ठ में परिबद्ध आवेश q होगा तथा बिन्दु P इस पृष्ठ पर होगा। अत: गाउस प्रमेय से इस गाउसीय पृष्ठ का निर्गत कुल वैद्युत फ्लक्स
\(\phi_{\mathrm{E}}=\frac{q}{\varepsilon_0}\) .............(1)
गाउसीय पृष्ठ के प्रत्येक बिन्दु पर विद्युत् क्षेत्र की तीव्रता समान होगी और त्रिज्या की दिशा बाहर की और होगी। बिन्दु P पर एक लघु क्षेत्रफल अवयव (element) dS लें तो इससे गुजरने वाला वैद्युत फ्लक्स
\(\phi_{\mathrm{E}}=\overrightarrow{\mathrm{E}} \cdot \overrightarrow{\mathrm{S}}\)
अतः सम्पूर्ण पृष्ठ (whole surface) से निर्गत (exit) वैद्युत फ्लक्स
\(\phi_{\mathrm{E}}=\oint_{\mathrm{S}} \overrightarrow{\mathrm{E}} \cdot d \overrightarrow{\mathrm{S}}=\oint_{\mathrm{S}} \mathrm{E} \cdot d \mathrm{~S} \cos \theta\)
∵ गोलाकार गाउसीय पृष्ठ के प्रत्येक बिन्दु पर E नियत रहता है और θ = 0°, अत:

∴ E = \(\frac{1}{4 \pi \varepsilon_0} \cdot \frac{q}{r^2}\) ............(3)
सदिश रूप में,
\(\overrightarrow{\mathrm{E}}=\frac{1}{4 \pi \varepsilon_0} \cdot \frac{q}{r^2} \cdot \hat{r}\) ...............(4)
जहाँ \(\hat{r}\) = OP दिशा में एकांक (unit) वेक्टर। यदि कोश पर आवेश का पृष्ठ घनत्व (surface density) σ हो, तो
q = 4πR²σ
अतः समीकरण (4) से,
E = \(\frac{\sigma}{\varepsilon_0} \frac{\mathrm{R}^2}{r^2}\) ...............(5)

(ii) जबबिन्दुगोलीय कोश के पृष्ठपर स्थित है (On the Surface of Spherical Shell) (r = R): इस स्थिति में गाउसीय पृष्ठ की त्रिज्या R होने पर भी परिबद्ध आवेश q ही रहेगा अतः समी- (3) में r = R रखने पर,
E =\(\frac{1}{4 \pi \varepsilon_0} \frac{q}{\mathrm{R}^2}\) .........................(6)
सदिश रूप में (vectorially),
\(\overrightarrow{\mathrm{E}}=\frac{1}{4 \pi \varepsilon_0} \frac{q}{\mathrm{R}^2} \hat{r}\) .........................(7)
अर्थात् E का मान नियत होता है और यह अधिकतम मान होता है।

(iii) जब बिन्दु P गोलीय कोश के अन्दर (Inside the spherical Shell) स्थित है (r < R): चूँक गोलीय कोश को दिया गया समस्त आवेश कोश के पृष्ठ पर समान रूप से वितरित होता है तथा कोश के अन्दर कोई आवेश मौजूद नहीं होता है, अत: यदि O को केन्द्र मानकर r त्रिज्या (r < R) का कोई गाउसीय पृष्ठ खाँचें तो इस पृष्ठ से परिबद्ध आवेश शून्य होगा, अर्थात् गाउसीय पृष्ठ से निर्गत फ्लक्स

अर्थात् गोलीय कोश के अन्दर प्रत्येक बिन्दु पर विद्युत् क्षेत्र की तीव्रता शून्य होगी।

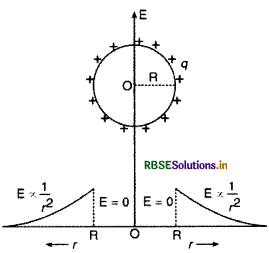
आवेशित गोलीय कोश के कारण उत्पन्न विद्युत् क्षेत्र की तीव्रता E कोश के केन्द्र O से दूरी r पर चित्र 1.60 की भाँति निर्भर करती है।

प्रश्न 4. 
किसी खोखले चालक गोले जिसकी आन्तरिक त्रिज्या r₁ तथा बाह्य त्रिज्या r₂ है, के पृष्ठ पर आवेश Q है। इस गोले के केन्द्र पर भी एक बिन्दु आवेश -q रखा है।
(a) इस गोले के (i) आन्तरिक और (ii) बाह्य पृष्ठ पर पृष्ठीय आवेश घनत्व क्या है?
(b) स्थिर - वैद्युतिकी के गाउस के नियम का उपयोग करके इस गोले से बाहर स्थित किसी बिन्दु पर विद्युत क्षेत्र के लिए व्यंजक प्राप्त कीजिए।
उत्तर:

(a) आन्तरिक पृष्ठ पर पृष्ठीय आवेश घनत्व
σ_i = \(\frac{q}{4 \pi r_1^2}\)
बाह्य पृष्ठ पर पृष्ठीय आवेश घनत्व
σ_out = \(\frac{\mathrm{Q}-q}{4 \pi r_2^2}\)

(b) गॉउस की प्रमेय से विद्युत फ्लक्स
Φ = \(\frac{\mathrm{Q}-q}{\varepsilon_0}\) ................(1)
कोश के बाहर स्थित बिन्दु P पर विद्युत क्षेत्र ज्ञात करना है, तब r त्रिज्या के गाउसीय पृष्ठ से संबद्ध विद्युत फलक्स
Φ = \(\int_s \overrightarrow{\mathrm{E}} \cdot d \overrightarrow{\mathrm{S}}=\int_s \mathrm{E} \cdot d s\)
Φ = E.4πr² ...............(2)
समी (1) व (2) की तुलना करने पर,
E.4πr² = \(\frac{\mathrm{Q}-q}{\varepsilon_0}\)
E = \(\frac{1}{4 \pi \varepsilon_0} \frac{\mathrm{Q}-q}{r^2}\)

प्रश्न 5.
(a) किसी अनन्त लम्बे पतले सीधे तार का एकसमान रैखिक आवेश घनत्व λ है। गाउस के नियम का उपयोग करके इस तार से x दूरी पर स्थित किसी बिन्दु पर विद्युत क्षेत्र (E) के लिए व्यंजक प्राप्त कीजिए।
(b) तार से दूरी x के फलन के रूप में विद्युत क्षेत्र E के विचरण को ग्राफ खींचकर दर्शाइए।
उत्तर:
अनन्त लम्बाई के एकसमान आवेशित सीधे तार के कारण विद्युत क्षेत्र (Electric Field due to a uniformly charged straight wire of Infinite Length)
माना AB एक अनन्त लम्बाई का सीधा तार है जिसकी एकांक लम्बाई (unit length) पर आवेश अर्थात् आवेश का रेखीय घनत्व λ है। इस रेखीय आवेश से r दूरी पर स्थित बिन्दु P पर विद्युत् क्षेत्र की तीव्रता ज्ञात करनी है। अब P बिन्दु पर विद्युत् क्षेत्र ज्ञात करने के लिए l लम्बाई एवं r त्रिज्या के एक बेलनाकार गाउसीय पृष्ठ की कल्पना करते हैं, जिसके बेलनाकार पृष्ठ (cylindrical surface) पर बिन्दु P स्थित है।

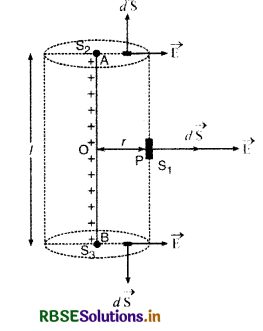
चूँकि आवेश का रेखीय घनत्व (linear density) λ है, अत: गाउसीय पृष्ठ द्वारा परिबद्ध आवेश (bounded charge)
q = λ.l
फ्लक्स की परिभाषानुसार,
\(\phi=\oint_{\mathrm{S}} \overrightarrow{\mathrm{E}} \cdot d \overrightarrow{\mathrm{S}}=\oint_{\mathrm{S}} \mathrm{E} d \mathrm{~S} \cos \theta\) ..................(1)
समीकरण (1) को हल करने के लिए गाउसीय पृष्ठ को निम्न तीन भागों में बाँट सकते हैं-

• बेलनाकार पृष्ठ S₁ जिस पर विद्युत् क्षेत्र की तीव्रता हर जगह समान है एवं θ = 0° ∴ cos 0° = 1
• सूक्ष्म पृष्ठ S₂ जहाँ वैद्युत क्षेत्र पृष्ठ के अनुदिश (along) है अतः θ = 90° ∴ cos 90° = 0
• सूक्ष्म पृष्ठ S₃, जहाँ θ = 90° ∴ cos 90° = 0 

अतः समी. (1) से,

अब गाउस के प्रमेय से,
\(\phi=\frac{1}{\varepsilon_0}(\Sigma q)=\frac{\lambda l}{\varepsilon_0}\) ...................(3)
समी. (2) व (3) की तुलना करने पर,

यदि रेखीय आवेश की लम्य दिशा (perpendicular direction) में एकांक वेक्टर \(\hat{n}\) हो तो सदिश रूप में
\(\overrightarrow{\mathrm{E}}=\frac{1}{4 \pi \varepsilon_0 K} \cdot \frac{2 \lambda}{r} \hat{n}\) ....................(5)
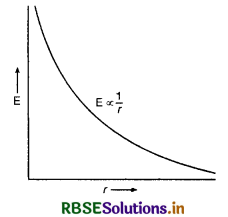
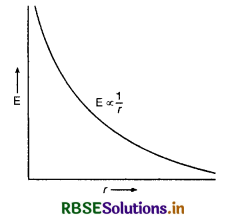
स्पष्ट है कि E ∝ \(\frac{1}{r}\)
अर्थात् अनन्त लम्बाई के रेखीय चालक के निकट बिन्दु पर विद्युत् क्षेत्र की तीव्रता चालक से बिन्दु की दूरी के व्युत्क्रमानुपाती (inversely proportional) होती है लेकिन आवेश की लम्बाई पर निर्भर नहीं करती है। दूरी के साथ विद्युत् क्षेत्र की तीव्रता का परिवर्तन (variation) चित्र 1.56 में दिखाया गया है।

प्रश्न 6. 
किसी वैधुत द्विधव की विषुवत रेखा के किसी बिन्दु पर विद्युत क्षेत्र के लिए व्यंजक व्युत्पन्न कीजिए।
उत्तर:
निरक्षीय स्थिति (equatorial position) में - वैद्युत द्विध्रुव की निरक्षीय स्थिति में दूरी r पर स्थित बिन्दु P पर विद्युत् क्षेत्र की तीव्रता ज्ञात करनी है। बिन्दु P से दोनों आवेों की दूरियाँ समान \((\sqrt{r^2+l^2})\) होंगी। अतः P पर +q आवेश के कारण उत्पन्न विद्युत् क्षेत्र की तीव्रता का परिमाण
E₁ = \(\frac{1}{4 \pi \varepsilon_0} \frac{q}{\left(r^2+l^2\right)}\) (AP दिशा में)

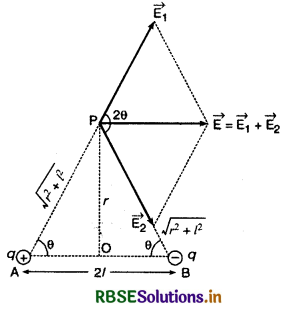
और -q आवेश के कारण P पर उत्पन्न विद्युत् क्षेत्र की तीव्रता का परिमाण
E₂ = \(\frac{1}{4 \pi \varepsilon_0} \frac{q}{\left(r^2+l^2\right)}\) (PB दिशा में) 
इस प्रकार \(\left|\overrightarrow{\mathrm{E}_1}\right|=\left|\overrightarrow{\mathrm{E}_2}\right|\)
या E₁ = E₂
बिन्दु P पर परिणामी विद्युत् क्षेत्र की तीव्रता
\(\overrightarrow{\mathrm{E}}=\overrightarrow{\mathrm{E}_1}+\overrightarrow{\mathrm{E}_2}\)
समान्तर चतुर्भुज के नियम से परिणामी विद्युत् क्षेत्र की तीव्रता का परिमाण

चित्र 1.36 में \(\overrightarrow{\mathrm{E}}\) की दिशा द्विध्रुव की अक्ष के समान्तर होगी। चूंकि \(\overrightarrow{\mathrm{p}}\) की दिशा ऋण आवेश से धन आवेश की ओर होती है अत: \(\overrightarrow{\mathrm{E}}\) व \(\overrightarrow{\mathrm{p}}\) की दिशाएँ परस्पर विपरीत होगी। इस प्रकार समी. (7) को सदिश रूप में निम्न प्रकार लिख सकते हैं-
\(\overrightarrow{\mathrm{E}}=\frac{1}{4 \pi \varepsilon_0} \frac{\vec{p}}{\left(r^2+l^2\right)^{3 / 2}}\) ......................(8)
दीर्घ दूरियों के लिए r >> l
∴ r² >> l²
अतः l² को r² की तुलना में छेड़ने पर समी. (7) से,
\(\mathrm{E}=\frac{1}{4 \pi \varepsilon_0} \frac{p}{r^3}\) ..................(9)
सदिश रूप में
\(\overrightarrow{\mathrm{E}}=-\frac{1}{4 \pi \varepsilon_0} \frac{\vec{p}}{r^3}\) ......................(10)

प्रश्न 7. 
गाउस के नियम का उपयोग करके आवेश धनत्व λ C/m की किसी सीधी एकसमान आवेशित अनन्त रेखा के कारण विद्युत क्षेत्र E के लिए व्यंजक व्युत्पन्न कीजिए।
आवेश रेखा से लम्बवत् दूरी r के साथ E के विचरण को दर्शाने के लिए ग्राफ खींचिए।
उत्तर:
अनन्त लम्बाई के एकसमान आवेशित सीधे तार के कारण विद्युत क्षेत्र (Electric Field due to a uniformly charged straight wire of Infinite Length)
माना AB एक अनन्त लम्बाई का सीधा तार है जिसकी एकांक लम्बाई (unit length) पर आवेश अर्थात् आवेश का रेखीय घनत्व λ है। इस रेखीय आवेश से r दूरी पर स्थित बिन्दु P पर विद्युत् क्षेत्र की तीव्रता ज्ञात करनी है। अब P बिन्दु पर विद्युत् क्षेत्र ज्ञात करने के लिए l लम्बाई एवं r त्रिज्या के एक बेलनाकार गाउसीय पृष्ठ की कल्पना करते हैं, जिसके बेलनाकार पृष्ठ (cylindrical surface) पर बिन्दु P स्थित है।

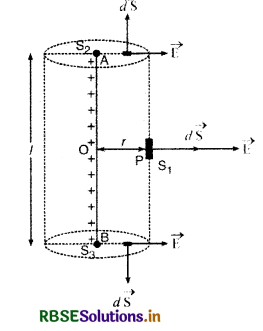
चूँकि आवेश का रेखीय घनत्व (linear density) λ है, अत: गाउसीय पृष्ठ द्वारा परिबद्ध आवेश (bounded charge)
q = λ.l
फ्लक्स की परिभाषानुसार,
\(\phi=\oint_{\mathrm{S}} \overrightarrow{\mathrm{E}} \cdot d \overrightarrow{\mathrm{S}}=\oint_{\mathrm{S}} \mathrm{E} d \mathrm{~S} \cos \theta\) ..................(1)
समीकरण (1) को हल करने के लिए गाउसीय पृष्ठ को निम्न तीन भागों में बाँट सकते हैं-

• बेलनाकार पृष्ठ S₁ जिस पर विद्युत् क्षेत्र की तीव्रता हर जगह समान है एवं θ = 0° ∴ cos 0° = 1
• सूक्ष्म पृष्ठ S₂ जहाँ वैद्युत क्षेत्र पृष्ठ के अनुदिश (along) है अतः θ = 90° ∴ cos 90° = 0
• सूक्ष्म पृष्ठ S₃, जहाँ θ = 90° ∴ cos 90° = 0 

अतः समी. (1) से,

अब गाउस के प्रमेय से,
\(\phi=\frac{1}{\varepsilon_0}(\Sigma q)=\frac{\lambda l}{\varepsilon_0}\) ...................(3)
समी. (2) व (3) की तुलना करने पर,

यदि रेखीय आवेश की लम्य दिशा (perpendicular direction) में एकांक वेक्टर \(\hat{n}\) हो तो सदिश रूप में
\(\overrightarrow{\mathrm{E}}=\frac{1}{4 \pi \varepsilon_0 K} \cdot \frac{2 \lambda}{r} \hat{n}\) ....................(5)
स्पष्ट है कि E ∝ \(\frac{1}{r}\)
अर्थात् अनन्त लम्बाई के रेखीय चालक के निकट बिन्दु पर विद्युत् क्षेत्र की तीव्रता चालक से बिन्दु की दूरी के व्युत्क्रमानुपाती (inversely proportional) होती है लेकिन आवेश की लम्बाई पर निर्भर नहीं करती है। दूरी के साथ विद्युत् क्षेत्र की तीव्रता का परिवर्तन (variation) चित्र 1.56 में दिखाया गया है।

प्रश्न 8.
गाउस प्रमेय का उपयोग करके पृष्ठीय आवेश घनत्व σ की किसी एकसामन आवेशित अनन्त बड़ी समतल पतली शीट के कारण विद्युत क्षेत्र ज्ञात कीजिए।
उत्तर:
एकसमान आवेशित अनन्त समतल चादर के कारण विद्युत क्षेत्र (Electrie Field due to an Uniformly Charged Infinite Plane Sheet)
(a) अनन्त विस्तार की आवेशित चालक परत के कारण वैद्युत क्षेत्र की तीव्रता (Intensity of Electric Field due to any Infinite Extent Charged Condueting Sheet): जब अनन्त विस्तार (infinite extent) की चालक परत को आवेश दिया जाता है तो आवेश पट्टिका के बाहरी पृष्ठ पर समान रूप से वितरित हो जाता है जिससे चालक के अन्दर विद्युत् क्षेत्र शून्य हो जाता है। चालक के पृष्ठ पर तथा उसके निकट बाह्य बिन्दु पर वैद्युत क्षेत्र परत के पृष्ठ के लम्बवत् होता है।

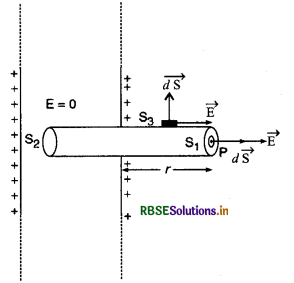
माना परत पर आवेश का पृष्ठ घनत्व σ है। इस परत के कारण लम्बवत् दूरी r पर स्थित किसी बिन्दु P पर वैद्युत क्षेत्र की तीव्रता ज्ञात करनी है।
अब एक बेलनाकार गाउसीय पृष्ठ की कल्पना करते हैं जिसका एक सूक्ष्म पृष्ठ S₁ बिन्दु P पर तथा दूसरा सूक्ष्म पृष्ठ S₂ परत के अन्दर स्थित है। इस गाउसीय पृष्ठ का अनुप्रस्थ परिच्छेद क्षेत्रफल S है अतः बेलनाकार गाउसीय पृष्ठ द्वारा परिबद्ध आवेश
q = σ.S ................(1)
अब फ्लक्स की परिभाषानुसार,
\(\phi_{\mathrm{E}}=\oint_{\mathrm{S}} \overrightarrow{\mathrm{E}} \cdot \overrightarrow{d \mathrm{~S}}=\oint_{\mathrm{S}} \mathrm{E} \cdot d \mathrm{~S} \cdot \cos \theta\) ..................(2)
समी. (2) को हल करने के लिए हम गाउसीय पृष्ठ को चीन भागों में बाँट सकते हैं-
(i) प्लेट के पृष्ठ के बाहर सूक्ष्म पृष्ठ S₁,
जहाँ θ = 0 ∴ cosθ = 1

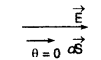
(ii) चालक प्लेट के अन्दर सूक्ष्म पृष्ठ S₂,
जहाँ E = 0 तथा 

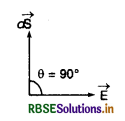
(iii) बेलनाकार पृष्ठ S₃,
जहाँ θ = 90°, अत: cosθ = 0 
∴ समीकरण (2) से,

या \(\phi_{\mathrm{E}}\) = E.S (क्योंकि \(\oint_{\mathrm{S}_1} \cdot d \mathrm{~S}\) = S) ...................(3)
गाउस के प्रमेय से,
Φ = \(\frac{1}{\varepsilon_0}\) x परिबद्ध आवेश
= \(\frac{q}{\varepsilon_0}=\frac{\sigma \mathrm{S}}{\varepsilon_0}\) (∵ q = σS) ..................(4)
समी, (3) व (4) की तुलना करने पर
E.S = \(\frac{\sigma S}{\varepsilon_0}\) या E = \(\frac{\sigma}{\varepsilon_0}\) .................(5)
यदि चालक के पृष्ठ के लम्बवत् एकांक सदिश हो तो सदिश रूप में विद्युत् क्षेत्र
\(\overrightarrow{\mathrm{E}}=\frac{\sigma}{\varepsilon_0} \hat{n}\) ...................(6)
इस प्रकार अनन्त विस्तार की आवेशित प्लेट के निकट किसी बिन्दु पर वैद्युत क्षेत्र की तीव्रता परत के क्षेत्रफल एवं परत से उस बिन्दु की दूरी पर निर्भर नहीं करती है।

(b) अनन्त विस्तार की आवेशित परावैधुत परत के कारण वैद्युत क्षेत्र की तीव्रता (Electric Field Intensity due to any Infinite Extent Charged Dielectric Sheet): चित्र 1.58 में पतली, अनन्त विस्तार की समान रूप से आवेशित परावैधुत परत प्रदर्शित की गयी है। जिस पर एकसमान आवेश का पृष्ठ घनत्व σ है। इस परत से r दूरी पर स्थित बिन्दु P पर विद्युत क्षेत्र की तीव्रता ज्ञात करनी है।

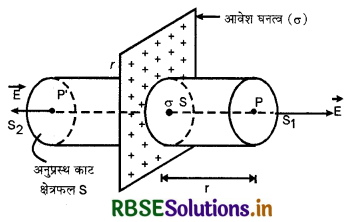
सममिति से, विद्युत क्षेत्र की तीव्रता परत से बाहर की ओर होगी। इसके अतिरिक्त परत से समान दूरी पर स्थित दो बिन्दुओं P और P' के लिए E का परिमाण समान पर दिशा में विपरीत होगा।
हम एक बेलनाकार गाउसीय पृष्ठ को चुनते हैं जिसकी अनुप्रस्थ कार का क्षेत्रफल S और लम्बाई 2r है, इसका अक्ष परत के लम्बवत् है।
चूँकि क्षेत्र रेखायें बेलन के वक़ पृष्ठ के समान्तर होंगी अत: वक्र पृष्ठ से निर्गत फ्लक्स शून्य होगा। बेलन के अन्त्यफलक (plane - end faces) S₁ व S₂ से निर्गत फ्लक्स
Φ_E = ES + ES = 2ES 
गाउसीय पृष्ठ से परिबद्ध आवेश
q = σS
गाउस की प्रमेय से,
Φ_E = \(\frac{q}{\varepsilon_0}\)

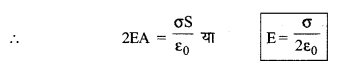
अत: E, r पर निर्भर नहीं है।

आंकिक प्रश्न

प्रश्न 1.
किसी धातु के गोले को 1C आवेश से धनावेशित करने में उससे कितने इलेक्ट्रॉन निष्कासित करने होंगे?
हल:
दिया है: आवेश q = 1C
इलेक्ट्रॉनों की संख्या = n
q = ne
n = \(\frac{q}{e}\)
n = \(\frac{1}{1.6 \times 10^{-19}}\)
= 6.25 x 10¹⁸ इलेक्ट्रॉन

प्रश्न 2.
किसी वस्तु को इतना आवेशित किया जाता है कि उसके दव्यमान में 9.1 ng की वृद्धि हो जाती है तब
(i) कितने इलेक्ट्रॉन वस्तु को दिए गए?
(ii) आवेश का मान एवं प्रकृति ज्ञात करो। 
उत्तर:
दिया है, ∆m = 9.1 ng = 9.1 x 10^-9 g
= 9.1 x 10^-12 kg 
(i) ∆m = nme
n = \(\frac{\Delta m}{m_e}=\frac{9.1 \times 10^{-12}}{9.1 \times 10^{-31}}\)
n = 10¹⁹ इलेक्ट्रॉन 

(ii) आवेश q = ne
q = 10¹⁹ x 1.6 x 10^-19
q = 1.6 C

प्रश्न 3.
निर्यात् में रखे दो बिन्दुवत आवेशों के मध्य बल 18 N है यदि 1 mm मोटाई तथा 6 परावैद्युतांक की एक कांच की पट्टिका इन आवेशों के मध्य रख दी जाये तब बल का मान ज्ञात कीजिए। 
हल: 
दिया है; F = 18 N
ε_r = 6
F_m = \(\frac{\mathrm{F}}{\varepsilon_{\mathrm{r}}}=\frac{18}{6}\) = 3 N

प्रश्न 4. 
समान आवेश से आवेशित दो धन आयनों के मध्य प्रतिकर्षण बल 3.7 x 10^-9 N है जब उनके मध्य दूरी 5Å है। ज्ञात कीजिए प्रत्येक आयन पर कितने इलेक्ट्रॉनों की कमी है?
हल: 
दोनों आयनों पर आवेश
q₁ = q₂ = q
प्रतिकर्षण बल F = 3.7 x 10^-9 N 
दूरी r = 5Å = 5 x 10^-10 m

प्रश्न 5. 
चार समान आवेश प्रत्येक q मान का, a भुजा वाले वर्ग के चारों कोनों पर स्थित हैं। प्रत्येक आवेश पर शेष आवेशों के कारण परिणामी बल ज्ञात कीजिए।
हलः

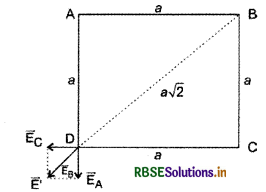
बिन्दु D पर उत्पन्न विद्युत क्षेत्र

∵ E_A = E_C, अत: इन दोनों का परिणामी \(\overrightarrow{\mathrm{E}}\) दोनों के मध्य कोण को समद्विभाजित करेगा।
∴ E' = \(\sqrt{E_A^2+E_C^2}\)
= E_A \(\sqrt{2}\) = 9 x 10⁹\(\frac{q}{a^2} \sqrt{2}\)
∵ E' और E_B एक ही दिशा में है, अत: इन दोनों का परिणामी
E = E' + E_B
= 9 x 10⁹ \(\frac{q}{a^2} \sqrt{2}\) + 9 x 10⁹\(\frac{q}{a^2}\)
या E = 9 x 10⁹\(\frac{q}{a^2}(\sqrt{2}+1)\)
अत: D पर आरोपित बल
F = E_q = 9 x 10⁹\(\frac{q^2}{a^2}(\sqrt{2}+1)\)

प्रश्न 6.
तीन बिन्दु आवेश q, -4q और 2q भुजा 'l' के समबाहु त्रिभुज ABC के शीर्षों पर आरेख में दाए अनुसार स्थित हैं। आवेश q पर कार्यरत परिणामी विद्युत बल के परिमाण के लिए व्यंजक ज्ञात कीजिए।

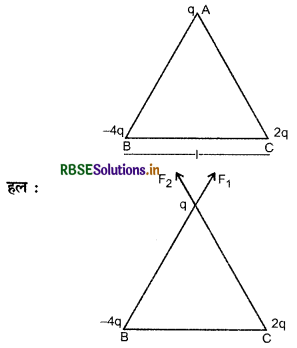
B पर स्थित -4q आवेश के कारण q पर कार्यरत बल
F₁ = \(\frac{1}{4 \pi \varepsilon_0} \frac{q \cdot 4 q}{l^2}=\frac{1}{4 \pi \varepsilon_0} \frac{4 q^2}{l^2}\)
C पर स्थित 2q आवेश के कारण q पर कार्यरत बल
F₂ = \(\frac{1}{4 \pi \varepsilon_0} \frac{q \cdot 2 q}{l^2}=\frac{1}{4 \pi \varepsilon_0} \frac{2 q^2}{l^2}\)
∴ 2F₁ = F₂
\(\overrightarrow{\mathrm{F}}_1 \text { व } \overrightarrow{\mathrm{F}}_2\) के मध्य कोण 60° है अतः परिणामी बल

प्रश्न 7.
भुजा a वाले एक समबाहु त्रिभुज के शीर्ष A और B पर समान आवेश q है। त्रिभुज के बिन्दु C पर विद्युत क्षेत्र का परिमाण ज्ञात कीजिए। 
हल:

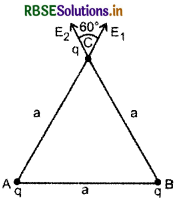
बिन्दु C पर बिन्दु C  पर स्थित आवेश के कारण विद्युत क्षेत्र की तीव्रता
E₁ = \(\frac{1}{4 \pi \varepsilon_0} \frac{q}{a^2}\) (AC की ओर) 
बिन्दु C पर बिन्दु B पर स्थित आवेश के कारण विद्युत क्षेत्र की तीव्रता
E₂ = \(\frac{1}{4 \pi \varepsilon_0} \frac{q}{a^2}\) (BC की ओर) 
E₁ व E₂ के मध्य बनने वाला कोण 60° है अतः बिन्दु C पर परिणामी तीव्रता

प्रश्न 8.
4 x 10^-9 Cm द्विध्रुव आघूर्णका कोई विद्युत द्विध्रुव 5 x 10⁴ NC^-1 परिमाण के किसी एकसमान विद्युत क्षेत्र की दिशा से 30° पर सरेखित है। द्विधुव पर कार्यरत बल आपूर्ण का परिमाण परिकलित कीजिए।
हल: 
दिया है, द्विध्रुव आधूर्ण
P = 4 x 10^-9 Cm 
विद्युत क्षेत्र की तीव्रता E = 5 x 10⁴ N/C 
विद्युत क्षेत्र के साथ द्विध्रुव का कोण
θ = 30°
द्विध्रुव पर आघूर्ण τ = ?
τ = PE sinθ
= 4 x 10^-9 x 5 x 10⁴ x sin30° 
= 4 x 10^-9 x 5 x 10⁴ x \(\frac{1}{2}\)
= 10^-4 N - m 

प्रश्न 9.
दो छोटे सर्वसम विद्युत द्विधुव AB तथा CD जिनमें प्रत्येक का द्विध्रुव आघूर्ण \(\overrightarrow{\mathbf{P}}\) है, आरेख में दर्शाए अनुसार, x - अक्ष की ओर संकेत करते किसी बाह्य विद्युत क्षेत्र \(\overrightarrow{\mathbf{E}}\) में एक - दूसरे से 120° के कोण पर स्थित हैं। ज्ञात कीजिए
(a) इस व्यवस्था का द्विधुव आघूर्ण, और 
(b) इस पर कार्यरत नेट बल - आघूर्ण का परिमाण और दिशा।

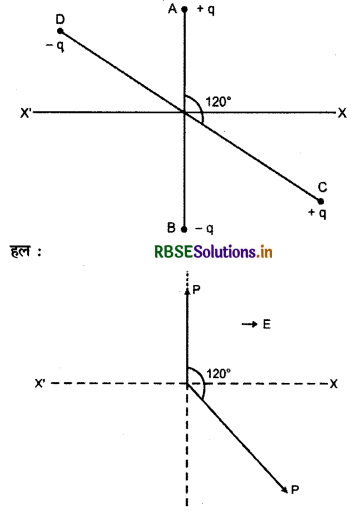
(a) चित्रानुसार, परिणामी द्विध्रुव आघूर्ण 
P_net = \(\sqrt{\mathrm{P}_1^2+\mathrm{P}_2^2+2 \mathrm{P}_1 \mathrm{P}_2 \cos 120^{\circ}}\)
P_net = \(\sqrt{\mathrm{P}^2+\mathrm{P}^2+2 \mathrm{P}^2 \times\left(\frac{-1}{2}\right)}\) (∵ P₁ = P₂ = P)
P_net = P\(\sqrt{3}\)

(b) AB पर आरोपित बल आघूर्ण
τ₁ = PE sin 90°
τ₁ =  PE अवधिर ऊपर की ओर
CD पर आरोपित बल आपूर्ण
τ₂ = P2E sin 120°
τ₂ = PE\(\frac{\sqrt{3}}{2}\)
τ₂ = \(\frac{\sqrt{3}}{2}PE\) (ऊध्वाधर नीचे की ओर) 
अतः परिणामी बल आघूर्ण
τ = τ₁ - τ₂
= PE - \(\frac{\sqrt{3}}{2}PE \)
= \(PE\left(1-\frac{\sqrt{3}}{2}\right)\) (ऊर्ध्वाधर ऊपर की ओर) 

प्रश्न 10. 
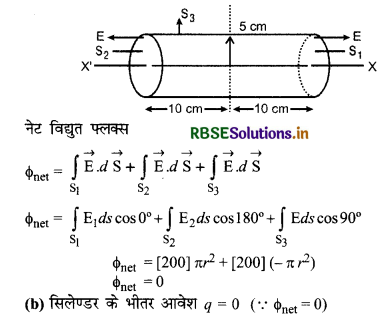
कोई विद्युत क्षेत्र एकसमान है तथा धनात्मक x के क्षेत्र में यह +x दिशा के अनुदिश कार्यरत है। परन्तु इसके साथ - साथ ऋणात्मक x के क्षेत्र में -x दिशा के अनुदिश यह समान परिमाण के साथ कार्यरत है। इस क्षेत्र का मान E = 200 N/C, x > 0 के लिए तथा E = - 200 N/C, x < 0 के लिए है। लम्बाई 20 cm और त्रिज्या 5 cm का कोई लम्बवृत्तीय सिलेण्डर x - अक्ष के अनुदिश इस प्रकार स्थित है कि इसका केन्द्र मूल बिन्दु पर तथा एक समतल फलक x = + 10 cm तथा दूसरा फलक x = -10 cm पर है। ज्ञात कीजिए-
(i) सिलेण्डर से होकर गुजरने वाला नेट बहिर्मुखी फ्लक्स 
(ii) सिलेण्डर के भीतर उपस्थित कुल आवेश
हल:

प्रश्न 11.
विद्युत क्षेत्र में \(\overrightarrow{\mathrm{E}}=200 \hat{i}+300 \hat{j} V-\mathrm{m}^{-1}\) में स्थित एक क्षेत्रफल सदिश \(\overrightarrow{\mathrm{S}}=5 \times 10^{-3} \hat{j} \mathrm{~m}^2\) से पारित विद्युत फ्लक्स का मान ज्ञात कीजिए।
हल: 
दिया है, \(\overrightarrow{\mathrm{E}}=200 \hat{i}+300 \hat{j} V-\mathrm{m}^{-1}\)
\(\overrightarrow{\mathrm{S}}=5 \times 10^{-3} \hat{j} \mathrm{~m}^2\)
अतः विद्युत फ्लक्स
Φ = \(\overrightarrow{\mathrm{E}} \cdot \overrightarrow{\mathrm{S}}\)
= ( 200\(\hat{i}\) + 300\(\hat{j}\)).(5 x 10^-3\(\hat{j}\))
= 1.5 V - m

प्रश्न 12.
आरेख में दर्शाए अनुसार कोई बिन्दु आवेश q भुजा d के किसी वर्ग के केन्द्र के ठीक ऊपर दूरी d/2 पर स्थित है। गाउस के नियम का उपयोग करके इस वर्ग से गुजरने वाले विद्युत फ्लक्स के लिए व्यंजक प्राप्त कीजिए।

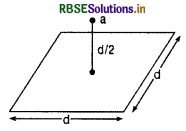
हल:

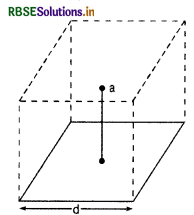
हम q आवेश को d भुजा के घन में रखा मानते हैं जिससे गुजरने वाला विद्युत फ्लक्स Φ_net = \(\frac{q}{\varepsilon_0}\)
अत: वर्ग से गुजरने वाला विद्युत फ्लक्स कुल विद्युत फ्लक्स का \(\frac{1}{6}\) वाँ भाग होगा अर्थात्
Φ = \(\frac{q}{6 \varepsilon_0}\)

प्रश्न 13.
σ और - 2σ C/m² आवेश घनत्व की दो वृहद् आवेशित समतल चादरें एक - दूसरे के बीच पृथक्कन d के साथ ऊर्ध्वाधर व्यवस्थित की गयी हैं। उस बिन्दु पर विद्युत क्षेत्र के लिए व्यंजक व्युत्पन्न कीजिए जो स्थित हैं (i) पहली चादर के बायीं ओर (ii) दूसरी चादर के दायीं ओर तथा (iii) दोनों चादरों के बीच
हल:

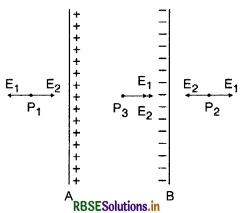
A प्लेट के कारण विद्युत क्षेत्र E₁ = \(\frac{\sigma}{2 \varepsilon_0}\)
B प्लेट के कारण विद्युत क्षेत्र E₂ =\(\frac{2 \sigma}{2 \varepsilon_0}=\frac{\sigma}{\varepsilon_0}\)
(i) P₁ बिन्दु पर विद्युत क्षेत्र \(\overrightarrow{\mathrm{E}_1} \text { व } \overrightarrow{\mathrm{E}_2}\) परस्पर विपरीत हैं अत: परिणामी विद्युत क्षेत्र
Eρ₁ = E₂ - E₁
\(=\frac{\sigma}{\varepsilon_0}-\frac{\sigma}{2 \varepsilon_0}\)
= \(\frac{-\sigma}{2 \varepsilon_0}\) (+x अक्ष की ओर) 

(ii) P₂ बिन्दु पर विद्युत क्षेत्र \(\overrightarrow{\mathrm{E}_1} \text { व } \overrightarrow{\mathrm{E}_2}\)  चित्रानुसार विपरीत दिशा में है-
Eρ₂ = E₁ - E₂
= \(\frac{\sigma}{2 \varepsilon_0}-\frac{\sigma}{\varepsilon_0}\)
= \(\frac{\sigma}{2 \varepsilon_0}\) - x अक्ष की ओर 

(iii) चादरों के बीच में Eρ₃ = E₁ + E₂
= \(\frac{\sigma}{\varepsilon_0}+\frac{\sigma}{2 \varepsilon_0}\)
Eρ₃ = \(\frac{3}{2} \frac{\sigma}{\varepsilon_0}\)

प्रश्न 14.
कोई रैखिक आवेश 2 cm दूरी पर 9 x 10⁴ NC^-1 विद्युत क्षेत्र उपन्न करता है। रैखिक आवेश घनत्व ज्ञात कीजिए।
हल: 
अनन्त विस्तार के रेखीय आवेश के कारण उत्पन्न विद्युत क्षेत्र की तीव्रता
E = \(\frac{1}{4 \pi \varepsilon_0} \frac{2 \lambda}{r}\)
जहाँ λ आवेश का रेखीय घनत्व है और r आवेश से प्रेक्षण बिन्दु की दूरी है। 
प्रश्नानुसार r = 2 cm = 2 x 10^-2 m
λ = ?, E = 9 x 10⁴ NC^-1
9 x 10⁴ = 9 x 10⁹ x \(\frac{2 \lambda}{2 \times 10^{-2}}\)
λ = 1.0 x 10^-7 Cm^-1
या λ = 0.1µ Cm^-1

प्रश्न 15.
एक गोले के केन्द्र से 20 सेमी दूरी पर विद्युत क्षेत्र की तीव्रता 10V/m है। गोले की त्रिज्या 5 सेमी है। गोले के केन्द्र से 8 सेमी दूरी पर विद्युत क्षेत्र की तीव्रता ज्ञात कीजिए।
हल: 
गोले के केन्द्र बिन्दु पर विद्युत क्षेत्र की तीव्रता
E = \(\frac{1}{4 \pi \varepsilon_0} \frac{q}{r^2}\)
प्रश्नानुसार r = 20 cm = 20 x 10^-2 m
E = 10V/m
10 = 9 x 10⁹ x \(\frac{q}{\left(20 \times 10^{-2}\right)^2}\)
q = \(\frac{400 \times 10^{-4} \times 10}{9 \times 10^9}\)
q = 4.45 x 10^-11 C

प्रतियोनी परीक्षा संबंधी प्रश्न

प्रश्न 1. 
+ σ C/m² पृष्ठ आवेश घनत्व की दो अपरिमित समतल इस प्रकार रखी हैं कि उनके मध्य 30° का कोण है। उनके मध्य दर्शाए क्षेत्र में विद्युत क्षेत्र होगा-

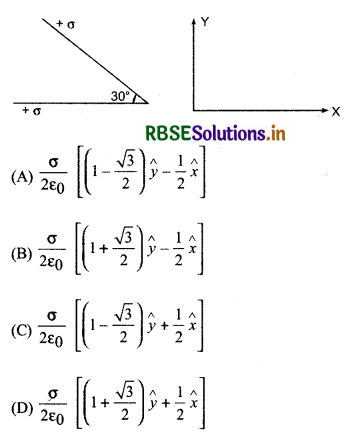
उत्तर:

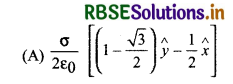
प्रश्न 2.
10 cm त्रिज्या के गोलीय चालक पर 3.2 x 10^-7 C आवेश समान रूप से वितरित है। इसके केन्द्र से 15 cm दूरी पर विद्युत क्षेत्र का परिमाण क्या होगा?
\(\left(\frac{1}{4 \pi \varepsilon_0}=9 \times 10^9 \mathrm{Nm}^2 / \mathrm{C}^2\right)\)
(A)1. 28 x 10³ N/C 
(B)1.28 x 10^-3 N/C 
(C) शून्य 
(D)1.28 x 10⁵ N/C
उत्तर:
(D) 1.28 x 10⁵ N/C

प्रश्न 3. 
त्रिज्या 'a' तथा 'b' के दो एक - केन्द्री गोलों के (चित्र देखिये) बीच के स्थान में आयतन आवेश घनत्व ρ = \(\frac{\mathbf{A}}{r}\) है, जहाँ A स्थिरांक है तथा r केन्द्र से दूरी है। गोलों के केन्द्र पर एक बिन्दु आवेश Q है। A का वह मान बताइये जिससे गोलों के बीच के स्थान में एकसमान वैद्युत क्षेत्र हो-

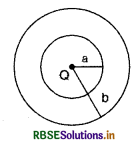
(A) \(\frac{\mathrm{Q}}{2 \pi\left(b^2-a^2\right)}\)
(B) \(\frac{2 Q}{\pi\left(a^2-b^2\right)}\)
(C) \(\frac{2 Q}{\pi a^2}\)
(D) \(\frac{\mathrm{Q}}{2 \pi a^2}\)
उत्तर:
(D) \(\frac{\mathrm{Q}}{2 \pi a^2}\)

प्रश्न 4.
लम्बाई l की दो द्रव्यमानहीन डोरियों द्वारा एक उभयनिष्ठ बिन्दु से दो एकसमान आवेशित गोले लटकाये गये हैं, जो कि प्रारम्भ में दूरी d (d << l) पर अपने अन्योन्य विकर्षण के कारण हैं। दोनों गोलों से आवेश एक स्थिर दर से लीक होना प्रारम्भ करता है। इसके परिणामस्वरूप आवेश एक - दूसरे की ओर y वेग से गति करना प्रारम्भ करते हैं, तब दोनों के बीच दूरी x के फलन के रूप में है-
(A) v ∝ x^-1/2
(B) v ∝ x^-1
(C)v ∝ x^-1/2
(D) v ∝ x
उत्तर:
(A) v ∝ x^-1/2

प्रश्न 5.
एक आवेशित अनन्त चालक तल पर रेखा AA' है जो कागज के तल के लम्बवत् है। समतल पर आवेश का पृष्ठ घनत्व σ है और B एक गेंद है जिसका द्रव्यमान m तथा आवेश परिमाण q है। B की डोरी से AA' रेखा पर एक बिन्दु से बाँधा गया है तब सरल रेखा AA' और डोरी के बीच निर्मित स्पर्श रेखा का कोण (θ) है-
(A) \(\frac{q \sigma}{2 \varepsilon_0 m g}\)
(B) \(\frac{q \sigma}{4 \pi \varepsilon_0 m g}\)
(C) \(\frac{q . \sigma}{2 \pi \varepsilon_0 m g}\)
(D) \(\frac{q \cdot \sigma}{\varepsilon_0 m g}\)
उत्तर: 
(D) \(\frac{q \cdot \sigma}{\varepsilon_0 m g}\)

प्रश्न 6.
एक लम्बे बेलनाकार कोश के ऊपरी आधे भाग में धनात्मक पृष्ठ आवेश σ तथा निचले आधे भाग में ऋणात्मक पृष्ठ आवेश -σ है। इस बेलन के चारों ओर विद्युत क्षेत्र रेखायें, यहाँ दर्शाये गये आरेख में से किस आरेख के समान होंगी? (यह केवल व्यवस्था आरेख है और स्केल के अनुसार नहीं है।)

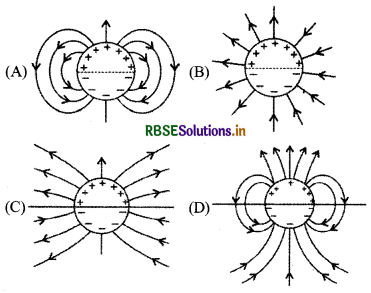
उत्तर:

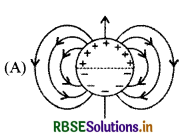
प्रश्न 7. 
एक खोखले सिलेण्डर के अन्दर q आवेश है यदि वक्रपृष्ठ B पर सम्बद्ध फ्लक्स Φ (वोल्ट/मी.) है, तब समतल पृष्ठ A पर वैद्युत फ्लक्स (वोल्ट/मीटर) में होगा-
(A) \(\frac{1}{2}\left[\frac{q}{\varepsilon_0}-d\right]\)
(B) \(\frac{q}{2 \varepsilon_0}\)
(C) \(\frac{\phi}{3}\)
(D) \(\frac{q}{\varepsilon_0}-\phi\)
उत्तर:
(A) \(\frac{1}{2}\left[\frac{q}{\varepsilon_0}-d\right]\)

प्रश्न 8.
दो R व 2R त्रिज्या वाले अचालक ठोस गोलकों को जिन पर क्रमशः ρ₁ तथा ρ₂ एकसमान आयतन आवेश घनत्व हैं, एक - दूसरे से स्पर्श करते हुए रखे गये हैं। दोनों गोलकों के केन्द्रों से गुजरती हुई रेखा खींची जाती है। इस रेखा पर छोटे गोलक के केन्द्र से 2R दूरी पर नेट विद्युत क्षेत्र शून्य है, तब अनुपात \(\frac{\rho_1}{\rho_2}\) का मान हो सकता है-
(A) -4
(B) \(-\frac{32}{25}\)
(C) \(\frac{32}{25}\)
(D) 4
उत्तर:
(C) \(-\frac{32}{25}\)

प्रश्न 9.
एक बिन्दु आवेश एकसमान रेखीय λ घनत्व वाले अनन्त लम्बाई के तार तथा एक एकसमान पृष्ठ आवेश घनत्व σ वाले अनन्त समतल चादर के कारण r दूरी पर विद्युत क्षेत्र की तीव्रताएँ क्रमश: E₁(r), E₂(r) तथा E₃(r) हैं यदि एक दी गई दूरी r₀ पर E₁(r₀) = E₂(r₀) = E₃(r₀) तब-
(A)Q = 4σπr₀²
(B) r₀ = \(\frac{\lambda}{2 \pi \sigma}\)
(C) E₁(r₀/2) = 2E₂(r₀/2)
(D) E₂(r₀/2) = 4E₃(r₀/4)
उत्तर:
(D) E₂ (r₀/2) = 4E₃(r₀/4)

प्रश्न 10.
किसी परिवेश (स्थान) में विद्युत क्षेत्र है जिसकी दिशा बाहर की ओर है तथा इसका मान E = Ar से निरूपित किया जाता है। एक ऐसे गोल पर जिसकी त्रिज्या 'a' है और जिसका केन्द्र इस विद्युत क्षेत्र के मूल बिन्दु पर है, आवेश की मात्रा होगी-
(A) Aε₀a²
(B) 4πε₀Aa²
(C) ε₀Aa³
(D) 4πε₀Aa³
उत्तर:
(D) 4πε₀Aa³

प्रश्न 11.
पिच की दो गेंदों (गोलियों) पर समान (बराबर) आवेश है। इन्हें समान लम्बाई की डोरियों (धागे) से एक बिन्दु से लटकाया गया है। सन्तुलन की अवस्था में इनके बीच की दूरी r दोनों डोरियों को उनकी आधी लम्बाई पर कसकर बाँध दिया जाता है। अतः सन्तुलन की स्थिति में दोनों गेंदों के बीच की दूरी होगी।

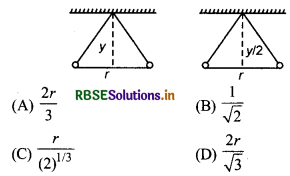
उत्तर:
 

प्रश्न 12.
निवांत में विद्युतशीलता का विमीय सूत्र (ε₀) से चिह्नित किया जाता है। यदि M = द्रव्यमान, L = लम्बाई, T = समय और A = विद्युत धारा है, तब
(A)[ε₀] = [M^-1L^-3T²A] 
(B) [ε₀] = [M^-1L^-3T⁴A²]
(C) [ε₀] = [M^-1L²T^-1A^-2] 
(D) [ε₀] = [M^-1L²T^-1A]
उत्तर:
(C) [ε₀] = [M^-1L²T^-1A^-2]

प्रश्न 13. 
प्रत्येक q मान के दो आवेश x = -a और x = a पर x - अक्ष पर रखे हैं। द्रव्यमान m और आवेश q₀ = \frac{q}{2} का एक कण मूलबिन्दु पर रखा है। यदि आवेश q₀ को y - अक्ष के अनुदिश एक अल्प - विस्थापन (y << a) दिया जाए, तब कण पर कार्यरत, परिणामी बल इसके समानुपाती है-
(A) y
(B) -y
(C) \(\frac{1}{y}\)
(D) \(-\frac{1}{y}\)
उत्तर:
(A) y