RBSE Class 12 Physics Important Questions Chapter 1 Electric Charges and Fields

Rajasthan Board RBSE Class 12 Physics Important Questions Chapter 1 Electric Charges and Fields Important Questions and Answers.

RBSE Class 12 Physics Chapter 1 Important Questions Electric Charges and Fields

Multiple Choice Questions

Question 1.
A charge q₁ exerts some force on a second charge q₂. A third charge q₃ is brought near them. Then, force exerted by q₁ on q₂ will:
(A) increase in magnitude
(B) decrease in magnitude
(C) remain unchanged
(D) first increase and then decrease.
Answer:
(C) remain unchanged

Question 2.
Two equal and similar charges are placed along a straight line. A third equal and similar charge is placed midway between the two charges. Then, the system, will:
(A) be in equilibrium
(B) not be in equilibrium
(C) oscillate
(D) lose charge.
Answer:
(B) not be in equilibrium

Question 3.
The unit of permittivity of free space ε₀ is:
(A) C²N^-1m^-2
(B) Nm²C^-2
(C) CN²m^-1
(D) C²N^-2m^-2.
Answer:
(A) C²N^-1m^-2

Question 4.
In a charged conductor the charge resides at the:
(A) Inner surface
(B) Outer surface
(C) Centre
(D) None of these.
Answer:
(B) Outer surface

Question 5.
What are the units of K = \(\frac{1}{4 \pi \varepsilon_0}\)?
(A) C²N^-2m^-2
(B) Nm²C^-2
(C) Nm²C²
(D) Unitless.
Answer:
(B) Nm²C^-2

Question 6.
The dielectric constant of metal is:
(A) 1
(B) Greater than 1
(C) Zero
(D) Infinite.
Answer:
(D) Infinite.

Question 7.
What is the dimensional formula of electric field intensity?
(A) [MLT^-3A^-1]
(B) [M²LT^-3A^-1]
(C) [ML²T^-2A¹]
(D) [ML²T^-3A^-1].
Answer:
(A) [MLT^-3A^-1]

Question 8.
When a body becomes negatively charged, its mass:
(A) decreases
(B) increases
(C) remains same
(D) None of these.
Answer:
(A) decreases

Question 9.
Electric field intensity due to an electric dipole at a point of distance r from its center varies as:
(A) r
(B) r²
(C) r³
(D) r^-3.
Answer:
(D) r^-3.

Question 10.
Quantization of charge means that charge on a body is integral multiple of smallest quantity of charge:
(A) Charge of electron
(B) Charge on proton
(C) Both A & B
(D) None of these.
Answer:
(C) Both A & B

Question 11.
The number of electrons in one coulomb of charge:
(A) 6 x 10¹⁸
(B) 6.05 x 10¹⁸
(C) 6.5 x 10¹⁸
(D) 6.25 x 10¹⁸.
Answer:
(D) 6.25 x 10¹⁸.

Question 12.
Can be body have charge of 4 x 10^-19 C?
(A) cannot say
(B) No
(C) question is incomplete
(D) Yes.
Answer:
(B) No

Question 13.
In non-uniform electric field, electric dipole experiences:
(A) Torque only
(B) Torque as well as force
(C) Force only
(D) None of these.
Answer:
(B) Torque as well as force

Question 14.
When electric dipole is in stable equilibrium, then the angle between electric dipole moment \(\vec{p}\) and electric field \(\vec{E}\) is:
(A) 0
(B) π
(C) \(\frac{\pi}{3}\)
(D) \(\frac{\pi}{2}\)
Answer:
(A) 0

Question 15.
A stationary charge produces:
(A) an electric field only
(B) a magnetic field only
(C) both electric and magnetic field
(D) none of these.
Answer:
(A) an electric field only

Question 16.
The torque acting on a dipole of moment \(\vec{p}\) in an electric field \(\vec{E}\) is:
(A) \(\vec{p}. \vec{E}\)
(B) \(\vec{p}\) x \(\vec{E}\)
(C) Zero
(D) \(\vec{E}\) x \(\vec{p}\)
Answer:
(B) \(\vec{p}\) x \(\vec{E}\)

Question 17.
What is the angle between the electric dipole moment and the electric field strength due to it on the equitorial line?
(A) 0°
(B) 90°
(C) 180°
(D) None of these.
Answer:
(C) 180°

Question 18.
Is it safe to be inside a car during a thunder storm?
(A) Cannot say
(B) Yes
(C) Statement is incomplete
(D) No.
Answer:
(B) Yes

Question 19.
What does q₁ + q₂ = 0 signify in electrostatics?
(A) Charges are equal
(B) Charges are of opposite sign
(C) Both A & B
(D) None of these.
Answer:
(C) Both A & B

Question 20.
A point charge + q is placed at the mid-point of a cube of side b. The electric flux emerging from the cube is:
(A) zero
(B) \(\frac{q}{\varepsilon_0}\)
(C) \(\frac{6 q l^2}{\varepsilon_0}\)
(D) \(\frac{q}{6 l^2 \varepsilon_0}\)
Answer:
(B) \(\frac{q}{\varepsilon_0}\)

Question 21.
A charge q is placed at the center of the line joining two exactly equal positive charges Q. The system of three charges will be in equilibrium if q is equal to:
(A) -\(\frac{\mathrm{Q}}{4}\)
(B) +Q
(C) -Q
(D) \(\frac{\mathrm{Q}}{2}\)
Answer:
(A) -\(\frac{\mathrm{Q}}{4}\)

Question 22.
The SI unit of electric charge is:
(A) Coulomb
(B) Ampere
(C) Weber
(D) Volt.
Answer:
(A) Coulomb

Question 23.
What is the value of permittivity (ε₀) of free space in SI system
(A) 8.85 x 10^-12 N^-1m^-2C²
(B) 8 x 10^-11N^-1m^-2C²
(C) 8.8 x 10^-10N^-1m^-2C²
(D) 8.8 x 10^-9N^-1m^-2C².
Answer:
(A) 8.85 x 10^-12 N^-1m^-2C²

Question 24.
The unit of permittivity (ε₀) of free space is:
(A) CN²m^-1
(B) Nm²C^-2
(C) C²N²m^-2
(D) C²N^-1m^-2.
Answer:
(D) C²N^-1m^-2.

Question 25.
In SI, unit of electric field is:
(A) Am^-1
(B) NC^-1
(C) Cm^-1
(D) Cm^-2
Answer:
(B) NC^-1

Fill in the blanks

Question 1.
Frictional electricity is also called ........................... electricity.
Answer:
static.

Question 2.
The electric charges developed on glass rod (rubbed with silk) is ........................... from charge developed on ebonite rod (rubbed with fur).
Answer:
different.

Question 3.
We can charge a conductor ........................... by induction.
Answer:
permanently.

Question 4.
The force between any two charges is not ........................... by the ........................... other charges.
Answer:
affected, presence.

Question 5.
Charge on an electron = ........................... C.
Answer:
- 1.6 x 10^-19.

Question 6.
The ........................... field inside a hollow conductor is ...........................
Answer:
electric, zero.

Question 7.
A solid sphere of charge is also called ........................... sphere.
Answer:
non-conducting.

Question 8.
Electric flux is a ........................... quantity.
Answer:
scalar.

Question 9.
Electric flux through a closed surface S = ...........................
Answer:
\(\oint_{\mathrm{S}} \overrightarrow{\mathrm{E}} \cdot \overrightarrow{d \mathrm{~S}}\)

Question 10.
In a sheet of charge, the same charge shows up on its ........................... sides. 
Answer:
two

Very Short Answer Type Questions

Question 1.
What is electrostatics?
Answer:
It is that branch of physics in which we study electric charges at rest.

Question 2.
What is frictional electricity?
Answer:
The electricity developed on bodies when they re rubbed with each other is called frictional electricity.

Question 3.
What is the minimum charge observed in nature?
Answer:
± 1.6 x 10^-19 C.

Question 4.
Is the unit of charge coulomb a basic unit in S.I.?
Answer:
No, the basic unit in SI is ampere, because 1 C = 1 As.

Question 5.
How does the Coulomb’s force between two point charges depend upon the dielectric constant of the intervening medium?
Answer:
Since Coulomb’s force between two point charges q₁, q₂ separated by distance r is given by:
F = \(\frac{1}{4 \pi \varepsilon_0 \mathrm{~K}} \frac{q_1 q_2}{r^2}\)
i.e. F ∝ \(\frac{1}{\mathrm{~K}}\)
So force between two charges is inversely proportional to dielectric constant K.

Question 6.
How absolute permittivity is related to relative permittivity?
Answer:
Absolute permittivity = permittivity of free space x relative permittivity of the medium.
i.e. ε = ε₀ ε_r

Question 7.
What is the importance of superposition principle in electrostatics?
Answer:
It is used to determine the effect of a number of charges on a given charge. Coulomb’s law as such is a two-charge interaction law and is applicable to point charges only.

Question 8.
Is the force of interaction between two point charges affected due to the presence of another charge?
Answer:
No, it is independent of the presence of charges.

Question 9.
What is the magnitude and unit of ε₀?
Answer:
It is ε₀ = 8.854 x 10^-12 C²N^-1m^-2.

Question 10.
For what order of distance is Coulomb's law true?
Answer:
It holds for all distances greater than nuclear distance (≃ 10^-15 m).

 
Question 11.
When a glass rod is rubbed with silk cloth, it acquires a charge +1.6 x 10^-13 C, what is the charge on silk cloth?
Answer:
Silk cloth acquires a charge of -1.6 x 10^-13 C, i.e., it has 10⁶ extra electrons on it.

Question 12.
An ebonite rod held in hand can be charged by rubbing with flannel but a copper rod cannot be charged like this. Why?
Answer:
Ebonite rod is an insulator. Hence when charged by rubbing, the charge remains at the same position. Since copper is a good conductor of electricity, the charge produced by rubbing flows to earth through our hands.

Question 13. 
What kind of charges are produced when glass rod is rubbed with silk?
Answer:
+ve charge is produced on glass rod and equal -ve charge is produced on silk cloth.

Question 14.
Define Coulomb charge.
Answer:
We know F = 9 x 10⁹ x \(\frac{q_1 q_2}{r^2}\) for vacuum
if q₁ = q₂ = q (say) r = 1 m;
F = 9 x 10⁹ N
Then
9 x 10⁹ = 9 x 10⁹ \(\frac{q \cdot q}{1^2}\) or
q = ± 1C
∴ 1 C charge is that which when placed before an equal and similar charge in vacuum at a distance of 1 m repels it with a force of 9 x 10⁹ N.

Question 15.
How many electrons are present in one coulomb of charge?
Answer:
Let n be the electrons in 1C of charge and charge on an electron is 1.6 x 10^-19 C.
∴ n 1.6 x 10^-19 = 1
or n = \(\frac{1}{1.6 \times 10^{-19}}=\frac{10 \times 10^{19}}{16}\)
or n = 0.625 x 10¹⁹
i.e. = 6.25 x 10¹⁸ electrons are there in 1C of charge.

Question 16.
What is the value of constant of proportionality?
Answer:
9 x 10⁹ Nm² C^-2.

Question 17.
How much is the charge on an electron in S.I. units?
Answer:
1.6 x 10^-19 C.

Question 18.
State Coulomb's law of force in electrostatics.
Answer:
It states that the force of interaction between two stationary point charges is directly proportional to the product of magnitude of their charges and inversely proportional to the square of the distance between them.

Question 19.
Name the property which tells about the charge exists in packet.
Answer:
Quantisation of charge.

Question 20.
Can a body have a charge of 0.8 x 10^-19 C? Justify your answer by comment.
Answer:
No. Because the minimum charge that a body can have is the charge of an electron or proton i.e. ± 1.6 x 10^-19 C.

Question 21.
What do you mean by point charges?
Answer:
When the distance between the charged bodies is very large as compared to the sizes of the charged bodies, then the charges are said to be point charges.

Question 22.
Define electric field intensity at a point.
Answer:
Electric field intensity at a point is the electrostatic force experienced by a unit positive test charge placed at that point.
\(\overrightarrow{\mathrm{E}}(\vec{r})=\operatorname{Lt}_{q_0 \rightarrow 0} \frac{\overrightarrow{\mathrm{F}}}{q_{11}}\)
It is assumed that the field due to test charge does not in any way alter the electric field due to the given charge and hence we take q₀ → 0.

Question 23.
Dielectric constant of water is 80. What is its permittivity?
Answer:
Permittivity of water
ε = ε₀ ε_r = ε₀ K
= 8.854 x 10^-12 x 80
= 708.32 x 10^-12 C² N^-1 m^-2

Question 24.
How many joules are there in MeV?
Answer:
1 MeV = 10⁶ eV
1 MeV = 10⁶ x 1.6 x 10^-19 C x \(​​\)\(\frac{\mathrm{J}}{\mathrm{C}}\)
1 MeV = 1.6 x 10^-13 J

Question 25.
Write dimensional formula of ε₀.
Answer:

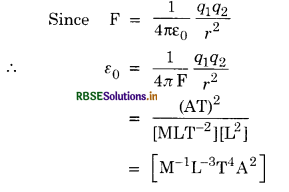
Question 26.
Does the force between two charges change when the medium air is replaced by water?
Answer:
Yes. it is reduced by \(\frac{1}{81}\) th of its value in air.

Question 27.
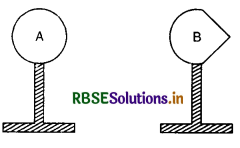
A and B are two negatively charged and insulated conductors. State, with reason, which conductor will tend to lose charge?
Answer:
B will lose charge. Electric field will be greater at the pointed end due to the concentration of electrons. In higher electric field, the force acting on the charge will be greater so the charges will lose from the pointed ends.

Question 28.
What happens when an electric dipole is held in a non-uniform electric field?
Answer:
When an electric dipole is held in a non-uniform electric field some net force and torque do act on the dipole. When the dipole sets itself parallel to the field, torque becomes zero, but the net force persists.

Question 29.
Name C.G.S. and S.I. units of charge. Give relation between them.
Answer:
CGS unit of charge is stat coulomb.
S.I. unit of charge is coulomb (C).
1 coulomb = 3 x 10⁹ stat coulomb.

Question 30.
Give the ratio of the electrostatic force to the gravitational force between a proton and an electron.
Answer:
The ratio is 2.4 x 10³⁹.

Question 31.
Give some examples supporting the fact that electrostatic forces are much more stronger than gravitational forces.
Answer:
A paper piece is lifted up by the electrostatic attraction of a charged tiny comb against the gravitational attraction of the huge earth.

Question 32.
Give the principle of superposition.
Answer:
According to this principle, the force on any single charge among many charges, is the vector sum of the forces due to each other charge on it. Force between two charges being unaffected by the presence of other charges.

Question 33.
Write general expression for force between two point charges.
Answer:
The general expression is,
\(\vec{F}=\dot{r} \frac{q_1 q 2}{r^2} \cdot \hat{r}\)

Question 34.
Which charges are transferred on rubbing?
Answer:
Negative charged electrons are transferred on rubbing of two bodies.

Question 35.
Which rubbed body acquires a positive charge and which acquires a negative charge?
Answer:
The body which loses electrons becomes positively charged. The body which gains electrons becomes negatively charged.

Question 36.
Define electric field at a point. What are its units? Is it a scalar or a vector quantity?
Answer:
Electric field at a point
It is defined as the electrostatic force per unit charge acting on a vanishing small test charge placed at that point.
Its unit is NC^-1. It is a vector quantity.

Question 37.
Two electric lines never cross each other. Why?
Answer:
This is because at the point of intersection, two tangents can be drawn to the two lines of force. Therefore, there would be two directions of electric intensity at the same point, which is not possible.

Question 38.
What is spherically symmetric field?
Answer:
It is that field for a given charge which depends only on the magnitude of position vector of a point of observation.

Question 39.
Why electric intensity at any point inside a charged conductor is zero?
Answer:
This is because there are no electric lines of force inside the body of a conductor.

Question 40.
Does motion of a body affect its charge?
Answer:
No, charge on a body does not change when the body starts moving.

Question 41.
Electric charge is additive. Explain.
Answer:
Electric charge is additive. By this statement, we mean that charges can be added. Therefore, the total electric charge on an extended body is the algebraic sum of the charges present in different parts of the body.

Question 42.
Name any three basic properties of electric charge.
Answer:

• Quantisation of charge.
• Conservation of charge.
• Independent of speed.

Question 43.
What is the origin of frictional forces?
Answer:
The frictional forces are electric in origin.

Question 44.
What is the use of electric lines 1 of force?
Answer:
Drawing the lines of force helps us to visualize the extent of the electric field in some region of space. Of course electric lines of force can only give us partial information about the nature of the electric field produced by given sources, but it is still valuable. While we could put an arrow on each line of force to indicate the direction of electric vector at each point on it, the line cannot indicate the magnitude of the electric vector.

Question 45.
Define an electric dipole.
Answer:
Electric dipole
A pair of equal and opposite point charges separated by a fixed distance is called an electric dipole. A molecule like that of water in which the centres of +ve and -ve charge are separated, is an example of electric dipole.

Question 46.
Define dielectric constant of a medium. Give its values for somse common media.
Answer:
Dielectric constant. Dielectric constant of a medium is defined as the ratio of the electrostatic force between the two charges placed at a certain distance apart in vacuum to the force between the same two charges placed at the same distance apart in the medium. Dielectric constants of some common media are as follows:
Vacuum - 1.00000
Air - 1.00054
Water - 78
Paper - 3.5
Mica - 5.4

Question 47.
What is the use of the concept of electric field intensity?
Answer:
If electric field intensity at a point is known, we can calculate the force experienced by any charge placed at that point. The force \(\overrightarrow{\mathrm{F}}\) on a charge q at a point, where electric intensity is \(\overrightarrow{\mathrm{E}}\) is
\(\overrightarrow{\mathrm{F}} = q\overrightarrow{\mathrm{E}}\)

Question 48.
From where did the term electricity get its origin?
Answer:
The Greek name for amber is 'Electrum' which is the origin of the term 'electricity'.

Question 49.
An ebonite rod is rubbed with fur/wool. What type of charges do they acquire?
Answer:
The ebonite rod acquires negative charge and fur/wool acquires an equal positive charge.

Question 50.
A glass rod is rubbed with silk. What type of charge do they acquire?
Answer:
A glass rod acquires positive charge and silk acquires an equal negative charge.

Question 51.
What is the cause of electrostatics?
Answer:
Electrostatics is explained on the basis of modern electron theory. On rubbing, there occurs transfer of some electrons in the outermost orbits from one body to the other. A body which loses electrons acquires positive charge and the other which gains electrons acquires an equal negative charge.

Question 52.
Is the mass of a body affected I on charging?
Answer:
Yes, but very slightly. The decrease in mass of positively charged body is equal to loss of electrons and gain in mass of negatively charged body is equal to gain of electrons.

Question 53.
What is a gaussian surface?
Answer:
A closed surface associated with a charge is called a gaussian surface (surface integral of electrostatic field is taken over it).

Question 54.
What must be the shape of a gaussian surface?
Answer:
The shape must be symmetrical about the charge distribution (spherical for a point charge and cylindrical for a line or a sheet charge).

Question 55.
Write Gauss’s theorem for a charge outside a closed surface.
Answer:
The theorem becomes,
\(\oint_{\mathrm{S}} \overrightarrow{\mathrm{E}}(\vec{r}) \cdot d \overrightarrow{\mathrm{S}}\) = 0 = 0

Question 56.
What is the condition for electric flux through an area to be maximum?
Answer:
The electric flux linked with an area will be maximum when lines of force are normal to area.

Question 57.
What is the importance of Gauss’ theorem?
Answer:
Gauss’ theorem is extremely useful in dealing with electrostatic problems. The solution of certain problems becomes very easy by the use of this theorem.

Question 58.
The electric flux through a certain closed surface is zero i.e.\(\oint_{\mathbf{S}} \overrightarrow{\mathbf{E}} \cdot \overrightarrow{\mathrm{dS}}\)  = 0. Does it necessarily imply that \(\vec{E}\) = 0?
Answer:
No. \(\oint_{\mathbf{S}} \overrightarrow{\mathbf{E}} \cdot \overrightarrow{\mathrm{dS}}\)  = 0 if \(\overrightarrow{\mathrm{E}} \perp d \overrightarrow{\mathrm{S}}\)

Question 59.
If the Coulomb’s law involved \(\frac{1}{r^3}\) dependence (instead of \(\frac{1}{r^2}\) ), would Gauss’ law be still true?
Answer:
No, in that case Gauss’s law would not be true.

Question 60.
An electric dipole is enclosed in a cube, but total electric flux linked will be zero. Discuss.
Answer:
Since, net charge is zero so
\(\oint_{\mathrm{S}} \overrightarrow{\mathrm{E}} \cdot d \overrightarrow{\mathrm{S}}=\frac{q}{\varepsilon_0}\) = 0

Question 61.
Conservation of charge is the law of nature. Explain.
Answer:
In all natural processes, the conservation of a charge is obeyed and till now the violation of this law is not observed. Hence, it is the law of nature.

Question 62.
Obtain the unit of e₀ with the help of the formula
E = \(\frac{1}{4 \pi \varepsilon_0} \frac{q}{r^2}\)
Answer:
Given

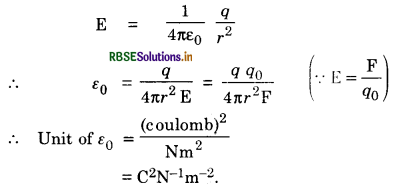
Question 63.
An electric dipole of dipole moment 20 x 10^-6 Cm is enclosed by a closed surface. What is the net flux coming?
Answer:
Zero, because total flux
Φ = \(\frac{q}{\varepsilon_0}+\frac{-q}{\varepsilon_0}\) = 0
(A dipole has two charges + q and - q)

Question 64.
What led us to conclude that there are two kinds of charges?
Answer:
Experiments showed that

• two rods of ebonite rubbed with fur repel each other.
• a rod of ebonite rubbed with fur attracts a glass rod rubbed with a piece of silk.

This meant that electrification of ebonite rod is different from the electrification of silk rod.

Question 65.
What is the direction of electric; field intensity vector \(\overrightarrow{\mathbf{E}}\)?
Answer:
Its direction is in the direction of the force acting on test charge.

Question 66.
What is the nature of the symmetry of the field due to a point charge?
Answer:
Field due to a point charge has spherical (radial) symmetry.

Question 67.
What is the nature of symmetry of the field due to a two-charge system?
Answer:
Field due to a two-charge system has a cylindrical symmetry. (It becomes spherical, when charges are too close or distance is too large).

Question 68.
How is the direction of \(\overrightarrow{\mathbf{E}}\) related with type of field charge?
Answer:
It is outward (away) for a positive field charge and inward (towards) for a negative field charge.

Question 69.
When is electric line of force curved?
Answer:
Electric line of force is curved in the field of more than one point charges.

Question 70.
What is induction?
Answer:
It is the phenomenon due to which charge appears on a conductor when put near another charged conductor.

Question 71.
Two charges of + 1C and +2C separated by a distance of 1 m, repel each other with a force of \(\vec{F}_1\) and \(\vec{F}_2\) respectively. What is the ratio of \(\vec{F}_1\) and \(\vec{F}_2\)?
Answer:
\(\vec{F}_1\) : \(\vec{F}_2\) = 1 : 1 because the forces are equal in magnitude and opposite in direction.

Question 72.
Two charges 1C and 2C are separated by a distance of 1 m, in air. If the force experienced by 1C is (2\(\hat{i}\) + 3\(\hat{j}\) - 4\(\hat{k}\)) find the force experienced by the charge of 2C when the charges are (i) like (ii) unlike.
Answer:
In both cases the force experienced by +2C is equal and opposite to that of + 1C,
∴ \(\vec{F}_2= (-2\hat{i} -3\hat{j} + 4\hat{k})\)

Question 73.
When the hand approaches a charged weight suspended on the silk thread, the weight is attracted towards the hand. Why?
Answer:
An equal and opposite charge is induced on the hand, hence the charged weight is attracted towards the hand.

Question 74.
Can a body have a charge of 0.8 x 10^-19 C? Justify your answer by comment.
Answer:
No. Because the minimum charge that a body can have is the charge of an electron or proton i.e. ± 1.6 x 10^-19 C.

Question 75.
Is electric field intensity a scalar or a vector quantity? Give its SI units.
Answer:
Electric field intensity is a vector quantity. Its direction is the same as the direction of force acting on the unit charge placed at the point of observation.
Units. In S.I. the units of electric field intensity is NC^-1.

Question 76.
What does q₁ + q₂ = 0 signify in electrostatics?
Answer:
It signifies that the electric charges are additive in nature.

Question 77.
A glass rod when rubbed with silk acquires a charge +1.6 x 10^-12 C. What is the charge on silk?
Answer:
The charge on silk will be -1.6 x 10^-12 C.

Question 78.
What is quantisation of charge?
Answer:
Quantisation of charge means that charge exists in the form of packets and not in continuous amounts and is always integral multiple of the smallest elementary quantity of charge (i.e. e)
So q = ± ne    (where n = 1, 2, ................)

Question 79.
At what points is the electric dipole field intensity parallel to the line joining the charges?
Answer:
At axial points and at bisector points.

Question 80.
Draw lines of force to represent a uniform electric field.
Answer:

Question 81.
State Coulomb’s law of force in electrostatics.
Answer:
It states that the force of interaction between two stationary point charges is directly proportional to the product of magnitude of their charges and inversely proportional to the square of the distance between them.

Question 82.
Name any two basic properties of electric charge.
Answer:

• The electric charge is quantized.
• The electric charge in a system is conserved.

Question 83.
What is the basic cause of quantization of charge?
Answer:
During charging, only integral number of electrons is transferred from one body to another hence the charge possessed by a body is always integral multiple of e (e = ± 1.6 x 10^-19 C).

Question 84.
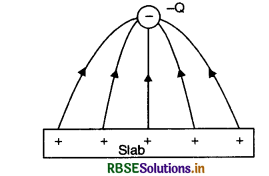
Draw the pattern of electric field lines, when a point charge-Q is kept near an uncharged conducting plates.
Answer:
The pattern is as shown in fig. VSAQ 84.

Question 85.
Define dielectric constant of a medium.
Answer:
Dielectric constant of a medium may be defined as the ratio of the force between two charges placed at a certain distance apart in air to the force between the same two charges placed at the same distance apart in that medium. 

Question 86.
How does the Coulomb’s force between two point charges depend upon dielectric constant of the intervening medium?
Answer:
The Coulomb’s force F ∝ \(\frac{1}{\mathrm{~K}}\).
(K is dielectric constant of the intervening medium)

Question 87.
Force between two point electric charges kept at a distance d apart in air is F. If these charges are kept at the same distance in water, how does the force between them change?
Answer:
The force will become \(\frac{\mathrm{F}}{\mathrm{K}}\) (K is dielectric constant of water.)

Question 88.
Define the term electric dipole moment.
Answer:
Electric dipole moment of an electric dipole is the product of magnitude of either charge and the distance between the two charges and the direction is from - ve to + ve charge.

Question 89.
Define dipole moment. Is it scalar or a vector quantity?
Answer:
Electric dipole moment of an electric dipole is the product of magnitude of either charge and the distance between the two charges and the direction is from - ve to + ve charge.
It is a vector quantity.

Question 90.
Give the S.I. unit of electric dipole moment.
Answer:
S.I. unit of dipole moment is Coulomb metre i.e. C m.

Question 91.
What is the angle between the direction of electric field at any (i) axial point and (ii) equatorial point due to an electric dipole?
Answer:
180° or anti-parallel.

Question 92.
What orientation of an electric dipole in a uniform electric field corresponds to its stable equilibrium?
Answer:
The dipole moment is parallel to the direction of electric field in stable equilibrium, (i.e. θ = 0).

Question 93.
Two point electric charges of unknown magnitude and sign are placed at a distance ‘d' apart. The electric intensity is zero at a point, not between the charges but on the line joining them. Write two essential conditions for this to happen.
Answer:

• The two charges should be of opposite nature.
• The magnitudes of the two charges should be different.

 
Question 94.
An electric dipole moment 20 x 10^-6 C is enclosed by closed surface. What is the net electric flux coming out of this surface?
Answer:
Zero.

Question 95.
An electrostatic field line cannot be discontinuous. Why?
Answer:
Since electrostatic field line is the path followed by a unit test positive charge in an electric field when free to do so, hence the field line must be continuous.

Questin 96.
The force acting between two point charges q₁ and q₂ kept at the same distance apart in air is attractive or repulsive when (i) q₁q₂ > 0 (ii) q₁q₂ < 0.
Answer:
When q₁q₂ > 0, the force between them is repulsive when q₁q₂ < 0, the force between them is attractive.

Question 97.
Is electric field intensity a scalar or a vector quantity? Give its S.I. units.
Answer:
Electric field is a vector quantity and its S.I. unit is NC^-1 or Vm^-1.

Question 98.
Define electric field intensity at a point.
Answer:
Electric field intensity at any point due to a source charge is the force experienced per unit positive test charge placed at that point without disturbing the source charge.

Question 99.
Name the physical quantity, whose S.I. unit is newton coulomb.
Answer:
It is the unit of electric field intensity.

Question 100.
The electric field lines never cross each other, why?
Answer:
If the electric field lines cross each other, then there will be two directions of electric field at that point, which is not possible.

Question 101.
Which physical quantity has unit NC^-1? Is it a vector or a scalar quantity?
Answer:
Electric field strength has unit NC^-1 and it is a vector quantity.

Question 102.
Write an expression for the flux Df of the electric field \(\overrightarrow{\mathrm{E}}\), through an area element ∆\(\overrightarrow{\mathrm{S}}\). 
Answer:
∆Φ = \(\overrightarrow{\mathrm{E}} . ∆\overrightarrow{\mathrm{S}}\).

Question 103.
In which orientation, a dipole placed in a uniform electric field is in (i) stable, (ii) unstable equilibrium?
Answer:

• The dipole will be in stable equilibrium when \(\vec{p} \| \overrightarrow{\mathrm{E}}\) i.e. Φ = 0°.
• The dipole will be in unstable equilibrium if \(\vec{p}\) is antiparallel to \(\vec{E}\) i.e. Φ = 180°.

Question 104.
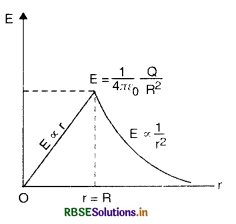
Draw a plot showing variation of electric field with distance from the center of a solid conducting sphere of radius R, having a charge of +Q on its surface.
Answer:
The graph showing the variation of E with distance from the center of a solid conducting sphere is given in Fig. VSAQ 104.

Short Answer Type Questions

Question 1.
What do you understand by quantisation of electric charge?
Answer:
Quantisation of charge. It is that property of charge by virtue of which charge on a body exists in the form of discrete packet of charge e, only, where e is the charge on an electron. The charge carried by anybody would be equal to ± ne, where n = 0, 1, 2, 3, 4, 5, etc. The charge on a body is thus some multiple of e and cannot exist as a fraction of e. So charge exists in the form of packets and not in continuous amounts. Thus, charge is said to have a discrete (discontinuous) nature or is said to be quantised. 

Question 2.
State Coulomb’s law. Define one Coulomb.
Answer:
Coulomb’s law. The law states that two stationary electric point charges attract or repel each other with a force which is directly proportional to the product of the magnitudes of the charges and inversely proportional to the square of the distance between them.
Let q₁, q₂ two point-like charges separated by a distance r, then the force between the two charges is:
F ∝ q₁q₂

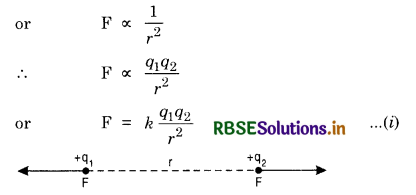
where k is the constant of proportionality and its value depends upon (i) system of unit adopted and (ii) the nature of medium separating q₁ and q₂.
In SI,
k = \(\frac{1}{4 \pi \varepsilon_0 \varepsilon_r}\)
∴ F = \(\frac{1}{4 \pi \varepsilon_0 \varepsilon_r} \frac{q_1 q_2}{r^2}\)
In air (or vacuum)
ε_r = 1
∴ F = \(\frac{1}{4 \pi \varepsilon_0} \frac{q_1 q_2}{r^2}\)
= 9 x 10⁹ \(\frac{q_1 q_2}{r^2}\)
Definition of one Coulomb (Unit of Charge)
In SI, the unit of charge is 1 C (1 coulomb).
In free space, the force of interaction between two point charges is given by
F = 9 x 10⁹\( \frac{q_1 q_2}{r^2}\)
If q₁ = q₂ = q, r = 1 m
and F = 9 x 10⁹ N, then
9 x 10⁹ = 9 x 10⁹.\(\frac{q_1 q_2}{r^2}\)
or q₂ = 1
or q = +1
Thus one Coulomb is a charge which repels equal and similar charge placed at one metre away in vacuum with a force of 9 x 10⁹ newton.

Question 3.
State Coulomb’s law in electrostatics. Write the law in vector form. Derive the definition of Coulomb.
Answer:
Coulomb’s law. It states that two stationary electric point charges attract or repel each other with a force which is directly proportional to the product of magnitude of the charges and inversely proportional to the square of the distance between them.
Coulomb’s law in Vector form
Let q₁ and q₂ charges be separated by a distance r (Fig. SAQ 3).

Adding (i), (ii), we get
\(\overrightarrow{\mathrm{F}}_{12}+\overrightarrow{\mathrm{F}}_{21}\) = 0
or \(\overrightarrow{\mathrm{F}}_{12}\) = -\(\overrightarrow{\mathrm{F}}_{21}\)
Definition of one Coulomb
Definition of one Coulomb (Unit of Charge)
In SI, the unit of charge is 1 C (1 coulomb).
In free space, the force of interaction between two point charges is given by
F = 9 x 10⁹ \(\frac{q_1 q_2}{r^2}\)
If q₁ = q₂ = q, r = 1 m
and F = 9 x 10⁹ N, then
9 x 10⁹ = 9 x 10⁹.\(\frac{q_1 q_2}{r^2}\)
or q₂ = 1
or q = +1
Thus one Coulomb is a charge which repels equal and similar charge placed at one metre away in vacuum with a force of 9 x 10⁹ newton.
Importance of Coulomb’s law

• In vector form, we find that the forces \(\overrightarrow{\mathrm{F}}_{12}\) and \(\overrightarrow{\mathrm{F}}_{21}\) are equal and opposite.
• It shows that the electrostatic force between two charges is a central force.

Question 4.
Write the Coulomb’s law in terms of position vector of charges.
Answer:
Let two charges q₁ and q₂ be located at point A and B having position vectors
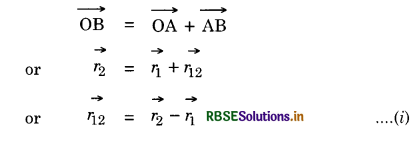
\(\overrightarrow{r_1}\) and \(\overrightarrow{r_2}\) respectively from origin O as shown in Fig. SAQ 4.

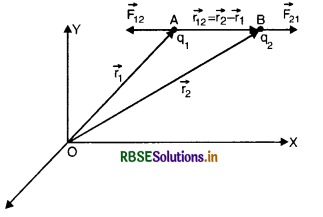
From the triangle law of vector addition. We have

Force on charge q₂ due to q₁ is given by

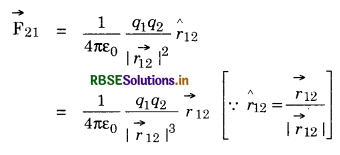
Using equation (i), we get
\(\overrightarrow{\mathrm{F}}_{21}=\frac{1}{4 \pi \varepsilon_0} \frac{q_1 q_2}{\left|\vec{r}_2-\vec{r}_1\right|^3}\left(\vec{r}_2-\vec{r}_1\right)\) .....................(ii)
Similarly,
\(\overrightarrow{\mathrm{F}}_{12}=\frac{1}{4 \pi \varepsilon_0} \frac{q_1 q_2}{\left|\vec{r}_1-\vec{r}_2\right|^3}\left(\vec{r}_1-\vec{r}_2\right)\) ........................(iii)
These eqns. (ii) and (iii) represent Coulomb’s law in terms of position vectors.

Question 5.
Derive an expression for the field intensity at a point on the axial line of an electric dipole.
Answer:
Consider an electric dipole consisting of charges -q and +q, separated by a distance 2a and placed in free space. Let P be a point on the axial line joining the two charges of the dipole at a distance r from the center O of the dipole (Fig. SAQ 5).

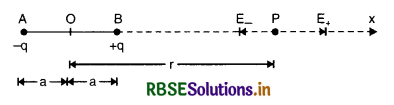
The electric field \(\overrightarrow{\mathrm{E}}\) at point P due to dipole will be the resultant of the electric field \(\overrightarrow{\mathrm{E}}\)_- (due to charge -q at point A) and \(\overrightarrow{\mathrm{E}}\)₊ (due to charge + q at point B)
i.e.,

Since \(\overrightarrow{\mathrm{E}}\)_- and \(\overrightarrow{\mathrm{E}}\)₊ act along the same line but in opposite directions, the magnitude of the electric field at point P is given by

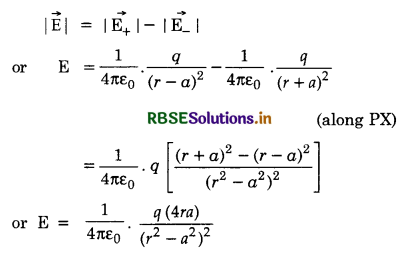
Now, q(2a) = p, the magnitude of the electric dipole moment of the dipole. Therefore,
E = \(\frac{1}{4 \pi \varepsilon_0} \cdot \frac{2 p r}{\left(r^2-a^2\right)^2}\) (along PX)
It may be noted that direction of electric field at a point on axial line of the dipole is from charge -q to +q i.e. the same as that of electric dipole moment of the dipole.
When the point P is very far away from the electric dipole, i.e. for a short dipole 2a << r. Therefore,
E = \(\frac{1}{4 \pi \varepsilon_0} \cdot \frac{2 p r}{r^4}\)
or E = \(\frac{1}{2 \pi \varepsilon_0} \cdot \frac{p}{r^3}\)

Question 6. 
Derive a relation for electric WM field of an electric dipole at a point on its equatorial line.
Answer:
Consider an electric dipole having two charges -q and +q lying at A and B at a distance 2a. Let us determine electric field intensity at point P on the equatorial line at a distance r from the center O of the dipole. Electric field intensity E₊ due to charge +q and E_- due to charge -q at P are given by
E₊ = k\(\frac{q}{\left(r^2+a^2\right)}\) [k = \(\frac{1}{4 \pi \varepsilon_0}\)]
E_- = k\(\frac{q}{\left(r^2+a^2\right)}\)
Resolving E+ and E- into rectangular components, we have E₊ cos θ + E_- cos θ along PD. E₊ sin θ and E_- sin θ being equal and opposite mutually cancel each other. (Fig. SAQ 6).

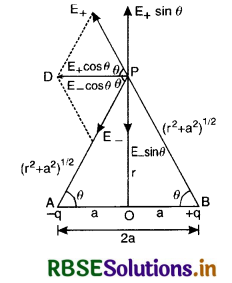
∴ Net electric field at P is given by
E_eq = E₊ cos θ + E_- cos θ
= 2E cos θ [∵ E₊ = E_- = E(say)]

-ve sign means that the direction of \(\overrightarrow{\mathrm{E}}_{e q}\) is opposite to \(\vec{p}\). When point P is very far away from the electric dipole i.e. for a short dipole 2a << r.
\(\left|\overrightarrow{\mathrm{E}}_{e q}\right|=\frac{|\vec{p}|}{4 \pi \varepsilon_0 r^3} \text { or } \mathrm{E}_{e q}=\frac{p}{4 \pi \varepsilon_0 r^3}\)

Question 7.
Calculate the force and torque acting on an electric dipole placed in an external uniform electric field, and define dipole moment.
Answer:
Consider a uniform electric field having constant magnitude and direction the same at all planes. Consider an electric dipole with its electric dipole moment vector, \(\vec{p}\) making an angle θ with the field. (Fig. SAQ 7).
Since \(\overrightarrow{\mathrm{E}}\) at any point is the force experienced per unit charge.

Hence, in a uniform electric field an electric field dipole experiences no net force; and therefore dipole does not undergo any translatory motion.
Torque acting on the dipole
These forces are equal in magnitude and opposite in direction, therefore, they form a couple.

Question 8.
What do you understand by conservation of charge?
Answer:
Conservation of Charge. The law of conservation of charge states that the total charge (algebraic sum of positive and negative charges) in an isolated system remains constant.

The electric charge can neither be created nor destroyed. This law has been found to be true for all events as well as for those at nuclear and atomic levels. In other words, there is no exception to the law. Like the law of conservation of energy, the law of conservation of charge is also a universal law.
Examples.

• When a glass rod is rubbed with silk the charges developed on the glass rod and the piece of silk are equal and opposite.
• Charge is conserved in all chemical and nuclear reactions.

Question 9.
Compare the properties of electric charge and mass which are not similar.
Answer:
table 1

Question 10.
How does rubbing of the two bodies produce electricity?
Answer:
When we rub two bodies, due to friction, some electrons are transferred from one body to another. The body which gains electrons becomes negatively charged and which loses electrons becomes positively charged by equal amount.
 
Question 11.
A comb after passing through dry hair attracts small pieces of paper. What happens if the hair is wet or if it is a rainy day?
Answer:
A dry comb, when passed through hair, gets charged due to friction and because of this it induces an opposite charge on the paper. The electrostatic force of attraction between the comb and the paper is much greater than the weight of paper, therefore, it is lifted. On a wet day, the hair is wet, the friction is quite less and hence, comb does not get charged.

Question 12.
You are given two metal spheres mounted on portable insulating supports. Find the way to give them equal and opposite charges. You may use a glass rod rubbed with silk but may not touch it to spheres. Do the spheres have to be of equal size for your method to work?
Answer:
By keeping the two spheres in contact and bringing a charged rod near one of the spheres, equal and opposite charges will be induced on two spheres as shown in Fig. SAQ 12 (a).

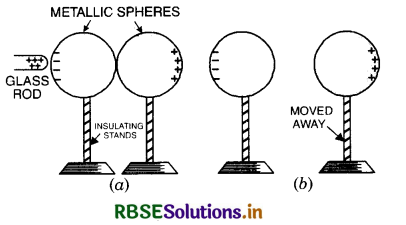
By keeping the rod in position, remove the sphere on the RHS by insulating stand to some distance apart Fig. SAQ 12 (b).
Next, remove the glass rod. Now the two spheres will carry equal and opposite charge. The charge on the two spheres will be equal irrespective of their sizes.

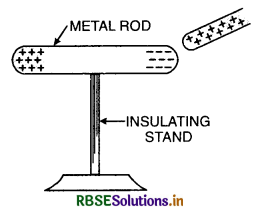
Question 13.
A charged glass rod is held on one end of an insulated uncharged metal rod as shown in Fig., electrons are drawn to one end, as shown. Why does the flow of electrons cease? There is almost an inexhaustible supply of them in the metal rod. Is there any net electrical force on the rod?
Answer:
The flow of electrons ceases because electrons repel further electrons.
Yes, there is a net force of attraction on the metal rod.

Question 14.
Three equal charges of+q C each placed at the three corners of an equilateral triangle. Find the total force experienced by a unit charge placed at the centroid of the triangle.

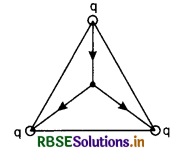
Answer:
Zero, because equal forces are inclined at angle of 120° so resultant is zero.

Question 15.
Compare the gravitational and electrical forces between proton-proton; proton-electron; electron-electron.
Answer:

(i) Between proton-proton.
m₁ = m₂ = 1.67 x 10^-27 kg;
q₁ = q₂ = 1.67 x 10^-19 C
∴ \(\frac{\mathrm{F}_e}{\mathrm{~F}_g}=\frac{9 \times 10^9 \times\left(1.6 \times 10^{-19}\right)^2}{6.67 \times 10^{-11} \times\left(1.67 \times 10^{-27}\right)^2}\)
= 1.239 x 10³⁶

(ii) Between proton-electron.
m₁ = 1.67 x 10^-27 kg; 
m₂ = 9.1 x 10^-31 kg
q₁ = q₂ = 1.6 x 10^-19 C (numerically)
∴ \(\frac{\mathrm{F}_e}{\mathrm{~F}_g}=\frac{9 \times 10^9 \times\left(1.6 \times 10^{-19}\right)^2}{6.67 \times 10^{-11}\left(1.67 \times 10^{-27}\right)\left(9.1 \times 10^{-31}\right)}\)
= 2.27 x 10³⁹

(iii) Between electron-electron.
m₁ = m₂ = 9.1 x 10^-31 kg;
q₁ = q₂ = 1.6 x 10^-19 C
∴\( \frac{\mathrm{F}_e}{\mathrm{~F}_g}=\frac{9 \times 10^9 \times\left(1.6 \times 10^{-19}\right)^2}{6.67 \times 10^{-11}\left(9.11 \times 10^{-31}\right)^2}\)
\(\frac{\mathrm{F}_e}{\mathrm{~F}_g}\) = 4.162 x 10⁴²
The ratio is quite huge. This shows that electric forces are much stronger than gravitational forces.

Question 16.
Compare the electric Helds due to a monopole (single charge) and dipole.
Answer:
table 2

Question 17.
Explain attraction and repulsion between two charges on the basis of electrostatic lines of force.
Answer:
1. The lines of force between a positively charged conductor A and a negatively charged conductor B are shown in Fig. (SAQ 17 (a)). These lines of force behave like stretched rubber bands and tend to contract lengthwise. Hence, when they become

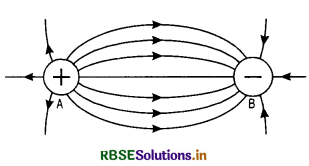
shorter the two bodies try to move towards each other. This explains electrostatic attraction.

2. The lines of force between two positive charges are as shown in Fig. (SAQ 17 (b)). Since the lines of force repel each other sideways, the lines of force due

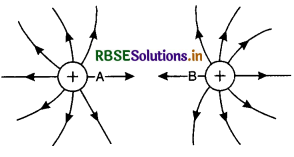
to one body push away from the lines of force due to the other body, the two bodies thus move away from each other. This explains electrostatic repulsion. It should be noted that in case no lines of force go from one body to the other.

Question 18.
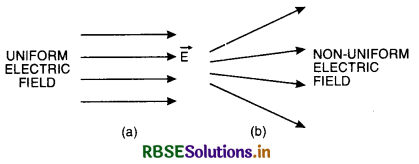
Define uniform and non-uniform electric fields. How are they represented geometrically?
Answer:
Uniform electric field.
A uniform electric field has the same intensity (both in magnitude and direction) at all points in it. Therefore, the electric field vectors at all the points must be of the same length and point in the same direction. Hence a uniform field is represented by a set of parallel lines pointing in the same direction.

A non-uniform field is that in which electric intensity is different at different parts, either in magnitude or direction or both.
A uniform and a non-uniform electric field are represented by the lines of force as shown in figures SAQ 18 (a) and (b) respectively.

Question 19.
How is electric field represented by diagram? What is the advantage of this representation?
Answer:
A point charge has an electric field whose strength decreases with an increase in distance. Let A, B and C be three points situated along a line at
increasing distances from Fig. SAQ 19. Let \(\overrightarrow{\mathrm{E}}_1, \overrightarrow{\mathrm{E}}_2\), \(\overrightarrow{\mathrm{E}}_3\) be the electric intensities at A, B and C respectively. These vectors are known as electric field vectors or force vectors. They have the same direction but decrease in magnitude with increase of distance. Therefore, they are represented by arrows of gradually decreasing lengths. A similar set of arrows, along another line, at A', B' and C' are also shown.


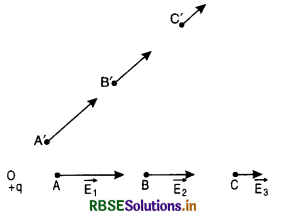
The direction of arrow represents the direction of field at that point. An electric field having these force vectors at its different points is said to be represented by force vectors or field vectors.

If a negative charge is placed at O, then the field vectors will point towards the charge.
The main advantage of this representation is that we can have an idea of the relative magnitude and the direction of electric intensity at a point in an electric field directly from the diagram.

Question 20.
Show that total electric flux over a closed surface due to charge outside the surface is zero.
Answer:
We can also show that the charges present outside the surface do not contribute to the electric flux. For this, suppose a charge + q is situated at a point O outside the closed surface.
Let a cone of small solid angle dΩ from O cut areas ds₁ and ds₂ of the closed surface at A and B respectively (Fig. SAQ 20).

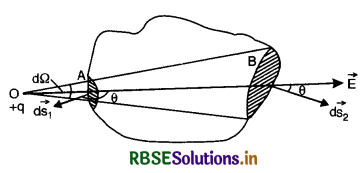
As \(\overrightarrow{\mathrm{E}}\) is inwards at A,
Flux at A = -\(\frac{q}{4 \pi \varepsilon_0}\) dΩ
(Negative sign because outdrawn normal at A makes obtuse angle with \(\overrightarrow{\mathrm{E}}\) for which cos θ is negative).
As \(\overrightarrow{\mathrm{E}}\) is outwards at B,
Flux at B = \(\frac{q}{4 \pi \varepsilon_0}\) dΩ
Total electric flux over these elements of closed surface
= -\(\frac{q d \Omega}{4 \pi \varepsilon_0}+\frac{q d \Omega}{4 \pi \varepsilon_0}\) = 0
Hence total electric flux over the closed surface due to charge outside the surface is zero.

Question 21.
Vehicles carrying inflammable materials usually have metallic ropes touching the ground during motion, why?
Answer:
When the vehicle is moving in earth’s magnetic field, its iron parts, cut the magnetic field. Due to change of magnetic fields in iron parts, an induced e.m.f. is set up. When the metallic rope from the vehicle touches the road, the induced current is grounded and the vehicle is saved from catching fire.

Question 22.
State and derive Gauss’ theorem in electrostatics for a spherically symmetrical closed surface.
Answer:
Gauss’ Theorem. It states that the total electric flux through a closed surface is equal to 1/ε₀ times the magnitude of the charge.
i.e. \(\oint \overrightarrow{\mathrm{E}} \cdot d \overrightarrow{\mathrm{S}}\) = q/ε₀
Proof. If a point charge q is placed at the center of a sphere of radius r, then the electric field at the surface of the sphere is given by

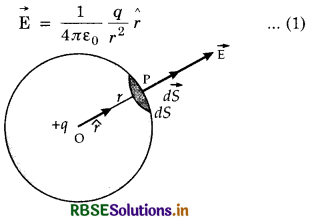
The electric flux linked with a small element dS around point P is given by

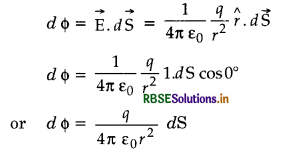
∴ Total electric flux through the whole spherical surface

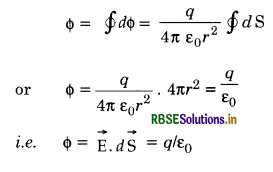
This is Gauss’ theorem.

Question 23.
Derive Coulomb’s law from Gauss’s theorem.
Answer:
Coulomb’s law from Gauss’ theorem
Consider an isolated positive charge +q at O. Imagine a sphere of radius r and center O (Fig. SAQ 23).
Electric field \(\overrightarrow{\mathrm{E}}\) at every point on the sphere is the same and is directed outwards. Direction of small area element \(\vec{d} \mathbf{s}\) is also along \(\overrightarrow{\mathrm{E}}\) i.e, the angle between \(\overrightarrow{\mathrm{E}}\) and \(\vec{d} \mathbf{S}\) = 0°.
According to Gauss’ theorem,


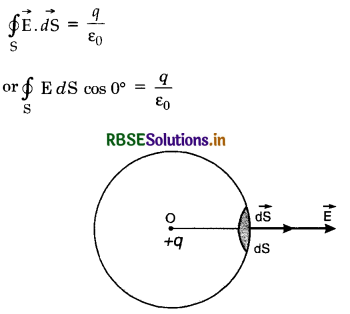
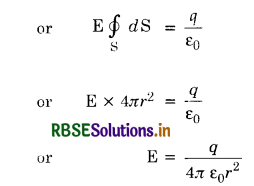
If another charge q₀ is placed on the sphere then, force F on it is
F = q₀E = \(\frac{q_0 q}{4 \pi \varepsilon_0 r^2}\)
which is Coulomb’s law.

Question 24.
Find the Electric Field due to two infinite plane parallel sheet of charge.
Answer:
Electric Intensity at any point outside two parallel, plane, oppositely charged conductors. Suppose there are two parallel plane sheets A and B with uniform charge densities σ₁ and σ₂. Let sheet A be to the left of sheet B. Then electric field at a point can be found by the superposition law. There are three regions.

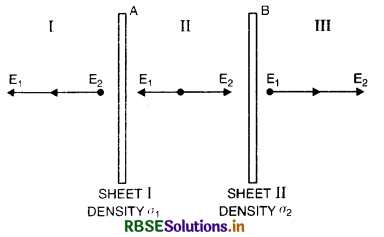
Region I is to the left of sheet A.
Region II between sheets A and B.
Region III is to the right of sheet B.
If the direction from left to right is taken +ve, then using the result, E = \(\frac{\sigma}{2 \varepsilon_0}\).
For region I
E = (-E₁ - E₂) = \(\frac{\sigma}{2 \varepsilon_0}\) (- σ₁ - σ₂) ......................(i)
For region II
E = (E₁ - E₂) = \(\frac{\sigma}{2 \varepsilon_0}\) ( σ₁ - σ₂) ......................(ii)
For region III
E = (E₁ + E₂) = \(\frac{\sigma}{2 \varepsilon_0}\) ( σ₁ + σ₂) ......................(iii)
A negative field means that it points from right to left and a + ve field means the opposite.
The case σ₁ > σ₂ > 0 is illustrated in Fig. SAQ 24.
If the two sheets are oppositely charged such that σ₁ = σ and σ₂ = σ, then
From eq. (i), (ii) and (iii), we get
E_I = 0, E_II = \(\frac{1}{2 \varepsilon_0}\) (2σ) = \(\frac{\sigma}{\varepsilon_0}\) and E_III = 0

Question 25.
Find the electric field intensity at any point on the axis of a uniformly charged ring or loop. What happens if the ring is far away from the point?
Answer:
Let us consider a circular loop of radius a held perpendicular to the plane of paper.
Let whole of loop carries a charge q. Charge on a small element of loop MN of length dl is

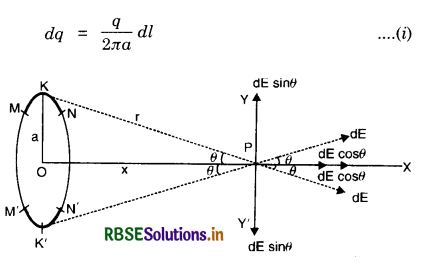
Electric field at P due to charge element MN is
dE = \(\frac{1}{4 \pi \varepsilon_0} \frac{d q}{r^2}\)
= \(\frac{1}{4 \pi \varepsilon_0} \frac{d q}{\left(x^2+a^2\right)}\) along KP
dE can be resolved into two rectangular components.
dE cos θ acting horizontally along PX and dE sin θ acting along PY.
For a pair of diagrammatically opposite element M'N', dE cos θ acts along PX and hence add up but dE sin θ along PY' cancel with dE sin θ along PY. ΣdE sin θ = 0 for full loop and dE cos θ add up
∴ E = ΣdE cos θ

Special case. When x > > a i.e., P lies far off, then a² < < x² and hence can be neglected
∴ E = \(\frac{q x}{4 \pi \varepsilon_0\left(x^2\right)^{3 / 2}}=\frac{q x}{4 \pi \varepsilon_0 x^3}\)
or E = \(\frac{1}{4 \pi \varepsilon_0} \times \frac{q}{x^2}\)

Question 26.
Two metallic spheres of exactly equal masses are taken. One is given a positive charge q Coulomb and the other an equal negative charge by friction. Are their masses after charging equal?
Answer:
No. Because when two bodies are rubbed together, there is transfer of electrons from one body to another. Since electrons are materials particles, so their transfer from one body to another causes a change in mass. The body from which electrons are removed becomes positively charged and body to which electrons get transferred becomes negatively  charged. Hence the mass of negatively charged body will be more than positively charged body.

Question 27.
State the limitations of Coulomb’s law in electrostatics.
Or
Is Coulomb’s law in electrostatics applicable in all situations?
Answer:
No, Coulomb’s law is not applicable in all situations. It is applicable only when:

• The electric charges are stationary.
• The electric charges are points in size.
• Both the charges should lie in an isolated system.

Thus we find that if two charges are finite in size like two charged spheres, the Coulomb’s law does not apply because when the charged spheres are brought together, the distribution of charge do not remain uniform.

Question 28.
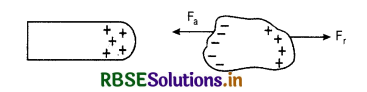
Why does a charged glass rod attract a piece of paper?
Answer:
When a charged rod (say positively charged) is brought near a piece of paper, equal and opposite charge is induced on the paper as shown in Fig. The force of attraction between the glass rod and the piece of paper is more than the force of repulsion between the glass rod and the piece of paper i.e. F_a > F_r . Hence the charged glass rod attract the piece of paper.

Question 29.
What is the value of charge on a body which carries (12) excess of protons?
Answer:
The charge on a body is given by
q = ne
Here n = 12
∴ q = 12e
= 12 x 1.6 x 10^-19 C
or q = 19.2 x10^-19 C

Question 30.
Find the magnitude of electric field which just balances a deuteron of mass 3.2 x 10^-27 kg. (Take g = 10 m s^-2)
Answer:
Given m = 3.2 x 10^-27 kg
q = 1.6 x 10^-19 C, g = 10 m s^-2
Since F = mg
Also F = qE
∴ qE = mg
or E = \(\frac{m g}{q}=\frac{3.2 \times 10^{-27} \times 10}{1.6 \times 10^{-19}}\)
or E = 2.0 x 10^-7 NC^-1

Question 31.
Prove that the net force acting on an electric dipole, inclined at an angle θ to the uniform electric field \(\overrightarrow{\mathbf{E}}\) is zero. Draw a suitable diagram.
Answer:
Let an electric dipole consisting of two charges (+q) and (-q) separated by a distance 2a is placed in a uniform electric field \(\overrightarrow{\mathbf{E}}\) as shown in Fig. SAQ 31.

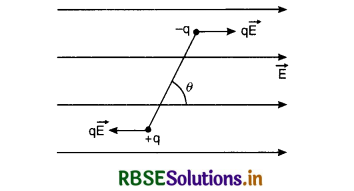
∴ Force experienced by +q charge
\(\overrightarrow{\mathrm{F}}=+q \overrightarrow{\mathrm{E}}\)
Force experienced by -q charge
\(\overrightarrow{\mathrm{F}}=-q \overrightarrow{\mathrm{E}}\)
∴ Net force on dipole in uniform electric field \(\overrightarrow{\mathbf{E}}\) is
\(\overrightarrow{\mathrm{F}}_{\text {total }}=q \overrightarrow{\mathrm{E}}-q \overrightarrow{\mathrm{E}}\) = 0
i.e. net force on the dipole is zero.

Question 32. 
We define the electric field strength as:
\(\overrightarrow{\mathrm{E}}=\lim _{\mathbf{q}_0 \rightarrow 0} \frac{\overrightarrow{\mathrm{F}}}{\mathrm{q}_0}\)
Keeping in mind that minimum value of the charge that exists in nature cannot be less than e = 1.6 x 10^-19 C, how can we justify the above definition?
Answer:
The minimum value of charge that exists in nature, no doubt is e = 1.6 x 10^-19 C. But this charge is very very small as compared to the actual charges we deal with. Hence we can say that the condition that q₀ → 0 is satisfied. But when we deal with microscopic cases like the charges within the atom or nucleus, this definition may not be strictly true.

Question 33.
Show that charge always resides on the outer surface of a conductor.
Or
Show that net charge in the interior of a conductor is zero.
Answer:
Consider a conductor of any shape or size, which is given a +ve charge +q. Consider a gaussian closed surface just inside the outer surface of the conductor as shown in the figure SAQ 33 by dotted lines.
From Gauss’ theorem,

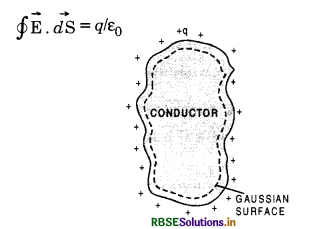
But \(\overrightarrow{\mathrm{E}}\) = 0 inside the conductor
∴ q = 0
i.e. charge inside the conductor is zero. Hence we find that charge always resides on the outer surface of the conductor.

Question 34. 
Find electric intensity at a point in between two parallel opposite-charged infinite sheets.
Answer:
Consider two parallel plane charged conductors A and B carrying + ve and - ve charges of density a (charge per unit area). According to Gauss’ theorem, the electric intensity at P due to the charge on sheet A is

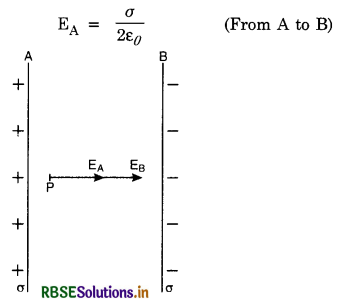
And due to charge on sheet B is
E_B = \(\frac{\sigma}{2 \varepsilon_0}\) (From A to B)
∴ E = E_A + E_B
= \(\frac{\sigma}{ \varepsilon_0}\)

Question 35.
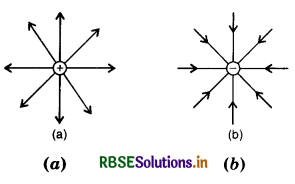
The electric field E due to any point charge is defined as E = \(\lim _{q \rightarrow 0} \frac{F}{q}\), while q is the test charge and F is the force acting on it. What is the physical significance of lim_q→0 in this expression? Draw the electric lines of point charge Q when (i) Q > 0 and (ii) Q < 0.
Answer:
The physical significance of defining the electric field, E = \(\lim _{q \rightarrow 0} \frac{F}{q}\), is that the field due to test charge does not in any way alter the electric field due to the source charge, hence we take q → 0. The electric field lines are as shown in Figs. SAQ 35 (a) and (b).

Question 36.
The force of attraction between two point charges placed at a distance 'd' apart in a medium is F. What should be the distance apart in the same medium so that the force of attraction between them becomes F/4?
Answer:
If 'd' be the distance between two charges q₁ and q₂ in a medium of dielectric constant k, then force between them
F = \(\frac{1}{4 \pi \varepsilon_0 k} \frac{q_1 q_2}{d^2}\) ........................(i)
Let F becomes \(\frac{\mathrm{F}}{4}\) and distance becomes d₁
So \(\frac{\mathrm{F}}{4} = \frac{1}{4 \pi \varepsilon_0 k} \frac{q_1 q_2}{d_1^2}\) ...............................(ii)
Dividing (i) by (ii), we get
4 = \(\frac{d_1^2}{d^2}\)
i.e. the distance between the charges is doubled.
d₁ = 2d

Question 37.
S₁ and S₂ are two hollow concentric spheres enclosing charges Q and 2Q respectively as shown in Fig. SAQ 37 (i) What is the ratio of electric flux through S₁ and S₂? (ii) How will the electric flux through the sphere S₁ change if a medium of dielectric constant 5 is introduced in the sphere inside S₁ in place of air?
Answer:
(i) Let Φ₁ and Φ₂ be the electric flux linked through sphere S₁ and S₂ respectively.

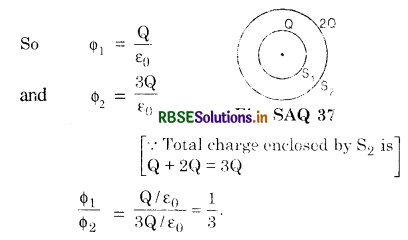
(ii) Let \(\overrightarrow{\mathrm{E}}\) be electric, field intensity on the surface of the sphere S₁ due to charge Q placed inside the sphere. Then, according to Gauss’ theorem.
Q₁ = \(x = {-b \pm \sqrt{b^2-4ac} \over 2a}\oint \overrightarrow{\mathrm{E}} \cdot d \mathrm{~S}=\frac{\mathrm{Q}}{\epsilon_0}\) ......................(i)
On introducing medium of dielectric constant K inside the sphere S₁ suppose that electric field on the surface of sphere becomes \(\overrightarrow{\mathrm{E}^{\prime}}\). Then,
\(\overrightarrow{\mathrm{E}^{\prime}}=\frac{\overrightarrow{\mathrm{E}}}{\mathrm{K}}\) ......................(ii)
If the electric flux through the sphere is now Q₁' then
Q₁' = \(\phi \overrightarrow{\mathrm{E}} \cdot d \overrightarrow{\mathrm{S}}=\phi \frac{\overrightarrow{\mathrm{E}}}{\mathrm{K}} \cdot d \overrightarrow{\mathrm{S}}=\frac{\mathrm{Q}}{\mathrm{K} \varepsilon_0}\)
Here, K = 5 [Using the equations (i) and (ii)]
Q₁' = \(\frac{\mathrm{Q}}{5 \varepsilon_0}\).

Question 38.
Derive an expression for the electric field at any point on the equitorial line of an elecric dipole.
Answer:
Consider an electric dipole having two charges -q and +q lying at A and B at a distance 2a. Let us determine electric field intensity at point P on the equatorial line at a distance r from the centre O of the dipole. Electric field intensity E₊ due to charge +q and E_- due to charge -q at P are given by
E₊ = k\(\frac{q}{\left(r^2+a^2\right)}\) [k = \(\frac{1}{4 \pi \varepsilon_0}\)]
E_- = k\(\frac{q}{\left(r^2+a^2\right)}\)
Resolving E₊ and E_- into rectangular components, we have E₊ cos θ + E_- cos θ along PD. E₊ sin θ and E_- sin θ being equal and opposite mutually cancel each other. (Fig. SAQ 6).

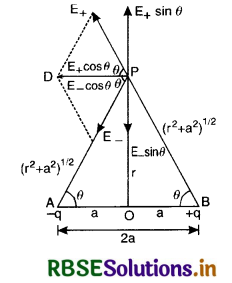
∴ Net electric field at P is given by
E_eq = E₊ cos θ + E_- cos θ
= 2E cos θ [∵ E₊ = E_- = E(say)]

-ve sign means that the direction of \(\overrightarrow{\mathrm{E}}_{e q}\) is opposite to \(\vec{p}\). When point P is very far away from the electric dipole i.e. for a short dipole 2a << r.
\(\left|\overrightarrow{\mathrm{E}}_{e q}\right|=\frac{|\vec{p}|}{4 \pi \varepsilon_0 r^3} \text { or } \mathrm{E}_{e q}=\frac{p}{4 \pi \varepsilon_0 r^3}\)

Long Answer Type Questions

Question 1.
What is frictional electricity? Give examples. What are two types of charges?
Answer:
Frictional Electricity. It is the charge produced by rubbing two bodies. Since the force of friction is responsible for the production of this charge, this is called frictional electricity. For example, ebonite or plastic objects rubbed with wool, or glass rubbed with silk acquires the ability to attract small objects and the bodies showing this effect are said to be charged.
Experiments. Suspend a glass rod by a piece of dry silk thread so that it is balanced horizontally and free to turn round.

1. If you charge the rod by rubbing it with silk, you will find that when this piece of silk is brought near the rod, it attracts the rod strongly than any other piece of silk will do.
2. If the suspended rod and another glass rod are both charged by rubbing with silk, the two rods will repel each other when they are brought close together as shown in Fig. LAQ 1 (a) below.
   
3. The same experiment can be performed with ebonite rod rubbed with wool, it will be found that the rods repel each other. If, however we charge glass rod by rubbing it with silk and then bring a piece of ebonite rod rubbed with wool close to it, these will attract each other as shown in Fig. LAQ 1 (b) below.

We may sum up the conclusions of these experiments as follow:

• The charge on a glass rod produced when rubbed with silk is called positive and an ebonite rod or amber when rubbed with wool is called negative,
• Like charges repel each other
• Unlike charges attract each other.

From the results of experiments producing frictional electricity one can make tip a table with one column listing substances acquiring a positive charge upon rubbing, and another column containing substances acquiring 'negative' charge.
Table. Frictional electricity leading to two kinds of charges.

table 3

The experimental result is that two electrified objects in the same column repel, but if they are in different columns they attract one another. The substances in the following list are arranged in such a way that on rubbing, i.e. by friction, one occurring earlier acquires a negative charge while that occurring later acquires a positive charge.
Rubber, Ebonite, Sulphur, Silk, Flannel, Glass, Fur.

Question 2.
What is electronic theory of electrification by friction? Hence define conductors and insulators.
Answer:
Electronic theory of Electrification. An atom consists of nucleus and electrons. Nucleus contains positively charged protons and uncharged neutrons. The electrons which are negatively charged revolve around the nucleus in certain orbits. Since the number of protons and electrons in an atom is the same, the atom is electrically neutral.

The electrons which are very close to the nucleus are called bound electrons and are tightly bound to the nucleus due to strong force of attraction between the charges of nucleus and electrons. The force of attraction between the nucleus and the electrons which are far away from the nucleus is very weak. These electrons are called free electrons and these are responsible for electrification of objects.

When glass rod is rubbed with silk, some electrons from the glass rod are removed and they are transferred to the silk. This is due to the fact that in glass, electrons are less tightly bound than in silk. Since electrons are removed from atoms of glass then due to loss (or deficit) of electrons, glass gets positively charged. On the other hand, due to gain of same number of electrons, the silk gets an equal negative charge.

Similarly, when ebonite rod is rubbed with fur, the free electrons from fur are transferred to the ebonite rod. Hence ebonite rod is negatively charged due to excess of electrons while the fur becomes positively charged due to deficit of the same number of electrons.

Conductors and insulators. Every metal contains large number of electrons which are less tightly bound to nucleus. These electrons do not remain attached to their respective atoms and hence are called free electrons. These cannot leave the metal.
A substance which has large number of free electrons is called good conductor of electricity.
e.g. Silver, copper, aluminium, mercury, tin, iron, human body, acid, alkali, salt, gold, brass etc. are good conductors of electricity.
A substance which has negligible number of free electrons is called bad conductor or insulator or dielectrics.
e.g. Quartz, glass, wood, dry air, gases, dry silk, pure water, bakelite, mica, amber, ebonite, sulphur, wax, oils are some examples of insulators.

Question 3.
State and explain dielectric constant (or relative permittivity).
Answer:
Definition of dielectric constant (or relative permittivity). The force between two charges q₁ and q₂ separated by distance r in a medium having relative permittivity ε_r is given by
F_m = \(\frac{1}{4 \pi \varepsilon_0 \varepsilon_r} \frac{q_1 q_2}{r^2}\) .......................(i)
The relative permittivity ε_r is also called the dielectric constant K of the medium i.e. ε_r = K
∴ F_m = \(\frac{1}{4 \pi \varepsilon_0 K} \frac{q_1 q_2}{r^2}\) .......................(ii)
For vacuum or air, K = 1
∴ F_v = \(\frac{1}{4 \pi \varepsilon_0} \frac{q_1 q_2}{r^2}\) ......................(iii)
Dividing (iii) by (ii), we get
\(\frac{\mathrm{F}_v}{\mathrm{~F}_m}\) = K
or K = \(\frac{\mathrm{F}_v}{\mathrm{~F}_m}\)
Hence, the dielectric constant (or relative permittivity) of a medium is defined as the ratio of the electrostatic force between two charges placed at certain distance apart in vacuum to the force between the same two charges placed at the same distance apart in that medium.
The value of K depends upon the nature of medium.
For vacuum, K = 10000, for air, K = 100054
For water, K = 81
Relative Permittivity or Dielectric constant or Specific Inductive Capacity (S.I.C.) ε = ε₀ K.
or K = \(\frac{\varepsilon}{\varepsilon_0}\)
or Relative permittivity = \(\frac{\text { absolute permittivity of medium }}{\text { absolute permittivity of vacuum }}\)

Question 4.
(a) State and explain superposition principle.
(b) Find an expression for the total force acting on a given charge due to a number of other charges, when the source charges are point charges.
Answer:
(a) Principle of Superposition. The resultant electric force at a point charge due to a number of charges in its neighborhood is the vector sum of the electric forces produced by each charge individually in the absence of other charges.
If a charge q₁ experiences forces \(\overrightarrow{\mathrm{F}}_{12}, \overrightarrow{\mathrm{F}}_{13}, \ldots, \overrightarrow{\mathrm{F}}_{1 n}\) due to other charge q₂, q₃ .................. respectively, then the total force \(\overrightarrow{\mathrm{F}}\) experienced by the charge q₁ is given by
\(\overrightarrow{\mathrm{F}} = \overrightarrow{\mathrm{F}}_{12}, \overrightarrow{\mathrm{F}}_{13}, \ldots, \overrightarrow{\mathrm{F}}_{1 n}\)

(b) Suppose we have many point charges q₁, q₂, q₃ ........................ at points P₁, P₂, P₃ .................. in space, with position vectors \(\vec{r}_1, \vec{r}_2, \vec{r}_3\) ................. The total force \(\overrightarrow{\mathrm{F}}_1\) on charge q₁ is the vector sum of the individual forces that each of the other charges q₂, q₃ ............... exert on it.

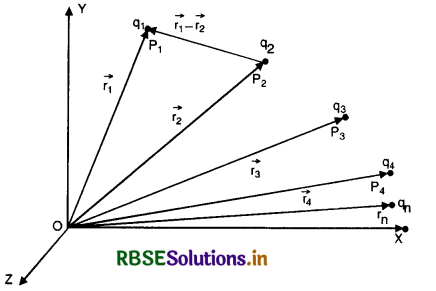
Therefore, using Coulomb’s law of electrostatics The force on charge q₁ due to q₂

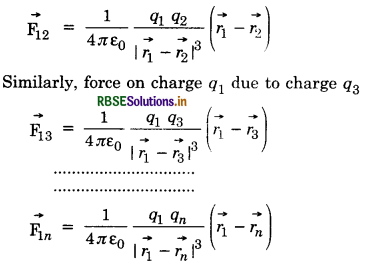
∴ total force on charge q₁ due to all other charges

Question 5.
(a) What is meant by continuous charge distribution? Describe different types of continuous charge distribution and give expression for total charge in each case.
(b) Derive an expression for the total force acting on a point charge due to general charge distribution.
Answer:
(a) Continuous charge distribution.
Point charges do not exist in real practice and are only imaginary charges. In practice we always deal with charged bodies having definite length, area or volume which possesses a continuous distribution of charges.
Types. There are three main types of charge distribution:

• Linear charge distribution
• Surface charge distribution and
• Volume charge distribution.

1. Linear charge distribution. When the charge is distributed uniformly along a line, and the distribution is one dimensional, it is called linear charge distribution.
If λ (r') be the line density of charge i.e. charge per unit length at position r' and dl be a small length element about that position, then charge on the element becomes λ (r') dl [Fig. (LAQ 5) (a)].

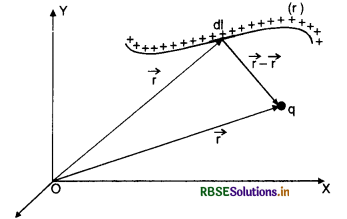
The total charge is given by \(\int_{\mathrm{L}} \lambda\left(r^{\prime}\right)\) dl. The expression is called line integral of linear charge distribution.
Expression for force
Let point charge q lie at a point on position vector \(\vec{r}\).
∴ Force on charge q due to linear charge distribution is 
\(\overrightarrow{\mathrm{F}}=\frac{1}{4 \pi \varepsilon_0} q \int \lambda\left(r^{\prime}\right) d l \cdot \frac{\left(\vec{r}-\overrightarrow{r^{\prime}}\right)}{\left|\vec{r}-\overrightarrow{r^{\prime}}\right|^3}\)

2. Surface charge distribution. When the charge is distributed over a surface and the distribution is two-dimensional, it is called surface charge distribution.
If σ(r') be the surface density of charge i.e., charge per unit area at position r' and ds be a small area element about that position, then charge on the element becomes σ(r') ds [Fig. LAQ 5 (b)].

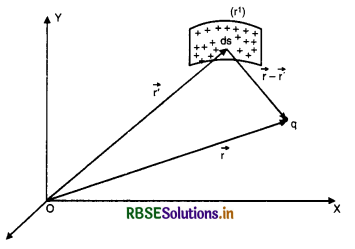
The total charge is given by \(\int_{\mathrm{S}} \sigma\left(r^{\prime}\right) \)ds. The expression is called surface integral of superficial charge distribution.
Expression for Force. Let point charge q lie at a point on position r.
∴ Force on charge q due to surface charge distribution is
\(\overrightarrow{\mathrm{F}}=\frac{1}{4 \pi \varepsilon_0} q^{\prime} \int_{\mathrm{S}} \sigma\left(r^{\prime}\right) d s \cdot \frac{\left(\vec{r}-\overrightarrow{r^{\prime}}\right)}{\left|\vec{r}-\overrightarrow{r^{\prime}}\right|^3}\)

3. Volume charge distribution. When charge is continuously distributed over a volume and distribution is three-dimensional, it is called volume charge distribution.
If ρ(r') be the volume density of charge i.e. charge per unit volume at position r' and dV be small volume element about that position, then charge on the element becomes ρ(r') dV [Fig. LAQ 5 (c)]

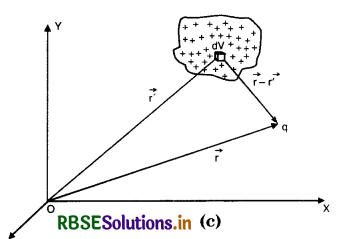
The total charge is given by \(\int_{\mathrm{V}} \rho\left(r^{\prime}\right) d \mathrm{~V}\). The expression is called volume integral of volume charge distrinution.
Expression for force. Let point charge q lie on position r.
∴ Force on charge q due to volume distribution is
\(\overrightarrow{\mathrm{F}}=\frac{1}{4 \pi \varepsilon_0} q \int_{\mathrm{V}} \rho\left(r^{\prime}\right) d \mathrm{~V} \cdot \frac{\left(\vec{r}-\overrightarrow{r^{\prime}}\right)}{\left|\vec{r}-\overrightarrow{r^{\prime}}\right|^3}\)

(b) Total force on a point charge. Let point charge q' lie at a point in position r'. Let λ (r), σ(r') and ρ(r') be the line charge density, the surface charge density and the volume charge density respectively at same position r'.
Let point charge q, lie at a point on position r.
Then Force on charge, q due to point charge q'
F = \(\frac{1}{4 \pi \varepsilon_0} q\left[\sum_{\text {point charges }} q^{\prime} \frac{\vec{r}-\overrightarrow{r^{\prime}}}{\left|\vec{r}-\overrightarrow{r^{\prime}}\right|^3}\right]\)
Total force on charge q, at position \(\vec{r}\) becomes

Question 6.
(a) Define electric field and electric field intensity at a point.
(b) Find the electric field intensity
(i) due to a group of point charges and
(ii) due to a general charge distribution.
Answer:
(a) Electric field. The electric field due to a point charge or a system of charges is the space around the charge within which the force of attraction/ repulsion due to the charge can be experienced. Theoretically, the electric field due to a charge extends upto infinity. But practically, it is confined only to some distance from the charge.

Electric field intensity. Electric, field intensity (\(\overrightarrow{\mathrm{E}})\) at any point in the electric field is equal to the force acting over a unit positive charge on a vanishingly small charge placed at that point.

If \(\overrightarrow{\mathrm{F}}\) is the coulomb force acting on a small positive test charge q₀, then by definition,
\(\overrightarrow{\mathrm{E}}=\operatorname{Lt}_{q_0 \rightarrow 0} \frac{\overrightarrow{\mathrm{F}}}{q_{\dot{0}}}\)

The S.I. unit of is newton/coulomb. It is a vector quantity and the direction of \(\overrightarrow{\mathrm{E}}\) is the direction in which the test charge will move if free to do so.

Field intensity due to a point charge. Suppose we have to calculate electric field intensity at any point P to a point charge q at O, where OP = r. Imagine a positive test charge q0 at P. According to Coulomb’s law, force at P is
\(\overrightarrow{\mathrm{F}}=\frac{1}{4 \pi \varepsilon_0} \frac{q q_0}{r^2} \hat{r} where \hat{r}\) is unit vector directed from q towards q₀ as shown in Fig. LAQ 6 (a) below.

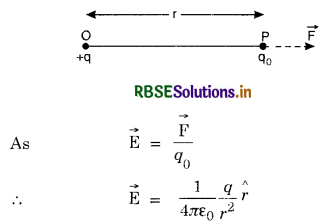
\(\hat{r}\) is the unit vector in the direction of force.
If q is + ve, the field intensity is directed radially outwards along OP. If q is negative, the field intensity is directed towards q, along PO. 

(b) (i) Electric field intensity due to a group of charges. The electric field intensity at any point due to a group of point charges is equal to the vector sum of the electric field intensities due to given charges at the same point. For this, we first calculate the electric field intensity at the given point due to individual charges and then add them vectorially. Let us consider a system of n charges q₁, q₂, ................. q_n with position vectors \(\vec{r}_1, \vec{r}_2, \ldots . . \overrightarrow{r_n}\) respectively relative to some origin O. Let a unit charge be placed at origin O as shown in Fig., then
Electric field due to q₁ at \(\vec{r}_1\) is
\(\vec{E}_1=\frac{1}{t . \tau \varepsilon_0} \frac{q_1}{r_1^2} \hat{r_1}\)
Electric field due to q₂ at \(\vec{r}_2\) is
\(\overrightarrow{\mathrm{E}}_2=\frac{1}{4 . \pi \varepsilon_0} \frac{q_2}{r_2^2} \hat{r_2}\)
Similarly
\(\overrightarrow{\mathrm{E}}_n=\frac{1}{4 . \pi \varepsilon_0} \frac{q_n}{r_n^2} \hat{r_n}\)

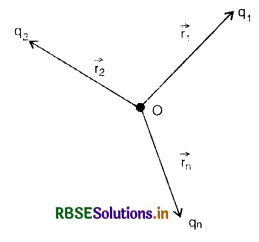
∴ Total electric field at 0 due to the system of charges is given by
\( \overrightarrow{\mathrm{E}}=\overrightarrow{\mathrm{E}}_1+\overrightarrow{\mathrm{E}}_2+\overrightarrow{\mathrm{E}}_3+\ldots \ldots \ldots . .+\overrightarrow{\mathrm{E}}_n\)
 \(\overrightarrow{\mathrm{E}}=\frac{1}{4 \pi \varepsilon_0} \sum_{i=1}^n \frac{q_i}{r_i^2} \hat{r_i}\)
 Here ri is the distance of the point P from the ith charge q_i and \(\hat{r}\) is unit vector directed from qi to the point P.
 
(ii) General expression for the electric field at a point. The general expression for the force on a charge q₀ at \(\hat{r}\) due to the most general (static) source distribution is given by

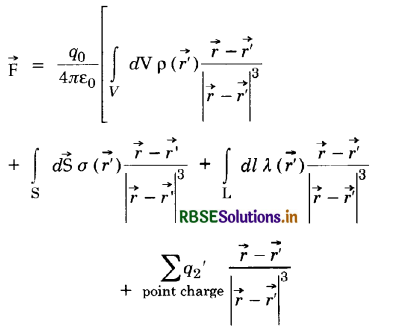
Now electric field \(\overrightarrow{\mathrm{E}}\) at a point is given by
\(\overrightarrow{\mathrm{E}} = \operatorname{Lt}_{q_0 \rightarrow 0} \frac{\overrightarrow{\mathrm{F}}}{q_0}\) ......................(i)
Putting the value of \(\overrightarrow{\mathrm{F}}\) , we get

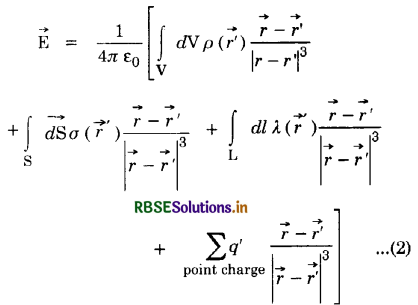
Question 7.
(a) Define electric dipole, dipole moment and dipole electric field. Draw lines of force for a dipole field.
(b) Derive expression for the intensity of dipole field.
Answer:
(a) Electric dipole. A system of two equal and opposite charges separated by certain distance is called electric dipole.

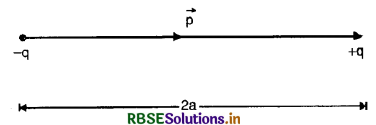
Fig. LAQ 7 (a) shows an electric dipole consisting of two equal and opposite point charges (± q) separated by a small distance 2a.
Dipole moment (\(\overrightarrow{\mathrm{P}}\)). It is defined as the product of magnitude of either charge and the distance between two charges.
i.e. \(\overrightarrow{\mathrm{P}} = q \overrightarrow{2 a}\)
The direction of \(\overrightarrow{p}\) is from -ve charge to +ve charge.
Units: In S.I.,
The unit of \(\overrightarrow{p}\) is Coulomb-metre (Cm).
Dipole field. The electric field produced by an electric dipole is called electric dipole field and is defined as the space around an electric dipole within which the effect of the dipole can be felt.

Electric lines of force. Below Fig. LAQ 7 (b) shows the section of the field in the plane of paper, containing dipole itself.


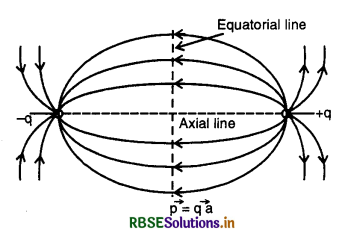
The lines of force are directed away from +q charge and towards -q charge. They are straight and open along the line containing the charges. This line is called axial line of dipole. On the broad side of the dipole, lines are curved. Near the dipole, they start from +q charge and end at -q charge, then closing their path at the ends of the dipole.

(b) Intensity of dipole field
Let an electric dipole have charge strength q and length a. So its dipole moment p = qa. Let it lie along z-axis with its centre at origin O, charges q at position z = a/2 and charges -q at position z = - a/2.
Let the poles have the position vectors \(\vec{r}_1\) and \(\vec{r}_2\) as shown in Fig. ahead. So \(\vec{r}_1\) has co-ordinates (0, 0, a/2) and \(\vec{r}_2\) has co-ordinates (0, 0, -a/2).



This expression holds true when r > > a.
In case of point dipole, a → 0, we write qa = p
Then \(\overrightarrow{\mathrm{E}}(\vec{r})=\frac{p}{\pi \varepsilon_0} \frac{1}{r^3}\left[3 x z \hat{i}+3 y z \hat{j}+\left(3 z^2-r^2\right) \hat{k}\right]\)
This is the expression for intensity of electric field of an ideal point dipole at all points in the space. The field has cylindrical symmetry with the axis of dipole as axis of the cylinder.

Question 8.
Find an expression for electric intensity due to a short electric dipole at any point situated along a line inclined at an angle from the dipole axis.
Answer:
Let AB be a short dipole of dipole moment p. Let P be a point at a distance r from mid-point of the dipole and inclined at an angle θ (See Fig.). The dipole moment can be resolved into two rectangular components:
(i) p cos θ along A₁B₁
(ii) p sin θ along A₂B₂.
Now P lies on axial line of p cos θ
∴ E₁ = 2k\(\frac{p \cos \theta}{r^3}\) along PL
And P lies on equatorial line of p sin θ
∴ E₂ = k\(\frac{p \cos \theta}{r^3}\) along PM
Since E₁ and E₂ are perpendicular to each other, so the resultant electric field E is given by

In rt ∠∆PLN

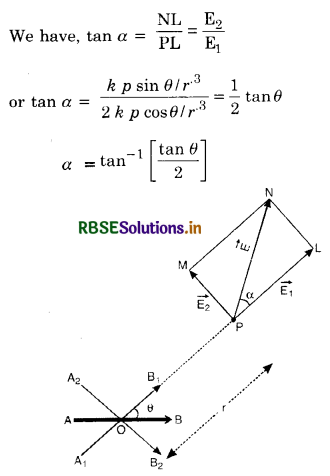
Case (i) When P lies on axial line of the dipole
i.e. θ = 0°
∴ E = \(\frac{k p}{r^3} \sqrt{3+1}=\frac{2 k p}{r^3}\)
And tan α = \(\frac{1}{2}\)tan 0°= 0
or α = 0°

Case (ii) When P lies on equatorial line of the dipole
i.e. θ = 90°
∴ E = \(\frac{k p}{r^3} \sqrt{0+1}=\frac{k p}{r^3}\)
And tan α = \(\frac{1}{2}\)tan 90° = ∞ or α = 90°

Question 9.
Calculate the force and torque acting on an electric dipole placed in an external uniform electric field, and define dipole moment and explain when the torque is maximum and minimum.
Answer:
Electric dipole and its units: 
Electric dipole. A system of two equal and opposite charges separated by certain distance is called electric dipole.

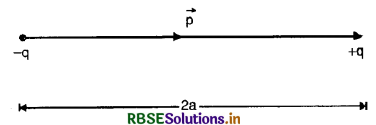
Fig. LAQ 7 (a) shows an electric dipole consisting of two equal and opposite point charges (± q) separated by a small distance 2a.
Dipole moment (\(\overrightarrow{\mathrm{P}}\)). It is defined as the product of magnitude of either charge and the distance between two charges.
i.e. \(\overrightarrow{\mathrm{P}} = q \overrightarrow{2 a}\)
The direction of \(\overrightarrow{p}\) is from -ve charge to +ve charge.
Units: In S.I.,
The unit of \(\overrightarrow{p}\) is Coulomb-metre (Cm).
Dipole field. The electric field produced by an electric dipole is called electric dipole field and is defined as the space around an electric dipole within which the effect of the dipole can be felt.
Electric lines of force. Below Fig. LAQ 7 (b) shows the section of the field in the plane of paper, containing dipole itself.

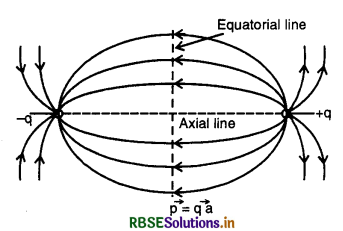
The lines of force are directed away from +q charge and towards -q charge. They are straight and open along the line containing the charges. This line is called axial line of dipole. On the broad side of the dipole, lines are curved. Near the dipole, they start from +q charge and end at -q charge, then closing their path at the ends of the dipole.

Expression for torque
Consider a uniform electric field having constant magnitude and directiori the same at all planes. Consider an electric dipole with its electric dipole moment vector, \(\vec{p}\) making an angle θ with the field. (Fig. SAQ 7).
Since \(\overrightarrow{\mathrm{E}}\) at any point is the force experienced per unit charge.

Hence, in a uniform electric field an electric field dipole experiences no net force; and therefore dipole does not undergo any translatory motion.
Torque acting on the dipole
These forces are equal in magnitude and opposite in direction, therefore, they form a couple.

From eq. (4), we have
i.e. |\(\vec{\tau}\)| = pE sin θ
(∴ qa = p = Electric Dipole Moment)
The forces acting on dipole, try to rotate the dipole clockwise and according to right hand rule of rotation, the torque acts downwards ⊥ to the plane containing \(\vec{p}\) and \(\vec{E}\)
i.e. \(\vec{\tau} \perp \vec{p}\)
or \(\vec{\tau} \perp \vec{E} \).....................(5)
The equations (4) and (5) satisfy the condition for cross-product of vector
∴ Either \(\vec{\tau}=\vec{p} \times \overrightarrow{\mathrm{E}}\) ........................(6)
or \(\vec{\tau}=\overrightarrow{\mathrm{E}} \times \vec{p}\) ......................(7)
According to right-hand rule of vector product of vectors, only the equation (6) is satisfactory.
Hence, the accepted relation is
\(\vec{\tau}=\vec{p} \times \overrightarrow{\mathrm{E}}\)
Thus, it is seen that in a uniform electric field, dipole experiences only a torque but no net force.
Maximum torque acts when θ = 90°
So τ_max = P E sin 90° = pE
Minimum torque acts when θ = 0°
τ_min = pE Sin 0° = 0
Definition of dipole moment
Since τ = pE sin θ
So if E = 1, θ = 90°, then
τ = p
or p = τ
i.e. dipole moment of an electric dipole is the torque acting on a dipole, placed at right angle to the uniform electric field of unit strength.

Question 10.
Discuss the motion of a charged particle in a uniform electric field.
Answer:
Suppose an electron carrying charge e, moving along X-axis is subjected to a uniform electric field of strength \(\overrightarrow{\mathrm{E}}\) along Y-axis.
∴ Force on the electron,
\(\overrightarrow{\mathrm{F}} = e\overrightarrow{\mathrm{E}}\)
As the electron carries negative charge, force on it is in a direction opposite to \(\overrightarrow{\mathrm{E}}\) (i.e. towards the positive plate).
Acceleration of electron 
\(\vec{a}=\frac{\text { force }}{\text { mass }}=\frac{e \overrightarrow{\mathrm{E}}}{m}\) .....................(1)
The electron moves under the combined action of its own uniform velocity (u) along X-axis and uniformly accelerated velocity along Y-axis due to the field.
At any time t, suppose the electron is at P(x,y).
Using
s = ut + \(\frac{1}{2}\) at²    
∴ x = ut    ...................(2)
and y = \(\frac{1}{2}\) at²     .................(3)
from eqn. (2), t = \(\frac{x}{u}\)

Putting in eqn. (3), we get
y = \(\frac{1}{2} a \cdot \frac{x^2}{u^2}\)
y = \(\frac{1}{2}\left(\frac{e \mathbf{E}}{m}\right) \cdot \frac{x^2}{u^2}\)
Clearly y ∝ x²
Thus, the path of charged particle is parabolic in nature.

Question 11.
Define electric flux density and electric flux. Give relation between them in different cases.
Answer:
Electric flux density. The number of electric lines of force passing normally per unit area about any point, is called electric flux density about that point. It is also called electric intensity. It is a vector quantity represented by \(\overrightarrow{\mathrm{E}}\). Its units is NC^-1.

Electric Flux. The surface integral of electric field over a surface is called electric flux linked with the surface. Thus total numbers of electric lines of force passing through a surface in a direction normal to the surface when the surface is placed inside an electric field is called electric flux. It is denoted by Φ.

Consider a small area element d \(\overrightarrow{\mathrm{S}}\) of a closed surface S. Let \(\overrightarrow{\mathrm{E}}\) be electric field at area element. Thus, electric flux through area.element is \(d \overrightarrow{\mathrm{s}}\) given by
dΦ = \(\overrightarrow{\mathrm{E}}.d \overrightarrow{\mathrm{S}}\)
(where area vector \(d \overrightarrow{\mathrm{s}}\) is a vector whose magnitude represents the area of the element and direction is normal to the element)
If θ is the angle between the direction of area element and the electric field, then,
dΦ = E dS cos θ = (E cos θ) dS
Now, E cos θ is normal component of the electric field (component of the electric field along normal to area element) and is denoted by En.

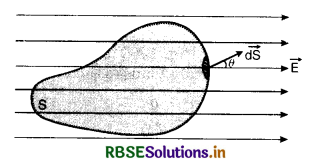
Therefore,
dΦ = \(\overrightarrow{\mathrm{E}} \cdot \overrightarrow{d \mathrm{~S}}\)
Total electric flux lined with a surface S is given by
Φ = ∫\(\overrightarrow{\mathrm{E}} \cdot \overrightarrow{d \mathrm{~S}}\)
If the surface S is closed. then total electric flux linked with the closed surface is given by
Φ = \(\oint \overrightarrow{\mathrm{E}} \cdot d \overrightarrow{\mathrm{S}}\)

Question 12.
State and prove Gauss’s theorem. What is its importance?
Answer:
Gauss’s Theorem
It states that the total electric flux through a closed surface enclosing a charge is equal to \(\frac{1}{\varepsilon_0}\) times the magnitude of the charge enclosed.
Here, ε₀ is permittivity of the free space. It may be pointed out the Gauss’s theorem is true for closed surface of any shape. Such a surface enclosing the charge is called gaussian surface.
Consider any closed surface S enclosing a charge q (Fig.). Consider an area element \(d \overrightarrow{\mathrm{s}}\) of the surface S such that its distance from the charge is r. If \(\overrightarrow{\mathrm{E}}\) is electric field at area element, then electric flux passing through the area element is given by
dΦ = \(\overrightarrow{\mathrm{E}} \cdot \overrightarrow{d \mathrm{~S}}\)
The total electric flux through the surface S is given by
Φ = \(\oint_{\mathrm{S}} \overrightarrow{\mathrm{E}} \cdot d \vec{S}\)

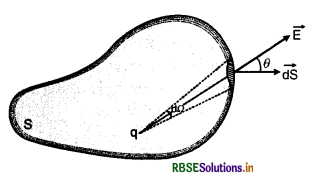
Then, mathematically, Gauss's theorem states that
Φ = \(\oint_{\mathrm{S}} \overrightarrow{\mathrm{E}} \cdot d \vec{S} = \frac{q}{\varepsilon_o}\)
Proof:
Since, \(\oint_{\mathrm{S}} \overrightarrow{\mathrm{E}} \cdot d \overrightarrow{\mathrm{S}}=\oint_{\mathrm{S}} \mathrm{E} d \mathrm{~S} \cos \theta\)
where θ is angle between \(\overrightarrow{\mathrm{E}}\) and \(\vec{d} \mathrm{~s}\). Further magnitude of electric field due to charge q, at the area element is given by
E = \(\frac{1}{4 \pi \varepsilon_0} \frac{q}{r^2}\)
Therefore,
\(\oint_{\mathrm{S}} \overrightarrow{\mathrm{E}} \cdot d \overrightarrow{\mathrm{S}}=\oint_{\mathrm{S}} \frac{1}{4 \pi \varepsilon_0} \frac{q}{r^2} d \mathrm{~S} \cos \theta\)
or \(\oint_{\mathrm{S}} \overrightarrow{\mathrm{E}} \cdot d \overrightarrow{\mathrm{S}}=\frac{q}{4 \pi \varepsilon_0} \oint_{\mathrm{S}} \frac{d \mathrm{~S} \cos \theta}{r^2}\)
For a closed surface,
\(\oint_{\mathrm{S}} \overrightarrow{\mathrm{E}} \cdot d \overrightarrow{\mathrm{S}}=\frac{q}{4 \pi \varepsilon_0} \times 4 \pi \quad\left[\because \oint_{\mathrm{S}} \frac{d \mathrm{~S} \cos \theta}{r^2}=4 \pi\right]\)
Hence Φ = \(\oint_{\mathrm{S}} \overrightarrow{\mathrm{E}} \cdot d \overrightarrow{\mathrm{S}}=\frac{q}{\varepsilon_0}\)
It proves Gauss’s theorem.
Importance of Gauss's theorem. Gauss’s theorem is of great importance. Those situations, in which calculation of electric field by applying Coulomb’s law becomes very difficult. The result can be obtained by applying Gauss’s theorem with great ease.

Question 13.
State Gauss’s law. Obtain an expression for electric field due to line charge (or infinite long wire) using this law.
Or
Using Gauss’s law, determine the electric field intensity due to a long thin wire of uniform linear charge density.
Answer:
Gauss’s law states that total electric flux over the closed surface S in vacuum is \(\frac{1}{\varepsilon_0}\) times the total charge contained inside surface S.
\(\phi_{\mathrm{E}}=\oint \overrightarrow{\mathrm{E}} \cdot \overrightarrow{d \mathrm{~S}}=\frac{q}{\varepsilon_0}\)
Electric field intensity due to a line charge.
Consider a thin charged rod with uniform linear charge density λ. We wish to find an expression for electric intensity at point P at a perpendicular distance r, from the rod. Consider a right circular cylinder of radius r and length l with the infinite long line of charge as its axis.
In surface I and III, \(\overrightarrow{\mathrm{E}}\) and \(d \overrightarrow{\mathrm{S}}\) are ⊥ to each other. In cases of surface II, \(\overrightarrow{\mathrm{E}}\) and \(d\overrightarrow{\mathrm{S}}\) are parallel to each other and hence θ = 0°.

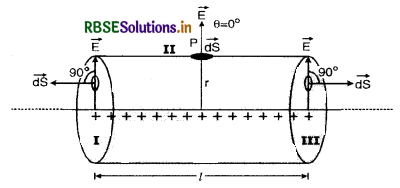
From Gauss's theorem, we have 

Question 14.
State Gauss’s theorem in electrostatics. Using this theorem, derive an expression for the electric field intensity due to an infinite plane sheet of charge density σ Cm².
Or
What is electric flux? Write its S.I. units. Using Gauss’s theorem, deduce an expression for the electric field at a point due to a uniformly charged infinite plane sheet.
Answer:
Gauss’s law states that total electric flux over the closed surface S in vacuum is \(\frac{1}{\varepsilon_0}\) times the total charge contained inside surface S.
\(\phi_{\mathrm{E}}=\oint \overrightarrow{\mathrm{E}} \cdot \overrightarrow{d \mathrm{~S}}=\frac{q}{\varepsilon_0}\)

Electric field intensity due to a line charge.
Consider a thin charged rod with uniform linear charge density λ. We wish to find an expression for electric intensity at point P at a perpendicular distance r, from the rod. Consider a right circular cylinder of radius r and length l with the infinite long line of charge as its axis.
In surface I and III, \(\overrightarrow{\mathrm{E}}\) and d \(\overrightarrow{\mathrm{S}}\) are ⊥ to each other. In cases of surface II, \(\overrightarrow{\mathrm{E}}\) and \(d\overrightarrow{\mathrm{S}}\) are parallel to each other and hence θ = 0°.

From Gauss's theorem, we have 


Electric flux density. The number of electric lines of force passing normally per unit area about any point, is called electric flux density about that point. It is also called electric intensity. It is a vector quantity represented by \(\overrightarrow{\mathrm{E}}\). Its units is NC^-1.

Electric Flux. The surface integral of electric field over a surface is called electric flux linked with the surface. Thus total numbers of electric lines of force passing through a surface in a direction normal to the surface when the surface is placed inside an electric field is called electric flux. It is denoted by Φ.

Consider a small area element \(d \overrightarrow{\mathrm{S}}\) of a closed surface S. Let \(\overrightarrow{\mathrm{E}} \) be electric field at area element. Thus, electric flux through area.element is \(d \overrightarrow{\mathrm{s}}\) given by
dΦ = \(\overrightarrow{\mathrm{E}}.d \overrightarrow{\mathrm{S}}\)
(where area vector \(d \overrightarrow{\mathrm{s}}\) is a vector whose magnitude represents the area of the element and direction is normal to the element)
If θ is the angle between the direction of area element and the electric field, then,
dΦ = E dS cos θ = (E cos θ) dS
Now, E cos θ is normal component of the electric field (component of the electric field along normal to area element) and is denoted by En.

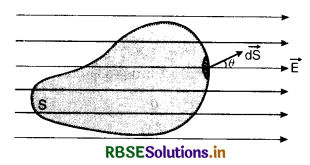
Therefore,
dΦ = \(\overrightarrow{\mathrm{E}} \cdot \overrightarrow{d \mathrm{~S}}\)
Total electric flux lined with a surface S is given by
Φ = ∫\(\overrightarrow{\mathrm{E}} \cdot \overrightarrow{d \mathrm{~S}}\)
If the surface S is closed. then total electric flux linked with the closed surface is given by
Φ = \(\oint \overrightarrow{\mathrm{E}} \cdot d \overrightarrow{\mathrm{S}}\)

Expression for electric field. Consider a non-conducting infinite thin sheet of area S having surface area charge density σ. Let P be a point at certain distance where electric field \(\overrightarrow{\mathrm{E}}\) is to be determined.
Consider a Gaussian surface passing through point P which is a cylinder passing through the sheet. Let us divide this cylinder in three sections S₁, S₂ and S₃. Consider an element of area dS in each section as shown in Fig.

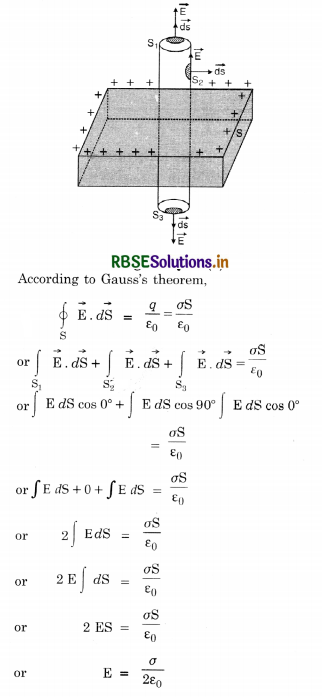
Note: For Conducting Sheet If we have a conducting thin sheet, the charge will be distributed on both the upper and lower surfaces as shown in Fig. ahead. Therefore, total charge enclosed by the cylindrical Gaussian surface will be 2σS. Hence, as explained above we will have E = σ/ε₀. That is the electric field due to an infinite conducting sheet is twice that due to a non-conducting sheet.

Question 15.
Find electric field due to charged spherical shell. At a point (i) outside the shell (ii) on the shell and (iii)    inside the shell.
Answer:
Spherical shell
A spherical shell is a hollow sphere of infinitesimally small thickness. Consider a spherical shell of radius R. Let q be charged on the shell. Let us find electric field at a point P at a distance r from the center O of the spherical shell.

Case I. When point P is lying outside the shell (i.e r > R)
From the point P, draw a Gaussian surface which will be a sphere of radius r. Let dS be small area element on the Gaussian surface P as shown in Fig. LAQ 15 (a) below.

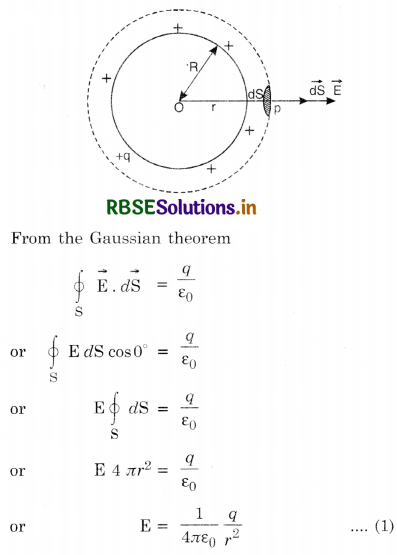
i.e. the electric field outside the spherical shell behaves as if whole charge is concentrated at the centre of the spherical shell.
In terms of surface charge density
If σ is the surface density, then
q = σ 4πR²
∴ From eq. (1), we have.
E = \(\frac{1}{4 \pi \varepsilon_0} \frac{\sigma 4 \pi \mathrm{R}^2}{r^2}\)
= \(\frac{\sigma}{\varepsilon_o} \frac{\mathrm{R}^2}{r^2}\) ........................(2)

Case II. When point P lies on the surface of spherical shell
On the surface of the shell. Fig. LAQ 15 (b).
r = R
So from equation (1), we have,
E = \(\frac{1}{4 \pi \varepsilon_0} \frac{q}{\mathrm{R}^2}\) ......................(3)
And from equation (2)
E = \(\frac{\sigma}{\varepsilon_{0}}\) .........................(4)


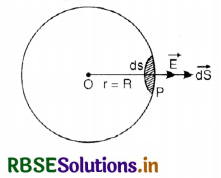
Case III When point P lies inside the spherical shell
From point P draw a gaussian surface which will be a sphere of radius r. [Fig. LAQ 15(c)]

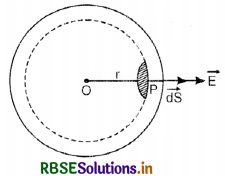
From the Gauss's theorem
\(\oint_{\mathrm{S}} \overrightarrow{\mathrm{E}} \cdot d \overrightarrow{\mathrm{S}}=\frac{0}{\varepsilon_0}\) = 0
[∵ No charge exists inside the sphereical shell]
or E = 0 .........................(5)
i.e. electric field inside the charged spherical shell is zero.
Variation of electric field E with distance
Fig. LAQ 15 (d) shows the variation of electric field with distance from the center of charged spherical shell.

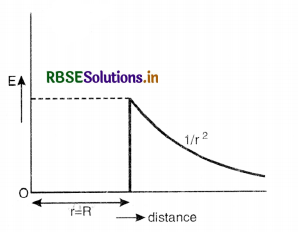
Question 16.
Find electric field due to solid sphere of charge at a point (i) outside (ii) on the surface and (iii) inside.
Answer:
Let charge q be distributed uniformly over a sphere of radius r. Let us find electric field intensity at a point P at distance r from the center O.

Case I. When point P lies outside the sphere (r > R)
Draw a Gaussian surface through point P which is a sphere of radius r. Consider a small element of area dS on the Gaussian surface at point P as shown in Fig. LAQ 16 (a).

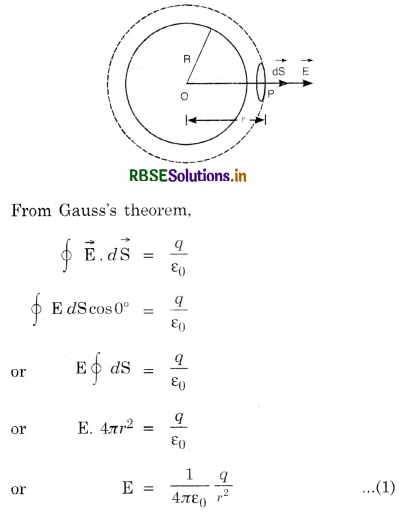
i.e. the electric field outside the charged sphere behaves as if whole charge is concentrated at the center of the sphere.
In terms of volume charge density
If ρ is the volume density of charge, then
q = pV = ρ\(\frac{4}{3}\)πR³
From Eq. (1), we have
E =\( \frac{1}{4 \pi \varepsilon_0} \frac{\rho}{r^2} \cdot \frac{4}{3} \pi \mathrm{R}^3\)
= \(​​\) .....................(2)

Case II. When point P lies on surface of the sphere
On the surface of the sphere, r = R (Fig. 1AQ 16 (b))
∴ From Eq. (1), we have 
E = \(\frac{1}{4 \pi \varepsilon_0} \frac{q}{\mathrm{R}^2}\) .......................(3)
And from (2), we have
E = \(\frac{\rho}{\varepsilon_0} \cdot \frac{\mathrm{R}}{3}\) ......................(4)

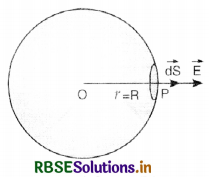
Case III. When point P lies inside the sphere
In this case, the Gaussian surface is a sphere of radius r. Let q' be the charge enclosed by the Gaussian surface Fig. LAQ 16 (c).
From Gauss’s theorem


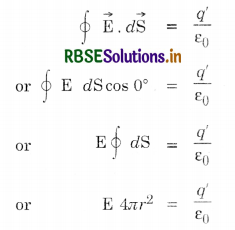
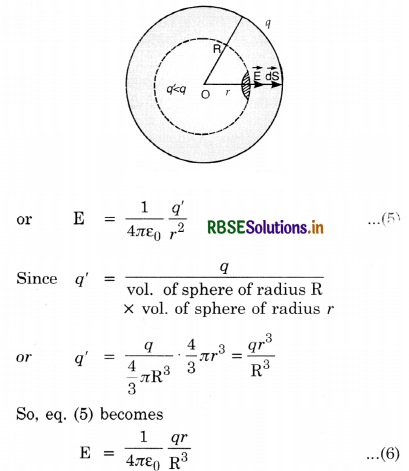
The variation of electric field \(\overrightarrow{\mathbf{E}}\) with distance 
Fig. LAQ 16 (d) shows the variation of electric field with distance from the center of charged sphere.

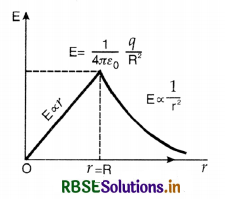
Question 17.
Using Gauss’s theorem, show mathematically that for any point outside the shell, the field due to a uniformly charged thin spherical shell is the same as if the entire charge is concentrated at the center. Why do you expect the electric field inside the shell to be zero according to this theorem?    
Or
Define electric flux. Write its S.I. units. Using Gauss’s theorem, derive an expression for the electric field intensity at a point outside the charged spherical shell.
Answer:
Spherical shell
A spherical shell is a hollow sphere of infinitesimally small thickness. Consider a spherical shell of radius R. Let q be charge on the shell. Let us find electric field at a point P at a distance r from the center O of the spherical shell.

Case I. When point P is lying outside the shell (i.e r > R)
From the point P, draw a Gaussian surface which will be a sphere of radius r. Let dS be small area element on the Gaussian surface P as shown in Fig. LAQ 15 (a) below.

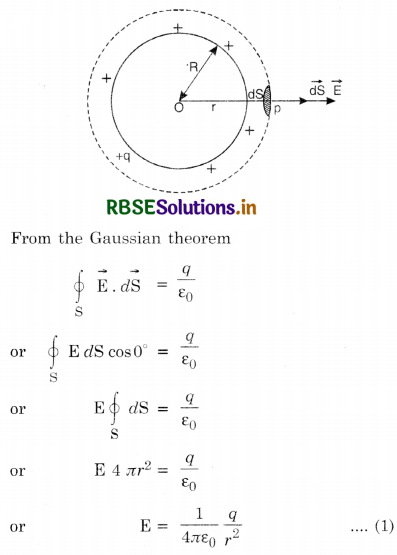
i.e. the electric field outside the spherical shell behaves as if whole charge is concentrated at the center of the spherical shell.
In terms of surface charge density
If σ is the surface density, then
q = σ 4πR²
∴ From eq. (1), we have.
E = \(\frac{1}{4 \pi \varepsilon_0} \frac{\sigma 4 \pi \mathrm{R}^2}{r^2}\)
= \(​​\) ........................(2)

Case II. When point P lies on the surface of spherical shell
On the surface of the shell. Fig. LAQ 15 (b).
r = R
So from equation (1), we have,
E =\( \frac{1}{4 \pi \varepsilon_0} \frac{q}{\mathrm{R}^2}\) ......................(3)
And from equation (2)
E = \(\frac{\sigma}{\varepsilon_{0}}\) .........................(4)


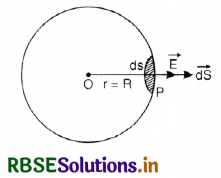
Case III When point P lies inside the spherical shell
From point P draw a gaussian surface which will be a sphere of radius r. [Fig. LAQ 15(c)]

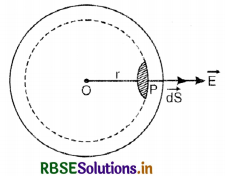
From the Gauss's theorem
\(\oint_{\mathrm{S}} \overrightarrow{\mathrm{E}} \cdot d \overrightarrow{\mathrm{S}}=\frac{0}{\varepsilon_0}\) = 0
[∵ No charge exists inside the spherical shell]
or E = 0 .........................(5)
i.e. electric field inside the charged spherical shell is zero.
Variation of electric field E with distance
Fig. LAQ 15 (d) shows the variation of electric field with distance from the center of charged spherical shell.

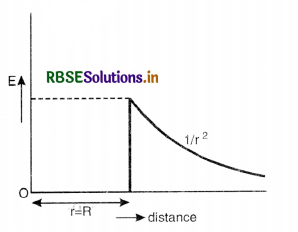
Question 18.
Define the term electric dipole moment. Give its units. Derive an expression for maximum torque acting on the electric dipole when held in a uniform electric field.
Answer:
Electric dipole and its units: 
Electric dipole. A system of two equal and opposite charges separated by certain distance is called electric dipole.

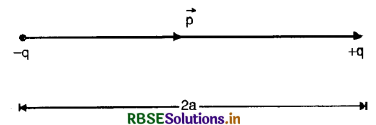
Fig. LAQ 7 (a) shows an electric dipole consisting of two equal and opposite point charges (± q) separated by a small distance 2a.
Dipole moment (\(\overrightarrow{\mathrm{P}}\)). It is defined as the product of magnitude of either charge and the distance between two charges.
i.e. \(\overrightarrow{\mathrm{P}} = q \overrightarrow{2 a}\)
The direction of \(\overrightarrow{p}\) is from -ve charge to +ve charge.
Units: In S.I.,
The unit of \(\overrightarrow{p}\) is Coulomb-metre (Cm).
Dipole field. The electric field produced by an electric dipole is called electric dipole field and is defined as the space around an electric dipole within which the effect of the dipole can be felt.

Electric lines of force. Below Fig. LAQ 7 (b) shows the section of the field in the plane of paper, containing dipole itself.

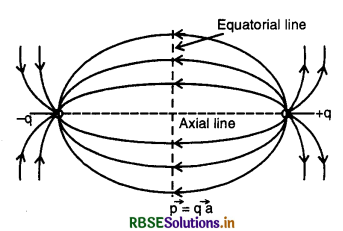
The lines of force are directed away from +q charge and towards -q charge. They are straight and open along the line containing the charges. This line is called axial line of dipole. On the broad side of the dipole, lines are curved. Near the dipole, they start from +q charge and end at -q charge, then closing their path at the ends of the dipole.

Expression for torque
Consider a uniform electric field having constant magnitude and directiori the same at all planes. Consider an electric dipole with its electric dipole moment vector, \(\vec{p}\) making an angle θ with the field. (Fig. SAQ 7).
Since \(\overrightarrow{\mathrm{E}}\) at any point is the force experienced per unit charge.

Hence, in a uniform electric field an electric field dipole experiences no net force; and therefore dipole does not undergo any translatory motion.
Torque acting on the dipole
These forces are equal in magnitude and opposite in direction, therefore, they form a couple.

From eq. (4), we have
i.e. |\(\vec{\tau}\)| = pE sin θ
(∴ qa = p = Electric Dipole Moment)
The forces acting on dipole, try to rotate the dipole clockwise and according to right hand rule of rotation, the torque acts downwards ⊥ to the plane containing \(\vec{p}\) and \(\vec{E}\)
i.e. \(\vec{\tau} \perp \vec{p}\)
or \(\vec{\tau} \perp \vec{E}\) .....................(5)
The equations (4) and (5) satisfy the condition for cross-product of vector
∴ Either \(\vec{\tau}=\vec{p} \times \overrightarrow{\mathrm{E}}\) ........................(6)
or \(\vec{\tau}=\overrightarrow{\mathrm{E}} \times \vec{p}\) ......................(7)
According to right-hand rule of vector product of vectors, only the equation (6) is satisfactory.
Hence, the accepted relation is
\(\vec{\tau}=\vec{p} \times \overrightarrow{\mathrm{E}}\)
Thus, it is seen that in a uniform electric field, dipole experiences only a torque but no net force.
Maximum torque acts when θ = 90°
So τ_max = P E sin 90° = pE
Minimum torque acts when θ = 0°
τ_min = pE Sin 0° = 0
Definition of dipole moment
Since τ = pE sin θ
So if E = 1, θ = 90°, then
τ = p
or p = τ
i.e. dipole moment of an electric dipole is the torque acting on a dipole, placed at right angle to the uniform electric field of unit strength.

Question 19.
A charge q is placed at the center of the line joining two equal charges Q, Show that the system of three charges will be in equilibrium if q =-\(\frac{Q}{4}\).
Answer:
Let the two charges each of magnitude Q be placed at points A and B at a distance r from each other. Let charges q be placed at O at the center of A and B on shown in figure LAQ 19. Charges A and B exert equal and opposite force on charge q, so the charge q is in equilibrium.
For equilibrium, of'charge Q at A

HOTS QUESTIONS

Question 1.
On what range of separation between the charges, the Coulomb’s force law is found valid?
Answer:
Experimentally the Coulomb’s force law is found to remain valid for a separation between the charges of the order of 10^-15 m to macroscopic distances of several kilometers. It is believed that the law should hold good, however large the separation between the charges may be.

Question 2.
A charged ball B hangs from a silk thread S, which makes an angle θ with a large charged conducting sheet P as shown in Fig. HQ 2 (a). Show that the surface charge density of the sheet is proportional to tan θ.

Answer:
The electric field at any point around the sheet P is given by
E = \(\frac{\sigma}{\varepsilon_0}\) (σ is surface charge density)
The force on ball B having charge q due to charge sheet P is given by Fig. HQ. 2(b)

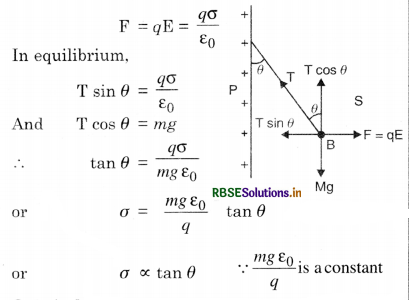
Question 3.
A charge is situated outside an uncharged hollow conductor experiences a force if another charge B is placed inside the conductor, but B does not experience any force. Why? Does it not violate the third law of motion?
Answer:
It happens because there is an electric field over A but no electric field over B as it lies inside a hollow conductor. Third law of motion is not violated because force arises between A and the hollow sphere, the charge B is simply an internal part of the sphere.

Question 4.
In the given figure HQ 4, calculate the total flux of the electrostatic field through the sphere S₁ and S₂. The wire AB, as shown here, has a linear charge density λ given by λ = kx, where x is the distance measured along the wire, from the end A.

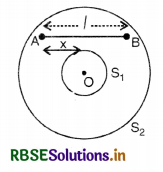
Answer:
Since linear charge density λ (λ = kx) depends on distance, so it is not constant. Thus consider a small element dx having charge dq, then
dq = λ dx = kx dx
∴ q = λdq = k\( \int_0^l x d x=\frac{k l^2}{2}\)
Electric flux through Gaussian surface is:
\(\phi_1=\oint \overrightarrow{\mathrm{E}} \cdot d \overrightarrow{\mathrm{S}}=\frac{q}{\varepsilon_0}=0\) (∵ q = 0 inside s₁)
Electric flux through Gaussian surface S₂ is:
\(\phi_2=\oint \overrightarrow{\mathrm{E}} \cdot d \overrightarrow{\mathrm{S}}=\frac{q}{\varepsilon_0}=\frac{k l^2}{2 \varepsilon_0} \left(\because q=\frac{k l^2}{2}\right)\)
Total electric flux thorugh the spheres S₁ and S₂
Φ = Φ₁ + Φ₂
or Φ = 0 + \(\frac{k l^2}{2 \varepsilon_0}=\frac{k l^2}{2 \varepsilon_0}\)

Question 5.
Can two balls have same kind of charge on them attract each other? Explain.
Answer:
Yes, two balls having same kind of charge can attract each other if charge possessed by one ball is very large as compared to that on the other ball because when two charged balls are placed near each other, they induced opposite charges on the faces of each other. On the ball having small amount of charge, very large amount of induced charge (opposite in nature) is produced, two balls get attracted towards each other.

Question 6.
We define the electric field strength as:
\(\overrightarrow{\mathrm{E}}=\operatorname{limit}_{q_0 \rightarrow 0} \frac{\overrightarrow{\mathrm{F}}}{q_0}\)
Keeping in mind that the minimum value of the charge that exist in nature cannot be less than e = 1.0 x 10^-19 C, how can we justify the above definition?
Answer:
The minimum value of charge that exists in nature, that is 1.0 x 10^-19 C is very very small as compared to the actual charges we deal with. Therefore, in general, the condition q₀ → 0 is satisfied. However in microscopic cases, for example, while dealing with charges within the atom or nucleus, the definition may not be strictly applicable.

Question 7.
A metal sheet is moved with constant acceleration 'a’ parallel to its plane. Does any charge develop on its surfaces, which are perpendicular to its motion?
Answer:
As the metal plate is accelerated, the electrons inside also possess the same acceleration. A force may be applied on an electron, only when an electric field is created. So there must develop charges on the faces that are perpendicular to the direction of motion, so that there develops an electric field inside the metal plate. The front face will be charged positively, and the rear one negatively. If E is the intensity of electric field, then surface density of charge σ developed is given by
e E = ma
or e\( \frac{\sigma}{\varepsilon_0}\) = ma [∵ E = \(\frac{\sigma}{\varepsilon_0}\)]
or σ = \(\frac{\varepsilon_0 m a}{e}\)