RBSE Class 12 Geography Practical Notes Chapter 2 आंकड़ों का प्रक्रमण

These comprehensive RBSE Class 12 Geography Notes Practical Chapter 2 आंकड़ों का प्रक्रमण will give a brief overview of all the concepts.

RBSE Class 12 Geography Practical Notes Chapter 2 आंकड़ों का प्रक्रमण

→ आँकड़ों के संगठन तथा प्रस्तुतीकरण से आँकड़ों का प्रक्रमण आसान हो जाता है। आंकड़ों के विश्लेषण के लिए केन्द्रीय प्रवृत्ति के माप, प्रकीर्णन के माप तथा सम्बन्ध के माप आदि सांख्यिकीय विधियों का उपयोग किया जाता है। केन्द्रीय प्रवृत्ति के माप जैसे-माध्य, माध्यिका तथा बहुलक पर्यवेक्षणों के समूह का आदर्श मूल्य प्रस्तुत करते हैं। प्रकीर्णन के माप जैसे-विस्तार, मानक विचलन, माध्य विचलन, प्रसरण तथा विचरण गुणांक एवं लारेंज वक्र आदि आँकड़ों की आन्तरिक विषमताओं को दर्शाते हैं। सह सम्बन्ध के माप दो या दो से अधिक घटनाओं, जैसे-वर्षा तथा बाढ़ की घटना साहचर्य की गहनता को प्रस्तुत करते हैं। 

→ केन्द्रीय प्रवृत्ति के माप
वर्षा, ऊँचाई, जनसंख्या का घनत्व, उपलब्धियों के स्तर या आयु वर्ग में विभिन्नताओं के वितरण का केन्द्र ज्ञात करने वाली सांख्यिकीय विधियों को केन्द्रीय प्रवृत्ति के माप से सम्बोधित किया जाता है। दूसरे शब्दों में, सांख्यिकी में सम्पूर्ण समंक श्रेणी की केन्द्रीय प्रवृत्ति को सरल और संक्षिप्त रूप से अभिव्यक्त करने वाला प्रतिनिधि मूल्य केन्द्रीय प्रवृत्ति की माप कहलाती है।
केन्द्रीय प्रवृत्ति की द्योतक संख्या आँकड़ों के समूह की प्रतिनिधि संख्या होती है। केन्द्रीय प्रवृत्ति के कई माप हैं; जैसे-माध्य, माध्यिका तथा बहुलक आदि। केन्द्रीय प्रवृत्ति के माप को सांख्यिकीय औसत के नाम से भी जानते हैं। 

→ माध्य (Mean)
माध्य वह मान है जो सभी मूल्यों के योग को कुल पदों की संख्या से विभाजित करके प्राप्त किया जाता है। दूसरे शब्दों में किसी चर के विभिन्न मूल्यों का साधारण अंकगणितीय औसत माध्य कहलाता है।

→ माध्य ज्ञात करने की विधियाँ
वर्गीकृत व अवर्गीकृत दोनों प्रकार के आँकड़ों के लिए माध्य प्रत्यक्ष व अप्रत्यक्ष विधियों के द्वारा ज्ञात किया जाता है। 

 

→ अवर्गीकृत आँकड़ों से माध्य की गणना
अवर्गीकृत आँकड़ों से माध्य की गणना प्रत्यक्ष या अप्रत्यक्ष विधि से की जाती है। 

→ प्रत्यक्ष विधि
अवर्गीकृत आँकड़ों से प्रत्यक्ष विधि द्वारा माध्य की गणना करने के लिए पदों के सभी मूल्यों को जोड़कर पदों की कुल संख्या से भाग देते हैं। इस प्रकार माध्य की गणना निम्नांकित सूत्र द्वारा की जाती है
X̄ = \(\frac{\Sigma x}{\mathrm{~N}}\)
जहाँ, X̄ = माध्य
Σ = मापों के सभी मूल्यों का योग
x = मापों की किसी श्रेणी में एक अपरिष्कृत समंकं 
Σx = मापों की सभी श्रेणी के अपरिष्कृत समंकों का योग
N = श्रेणी के पदों की संख्या 

→ अप्रत्यक्ष विधि
श्रेणी में जहाँ पदों की संख्याएँ बहुत अधिक होती हैं, वहाँ अप्रत्यक्ष विधि से माध्य की गणना की जाती है। इस विधि में एक स्थिरांक (कल्पित माध्य) को सभी मूल्यों से घटाने पर पदों का संख्या विस्तार कम हो जाता है। कल्पित माध्य द्वारा संख्याओं के विस्तार को कम करने की क्रिया को 'कूट पद्धति' कहते हैं।
अप्रत्यक्ष विधि से माध्य की गणना निम्न सूत्र से की जाती है
X̄ = A + \(\frac{\Sigma d}{\mathrm{~N}}\)
जहाँ, A = घटाया हुआ स्थिरांक (कल्पित माध्य)
Σd = स्थिरांक घटाए हुए मूल्यों का योग
N = उक्त श्रेणी में कुल प्रेक्षणों की संख्या

→ वर्गीकृत आँकड़ों से माध्य की गणना
वर्गीकृत आँकड़ों से माध्य की गणना प्रत्यक्ष या अप्रत्यक्ष विधियों से की जाती है।

→ प्रत्यक्ष विधि:
प्रत्यक्ष विधि से वर्गीकृत आँकड़ों के लिए माध्य की गणना करते समय प्रत्येक वर्ग के मध्य बिन्दुओं से सम्बन्धित आवृत्ति ()f को गुणा किया जाता है fx (जहाँ x मध्य बिन्दु है) के सभी मानों को जोड़कर प्राप्त Σfx में पदों की संख्या (N) से भाग दिया जाता है। इस प्रकार निम्नांकित सूत्र द्वारा माध्य की गणना की जाती है
X̄ = \(\frac{\Sigma f x}{\mathrm{~N}}\)
जहाँ, X̄ = माध्य
f = आवृत्ति 
x = वर्ग अन्तराल का मध्य बिन्दु
N = पदों की संख्या (इसे Σf भी कहते हैं) 

→ अप्रत्यक्ष विधि:
वर्गीकृत आँकड़ों से अप्रत्यक्ष विधि द्वारा माध्य की गणना निम्नांकित सूत्र से की जाती है
X̄ = A + \(\frac{\Sigma f d}{\mathrm{~N}}\)
जहाँ, A = कल्पित माध्य
f = आवृत्ति
d = कल्पित माध्य से पद का विचलन
N = कुल पदों की संख्या अथवा Σf 

→ माध्यिका (Median)
जब किसी श्रेणी के पदों को आरोही अथवा अवरोही क्रम में रखा जाता है, तो मध्य का पद माध्यिका कहलाती है। अन्य शब्दों में, माध्यिका उस कोटि का मान होती है जो व्यवस्थित श्रेणी को दो बराबर भागों में विभाजित करती है। 

→ माध्यिका ज्ञात करने की विधियाँ
अवर्गीकृत आँकड़ों तथा वर्गीकृत आँकड़ों के लिए माध्यिका की गणना अलग-अलग सूत्र द्वारा की जाती है।

→ अवर्गीकृत आँकड़ों के लिए माध्यिका की गणना
आँकड़े अवर्गीकृत होने पर उन्हें बढ़ते या घटते क्रम में व्यवस्थित कर लिया जाता है। इस व्यवस्थित श्रेणी में मध्यवर्ती पद के मान की स्थिति ज्ञात करके माध्यिका प्राप्त की जाती है। माध्यिका की गणना करने के लिए निम्नांकित सूत्र का प्रयोग किया जाता है
M = \(\frac{\mathrm{N}+1}{2}\) वाँ पद

→ वर्गीकृत आँकड़ों से माध्यिका की गणना
आँकड़े वर्गीकृत होने पर उस बिन्दु का मान ज्ञात करना होता है, जहाँ कोई व्यक्त प्रेक्षण किसी वर्ग के माध्य में स्थित होता है। इस प्रकार माध्यिका की गणना निम्नांकित सूत्र के द्वारा की जाती है
M = l + \(\frac{i}{f}\)(\(\frac{\mathrm{N}}{2}\) - C)
जहाँ, M = वर्गीकृत आँकड़ों के लिए माध्यिका
l = माध्यिका वर्ग की निम्न सीमा ।। 
i = वर्ग अन्तराल
f = माध्यिका वर्ग की आवृत्ति .
N = आवृत्ति का कुल योग अथवा पदों की संख्या
c = माध्यिका वर्ग से ठीक पहले वाले वर्ग की संचयी आवृत्ति 

→ बहुलक (Mode):

• बहुलक पद का वह मान है जिसकी बारम्बारता या आवृत्ति सबसे अधिक होती है। किसी श्रेणी में एक या एक से अधिक बहुलक हो सकते हैं। यदि किसी श्रेणी में एक मान की पुनरावृत्ति अधिक है तो एक बहुलक, दो मान की पुनरावृत्ति समान है तो द्वि-बहुलक तथा तीन मानों की पुनरावृत्ति समान है तो उसे त्रि-बहुलक श्रेणी कहते हैं। ऐसे ही कई मानों की समान बार पुनरावृत्ति होने पर उसे बहु-बहुलक श्रेणी कहते हैं। किसी श्रेणी में एक भी मान की पुनरावृत्ति न होने पर वह बहुलक-रहित श्रेणी कहलाती है।
• अवर्गीकृत श्रेणी में बहुलक की गणना निरीक्षण एवं समूहन विधि द्वारा की जाती है जबकि वर्गीकृत श्रेणी में बहुलक ज्ञात करने के लिए अग्र सूत्रों का प्रयोग करते हैं

1. Z = L + \(\frac{f_{1}-f_{0}}{2 f_{1}-f_{0}-f_{2}}\) × i

2. Z = L + \(\frac{f_{2}}{f_{0}+f_{2}}\) × i

• Z = बहुलक
• L = बहुलक वर्ग की निम्न सीमा
• f₁ = बहुलक वर्ग की आवृत्ति
• f₀ = बहुलक वर्ग से पहले वाले वर्ग की आवृत्ति
• f₂ = बहुलक वर्ग से बाद वाले वर्ग की आवृत्ति
• i = वर्ग-अन्तराल 

किसी समंक के समान्तर माध्य से उनके विभिन्न मूल्यों के विचलनों के वर्गों के समान्तर माध्य के वर्गमूल को मानक विचलन कहते हैं।

→ प्रकीर्णन के माप:

• आँकड़ों के वितरण का उपयुक्त प्रतिरूप प्राप्त करने के लिए केन्द्रीय प्रवृत्ति के माप के साथ प्रकीर्णन या बिखराव या विषमता के माप की भी आवश्यकता होती है।
• प्रकीर्णन से तात्पर्य केन्द्रीय प्रवृत्ति के माप से विभिन्न मूल्यों के बिखराव अथवा विषमता की मात्रा से है। यह माप औसत मूल्य से किसी इकाई अथवा संख्यात्मक मान की विषमता की प्रवृत्ति का मापन करता है। 

→ प्रकीर्णन के मापन की विधियाँ
प्रकीर्णन के मापन की कई विधियाँ हैं

• विस्तार (R),
• चतुर्थक विचलन,
• माध्य विचलन,
• मानक विचलन (SD) तथा विचरण गुणांक (CV)
• लॉरेंज वक्र।

लेकिन इसमें विस्तार (R) के साथ-साथ प्रकीर्णन के सापेक्ष माप के रूप में मानक विचलन तथा प्रकीर्णन के सापेक्षिक माप के रूप में विचरण गुणांक, प्रकीर्णन के सबसे अधिक प्रचलित माप हैं। 

→ विस्तार (Range):
किसी श्रेणी में अधिकतम व न्यूनतम मूल्य के अन्तर को विस्तार (Range) कहते हैं। इस प्रकार यह किसी श्रेणी में सबसे. छोटे से लेकर सबसे बड़े माप के बीच अन्तर है। विस्तार की गणना के लिए निम्नांकित सूत्र का प्रयोग किया जाता है- .
R = L - S 
जहाँ, R = विस्तार
L = अधिकतम मान (सबसे बड़ा पद)
S = न्यूनतम मान (सबसे छोटा पद) 
प्रकीर्णन के माप के रूप में विस्तार (R) का मान पूर्णत: दो चरम मूल्यों पर आधारित होता है। जिसके कारण समूची समंक श्रेणी की बनावट को समझना सम्भव नहीं है। 

→ मानक विचलन (Standard Deviation):
प्रकीर्णन के माप के रूप में मानक विचलन (SD) सबसे अधिक प्रचलित माप है। किसी समंक के समान्तर माध्य से उसके विभिन्न मूल्यों के विचलनों के वर्गों के समान्तर माध्य के वर्गमूल को मानक विचलन कहते हैं। मानक विचलन प्रकीर्णन का सर्वाधिक स्थिर माप है। मानक विचलन के लिए ग्रीक अक्षर (लघु सिग्मा) का प्रयोग किया जाता है। अवर्गीकृत श्रेणी में मानके विचलन के लिए निम्नांकित सूत्र का प्रयोग किया जाता है
σ = \(\sqrt{\frac{\Sigma x^{2}}{\mathbf{N}}}\)
जहाँ, σ = मानक विचलन 
Σx² = विचलनों के वर्गों का योग
N = पदों की संख्या
इस सूत्र का प्रयोग अवर्गीकृत आँकड़ों का मानक विचलन ज्ञात करने के लिए किया जाता है। विचलन वर्गों के योग में N का भाग देने पर प्राप्त मूल्य वर्ग प्रसरण कहलाता है अर्थात् प्रसरण का वर्गमूल ही मानक विचलन होता है।

→ वर्गीकृत आँकड़ों का मानक विचलन
वर्गीकृत आँकड़ों का मानक विचलन ज्ञात करने के लिए निम्नांकित सूत्र का प्रयोग किया जाता है
σ = i × \(\sqrt{\frac{\Sigma f x^{2}}{\mathrm{~N}}-\left(\frac{\Sigma f x}{N}\right)^{2}}\)
जहाँ, σ = मानक विचलन
i = वर्ग-विस्तार
N = आवृत्तियों का कुल योग
f = आवृत्ति
dx = कल्पित माध्य से पद विचलन

→ विचलन गुणांक (CV):
विचलन गुणांक मानक विचलन के माध्यम को माध्य के प्रतिशत के रूप में अभिव्यक्त करता है। विचलन गुणांक ज्ञात करने के लिए निम्नांकित सूत्र को उपयोग में लाया जाता है

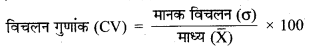
→ सह-सम्बन्ध (Correlation)
जब कोई दो चर मूल्य परस्पर एक दिशा में या विपरीत दिशा में घटने-बढ़ने की प्रवृत्ति रखते हैं तो ऐसी स्थिति में उनके मध्य एक विशेष प्रकार का सम्बन्ध पाया जाता है। इस सम्बन्ध को ही सह-सम्बन्ध कहते हैं। 

→ सह-सम्बन्ध की दिशा
जब दोनों चरों की दिशा एक हो, तो धनात्मक सह-सम्बन्ध होता है तथा जब दोनों चरों के मध्य की दिशा विपरीत हो, तो ऋणात्मक सह-सम्बन्ध होता है। 

→ सह-सम्बन्ध की गहनता
सह-सम्बन्ध की दिशा की दृष्टि से इसका अधिकतम विस्तार -1 से शून्य की ओर होते हुए +1 तक होता है। सह-सम्बन्ध पूरा ± 1 होने पर (धनात्मक या ऋणात्मक) इसे पूर्ण सह-सम्बन्ध कहते हैं। इस प्रकार गहनतम सह-सम्बन्ध के दो विपरीत सिरों के मध्य शून्य (0) सह-सम्बन्ध स्थित होता है, जहाँ पर चरों के मध्य सह-सम्बन्ध का अभाव पाया जाता है।

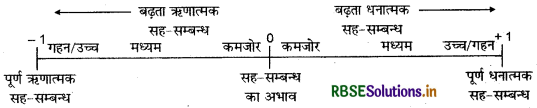
→ सह-सम्बन्ध की दिशा व गहनता का विस्तार
इसे निम्न रैखिक चित्र के द्वारा प्रदर्शित किया जा सकता है

→ पूर्ण धनात्मक सह-सम्बन्ध
जब सरल रेखा प्रकीर्ण आरेख के निचले बाएँ से ऊपरी दाएँ भाग की ओर जाती है, तो यह पूर्ण धनात्मक सह-सम्बन्ध कहलाता है जिसका मान +1:00 होता है। 

→ पूर्ण ऋणात्मक सह-सम्बन्ध
जब सरल रेखा प्रकीर्ण आरेख के ऊपरी बाएँ भाग से निचले दाएँ भाग की ओर जाती है, तो यह पूर्ण ऋणात्मक सह-सम्बन्ध कहलाता है जिसका मान - 1.00 होता है।

→ शून्य सह-सम्बन्ध
जब दोनों चरों के मध्य कोई सह-सम्बन्ध नहीं होता तो उसे शून्य सह-सम्बन्ध अथवा सह-सम्बन्ध का अभाव कहते हैं। 

→ अन्य सह-सम्बन्ध
पूर्ण सह-सम्बन्ध (±1) व शून्य सह-सम्बन्ध के बीच साहचर्य की सामान्य प्रवृत्ति मिलती है, जिन्हें कमजोर, मध्यम व गहन सह-सम्बन्ध कहा जाता है। प्रकीर्णन या बिखराव अधिक होने से सह-सम्बन्ध कमजोर, प्रकीर्णन कम होने से सह-सम्बन्ध गहन होता है। 

→ सह-सम्बन्ध की गणना करने की विधि
स्पीयरमैन ने कोटि सह-सम्बन्ध के आधार पर सह-सम्बन्ध की गणना के लिए निम्नांकित सूत्र का प्रयोग किया है
ρ = 1 - \(\frac{6\left[\sum D^{2}\right]}{\mathrm{N}\left(\mathrm{N}^{2}-1\right)}\)
जहाँ, ρ(रो - rho) = कोटि सह-सम्बन्ध
ΣD² = कोटियों के अन्तर के वर्गों का योग
N = X - Y युग्मों की संख्या