RBSE Class 10 Science Important Questions Chapter 12 Electricity

 

Question 1.    
Ohm x  Meter is the unit of which of the following physical quantity ?
(a) Resistance
(b) Resistivity
(c) Current
(d) Potential Difference
Answer:
(b) Resistivity

 

 

Question 2. 
Value of charge on an electron is 1.6 x 10^-19 coulomb. The no. of electrons flowing in a wire of 1 A current in one second is -
(a) 0.625 x 10^-19 
(b) 1.6 x 10^-19  
(c) 1.6 x 10^-19    
(d) 0.625 x 10⁺¹⁹ 
Answer:
(d) 0.625 x 10⁺¹⁹

 

Question 3.    
How much work is done to carry a 1 C charge between two points of 6 V potential difference ?
(a) 24 J    
(b) 6 J
(c) 12 J    
(d) 3 J
Answer:
(b) 6 J

 

Question 4.    
When resistance wire of different resistors are joined in series in an electric circuit then in each resistance -
(a) Value of current and potential difference is different.
(b) Value of current and potential difference is same
(c) Current is same but potential difference is different
(d) Value of current is different but potential difference is same in each
Answer:
(a) Value of current and potential difference is different.

 

Question 5.    
The device through which value of current is measured in an electric circuit is -
(a) Ammeter    
(b) Voltmeter
(c) Ohm meter    
(d) None of these
Answer:
(c) Ohm meter

 

 

Question 6.    
The specific resistance of a conductor depends upon - 
(a) Length of conductor
(b) Area of cross - section of conductor
(c) Matter of conductor
(d) Structure of conductor
Answer:
(c) Matter of conductor

 

Question 7.    
The value of current in ampere at a point when 30 coulomb of charge is flows in an electric circuit for 3 secs is -
(a) 0.1    
(b) 10
(c) 90    
(d) 33
Answer:
(b) 10

 

Question 8.    
The resistance of a 10 m long wire is 15 Ohm. If its length is reduced to 5 m, then the resistance of wire in Ohm will be -
(a) 75    
(b) 15
(c) 25    
(d) 30
Answer:
(a) 75    

 

 

 

Question 1. 
In the given circuit diagram, find the current I, flowing with 10 Ω resistance.

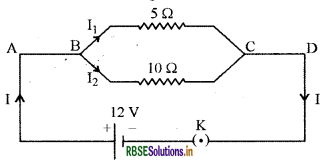
Answer:
\(I_{2}=\frac{V}{R}\)
\(\mathrm{I}_{2}=\frac{10}{12}\)
I₂ = 1.2 A.

 

Question 2. 
Write two function of battery in vehicle.
Answer:

 

Question 3. 
A 0.25 ampere current flows through the filament of an electric bulb for 20 minutes. Find the magnitude of the electric charge flowing through the electric circuit.
Answer: 
I = 0.25 A, t = 20 min = 1200 sec.
We know, Q = It
= 0.25 x 1200 
Charge = 300 columb.

 

 

Question 4. 
A 12 Ω resistance is cut into thru equal parts and then connected in triangular form. Determine the equivalent resistance between two ends of any side of the triangle.
Answer:

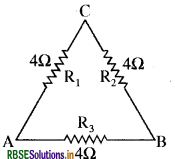
The resistance between points A and B. R₁ and R₂ are in the series, therefore
\(R=R_{1}+R_{2}\)
R = 4 + 4 = 8 Ω
\(\begin{aligned} &\frac{1}{\mathrm{R}^{\prime}}=\frac{1}{\mathrm{R}}+\frac{1}{\mathrm{R}_{3}} \\ &\frac{1}{\mathrm{R}^{\prime}}=\frac{1}{8}+\frac{1}{4} \\ &\frac{1}{\mathrm{R}^{\prime}}=\frac{1+2}{8}=\frac{3}{8} \end{aligned} \mathrm{R}^{\prime}=\frac{8}{3}\)
= 2.66 Ω

 

Question 5.
 2 Ω, 3 Ω and 6 Ω can be connected in which manner so that the total resistance of the combination is 1 Ω.
Answer: 
When the three resistances are connected in parallel, then, their combined resistance is 1 Ω.
\(\begin{aligned} &\frac{1}{\mathrm{R}}=\frac{1}{\mathrm{R}_{1}}+\frac{1}{\mathrm{R}_{2}}+\frac{1}{\mathrm{R}_{3}} \text { or } \frac{1}{\mathrm{R}}=\frac{1}{2}+\frac{1}{3}+\frac{1}{6} \\ &\frac{1}{\mathrm{R}}=\frac{3+2+1}{6}=\frac{6}{6} \end{aligned} \)
R = 1 Ω

 

Question 6. 
The resultant resistance in the given electric circuit is -

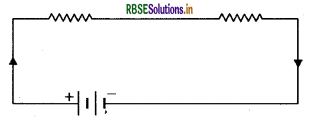
Answer: 
In the circuit the resistance is connected in series.
R = R₁ + R₂
R = 2 + 2 = 4 Ω

 

Question 7. 
Write Ohm’s law.
Answer: 
Ohm’s Law states that, “The electric current flowing through a conductor is directly proportional to the potential difference across the ends of the conductors.”
Hence, V  ∝ I or V = IR (Here R is a constant.)

 

Question 8. 
What is electric energy ?
Answer: 
It is the work done by the electricity to maintain current in an electric circuit.

 

Question 9. 
What is the SI unit of resistance and what is its symbol?
Answer: 
SI unit of resistance is ‘ohm’ and it is represented by a Greek word Ω.

 

Question 10. 
What is variable resistance?
Answer: 
A component used to regulate current without changing the voltage source is called variable resistance.

 

Question 11. 
What is resistance ?
Answer: 
It is the property of a conductor to resist the flow of charges through it.

 

 
 Question 12. 
 What is ‘resistor’ ?
Answer: 
A conductor having some appreciable resistance is called a resistor.

 

Question 13. 
What is a poor conductor ?
Answer: 
A component of identical size that offers a higher resistance is a poor conductor. 

 

Question 14. 
What is the unit of electric charge?
Answer:
Coulomb.

 

Question 15. 
Kilowatt hour is the unit of what?
Answer: 
Electric energy.

 

Question 16. 
Define 1 Kilowatt hour.
Answer: 
It is the amount of energy consumed when an electrical power of 1 KW is used for 1 hour.

 

Question 17. 
Write the SI unit of electric current.
Answer:

Ampere.

 

 

Question 18.

How does electric fuse protects the electric circuit and appliances ?
Answer: 
When the current exceed in the circuit then the temperature of fuse wire increases and melts due to which current stops flowing in the circuit and electrical appliances are saved from burning.

 

Question 19. 
What is electric current ?
Answer: 
It is the amount of charge flowing through a conductor per unit time.

 

Question 20. 
Write the value of charge on an electron.
Ans. 
1.6 x 10^-19 coulomb.

 

Question 21. 
What is the resistance of an ammeter ?
Answer: 
Its resistance is very less (nearly zero).

 

Question 22. 
Define 1 ampere.
Answer: 
One ampere is the current flowing through a conductor when one coulomb of charge flowing for one second through a conductor.

 

Question 23. 
Why are nitrogen and argon gas often filled in bulbs?
Answer: 
Bulbs are often filled with chemically inert gas like nitrogen and argon because they increase the lifespan of its filament.

 

Question 24. 
What does ‘unit’ mean ?
Answer: 
The commercial unit of electric energy is kilowatt hour (kWh), which is commonly called unit.

 

Question 25. 
Joule/coulomb is the unit of which physical quantity?
Answer: 
Potential difference.

 

Question 26. 
Ammeter is connected in which manner in an electric circuit.
Answer: 
Ammeter is always connected in series in the circuit.

 

 

Question 27. 
On what factor does the resistance of a matter depend upon?
Answer: 
Nature of the material.

 

Question 28. 
Unit of specific resistivity is ?
Answer: 
Ohm x Meter.

 

Question 29. 
What is the nature of graph between V-I in the Ohm’s Law ?
Answer: 
The nature of graph is a straight line.

 

Question 30. 
Why is lead - tin alloy used for making fuse-wire ?
Answer: 
Lead tin alloy has low melting point due to which fuse wire melts when current exceed a particular value. So it is used for making fuse wire.

 

Question 31. 
What do you mean by electric resistivity ?
Answer: 
The resistivity of a conductor is equal to the resistance of conductor of 1 m² area of cross-section and 1 m length. Its S.I. unit is Ohm-meter.

 

Question 32. 
What is series combination ?
Answer: 
In series combination the resistances are joined in such manner that the second end of each resistances is joined to the first end of the next resistance and so on.

 

Question 33.
What is parallel combination ?
Answer: 
When two or more then two resistances are connected in such a way that their first ends are connected to one point and the second ends to another point then this combination is called parallel combination.

 

 
Question 34.
What should be done to reduce the resistance in an circuit?
Answer: 
To reduce the resistance in an circuit, it should be connected in parallel.

 

Question 35. 
Which metal is used to make fuse wire ?
Answer: 
Copper or tin lead alloy.

 

Question 36. 
The heat produced in a conductoris directly proportional to the of current in it ?
Answer: 
Square.

 

Question 37. 
Heat produced in a conductor is directly proportional to the of conductor.
Answer:
Resistance.

 

Question 38. 
In which combination the value of total resistance is maximum?
Answer: 
In series combination.

 

Question 39. 
Which physical quantity is same in the parallel combination of resistances ?
Answer: 
Potential difference (V) between the two ends.

 

Question 40. 
What is the effect of increase in temperature in the resistance of semiconductors ?
Answer: 
On increasing temperature the resistance of conductors increases whereas the resistance of semiconductors decreases.

 

Question 41. 
A wire is stretched and its radius becomes half of its original one ? What is the resistance of the wire now ?
Answer: 
When radius becomes half, the area of cross - section of surface becomes one fourth and its length becomes four times. Hence now the resistance of wire becomes 16 times that of original one.

 

 

 

Question 1. 
Some components provide a simple path for the current to flow while others oppose this flow. Why does this happen ?
Answer: 
We know that motion of electrons in a electric circuit constitutes an electric current. The electrons, however, are notcompletely free to move within a conductor. They are restrained by the attraction of the atoms among which they move. Thus, motion of electrons through a conductor is retarded by its resistance. A component of a given size that offers a low resistance is a good conductor. A conductor having some appreciable resistance is called a resistor.

 

Question 2. 

Column ‘X’ (Physical amount/Rule)	Column ‘Y’ (Formula)
(i) Electric Current	(a) R = R1+ R2 + R3
(ii) Potential	(b) P = RA/l
(iii) Ohm’s law	(c)\(\frac{1}{R}=\frac{1}{R_{1}}+\frac{1}{R_{2}}\)
(iv) Resistivity	(d)v = W/Q
(v) Series Combination	(e) I = Q/t
(vi) Parallel Combination	(f) v = IR

Answer:
(i) (e) 
(ii) (d) 
(iii) (f)
(iv) (b)
(v) (a)
(vi) (c)

 

Question 3. 
An electric refrigerant of 600 W is allowed to run for 8 hours/day. What is the cost of energy to run it for 30 days at the rate of Rs. 4.00 per kWh ?
Answer: 
P = 600 W 
t = 8 h/day
No. of days = 30 days
Total energy consumed by refrigerant in 30 days
= 600 W x 8.00 h/day x 30 days 
= 600 x 8 x 30 watt x hour 
= 144000 watt x hour
\(\frac{144000}{1000} K Wh\)
= 144 kWh
In this way the value of total energy used to run the refrigerant for 30 days is
= 144 kWh x 4.00 Rs./kWh 
= 576.00 Rs.

 

 

Question 4. 
Explain the practical application of heating effect of electric current.
Answer: 
The generation of heat in a conductor is an inevitable consequence of electric current. In many cases, it is undesirable as it converts useful electrical energy into heat. In electric circuits, the unavoidable heating can increase the temperature of the components and alter their properties. However, heating effect of electric current has many useful applications. The electric laundry iron, electric toaster, electric oven, electric kettle and electric heater. The electric heating is also used to produce light, as in an electric bulb.

 

Question 5. 
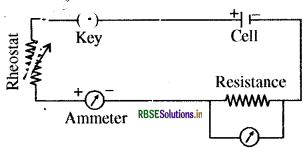
Draw the schematic diagram of electric circuit and explain it.
Answer: 
In the given diagram a schematic presentation of electric circuit is shown.

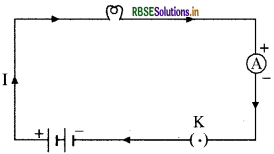
An instrument called ammeter measures electric current in a circuit. It is always connected in series in a circuit through which the current is to be measured. Figure shows the schematic diagram of a typical electric circuit comprising a cell, an electric bulb, an ammeter and a plug key. Note that the electric current flows in the circuit from the positive terminal of the cell to the negative terminal of the cell through the bulb and ammeter.

 

Question 6. 
Define electric potential and potential difference.
Answer:
Electric Potential and Potential difference: We define the electric potential difference between two points in an electric circuit carrying some current as the work done to move a unit charge from one point to the other -
Potential difference (V) between two points = Work done (W)/Charge (Q)
V = W/Q

 

The SI unit of electric potential difference is volt (V), named after Alessandro Volta (1745-1827), an Italian physicist. One volt is the potential difference between two points in a current carrying conductor when 1 joule of work is done to move a charge of 1 coulomb from one point to the other.
Therefore, \(\text { volt }=\frac{1 \text { Joule }}{1 \text { coulomb }}\)
1 V = 1 J C ^-1

The potential difference is measured by means of an instrument called the voltmeter. The voltmeter is always connected in parallel across the points between which the potential difference is to be measured.

 

 

Question 7. 
Electric bulb is based on which property of electric current ? What measures are taken in the electric bulb to get proper and continuous light ?
Answer: 
Electric bulb is based on the property of heating effect of electric current. The filament must retain as much of the heat generated as in possible, so that it gets very hot and emits light. It must not melt at such high temperature. A strong metal with high melting point such as tungsten (melting point 3380°C) is used for making bulb filaments. The filament should be thermally isolated as much as possible, using insulating support, etc. The bulbs are usually filled with chemically inactive nitrogen and organ gases to prolong the life of filament.

 

Question 8. 
What is 1 ohm resistance ?
Answer: 
If the potential difference across the two ends, of a conductor is 1 V and the current through it is 1 A, then the resistance R, of the conductor is 1 Q. That is, 1 ohm
\(=\frac{1 \text { volt }}{1 \text { ampere }}\)
If I = 1 Ampere, V = 1 Volt, then R = 1 ohm.

 

Question 9. 
Differentiate between series and parallel combination of resistances.
Answer: 
Difference between series and parallel combination are:

Series	Parallal
1. In this the value of current flowing in each resistor is same.	1. In this the value of current flowing in each resistor is different.
2. In it the potential difference between the two ends is different.	2. In it the potential difference between the two ends is same.
3. In it the value of total resistance is maximum.	3. In it the value of total resistance is minimum.

 

Question 10. 
What should be the ratio of resistances of two conductors made of same material whose width is same and the ratio of lengths is 1 : 2 ?
Answer:
Since both conductors are of same material, hence their area of cross - section of surface and specific resistivity constant will be -
Resistance \( \mathrm{R}_{1}=\frac{\rho l_{1}}{\mathrm{~A}}\) .....(1)
Similarly, Resisiance \( \mathrm{R}_{2}=\frac{\rho l_{2}}{\mathrm{~A}} \) .....(2)
On dividing eq. (i) by (ii) we get
\(\frac{\mathrm{R}_{1}}{\mathrm{R}_{2}}=\frac{l_{1}}{l_{2}}\)
 But given that  

\(\frac{l_{1}}{l_{2}}=\frac{1}{2} \quad \therefore \frac{\mathrm{R}_{1}}{\mathrm{R}_{2}}=\frac{1}{2}\)
R₁ : R₂  = 1 : 2

 

Question 11. 
Differentiate between ammeter and voltmeter.
Answer: 
The differences between ammeter and voltmeter are:

Ammeter	Voltmeter
1. Used to measure the value of current flowing in a circuit.	1. Used to measure the potential difference between the two terminals of circuit.
2. Its resistance is minimum.	2. Its resistance is maximum.
3. It is connected in series.	3. It is connected in parallel.

 

Question 12. 
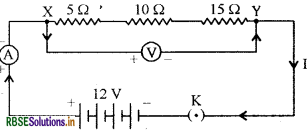
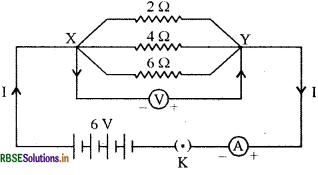
Draw a suitable circuit diagram when -
(a) The total potential are determined by adding resistors of 5 Ω, 10  Ω and 15 Ω in series with a 12 V battery.
(b) The total potential are determined by adding the resistors of 2  Ω, 4  Ω and 6 Ω in parallel with a 6 V battery.
Answer: 
(a) Total potential when resistors are joined in series.

 

(b) Total potential when resistors are joined in parallel -

 

Question 13. 
What do you mean by electrical energy ? Explain.
Answer: 
We know that
\(\text { Power } \mathrm{P}=\frac{\text { Electric Energy }[\mathrm{H}]}{\text { Time }[t]}\)
\(\therefore \quad \mathrm{P}=\frac{\mathrm{H}}{t} \text { or } \mathrm{H}=\mathrm{P} \times t\)
If power (P) is expressed in watt and time (t) is expressed in secs, then electric energy is in Joules.
⇒ Joule = Watt x Sec.
Hence, the electric energy of an appliance is equal to the product of its power and time.

 

Question 14. 
What do you mean by Kilowatt hour ? Calculate the no. of Joules in 10 Kilowatt hour.
Answer: 
Kilowatt hour is the commercial unit of electric energy. Commonly 1 Kilowatt hour is termed as 1 unit
Hence 1 Kilowatt hour
= 1000 Watt x 1 hour
⇒ 1,000 Watt x 60 x 60 secs.
⇒ 3.6 x 10⁶ Joules
.'. The number of Joules is 10 Kilowatt hour.
= 10 x 3.6 x 10⁶ = 36 x 10⁶ Joules 

 

 

Question 15. 
When an electric heater extract 4A current from a source, then the potential difference between its terminal is 60V. Calculate the amount of current when the potential difference becomes 120 V.
Answer: 
Given,
I = 4 Ampere, V = 60 Volts.
We know that,
V = IR
\(\therefore \quad \mathrm{R}=\frac{\mathrm{V}}{\mathrm{I}} R=\frac{60}{4} = 15  Ω\)
Again V=IR
or  \(\begin{aligned} &I=\frac{V}{R} \\ &I=\frac{120}{15} \end{aligned}\)
= 8 Ω
Hence at 120 V the heater extracts 8 ohm current.

 

Question 16. 
4 Ω, 6 Ω and 8 Ω resistances are connected in series with 9 V battery - 
(a) Draw the circuit diagram.
(b) Calculate the total current flows in circuit. 
Answer:

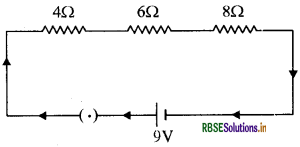
(b) Total resistance in series combination of 4 Ω, 6 Ω and 8 Ω
R = R₁ + R₂ + R₃
R = 4 + 6 + 8
R = 18 Ω
 Now, V=IR
\(\mathrm{I}=\frac{\mathrm{V}}{\mathrm{R}} I=\frac{9}{18} = 0.5 Ampere\)

 

Question 17. 
In parallel combination, find out -
(a) Total Resistance in circuit.
(b) Current flown in the circuit.

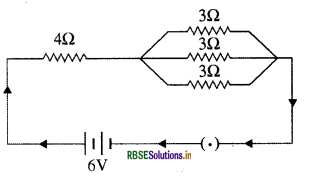
Answer: 
(a) Total resistance of 3 Ω each resistances connected in parallel is
\(\begin{aligned} &\frac{1}{R}=\frac{1}{R_{1}}+\frac{1}{R_{2}}+\frac{1}{R_{3}} \\ &\frac{1}{R}=\frac{1}{3}+\frac{1}{3}+\frac{1}{3}=\frac{1+1+1}{3} \end{aligned} =\frac{3}{3}  =1 Ω\) 
This 1Ω resistance is connected in series with  4Ω  resistance,
Hence R = R₁ + R₂
R = 4 Ω + l Ω= 5 Ω.

 

(b) Given,
R = 5Ω , V = 6V Now V = IR
\(\mathbf{I}=\frac{\mathbf{V}}{\mathbf{R}} =\frac{6 \mathrm{~V}}{5 \Omega}\)
= 1.2 Ampere

 

 

Question 18. 
An electric device uses 2 kW of electric power when operating at 220 V. In this set up, how much ampere fuse should be used ?
Answer: 
Given,
P = 2 kW 
= 2000 W 
V = 220 V 
From formula
p = VI
2000 W = 220 V x I
\(I=\frac{2000 \mathrm{~W}}{220 \mathrm{~V}}\)
I  = 9.09 A.
Therefore, in this electric circuit 9.09 A of electric current is flowing, so, in this set up 10 A fuse should be used.

 

Question 19. 
In a house, 400 W refrigerator is used for 8 hours daily and 120 W electric heater is used for 2 hours daily. How much is consumed in 30 days at the rate of 4 Rs. per unit?
Answer: 
Energy consumed daily in refrigerator
= 400 W x 8h 
= 3200 Wh.
Energy consumed daily in electric heater 
= 120 W x 2h 
= 240 Wh.
Hence, electric energy consumed in 30 days is
= 3200 + 240 x 30 
= 3440 x 30 
= 1,03,200 Wh
= 103.2 Kwh
= 103.2 unit (Y 1 Kwh = 1 unit) At the rate of 4 Rs. total investment
= 4 x 103.2 = 412.8 Rs

 

Question 20. 
A 100 W bulb is used daily for 10 hours. If the rate of electric energy is 4 Rs. per unit, then calculate electric cost in 30 days.
Answer: 
Energy consumed daily in bulb 
= 100 W x 10 h = 1,000 wh.
∴ In 30 days total energy consumed 
= 1,000 x 30 = 30,000 wh.
or 30 Kwh 
or 30 unit
[∵1 Kwh = 1 unit] 
Cost of electric energy consumed = 4 x 30 = 120 Rs.

 

Question 21.

Match the following -

Column X	Column Y
(i) Current measuring device	(A) Joules heating effect
(ii) Potential difference measuring device	(B) Commercial unit of electric energy
(iii) IR	(C) Ammeter
(iv) I2Rt	(D) Voltmeter
(v) Ohm-meter (Q-m)	(E) Ohm’s law
(vi) Unit (Kwh)	(F) Resistance

 

 

Question 1. 
(a) What are the factors in which the resistance of the conductor depends ? Define resistivity and write its SI unit.
(b) In the given circuit, give the value of total resistance and total current.

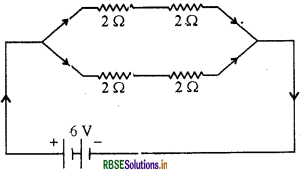
Answer: 
(a) The resistance of the conductor depends on the following factors -

Resistance of at uniform metallic conductor is directly proportional to its length ( l ) and inversely proportional to the area of cross-section (A), that is,
R ∝ l
and\( \mathrm{R} \propto \frac{1}{\mathrm{~A}}\)
∴\( \mathrm{R} \propto \frac{l}{\mathrm{~A}}\)
Or 
\( \mathrm{R}=\rho \frac{l}{\mathrm{~A}}\)

Here, p (rho) is at constant of proportionality and is called the electrical resistivity of the material of the conductor.
Resistivity: The resistance of one meter long and one square meter transverse cut cross-section area of a conducting wire is called resistivity. Kts SI unit is Q m (ohm meter). Resistivity depends only on the nature of the substance.

(b) In the given circuit, th'e resistors of 2Ω and 2 Ω are in series. Therefore, its total resistance is -
R₁ = 2 + 2 = 4  Ω 
R₂ = 2 + 2 = 4  Ω 
Here, both 4  Ω resistors are arranged in parallel. Therefore, its total resistance will be -
\(\frac{1}{R}=\frac{1}{R_{1}}+\frac{1}{R_{2}} =\frac{1}{4}+\frac{1}{4}=\frac{2}{4}=\frac{1}{2}\)
R = 2 Ω
Therefore, total resistance R is 2 Ω .
We know, Current I = \(\frac{V}{R}\)
Here V = 6V and R = 2 Ω
Therefore,  \(I=\frac{6}{2}\) =3 Ampere

 

Question 2. 
Explain the working of fuse used in the electric circuits.
Answer: 
The fuse used in electric circuits protects circuits and appliances by stopping the flow of any undu'iy high electric current. The fuse is placed in series with the device. It consists of a pitjce of wire made of a metal or an alloy of appropriate melting point, for example aluminium, copper, iron, lead etc. If a current larger than the specified value flows through the circuits, the temperature of the fuse wire increases. This melts the fuse wire and breaks the circuit. The fuse wire is usually encased in a cartridge of procelain or similar material with metal ends. The fuses used for domestic purposes are rated as 1A., 2A, 3A, 5 A, 10A etc.

 

 

Question 3. 
State Ohm’s laiw. Describe an experiment to verify this law.
Answer: 
Ohm’s law states that the electric current flowing through a metallic wire is directly proportional to the potential difference V, across its ends provided its t emperature remains the same. This is called Ohm’s law. In other words -
V  ∝ I
or  V/I = constant
    = R
or    V = IR

In Eq., R is a constant for the given metallic wire at a given temperature and is called its resistance. It is the property of a conductor to resist the flow of charges.

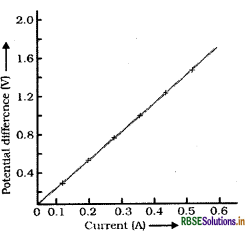
As soon as key is on, the current starts flowing in the circuit. Note the current in ammeter and potential difference in voltmeter. Now, with the help of rheostat change the value of current and note the readings of ammeter and voltmeter in the table. Draw a graph between V and I. Graph obtained is linear.

 

Question 4. 
On which factors does the resistance of a conductor depends ? Define resistivity and state its SI unit.
Answer: 
There are a number of factors which affect the resistance of a conductor :
At a given temperature, the resistance of a conductor depends on the following factors -

1. For a wire of given material and same cross-section, the resistance of a conductor is directly proportional to length,

R∝l ... (1)

2. For a wire of given material and given length, the resistance of a conductor varies inversely to the area of cross-section (A) of the wire.

\(R \propto \frac{1}{A} \) ... (2)

Using equation (1) and (2), R ∝ \(\frac{l}{\mathrm{~A}}\)

Or  
\(\mathbf{R}=\rho \cdot \frac{l}{\mathrm{~A}}\)

where p is a constant. It is called as specific resistance or resistivity of the wire. The unit of p is ohm - meter (Q - m).

If l = lm, A = lm², then R = p so resistivity is defined as the resistance of a conductor of unit length per unit area of cross-section.

The SI unit of resistivity is Ohm - meter,

3. Depends upon the nature of the material of resistance. If we take two wires one of copper and other of iron and arrange them systematically in the electric circuit and switch on the current then we observe that more current flows in copper wire. Hence the resistance of copper is less than iron. Thus resistance depends upon the material of resistor.

4. The resistance of a metallic conductor also depends on temperature. The resistance of conductors increases with increase in temperature; but when temperature is decreased there is a decrease in their resistance. At a very low temperature certain metals lose their resistance considerably, which is known as super conductivity.

 

Question 5. 
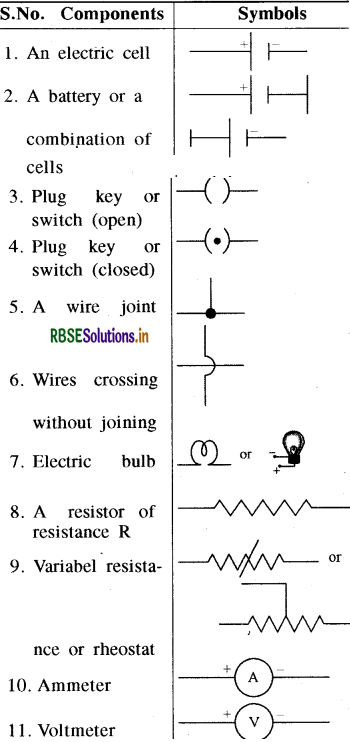
Show the symbols of some commonly used components in circuit diagrams.
Answer:

 

Question 6. 
Draw the circuit diagram showing series combination of resistance and formulate its formula.
Answer: 
In a electric circuit, connect three resistors R₁, R₂ and R₃ in series. Connect voltmeter V₁ , V₂ and V₃ parallel to R₁ , R₂ and R₃ respectively. Cell E, ammeter A and key K are connected in sequence in the circuit. Applying the key K, current I flows from the cell E in the circuit. With the flow of current, potential difference V₁, V₂, V₃ is created across the series combination which is equal to the potential difference V between P and Q. Therefore, 

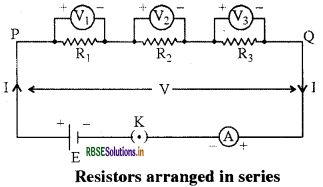
v = v₁ + v₂ + v₃ ....... (1)
Since, the current flowing in the circuit is I, then current through each resistance is also I. It is possible to replace the three resistors joined in series by an equivalent single resistor of resistance R, such that the potential difference V across it, and the current I through the circuit remains the same. Applying the ohm’s law to the entire circuit,
V = IR ...... (2)
On applying Ohm’s Law to the three resistors separately,
V₁ = IR₁ ...... (3)
V₂ = IR₂ ...... (4)
V₃ = IR₃ ...... (5)
From (1) and (2)
IR = IR₁ + IR₂ + IR₃ 
Or    
R_s = R₁ + R₂ + R₃
We can conclude that when several resistors are joined in series, the resistance of the combination R_s equals the sum of their individual resistances, R_1, R₂, R₃ and is thus greater than any individual resistance. When resistance is more than three -
R = R ₁ + R₂ + R₃ + ...... R_n
Or    
R_s= R₁ + R₂ + R₃ + R₄ ...... + R_n

 

 

Question 7. 
Draw the circuit diagram for parallel combination of resistance and derive formula for equivalent resistance.
Answer: 
Parallel Combination: Three resistors joined in parallel in a combination of cells or battery (E), one key (K) and an ammeter (A). A voltmeter is also connected in parallel with the combination of resistors.

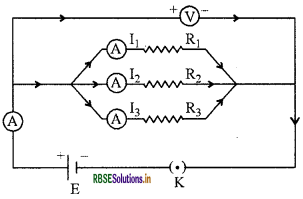
the potential difference across the combination. The potential difference across each resistor is also V. This can be checked by connecting the voltmeter across each individual resistor. Plug the key, and note the ammeter and voltmeter reading. Let the current be I and V is the potential difference across the combination. The potential difference acrosseach resistor is also V. This can be checked by connecting the voltmeter across each individual resistor.
It is observed that the total current I, is equal to the sum of the separate currents through each branch of combination.
I₁ = I₁ + I₂ + I₃  ......... (1)
Let Rp be the equivalent resistance of the parallel combination of resistors. By applying ohm’s law to the parallel combination of resistors, we have,
\(I=\frac{V}{R_{\rho}}\) ......... (2)
On applying ohm’s law to each resistor, we have
\(\mathrm{I}_{1}=\frac{\mathrm{V}}{\mathrm{R}_{1}}\); \(\mathrm{I}_{2}=\frac{\mathrm{V}}{\mathrm{R}_{2}}\); \(\mathrm{I}_{3}=\frac{\mathrm{V}}{\mathrm{R}_{3}} \) .......... (3)
From (1) and (2)
\(\begin{aligned} &\frac{V}{R_{\rho}}=\frac{V}{R_{1}}+\frac{V}{R_{1}}+\frac{V}{R_{2}}+\frac{V}{R_{3}} \\ &\frac{1}{R_{\rho}}=\frac{V}{R_{1}}+\frac{V}{R_{2}}+\frac{V}{R_{3}} \end{aligned}\)
Thus, we may conclude that the reciprocal of the equivalent resistance of a group of resistances joined in parallel is equal to the sum of the reciprocals of the individual resistances. Thus, we may conclude that the reciprocal of the equivalent resistance of a group of resistances joined in parallel is equal to the sum of the reciprocals of the individual resistances.

 

Question 8. 
Explain the heating effect of electric current and define Joule’s heating law.
Answer: 
Heating Effect of Electric Current: An electric fan becomes warm if used continuously for longer time etc. On the other hand, if the electric circuit is purely resistive, that is, a configuration of resistors only connected to a battery; the source energy continually gets dissipated entirely in the form of heat. This is known as the heating effect of electric current. This effect is utilised in devices such as electric heater, electric iron, etc.

 

Consider a current I flowing through a resistor of resistance R. Let the potential difference across it be V. Let t be the time during which a charge Q flows across. The work done in moving the charge Q through a potential difference V is VQ. Therefore, the source must supply energy equal to VQ in time t. Hence, the power input to the circuit by the source is :
\(\mathrm{P}=\mathrm{V} \frac{\mathrm{Q}}{t}=\mathrm{VI}\)
Or the energy supplied to the circuit by the source in time t is P x t, that is VIr. What happens to this energy expended by the source ? This energy gets dissipated in the resistor as heat. Thus for a steady current I, the amount of heat H produced in time t is H = VIt

 

Question 9. 
What is electric power ? Define the formula for it.
Answer: 
The rate at which electric energy is dissipated or consumed in an electric circuit is termed as electric power. The power P is given by    
P = VI
Or
P = I²R = V²/R
The SI unit of electric power is watt (W). It is the power consumed by a device that carries 1 A of current when operated at a potential difference of 1 V. Thus,
1 W = 1 volt x 1 ampere = 1 V A 
The unit watt is very small. Its other big units are kilowatt, magawatt, horse power etc.
1 Kilowatt = 1000 watt = 103 watt 
1 Megawatt = 1000000 = 106 watt 
1 Horse power = 746 watt.

 

 
 Numerical Questions

 

Question 1. 
A domestic electric circuit has a fuse of 5 ampere. What will be the maximum number of 100 W (220 V) bulbs that can be safely used in this circuit ? 
Answer:

P = 100 W
V = 220 V
Current taken by one bulb, 
\(I=\frac{P}{V}=\frac{100}{220}=\frac{5}{11} \mathrm{~A}\)
Current in circuit = 5A
Number of bulb used \(\frac{5}{5}\) x 11 = 11 

 

Question 2. 
A current of 0.5 A is drawn by a filament of an electric bulb for 10 mins. Find the amount of electric charge that flows through the circuit.
Answer: 
Given,

I = 0.5 A,
t = 10 mins = 10 x 60 sec,
Q = ?
Q= I x t
Q= 0.5 x 10 x 60 
= 300 coulomb

 

Question 3. 
Calculate the current flowing in an electric bulb of 40 W, 220 V ?
Answer: 
Given,
P = 40 W
V  = 220 V
From formula - P = VI
\(I=\frac{\mathbf{P}}{\mathbf{V}}\)
By putting the value -
\(I=\frac{40 \mathrm{~W}}{220 \mathrm{~V}} I=\frac{40}{220}\)
I = 0.18 A

Question 4. 
(a) If the resistance of the filament of an electric bulb is 1200 Q, then calculate the amount of current drawn by it from source of 220 V.
(b) How much current will an electric heater coil draw from a source of 220 V, if the resistance of the heater coil is 100Q.
Answer: 
(a) Given,  
R = 1200 Ω,
V = 220 V, I = ?
\(\mathbf{I}=\frac{\mathbf{V}}{\mathbf{R}}\)
On substituting values,
\(I=\frac{220}{1200} = 0.18 A\)

(b) Given - R = 100 Ω, V = 220 V, I = ?
\(\begin{aligned} &I=\frac{V}{R} \\ &I=\frac{220}{100} \end{aligned}\) = 2.2A

 

 

Question 5. 
A 100 W electric device is used for 6 hours daily. How much energy (in units) is used by it is 30 days ?
Answer: 
Given - P = 100 W 
1 unit = 1 kWh Therefore,
No. of units
\(\begin{aligned} &=\frac{\text { Watt } \times \text { hour } \times \text { number of days }}{1000} \\ &=\frac{100 \times 6 \times 30}{1000} \end{aligned} \)
= 18 units.

 

Question 6. 
If, the resistance of a wire of length 1 m and diametre 0.3 mm at 20°C is 26Ω, then calculate the specific resistivity of the wire at this temperature.
Answer: 
Given,
l = 1 m
R = 26 Ω
d = 0.3 mm = 0.3 x 10 ^-3 m = 3 x 10^-4 m.
 ρ = ?
We know that  ρ = \(\frac{\mathrm{RA}}{l}=\frac{\mathrm{R} \pi\left(\frac{\mathrm{d}}{2}\right)^{2}}{l}\)
ρ  = \(\frac{\mathrm{R} \pi \mathrm{d}^{2}}{4 l}\)
On substituting value, we get
\(\begin{aligned} \rho &=\frac{26 \times 3.14 \times\left(3 \times 10^{-4}\right)^{2}}{4 \times 1} \\ &=\frac{26 \times 3.14 \times 9 \times 10^{-8}}{4} \end{aligned}\)
183.69 x 10 ^-8 
Or      
ρ  = 1.84 x 10 ^-6 Ωm.

 

Question 7. 
A wire of given material having length l and area of cross - section A has a resistance of 4 Ω. What would be the resistance of another wire of the same material having length 1/2 and area of cross - section 2A ?
Answer: 
For first wire\( \mathrm{R}_{1}=\frac{\rho l}{\mathrm{~A}}=4 \Omega\)
For second wire -
\(\begin{aligned} \mathrm{R}_{2} &=\rho \frac{l / 2}{2 \mathrm{~A}} \\ &=\frac{1}{4} \cdot \rho \frac{l}{\mathrm{~A}} \\ &=\frac{1}{4} \mathrm{R}_{1} \\ &=\frac{1}{4} \times 4 \end{aligned}  \)
=1 Ω
.'. The resistance of new wire is 1 Ω.

 

Question 8. 
A wire of given material having length / and area of cross-section A has a resistance 8 Ω. Determine the resistance of another wire of same material having length 21 and area of cross-section\(\frac{A}{2}\)?
Answer: 
Given,
R₁ = 8 Ω, length = l, Area = A
R₂ = ?, length = 21, Area =\( \frac{A}{2}\)
We know that,
\(\mathrm{R}=\rho \times \frac{l}{\mathrm{~A}}\)
Here  is ρ specific resistivity.
\(\begin{aligned} \mathbf{R}_{1} &=\rho \times \frac{l}{\mathrm{~A}} \\ 8 &=\rho \times \frac{l}{\mathrm{~A}} \end{aligned}\)  ............(1)
Similarly  \(\begin{aligned} &\mathrm{R}_{2}=\rho \times \frac{2 l}{\mathrm{~A} / 2} \\ &\mathrm{R}_{2}=\rho \times \frac{2 \times 2 l}{\mathrm{~A}} \\ &\mathrm{R}_{2}=4 \times \frac{\rho l}{\mathrm{~A}} \end{aligned}\)
R₂ = 4 x 8
Substituting value of  ρ x \(\frac{l}{\mathrm{~A}} \)= 8  [from eq.1]
R₂ = 32 Ω,

 

 

Question 9. 
Two electric bulb of 100 W and 60 W are connected in parallel of a 200 V power line. They are burnt for 5 hours daily. What will be the 20 day electric energy consumption and if electricity consumption rate is Rs. 6 per unit, then calculate the bill amount.
Answer: 
Electric power used by two bulb of 100 W and 60 W and number of unit -
\(\text { Number of unit }=\frac{\text { Watt } \times \text { Hour } \times \text { Day }}{1000}\)
Total unit used
\(\begin{aligned} &=\frac{100 \mathrm{~W} \times 5 \times 30+60 \mathrm{~W} \times 5 \times 30}{1000} \\ &=\frac{15000 \mathrm{Wh}+9000 \mathrm{Wh}}{1000} \end{aligned}\)
 = 24 kWh 
 Therefore = 24 unit.
So, the total electric energy used is 24 unit.
Rate of one unit = Rs. 6
Then rate for 24 unit = 6 x 24
= Rs. 144
Therefore, bill amount will be Rs. 144.

 

Question 10. 
An electric lamp, whose resistance is 20  Ω, and a conductor of 4  Ω resistance are connected to a 6 V battery as shown in figure. Calculate - (a) the total resistance of the circuit (b) the current through the circuit (c) the potential difference across the electric lamp and the conductor.

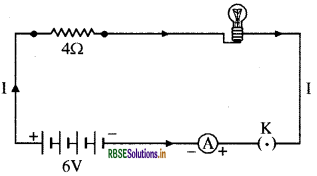
Answer: 
(a) The resistance of the electric lamp R1= 20 Ω,
The resistance of the conductor = 4 Ω (connected in series)
Then the total resistance in the circuit R = R1 + R2
= 20 Ω+ 4 Ω = 24 Ω

(b) The potential difference across the two terminals of a battery 
V = 6V
From Ohm’s law the current through the circuit is given by -
\(I=\frac{V}{R_{s}}=\frac{6 \mathrm{~V}}{24 \Omega}=0.25 \mathrm{~A}\)

(c)    Potential difference between the two terminals of lamp - 
\(\begin{aligned} \mathrm{V}_{1} &=\mathrm{I} \mathrm{}_{1} \\ &=0.25 \times 20=5 \mathrm{~V} \end{aligned}\) 
Potential difference across the terminals of conductor -
\(\begin{aligned} \mathbf{V}_{2} &=\mathrm{I} \mathrm{R}_{2} \\ &=0.25 \times 4=1 \mathrm{~V} \end{aligned}\)

 

Question 11. 
In the circuit diagram given in figure, suppose the resistors R₁, R₂, R₃, have the values 5 Ω, 10 Ω, 30 Ω respectively. Which have been connected to a battery of 12V? Calculate - 
(a) the current through each resistor,
(b) the total current In the circuit, and
(c) the total resistance of the circuit.

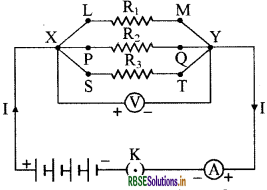
Answer: 
(a) Given,
R₁ = 5 Ω , R₂ = 10 Ω and R₃ = 30Ω
Potential difference across the battery
V = 12V
Using Ohm’s Law
The current I₁ through R₁ =\( \frac{\mathrm{V}}{\mathrm{R}_{1}}\)
\(\mathrm{I}_{1}=\frac{12 \mathrm{~V}}{5 \Omega}=2.4 \mathrm{~A}\)
The current I₂ through R₂ = \(\frac{\mathrm{V}}{\mathrm{R}_{2}}\)
\(\mathrm{I}_{2}=\frac{12 \mathrm{~V}}{10 \Omega}=1.2 \mathrm{~A}\)
The current I₃ through R₃ =  \(\frac{\mathrm{V}}{\mathrm{R}_{3}}\)
\(I_{3}=\frac{12 V}{30 \Omega}=0.4 \mathrm{~A}\)

(b) The total current in the circuit
\(\begin{aligned} \mathrm{I} &=\mathrm{I}_{1}+\mathrm{I}_{2}+\mathrm{I}_{3} \\ &=(2.4+1.2+0.4) \mathrm{A}=4 \mathrm{~A} \end{aligned}\)

(c) Total Resistance  
\(\begin{aligned} \frac{1}{\mathrm{R}_{\mathrm{p}}} &=\frac{1}{\mathrm{R}_{1}}+\frac{1}{\mathrm{R}_{2}}+\frac{1}{\mathrm{R}_{3}} \\ &=\frac{1}{5}+\frac{1}{10}+\frac{1}{30} \\ \frac{1}{\mathrm{R}_{\mathrm{p}}} &=\frac{6+3+1}{30}=\frac{10}{30} \\ \mathrm{R}_{\mathrm{p}} &=\frac{30}{10}=3 \Omega \end{aligned}\)

 

 

Question 12. 
If in fig., R₁= 10  Ω, R₂ = 40  Ω, R₃ = 30  Ω, R₄ = 20  Ω, R₅ = 60  Ω and a 12 V battery is connected to the arrangement.
Calculate - 
(a) the total resistance in the circuit.
(b) the total current flowing in the circuit.

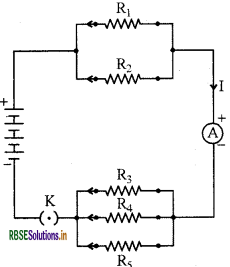
Answer: 
Given -
R₁ = 10  Ω , R₂ = 40  Ω , R₃ = 30  Ω, R₄ = 20  Ω,  R₅ = 60 Ω
(a) Equivalent resistance of R₁ and R₂ = Rρ  for parallel connection
\(\begin{aligned} &\frac{1}{R_{p}}=\frac{1}{R_{1}}+\frac{1}{R_{2}} \\ &\frac{1}{R_{p}}=\frac{1}{10}+\frac{1}{40}=\frac{4+1}{40}=\frac{5}{40} \\ &R_{p}=\frac{40}{5}=8 \Omega \end{aligned}\)
Similarly, for R₃, R₄ and R₅
\(\begin{aligned} \frac{1}{\mathrm{R}_{\mathrm{p}}^{\prime}} &=\frac{1}{\mathrm{R}_{3}}+\frac{1}{\mathrm{R}_{4}}+\frac{1}{\mathrm{R}_{5}} \\ &=\frac{1}{30}+\frac{1}{20}+\frac{1}{60}=\frac{2+3+1}{60}=\frac{6}{60}=\frac{1}{10} \end{aligned}\)
.'. R'p = 10 Ω
Thus, the total resistance, 
R = R_P + R'_p
= 8 Ω+10 Ω=18 Ω 

(b) To calculate the current, we use Ohm’s  Law and get
\(I=\frac{V}{R}=\frac{12 V}{18 \Omega}=\frac{2}{3}\)=0.67
I = 0.67 A

 

Question 13. 
An electric iron consumes energy at a rate of 840 W for maximum heating rate and 360 W for minimum heating rate. If the potential difference of the source is 220 V, then in both cases calculate the current and resistance.
Answer: 
(a) When heating rate is maximum 
P = 840 W 
V = 220 V 
I = ?
\( \begin{aligned} &I=\frac{P}{V} \\ &I=\frac{840}{220}=3.82 \mathrm{~A} \end{aligned}\)
And resistance of electric iron 
\(\mathrm{R}=\frac{\mathrm{V}}{\mathrm{I}}=\frac{220 \mathrm{~V}}{3.82 \mathrm{~A}}=57.60 \Omega\)

(b) When heating rate is minimum
\( \begin{aligned} &I=\frac{P}{V} \\ &I=\frac{360 \mathrm{~W}}{220 \mathrm{~V}}=1.64 \mathrm{~A} \end{aligned}\)
And resistance of electric iron
\(\mathrm{R}=\frac{\mathrm{V}}{\mathrm{I}}=\frac{220 \mathrm{~V}}{1.64 \mathrm{~A}}=134.15 \Omega\)

 

Question 14. 
100 J of heat, is produced each second in a 4  Ω resistor. Calculate the potential difference across the resistor.
Answer: 
Given,
H = 100 J 
 R = 4 Ω
 t = 1 sec.
V = ?
We know that the heat produced in the wire H = I²Rt
\(\mathrm{I}^{2}=\frac{\mathrm{H}}{\mathrm{RT}}\)
On substituting values 
\(\begin{aligned} \mathbf{I}^{2} &=\frac{100}{4 \times 1}=25 \\ I &=\sqrt{25}=5 \mathrm{~A} \end{aligned}\)
From Ohm’s Law V = IR
V = 5 x 4 = 20 V 

 

Question 15. 
A bulb is connected to a battery of 220 V. If a current of 0.50 A flows through the bulb, calculate the power of bulb.
Answer: 
Given,
V = 220 V 
I = 0.50 A 
P = ?
We know that Power P = VI
= 220 V x 0.50 A = 110 J/s
= 110 W    

 

Question 16. 
If a 220 V or 100 W bulb is connected to a 110 V source then find the value of the power consumed by the bulb.
Answer: 
Given,
V = 220 V
Power of bulb P = 100 W
Resistance of bulb \(\mathrm{R}=\frac{\mathrm{V}^{2}}{\mathrm{P}}\)
R=\(\frac{220 \times 220}{100}\)
R = 484 Ω
Here, Voltage of source  V₁ = 110 V
∴ Power used by bulb  P₁ = \(\frac{\mathrm{V}_{1}^{2}}{\mathrm{R}}\)
\(P_{1}=\frac{110 \times 110}{484}\)
P₁ = 25 W

 

 

Question 17. 
An electric refrigerator rated 400 W operates 8 hour/day. What is the cost of energy to operate it for 30 days at Rs. 3.00 per Kwh ?
Answer: 
Given,
P = 400 W 
t = 8 hr/day
Number of days = 30 days
The total energy consumed by the refrigerator in 30 days
= 400 W x 8.0 x 30 
= 400 x 8 x 30 
= 96000 watt / hour
Thus, the cost of energy operated in refrigerator for 30 days
= 96 Kwh x 3.00 
= 288.00 Rs. 

 

Question 18. 
The resistors of 20 Ω, 30 Ω and 50 Ω are connected in series which have been connected to a source of 150 V. Calculate the current through each resistor, and the potential difference between its terminals.
Answer:

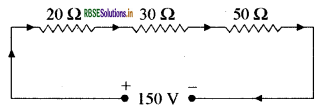
Since the resistances are connected, in series, hence equal current flows through there
R = R₁ + R₂ + R₃
= 20 + 30 + 50 = 100 Ω 
Therefore, current flows in each resistor is 
\(\begin{aligned} &\mathrm{I}=\frac{\mathrm{V}}{\mathrm{R}} \\ &\mathbf{I}=\frac{150}{100}=1.5 \mathrm{~A} \end{aligned}\)
Potential difference across 20Ω  is  
V₁ = IR₁
1.5 x 20 = 30 V    
Potential difference across 30 Ω is
V₂ = I R₂
1.5 x 30 = 45 V    
Potential difference across 50 Ω is
V₃ = I R₃ 
1.5 x 50 = 75 Volts

 

Question 19. 
In figure R₁ = 2 Ω, R₂ = 4 Ω and R₃ = 4 Ω and the circuit of these resistors is connected to 6 V, then calculate -
(a) Total resistance in the circuit.
(b) Total current in the circuit.
(c) Current flowing in resistance of R = 2 Ω.

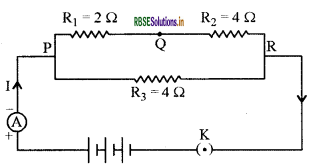
 Answer:
 Given, 
 R₁ = 2Ω , R₂ = 4Ω, R₃ = 4Ω, V = 6V
(a) R₁ and R₂ are in series, so their total resistance Rs will be -
R_s = R₁ + R₂ 
R_S = 2 + 4= 6Ω
R_s and R₃ are parallel, so their total resistance Rp will be -
\(\begin{aligned} \frac{1}{R_{P}} &=\frac{1}{R_{S}}+\frac{1}{R_{3}} \\ \frac{1}{R_{P}} &=\frac{1}{6}+\frac{1}{4}=\frac{10}{24} \\ R &=\frac{24}{10}=2.4 \Omega \end{aligned}\)

(b) To know the flow of current, ohm’s law is used - 
\(I=\frac{V}{R}\)
[Here,\( \mathrm{V}=6 \mathrm{~V}, \mathrm{R}=2.4 \Omega\) ]
\(I=\frac{6}{2.4} \quad I=2.5 \mathbf{A}\)

(c) Current flowing in resistance Rt = 2 Ω from ohm’s law - 
I = \(\frac{V}{R}\) [Here V = 6V , R = 6 Ω]
I = \(\frac{6}{6}, \quad\) I = 1 A

 

Question 20. 
The work done in carrying a positive particle whose value of charge is lO^-6C from infinity to a point in electric circuit is 6 x 10 ^-5 Joule. Calculate the potential difference at that point.
Answer: 
Given,
Q = 10 ^-6C, 
W = 6 x 10^-5 J, 
V = ?
\(\text { Potential }(\mathrm{V})=\frac{\text { Work }(\mathrm{W})}{\text { Charge }(\mathrm{Q})}\)
\(\frac{6 \times 10^{-5}}{10^{-6}}=6 \times 10 \mathrm{~J} / \mathrm{C}\)
= 60 Volts

 

Question 21. 
In the given circuit diagram, Calculate -

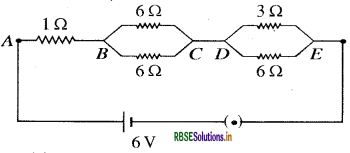
(a) Total resistance of combination
(b) Current in I  resistance
(C) Potential difference between points B and C. .
Answer: 
(a) Total resistance of combination: Between B and C the resistors are connected in parallel, hence, resistance is
\(\frac{1}{R_{1}}=\frac{1}{6}+\frac{1}{6}=\frac{2}{6}=\frac{1}{3}\)
R₁ = 3 Ω 
Similarly between D and E the resistors are connected in parallel hence resistance
\(\begin{aligned} R_{2} &=\frac{1}{R_{2}}=\frac{1}{3}+\frac{1}{6} \\ &=\frac{2+1}{6}=\frac{3}{6}=\frac{1}{2} \end{aligned}\)
R₂ = 2  Ω
Now, 1 Ω, 2 Ω and 3  Ω resistances are combined in series, hence their total resistances is
R = 1+ 3 + 2  =6
R = 6 Ω

(b) Current through 1 Ω resistance
\(I=\frac{V}{R}\)
Here V = 6V and R = 1 Ω  
\(I=\frac{6 V}{1 \Omega}\)= 6
I = 6 Ω

(c) Potential difference between points B and C
Total potential difference between two terminals circuit is -
V = 6V
Using Ohm’s law, current between point B and C is
\(\mathrm{I}_{1}=\frac{\mathrm{V}}{\mathrm{R}_{1}}\)
Here V = 6V and R1 = 3 Ω
\(I_{1}=\frac{6 V}{3 \Omega}=2 \mathrm{~A}\)
Now, potential difference between point B and C is
V₁ = I₁ x R₁ 
V₁  =  2A x 3 Ω
⇒ V₁ = 6V
Hence, the potential difference between point B and C is 6 Volts

 

 

Question 22. 
Two lamps one rated 60 W, 220 V and the other 40 W, 220 V are connected in parallel to a 220 V electric mains supply. What current is drawn from the line if the supply voltage is 220 V ?
Answer: 
Since both lamps are connected in parallel, so the value of potential difference will be same.
Electric current taken by 60 W electric lamp - 
P = V x I 
I = \(\frac{P}{V}\)
Here, P = 60 W, V = 220 V
So\(,I_{1}=\frac{60 \mathrm{~W}}{220 \mathrm{~V}}=\frac{60}{220} \mathrm{~A}\)
Similarly, electric current taken by 40 W electric lamp -
\(I_{2}=\frac{40 \mathrm{~W}}{220 \mathrm{~V}}=\frac{40}{220} \mathrm{~A}\)
Total current flowing in parallel circuit 
I = I₁ + I₂
So,\( \begin{aligned} &I=\frac{60}{220}+\frac{40}{220} \\ &I=\frac{100}{220} \end{aligned}\)
I = 0.454 A