RBSE Class 10 Science Important Questions Chapter 10 Light Reflection and Refraction

Rajasthan Board RBSE Class 10 Science Important Questions Chapter 10 Light Reflection and Refraction Important Questions and Answers.

RBSE Class 10 Science Chapter 10 Important Questions Light Reflection and Refraction

Objective Type Questions

Question 1.
The velocity of light is maximum in -
(a) Glass
(b) Water
(c) Air
(d) Vacuum
Answer:
(d) Vacuum

 

Question 3.
A beam of light is incident on a plane mirror normally, the value of angle of reflection is -
(a) 90°
(b) 180°
(c) 0°
(d) 45°
Answer:
(c) 0°

Question 4.
The image formed by an object kept in front of a concave lens is always -
(a) Virtual and erect
(b) Real and erect
(c) Virtual and inverted
(d) Real and inverted
Answer:
(a) Virtual and erect

Question 5.
Dioptre is the unit of -
(a) Focal length
(b) Magnification
(c) Power of lens
(d) None of these
Answer:
(c) Power of lens

Question 6.
A presbyopic person uses spectacles of double lens in which -
(a) Upper is convex and lower is concave lens
(b) Lower is convex and upper is concave lens
(c) Both are convex lens with different focal length
(d) Both are concave lens with different focal length
Answer:
(b) Lower is convex and upper is concave lens

Question 7.
On seeing distant source of light through smoke, it seems twinkling due to -
(a) Reflection
(b) Refraction
(c) Diffusion
(d) None of these
Answer:
(b) Refraction

Question 8.
An incident ray travels straight on its path without diverting while passing through this lenses. Such point diverting while passing through this lenses. Such point on the principal focus is termed as -
(a) Focus
(b) Optical
(c) Image
(d) Centre of curvature
Answer:
(b) Optical

Very Short Answer Type Questions

Question 1.
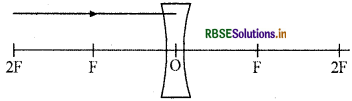
Complete the given ray diagram -

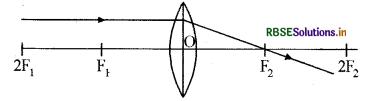
Answer:

Question 2.
Define focal length.
Answer:
The distance between principal focus and optical centre of a lens is known as the focal length.

Question 3.
Radius of curvature of a spherical mirrors is 30 cm. Calculate its focal length.
Answer:
∵ R = 2f
∴ f = \(\frac{\mathrm{R}}{2}=\frac{30}{2}\)  = 15 cm

Question 4.
What is ‘diffraction’?
Answer:
If an opaque object on the path of light becomes very small, light has a tendency to bend around it and not walk in a straight line - an effect known as diffraction of light.

Question 5.
By what nature of light can the diffraction effect be interpreted ?
Answer:
The diffraction effect can be explained based on the wave nature of the light.

Question 6.
What is modern quantum theory of light ?
Answer:
A modem quantum theory of light emerged in which light is neither a ‘wave’ nor a ‘particle’ - the new theory reconciles the particle properties of light with the wave nature.

Question 7.
How do we see our reflection in a showing mirror?
Answer:
The image formed is virtual and large.

Question 8.
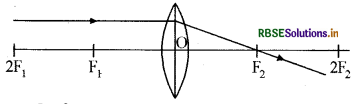
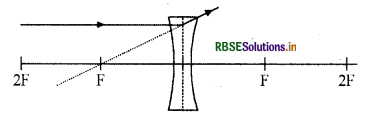
Complete the given ray diagram -

Answer:

Question 9.
If the ray of light is incident normally on a mirror then, the angle of reflection is ?
Answer:
The value of angle of reflection is zero [0°].

Question 10.
Which lens is used in hypermetropia ?
Answer:
A convex lens of short focal length is used.

Question 11.
Name the lens that diverges the rays of light ?
Answer:
Concave lens.

Question 12.
On what factors does the focal length of lens depend upon ?
Answer:
The focal length of a lens depends upon the following factors -

• Refractive index of the lens material.
• Radius of curvatures of both surfaces of lens.
• Wavelength of light.

Question 13.
The radius of curvature of a concave mirror is 10 cm. Calculate its focal length ?
Answer:
∵ f =\( \frac{\mathrm{R}}{2}\)
∴ f = \(\frac{-10}{2}\)
= -5 cm
Hence focal length is 5 cm.

Question 14.
What is ‘concave mirror’?
Answer:
The spherical mirror whose reflective surface is curved inwards, that is, faces towards the centre of the sphere, is called concave mirror.

Question 15.
What is ‘pole of mirror’?
Answer:
The centre of the reflecting surface of a spherical mirror is a point called the pole.

Question 16.
What is the relation between radius of curvature and focal length of spherical mirror?
Answer:
For spherical mirrors of small apertures, the radius of curvature is found to be equal to twice the focal length, that is R = 2f.

Question 17.
Which type of mirror is fitted on the wall of Agra Fort facing Taj Mahal ?
Answer:
Convex mirror.

Question 18.
What do you mean by object distance (u) and image distance (v) ?
Answer;
The distance of the object from its pole is called the object distance (u) and the distance of the image from the pole of the mirror is called the image distance (v).

Question 19.
What is a ‘lens’?
Answer:
A transparent material bound by two surfaces, of which one or both surfaces are spherical, forms a lens.

Question 20.
Name the mirror that makes large and virtual image of an object.
Answer:
Concave mirror.

Question 21.
If an object is placed between the pole and infinity of a convex mirror. Where its image will be formed ?
Answer:
Its image will be formed between the focus and pole of the mirror and behind the mirror.

Question 22.
Which mirror is used by the dentist to check the teeth of patients?
Answer:
Concave mirror.

Question 23.
Where should an object be placed on the principal axis of a concave mirror to get a real image of equal size to that of the object ?
Answer:
Object should be placed at the radius of curvature (R) of the mirror.

Question 24.
Define the linear magnification of a mirror.
Answer:
It is defined as the ratio between the height of the image (h') and the height , of the object (h).

Question 25.
When should both the focal lengths of a lens equalise ?
Answer:
When the medium on both the sides of the lens is the same and both the radius of curvature are the same, their focal lengths are also the same.

Question 26.
Write the first law of refraction.
Answer:
The incident ray, the refracted ray and the normal to the interface at the point of incidence all lie in the same plane.

Question 27.
Name the lens used to converge the rays of light at a point.
Answer:
Convex lens or converging lens.

Question 28.
What is the effect on velocity of the light ray when it enters from a denser to a rarer medium?
Answer:
The velocity of the light wave increases.

Question 29.
Which have greater value, angle of incidence or angle of refraction, when a light ray enters from rarer to denser medium?
Answer:
The angle of incidence has greater value than the angle of refraction.

Question 30.
What is the main difference between rarer and denser medium ?
Answer:
In denser medium the velocity of light is lesser than vacuum whereas in rarer medium the velocity of light is greater than the denser medium.

Question 31.
What do you mean by refraction?
Answer:
The bending of the light ray from its path in passing from one medium to the other is called refraction of light.

Question 32.
An convex lens forms a real and highly enlarged image of an object. What should be the position of the object on the principal axis?

Question 33.
What is a ‘convex mirror’?
Answer:
A spherical mirror whose reflecting surface is curved outwards, is called a convex mirror.

Question 34.
Differentiate between the focal length ( f ) of mirror and lens.
Answer:

Question 36.
What is refraction of light?
Answer:
When light travel obliquely from one medium to another, the direction of propagation of light in the second medium changes. This phenomenon is known as refraction of light.

Question 37.
The ability of a lens to converge or diverge light rays depends on what ?
Answer:
The ability of a lens to converge . or diverge light rays depends on its focus distance.

Question 38.
Name that physical quantity that remains unaltered or unchanged when the light ray enters from one medium to another medium?
Answer:
Frequency.

Question 39.
What do you mean by the optical centre of the lens?
Answer:
The central point of a lens through which the ray of light passes without suffering any deviation is known as the optical centre of the lens.

Question 40.
A convex lens forms a virtual and enlarged image of an object. What should be the position of the object on the principal axis ?
Answer:
The object must be placed between the focus and the optical centre of the lens.

Question 41.
A point on the principal axis on which light rays coming parallel principal axis converge is known as of a lens.
Answer:
Focus.

Question 42.
Where should we use more than one lens?
Answer:
The use of more than one lens in the following -
(a) Construction of camera
(b) Objective lens of the remedial lens for shortsightedness and longsightedness.

Short Answer Type Questions

Question 1.
Define the power of a lens. Write its unit and formula.
Answer:
Power of lens: The degree of convergence or divergence of light rays achieved by a lens is expresed in terms of its power. The power of a lens is defined as the reciprocal of its focal length. It is represented by the letter P.
The power P of a lens of focal length f is given by.
P = \(\frac{1}{f}\)
The SI unit of power of lens is ‘dioptre’. It is denoted by the letter D. If f is expressed in metres, then, power is expressed in dioptres. Thus, 1 dioptre is the power of the lens whose focal length is 1 metre.
1D = 1m ^-1
The power of a convex lens is positive and that of a concave lens is negative.

Question 2.
Explain the nature of light.
Answer:
If an opaque object on the path of light becomes very small, light has a tendency to bend around it and not walk in a straight line - an effect known as the diffraction of light. Then the straight line treatment of optics using ray fails. To explain phenomena such as diffraction, light is thought of as a wave.

But the wave theory of light often becomes inadequate for treatment of the interaction of light with matter, and light often behaves somewhat like a stream of particles, A modern quantum theory of light emerged in which light is neither a ‘wave’ nor a ‘particle’ the new theory reconciles the particle properties of light with the wave nature.

Question 3.
(A) What do you mean by reflection of light?
(B) Give the laws of reflection with the help of diagram.
Answer:
(A) Reflection of light is the process where the incident light on a surface is bounced back into the same medium.
(B) The laws of reflection are as follows -

• Incident ray, reflected ray and the normal at the point of incidence, all lie in the same plan.
• The angle of incidence is equal to the angle of reflection i.e. ∠i =∠r.

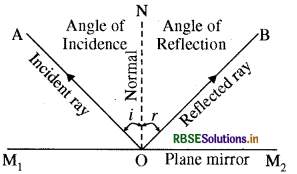
Question 4.
What are the properties of the image formed by a plane mirror ?
Answer:
Image formed by a plane mirror is always virtual and erect. The size of the image is equal to that of the object. The image formed is as far behind the mirror as the object is in front of it. Further, the image is laterally inverted.

Question 5.
(A) Why does the ray of light bends while travelling from one medium to other ?
(B) Power of a lens is -4.0D. What is the nature of the lens?
Answer:
(A) The light ray bends while travelling from one medium to other due to refraction.
(B) The power of the lens is negative. Therefore its focal length is also negative. Hence the nature of the lens is concave.

Question 6.
An object of size 4.00 cm is placed 30 cm far from a concave mirror of 15.0 cm focal length. At what distance from the mirror a screen is placed to get a clear image of the object ? Find out the nature and size of the image.
Answer:
Size of object h = 4 cm
Focal length f = - 15 cm
Object distance u = - 30 cm
Image distance v = ?
According to the mirror formula -
\(\frac{1}{v}+\frac{1}{u}=\frac{1}{f}\)
\(\frac{1}{v}=\frac{1}{f}-\frac{1}{u}\)
\(\frac{1}{v}=\frac{1}{15}-\frac{1}{-30}\)
\(\frac{-2+1}{30}=\frac{1}{-30}\)
v = -30
Therefore the screen should be placed 30 cm away from the mirror.

Magnification of mirror
m = \(\frac{h^{\prime}}{h}=\frac{-v}{u}\)
h' = -\(\left(\frac{v}{u}\right) \times h\)
h' = \(\left(\frac{-30}{-30}\right) \times 4\)
=\(\frac{-120}{30}\)
- 40 cm
Height of image h' = - 40 cm.
Hence image obtained is real, inverted and magnified.

Question 7.
Differentiate between lens and mirror.
Answer:

Question 9.
With the help of a ray diagram, show the nature and position of the image for the following positions of object in a concave mirror -
(a) Between F and C
(b) Between F and P.
Answer:
(a) Between F and C.

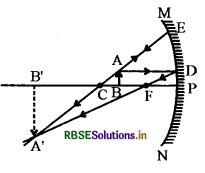
Image is formed between C and ∞ (infinity), real and inverted.

(b) Between F and P.

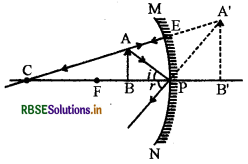
Question 10.
Light ray enters from air into water, whose refractive index is 1.33. If speed of light in air is 3 x 10₈ m/s, find the speed of light in water ?
Answer:
Given -
Speed of light in air c = 3 x 10⁸ m/s.
Refractive index of water n =1.33
Speed of light in water v = ?
∵ Refractive index n = \(\frac{C}{v}\)
∴\(\nu=\frac{c}{n}\)
\(v=\frac{3 \times 10^{8}}{1.33}\)
= 2.25 x 10⁸
Therefore speed of light in water is 2.25 x 10⁸m/s.

Question 11.
Draw the image of object AB in the given ray diagram.

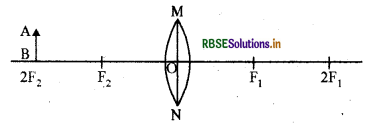
Answer:

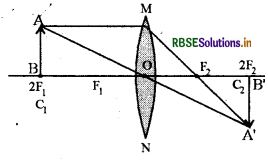
Question 12.
An object is placed at the centre of curvature of a concave mirror. Draw the ray diagram of the image so formed.
Answer:

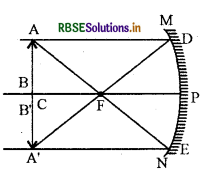
Question 13.
Focal length of an convex lens is 20 cm. What is the power of lens ?
Answer:
Given,
Focal length f = 20cm
\(\frac{20}{100}=\frac{1}{5} \mathrm{~m}\)
∵ Power of lens P =\( \frac{1}{f}\)
∴ P=\(\frac{1}{1 / 5}\)
P = +5 Dioptre

Question 14.
What is mirror formula ? Explain.
Answer:
In a spherical mirror, the distance of the object from its pole is called the object distance (u). The distance of the image from the pole of the mirror is called the image distance (v). The distance of the principal focus from the pole is called the focal length (f ). There is a relationship between these three quantities given by the mirror formula which is expressed as -
\(\frac{1}{v}+\frac{1}{u}=\frac{1}{f}\)
This formula is valid in all situations for all spherical mirrors for all positions of the object.

Question 15.
Define the following -
(i) Plane mirror
(ii) Spherical mirror.
Answer:
(i) Plane Mirror: A plane mirror is simply a mirror with flat surface polished from one side.
(ii) Spherical Mirror: A spherical mirror is a part of hollow sphere whose inner or outer surface is polished. Their reflecting surface is curved.

They are of two types -
(a) Concave mirror: A concave mirror is one whose reflecting surface is curved inwards towards the centre of sphere.(b) Convex mirror: A convex mirror is one whose reflecting surface is curved outwards away from the centre of sphere.

Question 16.
Explain the laws of reflection by spherical mirror.
Answer:

1. A ray parallel to principal axis is reflected in such a way that after reflection it passes through the principal focus or appears to come from focus.
2. A ray passing through the centre of curvature hits the mirror along the direction the normal to the mirror at the point and retraces its path after reflection.
3. A ray of light heading towards the focus or incident in the mirror after passing through the focus returns parallel to the principal axis.

Question 17.
Differentiate between convergent and divergent lens.
Answer:

Question 18.
Write the differences between real and virtual image.
Answer:

Question 19.
Define the following terms (any three) related to spherical mirrors -
(i) Pole
(ii) Principal axis
(iii) Principal focus
(iv) Focal length.
Answer:
(i) Pole: It is the mid point of spherical mirror.
(ii) Principal Axis: It is an imaginary line joining the pole to the centre of curvature.
(iii) Principal Focus: The point on the principal axis at which light rays parallel to the principal axis, after reflection from the mirror, actually meet or appear to come from, is called the principal focus of the mirror.
(iv) Focal Length: The distance of the principal focus from the pole of the mirror is called the focal length of the mirror.

Question 20.
Define centre of curvature, radius of curvature and aperture for a spherical mirror.
Answer:

1. Centre of Curvature:The centre of the sphere of which the mirror forms a part, is called the centre of curvature of the mirror.
2. Radius of Curvature: The radius of the sphere of which the mirror forms a part, is called the radius of curvature of a mirror.
3. Aperture: The diameter of the periphery of the mirror is called the aperture of the mirror.

Question 21.
Why does the paper burn when sunlight is focused on a sheet of paper with a convex lens?
Answer:
The light from the sun is converged at a point, as a sharp, bright spot by the mirror. In fact, this spot of light is the image of the sun on the sheet of paper. This point is the focus of the concave mirror. The heat produced due to the concentration of sunlight ignites the paper.

Question 22.
Give informations for the image formation by a concave mirror for different positions of an object.
Answer:

Question 23.
Draw the ray diagram for the image formation object at following positions by a concave mirror -
(i) At infinity
(ii) Far from centre of curvature.
Answer:

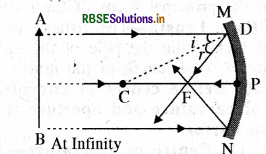
Question 24.
What is the difference in marking pattern for spherical mirror and spherical lens ?
Answer:

Question 25.
Draw the ray diagrams for a concave mirror, if the object is placed at focus.
Answer:

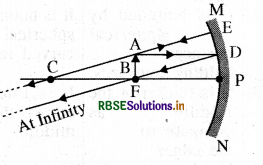
Question 26.
Give the uses of concave mirror.
Answer:

• As a reflector in search light, headlights of motor cars and projectors etc.
• By dentist for obtaining enlarged image of patient’s teeth.
• For converging solar radiations in solar cooker.
• Used as sharing mirrors, for obtaining large image of face.

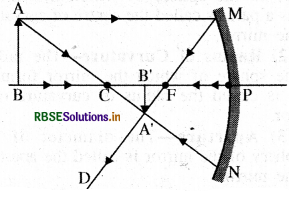
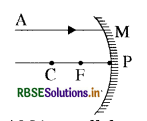
Question 27.
A ray AM falls on a spherical mirror as shown in the figure. Redraw the figure to show the reflected ray, angle of reflection and angle of incidence.

Answer:
Ray AM is parallel to principal axis, therefore after reflection it passes through focus as shown in figure.

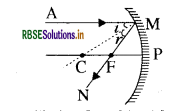
(i) Angle of incidence =∠AMC
(ii) Angle of reflection =∠NMC.

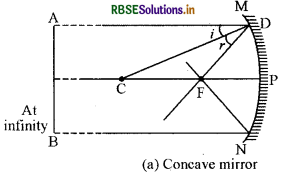
Question 28.
Draw a ray diagram to determine the principal focus (F) of concave mirror and convex mirror by parallel light rays.
Answer:

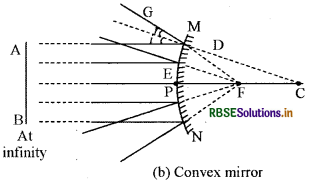
Question 29.
What do you mean by mirror formula and magnification or linear magnification.
Answer:
In spherical mirror, distance of object from the pole is called object distance (u). Distance of image from the pole of mirror is called image distance (v). Distance between pole and principal focus is called focal length (f ). Relation between these three quantities is called mirror formula and is represented by -
\(\frac{1}{v}+\frac{1}{u}=\frac{1}{f}\)

Magnification or linear magnification -
Magnification produced by spherical mirror is that which tells that how much magnified an image is in comparison to an object. The ratio of the size of the image to the size of the object is termed as linear magnification.
i.e\( m =\frac{\text { Height of the image }\left(h^{\prime}\right)}{\text { Height of the object }(h)}\)
\(m =\frac{h^{\prime}}{h}\)
The linear magnification m is also related to the object distance (u) and the image distance (v), as
\(m = \frac{h^{\prime}}{h}=\frac{v}{u}\)
There is no unit for linear magnification. A negative sign in the value of magnification indicates that the image is real. A positive sign in the value of magnification indicates that the image is virtual.

Question 30.
Refrative index of some medium is given in the table given below. Write the name of that medium whose optical density is maximum and minimum -

Answer:
Optical density of a medium is proportional to its refractive index, hence optical density of diamond is maximum and that of ice is minimum.

Question 31.
Refractive index of mediums A, B, C and D are given below -

In which of the given medium the speed of light is maximum and in which it is minimum.
Answer:
Speed of light in medium
\(=\frac{1}{\text { Refractive Index }}\)
Refractive index of medium'A is minimum, hence speed of light in medium A is maximum and speed of light is minimum in medium D.

Question 32.
Find the refractive index of that liquid in which the angle of incidence of a light ray is 45° and the angle of refraction is 30°.
Answer:
Given,
Angle of incidence (f ) =45°
Angle of refraction (r) = 30°
Formula:
\(n=\frac{\sin i}{\sin r}\)
\(n=\frac{\sin 45^{\circ}}{\sin 30^{\circ}}=\frac{\frac{1}{\sqrt{2}}}{\frac{1}{2}}=\frac{2}{\sqrt{2}}\)
\(n=\sqrt{2}\)= 1.414
Hence refractive index of the liquid is 1.414.

Question 33.
For opticians why it is convenient to use power instead of the focal length of the lens ?
Answer:
Many optical instruments consist of a number of lenses. They are combined to increase the magnification and sharpness of the image. The net power (P) of the lenses placed in contact is given by the algebric
sum of the indivisual powers P1, P2, P3,
as P = P1 + P2+ P3 + ...............
The use of powers, instead of focal lengths, for lenses is quite convenient for opticians. During eye-testing, an optician puts serveral different combinations of corrective lenses of known power, in contact, inside the testing spectacles frame. The optician calculates the power of the lens required by simple algebric addition.

For example, a combination of 2 lenses of power + 2.0D and + 0.25 D is equivalents to a single lens of power + 2.25 D. The simple additive property of the powers of lenses can be used to design lens systems to minimise certain defects in images produced by a single lens. Therefore, for opticians it is convenient to use power instead of focal length of lens.

Question 34.
What do you mean by lens ? How many types of lenses are there ?
Answer:
A lens is a transparent refracting medium bounded by two curved surfaces which are generally spherical or one of the surface is plane.

Lenses are of following two types -

1. Convex lens or converging lens: Convex lens has its two surfaces bulging outwards. These lens are thick at the middle and thin at the edges. They are often used as magnified lens.
2. Concave lens: A concave lens has its two surfaces caring inwards. These lenses are thick at the edges and thin at the middle.

In the given figure concave lens diverging the ray of light and convex lens is converging the ray of light is shown -

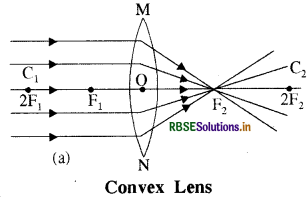
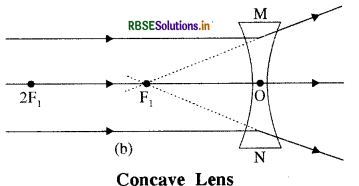
Question 35.
Define the following terms related to lens -
(i) Centre of Curvature
(ii) Radius of Curvature
(iii) Principal Axis
(iv) Principal Focus
(v) Focal Length.
Answer:
(i) Centre of Curvature: A lens has two spherical surfaces and each surface is a part of sphere. The centre of sphere of which the surface forms a part is called the centre of curvature of that surface.

(ii) Radius of Curvature: The radius of the sphere of which the refracting surface forms a part is called the radius of curvature of the surface.

(iii) Principal Axis: A straight line passing through the centres of curvatures of two surfaces of a lens is called principal axis.

(iv) Principal Focus: A point on principal axis on which light rays coming parallel to principal axis coverge or appear to diverge is known as principal focus.

(v) Focal Length: The distance between principal focus and optical centre is known as focal length. It is represented by ‘f'.

Question 36.
In a microscope four lenses of power + 0.5 D, + 1.0 D, + 2.0 D, and + 2.5 D are assembled. Find the net power.
Answer:
The net power (P) of the lenes placed in contact is given by the algebraic
sum of the individual powers P₁, P₂, P₃ as -
P = P₁ + P₂ + P₃ +
Here, it is given -
P₁ = + 0.5 D P₂ = + 1.0 D P₃ =.+ 2.0 D P₄ = + 2.5 D
Therefore, from the formula of net power -
P = (+ 0.5) + (+ 1.0) + (2.0) + (2.5)
P = + 6D

Question 37.
What is the nature, position and relative size of the image formed by a concave lens for the following positions of objects -
(i) At infinite
(ii) Between infinity and optical centre O of lens.
Answer:

Question 38.
What do you mean by cartesian sign convention for a spherical lens ?
Answer:
For a spherical lens following rules are to be followed -

1. All distances in a lens are to be measured from the optical centre of the lens.
2. Distances measured in the direction of incident ray are taken to be positive.
3. Distances opposite to the direction of incident ray are to be taken negative.
4. The height of the object or image measured above the principal axis are to be taken positive. Whereas below it are taken as negative.

The cartesian sign convention is clear from the'figure given below -

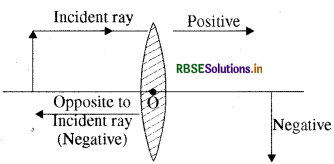
Question 39.
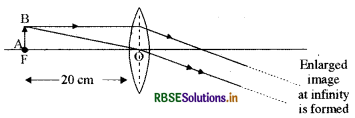
You are provided with a convex lens of 20 cm focal length. Where will you place an object to get its real inverted and enlarged image. Draw ray diagram.
Answer:
In convex lens the image formed is real inverted and enlarged if the object is placed at its focus. Hence object is placed 20 cm in front of the lens.

Question 40.
Explain the power and focal length for a combination of lenses.
Answer:
If two lenses of focal length f₁ and f₂ are placed in contact, this combination behaves like a single lens whose focal length F is given by
Since power of lens P = \(\frac{1}{f}\) Power of combination of lens
P = P₁ + P₂
If there is a combination of a number of lenses having power P₁, P₂, P₃ etc.
1 then The power of combination lens P = P₁+P₂+P₃+P₄

Question 41.
If a concave lens and a convex are placed together and their combined power is positive, at which lens power the combined lense power will work ?
Answer:
Since the combined power of lenses is positive, therefore the focal length of combined lenses is positive. Hence it will work as a convex lens.

Question 42.
If a convex lens is placed with a concave lens and their combined power is negative, at which lens power the combined lense power will work ?
Answer:
Since the value of power of combined lens is negative therefore the focal length of the combined lens is also negative. Hence it works as a concave lens.

Essay Type Questions

Question 1.
Determine the formation of images by spherical mirrors by drawing ray diagram.
Answer:
To study the formation of images by spherical mirror by drawing ray diagrams, consider an extended object, of finite size, placed in front of a spherical mirror. Each small portion of the extended object acts like a point source. An infinite number of rays originate from each of these points.

To construct the ray diagrams, in order to locate the image of an object, an arbitrarily large number of rays emanating from a point could be considered. However, it is more convenient to consider only two rays, for the sake of clarity of the ray diagram. These rays are so chosen that it is easy to know their directions after reflection from the mirror.

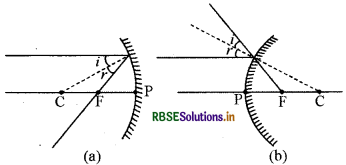
The intersection of at least two reflected rays give the position of image of the point object. Any two of the following rays can be considered for locating the image.
(i) A ray parallel to the principal axis, after reflection, will pass through the principal focus in case of a concave mirror or appear to diverge from the principal focus in case of a convex mirror.

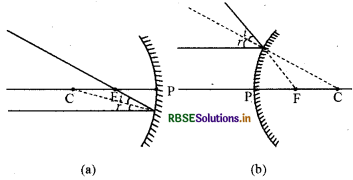
(ii) A ray passing through the principal focus of a concave mirror or a ray which is directed towards the principal focus of a convex mirror after reflection, will emerge parallel to the principal axis.

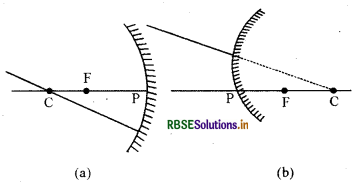
(iii) A ray passing through the center of a curvature of a concave mirror or directed in the direction of the center of curvature of a convex mirror, after reflection, is reflected back along the same path.

A ray incident obliquely to the principal axis, towards a point P (pole of the mirror), on the concave mirror or a convex mirror, is reflected obliquely.

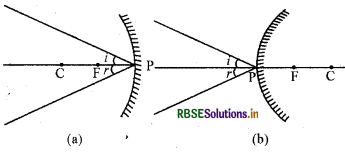
Question 2.
(a) Write the formula of magnification produced by a spherical mirror.
(b) Name the mirror which can form erect and magnified.
(c) Define principal focus of the convex mirror.
Answer:
(a) If h is the height of the object and h' is the height of the image, then the magnification ‘m’ produced by a spherical mirror is given by
\(m =\frac{\text { Heiht of the image }\left(h^{\prime}\right)}{\text { Height of the object }(h)}\)
\(m =\frac{h^{\dagger}}{h}\)

The magnification m is also related to the object distance (u) and image distance (v). It can be expressed as :
Magnification \((m) = \frac{h^{\prime}}{h}=-\frac{v}{u}\)

(b) Concave mirror can form an erect and magnified image.
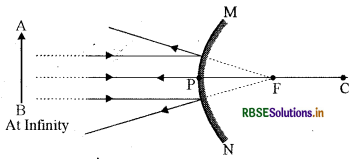
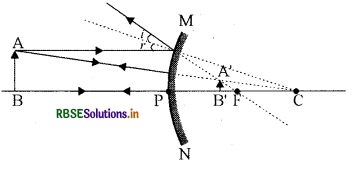
(c) When the rays parallel to the principal axis are reflected, then they appear to come from a point on the principal axis. This point is called the principal focus of the convex mirror.

Question 3.
Give the information of image formation by a convex mirror for the given positions of object and draw the ray diagrams for images -
(i) When object is at infinity (∞)
(ii) When object is in between P and infinity (∞)
Answer:

Question 4.
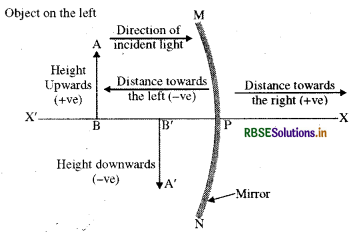
What do you mean by new cartesian sign convention for the spherical mirrors. Explain it with the help of diagram.
Answer:
While dealing with the reflection of light by spherical mirrors we shall follow a set of sign conventions called the New Cartesian sign convention. In this convention, the pole (P) of the mirror is takes as the origin. The principal axis of the mirror is taken as the x-axis (x'x) of the coordination system. The convention are as follows -

1. The object is always placed to the left of the mirror. This implies that the light from the object falls on the mirror from the left hand side.
2. All the distances parallel to the principal axis are measured from the pole of the mirror.
3. All distances measured to the right of the origin (along + x-axis) are taken as positive while those measured to the left of the origin (along x-axis) are taken as negative.
4. Distances measured perpendicular to and above the principal axis (along + yaxis) are taken as positive.
5. Distances measured perpendicular to and below the principal axis (along - yaxis) are taken as positive.

Question 5.
What is refraction of light ? What is the reason for refraction ? Explain the laws of refraction with the help of a ray diagram.
Answer:
Refraction:
The bending of light ray from its path in passing from one medium to other medium is called refraction of light.

Cause of Refraction:
The refraction of light causes due to the difference in velocities of light in both mediums.

Laws of Refraction:
Refraction of light is based on the following laws -
(i) The incident ray, the refracted ray and the normal to the interface at the point of incidence, all lie in the same plane.

(ii) The ratio of sine of angle of incidence to the sine of angle of refraction is a constant, for light of a given colour and for the given pair of media. If the angle of incidence be and the angle of refraction be ‘r’ then,
\(\frac{\sin i}{\sin r} \)= constant sinr.
This law is called the snell’s law and the constant is called the refractive index. Verification of the laws of refraction -
For verifying first law of refraction take a rectangular glass slab ABCD as shown in figure. Keep the slab on a white sheet.

PQ is a light ray which is incident on the surface AB of the slab. When it enters the glass slab at Q, it diverts from its original path and refracted in QR direction and afterwards escapes out from the glass slab is RS direction. QR and RS are called refracted ray and emergent ray respectively.

We observe that the incident ray PQ, refracted ray QR and normal QN all the three are in same plane of paper. Hence incident ray, refracted ray and normal all are in same plane. This is the first law of refraction.

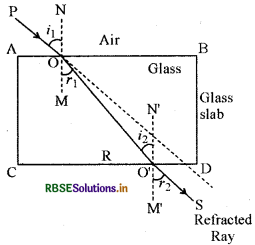
Refraction of light through rectangular glass slab. On joining Q to R we get refracted ray. Now draw a perpendicular at point Q and find out the angle of incidence (f) and angle of refraction (r).

On incidenting the ray of light at different angles on the slab we find the different values of i and r. On calculating we will find that value of remains constant. We call it as constant p. This is the second law of refraction. Hence
₁µ₂ orµ₁₂; \(\frac{\sin i}{\sin r} \)= a constant

Question 6.
Draw a ray diagram of refraction from a denser medium of light to rarer medium.
Answer:

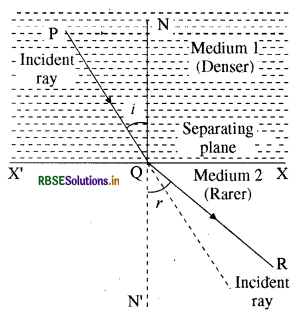
Question 7.
Define the refractive index of medium. Write three factors affecting it.
Answer:
Refractive index of a medium is defined as the ratio of the speed of light in air to that of, the speed in the material medium. Consider a ray of light travelling from medium 1 into medium 2, as shown in Figure. Let be the speed of light in medium 1 and v, be the speed of light in medium 2.

The refractive index of medium 2 with respect to medium 1 is given by the ratio of the speed of light in medium 1 and the speed of light in medium 2. This is usually represented by the symbol n₂₁ This can be expressed in an equation form as

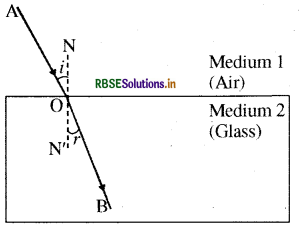
\(n_{21}=\frac{\text { Speed of light in medium } 1}{\text { Speed of light in medium } 2}=\frac{v_{1}}{v_{2}}\)

By the same argument, the refractive index of medium 1 with respect to medium 2 is represented as n₁₂. It is given by
\(n_{12}=\frac{\text { Speed of light in medium } 2}{\text { Speed of light in medium } 1}=\frac{v_{2}}{v_{1}}\)

If medium 1 is vacuum or air, then the refractive index of medium 2 is considered with respect to vacuum. This is called the absolute refractive index of the medium. It is simply represented as nr If c is the speed of light in air and v is the speed of light in the medium, then, the refractive index of the medium nm is given by
n_m = \(\frac{\text { Speed of light in air }}{\text { Speed of light in the medium }}=\frac{c}{v}\)

The absolute refractive index of a medium is simply called its refractive index. Factors affecting the refractive index are as follows -

• Nature of Medium
• Density
• Colour of the light.

Question 8.
On the basis of different rays, determine the location of reflections made by the lens by making a ray diagram.
Answer:
For drawing ray diagrams in lenses, we consider any two of the following rays -
(i) A ray of light from the object, parallel to the principal axis, after refraction from a convex lens, passes through the principal focus on the other side of the lens. In case of a concave lens, the ray appears to diverge from the principal focus located on the same side of the lens.


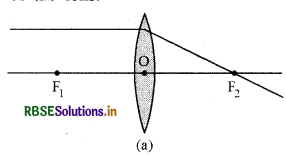
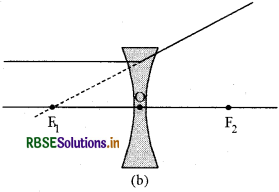
(ii) A ray of light passing through a principal focus, after refraction from a convex lens, will emerge parallel to the principal axis. A ray of light appearing to meet at the principal focus of a concave lens, after refraction, will emerge parallel to the principal axis.


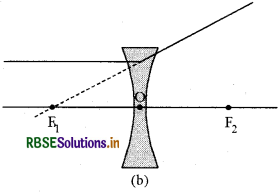
(iii) A ray of light passing through the optical centre of a lens will emerge without any deviation.

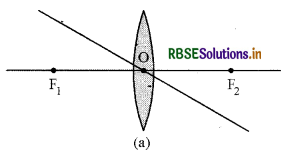
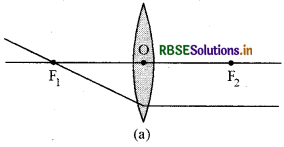
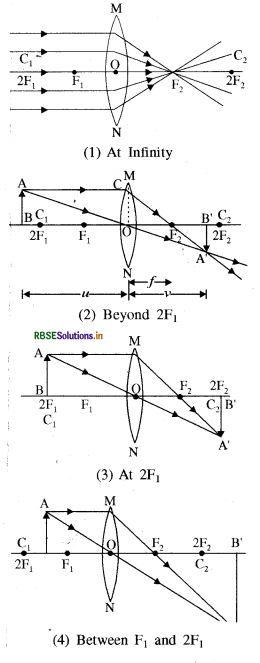
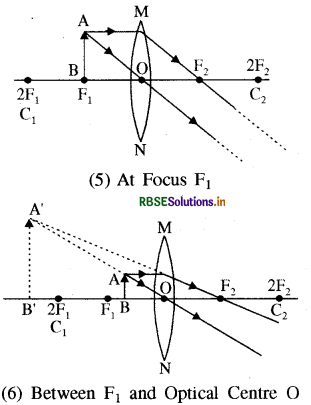
Question 9.
Draw the image formed by a convex lens of the object kept at following position -
(i) At infinity
(ii) Beyond 2F₁
(iii) At 2F₁
(iv) Between F₁and 2F₁
(v) At Focus F₁
(vi) Between Focus F₁ and Optical Centre O.
Answer:
Nature, position and size of image formed by a convex lens at different position of object is :




Question 10.
What is meant by ‘denser medium’ and ‘rarer medium’?
Answer:
The ability of a medium to refract light is also expressed in terms of its optical density. Optical density has a definite connotation, it is not the same as mass density. The terms ‘rarer medium’ and ‘denser medium’ actually means, ‘optically rarer medium’ and optically denser medium’ respectively. In comparing two media, the one with the larger refractive index is optically denser medium than the other.

The other medium of lower refractive index is optically rarer. The speed of light is higher in a rarer medium than a denser medium. Thus, a ray of light travelling from a rarer medium to a denser medium slows down and bends towards the normal. When it travels from a denser medium to a rarer medium, it speeds up and bends away from the normal.

Question 11.
Draw the ray diagram of the image formed when the object is placed between the f1 and 2f1 from the optical centre of following lenses -
(i) Convex Lens
(ii) Concave Lens. Here f₁ is the focal length of the lens.
Answer:
(i) Convex Lens: Object placed between 2F₁ and F₁ at a convex lens forms image which is real, inverted and large -

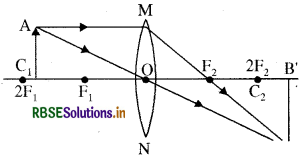
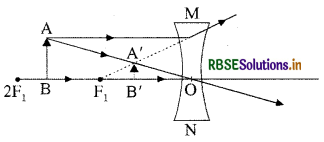
(ii) Concave Lens: Object placed between F₁ and 2F₁ of a concave lens formsvirtual, erect and small image-

Numerical Questions

Question 1.
The focal length of a concave lens is 40 cm. What will be its power ?
Answer:
Power of lens -
P =\( \frac{1}{f}\)meter
Here.
f= -40cm
P = \(-\frac{100}{40}\)
P = -2.5 D

Question 2.
The rear view convex mirror of an automobile has radius of curvature 3.00 m. If a bus is situated 5 m away from the mirror then find the nature, position and size of the image.
Answer:
Given :
Radius of curvature R = + 3 m
Object distance u = - 5 m ' (From sign convention)
Image distance v = ?
Image’s heìght h’ = ?
We know that\(\begin{gathered} f=\frac{\mathrm{R}}{2} \\ f=\frac{+3.00 m}{2}=+1.50 \mathrm{~m} \end{gathered}\)
From Mirror formula
\(\frac{1}{v}+\frac{1}{u}=\frac{1}{f}\)
\(\frac{1}{v}=\frac{1}{f}-\frac{1}{u}\)
Substituting the values.
\(m=-\left(\frac{1.15 m}{-5.00 m}\right)\)
\(m=\frac{115}{500}=+0.23\)
Here the value of magnification is +ve.
Hence the image is virtual, erect and small in size to object (0.23 times).

Question 3.
If an ophtalmologist suggest a corrective lens of power + 2.5 D and - 4.0 D, then determine the focal length of the lens.
Answer:
Lens power P = \(\frac{1}{8}\)metre 
(i) Here, P = + 2.5D
‘I’hen, 2.5 D = \(\frac{1}{f}\)
f=\(\frac{1}{2.5}\)meter
 = \(\frac{100}{2.5}\) cm
= +40 cm
Therefore, the positive sign shows that the lens will be convex lens whose focal length will be 40 cm.

(ii) When P = - 4.0 D
Then -40 =\(\frac{1}{f}\)
f =\(\frac{1}{-4.0} \mathrm{~m}\)
\(-\frac{100}{4} \mathrm{~m}\)
f = -25cm
The negative sign shows thai the lens will he concave, whose focal length will be 25 cm.

Question 4.
An object of height 4 cm is placed 6 cm in front of an concave mirror of 12 cm focal length. Find the position, nature and size of the image kept nearer.
Answer:
Given :
u = - 6 cm [Sign convention]
f= - 12 cm [Sign convention]
height of object h' = 4 cm
From Mirror formula -
\(\frac{1}{u}+\frac{1}{v}=\frac{1}{f}\)
On substituting the values, we get
\(-\frac{1}{6}+\frac{1}{v}=-\frac{1}{12}\)
\(\frac{1}{v}=-\frac{1}{12}+\frac{1}{6}=\frac{-1+2}{12}\)
\(\frac{1}{v}=\frac{1}{12}\)
v = 12 cm
Hence, the image is formed behind the mirror at a distance 12 cm. Here the value of v is positive, hence the image is virtual.

Magnification m =\(\frac{h^{\prime}}{h}=-\frac{v}{u}\)
\(\begin{aligned} \frac{h^{\prime}}{h} &=-\frac{v}{u} \\ h^{\prime} &=-\left(\frac{v}{u}\right) \times h \end{aligned}\)
On substituting the values, we get
\(h^{\prime}=-\left(\frac{12}{-6}\right) \times 4\)
h' = 8 cm
Hence, the height of image is 8 cm. Here the sign is positive, therefore the image is erect.

Question 5.
The image of an object placed in front of a concave mirror is formed at 100 cm in front of the mirror. If the focal length of the mirror is 98 cm, find the distance of the object.
Answer:
From Mirror Formula:  \(\frac{1}{f}=\frac{1}{v}+\frac{1}{u}\)
Here.
f= - 98 cm
u = -100 cm
v = ?
By putting values.
\(\frac{1}{-98}=\frac{1}{u}+\frac{1}{-100}\)
\(\frac{1}{u}=\frac{1}{100}-\frac{1}{98}\)
\(-\frac{1}{4900}\)
u = - 4900 cm.

Question 6.
Radius of Curvature of a convex lens of moving vehicle is 2.0 m. A truck comes from a distance of 3.5 m behind it. Find
(i) The position of image
(ii) The size and nature of image in comparison to truck.
Answer:
According to the Question: Radius of Curvature R = 2.0 m v
R = 2f
\(f=\frac{\mathrm{R}}{2}=\frac{2.0}{2}=1 \mathrm{~m}\)
u - -3.5 m [From sign convention]

Mirror formula:
\(\frac{1}{u}+\frac{1}{v}=\frac{1}{f}\)
\(\frac{1}{v}=\frac{1}{f}-\frac{1}{u}\)
\(\frac{1}{v}=\frac{1}{1}-\left(-\frac{1}{3.5}\right)=1+\frac{1}{3.5}\)
\(\frac{1}{v}=1+\frac{10}{35}=1+\frac{2}{7}\)
\(=\frac{7+2}{7}=\frac{9}{7}\)
\(v=\frac{7}{9}=0.78 \mathrm{~m}\)
Truck is 0.78 m behind the mirror. The nature and size of image can be find out by following formula -
\(m=-\frac{v}{u}\)
\(=-\left(\frac{\frac{7}{9}}{-3.5}\right)=\frac{7}{9} \times \frac{1}{3.5}=\frac{2}{9}\)
Hence the image of truck is\( \frac{2}{9}\)times the size of truck. Here the value of m is positive. Hence the image is virtual and erect.

Question 7.
Refractive index of dense flint glass is 1.65 and refractive index of alcohol to air is 1.36. What is the refractive index of flint glass in comparison to alcohol ?
Given -  n_g = 1.65
n_al= 1.36
\({ }^{a l} n_{g}=\frac{n_{g}}{n_{a l}}=\frac{1.65}{1.36}=1.213\)

Question 8.
A object is placed 15 cm in front of a concave mirror. Find the nature, position and magnification of the image made by the mirror. The focal length of the mirror is 10 cm.
Answer:
Mirror formula
\(\frac{1}{f}=\frac{1}{v}+\frac{1}{u}\)
Here,
u = - 15 cm
f = - 10 cm
v = ?
\(\frac{1}{-10}=\frac{1}{v}+\frac{1}{-15}\)
\(\frac{1}{v}=\frac{1}{15}-\frac{1}{10}=-\frac{1}{30}\)
v = - 30 cm.
So, the image will be formed to the left of the mirror and will be real and inverted.

Question 9.
Light enters into glass from air having refractive index 1.5. Find out the time taken by the light to pass a glass strip of 50 cm thickness.
Answer:
Given -
Speed of light in air c = 3 x 10⁸ m/s
Refractive index of glass n = 1.5
∵ Refractive index\( n=\frac{c}{v}\)
\(v=\frac{c}{n}\)
On substituting values,
\(v=\frac{3 \times 10^{8}}{1.5}=2 \times 10^{8} \mathrm{~m} / \mathrm{s}\)
Hence speed of light in glass = 2 x 10⁸ m/s
\(\text { Time taken } \begin{aligned} &=\frac{\text { Distance }}{\text { Speed }}=\frac{0.5 \mathrm{~m}}{2 \times 10^{8}} \\ &=25 \times 10^{-9} \mathrm{sec} \end{aligned}\)

Question 10.
Focal lengths of a concave lens is 15 cm. At what distance should the object be placed from the lens so as to obtain an image at 10 cm. from the lens. Find out the magnification produced by the lens also.
Answer:
We know that in a concave lens, the image formed is always virtual, erect and in the same direction where the object is placed.
Given -
Image distance v = - 10 cm
Focal length f = - 15 cm
Object distance u = ?
From lens formula -
\(\frac{1}{v}-\frac{1}{u}=\frac{1}{f}\)
\(\frac{1}{u}=\frac{1}{v}-\frac{1}{f}\)
On substituting the values, we get
\(\frac{1}{u}=-\frac{1}{10}-\left(-\frac{1}{15}\right)=\frac{-1}{10}+\frac{1}{15}\)
\(\frac{1}{u}=\frac{-3+2}{30}=\frac{-1}{30}\)
u = -30 cm
Hence object distance = 30 cm.

Magnification \(m =\frac{v}{u}\)
\(m=\frac{-10 \mathrm{~cm}}{-30 \mathrm{~cm}}=\frac{1}{3}=+0.33\)
Here the positive sign shows that the image formed is virtual and erect. The size of image is 1/3 rd the size of the object.

Question 11.
A concave mirror produces a virtual image three times larger than the image. The curvature radius of the mirror is 36 cm. Find the position of the object.
Answer:
Imagine that the object is at x distance. Then
From Magnification formula -
\(m=\frac{-v}{u}\)
Here, m = + 3
u = - x cm
By putting the values
\(=3=\frac{-v}{-x}=v=3 x\)
From mirror formula -
\(\frac{1}{f}=\frac{1}{v}+\frac{1}{u}\)
Here,
R = -36 cm
\(\begin{aligned} &f=\frac{\mathrm{R}}{2} \\ &f=\frac{-36}{2}=-18 \end{aligned}\)
So,
\(\frac{1}{-18}=\frac{1}{3 x}-\frac{1}{x}\)
x = 12 cm
u = -12 cm.

Question 12.
An object of 2.0 cm height is placed vertical to the principal axis of a convex lens of focal length 10 cm. The distance of object from lens is 15 cm. Find the nature, position and size of the image. Also find out its magnification.
Answer:
Given -
Height of object h = + 2.0 cm
Focal length f = + 10 cm
Object distance u = - 15 cm
Image distance v = ?
Height of image h' = ?
From lens formula -
\(\begin{aligned} \frac{1}{v}-\frac{1}{u} &=\frac{1}{f} \\ \frac{1}{v} &=\frac{1}{u}+\frac{1}{f} \end{aligned}\)
On substituting values, we get
\(\begin{aligned} &\frac{1}{v}=-\frac{1}{15}+\left(+\frac{1}{10}\right)=\frac{-1}{15}+\frac{1}{10} \\ &\frac{1}{v}=\frac{-2+3}{30}=\frac{1}{30} \end{aligned}\)
v = + 30 cm
Positive value of v shows that the image formed towards the right side of the optical centre of lens at 30 cm distance. Hence the image is virtual and erect.

Magnification \(m =\frac{h^{\prime}}{h}=\frac{v}{u}\)
\(\text { Or } h^{\prime}=\left(\frac{v}{u}\right) \times h\)
On substituting values, we get
\(h^{\prime}=\left(\frac{+30}{-15}\right) \times 2.0\)
h' = - 4Ocm
Height of image = - 4.0 cm .
\(\text { Magnification } m=\frac{+30 \mathrm{~cm}}{-15 \mathrm{~cm}}=-2\)
Negative values of m and h' shows that image is real and inverted. It is formed below the principal axis. This image is two times magnified.
Question 13.
A converging lens having power 5D is placed with a diverging lens having power 3D. Calculate the focal length of lens combination.
Answer:
Power of Convex lens P₁ = 5 D
Power of Convex lens PP₂ = - 3 D
Power of combined lens P = PP₁ + PP₂
= 5 D + (-3 D)
= 2 D
Focal length of the lens
\(\begin{aligned} &f=\frac{1}{\mathrm{P}(\mathrm{in} \mathrm{} \mathrm{m})}=\frac{1}{2} \mathrm{~m} \\ &f=\frac{1}{2} \mathrm{~m}=50 \mathrm{~cm} \end{aligned}\)

Question 14.
A concave mirror forms two timer magnified and real image of an object placed at 15 cm from its pole. Determine the distance of image from mirror and focal length of the mirror.
Answer:
Given -
u = - 15 cm
\(m = 2 = +\frac{v}{u}\) [ ∵ Image is real]
\(2 = \frac{v}{-15}\)
Image distance v = 2 x - 15 = - 30 cm
Spherical Mirror formula -
\(\begin{aligned} &\frac{1}{f}=\frac{1}{v}+\frac{1}{u} \\ &\frac{1}{f}=-\frac{1}{30}-\frac{1}{15} \\ &\frac{1}{f}=\frac{-1-2}{30}=\frac{-3}{30} \end{aligned}\)
f₂ - 10 cm
Hence the focal length of mirror is - 10 cm.

Question 15.
The refractive index of glass with respect to air is \(\frac{3}{2}\)and the refractiveindex of water with respect to air is 3. If the speed of light in air is 3 x 10⁸ m/s, then (a) in glass, (b) in water, calculate the speed of light ?
Answer:
Given-
n_g = \(\frac{3}{2}\)and n_w =\(\frac{4}{3}\), c= 3 x10⁸ m/s
∵\(ng =\frac{c}{v}\)
∴ v (Speed of light in glass)
\(\frac{c}{n_{g}} \)
\(\frac{3 \times 10^{8}}{\frac{3}{2}}=\frac{3 \times 10^{8} \times 2}{3}\)
Again, n_w =\(\frac{C}{v^{\prime}}\)
∴\( v (Speed of light in water) =\frac{c}{n_{w}} \frac{3 \times 10^{8}}{\frac{4}{3}}=\frac{3 \times 10^{8} \times 3}{4} \frac{9}{4} \times 10^{8}=2.25 \times 10^{8} \mathrm{~m} / \mathrm{s}\)
Therefore.
Speed of light in glass = 2 x 10⁸ m/s. and
Speed of light in water = 2.25 x m/s