RBSE Class 10 Maths Notes Chapter 9 त्रिकोणमिति का अनुप्रयोग

These comprehensive RBSE Class 10 Maths Notes Chapter 9 त्रिकोणमिति का अनुप्रयोग will give a brief overview of all the concepts.

RBSE Class 10 Maths Chapter 9 Notes त्रिकोणमिति का अनुप्रयोग

→ दृष्टि-रेखा प्रेक्षक की आँख से प्रेक्षक द्वारा देखी गई वस्तु के बिन्दु को मिलाने वाली रेखा होती है।

→ उन्नयन कोण (Angle of Elevation)-जब भी कोई व्यक्ति/दर्शक अथवा अन्वेषक अपनी आँख से | स्वाभाविक क्षैतिज तल से ऊपर की ओर स्थित वस्तु को देखता है, उस वक्त उस व्यक्ति की आंख के स्वाभाविक क्षैतिज तल और देखी जाने वाली वस्तु के मध्य जो कोण बनता है उसे उन्नयन कोण (Angle of Elevation) कहते हैं। जैसे
यदि P उड़ती हुई पतंग को जब उड़ाने वाला देखता है तो उसकी आँख का स्वाभाविक तल अर्थात् क्षैतिज अक्ष 'OX' होगा और PM पतंग की क्षैतिज अक्ष 'OX' से ऊर्ध्वाधर दूरी तथा OP आँख से पतंग तक की सीधी दूरी कहलाएगी।

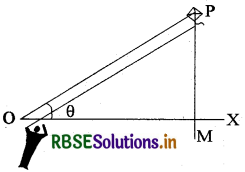
इस प्रकार एक समकोण त्रिभुज OMP आकृति बनती है। जहाँ 0 0 ∠PMO = समकोण तथा ∠POM = 0 उन्नयन कोण कहलाएगा। उन्नयन कोण क्षैतिज से ऊपर की ओर नापे जाते हैं। अर्थात् देखी गई। वस्तु का उन्नयन कोण दृष्टि रेखा और क्षैतिज रेखा से बना कोण होता है जबकि यह क्षैतिज स्तर से ऊपर होता है अर्थात् वह स्थिति जबकि वस्तु को देखने के लिए हमें अपने सिर को ऊपर उठाना पड़ता है।
और फिर समकोण त्रिभुज के लिए पाइथागोरस प्रमेय का प्रयोग करते हुए त्रिकोणमिति की सहायता से OP, OM या PM दूरी ज्ञात करना सम्भव हो जाता है।
. क्षैतिज रेखा

→ अवनमन कोण (Angle of Depression)—जब कोई व्यक्ति -
अवनमन कोण स्वयं उच्च तल पर हो और आँख के स्वाभाविक क्षैतिज तल से नीचे स्थापित किसी वस्तु को नेत्र से देखता है, अर्थात् जब वस्तु को देखने के लिए व्यक्ति को नीचे की ओर देखना पड़ता है, उस अवस्था में आँख के स्वाभाविक क्षैतिज तल और वस्तु के मध्य में जो कोण बनता है उसे अवनमन कोण कहते हैं।

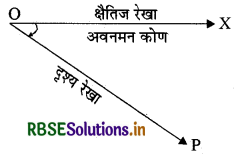
जैसे - जब कोई दर्शक जो बिन्दु 0 पर स्थित है, बिन्दु P को देखता है तो दृश्य रेखा OP तथा क्षैतिज | रेखा ox के बीच का कोण ∠XOP, P का O के सापेक्ष अवनमन कोण कहलाता है। देखी गई वस्तु का अवनमन कोण दृष्टि रेखा और क्षैतिज रेखा से बना कोण होता है जबकि क्षैतिज रेखा क्षैतिज स्तर से नीचे होता है अर्थात् वह स्थिति जबकि वस्तु को देखने के लिए हमें अपने सिर को झुकाना पड़ता है।

→ O का P के सापेक्ष उन्नयन कोण =P का O के सापेक्ष अवनमन कोण जैसा कि दिए गए चित्र में दर्शाया गया है कि अवनमन कोण व उन्नयन कोण बराबर हैं।

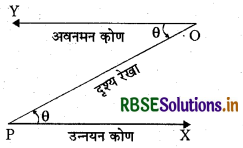
→ त्रिकोणमितीय अनुपातों की सहायता से किसी वस्तु की ऊँचाई या लम्बाई या दो सुदूर वस्तुओं के बीच की दूरी ज्ञात की जा सकती है।