RBSE Class 10 Maths Notes Chapter 8 त्रिकोणमिति का परिचय

These comprehensive RBSE Class 10 Maths Notes Chapter 8 त्रिकोणमिति का परिचय will give a brief overview of all the concepts.

RBSE Class 10 Maths Chapter 8 Notes त्रिकोणमिति का परिचय

→ अंग्रेजी शब्द "trigonometry' की व्युत्पत्ति ग्रीक शब्दों ‘tri' (जिसका अर्थ है तीन), "gon' (जिसका अर्थ है, भुजा) और 'metron' (जिसका अर्थ है माप) से हुई है। वस्तुतः त्रिकोणमिति में एक त्रिभुज की भुजाओं और कोणों के बीच के सम्बन्धों का अध्ययन किया जाता है।

→ प्राचीनकाल के खगोलविद् त्रिकोणमिति का प्रयोग पृथ्वी से तारों और ग्रहों की दूरियाँ मापने में करते। थे। आज भी इसका उपयोग इंजीनियरिंग और भौतिक विज्ञान में आज भी किया जाता है।।

→ पाइथागोरस प्रमेय (Pythagoras Theorem) "किसी समकोण त्रिभुज में समकोण बनाने वाली भुजाओं के वर्गों का योग त्रिभुज के कर्ण के वर्ग के बराबर होता

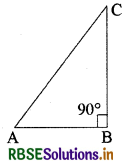
(AC)² = (AB)² + (BC)²
इस प्रमेय की सहायता से यदि हमें दो भुजाओं की माप ज्ञात हो, तो तीसरी भुजा की माप ज्ञात कर सकते हैं।

→ त्रिकोणमितीय अनुपात - समकोण त्रिभुज की भुजाओं के कुछ अनुपातों का उसके न्यूनकोणों के सापेक्ष अध्ययन को त्रिकोणमितीय अनुपात कहते हैं।


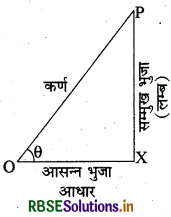
tan θ = सम्मुख भुजा/आसन्न भुजा
= लम्ब/आधार या स्पर्श ज्या θ

cot θ = आसन्न भुजा/सम्मुख भुजा
= आधार/लम्ब या कोटिस्पर्शज्या θ

sec θ = कर्ण/आसन्न भुजा
= कर्ण/आधार या व्युत्क्रम कोटिज्या θ

cosec θ = कर्ण/सम्मुख भुजा
= कर्ण/लम्ब या व्युत्क्रम ज्या θ

→ व्युत्क्रम त्रिकोणमितीय अनुपात

• \(\frac{1}{\sin \theta}\) = cosec θ ⇒ sin θ cosec θ = 1
• \(\frac{1}{\cos \theta}\) = sec θ ⇒ cot θ sec θ = 1
• \(\frac{1}{\tan \theta}\) = cot θ ⇒ tan θ cot θ = 1
• cosec A = \(\frac{1}{\sin \mathrm{A}}\), sec A = \(\frac{1}{\cos A}\)
• tan A = \(\frac{1}{\cot \mathrm{A}}\) cotA , tan A = \(\frac{\sin A}{\cos A}\)

→ यदि एक न्यूनकोण का एक त्रिकोणमितीय अनुपात ज्ञात हो, तो कोण के शेष त्रिकोणमितीय अनुपात सरलता से ज्ञात किए जा सकते हैं।

→ sin A या cos A का मान कभी भी 1 से अधिक नहीं होता, जबकि sec A या cosec A का मान सदैव 1 से अधिक या 1 के बराबर होता है।

→ विशेष कोणों के त्रिकोणमितीय अनुपातों की सारणी

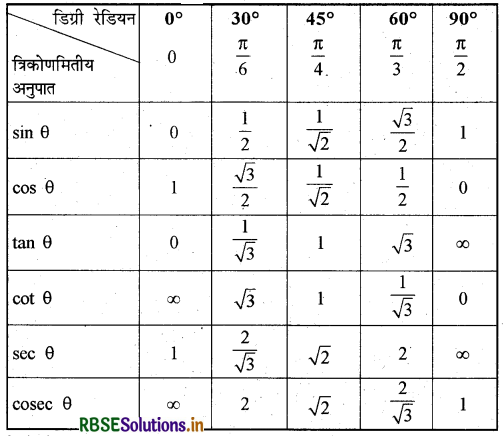
→ पूरक कोणों के त्रिकोणमितीय अनुपात-पूरक कोण कोई दो कोण परस्पर पूरक कोण कहलाते हैं यदि इनकी माप का योगफल 90° हो।

• sin (90° - θ) = cos θ
• cot (90° - θ) = tan θ
• cos (90° - θ) = sin θ
• sec (90° - θ) = cosec θ
• tan (90° - θ) = cot θ
• cosec (90° - θ) = sec θ

इसी प्रकार किसी कोण का sin θ = उसके पूरक कोण का cosine
किसी कोण का tangent = उसके पूरक कोण का cotangent
किसी कोण का secant = उसके पूरक कोण का cosecant
इनका विलोम भी सत्य है।

→ त्रिकोणमितीय सर्वसमिकायें-एक कोण के त्रिकोणमितीय अनुपातों से सम्बन्धित सर्वसमिका को त्रिकोणमितीय सर्वसमिका कहा जाता है। सर्वसमिकाओं को सिद्ध करते समय निम्नलिखित बिन्दुओं को ध्यान में रखना चाहिए

• सर्वसमिका को जटिल पक्ष में हल प्रारम्भ करते हैं और इसमें मूलभूत सर्वसमिकाओं को प्रयोग कर दूसरा पक्ष ज्ञात करते हैं।
• यदि सर्वसमिकाओं में कई त्रिकोणमितीय अनुपात विद्यमान हों, तो उनको sine अथवा cosine के रूप में | व्यक्त करना सामान्यतया सुविधाजनक होता है।
• यदि करणी चिह्न (radical sign) लगा हो तो उसे यथासम्भव हटाना चाहिए।
• यदि सर्वसमिका के एक पक्ष से दूसरा पक्ष सरलतापूर्वक ज्ञात नहीं किया जा सकता हो, तो दोनों पक्षों को सरल करके एक ही राशि अथवा पद के समानक सम (identically equal) सिद्ध करना चाहिए।

→ वर्ग सम्बन्ध

• sin²θ+ cos²θ = 1 ⇒ sin²θ = 1 - cos²θ या cos²θ = 1 - sin²θ
• sec²θ - tan²θ = 1 ⇒ sec²θ = 1 + tan²θ या tan²θ = sec²θ - 1
• cosec²θ - cot²θ = 1 ⇒ cosec²θ = 1 + cot²θ या cot²θ = cosec²θ - 1