RBSE Class 10 Maths Notes Chapter 7 निर्देशांक ज्यामिति

These comprehensive RBSE Class 10 Maths Notes Chapter 7 निर्देशांक ज्यामिति will give a brief overview of all the concepts.

RBSE Class 10 Maths Chapter 7 Notes निर्देशांक ज्यामिति

→ निर्देशांक ज्यामिति - इस ज्यामिति में बिन्दु की स्थिति विशिष्ट संख्याओं, जिन्हें निर्देशांक कहते हैं, के द्वारा निरूपित की जाती है तथा उनसे बनी विभिन्न आकृतियों (रेखाओं, वक्रों आदि) को बीजीय समीकरणों द्वारा. निरूपित किया जाता है। इस प्रकार ज्यामिति की यह शाखा रेखागणित तथा बीजगणित के सम्मिश्रण से विकसित हुई है। अतः निर्देशांकों के प्रयोग के कारण गणित की इस शाखा को निर्देशांक ज्यामिति (Co-ordinate geometry) कहा जाता है।

→ कार्तीय निर्देशांक (Cartesian co-ordinate)-माना किसी समतल में दो परस्पर लम्बवत् रेखाएँ XOX' और YOY' हैं जो कि बिन्दु 0 पर प्रतिच्छेद करती हैं। इन्हें निर्देशांक अक्ष (Co-ordinate axes) कहते हैं और 0 को मूल बिन्दु (origin) कहते हैं। XOX' तथा YOY' परस्पर लम्बवत् + हैं, अत: XOX' और YOY' को समकोणिक अक्ष या आयतीय निर्देशांक अक्ष । (भज) कहते हैं।

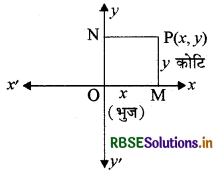
→ x-अक्ष पर स्थित प्रत्येक बिन्दु का y-निर्देशांक = 0

→ y-अक्ष पर स्थित प्रत्येक बिन्दु का x-निर्देशांक = 0

→ चतुर्थांश में निर्देशांकों के चिह्न –यदि समतल में किसी बिन्दु p के निर्देशांक (x, y) हों, तो

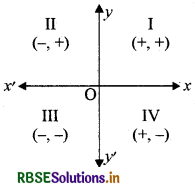
• प्रथम चतुर्थांश में x > 0, y > 0; निर्देशांक (+, +)
• द्वितीय चतुर्थांश में x < 0, y > 0; निर्देशांक (-, +)
• तृतीयं चतुर्थांश में x < 0, y < 0; निर्देशांक (-, -)
• चतुर्थ चतुर्थांश में x > 0, y <.0; निर्देशांक (+, -)

स्मरणीय -

• किसी बिन्दु P के निर्देशांक (x, y) हैं, तो इसे P(x, y) लिख सकते हैं।
• किसी बिन्दु का भुज, बिन्दु की y-अक्ष के लम्बवत् दूरी पर होती है।
• किसी बिन्दु की कोटि, बिन्दु की x-अक्ष के लम्बवत् दूरी होती है।
• किसी बिन्दु का भुज, y-अक्ष के दायीं ओर धनात्मक और बायीं ओर ऋणात्मक होता है।
• किसी बिन्दु की कोटि x-अक्ष के ऊपर धनात्मक और नीचे ऋणात्मक होती है।
• यदि y = 0 हो, तो बिन्दु x-अक्ष पर स्थित होता है।
• यदि x = 0 हो, तो बिन्दु y-अक्ष पर स्थित होता है।
• यदि x = 0, y = 0 हो, तो बिन्दु मूल बिन्दु है।

→ दो बिन्दुओं के बीच की दूरी (Distance between two points) समतल में स्थित दो बिन्दुओं P(x₁, y₁) तथा Q(x₂, y₂) के बीच की दूरी

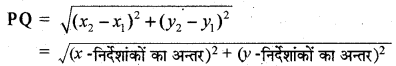
→ विशेष स्थिति—मूल बिन्दु 0(0, 0) से किसी बिन्दु P(x, y) की दूरी
OP = \(\sqrt{x^{2}+y^{2}}\)

→ दो बिन्दुओं के मध्य दूरी का अन्तःविभाजन-माना समतल में दो बिन्दु A और B हैं, यदि रेखा AB पर कोई बिन्दु P, A व B के मध्य स्थित हो, तो इस प्रकार के विभाजन को अन्तःविभाजन कहते हैं।

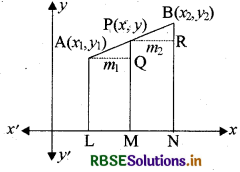
माना समतल में स्थित दो बिन्दु A(x₁, y₁) और B(x₂, y₂) हैं और बिन्दु P(x, y) रेखाखण्ड AB को m₁ : m₂, में अन्त:विभाजित करता है तो बिन्दु P के अभीष्ट निर्देशांक \(\left[\frac{m_{1} x_{2}+m_{2} x_{1}}{m_{1}+m_{2}}, \frac{m_{1} y_{2}+m_{2} y_{1}}{m_{1}+m_{2}}\right]\) इसे विभाजन सूत्र भी कहते हैं।

→ यदि P रेखाखण्ड AB को k : 1 के अनुपात में विभाजित करें तो बिन्दु P के निर्देशांक \(\left(\frac{k x_{2}+x_{1}}{k+1}, \frac{k y_{2}+y_{1}}{k+1}\right)\) होंगे।

→ यदि बिन्दु P रेखाखण्ड AB का मध्य बिन्दु हो, अर्थात् P, AB को 1 : 1 में विभाजित करता हो, तो P के निर्देशांक \(\left(\frac{x_{2}+x_{1}}{2}, \frac{y_{2}+y_{1}}{2}\right)\) होंगे।

→ बिन्दुओं (x₁, y₁), (x₂, y₂) और (x₃, y₃) से बनने वाले त्रिभुज का क्षेत्रफल व्यंजक \(\frac{1}{2}\)[x₁[x₂(y₂ - y₁) + x₂(y₃ - y₁) + x₃(y₁ - y₂)] का संख्यात्मक मान होता है।