RBSE Class 10 Maths Notes Chapter 3 दो चरों वाले रखिक समीकरण का युग्म

These comprehensive RBSE Class 10 Maths Notes Chapter 3 दो चरों वाले रखिक समीकरण का युग्म will give a brief overview of all the concepts.

RBSE Class 10 Maths Chapter 3 Notes दो चरों वाले रखिक समीकरण का युग्म

→ वह समीकरण जिसको ax² + by + c = 0 के रूप में रखा जा सकता है, जहाँ a, b और c वास्तविक संख्याएँ हैं और a तथा b दोनों शून्य नहीं हैं, दो चरों x और y में एक रैखिक समीकरण कहलाता है। प्रतिबन्ध a और b दोनों शून्य नहीं हैं, को हम प्रायः a² + b² + 0 से प्रदर्शित करते हैं।

→ समीकरण का प्रत्येक हल उसको निरूपित करने वाली रेखा पर स्थित एक बिन्दु होता है।

→ दो चरों में दो रैखिक समीकरण एक रैखिक समीकरणों का युग्म कहलाता है। दो चरों x और y में रैखिक समीकरण युग्म का व्यापक रूप
a₁x + b₁y + c₁ = 0
और a₂x + b₂y + c₂ = 0 है।
जहाँ a₁, a₂, b₁, b₂, c₁, तथा c₂, ऐसी वास्तविक संख्याएँ हैं कि a₁² + b₁² ≠ 0, a₂² + b₂² ≠ 0 है।

→ एक रैखिक समीकरण युग्म को निम्नांकित रूप में निरूपित किया जा सकता है तथा हल किया जा सकता

• ग्राफीय विधि द्वारा तथा
• बीजगणितीय विधि द्वारा।

→ ग्राफीय विधि - दो चरों में एक रैखिक समीकरण युग्म का ग्राफ दो रेखाएँ निरूपित करता है जो निम्नलिखित गुण प्रदर्शित करती हैं।

• यदि रेखाएँ एक बिन्दु पर प्रतिच्छेद करती हैं, तो वह बिन्दु दोनों समीकरणों का अद्वितीय हल होता है। इस स्थिति में समीकरण युग्म संगत होता है।
• यदि रेखाएँ संपाती हैं, तो उनके अपरिमित रूप से अनेक हल होते हैं। रेखा पर स्थित प्रत्येक बिन्दु हल होता है। इस स्थिति में समीकरण युग्म आश्रित (संगत) होता है।
• यदि रेखाएँ समान्तर हैं, तो समीकरण युग्म का कोई हल नहीं होता है। इस स्थिति में समीकरण युग्म असंगत होता है।

→ बीजगणितीय विधि - हम एक रैखिक समीकरण युग्म के हल ज्ञात करने की निम्नांकित विधियों को जानते हैं

• प्रतिस्थापन विधि - इस विधि में हम एक चर का मान दूसरे चर के पद में व्यक्त करके रैखिक समीकरण युग्म को हल करने के लिए प्रतिस्थापित करते हैं। इसलिये इस विधि को प्रतिस्थापन विधि कहते हैं।
• विलोपन विधि - इस विधि में हम किसी भी एक चर को विलुप्त करके, एक चर में एक रैखिक समीकरण प्राप्त करते हैं। उस रैखिक समीकरण को हल करके किसी भी एक चर राशि का मान प्राप्त करते हैं। उस मान को किसी भी समीकरण में रखकर दूसरी चर राशि का मान निकाला जा सकता है।
• वज्रगुणन विधि - इस विधि में दोनों समीकरणों को इस प्रकार लिख लेते हैं कि उनके दायें पक्ष में शून्य हो।

माना समीकरण
a₁x + b₁y + c₁ = 0
तथा a₂x + b₂y + c₂ = 0 है।
\(\frac{x}{b_{1} c_{2}-c_{1} b_{2}}=\frac{y}{c_{1} a_{2}-a_{1} c_{2}}=\frac{1}{a_{1} b_{2}-b_{1} a_{2}}\)

संजीव पास बुक्स उपर्युक्त को सारणिक रूप में निम्न प्रकार से लिख सकते हैं

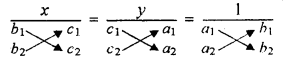
इस आरेख के अनुसार नीचे की तरफ तीर वाली (1) संख्याओं के गुणनफल में से ऊपर की ओर तीर वाली (1) संख्याओं के गुणनफल को घटाकर लिखा जा सकता है।

→ यदि दिए गए रैखिक समीकरण a₁x + b₁y + c₁ = 0 और a₂x + b₂y + c₂ = 0 एक रैखिक समीकरण को प्रदर्शित करते हैं, तो निम्न स्थितियाँ उत्पन्न हो सकती हैं

• \(\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}}\): इस स्थिति में रैखिक समीकरण युग्म संगत होता है।
• \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}\): इस स्थिति में रैखिक समीकरण युग्म असंगत होता है।
• \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}} \): इस स्थिति में रैखिक समीकरण युग्म आश्रित (संगत) होता है।

→ अनेक स्थितियाँ होती हैं जिन्हें गणितीय रूप में ऐसी दो समीकरणों से प्रदर्शित किया जा सकता है जो प्रारम्भ में रैखिक नहीं हों, परन्तु हम उन्हें परिवर्तित कर एक रैखिक समीकरण युग्म में बदल सकते हैं।

→ युगपत रैखिक समीकरणों के अनुप्रयोग -

• जिन अज्ञात राशियों को ज्ञात करना है उन्हें चरों x तथा y से निरूपित करते हैं।
• समस्या में शब्दों के रूप में दिये गये प्रतिबन्धों को दो चरों x तथा y वाले युगपत समीकरण में बदलते हैं।
• हल करके समस्या का हल निकालते हैं।

→ युगपत समीकरण का लेखाचित्र द्वारा हल ग्राफ - यह एक आकृति होती है जो कि ग्राफ पेपर पर बिन्दुओं के समुच्चय के रूप में रेखाओं और वक्रों को प्रदर्शित करती है जिससे दो चर राशियों के बीच सम्बन्ध ज्ञात होता है।
एक दिये हुए सम्बन्ध (चर राशियों के मध्य) का ग्राफ चित्रित करने के लिए सर्वप्रथम एक ग्राफ पेपर पर बीचों-बीच Xox' अक्ष पर और YoY' अक्ष पर गहरी आड़ी रेखा और खड़ी रेखा खींचते हैं।

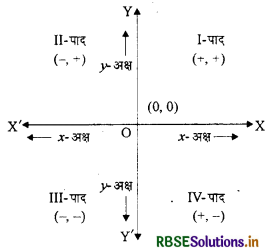
• आड़ी रेखा XOX'-x-अक्ष कहलाती है।
• खड़ी रेखा YOY'-y-अक्ष कहलाती है।

इस प्रकार इन दो रेखाओं के खींचने से ग्राफ पेपर चार खानों में X': Y, विभक्त हो जाता है जिन्हें क्रमशः I, II, III, IV पाद कहते हैं। प्रथम पाद में वे सभी निर्देशांक आते हैं जो कि दोनों ही (+, +) होते हैं, II पाद में X के ऋणात्मक और Y के धनात्मक निर्देशांक चित्रित होते हैं, III-पाद III पाद में दोनों ही ऋणात्मक निर्देशांक स्थान लेते हैं और IV पाद में X के धनात्मक और Y के ऋणात्मक मान वाले निर्देशांक स्थान पाते हैं।

रेखाएँ XOX' और YOY' जहाँ एक-दूसरे को काटती हैं इसे मूल बिन्दु कहते हैं और मूल बिन्दु के निर्देशांक सदैव (0, 0) होते हैं। निर्देशांक-ग्राफ पेपर पर इन्हें स्थापित करना। वह सभी क्रमित युग्म जो कि x और y अक्ष पर क्रमशः किसी बिन्दु की दूरी को प्रदर्शित करते हैं उन्हें निर्देशांक कहते हैं।

→ युगपत समीकरणों का निरूपण और हल-इस प्रकार जब दो चर राशि के युगपत समीकरणों के निर्देशांकों को ग्राफ पेपर पर चित्रित कर मिला देने से सदैव दो सरल रेखाओं की आकृति मिलेगी जो आपस में या बढ़ाये जाने पर एक-दूसरे को अवश्य काटेंगी।

→ प्रतिच्छेदन बिन्दु-वह बिन्दु जहाँ पर दो सरल रेखाओं के ग्राफ एक-दूसरे को काटते हैं इस बिन्दु से ग्राफ पेपर के अक्ष-X और अक्ष-Y पर परस्पर लम्ब डालने पर यह लम्ब मूल बिन्दु 0 से जिस दूरी पर XOX' अक्ष को और YOY' अक्ष को काटते हैं वह दूरी ही समीकरणों का हल होगी।