RBSE Class 10 Maths Notes Chapter 14 सांख्यिकी

These comprehensive RBSE Class 10 Maths Notes Chapter 14 सांख्यिकी will give a brief overview of all the concepts.

RBSE Class 10 Maths Chapter 14 Notes सांख्यिकी

→ केन्द्रीय प्रवृत्ति—दिए गए आँकड़ों में से श्रेणी के अधिकांश पद जिस आँकड़े के आस-पास केन्द्रित होते हैं, उसे आँकड़ों की केन्द्रीय प्रवृत्ति कहते हैं। इसे ही केन्द्रीय प्रवृत्ति की माप अथवा माध्य भी कहा जाता है। ये तीन प्रकार के होते हैं

• माध्य
• बहुलक
• माध्यक।

→ समान्तर माध्य–यदि किसी चर राशि के x मान क्रमशः x₁, x₂, x₃, ....... x_n, हों तो उनका समान्तर माध्य होगा -
(x̄) = \(\frac{x_{1}+x_{2}+x_{3}+\ldots \ldots \ldots x_{n}}{n}\)
या x̄ = \(\frac{\sum_{i=1}^{n} x_{i}}{n}\)
यहाँ पर प्रतीक Σ (सिग्मा) योग की प्रक्रिया को दर्शाने के लिये किया गया है।

→ माध्य-यदि प्रेक्षणों x₁, x₂, x₃, ....... x_n, की बारम्बारताएँ क्रमशः f₁, f₂, f₃, ....... f_n, हों, तो इन सभी प्रेक्षणों के मानों का योग = f₁x₁ + f₂x₂ + f₃x₃ + .......... + f_nx_n है तथा प्रेक्षणों की संख्या f₁ + f₂ + ........ + f_n, है तब
माध्य (x̄) = \(\frac{f_{1} x_{1}+f_{2} x_{2}+f_{3} x_{3}+\ldots \ldots f_{n} x_{n}}{f_{1}+f_{2}+f_{3}+\ldots \ldots \ldots f_{n}}\)
या x̄ = \(\frac{\sum_{i=1}^{n} f_{i} x_{i}}{\sum_{i=1}^{n} f_{i}}\)
या x̄ = \(\frac{\sum f_{i} x_{i}}{\sum f_{i}}\)
यहाँ i का मान l से n तक विचरण करता है। यह विधि प्रत्यक्ष विधि कहलाती है।

→ अवर्गीकृत बारम्बारता बंटन से समान्तर माध्य क्रिया पद

• प्रत्येक विचर को उसकी बारम्बारता से गुणा करके (f_i × x_i) का योग ज्ञात करते हैं।
• योगफल में बारम्बारता के योगफल का भाग देते हैं।
• इस प्रकार प्राप्त भागफल समान्तर माध्य होगा।

→ वर्ग:चिह्न या मध्य-बिन्दु-किसी भी अन्तराल का मध्य-बिन्दु या वर्ग-चिह्न उसकी ऊपरी सीमा और | निचली सीमाओं का औसत निकालकर ज्ञात करते हैं। अर्थात्

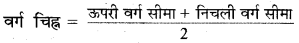
→ कंल्पित माध्य विधि (x̄) = a + \(\frac{\sum f_{i} d_{i}}{\sum f_{i}}\)
संजीव पास बुक्स जहाँ पर d_i = x_i - a, a = कल्पित माध्य
Σf_i = N = बारम्बारताओं का योग
नोट-कल्पित माध्य विचर (x) का वह मान लिया जाता है जिसकी बारम्बारता अधिकतम हो। ऐसा करने पर गणितीय परिकलन आसान हो जाता है।

→ पग-विचलन विधि - इस विधि में विचलनों d_i = x_i - a के सभी मानों को किसी एक उभयनिष्ठ संख्या (माना h) से भाग देते हैं। ऐसी स्थिति में इन सभी विचलनों को h से विभाजित करते हुए नये विचलन u_i = \(\frac{x_{i}-a}{h}\) के रूप में लेते हैं,

a = कल्पित माध्य
h = वर्ग माप
Σf_i = N = बारम्बारताओं का योग
पग-विचलन विधि तभी सुविधाजनक होगी, जबकि सभी d. में कोई सार्व गुणनखण्ड होगा।

→ बहुलक-दिए हुए प्रेक्षणों में बहुलक का वह मान है जो सबसे अधिक बार आता है अर्थात् उस प्रेक्षण का मान जिसकी बारम्बारता अधिकतम हो, बहुलक कहलाता है।
बहुलक = l + \(\left[\frac{f_{1}-f_{0}}{2 f_{1}-f_{0}-f_{2}}\right]\) × h
वर्गीकृत आँकड़ों का बहुलक इसी सूत्र से ज्ञात करते हैं। यहाँ
l = बहुलक वर्ग की निम्न सीमा
h = वर्ग अन्तराल की माप
f₁ = बहुलक वर्ग की बारम्बारता
f₀ = बहुलक वर्ग से ठीक पहले वर्ग की बारम्बारता तथा
f₂ = बहुलक वर्ग के ठीक बाद में आने वाले वर्ग की बारम्बारता है।

→ माध्यक या माध्यिका (A) यदि किसी चर राशि x के मानों को आरोही (ascending) या अवरोही (descending) क्रम में रखा
जाये, तो इस श्रेणी के मध्य के पद को श्रेणी की माध्यिका या माध्यक कहते हैं।
(i) यदि पदों की संख्या विषम है इस स्थिति में मध्य पद एक ही होगा
∴ माध्यक (M) = \(\left(\frac{n+1}{2}\right)\)वाँ पद

(ii) यदि पदों की संख्या सम है, तो

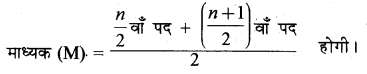
(B) अवर्गीकृत बारम्बारता बंटन से माध्यक ज्ञात करना - अवर्गीकृत बारम्बारता बंटन से माध्यक ज्ञात करने की निम्न विधि है

• संचयी बारम्बारता सारणी को तैयार कीजिये।
• \(\frac{\mathrm{N}}{2}\) = का मान ज्ञात करना, जहाँ पर N = Σf_i
• \(\frac{\mathrm{N}}{2}\), से ठीक अधिक संचयी बारम्बारता वाला चर मान माध्यक होगा।

(C) वर्गीकृत बारम्बारता बंटन से माध्यक-वर्गीकृत बारम्बारता बंटन से माध्यक ज्ञात करने के लिये निम्न | बिन्दु हैं

• (i) संचयी बारम्बारता सारणी तैयार कीजिये।
• (ii) \(\frac{\mathrm{N}}{2}\) ज्ञात कर ठीक अधिक संचयी बारम्बारता वाले वर्ग-अन्तराल को ज्ञात कीजिये।
• (iii) अब इस वर्ग-अन्तराल के लिये निम्न सूत्र की सहायता से माध्यक ज्ञात कीजिये
  माध्यक = l + \(\left[\frac{\frac{n}{2}-c . f}{f}\right]\) × h
  यहाँ । = माध्यक वर्ग की निम्न सीमा
  n = प्रेक्षणों की संख्या
  c.f. = माध्यक वर्ग से ठीक पहले वाले वर्ग की संचयी बारम्बारता
  f = माध्यक वर्ग की बारम्बारता तथा
  h = वर्ग माप है।

→ तीनों केन्द्रीय प्रवृत्ति के मापकों में निम्नलिखित सम्बन्ध होता है
3 × माध्यक = बहुलक + 2 × माध्य

→ संचयी बारम्बारता बंटनों को आलेखीय रूप से संचयी बारम्बारता वक्रों या 'से कम प्रकार के' या 'से अधिक प्रकार के' तोरण द्वारा निरूपित किया जा सकता है।

→ वर्गीकृत आँकड़ों का माध्यक इनके दोनों प्रकार के तोरणों के प्रतिच्छेद बिन्दु से क्षैतिज अक्ष पर लम्ब डालकर लम्ब और क्षैतिज अक्ष के प्रतिच्छेद बिन्दु के संगत मान से प्राप्त हो जाता है।