RBSE Class 10 Maths Notes Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन

These comprehensive RBSE Class 10 Maths Notes Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन will give a brief overview of all the concepts.

RBSE Class 10 Maths Chapter 13 Notes पृष्ठीय क्षेत्रफल एवं आयतन

→ (A) [घन और घनाभ का पृष्ठीय क्षेत्रफल और आयतन]
क्षेत्रफल :

• घनाभ का सम्पूर्ण पृष्ठीय क्षेत्रफल = 2 (ल. × चौ. + चौ. × ॐ. + ॐ. × ल.) वर्ग इकाई
• घन का सम्पूर्ण पृष्ठीय क्षेत्रफल = 6 (भुजा)²
• घनाभ की चारों दीवारों का क्षेत्रफल = 2 × ऊँचाई (लम्बाई + चौड़ाई) वर्ग इकाई
  अथवा
  = ऊँचाई × परिमाप वर्ग इकाई

→ आयतन :

• घनाभ का आयतन = लम्बाई × चौड़ाई × ऊँचाई घन इकाई
• घन का आयतन = (भुजा)³ घन इकाई

घन और घनाभ के विकर्ण
(1) घनाभ के विकर्ण की लम्बाई

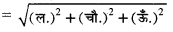
(2) घन के विकर्ण की लम्बाई = √3 × भुजा

→ (B) [ लम्बवृत्तीय बेलन : पृष्ठीय क्षेत्रफल एवं आयतन]
लम्बवृत्तीय बेलन वह ठोस आकृति है जिसमें एक वक्रपृष्ठ और सर्वांगसम वृत्तीय अनुप्रस्थ काट हो तथा बेलन का अक्ष वृत्तीय अनुप्रस्थ काट पर लम्बवत् हो। सामान्य-.

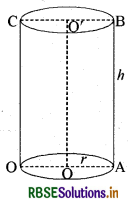
• यहाँ बेलन को 'लम्बवृत्तीय बेलन' (Right circular cylinder) के अर्थ में प्रयोग किया गया है।
• बेलन को ऊर्ध्वाधर स्थिति में रखने पर नीचे के वृत्तीय सिरे को बेलन का आधार कहते हैं और बेलन की लम्बाई उसकी ऊँचाई (h) कही जाती है । वृत्तीय सिरे की त्रिज्या को बेलन की त्रिज्या (r) कहते हैं।
• खोखले बेलन में दोनों सिरे खुले होते हैं । ठोस बेलन में दोनों सिरे बन्द होते हैं।

क्षेत्रफल

• ठोस बेलन का वक्र पृष्ठ का क्षेत्रफल = 2πrh वर्ग इकाई
• बेलन के एक सिरे की परिधि जिसकी त्रिज्या r है = 2πr वर्ग इकाई
• बेलन के आधार का क्षेत्रफल = πr² वर्ग इकाई -
• बेलन का सम्पूर्ण पृष्ठ क्षेत्रफल = वक्र पृष्ठ + 2 × आधार का. क्षेत्रफल
  = 2πrh + 2πr²
  = 2πr (h + r) वर्ग इकाई
• खोखले बेलन का सम्पूर्ण पृष्ठीय क्षेत्रफल
  = 2πr₁h + 2πr₂h + 2πr₁² - 2πr₂²
  = 2πh (r₁ + r₂) + 2π (r₁² - r₂²)
  = 2πh (r₁ + r₂) + 2π (r₁ + r₂) (r₁ - r₂)
  = 20 (r₁ - r₂) (h + r₁ - r₂)

आयतन

• बेलन का आयतन = πr²h घन इकाई
• खोखले बेलन का आयतन = π(r₁² – r₁²) h घन. इकाई
  नोट-खोखले बेलन में दो त्रिज्याएँ (आन्तरिक और बाह्य) होती हैं, जिन्हें 'r₁,' और r₂,' मानकर चला जाता है।

→ (C) (Pica (Cone)]:
लम्बवृत्तीय शंकु वह ठोस आकृति है जब कोई रेखाखण्ड एक स्थिर बिन्दु पर एक स्थिर रेखा से अचर कोण पर परिक्रमण करती है।

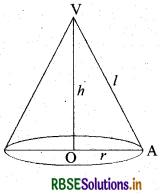
• शंकु का आकार आइसक्रीम कोन या जोकर की टोपी जैसा होता है।
• लम्बवृत्तीय शंकु की ऊँचाई = h
  शंकु की त्रिज्या = r तथा उसकी
  तिरछी ऊँचाई = l मानी जाती है।

क्षेत्रफल

• शंकु'का वक्र पृष्ठीय (तिर्यक पृष्ठीय) क्षेत्रफल का सूत्र है = πrl
• शंकु का सम्पूर्ण पृष्ठीय क्षेत्रफल का सूत्र है = πr(r + l)

आयतन

• शंकु का आयतन = \(\frac{1}{3}\)πr²h
• शंकु की तिरछी ऊँचाई l = \(\sqrt{r^{2}+h^{2}}\)

(D) [गोला (Sphere)]:

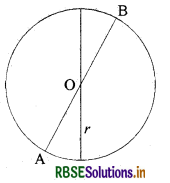
अर्थ

• एक वृत्त या अर्द्धवृत्त द्वारा उसके एक व्यास को अक्ष मानकर उसके चारों ओर क्रमशः पूरा चक्कर या आधा चक्कर लगाने पर जो ठोस जनित होता है, उसे गोला कहते हैं।
• आकाश में स्थित उन सभी बिन्दुओं के समुच्चय को गोला कहा जा सकता है जो एक नियत बिन्दु से समान दूरी पर हों।
• नियत बिन्दु को गोले का केन्द्र कहते हैं।
• केन्द्र से इसके किसी बिन्दु की दूरी को त्रिज्या कहते हैं।
• उस रेखाखण्ड को, जो गोले के केन्द्र से गुजरता है और जिसके दोनों सिरे गोले पर-हों, गोले का व्यास कहलाता है। गोले की त्रिज्या उसके व्यास की आधी होती है।
• गोले द्वारा आकाश (space) में घेरा गया स्थान उसका आयतन कहलाता है।

क्षेत्रफल

• गोले का पृष्ठीय क्षेत्रफल = 4πr²
• अर्द्ध गोले का वक्र पृष्ठ का क्षेत्रफल = 2πr²
• अर्द्ध गोले के सम्पूर्ण पृष्ठ का क्षेत्रफल = 3πr²
• यदि गोलीय कोश की बाहरी त्रिज्या तथा भीतरी त्रिज्या । है, तो गोलीय कोश का सम्पूर्ण पृष्ठीय क्षेत्रफल = 4π (r₁² + r₂²)

आयतन

• गोले का आयतन = \(\frac{4}{3}\)πr³
• अर्द्धगोले का आयतन = \(\frac{2}{3}\)πr³
• गोलीय कोश का आयतन = \(\frac{4}{3}\)π(r₁³ - r₂³)

जब किसी शंकु को उसके आधार के समान्तर किसी तल द्वारा काटकर एक छोटा शंकु हटा देते हैं, तो जो ठोस बचता है, वह शंकु का एक छिन्नक कहलाता है। शंकु के छिन्नक से सम्बद्ध सूत्र निम्नलिखित हैं :

• शंकु के छिन्नक का आयतन = \(\frac{1}{3}\)πh (r₁² + r₂² +r₁r₂)
• शंकु के छिन्नक का वक्र पृष्ठीय क्षेत्रफल = πl (r₁ + r₂)
  जहाँ l = \(\sqrt{h^{2}+\left(r_{1}-r_{2}\right)^{2}}\)
• शंकु के छिन्नक का सम्पूर्ण पृष्ठीय क्षेत्रफल
  = rl (r₁ + r₂) + (r₁² + r₂²)
  उपर्युक्त सूत्रों में, h = छिन्नक की (ऊर्ध्वाधर) ऊँचाई, l = छिन्नक की तिर्यक ऊँचाई तथा r₁ और r₂, छिन्नक के दोनों वृत्तीयं सिरों की त्रिज्याएँ हैं।