RBSE Class 10 Maths Notes Chapter 12 वृतों से संबंधित क्षेत्रफल

These comprehensive RBSE Class 10 Maths Notes Chapter 12 वृतों से संबंधित क्षेत्रफल will give a brief overview of all the concepts.

RBSE Class 10 Maths Chapter 12 Notes वृतों से संबंधित क्षेत्रफल

→ वृत्त की परिधि (Circumference of a Circle) - वृत्त एक समतलीय ज्यामितीय आकृति है, जिसका प्रत्येक बिन्दु, उसी समतल के एक निश्चित बिन्दु से सदैव निश्चित दूरी पर रहता है। यह निश्चित बिन्दु वृत्त का केन्द्र है और अचर दूरी को वृत्त की त्रिज्या कहते हैं। त्रिज्या का दोगुना व्यास होता है। वृत्त का एक चक्कर लगाने पर चलित दूरी, वृत्त का परिमाप या परिधि कहलाती है। वृत्त की त्रिज्या को अंग्रेजी वर्णमाला के अक्षर से दर्शाते हैं।

→ किसी भी वृत्त की परिधि और व्यास का अनुपात एक निश्चित अचर राशि होती है। इस अनुपात की अचर राशि को ग्रीक अक्षर स द्वारा प्रदर्शित करते हैं। अतः

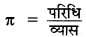
= पाराध = π × व्यास
= π × 2 = 2πr
व्यावहारिक रूप में L का सन्निकट मान \(\frac{22}{7}\) या 3.14 लेते हैं।

→ वृत्त का क्षेत्रफल = πr²

→ अर्द्ध वृत्त का क्षेत्रफल = \(\frac{1}{2}\)πr²

→ अर्द्ध वृत्त का परिमाप = πr + 2r = r (π + 2)

→ वलयिका का क्षेत्रफल (Area of an annullus) - चित्रानुसार दो वृत्ताकार वलयों का केन्द्र 0 और जिनकी बाह्य और अन्तः त्रिज्याएँ क्रमशः r₁, और r₂, (r₁ >r₂) हैं।

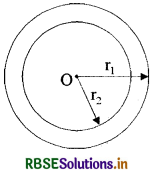
वलयिका का क्षेत्रफल = दोनों वृत्तों के बीच का क्षेत्रफल
= बड़े वृत्त का क्षेत्रफल - छोटे वृत्त का क्षेत्रफल
= πr₁² - πr₂²
= π(r₁² - r₂²)
= π × (त्रिज्याओं के वर्गों का अन्तर)
अतः वलयिका का क्षेत्रफल = π(r₁² - r₂²)

→ वत्त के त्रिज्य खण्ड का क्षेत्रफल (Area of a sector of a circle) - किसी भी वृत्त की दो त्रिज्याओं और एक चाप से घिरे हुए क्षेत्र को वृत्त का त्रिज्यखण्ड (sector) सामने चित्र में दिये गये वृत्त का त्रिज्यखण्ड AOB है। माना कि ∠AOB = 0 है और θ < 180° । जब θ का मान बढ़ता है तो चाप AB की लम्बाई भी उसी अनुपात में बढ़ती है।

इस प्रकार त्रिज्या r वाले वृत्त के एक त्रिज्यखण्ड, जिसका कोण अंशों में θ है, का क्षेत्रफल \(\frac{\theta}{360}\) × πr² होता है। साथ ही त्रिज्या r वाले वृत्त के एक त्रिज्यखण्ड, जिसका कोण अंशों में θ है, के संगत चाप की लम्बाई \(\frac{\theta}{360}\) × 2πr होती है।

→ वृत्त के त्रिज्यखण्ड की चाप की लम्बाई (L) और क्षेत्रफल (A) में सम्बन्ध यदि r त्रिज्या के वृत्त में कोण θ के त्रिज्यखण्ड की चाप की लम्बाई L और क्षेत्रफल A है, तो
L = \(\frac{\pi r \theta}{180}\) = 2πr × \(\frac{\theta}{360}\)
A = \(\frac{\pi r^{2} \theta}{360}\) = πr² × \(\frac{\theta}{360}\)

वृत्त के त्रिज्यखण्ड की चाप की लम्बाई (L) और वृत्त की त्रिज्या ज्ञात होने पर त्रिज्यखण्ड का क्षेत्रफल
A = \(\frac{1}{2}\)(Lr)

→ वृत्तखण्ड (Segment) - वृत्त की प्रत्येक जीवा वृत्त को दो भागों में विभाजित करती है। इनमें से प्रत्येक भाग को वृत्तखण्ड कहते हैं। बड़े भाग को. दीर्घवृत्तखण्ड और छोटे भाग को लघुवृत्तखण्ड कहते हैं।
दिये गये चित्र में ABC लघु वृत्तखण्ड है तथा ADC दीर्घ वृत्तखण्ड है।

→ एक वृत्तखण्ड का क्षेत्रफल = संगत त्रिज्यखण्ड का क्षेत्रफल - संगत त्रिभुज का क्षेत्रफल

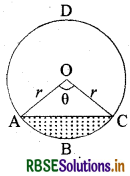
वृत्तखण्ड ABC का क्षेत्रफल = त्रिज्यखण्ड OABC का क्षेत्रफल - ∆OAC का क्षेत्रफल
= \(\frac{\theta}{360^{\circ}}\) × πr² - ∆OAC का क्षेत्रफल
= \(\frac{\theta \times \pi r^{2}}{360^{\circ}}-\frac{1}{2}\)r²sin θ
चूँकि ∆OAC एक समद्विबाहु त्रिभुज है।

→ ∴ दीर्घ वृत्तखण्ड ADC का क्षेत्रफल
= πr² - लघु वृत्तखण्ड ABC
= πr² - (\(\frac{\theta}{360^{\circ}}\) × πr² - \(\frac{1}{2}\)r²sin θ)