RBSE Class 10 Maths Important Questions Chapter 9 त्रिकोणमिति का अनुप्रयोग

Rajasthan Board RBSE Class 10 Maths Important Questions Chapter 9 त्रिकोणमिति का अनुप्रयोग Important Questions and Answers.

RBSE Class 10 Maths Chapter 9 Important Questions त्रिकोणमिति का अनुप्रयोग

वस्तुनिष्ठ प्रश्न

प्रश्न 1.
10 मीटर ऊँचे एक वृक्ष की छाया 10√3 मीटर लम्बी हो, तो सूर्य का उन्नतांश कोण है
(A) 90°
(B) 60°
(C) 45°
(D) 30°
उत्तर:
(D) 30°

प्रश्न 2.
किसी मीनार की छाया उसकी ऊँचाई के बराबर हो तो सूर्य का उन्नयन कोण है
(A) 90°
(B) 60°
(C) 45°
(D) 30°
उत्तर:
(C) 45°

प्रश्न 3.
यदि किसी वृक्ष की छाया उसकी ऊँचाई की 5 गुना हो, तो सूर्य का उन्नयन कोण है
(A) 90°
(B) 60°
(C) 45°
(D) 30°
उत्तर:
(B) 60°

प्रश्न 4.
एक पहाड़ी का ढलान क्षैतिज से 60° कोण बनाता है। यदि शिखर तक पहुँचने में 500 मीटर चलना पड़ता है, तो पहाड़ी की ऊँचाई है
(A) 50√3 मीटर
(B) \(\frac{500}{\sqrt{3}}\) मीटर
(C) 250√3 मीटर
(D) \(\frac{250}{\sqrt{3}}\) मीटर
उत्तर:
(C) 250√3 मीटर

प्रश्न 5.
यदि एक मीनार की ऊँचाई उसकी छाया 13 गुनी है तो सूर्य का उन्नतांश कोण है|
(A) 30°
(B) 45°
(C) 75°
(D) 60°
उत्तर:
(D) 60°

प्रश्न 6.
50 मीटर ऊँचे एक प्रकाश स्तम्भ के शिखर से | किसी नाव का अवनमन कोण 60° है। नाव की प्रकाश स्तम्भ से दूरी होगी
(A) 50√3 मीटर
(B) \(\frac{50}{\sqrt{3}}\) मीटर
(C) 50 × 3 मीटर
(D) 50 मीटर
उत्तर:
(B) \(\frac{50}{\sqrt{3}}\) मीटर

अतिलघूत्तरात्मक प्रश्न

प्रश्न 1.
3 मीटर ऊँचे खम्भे की परछाईं की लम्बाई 3 मीटर है। उस समय सूर्य का उन्नयन कोण ज्ञात कीजिये।
हल:
tan θ = \(\frac{3}{3}\) = 1
θ = 45°

प्रश्न 2.
दी गई आकृति में कोण का मान ज्ञात कीजिए।

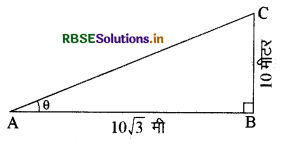
हल:
tan θ = \(\frac{10}{10 \sqrt{3}}\)
= \(\frac{1}{\sqrt{3}}\)
= 30°

प्रश्न 3.
चित्र के अनुसार 'x' का मान लिखिए

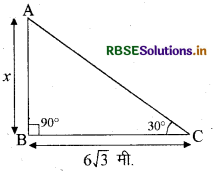
AB = x,
BC = 6√3 मीटर
तथा ∠C = 30°
हल:
tan 30° = \(\frac{x}{6 \sqrt{3}}\)
अतः x = 6√3 × tan 30°
= 6√3 × \(\frac{1}{\sqrt{3}}\)
= 6 मीटर

प्रश्न 4.
सूर्य के उन्नयन कोण में वृद्धि (0° से 90° तक) होने से किसी स्तम्भ की परछाईं की लम्बाई में क्या परिवर्तन होता है? लिखिए।
उत्तर:
परछाईं की लम्बाई कम होती जाएगी।

प्रश्न 5.
एक चिमनी के आधार से 200 मीटर दूरी पर से उसके शिखर का उन्नयन कोण 60° है। चिमनी की ऊँचाई ज्ञात कीजिए।
हल:
tan 60° = \(\frac{x}{200}\)
या x = 200 × 13
अतः x = 200 × 1.732 = 346.4 मीटर

प्रश्न 6.
20 मीटर ऊँचे नदी के पुल से एक नाव का अवनमन कोण 300 है। नाव को पल के नीचे में कितनी दूरी चलना होगा?
हल:
tan 30° = \(\frac{20}{x}\) [∵ tan 30° = \(\frac{1}{\sqrt{3}}\)]
\(\frac{1}{\sqrt{3}}=\frac{20}{x}\)
या x = 20√3 मीटर उत्तर

प्रश्न 7.
टेलीफोन के खम्भे की भूमि से ऊँचाई 17 मीटर है। उसके ऊपरी सिरे से बंधा हआ तार भूमि से 45° का कोण बनाता है। तार की लम्बाई ज्ञात कीजिए।
हल:
sin 45° = \(\frac{17}{x}\) (∵ sin45° = \(\frac{1}{\sqrt{2}}\))
∴ \(\frac{1}{\sqrt{2}}=\frac{17}{x}\) या x = 17√2 = 17 × 1.414
= 24.04 मीटर

लघूत्तरात्मक प्रश्न

प्रश्न 1.
एक वृक्ष पृथ्वी से 4 मीटर की ऊँचाई से टूटकर इस प्रकार गिरता है कि इसका ऊपरी सिरा पृथ्वी से 30° का कोण बनाता है। वृक्ष की कुल ऊँचाई ज्ञात कीजिए।
हल:
यहाँ BC पेड़ का टूटा हुआ भाग है।

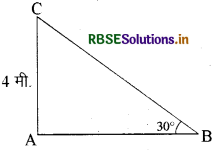
अतः sin 30° = \(\frac{\mathrm{AC}}{\mathrm{BC}}\)
BC = \(\frac{\mathrm{AC}}{\sin 30}\)
\(\frac{4}{\frac{1}{2}}\) = 8 मीटर
अतः वृक्ष की कुल ऊँचाई (AC + BC) = 4 + 8 = 12 मीटर

प्रश्न 2.
एक मकान की छत से मैदान में पड़े एक पत्थर का अवनमन कोण 60° है। यदि पत्थर से छत की तिरछी दूरी 4/3 मीटर हो तो मकान की ऊँचाई ज्ञात कीजिए।
हल:
यहाँ AC = 4√3 मीटर

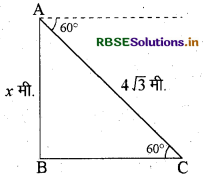
AB = x मीटर
AB _ लम्ब sin e = AC = कर्ण : -
sin 60° = \(\frac{x}{4 \sqrt{3}}\)
\(\frac{\sqrt{3}}{2}=\frac{x}{4 \sqrt{3}}\)
अतः x = \(\frac{4 \sqrt{3} \times \sqrt{3}}{2}\)
= 2 × 3 = 6 मीटर
अतः मकान की ऊँचाई = 6 मीटर

प्रश्न 3.
किसी स्तम्भ की चोटी का उन्नतांश समतल पर स्थित एक बिन्दु से 150 है। स्तम्भ की ओर 100 मीटर चलने पर उन्नतांश 30° हो जाता है। स्तम्भ की ऊँचाई ज्ञात कीजिए।
हल:
माना कि स्तम्भ की चोटी C का उन्नतांश कोण समतल पर बिन्दु 0 से 15° और बिन्दु A से 30° है, जहाँ OA = 100 मी. है।

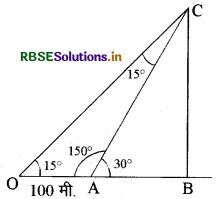
∠COB = 15° और ∠CAB = 30°
∠OCA = 15° और OA = AC = 100 मीटर समकोण त्रिभुज CBA में,
sin 30° = \(\frac{\mathrm{BC}}{\mathrm{AC}}\)
∴ BC = AC sin 30°
= 100 × \(\frac{1}{2}\) = 50 मी.
अतः स्तम्भ की ऊँचाई = 50 मीटर

प्रश्न 4.
एक स्तम्भ के आधार से 40 मीटर दूर स्थित बिन्दु पर स्तम्भ के ऊपरी सिरे का उन्नयन कोण 60° है। स्तम्भ की ऊँचाई ज्ञात कीजिए।
हल:
माना कि स्तम्भ की ऊँचाई h मीटर है। समकोण त्रिभुज ABC से

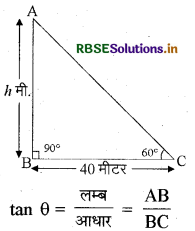
या tan 60° = \(\frac{h}{40}\)
या \(\frac{\sqrt{3}}{1}=\frac{h}{40}\)
h= 40 × √3
= 40 × 1.732 = 69.280
∴ h = 69.28 मीटर अतः स्तम्भ की ऊँचाई = 69.28 मीटर

प्रश्न 5.
किसी मीनार के आधार से होती हुई एक ही रेखा में दूरियों x और y पर स्थित बिन्दुओं से मीनार के सिरों से उन्नतांश कोण एक-दूसरे के पूरक हैं। सिद्ध कीजिये कि मीनार की ऊँचाई \(\sqrt{xy}\) है।
हल:
माना मीनार की ऊँचाई h मीटर है। OB = x और AB = y

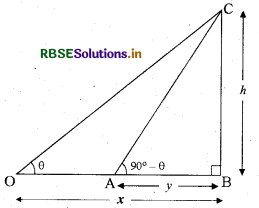
अब समकोण त्रिभुज CBO में,
tan θ = \(\frac{\mathrm{BC}}{\mathrm{OB}}=\frac{h}{x}\)
∴ h = x tan θ .... (i)
पुनः समकोण त्रिभुज CBA
tan (90° - θ) = \(\frac{h}{y}\)
h = y cot θ
∴ tan (90° - θ) = cot θ .... (ii)

समीकरण (i) तथा (ii) का गुणा करने पर
h² = x tan θ × y cot θ = xy
[∵ tan θ x cot θ = 1]
∴ h = /xy
अतः मीनार की ऊँचाई = \(\sqrt{x y}\) है। ( इतिसिद्धम्)

प्रश्न 6.
एक सीढ़ी ऊर्ध्वाधर दीवार के सहारे इस प्रकार टिकी है कि इसका नीचे का सिरा क्षैतिज भूमि पर दीवार से 3 मीटर दूर है। यदि सीढ़ी भूमि से 60° का कोण बनाए तो सीढ़ी दीवार पर कितनी ऊँचाई तक पहुँचती है? सीढ़ी की लम्बाई भी ज्ञात कीजिए।
हल:
माना कि सीढ़ी AC दीवार AB पर h ऊँचाई तक पहुँचती है।

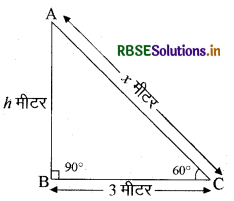
अब समकोण त्रिभुज ABC से

या tan 60° =
या \(\frac{\sqrt{3}}{1}=\frac{h}{3}\)
∴ h = 3 × √3
= 3 × 1.732 = 5.196 मीटर
∴ h = 5.196 मीटर
अतः सीढ़ी दीवार पर h = 5.196 मीटर ऊँचाई तक पहुँचती है।

सीढ़ी की लम्बाई के लिए माना कि सीढ़ी की लम्बाई x मीटर है। अतः समकोण त्रिभुज ABC से

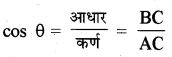
या cos 60° = \(\frac{3}{x}\)
या \(\frac{1}{2}=\frac{3}{x}\)
x = 6 मीटर
अतः सीढ़ी की लम्बाई = 6 मीटर होगी।

प्रश्न 7.
1.5 m लम्बा एक प्रेक्षक एक चिमनी से 28.5 m की दूरी पर है। उसकी आँखों से चिमनी के शिखर का उन्नयन कोण 45° है। चिमनी की ऊँचाई बताइए।
हल:
यहाँ AB चिमनी है, CD प्रेक्षक है और ∠ADE उन्नयन कोण है (देखिए आकृति)। यहाँ ADE एक त्रिभुज है जिसमें कोण E समकोण है और हमें चिमनी की ऊँचाई ज्ञात करनी है।

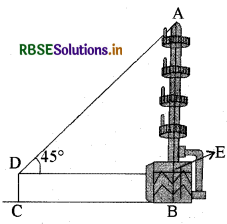
यहाँ AB = AE + BE = (AE + 1.5) m
BE = CD = 1.5 m
और DE = CB = 28.5 m
AE ज्ञात करने के लिए हमें एक ऐसा त्रिकोणमिति अनुपात लेना चाहिए जिसमें AE और DE दोनों हों। अतः
tan 45° = \(\frac{\mathrm{AE}}{\mathrm{DE}}\)
अर्थात् 1 = \(\frac{\mathrm{AE}}{28.5}\)
इसलिए AE = 28.5
अतः चिमनी की ऊँचाई (AB) = (28.5 + 1.5) m = 30 m

प्रश्न 8.
धरती पर एक मीनार ऊर्ध्वाधर खड़ी है। धरती के एक बिन्दु से, जो मीनार के पाद-बिन्दु से 15 | m दूर है, मीनार के शिखर का उन्नयन कोण 60° है। मीनार की ऊँचाई ज्ञात कीजिए।
हल:
चित्र में AB मीनार को निरूपित करता है, CB मीनार से बिन्दु की दूरी है और ∠ACB उन्नयन कोण है। हम मीनार की ऊँचाई अर्थात् AB ज्ञात करना चाहते हैं और, यहाँ ACB एक त्रिभुज है जो B पर समकोण

अब हम त्रिकोणमितीय अनुपात tan 60° (या cot 60°) लेते हैं, क्योंकि इस अनुपात में AB और BC दोनों होते हैं

tan 60° = \(\frac{\mathrm{AB}}{\mathrm{BC}}\)
अर्थात् √3 = \(\frac{\mathrm{AB}}{15}\)
अर्थात् AB = 15√3
मीनार की ऊँचाई = 15√3 m

प्रश्न 9.
एक नदी के पुल के एक बिन्दु से नदी के सम्मुख किनारों के अवनमन कोण क्रमशः 30° और 45° हैं। यदि पुल किनारों से 3 m की ऊँचाई पर हो तो नदी की चौड़ाई ज्ञात कीजिए।
हल:
आकृति में, A और B नदी के सम्मुख किनारों के बिन्दुओं को प्रकट करते हैं, जिससे कि AB नदी की चौड़ाई है। 3 m की ऊँचाई पर बने पुल पर एक बिन्दु P है अर्थात् DP = 3 m है। हम नदी की चौड़ाई ज्ञात करना चाहते हैं जो कि AAPB की भुजा AB की लम्बाई है।

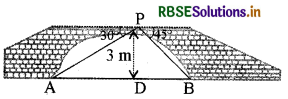
अब AB = AD + DB.
समकोण ΔAPD में, ∠A = 30°
अतः tan 30° = \(\frac{\mathrm{PD}}{\mathrm{AD}}\)
अर्थात् \(\frac{1}{\sqrt{3}}=\frac{3}{A D}\)
या AD = 3√3 m

अतः समकोण ΔPBD में, ∠B = 45° है।
इसलिए BD = PD = 3 m
अब AB = BD + AD = 3 + 3√3
= 3 (1 + 3) m
इसलिए नदी की चौड़ाई = 3 (√3 + 1) m

प्रश्न 10.
10 मी. ऊँचे भवन के शिखर से एक टॉवर के शिखर का उन्नयन कोण 60° है और उसके पाद का अवनमन कोण 45° है। टॉवर की ऊँचाई ज्ञात कीजिए।
हल:
माना कि टॉवर की ऊँचाई h मी. है। टॉवर के शिखर का उन्नयन कोण 60° तथा पाद का अवनमन कोण 45° है।
अब ΔABD में

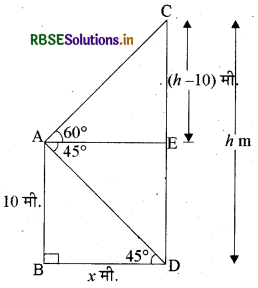
\(\frac{\mathrm{BD}}{\mathrm{AB}}\) = cot 45°
या \(\frac{\mathrm{BD}}{10}\) = 1
या BD = 10 मी. ..........(i)
अब समकोण त्रिभुज AEC में
\(\frac{\mathrm{AE}}{\mathrm{EC}}\) = cot 60°
या \(\frac{\mathrm{AE}}{h-10}=\frac{1}{\sqrt{3}}\)
या AE = \(\frac{h-10}{\sqrt{3}}\) ..............(ii)
परन्तु BD = AE
∴ 10 = \(\frac{h-10}{\sqrt{3}}\) [(i) और (ii) के प्रयोग से]
या 10√3 = h - 10
या = 10√3 + 10 = 10 (√3 +1) मी.
अतः टॉवर की ऊँचाई = 10(√3 +1) मी.

प्रश्न 11.
एक नदी के पुल के एक बिन्दु से नदी के सम्मुख किनारों के अवनमन कोण क्रमश: 30° और 45° है। यदि पुल किनारों से 4 मीटर की ऊँचाई पर हो, तो नदी की चौड़ाई ज्ञात कीजिए।
हल:
माना आकृति में A और B नदी के सम्मुख किनारों के बिन्दुओं को प्रकट करते हैं जिससे कि AB नदी की चौड़ाई है। 4 m की ऊँचाई पर बने पुल पर एक बिन्दु P है अर्थात् DP = 4 m है। हम नदी की चौड़ाई ज्ञात करना चाहते हैं जो कि ΔAPB की भुजा AB की लम्बाई है।

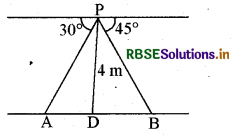
अब AB = AD + DB
समकोण ΔAPD में ∠A = 30°
अतः tan 30° = \(\frac{P D}{A D}\)
अर्थात् \(\frac{1}{\sqrt{3}}=\frac{4}{\mathrm{AD}}\)
या AD = 4√3 m

अतः समकोण ΔPBD में ∠B = 45° है।
∴ BD = PD = 4 m
अब AB = BD + AD = 4 + √3
= 4(1 + √3) m
अतः नदी की चौड़ाई = 4(1 + √3) m

प्रश्न 12.
एक मीनार के पाद से एक भवन के शिखर का उन्नयन कोण 30° है और भवन के पाद से मीनार के शिखर का उन्नयन कोण 60° है। यदि मीनार की ऊँचाई 48 मीटर है तो भवन की ऊँचाई ज्ञात कीजिए।
हल:
माना कि BC = 48 m मीनार की ऊँचाई है और AD = h m भवन की ऊँचाई है। मीनार के पाद-बिन्दु से भवन के शिखर का और भवन के पाद-बिन्दु से मीनार के शिखर का उन्नयन कोण क्रमशः 30° और 60° हैं।

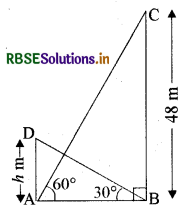
समकोण ΔABC में,
\(\frac{A B}{B C}\) = cot 60°
या \(\frac{A B}{48}=\frac{1}{\sqrt{3}}\)
या AB = \(\frac{48}{\sqrt{3}}\) ....... (i)

साथ ही, समकोण ΔDAB में,
\(\frac{\mathrm{AB}}{\mathrm{DA}}\) = cot 30°
या \(\frac{\mathrm{AB}}{h}\) = √3
या AB = h√3
(i) और (ii) से,
\(\frac{48}{\sqrt{3}}\) = h√3
या \(\frac{48}{\sqrt{3}} \times \frac{1}{\sqrt{3}}\) = h
या h = \(\frac{48}{3}\) = 16 मीटर
अतः, भवन की ऊँचाई = 16 मीटर

निबन्धात्मक प्रश्न

प्रश्न 1.
एक बिजली मिस्त्री को एक 5 m ऊँचे खम्भे पर आ गई खराबी की मरम्मत करनी है। मरम्मत का काम करने के लिये उसे खम्भे के शिखर से 1.3 m नीचे एक बिन्दु तक पहुँचना चाहती है। यहाँ पर पहुँचने | के लिये प्रयुक्त सीढ़ी की लम्बाई कितनी होनी चाहिये जिससे कि क्षैतिज से 60° के कोण से झुकने पर वह अपेक्षित स्थिति तक पहुँच जाये? और यह भी बताइये कि खम्भे का पाद-बिन्दु कितनी दूरी पर सीढ़ी के पादबिन्दु से होना चाहिये?
हल:
बिजली मिस्त्री को खम्भे AD पर बिन्दु B तक पहुँचना है।

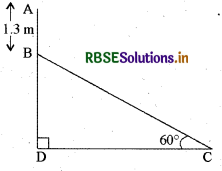
अतः BD = AD - AB
= 5 - 1.3 = 3.7 m

यहाँ पर BC सीढ़ी की लम्बाई को प्रकट करती है। हमें इसकी लम्बाई अर्थात् समकोण त्रिभुज BDC का कर्ण ज्ञात करना है।

अर्थात् सीढ़ी की लम्बाई 4.28 m होनी चाहिये। अब cot 60° = आधार

अतः उसे सीढ़ी के पाद को खम्भे से 2.14 m की दूरी पर रखना चाहिये।

प्रश्न 2.
100 मीटर ऊँचे एक प्रकाश स्तम्भ की चोटी से एकं प्रेक्षक समुद्र में एक जहाज को ठीक अपनी ओर आते हुए देखता है। यदि जहाज का अवनमन कोण 30° से बदलकर 450 हो जाता है तो प्रेक्षक की इस अवधि में जहाज द्वारा तय की गई दूरी ज्ञात कीजिए।
हल:
माना AB एक प्रकाश स्तम्भ है जिसकी ऊँचाई 100 मीटर है। माना जहाज D से C बिन्दु पर आ जाता है।

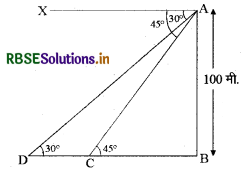
तब ∠XAD = 30° = ∠ADB
तथा ∠XAC = 45° = ∠ACB

समकोण त्रिभुज ABC में
tan 45° = \(\frac{100}{\mathrm{BC}}\)
BC = \(\frac{100}{1}\)
= 100 मीटर
BD = (CD + 100)

पुनः समकोण ΔABD में
tan 30° = \(\frac{100}{\mathrm{DB}}\)
\(\frac{1}{\sqrt{3}}=\frac{100}{(\mathrm{CD}+100)}\)
(CD + 100) = -√3 (100)
CD = 100√3 - 100 = 100
(√3 - 1) = 100(1.732 – 1)
CD = 100 × 0.732 = 73.2 मीटर
अतः जहाज द्वारा तय की गई दूरी = 73.2 मीटर

प्रश्न 3.
क्षैतिज तल पर स्थित मीनार ऊर्ध्वाधर खड़ी है और उसके शिखर पर 7 मीटर लम्बाई का एक ध्वज दण्ड लगा है। तल पर स्थित किसी बिन्दु से ध्वज दण्ड के आधार और ऊपरी सिरे के उन्नयन कोण क्रमशः 30° और 45° हैं। मीनार की ऊँचाई ज्ञात कीजिए।
हल:
माना मीनार की ऊँचाई BD = h मीटर है।
तथा ध्वज दण्ड की लम्बाई AD = 7 मीटर है।

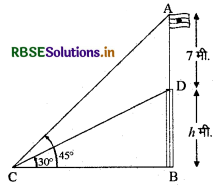
समकोण ΔABC से.
\(\frac{A B}{B C}\) = tan 45°
या \(\frac{h+7}{\mathrm{BC}}\) = 1
BC = (h + 7) मीटर

तथा समकोण ΔDBC से
\(\frac{\mathrm{DB}}{\mathrm{BC}}\) = tan 30°
या \(\frac{h}{\mathrm{BC}}=\frac{1}{\sqrt{3}}\)
BC = h√3 .... (ii)

समीकरण (i) व (ii) की तुलना करने पर
h√3 = h + 7
या h(√3 - 1) = 7
h = \(\frac{7}{\sqrt{3}-1}=\frac{7}{1.732-1} = \frac{7}{0.732}\)
h = \(\frac{7000}{732}\) = 9.56 मीटर
∴ मीनार की ऊँचाई = 9.56 मीटर

प्रश्न 4.
4000 मीटर की ऊँचाई पर उड़ते हुए वायुयान के ठीक नीचे जिस क्षण दूसरा वायुयान आता है, उसी क्षण क्षैतिज तल पर किसी बिन्दु से इन वायुयानों के उन्नयन कोण क्रमशः 60° और 45° हैं। उस क्षण पर दोनों वायुयानों के बीच की ऊर्ध्वाधर की दूरी ज्ञात कीजिए।
हल:
माना कि पहले हवाई जहाज (वायुयान) की ऊँचाई AC तथा दूसरे वायुयान की ऊँचाई BC = h मीटर है।
माना CD = x मीटर

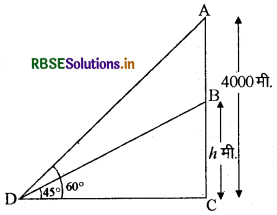
समकोण त्रिभुज ACD से
\(\frac{\mathrm{AC}}{\mathrm{CD}}\) = tan 600
⇒ \(\frac{4000}{x}\) = √3
∴ 4000 = √3x .... (i)

पुनः समकोण त्रिभुज BCD से
\(\frac{h}{x}\) = tan 45°
⇒ h = x . 1
⇒ h = x ........(ii)

समीकरण (i) तथा (ii) से
h√3 = 4000 मीटर
⇒ h = \(\frac{4000}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}}\) मीटर
(अंश तथा हर में 13 से गुणा करने पर)
= \(\frac{4000 \times \sqrt{3}}{3}\) मीटर

दोनों वायुयानों के बीच लम्बवत् दूरी

प्रश्न 5.
एक मीनार क्षैतिज तल पर खड़ी है। सूर्य के उन्नतांश कोण 30° पर मीनार की छाया, सूर्य के उन्नतांश 60° पर मीनार की छाया से 45 मीटर अधिक है। मीनार की ऊँचाई ज्ञात कीजिए।
हल:
माना मीनार की ऊँचाई AB = h मीटर है।
अब BD मीनार की छाया है जबकि सूर्य का उन्नतांश कोण 30° है तथा BC भी मीनार की छाया है जबकि सूर्य का उन्नतांश कोण 60° है।

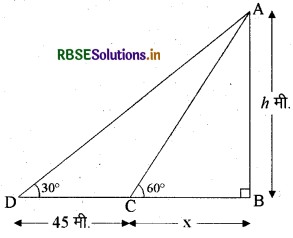
यहाँ DC = 45 मीटर तथा माना BC = x मीटर है।
∴ BD = 45 + x मीटर

अब समकोण ΔABD से
\(\frac{\mathrm{AB}}{\mathrm{BD}}\) = tan 300
या \(\frac{h}{45+x}=\frac{1}{\sqrt{3}}\)
√3 h = 45 + x
x = (h√3 - 45) मीटर .... (i)

पुनः समकोण त्रिभुज ABC से
\(\frac{h}{x}\) = tan 60°
या x = \(\frac{h}{\sqrt{3}}\) ...... (ii)

समीकरण (i) व (ii) की समानता या तुलना करने पर
h√3 - 45 = \(\frac{h}{\sqrt{3}}\)
या 3h - 45√3 = h
या 2h = 45√3
या h = 22.5 × 1.732
अर्थात = 38.97 मीटर
अतः मीनार की ऊँचाई = 38.97 मीटर

प्रश्न 6.
100 मीटर ऊँचाई एक मीनार की चोटी और उसके आधार से, एक चट्टान की चोटी के उन्नयन कोण क्रमशः 30° और 45° हैं। चट्टान की ऊँचाई ज्ञात कीजिए।
हल:
माना चट्टान की ऊँचाई AB है तथा वह (h + 100) मीटर है और मीनार की ऊँचाई CD है तथा वह | 100 मीटर है।

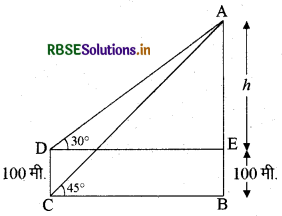
∴ ∠ADE = 30°
तथा ∠ACB = 45°

समकोण त्रिभुज AED से
\(\frac{h}{\mathrm{DE}}\) = tan 30° = \(\frac{1}{\sqrt{3}}\)
DE = √3h

तथा समकोण त्रिभुज ABC से
\(\frac{h+100}{\mathrm{BC}}\) = tan 450
या \(\frac{h+100}{\mathrm{DE}}\) = 1 [∵ DE = BC]
h + 100 = DE
h + 100 = 1√3h
DE = √3 h समी. (i) से

h(√3 - 1) = 100
⇒ h = \(\frac{100}{\sqrt{3}-1} \times \frac{\sqrt{3}+1}{\sqrt{3}+1}\)
[अंश तथा हर में (√3 + 1) से गुणा करने पर]
= \(\frac{100(\sqrt{3}+1)}{3-1}\)
= \(\frac{100(\sqrt{3}+1)}{2}\)
= 50(1.732 + 1)
= 50 x 2.732
⇒ h = 136.60 मीटर
अतः चट्टान की ऊँचाई = h + 100
= 136.60 + 100
= 236.60 मीटर

प्रश्न 7.
पहाड़ी पर खड़ा एक व्यक्ति एक नाव को देखता है, जिसका उस समय अवनमन कोण 30° है और यह नाव समुद्र के किनारे उस व्यक्ति के ठीक नीचे के स्थान की ओर आ रही है। नाव समान चाल से आ रही है। 6 मिनट पश्चात् उसका अवनमन कोण 60° हो जाता है। पहाड़ी की ऊँचाई और नाव को किनारे तक पहुँचने में लगने वाला समय ज्ञात कीजिए।
हल:
माना पहाड़ी की ऊँचाई h मीटर अर्थात् चित्रानुसार AB है तथा प्रेक्षक व्यक्ति A बिन्दु पर खड़ा है। एक नाव D बिन्दु की ओर से 6 मिनट में बिन्दु C पर पहुँचती : है। माना
DC = x₁, CB = x₂

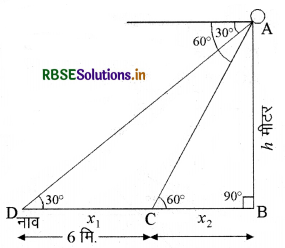
अब समकोण त्रिभुज ABC से
\(\frac{h}{x_{2}}\) = tan 60°
⇒ h = x₂ . √3 ........(i)

पुनः समकोण त्रिभुज ABD से
\(\frac{h}{x_{1}+x_{2}}\) = tan 30° = \(\frac{1}{\sqrt{3}}\)
⇒ h = \(\frac{x_{1}+x_{2}}{\sqrt{3}}\) ....(ii)

समीकरण (i) व (ii) से
⇒ x₂√3 = \(\frac{x_{1}+x_{2}}{\sqrt{3}}\)
⇒ x₂ × √3 × √3 = x₁ + x₂
⇒ 3x₂ = x₁ + x₂
या 2x₂ = x₁
या x₂ = \(\frac{x_{1}}{2}\)
लेकिन दिया गया है कि x, दूरी तय करने में 6 मिनट लगते हैं।

∴ x₂, दूरी तय करने में समय = \(\frac{1}{2}\) × 6 = 3 मिनट
⇒ बिन्दु D से B तक पहुँचने में लगा समय = 6 + 3 = 9 मिनट

प्रश्न 8.
भूमि के एक बिन्दु P से एक 10 m ऊँचे भवन के शिखर का उन्नयन कोण 30° है। भवन के शिखर पर एक ध्वज को लहराया गया है और P से ध्वज के शिखर का उन्नयन कोण 45° है। ध्वजदंड की लम्बाई और बिन्दु P से भवन की दूरी ज्ञात कीजिए। (यहाँ आप √3 = 1.732 ले सकते हैं।)
हल:
आकृति में, AB भवन की ऊँचाई है, BD ध्वजदंड प्रकट करता है और P दिया हुआ बिन्दु प्रकट करता है। यहाँ पर दो समकोण त्रिभुज PAB और PAD हैं। हमें ध्वजदण्ड की लम्बाई अर्थात् DB और बिन्दु P से भवन की दूरी अर्थात् PA ज्ञात करना है।

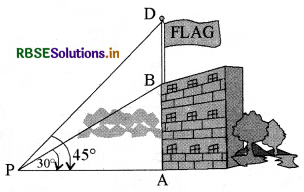
समकोण ΔPAB में
tan 30° = \(\frac{\mathrm{AB}}{\mathrm{AP}}\)
अर्थात \(\frac{1}{\sqrt{3}}=\frac{10}{A P}\)
∴ AP = 10√3
अर्थात् P से भवन की दूरी 10√3 m = 17.32 m.
माना DB = x m है तब AD = (10 + x) m

अब समकोण APAD में
tan 45° = \(\frac{\mathrm{AD}}{\mathrm{AP}}=\frac{10+x}{10 \sqrt{3}}\)
∴ 1 = \(\frac{10+x}{10 \sqrt{3}}\) या 10√3 = 10 +
x = 10√3 - 10 = x
अर्थात् x = 10(√3 - 1) = 10 (1.732 - 1)
= 10 × 0.732 = 7.32 m
अतः ध्वजदंड की लम्बाई = 7.32 m है।

प्रश्न 9.
एक समतल जमीन पर खड़ी मीनार की छाया उस स्थिति में 40 m अधिक लम्बी हो जाती है जबकि सूर्य का उन्नतांश (altitude) 60° से घटकर 30° हो जाता है अर्थात् छाया के एक सिरे से मीनार के : शिखर का उन्नयन कोण 60° है और DB छाया की लम्बाई है जबकि उन्नयन कोण 30° है। मीनार की ऊँचाई ज्ञात कीजिए।

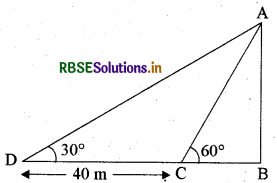
अथवा
एक समतल जमीन पर खड़ी मीनार की छाया उस स्थिति में 40 मीटर अधिक लम्बी हो जाती है जबकि सूर्य की उन्नतांश 60° से घटकर 30° हो जाता है। मीनार की ऊँचाई ज्ञात कीजिए।
हल:
माना कि AB की लम्बाई १ मीटर है और BC, x मीटर है। प्रश्न के अनुसार DB, BC से 40 m अधिक लम्बा है।
अतः DB = (40 + x) m
यहाँ दो समकोण त्रिभुज ABC और ABD हैं।

ΔABC में tan 60° = \(\frac{\mathrm{AB}}{\mathrm{BC}}\)
या √3 = \(\frac{h}{x}\) .......(i)

ΔABD में tan 30° = \(\frac{A B}{B D}\)
अर्थात् \(\frac{1}{\sqrt{3}}=\frac{h}{x+40}\) ..............(ii)
(i) से,
h = x√3
इस मान को (ii) में प्रतिस्थापित करने पर
(x√3)√3 = x + 40,
अर्थात् 3x = x + 40 अर्थात्
x= 20
इसलिए h = 20√3 [(i) से]
अतः मीनार की ऊँचाई = 20 13 m

प्रश्न 10.
एक बहुमंजिल भवन के शिखर से देखने पर एक 8 m ऊँचे भवन के शिखर और तल के अवनमन |कोण क्रमशः 30° और 45° हैं। बहुमंजिल भवन की ऊँचाई और दो भवनों के बीच की दूरी ज्ञात कीजिए।
हल:
आकृति में PC बहुमंजिल भवन को और AB, 8 m ऊँचे भवन को प्रकट करता है। हम बहुमंजिल भवन की ऊँचाई, अर्थात् PC और दो भवनों के बीच की दूरी अर्थात् AC ज्ञात करना चाहते हैं।

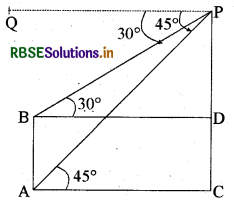
PB समान्तर रेखाओं PQ और BD की एक तिर्यकछेदी रेखा है। अतः ∠QPB और ∠PBD एकान्तर कोण हैं और इसलिए बराबर हैं।
अतः ∠PBD = 30°,
इसी प्रकार ∠PAC = 45°

समकोण ΔPBD में \(\frac{P D}{B D}\) = tan 30° = \(\frac{1}{\sqrt{3}}\)
या BD = PD√3 .... (i)

समकोण ΔPAC में \(\frac{\mathrm{PC}}{\mathrm{AC}}\) = tan 45° = 1
अर्थात् PC = AC
और PC = PD + DC
∴ PD + DC = AC
∴ AC = BD और DC = AB = 8 m,
∴ BD = PD + 8 .... (ii)

समीकरण (i) तथा (ii) से
⇒ PD + 8 = PD√3
⇒ 8 = PD√3 – PD
⇒ 8 = PD (√3 - 1)
अतः PD = \(\frac{8}{\sqrt{3}-1}\)
अंश तथा हर में (√3 + 1) से गुणा करने पर
PD = \(\frac{8(\sqrt{3}+1)}{(\sqrt{3}-1)(\sqrt{3}+1)}\)
= \(\frac{8(\sqrt{3}+1)}{3-1}=\frac{8(\sqrt{3}+1)}{2}\)
= 4(√3 + 1) m

अतः बहुमंजिल भवन की ऊँचाई PC = PD + DC = PD + AB
∵ DC = AB
= 4(√3 + 1) + 8 ∵ AB = 8 m है
= 4√3 + 4 + 8 = 4√3 + 12
= 4(3 + √3) m
दो भवनों के बीच की दूरी = AC है। लेकिन AC = PC है। अतः दो भवनों के बीच की दूरी = 4(3 + √3) m
अतः बहुमंजिल भवन की ऊँचाई और दो भवनों के बीच की दूरी आपस में बराबर है।