RBSE Class 10 Maths Important Questions Chapter 7 निर्देशांक ज्यामिति

Rajasthan Board RBSE Class 10 Maths Important Questions Chapter 7 निर्देशांक ज्यामिति Important Questions and Answers.

RBSE Class 10 Maths Chapter 7 Important Questions निर्देशांक ज्यामिति

वस्तुनिष्ठ प्रश्न

प्रश्न 1.
बिन्दु (3, 4) की y-अक्ष से दूरी होगी
(A) 1
(B) 4
(C) 2
(D) 3
उत्तर:
(D) 3

प्रश्न 2.
(- 2, 1), (2, - 2) और (5, 2) शीर्ष वाला त्रिभुज है
(A) समकोण
(B) समबाहु
(C) समद्विबाहु
(D) इनमें से कोई नहीं
उत्तर:
(C) समद्विबाहु

प्रश्न 3.
बिन्दु (5, 0) और (0, 4) को मिलाने वाले रेखाखण्ड को बिन्दु P, 2 : 3 के अनुपात में अन्त:विभाजित करता है। P के निर्देशांक हैं-
(A) (3, \(\frac{8}{5}\))
(B) (1, \(\frac{4}{5}\))
(C) \(\left(\frac{5}{2}, \frac{3}{4}\right)\)
(D) (2, \(\frac{12}{5}\))
उत्तर:
(A) (3, \(\frac{8}{5}\))

प्रश्न 4.
यदि बिन्दु (1, 2), (- 1, x) और (2, 3) संरेख हों, तो x का मान होगा
(A) 2
(B) 0
(C) - 1
(D) 1
उत्तर:
(B) 0

प्रश्न 5.
यदि बिन्दु (x, y), बिन्दुओं (2, 1) और (1, -2) से समान दूरी पर हों, तो
(A) x + 3y = 0
(B) 3x + y = 0
(C) x + 2y = 0
(D) 2y + 3x = 0
उत्तर:
(A) x + 3y = 0

प्रश्न 6.
यदि A(4, - 3), B(3, - 2) तथा C(2, 8) किसी त्रिभुज के शीर्ष हों, तो y-अक्ष से इसके केन्द्रक की दूरी होगी
(A) 1
(B) 4
(C) 3
(D) 2
उत्तर:
(C) 3

प्रश्न 7.
दो बिन्दुओं (0, cos θ) तथा (sin θ, 0) के मध्य दूरी है-
(A) 1
(B) sin θ + cos θ
(C) \(\frac{1}{2}\)(sin θ + cos θ)
(D) 0
उत्तर:
(A) 1

अतिलघूत्तरात्मक प्रश्न

प्रश्न 1.
बिन्दु (5, - 2) की y-अक्ष से दूरी लिखिए।
उत्तर:
5 चूँकि -अक्ष पर लम्ब दूरी 5 है।

प्रश्न 2.
बिन्दु (- 2, 2), (8, - 2) तथा (-4, - 3) किस तरह के त्रिभुज के शीर्ष हैं?
हल:
यदि दिये गये बिन्दु क्रमशः A, B, C हों तो
AB = \(\sqrt{100+16}=\sqrt{116}\)
BC = \(\sqrt{144+1}=\sqrt{145}\)
CA = \(\sqrt{4+25}=\sqrt{29}\)
∴ AB² + CA² = BC²
⇒ A, B, C समकोण त्रिभुज के शीर्ष हैं।

प्रश्न 3.
यदि (4,3) और (-. 2, - 1) किसी समान्तर चतुर्भुज.के सम्मुख शीर्ष हों तथा इसका तीसरा शीर्ष (1,0) हो तो चौथे शीर्ष के निर्देशांकों का गुणनफल क्या होगा?
उत्तर:
दिये गये सम्मुख शीर्षों को मिलाने वाले विकर्ण का मध्य बिन्दु है :\(\left(\frac{4-2}{2}, \frac{3-1}{2}\right)\) अर्थात् (1, 1) जो कि दूसरे विकर्ण का भी मध्य-बिन्दु है। अतः यदि चौथा शीर्ष
(x,y) हो तो \(\frac{x+1}{2}\) = 1 तथा \(\frac{y+0}{2}\) = 1
x = 1, y = 2 अतः गुणनफल 1 × 2 = 2

प्रश्न 4.
यदि बिन्दु (k, 2) तथा (3, 4) के बीच की दूरी √8 हो, तो k का मान लिखिए।
हल:
प्रश्नानुसार (√8)² = (K - 3)² + (2 – 4)²
8 = (K - 3)² + 4
4 = (K - 3)²
(K - 3) = ± 2
K = ± 2 + 3
∴ K = 5 और K = 1

प्रश्न 5.
(-3, - 4) तथा (1, - 2) बिन्दुओं को मिलाने वाली रेखाखण्ड को y-अक्ष किस अनुपात में विभाजित करता है? लिखिए।
हल:
y-अक्ष पर x = 0
माना रेखाखण्ड λ : 1 में विभाजित करता है। अन्तः विभाजन सूत्र
x = \(\frac{m_{1} x_{2}+m_{2} x_{1}}{m_{1}+m_{2}}\)
∴ 0 = \(\frac{\lambda \times 1+1 \times(-3)}{\lambda+1}\)
0 = λ - 3
∴ λ = 3
अतः अनुपात 3 : 1

प्रश्न 6.
यदि (a, 0), (0, b) तथा (1, 1) संरेख हों, इसकी क्या शर्त होगी?
हल:
तीन बिन्दु संरेख के लिये इनसे निर्मित होने वाले त्रिभुज का क्षेत्रफल शून्य होना चाहिए।
त्रिभुज का क्षेत्रफल = \(\frac{1}{2}\)[x₁(y₂ - y₂₃) + x₂ (y₃ - y₁) + x₃ (y₁ - y₂)] = 0
या x₁(y₂ - y₃) + x₂ (y₃ - y₁) + x₃ (y₁ - y₂) = 0
a(b - 1) + 0(1 - 0) + 1(0 - b)= 0
ab - a - b = 0
a + b = ab

प्रश्न 7.
बिन्दुओं (6, 8) और (2, 4) को मिलाने वाले रेखाखण्ड के मध्य बिन्दु के निर्देशांक ज्ञात कीजिये।
हल:
मध्य बिन्दु के निर्देशांक होते हैं।
x = \(\frac{x_{1}+x_{2}}{2}\), y = \(\frac{y_{1}+y_{2}}{2}\)

अतः x = \(\frac{6+2}{2}=\frac{8}{2}\) = 4
y = \(\frac{8+4}{2}=\frac{12}{2}\) = 6
अतः मध्य बिन्दु के निर्देशांक (4, 6) होंगे।

प्रश्न 8.
किसी वर्ग के सम्मुख शीर्ष (-5, - 4) और (3, 2) हैं। इसके विकर्ण की लम्बाई लिखिए।
हल:
वर्ग के विकर्ण की लम्बाई = \(\sqrt{(3+5)^{2}+(2+4)^{2}}\)
= \(\sqrt{(8)^{2}+(6)^{2}}=\sqrt{64+36}\)
= \(\sqrt{100}\) = 10

प्रश्न 9.
मूल बिन्दु से बिन्दु (3, 4) की दूरी ज्ञात कीजिए।
हल:
मूल बिन्दु से दूरी
= \(\sqrt{(3-0)^{2}+(-4-0)^{2}}\)
= \(\sqrt{9+16}=\sqrt{25}\) = 5

प्रश्न 10.
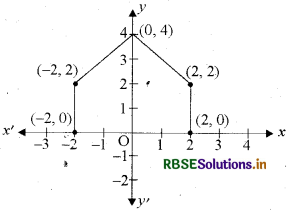
बिन्दुओं (- 2, 0), (2, 0), (2, 2), (0, 4), (-2, 2) को क्रम से मिलाने पर कौनसी आकृति प्राप्त होगी?
हल:
दिये गये बिन्दु मिलाने पर पंचभुज प्राप्त होता है।

प्रश्न 11.
बिन्दु (1, 2) और (6, 7) को मिलाने वाले .रेखाखण्ड को बिन्दु (3, 4) किस अनुपात में विभाजित करता है?
हल:
माना (1, 2) और (6, 7) को मिलाने वाला रेखाखण्ड m₁ : m₂ में विभाजित करते हैं।
3 = \(\frac{m_{1} \times 6+m_{2} \times 1}{m_{1}+m_{2}}\)
3 (m₁ + m₂) = 6m₁ + m₂
3m₁ + 3m₂ = 6m₁ + m₂
3m₂ - m₂ = 6m₁ - 3m₁
2m₂ = 3m₁
\(\frac{m_{1}}{m_{2}}=\frac{2}{3}\)
अतः m₁ : m₂ = 2 : 3

प्रश्न 12.
यदि बिन्दुओं (3, 6) और (k, 5) से बिन्दु | (0, 2) की दूरियाँ बराबर हों, तो k का मान ज्ञात कीजिए।
हल:
प्रश्नानुसार बिन्दु (3,k) और (0, 2) के बीच | की दूरी = (k, 5)और (0, 2) के बीच की दूरी
(0 - 3)² + (2 - k)² = (0 - k) + (2 - 5)²
⇒ 9 + 4 - 4k + k² = k² + 9
⇒ 4 - 4k = 0
⇒ - 4k = - 4
∴k = 1

प्रश्न 13.
यदि तीन बिन्दु (2, 1), (k, 1) तथा (2k + 1, 2) संरेखी हों, तो k का मान ज्ञात कीजिये।
हल:
यहाँ x₁ = 2, x₂ = k, x₃ = 2k + 1
तथा y₁ = 1, y₂ = 1, y₃ = 2

तीनों बिन्दु संरेख हैं अतः
x₁(y₂ - y₃) + x₂ (y₃ - y₁) + x₃ (y₁ - y₂) = 0
⇒ 2(1 - 2) + k(2 - 1) + (2k + 1) (1 - 1) = 0
⇒ - 2 + k + 0 = 0
k = 2

प्रश्न 14.
बिन्दु (-2, 9) की x-अक्ष से दूरी लिखिये।
हल:
x-अक्ष से दूरी 9 होगी।
चूँकि x-अक्ष से लम्बवत् दूरी 9 है।

प्रश्न 15.
बिन्दुओं (4, - 3) और (8, 5) को मिलाने वाले रेखाखण्ड को 3 : 1 में अन्तःविभाजन करने वाले बिन्दु के निर्देशांक लिखिये।
हल:
अन्तःविभाजन का सूत्र
\(\left(\frac{m_{1} x_{2}+m_{2} x_{1}}{m_{1}+m_{2}}, \frac{m_{1} y_{2}+m_{2} y_{1}}{m_{1}+m_{2}}\right)\)

माना वह बिन्दु P(x, y) है।
विभाजन सूत्र का प्रयोग करने पर
x = \(\frac{3(8)+1(4)}{3+1}=\frac{24+4}{4}=\frac{28}{4}\)
x = 7,
और y = \(\frac{3(5)+(-3)}{3+1}=\frac{15-3}{4}=\frac{12}{4}\)
y = 3 प्राप्त होता है।
अतः विभाजन वाला अभीष्ट बिन्दु P(7, 3) है।

प्रश्न 16.
बिन्दु (7,- 3) की y-अक्ष से दूरी लिखिए।
हल:
7, क्योंकि y-अक्ष पर लम्ब दूरी 7 है।

प्रश्न 17.
बिन्दु (3,-2) की y-अक्ष से दूरी लिखिए।
हल:
3, क्योंकि y-अक्ष पर लम्ब दूरी 3 है।

प्रश्न 18.
यदि M (4, 5), रेखाखण्ड AB का मध्य बिन्दु है तथा A का निर्देशांक (3, 4) है, तो बिन्दु B के निर्देशांक ज्ञात कीजिए।
हल:
माना कि बिन्दु B के निर्देशांक (x, y) हैं।

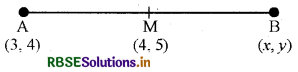
∴ मध्य बिन्दु 4 = \(\frac{3+x}{2}\)
या 3 + x = 8
∴ x = 8 - 3 = 5
तथा 5 = \(\frac{4+y}{2}\)
या 4 + y = 10
∴ y = 10 - 4 = 6
अतः बिन्दु B के निर्देशांक (5, 6) होंगे।

प्रश्न 19.
बिन्दु (-5, 4) की x-अक्ष से दूरी लिखिए।
हल:
बिन्दु (-5, 4) की x-अक्ष से दूरी 4 होगी।

प्रश्न 20.
यदि K (5, 4) रेखाखण्ड PQ का मध्य बिन्दु है तथा Q के निर्देशांक (2, 3) है, तो P के निर्देशांक ज्ञात कीजिए।
हल:
माना कि बिन्दु P के निर्देशांक (x, y) हैं।

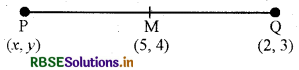
∴ मध्य बिन्दु 5 = \(\frac{x+2}{2}\)
या x + 2 = 10
∴ x = 10 - 2 = 8
तथा ∴ 4 = y + 3
या + 3 = 8
∴ y = 8 - 3 = 5
अतः बिन्दु P के निर्देशांक (8, 5) होंगे।

प्रश्न 21.
यदि दो बिन्दु A(-2, 5) और B(-5, Y) का मध्य बिन्दु (\(\frac{-7}{2}\), 3) है, तो बिन्दु A, B के मध्य दूरी ज्ञात कीजिए।
हल:

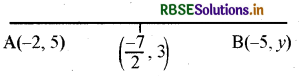
प्रश्नानुसार ȳ = \(\frac{y_{1}+y_{2}}{2}\)
3 = \(\frac{5+y}{2}\)
या 5 + y = 6.
∴ y = 6 - 5 = 1

इस प्रकार दो बिन्दु A(-2. 5) तथा B(-5. 1) हैं।
AB = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
= \(\sqrt{(-5+2)^{2}+(1-5)^{2}}\)
= \(\sqrt{(-3)^{2}+(-4)^{2}}\)
= \(\sqrt{9+16}=\sqrt{25}\) = 5
अतः बिन्दु A, B के मध्य की दूरी = 5 इकाई।

लघूत्तरात्मक प्रश्न

प्रश्न 1.
यदि एक चतुर्भुज के शीर्ष (1, 4), (5, 4), (-5, - 3) और (1, - 3) हों तो चतुर्भुज का प्रकार बताइए।
हल:


अतः AB = CD और BC = AD
तथा विकर्ण AC = BD
अतः दिये गये बिन्दु आयत के शीर्ष हैं।

प्रश्न 2.
वहअनुपात ज्ञात कीजिए जबकि बिन्दु (-3,p) बिन्दुओं (-5, - 4) और (- 2, 3) को अन्तःविभाजित करता है।p का मान भी ज्ञात कीजिए।
हल:
माना C(- 3, p) AB को अनुपात k : 1 में विभाजित करता है।
∴ विभाजन के नियम से
x = \(\frac{m_{1} x_{2}+m_{2} x_{1}}{m_{1}+m_{2}} \)और
y = \(\frac{m_{1} y_{2}+m_{2} y_{1}}{m_{1}+m_{2}}\)
∴ -3 = \(\frac{-2 k-5}{k+1}\)
या- 3k - 3 = - 2k - 5
या k = - 3 + 5 = 2

अर्थात् अनुपात k : 1 या 2 : 1 होगा।
तथा p = \(\frac{2 \times 3+1 \times(-4)}{2+1}=\frac{2}{3}\)
∴ p = \(\frac{2}{3}\)

प्रश्न 3.
बिन्दुओं (5, - 6) और (- 1, - 4) को जोड़ने वाले रेखाखण्ड को y-अक्ष किस अनुपात में विभाजित करती है? इस प्रतिच्छेद बिन्दु के निर्देशांक भी ज्ञात कीजिये।
हल:
माना वांछित अनुपात k : 1 है। तब विभाजन सूत्र से .
x = \(\frac{m_{1} x_{2}+m_{2} x_{1}}{m_{1}+m_{2}}\) और
y = \(\frac{m_{1} y_{2}+m_{2} y_{1}}{m_{1}+m_{2}}\)
अत: k : 1 के अनुपात में विभाजित करने वाले बिन्दु के निर्देशांक हैं :
\(\left(\frac{-k+5}{k+1}, \frac{-4 k-6}{k+1}\right)\)
चूँकि दिया गया है कि यह बिन्दु y-अक्ष पर स्थित है और हम जानते हैं कि y-अक्ष पर x का मान शून्य होता है।
अतः \(\frac{-k+5}{k+1}\) = 0
इसलिए k = 5
अर्थात् वांछित अनुपात 5 : 1 है। k का मान 5 रखने पर हमें प्रतिच्छेद बिन्दु (0, \(\frac{-13}{3}\)) प्राप्त होता है।

प्रश्न 4.
k का मान ज्ञात कीजिये, यदि बिन्दु A(2, 3), B(4, k) और C(6, - 3) संरेखी हैं।
हल:
चूँकि दिया गया है कि तीनों बिन्दु संरेखी हैं, इसलिये इससे बनने वाले त्रिभुज का क्षेत्रफल शून्य होगा। अर्थात्
\(\frac{1}{2}\)[2(k + 3) + 4(- 3 - 3) + 6(3 – k)] = 0
अर्थात् 2k + 6 - 4 × 6 + 18 - 6k = 0
2k + 6 - 24 + 18 - 6k = 0
4k = 0 या k = 0
अतः k का वांछित मान 0 है।

प्रश्न 5.
y-अक्ष पर एक ऐसा बिन्दु ज्ञात कीजिये जो बिन्दुओं A(6, 5) और B(-4, 3) से समदूरस्थ है।
हल:
हम जानते हैं कि y-अक्ष पर स्थित कोई भी बिन्दु (0, y) के रूप का होता है। अतः माना कि बिन्दु P(0, y) बिन्दुओं A और B से समदूरस्थ है।
तब (6 - 0)² + (5 - y)² = (- 4 - 0)² + (3 - y)²
या 36 + 25 + y² - 10y = 16 + 9 + y² - 6y
या 4y = 36
या y = \(\frac{36}{4}\) = 4
अतः वांछित बिन्दु (0, 9) है।

प्रश्न 6.
एक रेखा का एक सिरा (4, 0) है और मध्य बिन्दु (4, 1) है, तो रेखा के दूसरे सिरे के निर्देशांक क्या होंगे? .
हल:
माना दूसरे सिरे के निर्देशांक (x₂, y₂) हैं।
मध्य बिन्दु
4 = \(\frac{4+x_{2}}{2}\)

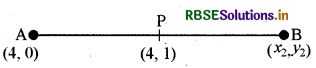
⇒ 4 × 2 = 4 + x₂
x₂ = 8 - 4 = 4
और 1 = \(\frac{0+y_{2}}{2}\)
2 = 0 + y₂
y₂ = 2
∴ (x₂, y₂) = (4, 2)
अतः दूसरे सिरे के निर्देशांक (4, 2) हैं।

प्रश्न 7.
बिन्दुओं (6, 8) और (2, 4) को मिलाने वाले रेखाखण्ड के मध्य बिन्दु से बिन्दु (1, 2) की दूरी ज्ञात कीजिए।
हल:
दिए गए बिन्दुओं (6, 8) तथा (2, 4) के मध्य बिन्दु के निर्देशांक

अतः अभीष्ट बीच की दूरी 5 होगी।

प्रश्न 8.
सिद्ध कीजिए कि बिन्दुओं (5, 7) और (3, 9) को मिलाने वाले रेखाखण्ड का मध्य बिन्दु वही है जो बिन्दुओं (8, 6) तथा (0, 10) को मिलाने वाले रेखाखण्ड का मध्य बिन्दु है।
हल:
बिन्दु A(5, 7) तथा B(3, 9) का मध्य बिन्दु
= \(\left[\frac{5+3}{2}, \frac{7+9}{2}\right]=\left(\frac{8}{2}, \frac{16}{2}\right)\) = (4, 8)
तथा बिन्दु C(8, 6) तथा D(0, 10) का मध्य बिन्दु
= \(\left[\frac{8+0}{2}, \frac{6+10}{2}\right]=\left(\frac{8}{2}, \frac{16}{2}\right)\) = (4, 8)
अतः दोनों बिन्दुओं के रेखाखण्ड का मध्य बिन्दु समान है।

प्रश्न 9.
यदि A, B और C के निर्देशांक क्रमशः (6, - 1), (1, 3) तथा (x, 8) हैं तो x का मान ज्ञात कीजिए जबकि AB = BC हो।
हल:
दिया गया है-AB = BC
(AB)² = (BC)²
(6 - 1)² + (- 1 - 3)² = (x - 1)² + (8 - 3)²
25 + 16 = (x - 1)² + 25
16 = (x - 1)²
± 4 = (x - 1)

धनात्मक चिह्न लेने पर
4 = x - 1
x = 5
इसी प्रकार ऋणात्मक चिह्न लेने पर
- 4 = x - 1
∴ - 4 + 1 = x
x = -3
अतः x का मान - 3 या 5 होगा।

प्रश्न 10.
बिन्दुओं (1, - 2) तथा (4, 7) को मिलाने वाले रेखाखण्ड को बिन्दु (2, 1) किस अनुपात में विभाजित करता है?
हल:
माना दिये हुए बिन्दुओं को मिलाने वाली रेखाखण्ड को बिन्दु (2, 1), λ : 1 में विभाजित करता है। अतः विभाजन सूत्र से
x̄ = \(\frac{m_{1} x_{2}+m_{2} x_{1}}{m_{1}+m_{2}}\)
2 = \(\frac{\lambda \times 4+1 \times 1}{\lambda+1}\)
2λ + 2 = 4λ + 1
2 - 1 = 4λ - 2λ
1 = 2λ
∴ λ = \(\frac{1}{2}\)
अतः अभीष्ट अनुपात 1 : 2 है।
नोट : कोटि के मान से भी हमें यही अनुपात प्राप्त होगा।

प्रश्न 11.
x-अक्ष पर वह बिन्दु ज्ञात कीजिये जो बिन्दुओं A(6, 5) व B(- 4, 5) से समदूरस्थ हैं।
हल:
माना x-अक्ष पर वह बिन्दु P(x, 0) है। जो बिन्दुओं A(6, 5) व B(- 4, 5) से समदूरस्थ है।
प्रश्नानुसार AP= BP ∴ (AP)² = (BP)²
दो बिन्दुओं के बीच की दूरी ज्ञात करने का सूत्र लगाने
d = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
∴ (x - 6)² + (0 - 5)² = (x + 4)² + (0 - 5)²
⇒ x² - 12x + 36 + 25 = x² + 8x + 16 + 25
⇒ - 12x + 36 = 8x + 16
⇒ - 12x - 8x = 16 - 36
⇒ - 20x = - 20
⇒ x = \(\frac{-20}{-20}\) = 1
x-अक्ष पर वह बिन्दु P(1, 0) है।

प्रश्न 12.
यदि बिन्दु A(6, 1), B(8, 2), C(9, 4) और D(x, y) क्रम में एक समान्तर चतुर्भुज के शीर्ष हैं, तो बिन्दु D(x, y) ज्ञात कीजिये।
हल:
हम जानते हैं कि समान्तर चतुर्भुज के विकर्ण परस्पर समद्विभाजित करते हैं।

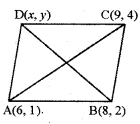
अतः विकर्ण AC के मध्य बिन्द के निर्देशांक
विकर्ण BD के मध्य बिन्दु के निर्देशांक
अर्थात्

अतः बिन्दु D(7, 3) होगा।

प्रश्न 13.
बिन्दुओं A(5,2), B(4,7) और C(7,-4) से बनने वाले त्रिभुज का क्षेत्रफल ज्ञात कीजिये।
हल-:
ΔABC का क्षेत्रफल व्यंजक का संख्यात्मक मान निम्न होता है :
\(\frac{1}{2}\)[x₁(y₂ - y₂₃) + x₂ (y₃ - y₁) + x₃ (y₁ - y₂)]
∴ शीर्षों A(5,2),B(4,7) और C(7,-4)वाले त्रिभुज ABC का क्षेत्रफल है।
= \(\frac{1}{2}\)[5(7 + 4) + 4(- 4 - 2) + 7(2 - 7)]
= \(\frac{1}{2}\)[5 × 11 + 4 × (- 6) + 7 × (-5)]
= \(\frac{1}{2}\)[55 - 24 - 35] = \(\frac{1}{2}\)[55 - 59]
= \(\frac{-4}{2}\) = -2
चूँकि क्षेत्रफल एक माप है, इसलिये यह ऋणात्मक नहीं हो सकता है। अतः हम क्षेत्रफल के रूप – 2 का संख्यात्मक मान 2 लेंगे इसलिये त्रिभुज का क्षेत्रफल 2 वर्ग मात्रक है।

निबन्धात्मक प्रश्न

प्रश्न 1.
किसी समतल में चार बिन्दु P(2,-1), Q (3,4), R(-2,3) और S(-3,-2) हैं, तो सिद्ध कीजिए कि PQRS वर्ग नहीं एक समचतुर्भुज है।
हल:
PQRS को समचतुर्भुज सिद्ध करने के लिए हमें सिद्ध करना होगा
(i) PQ = QR = RS = SP तथा PR ≠ OS
(ii) PR का मध्य बिन्दु = QS का मध्य बिन्दु

PR विकर्ण के बीच की दूरी

इस प्रकार विकर्ण PR का मध्य बिन्दु = विकर्ण QS का मध्य बिन्दु
⇒ PQRS के विकर्ण परस्पर समद्विभाजित हो रहे हैं। अतः ये एक सम- चतुर्भुज के विकर्ण हैं तथा चारों भुजाएँ भी बराबर हैं तथा विकर्ण आपस में बराबर नहीं हैं। अतः ये वर्ग नहीं हैं।

प्रश्न 2.
सिद्ध कीजिए कि समकोण त्रिभुज AOB में कर्ण का मध्य बिन्दु C त्रिभुज के शीर्षों O,A और B से बराबर दूरी पर स्थित है।
हल:
माना A= (2a, 0) तथा B = (0, 2b)
∴ मध्य बिन्दु = (C)
C = \(\left[\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\right]\)
= \(\left[\frac{2 a+0}{2}, \frac{0+2 b}{2}\right]\)= (a, b)


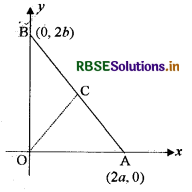
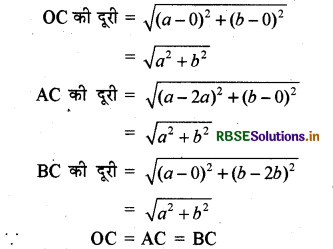
अर्थात् C बिन्दु, 0, A व B से बराबर दूरी पर हैं।

प्रश्न 3.
उस त्रिभुज की माध्यिकाओं की लम्बाइयाँ - ज्ञात कीजिए, जिसके शीर्ष (1, - 1), (0, 4) तथा (-5, 3) हैं।
हल:
BC के मध्य बिन्दु D के निर्देशांक
\(\left[\frac{0-5}{2}, \frac{4+3}{2}\right]=\left(-\frac{5}{2}, \frac{7}{2}\right)\)

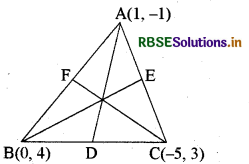
AC के मध्य बिन्दु E के निर्देशांक

अत: माध्यिकाओं की लम्बाइयाँ \(\frac{\sqrt{130}}{2}, \sqrt{13}\) और \(\frac{\sqrt{130}}{2}\) होंगी।

प्रश्न 4.
यदि त्रिभुज की भुजाओं के मध्य बिन्दु (1, 2), (0, - 1) तथा (2, - 1) हैं, तो त्रिभुज के शीर्षों के निर्देशांक ज्ञात कीजिए।
हल:
(x₁, y₁) व (x₂, y₂) बिन्दुओं को मिलाने वाली रेखा का मध्य बिन्दु होगा

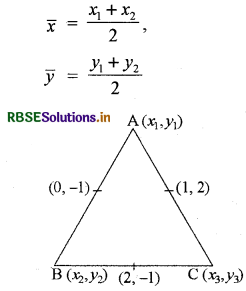
या x + x = 2 एवं y + y = 4 .... (1)
इसी प्रकार AB रेखा के लिए
\(\frac{x_{1}+x_{2}}{2}\) = 0, \(\frac{y_{1}+y_{2}}{2}\) = -1
या x₁ + x₂ = 0 एवं y₁ + y₂ = - 2 .... (2)

BC रेखा के लिए.
\(\frac{x_{2}+x_{3}}{2}\) = 2, \(\frac{y_{2}+y_{3}}{2}\) = -1
x₂ + x₃ = 4 एवं y₂ + y₃ = - 2 .... (3)

समीकरण 1, 2 व 3 को हल करने पर
2x₁ + 2x₂ + 2x₃ = 6
या x₁ + x₂ + x = 3 ..............(4)

या 2y₁ + 2y₂ + 2y₃ = 0
या y₁ + y₂ + y₃ = \(\frac{0}{2}\) = 0
या y₁ + y₂ + y₃ = 0

समीकरण (4) से
x₁ + x₂ + x₃ = 3
0 + x₃ = 3
समी. (1) से x + x = 0
इसी तरह से x₁ + x₂ = 0
x₃ = 1

इसी तरह से x₁ + x₂ = 0
x₂ = 1

इसी तरह से x₁ + 4 = 3
∴ x₁ = 3 - 4 = - 1
x₁ = -1

समीकरण (5) से y + y + y = 0
समीकरण (1), (2) तथा (3) के मान समीकरण (5) में रखने पर निम्न मान प्राप्त होते हैं
y₁ + y₂ + y₃ = 0
या 4 + y₂ = 0 ∴y₂ = -4
या - 2 + y₃ = 0 ∴ y₃ = 2
y₁ - 2 = 0 ∴ y₁ = 2

अतः हमें निम्न मान प्राप्त होते हैं
x₁ = - 1, y₁ = 2
x₂ = 1, y₂ = - 4
x₃ = 3, y₃ = 2

अतः अभीष्ट बिन्दु है (-1, 2), (1, - 4) तथा (3, 2)

प्रश्न 5.
बिन्दु (- 4, 6), बिन्दुओं A(- 6, 10) और B(3, - 8) को जोड़ने वाले रेखाखण्ड को किस अनुपात में विभाजित करता है?
हल:
माना कि (-4, 6) रेखाखण्ड AB के आन्तरिक रूप से m₁ : m₂ के अनुपात में विभाजित करता है। अतः विभाजन सूत्र से
x = \(\frac{m_{1} x_{2}+m_{2} x_{1}}{m_{1}+m_{2}}\)
और y =\(\frac{m_{1} y_{2}+m_{2} y_{1}}{m_{1}+m_{2}}\)
का प्रयोग करने पर
(-4, 6) = \(\frac{m_{1} x_{2}+m_{2} x_{1}}{m_{1}+m_{2}}\)
संगत पद लेने पर
-4 = \(\frac{3 m_{1}-6 m_{2}}{m_{1}+m_{2}}\)
या -4m₁ - 4m₂ = 3m₁ - 6m₂
या - 7m₁ = -2m₂
या m₁ : m₂ = 2 : 7

हमें इसकी जाँच करनी होगी कि यह अनुपात yनिर्देशांक को भी सन्तुष्ट करता है।

अतः बिन्दु (-4, 6), बिन्दुओं A(- 6, 10) और B(3, - 8) को जोड़ने वाले रेखाखण्ड को 2 : 7 के अनुपात में विभाजित करता है।

प्रश्न 6.
ज्ञात कीजिए कि रेखा 3x + y = 9. बिन्दुओं (1,3) तथा (2, 7) को मिलाने वाले रेखाखण्ड को किस अनुपात में विभाजित करती है?
हल:
माना बिन्दु (1, 3) तथा (2, 7) को मिलाने वाला रेखाखण्ड 3x + y = 9 को 2 : 1 में विभाजित करता है। अतः विभाजन बिन्दु के निर्देशांक

यह बिन्दु रेखा 3x + y = 9 पर स्थित होंगे और इसको सन्तुष्ट करेंगे। अतः मान रखने पर
⇒ 3. \(\left(\frac{2 \lambda+1}{\lambda+1}\right)+\frac{7 \lambda+3}{\lambda+1}\) = 9
⇒ \(\frac{6 \lambda+3}{\lambda+1}+\frac{7 \lambda+3}{\lambda+1}\) = 9
⇒ 6λ + 3 + 7λ + 3 = 9 (λ + 1)
⇒ 13λ + 6 = 9λ + 9
⇒ 13λ - 9λ = 9 - 6
⇒ 4λ = 3
∴ λ = \(\frac{3}{4}\)

∴ अभीष्ट अनुपात = \(\frac{3}{4}\) : 1 या 3 : 4

प्रश्न 7.
बिन्दुओं P (-3, 4) और Q (4, 5) को जोड़ने वाले रेखाखण्ड को समत्रिभाजित करने वाले बिन्दुओं के निर्देशांक ज्ञात कीजिए।
हल:
माना कि R (x, y) और S (x, y,) अभीष्ट बिन्दु हैं जो बिन्दुओं P (-3, 4) और Q (4, 5) को जोड़ने वाले रेखाखण्ड को समत्रिभाजित करते हैं अर्थात् R (x, y) PQ को 1 : 2 के अनुपात में और S (x, y) PQ को 2 : 1 के अनुपात में विभाजित करते हैं।

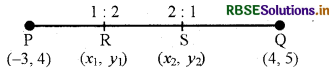
बिन्दु R के लिए

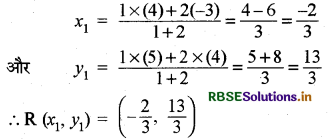
बिन्दु s के लिए-

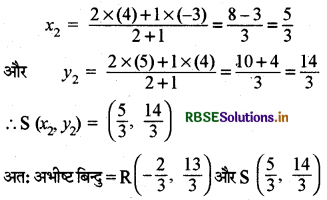
प्रश्न 8.
उस त्रिभुज का क्षेत्रफल ज्ञात कीजिए जिसके शीर्ष (-5, 7), (4, 5) और (-4, -5) हैं।
हल:
माना कि AABC के शीर्ष A(-5, 7), B(4, -5) और C(-4, -5) हैं।
यहाँ x₁ = -5, x₂ = 4, x₃ = -4
y₁ = 7, y₂ = 5, y₃ = -5
∴ ΔABC का क्षेत्रफल
= \(\frac{1}{2}\)[x₁(y₂ - y₂₃) + x₂ (y₃ - y₁) + x₃ (y₁ - y₂)]
= \(\frac{1}{2}\)[-5(5 + 5) + 4(-5 - 7) - 4(7 - 5)]
= \(\frac{1}{2}\)[-5(10) + 4(-12) - 4(2)]
= \(\frac{1}{2}\)[-50 - 48 - 8]
= -\(\frac{106}{2}\) = -53
चूँकि क्षेत्रफल एक माप है, इसलिए यह ऋणात्मक नहीं हो सकता है। अतः हम क्षेत्रफल के रूप -53 का संख्यात्मक मान 53 लेंगे। इसलिए त्रिभुज का क्षेत्रफल 53 वर्ग मात्रक है।