RBSE Class 10 Maths Important Questions Chapter 6 त्रिभुज

Rajasthan Board RBSE Class 10 Maths Important Questions Chapter 6 त्रिभुज Important Questions and Answers.

RBSE Class 10 Maths Chapter 6 Important Questions त्रिभुज

वस्तुनिष्ठ प्रश्न

प्रश्न 1.
दो सरल रेखाएँ जो एक ही रेखा के लम्बवत् हों, परस्पर कहलाती हैं
(A) लम्ब रेखाएँ
(B) समान्तर रेखाएँ
(C) समद्विभाजित रेखाएँ
(D) समान रेखाएँ
उत्तर:
(B) समान्तर रेखाएँ

प्रश्न 2.
दी गई आकृति में AD, ∠A का अन्तः समद्विभाजक है। यदि AB = 6 सेमी., BD = 4 सेमी. और DC = 3 सेमी., हो तो AC का मान है

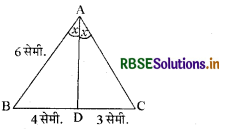
(A) 3 सेमी.
(B) 4 सेमी.
(C) 4.5 सेमी.
(D) 5 सेमी.
उत्तर:
(C) 4.5 सेमी.

प्रश्न 3.
संलग्न आकृति में यदि AB ∥ CD हो तो x का मान है

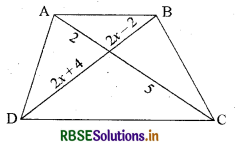
(A) 1
(B) 2
(C) 3
(D) 4
उत्तर:
(C) 3

प्रश्न 4.
दो समरूप त्रिभुजों के क्षेत्रफल क्रमशः 25 सेमी.² तथा 36 सेमी.2 हैं। यदि छोटे त्रिभुज की एक माध्यिका की लम्बाई 10 सेमी. है तो बड़े त्रिभुज की संगत माध्यिका की लम्बाई है
(A) 12 सेमी.
(B) 15 सेमी.
(C) 16 सेमी.
(D) 18 सेमी.
उत्तर:
(A) 12 सेमी.

प्रश्न 5.
दी गई आकृति में QA और PB, AB पर लम्बवत् हैं। यदि AO = 10 सेमी., BO = 6 सेमी. तथा PB = 9 सेमी. हो तो AQ की लम्बाई है.

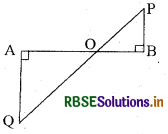
(A) 12 सेमी.
(B) 15 सेमी.
(C) 18 सेमी.
(D) 21 सेमी.
उत्तर:
(B) 15 सेमी.

प्रश्न 6.
ΔABC ~ ΔDEF है, यदि ∠A = 40°, ∠E = 80° है तो ∠C का मान है
(A) 70°
(B) 60°
(C) 50°
(D) 40°
उत्तर:
(B) 60°

प्रश्न 7.
यदि ΔABC में D भुजा BC का मध्य बिन्दु हो और AB² + AC² = x (BD² + AD²) तो x का मान होगा
(A) 1
(B) 2
(C) 4
(D) शून्य
उत्तर:
(B) 2

प्रश्न 8.
चित्र में ABC एक समकोण समद्विबाहु त्रिभुज है जहाँ ∠B = 90° है। यदि BC = 8 सेमी. है तो AD की लम्बाई क्या होगी? जहाँ D, BC का मध्य बिन्दु है

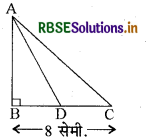
(A) 20 सेमी.
(B) \(\sqrt{20}\) सेमी.
(C) 2\(\sqrt{20}\) सेमी.
(D) 4\(\sqrt{20}\) सेमी.
उत्तर:
(C) 2\(\sqrt{20}\) सेमी.

अतिलघूत्तरात्मक प्रश्न

प्रश्न 1.
ΔABC में AD कोण ∠BAC का समद्विभाजक है। यदि AB = 4 cm, AC = 6 cm, BD = 2 cm है तो BC का मान ज्ञात कीजिए।

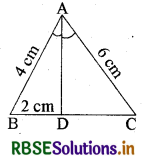
हल:
आधारभूत समानुपातिक प्रमेय से
\(\frac{\mathrm{BD}}{\mathrm{DC}}=\frac{\mathrm{AB}}{\mathrm{AC}}\)
या DC = \(\frac{\mathrm{BD} \times \mathrm{AC}}{\mathrm{AB}}\)

मान रखने पर
= \(\frac{6 \times 2}{4}\) = 3 cm
∴ BC = BD + DC
= 2 + 3 = 5 cm

प्रश्न 2.
किसी त्रिभुज की बराबर भुजाओं के सम्मुख कोण कैसे होते हैं?
उत्तर:
बराबर भुजाओं के सम्मुख कोण समान होते हैं।

प्रश्न 3.
दो समरूप त्रिभुजों की भुजाएँ 4:5 के अनुपात में हैं। इन त्रिभुजों के क्षेत्रफलों का अनुपात ज्ञात कीजिये।
हल:
समरूप त्रिभुजों के क्षेत्रफलों का अनुपात भुजाओं के अनुपात के वर्ग के बराबर है, अतः त्रिभुजों के क्षेत्रफलों में अनुपात
= (4 : 5)²
= 16 : 25

प्रश्न 4.
बौधायन प्रमेय का कथन लिखिए।
हल:
बौधायन प्रमेय-किसी आयत के विकर्ण से बने वर्ग का क्षेत्रफल इसकी दोनों आसन्न भुजाओं पर बने वर्गों के योग के बराबर होता है।

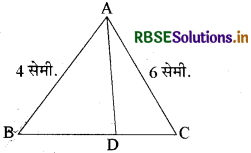
प्रश्न 5.
दी गई आकृति में AD, ∠A का अन्तः समद्विभाजक है। यदि AB = 4 सेमी., AC = 6 सेमी. है तो BD : DC लिखिए।
हल:
\(\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{\mathrm{BD}}{\mathrm{DC}}\)
अतः \(\frac{4}{6}=\frac{B D}{D C}\)
अतः BD : DC = 4 : 6 = 2 : 3

प्रश्न 6.
यदि ΔABC ~ ΔDEF, AB = 5 सेमी., DE = 3 सेमी. तथा ΔABC का क्षेत्रफल = 50 सेमी. है, तो ΔDEF का क्षेत्रफल लिखिए।
हल:

प्रश्न 7.
संलग्न आकृति में BC ∥ PQ यदि AP = 4 सेमी., AQ = 5 सेमी. तथा QC = 2.5 सेमी. तो PB का मान ज्ञात कीजिए।
हल:
\(\frac{\mathrm{AQ}}{\mathrm{QC}}=\frac{\mathrm{AP}}{\mathrm{PB}}\)
= \(\frac{5}{2.5}=\frac{4}{\mathrm{~PB}}\)
अतः PB = \(\frac{4}{2}\) = 2 सेमी.

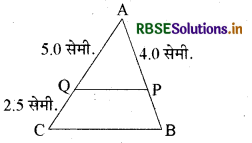
प्रश्न 8.
उपर्युक्त प्रश्न के चित्र में यदि AB = 7 सेमी., AP = 5 सेमी. तथा AC = 10.5 सेमी. तो AQ का मान ज्ञात कीजिए।
हल:
\(\frac{\mathrm{AC}}{\mathrm{AQ}}=\frac{\mathrm{AB}}{\mathrm{AP}}\)
= \(\frac{10.5}{\mathrm{AQ}}=\frac{7}{5}\)
अतः AQ = \(\frac{10.5 \times 5}{7}\) = 7.5 सेमी.

प्रश्न 9.
त्रिभुज ABC की भुजा BC पर P तथा Q बिन्दु इस प्रकार हैं कि BP = 3 सेमी., BQ = 5 ΔABP सेमी. तथा BC = 6 सेमी., तो अनुपात \(\frac{\triangle \mathrm{ABP}}{\triangle \mathrm{APQ}}\) का |मान ज्ञात कीजिए।
हल:
\(\frac{\triangle \mathrm{ABP}}{\Delta \mathrm{APQ}}=\frac{(\mathrm{BP})^{2}}{(\mathrm{PQ})^{2}}=\frac{(3)^{2}}{(2)^{2}}=\frac{9}{4}\)

प्रश्न 10.
दो समरूप त्रिभुज ABC तथा PQR के -परिमाप क्रमशः 36 सेमी. तथा 24 सेमी. हैं। यदि PQ 10 सेमी. हो तो AB ज्ञात कीजिए।
हल:

अतः AB = 15 सेमी.

प्रश्न 11.
यदि दो त्रिभुज ABC और XYZ में \(\frac{{AB}}{{XY}}=\frac{{BC}}{{YZ}}=\frac{{AC}}{{ZX}}\) तो ΔABC के कोण A का मान त्रिभुज XYZ के किस कोण के बराबर होगा?
उत्तर:
∠X के समान।

प्रश्न 12.
यदि ΔABC में ΔDEF में = BC \(\frac{AB}{DE}=\frac{BC}{EF}=\frac{AC}{DF}\) हो, तो वे आपस में कैसे त्रिभज होंगे?
उत्तर:
समरूप त्रिभुज।

प्रश्न 13.
दो त्रिभुजों के समरूप होने की दो दशाएँ बताइए।
उत्तर:
दो त्रिभुज समरूप होते हैं यदि
(i) उनके संगत कोण समान हों।
(ii) उनकी संगत भुजाएँ समानुपाती हों।

प्रश्न 14.
SSS नियम लिखिए।
उत्तर:
sss नियम-यदि दो त्रिभुजों की संगत भुजाएँ समानुपाती हैं, तो वे दोनों समरूप होते हैं।

प्रश्न 15.
ΔABC की भुजाओं AB और AC पर बिन्दु D और E इस प्रकार हैं कि DE ∥ BC यदि AD = 8 सेमी., AB = 12 सेमी. तथा AE = 12 सेमी. हो तो CE का माप लिखिए।

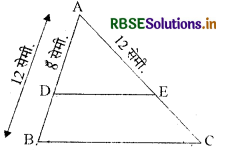
हल:
आधारभूत आनुपातिक प्रमेय से
\(\frac{A D}{B D}=\frac{A E}{C E}\)
यहाँ AD = 8 सेमी., BD = (12 - 8) = 4 सेमी. तथा AE = 12 सेमी. है।
अतः मान रखने पर
\(\frac{A D}{B D}=\frac{A E}{C E}\)
CE = \(\frac{12}{8}\) × 4 = 6 सेमी.

प्रश्न 16.
ΔABC में यदि D, BC पर कोई बिन्दु इस प्रकार है कि \(\frac{A B}{A C}=\frac{B D}{D C}\), ∠B = 70° तथा ∠C = 50° हो तो ∠BAD का माप लिखिए।
हल:
दिया है : ΔABC जिसमें D, BC पर बिन्दु इस प्रकार है कि \(\frac{A B}{A C}=\frac{B D}{D C}\) तथा ∠B = 70° व ∠C = 50°

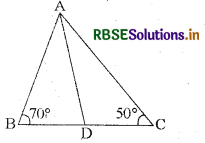
ज्ञात करना है : ∠BAD (दिया है)
उपपत्ति : यहाँ \(\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{\mathrm{BD}}{\mathrm{CD}}\) (लिख सकते हैं)
अतः ΔABD ~ ΔADC
∠A = [180 - (70 + 50)] = 60°
अतः ∠BAD = \(\frac{1}{2}\) ∠A= \(\frac{60}{2}\)  = 30°

प्रश्न 17.
दी गई आकृति में ∠ABC = 90° तथा BD ⊥ AC है। यदि BD = 8 सेमी. तथा AD = 4 सेमी. हो तो CD का माप लिखिए।
हल:
ΔABD व ΔBDC में

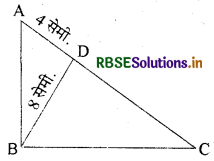
∠BDC = ∠BDA (प्रत्येक 90°)
∠DBC = ∠BAD
अत: ΔABD ~ ΔBDC
\(\frac{\mathrm{AB}}{\mathrm{BD}}=\frac{\mathrm{BD}}{\mathrm{CD}}\)
\(\frac{4}{8}=\frac{8}{C D}\) या 4CD = 64
अतः CD = \(\frac{64}{4}\) = 16. सेमी.

प्रश्न 18.
चित्र में EF ∥ BC, यदि AE : BE = 4 : 1 और CF = 1.5 सेमी. हो, तो AF की लम्बाई क्या होगी?

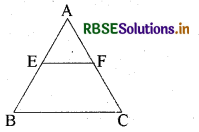
हल:
चित्र में EF ∥ BC
∴ \(\frac{\mathrm{AE}}{\mathrm{BE}}=\frac{\mathrm{AF}}{\mathrm{CF}}\)
⇒ \(\frac{4}{1}=\frac{\mathrm{AF}}{1.5}\)
⇒AF = 4 × 1.5
= 6.0 सेमी.

प्रश्न 19.
दो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात 16: 81 है तो इनकी भुजाओं का अनुपात ज्ञात कीजिए।
हल:
समरूप त्रिभुजों के क्षेत्रफलों का अनुपात भुजाओं के अनुपात के वर्ग के बराबर होता है। अतः इनकी भुजाओं का अनुपात
= \(\sqrt{\frac{16}{81}}=\frac{4}{9}\)
अतः इनकी भुजाओं का अनुपात = 4 : 9

लघूत्तरात्मक प्रश्न

प्रश्न 1.
यदि कोई रेखा एक ΔABC की भुजाओं AB और AC को क्रमशः D और E पर प्रतिच्छेद करे तथा भुजा BC के समान्तर हो, तो सिद्ध कीजिए कि \(\frac{A D}{A B}=\frac{A E}{A C}\) होगा ( देखिए आकृति)।

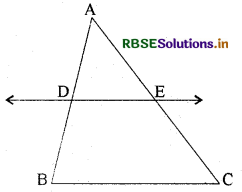
हल:

प्रश्न 2.
ABCD एक समलम्ब है जिसमें AB ∥ DC है। असमान्तर भुजाओं AD और BC पर क्रमशः बिन्दु E और F इस प्रकार स्थित हैं कि EF भुजा AB के समान्तर है (देखिए आकृति)। दर्शाइए कि \(\frac{A E}{E D}=\frac{B E}{F C}\) है।

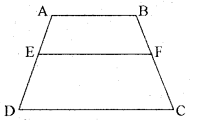
हल:
A और C को मिलाएँ जो EF को G पर | प्रतिच्छेद करे (देखिए आकृति)।
AB ∥ DC और EF ∥ AB (दिया है)
इसलिए EF ∥ DC (एक ही रेखा के समान्तर रेखाएँ परस्पर समान्तर होती हैं)

अब ΔADC में,
EG ∥ DC (क्योंकि EF ∥ DC)
अतः \(\frac{\mathrm{AE}}{\mathrm{ED}}=\frac{\mathrm{AG}}{\mathrm{GC}}\) (प्रमेय 6.1 के अनुसार) ....... (i)

इसी प्रकार ΔCAB में,
\(\frac{\mathrm{CG}}{\mathrm{AG}}=\frac{\mathrm{CF}}{\mathrm{BF}}\)
अर्थात् \(\frac{\mathrm{AG}}{\mathrm{GC}}=\frac{\mathrm{BF}}{\mathrm{FC}}\) ....(ii)

अतः (i) और (ii) से,
\(\frac{\mathrm{AE}}{\mathrm{ED}}=\frac{\mathrm{BF}}{\mathrm{FC}}\) (इतिसिद्धम्)

प्रश्न 3.
आकृति में \(\frac{P S}{S Q}=\frac{P T}{T R}\) है तथा ∠PST = ∠PRQ है। सिद्ध कीजिए कि ΔPQR एक समद्विबाहु त्रिभुज है।

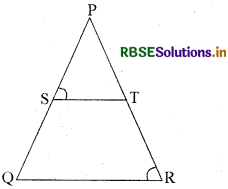
हल:
यह दिया है कि,
\(\frac{P S}{S Q}=\frac{P T}{T R}\)
अतः ST ∥ QR (प्रमेय 6.2 के अनुसार)

इसलिए ∠PST = ∠PQR (संगत कोण) ....(i)
साथ ही यह दिया है कि ∠PST = ∠PRQ .... (ii)
अतः ∠PRQ = ∠PQR [(i) और (ii) से]
इसलिए PQ = PR (समान कोणों की सम्मुख भुजाएँ)
अर्थात् ΔPQR एक समद्विबाहु त्रिभुज है। (इतिसिद्धम्)

प्रश्न 4.
दी गयी आकृति में, यदि PQ ∥ RS है, तो सिद्ध कीजिये कि
ΔPOQ ~ ΔSOR है।

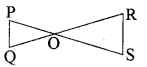
हल:
PQ ∥ RS (दिया है)
अतः ∠P = ∠S (एकान्तर कोण)
और ∠Q = ∠R (एकान्तर कोण)
साथ ही ∠POO = ∠SOR (शीर्षाभिमुख कोण)
इसलिये ΔPOQ ~ ΔSOR (AAA समरूपता कसौटी) (इतिसिद्धम्)

प्रश्न 5.
दी गयी आकृति में ∠P ज्ञात कीजिये।

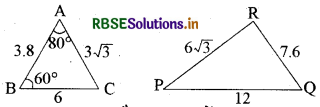
हल:
ΔABC और ΔPQR में,

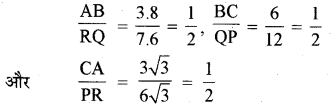
अर्थात्
इसलिये ΔABC ~ ΔRQP (SSS समरूपता)
इसलिये ∠C = ∠P (समरूप त्रिभुजों के संगत कोण)
लेकिन ∠C = 180° - ∠A - ∠B (Δ का कोण योग गुणधर्म)
∠C = 180° - 80° - 40° = 40°
अतः ∠P = 40°

प्रश्न 6.
दी गयी आकृति में, OA . OB = OC . OD है। दर्शाइये कि ∠A = ∠C और ∠B = ∠D है।

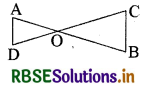
हल:
OA . OB = OC . OD (दिया है)
अतः \(\frac{\mathrm{OA}}{\mathrm{OC}}=\frac{\mathrm{OD}}{\mathrm{OB}}\) .... (1)
साथ ही, हमें प्राप्त है ∠AOD = ∠COB (शीर्षाभिमुख कोण) .... (2)

समीकरण (1) और (2) से
ΔAOD ~ ΔCOB (SAS समरूपता कसौटी)
इसलिये ∠A = ∠C और ∠D = ∠B (समरूप त्रिभुजों के संगत कोण)

प्रश्न 7.
दी गयी आकृति में ∠ACB = 90° तथा CD ⊥ AB है। सिद्ध कीजिये कि \(\frac{B^{2}}{A C^{2}}=\frac{B D}{A D}\)
हल:
ΔACD ~ ΔABC
चूँकि हम जानते हैं कि यदि किसी समकोण त्रिभुज के समकोण वाले शीर्ष से कर्ण पर लम्ब डाला जाये तो इस लम्ब के दोनों ओर बने त्रिभुज सम्पूर्ण त्रिभुज के समरूप होते हैं तथा परस्पर भी समरूप होते हैं।
अतः \(\frac{\mathrm{AC}}{\mathrm{AB}}=\frac{\mathrm{AD}}{\mathrm{AC}}\)
या AC² = AB . AD .... (1)

इसी प्रकार उपर्युक्त प्रमेय से
ΔBCD ~ ΔBAC
अतः \(\frac{B C}{B A}=\frac{B D}{B C}\)
या BC² = BA . BD . .... (2)

समीकरण (1) तथा (2) से
\(\frac{\mathrm{BC}^{2}}{\mathrm{AC}}=\frac{\mathrm{BA} \cdot \mathrm{BD}}{\mathrm{AB} \cdot \mathrm{AD}}=\frac{\mathrm{BD}}{\mathrm{AD}}\) (इतिसिद्धम्)

प्रश्न 8.
एक सीढ़ी किसी दीवार पर इस प्रकारटिकी हुई है कि इसका निचला सिरा दीवारसे 2.5 m की दूरी पर है तथा इसका ऊपरी सिरा भूमि से 6 m की ऊँचाई पर बनी एक खिड़की तक पहुँचता है।सीढ़ी की लम्बाई ज्ञात कीजिये।
हल:
माना AB सीढ़ी है तथा CA दीवार है जिसमें खिड़की A पर है। जैसा आकृति में दिखाया गया है।

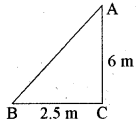
साथ ही BC = 2.5 m
CA = 6 m है।
पाइथागोरस प्रमेय से
AB² = BC² + CA²
= (2.5)² + (6)²
= 6.25 + 36

AB² = 42.25
∴ AB = 142.25 = 6.5 m
अतः AB = 6.5 m
इस प्रकार, सीढ़ी की लम्बाई 6.5 m है।

प्रश्न 9.
दी गयी आकृति में, AD ⊥ BC है। सिद्ध कीजिये कि AB² + CD² = BD² + AC² है।

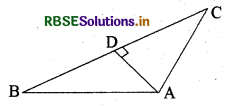
हल:
ΔADC से
AC² = AD² + CD² .... (1) (पाइथागोरस प्रमेय से)

ΔADB से
AB² = AD² + BD² .... (2) (पाइथागोरस प्रमेय से)

समीकरण (2) में से समीकरण (1) को घटाने पर
AB² - AC² = BD² - CD²
या AB² + CD² = BD² + AC² (इतिसिद्धम्)

प्रश्न 10.
एक समतल जमीन पर 2 मी. लम्बे छात्र की छाया की लम्बाई 1 मी. है। उसी समय एक मीनार की छाया की लम्बाई 5 मी. हो, तो मीनार की ऊँचाई ज्ञात कीजिए।
हल:
माना कि मीनार की ऊँचाई hm है। चित्रानुसार हम देखते हैं कि ΔABC तथा ΔDEC समरूप हैं अर्थात्

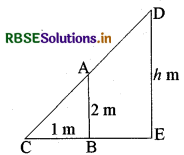
ΔABC - ΔDEC
अत: \(\frac{\mathrm{AB}}{\mathrm{DE}}=\frac{\mathrm{CB}}{\mathrm{CE}}\)
⇒ \(\frac{2}{h}=\frac{1}{5}\)
या h = 5 × 2
= 10 m.

प्रश्न 11.
आकृति में कोणों ∠OKS व ∠ROPका मान ज्ञात कीजिए, यदि त्रिभुज ΔOPR ~ ΔOSK तथा ∠POS = 1250 और ∠PRO = 70° है।

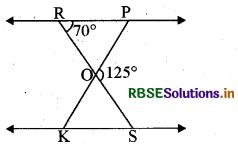
हल:
प्रश्नानुसार ∠POS = 125° तथा ∠PRO = 70°

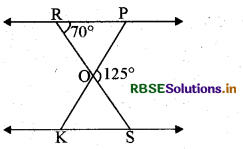
चित्रानुसार ROS एक सरल रेखा है।
∴ ∠ROP + ∠POS = 180°
या ∠ROP + 125° = 180°
∠ROP = 180° - 1250
= 550

जब ∠ROP = 55° तो ∠KOS भी 55° का होगा क्योंकि ये शीर्षाभिमुख कोण या सम्मुख कोण है।
∴ ΔOPR ~ ΔOSK
∴ ∠R = ∠S = 70°
अतः AROP में ∠R + ∠O + ∠P = 180°
70° + 550 + ∠P = 180°
या ∠P = 180° – 70° - 55°
∠P = 55°
∴ ∠P = ∠K = 55°
अतः ∠OKS = 55° तथा ∠ROP = 55°

निबन्धात्मक प्रश्न

प्रश्न 1.
किसी त्रिभुज की एक भुजा के समान्तर खींची गई रेखां अन्य दो भुजाओं को जिन दो बिन्दुओं पर प्रतिच्छेद करती है, वे बिन्दु उन भुजाओं को समान अनुपात में विभाजित करते हैं। सिद्ध कीजिए।
अथवा यदि किसी त्रिभुज की एक भुजा के समान्तर अन्य दो भुजाओं को भिन्न-भिन्न बिन्दुओं पर प्रतिच्छेद करने के लिए एक रेखा खींची जाए, तो सिद्ध कीजिए कि ये अन्य दो भुजाएँ एक ही अनुपात में विभाजित होती हैं।
हल:
दिया है-ΔABC में DE ∥ BC खींची गई है और यह AB को D पर तथा AC को E पर प्रतिच्छेदित करती है।

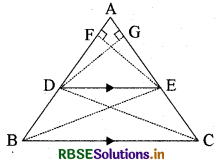
सिद्ध करना है- \(\frac{\mathrm{AD}}{\mathrm{DB}}=\frac{\mathrm{AE}}{\mathrm{EC}}\)

रचना-B को E से तथा C को D से मिलाइए और EF ⊥ BA तथा DG ⊥ AC खींचिए।
उपपत्ति: ∵ ΔBDE तथा ΔCED एक ही आधार DE पर तथा समान्तर रेखाओं DE तथा BC के बीच स्थित हैं।
∴ ΔBDE का क्षेत्रफल = ΔCED का क्षेत्रफल .... (1)
∵ ΔADE तथा ΔBDE की उभयनिष्ठ ऊँचाई EF है।

अब समीकरण (1), (2) व (3) से
\(\frac{\mathrm{AD}}{\mathrm{DB}}=\frac{\mathrm{AE}}{\mathrm{EC}}\) (इतिसिद्धम्)

प्रश्न 2.
90 cm की लम्बाई वाली एक लड़की बल्ब लगे एक खम्भे के आधार से परे 1.2 m/s की चाल से चल रही है। यदि बल्ब भूमि से 3.6 cm की ऊँचाई पर है, तो 4 सेकण्ड बाद उस लड़की की छाया
की लम्बाई ज्ञात कीजिए।
हल:
मान लीजिए AB बल्ब लगे खम्भे को तथा CD लड़की द्वारा खम्भे के आधार से परे 4 सेकण्ड चलने के बाद उसकी स्थिति को प्रकट करते हैं (देखिए आकृति)।

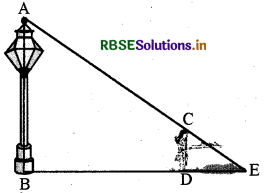
आकृति के अनुसार DE लड़की की छाया की लम्बाई है। माना कि DE, x m है।
BD = 1.2 m × 4 = 4.8 m
अब ΔABE और ΔCDE में,
∠B = ∠D (प्रत्येक 90° का है, क्योंकि बल्ब लगा खम्भा और लड़की दोनों ही भूमि से ऊर्ध्वाधर खड़े हैं)
तथा ∠E = ∠E (समान कोण)
अतः ΔABE ~ ΔCDE (AA समरूपता कसौटी)
इसलिए \(\frac{\mathrm{BE}}{\mathrm{DE}}=\frac{\mathrm{AB}}{\mathrm{CD}}\) (समरूप त्रिभुजों की संगत भुजाएँ)
अर्थात् \(\frac{4.8+x}{x}=\frac{3.6}{0.9}\) (90 cm = \(\frac{4.8+x}{x}=\frac{3.6}{0.9}\) m = 0.9 m)
अर्थात् 4.8 + x = 4x
अर्थात् 3x = 4.8
अर्थात् x = 1.6
अतः 4 सेकण्ड चलने के बाद लड़की की छाया की लम्बाई 1.6 m है।

प्रश्न 3.
आकृति में CM और RN क्रमशः ΔABC और ΔPQR की माध्यिकाएँ हैं। यदि ΔABC ~ ΔPQR है तो सिद्ध कीजिए कि-
(i) ΔAMC ~ ΔPNR
(ii) \(\frac{\mathrm{C M}}{\mathrm{R N}}=\frac{\mathrm{A B}}{\mathrm{P Q}}\)
(iii) ΔCMB ~ ΔRNQ

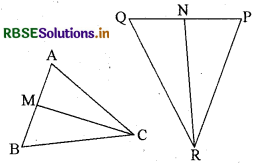
अथवा
आकृति में CD और RS क्रमशः ΔABC और ΔPQR की माध्यिकाएँ हैं। यदि ΔABC ~ ΔPQR हो, तो सिद्ध कीजिए कि
(i) ΔADC ~ ΔPSR
(ii) \(\frac{\mathrm{CD}}{\mathrm{R S}}=\frac{\mathrm{AB}}{\mathrm{P Q}}\)

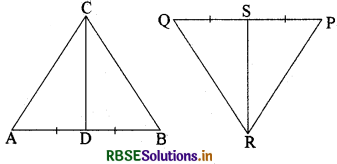
हल:
(i) ΔABC ~ ΔPQR (दिया है)
अतः \(\frac{\mathrm{AB}}{\mathrm{PQ}}=\frac{\mathrm{BC}}{\mathrm{QR}}=\frac{\mathrm{CA}}{\mathrm{RP}}\) .... (i)
तथा ∠A = ∠P, ∠B = ∠Q और ∠C = ∠R .... (ii)
AB = 2AM और PQ = 2PN (क्योंकि CM और RN माध्यिकाएँ हैं)

इसलिए (i) से \(\frac{2 \mathrm{AM}}{2 \mathrm{PN}}=\frac{\mathrm{CA}}{\mathrm{RP}}\)
अर्थात् \(\frac{\mathrm{AM}}{\mathrm{PN}}=\frac{\mathrm{CA}}{\mathrm{RP}}\) ....... (iii)
साथ ही ∠MAC = ∠NPR [(ii) से].... (iv)
इसलिए (iii) और (iv) से, .
ΔAMC ~ ΔPNR (SAS समरूपता) .... (v)

(ix) और (x) से]
अतः ΔCMB ~ ΔRNQ (SSS समरूपता) (इतिसिद्धम्)

प्रश्न 4.
सिद्ध कीजिये कि दो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात इनकी संगत भुजाओं के अनुपात के वर्ग के बराबर होता है।
हल:
दिया गया हैदो त्रिभुज ABC और PQR
ऐसे दिये गये हैं कि ΔABC ~ ΔPQR

सिद्ध करना है :

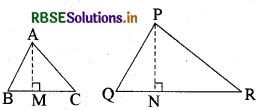
रचना शीर्ष A तथा P से भुजा BC और QR पर लम्ब AM और PN खींचे गये हैं।

अब ar (ABC) = \(\frac{1}{2}\)BC - AM
तथा ar (PQR) = \(\frac{1}{2}\)QR × PN

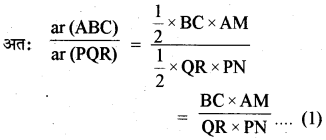
अब ΔABM और ΔPQN में,
और ∠B = ∠Q(∵ ΔABC ~ ΔPQR है।)
∠M = ∠N (प्रत्येक 90° का है।)

अतः ΔABM ~ ΔPQN (AA समरूपता कसौटी)

इसलिये \(\frac{\mathrm{AM}}{\mathrm{PN}}=\frac{\mathrm{AB}}{\mathrm{PQ}}\) .... (2)
साथ ही ΔABC ~ ΔPQR (दिया है)
इसलिये \(\frac{\mathrm{AB}}{\mathrm{PQ}}=\frac{\mathrm{BC}}{\mathrm{QR}}=\frac{\mathrm{CA}}{\mathrm{RP}}\) .... (3)
अतः \(\frac{{ar}(\mathrm{ABC})}{{ar}(\mathrm{PQR})}=\frac{\mathrm{AB}}{\mathrm{PQ}} \times \frac{\mathrm{AM}}{\mathrm{PN}}\) [समी. (1) और (3) से]
\(\frac{{ar}(\mathrm{ABC})}{{ar}(\mathrm{PQR})}=\frac{\mathrm{AB}}{\mathrm{PQ}} \times \frac{\mathrm{AB}}{\mathrm{PQ}}\) (समीकरण (2) से)

अब समीकरण (3) का प्रयोग करने पर
\(\frac{{ar}(\mathrm{ABC})}{{ar}(\mathrm{PQR})}=\left(\frac{\mathrm{AB}}{\mathrm{PQ}}\right)^{2}=\left(\frac{\mathrm{BC}}{\mathrm{QR}}\right)^{2}=\left(\frac{\mathrm{CA}}{\mathrm{RP}}\right)^{2}\) (इतिसिद्धम्)

प्रश्न 5.
ΔARC की भुजाओं AB और AC पर क्रमशः बिन्दु D और E इस प्रकार हैं कि DE ∥ BC है। यदि रेखा DE, ΔABC को बराबर क्षेत्रफल वाली आकृतियों में बाँटती हो तो सिद्ध कीजिए कि
\(\frac{\mathrm{BD}}{\mathbf{A B}}=\frac{2-\sqrt{2}}{2}\)
हल:
दिया हुआ है-ΔABC जिसमें DE ∥ BC
सिद्ध करना है_
\(\frac{\mathrm{BD}}{\mathbf{A B}}=\frac{2-\sqrt{2}}{2}\)
उपपत्ति : ΔABC में DE ∥ BC
∴ ∠1 = ∠2, ∠3 = ∠4
ΔABC ~ ΔADE

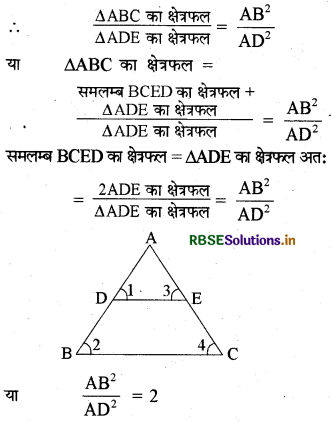
तथा \(\frac{\mathrm{AB}}{\mathrm{AD}}\) = √2
अतः AD = AB - BD.
AB = √2 (AB - BD)
√2 BD = √2 AB - AB

या BD = \(\frac{\mathrm{AB}(\sqrt{2}-1)}{\sqrt{2}}\)
या \(\frac{\mathrm{BD}}{\mathrm{AB}}=\frac{(\sqrt{2}-1)}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}}\)
अशं तथा हर में √2 से गुणा करने पर
= 2√2 (इतिसिद्धम्)

प्रश्न 6.
किसी भी समकोण त्रिभुज में कर्ण का वर्ग शेष दोनों भुजाओं के वर्गों के योग के बराबर होता है। सिद्ध कीजिए।
हल:
दिया है - एक ΔABC में ∠B = 90° है।
सिद्ध करना है.-AC² = AB² + BC²
रचना-BD ⊥ AC खींचिए।

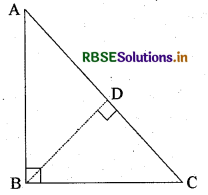
उपपत्ति-ΔABC और ΔADB में
∠ABC = ∠ADB (प्रत्येक 90°)
∠A = ∠A (उभयनिष्ठ)

कोण-कोण समरूपता उप प्रमेय से.
∴ ΔABC ~ ΔADB

∵ समरूप त्रिभुजों की संगत भुजा समानुपाती होती है।
अतः \(\frac{\mathrm{AB}}{\mathrm{AD}}=\frac{\mathrm{AC}}{\mathrm{AB}}\)
⇒ AB² = AC × AD

इस प्रकार ΔABC ~ ΔBDC में
\(\frac{\mathrm{BC}}{\mathrm{DC}}=\frac{\mathrm{AC}}{\mathrm{BC}}\)
⇒ BC² = AC × DC .... (2)

समीकरण (1) व (2) को जोड़ने से
AB²+ BC² = AC × AD + AC - DC
= AC × (AD + DC)
= AC × AC
= AC²
AC² = AB² + BC² (इतिसिद्धम्)

प्रश्न 7.
BL और CM एक समकोण त्रिभुज ABC की माध्यिकाएँ हैं तथा ∠A = 90° है, तो सिद्ध कीजिये कि
4(BL² + CM²) = 5BC²
अथवा
BE और CF एक समकोण त्रिभुज ABC की माध्यिकाएँ हैं तथा इस त्रिभुज का कोण A समकोण है। सिद्ध कीजिये कि 4(BE² + CF²) = 5BC².
हल:
BL और CM एक ΔABC की माध्यिकाएँ हैं | जिसमें ∠A = 90° है, जैसा कि आकृति में दिखाया गया है।

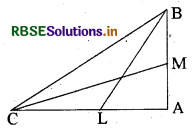
ΔABC से
BC² = AB² + AC² .... (i) (पाइथागोरस प्रमेय)

ΔABL से
BL² = AL² + AB²
या BL² = \(\left(\frac{\mathrm{AC}}{2}\right)^{2}\) + AB² ( AC का मध्य बिन्दु L है)
या BL² = \(\frac{\mathrm{AC}^{2}}{4}\) + AB²
या 4BL² = AC² + 4AB² .... (ii)

ΔCMA से
CM² = AC² + AM²
CM = AC² + \(\left(\frac{\mathrm{AB}}{2}\right)^{2}\) (AB का मध्य बिन्दु M है)
या CM² = AC² + \(\frac{\mathrm{AB}^{2}}{4}\)
या 4CM² = 4AC² + AB² .... (iii)

समीकरण (ii) तथा (iii) को जोड़ने पर
4BL² + 4CM² = AC² + 4AB² + 4AC² + AB²
या 4(BL² + CM²) = 5AC² + 5AB²
या 4(BL² + CM²) = 5(AC² + AB²)
या 4(BL² + CM²) = 5BC² [समी. (i) से] (इतिसिद्धम्)

प्रश्न 8.
आयत ABCD के अन्दर स्थित एक बिन्दु O को शीर्ष A, B, C और D से मिलाया गया गया है। सिद्ध कीजिए कि
OB² + OD² = OC² + OA²
हल:
दिया है-आयत ABCD इसके अन्दर बिन्दु 0 है, OA, OB, OC व OD को मिलाया।
सिद्ध करना है
OB² + OD² = OC² + OA²

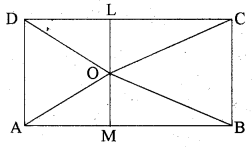
रचना–O में से LM ∥ AD खींचा जो DC और AB को क्रमशः L और M पर मिलती है।
उपपत्ति: हम जानते हैं कि- OB² = OM² + MB² (पाइथागोरस प्रमेय से)
= OM² + CL²
तथा OD² = OL² + DL² = OL² + AM²
∴ OB² + OD² = OM² + CL² + OL² + AM²
= (OM² + AM²) + (CL² + OL²)
= OA² + OC²
अत: OB² + OD² = OC² + OA² (इतिसिद्धम्)

प्रश्न 9.
सिद्ध कीजिए कि यदि किसी त्रिभुज की एक भुजा का वर्ग.अन्य दो भुजाओं के वर्गों के योग के बराबर हो, तो पहली भुजा का सम्मुख कोण समकोण होता है।
हल:
दिया है - एक त्रिभुज ABC है जिसमें AC² = AB² + BC²
सिद्ध करना है - ∠ABC = 90°
रचना-एक अन्य त्रिभुज DEF इस प्रकार बनाया कि DE = AB, EF = BC तथा ∠E = 90°

उपपत्ति - यह सिद्ध करने के लिए कि ∠ABC = 90° है,
हमें केवल यह सिद्ध करना होगा कि ΔABC ~ ΔDEF है।
∴ ΔDEF एक समकोण त्रिभुज है जिसमें ∠DEF समकोण है।

अतः पाइथागोरस प्रमेय से
DF² = DE² + EF²
⇒ DF² = AB² + BC²
[∵ DE = AB तथा EF = BC (रचना से)]
⇒ DF² = AC²
[∵ दिया है कि AB² + BC² = AC²]
⇒ DF = AC ....(i)

अतः ΔABC और ΔDEF में
AB = DE (रचना से)
BC = EF (रचना से)
तथा AC = DF [ (i) से]

अतः सर्वांगसमता की Sss कसौटी से
ΔABC ≅ ΔDEF
∠B = ∠E [∵ सर्वांगसम त्रिभुजों के संगत कोण समान होते हैं।]
∠B = ∠E = 90° [∵ ∠E = 90° (रचना से)]
अत: ΔABC एक समकोण त्रिभुज है। (इतिसिद्धम्)

प्रश्न 10.
आयत ABCD के अन्दर स्थित O कोई बिन्द है, सिद्ध कीजिए
OB² + OD² = OA² + OC²

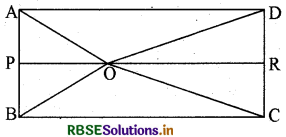
हल:
आयत ABCD के अन्दर एक बिन्दु O स्थित है जिससे गुजरती हुई BC के समान्तर रेखा भुजाओं AB और DC को क्रमशः P और R पर काटती है।

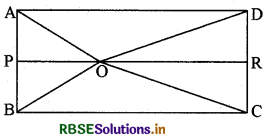
समकोण त्रिभुजों OPB और ORD में पाइथागोरस प्रमेय से
OB² = OP² + PB² और OD² = OR² + DR²

इन दोनों को जोड़ने पर
⇒ OB² + OD² = OP² + PB² + OR² + DR²
⇒ OB² + OD² = OP² + OR² + PB² + DR² ......(i)

पुनः समकोण त्रिभुजों ORC तथा OPA में पाइथागोरस प्रमेय से
OC² = OR² + RC² तथा OA² = OP² + PA²

इन दोनों को जोड़ने पर
⇒ OC² + OA² = OR² + RC² + OP² + PA²
⇒ OC² + OA² = OR² + OP² + RC² + PA²
⇒ OC² + OA² = OR² + OP² + PB² + DR² [∵ RC = PB तथा PA = DR]
⇒ OC² + OA² = (OR² + OP²) + (PB² + DR²)

(i) व (ii) से
⇒ OB² + OD² = OC² + OA²
⇒ OB² + ² = OA² + OC² (इतिसिद्धम्)

प्रश्न 11.
निम्न में से दी गई आकृति में \(\frac{P K}{K S}=\frac{P T}{T R}\) हैं तथा ∠PKT = ∠PRS है। सिद्ध कीजिए कि ΔPSR एक समद्विबाहु त्रिभुज है।

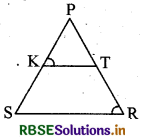
हल:
प्रश्नानुसार दिया गया है \(\frac{\mathrm{PK}}{\mathrm{KS}}=\frac{\mathrm{PT}}{\mathrm{TR}}\)
अत: KT ∥ SR
∴ ∠PKT = ∠PSR (संगत कोण) ....(i)

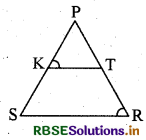
साथ ही यह दिया हुआ है कि
∠PKT = ∠PRS . ....(ii)

अतः ∠PRS = ∠PSR [(i) व (ii) से]
इसलिए PS = PR (समान कोणों की सम्मुख भुजाएँ)
अर्थात् APSR एक समद्विबाहु त्रिभुज है। (इतिसिद्धम्)

प्रश्न 12.
दी गई आकृति में ABC एक त्रिभुज है। यदि \(\frac{A D}{A B}=\frac{A E}{A C}\) तो सिद्ध कीजिए DE ∥ BC

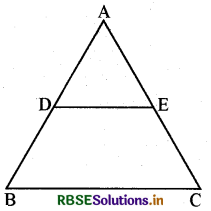
हल:

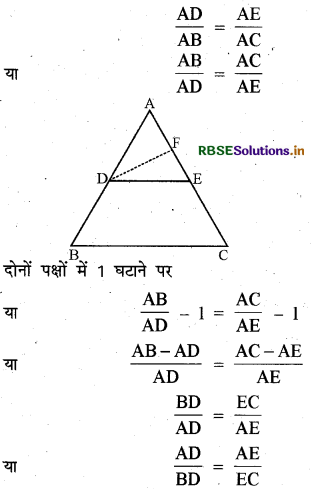
अतः एक त्रिभुज की भुजाओं AB एवं AC को DE समान अनुपात में विभाजित करती है।
सिद्ध करना है - DE ∥ BC
रचना - D से जाने वाली एक अन्य रेखा DF खींची।
उपपत्ति-माना कि रेखा DE भुजा BC के समान्तर नहीं है तथा D से होकर जाने वाली एक अन्य रेखा DF भुजा BC के समान्तर है।

अर्थात् DF ∥ BC
अतः आधारभूत आनुपातिकता प्रमेय से,
\(\frac{\mathrm{AD}}{\mathrm{DB}}=\frac{\mathrm{AF}}{\mathrm{FC}}\) .......(i)
लेकिन दिया हुआ है
\(\frac{\mathrm{AD}}{\mathrm{DB}}=\frac{\mathrm{AE}}{\mathrm{EC}}\)
समी. (1) तथा (2) को बराबर करने पर
\(\frac{\mathrm{AF}}{\mathrm{FC}}=\frac{\mathrm{AE}}{\mathrm{EC}}\)

दोनों पक्षों में 1 जोड़ने पर

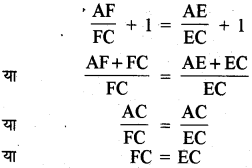
यह तब ही सम्भव है जब F एवं E दोनों बिन्दु सम्पाती हों, अर्थात् DF एवं DE सम्पाती रेखाएँ हैं। अतः DE ∥ BC इतिसिद्धम् ।

प्रश्न 13.
एक चतुर्भुज PQRS के विकर्ण परस्पर 0 बिन्दु पर इस प्रकार प्रतिच्छेद करते हैं कि \(\frac{\mathrm{PO}}{\mathrm{QO}}=\frac{\mathrm{RO}}{\mathrm{SO}}\) हैं। दर्शाइए कि PQRS एक समलम्ब है।
हल:
दिया है-चतुर्भुज PQRS में विकर्ण PR और QS परस्पर बिन्दु O पर इस प्रकार प्रतिच्छेद करते हैं कि \(\frac{\mathrm{PO}}{\mathrm{QO}}=\frac{\mathrm{RO}}{\mathrm{SO}}\) है।

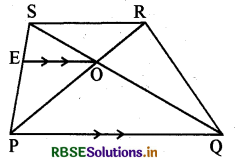
सिद्ध करना है-चतुर्भुज PQRS एक समलम्ब है।
रचना-'0' से रेखा EO ∥ PQ खींची, जो PS को E पर मिलती है।
उपपत्ति ΔSPQ में, EO ∥ PQ

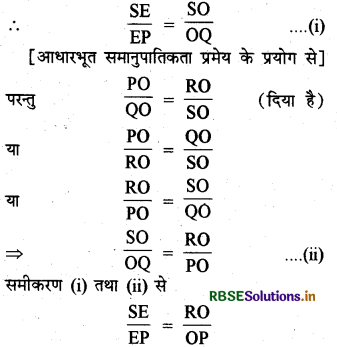
∴ आधारभूत समानुपातिकता प्रमेय के प्रयोग से
EO ∥ SR
साथ ही, EO ∥ PQ
∴ चतुर्भुज PQRS एक समलम्ब है जिसमें PQ || SR (इतिसिद्धम्)