RBSE Class 10 Maths Important Questions Chapter 4 द्विघात समीकरण

Rajasthan Board RBSE Class 10 Maths Important Questions Chapter 4 द्विघात समीकरण Important Questions and Answers.

RBSE Class 10 Maths Chapter 4 Important Questions द्विघात समीकरण

वस्तुनिष्ठ प्रश्न

प्रश्न 1.
समीकरण 5x² - \(\frac{49}{5}\) = 0 के हल हैं
(A) \(\frac{49}{25}\), - \(\frac{49}{25}\)
(B) \(\frac{5}{7}\) - \(\frac{5}{7}\)
(C) - \(\frac{7}{5}\), \(\frac{7}{5}\)
(D) - \(\frac{7}{\sqrt{5}}\), \(\frac{7}{\sqrt{5}}\)
उत्तरः
(C) - \(\frac{7}{5}\), \(\frac{7}{5}\)

प्रश्न 2.
यदि समीकरण x² + 3ax + k = 0 का एक हल x = - a हो तो k का मान होगा
(A) 0
(B) 2a²
(C) a²
(D) - 2a
उत्तरः
(B) 2a²

प्रश्न 3.
किसी संख्या का वर्ग उसके तिगुने से 70 अधिक है। इस कथन को प्रकट करने वाला समीकरण है
(A) x² + 3r - 70 = 0
(B) x² - 3x - 70 = 0
(C) x² - 3r + 70 = 0
(D) x² + 3x + 70 = 0
उत्तरः
(B) x² - 3x - 70 = 0

प्रश्न 4.
समीकरण (x - 3)² = 3 के मूल हैं
(A) 3 ± √3
(B) - 3 ± √3
(C) 0
(D) 6
उत्तरः
(A) 3 ± √3

प्रश्न 5.
द्विघात समीकरण px² + qx + r = 0, p ≠ 0 के मूल समान होंगे यदि-
(A) p² < 4qr
(B) p² > 4qr
(C) q² = 4pr
(D) p² = 4qr
उत्तरः
(C) q² = 4pr

प्रश्न 6.
समीकरण ax² + bx + c = 0, a ≠ 0 के मूल वास्तविक नहीं होंगे यदि
(A) b² < 4ac
(B) b² > 4ac
(C) b² = 4ac
(D) b = 4ac
उत्तरः
(A) b² < 4ac

प्रश्न 7.
समीकरण x² - 4x = 0 के हल हैं
(A) 4, 4
(B) 2, 2
(C) 0, 4
(D) 0, 2
उत्तरः
(C) 0, 4

अतिलघूत्तरात्मक प्रश्न

प्रश्न 1.
यदि 6x² = 54 हो तो x का मान लिखिए।
हल:
x² = \(\frac{54}{6}\) = 9 अतः x = ± 3

प्रश्न 2.
समीकरण x² - \(\frac{x}{3}\) के हल लिखिए।
हल:
x² - \(\frac{x}{3}\) = 0 या x\(\left(x-\frac{1}{3}\right)\) = 0 या x = 0, \(\frac{1}{3}\)

प्रश्न 3.
जाँच कीजिये कि क्या x(2x + 3) = x² + 1 एक द्विघात समीकरण है?
हल:
x(2x + 3) = x² + 1
⇒ 2x² + 3x = x² + 1
⇒ 2x² + 3x - x² - 1 = 0.
⇒ x² + 3x - 1 = 0
अतः उपर्युक्त समीकरण द्विघात समीकरण है।

प्रश्न 4.
यदि समीकरण x² - 8x + a = 0 का एक मूल 5 है, तो दूसरा मूल लिखिए।
हल:
यहाँ मूलों का योग 8 है अतः दूसरा मूल 8 - 5 = 3 होगा।

प्रश्न 5.
दो क्रमागत प्राकृत संख्याओं के वर्गों का योग 25 है। यदि छोटी संख्या x हो तो इस तथ्य को अभिव्यक्त करने वाला समीकरण लिखिए।
हल:
x² + (x + 1)² = 25

प्रश्न 6.
संख्या x तथा उसके व्युत्क्रम का योग \(\frac{5}{2}\) है, इसे बीजीय समीकरण के रूप में लिखिए।
हल:
x + \(\frac{1}{x}\) = \(\frac{5}{2}\)

प्रश्न 7.
एक घन संख्या x अपने वर्ग से 56 कम है। इस वाक्य को प्रकट करने वाला समीकरण लिखिए।
हल:
x² - 56 = x, या x² - x = 56 ∴ x² - x - 56 = 0

प्रश्न 8.
समीकरण \(\frac{x}{5}\) - \(\frac{5}{x}\) = 0 को सन्तुष्ट करने वाले x के मान लिखिए।
हल:
x = ± 5

प्रश्न 9.
यदि समीकरण x² - 8x + k = 0 के मूल समान हों तोk का मान ज्ञात कीजिए।
हल:
मूल समान होने पर b² - 4ac = 0
∴ (-8)² - 4 × 1 × k = 0
∵ यहाँ पर a = 1, b = - 8, c = k
64 - 4k = 0
∴ k = \(\frac{64}{4}\) = 16 उत्तर

प्रश्न 10.
समीकरण \(\frac{x}{4}\)-\(\frac{4}{x}\) के मूल ज्ञात कीजिए
हल:

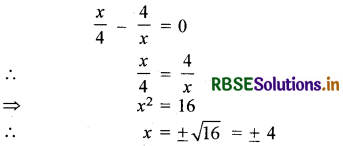
प्रश्न 11.
समीकरण x - \(\frac{1}{x}\) = 0 को हल कीजिए।
हल:

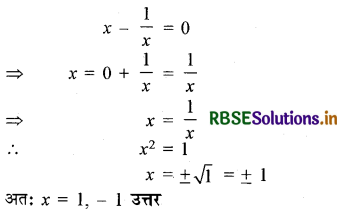
प्रश्न 12.
समीकरण 2x² - 8 = 0 को हल कीजिए।
हल:
दिया गया समीकरण
2x² - 8 = 0
⇒ 2 (x² - 4) = 0
⇒ 2 (x + 2) (x - 2) = 0
∴ x = 2, - 2

प्रश्न 13.
जाँच कीजिये कि क्या (x - 2)² + 1 = 2x - 3 एक द्विघात समीकरण है?
हल:
(x - 2)² + 1 = 2x - 3
⇒ x² - 4x + 4 + 1 = 2x - 3
⇒ x² - 4x + 5 - 2x + 3 = 0
⇒ x² - 6x + 8 = 0
अतः उपर्युक्त समीकरण द्विघात समीकरण है।

प्रश्न 14.
समीकरण 2x⇒ + 3x + 4 = 0 के मूलों की प्रकृति ज्ञात कीजिए।
हल:
a = 2, b = 3, c = 4
∴ विविक्तकर का मान D = b² - 4ac
= (3)² - 4 × 2 × 4
= 9 - 32
= - 23 < 0
∵ विविक्तकर का मान ऋणात्मक है अतः मूल विद्यमान नहीं है। अर्थात् मूल काल्पनिक होंगे।

प्रश्न 15.
द्विघात सूत्र लिखिए।
हल:
यदि b² - 4ac ≥ 0 हो, तो द्विघात समीकरण ax² + bx + c = 0 के मूल \(\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}\) होते हैं| यही सूत्र द्विघात सूत्र कहलाता है।

प्रश्न 16.
k का मान ज्ञात कीजिये जिसके लिये x = 2 द्विघात समीकरण 3x² - kx - 2 = 0 का एक मूल है।
हल:
∵ x = 2 समीकरण 3x² - kx - 2 = 0 का एक मूल है अतः x = 2 समीकरण में रखने पर
3(2)² - k(2) - 2 = 0
⇒ 12 - 2k - 2 = 0
⇒ - 2k = - 10
∴ k = 5

लघूत्तरात्मक प्रश्न

प्रश्न 1.
6 तथा-1 मूलों वाली समीकरण ज्ञात कीजिए।
हल:
मूलों का योग 6 + (- 1) = 5
मूलों का गुणनफल 6 × - 1 = - 6
हम जानते हैं कि
x² - (मूलों का योग) x + मूलों का गुणनफल = 0
x² - 5x – 6 = 0

प्रश्न 2.
समीकरण (3x + 2) (2x + 3) = 6 को हल कीजिए।
हल:
दिये गये समीकरण से
(3x + 2) (2x + 3) = 6
⇒ 6x² + 9x + 4x + 6 = 6
⇒ 6x² + 13x = 0
⇒ x (6x + 13) = 0
या x = 0
या 6x + 13 = 0 ∴ 6x = - 13
अतः x = 0, - \(\frac{13}{6}\)

प्रश्न 3.
निम्नलिखित द्विघात समीकरण को हल कीजिए
4x² + 4bx - (a² - b²) = 0
हल:
दी गई समीकरण
4x² + 4bx - (a² - b²) = 0
⇒ 4x² + 4bx + b² - a² = 0
⇒ (2x + b)² - a² = 0
⇒ (2x + b + a) (2x + b - a) = 0
[∵ a² - b² = (a + b) (a - b)]
∴ या तो 2x + b + a = 0
⇒ x = \(\frac{-a-b}{2}\) = \(-\left(\frac{a+b}{2}\right)\)
या 2x + b - a = 0 ⇒ x = \(\frac{a-b}{2}\)
अतः दी गई समीकरण के मूल हैं
x = -\(\left(\frac{a+b}{2}\right)\),
x = \(\frac{a-b}{2}\)

प्रश्न 4.
समीकरण x + \(\frac{1}{x}\) = 3\(\frac{1}{3}\) को हल कीजिये।
हल:
समीकरण
x + \(\frac{1}{x}\) = 3\(\frac{1}{3}\)
x + \(\frac{1}{x}\) = \(\frac{10}{3}\)
3x² + 3 = 10x
3x
⇒ 3x² + 3 = 10x
∴ 3x² - 10x + 3 = 0
3x² - 9x - x + 3 = 0
3x(x - 3) - 1(x - 3) = 0
(3x - 1) (x - 3) = 0
∴ x = 3, \(\frac{1}{3}\)

प्रश्न 5.
अंकित तथा उसके पिताजी की आयु में 30 वर्षों का अन्तर है। उनकी आयु के वर्गों का अन्तर 1560 है। अंकित तथा उसके पिताजी की आयु ज्ञात कीजिए।
हल:
माना पिता की आयु = x वर्ष
अंकित की आयु = x - 30 वर्ष
प्रश्नानुसार
x² - (x - 30)² = 1560
⇒ x² - x² + 60x - 900 = 1560
⇒ 60x = 1560 + 900
⇒ 60x = 2460
⇒ x = \(\frac{2460}{60}\) = 41
अतः पिता की आयु = 41 वर्ष तथा पुत्र की आयु = 41 - 30 = 11 वर्ष उत्तर

प्रश्न 6.
द्विघात समीकरण 6x² - x - 2 = 0 के मूल ज्ञात कीजिए।
हल:
प्रश्नानुसार 6x² - x - 2 = 6x² + 3x - 4x - 2
= 3x (2x + 1) - 2 (2x + 1)
= (3x - 2) (2x + 1)
6x² - x - 2 = 0 के मूल x के वे मान हैं, जिनके लिए (3x - 2) (2x + 1) = 0 हो।
इसलिए 3x - 2 = 0 या 2x + 1 = 0
अर्थात् x = \(\frac{2}{3}\) या x = -\(\frac{1}{2}\)
अत: 6x² - x - 2 = 0 के मूल \(\frac{2}{3}\) और - \(\frac{1}{2}\) हैं। उत्तर

प्रश्न 7.
द्विघात समीकरण 3x² - 2√6x + 2 = 0 के मूल ज्ञात कीजिए।
हल:
3x² - 2√6x + 2
= 3x² - √6x - √6x + 2
= √3x(√3x - √2) - √3(√3x - √2)
= (√3x - √2) (√3x - √2)
अतः समीकरण के मूल x के वे मान हैं, जिनके लिए
(√3x - √2) (√3x - √2) = 0
अब x = \(\sqrt{\frac{2}{3}}\) के लिए, √3x - √2 = 0 है।
अतः यह मूल, गुणनखण्ड √3x - √2 के दो बार आने के कारण, दो बार आता है, अर्थात् इस मूल की पुनरावृत्ति होती है।
इसलिए 3x² - 2√6x + 2 = 0 के मूल \(\sqrt{\frac{2}{3}}, \sqrt{\frac{2}{3}}\) हैं।

प्रश्न 8.
सामने दिया गया चित्र एक प्रार्थना कक्ष का है। इस कक्ष की विमाएँ ज्ञात कीजिए।

हल:
कक्ष की लम्बाई = 2x + 1
कक्ष की चौड़ाई = x
∴ कक्ष का क्षेत्रफल = (2x + 1) . x m²
= (2x² + x) m²
∴ 2x² + x = 300 (दिया है)
अतः 2x² + x - 300 = 0
इसलिए कक्ष की चौड़ाई समीकरण 2x² + x - 300 = 0 जो एक द्विघात समीकरण है, को सन्तुष्ट करना चाहिए।
गुणनखण्डन विधि का प्रयोग करने पर
2x² - 24x + 25x - 300 = 0
या 2x (x - 12) + 25 (x - 12) = 0
अर्थात् (x - 12) (2x + 25) = 0
अतः, दिए गए समीकरण के मूल x = 12 या x = - 12.5 हैं। क्योंकि x कक्ष की चौड़ाई है, यह ऋणात्मक नहीं हो सकती। इसलिए, कक्ष की चौड़ाई 12 m है।
इसकी लम्बाई = 2x + 1 = 25 m होगी। उत्तर

प्रश्न 9.
समीकरण 2x² - 5x + 3 = 0 को पूर्ण वर्ग बनाने की विधि से हल कीजिए।
हल:

प्रश्न 10.
पूर्ण वर्ग बनाने की विधि से समीकरण 5x² - 6x - 2 = 0 के मूल हल कीजिए।
हल:
दिए हुए समीकरण को 5 से गुणा करने पर, 25x² - 30x - 10 = 0
यह निम्न के तुल्य है:
(5x)² - 2 × (5x) × 3 + 3² - 3² - 10 = 0
अर्थात् (5x - 3)² - 9 - 10 = 0
अर्थात् (5x - 3)² - 19 = 0
अर्थात् (5x - 3)² = 19
अर्थात् 5x - 3 = ± √19
अर्थात् 5x = 3 ± √19
अतः x = \(\frac{3 \pm \sqrt{19}}{5}\)
इसलिए मूल \(\frac{3 \pm \sqrt{19}}{5}\) और \(\frac{3 \pm \sqrt{19}}{5}\) हैं।

प्रश्न 11.
हंसों की एक टोली में से हंसों की कुल संख्या के वर्गमूल के \(\frac{7}{2}\) गुना हंस तालाब के किनारे खेल रहे हैं। शेष 2 हंस तालाब के पानी में खेल रहे हैं। हंसों की कुल संख्या ज्ञात कीजिए।
हल:
माना कुल हंसों की संख्या = x है।
∴ x के वर्गमूल \(\frac{7}{2}\) का गुना = \(\frac{7}{2}\) √x प्रश्नानुसार
\(\frac{7}{2}\)√x + 2 = x
⇒ \(\frac{7}{2}\)√x = x - 2
दोनों पक्षों का वर्ग करने पर
\(\frac{49}{4}\)x = x² - 4x + 4
⇒ 49x = 4x² - 16x + 16
⇒ 4x² - 16x + 16 - 49x = 0
⇒ 4x² - 65x + 16 = 0
⇒ 4x² - 64x - x + 16 = 0
⇒ 4x(x - 16) - 1(x - 16) = 0
= (4x - 1) (x - 16) = 0
यदि 4x - 1 = 0
तब x = \(\frac{1}{4}\)
यदि x - 16 = 0
तब x = 16
⇒ x = 16, \(\frac{1}{4}\)
अतः हंसों की कुल संख्या = 16

निबन्धात्मक प्रश्न

प्रश्न 1.
एक त्रिभुज की दो भुजाएँ x सेमी. तथा 3 (x + 1) सेमी. समकोण बनाती हैं। यदि त्रिभुज का क्षेत्रफल 84 वर्ग सेमी. हो तो त्रिभुज की सभी भुजाएँ ज्ञात कीजिए।
हल:
प्रश्नानुसार \(\frac{1}{2}\)x × 3 (x + 1) = 84
(∵ Δ का क्षेत्रफल = \(\frac{1}{2}\) × आधार × ऊँचाई)
या \(\frac{3 x^{2}+3 x}{2}\) = 84
⇒ 3x² + 3x = 168
या 3x² + 3x = 168
⇒ 3x² + 3x - 168 = 0
∴ x² + x - 56 = \(\frac{0}{3}\) = 0
अतः x² + 8x - 7x - 56 = 0
या x (x + 8) - 7 (x + 8) = 0
या (x + 8) (x - 7) = 0
अतः x - 7 = 0 तब x = 7
यदि x + 8 = 0
तो x = - 8 जो कि सम्भव नहीं है चूँकि त्रिभुज की भुजा की लम्बाई ऋणात्मक नहीं होती है।
एक भुजा = 7 तथा दूसरी भुजा = 3 (7 + 1) = 24
तथा तीसरी भुजा = \(\sqrt{7^{2}+24^{2}}\) = √625 = 25 सेमी. उत्तर

प्रश्न 2.
दो संख्याओं का योग 48 है तथा उनका गुणनफल 432 है। संख्याएँ ज्ञात कीजिए।
हल:
माना कि . पहली संख्या = x है।
∴ दूसरी संख्या = (48 - x)
प्रश्नानुसार x (48 - x) = 432
⇒ 48x - x² = 432
⇒ x² - 48x + 432 = 0
⇒ x² - 36x - 12x + 432 = 0
⇒ x (x - 36) - 12 (x - 36) = 0
⇒ (x - 36) (x - 12) = 0
यदि x - 36 = 0 तब x = 36
यदि x - 12 = 0 तब x = 12
अतः संख्याएँ 12, 36 होंगी।

प्रश्न 3.
6500 रुपये कुछ व्यक्तियों के मध्य समान रूप से विभाजित किये गये। यदि 15 व्यक्ति और होते तो प्रत्येक के हिस्से में 30 रु. कम आते। ज्ञात कीजिये कि प्रारम्भ में कितने व्यक्ति थे?
हल:
माना प्रारम्भ में व्यक्तियों की संख्या = x
अतः प्रत्येक के हिस्से में रुपये = \(\frac{6500}{x} \)प्रश्नानुसार
(x + 15)\(\left(\frac{6500}{x}-30\right)\) = 6500
(x + 15) (6500 - 30x) = 6500x
⇒ 6500x - 30x² + 97500 - 450x - 6500 x = 0
⇒ - 30x² - 450x + 97500 = 0
⇒ - 30 (x² + 15x - 3250) = 0
⇒ x² + 15x - 3250 = 0
⇒ x² + 65x - 50x - 3250 = 0
⇒ x (x + 65) - 50 (x + 65) = 0
⇒ (x + 65) (x - 50) = 0
∴ या तो x + 65 = 0
⇒ x= - 65 (उपेक्षा करने पर)
या x - 50 = 0 ⇒ x = 50
अतः प्रारम्भ में व्यक्तियों की संख्या = 50

प्रश्न 4.
एक समकोण त्रिभुज के कर्ण की लम्बाई 3√10 सेमी. है। यदि छोटी भुजा को तिगुना तथा बड़ी भुजा को दुगुना कर दिया जाये तो नये कर्ण की लम्बाई 9√5 सेमी. हो जाती है। त्रिभुज की तीनों भुजाओं को ज्ञात कीजिए।
हल:
माना छोटी भुजा = x सेमी. तो पायथागोरस प्रमेय से बड़ी भुजा = \(\sqrt{(3 \sqrt{10})^{2}-x^{2}}\) = \(\sqrt{90-x^{2}}\)
प्रश्नानुसार
(3x)² + \(\left(2 \sqrt{90-x^{2}}\right)^{2}\) = (9√5)²
9x² + 4 (90 - x2) = 81 x 5 . 9x2 + 360 - 4x2 = 405
5x² = 405 - 360
5x² = 45
x² = \(\frac{45}{5}\) = 9.
x = + 3
∵ भुजा ऋणात्मक नहीं हो सकती अतः x = + 3
अतः छोटी भुजा = 3 सेमी. तथा बड़ी भुजा = \(\sqrt{90-(3)^{2}}\)
= \(\sqrt{90-9}\) = √81 = ±9
अतः बड़ी भुजा = ± 9 सेमी.
अतः छोटी भुजा = 3 सेमी. तथा बड़ी भुजा = + 9 सेमी.

प्रश्न 5.
एक आयताकार भूखण्ड का क्षेत्रफल 528 m² है। क्षेत्र की लम्बाई (मीटरों में) चौड़ाई के दुगुने से एक अधिक है। इसे द्विघाती सूत्र से हल कीजिए।
हल:
माना भूखण्ड की चौड़ाई x मीटर है। तब, लम्बाई (2x + 1) मीटर है। हमें दिया है कि x (2x + 1) = 528, अर्थात् 2x² + x - 528 = 0 है।
यह ax² + bx + c = 0 के प्रकार का है, जहाँ a = 2, b = 1, c = - 528 है।
अतः द्विघाती सूत्र से,

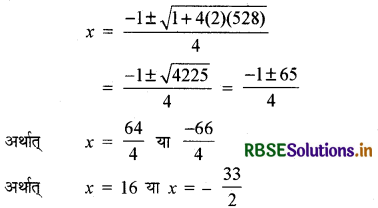
क्योंकि x एक विमा होने के कारण ऋणात्मक नहीं हो सकता है, इसलिए भूखण्ड की चौड़ाई 16m है और लम्बाई (2 × 16 + 1) = 33m है।

प्रश्न 6.
दो ऐसे क्रमागत विषम धनात्मक पूर्णांक ज्ञात कीजिए जिनके वर्गों का योग 290 हो।
हल:
माना दोनों क्रमागत विषम धनात्मक पूर्णांकों में छोटा पूर्णांक x है। तब, दूसरा पूर्णांक x + 2 होगा। प्रश्न के अनुसार,
x² + (x + 2)² = 290
अर्थात् x² + x² + 4x + 4 = 290
अर्थात् 2x² + 4x - 286 = 0
अर्थात् x² + 2x - 143 = 0,
जो x में एक द्विघात समीकरण है।
इसी द्विघात समीकरण की ax² + bx + c = 0 से तुलना करने पर
a = 1, b = 2 और c = - 143
द्विघाती सूत्र का प्रयोग करने पर
x = \(\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}\)

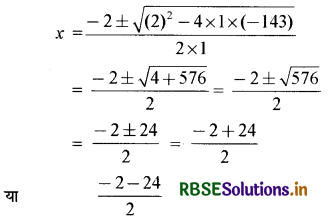
अर्थात् x = 11 या x = - 13
परन्तु x एक धनात्मक विषम पूर्णांक दिया है। अतः x = 11 होगा, क्योंकि x ≠ - 13 है।
अतः, दोनों क्रमागत विषम धनात्मक पूर्णांक 11 और 13 हैं।

प्रश्न 7.
एक ऐसे आयताकार पार्क को बनाना है जिसकी चौड़ाई इसकी लम्बाई से 3 m कम हो। इसका क्षेत्रफल पहले से निर्मित समद्विबाहु त्रिभुजाकार पार्क जिसका आधार आयताकार पार्क की चौड़ाई के बराबर तथा ऊँचाई 12 m है, से 4 वर्ग मीटर अधिक हो ( देखिए आकति)। इस आयताकार पार्क की लम्बाई और चौड़ाई ज्ञात कीजिए।
हल:

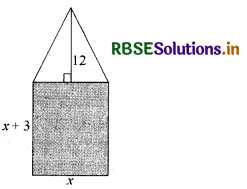
माना कि आयताकार पार्क की चौड़ाई x m है। इसलिए, इसकी लम्बाई = (x + 3) m होगी।
अतः आयताकार पार्क का क्षेत्रफल = x (x + 3) m² = (x² + 3x) m²
अब समद्विबाहु त्रिभुज का आधार = x m
अतः इसका क्षेत्रफल = \(\frac{1}{2}\) × x × 12 = 6x m²
प्रश्न के अनुसार
x² + 3x = 6x + 4
अर्थात् x² - 3x - 4 = 0
उपर्युक्त द्विघात समीकरण की तुलना द्विघात समीकरण,
ax² + bx + c = 0 से करने पर
a = 1, b = - 3 और c = - 4
द्विघाती सूत्र का उपयोग करने पर,

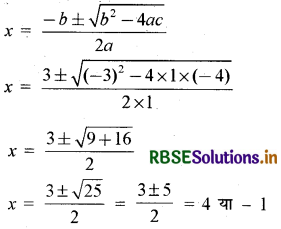
परन्तु x ≠ - 1 है। अतः x = 4 है।
इसलिए, पार्क की चौड़ाई = 4m और लम्बाई 7 m होगी।

प्रश्न 8.
निम्न द्विघात समीकरणों के मूल, यदि उनका अस्तित्व हो तो द्विघाती सूत्र का उपयोग करके ज्ञात कीजिए :
(i) 3x² - 5x + 2 = 0
(ii) x² + 4x + 5 = 0
(ii) 2x² - 2√2x + 1 = 0
हल:
(i) 3x² - 5x + 2 = 0 के लिए : यहाँ a = 3, b = - 5, c = 2 है। इसलिए, b² - 4ac = 25 - 24 = 1 > 0
अत: x = \(\frac{5 \pm \sqrt{1}}{6}\) = \(\frac{5 \pm 1}{6}\) है, अर्थात् x = 1 या x = \(\frac{2}{3}\) है।
इसलिए मूल \(\frac{2}{3}\) और 1 हैं।

(ii) x² + 4x + 5 = 0 के लिए यहाँ a = 1, b = 4, c = 5 है। इसलिए b² - 4ac = 16 - 20 = - 4 < 0
परन्तु, क्योंकि किसी वास्तविक संख्या का वर्ग ऋणात्मक नहीं हो सकता है, इसलिए \(\sqrt{b^{2}-4 a c}\) का मान वास्तविक नहीं होगा।
अतः दिए हुए समीकरण के कोई वास्तविक मूल नहीं हैं।

(iii) 2x² - 2√2x + 1 = 0 के लिए : यहाँ a = 2, b = - 2√2 , c = 1 है।
इसलिए b² - 4ac = 8 - 8 = 0 है।
अत: x = \(\frac{2 \sqrt{2} \pm \sqrt{0}}{4}\) = \(\frac{\sqrt{2}}{2}\) ± 0 अर्थात् x = \(\frac{1}{\sqrt{2}}\) है।
इसलिए मूल \(\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}\) हैं।

प्रश्न 9.
निम्न समीकरणों के मूल ज्ञात कीजिए:
(i) x + \(\frac{1}{x}\) = 3, x ≠ 0
(ii) \(\frac{1}{x}\)-\(\frac{1}{x-2}\) = 3, x ≠ 0, 2
हल:
(i) x + \(\frac{1}{x}\) = 3 के लिए : सभी पदों को x ≠ 0 से गुणा करने पर,
x² + 1 = 3x
अर्थात् x² - 3x + 1 = 0,
जो एक द्विघात समीकरण है।
यहाँ a = 1, b = - 3. c = 1 है।
अतः b² - 4ac = 9 - 4 = 5 > 0
अतः x = \(\frac{3 \pm \sqrt{5}}{2}\)
इसलिए मूल \(\frac{3 \pm \sqrt{5}}{2}\) और \(\frac{3 \pm \sqrt{5}}{2}\) हैं।

(ii) \(\frac{1}{x}\) - = 3, x ≠ 0, 2 :
चूँकि x ≠ 0, 2 है, इसलिए समीकरण को x (x - 2) से गुणा करने पर,
(x - 2) - x = 3x (x - 2)
= 3x² - 6x
अतः, दी गई समीकरण परिवर्तित होकर 3x² - 6x + 2 = 0 बन जाती है, जो एक द्विघात समीकरण है।
यहाँ a = 3, b = - 6, c = 2 है। इसलिए b² - 4ac = 36 - 24 = 12 > 0 है।

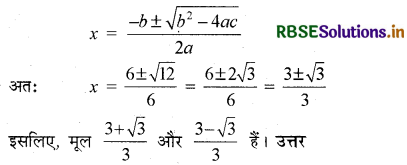
प्रश्न 10.
एक मोटर बोट, जिसकी स्थिर जल में चाल 18 km./h है, 24 km. धारा के प्रतिकूल जाने में, वही दूरी धारा के अनुकूल जाने की अपेक्षा 1 घण्टा अधिक लेती है। धारा की चाल ज्ञात कीजिए। .
हल:
माना कि धारा की चाल x km./h है।
इसलिए, धारा के प्रतिकूल नाव की चाल = (18 - x) km./h और धारा के अनुकूल नाव की चाल = (18 + x) km./h है।
धारा के प्रतिकूल जाने में लिया गया समय

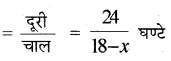
इसी प्रकार, धारा के अनुकूल जाने में लिया गया समय = \(\frac{24}{18+x}\) घण्टे
प्रश्नानुसार
\(\frac{24}{18-x}\) - \(\frac{24}{18+x}\) = 1
अर्थात् 24 (18 + x) - 24 (18 - x) = (18 - x) (18 + x)
अर्थात् 24 × 18 + 24x - 24 × 18 + 24x = (18)² - (x)²
अर्थात् 48x = 324 - x²
अर्थात् x² + 48x - 324 = 0
उपर्युक्त समीकरण की तुलना द्विघात समीकरण
ax² + bx + c = (0 से करने पर
a = 1, b = 48 तथा c = - 324
द्विघात सूत्र का उपयोग करने पर,

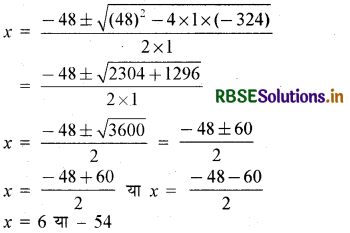
क्योंकि x धारा की चाल है, इसलिए यह ऋणात्मक नहीं हो सकती है। अतः, हम मूल x = - 54 को छोड़ देते हैं। इसलिए, x = 6 से हम प्राप्त करते हैं कि धारा | की चाल 6 km./h है।

प्रश्न 11.
13 मीटर व्यास वाले एक वृत्ताकार पार्क की परिसीमा के एक बिन्दु पर एक खम्भा इस प्रकार गाड़ना है कि इस पार्क के एक व्यास के दोनों अन्तः बिन्दुओं पर | बने फाटकों A और B से खम्भे की दूरियों का अन्तर 7. मीटर हो। क्या ऐसा करना सम्भव है? यदि है, तो दोनों | फाटकों से कितनी दूरियों पर खम्भा गाड़ना है?
हल:
चित्रानुसार माना खम्भे की अभीष्ट स्थिति P है। खम्भे की फाटक B से दूरी x m है अर्थात् BP = x m है।अब खम्भे की दोनों फाटकों की दूरियों का अन्तर =AP-BP (या BP- AP) = 7 m है। इसलिए, AP = (x +7) m होगा।

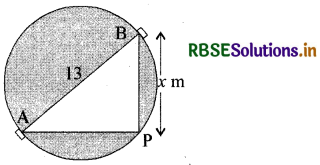
साथ ही, AB = 13 m है । चूँकि AB व्यास है, इसलिए
∠APB = 90°
इसलिए AP² + PB² = AB²
(पाइथागोरस प्रमेय द्वारा)
अर्थात् (x + 7)² + x² = 13²
अर्थात् x² + 14x + 49 + x² = 169
अर्थात् 2x² + 14x – 120 = 0
या x² + 7x - 60 = 0
अतः खम्भे की फाटक B से दूरी 'x' समीकरण x² + 7x - 60 = 6 को सन्तुष्ट करती है। अतः b² - 4ac = 7² - 4 × 1 × (- 60) = 289 > 0
अतः दिए गए द्विघात समीकरण के दो वास्तविक मूल हैं और इसीलिए खम्भे को पार्क की परिसीमा पर गाड़ा जा सकना सम्भव है।
द्विघात समीकरण x² + 7x - 60 = 0 को द्विघाती सूत्र से हल करने पर,
द्विघात समीकरण x² + 7x - 60 = 0 की तुलना ax² + bx + c = 0 से करने पर a = 1, b = 7 तथा c = - 60

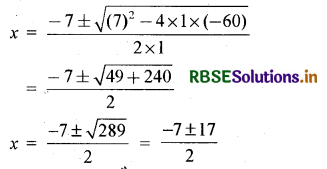
इसलिए, x = 5 या - 12 है।
चूँकि खम्भे और फाटक B के बीच की दूरी है, यह धनात्मक होना चाहिए। इसलिए, x = - 12 को छोड़ देते हैं। अतः, x = 5 है।
इस प्रकार, खम्भे को पार्क की परिसीमा पर फाटक B से 5 m और फाटक A से \(\sqrt{13^{2}-5^{2}}\) = 12 m की दूरी पर गाड़ना है।

प्रश्न 12.
दो स्टेशनों के बीच के 400 किमी यात्रा | करने में एक एक्सप्रेस रेलगाड़ी, सवारी गाड़ी से 2 घंटा | समय कम लेती है। (मध्य के स्टेशनों पर ठहरने का समय ध्यान में न रखते हुए ) यदि एक्सप्रेस रेलगाड़ी की औसत चाल, सवारी गाड़ी की औसत चाल से 10 किमी/ | घं. अधिक हो, तो दोनों रेलगाड़ियों की औसत चाल ज्ञात कीजिए।
हल:
माना कि सवारी गाड़ी की चाल - किमी/घं. है। अतः एक्सप्रेस गाड़ी की चाल = (x + 10) किमी/ घं. होगी। क्योंकि एक्सप्रेस गाड़ी की औसत चाल, सवारी गाड़ी से 10 किमी/घं. अधिक है।

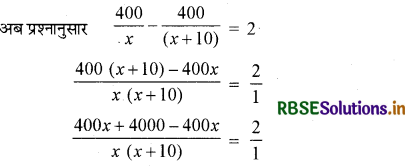
या 2x (x + 10) = 4000
या x² + 10x - 2000 = 0
x² + 50x - 40x - 2000 = 0
x (x + 50) - 40 (x + 50) = 0
(x + 50) (x - 40) = 0
∴ x = 40, -50
∵ चाल ऋणात्मक नहीं हो सकती अतः x = 40 किमी/घंटा
तथा x + 10 = 40+ 10 = 50 किमी/घंटा
अर्थात् सवारी गाड़ी की औसत चाल 40 किमी/घंटा तथा एक्सप्रेस गाड़ी की चाल 50 किमी. होगी।

प्रश्न 13.
एक मोटर बोट जिसकी स्थिर जल में चाल 18 किमी/घण्टा है। उस बोट ने 12 किमी धारा के प्रतिकूल जाने में, वही दूरी धारा के अनुकूल जाने की अपेक्षा , घण्टा अधिक लेती है।धारा की चाल ज्ञात कीजिए।
हल:
माना कि धारा की चाल x km/h है।
∴ धारा के प्रतिकूल नाव की चाल = (18 - x) km/h
और धारा के अनुकूल नाव की चाल = (18 + x) km/h होगी।
धारा के प्रतिकूल जाने में लिया गया समय

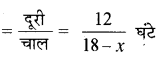
इसी प्रकार धारा के अनुकूल जाने में लिया गया समय = \(\frac{12}{18+x}\) घंटे
प्रश्नानुसार \(\frac{12}{18-x}-\frac{12}{18+x}=\frac{1}{2}\)
या 2 × 12 (18 + x) - 2 × 12 (18 - x) = (18 - x) (18 + x)
या 24 × 18 + 24x - 24 × 18 + 24x = (18)² - (7)²
या 48x = 324 - x²
या x² + 48x - 324 = 0
उपर्युक्त समीकरण की तुलना द्विघात समीकरण ax² + bx + c = 0 से करने पर a = 1, b = 48 तथा c = - 324 द्विघात सूत्र का उपयोग करने पर

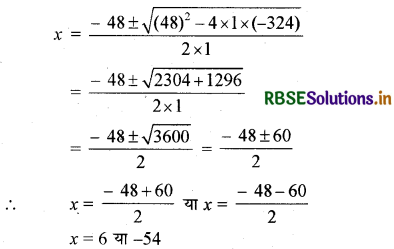
क्योंकि x धारा की चाल है इसलिए यह ऋणात्मक नहीं हो सकती है। अतः हम मूल x = -54 को छोड़ देते हैं। इसलिए x = 6 अर्थात् धारा की चाल = 6 km/h है।

प्रश्न 14.
एक आयताकार खेत का विकर्ण उसकी छोटी भुजा से 40 मीटर अधिक लम्बा है। यदि बड़ी भुजा छोटी भुजा से 20 मीटर अधिक हो तो खेत की भुजाएँ ज्ञात कीजिए।
हल:
माना कि आयताकार खेत की छोटी भुजा = AD = x मी.
आयताकार खेत की लम्बी भुजा = AB = (x + 20) मी.
और आयताकार खेत का विकर्ण = DB= (x +40) मी..
एक आयत में लम्बाई और चौड़ाई के बीच का कोण समकोण होता है।
∴ ∠DAB = 90°
अब समकोण त्रिभुज DAB में

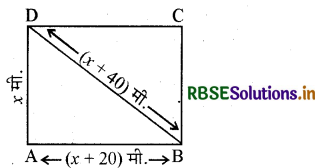
पाइथागोरस प्रमेय से
(DB)² = (AD)² + (AB)²
या (x + 40)² = (x)² + (x + 20)²
या x² + 80x + 1600 = x² + x² + 40x + 400
या x² + 80x + 1600 = 2x² + 40x + 400
या x² + 80x + 1600 - 2x² - 40x - 400 = 0
या- x² + 40x + 1200 = 0
या x² - 40x – 1200 = 0
इसकी तुलना ax² + bx + c से करने पर
∴ a = 1, b = -40, c = -1200
और b² - 4ac = (-40)² - 4 × 1 × (-1200)
= 1600 + 4800
= 6400 > 0

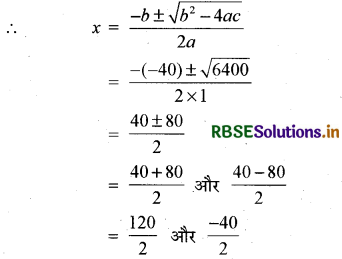
∵ किसी भी भुजा की लम्बाई ऋणात्मक नहीं होती है।
इसलिए x = -20 को छोड़ने पर
∴ x = 60 मी.
अतः आयताकार खेत की सबसे छोटी भुजा = 60 मी.
आयताकार खेत की लम्बी भुजा = (60 + 20) मी. = 80 मी.

प्रश्न 15.
17 मीटर व्यास वाले एक वृत्ताकार पार्क की परिसीमा के एक बिन्दु पर एक खम्भा इस प्रकार - गाड़ना है कि इस पार्क के एक व्यास के दोनों अन्त बिन्दुओं पर बने फाटकों A और B से खम्भे की दूरियों का अन्तर 7 मीटर हो। क्या ऐसा करना सम्भव है? यदि है तो दोनों फाटकों से कितनी दूरियों पर खम्भा गाड़ना है?
हल:
माना खम्भे की अभीष्ट स्थिति P है। माना खम्भे की फाटक B से दूरी x मीटर है अर्थात् BP = x मीटर है। अब खम्भे की दोनों फाटकों की दरियों का अन्तर = AP - BP (या BP – AP) = 7 मीटर है। इसलिये. AP = 7 + BP = (7 + x) मीटर होगा।
साथ ही, AB = 17 मीटर है। चूंकि AB व्यास है, इसलिए

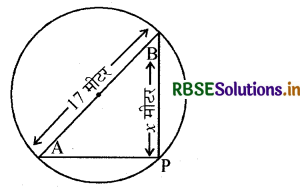
∠APB = 90°
चूँकि अर्द्धवृत्त में बना कोण समकोण होता है।
इसलिए (AP)² + (BP)² = (AB)²
पाइथागोरस प्रमेय से
अर्थात् (7 + x)² + x² = (17)²
अर्थात् x² + 14x + 49 + x² = 289
अर्थात् 2x² + 14x + 49 - 289 = 0
अर्थात् 2x² + 14x - 240 = 0
या 2(x² + 7x - 120) = 0
या x² - 7x - 120 = \(\frac{0}{2}\) = 0
या x² + 7x - 120 = 0
गुणनखण्ड करने पर
x² + 15x - 8x - 120 = 0
⇒ x(x + 15) - 8(x + 15) = 0
⇒ (x - 8) (x + 15) = 0
∴ x = 8 या -15 है।
चूँकि x खम्भे की फाटक B के बीच की दूरी है। यह धनात्मक होनी चाहिए इसलिए x = -15 को छोड़ | देते हैं। अतः x = 8 है। इस प्रकार, खम्भे की पार्क की परिसीमा पर फाटक B से 8 मीटर और फाटक A से
\(\sqrt{(17)^{2}-(8)^{2}}\) = \(\sqrt{289-64}\)
= √225 = 15 मीटर
की दूरी पर गाड़ना है।