RBSE Class 10 Maths Important Questions Chapter 3 दो चरों वाले रखिक समीकरण का युग्म

Rajasthan Board RBSE Class 10 Maths Important Questions Chapter 3 दो चरों वाले रखिक समीकरण का युग्म Important Questions and Answers.

RBSE Class 10 Maths Chapter 3 Important Questions दो चरों वाले रखिक समीकरण का युग्म

वस्तुनिष्ठ प्रश्न

प्रश्न 1.
यदि 2x + y = 6 हो तो इसको सन्तुष्ट करने वाला युग्म है
(A) (1, 2)
(B) (2, 1)
(C) (2, 2)
(D) (1, 1)
उत्तर:
(C) (2, 2)

प्रश्न 2.
यदि \(\frac{4}{x}\) + 5y = 7 तथा x = -\(\frac{4}{3}\) हो, तो y का मान होगा
(A) \(\frac{37}{15}\)
(B) 2
(C) \(\frac{1}{2}\)
(D) \(\frac{1}{3}\)
उत्तर:
(B) 2

प्रश्न 3.
समीकरण \(\frac{y-3}{7}-\frac{x}{2}\) = 1 में यदि y = 10 हो, तो x बराबर है
(A) 0
(B) 1
(C) - 2
(D) 2
उत्तर:
(A) 0\(\frac{x+5}{3}\)

प्रश्न 4.
पिता की आयु पुत्र की आयु की तिगुनी है, यदि पिता की आयु x वर्ष है, तो 5 वर्ष बाद पुत्र की आयु होगी
(A) 3x + 5
(B) x + 5
(C) \(\frac{x}{3}\) +5
(D)
उत्तर:
(C) \(\frac{x}{3}\) +5

प्रश्न 5.
x-अक्ष पर बिन्दु है-
(A) (2, 3)
(B) (2, 0)
(C) (0, 2)
(D) (2, 2)
उत्तर:
(B) (2, 0)

प्रश्न 6.
बिन्दु P(3, - 4) जिस चतुर्थांश में है, वह है
(A) प्रथम
(B) द्वितीय
(C) तृतीय
(D) चतुर्थ
उत्तर:
(D) चतुर्थ

प्रश्न 7.
यदि किसी संख्या में इकाई का अंक a तथा दहाई का अंक b हो, तो वह संख्या है
(A) 10a + b
(B) a + 10b
(C) a + b
(D) ab
उत्तर:
(B) a + 10b

अतिलघूत्तरात्मक प्रश्न

प्रश्न 1.
K के किस मान के लिए समीकरण निकाय 2x + Ky = 1; 3x - 5y = 7 का कोई हल विद्यमान नहीं है?
हल:
कोई हल नहीं होने के लिए
\(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}\)
⇒ \(\frac{2}{3}=\frac{K}{-5} \neq \frac{1}{7}\)
यह प्रतिबन्ध सत्य होगा यदि \(\frac{2}{3}=\frac{K}{-5}\)
K = \(\frac{-10}{3}\)
अतः, K = \(\frac{-10}{3}\) होने पर निकाय का कोई हल नहीं होगा।

प्रश्न 2.
अनुपातों \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}\) और \(\frac{c_{1}}{c_{2}}\) कर ज्ञात कीजिये कि रैखिक समीकरणों 2x - 2y - 12 = 0 तथा 4x - 4y - 5 = 0 के युग्म संगत हैं या असंगत।
हल:
समीकरणों 2x - 2y - 2 = 0 तथा 4x - 4y - 5 = 0 की तुलना करने पर
\(\frac{a_{1}}{a_{2}}=\frac{2}{4}=\frac{1}{2}\) तथा \(\frac{b_{1}}{b_{2}}=\frac{4}{4} \)= 1
∵ \(\frac{c_{1}}{c_{2}} \neq \frac{b_{1}}{b_{2}}\)
अतः समीकरणों का युग्म संगत है।

प्रश्न 3.
दिखाइये रेखाएँ x - 4y + 5 = 0 और 3x - 12y + 8 = 0 समान्तर हैं।
हल:
दी गयी रेखाओं के समीकरण
x - 4y + 5 = 0 तथा
3x - 12y + 8 = 0
उपर्युक्त समीकरण युग्म की व्यापक समीकरण युग्म से तुलना करने पर
a₁ = 1, b₁ = - 4, c₁ = 5
तथा a₂ = 3, b₂ = - 12, c₂ = 8
अब \(\frac{a_{1}}{a_{2}}=\frac{1}{3}, \frac{b_{1}}{b_{2}}=\frac{-4}{-12}=\frac{1}{3}\)
तथा \(\frac{c_{1}}{c_{2}}=\frac{5}{8}\)
∵ \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}\)
दिये गये सनीकरण युग्म असंगत हैं। अतः दी गयी रेखाएँ समान्तर हैं।

प्रश्न 4.
एक संख्या x का दुगुना y से 24 अधिक है। इस वाक्य को प्रकट करने वाला समीकरण लिखिए।
हल:
2x - y = 24

प्रश्न 5.
राम की आयु x वर्ष तथा श्याम की आयु y वर्ष है। पाँच वर्ष पूर्व राम की आयु श्याम की आयु की दुगुनी थी। इस कथन को प्रकट करने वाले समीकरण को ax + by + c = 0 के रूप में लिखिए।
हल:
x - 2y + 5 = 0

प्रश्न 6.
दो चर वाले रैखिक समीकरण युग्म का निरूपण एवं हल प्रस्तुत करने की विधियाँ लिखिए।
हल:

• ग्राफीय विधि,
• बीजीय विधि।

प्रश्न 7.
रैखिक समीकरणों के असंगत युग्म से आप क्या समझते हो?
उत्तर:
यदि दोनों रेखाएँ समान्तर हों, तब इस रैखिक समीकरण युग्म का कोई हल नहीं होता है।
इस दशा में यह रैखिक समीकरणों का असंगत युग्म कहलाता है।

प्रश्न 8.
निम्न समीकरण निकाय के हलों की प्रकृति ज्ञात कीजिए
2x + 4y = 7, 3x + 6y = 10
हल:
2x + 4y - 7 = 0
3x + 6y - 10 = 0
a₁x + b₁y+ c = 0 तथा a₂x + b₂y + c₂ = 0 से तुलना करने पर
\(\frac{a_{1}}{a_{2}}=\frac{2}{3}\) तथा \(\frac{b_{1}}{b_{2}}=\frac{4}{6}=\frac{2}{3}\) तथा \(\frac{c_{1}}{c_{2}}=\frac{7}{10}\)
अतः \(\frac{2}{3}=\frac{2}{3} \neq \frac{7}{10}\)
अतः समीकरण निकाय असंगत है और निकाय का कोई हल नहीं है।

प्रश्न 9.
यदि एक भिन्न के अंश और हर में 1 जोड़ते हैं तो भिन्न का मान \(\frac{1}{2}\) हो जाता है। इसे समीकरण में कैसे लिखेंगे?
हल:
माना भिन्न \(\frac{x}{y}\) है।
\(\frac{x+1}{y+1}=\frac{1}{2}\)

प्रश्न 10.
निम्न समीकरण निकाय में x का मान ज्ञात कीजिए-
2x + 3y = 4
3x + 4y = 5
हल:
दिये गये समीकरण से
2x + 3y - 4 = 0 .... (1)
3x + 4y - 5 = 0 .... (2)

समीकरण (1) में 4 से और समीकरण (2) में 3 से गुणा करने पर
8x + 12y - 16 = 0
9x + 12y - 15 = 0

घटाने पर-
- x - 1 = 0
- x = 1
या x = - 1

प्रश्न 11.
समीकरण x + y = 2xy तथा \(\frac{1}{x}+\frac{2}{y}\) = 10 को हल करके केवल का मान ज्ञात कीजिए।
हल:
x + y = 2xy
दोनों तरफ xy से भाग देने पर
\(\frac{x}{x y}+\frac{y}{x y}=\frac{2 x y}{x y}\)
\(\frac{1}{y}+\frac{1}{x}\) = 2

दूसरे समीकरण से
\(\frac{1}{x}+\frac{2}{y}\) = 10

समीकरण (1) में से समीकरण (2) घटाने पर
-\(\frac{1}{y}\) = -8
∴ y = \(\frac{1}{8}\)

प्रश्न 12.
बीजीय रूप में रैखिक समीकरण युग्म को हल करने की विधियों का नाम लिखिए।
हल:

• प्रतिस्थापन विधि,
• विलोपन विधि,
• वज्रगुणन विधि।

प्रश्न 13.
यदि रैखिक समीकरण a₁x + b₁y + c₁ = 0 और a₂x + b₂y + c₂ = 0 में यदि \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}\neq \frac{c_{1}}{c_{2}}\) हो, तो इस स्थिति का अर्थ स्पष्ट कीजिए।
हल:
यदि \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}\neq \frac{c_{1}}{c_{2}}\) हो, तो रैखिक समीकरण हला a, b C2. युग्म असंगत होता है।

प्रश्न 14.
समीकरण 5y - 3x – 10 = 0 में y को x के रूप में व्यक्त कीजिए। वह बिन्दु ज्ञात कीजिए जहाँ समीकरण 5y - 3x - 10 = 0 द्वारा निरूपित रेखा y-अक्ष को काटती है।
हल:
समीकरण 5y - 3x - 10= 0
5y = 3x + 10
∴ y = \(\frac{3 x+10}{5}\)
समीकरण 5y – 3x – 10 = 0 में u रेखा y-अक्ष पर तब काटेगी जब x = 0 हो तो y = \(\frac{3 \times 0+10}{5}\) = 2
अतः वह बिन्दु (0, 2) होगा।

प्रश्न 15.
यदि रैखिक समीकरण a₁x + b₁y + c₁ = 0 तथा a₂x + b₂y + c₂ = 0 में \(\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}}\) हो, तो इस स्थिति का अर्थ स्पष्ट कीजिए।
हल:
यदि \(\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}}\) हो, तो रैखिक समीकरण युग्म संगत होता है।

प्रश्न 16.
रैखिक समीकरण युग्म √2x + √3y = 0 तथा √3x - √2y = 0 का हल लिखिये।
हल:
दी गई रैखिक समीकरण-युग्म है :
√2x + √3y = 0 .... (1)
√3x - √2y = 0 ... (2)

समीकरण (2) से
√3x = √2y
∴ x = \(\frac{\sqrt{2}}{\sqrt{3}}\)y

x का यह मान समीकरण (1) में रखने पर
√2 + \(\frac{\sqrt{2}}{\sqrt{3}}\)y + √3y = 0
⇒ \(\frac{2}{\sqrt{3}}\)y + √3y
2y + 3y = 0 × √3 = 0
5y = 0
∴ y = \(\frac{0}{5}\) = 0

y का यह मान समीकरण (1) में रखने पर
√2x + √3 × 0 = 0
⇒ √2x = 0
x = \(\frac{0}{\sqrt{2}}\) = 0
अतः x = 0, y = 0

प्रश्न 17.
7 पेंसिल तथा 5 पेन का कुल मूल्य 29 रु. है। इसको बीजगणितीय रूप में लिखिए।
हल:
माना कि 1 पेंसिल का मूल्य = x रु.
और 1 पेन का मूल्य = y रु.
अतः प्रश्नानुसार 7x + 5y = 29

प्रश्न 18.
रैखिक समीकरण युग्म 3x + 4y = 0 तथा 2x - y = 0 का हल लिखिए।
हल:
x = 0 तथा y = 0

प्रश्न 19.
रैखिक समीकरण युग्म 4x + 2 = 5 तथा x - 2y = 0 का हल लिखिए।
हल:
समीकरण युग्म 4x + 2y = 5 .... (1)
तथा x - 2y = 0 .... (2)

समीकरण (2) से x = 2y मान समीकरण (1) में रखने पर
4(2y) + 2y = 5
8y + 2y = 5
∴ 10y = 5 या y = \(\frac{5}{10}=\frac{1}{2}\)
y का यह मान समीकरण (2) में रखने पर
x - 2.\(\frac{1}{2}\) = 0
या x - 1 = 0
∴ x = 1
अतः x = 1 तथा y = \(\frac{1}{2}\)

लघूत्तरात्मक प्रश्न

प्रश्न 1.
दो अंकों की एक संख्या ऐसी है कि इसके अंकों का गुणनफल 12 है। जब इस संख्या में 36 जोड़ दिया जाये तो संख्या के अंक परस्पर बदल लेते हैं। संख्या ज्ञात कीजिए।
हल:
माना संख्याएँ x व हैं। प्रश्नानुसार x × y = 12 .... (i)
तथा 10x + y + 36 = 10y + x .... (ii)
या 9x - 9y = - 36
x - y = - 4 .... (iii)
समीकरण (iii) से
(x - y)² = x² + y² - 2xy
(- 4)² = x² + y² - 2 × 12
x² + y² = 16 + 24 = 40
पुनः . (x + y)² = x² + y² + 2xy
= 40 + 2 × 12
(x + y)² = 64
x + y = \(\sqrt{64}\) = ± 8.... (iv)

समीकरण (iii) तथा (iv) से
x = 2 तथा y = 6
अतः संख्या 26 होगी।

प्रश्न 2.
दो अंकों का संख्या का योग 9 है। इस संख्या का चार गुना, संख्या के अंकों को पलटने से बनी संख्या का सात गुना है। वह संख्या ज्ञात कीजिये।
हल:
माना दहाई का अंक x तथा इकाई का अंक y है।
तब अभीष्ट संख्या = 10x + y
प्रश्नानुसार x + y = 9 .... (i)

पुनः प्रश्नानुसार
4(10x + y) = 7(10y + x)
⇒ 40x + 4y = 70y + 7x
⇒ 33x - 66y = 0
⇒ x - 2y = 0 .... (ii)

समीकरण (i) में से (ii) को घटाने पर।

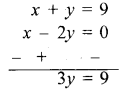
y = \(\frac{9}{3}\) = 3

y का मान समीकरण (ii) में रखने पर
x - 2 × 3 = 0
x = 6

अतः अभीष्ट संख्या= 10x + y
= 10 × 6 + 3 = 60 + 3
= 63

प्रश्न 3.
एक कस्बे के एक राजकीय विद्यालय तथा प्राइवेट विद्यालय में अध्यापकों की संख्या 210 है। जब 10 अध्यापक प्राइवेट विद्यालय से इस्तीफा देकर राजकीय विद्यालय में चले जाते हैं तो दोनों विद्यालयों में अध्यापकों की संख्या समान हो जाती है। प्रत्येक विद्यालय में अध्यापकों की संख्या ज्ञात कीजिए।
हल:
माना राजकीय विद्यालय में अध्यापकों की संख्या = x तथा प्राइवेट में अध्यापकों की संख्या = y है।
अतः प्रश्नानुसार x + y = 210 .... (i)
तथा (x + 10) = (1 - 10)
x - y = - 20 .... (ii)

समीकरण (i) व (ii) को जोड़ने पर।
2x = 190
x = \(\frac{190}{2}\) = 95

x का मान समीकरण (i) में रखने पर
95 + y = 210
y = 210 - 95 = 115
अतः राजकीय विद्यालय में संख्या 95 व प्राइवेट में 115

प्रश्न 4.
दो अंकों वाली संख्या के अंकों का योगफल 7 है। अंकों का क्रम उलट देने पर प्राप्त संख्या मूल संख्या से 9 अधिक होती है। वह संख्या ज्ञात कीजिए।
हल:
माना संख्या में दहाई अंक = x
और इकाई अंक = y
तब दी हुई संख्या = (10x + y)
अंकों का क्रम उलट करने पर संख्या = (10y + x)
प्रश्नानुसार - x + y = 7
या x + y - 7 = 0.... (1)
और (10x + y) + 9 = 10y + x
या 10x + y + 9 = 10y + x
या 9x + 9 = 9y
x - y + 1 = 0 .........(2)

समीकरण (1) व (2) को हल करने पर

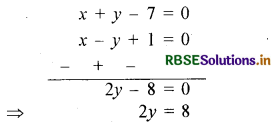
y = \(\frac{8}{2}\) = 4

y = 4 मान को समीकरण (1) में रखने पर
x + 4 - 7 = 0
x - 3 = 0
⇒ x = 3
संख्या = 10x + 1 = 10 × 3 + 4 = 30 + 4 = 34

प्रश्न 5.
6 वर्ष बाद एक आदमी की आयु उसके पुत्र की आयु की 3 गुना हो जायेगी और 3 वर्ष पूर्व वह अपने पुत्र की आयु का 9 गुना था। उनकी वर्तमान आयु ज्ञात कीजिए।
हल:
माना आदमी एवं उसके पुत्र की वर्तमान आयु क्रमशः x वर्ष व y वर्ष है। 6 वर्ष बाद पिता की आयु
= x + 6

तथा 6 वर्ष बाद पुत्र की आयु = y + 6 अतः प्रश्नानुसार
x + 6 = 3(y + 6)
⇒ x + 6 = 3y + 18
या x - 3y = 12 .... (i)

पुनः 3 वर्ष पूर्व पिता एवं पुत्र की आयु क्रमशः (x - 3) व (v - 3) होगी।
अतः प्रश्नानुसार
x - 3 = 9(y - 3)
⇒ x - 3 = 9y - 27
या x - 9y = - 24 .... (ii)

अतः दोनों समीकरणों को लिखने पर।

y = \(\frac{36}{6}\) = 6
y का मान (i) में रखने पर
x - 3 × 6 = 12
x - 18 = 12
x = 12 + 18 = 30
अतः पिता की आयु = 30 वर्ष तथा पुत्र की आयु = 6 वर्ष ।

प्रश्न 6.
आफ़ताब अपनी पुत्री से कहता है, 'सात वर्ष पूर्व मैं तुमसे सात गुनी आयु का था। अब से 3 वर्ष बाद मैं तुमसे केवल तीन गनी आय का रह जाऊँगा। (क्या यह मनोरंजक है?) इस स्थिति को बीजगणितीय एवं ग्राफीय रूपों में व्यक्त कीजिए।
हल:
माना आफ़ताब और उसकी पुत्री की आयु (वर्षों में) क्रमशः 5 और 1 हैं। तब रैखिक समीकरण युग्म होंगे
s - 7 = 7 (t - 7),
अर्थात् s - 7t + 42 = 0 .... (1)
तथा s + 3 = 3 (t + 3)
अर्थात् s - 3t = 6 .... (2)

समीकरण (2) का प्रयोग करने पर
s = 3t + 6

समीकरण (1) में s का मान रखने पर
(3t + 6) - 7t + 42 = 0

अर्थात् - 4t = 48, जिससे t = 12
t के इस मान को समीकरण (2) में रखने पर
s = 3 (12) + 6 = 42
अतः, आफ़ताब और उसकी पुत्री क्रमशः 42 वर्ष और 12 वर्ष के हैं।

प्रश्न 7.
दो रेल पटरियाँ समीकरणों x + 2y - 4 = 0 और 2x + 4y - 12 = 0 द्वारा निरूपित की गई हैं। क्या रेल पटरियाँ एक-दूसरे को काटेंगी?
हल:
प्रश्नानुसार रैखिक समीकरण
x + 2y - 4 = 0 .... (1)
2x + 4y - 12 = 0 .... (2)

समीकरण (1) से x को y के पदों में व्यक्त करने पर
x = 4 - 2y

अब, x के इस मान को समीकरण (2) में प्रतिस्थापित करने पर
2 (4 - 2y) + 4y - 12 = 0
अर्थात् 8 - 12 = 0
अर्थात् -4 = 0
जो कि एक असत्य कथन है।
अतः, दिए गए समीकरणों का कोई सार्व हल नहीं है। इसलिए, दोनों पटरियाँ एक-दूसरे को नहीं काटेंगी।

प्रश्न 8.
p के किन मानों के लिए, निम्न समीकरणों के युग्म का एक अद्वितीय हल है?
4x + py + 8 = 0
2x + 2y + 2 = 0
हल:
यहाँ a₁ = 4, a₂ = 2, b₁ = p, b₂ = 2 है।
अब दिए गए युग्म का एक अद्वितीय हल होने के लिए, \(\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}}\) होगा।
अर्थात् \(\frac{4}{2} \neq \frac{p}{2}\)
अर्थात् p ≠ 4
अतः, 4 के अतिरिक्त, p के प्रत्येक मान के लिए दिए हुए समीकरण युग्म का एक अद्वितीय हल होगा।

प्रश्न 9.
आलेखीय विधि से प्रदर्शित कीजिए कि निम्न समीकरण निकाय 2x + 4y = 10; 3x + 6y = 12 कोई हल नहीं रखता है।
हल:
समीकरण 2x + 4y = 10 से
4y = 10 - 2xy
या y = \(\frac{10-2 x}{4}\)

समीकरण 3x + 6y = 12
= \(\frac{12-3 x}{6}\)

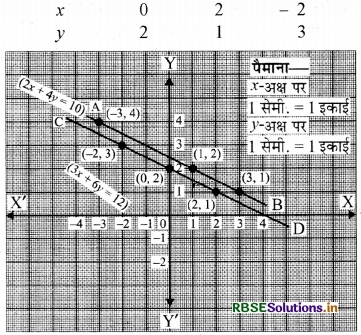
बिन्दु (1, 2) (-3, 4) व (3, 1) का आलेखन कर मिलाने से समीकरण 2x +4y= 10 आलेख AB प्राप्त होगा तथा बिन्दु (0, 2), (2, 1) व (- 2, 3) को आलेखन कर मिलाने पर 3x + 6y = 12 का आलेख CD प्राप्त होता है। ये दोनों रेखाएँ परस्पर समान्तर हैं अतः दिया गया समीकरण निकाय असंगत है तथा इसका कोई हल नहीं है।

प्रश्न 10.
k के किस मान के लिए निम्न रैखिक समीकरण के युग्म के अपरिमित रूप से अनेक हल होंगे?
kx + 3y = k - 3
12x + ky = k
हल:
अनन्त हल के लिये

अतः k = 6

निबन्धात्मक प्रश्न

प्रश्न 1.
ग्राफ द्वारा जाँच कीजिये कि समीकरण युग्म
x + 3y = 6 और
2x - 3y = 12
संगत है। यदि ऐसा है, तो उन्हें ग्राफ द्वारा हल कीजिये।
अथवा
निम्न रैखिक समीकरणों को लेखाचित्र (ग्राफ) द्वारा हल कीजिए :
x + 3y = 6
2x - 3y = 12
हल:
दिये गये समीकरण से सारणी तैयार करने पर
x + 3y = 6
3y = 6 - x
y = \(\frac{6-x}{3}\)

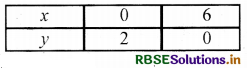
दूसरे समीकरण से
2x - 3y = 12
या 2x - 12 = 33
या y = \(\frac{2 x-12}{3}\)

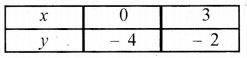
एक ग्राफ पेपर पर बिन्दुओं A(0, 2), B(6, 0), P(0, - 4) और Q(3, – 2) को आलेखित कीजिये और बिन्दुओं को मिलाकर रेखा AB और PQ खींची गयी है जैसा कि आकृति में दिखाया गया है। हम देखते हैं कि रेखाओं AB और PQ में एक उभयनिष्ठ बिन्दु B(6; 0) है। इसलिये रैखिक समीकरण | युग्म का एक हल x = 6, y = 0 है, अर्थात् समीकरण युग्म संगत है।

प्रश्न 2.
समीकरण निकाय 2x - y = 1; x + 2y = 8 का आलेख विधि से हल ज्ञात कीजिए तथा इनकी संगत रेखाएँ y-अक्ष को जिन बिन्दुओं पर मिलती हैं उन बिन्दुओं के निर्देशांक ज्ञात कीजिए।
हल:
समीकरण 2x - y = 1
अतः y = 2x - 1

समीकरण
x + 2y = 8
y = \(\frac{8-x}{2}\)

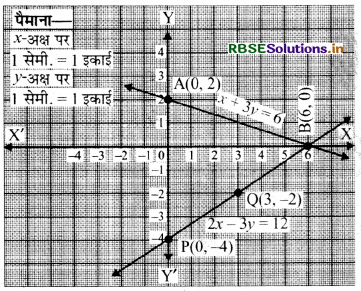
बिन्दु (1, 1) (2, 3) (3, 5) से तथा बिन्दु (2, 3) (4, 2) (6, 1) से आलेख खींचकर बिन्दु (2, 3) वह है जहाँ दोनों लेखाचित्र कटते हैं प्राप्त किया, यह समीकरणों का अभीष्ट हल है अत: x = 2, y = 3 प्रथम रेखा yअक्ष को बिन्दु (0, - 1) पर प्रथम द्वितीय रेखा y-अक्ष को बिन्दु (0, 4) पर मिलती है।

प्रश्न 3.
दो अंकों की एक संख्या एवं उसके अंकों को उलटने पर बनी संख्या का योग 66 है। यदि संख्या के अंकों का अन्तर 2 हो, तो संख्या ज्ञात कीजिए। ऐसी संख्याएँ कितनी हैं?
हल:
माना प्रथम संख्या की दहाई तथा इकाई के अंक क्रमशः x और y हैं। इसलिए, प्रथम संख्या को प्रसारित रूप में 10x + y लिखने पर जब अंक उलट जाते हैं, तो x इकाई का अंक बन जाता है तथा y दहाई का अंक। यह संख्या प्रसारित रूप में 10y + x है।

दिए हुए प्रतिबंधों के अनुसार,
(10x + y) + (10y + x) = 66
अर्थात् 11 (x + y) = 66
अर्थात् x + y = 6 .... (1)

हमें यह भी दिया गया है कि अंकों का अन्तर 2 है। इसलिए,
या तो x - y = 2 .... (2)
या y - x = 2 .... (3)
यदि x - 1 = 2 है, तो (1) और (2) को विलोपन विधि से हल करने पर x = 4 और y = 2 इस स्थिति में, हमें संख्या 42 प्राप्त होती है।
यदि y - x = 2 है, तो (1) और (3) को विलोपन विधि से हल करने पर, हमें x = 2 और y = 4 इस स्थिति में, हमें संख्या 24 प्राप्त होती है।
इस प्रकार ऐसी दो संख्याएँ 42 और 24 हैं।
सत्यापन : यहाँ 42 + 24 = 66 और 4 - 2 = 2 है तथा 24 + 42 = 66 और 4 - 2 = 2 है।

प्रश्न 4.
k के किस मान के लिए, निम्न रैखिक समीकरणों के युग्म के अपरिमित रूप से अनेक हल होंगे?
kx + 3y - (k - 3) = 0
12x + ky - k = 0
हल:
यहाँ \(\frac{a_{1}}{a_{2}}=\frac{k}{12}, \frac{b_{1}}{b_{2}}=\frac{3}{k}, \frac{c_{1}}{c_{2}}=\frac{k-3}{k}\) रैखिक समीकरणों के युग्म के अपरिमित रूप से अनेक हल होने के लिए, \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}\) होना चाहिए।
अर्थात् \(\frac{k}{12}=\frac{3}{k}=\frac{k-3}{k}\)
या \(\frac{k}{12}=\frac{3}{k}\)
जिसमें k² = 36 प्राप्त होता है, अर्थात् k = ± 6 हैं।
साथ ही \(\frac{3}{k}=\frac{k-3}{k}\)
जिससे 3k = k² - 3k प्राप्त होता है, अर्थात् 6k = k² है।
जिसका अर्थ k = 0 या k = 6 है।
इसलिए, k का मान, जो दोनों प्रतिबन्धों को सन्तुष्ट करता है, k = 6 है। इस मान के लिए समीकरणों के युग्म के अपरिमित रूप से अनेक हल हैं।

प्रश्न 5.
बैंगलोर के एक बस स्टैण्ड से यदि हम दो टिकट मल्लेश्वरम के तथा 3 टिकट यशवंतपुर के खरीदें, तो कुल लागत 46 रु. है। परन्तु यदि हम 3 टिकट मल्लेश्वरम के और 5 टिकट यशवंतपुर के खरीदें, तो कुल लागत 74 रु. है। बस स्टैण्ड से मल्लेश्वरम का किराया तथा बस स्टैण्ड से यशवंतपुर का किराया ज्ञात कीजिए।
हल:
माना बैंगलोर के बस स्टैण्ड से, मल्लेश्वरम का किराया x रु. तथा यशवंतपुर का किराया y रु. है। दी गई सूचनाओं से,
2x + 3y = 46
अर्थात् 2x + 3y - 46 = 0 ....(1)

3x + 5y = 74,
अर्थात् 3x + 5y - 74 = 0 ....(2)

वज्रगुणन विधि से इन समीकरणों को हल करने पर

अतः, बैंगलोर के बस स्टैण्ड से, मल्लेश्वरम का किराया 8 रु. तथा यशवंतपुर का किराया 10 रु. है।

प्रश्न 6.
निम्न समीकरण युग्म को रैखिक समीकरणों के युग्म में बदल कर हल कीजिए :
\(\frac{5}{x-1}+\frac{1}{y-2}\) = 2
\(\frac{6}{x-1}-\frac{3}{y-2}\) = 1
हल:
\(\frac{1}{x-1}\) =p और \(\frac{1}{y-2}\) = q रखने पर दी गई समीकरण
5\(\left(\frac{1}{x-1}\right)+\frac{1}{y-2}\) = 2 ............(1)
6\(\left(\frac{1}{x-1}\right)\) - 3\(\left(\frac{1}{y-2}\right)\) = 1 ..........(2)
5p + q = 2 .... (3)
6p - 34 = 1 .... (4)

समीकरण (3) और (4) व्यापक रूप में एक रैखिक समीकरण युग्म बनाती हैं। अब इन समीकरणों को हल करने के लिए, किसी भी विधि का प्रयोग कर सकते हैं। हम पाते हैं, p = \(\frac{1}{3}\) और q = \(\frac{1}{3}\)
अब p के लिए \(\frac{1}{x-1}\) प्रतिस्थापित करने पर
\(\frac{1}{x-1}=\frac{1}{3}\)
अर्थात् x - 1 = 3, अर्थात् x = 4 है।

इसी प्रकार q के लिए \(\frac{1}{y-2}\) रखने पर
\(\frac{1}{y-2}=\frac{1}{3}\)
अर्थात् 3 = y - 2, अर्थात् y = 5 है।
अतः, दिए गए समीकरण युग्म का अभीष्ट हल x = 4, y = 5 है।

प्रश्न 7.
दो व्यक्तियों की आय का अनुपात 9 : 7 है और उनके खर्चों का अनुपात 4 : 3 है। यदि प्रत्येक व्यक्ति प्रति महीने में 2000 रु. बचा लेता है, तो उनकी मासिक आय ज्ञात कीजिए।
हल:
माना कि दोनों व्यक्तियों की मासिक आय क्रमश: 9x रु. तथा 7x रु. और उनके खर्च क्रमशः 4y रु. और 3y रु. हैं । तब, उस स्थिति में बने समीकरण हैं :
9x - 4y = 2000.... (1)
और 7x - 3y = 2000.... (2)

चरण 1: के गुणकों को समान करने के लिए समीकरण (1) को 3 से तथा समीकरण (2) को 4 से गुणा करने पर
- 27x - 12y = 6000.... (3)
28x - 12y = 8000.... (4)

चरण 2 :y को विलुप्त करने के लिए समीकरण (3) को समीकरण (4) में से घटाने पर क्योंकि । के गुणांक समान हैं, इसलिए
(28x - 27x) - (12y - 12y) = 8000 - 6000 अर्थात्
x = 2000

चरण 3 : x का मान (1) में प्रतिस्थापित करने पर,
9 (2000) - 4y = 2000
y = 4000
अतः समीकरणों के युग्म का हल x = 2000, y = 4000 है। इसलिए, व्यक्तियों की मासिक आय क्रमशः 18000 रु. तथा 14000 रु. है।

प्रश्न 8.
एक नाव 10 घण्टे में धारा के प्रतिकूल 30 km. तथा धारा के अनुकूल 44 km. जाती है। 13 घण्टे में वह 40 km. धारा के प्रतिकूल एवं 55 km. धारा के अनुकूल जाती है। धारा की चाल तथा नाव की स्थिर पानी में चाल ज्ञात कीजिए।
हल:
माना, नाव की स्थिर जल में चाल x km./h है तथा धारा की चाल y km./h है। साथ ही, नाव की धारा के अनुकूल चाल = (x + y) km./h तथा नाव की धारा के प्रतिकूल. चाल = (x - y) km./h होगी।
अर्थात
साथ ही,

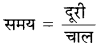
प्रथम स्थिति में, जब नाव 30 km. धारा के प्रतिकूल चलती है, माना घण्टों में लिया गया समय t₁, है। तब
t₁ = \(\frac{30}{(x-y)}\)

माना t₂, घण्टों में वह समय है जिसमें नाव 44 km. धारा के अनुकूल चलती है। तब, t₂ = \(\frac{44}{x+y}\) है। कुल लगा समय t₁ + t₂ = 10 घण्टे है। अतः
\(\frac{30}{x-y}+\frac{44}{x+y}\) = 10 .... (1)

दूसरी स्थिति में, 13 घण्टों में वह 40 km. धारा के प्रतिकूल और 55 km. धारा के अनुकूल चलती है। तब
\(\frac{40}{x-y}+\frac{55}{x+y}\) = 13 .... (2)
\(\frac{1}{x-y}\) = u और हर \(\frac{1}{x+y}\) = v रखने पर .... (3)

इन मानों को समीकरण (1) और (2) में प्रतिस्थापित | करने पर .
30n + 44v = 10
या 30u + 44v – 10 = 0 ....(4)
40u + 55v = 13
या 40u + 55v - 13 = 0 ....(5)

वज्रगुणन विधि प्रयोग करने पर,

अब u, v के इन मानों को समीकरण (3) में रखने पर,
\(\frac{1}{x-y}=\frac{1}{5}\) और \(\frac{1}{x+y}=\frac{1}{11}\)
अर्थात् x - y = 5
और x + y = 11 .... (6)

इन समीकरणों को जोड़ने पर
2x = 16
अर्थात् x = 8

(6) में दी हुई समीकरणों को घटाने पर
2y = 6
अर्थात् y = 3
अतः नाव की स्थिर जल में चाल 8 km./h तथा धारा की चाल 3 km./h है।

प्रश्न 9.
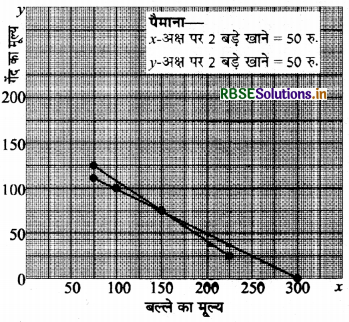
क्रिकेट टीम के एक कोच ने एक बल्ला और 2 गेंदें 300 रु. में खरीदी। बाद में एक ही प्रकार के अन्य 2 बल्ले तथा 3 गेंदें 525 रु. में खरीदी। इस स्थिति को बीजगणितीय रूपों में व्यक्त कीजिए एवं इसको ग्राफीय विधि से हल कीजिए। यह भी ज्ञात कीजिए कि कोच एक बल्ला तथा एक गेंद कितने रुपयों में खरीद सकेगा?
हल:
माना कि एक बल्ले का मूल्य = x रु. तथा
एक गेंद का मूल्य = y रु.

बीजगणितीय रूप
प्रश्न की पहली शर्त के अनुसार
x + 2y = 300

प्रश्न की दूसरी शर्त के अनुसार
2x + 3y = 525

∴ दो चरों में रैखिक समीकरण युग्म हैं
x + 2 = 300
2x + 31 = 525

आलेखीय रूप
x + 2y = 300
x = 300 - 21 ....(1)

y = 10 को (1) में प्रतिस्थापित करने पर
x = 300 - 2 × 0
x = 300

y = 75 को (1) में प्रतिस्थापित करने पर
x = 300 - 2 × 75
= 300 - 150
x = 150

y = 100 को (2) में प्रतिस्थापित करने पर
x = 300 - 2 × 100
= 300 - 200
x = 100

2x + 3y = 525 ....(2)
2x = 525 - 3y
x = \(\frac{525-3 y}{2}\)

y = 25 को (2) में प्रतिस्थापित करने पर
x = \(\frac{525-3 \times 25}{2}=\frac{525-75}{2}\)
x = \(\frac{450}{2}\) = 225

y = 75 को (2) में प्रतिस्थापित करने पर
x = \(\frac{525-3 \times 75}{2}=\frac{525-225}{2}\)
x = \(\frac{300}{2}\) = 150

y = 125 को (2) में प्रतिस्थापित करने पर
x = \(\frac{525-3 \times 125}{2}=\frac{525-375}{2}\)
x = \(\frac{150}{2}\) = 75

ग्राफीय विधि से हल करने पर x = 150 तथा y = 75 तथा कोच एक बल्ला तथा एक गेंद खरीद सकेगा
= 150 + 75 = 225 रु.

प्रश्न 10.
अशोक ने एक टेस्ट में 65 अंक अर्जित किए, जब उसे प्रत्येक सही उत्तर का 5 अंक मिले तथा प्रत्येक अशुद्ध उत्तर पर 2 अंक की कटौती की गई। यदि उसे सही उत्तर पर 3 अंक मिलते तथा अशुद्ध उत्तर पर 1 अंक कटते, तो अशोक 40 अंक अर्जित करता। इस समस्या को बीजगणितीय रूप में व्यक्त कर ग्राफ विधि से हल कीजिए। टेस्ट में कुल कितने प्रश्न थे ?
हल:
माना कि सही उत्तर का अर्थ x तथा अशुद्ध उत्तर का अर्थ y है । अब प्रश्नानुसार (प्रथम शर्त के अनुसार)
5x - 2y = 65 ....(i)

द्वितीय शर्त के अनुसार
3x - y = 40 ....(ii)

समीकरण (i) से 5x = 65 + 2y
∴ x = \(\frac{65+2 y}{5}\)

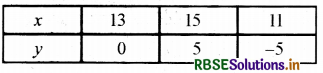
y= 0 रखने पर x = \(\frac{65+0}{5}\) = 13

y= 5 रखने पर x = \(\frac{65+10}{5}\) = 15

y = - 5 रखने पर x = \(\frac{65-10}{5}\) = 11

समीकरण (ii) से 3x - y = 40
-y = 40 - 3x
y = 3x - 40

x= 10 रखने पर y = 30 - 40 = - 10
x = 15 रखने पर y = 45 - 40 = 5
x = 20 रखने पर y = 60 - 40 = 20

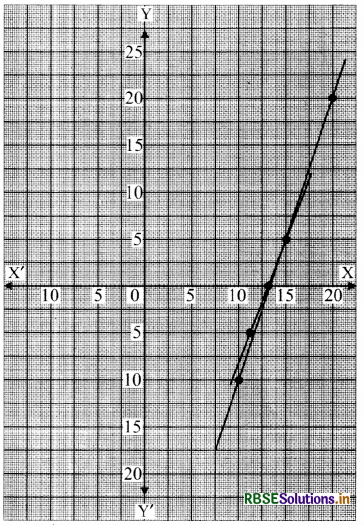
पैमाना
x-अक्ष पर 2 बड़े खाने = 5 इकाई
y-अक्ष पर 2 बड़े खाने = 5 इकाई
∴ दोनों लेखाचित्रों का मिलान बिन्दु (15, 5) है। अतः कुल प्रश्न = 15 + 5 = 20

प्रश्न 11.
5 सेबों और 3 सन्तरों का कुल मूल्य 35 रुपये है जबकि 2 सेबों और 4 सन्तरों का कुल मूल्य 28 रुपये है। इस समस्या को बीजगणितीय रूप में व्यक्त कर ग्राफ विधि से हल कीजिए।
हल:
माना कि सेबों को x से तथा सन्तरों को y से प्रदर्शित करें तो प्रश्नानुसार
प्रथम शर्त = 5x + 3y = 35
3y = 35 - 5x
∴ y = \(\frac{35-5 x}{3}\) .... (i)


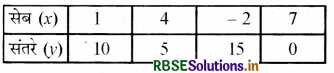
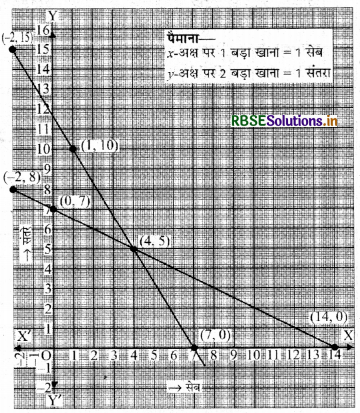
तथा द्वितीय शर्त = 2x + 4y = 28
4y = 28 - 2x
y = \(\frac{28-2 x}{4}\) .... (ii)

दोनों वक्र बिन्दु (4,5) पर मिलते हैं। वहाँ से :-अक्ष तथा -अक्ष पर लंब डालने पर हल x = 4 सेब तथा V=5 संतरे

प्रश्न 12.
2 अभ्यास पुस्तिका और 3 पेन्सिलों का कुल मूल्य 17 रुपये है, जबकि 3 अभ्यास पुस्तिका और 4 पेन्सिलों का कुल मूल्य 24 रुपये है। इस समस्या को बीजगणितीय रूप में व्यक्त कर ग्राफ विधि से हल कीजिए।
हल:
माना कि 1 अभ्यास पुस्तिका का मूल्य = x रु.
और 1 पेन्सिल का मूल्य = y रु.

पहली शर्त के अनुसार,
2x + 3y = 17

दूसरी शर्त के अनुसार,
3x + 4y = 24

इसलिए रैखिक समीकरण युग्म हैं
2x + 3y = 17
3x + 4 = 24

अब इन रैखिक समीकरणों का आलेख खींचने पर |
2x + 3y = 17
2x = 17 - 3y
या 2x = 17 - 3y
या x = \(\frac{17-3 y}{2}\) ....(1)

y = 1 को समी. (1) में प्रतिस्थापित करने पर
x = \(\frac{17-3 \times 1}{2}=\frac{17-3}{2}=\frac{14}{2}\) = 7

y = 3 को समी. (1) में प्रतिस्थापित करने पर
x = \(\frac{17-3 \times 3}{2}=\frac{17-9}{2}=\frac{8}{2}\) = 4
x = 4

y = 5 को समी. (1) में प्रतिस्थापित करने पर
x = \(\frac{17-3 \times 5}{2}=\frac{17-15}{2}=\frac{2}{2}\) = 1
x = 1

बिन्दुओं A(7, 1), B(4, 3), C(1, 5) को आलेखित करने और उनको मिलाते हुए रेखा खींचने पर हमें समीकरण 2x + 3y = 17 का आलेख प्राप्त होता है।

अब दूसरे समीकरण से ।
3x + 4 = 24

या 3x = 24 - 4y
या x = \(\frac{24-4 y}{3}\)

समी. (2) में y = 0 प्रतिस्थापित करने पर
x = \(\frac{24-4 \times 0}{3}=\frac{24-0}{3}=\frac{24}{3}\) = 8
x = 8

समी. (2) में y = 3 प्रतिस्थापित करने पर
x = \(\frac{24-4 \times 3}{3}=\frac{24-12}{3}=\frac{12}{3}\) = 4
x = 4

समी. (2) में y = 6 प्रतिस्थापित करने पर
x = \(\frac{24-4 \times 6}{3}=\frac{24-24}{3}=\frac{0}{3}\) = 0
x = 0

बिन्दु D(8, 0), B(4, 3), E(0, 6) को आलेखित करने और उनको मिलाते हुए रेखा खींचने पर हमें समीकरण 3x + 4 = 24 का आलेख प्राप्त होता है।

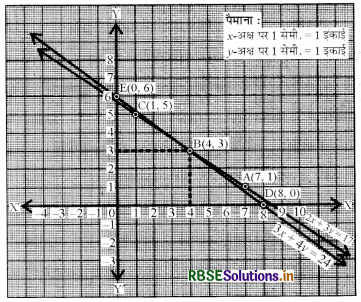
आलेख से यह स्पष्ट है कि दोनों रैखिक समीकरण बिन्दु (4. 3) पर मिलते हैं।
इसलिए बिन्दु B(4, 3) आलेखीय स्थिति है।
अतः, 1 अभ्यास पुस्तिका का मूल्य = 4 रु.
1 पेन्सिल का मूल्य = 3 रु.