RBSE Class 10 Maths Important Questions Chapter 2 बहुपद

Rajasthan Board RBSE Class 10 Maths Important Questions Chapter 2 बहुपद Important Questions and Answers.

RBSE Class 10 Maths Chapter 2 Important Questions बहुपद

वस्तुनिष्ठ प्रश्न

प्रश्न 1.
बहुपद p(x) का शून्यक, जहाँ p(x) = ax + 1 . है, a ≠ 0 है
(A) 1
(B) - a
(C) 0
(D) -\(\frac{1}{a}\)

प्रश्न 2.
एक त्रिघात बहुपद के अधिक से अधिक शून्यकों की संख्या होती है
(A) 1
(B) 2
(C) 3
(D) 4

प्रश्न 3.
यदि α, β तथा γ त्रिघात बहुपद ax³+ bx² + cx + d = 0 के शून्यक हों, तो α + β + γ का मान होगा
(A) a
(B) b
(C) c
(D)

प्रश्न 4.
विभाजन एल्गोरिथ्म का प्रयोग कर x⁴ - 3x² + 2x + 5 में x - 1 का भाग देने पर भागफल व शेषफल होगा
(A) भागफल = x⁴ - 3x² + 2x + 5, शेषफल = 6
(B) भागफल = x³ - 3x + 2, शेषफल = - 5
(C) भागफल = x³ + x² - 2x, शेषफल = 5
(D) भागफल = 3x² + 2x + 5, शेषफल = 3

प्रश्न 5.
व्यंजक (x - 3) बहुपद p(x) = x³ + x² - 17x + 5 का गुणनखण्ड होगा यदि.
(A) p(3) = 0
(B) p(-3) = 0
(C).p(-3)= 3
(D) p(-3)= -3

प्रश्न 6.
यदि α, β तथा γ त्रिघात बहुपद ax³ + bx² + cx + d = 0 के शून्यक हों, तो αβ + βγ + γα का मान होगा
(A) c
(B) \(\frac{c}{a}\)
(C) a
(D) ac

प्रश्न 7.
यदि x + a में (x + a) का भाग दिया जाए तो शेषफल होगा-
(A) x² + a²
(B) x + a
(C) 0
(D) a

प्रश्न 8.
यदि विधात बहुपद ax³ + bx² + cx + d = 0 के शून्यक α, β तथा γ हों, तो αβγ का मान होगा-
(A) -\( \frac{d}{a}\)
(B) d
(C) a
(D) ad

अतिलघूत्तरात्मक प्रश्न

प्रश्न 1.
बहुपद का शून्यक क्या होता है?
उत्तर:
एक वास्तविक संख्या a किसी बहुपद p(x) का शून्यक कहलाएगी यदि p(a) = (0 हो अर्थात् चर का वह मान जिससे बहुपद का मान शून्य हो जाए।

प्रश्न 2.
रैखिक बहुपद का उदाहरण लिखिए।
उत्तर:
ax + b, जहाँ a, b ∈ R तथा a ≠ 0

प्रश्न 3.
यदि द्विघात बहुपद ax² + bx+ c के शून्यक α और β हों तो α + β तथा αβ का मान लिखिए।
उत्तर:
α + β = - \(\frac{b}{a}\) तथा αβ = \(\frac{c}{a}\)

प्रश्न 4.
विभाजन एल्गोरिथ्म लिखिए।
उत्तर:
यदि दिए गए बहुपद p(x) और शून्येतर बहुपद g(x) के लिए दो ऐसे बहुपदों q(x) तथा r(x) का अस्तित्व होता है कि p(x) = g(x) q(x) + r(x) जहाँ r(x) = 0 है या घात r(x) < घात g(x) है।

प्रश्न 5.
बहुपद किसे कहते हैं?
उत्तर:
एक से अधिक पदों के बीजगणितीय व्यंजक बहुपद कहलाते हैं यदि इसके पदों में किसी भी चर की घात ऋणात्मक नहीं होनी चाहिए।

प्रश्न 6.
एक द्विघात बहुपद का उदाहरण लिखिए।
उत्तर:
y² - 2

प्रश्न 7.
त्रिघात बहुपद की परिभाषा उदाहरण सहित लिखिए।
उत्तर:
एक ऐसा बहुपद जिसमें घातों की अधिकतम संख्या तीन हो, त्रिघात बहुपद कहलाता है। जैसे 3x³ - 2x² + x - 1

प्रश्न 8.
बहुपद का मान क्या होता है?
उत्तर:
यदि x में p(x) कोई बहुपद है और यदि k कोई वास्तविक संख्या है, तो p(x) में x को k से प्रतिस्थापित करने पर जो वास्तविक संख्या प्राप्त होती है, वह p(x) का x = k पर मान कहलाती है और इसे p(k) से निरूपित किया जाता है।

प्रश्न 9.
यदि व्यंजक x³ - 2x + 1 का एक भाजक (x - 1) है तो शेषफल लिखिए।
उत्तर:
माना कि व्यंजक f(x) = x³ - 2x + 1 का एक गुणनखण्ड (x - 1) है।
अतः (1) = (1)³ – 2(1) + 1 = 1 - 2 + 1
= 0
∴ शेषफल = शून्य

प्रश्न 10.
द्विघात बहुपद x² + 7x + 10 के शून्यक ज्ञात कीजिए।
उत्तर:
x² + 7x + 10
x² + 5x + 2x + 10
(x + 5) + 2(x + 5) = (x + 2) (x + 5)
∴ x² + 7x + 10 का मान शून्य है, जब x + 2 = 0 या x + 5 = 0 है अर्थात् जब x = - 2 या x = - 5 हो।
∴ x² + 7x + 10 के शून्यक - 2 और - 5 हैं।

प्रश्न 11.
यदि 2 बहुपद f(x) = x⁴ - x³ - 4x² + kx + 10 का गुणनखण्ड हो तो k का मान लिखिए।
हल:
f(2) = 2⁴ - x³ - 4 × 2² + k × 2 + 10
या 0 = 16 - 8 - 16 + 2k + 10
0 = 2k + 2
∴ k = \(\frac{-2}{2}\) = - 1

प्रश्न 12.
यदि (x - 2) व्यंजक x² + 2x - a का एक गुणनखण्ड है तो a का मान लिखिए।
उत्तर:
x - 2 = 0 या x = 2
व्यंजक में रखने पर इसका मान शून्य होना चाहिए। अतः
(2)² + 2 × 2 - a = 0
4 + 4 - a = 0
a = 8

प्रश्न 13.
यदि x + y + 3 - 3xyz = (x + y + z) (x + y + 2 + k) हो, तो k का मान लिखिए।
उत्तर:
k = - xy – yz - zx

प्रश्न 14.
एक द्विघात बहुपद ज्ञात कीजिये जिसके शून्यकों के योग और गुणनफल क्रमशः -4 और 3 हों।
हल:
x² - (मूलों का योग) x + मूलों का गुणनफल
x² - (- 4) x + 3
x² + 4x + 3

प्रश्न 15.
एक n घात वाले बहुपद के अधिकतम शून्यकों की संख्या लिखिए।
उत्तर:
n शून्यक।

प्रश्न 16.
द्विघात बहुपद ax + bx + c के आलेख की आकृति किस प्रकार की प्राप्त होती है?
उत्तर:
परवलंया आकृति।

प्रश्न 17.
वह बहुपद ज्ञात कीजिये जिसके शून्यक - 5 और 4 हों।
हल:
[x - (- 5)] (x - 4)
⇒ (x + 5) (x - 4)
⇒ x² - 4x + 5x - 20
⇒ x² + x - 20

प्रश्न 18.
यदि बहुपद f(x) = x² - 5x + k के शून्यक α तथा β इस प्रकार हों कि α - β = 1 तो k का मान लिखिये।
हल:
दिया गया है कि α तथा β बहुपद x² - 5x + k के शून्यक हैं।
α + β = \(\left(\frac{-5}{1}\right)\) = 5
αβ = \(\frac{k}{1}\) = k
α - β = 1
या (α - β) = 1
(α + β) - 4αβ = 1
या 25 - 4k = 1
4k =24 ∴ k = \(\frac{24}{4}\) = 6

प्रश्न 19.
x² - 9 के शून्यक ज्ञात कीजिये।।
हल:
x² - 9 = (x)² - (3)² = (x + 3) (x - 3)
बहुपद के शून्यक के लिये
x + 3 = 0 ⇒ x = - 3 तथा
x - 3 = 0 ⇒ x = 3
अतः बहुपद x² - 9 के शून्यक = - 3

प्रश्न 20.
यदि बहुपद ax² - 6x - 6 के शून्यकों का गुणनफल 6 हो, तो a का मान ज्ञात कीजिये।
हल:
दिये गये बहुपद के शून्यक a तथा B हैं । तब शून्यकों का गुणनफल
αβ = \(\frac{c}{a}\) से
⇒ αβ = \(\frac{-6}{a}\)
⇒ 6 = \(\frac{-6}{a}\)
∴ a = -1

लघुत्तरात्मक प्रश्न

प्रश्न 1.
भाग की क्रिया सम्पन्न किये बिना ही सिद्ध कीजिए कि
(i) x² + (a - 3) x - 3a (x + a) से पूर्णतः विभाजित होता है।
(ii) 3x³ + 11x² + x - 15 व्यंजक (x-1) से पूर्णतः विभाजित होता है।
हल:
(i) यदि (x + a) से पूर्णतः विभाजित है तो x = - a मान रखने पर व्यंजक का मान शून्य हो जायेगा। अतः व्यंजक में x = - a मान रखने पर
= (- a)² + (a - 3) (- a) - 3a
= a² - a² + 3a - 3a = 0
अतः (x + a) से व्यंजक x² + (a - 3) x - 3a पूर्णतः विभाजित है।

(ii) व्यंजक में x = 1 मान रखने पर
3(1)³ + 11(1)² + 1 - 15
3 + 11 + 1 - 15 = 0
अतः व्यंजक 3x + 11x² + x – 15 व्यंजक (x - 1) से पूर्णतः विभाजित है।

प्रश्न 2.
a के किस मान के लिए बहुपद x³ + 2x² - 3ax - 8 में व्यंजक (x - 4) का पूरा-पूरा भाग जाता है।
हल:
हम जानते हैं (x - 4) का भाग देने पर शेषफल f(a) प्राप्त होगा।
∴ f(a) जहाँ
f(x) = x³ + 2x² - 3ax - 8
f(4) = (4)³ + 2(4)² - 3a × 4 - 8
= 64 + 32 - 12a - 8 = 0
या 12a = 88
a = \(\frac{88}{12}=\frac{22}{3}\)

प्रश्न 3.
सिद्ध कीजिए कि बहुपद x² + 2x + 3 के शून्य विद्यमान नहीं हैं।
हल:
माना कि f(x) = x² + 2x + 3
f(x) = {x² + 2 × x + 1} + 2
= (x + 1)² + 2
यहाँ x के वास्तविक मान के लिए (x + 1)² का मान ऋणात्मक नहीं होगा। अत: (x + 1)² हमेशा शून्य से अधिक होगा अतः (x) का मान 2 से अधिक होगा।

प्रश्न 4.
p के किस मान के लिए बहुपद px³ + 9x² + 6x - 1 व्यंजक (3x + 2) से पूर्णतः विभाजित | होता है।
हल:
दिया गया है कि (3x + 2) दिये गये व्यंजक | का एक गुणनखण्ड है।
∴ 3x + 2 = 0
या 3x = -2 ∴ x = \(\frac{-2}{3}\)
व्यंजक f(x)= px³ + 9x² + 6x - 1 में x = \(\frac{2}{3}\) मान रखने पर

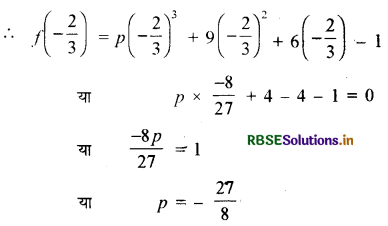
प्रश्न 5.
एक द्विघात बहुपद ज्ञात कीजिये जिसके शून्यकों के योग तथा गुणनफल क्रमशः 4 तथा 1 हैं।
हल:
दिया गया है
α + β = 4
तथा αβ = 1
माना द्विघात बहुपद के शून्यक α व β हैं।
∴ द्विघात बहुपद = (x - α) (x - β)
= x² - (α + β) x + αβ
= x² - 4x + 1
अतः अभीष्ट बहुपद = x² - 4x + 1

प्रश्न 6.
द्विघात बहुपद 2x² - 6x +4 के शून्यांकों का योग व गुणनफल ज्ञात कीजिए।
हल:
दिया गया बहुपद 2x² - 6x + 4

प्रश्न 7.
यदि (x - 1) तथा (x + 2) बहुपद 2x³ + mx² + nx - 14.के गुणनखण्ड है तो m तथा. n के मान ज्ञात कीजिए।
हल:
माना कि f(x) = 2x³ + mx² + nx - 14 है
अतः (x - 1). तथा (x + 2) f(x) के गुणनखण्ड होने चाहिए।
अत: f(1) = 0 व f(-2) = 0
व्यंजक :2x³ + mx² + nx - 14 में
f(1) = m(1)² + n(1) - 14 = 0
⇒ m + n - 12 = 0

व्यंजक 2x³ + mx² + nx - 14 में
f(- 2) = 2(-2)³ + m(- 2)² + n(-2) - 14 = 0
f(-2) = - 16 + 4m - 2n - 14
⇒ 4m - 2n - 30 = 0 .... (ii)

समीकरण (i) व (ii) से
m + n = 12 ...... (iii)
2m - n = 15 .... (iv)
जोड़ने पर 3m = 27 ⇒ अतः m = 9
समीकरण (iii) से n = 3

प्रश्न 8.
यदि बहुपद x³ + lx + m में (x - 1) या (x + 1) का भाग दिया जाये तो शेषफल 7 बचता है, । तथा m के मान ज्ञात कीजिए।
हल:
f(x) = x³ + lx + m तथा (x - 1) या (x + 1)
इसके गुणनखण्ड हैं जब 7 इसमें से घटा दें अतः
(1) = 1 + l + m - 7 - 0
⇒ l + m - 6 = 0 .... (i)
f(1) = - 1 - l + m - 7 = 0
⇒ - 1 + m - 8 = 0 .... (ii)
समीकरण (i) व (ii) को हल करने पर l = - 1 तथा m = 7

प्रश्न 9.
द्विघात बहुपद x² + 7x + 10 के शून्यक ज्ञात कीजिए और शून्यकों तथा गुणांकों के बीच के सम्बन्ध की सत्यता की जाँच कीजिए।
हल:
प्रश्नानुसार
x² + 7x + 10 = (x + 2) (x + 5)
इसलिए x² + 7x + 10 का मान शून्य है, जब x + 2 = 0 है या x + 5 = 0 है, अर्थात् जब x = - 2
या x = - 5 हो। इसलिए, x² + 7x + 10 के शून्यक - 2 और - 5 हैं।
अब, शून्यकों का योग = - 2 + (-5) = (-7)

अतः शून्यकों -- 2 और - 5 द्वारा भी योगफल व गुणनफल वही हैं, जो कि इनमें हैं।
∴ बहुपद के शून्यकों और गुणांकों के बीच सम्बन्ध 'सही है। .

प्रश्न 10.
एक द्विधात बहुपद ज्ञात कीजिये जिसके शून्यकों के योग तथा गुणनफल क्रमशः 0 और √5 हैं।
हल:
माना द्विघात बहुपद के शून्यक a तथा हैं।
दिया गया है α + β = 0
αβ = √5
α तथा β शून्यक हैं।
∴ द्विघात बहुपद = (x - α) (x - β)
= x² - (α + β) x + αβ
= x² - 0.x + √5 = x² + √5
अतः अभीष्ट बहुपद = x² + 5

प्रश्न 11.
यदि द्विघात व्यंजक kx² + 5x + 3k के शून्यकों का योग उनके गुणनफल के बराबर हो, तो k का मान ज्ञात कीजिये।
हल:
दिए गए व्यंजक kx² + 5x + 3k के अनुसार
शून्यकों का योग (α + β) = -\(\frac{5}{k}\)
तथा शून्यकों का गुणनफल (αβ) = \(\frac{3 k}{k}\) = 3

अब प्रश्नानुसार -\(\frac{5}{k}=\frac{3}{1}\)
या 3k = - 5
∴ k = 5

प्रश्न 12.
3x³ + x² + 2x + 5 को 1 + 2x + x² से भाग दीजिए।
हल:
यहाँ f(x) = 3x³ + x² + 2x + 5
तथा g(x) = 1 + 2x + x²

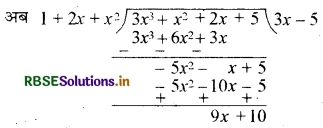
भागफल = 3x - 5 तथा शेषफल = 9x + 10

प्रश्न 13.
द्विघात बहुपद x² + x - 2 के शून्यक ज्ञात कीजिए और शून्यकों तथा गुणांकों के बीच के सम्बन्ध की सत्यता की जाँच कीजिए।
हल:
प्रश्नानुसार
x² + x - 2 = x² + 2x - x - 2
= x(x + 2) - 1(x + 2)
= (x + 2) (x - 1)
x² + x - 2 का मान शून्य होगा यदि (x + 2) (x - 1) के मान शून्य हों अर्थात् x + 2 = 0
या x - 1 = 0 अर्थात् x = -2 या x = 1
अत: x² + x - 2 के शून्यक -2 और 1 हैं।
अब, शून्यकों का योग = -2 + 1

निबन्धात्मक प्रश्न

प्रश्न 1.
शेषफल प्रमेय का प्रयोग करते हुए निम्नलिखित बहुपदों के गुणनखण्ड ज्ञात कीजिए
(i) x³ - x² - 5x + 6
(ii) 2x³ - x² - 13x - 6
(iii) y³ - 7y + 6
(iv) x³ - 6x² + 3x + 10
हल:
(i) f(x)= x³ - 2x² - 5x + 6
x = 1 रखने पर
f(1)= 1³ - 2.1² - 5.1 + 6
= 1 - 2 - 5 + 6 = 0
f(x) का एक गुणनखण्ड (x - 1) है।
∴ अतः व्यंजक x³ - x² - x² + x – 6x + 6
(पहले दो पदों को इस प्रकार व्यवस्थित करते हैं कि उभयनिष्ठ लेने के पश्चात् (x - 1) बचे, आगे भी दो-दो पदों के युग्म ऐसे बनाते हैं कि यह प्रक्रिया चलती रहे)
= x² (x - 1) - x (x - 1) - 6 (x - 1)
= (x - 1) (x² - x - 6)
= (x - 1) (x + 2) (x - 3)
दूसरी विधि-: ∴ f(x) का मान गुणनखण्ड (x - 1) है भाग की क्रिया से

अतः x³ - 2x² - 5x + 6
= (x - 1) (x² - x + 6)
= (x - 1) (x - 3) (x + 2)

(ii) f(x) = 2x³ - x² - 13x - 6 x = - 2 मान रखने पर।
2(-2)³ - (- 2)² - 13(-2) - 6
= - 16 - 4 + 26 - 6 = 0
अतः f(x)= (x + 2) एक गुणनखण्ड होगा
अतः 2x³ + 4x² - 5x² - 10x - 3x - 6
= 2x(x + 2) - 5x(x + 2) - 3(x + 2)
= (x + 2) (2x² - 5x - 3)
= (x + 2) {2x² - 6x + x - 3}
= (x + 2) {2x(x - 3) + 1(x - 3)}
= (x + 2) (x - 3) (2x + 1)

(iii) f(x) = y³ - 7y + 6 दिये गये व्यंजक में y = 1 रखने पर,
(1)³ - 7(1) + 6 = 1 - 7 + 6 = 0
अतः (y - 1) दिये गये व्यंजक का एक गुणनखण्ड होगा।
अब हम दिये गये व्यंजक के पदों को दो-दो में इस प्रकार समूहित करते हैं कि इनमें (y - 1) सार्वगुणनखण्ड हो जाये।
y³ - 7y + 6
= y³ - y² + y² - 7y + 6. (∵ y² - y² = 0)
= y²(y - 1) + y² - y + y - 7y + 6( y = 0)
= y²(y - 1) + y(y - 1) - 6y + 6
= y²(y - 1) + y(y - 1) - 6y - 1)

पूरे व्यंजक में से (y - 1) को सार्वगुणनखण्ड लेने पर
(y - 1) (y² + y - 6)
= (y - 1) {y² + 3y - 2y - 6}
= (y - 1) {y² + 3) - 2 + 3)}
= (y - 1) {(y - 2) (y + 3)}
= (y - 1) (y - 2) (y + 3)

(iv) f(x) = x³ - 6x² + 3x + 10 दिये गये व्यंजक में x = - 1 रखने पर
(- 1)³ - 6(- 1)² + 3(- 1) + 10
= - 1 - 6 - 3 + 10
= - 10 + 10 = 0
अतः (x + 1) दिये गये व्यंजक का एक गुणनखण्ड होगा।

अब हम दिये गये व्यंजक के पदों को दो-दो में इस | प्रकार समूहित करते हैं कि इनमें (x + 1) सार्वगुणनखण्ड हो जाये।
x³ - 6x² + 3x + 10
= x³ + x² - x² - 6x² + 3x + 10 (∵ x² - x² = 0)
= x²(x + 1) - 7x² - 7x + 7x+ 3x + 10 (∵ 7x - 7x = 0)
= x(x + 1) - 7x(x + 1) + 10x + 10
= x (x + 1) - 7x(x + 1) + 10(x + 1)

पूरे व्यंजक में से (x + 1) को सार्वगुणनखण्ड लेने पर
= (x + 1) (x² - 7x + 10)
= (x + 1) (x² - 5x - 2x + 10)
= (x + 1) {x(x - 5) - 2(x - 5)}
= (x + 1) {(x - 2) (x - 5)}
= (x + 1) (x - 2) (x - 5)

प्रश्न 2.
यदि (x + 1) तथा (x - 2) बहुपद x³ + kx² + hx + 6 के गुणनखण्ड हों तो h तथा k के मान ज्ञात कीजिए।
हल:
माना कि f(x)= x³ + kx² + hx + 6 इसके (x + 1) (x - 2) गुणनखण्ड होने चाहिए।
अतः f(- 1) = 0 तथा f(2) = 0
f(- 1) = (- 1)³ + (-1)² + h(-1) + 6 = 0
= - 1 + k - h + 6 = 0
⇒ k - h + 5 = 0 .... (i)
तथा f(2) = (2)³ + k(2)² + h(2) + 6 = 0
= 8 + 4k + 2h + 6 = 0
⇒ 4k + 2h + 14 = 0 .... (ii)

समीकरण (i) व (ii) को हल करने पर
समीकरण (i) को 2 से गुणा करके समीकरण (ii) में जोड़ने पर
2k - 2h = - 10
4k + 2h = -14
6k = -24
k = -\(\frac{24}{6}\) = - 4

k का मान समीकरण (i) में रखने पर
k - h = - 5
- 4 - h = - 5
- h = - 5 + 4 = - 1
h = 1
अत: h = 1 तथा k = - 4 प्राप्त होगा।

प्रश्न 3.
बहुपद f(x) = 3x³ + ax² + 4x + b का एक गुणनखण्ड (x + 2) है। यदि इसमें (x - 3) का भाग दिया जाये तो शेषफल - 5 बचता है। a तथा b के मान ज्ञात कीजिए।
हल:
f(x) = 3x³ + ax² + 4x + b है, इसका गुणनखण्ड (x + 2) है।
अतः f(- 2) = 3(-2)³ + a(-2)² + 4(-2) + b = 0
= - 24 + 4a - 8 + b = 0
या 4a + b - 32 = 0 .......(i)

तथा + 5 जोड़ने पर गुणनखण्ड (x - 3) है अतः
f(x) = 3x² + ax² + 4x + b
f(3) = 3(3)² + a(3)² + 4 × 3 + b + 5
= 81 + 9a + 12 + b + 5 = 0
या 9a + b + 98 = 0 .........(iii)

समीकरण (i) व (ii) को हल करने पर

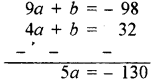
a = \(\frac{130}{5}\) = - 26

a का मान समीकरण (i) में रखने पर
4a + b = 32
4(- 26) + b = 32
- 104 + b = 32
b = 104 + 32 = 136
अतः a = - 26, b = 136

प्रश्न 4.
जाँच कीजिए कि त्रिघात बहुपद p(x) = 3x³ - 5x² - 11x - 3 के शून्यक 3, - 1 और - \(\frac{1}{3}\) हैं। इसके पश्चात् शून्यकों तथा गुणांकों के बीच के सम्बन्ध की सत्यता की जाँच कीजिए।
हल:
दिए हुए बहुपद की ax³ + bx² + cx + d से तुलना करने पर, a = 3, b = - 5, c = - 11, d = - 3 है।
पुनः, p(3) = 3 × 3³ – (5 × 3²)- (11 × 3) - 3
= 81 - 45 - 33 - 3 = 0
p(- 1) = 3 × (- 1)³ - 5 × (- 1)² - 11 × (-1) - 3
= - 3 - 5 + 11 - 3 = 0
p\(\left(-\frac{1}{3}\right)\) = 3 × \(\left(-\frac{1}{3}\right)^{3}\) - 5 × \(\left(-\frac{1}{3}\right)^{2}\) - 11 × \(\left(-\frac{1}{3}\right)\) - 3
= \(-\frac{1}{9}-\frac{5}{9}+\frac{11}{3}-3=-\frac{2}{3}+\frac{2}{3}\) = 0

अतः, 3x³ - 5x² - 11x - 3 के शून्यक 3, - 1 और - \(\frac{1}{3}\) हैं।
इसलिए, हम α = 3, β = - 1 और γ = -\(\frac{1}{3}\) लेते हैं। अब,

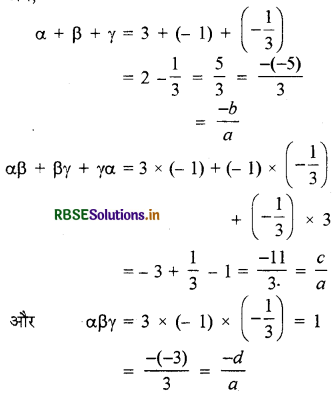
अतः शून्यकों 3, - 1 और \(\frac{1}{3}\) द्वारा भी योगफल व गुणनफल वही है जो कि इनमें है।
∴ बहुपद के शून्यकों और गुणांकों के बीच सम्बन्ध सही है।

प्रश्न 5.
3x³ - x³ - 3x + 5 को x - 1 - x² से भाग दीजिए और विभाजन एल्गोरिथ्म की सत्यता की
हल:
दिए हुए बहुपद मानक रूप में नहीं हैं। भाग की क्रिया करने के लिए, हम सर्वप्रथम भाज्य और भाजक दोनों को उनकी घातों के घटते क्रम में लिखते हैं।

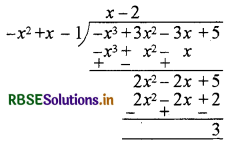
इसलिए, भाज्य = - x³ + 3x² - 3x + 5 तथा भाजक = - x² + x - 1 है। भाग देने की क्रिया दायीं ओर दिखाई गई है। हम यहाँ रुकते हैं, क्योंकि 3 की घात 0, - x² + x - 1 की घात 2 से कम है।
इसलिए भाग की क्रिया करके शेषफल 3 तथा भागफल x - 2 प्राप्त होता है।

अब भाजक × भागफल + शेषफल
= (- x² + x - 1) (x - 2) + 3
= - x³ + x² - x + 2x² - 2x + 2 + 3
= - x + 3x² - 3x + 5
= भाज्य
अतः, विभाजन एल्गोरिथ्म सत्यापित हो गया।

प्रश्न 6.
2x⁴ - 3x³ - 3x² + 6x - 2 के सभी शून्यक ज्ञात कीजिए, यदि आपको इसके दो शून्यक √2 और -√2 ज्ञात हैं।
हल:
क्योंकि दो शून्यक √2 और - √2 हैं, इसलिए (x - √2) (x + √2) = x² - 2 दिए गए बहुपद का एक गुणक है। अतः

भागफल का प्रथम पद \(\frac{2 x^{4}}{x^{2}}\) = 2x² है।
भागफल का दूसरा पद \(\frac{-3 x^{3}}{x^{2}}\) = - 3x है।
भागफल का तीसरा पद \(\frac{x^{2}}{x^{2}}\) = 1 है।
∴ 2x⁴ - 3x³ - 3x² + 6x - 2
= (x² - 2) (2x² - 3x + 1)
अब - 3x को विभक्त करके 2x² - 3x + 1 के गुणनखण्ड (2x - 1) (x - 1) प्राप्त होते हैं। इसलिए, इसके शून्यक x = \(\frac{1}{2}\) और x = 1 द्वारा दिए जाएंगे। अतः, दिए हुए बहुपद के शून्यक √2, -√2 , \(\frac{1}{2}\) और 1 हैं।

प्रश्न 7.
x³ - 3x² + 3x - 5 को x - 1 - x² से भाग कीजिए और विभाजन एल्गोरिथ्म की सत्यता की जाँच कीजिए।
हल:
यहाँ f(x) = x³ - 3x² + 3x - 5 तथा
g(x) = –x² + x - 1
अब

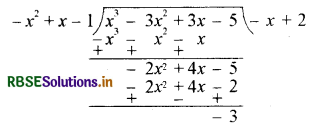
हम पाते हैं कि भागफल q(x) = x + 2 तथा शेषफल r(x) = -3
अब भाज्य = भागफल × भाजक + शेषफल
= (x + 2) (-x² + x - 1) - 3
= x³ - x² + x - 2x² + 2x - 2 - 3
= x³ - 3x² + 3x - 5 = भाज्य
अतः विभाजन एल्गोरिथ्म सत्यापित होता है।