RBSE Class 10 Maths Important Questions Chapter 14 Statistics

Rajasthan Board RBSE Class 10 Maths Important Questions Chapter 14 Statistics Important Questions and Answers.

RBSE Class 10 Maths Chapter 14 Important Questions Statistics

Objective Type Questions

Question 1.
The modal value of any series is
(A) intermediate value
(B) value with the maximum frequency
(C) value with the least frequency
(D) limiting value
Answer:
(B) value with the maximum frequency

Question 2.
The median value of the following series is
520, 20, 340, 190, 35, 800, 1210, 50, 80
(A) 1210
(B) 520
(C) 190
(D) 35
Answer:
(C) 190

Question 3.
If the mean of 5, 7, 9, x is 9, then the value of x is
(A) 11
(B) 15
(C) 18
(D) 16
Answer:
(B) 15

Question 4.
The median of the distribution 2, 3, 4, 7, 5, 1 is
(A) 4
(B) 7
(C) 11
(D) 3.5
Answer:
(D) 3.5

Question 5.
The mode of the distribution 3, 5, 7, 4, 2, 1, 4, 3, 4 is
(A) 7
(B) 4
(C) 3
(D) 1
Answer:
(B) 4

Question 6.
The number of students in a school according to their ages is as follows:

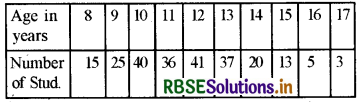
Their mode will be
(A) 41
(B) 12
(C) 3
(D) 17
Answer:
(B) 12

Question 7.
If the mean of the following distribution is 5, then the value of P is

(A) 8
(B) 7.5
(C) 7
(D) 6.5
Answer:
(B) 7.5

Very Short Answer Type Questions

Question 1.
Find the mean of the first ten even natural numbers.
Solution:
First ten even numbers = 2, 4, 6, 8, 10, 12, 14, 16, 18, 20
So Mean \((\bar{x}) = \frac{2+4+6+8+10+12+14+16+18+20}{2}\)
= \(\frac{110}{10}\)
= 11

Question 2.
Write the mode of distribution 3, 5, 7, 4, 2, 1, 4, 3, 4
Solution:
In the above distribution 4 has appeared a maximum number of times, so mode = 4
 
Question 3.
Write the median of the following distribution:

Solution:
\(\frac{n}{2}=\frac{10}{2}\) = 5
Here 5 comes in cumulative frequency 5 where the value is 6.
So median = 6

Question 4.
Write the value of P in the following distribution:

Solution:
10 - 7 = 3 So P = 3

Question 5.
Write the value of a firm the following table:

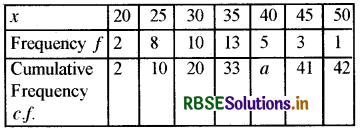
Solution:
a = 33 + 5 = 38

Question 6.
Find the arithmetic mean of the following frequency distribution by the direct method.

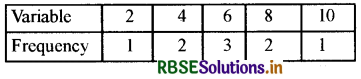
Solution:

∴ Arithmetic Mean = \(\frac{\sum f x}{\sum f}\)
= \(\frac{54}{9}\)
= 6

Question 7.
If the arithmetic means of terms 5, 6, 7, 9, k, and 20 is 11. Then find the value of k.
Solution:
Arithmetic Mean = \(\frac{Sum of terms}{Total terms}\)
⇒ 11 = \(\frac{5+6+7+9+k+20}{6}\)
⇒ 66 = 47 + k
⇒ k = 66 - 47 = 19

Question 8.
In 32 families of a village the number of members is according to the following table:

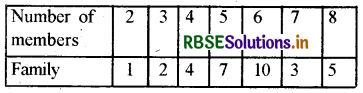
Write the mode of the distribution.
Solution:
Mode = 6
∴ The value of the frequency of 6 is maximum.

Question 9.
A situation of solving any question of mode is as follows:
Z = \(18+\frac{15-8}{30-8-7} \times 5\)
Write the frequency of the modal class.
Solution:
15

Question 10.
Read the following frequency distribution carefully and find the values of b and d.

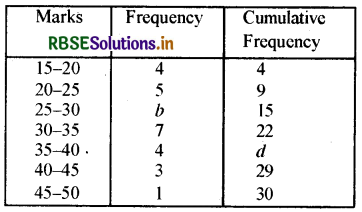
Solution:
From Table it is clear that
9 + b = 15
b = 15 - 9 = 6
and 22 + 4 = d
d = 26

Question 11.
Find the median and mode of the distribution 1, 6, 3, 5, 7, 9, 11, 4, 9.
Solution:
Writing in ascending order 1, 3, 4, 5, 6, 7, 9, 9, 11
Number of terms = 9 which is an odd number
So, Median = \(\left(\frac{9+1}{2}\right)^{\text {th }}\) term
= 5th term
= 6
In the given distribution the frequency of 9 is 2 which is the maximum.
Hence the mode of the given distribution = 9

Question 12.
The mean of a₁, a₂, a₃, ........, a_n is A, then find the value of A.
Solution:

Question 13.
If the mode and arithmetic mean of data are 70 and 100 respectively. Then find the median.
Solution:
Mode = 70
Arithmetic Mean = 100
3 × Median = Mode + 2 × Mean
⇒ 3 × Median = 70 + 2 × 100
⇒ 3 × Median = 70 + 200 = 270
∴ Median = \(\frac{270}{3}\) = 90
Hence Median = 90

Short Answer Type Questions

Question 1.
Find the mean of the following distribution.

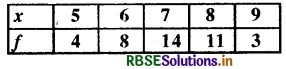
Solution:

Question 2.
Find the mean from the following frequency distribution.

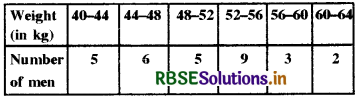
Solution:

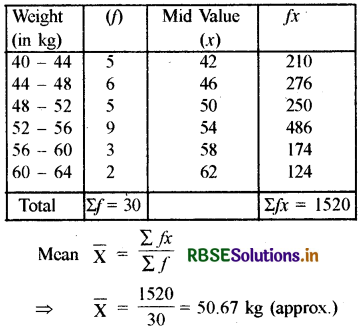
Question 3.
Find the median of the following distribution:

Solution:

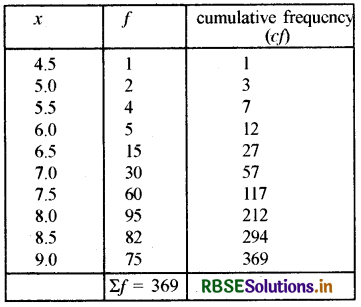
Median = \(\frac{n}{2}\)
= \(\frac{369}{2}\)
= 184.5
184.5 comes under the cumulative frequency 212 which is in the variable = 8
Hence median = 8

Question 4.
The number of sums scored by players of a cricket team is as follows:
57, 17, 26, 91, 115, 26, 83, 41, 57, 0, 26.
Find their mean, mode, and median.
Solution:
(i) Mean \(\overline{\mathbf{X}}=\frac{\sum x}{n}\)
= \(\frac{57+17+26+91+115+26+83+41+57+0+26}{11}\)
= \(\frac{539}{11}\)
= 49 runs
(ii) According the numbers under consideration in ascending order 0, 17, 26, 26, 26, 41, 57, 57, 83, 91, 115.
Here n = 11
So Median (M) = \(\frac{n+1^{\text {th }}}{2}\) number
= \(\frac{11+1^{\text {th }}}{2}\) number
= 6th number
So Median (M) = 41 runs.
(iii)

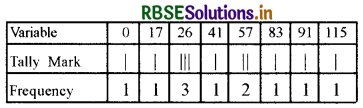
Here frequency 3 is maximum.
The value of its corresponding variable is 26.
So Mode = 26 runs.

Question 5.
If the mean of the following frequency distribution is 7.5 then find the value of P.

Solution:

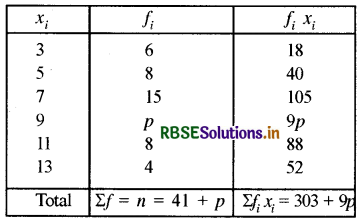
∵ Σf_i = 41 + p and Σf_ix_i = 303 + 9p
∴ Arithmatic Mean = \(\frac{\sum f_{i} x_{i}}{\sum f_{i}}\)
⇒ 7.5 = \(\frac{303+9 p}{41+p}\)
⇒ 7.5 × (41 + p) = 303 + 9p
⇒ 307.5 + 7.5p = 303 + 9p
⇒ 1.5p = 4.5
⇒ p = 3

Question 6.
Find the mean for the following frequency distribution.

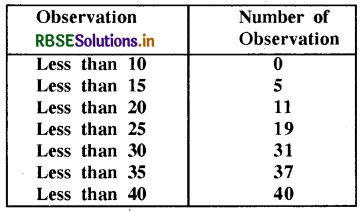
Solution:
We can rewrite the frequency distribution as follows:

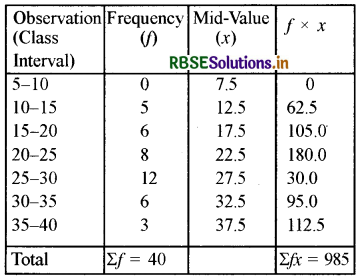
∴ Arithmetic Mean = \(\frac{\sum f x}{\sum f}\)
= \(\frac{985}{40}\)
= 24.63

Long Answer Type Questions

Question 1.
Find the median of the following grouped frequency distribution:

Solution:

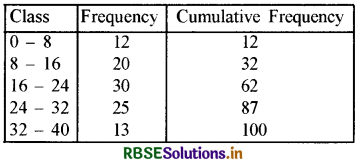
Median number = 100/2 = 50
So median class = (16 - 24)
l = 16, f = 30, C = 32, h = 8

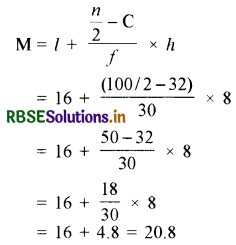
Question 2.
Find the mode of the following frequency distribution:

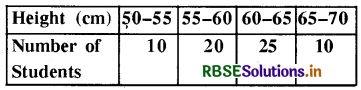
Solution:
Here the maximum frequency of 25 is of class 60-65.
So modal class is = (60 - 65)
So, l = 60, f₁ = 25, f₂ = 10, f₀ = 20, h = 5

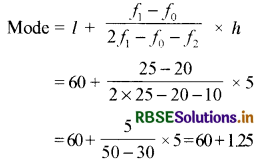
So Mode = 61.25 cm

Question 3.
The median of the following data is 525. If the sum of the frequencies is 100. Then find the values of x and y.

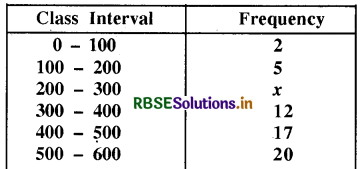
Solution:

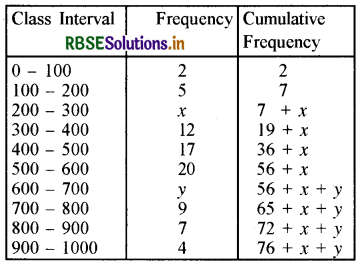
It is given that n = 100.
So, 76 + x + y = 100 i.e., x + y = 24 ......(i)
Median = 525 which lies in the class 500 - 600.
So, l = 500, f = 20, cf = 36 + x, h = 100
∴ Median = \(l+\left(\frac{\frac{n}{2}-c f}{f}\right) \times h\)
⇒ 525 = \(500+\left(\frac{50-36-x}{20}\right) \times 100\)
⇒ 525 - 500 = (14 - x) × 5
⇒ 25 = 70 - 5x
⇒ 5x = 70 - 25 = 45
⇒ x = 9
So from (i), 9 + y = 24
∴ y = 15

Question 4.
The weights of 30 students of a class at the time of their medical check-up were recorded as follows. Find the mean weight of the students.

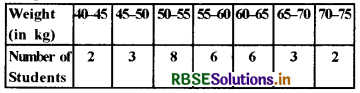
Solution:
Let assumed mean (a) = 57.5 and class size (h) = 5

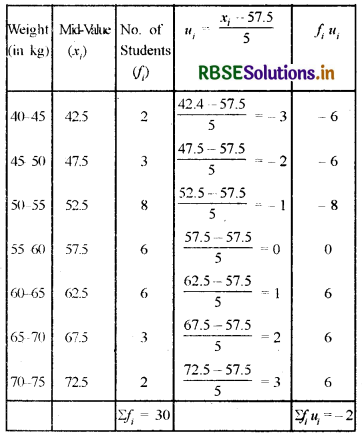
So Mean Weight of Students = 57.167 kg

Question 5.
Find the median from the following data:

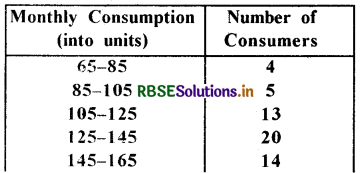
Solution:
Median

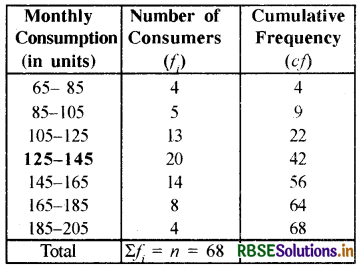
Here, Σf_i = n = 68 Then \(\frac{n}{2}=\frac{68}{2}\) = 34
Which lies in the class interval 125-145
∴ Median Class = 125-145
So l = 125; n = 68; f = 20; c.f = 22 and h = 20

Question 6.
The following data of 100 students of class X at any school in a special session are given. Find the mode of this distribution.

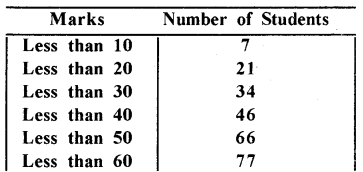
Solution:
Forming the right grouped table

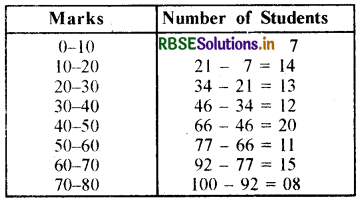
Here it is clear that the maximum frequency (number of students) is 20, where class interval is 40-50.
So here model class will be class interval (40-50)
and here f₁ = 20, f₀ = 12, f₂ = 11, l = 40 and h = 10

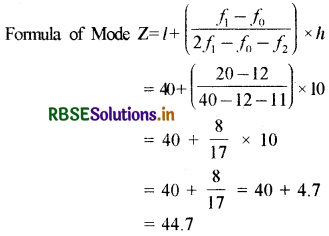
Question 7.
The annual profits earned by 30 shops of a shopping complex in a locality give rise to the following distribution:

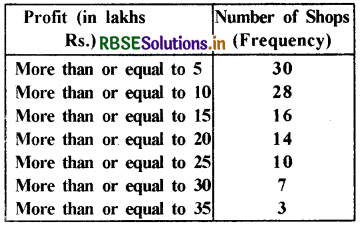
Draw both ogives for the data above. Hence obtain the median profit.
Solution:
We first draw the horizontal and vertical axes, with lower limits of the profit along the horizontal axis, and the cumulative frequency along the vertical axes.
Then, we plot the points (5, 30), (10, 28), (15, 16), (20, 14), (25, 10), (30, 7) and (35, 3).
We join these points with a smooth curve to get the ‘more than' ogive, as shown in Fig.

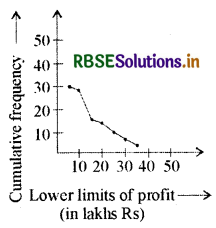
Now, let us obtain the classes, their frequencies, and the cumulative frequency from the table above.

Using these values, we plot the points (10, 2), (15, 14), (20, 16), (25, 20), (30, 23), (35, 27), (40, 30) on the same axes as in Fig. to get the ‘less than' ogive, as shown in Fig.

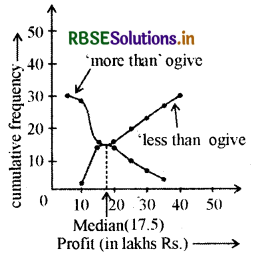
The abcissa of their point of intersection is nearly 17.5, which is the median. This can also be verified by using the formula. Hence, the median profit (in lakhs) is Rs. 17.5.

Question 8.
The distribution of the marks obtained by 30 students on a test of Mathematics is as follows:

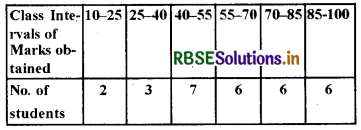
From these data find the mean by assumed mean method and also find the mode.
Solution:

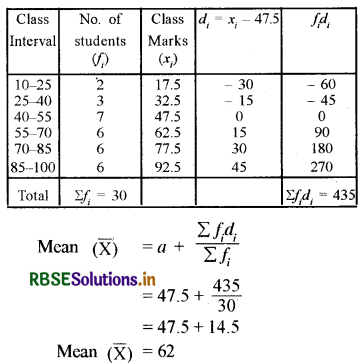
Hence the mean of the marks obtained by the students is 62.
From the given frequency table the maximum frequency is 7.
So modal class = 40 - 55
Lower limit of modal class (l) = 40
Class Size (h) = 15
Frequency of the modal class (f₁) = 17
Frequency of the class just preceding the modal class (f₀) = 3
The frequency of the class just exceeding the modal class (f₂) = 6

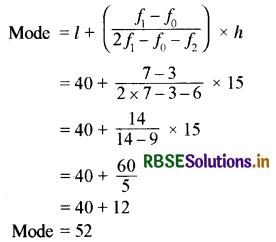
So the mode of the above data is 52.

Question 9.
If the mean of the distribution given below is 50, then find the values of x and y.

Solution:

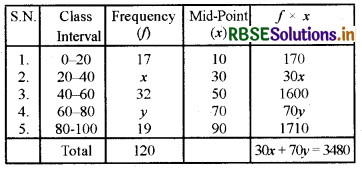
Sum of the products (f × x) = 170 + 30x + 1600 + 70y + 1710
= 30x + 70y + 3480
Sum of the frequencies (f) = 17 + x + 32 + y + 19 = 120
x + y + 68 = 120
x + y = 120 - 68 = 52
x + y = 52 ......(1)
\(\overline{\mathbf{X}}=\frac{\sum \mathrm{f} \times x}{\mathrm{~N}}\)
\(\frac{50}{1}=\frac{30 x+70 y+3480}{120}\)
6000 = 30x + 70y + 3480
30x + 70y = 6000 - 3480 = 2520
3x + 7y = 252 .....(2)
Multiplying (1) by 7 and subtracting from equation (2)

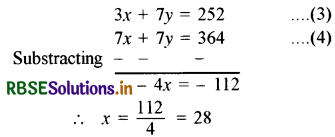
Putting this value of x in equation (1)
x + y = 52
28 + y = 52
y = 52 - 28 = 24
∴ x = 28 and y = 24

Question 10.
In the following distribution calculate mean x from the assumed mean:

Or
Find the mode of the following distribution:

Solution:

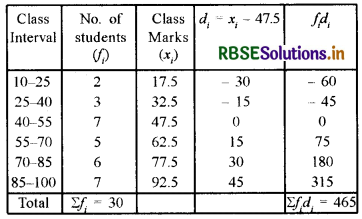
Mean \((\overline{\mathrm{X}}) = a+\frac{\sum f_{i} d_{i}}{\sum f_{i}}\)
Here assumed Mean (a) = 47.5
= 47.5 + \(\frac{465}{30}\)
= 47.5 + 15.5
Mean \((\overline{\mathrm{X}})\) = 63
So Mean by method of assumed Mean = 63
Or
The maximum frequency is 61 in the given data and the corresponding interval is 60-80.
∴ Modal Class = 60 - 80
So Here, l = 60, f₁ = 61, f₀ = 52, f₂ = 38 and h = 20