RBSE Class 10 Maths Important Questions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन

Rajasthan Board RBSE Class 10 Maths Important Questions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Important Questions and Answers.

RBSE Class 10 Maths Chapter 13 Important Questions पृष्ठीय क्षेत्रफल एवं आयतन

वस्तुनिष्ठ प्रश्न

प्रश्न 1.
यदि किसी शंकु की ऊँचाई एवं त्रिज्या क्रमशः 12 सेमी. और 5 सेमी. है तो इसके वक्र पृष्ठ का क्षेत्रफल है
(A) 60π सेमी.²
(B) 65π सेमी.²
(C) 100π सेमी.²
(D) 120π सेमी.²
उत्तर:
(B) 65π सेमी.²

प्रश्न 2.
एक ठोस गोले की त्रिज्या, वक्र पृष्ठ और उसका आयतन क्रमशः r, S व V हैं, उनके बीच में निम्न में से सही सम्बन्ध होगा
(A) 3r = VS
(B) 3rs = V
(C) 3rV = S
(D) 3V = rS
उत्तर:
(D) 3V = rS

प्रश्न 3.
दो गोलों की त्रिज्याएँ क्रमशः r तथा 2r हैं, उनके आयतनों का अनुपात है
(A) 1 : 2
(B) 1 : 4
(C) 1 : 1
(D) 1 : 8
उत्तर:
(D) 1 : 8

प्रश्न 4.
एक बेलनाकार बोतल का व्यास 10 सेमी. है। यदि उसमें 14 सेमी. ऊँचाई तक द्रव भरा हो, तो द्रव का आयतन है-
(A) 1200 घन. सेमी.
(B) 1100 घन सेमी.
(C) 1500 घन सेमी.
(D) 1150 घन सेमी.
उत्तर:
(B) 1100 घन सेमी.

प्रश्न 5.
सीसे के एक घन की कोर 11 सेमी. है। घन को पिघलाकर 1 सेमी. व्यास की गोलियाँ बनाई जा सकती
(A) 2541
(B) 2154
(C) 5245
(D) 1245
उत्तर:
(A) 2541

प्रश्न 6.
14 सेमी. भुजा के एक घन से एक बड़े से बड़ा शंकु काटा जाता है। शंकु का आयतन है
(A) 766.18 घन सेमी.
(B) 817.54 घन सेमी.
(C) 1232 घन सेमी.
(D) 718.66 घन सेमी.
उत्तर:
(D) 718.66 घन सेमी.

अतिलघूत्तरात्मक प्रश्न

प्रश्न 1.
यदि एक अर्द्धगोले का सम्पूर्ण पृष्ठीय क्षेत्रफल 48 वर्ग सेमी. है तो इसकी त्रिज्या की लम्बाई | लिखिए।
हल:
यहाँ 3πr² = 48π
r² = \(\frac{48 \pi}{3 \pi}\) = 16
अतः त्रिज्या = \(\sqrt{16}\) = 4 सेमी.

प्रश्न 2.
एक बेलन के आधार की त्रिज्या 7 सेमी. तथा ऊँचाई 5 सेमी. है। बेलन के वक्रपृष्ठ का क्षेत्रफल लिखिए।
हल:
बेलन का वक्रपृष्ठ क्षेत्रफल = 2πrh
यहाँ r = 7 सेमी.
तथा h = 5 सेमी.

वक्रपृष्ठ का क्षेत्रफल = 2 × \(\frac{22}{7}\) × 7 × 5 वर्ग सेमी.
= 220 वर्ग सेमी.

प्रश्न 3.
यदि एक गोले का सम्पूर्ण पृष्ठीय क्षेत्रफल 36 सेमी. है तो उसकी त्रिज्या ज्ञात कीजिए।
हल:
गोले का सम्पूर्ण पृष्ठीय क्षेत्रफल = 4πr² = 36
r² = \(\frac{36 \times 7}{4 \times 22}=\frac{63}{22}\)
r² = 2.8636
r = 1.69 सेमी.

प्रश्न 4.
एक बेलन जिसकी ऊँचाई 3 सेमी. है तथा बेलन का वक्रपृष्ठ 66 सेमी.² है, तो उसकी त्रिज्या लिखिए।
हल:
बेलन का वक्र पृष्ठ = 2πrh
66 = 2 × \(\frac{22}{7}\) × r × 3
\(\frac{66 \times 7}{2 \times 22 \times 3}\) = r
r = 3.5 सेमी.

प्रश्न 5.
किसी शंकु की ढालू (तिर्यक ) लम्बाई 5 सेमी. तथा ऊँचाई 4 सेमी. है, तो उसका व्यास लिखिए।
हल:
r = \(\sqrt{5^{2}-4^{2}}\)
= \(\sqrt{25-16}=\sqrt{9}\) = 3
व्यास = 2 × 3 = 6 सेमी.

प्रश्न 6.
एक आयताकार कागज की लम्बाई 28 सेमी. तथा चौड़ाई 14 सेमी. है। इस कागज को लम्बाई में मोड़ने पर बने बेलन का वक्रपृष्ठीय क्षेत्रफल लिखिए।
हल:
वक्र पृष्ठ = 28 × 14
= 392 वर्ग सेमी.

प्रश्न 7.
एक ठोस गोले का व्यास 6 सेमी. है। गोले का आयतन लिखिए। (उत्तर π में दीजिए।)
हल:
आयतन = \(\frac{4}{3}\)πr³
= \(\frac{4}{3}\) × π × 3 × 3 × 3
= 36π घन सेमी.

प्रश्न 8.
एक गोले का पृष्ठीय क्षेत्रफल 1000 वर्ग मीटर है। उसकी त्रिज्या लिखिए।
हल:

प्रश्न 9.
एक बेलन और एक शंकु के आधार तथा ऊँचाइयाँ समान हैं। उनके आयतनों का अनुपात ज्ञात कीजिये।
हल:
माना शंकु व बेलन के आधार की त्रिज्या r. cm और ऊँचाई h cm है।

प्रश्न 10.
एक लम्बवृत्तीय बेलन की ऊँचाई और उसकी त्रिज्या समान है। उसके सम्पूर्ण पृष्ठ एवं वक्र पृष्ठ में अनुपात ज्ञात कीजिये।
हल:
माना बेलन की ऊँचाई h और उसकी त्रिज्या r है।
∴ h = r दिया है।

प्रश्न 11.
एक ठोस अर्द्धगोले की त्रिज्या 7 cm. है। इसका सम्पूर्ण पृष्ठीय क्षेत्रफल ज्ञात कीजिये।
हल:
r = 7 cm.
अत:अर्द्धगोले का सम्पूर्ण पृष्ठ = 3πr²
= 3 × \(\frac{22}{7}\) × 7 × 7
= 66 × 7 = 462 cm²

प्रश्न 12.
एक ठोस अर्धगोले का सम्पूर्ण पृष्ठीय क्षेत्रफल 462 वर्ग सेमी. है। इसकी त्रिज्या ज्ञात कीजिए।
हल:
अर्धगोले का सम्पूर्ण पृष्ठीय क्षेत्रफल = 3πr²
मान रखने पर 462 = 3 × \(\frac{22}{7}\) × r²
इसलिए r² = \(\frac{462 \times 7}{3 \times 22}=\frac{21 \times 7}{3}\) = 7 × 7
r² = 49
r = \(\sqrt{49}\) = 7 सेमी.
अतः अर्धगोले की त्रिज्या = 7 सेमी.

लघूत्तरात्मक प्रश्न

प्रश्न 1.
यदि 11 सेमी. × 3.5 सेमी. × 2.4 सेमी. मोम के एक घनाभ से 2.8 सेमी. व्यास की एक मोमबत्ती बनाई जाती है। मोमबत्ती की लम्बाई ज्ञात कीजिए।
हल:
घनाभाकार मोमबत्ती का आयतन = (ल. × चौ. × ॐ.) घन सेमी.
= 11 × 3.5 × 2.4 घन सेमी.
बेलनाकार मोमबत्ती का आयतन = πr²h
अर्थात् πr²h = 11 × 3.5 × 2.4 (∵ दोनों का आयतन बराबर होगा।)
h = \(\frac{11 \times 3.5 \times 2.4}{\pi \times r^{2}}\)
h = \(\frac{11 \times 3.5 \times 2.4 \times 7}{22 \times 1.4 \times 1.4}\)
[∵ r = \(\frac{2.8}{2}\)= 14]
h = 15 सेमी.

प्रश्न 2.
व्यास 1 cm. वाली 8 cm. लम्बी ताँबे की एक छड़ को एकसमान चौड़ाई वाले 18 m लम्बे एक तार के रूप में खींचा जाता (बदला जाता) है। तार की मोटाई ज्ञात कीजिए।
अथवा
1 सेमी. व्यास वाली 8 सेमी. लम्बी ताँबे की छड़ को एक समान चौड़ाई वाले 18 मी. लम्बे एक तार के रूप में खींचा जाता (बदला जाता है)। तार की मोटाई ज्ञात कीजिए।
हल:
छड़ का आयतन = π × \(\left(\frac{1}{2}\right)^{2}\) × 8 cm³ = 2π cm³
समान आयतन वाले तार की लम्बाई = 18 m = 1800 cm.
यदि तार के अनुप्रस्थ काट (cross-section) की त्रिज्या है, तो तार का आयतन = π × r² × 1800 cm
अतः π × r² × 1800 = 2π
∵ दोनों का आयतन बराबर होगा। अर्थात् r² = \(\frac{1}{900}\)
अर्थात् r = \(\frac{1}{30}\) cm.
अतः, तार के अनुप्रस्थ काट का व्यास, तार की चौड़ाई \(\frac{1}{15}\) cm., अर्थात् 0.67 mm (लगभग)

प्रश्न 3.
पानी से पूरी भरी हुई एक अर्द्धगोलाकार टंकी को एक पाइप द्वारा 3\(\frac{4}{7}\) लीटर प्रति सेकण्ड की दर से खाली किया जाता है। यदि टंकी का व्यास 3 m है, तो वह कितने समय में आधी खाली हो जाएगी? (π = \(\frac{22}{7}\) लीजिए।)
हल:
अर्द्धगोलाकार टंकी की त्रिज्या = \(\frac{3}{2}\)m
अतः, टंकी का आयतन = \(\frac{2}{3} \times \frac{22}{7} \times\left(\frac{3}{2}\right)^{3}\) m³
= \(\frac{99}{14}\)m³
उस पानी का आयतन, जिसे खाली किया जाना है
= \(\frac{1}{2} \times \frac{99}{14}\) m³
= \(\frac{99}{28}\) × 1000
= \(\frac{99000}{28}\) लीटर
अब, \(\frac{25}{7}\) लीटर पानी खाली होता है 1 सेकण्ड में, इसलिए \(\frac{99000}{28}\) लीटर पानी खाली होगा \(\frac{99000}{28} × \frac{7}{25}\) सेकण्ड में, अर्थात् 16.5 मिनट में।

प्रश्न 4.
हनुमप्पा और उसकी पत्नी गंगाम्मा गन्ने के रस से गुड़ बना रहे हैं। उन्होंने गन्ने के रस को गर्म करके राब (शीरा) बना ली है, जिसे शंकु के छिन्नक के आकार के साँचों में डाला जाता है, जिनमें से प्रत्येक के दोनों वृत्तीय फलकों के व्यास क्रमशः 30 cm. और 35 cm. हैं तथा साँचे की ऊर्ध्वाधर ऊँचाई 14 cm. है ( देखिए आकृति)। यदि 1 cm राब का द्रव्यमान लगभग 1.2g है तो प्रत्येक साँचे में भरी जा सकने वाली राब का द्रव्यमान ज्ञात करें। (π = \(\frac{22}{7}\) लीजिए)

हल:
चूँकि साँचा एक शंकु के छिन्नक के आकार का | है, इसलिए इसमें भरी जा सकने वाली राब का आयतन
= \(\frac{\pi}{3}\)h(r₁² + r₂² + r₁r₂),
जहाँ r₁, बड़े आधार की त्रिज्या है और r₂, छोटे आधार की त्रिज्या है।

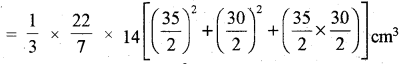
= 11641.7 cm³
यह दिया है कि 1 cm³ राब का द्रव्यमान 1.2 g है। अतः प्रत्येक साँचे में भरी जा सकने वाली राब का भार द्रव्यमान
= (11641.7 × 1.2) g
= 13970.04g
= 13.97kg. = 14kg. (लगभग)

प्रश्न 5.
20 मीटर गहरा और 7 मीटर व्यास का एक कुआँ खोदा गया है। इससे निकली मिट्टी से 22 मीटर × 14 मीटर माप का एक चबूतरा बनाया गया है। चबूतरे की ऊँचाई ज्ञात कीजिए। .
हल:
चूँकि कुआँ बेलनाकार है, इसकी गहराई (ऊँचाई) है = 20 मीटर
इसकी त्रिज्या है = \(\frac{7}{2}\) मीटर = 3.5
मीटर बेलनाकार कुएँ का आयतन = चबूतरे का आयतन बेलनाकार कुएँ का आयतन है = πr²h
= \(\frac{22}{7} \times \frac{7}{2} \times \frac{7}{2}\) × 20 घन मीटर
= 22 × 7 × 5 घन मीटर
= 770 घन मीटर
अतः चबूतरे का आयतन = 770 घन मीटर

= 2.5 मीटर

प्रश्न 6.
धातु के एक गोले का व्यास 6 सेमी. है। गोले को पिघलाकर एक समान वृत्तीय अनुप्रस्थ-परिच्छेद वाला तार बनाया गया है। यदि तार की लम्बाई 36 मीटर हो, तो उसकी त्रिज्या ज्ञात कीजिए।
हल:
गोले का व्यास = 6 सेमी.
त्रिज्या (r) = \(\frac{6}{2}\) = 3 सेमी.
तार की लम्बाई (h) = 36 मीटर = 3600 cm.
गोले का आयतन = \(\frac{4}{3}\)πr³ धन इकाई
= \(\frac{4}{3} \times \frac{22}{7}\) × (3)³ घन सेमी.
तथा बेलन का आयतन = πr²h
अतः दोनों के आयतन समान होंगे।

प्रश्न 7.
एक शंकु, जिसकी ऊँचाई 24 सेमी. और आधार की त्रिज्या 6 सेमी. है., प्रतिमा बनाने वाली चिकनी मिट्टी से बनाया गया है। एक बच्चा उसको पुनः गोले का आकार देता है। गोले की त्रिज्या ज्ञात कीजिए।
हल:
शंकु की ऊँचाई (h) = 24 सेमी.
तथा त्रिज्या (r) = 6 सेमी.

∴ शंकु का आयतन = \(\frac{1}{3}\)πr³ घन इकाई
= \(\frac{4}{3}\) × π × (6)³ × 24 घन सेमी.
गोले का आयतन = 4
प्रश्नानुसार, गोले का आयतन = शंकु का आयतन

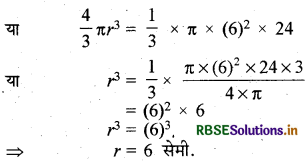
अतः गोले की त्रिज्या 6 सेमी.

प्रश्न 8.
दो घनों, जिनमें से प्रत्येक का आयतन 27 सेमी. है, के संलग्न फलकों को मिलाकर एक ठोस बनाया जाता है। प्राप्त घनाभ का पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
हल:
माना कि धन की प्रत्येक भुजा = x cm. है।
घन का आयतन = 27 cm.3
⇒ x³ = 27
⇒ x = \(\sqrt[3]{27}\)
= \(\sqrt[3]{3 \times 3 \times 3}\)
x = 3 cm.

∴ घन की भुजा =3 cm.
∴ दोनों घनों को जोड़ने पर वह घनाभ बन जाएगा। इसकी लम्बाई = 2x cm.
= 2 × 3 = 6 cm.
चौड़ाई = x = 3 cm.
तथा ऊँचाई = x = 3 cm.
अब घनाभ का पृष्ठीय क्षेत्रफल = 2 [ल. × चौ. + चौ. × ऊँ. + ऊँ. × ल.]
= 2 [6 × 3 + 3 × 3 + 3 × 6]
= 2 [18 + 9 + 18]
= 2[45] = 90 cm.²
अर्थात् घनाभ का क्षेत्रफल 90 cm.² है।

प्रश्न 9.
पानी से भरी हुई एक अर्धगोलाकार टंकी को एक पाइप द्वारा 5 लीटर प्रति सेकंड की दर से खाली किया जाता है। यदि टंकी का व्यास 3.5 मी. है, तो वह कितने समय में आधी खाली हो जाएगी? ।
हल:
अर्ध गोले का आयतन = \(\frac{2}{3}\)πr³
यहाँ टंकी की त्रिज्या = \(\frac{3.5}{2}\)मी.

5 लीटर पानी खाली होने का समय = 1 सैकण्ड
∴ 1 लीटर पानी खाली होने का समय = \(\frac{1}{5}\) सैकण्ड
∴ \(\frac{110 \times 1225}{24}\) लीटर पानी खाली होने का समय = \(\frac{1}{5} \times \frac{110 \times 1225}{24}\) सैकण्ड
= \(\frac{110 \times 245}{24}\) सैकण्ड
= \(\frac{110 \times 245}{24 \times 60}\) मिनट = \(\frac{11 \times 245}{144}\) मिनट
= 18.7 मिनट (लगभग)
अर्थात् वह टंकी 18.7 मिनट में आधी खाली हो जाएगी।

प्रश्न 10.
1 सेमी त्रिज्या और 2 सेमी लम्बी तांबे की एक छड़ को एक समान चौड़ाई वाले 18 मीटर लम्बे एक तार के रूप में बदला जाता है। तार की मोटाई ज्ञात कीजिए।
हल:
छड़ का आयतन = π × (1)² × 2 cm.³ = 2π cm.³
समान आयतन वाले तार की लम्बाई = 18 m. = 1800 cm.
यदि तार के अनुप्रस्थ काट की त्रिज्या r है तो तार का आयतन = π × r² × 1800 cm.²
अतः π × r² × 1800 = 2π [∵: दोनों का आयतन बराबर होगा।]
अर्थात् r² = \(\frac{1}{900}\)
अर्थात् r = \(\frac{1}{30}\)

अतः तार के अनुप्रस्थ काट का व्यास अर्थात् मोटाई
= 2 × \(\frac{1}{30}\) cm.
= \(\frac{1}{15}\) cm.

प्रश्न 11.
एक चाँदी के घनाभ जिसकी विमाएँ 8 cm. × 9 cm. × 11 cm. को पिघलाकर समान त्रिज्या के सात गोले बनाए गए हैं। एक चाँदी के गोले की त्रिज्या ज्ञात कीजिए।
हल:
चाँदी के घनाभ का आयतन = ल. × चौ. × ॐ.
= 8 × 9 × 11
= 792 घन सेमी.

इस आयतन में से समान त्रिज्या के सात गोले बनाये गये हैं। माना प्रत्येक गोले की त्रिज्या R सेमी. है। अतः
प्रश्नानुसार,
चाँदी के घनाभ का आयतन = 7 × गोले का आयतन
792 = 7 × \(\frac{4}{3}\)πR³
792 = 7 × \(\frac{4}{3} \times \frac{22}{7}\) × R³
792 = \(\frac{88 R^{3}}{3}\)
∴ R³ = \(\frac{792 \times 3}{88}\)
= 9 × 3 = 27
R = (27)^1/3 = (33)^1/3 = 31
R = 3 सेमी.
अतः चाँदी के गोले की त्रिज्या = 3 सेमी.

निबन्धात्मक प्रश्न

प्रश्न 1.
सीसे के 3 सेमी. व्यास वाले एक गोले को पिघलाकर तीन गोलियों में परिवर्तित किया जाता है। इनमें से दो गोलियों के व्यास 1 सेमी. और 1.5 सेमी. हैं। तीसरी गोली का व्यास ज्ञात कीजिए।
हल:
माना तीसरी गोली की त्रिज्या r सेमी. है।
∵ गोले का व्यास = 3 सेमी.

या त्रिज्या = \(\frac{3}{2}\) = 1.5 सेमी.
पहली गोली का व्यास = 1 सेमी.

∴ त्रिज्या = \(\frac{1}{2}\) सेमी. = 0.5 सेमी.
दूसरी गोली का व्यास = 1.5 सेमी.
त्रिज्या = \(\frac{1.5}{2}\) = 0.75 सेमी.

∵ 1.5 सेमी. त्रिज्या के गोले को पिघलाकर तीन गोलियाँ बनाई गई हैं।
∴ तीन गोलियों का कुल आयतन = गोले का आयतन

अत: तीसरी गोली का व्यास \(\frac{1}{2}\)(181)^1/3 होगा।

प्रश्न 2.
धातु से बनी एक खुली बाल्टी शंकु के एक छिन्नक के आकार की है, जो उसी धातु के बने एक खोखले बेलनाकार आधार पर आरोपित है ( देखिए आकृति)। इस बाल्टी के दोनों वृत्ताकार सिरों के व्यास 45 cm. और 25 cm. हैं तथा बाल्टी की कुल ऊर्ध्वाधर ऊँचाई 40 cm. और बेलनाकार आधार की ऊँचाई 6 cm. है। इस बाल्टी को बनाने में प्रयुक्त धातु की चादर का क्षेत्रफल ज्ञात कीजिए जबकि हम बाल्टी की मुठिया (या हत्थे) को इसमें सम्मिलित नहीं कर रहे हैं। साथ ही, उस पानी का आयतन ज्ञात कीजिए जो इस बाल्टी में धारण कर सकता है। (π = \(\frac{22}{7}\) लीजिए)

हल:
बाल्टी की कुल ऊँचाई = 40 cm. है, जिसमें आधार की ऊँचाई भी सम्मिलित है।
इसलिए शंकु के छिन्नक की ऊँचाई (40 - 6) cm. = 34 cm. है।
अतः, शंकु के छिन्नक की तिर्यक ऊँचाई l = \(\sqrt{h^{2}+\left(r_{1}-r_{2}\right)^{2}}\)
जहाँ r₁ = 22.5 cm., r₂ = 12.5 cm. और h = 34 cm.
अतः l = \(\sqrt{34^{2}+(22.5-12.5)^{2}}\) cm.
= \(\sqrt{34^{2}+10^{2}}\) = 35.44 cm.
इसमें प्रयुक्त धातु की चादर का क्षेत्रफल
= शंकु के छिन्नक का वक्र पृष्ठीय क्षेत्रफल + वृत्तीय आधार का क्षेत्रफल + बेलन का वक्र पृष्ठीय क्षेत्रफल
= [π × 35.44 (22.5 + 12.5) + π × (12.5)2 + 2π × 12.5 × 6] .cm²
= \(\frac{22}{7}\)[1240.4 + 156.25 + 150] cm²
= 4860.9 cm²

अब, बाल्टी में आ सकने वाले पानी का आयतन, जिसे बाल्टी की धारिता भी कहते हैं ।
= \(\frac{\pi \times h}{3}\) × (r₁² + r₂² + r₁r₂)
= \(\frac{22}{7} \times \frac{34}{3}\) × [(22.5)2 + (12.5)2 + 22.5 × 12.5] cm²
= \(\frac{22}{7} \times \frac{34}{3}\) × 943.75
= 33615.48 cm³ ≈ 33.62 लीटर (लगभग)
∵ 1000 cm³ = 1 लीटर
अतः प्रयुक्त धातु की चादर का क्षेत्रफल 4860.9 cm² तथा पानी का आयतन 33.62 लीटर होगा।

प्रश्न 3.
एक शंकु के छिन्नक, जो 45 cm. ऊँचा है, के सिरों की त्रिज्याएँ 28 cm. और 7 cm. हैं। इसका आयतन, वक्र पृष्ठीय क्षेत्रफल और सम्पूर्ण पृष्ठीय क्षेत्रफल ज्ञात कीजिए। (π = \(\frac{22}{7}\) लीजिए)
हल:
इस छिन्नक को दो लम्ब वृत्तीय शंकुओं OAB और OCD के अन्तर के रूप में देखा जा सकता है (देखिए आकृति)। माना कि सेन्टीमीटर में शंकु OAB की ऊँचाई h₁, है और तिर्यक ऊँचाई l₁ है, अर्थात् OP = h₁, और OA = OB = l₁, है। माना कि शंकु OCD की सेन्टीमीटर में ऊँचाई h₂, और तिर्यक ऊँचाई l₂ है।

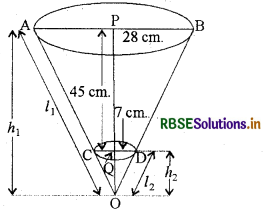
हमें r₁ = 28 cm., r₂ = 7 cm. और छिन्नक की ऊँचाई (h) = 45 cm.
तथा h₁ = 45 + h₂ .... (i)
सबसे पहले हमें क्रमशः शंकुओं OAB और OCD की ऊँचाइयों h, और h, को निर्धारित करना आवश्यक है।

चूँकि त्रिभुज OPB और OQD समरूप हैं, इसलिए
\(\frac{h_{1}}{h_{2}}=\frac{28}{7}=\frac{4}{1}\)
या h₁ = 4h₂ .... (ii)

समीकरण (i) तथा (ii) को हल करने पर
4h₂ = 45 + h₂
या 3h₂ = 45
या h₂ = \(\frac{45}{3}\) = 15 cm.

समीकरण (i) से h₁ = 45 + 15 = 60 cm.
अब, छिन्नक का आयतन
= शंकु OAB का आयतन - शंकु OCD का आयतन

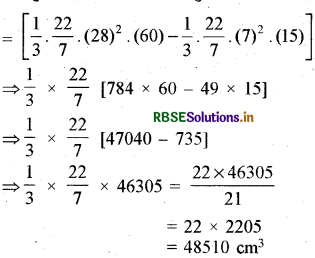
शंकु OAB तथा शंकु OCD की तिर्यक ऊँचाइयाँ क्रमशः l₁, और l₂ नीचे दर्शाए अनुसार प्राप्त होती हैं :

अब, छिन्नक का सम्पूर्ण पृष्ठीय क्षेत्रफल = वक्र पृष्ठीय क्षेत्रफल + πr₁² + πr₂²
= 5461.5 cm² + \(\frac{22}{7}\) (28)² cm² + \(\frac{22}{7}\) (7)² cm²
= 5461.5 cm² + 2464 cm² + 154 cm²
= 8079.5 cm²
अर्थात् छिन्नक का आयतन 48510 cm², वक्र पृष्ठीय क्षेत्रफल 5461.5 cm² तथा सम्पूर्ण पृष्ठीय क्षेत्रफल 8079.5 cm² होगा।

प्रश्न 4.
7 सेमी. व्यास वाला एक गोला पानी से आंशिक भरे एक बेलनाकार बर्तन में डाला जाता है। बर्तन के आधार का व्यास 14 सेमी. है। यदि गोला पूर्णतया पानी में डूबा हो, तो पानी का स्तर कितना ऊपर उठ जायेगा?
हल:
गोले का व्यास = 7 सेमी. .
∴ गोले की त्रिज्या = \(\frac{7}{2}\) = 3.5 सेमी.
∴ गोले का आयतन = \(\frac{4}{3}\)πr³
= \(\frac{4}{3}\)π × (3.5)³ घन सेमी. ..... (i)
पुनः बेलनाकार बर्तन के आधार का व्यास = 14 सेमी.

∴ त्रिज्या (r) = \(\frac{14}{2}\) = 7 सेमी.
∴ बेलन का आयतन = πr²h
= π (7)² × h . .... (ii)

समीकरण (i) तथा (ii) को बराबर करने पर

अतः गोला डालने पर पानी का स्तर \(\frac{7}{6}\) सेमी. ऊपर उठ जायेगा।

प्रश्न 5.
एक शंकु के छिन्नक जो 45 cm. ऊँचा हैं, के सिरों की त्रिज्यायें 28 cm. और 7. cm. हैं। इसका आयतन ज्ञात कीजिये।
हल:
माना कि शंकु OAB की ऊँचाई h₁, है । अर्थात्
OP = h₁

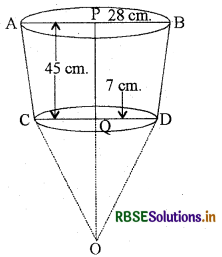
माना कि शंकु OCD की ऊँचाई h₂ है।
अर्थात् OQ = h₂
यहाँ पर r₁ = 28 cm., r₂ = 7 cm.
और छिन्नक की ऊँचाई h = 45 cm OP = h₁ OQ = h₂
∴ h₁ = 45 + h₂ .....(i)

ΔOPB और ΔOQD समरूप हैं
\(\frac{h_{1}}{h_{2}}=\frac{28}{7}\) = 4
h₁ = 4h₂ .....(ii)

समीकरण (i) तथा (ii) से
⇒ 3h₂ = 45
⇒ h₂ = 45
⇒ h₂ = \(\frac{45}{3}\) = 15 cm

समीकरण (ii) से h₁ = 4 × 15 = 60 cm.
छिन्नक का आयतन = शंकु OAB का आयतन - शंकु OCD का आयतन

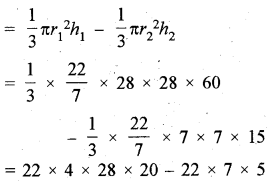
= 49280 - 770 = 48510 cm³
अर्थात् छिन्नक का आयतन 48510 cm² होगा।

प्रश्न 6.
4.2 सेमी. त्रिज्या वाले धातु के एक गोले को पिघलाकर 7 सेमी. त्रिज्या वाले बेलन के रूप में ढाला जाता है। बेलन की ऊँचाई ज्ञात कीजिए।
हल:
प्रश्नानुसार,
गोले की त्रिज्या (r) = 4.2 सेमी.
बेलन की त्रिज्या (R) = 6 सेमी.
माना कि बेलन की ऊँचाई = H सेमी.
ढालने पर आयतन पहले जितना ही रहता है। अर्थात् यहाँ
गोले का आयतन = बेलन का आयतन
\(\frac{4}{3}\)πr³ = πR³H

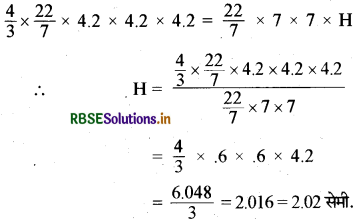
∴ बेलन की ऊँचाई (H) = 2.02 सेमी. (लगभग)