RBSE Class 10 Maths Important Questions Chapter 13 Surface Areas and Volumes

Rajasthan Board RBSE Class 10 Maths Important Questions Chapter 13 Surface Areas and Volumes Important Questions and Answers.

RBSE Class 10 Maths Chapter 13 Important Questions Surface Areas and Volumes

Objective Type Questions

Question 1.
If the height and radius of a cone are respectively 12 cm and 5 cm, then the area of its curved surface is
(A) 60π cm²
(B) 65π cm²
(C) 100π cm²
(D) 120π cm²
Answer:
(B) 65π cm²

Question 2.
If the radius, curved surface, and volume of a solid sphere are respectively r, S, and V, then the correct relation among them will be
(A) 3r = VS
(B) 3rS = V
(C) 3rV = S
(D) 3V = rS
Answer:
(D) 3V = rS

Question 3.
The radii of spheres are r and 2r respectively, the ratio of their volume is
(A) 1 : 2
(B) 1 : 4
(C) 1 : 1
(D) 1 : 8
Answer:
(D) 1 : 8

Question 4.
The diameter of a cylindrical bottle is 10 cm. If it is filled with a liquid upto a height of 14 cm, then the volume of the liquid is
(A) 1200 cubic cm
(B) 1100 cubic cm
(C) 1500 cubic cm
(D) 1150 cubic cm
Answer:
(B) 1100 cubic cm

Question 5.
The edge of a cube of lead is 11 cm. By melting the cube the shorts of diameter 1 cm can be formed
(A) 2541
(B) 2154
(C) 5245
(D) 1245
Answer:
(A) 2541

Question 6.
From a cube of side 14 cm, the largest cone is cut. The volume of the cone is
(A) 766.18 cubic cm
(B) 817.54 cubic cm
(C) 1232 cubic cm
(D) 718.66 cubic cm
Answer:
(D) 718.66 cubic cm

Very Short Answer Type Questions

Question 1.
If the total surface area of a hemisphere is 48π sq cm, then write the length of its radius.
Solution:
Here 3πr² = 48π
⇒ r² = \(\frac{48 \pi}{3 \pi}\) = 16
So Radius = \(\sqrt{16}\) = 4 cm

Question 2.
The radius of the base of a cylinder is 7 cm and the height is 5 cm. Write the area of the curved surface of the cylinder.
Solution:
Curved surface area of cylinder = 2πrh
Here r = 7 cm and h = 5 cm
∴ Curved surface area = 2 × \(\frac{22}{7}\) × 7 × 5 cm² = 220 cm²

Question 3.
If the total surface area of a sphere is 36 cm² then find its radius.
Solution:
Total surface area of sphere = 36
4πr² = 36
⇒ r² = \(\frac{36 \times 7}{4 \times 22}=\frac{63}{22}\)
⇒ r² = 2.8636
⇒ r = 1.69 cm

Question 4.
Write the radius of a cylinder whose height is 3 cm and whose curved surface is 66 cm².
Solution:
Curved surface area of cylinder = 2πrh
⇒ 66 = 2 × \(\frac{22}{7}\) × r × 3
⇒ r = \(\frac{66 \times 7}{2 \times 22 \times 3}\)
⇒ r = 3.5 cm

Question 5.
The slant height of a cone is 5 cm and the height is 4 cm, then write its diameter.
Solution:
r = \(\sqrt{5^{2}-4^{2}}\)
⇒ r = \(\sqrt{25-16}\)
⇒ r = 3
So Diameter = 2 × 3 = 6 cm

Question 6.
The radius of a solid hemisphere is 7 cm. Find its total surface area.
Solution:
r = 7 cm
So Total surface area of hemisphere = 3πr²
= 3 × \(\frac{22}{7}\) × 7 × 7
= 66 × 7
= 462 cm²

Short Answer Type Questions

Question 1.
From a cuboid 11 cm × 3.5 cm × 2.4 cm of the way a candlestick of diameter 2.8 cm is made. Find the length of the candlestick.
Solution:
Volume of cuboidal wax = (Length × Breadth × Height) cubic cm
= 11 × 3.5 × 2.4 cubic cm
Now volume of Cylindrical candlestick = πr²h
i.e., πr²h = 11 × 3.5 × 2.4 (∵ The volume of both will be equal)
∴ h = \(\frac{11 \times 3.5 \times 2.4}{\pi \times r^{2}}\)
⇒ h = \(\frac{11 \times 3.5 \times 2.4 \times 7}{22 \times 1.4 \times 1.4}\) [∵  r = \(\frac{2.8}{2}\) = 1.4]
⇒ h = 15 cm

Question 2.
A copper rod of diameter 1 cm and length 8 cm is drawn into a wire of uniform width and 18 m length (transformed). Find the thickness of the wire.
OR
A copper rod of diameter 1 cm and length 8 cm is drawn (transformed) in the form of a wire of uniform width and 18 m length. Find the thickness of the wire.
Solution:
Voume of rod = π × \(\left(\frac{1}{2}\right)^{2}\) × 8 cm³ = 2π cm³
Length of wire of uniform width = 18 m = 1800 cm
If the radius of the transverse cross-section of the wire is r,
then the volume of the wire = π × r² × 1800 cm³
So π × r² × 1800 = 2π
The volume of both will be the same
i.e. r² = \(\frac{1}{900}\)
i.e. r = \(\frac{1}{30}\) cm
Hence the diameter of the transverse cross-section of the wire, i.e., the thickness of the wire is \(\frac{1}{15}\) cm., i.e. 0.67 mm (approx.)

Question 3.
A hemispherical tank full of water is emptied by a pipe at the rate of 3\(\frac{4}{7}\) litres per second. How much time will it take to empty half the tank, if it is 3m in diameter? (Take π = \(\frac{22}{7}\))
Solution:
The radius of the hemispherical tank = \(\frac{3}{2}\)

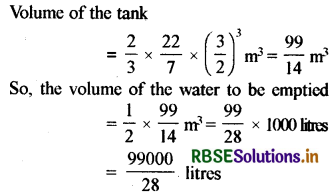
Since, \(\frac{25}{7}\) litres of water are emptied in 1 second, \(\frac{99000}{28}\) litres of water will be emptied in \(\frac{99000}{28} \times \frac{7}{25}\) seconds, i.e., in 16.5 minutes.

Question 4.
Hanumappa and his wife Gangamma are busy making jaggery out of sugarcane juice. They have processed the sugarcane juice to make the molasses, which is poured into moulds in the shape of a frustum of a cone having the diameters of its two circular faces as 30 cm and 35 cm and the vertical height of the mould is 14 cm (see Fig.). If each cm3 of molasses has a mass of about 1.2 g, find the mass of the molasses that can be poured into each mould. (Take π = \(\frac{22}{7}\))

Solution:
Since the mould is in the shape of a frustum of a cone, the quantity (volume) of molasses that can be poured into it = \(\frac{\pi}{3} h\left(r_{1}^{2}+r_{2}^{2}+r_{1} r_{2}\right)\)
where, r₁ is the radius of the larger base and r₂ is the radius of the smaller base = \(\frac{1}{3} \times \frac{22}{7} \times 14\left[\left(\frac{35}{2}\right)^{2}+\left(\frac{30}{2}\right)^{2}+\left(\frac{35}{2} \times \frac{30}{2}\right)\right]\) cm³
= 11641.7 cm³
It is given that 1 cm³ of molasses has a mass of 1.2 g.
So, the mass of the molasses that can be poured into each mould = (11641.7 × 1.2) g
= 13970.04 g
= 13.97 kg
= 14 kg (approx.)

Question 5.
A well 20 m deep and of 7 m diameter is dug. From the earth from digging an embankment of measure 22 m × 14 m is formed. Find the height of the embankment.
Solution:
Since the well is cylindrical, Therefore its depth (height) is = 20 m
Its radius is = \(\frac{7}{2}\) m = 3.5 m
Volume of cylindrical well = Volume of embankment
Volume of cylindrical well is = πr²h
= \(\frac{22}{7} \times \frac{7}{2} \times \frac{7}{2} \times 20\) cubic m
= 22 × 7 × 5 cubic m
= 770 cubic m
So, Volume of embankment = 770 cubic m

Question 6.
The diameter of a sphere of metal is 6 cm. By melting the sphere a wire of uniform circular transverse cross-section is made. If the length of the wire is 36 m, then find its radius.
Solution:
∵ Diameter of sphere = 6 cm
∴ Radius (r) = \(\frac{6}{2}\) = 3 cm
Length of wire (h) = 36 m = 3600 cm
Volume of sphere = \(\frac{4}{3}\) πr³ cubic units
= \(\frac{4}{3} \times \frac{22}{7} \times(3)^{3}\) cubic cm
and Volume of cylinder = πr²h
Hence both the volumes will be the same

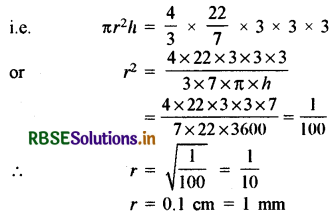
Question 7.
A cone of the height of 24 cm and a radius of the base of 6 cm was made-up modelling clay. A child reshapes it in the form of a sphere. Find the radius of the sphere.
Solution:
Height of cone (h) = 24 cm
and radius (r) = 6 cm
∴ Volume of cone = \(\frac{1}{3}\) πr²h cubic units
= \(\frac{1}{3}\) × π × (6)² × 24 cubic cm
Volume of sphere = \(\frac{4}{3} \pi r^{3}\)
According to the question,
The volume of the sphere = Volume of a cone

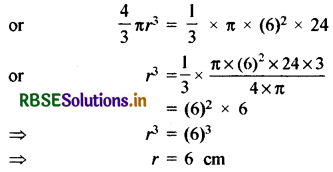
Therefore, the radius of the sphere is 6 cm.

Question 8.
2 cubes, each of volume 27 cm3, are joined end to end to make a solid. Find the surface area of the cuboid so obtained.
Solution:
Let each side of cube = x cm
Volume of cube = 27 cm³
⇒ x³ = 27
⇒ x = 3 cm
∴ Side of cube = 3 cm
∵ Adding the two cubes, a cuboid will be formed. Its
Length = 2x cm = 2 × 3 = 6 cm
Breadth = x = 3 cm
and Height = x = 3 cm
Now therefore area of cuboid = 2 [Length × Breadth + Breadth × Height + Height × Length]
= 2|6 × 3 + 3 × 3 + 3 × 6]
= 2 [18 + 9 + 18]
= 2 [45]
= 90 cm²
i.e. area of cuboid is 90 cm²

Question 9.
A hemispherical tank full of water is emptied by a pipe at the rate of 5 litres per second. If the diameter of the tank is 3.5 m, then in how much time will the tank be half-emptied?
Solution:
The volume of hemisphere = \(\frac{2}{3} \pi r^{3}\)
Here radius of the tank = \(\frac{3.5}{2}\) m

i.e. that tank will be half-emptied in 18.7 minutes.

Question 10.
A copper rod of radius 1 cm and length 2 cm is drawn into a wire of length 18 m of uniform thickness. Find the thickness of the wire.
Solution:
The volume of the rod = π × (1)² × 2 cm³ = 2π cm³
The length of the new wire of the same volume = 18 m = 1800 cm
If r is the radius (in cm) of cross-section of the wire, its volume = π × r² × 1800 cm²
therefore, π × r² × 1800 = 2π
i.e., r² = \(\frac{1}{900}\)
i.e., r = \(\frac{1}{30}\) cm
So, the diameter of the cross-section, i.e., the thickness of the wire is \(\frac{1}{15}\) cm, i.e. 0.67 mm (approx.)

Long Answer Type Questions

Question 1.
A sphere of lead of diameter 3 cm is melted and transformed into three shots. Out of these the diameters of the two shots are 1 cm and 1.5 cm. Find the diameter of the third shot.
Solution:
Let the radius of the third shot be r cm
∵ Diameter of sphere = 3 cm
∴ Radius = \(\frac{3}{2}\) = 1.5 cm
Diameter of first shot = 1 cm
Radius = \(\frac{1}{2}\) cm = 0.5 cm
Diameter of second shot = 1.5 cm
Radius = \(\frac{1.5}{2}\) cm = 0.75 cm
∵ By melting a sphere of radius 1.5 cm, three shots are made.
∴ Total volume of the three shots = Volume of sphere

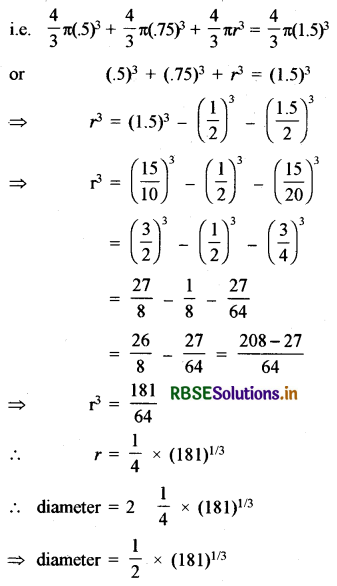
Question 2.
An open metal bucket is in the shape of a frustum of a cone, mounted on a hollow cylindrical base made of the same metallic sheet (see Fig.). The diameters of the two circular ends of the bucket are 45 cm and 25 cm, the total vertical height of the bucket is 40 cm and that of the cylindrical base is 6 cm. Find the area of the metallic sheet used to make the bucket, where we do not take into account the handle of the bucket. Also, find the volume of water the bucket can hold. (Take π = \(\frac {22}{7}\))

Solution:
The total height of the bucket = 40 cm, which includes the height of the base.
So, the height of the frustum of the cone = (40 - 6) cm = 34 cm
Therefore, the slant height of the frustum l = \(\sqrt{h^{2}+\left(r_{1}-r_{2}\right)^{2}}\)
where r₁ = 22.5 cm, r₂ = 12.5 cm and h = 34 cm
So, l = \(\sqrt{34^{2}+(22.5-12.5)^{2}}\) cm.
= \(\sqrt{34^{2}+10^{2}}\)
= 35.44 cm
The area of metallic sheet used = Curved surface area of frustum of cone + area of circular base + curved surface area of cylinder 
= π × 35.44 (22.5 + 12.5) + π × (12.5)2 + 2π × 12.5 × 6] m²
= \(\frac {22}{7}\) [1240.4 + 156.25 + 150] cm²
= 4860.9 cm²
Now, the volume of water that the bucket can hold (also, known as the capacity of the bucket)

Question 3.
The radii of the ends of a frustum of a cone 45 cm high are 28 cm and 7 cm (see Fig.). Find its volume, the curved surface area, and the total surface area (Taken π = \(\frac {22}{7}\))
Solution:
The frustum can be viewed as a difference between the two right circular cones OAB and OCD (see Fig.).
Let the height (in cm) of the cone OAB be h₁ and its slant height l₁
i.e., OP = h₁, and OA = OB = l₁.
Let h₂ be the height of cone OCD and l₂ its slant height.

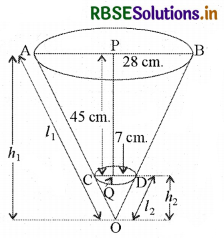
We have r₁ = 28 cm, r₂ = 7 cm
and the height of frustum (h) = 45 cm.
Also, h₁ = 45 + h₂ ......(i)
We first need to determine the respective heights h₁ and h₂ of the cone. OAB and OCD.
Since the triangles OPB and OQD are similar (Why?), we have
\(\frac{h_{1}}{h_{2}}=\frac{28}{7}=\frac{4}{1}\)
or h1 = 4h2 ......(ii)
Solving equations (i) and (ii)
4h2 = 45 + h₂
⇒ 3h₂ = 45
⇒ h₂ = 15 cm
From equation (i)
h₁ = 45 + 15 = 60 cm
Now, the volumes of the frustum = Volume of the cone OAB - Volume of the cone OCD

Thus, the curved surface area of the frustum = πr₁l₁ - πr₂l₂
= \(\frac {22}{7} (28)(66.20) - \frac {22}{7} (7)(16.55)\)
= 5461.5 cm²
Now, the total surface area of the frustum = the curved surface area + \(\pi r_{1}^{2}+\pi r_{2}^{2}\)
= 5461.5 cm² + \(\frac {22}{7}\) (28)² cm² + \(\frac {22}{7}\) (7)² cm²
= 5461.5 cm² + 2464 cm² + 154 cm²
= 8079.5 cm²

Question 4.
A sphere of diameter 7 cm is dropped into a cylindrical vessel partially filled with water. The diameter of the base of the vessel is 14 cm of the sphere is completely submerged in water, then by how much will the level of water rise?
Solution:
Diameter of sphere = 7 cm
∴ Radius of sphere = \(\frac{7}{2}\) = 3.5 cm
∴ Volume of sphere = \(\frac{4}{3} \pi r^{3} = \frac{4}{3} \pi \times(3.5)^{3}\) ........(i)
Again diameter of die base of the cylindrical vessel = 14 cm
∴ Radius (r) = \(\frac{14}{2}\) = 7 cm
Volume of cylinder = πr²h = π × (7)² × h ......(ii)
Equating equations (i) and (ii)

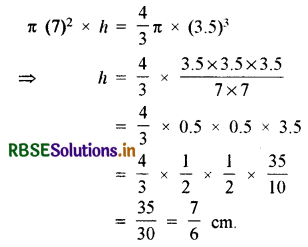
Hence the level of water will rise by \(\frac{7}{6}\) cm on dropping the sphere.

Question 5.
A frustum of a cone which is 45 cm high, has its radii of ends as 28 cm and 7 cm. Find its volume.
Solution:
Let the height of cone OAB be h₁ i.e. OP = h₁
Let the height of cone OCD be h₂ i.e. OQ = h₂

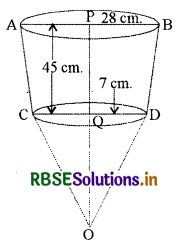
Here, r₁ = 28 cm, r₂ = 7 cm
and height of frustum h = 45 cm
OP = h₁, OQ = h₂
∴ h₁ = 45 + h₂  .... (i)
∆OPB and ∆OQD are similar
∴ \(\frac{h_{1}}{h_{2}}=\frac{28}{7}\) = 4
⇒ h₁ = 4h₂ ......(ii)
From equations (i) and (ii)
4h₂ = 45 + h₂
⇒ 3h₂ = 45
⇒ h₂ = 15 cm
From equation (ii), h₁ = 4 × 15 = 60 cm
Volume of frustum = Volume of cone OAB - Volume of cone OCD
= \(\frac{1}{3} \pi r_{1}^{2} h_{1}-\frac{1}{3} \pi r_{2}^{2} h_{2}\)
= \(\frac{1}{3} \times \frac{22}{7}\) × 28 × 28 × 60 - \(\frac{1}{3} \times \frac{22}{7}\) × 7 × 7 × 15
= 22 × 4 × 28 × 20 - 22 × 7 × 5
= 49280 - 770
= 48510 cm³

Question 6.
A sphere of metal of radius 4.2 cm is melted and recast in the shape of a cylinder of radius 7 cm. Find the height of the cylinder.
Solution:
According to the question,
Radius of sphere (r) = 4.2 cm
Radius of cylinder (R) = 6 cm
Let the height of the cyliner be = H cm
On casting the volume remains the same,
i.e. here volume of sphere = Volume of cylinder

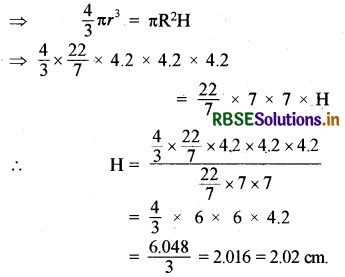
∴ Height of cylinder (H) = 2.02 cm (approx.)