RBSE Class 10 Maths Important Questions Chapter 12 वृतों से संबंधित क्षेत्रफल

Rajasthan Board RBSE Class 10 Maths Important Questions Chapter 12 वृतों से संबंधित क्षेत्रफल Important Questions and Answers.

RBSE Class 10 Maths Chapter 12 Important Questions वृतों से संबंधित क्षेत्रफल

वस्तुनिष्ठ प्रश्न

प्रश्न 1.
π संख्या है
(A) परिमेय
(B) अपरिमेय
(C) काल्पनिक
(D) इनमें से कोई नहीं
उत्तरः
(B) अपरिमेय

प्रश्न 2.
एक वृत्त की त्रिज्या 7 सेमी. है, तो उसका | क्षेत्रफल है
(A) 154 वर्ग सेमी.
(B) 308 वर्ग सेमी.
(C) 44 वर्ग सेमी.
(D) 606 वर्ग सेमी.
उत्तरः
(A) 154 वर्ग सेमी.

प्रश्न 3.
चित्र में वृत्त का केन्द्र 0 है। वृत्त की त्रिज्या 18 सेमी. है तथा ∠AOB = 30° है, तो लघु चाप AB की लम्बाई है-

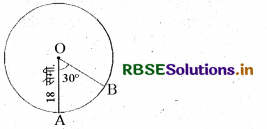
(A) 2π
(B) 3π
(C) 6π
(D) 4π
उत्तरः
(B) 3π

प्रश्न 4.
एक वृत्त की परिधि 176 सेमी. है, तो उसकी त्रिज्या है
(A) 21 सेमी.
(B) 14 सेमी.
(C) 28 सेमी.
(D) 7 सेमी.
उत्तरः
(C) 28 सेमी.

प्रश्न 5.
एक वृत्तखण्ड की त्रिज्या 5 सेमी. है। इस वृत्त के 9 सेमी. लम्बाई के चाप द्वारा बने त्रिज्यखण्ड का क्षेत्रफल है
(A) 45 वर्ग सेमी.
(B) 22.5 वर्ग सेमी.
(C) 67.5 वर्ग सेमी.
(D) 2.25 वर्ग सेमी.
उत्तरः
(B) 22.5 वर्ग सेमी.

प्रश्न 6.
एक वृत्ताकार मार्ग का बाह्य और अन्तः व्यास क्रमशः 10 मीटर व 6 मीटर है। वृत्ताकार मार्ग का क्षेत्रफल है।
(A) 250 वर्ग मीटर
(B) 160 वर्ग मीटर
(C) 90 वर्ग मीटर
(D) 70 वर्ग मीटर
उत्तरः
(B) 160 वर्ग मीटर

अतिलघुत्तरात्मक प्रश्न

प्रश्न 1.
एक वृत्त की परिधि 147 सेमी. है। इसकी त्रिज्या लिखिए।
हल:
परिधि = 2πr
∴ 2πr = 14π
या r = \(\frac{14 \pi}{2 \pi}\)
∴ r = 7 सेमी.

प्रश्न 2.
वृत्त की परिधि किसे कहते हैं?
उत्तर:
वृत्त के अनुदिश एक पूरे चक्कर में तय की गयी दूरी को वृत्त की परिधि कहते हैं।

प्रश्न 3.
π के मान की गणना किस गणितज्ञ ने की थी?
उत्तर:
भारतीय गणितज्ञ आर्यभट्ट ने π के मान की गणना की थी।

प्रश्न 4.
दो संकेन्द्रीय वृत्तों द्वारा परिबद्ध क्षेत्र के क्षेत्रफल का सूत्र लिखिए।
उत्तर:
π(r₁² - r₂²)

प्रश्न 5:
दो वृत्तों की त्रिज्याएँ क्रमशः 6 सेमी. और 4 सेमी. हैं। उनके क्षेत्रफलों का अनुपात लिखिए।
हल:
पहले वृत्त का क्षेत्रफल = πr²
= π(6)² = 36π
दूसरे वृत्त का क्षेत्रफल= πr² = π × (4)² = 16π
अनुपात लेने पर \(\frac{36 \pi}{16 \pi}\) = \(\frac{9}{4}\) = 9 : 4

प्रश्न 6.
एक घड़ी की मिनट की सई द्वारा 20 मिनट में केन्द्र पर अन्तरित कोण का मान ज्ञात कीजिए।
हल:
अन्तरित कोण = \(\frac{360}{60}\) × 20 = 120°

प्रश्न 7.
उस त्रिज्यखण्ड का क्षेत्रफल ज्ञात कीजिए जिसके चाप की लम्बाई 10 सेमी. और त्रिज्या 6 सेमी. हो।
हल:
यहाँ त्रिज्या = 6 सेमी., चाप (L) = 10 सेमी.
त्रिज्यखण्ड का क्षेत्रफल = \(\frac{1}{2}\) × L × r
= \(\frac{1}{2}\) × 10 × 6 = 30 सेमी.²

प्रश्न 8.
21 सेमी. त्रिज्या के वृत्त से काटे गये त्रिज्यखण्ड का कोण 60° है। त्रिज्यखण्ड की चाप की लम्बाई और क्षेत्रफल ज्ञात कीजिए।
हल:
त्रिज्या r = 21 सेमी.
त्रिज्यखण्ड का कोण C = 60°
केन्द्र पर कोण अन्तरित करने वाले चाप की लम्बाई
= \(\frac{\pi r \theta}{180^{\circ}}\) = \(\frac{22 \times 21 \times 60^{\circ}}{7 \times 180^{\circ}}\) = 22 सेमी.
त्रिज्यखण्ड का क्षेत्रफल = \(\frac{\pi \mathrm{R}^{2} \theta}{360^{\circ}}\)
= \(\frac{22 \times 21 \times 21 \times 60^{\circ}}{7 \times 360^{\circ}}\) = 231 वर्ग सेमी.

प्रश्न 9.
यदि एक अर्द्धवृत्ताकार चाँदे का व्यास 14 cm. है, तो इसकी परिधि ज्ञात कीजिये।
हल:
व्यास = 14 cm., ∴ त्रिज्या (r) = \(\frac{14}{2}\) = 7 cm
∴ परिधि = 2πr = 2 × \(\frac{22}{7}\) × 7
= 44 cm.

प्रश्न 10.
दो वृत्तों की परिधियों का अनुपात 2 : 3 है। उनकी त्रिज्याओं का अनुपात ज्ञात कीजिये।
हल:
माना दो वृत्तों की त्रिज्याएँ क्रमशः r₁ वा r₂ हैं।
∴ \(\frac{2 \pi r_{1}}{2 \pi r_{2}}=\frac{2}{3}\) ⇒ \(\frac{r_{1}}{r_{2}}=\frac{2}{3}\)
⇒ r₁ : r₂ = 2 : 3

प्रश्न 11.
यदि एक वृत्त का परिमाप और क्षेत्रफल संख्यात्मक रूप से बराबर है तो वृत्त की त्रिज्या ज्ञात कीजिये।
हल:
माना वृत्त की त्रिज्या = r है।
∴ प्रश्नानुसारवृत्त का परिमाप = वृत्त का क्षेत्रफल
2πr = πr²
∴ r = 2 मात्रक

प्रश्न 12.
त्रिज्या R वाले वृत्त के उस त्रिज्यखण्ड का क्षेत्रफल लिखिये जिसका कोण θ° है।
अथवा
त्रिज्या r वाले वृत्त के एक त्रिज्यखण्ड, जिसका कोण अंशों में 0 है, का क्षेत्रफल लिखिए।
हल:
त्रिज्यखण्ड का क्षेत्रफल = \(\frac{\theta}{360^{\circ}}\) × πr² वर्ग इकाई या \(\frac{\theta}{360^{\circ}}\) × πr² वर्ग इकाई

प्रश्न 13.
r त्रिज्या वाले वृत्त के एक त्रिज्यखण्ड, जिसका कोण अंशों में θ है, के संगत चाप की लम्बाई लिखिये।
अथवा
त्रिज्या r वाले वृत्त के एक त्रिज्यखण्ड जिसका कोण अंशों में θ है, तो संगत चाप की लम्बाई का सूत्र लिखिए।
हल:
कोण θ वाले त्रिज्यखण्ड के संगत चाप की लम्बाई = \(\frac{\theta}{360^{\circ}}\) × 2πr

प्रश्न 14.
यदि एक वृत्त की त्रिज्या 14 सेमी. हो, तो वृत्त का क्षेत्रफल ज्ञात कीजिए।
हल:
यहाँ वृत्त की त्रिज्या (r) = 14 सेमी.
∵ वृत्त का क्षेत्रफल = πr²
= \(\frac{22}{7}\) × (14)² = \(\frac{22}{7}\) × 14 × 14
= 22 × 2 × 14 = 616 वर्ग सेमी.

प्रश्न 15.
44 सेमी. परिधि वाले वृत्त का क्षेत्रफल ज्ञात कीजिए।
हल:
प्रश्नानुसार परिधि = 44 सेमी.
या 2πr = 44
∴ r = \(\frac{44 \times 7}{2 \times 22}\) = 7 सेमी.
∴ वृत्त का क्षेत्रफल = πr²
= \(\frac{22}{7}\) × 7 × 7
= 154 सेमी.

प्रश्न 16.
14 सेमी. व्यास वाले वृत्त की परिधि ज्ञात कीजिए।
हल:
∴ व्यास = 14 सेमी.
∴ त्रिज्या (7) = \(\frac{14}{2}\) = 7 सेमी.
वृत्त की परिधि = 2πr
= 2 × \(\frac{22}{7}\) × 7 = 44 सेमी.

प्रश्न 17.
उस वृत्त की त्रिज्या ज्ञात कीजिए जिसका क्षेत्रफल 616 वर्ग सेमी. है।
हल:
दिया है वृत्त का क्षेत्रफल = 616 वर्ग सेमी.
वृत्त का क्षेत्रफल = πr²
616 = \(\frac{22}{7}\) × r²
∴ r² = \(\frac{616 \times 7}{22}\) × 7
r² = 196
∴ r = √ 196 = 14 सेमी.
अतः वृत्त की त्रिज्या = 14 सेमी.

प्रश्न 18.
यदि एक वृत्त के दीर्घत्रिज्यखण्ड का कोण 250° है तो लघुत्रिज्य खण्ड का कोण ज्ञात कीजिए।
हल:
दीर्घत्रिज्यखण्ड का कोण + लघुत्रिज्यखण्ड का कोण = 360° होता है।
इसलिए लघुत्रिज्यखण्ड का कोण = 360° - दीर्घत्रिज्यखण्ड का कोण
= 360° - 250°
= 110°

लघूत्तरात्मक प्रश्न

प्रश्न 1.
एक वृत्तांकार खेत पर 24 रु. प्रति मीटर की दर से बाड़ लगाने का व्यय 5280 रु. है। इस खेत की 0.50 रु. प्रति वर्ग मीटर की दर से जुताई कराई जानी है। खेत की जुताई कराने का व्यय ज्ञात कीजिए। (π = \(\frac{22}{7}\) लीजिए।)
हल:
बाड़ की लम्बाई (मीटर में)

= 220 मीटर
अतः खेत की परिधि = 220 मीटर
इसलिए यदि खेत की त्रिज्या r मीटर है, तो
2πr = 220
या 2 × \(\frac{22}{7}\) × r = 220
या r = \(\frac{220 \times 7}{2 \times 22}\) = 35 मीटर
अर्थात् खेत की त्रिज्या 35 मीटर है।
अतः खेत का क्षेत्रफल = πr²
= \(\frac{22}{7}\) × 35 × 35 मीटर²
= 22 × 5 × 35 मीटर²
अब 1 मीटर² खेत की जुताई का व्यय = 0.50 रु.
अतः खेत की जुताई कराने का कुल व्यय = 22 × 5 × 35 × 0.50 = 1925 रु.

प्रश्न 2.
चित्र में अर्द्धवृत्त की त्रिज्या 7 सेमी. है। अर्द्धवृत्त में बने वृत्त का क्षेत्रफल ज्ञात कीजिए।

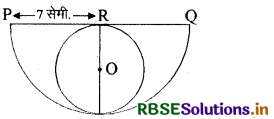
हल:
दी गई आकृति में
अर्द्धवृत्त की त्रिज्या, अर्द्धवृत्त के अन्दर बने वृत्त के व्यास के बराबर है।
अर्थात् अन्दर बने वृत्त की त्रिज्या (r) = \(\frac{P Q}{2}\)
r = \(\frac{7}{2}\) सेमी. = 3.5 सेमी.
अन्दर बने वृत्त का क्षेत्रफल = πr²
= \(\frac{22}{7}\) × 3.5 × 3.5 सेमी.²
= 38.5 सेमी.²

प्रश्न 3.
एक वृत्त के चतुर्थांश (Quadrant) का क्षेत्रफल ज्ञात कीजिये, जिसकी परिधि 22 cm. है।
हल:
वृत्त की परिधि = 22 cm.
2πr = 22
∴ r = \(\frac{22}{2 \pi}\) = \(\frac{22}{2 \times \frac{22}{7}}\)
r = \(\frac{7}{2}\) cm.
केन्द्रीय कोण (चतुर्थांश) (9) = 90°

चतुर्थांश का क्षेत्रफल = 9.625 cm²

प्रश्न 4.
त्रिज्या 21 सेमी. वाले वृत्त का एक चाप केन्द्र पर 60° का कोण अन्तरित करता है, तो संगत दीर्घ त्रिज्यखण्ड का क्षेत्रफल ज्ञात कीजिये।
हल:
दिया गया है
वृत्त की त्रिज्या r = 21 सेमी.

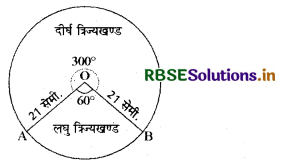
चाप द्वारा बनाये गये दीर्घ त्रिज्यखण्ड का क्षेत्रफल

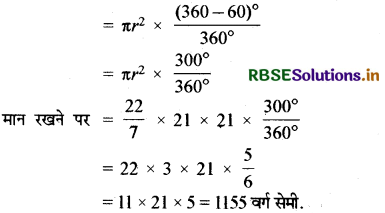
प्रश्न 5.
दी गयी आकृति में छायांकित क्षेत्र का | क्षेत्रफल ज्ञात कीजिए, जहाँ ABCD भुजा 14 cm का एक वर्ग है।

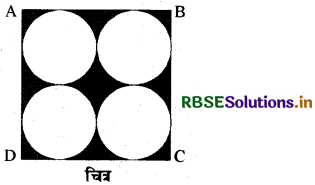
हल:
वर्ग ABCD का क्षेत्रफल = 14 × 14 cm² = 196 cm²
प्रत्येक वृत्त का व्यास = \(\frac{14}{2}\) cm = 7 cm .
∴ प्रत्येक वृत्त की त्रिज्या = \(\frac{7}{2}\) cm

अतः छायांकित भाग का क्षेत्रफल = (196 - 154)cm² = 42 cm²

प्रश्न 6.
दी गयी आकृति में छायांकित डिजाइन का क्षेत्रफल ज्ञात कीजिए, जहाँ ABCD भुजा 10 cm का एक वर्ग है तथा इस वर्ग की प्रत्येक भुजा को व्यास मान कर अर्द्धवृत्त खींचे गए हैं। (π = 3.14 का प्रयोग कीजिए।)

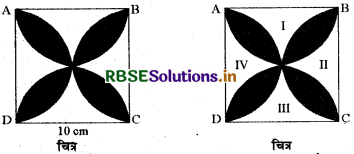
हल:
यहाँ पर हमने अछायांकित क्षेत्रों I, II, III और IV से अंकित किया है। जैसा कि चित्र में दिखाया गया है।
I का क्षेत्रफल + III का क्षेत्रफल
= ABCD,का क्षेत्रफल - दोनों अर्द्धवृत्तों का क्षेत्रफल, जिनमें से प्रत्येक की त्रिज्या 5 cm है।
= (10 × 10 - 2 × \(\frac{1}{2}\) × π × 5²) cm²
= (100 - 3.14 × 25) cm²
= (100 - 78.5) cm² = 21.5 cm²
इसी प्रकार, II का क्षेत्रफल + IV का क्षेत्रफल = 21.5 cm²
अतः छायांकित डिजाइन का क्षेत्रफल = ABCD का क्षेत्रफल - (I + II + III + IV) का क्षेत्रफल -
= (100 - 2 × 21.5) cm²
= (100 - 43) cm² = 57 cm²

प्रश्न 7.
7 सेमी. त्रिज्या वाले वृत्त में कोण 1200 के संगत दीर्घ त्रिज्यखण्ड का क्षेत्रफल ज्ञात कीजिए।
हल:
प्रश्नानुसार वृत्त के त्रिज्यखण्ड की त्रिज्या (R)= 7 cm,
केन्द्रीय कोण = 120°

प्रश्न 8.
एक वृत्त का चाप केन्द्र पर 45° का कोण अन्तरित करता है। यदि इसके लघु त्रिज्यखण्ड का क्षेत्रफल 77 cm² है, तो वृत्त की त्रिज्या ज्ञात कीजिए।
हल:
दिया हुआ त्रिज्यखण्ड OAPB है।
त्रिज्यखण्ड का क्षेत्रफल = \(\frac{\theta}{360}\) × πr²

मान रखने पर

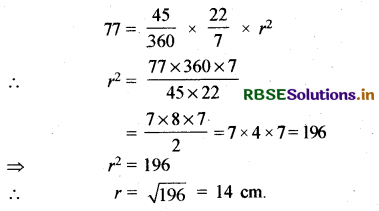
अतः वृत्त की त्रिज्या = 14 cm. 

निबन्धात्मक प्रश्न

प्रश्न 1.
चित्र में, PQRS एक आयत है। भुजा PQ = 10 सेमी. तथा QR = 7 सेमी. है। आयत के प्रत्येक शीर्ष पर 3.5 सेमी. त्रिज्या के वृत्त खींचे गए हैं। छायांकित भाग का क्षेत्रफल ज्ञात कीजिए।

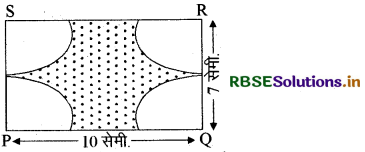
हल:
आयत PQRS का क्षेत्रफल = लम्बाई × चौड़ाई
= PQ × QR
= 10 × 7 = 70 सेमी.²
आयत का प्रत्येक कोण 90° होता है अतः चारों त्रिज्यखण्डों का क्षेत्रफल समान होगा।
∴ चारों त्रिज्यखण्डों का क्षेत्रफल = \(\frac{4 \pi r^{2} \theta}{360^{\circ}}\)
= 4 × \(\frac{22}{7}\) × \(\frac{3.5 \times 3.5 \times 90^{\circ}}{360^{\circ}}\) सेमी.²
= \(\frac{4 \times 22 \times 12.25}{7 \times 4}\) सेमी.²
= \(\frac{1078}{28}\) सेमी.² = 38.5 सेमी.²
छायांकित भाग का क्षेत्रफल = (आयत का क्षेत्रफल - चारों त्रिज्यखण्डों का क्षेत्रफल)
= (70 - 38.5) सेमी.²
= (31.5) सेमी.²
अतः छायांकित भाग का क्षेत्रफल=31.5 सेमी.² है।

प्रश्न 2.
चित्र में छायांकित भाग का क्षेत्रफल ज्ञात कीजिए।

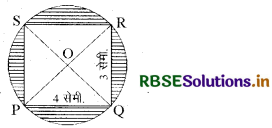
हल:
दी गई आकृति में
PR = \(\sqrt{(P Q)^{2}+(Q R)^{2}}\)
PR = \(\sqrt{16+9}\) सेमी.
PR = 25 सेमी.
PR = 5 सेमी.
वृत्त की त्रिज्या (OP) = \(\frac{\mathrm{PR}}{2}\)
वृत्त की त्रिज्या (OP) = \(\frac{5}{2}\) सेमी. = 2.5 सेमी.
वृत्त का क्षेत्रफल = πr²
= \(\frac{22}{7}\) × 2.5 × 2.5 सेमी.²
= 19.642 सेमी.²
आयत PQRS का क्षेत्रफल = PO × OR
= 4 × 3 सेमी.²
= 12 सेमी.²
छायांकित भाग का क्षेत्रफल = (वृत्त का क्षेत्रफल - आयत का क्षेत्रफल)
= (19.642 - 12) सेमी.²
= 7.642 सेमी.²

प्रश्न 3.
चित्र में, अर्द्धवृत्त का केन्द्र 0 है तथा अर्द्धवृत्त की त्रिज्या 5 सेमी. है। यदि PR = 8 सेमी. हो तो छायांकित भाग का क्षेत्रफल ज्ञात कीजिए।

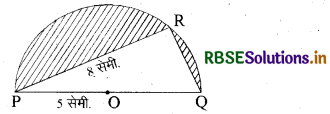
हल:
अर्द्धवृत्त का क्षेत्रफल = \(\frac{\pi r^{2}}{2}\)
= \(\frac{22}{7} \times \frac{5 \times 5}{2}\) सेमी.²
= \(\frac{275}{7}\) सेमी.²
= 39.28 सेमी.²
∆PQR में, PQ = 2 PO
PQ = 2(5) सेमी.
PQ = 10 सेमी.
QR = \(\sqrt{(P Q)^{2}-(P R)^{2}}\)
(पाइथागोरस प्रमेय से)
QR = \(\sqrt{(10)^{2}-(8)^{2}}\) सेमी
QR = \(\sqrt{100-64}\) सेमी.
QR = √36 = 6 सेमी.
∆PQR का क्षेत्रफल = \(\frac{1}{2}\) × QR × PR
= \(\frac{1}{2}\) × 6 × 8 सेमी.²
= 3 × 8 सेमी.² = 24 सेमी.²
छायांकित भाग का क्षेत्रफल = (अर्द्धवृत्त का क्षेत्रफल - त्रिभुज PQR का क्षेत्रफल)
= (39.28 - 24) सेमी.²
= 15.28 सेमी.²
∴ छायांकित भाग का क्षेत्रफल = 15.28 सेमी.²

प्रश्न 4.
चित्र में PQRS एक वर्ग है जिसकी एक भुजा 7 सेमी. है। वर्ग के प्रत्येक शीर्ष पर 3.5 सेमी. त्रिज्या के वृत्त खींचे गये हैं। छायांकित भाग का क्षेत्रफल ज्ञात कीजिए।

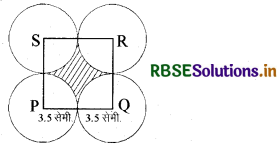
हल:
संलग्न आकृति में वर्ग की भुजा = 7 सेमी.
वर्ग का क्षेत्रफल = 7 × 7 सेमी.²
= 49 सेमी.²
दी गई आकृति में चारों वृत्त समान क्षेत्रफल के हैं।
इन वृत्तों में त्रिज्यखण्ड कटता है।
चारों वृत्तों में त्रिज्यखण्ड का कोण (θ) = 90°
त्रिज्या (r) = 3.5 सेमी
चारों वृत्तों के त्रिज्यखण्डों का क्षेत्रफल समान होगा।
अतः चारों त्रिज्यखण्डों का क्षेत्रफल = 4 × \(\frac{\pi r^{2} \theta}{360}\)
= 4 × \(\frac{22}{7}\) × \(\frac{3.5 \times 3.5 \times 90^{\circ}}{360^{\circ}}\) सेमी.²
= \(\frac{22}{7}\) × 3.5 × 3.5 सेमी.²
= 38.5 सेमी.²
छायांकित भाग का क्षेत्रफल= (वर्ग का क्षेत्रफल - चारों त्रिज्यखण्डों का क्षेत्रफल)
= (49 - 38.5) सेमी.²
= 10.5 सेमी.²

प्रश्न 5.
56 मीटर भुजा वाले एक वर्गाकार बगीचे ABCD के AB व CD भुजा पर दो वृत्ताकार फूलों की क्यारियाँ बनाई गयी हैं। यदि प्रत्येक वृत्ताकार क्यारी का केन्द्र बगीचे के विकर्णों का प्रतिच्छेद बिन्दु 0 है, तो बगीचे और क्यारियों के क्षेत्रफल का योग ज्ञात कीजिये।
हल:
वर्गाकार बगीचा ABCD का क्षेत्रफल
= भुजा × भुजा
= 56 × 56 वर्ग मी. .......... (i)

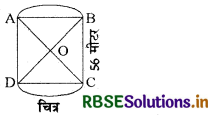
माना OA = OB = x मीटर है।
अतः x² + x² = (56)²
या 2x² = 56 × 56
या 2x² = \(\frac{56 \times 56}{2}\) = 28 × 56 .... (ii)
अब त्रिज्यखण्ड OAB का क्षेत्रफल
= \(\frac{90^{\circ}}{360^{\circ}}\) × πx²
= \(\frac{1}{4}\) × πx²

प्रश्न 6.
दो वृत्त बाह्यतः स्पर्श करते हैं। यदि इनके क्षेत्रफलों का योग 130rn cm है तथा इनके केन्द्रों के बीच | की दूरी 14 cm है, तो इन वृत्तों की त्रिज्याएँ ज्ञात कीजिये।
हल:
माना कि c₁ तथा c₂ दिये गये वृत्त के केन्द्र हैं और इनकी त्रिज्यायें क्रमशः r₁ और r₂ हैं। चूंकि दोनों | वृत्त बाह्यतः स्पर्श करते हैं।

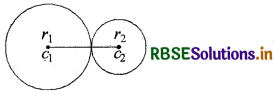
c₁c₂ = r₁ + r₂
⇒ 14 = r₁ + r₂
⇒ r₁ + r₂ = 14 .......... (i)
प्रश्नानुसार दोनों वृत्तों के क्षेत्रफलों का योग = 130π cm²

समीकरण (i) तथा (iv) को जोड़ने पर
2r₁ = 22
∴ r₁ = 11 cm
r₁ का मान, समीकरण (i) में रखने पर r₂ = 3 cm प्राप्त होता है।
अतः दोनों वृत्तों की त्रिज्यायें क्रमशः 11 cm तथा 3 cm हैं।

प्रश्न 7.
संलग्न आकृति में ∆ABC के शीर्ष बिन्दु A पर एक समकोण त्रिभुज है। जहाँ AB = 6 cm, BC = 10 cm तथा I, त्रिभुज ABC के अन्तःवृत्त का केन्द्र है तो छायांकित भाग का क्षेत्रफल ज्ञात कीजिये।

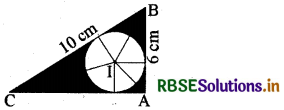
हल:
समकोण ∆ABC में
(BC)² = (AB)² + (AC)²
या (AC)² = (BC)² - (AB)²
या (AC)² = (10)² - (6)²
= 100 - 36 = 64
∴ AC = 8 cm
∴ ∆ABC का क्षेत्रफल = \(\frac{1}{2}\) × AB × AC
⇒ ∆ABC का क्षेत्रफल = \(\frac{1}{2}\) × 6 × 8 = 24 cm² माना अन्तःवृत्त की त्रिज्या r cm है।
∴ ∆ABC का क्षेत्रफल = ∆IBC का क्षेत्रफल + ∆ICA का क्षेत्रफल + ∆IAB का क्षेत्रफल

प्रश्न 8.
4 सेमी. त्रिज्या वाले एक वृत्त के उस त्रिज्यखण्ड का क्षेत्रफल ज्ञात कीजिए, जिसका कोण 60° है। साथ ही संगत दीर्घ त्रिज्यखण्ड का क्षेत्रफल भी ज्ञात कीजिए। (π = 3.14 का प्रयोग करें।)
हल:
प्रश्नानुसार वृत्त के त्रिज्यखण्ड की त्रिज्या (R) = 4 cm.
केन्द्रीय कोण (θ) = 60°

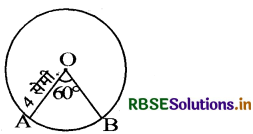
∵ त्रिज्यखण्ड का क्षेत्रफल = \(\frac{\pi \mathbf{R}^{2} \theta}{360^{\circ}}\)
= \(\frac{3.14 \times 4 \times 4 \times 60^{\circ}}{360^{\circ}}\)
= \(\frac{3.14 \times 2 \times 4}{3}\) = 8.37 सेमी.²
अतः त्रिज्यखण्ड का क्षेत्रफल = 8.37 सेमी.² उत्तर
संगत दीर्घ त्रिज्यखण्ड का क्षेत्रफल = \(\frac{\left(360^{\circ}-\theta\right)}{360^{\circ}}\) × πR²
= \(\frac{\left(360^{\circ}-60^{\circ}\right)}{360^{\circ}}\) × 3.14 × 4 × 4
= \(\frac{300^{\circ}}{360^{\circ}}\) × 300 × 3.14 × 16
= \(\frac{15}{18}\) × 3.14 × 16 = 41.87 सेमी.²

प्रश्न 9.
आकृति में छायांकित क्षेत्र का क्षेत्रफल ज्ञात कीजिए, यदि AB = 5 सेमी., AC = 12 सेमी. और O वृत्त का केन्द्र है।

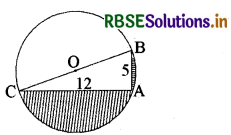
हल:
दी गई वृत्त के अन्दर की आकृति एक समकोण त्रिभुज की है जिसका आधार = 12 सेमी. तथा लम्ब = 5 सेमी. है।
अत: ∆ABC में CB² = CA²+ AB²
= (12)² + (5)²
= 144 + 25 = 169
∴ CB² = 169
∴ कर्ण CB = √169 = 13 सेमी.
समकोण ∆ का क्षेत्रफल = \(\frac{1}{2}\) × 12 × 5 = 6 × 5
= 30 सेमी.²
∴ अभीष्ट छायांकित क्षेत्रफल = अर्द्धवृत्त का क्षेत्रफल - ∆ABC का क्षेत्रफल